Thermodynamic modelling of mixtures of water, carbon dioxide and hydrogen at high pressure and temperature for hydrothermal CO2 reduction processes

In the context of the increasing CO₂ emissions and the corresponding environmental problems, CO₂ utilization processes that transform CO₂ into valuable compounds rather than just capturing and storing it can contribute to the transition to a carbon-free economy, giving value to unavoidable CO₂ emissions. Among the different technologies studied, hydrothermal conversion stands out by the high yields achieved in comparatively short reaction times and by the possibility to scale-up the process. The hydrothermal conversion uses CO₂ dissolved in aqueous solutions as feedstock, in which bicarbonate is the reacting species. Therefore, knowledge of the equilibrium concentrations of dissolved species is of interest for the development of the process. In this work, a thermodynamic model based on the activity coefficient model developed by Pitzer, Sun and Duan model is implemented and solved. The influence of different process conditions: temperature, pressure, composition of the initial solution, on the equilibrium composition of the dissolution is analyzed with the model. Experimental results obtained in hydrothermal reduction experiments are thus interpreted with the aid of the model. It is observed that the process is favored by moderate temperatures (<500 K), high initial concentrations of sodium bicarbonate (up to 2 mol/kg) and moderate initial concentrations of sodium hydroxide (below 1.5 mol/kg).

1 Introduction

Carbon dioxide emissions are a huge contributor to global warming and climate change. Human activities, such as burning fossil fuels, deforestation, and industrial activities, are significant sources of carbon dioxide emissions, which have several negative impacts on the environment [1–3]. Hence, reducing carbon dioxide emissions is a global concern as it is necessary for mitigating the impacts of climate change. Governments, businesses, and individuals all have a role to play in reducing carbon dioxide emissions through a variety of measures, including transitioning to clean energy sources, improving energy efficiency, and reducing reliance on fossil fuels.

Among the potential solutions, the capture, storage, utilization, and conversion of carbon dioxide into useful and highly value-added chemical products stand out, since carbon dioxide is a safe, cheap, and abundant carbon source; this represents a highly positive impact on the environment because it reintroduces carbon dioxide into the carbon cycle [4–8].

Some alternatives for carbon dioxide conversion into valuable chemical products are: electrochemical reduction, photochemical reduction, and hydrogenation of carbon dioxide [9]; here green hydrogen from water hydrolysis could play a key role. A common limitation of these approaches is the high thermodynamic stability of carbon dioxide, which means that for its chemical transformation, elevated external energy is needed.

One option to overcome carbon dioxide stability is through hydrothermal reduction, i.e., the conversion of CO₂ dissolved in high-temperature, high-pressure water, in a process that mimics the reactions that take place in the natural environment of submarine volcanoes [10]. This process offers the potential to turn a harmful greenhouse gas into valuable chemical products that can be used in a variety of industries, such as formic acid, methanol or methane. Furthermore, a useful characteristic of hydrothermal reduction is that it works with aqueous feeds, which means that the solutions obtained by absorption of CO₂ into alkaline water streams, which is the most technically developed carbon capture process available at the moment, can be directly used as feed for the hydrothermal reduction process. For example, if CO₂ is captured with aqueous solutions of sodium hydroxide, the resulting solution, rich in sodium bicarbonate, is a suitable inorganic carbon source for the hydrothermal reduction process [11–13].

The performance of the hydrothermal reduction process is based on the peculiar properties of water at high-temperature, high-pressure conditions, close to the critical point of water (T_C = 647.3 K and P_C = 221.2 bar). For example, properties such as dielectric constant reduce from 78 at ambient conditions (298 K and 1 bar) to 6 at the critical point, a value typical of a nonpolar solvent [14]. Besides, the solubility of some gases such as carbon dioxide increase close to the critical point. The ionic product of water (pKw) rises with temperature from 14 at ambient conditions until a maximum of around 11.2 close to 473 K, and then under supercritical conditions decreases until a value below 22. For that reason, pure water near 473 K behaves as if it were simultaneously more acid and more basic than pure water under normal conditions [15].

The hydrothermal reduction process can be carried out either using gaseous hydrogen as reductant, or using water itself as hydrogen source; in the second case, an additional reductant to promote the decomposition of water into hydrogen and oxygen, such as a metal [16, 17] or an organic reductant [18, 19], must be provided. Typically, formic acid is the main product yielded by this process [12, 18], but several products can be obtained from carbon dioxide under hydrothermal reduction using metal reductants and catalysts. For instance, methane was obtained from sodium bicarbonate using Raney Ni nanoparticles as a catalyst [20], and acetate was produced using a catalyst based on cobalt [21].

For the elucidation of the reaction mechanisms and the optimization of the process, a crucial aspect is to determine the ionic species present in the solution as a function of the reaction conditions. Indeed, upon dissolution in water, CO₂ undergoes transformations to carbonic acid, bicarbonate and carbonate according to its acid-base equilibrium. Of this species, it is considered that bicarbonate is the most reactive one, while carbonic acid and carbonate show a lower reactivity [11, 12]. Hence, it is of the highest significance to determine if the dissolution equilibrium of CO₂ is displaced towards bicarbonate.

This acid-base equilibrium is influenced by several factors, such as, of course, pressure and temperature, but also by the presence of other substances dissolved in the medium, and particularly ionic species such as those produced by the dissolution of salts. This equilibrium is also significant for geological studies, and as such has been studied by different authors [22], as discussed in detail in the following Section 2.

Based on these considerations, the objective of this work is to model the thermodynamic behavior of a mixture of water, carbon dioxide, and hydrogen under high temperature and pressure conditions, relevant for the development of the hydrothermal CO₂ reduction technology, in order to determine the molality of the species in reaction conditions for these process. In particular, conditions that favor the displacement of the equilibrium towards bicarbonate, which is the reactive species, are sought. The study aims to contribute to the field of carbon dioxide reduction transforming waste into economically valuable chemical products helping achieve the Sustainable Development Goal (SDG) due to the potential of hydrothermal reduction as a viable method for capturing and converting carbon dioxide into useful chemical products, with a focus on the production of formic acid.

2 Thermodynamic equilibrium of the electrolytic solution

The thermodynamic model considered in this work describes the speciation equilibrium of H⁺, Na⁺, OH⁻, Cl⁻, HCO₃⁻, CO₃^2-, CO₂, and H₂ in an aqueous solution of carbon dioxide, hydrogen, sodium chloride and sodium bicarbonate at hydrothermal conditions.

The equilibrium between the different species is a function of pressure, temperature, and composition. Two sorts of physicochemical equilibrium are essential to have a whole understanding of the systems; these are chemical equilibrium and phase equilibrium. Both are complex functions of pressure, temperature, and molality.

The model developed by [22] for the phase equilibrium of water, carbon dioxide, and sodium chloride was used to describe the behavior of the mixtures applied in the hydrothermal reduction of CO₂. This model considers a temperature range from 273.15 to 523.15 K and a pressure range from 0 to 1,000 bar; it is based on the previous model of [23] which considers a hydrate phase and an aqueous phase [24]. The parameters required to apply this model were taken from the literature, as detailed below. This model has been coupled with adequate Henry constants of the gas species, CO₂ and hydrogen, also collected from the literature [25].

The amount of carbon dioxide and hydrogen present in the aqueous dissolution of the system depends on its solubility in the vapor-liquid equilibrium according to Eqs 1, 2. This solubility was calculated as a function of temperature, pressure and gas composition with the corresponding Henry constants [25]. The equilibrium acid-base reactions involved in the aqueous dissolution are:

$C{O}_{2\left(g\right)}\leftrightarrow C{O}_{2\left(aq\right)}(1)$

$H_{2\left(g\right)}\leftrightarrow H_{2\left(aq\right)}(2)$

$H_{2}O+C{O}_{2\left(aq\right)}\leftrightarrow HC{O}_3^{-}+H^{+}(3)$

$HC{O}_3^{-}\leftrightarrow C{O}_3^{2-}+H^{+}(4)$

$H_{2}O\leftrightarrow H^{+}+{OH}^{-}(5)$

Eqs 3, 4 represent the dissociation of the carbonic acid, and Eq 5 the autoionization of water. The respective equilibrium constants (K) are defined as follows:

$K_1=\frac{\left(m_{H^{+}}{\gamma }_{H^{+}}\right)\left(m_{{HCO}_3^{-}}{\gamma }_{{HCO}_3^{-}}\right)}{\left(m_{C{O}_2}{\gamma }_{C{O}_2}\right)a_{H_{2}O}}(6)$

$K_2=\frac{\left(m_{H^{+}}{\gamma }_{H^{+}}\right)\left(m_{{CO}_3^{2-}}{\gamma }_{{CO}_3^{2-}}\right)}{\left(m_{{HCO}_3^{-}}{\gamma }_{{HCO}_3^{-}}\right)}(7)$

$K_w=\frac{\left(m_{H^{+}}{\gamma }_{H^{+}}\right)\left(m_{O{H}^{-}}{\gamma }_{O{H}^{-}}\right)}{a_{H_{2}O}}(8)$

Here m represents molality, γ molal activity coefficient, and $a_{H_{2}O}$ is molal activity of water.

The ionic product of water (8) was calculated following the model developed by [15], shown in Eq 9; this model was selected because of its wide T-P range of applicability. The parameters from A to G can be found in [22].

$\mathit{log}{K}_w=A+B{T}^{-1}+C{T}^{-2}+D{T}^{-3}+\left(E+F{T}^{-1}+G{T}^{-2}\right)\mathit{log}{\rho }_w(9)$

The other equilibrium constants (6) and (7) were obtained with the following Eq (10):

$\ln K=a_1+a_{2}T+a_3{T}^{-1}+a_4{T}^{-2}+a_5\ln T+\left(a_6{T}^{-1}+a_7{T}^{-2}+a_8{T}^{-1}\ln T\right)\left(P-P_s\right)+\left(a_9{T}^{-1}+a_{10}{T}^{-2}+a_{11}{T}^{-1}\ln T\right){\left(P-P_s\right)}^2(10)$

Where P_S is the saturation pressure of water calculated through the IAPWS-IF97 [26]. Parameters a₁ to a₁₁ were provided by [22]; these parameters were obtained by fitting experimental data.

To find the equilibrium of the different species: cations, anions, and neutral molecules of the system, it is necessary to calculate the activity coefficient ($\gamma$) in the electrolytic dissolutions. Thus, the activity coefficients of the different species were obtained with the model developed by Pitzer and co-workers [27–32]. The model is based on the Debye-Hückel model. For the activity coefficient of hydrogen, the Eq 20 listed below, presented by [33], was used, which estimates the molality of hydrogen in aqueous sodium chloride solutions (0–5 mol/kg) at temperatures and pressures of 273.15–373.15 K and 0–230 bars; this equations is also based on the Pitzer model.

All the different Virial Pitzer parameters (${\beta }^{\left(0\right)},{\beta }^{\left(1\right)},C^{\phi },\lambda ,\theta ,$ and $\psi$) for the mixture H₂O-CO₂-NaCl at different temperatures and pressures were obtained from the work of [22]; these parameters were used to solve the equilibrium compositions of the system H₂O-CO₂-NaHCO₃-NaCl-H₂. For the case of hydrogen, the parameters were obtained from [33]. Besides, experimental data on activity coefficients of hydrogen and other gases in different aqueous salt solutions can be found in [34].

The equations presented below describe the proposed model based in the model of Pitzer and co-workers [27–32] for the studied mixture. The Eqs 16–18 describe the activity coefficients, where M, X, and N in equations represent specific cations, anions, or neutral molecules, respectively. Eq. 19 calculates the water activity and with Eq. 20 the activity coefficient of hydrogen is obtained. Eqs 21–27 show how those parameters were obtained, the remaining parameters used to determine the activity coefficients were calculated with the polynomial functions of T and P developed by [22].

$A^{\phi }=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.{\left(2\pi N_A{\rho }_{w}1000\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\left(\frac{e^2}{{4\pi ϵ}_0{ϵ}_{r}kT}\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}(11)$

$I=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\sum m_i{z}_i(12)$

$Z={\displaystyle \sum _i}{m}_i\left|z_i\right|(13)$

$F=-A^{\phi }\left(\frac{I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{1+1.2I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{2}{1.2}\ln \left(1+1.2I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right)+{\displaystyle \sum _{c=1}^{N_c}}{\displaystyle \sum _{a=1}^{N_a}}{m}_c{m}_a{B}_{ca}^{\prime }+{\displaystyle \sum _{c=1}^{N_c-1}}{\displaystyle \sum _{c^{\prime }=c+1}^{N_c}}{m}_c{m}_{c^{\prime }}{\mathrm{\Theta }}_{c{c}^{\prime }}^{\prime }+{\displaystyle \sum _{a=1}^{N_a-1}}{\displaystyle \sum _{a^{\prime }=a+1}^{N_a}}{m}_a{m}_{a^{\prime }}{\mathrm{\Theta }}_{a{a}^{\prime }}^{\prime }(14)$

$\begin{array}{ll}\hfill \varphi -1& =\left(\frac{2}{{\displaystyle \sum _i}{m}_i}\right)\left(-\frac{A^{\phi }{I}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{1+1.2I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right)+{\displaystyle \sum _{c=1}^{N_c}}{\displaystyle \sum _{a=1}^{N_a}}{m}_c{m}_a\left(B_{ca}^{\phi }+Z{C}_{ca}\right)+{\displaystyle \sum _{c=1}^{N_c-1}}{\displaystyle \sum _{c^{\prime }=c+1}^{N_c}}{m}_c{m}_{c^{\prime }}\left({\mathrm{\Theta }}_{c{c}^{\prime }}^{\varphi }+{\displaystyle \sum _{a=1}^{N_a}}{m}_a{\psi }_{c{c}^{\prime }a}\right)\hfill \\ \hfill & +{\displaystyle \sum _{a=1}^{N_a-1}}{\displaystyle \sum _{a^{\prime }=a+1}^{N_a}}{m}_a{m}_{a^{\prime }}\left({\mathrm{\Theta }}_{a{a}^{\prime }}^{\varphi }+{\displaystyle \sum _{c=1}^{N_c}}{m}_a{\psi }_{a{a}^{\prime }c}\right)+{\displaystyle \sum _{n=1}^{N_n}}{\displaystyle \sum _{c=1}^{N_c}}{m_{n}m}_c{\lambda }_{nc}+{\displaystyle \sum _{n=1}^{N_n}}{\displaystyle \sum _{a=1}^{N_a}}{m}_n{m}_a{\lambda }_{na}+{\displaystyle \sum _{n=1}^{N_n}}{\displaystyle \sum _{c=1}^{N_c}}{\displaystyle \sum _{a=1}^{N_a}}{m_{n}m}_c{m}_a{\zeta }_{nca}\hfill \end{array}(15)$

The equations for determining the activity coefficients of the various ions and neutral molecules are given below, in addition to the equation for calculating the activity of water.

$\begin{array}{ll}\hfill \mathrm{Ln}{\gamma }_M& =z_M^{2}F+{\displaystyle \sum _{a=1}^{N_a}}{m}_a\left(2B_{Ma}+Z{C}_{Ma}\right)+{\displaystyle \sum _{c=1}^{N_c}}{m}_c\left(2{\mathrm{\Theta }}_{Mc}^{\varphi }+{\displaystyle \sum _{a=1}^{N_a}}{m}_a{\psi }_{Mca}\right)+{\displaystyle \sum _{a=1}^{N_a-1}}{\displaystyle \sum _{a^{\prime }=a+1}^{N_a}}{m}_a{m}_{a^{\prime }}{\psi }_{a{a}^{\prime }M}\hfill \\ \hfill & +\left|z_M\right|{\displaystyle \sum _{c=1}^{N_c}}{\displaystyle \sum _{a=1}^{N_a}}{m_c{m}_{a}C}_{ca}+2{\displaystyle \sum _{n=1}^{N_n}}{m}_n{\lambda }_{nM}+6{\displaystyle \sum _{n=1}^{N_n}}{\displaystyle \sum _{a=1}^{N_a}}{m}_n{m}_a{\zeta }_{Mna}\hfill \end{array}(16)$

$\begin{array}{ll}\hfill \ln {\gamma }_X& =z_X^{2}F+{\displaystyle \sum _{c=1}^{N_c}}{m}_c\left(2B_{cX}+Z{C}_{cX}\right)+{\displaystyle \sum _{a=1}^{N_a}}{m}_a\left(2{\mathrm{\Theta }}_{Xa}+{\displaystyle \sum _{c=1}^{N_c}}{m}_c{\psi }_{Xac}\right)+{\displaystyle \sum _{c=1}^{N_c-1}}{\displaystyle \sum _{c^{\prime }=c+1}^{N_c}}{m}_c{m}_{c^{\prime }}{\psi }_{c{c}^{\prime }X}\hfill \\ \hfill & +\left|z_X\right|{\displaystyle \sum _{c=1}^{N_c}}{\displaystyle \sum _{a=1}^{N_a}}{m_c{m}_{a}C}_{ca}+2{\displaystyle \sum _{n=1}^{N_n}}{m}_n{\lambda }_{nX}+6{\displaystyle \sum _{n=1}^{N_n}}{\displaystyle \sum _{c=1}^{N_c}}{m}_n{m}_c{\zeta }_{ncX}\hfill \end{array}(17)$

$\ln {\gamma }_N=2{\displaystyle \sum _{n=1}^{N_n}}{m}_n{\lambda }_{Nn}+2{\displaystyle \sum _{c=1}^{N_c}}{m}_c{\lambda }_{Nc}+2{\displaystyle \sum _{a=1}^{N_a}}{m}_a{\lambda }_{Na}+{\displaystyle \sum _{c=1}^{N_c}}{\displaystyle \sum _{a=1}^{N_a}}{m}_c{m}_a{\zeta }_{Nca}(18)$

$a_{H_{2}O}=\exp \left(-\frac{M_{H_{2}O}\varphi }{1000}{\displaystyle \sum _j}{m}_j\right)(19)$

$\ln {\gamma }_{H_2}=2{\displaystyle \sum _{c=1}^{N_c}}{m}_c{\lambda }_{H_{2}c}+2{\displaystyle \sum _{a=1}^{N_a}}{m}_a{\lambda }_{H_{2}a}+{\displaystyle \sum _{c=1}^{N_c}}{\displaystyle \sum _{a=1}^{N_a}}{m}_c{m}_a{\zeta }_{H_{2}ca}(20)$

The different Virial parameters of the Pitzer model are described in the following equations:

$B_{ca}^{\prime }=\frac{2{\beta }_{ca}^{\left(1\right)}}{{\alpha }^2{I}^2}\left(-1+\left(1+\alpha I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\frac{1}{2}{\alpha }^{2}I\right)\exp \left(-\alpha I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right)(21)$

$B_{ca}^{\phi }={\beta }_{ca}^{\left(0\right)}+{\beta }_{ca}^{\left(1\right)}\exp \left(-\alpha I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)(22)$

$B_{MX}={\beta }_{ca}^{\left(0\right)}+\frac{2{\beta }_{ca}^{\left(1\right)}}{{\alpha }^{2}I}\left(1-1\left(1+\alpha I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\exp \left(\alpha I^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right)(23)$

$C_{ca}=\frac{C_{ca}^{\phi }}{2{\left|z_M{z}_X\right|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}(24)$

${\mathrm{\Theta }}_{ij}^{\varphi }={\theta }_{ij}+{}_{.}{}^E{\theta }_{ij}\left(I\right)+I{}_{.}{}^E{\theta }_{ij}^{\prime }\left(I\right)(25)$

${\mathrm{\Theta }}_{ij}={\theta }_{ij}+{}_{.}{}^E{\theta }_{ij}\left(I\right)(26)$

${\mathrm{\Theta }}_{ij}^{\prime }={}_{.}{}^E{\theta }_{ij}^{\prime }\left(I\right)(27)$

Where ${\theta }_{ij}$ is the second Virial parameter for each pair of cations or each pair of anions. The terms ${}_{.}{}^E{\theta }_{ij}\left(I\right)$ and ${}_{.}{}^E{\theta }_{ij}^{\prime }\left(I\right)$ describes the electrostatic effects of unsymmetrical ion mixtures [35]. The Eqs 25–27 were obtained by [30]. The most important characteristic of ${}_{.}{}^E{\theta }_{ij}\left(I\right)$ and ${}_{.}{}^E{\theta }_{ij}^{\prime }\left(I\right)$ is that they only depend on the charges of the ions and the total ionic strength ($I$). Furthermore, they do not represent an extra parameterization of the model. ${}_{.}{}^E{\theta }_{ij}\left(I\right)$ and ${}_{.}{}^E{\theta }_{ij}^{\prime }\left(I\right)$ are set to zero when the ions have the same charge.

Some Virial parameters were set to zero; for instance, the second virial parameter (${\beta }_{ca}^{\left(0\right)}$, ${\beta }_{ca}^{\left(1\right)}$, and $C_{ca}^{\phi }$) of the following combinations: H⁺-OH^-, H⁺-HCO₃^-, and H⁺-CO₃^2-, because their influence on the activity coefficient is small. Furthermore, the third virial coefficients (${\theta }^{\prime }s$ and ${\psi }^{\prime }s$) related to H⁺, OH⁻, HCO₃⁻, and CO₃^2- also can be fixed to zero due to their minor impact on free energy. Besides, the third-order interaction ($\zeta$) of CO₂-Na⁺-HCO₃^- also can be set to zero because of the small contribution of the third virial coefficient. These assumptions were taken before by other researchers [22, 36].

It must be emphasized that the parametrization of the model used in this work, based on the work of [22], considered all species present in the hydrothermal conversion process, except hydrogen. Due to its nature and its relatively low concentration in the solution, it is not expected that hydrogen has a significant impact on the activity coefficients of other compounds in the solution. However, the inverse may not be true, and in particular the dissolved CO₂ species, that are not included in the parametrization of the activity coefficient model for hydrogen, may have a certain influence on this activity coefficient that is not considered in the model used.

Finally, the pH was calculated as the product between the concentration and the activity coefficient while the pOH as the difference between pK_w and pH.

$pH=-\mathit{log}\left(m_{H^{+}}·{\gamma }_{H^{+}}\right)(28)$

$pOH=pKw-pH(29)$

3 Methodology

The speciation equilibrium was represented by a nonlinear problem formed by four equations (ecs. 30–33 listed below) and four variables: mH⁺, mOH⁻, mHCO₃^-, and mCO₃^2-. The thermodynamic system was calculated and solved using the commercial computing software MATLAB^® R2022b. The program was divided into three main parts: auxiliary functions, equilibrium functions, and a solution file. The flow diagram of the code can be seen in Figures 1, 2.

FIGURE 1

FIGURE 1. Flow diagram of the algorithm with the functions that must be solved to calculate the molalities.

FIGURE 2

FIGURE 2. Flow diagram of the main program.

The auxiliary functions consist of five function codes that resolve different parts of the system: equilibrium constants, activity coefficients, Henry’s Law, saturation pressure of water and water density. The equilibrium constant function solves Eqs 6–8. The activity coefficient function computes the activity coefficient of every specie in the dissolution through the Pitzer model according to the Eqs 11–19. The density function returns the density of water according to the PC-SAFT equation of state [37], using an open-source program from [38].

The equilibrium functions file contains the four functions: obj_F (1), obj_F (2), obj_F (3), and obj_F (4), which are described in equations from (30) to (33); these are the function that must be solved by the computing software to calculate the thermodynamic equilibrium. The functions obj_F (1), obj_F (2), and obj_ F (3) represent the difference between the reference equilibrium constants calculated with Eqs 9, 10; and the named in Eqs 6–8 after dividing by its respective reference K to scale the function and facilitate the convergence of the numerical resolution method; and the fourth equation obj_F (4) describes the charge balance between the different ions, again scaled to facilitate convergence.

To solve the nonlinear equation system, formed by the four equilibrium functions named above, the fsolve function of MATLAB^® was used; this command takes an initial vector as initial guess and iterates until made zero the functions established in the equilibrium functions file by minimizing the sum of squares of the functions. Then the solution obtained is taken as the initial point for the next iterations. Some of the initial points were taken from the condition of pure water or water and carbon dioxide mixtures.

$obj\_F\left(1\right)=1-\frac{K_{1calc}}{K_1}(30)$

$obj\_F\left(2\right)=1-\frac{K_{2calc}}{K_2}(31)$

$obj\_F\left(3\right)=1-\frac{K_{wcalc}}{K_w}(32)$

$obj\_F\left(4\right)=\left(m_{H^{+}}+m_{{Na}^{+}}-m_{{OH}^{-}}-m_{{Cl}^{-}}-m_{{HCO}_3^{-}}-2m_{{CO}_3^{2-}}\right)/\left(m_{H^{+}}+m_{{Na}^{+}}\right)(33)$

The algorithm used by the MATLAB^® function fsolve to find solutions to the nonlinear systems is the trust-region-dogleg algorithm: fsolve tries to solve a system of equations by minimizing the sum of squares of the components. If the sum of squares is zero, the system of equations is solved. The trust-region-dogleg algorithm is an iterative method for solving nonlinear systems of equations. The algorithm starts with an initial approximate solution and then uses a trust region to gradually adjust the solution until a satisfactory solution is found. The trust region is a set of possible solutions that are considered “reasonably close” to the true solution. At each iteration, the algorithm uses a root-finding method to find the closest solution within the trust region. If this solution is satisfactory, the process is stopped, and the solution is returned. If it is not satisfactory, the trust region is adjusted, and the process is repeated. The root-finding method used by the trust-region-dogleg algorithm is the dogleg method. This method combines two simpler methods: the Newton method and the gradient direction method.

The Newton method uses information about the curvature of the function to find a faster solution. However, this method can fail if the curvature of the function changes a lot from one iteration to the next. The gradient direction method, on the other hand, uses information about the slope of the function to slowly move in the direction of the solution. This method is more stable, but also slower. The dogleg method combines these two methods to achieve a balance between stability and speed. It uses the Newton method when possible, and the gradient direction method when necessary.

4 Results and discussion

Several parameters of interest for the hydrothermal reduction of CO₂ were analyzed with the thermodynamic model: temperature, pressure, concentration of bases and concentration of sodium chloride (which would be applicable in case that CO₂ dissolved as bicarbonate in sea water is used as feedstock for the reduction process).

4.1 Effect of pressure and temperature

Figure 3 presents the results obtained at different pressures and temperatures, considering a fixed initial concentration of NaHCO₃ of 0.5 mol/kg in the dissolution (matching the conditions used in experimental works, in which the aqueous CO₂ solution was prepared dissolving this concentration of sodium bicarbonate in water [18, 19]) and a fixed hydrogen partial pressure of 20 bar. The range of conditions analyzed comprised temperatures ranging from 300 K to 500 K and CO₂ partial pressures in the gas of 20 bar, 50 bar, 75 bar and 125 bar. It must be noted that to facilitate visualization, results are presented in logarithmic scale.

FIGURE 3

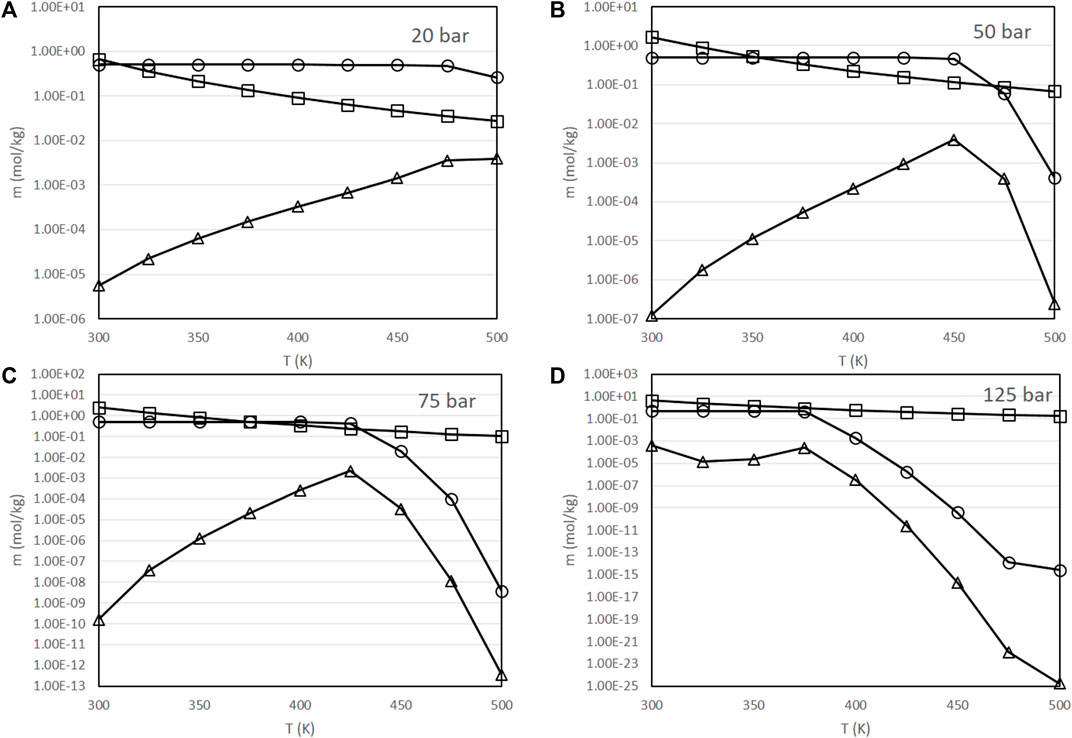
FIGURE 3. Variation of the molality of dissolved species as a function of pressure and temperature [(A): partial pressure of CO2 of 20 bar, (B): 50 bar, (C): 75 bar, (D): 125 bar], with a fixed initial concentration of NaHCO₃ of 0.5 mol/kg and a fixed H₂ partial pressure of 20 bar. ○: molality of H₂CO₃, □: molality of HCO₃⁻, △: molality of CO₃^2-

As presented in Figure 3, at comparatively low pressures and temperatures, sodium bicarbonate maintains a concentration very close to the initial value of 0.5 mol/kg. At a fixed pressure, the concentration of sodium bicarbonate eventually drops to very low values once that a threshold temperature is achieved; this threshold temperature is lower at higher CO₂ partial pressures, being about 500 K at 20 bar, 475 K at 50 bar, 450 K at 75 bar and 425 K at 125 bar. Conversely, the carbonate concentration slightly increases in these ranges.

This behavior is relevant to explain the experimental results of the performance of the process in terms of the yield of formic acid obtained. Experimentally, it is observed that this yield increases with temperature over a certain range of temperatures, while at higher temperatures it drops drastically [10, 39]. In the original experimental work, it was hypothesized that this result was due to the evolution of kinetic factors: at high temperatures, the rate of the decomposition reactions of formic acid would increase, decreasing its yield [39]. Figure 3 provides an alternative explanation in terms of the equilibrium composition: as the concentration of sodium bicarbonate drops at high temperatures, and, as already mentioned, bicarbonate is the reactive species, this would justify the lower yields obtained in these conditions.

Figure 4 presents the evolution of pH and pOH in the same range of conditions. As it can be observed, pH tends to increase at higher temperatures and higher pressures, with pOH following the opposing trends. In experiments with biomass materials as reductants, it is known that alkaline conditions favor the decomposition of biomass into the sugars and other reducing compounds that can react with inorganic CO₂ [11, 19]. According to Figure 4, higher temperatures favor the decomposition of biomass, in agreement with experimental results [18, 19]. Finally, Figure 5 presents the evolution of the dissolved H₂ concentration, which follows the typical behavior of a dissolved gas, with lower concentrations at higher temperatures.

FIGURE 4

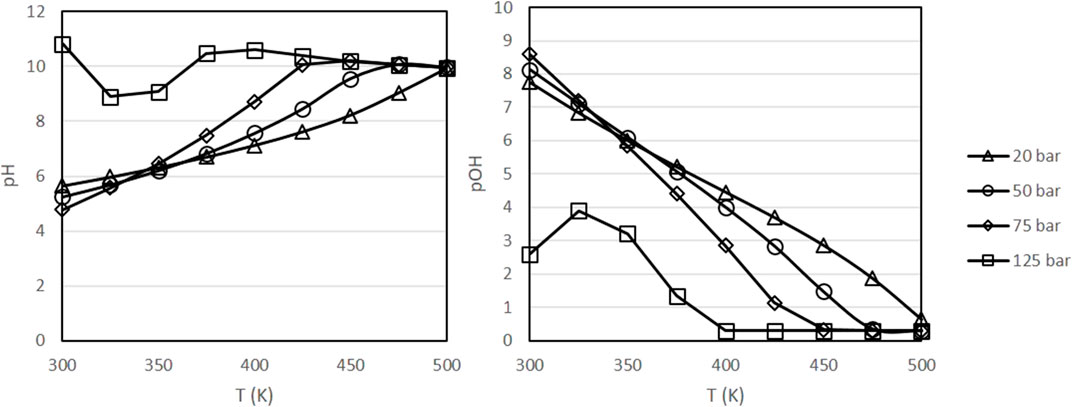
FIGURE 4. Variation of pH and pOH as a function of pressure and temperature with a fixed initial concentration of NaHCO₃ of 0.5 mol/kg and a fixed H₂ partial pressure of 20 bar.

FIGURE 5

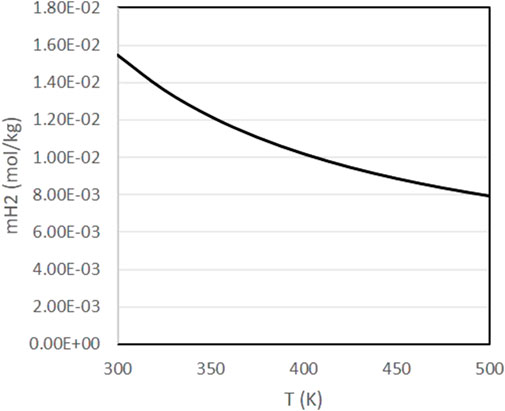
FIGURE 5. Variation of H₂ molality as a function of pressure and temperature with a fixed initial concentration of NaHCO₃ of 0.5 mol/kg and a fixed H₂ partial pressure of 20 bar.

4.2 Effect of the concentration of sodium bicarbonate

Figure 6 presents the equilibrium species and the pH of solutions at a fixed temperature of 400 K and fixed partial pressure of CO₂ of 50 bar as a function of the initial concentration of sodium bicarbonate in the solution. As presented in this figure, an increase in the initial concentration of sodium bicarbonate results in a near proportional increase of the concentration of bicarbonate in the equilibrium; this is, formation of bicarbonate is favored by the acid-base equilibrium under the considered conditions. On the other hand, pH increases and pOH decreases as a result of the addition of sodium bicarbonate, which is favourable for the decomposition reactions of biomass, that are promoted by alkaline conditions. Both results agree with the experimental observation of an improved reaction performance in presence of higher initial concentrations of sodium bicarbonate [19].

FIGURE 6

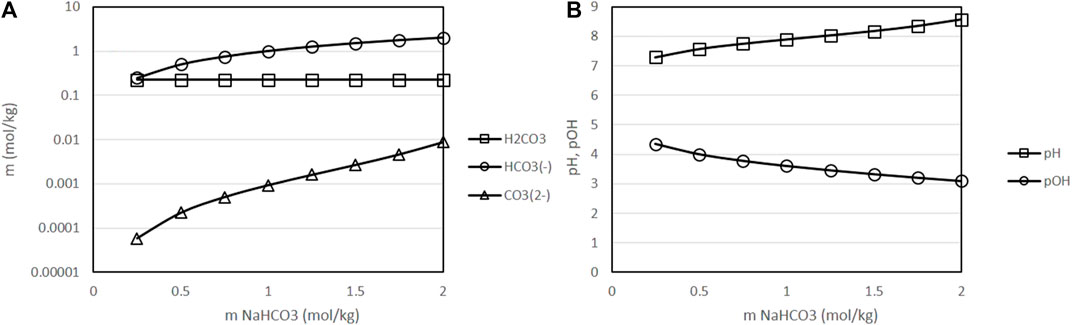
FIGURE 6. Variation of the molality of dissolved species as a function of the initial concentration of sodium bicarbonate [(A): molality of H₂CO₃, HCO₃⁻ and CO₃^2-, results presented in logarithmic scale (B): pH and pOH], with a fixed temperature of 400 K, fixed CO₂ partial pressure of 50 bar and a fixed H₂ partial pressure of 20 bar. ○: molality of H₂CO₃, □: molality of HCO₃⁻, △: molality of CO₃^2-

4.3 Effect of the addition of NaOH

Figure 7 presents the equilibrium species and the pH of solutions at a fixed temperature of 400 K, fixed partial pressure of CO₂ of 50 bar and fixed initial concentration of sodium bicarbonate of 0.5 mol/kg, as a function of the initial concentration of sodium hydroxide in the solution. This figure shows that the addition of sodium hydroxide increases pH/decreases pOH in a larger extent than the addition of the same initial concentration of sodium bicarbonate (see Figure 6). Acid base equilibrium, while displaced towards bicarbonate, shows also higher concentrations of carbonate than in simulations in which sodium bicarbonate was added. Especially at higher initial concentrations of sodium hydroxide, the concentration of carbonate increases significantly. This result is in agreement with experimental observations that show a lower performance of the reaction when high amounts of sodium hydroxide are added to the initial solution [11]; this reduction in the performance can be correlated with the displacement of equilibrium towards carbonate.

FIGURE 7

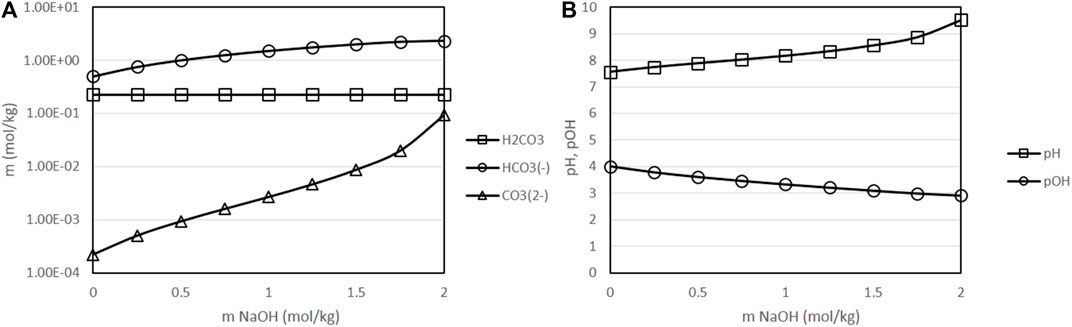
FIGURE 7. Variation of the molality of dissolved species as a function of the initial concentration of sodium hydroxide [(A): molality of H₂CO₃, HCO₃⁻ and CO₃^2--, results presented in logarithmic scale (B): pH and pOH), with a fixed temperature of 400 K, fixed initial concentration of NaHCO₃ of 0.5 mol/kg, fixed CO₂ partial pressure of 50 bar and a fixed H₂ partial pressure of 20 bar. ○: molality of H₂CO₃, □: molality of HCO₃⁻, △: molality of CO₃^2-].

4.4 Effect of the concentration of NaCl

Seawater is a natural sink for atmospheric CO₂. Thus, CO₂ dissolved in seawater, mostly as sodium bicarbonate, is a relevant feedstock for a hydrothermal CO₂ conversion process, as an alternative to solutions produced by absorption of CO₂ produced in industrial focal points. A major difference between these solutions produced by an industrial absorption process and seawater is the presence of NaCl in seawater. Besides the effect that this compound may have in practical aspects such as the required use of corrosion-resistant materials or modifications in the design of equipment, NaCl may also have a significant influence over the speciation equilibria studied in this work.

Thus, Figure 8 presents the results obtained, again at fixed conditions of 400 K, 50 bar of partial pressure of CO₂ and 0.5 mol/kg initial concentration of sodium bicarbonate, as a function of the concentration of NaCl in the solution. The range of NaCl concentrations considered correspond to the natural variations of the concentration of salt in different seas and oceans, which on average is about 35 g/L (0.6 mol/kg). As it can be seen in Figure 8, low concentrations of salt, in the range of this typical average value of 0.6 mol/kg, have a very minor effect on the speciation equilibria. Only at very high concentrations, an increase of pH and a gradual displacement of equilibrium towards carbonate is observed. Thus, the presence of dissolved NaCl is not expected to have a major impact on the process from the point of view of the concentration of the dissolved species.

FIGURE 8

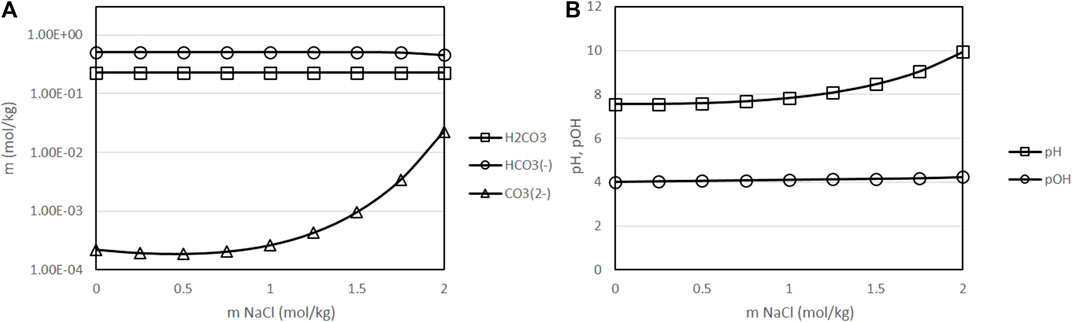
FIGURE 8. Variation of the molality of dissolved species as a function of the initial concentration of sodium chloride [(A): molality of H₂CO₃, HCO₃⁻ and CO₃^2--, results presented in logarithmic scale (B): pH and pOH), with a fixed temperature of 400 K, fixed initial concentration of NaHCO₃ of 0.5 mol/kg, fixed CO₂ partial pressure of 50 bar and a fixed H₂ partial pressure of 20 bar. ○: molality of H₂CO₃, □: molality of HCO₃⁻, △: molality of CO₃^2-].

5 Conclusion

A thermodynamic model of the equilibrium species in the hydrothermal conversion of CO₂ dissolved in aqueous solutions has been presented. The influence of different process conditions on the equilibrium concentrations has been analyzed, including: the effect of pressure and temperature, sodium bicarbonate concentration, sodium hydroxide concentration and sodium chloride concentration, with a focus on the concentration of bicarbonate, which is the main reacting species, in the equilibrium achieved under each of these conditions. It has been observed that high concentrations of sodium bicarbonate, which in turn favor the performance of the reaction, are favoured by moderate temperatures, high initial concentrations of sodium bicarbonate and moderate initial concentrations of sodium hydroxide. The presence of sodium chloride in the range of typical concentrations in natural seawater has a negligible influence on the equilibrium concentrations of dissolved species. These results provide valuable guidelines for the development and optimization of hydrothermal CO₂ conversion processes.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

IN-C implemented the thermodynamic model, performed calculations and elaborated the discussion of results. AM supervised the work, revised the model implementation and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This project has been funded by the Ministry of Science and Universities through project RTI2018-097456-B-I00 and by the Junta de Castilla y León through project by FEDER FUNDS under the BioEcoUVa Strategic Program (CLU-2019-04).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jeffry L, Ong MY, Nomanbhay S, Mofijur M, Mubashir M, Show PL. Greenhouse gases utilization: A review. Fuel (2021) 301:121017. doi:10.1016/j.fuel.2021.121017

CrossRef Full Text | Google Scholar

2. Lamb WF, Wiedmann T, Pongratz J, Andrew R, Crippa M, Olivier JGJ, et al. A review of trends and drivers of greenhouse gas emissions by sector from 1990 to 2018. Environ Res Lett (2021) 16(7):073005. doi:10.1088/1748-9326/abee4e

CrossRef Full Text | Google Scholar

3. Spigarelli BP, Kawatra SK. Opportunities and challenges in carbon dioxide capture. J CO2 Utilization (2013) 1:69–87. doi:10.1016/j.jcou.2013.03.002

CrossRef Full Text | Google Scholar

4. He M, Sun Y, Han B. Green carbon science: scientific basis for integrating carbon resource processing, utilization, and recycling. Angew Chem Int Edition (2013) 52(37):9620–33. doi:10.1002/anie.201209384

PubMed Abstract | CrossRef Full Text | Google Scholar

5. He D, Wang X, Yang Y, He R, Zhong H, Wang Y, et al. Hydrothermal synthesis of long-chain hydrocarbons up to C24with NaHCO₃ assisted stabilizing cobalt. Proc Natl Acad Sci (2021) 118(51):e2115059118. doi:10.1073/pnas.2115059118

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Ma S, Chen G, Guo M, Zhao L, Han T, Zhu S. Path analysis on CO₂ resource utilization based on carbon capture using ammonia method in coal-fired power Plants. Renew Sustain Energ Rev (2014) 37:687–97. doi:10.1016/j.rser.2014.05.048

CrossRef Full Text | Google Scholar

7. Sakakura T, Choi J-C, Yasuda H. Transformation of carbon dioxide. Chem Rev (2007) 107(6):2365–87. doi:10.1021/cr068357u

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhou H, Chen Z, López AV, López ED, Lam E, Tsoukalou A, et al. Engineering the Cu/Mo₂CTx (MXene) interface to drive CO2 hydrogenation to methanol. Nat Catal (2021) 4(10):860–71. doi:10.1038/s41929-021-00684-0

CrossRef Full Text | Google Scholar

9. Mikkelsen M, Jørgensen M, Krebs FC. The teraton challenge. A review of fixation and transformation of carbon dioxide. Energ Environ Sci (2010) 3(1):43–81. doi:10.1039/B912904A

CrossRef Full Text | Google Scholar

10. Martín A, Bermejo MD, Pérez E, Quintana-Gómez L, Queiroz J, Andérez M, et al. Chapter 24 hydrothermal CO₂ reduction using metals and biomass derivatives as reductants. In: Chemical valorisation of carbon dioxide. London, UK: The Royal Society of Chemistry (2023). p. 520–43. doi:10.1039/9781839167645-00520

CrossRef Full Text | Google Scholar

11. Andérez-Fernández M, Pérez E, Martín A, Bermejo MD. Hydrothermal CO₂ reduction using biomass derivatives as reductants. J Supercrit Fluids (2018) 133:658–64. doi:10.1016/j.supflu.2017.10.010

CrossRef Full Text | Google Scholar

12. del Río JI, Pérez E, León D, Martín Á, Bermejo MD. Catalytic hydrothermal conversion of CO₂ captured by ammonia into formate using aluminum-sourced hydrogen at mild reaction conditions. J Ind Eng Chem (2021) 97:539–48. doi:10.1016/j.jiec.2021.03.015

CrossRef Full Text | Google Scholar

13. Shen Z, Zhang Y, Jin F. The alcohol-mediated reduction of CO₂ and NaHCO₃ into formate: A hydrogen transfer reduction of NaHCO₃ with glycerine under alkaline hydrothermal conditions. RSC Adv (2012) 2(3):797–801. doi:10.1039/C1RA00886B

CrossRef Full Text | Google Scholar

14. Adeniyi KI, Zirrahi M, Hassanzadeh H. Phase equilibria of water-hydrocarbon (pentane to heavy oils) systems in the near-critical and supercritical water regions - a literature review. J Supercrit Fluids (2021) 178:105356. doi:10.1016/j.supflu.2021.105356

CrossRef Full Text | Google Scholar

15. Marshall WL, Franck EU. Ion product of water substance, 0–1000 °C, 1–10,000 bars New International Formulation and its background. J Phys Chem Reference Data (1981) 10(2):295–304. doi:10.1063/1.555643

CrossRef Full Text | Google Scholar

16. Quintana-Gómez L, Martínez-Álvarez P, Segovia JJ, Martín Á, Bermejo MD. Hydrothermal reduction of CO₂ captured as NaHCO₃ into formate with metal reductants and catalysts. J CO₂ Utilization (2023) 68:102369. doi:10.1016/j.jcou.2022.102369

CrossRef Full Text | Google Scholar

17. del Rio J, Martín A, Bermejo MD. Coupling the solvent-based CO₂ capture processes to the metal water-splitting for hydrogen generation in a semi-continuous system. Int J Hydrogen Energ (2023) 48:27892–906. doi:10.1016/j.ijhydene.2023.04.021

CrossRef Full Text | Google Scholar

18. Andérez-Fernández M, Pérez E, Ferrero S, Álvarez CM, Gumiel J, Martín Á, et al. Simultaneous formic acid production by hydrothermal CO₂ reduction and biomass derivatives conversion in a continuous reactor. Chem Eng J (2023) 453:139741. doi:10.1016/j.cej.2022.139741

CrossRef Full Text | Google Scholar

19. Andérez-Fernández M, Pérez E, Martín Á, McGregor J, Bermejo MD. Synergistic hydrothermal conversion of aqueous solutions of CO₂ and biomass waste liquefaction into formate. ACS Sustain Chem Eng (2022) 10(50):16948–57. doi:10.1021/acssuschemeng.2c06218

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zhong H, Yao G, Cui X, Yan P, Wang X, Jin F. Selective conversion of carbon dioxide into methane with a 98% yield on an in situ formed Ni nanoparticle catalyst in water. Chem Eng J (2019) 357:421–7. doi:10.1016/j.cej.2018.09.155

CrossRef Full Text | Google Scholar

21. Wang X, Yang Y, Wang T, Zhong H, Cheng J, Jin F. In situ formed metal oxide/metal interface enhanced C–C coupling in CO₂ reduction into CH₃COOH over hexagonal closed-packed cobalt. ACS Sustain Chem Eng (2021) 9(3):1203–12. doi:10.1021/acssuschemeng.0c06717

CrossRef Full Text | Google Scholar

22. Li D, Duan Z. The speciation equilibrium coupling with phase equilibrium in the H₂O–CO₂–NaCl system from 0 to 250 °C, from 0 to 1000 bar, and from 0 to 5 molality of NaCl. Chem Geology (2007) 244(3):730–51. doi:10.1016/j.chemgeo.2007.07.023

CrossRef Full Text | Google Scholar

23. Sun R, Duan Z. Prediction of CH₄ and CO₂ hydrate phase equilibrium and cage occupancy from ab initio intermolecular potentials. Geochimica et Cosmochimica Acta (2005) 69(18):4411–24. doi:10.1016/j.gca.2005.05.012

CrossRef Full Text | Google Scholar

24. Duan Z, Sun R, Zhu C, Chou IM. An improved model for the calculation of CO₂ solubility in aqueous solutions containing Na+, K+, Ca2+, Mg2+, Cl−, and SO42. Mar Chem (2006) 98(2):131–9. doi:10.1016/j.marchem.2005.09.001

CrossRef Full Text | Google Scholar

25.In:PJ Linstrom, and WG Mallard, editors. NIST Chemistry WebBook, NIST standard reference database number 69. Gaithersburg MD: National Institute of Standards and Technology (2023). doi:10.18434/T4D30320899

CrossRef Full Text | Google Scholar

26. Wagner W, Kruse A. Properties of water and steam: The industrial standard IAPWS-IF97 for the thermodynamic properties and supplementary equations for other properties. Berlin, Germany: Springer-Verlag (1998).

Google Scholar

27. Pitzer KS. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J Phys Chem (1973) 77(2):268–77. doi:10.1021/j100621a026

CrossRef Full Text | Google Scholar

28. Pitzer KS, Mayorga G. Thermodynamics of electrolytes. II. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent. J Phys Chem (1973) 77(19):2300–8. doi:10.1021/j100638a009

CrossRef Full Text | Google Scholar

29. Pitzer KS, Kim JJ. Thermodynamics of electrolytes. IV. Activity and osmotic coefficients for mixed electrolytes. J Am Chem Soc (1974) 96(18):5701–7. doi:10.1021/ja00825a004

CrossRef Full Text | Google Scholar

30. Pitzer KS. Thermodynamics of electrolytes. V. effects of higher-order electrostatic terms. J Solution Chem (1975) 4(3):249–65. doi:10.1007/BF00646562

CrossRef Full Text | Google Scholar

31. Pitzer KS. Electrolyte theory - improvements since Debye and hueckel. Acc Chem Res (1977) 10(10):371–7. doi:10.1021/ar50118a004

CrossRef Full Text | Google Scholar

32. Pitzer KS. Characteristics of very concentrated aqueous solutions. Phys Chem Earth (1981) 13-14:249–72. doi:10.1016/0079-1946(81)90013-6

CrossRef Full Text | Google Scholar

33. Zhu Z, Cao Y, Zheng Z, Chen D. An accurate model for estimating H₂ solubility in pure water and aqueous NaCl solutions. Energies (2022) 15(14):5021. doi:10.3390/en15145021

CrossRef Full Text | Google Scholar

34. Randall M, Failey CF. The activity coefficient of gases in aqueous salt solutions. Chem Rev (1927) 4(3):271–84. doi:10.1021/cr60015a003

CrossRef Full Text | Google Scholar

35. Friedman HL. Ionic solution theory. Interscience Publ (1962).

Google Scholar

36. Harvie CE, Møller N, Weare JH. The prediction of mineral solubilities in natural waters: The Na-K-Mg-Ca-H-Cl-SO4-OH-HCO3-CO3-CO2-H2O system to high ionic strengths at 25°C. Geochimica et Cosmochimica Acta (1984) 48(4):723–51. doi:10.1016/0016-7037(84)90098-X

CrossRef Full Text | Google Scholar

37. Gross J, Sadowski G. Perturbed-Chain SAFT: An equation of state based on a perturbation theory for chain molecules. Ind Eng Chem Res (2001) 40(4):1244–60. doi:10.1021/ie0003887

CrossRef Full Text | Google Scholar

38. Martín Á, Bermejo MD, Mato FA, Cocero MJ. Teaching advanced equations of state in applied thermodynamics courses using open source programs. Edu Chem Eng (2011) 6(4):e114–21. doi:10.1016/j.ece.2011.08.003

CrossRef Full Text | Google Scholar

39. Román-González D, Moro A, Burgoa F, Pérez E, Nieto-Márquez A, Martín Á, et al. 2Hydrothermal CO2 conversion using zinc as reductant: Batch reaction, modeling and parametric analysisof the process. J Supercrit Fluids (2018) 140:320–8. doi:10.1016/j.supflu.2018.07.003

CrossRef Full Text | Google Scholar

Nomenclature