- Institut für Theoretische Physik, Universität Leipzig, Leipzig, Germany
We derive a formula that expresses the density of states of a system with continuous degrees of freedom as a function of microcanonical averages of squared gradient and Laplacian of the Hamiltonian. This result is then used to propose a novel flat-histogram Monte Carlo algorithm, which is tested on a three-dimensional system of interacting Lennard-Jones particles, the O(n) vector spin model on hypercubic lattices in D = 1 to 5 dimensions, and the O(3) Heisenberg model on a triangular lattice featuring frustration effects.
1 Introduction
Central to statistical physics are the canonical ensemble, its partition function, and as defining quantity the temperature on the one hand as well as the microcanonical ensemble and the density of states defined by energy on the other. While the energy in the canonical ensemble takes the form of a weighted average over all microstates, the temperature in the microcanonical ensemble becomes the inverse of the derivative of the logarithmic density of states. However, in 1997 Rugh [1] showed that it too can be expressed as an average of an observable comprising various derivatives of the Hamiltonian. The same formula had already been found by Gilat [2], but—judging by the number of citations—received very little attention. With Rugh’s work at hand, it was soon realized [3] that this relation among other things offers a way to verify the correctness of Monte Carlo (MC) computer simulations. Unfortunately, the formula involves a rather unwieldy term containing the Hamiltonian’s Hessian that is computationally demanding. In this study, we develop a formula that expresses the density of states of the system as a function of microcanonical averages of squared gradient and Laplacian of the Hamiltonian while avoiding this term.
In the last decades, MC simulations have become an important tool to investigate thermodynamic properties of models of complex systems. Today, many different techniques are used. In addition to the famous Metropolis algorithm [4] which samples from the canonical ensemble nowadays generalized ensemble methods have become more prevalent. Among these, flat-histogram methods such as multicanonical (MUCA) [5], the Wang-Landau method [6], and Statistical Temperature MC [7] aim to create the same ensemble where the distribution as a function of energy is constant. On the one hand, this allows one to reweight the data to a canonical ensemble with any desirable temperature, while on the other hand even if one is only interested in low-temperature behavior the inclusion of high energies allows the system to decorrelate more easily. To bias the system’s random walk such that this ensemble becomes the stationary distribution the logarithm of the density of states (DoS) or its derivative must be known with sufficient precision. This can be achieved in an iterative process [8,9] that analyses and incorporates successively created histograms or on the fly by permanently altering the estimate of the DoS [6] or its derivative [7] based only on the energy of the current state of the system. Either way, the estimate of the DoS that is created and employed to drive the algorithm is solely based on the energy time series. No other information is utilized.
It is an interesting exercise and test of the accuracy and precision achieved with our formula to measure the microcanonical properties of the energy landscape and use them to estimate the DoS during a flat-histogram MC simulation that at the same time is using that estimate to achieve a flat distribution in energy. In this study, we demonstrate this idea with two examples: A system of interacting Lennard-Jones particles and the O(n) vector spin model.
The paper is organized as follows: In Section 2 we once more derive the formula of Gilat and Rugh and proceed to calculate our alternative. In Section 3 we discuss how a flat-histogram algorithm can be formulated and develop a suitable method for numerical integration. We then apply the method to a Lennard-Jones system in Section 4 and to the O(n) vector spin model in Section 5. In Section 6 we finish with some concluding remarks.
2 Calculating the density of states
The DoS or partition sum of the microcanonical ensemble at energy E is given by
where
with
To be able to apply the divergence theorem we rewrite (2) again:
Here,
We insert (5), apply the divergence theorem, and integrate perpendicular to the surfaces by multiplying the thickness of the integration volume
Dividing by g(E) on both sides we obtain the known result [1,2,10–13]
with
where
where E0 can be chosen freely. It is worth noting that B relates directly to temperature. It is true by definition that its microcanonical average equals the inverse microcanonical temperature if the latter is defined as
and it can easily be shown that its canonical average is equal to the inverse canonical temperature:
While gradient and Laplace operator can be applied to
and now consider its energy derivative
The integral can be transformed,
and the derivative be calculated similarly to the procedure used above. Using differential quotient and divergence theorem we find
It follows that
and in particular by choosing
We obtain for the inverse microcanonical temperature:
Integrating on both sides and exponentiating gives
We first derived (20) in a different way: If one formally considers a random walk in configuration space with sufficiently small step length and equilibrates the system after every single step on the respective surface of constant energy, one obtains a one-dimensional stochastic process in energy with a stationary distribution proportional to g(E). The change in energy for a small step X → X′ = X + x is given by
and it follows that the drift for such a process is
In the context of MC simulations, the DoS is virtually always determined via histograms. The distribution of energies within the employed ensemble is estimated and allows to calculate g(E). Although rare, faulty simulations with the detailed balance criterion violated are not unheard-of and it is sometimes not easy to spot such problems. It is worth noting that Eqs 10, 20 provide an alternative way to determine the DoS and a comparison with the histogram-derived DoS can, therefore, be used to test whether an algorithm is in balance.
3 Algorithm
It is well well-known and widely utilized that within a Monte Carlo simulation, a flat histogram can be produced if the acceptance probability for proposed moves is given by
which can now be written as
The arguments X have been removed for the sake of clarity.
One main challenge is the accurate numeric evaluation of the integral. Since the energy is continuous, it is natural to employ a binning procedure. It might be worthwhile to use an adaptive binwidth with higher resolution in regions where the integrand
changes rapidly with E, but here we use intervals Ik = [E0 + (k − 1)h, E0 + kh] of constant width h and estimate microcanonical averages of an observable O as the mean of all measurements with an energy Et ∈ Ik:
where t is the time index of the measurements. It is useful to also measure [E]k and use it instead of the midpoint of Ik for the integration. We use the notation Ek = [E]k and
Following the standard approach for quadrature (numerical integration) we locally approximate the data by an analytical function and integrate the latter. However, the usual choice of polynomials does not represent the underlying mathematical relation well. Since it is
we use the Ansatz
which corresponds to a system with lowest energy η and constant (canonical) specific heat C = kB(μ + 1). Assuming equality in Eq. 26 it is
and for two points (Ei, fi) and (Ei+1, fi+1) we obtain
Thus we arrive at
For the actual simulation, we use the function
with some suitable E0 and using Eqs 29–31 calculate G(Ek) for all bins (intervals) Ik. Inside each bin we approximate G(E) ≈ G(Ek) + G′(Ek)(E − Ek) linearly by using G(Ek) from the numerical integration and G′(Ek) = fk. The acceptance probability from Eq. 23 becomes
A concrete prescription for a simulation procedure in an iterative way proceeds as follows: At the start of the simulation usually no estimates of
During the simulation we always use the current estimate for
As we will show in the next section, in the form presented the algorithm is able to simulate quite large systems. However, there also is a drawback. The estimate of the DoS is necessarily based on information that has been gathered only in regions of state space that already have been sampled. This can include states that represent rare events in the converged ensemble, e.g., configurations that correspond to a supercritical gas. If the “correct” state—the condensate or droplet in the example—has not been found yet, then the estimates of microcanonical averages are dominated by the “wrong” data and it can take a very long time to correct this bias. Thus first-order phase transitions or rough energy landscapes can pose a challenge for the algorithm in its basic form. A more refined method of averaging than Eq. 25 which attributes higher weight to later measurements might turn out to be a solution for this problem.
4 Lennard-Jones particles
Clusters of Lennard-Jones particles and their morphology at low temperatures have been under study for a long time. Modeling noble gas atoms, Lennard-Jones particles are an interesting object of inquiry in their own right and they provide challenging benchmark systems for numerical optimization since their energy landscape contains numerous minima belonging to competing geometric structures. For small sizes, the ground states have been determined some time ago [14–16], and the behavior is well understood. If the number of atoms is a few thousands or less, the low-temperature phase is dominated by icosahedral geometry [17]. In many cases, there are solid-solid transitions [18] where the outer layer of the cluster changes from a so-called anti-Mackay shape that maximizes entropy to a Mackay structure minimizing energy. In some rare cases N = 38, 75, 76, 77, 98, 102, 103, 104, … non-icosahedral states are occupied at a very low temperature leading to solid-solid transitions that can be extremely challenging to investigate by means of MC simulations [19].
We consider N particles in three-dimensional space which interact pairwise through a 12–6 Lennard-Jones potential
With this parametrization, the potential has its minimum at r0 = 1. The particles are freely mobile within a cubic volume of linear extension L and we label their positions as x ∈ [0,L]3. The Hamiltonian reads
One finds that
and calculating or refreshing
is, therefore, somewhat cumbersome. Thankfully,
is simpler.
We performed a simulation of N = 100 particles confined in a steric cube with L = 5r0. The ground-state energy of this system is Eg = −557.039820 [14] and we restrict the energy to −520 < E < 0. The energy as a function of simulation time in units of N single-atom displacement moves can be seen in Figure 1. It is apparent that the simulation is able to reach all energies in the interval within a relatively short time. The early wedge-shaped blocks at low energy indicate that the averages are not converged yet and balance is established by repeatedly transitioning in and out of the low-energy state. Figure 2 shows the microcanonical averages
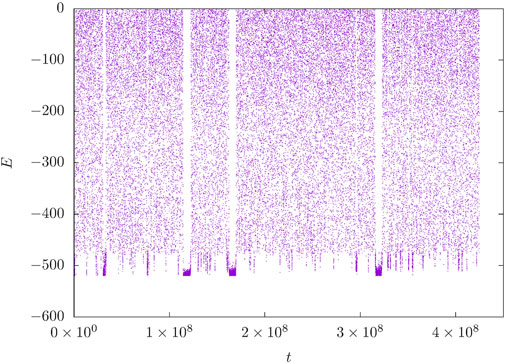
FIGURE 1. Time series of the energy E throughout a simulation of N = 100 Lennard-Jones particles. The energy was restricted to E > − 520.
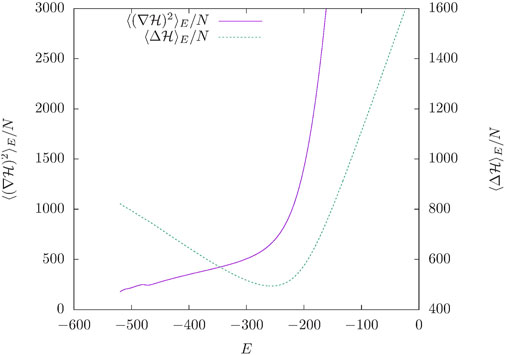
FIGURE 2. The microcanonical averages
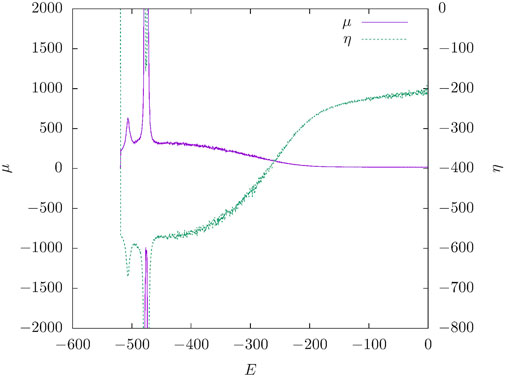
FIGURE 3. The integration parameters μ and η from the same simulation as the data in Figure 1.
5 O(n) spin model
The O(n) spin model is the generalization of the Ising (n = 1), XY (n = 2), and Heisenberg (n = 3) spin models. In this model spins
where the sum runs over all lattice bonds and J is the spin-spin interaction strength. To evaluate
where hk is the local field
and nb(k) the set of neighbors of spin σk. In the following, we set J = 1 and refrain from displaying it in the formulae. This is equivalent to assuming that ek, hk, and E are measured in units of J. It is convenient to divide by |σk| in Eq. 40 and for the moment to relax the n-sphere constraint to |σk| ≠ 1 since this allows one to use the one-particle gradient
and since hk − (hkσk)σk, (hkσk)σk, and hk form a right-angled triangle it follows 3
If the system is homogeneous, i.e., if all spins are equivalent we can drop the index k, and if the total number of spins is given by N it is
Next, we calculate that
and noting that ⟨e⟩E = 2E/N we find
Finally, we arrive at the surprisingly simple result
Unfortunately, this formula does not generalize to the Ising model n = 1 since on the one hand a continuous energy scale is implicitly required and on the other hand for the Ising model
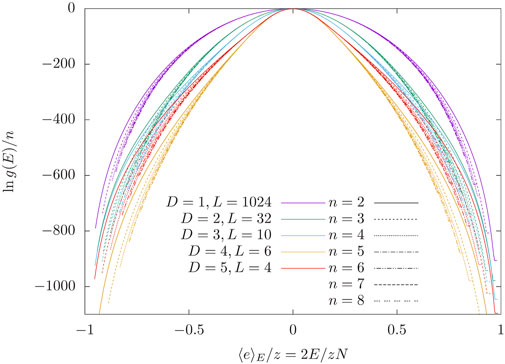
We now consider hypercubic lattices in D dimensions with linear extension L, N = LD spins, and periodic boundary conditions. For these lattices, the number of neighbors of any site (spin), the so-called coordination number, is z = 2D. During the simulation, we use N bins and integrate after every 103N individual spin updates. The single concern for selecting this value was to choose it large enough to not slow down the simulation by the computational effort of integrating. Proposed values for spins are selected randomly and independently of the current value. They are drawn using the rejection method for n = 2, Marsaglia’s methods [21] for n = 3, 4 and our own technique [22] for n ≥ 5. Time series of the energy per bond 2E/zN for different values of D and n and about N ≈ 103 spins are shown in Figure 4. For these cases, the simulation is able to cover most of the available energy interval within about 107 sweeps. We point out that for all simulations shown the ratio between the maximum of the DoS and the minimal value reached is between 10780 and 102000. Of course, such values can also be achieved with established state-of-the-art flat-histogram methods, but it is satisfying that this is possible with this method as well since it implies that the integration is done with adequate accuracy. The simulations fall a little bit short of the extremal energies Emax = −Emin = ND. We suspect that one reason is the comparatively large bin width which can become problematic if G or its derivative becomes very steep. From the measured densities of states
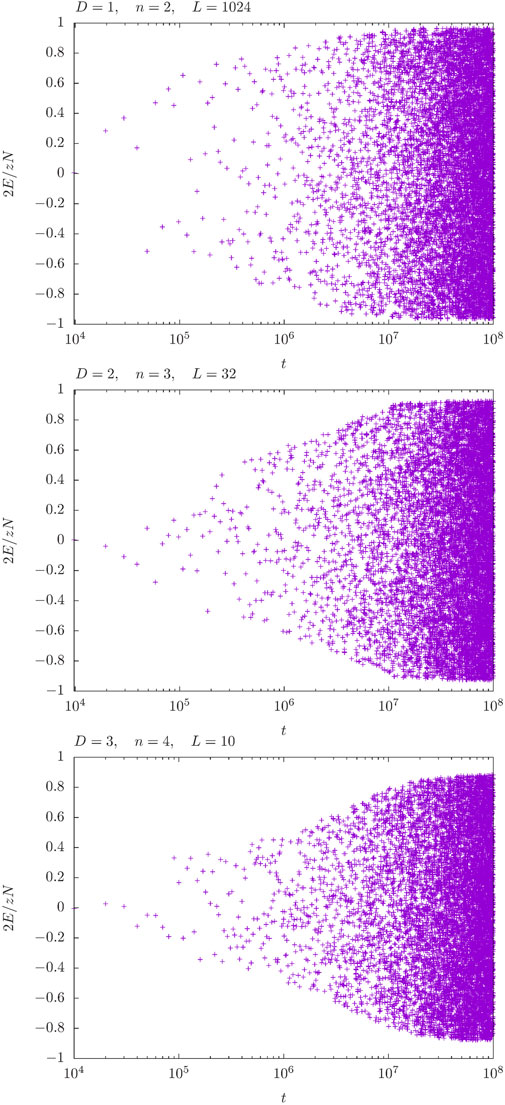
FIGURE 4. Time series of the energy per bond 2E/zN throughout simulations of N ≈ 1000 spins for different values of D and n. The time t is measured in units of N updates.
We find that for large enough systems
and
where from any spin σ* the spins σ|, σ‖, and σ⌞ are reached by one bond, two parallel bonds and two non-parallel bonds, respectively. This allows one to show that in one dimension
which is in very good agreement with our data and would be indistinguishable from the graphs for D = 1 in Figure 6. For the other values of D all curves for different n in Figure 6 also are very close to identical. Separate simulations for D = 2, 3 at energies close to the transition revealed that in the thermodynamic limit, the difference in
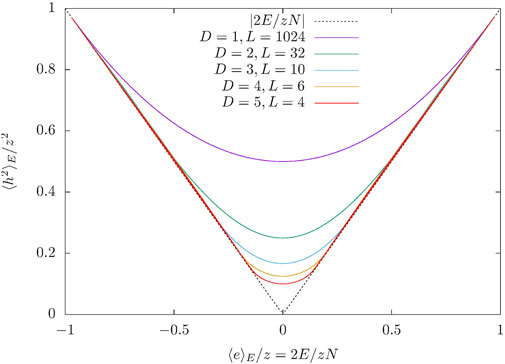
FIGURE 6. Microcanonical average
The situation is different for
with additional corrections. Here, fD(x) is a function that can easily be calculated in D = 1 dimension. We find
However, it appears that this function is also valid for D > 1 and we are led to believe by Figure 7B that the next correction is of the order z/n1/D. This is of course a somewhat speculative heuristic analysis and even though the systems are of medium size N ≈ 103 the linear extension of the lattices for D > 2 is small.
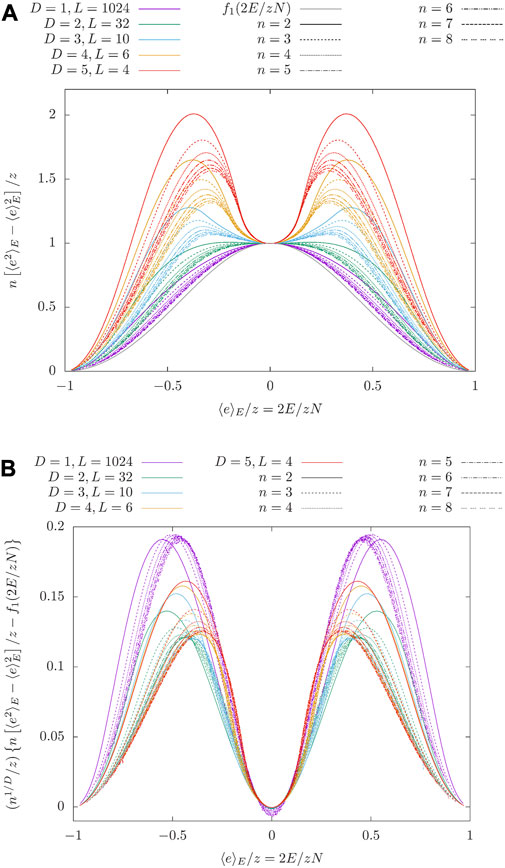
FIGURE 7. (A) The difference of the measured microcanonical average of
Finally we applied the method to the Heisenberg model on a triangular lattice with 1024 spins again with 1000 bins. Now the system experiences frustration at positive energies or negative temperatures which for J = 1 correspond to the antiferromagnet that for this lattice type has a maximal energy 2Emax/zN = 0.5. Again the algorithm is able to explore most of the energy range without getting trapped and the time series (not shown here) looks very similar to the previous cases. In Figure 8 the resulting data for
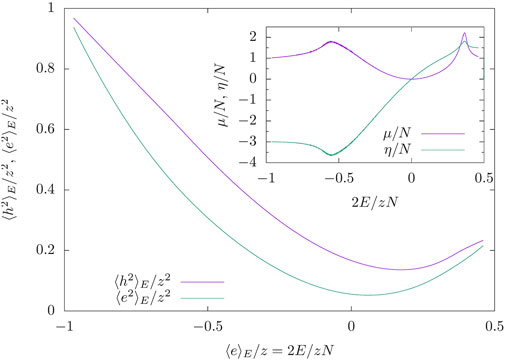
FIGURE 8. Microcanonical averages
6 Conclusion
In this study, we reviewed how the density of states of a system can be calculated via the inverse microcanonical temperature, i.e., the derivative of the logarithmic density of states, and how the latter can be obtained by means of microcanonical averages. We then introduced an alternative method that avoids mixed derivatives of the Hamiltonian, such that instead of the Hessian only the Laplacian and the gradient are required thus reducing computational demands. Since the ratio of Laplacian and squared gradient needs to be integrated, preferably with high accuracy, we devised a simple method for numerical integration adapted to the mathematical properties of that function.
Once the density of states can be calculated with sufficient accuracy and precision it can be used to verify the results of established histogram-based methods or—as shown in this study—to design a novel flat-distribution Monte Carlo method. This method is similar to the multicanonical method, the Wang-Landau method, or Statistical Temperature MC with the important difference that the information required to bias the ensemble towards a flat distribution is not indirectly obtained through the distribution of energy values but directly measured from the gradient and curvature of the Hamiltonian at the surfaces of constant energy.
The simulations we conducted are intended to be a proof-of-concept and we did not focus on optimizing the algorithm. We deem it likely that improvements can be made in various ways just as there are various histogram-based methods. Even hybrid strategies are conceivable. We observe that the algorithm is able to produce flat histograms on intervals of energy over which the density of states differs by hundreds to thousands of orders of magnitude, which in turn is convincing evidence that our formula for the density of states is correct and that our method for numerical integration works well for this particular type of function.
We applied the method first to a system of one hundred interacting Lennard-Jones particles. In order to ensure a stable simulation and converging microcanonical averages we had to exclude the lowest part of the energy spectrum. Nevertheless, even in the current basic form, the algorithm was able to cover all three phases—gaseous, liquid droplet, and frozen crystal-like—and also managed to map the low-temperature structural transition of the surface atoms. It turned out that the auxiliary data that are produced during the integration can be used to identify the transitions and the energies at which they occur.
Second, we considered the O(n) vector-spin model. After deriving expressions for the Laplacian and gradient of the Hamiltonian it became clear that only the average squared spin energy and the average of the square of a spin’s local field are required to calculate the density of states. Both of these can easily be measured during the simulation. We conducted a number of simulations for various spin and lattice dimensions and system sizes of up to about a thousand spins. In each case, it was easily possible to sample most of the state space. This was even true for the case of a system with frustration: The Heisenberg model on a triangular lattice. We found that the average squared local field depends on D but surprisingly only very little on n. The defining condition of the microcanonical ensemble is of course the system’s fixed total energy which translates to a known value for the nearest-neighbor spin-spin correlation. This in turn is closely related to the quantities needed to calculate the density of states: The squared local field comprises next-nearest-neighbor spin-spin correlations and the squared local energy is the second moment of nearest-neighbor spin products. A more rigorous theoretical analysis of the mutual dependencies of these quantities for the O(n) spin model would be of great interest.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
SS developed the method and performed the simulations. WJ and SS reviewed literature compiled and reviewed the manuscript. All authors contributed to the article and approved the submitted version.
Funding
The project was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the Collaborative Research Centre under Grant No. 189 853 844–SFB/TRR 102 (project B04).
Acknowledgments
SS thanks Franziska Facius for their hospitality.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Here, we assume that the potentials are not uncommonly complicated.
2In each iteration step we perform 1000 N moves, where N is the number of atoms or spins, respectively.
3In the case of the Heisenberg model (n = 3) an alternative expression is
References
1. Rugh HH. Dynamical approach to temperature. Phys Rev Lett (1997) 78:772–4. doi:10.1103/PhysRevLett.78.772
2. Gilat G. Calculation of derivatives of spectral functions in solids. Solid State Commun (1974) 14:263–5. doi:10.1016/0038-1098(74)90849-7
3. Butler BD, Ayton G, Jepps OG, Evans DJ. Configurational temperature: Verification of Monte Carlo simulations. J Chem Phys (1998) 109:6519–22. doi:10.1063/1.477301
4. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J Chem Phys (1953) 21:1087–92. doi:10.1063/1.1699114
5. Berg BA, Neuhaus T. Multicanonical algorithms for first order phase transitions. Phys Lett B (1991) 267:249–53. doi:10.1016/0370-2693(91)91256-U
6. Wang F, Landau DP. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys Rev Lett (2001) 86:2050–3. doi:10.1103/PhysRevLett.86.2050
7. Kim J, Straub JE, Keyes T. Statistical-temperature Monte Carlo and molecular dynamics algorithms. Phys Rev Lett (2006) 97:050601. doi:10.1103/PhysRevLett.97.050601
8. Janke W. Histograms and all that. In: B Dünweg, DP Landau, and AI Milchev, editors. Computer simulations of surfaces and interfaces, NATO science series, II. Mathematics, physics and chemistry. Dordrecht: Kluwer (2003). p. 137–57.
9. Ferrenberg AM, Swendsen RH. Optimized Monte Carlo data analysis. Phys Rev Lett (1989) 63:1195–8. doi:10.1103/PhysRevLett.63.1195
10. Giardina C, Livi R. Ergodic properties of microcanonical observables. J Stat Phys (1998) 91:1027–45. doi:10.1023/A:1023036101468
11. Nurdin WB, Schotte K-D. Dynamical temperature for spin systems. Phys Rev E (2000) 61:3579–82. doi:10.1103/PhysRevE.61.3579
12. Nurdin WB, Schotte K-D. Dynamical temperature study for classical planar spin systems. Physica A: Stat Mech its Appl (2002) 308:209–26. doi:10.1016/S0378-4371(02)00558-7
13. Gutiérrez G, Davis S, Palma G. Configurational temperature in constrained systems: The case of spin dynamics. J Phys A: Math Theor (2018) 51:455003. doi:10.1088/1751-8121/aae163
14. Northby JA. Structure and binding of Lennard-Jones clusters: 13 ≤ n ≤ 147. J Chem Phys (1987) 87:6166–77. doi:10.1063/1.453492
15. Wales DJ, Doye JPK. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J Phys Chem A (1997) 101:5111–6. doi:10.1021/jp970984n
16. Xiang Y, Jiang H, Cai W, Shao X. An efficient method based on lattice construction and the genetic algorithm for optimization of large Lennard-Jones clusters. J Phys Chem A (2004) 108:3586–92. doi:10.1021/jp037780t
17. Mackay AL. A dense non-crystallographic packing of equal spheres. Acta Crystallogr (1962) 15:916–8. doi:10.1107/S0365110X6200239X
18. Frantsuzov PA, Mandelshtam VA. Size-temperature phase diagram for small Lennard-Jones clusters. Phys Rev E (2005) 72:037102. doi:10.1103/PhysRevE.72.037102
19. Schnabel S, Janke W, Bachmann M. Advanced multicanonical Monte Carlo methods for efficient simulations of nucleation processes of polymers. J Comput Phys (2011) 230:4454–65. doi:10.1016/j.jcp.2011.02.018
20. Schnabel S, Seaton DT, Landau DP, Bachmann M. Microcanonical entropy inflection points: Key to systematic understanding of transitions in finite systems. Phys Rev E (2011) 84:011127. doi:10.1103/PhysRevE.84.011127
21. Marsaglia G. Choosing a point from the surface of a sphere. Ann Math Stat (1972) 43:645–6. doi:10.1214/aoms/1177692644
22. Schnabel S, Janke W. A simple algorithm for uniform sampling on the surface of a hypersphere (2022). arXiv preprint arXiv:2204.14004.
23. Nerattini R, Trombettoni A, Casetti L. Critical energy density of O(n) models in d = 3. J Stat Mech Theor Exp (2014) 2014:P12001. doi:10.1088/1742-5468/2014/12/P12001
Appendix
Calculation of ⟨e2⟩ for D = 1
For D = 1 and large N the spin products σk−1σk and σkσk+1 belonging to adjacent bonds are uncorrelated. The average of one product is given by
To calculate the second moment
we consider the (reduced) O(
with s = σkσk+1 and
where Ik are modified Bessel functions. It is
and
leading for example with n = 3 to
and
For general n (and D = 1) the second moment of e is given by
which with Eqs 67, 68 approaches in the limit of large n the closed form expressions Eqs 53, 54 of the main text.
Keywords: density of states, microcanonical analysis, microcanonical temperature, spin temperature, Monte Carlo method, flat histogram Monte Carlo, Markov chain Monte Carlo methods, vector spin model
Citation: Schnabel S and Janke W (2023) Surveying an energy landscape. Front. Phys. 11:1218107. doi: 10.3389/fphy.2023.1218107
Received: 06 May 2023; Accepted: 23 August 2023;
Published: 05 October 2023.
Edited by:
Jevgenijs Kaupužs, Liepaja University, LatviaReviewed by:
Omar Abu Arqub, Al-Balqa Applied University, JordanMilan Žukovič, University of Pavol Jozef Šafárik, Slovakia
Copyright © 2023 Schnabel and Janke. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefan Schnabel, c3RlZmFuLnNjaG5hYmVsQGl0cC51bmktbGVpcHppZy5kZQ==
 Stefan Schnabel
Stefan Schnabel Wolfhard Janke
Wolfhard Janke