Ground-state cooling in cavity optomechanical systems

The development of quantum optomechanics enables the manipulation of the quantum state of a macroscopic object and the conversion of frequency in different domains in quantum information processing, which prompts the process of quantum network and quantum computing. However, to enter the regime of quantum optomechanics, it’s necessary to prepare a mechanical object in its ground state. In this review, we briefly introduce the process of ground-state cooling in cavity optomechanical system. We first elucidate the theory of optomechanical cooling from both the classical and quantum perspective. Then we review experimental process about ground-state cooling in cavity optomechanical systems in these years, which includes the active feedback cooling and intrinsic optomechanical cooling. We selectively introduce the apparatus, samples and final cooling performance of some remarkable experiments. Finally, theoretical discussions on novel cooling approach will be reviewed, including cooling beyond resolved-sideband regime and multimode cooling, which may serve as a guidance for future experiment design.

1 Introduction

The area of optomechanics can be dated back to as early as 17th century, when Kepler noted that the dust tails of comets always point away from the sun. Kepler attributed this phenomenon to the existence of the radiation pressure force, which is a kind of action that light exerts on the object. Radiation pressure force, also dubbed as scattering force, forms the cornerstone of the optomechanical interaction. A strong evidence for its existence is the fact that laser could be utilized to trap and control atoms [1], which is known as “optical tweezer” that plays an important role in manipulating small objects like cells and bacteria in medicine. Besides the manipulation of atoms, laser could also be utilized to cool the atom to its motional ground state (see [2]; [3]) and this technology has become the base of current ultracold atom experiments.

Inspired by the remarkable achievement in laser cooling in atom systems, the idea of using radiation pressure to cool a larger object arose naturally. By bringing a mechanical resonator into quantum regime, we arrive at the region of quantum optomechanics, which is an emerging area that attracts extensive attention for both its rich physics content and wide range of applications. By preparing an optomechanical system in the quantum regime, it is possible to observe or even manipulate the quantum state of a macroscopic object, which offers a different view of quantum mechanics since former related experiments were all performed in extremely tiny systems. Quantum optomechanics offers us the possibility to create non-classical correlations (quantum entanglement) between mechanical modes and optical modes [4] and [5] or between two mechanical modes [6]. Moreover, due to its frequency being in a wide range, the mechanical mode is viewed as a perfect candidate for a quantum transducer between the microwave domain and the optical domain, which makes it an important constituent for quantum information processing network (see [7]; [8]). For example, an optomechanical device can serve as an interface between the solid superconducting qubits and the flying photonic qubits. Another important application of quantum optomechanics is quantum precision measurement, where squeezed light can be harnessed to improve the measurement precision even near the standard quantum limit (see [9]; [10]).

However, all fantastic applications about quantum mechanics mentioned above are all based on the prerequisite that the mechanical resonator is in its quantum ground-state. A macroscopic mechanical resonator is usually surrounded by complex thermal bath, which makes it hard to stay in its quantum ground state. Besides, the radiation pressure between the optical field and a mechanical resonator is generally weak, which is insufficient to bring a mechanical resonator to its quantum ground state. Thanks to the pioneered work of Braginsky (see [11]; [12]), the field of cavity optomechanics has achieved prominent enhancement of light-matter interaction by fabricating a high-finesse optical cavity. Various cavity optomechanics systems have been shown in experiments, including Fabry-Perot cavities [13], whispering-gallery mode cavities [14], photonic crystal cavities [15], microwave circuits [16], membranes [17], levitated particles [18] and so on. The structures listed above and references attached to them are not adequate, for more discussion on cavity optomechanics one can refer to previous reviews [19], [20], [21], [22], [23].

With the rapid development in cavity optomechanics and the implementation of cryogenic technology, ground-state cooling of mechanical modes has become possible, which paved the way to further manipulation of the quantum state of macroscopic object. So, the importance of preparing optomechanical systems in ground state is self-evident. Although there is a remarkable review about optomechanical cooling published [24], we would still like to complement the progress in recent years here. In this review, we briefly introduce the process of the ground-state cooling of cavity optomechanical system. In Section 2, we introduce the basic theory of the optomechanical cooling, including the classical version and the quantum version. In Section 3, we introduce the experimental process of ground-state cooling, including the active feedback cooling and the intrinsic optomechanical cooling. In Section 4, we introduce more theoretical discussions about ground-state cooling of optomechanical cooling, including cooling beyond resolved-sideband regime and multimode cooling. Finally, we make a summary and outlook.

2 Basic theory of optomechanical cooling

In this section, we provide the basic theory of optomechanical cooling, which can be divided into the classical version and the quantum version. The former helps us understand the picture of the cooling process while the latter gives a more strict description in the cooling limit.

2.1 Classical theory of optomechanical cooling

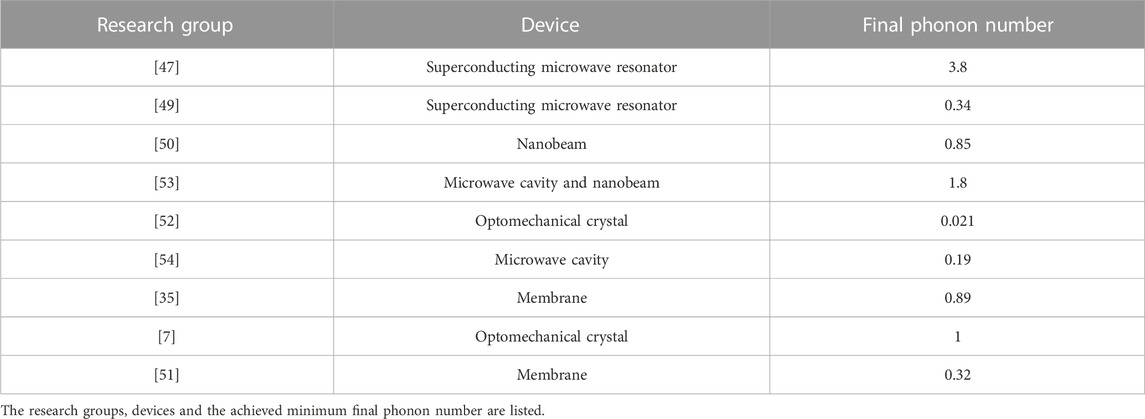
To understand why the radiation pressure can be utilized to cool a mechanical resonator, let’s start from an intuitive classical version of view. A typical optomechanical system can be modeled as a FP cavity shown in Figure 1. The FP cavity consists of two mirrors, one of which is fixed and the other can oscillate due to its connection with a spring. Since the radiation pressure will push the right mirror in Figure 1 to oscillate, the cavity length of the FP cavity varies as well. Different cavity length corresponds to different optical resonant frequency, so the optical resonant frequency is modulated by the mechanical mode, which causes the rebuilding of the cavity optical field during the oscillation of the mirror. However, the rebuilding of the cavity optical field is not instantaneous but requires some time due to the finite lifetime of the photon in the cavity. Thus, the radiation force is proportional to the velocity of the moving mirror, which behaves like a viscous force and causes extra damping γ_OM to the mechanical mode. The resulting effective temperature is

$T_{\mathit{eff}}=\frac{\gamma T}{\gamma +{\gamma }_{OM}}(1)$

where T is the thermal bath temperature and γ is the intrinsic mechanical dissipation rate. From 1 it seems like there is no cooling limit as long as γ_OM is strong enough, which corresponds to the cooling laser power. However, when the effective temperature reaches a sufficiently low level, the unavoidable quantum shot noise begins manifesting, which prohibits the realization of arbitrary low effective temperature. For the discussion of the optomechanical cooling in this region, we have to take a quantum point of view.

FIGURE 1

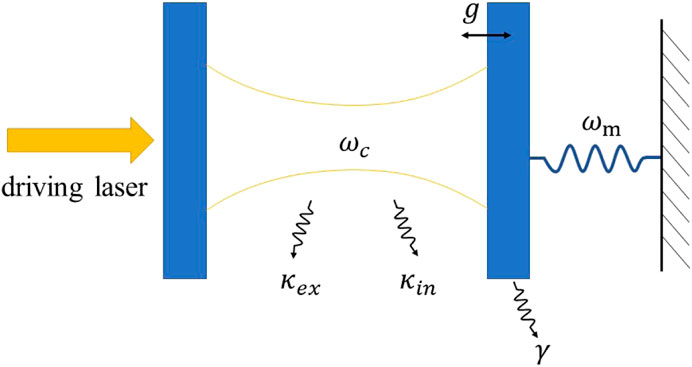
FIGURE 1. A typical optomechanical can be viewed as a FP cavity. The left mirror is fixed while the right mirror is movable with an oscillation frequency ω_m, which can be viewed as a mechanical harmonic mode. The light field in FP cavity can be viewed as an harmonic oscillator with a frequency ω_c, namely, the optical mode. Both the optical and mechanical mode will decay due to its coupling to the environment through decay channels. The mechanical mode decays with a rate γ. The optical mode’s decay rate can be distinguished as the extrinsic decay rate κ_ex and the intrinsic decay rate κ_in which corresponds to the detected and undetected channels, respectively. The optical mode and the mechanical mode couples each other with vacuum optomechanical strength g. A driving laser is input from the left side.

2.2 Quantum theory of optomechanical cooling

Quantum theory for optomechanical cooling has been well discussed in [25], [26] and [27]. Here we give a concise discussion. Similar to the classical version, a typical optomechanical system can be modeled as a FP cavity shown in Figure 1. But now we use operator to describe the optomechanical system, the Hamiltonian of which is

$H={\omega }_c{a}^{†}a+{\omega }_m{b}^{†}b+g{a}^{†}a\left(b^{†}+b\right)+\left({\mathrm{\Omega }}^{*}{e}^{i{\omega }_{L}t}a+\mathrm{\Omega }{e}^{-i{\omega }_{L}t}{a}^{†}\right).(2)$

From the first two terms one can see that we have considered both the optical and the mechanical mode as quantum harmonic oscillators with frequency ω_c and ω_m, where a(a^†) is the bosonic annihilation (creation) operator for the optical mode and b (b^†) is the bosonic annihilation (creation) operator for the mechanical mode. Now we explain the origin of the third term, i.e., the optomechanical interaction term. Similar to the classical description, the radiation pressure will cause the right mirror of Figure 1 to oscillate, which modulates the cavity length as a result. The change of the cavity length leads to the change of the resonance frequency. We can use the Taylor expansion to describe the change of the cavity resonance frequency as ω_c(x) = ω_c + x∂ω_c(x)/∂x + O(x). So the Hamiltonian for the optical mode becomes (ω_c + x∂ω_c(x)/∂x)a^†a, which indicates that (x∂ω_c(x)/∂x)a^†a is an emerging interaction term due to optomechanical coupling. Generally, we define G′ = ∂ω_c(x)/∂x as the frequency shift per displacement. Since the mechanical mode has been viewed as a quantum harmonic oscillator, the displacement operator x can be expressed as x = x_ZPF(b^† + b), where the zero-point fluctuation x_ZPF is defined as $x_{\mathit{ZPF}}=\sqrt{\hslash /2m_{\mathit{eff}}{\omega }_m}$ with m_eff denoting the effective mass of the mechanical mode. So the optomechanical interaction term can be rewritten as ga^†a(b^† + b), where the vacuum optomechanical coupling strength g is defined as g = G′x_ZPF. We note that g is more fundamental than G′ since it describes the interaction strength between a single photon and a single phonon. However, G′ may be affected by the specific geometric structure of the optomechanical system. The fourth term ${\mathrm{\Omega }}^{*}{e}^{i{\omega }_{L}t}a+\mathrm{\Omega }{e}^{-i{\omega }_{L}t}{a}^{†}$ is the driving term, where ω_L is the driving laser frequency and Ω is the driving laser amplitude. We note that Ω is defined as $\mathrm{\Omega }=\sqrt{{\kappa }_{ex}P/(\hslash {\omega }_L)}{e}^{i\varphi }$, where κ_ex denotes coupling rate, P denotes the driving laser power and ϕ denotes the initial phase of the driving laser. Under the rotation frame with ω_L the Hamiltonian becomes

$H=-\mathrm{\Delta }{a}^{†}a+{\omega }_m{b}^{†}b+g{a}^{†}a\left(b^{†}+b\right)+\left({\mathrm{\Omega }}^{*}a+\mathrm{\Omega }{a}^{†}\right),(3)$

where the detuning is defined as Δ = ω_L − ω_c. The quantum Langevin equations are then given by

$\dot{a}=\left(i\mathrm{\Delta }-\frac{\kappa }{2}\right)a-iga\left(b^{†}+b\right)-i\mathrm{\Omega }-\sqrt{{\kappa }_{ex}}{a}_{in,ex}-\sqrt{{\kappa }_{in}}{a}_{in,in},(4)$

$\dot{b}=\left(-i{\omega }_m-\frac{\gamma }{2}\right)b-ig{a}^{†}a-\sqrt{\gamma }{b}_{in}.(5)$

We have distinguished between the extrinsic (detected) and the intrinsic (undetected) dissipation channels here by the noise operator a_in,ex and a_in,in, with extrinsic dissipation rate κ_ex and intrinsic dissipation rate κ_in, respectively. The total dissipation rate κ is defined as κ = κ_ex + κ_in. The noise operator b_in is associated with the mechanical dissipation and γ is the corresponding dissipation rate.

Now we take the standard linearization approach to handle the quantum Langevin equations above. The so-called linearization is to split the classic coherent part $<a>=\alpha$ and the quantum fluctuation part δa of an operator a, or say doing the transformation

$\begin{array}{c}\hfill a\to \alpha +\delta a,\\ \hfill b\to \beta +\delta b.\end{array}(6)$

The classic part and the quantum fluctuation part separately satisfies the equations

$\dot{\alpha }=\left(i{\mathrm{\Delta }}^{\prime }-\frac{\kappa }{2}\right)\alpha -i\mathrm{\Omega },(7)$

$\dot{\beta }=\left(-i{\omega }_m-\frac{\gamma }{2}\right)\beta -ig|\alpha {|}^2,(8)$

$\delta \dot{a}=\left(i{\mathrm{\Delta }}^{\prime }-\frac{\kappa }{2}\right)\delta a-ig\alpha \left(\delta b+\delta b^{†}\right)-\sqrt{{\kappa }_{ex}}{a}_{in,ex}-\sqrt{{\kappa }_{in}}{a}_{in,in},(9)$

$\delta \dot{b}=\left(-i{\omega }_m-\frac{\gamma }{2}\right)\delta b-ig\left({\alpha }^{*}\delta a+\alpha \delta a^{†}\right)-\sqrt{\gamma }{b}_{in},(10)$

where the effective detuning Δ′ is defined as Δ′ = Δ − g(β + β*). The steady-state value for α can be obtained by letting the left side of Eq. 7 equals 0, which means that α = iΩ/(iΔ′ − κ/2). In the weak-coupling regime we can assume that Δ′ = Δ. And without losing the generality we let α be real by choosing a proper phase of Ω. To make the form simpler we replace δa, δb with a, b. The quantum fluctuation part becomes

$\dot{a}=\left(i\mathrm{\Delta }-\frac{\kappa }{2}\right)a-iG\left(b+b^{†}\right)-\sqrt{{\kappa }_{ex}}{a}_{in,ex}-\sqrt{{\kappa }_{in}}{a}_{in,in},(11)$

$\dot{b}=\left(-i{\omega }_m-\frac{\gamma }{2}\right)b-iG\left(a+a^{†}\right)-\sqrt{\gamma }{b}_{in},(12)$

where G = gα is the optomechanical coupling strength enhanced by the intracavity field. The above time-evolution equations are easier to handle in the frequency domain by doing the Fourier transformation

$a\left(\omega \right)=\frac{-iG\left(b\left(\omega \right)+b^{†}\left(\omega \right)\right)-\sqrt{{\kappa }_{ex}}{a}_{in,ex}\left(\omega \right)-\sqrt{{\kappa }_{in}}{a}_{in,in}\left(\omega \right)}{-i\left(\omega +\mathrm{\Delta }\right)+\frac{\kappa }{2}},(13)$

$b\left(\omega \right)=\frac{-iG\left(a\left(\omega \right)+a^{†}\left(\omega \right)\right)-\sqrt{\gamma }{b}_{in}\left(\omega \right)}{i\left({\omega }_m-\omega \right)+\frac{\gamma }{2}}.(14)$

From the expression above one can see that the mechanical mode b(ω) has a much narrower linewidth than the optical mode a(ω) since for general optomechanical system we have γ ≪ κ. By substituting Eq. 13 into Eq. 14 we get

$\begin{array}{cc}\hfill b\left(\omega \right)& =\frac{-\sqrt{\gamma }{b}_{in}\left(\omega \right)}{i\left({\omega }_m-\omega \right)+\frac{\gamma }{2}}-\frac{iG}{i\left({\omega }_m-\omega \right)+\frac{\gamma }{2}}\left(\frac{-iGb\left(\omega \right)-\sqrt{{\kappa }_{ex}}{a}_{in,ex}\left(\omega \right)-\sqrt{{\kappa }_{in}}{a}_{in,in}\left(\omega \right)}{-i\left(\omega +\mathrm{\Delta }\right)+\frac{\kappa }{2}}\right.\hfill \\ \hfill & \left.+\frac{iGb\left(\omega \right)-\sqrt{{\kappa }_{ex}}{a}_{in,ex}^{†}\left(\omega \right)-\sqrt{{\kappa }_{in}}{a}_{in,in}^{†}\left(\omega \right)}{i\left(-\omega +\mathrm{\Delta }\right)+\frac{\kappa }{2}}\right),\hfill \end{array}(15)$

where we have used the property o^†(ω) = [o(−ω)]^† and dropped the b^†(ω) term since it’s sharply peaked around −ω_m. We can rearrange the above expression as

$\begin{array}{cc}\hfill b\left(\omega \right)& =\frac{-\sqrt{\gamma }{b}_{in}\left(\omega \right)}{i\left({\omega }_m^{\prime }-\omega \right)+\frac{\mathrm{\Gamma }}{2}}+\frac{iG}{i\left({\omega }_m^{\prime }-\omega \right)+\frac{\mathrm{\Gamma }}{2}}\left(\frac{\sqrt{{\kappa }_{ex}}{a}_{in,ex}\left(\omega \right)+\sqrt{{\kappa }_{in}}{a}_{in,in}\left(\omega \right)}{-i\left(\omega +\mathrm{\Delta }\right)+\frac{\kappa }{2}}\right.\hfill \\ \hfill & \left.+\frac{\sqrt{{\kappa }_{ex}}{a}_{in,ex}^{†}\left(\omega \right)+\sqrt{{\kappa }_{in}}{a}_{in,in}^{†}\left(\omega \right)}{i\left(-\omega +\mathrm{\Delta }\right)+\frac{\kappa }{2}}\right),\hfill \end{array}(16)$

where we have defined ${\omega }_m^{\prime }={\omega }_m+\delta {\omega }_m$ and Γ = γ + γ_OM. The frequency shift δω_m is named as optical spring effect, which comes as a result of the modification of the resonance frequency of the mechanical oscillator due to its coupling to the light field. In the Doppler regime (the cavity decay rate κ is much larger than the mechanical frequency ω_m, i.e., κ ≪ ω_m), one can show that different detuning corresponds to the stiffening (Δ > 0) or softening (Δ < 0) of the mechanical oscillator “spring.” The extra damping rate γ_OM are called optomechanical damping rate, which is caused by the retardation between the build-up of radiation pressure force and the mechanical motion of the cavity due to the finite cavity life time (proportional to 1/κ). Thus, the radiation pressure may act as a viscous force which damps the mechanical motion or a force that amplifies the mechanical motion, which corresponds to cooling or amplification, depending on the detuning for most cases. The optical spring shifted mechanical frequency δω_m and the optomechanical damping rate γ_OM have the form

$\delta {\omega }_m=\mathrm{I}\mathrm{m}\left\{|G{|}^2\left(\frac{1}{-\mathrm{i}\left({\omega }_{\mathrm{m}}+\mathrm{\Delta }\right)+\frac{\kappa }{2}}-\frac{1}{\mathrm{i}\left(\mathrm{\Delta }-{\omega }_{\mathrm{m}}\right)+\frac{\kappa }{2}}\right)\right\},(17)$

${\gamma }_{OM}=2\mathrm{R}\mathrm{e}\left\{|G{|}^2\left(\frac{1}{-\mathrm{i}\left({\omega }_{\mathrm{m}}+\mathrm{\Delta }\right)+\frac{\kappa }{2}}-\frac{1}{\mathrm{i}\left(\mathrm{\Delta }-{\omega }_{\mathrm{m}}\right)+\frac{\kappa }{2}}\right)\right\},(18)$

where we have let ω = ω_m in Eqs 17, 18 since both δω_m and γ_OM have a linewidth κ and can therefore be viewed as constants over the linewidth of mechanical mode. Since we are discussing in the weak coupling region, it’s safe to make the approximation ${\omega }_m^{\prime }={\omega }_m$. The noise operator satisfies the following relationship

$<a_{in}^{†}\left(\omega \right)a_{in}\left({\omega }^{\prime }\right)>=0,(19)$

$<a_{in}\left(\omega \right)a_{in}^{†}\left({\omega }^{\prime }\right)>=\delta \left(\omega +{\omega }^{\prime }\right),(20)$

$<b_{in}^{†}\left(\omega \right)b_{in}\left({\omega }^{\prime }\right)>=n_{th}\delta \left(\omega +{\omega }^{\prime }\right),(21)$

$<b_{in}\left(\omega \right)b_{in}^{†}\left({\omega }^{\prime }\right)>=\left(n_{th}+1\right)\delta \left(\omega +{\omega }^{\prime }\right),(22)$

with $n_{th}=1/(e^{\hslash {\omega }_m/k_{B}T}-1)$ being the thermal phonon equilibrium with the environment, k_B being the Boltzmann constant and T being the bath temperature. Now we come to the step of calculating the final steady phonon number, which is defined as n_f =< b^†(t)b(t) > and can be easier to handle in frequency domain

$<b^{†}\left(t\right)b\left(t\right)>=\frac{1}{2\pi }{\int }_{\infty }^{-\infty }d\omega {\int }_{\infty }^{-\infty }d{\omega }^{\prime }<e^{-i\omega t}{e}^{-i{\omega }^{\prime }t}{b}^{†}\left(\omega \right)b\left({\omega }^{\prime }\right)>,(23)$

$=\frac{1}{2\pi }{\int }_{\infty }^{-\infty }d\omega \frac{\mathrm{\Gamma }}{{\left({\omega }_m+\omega \right)}^2+{\left(\frac{\mathrm{\Gamma }}{2}\right)}^2}\left(\frac{\gamma n_{th}}{\mathrm{\Gamma }}+\frac{|G{|}^2\kappa }{\mathrm{\Gamma }}\frac{1}{{\left(\mathrm{\Delta }+\omega \right)}^2+{\left(\frac{\kappa }{2}\right)}^2}\right),(24)$

$=\frac{\gamma n_{th}}{\mathrm{\Gamma }}+\frac{|G{|}^2\kappa }{\mathrm{\Gamma }}\frac{1}{{\left(\mathrm{\Delta }-{\omega }_m\right)}^2+{\left(\frac{\kappa }{2}\right)}^2},(25)$

where we have let ω = −ω_m in the second term in the bracket of Eq. 24 because this term can be treated as a constant over the linewidth of the mechanical mode under the condition κ ≫Γ. We can rearrange the Eq. 25 in a more concise form

$n_f=\frac{\gamma n_{th}+{\gamma }_{OM}{n}_M^O}{\gamma +{\gamma }_{OM}},(26)$

with $n_M^O=\left[-{({\omega }_m+\mathrm{\Delta })}^2-{(\frac{\kappa }{2})}^2\right]/4{\omega }_m\mathrm{\Delta }$ denoting the quantum limited phonon number which indicates that we can view the input laser source as an effective thermal bath. In the resolved-sideband regime (κ ≪ ω_m) and the red-detuning regime (Δ = −ω_m), the final phonon number can be approximated as

$n_f=\frac{\gamma n_{th}}{\mathrm{\Gamma }}+\frac{{\gamma }_{OM}}{\mathrm{\Gamma }}{\left(\frac{\kappa }{4{\omega }_m}\right)}^2.(27)$

When the mechanical bath temperature is low enough (n_th ≪ 1), one can see that the final phonon number is far less 1 from Eq. 27 in both the resolved-sideband regime and the red-detuning regime, which indicates us that the ground-state cooling of the mechanical mode is achieved.

Another way to derive Eq. 26 is to calculate the noise spectrum of the radiation pressure force, which is defined as S_FF(ω) = ∫ < F(t)F(0) > e^iωtdt. The radiation pressure force has the form of F = −G(a + a^†)/x_ZPF, which can be derived from the linearized optomechanical interaction Hamiltonian H_int,lin = G(a + a^†)(b + b^†) = Fx. One can see that S_FF is asymmetric in frequency since F(t) and F(0) are operators that do not commute. By performing the Fourier transformation, one can show that S_FF(ω) has the form

$S_{FF}\left(\omega \right)=\frac{|G{|}^2\kappa }{x_{\mathit{ZPF}}}\frac{1}{{\left(\mathrm{\Delta }+\omega \right)}^2+{\left(\frac{\kappa }{2}\right)}^2}.(28)$

The positive frequency part of S_FF(ω) means the process that the environment absorbs energy from the mechanical oscillator, while the negative frequency part of it implies the process that the mechanical oscillator absorbs energy from the environment. By using Fermi’s Golden Rule one can show that ${\gamma }_{\downarrow }^{OM}=x_{\mathit{ZPF}}^2{S}_{FF}({\omega }_m)$ and ${\gamma }_{\uparrow }^{OM}=x_{\mathit{ZPF}}^2{S}_{FF}(-{\omega }_m)$ represent the rate for emitting and absorbing a phonon by the mechanical oscillator, respectively. So the optomechanical damping rate γ_OM can be expressed as

$\begin{array}{cc}\hfill {\gamma }_{OM}& ={\gamma }_{\downarrow }^{OM}-{\gamma }_{\uparrow }^{OM}\hfill \\ \hfill & =x_{\mathit{ZPF}}^2\left[S_{FF}\left({\omega }_m\right)-S_{FF}\left(-{\omega }_m\right)\right].\hfill \end{array}(29)$

The master equation for the density matrix ρ of the mechanical mode b is

$\dot{\rho }=\left[\left({\gamma }_{\downarrow }^{OM}+\gamma \left(n_{th}+1\right)\right)\mathcal{D}\left[b\right]+\left({\gamma }_{\uparrow }^{OM}+\gamma n_{th}\right)\mathcal{D}\left[b^{†}\right]\right]\rho ,(30)$

where the Lindblad operator is defined as

$\mathcal{D}\left[o\right]\rho =\frac{1}{2}\left(2o\rho o^{†}-o^{†}o\rho -\rho o^{†}o\right).(31)$

With the master equation above one can show that the mean phonon number $\bar{n}=<n>=\mathit{Tr}<b^{†}b\rho >$ satisfies

$\dot{\stackrel{̄}{n}}=\gamma n_{th}+{\gamma }_{\uparrow }^{OM}-\left(\gamma +{\gamma }_{OM}\right)n,(32)$

which implies that the final steady phonon number is

$n_f=\frac{\gamma n_{th}+{\gamma }_{OM}{n}_M^O}{\gamma +{\gamma }_{OM}}(33)$

with $n_M^O={\gamma }_{\uparrow }^{OM}/{\gamma }_{OM}$ being the quantum limited phonon number.

3 Experimental process

In this section, we introduce the experimental process of the ground-state cooling of optomechanical systems. There are two kinds of cooling approach, one is the active feedback cooling and the other one is the passive radiation pressure cooling (dubbed as optomechanical cooling in this review). In Section 3.1, we introduce the active feedback cooling, including a simple description of its implementation principle and some remarkable experimental outcomes of it. In Section 3.2, we discuss the development process of optomechanical cooling, including its physical picture, its performance in different experimental parameter regime and its performance combined with cryogenic pre-cooling.

3.1 Active feedback cooling

From the classical optomechanical cooling picture one can see that the radiation pressure force acts like a viscous force due to the retardation of the establishment of the cavity. Since the cavity readout reveals the mechanical displacement with high precision, one can utilize this readout to generate a feedback force which is proportional to the velocity of the mechanical oscillator, i.e., a force $F=-m_{\mathit{eff}}\delta \gamma \dot{x}$ with δγ denoting the extra damping rate caused by the feedback loop. The extra damping rate δγ can be positive or negative, corresponding to cooling or amplification of the mechanical mode, respectively. This cooling method is called active feedback cooling, or say cold damping, which was first suggested by [28]. The following experiments [29]; [30]; [31]; [32]; [33]; [34] have show its ability to cool a mechanical system to a low final effective temperature. In the work of [32], the researchers utilize the active feedback method to cool the fundamental mechanical mode of an ultrasoft silicon cantilever from a base temperature 2.2 K to the lowest temperature 2.9 ± 0.3 mK, which is shown in Figure 2. One can see that with the increase of the feedback gain g, the effective mode temperature T_mode decreases as long as g is not very strong. A strong feedback gain g may lead to the occurrence of noise “squashing.” In a recent experiment, [35] designed an electronic feedback loop to convert the position measurement to a force which cools the mechanical mode of a 20-nm-thick Si₃N₄ membrane to its quantum ground state with a lowest thermal occupation around 0.89. This admirable advancement was due to the improvement of the measurement efficiency, which was reported as strong as η = 59% in [35].

FIGURE 2

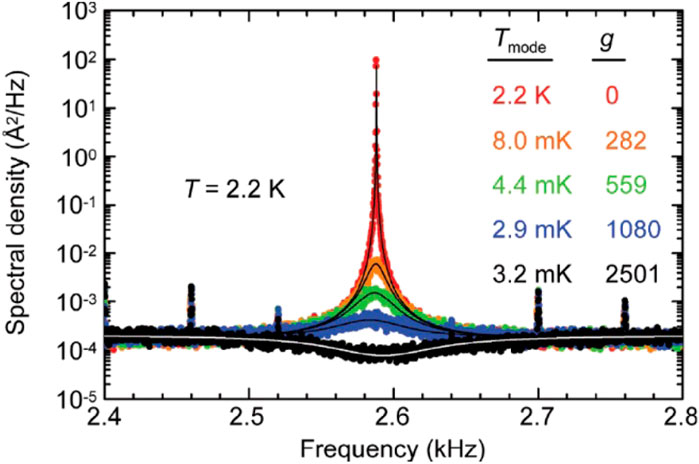
FIGURE 2. Active feedback cooling of a cantilever. The figure demonstrates the measured spectral density for different feedback gain g with base temperature 2.2 K. Reproduced with permission from [32]. Copyright 2007 American Physical Society.

3.2 Optomechanical cooling

Different from active feedback cooling, optomechanical cooling utilize the intrinsic radiation pressure force as the source of the feedback to damp the mechanical motion, which is dubbed as passive cooling. The process of optomechanical cooling can be understood in Figure 3B, in which the anti-Stokes process is demonstrated. During the anti-Stokes process, a driving laser photon with energy ℏω_L and a phonon with energy ℏω_m are converted into a cavity mode photon with energy ℏω_cav. On the contrary, for optomechanical amplification, a driving laser photon with energy ℏω_L is converted into a cavity mode photon with energy ℏω_cav and a phonon with energy ℏω_m, which corresponds to the Stokes process as shown in Figure 3A. Early demonstration of optomechanical cooling was performed as early as in 1970s by [12], who observed the modification of the damping rate of a pendulum placed in a microwave cavity. For optical domain, early experiments to realize dynamical back-action cooling were performed in systems like microtoroids [36] and micromirrors [37]; [38].

FIGURE 3

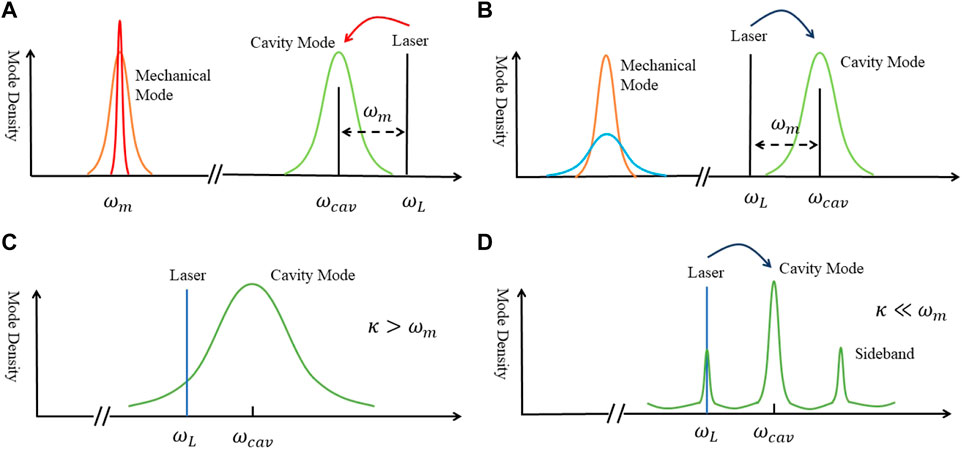
FIGURE 3. (A) Stokes process. A driving laser photon is converted into a cavity photon and a phonon, which causes the amplification of the mechanical motion. (B) Anti-Stokes process. A driving laser photon and a phonon are converted into a cavity photon, which corresponds to the cooling of the mechanical motion. (C) In the Doppler regime (κ > ω_m), the sidebands are hindered by the cavity mode, which limits the efficiency of the cooling. (D) In the resolved-sideband regime (κ ≪ ω_m), the sidebands are resolved and the difference between the rate of the anti-Stokes process and the Stokes process is large, which leads to efficient cooling.

Although these experiments showed great success in reducing the effective temperature of the mechanical mode, the quantum ground state is not achieved because they are operated in the Doppler regime (κ > ω_m), where the cooling rate γ_OM is limited since it is inversely proportional to the cavity decay rate κ (see [20]). However, this limitation can be overcome in the so-called resolved-sideband regime (ω_m ≪ κ), which can be clearly seen in Figure 3. We can define the rate for anti-Stokes process (Stokes process) as R_as(R_s), which is proportional to the density of states of its relative sideband. As a consequence, the cooling rate is proportional to (R_as − R_s). From Figure 3C we can see that two sidebands are hindered, which results in a small (R_as − R_s) and explains limited cooling rate in the unresolved-sideband regime. However, in Figure 3D, two sharp sidebands can be seen and one can show that (R_as − R_s) can obtain a large value, which permits the ground-state cooling (see [39]).

The experiments for resolved-sideband cooling has been performed both in the microwave regime and the optical domain. The first experiment for optical domain was conducted by [40], who achieved a cooling rate as strong as 1.5 MHz in a silica microtoroid optical cavity, which is three orders of magnitude larger than its intrinsic mechanical dissipation rate. Soon later, [41] achieved strong dynamical backaction by fabricating a novel double-disk whispering gallery mode cavity (shown in Figure 4), which lowered the threshold for mechanical oscillation. This strong dynamical backaction also facilitates efficient cooling with a temperature suppression of 14 dB. It’s notable that [41] used optical gradient force rather than the radiation pressure force (named as scattering force in some literature) to cool the mechanical mode. In addition to whispering gallery mode cavity, the resolved-sideband cooling was also successfully performed in other systems by achieving strong optomechanical coupling. By placing a dielectric membrane between two mirrors, [42] made optical elements and mechanical elements no longer compromises each other, which guaranteed a direct measurement of the mechanical mode. In this work, [42] not only cooled membrane to an effective temperature as low as 6.82 mK, but also paved the way to observing quantum jump of the mechanical mode. For microwave regime, [43] showed that the coupling between a superconducting microwave field and the mechanical motion is strong enough to cool the mechanical mode with a final phonon number of 140 quanta.

FIGURE 4

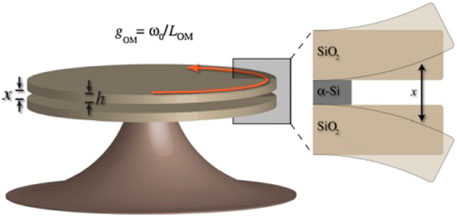
FIGURE 4. Schematic of a double-disk nano-optomechanical system. Two silica disks are separated by a sacrificial amorphous silicon with a nanoscale gap. The disks would vibrate due to its coupling to the optical gradient force, which leading to the oscillation of the disk spacing x. Reproduced with permission from [41]. Copyright 2009 American Physical Society.

The above discussions are all focused on increasing the optomechanical damping rate γ_OM and decreasing the dynamical backaction limited phonon number $n_M^O$ in Eq. 26 by endeavoring to achieve stronger optomechanical interaction or fabricating high-finesse microcavity. While lowering the thermal bath phonon number n_th should also not be ignored. With the development of cryogenics, the prominent reduction of the initial thermal occupancy phonon number n_th becomes possible, which is beneficial for achieving a small final phonon number. [44] have cooled a Si₃N₄ that carries a Bragg mirror down to the level of 30 quantum in a cryogenic ⁴He environment. Optomechanical cooling combined with Cryostat precooling is also performed in whispering gallery mode systems. With a precooled thermal bath of 1.4 K, [45] demonstrated that they could cool a mechanical breathing mode of a deformed microsphere down to 37 quanta through free-space evanescent excitation in a ⁴He cryostat. The lowest final phonon number was limited by the ultrasonic attenuation, which might be improved by placing the system in a ³He cryostat according to [45]. For the microtoroid system, [46] demonstrated a final phonon number of 63 can be achieved by optomechanical cooling combined with precooling in a ⁴He cryostat. [46] also compared their optical measurements to the previous nano-electromechanical counterparts and found that their imprecision-backaction was one order smaller than those in nano-electromechanical systems. [47] demonstrated the cooling of a superconducting microwave resonator (Nb-Al-SiN sample) from a initial phonon of 480 quanta to a lowest phonon around 3.8 quanta in a dilution refrigerator stabilized at T = 146 mK. [48] not only cooled a microtoroid resonator down to 9 quanta from an initial precooled atmosphere of 600 mK, but also utilized the two-level-system induced damping as a thermometry to determine the final effective temperature. One can see their cooling results in Figure 5, where the cooling factor of different laser power is shown.

FIGURE 5

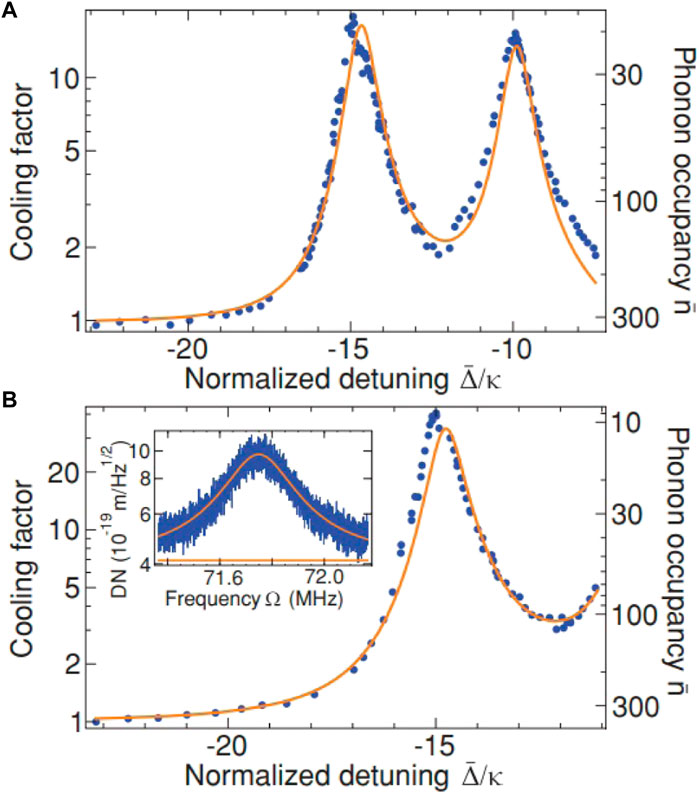
FIGURE 5. Cooling factor and phonon occupancy of the mechanical radial breathing mode versus laser detuning in different laser power. (A) P_in = 2 mW and (B) P_in = 4 mW. A minimum phonon number of n_f = 9 ± 1 can be achieved. Reproduced with permission from [48]. Copyright 2011 American Physical Society.

The work mentioned above is excellent, but they are still some distance from achieving quantum ground state since their final phonon number is still larger than 1, which is viewed as a landmark for a macroscopic object entering quantum regime since the probability of finding a system in the ground state is P = 1/(1 + n_f) with n_f being the final phonon number. Immediately following in 2011, two groups achieved final number less than 1. By embedding a micromechanical membrane into a superconducting microwave circuit, [49] achieved a strong electromechanical interaction between the microwave filed and a 10 MHz mechanical mode, which ensured a lowest phonon occupation of 0.34 from a beginning cryostat temperature 20 mK. It’s notable that [49] performed a near-Heisenberg measurement to extract the information of final phonon number, where they used a Josephson parametric amplifier to reduce the noise during the measurement. For optical regime, [50] demonstrated that they cooled a nanobeam mechanical resonator which is coupled to a laser with wavelength around 1,550 nm in a continuous-flow helium cryostat down to its quantum ground state by achieving a final phonon occupancy number around 0.85. This cooling was realized at an atmosphere temperature around 20 by placing the optomechanical devices into a continuous-flow helium cryostat K. As for the optomechanical devices, the nanobeam is periodical patterned based on a silicon-on-insulator chip. An introduction of imperfection of periodicity at the center of the beam will bound an optical mode and a mechanical mode at this location, which are coupled to each other through radiation pressure. A two-dimensional “cross” patterning acoustic radiation shield was also designed to reduce the mechanical dissipation. Similar to the former work, resolved-sideband regime was satisfied (κ/2π = 500 MHz, ω_m/2π = 3.68 GHz), which ensured the remarkable cooling effect with the help of efficient optomechanical coupling. Figure 6 demonstrates the main results of their experiment. Chan et al. determined the mechanical damping γ by sweeping a second probe laser to measure the electromagnetically induced transparency spectrum, which is shown in Figure 6A. By plotting the calibrated noise power spectral density, Chan et al. measured a minimum phonon number of 0.85 with an intracavity photon number n_c ≈ 2000 as shown in Figure 6B. Besides, Chan et al. analyzed the deviation of the measured phonon from the ideal cooling limit from the perspective of the optical absorption and the increase of the intrinsic mechanical damping, which is shown in Figures 6C, D. Optomechanical cooling also helps overcome the impediment to quantum electro-optic transduction. In 2022, Brubaker et al. achieved a maximum electro-optical transduction efficiency of 47% and minimum input-referred added noise of 3.2 photons in upconversion with the mechanical mode of the device sideband cooled to quantum ground state (see [51]). The transducer is made of a silicon nitride membrane whose vibrational mode is coupled to a microwave resonator and an optical resonator. The microwave resonator is a superconducting niobium titanium nitride LC circuit whose capacitance is modulated by the vibrating membrane. The optical resonator is a single-sided Fabry-Perot cavity with one of the cavity mirrors integrated into the silicon chip. Similarly, the light field of the optical resonator is also modulated by the mechanical motion of the membrane, such that both the microwave field and optical field can be utilized to cool the mechanical motion with their driving frequency (ω_e and ω_o) red-detuned by the mechanical frequency (ω_m). The cooling result of their work is shown in Figure 7. In Figure 7A, one can see that the final phonon number can be well cooled down less than 1 with only the optical field. From Figure 7B one can also see that although the introduction of the microwave field worsen the cooling effect, the final phonon number is still below 1, which ensures the preparation of the quantum ground state.

FIGURE 6

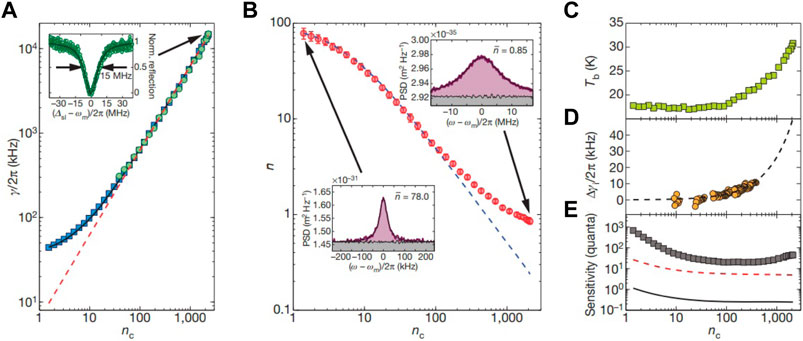
FIGURE 6. Optomechanical cooling of [50]. (A) Measured mechanical mode linewidth (blue squares), EIT window width (green circles) and theoretical predicted mechanical damping rate (red dashed line). The inset shows the EIT window of 15 MHz with an intracavity photon number n_c ≈ 50. (B) Measured average phonon number (Red circles). The phonon number is obtained by calculating the area of the mechanical noise power spectrum (purple area). Chan et al. achieved a minimum phonon number of 0.85 which indicates the mechanical mode was prepared in its ground state with a probability greater than 50%. The dashed blue line indicates the ideal cooled phonon number. (C) Estimated bath temperature versus the intracavity photon number. (D) Measured intrinsic mechanical damping rate versus the intracavity photon number. (E) The measured background noise power spectral density versus drive-laser power. Copyright 2011, Springer Nature.

FIGURE 7

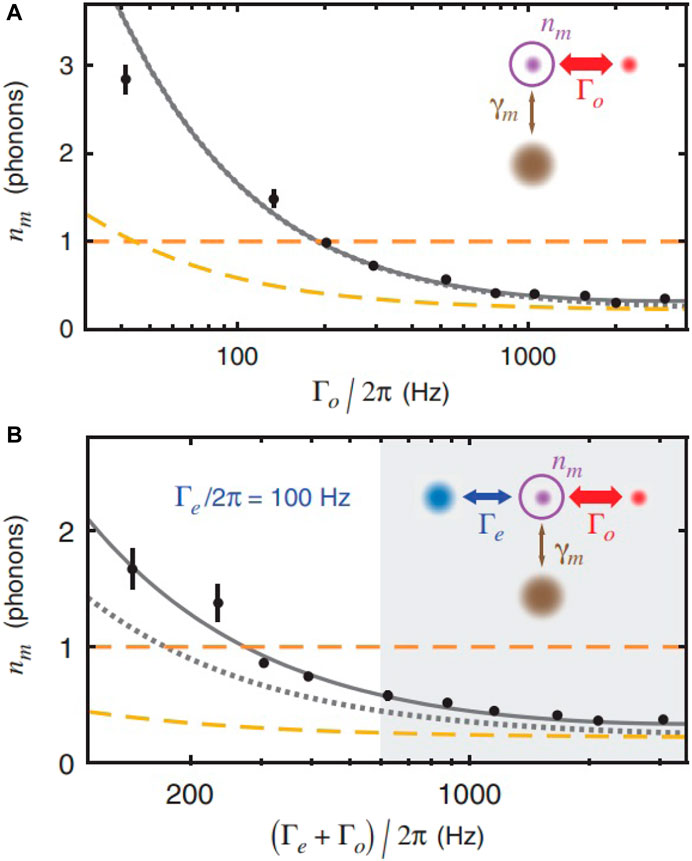
FIGURE 7. Ground-state cooling of electro-optomechanical transducer. (A) Membrane mechanical mode occupancy n_m versus optomechanical damping rate Γ_o with no electromechanical damping (Γ_e = 0). Black points are data and gray line is a fit. The lowest achieved phonon number is 0.32. The yellow dashed line indicates the backaction cooling limit. (B) n_m versus the total damping Γ_o + Γ_e with electromechanical damping fixed at Γ_e/2π = 100 Hz. The cooling effect deviates from (A) because of the additional noise. The ground-state cooling can still be achieved. Reproduced with permission from [51]. Copyright 2022 American Physical Society.

In order to provide readers with a more comprehensive perspective of the recent progress of the optomechanical cooling, we have listed the recent remarkable experimental process in Table 1 wherein the research groups, devices and final phonon number are shown. It’s notable that using pulsed optical excitation will end up with a pronounced asymmetry of the Stokes process and anti-Stokes process, which results in a remarkable cooling effect in the work of [52].

TABLE 1

TABLE 1. Recent experimental progress of ground-state cooling of optomechanical systems.

4 Theoretical discussion on ground-state cooling in optomechanical systems

Although the basic theory for optomechanical cooling has been introduced in Section 2, there is still extensive theoretical work about optomechanical cooling. Considering the fact that the resolved-sideband regime is hard to reach in the real experiments, researchers proposed alternative ways to achieve cooling beyond the resolved-sideband regime. Another important issue is to cool many mechanical modes in a large frequency bandwidth, which is dubbed as multimode cooling, different from the above discussion based on selective cooling on a single mechanical mode. An obstacle to realize multimode cooling is the dark-mode effect and various proposals to break it have been made.

4.1 Cooling beyond resolved-sideband regime

In Section 2.2 and Section 3.2 we have discussed about the importance of putting the optomechanical system in the so-called resolved-sideband regime, i.e., the mechanical mode frequency ω_m far exceeds the cavity decay rate κ. However, this is not the necessary condition for an optomechanical system to reach quantum ground state. Especially for some experimental optomechanical systems, satisfying the sideband condition is not easy. By coupling the mechanical motion to the cavity damping rate κ, [55] showed that the cavity would act like a zero-temperature bath due to the destructive interference of quantum noise, which ensures the realization of ground-state cooling even when the system is not in the resolved-sideband regime. The coupling between the mechanical mode and the cavity linewidth is called dissipative coupling, different from the previously mentioned coupling between the mechanical mode and the cavity resonance frequency, which is called dispersive coupling. [56] and [57] also considered the situation where both two different coupling patterns exists and discussed the best way to combine them to reach the best cooling performance. Also considering working on dissipation channels, [58] proposed to dynamically control the dissipation in the strong coupling regime to achieve a cooling limit which is several orders of magnitude smaller than the traditional one.

The idea of utilizing dissipative coupling to avoid resolved sideband-regime relies on the introduction of new destructive interference to suppress the Stokes process which leads to heating. Similar idea holds for introducing an auxiliary cavity to form the electromagnetically induced transparency (EIT) cooling scheme in the cold atom system. Such work includes but is not limited to [59], [60], [61] and [62]. In the work of [59], the authors proposed to couple a nanomechanical resonator to a superconducting flux qubit, which allows the existence of EIT interference that leads to the suppression of detrimental carrier excitations which prohibit cooling.

Another way to avoid the requirement of the resolved-sideband regime is to introduce a third system into the optomechanical system. [63] introduced two clouds of two-level atoms into the optical cavity, which tailored its noise spectrum into an asymmetric one that inhibits the Stokes process and prompts the anti-Stokes process. Similar idea holds for the work of [64], in which they introduced a quantum well into an optomechanical system and found that the average phonon occupancy tends to 0 with time.

Since [65] proposed that pulsed quantum optomechanics can be utilized to observe the quantum feature of macroscopic mechanical resonator by preparing it into quantum ground state, several cooling schemes based on pulsed driving has been proposed to break the resolved-sideband restraint. By modulating the optomechanical coupling strength over a time on the order of the period of the mechanical oscillator, [66] demonstrated that they could cool the mechanical mode colder than the traditional resolved-sideband limit. [67] also achieved faster cooling performance by pulsed laser, which was believed to induce quantum interference during the cooling process. Besides considering changing continuously pumped cooling scheme to the pulsed laser one, efforts on discussing the effect of frequency modulation on cooling has also been made (See [68]; [69]; [70]) and proved to be beneficial in promoting cooling in the unresolved-sideband regime. Since [71] proposed to use parametric process inside the cavity to improve cooling performance, nonlinearity has been considered as a method to realize ground-state cooling in the unresolved-sideband regime. Similar work can be found in [72], [73] and [74]. [75] also mentioned that parametric driving could be utilized to cancel the effect of the detrimental two-mode-squeezing process, which in the end realizes ground-state cooling without working in the sideband-resolved regime. Not only in theory, squeezed light has also been demonstrated to be able to cool the motion of a macroscopic mechanical resonator below its quantum backaction cooling limit in experiment (see [54]).

4.2 Multimode cooling

The previously discussed issues are all based on a standard optomechanical model, i.e., there is only one mechanical mode coupling to an optical mode. However, multimode optomechanical systems have also drawn people’s attention for its application in sensitive sensing and measurement. Since [76] reported that the introduction of another mechanical mode which has a close frequency to the one that has already coupled to the optical mode would hinder simultaneous cooling of these two mechanical modes. This phenomenon was called dark-mode effect (see [77]), where two degenerate mechanical modes hybrid to form a bright mode which couples strongly to the optical mode and a dark mode which almost decouples from the system. The related experiment has proved the existence of the dark mode (see [78]) and proposals on using cold-damping feedback to partially cool multimode mechanical resonator within a large frequency window (see [79]) has been made. Theoretical proposals on breaking dark-mode to achieve simultaneous ground-state cooling of multiple degenerate mechanical modes have been made, they include introducing a phase-dependent phonon exchange interaction [80], considering bath spectral filtering [81], employing different optical dissipation channels [82], introducing auxiliary cavity mode [83] and introducing cross-Kerr nonlinearity [84].

5 Summary and outlook

In this review, we first elucidated the basic theory of optomechanical cooling from both the classical and quantum perspective. We emphasize the importance of the retardation nature of the radiation pressure force, which gives rise to the damping of the mechanical mode. Besides, the dynamical backaction cooling limit was also analyzed with quantum noise approach, which can serve as a guidance for the striving direction for experimental realization. Then we briefly reviewed the experimental process of ground-state cooling of optomechanical systems, including active feedback cooling and optomechanical cooling. We have selectively introduced some important experimental results, including their experimental apparatus, methods and samples. Finally, we introduced various novel theoretical proposals about ground-state cooling, including cooling beyond resolved-sideband limit and multimode cooling, which can serve as a complement for present experiments.

Ground-state cooling of optomechanical systems has brought quantum physics in an unprecedented large scale, thus offering people a new perspective of quantum mechanics. Besides, the booming area of quantum optomechanics also provides the possibility of its functionality in macroscopic non-classical state generation, high precision quantum measurement and long-sought quantum communication and quantum computing.

Author contributions

PW wrote the first draft of the manuscript. MW and G-LL revised the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (62131002), Beijing Advanced Innovation Center for Future Chip (ICFC), and Tsinghua University Initiative Scientific Research Program. MW acknowledges the Young Elite Scientists Sponsorship Program by China Association for Science and Technology (2022QNRC001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ashkin A. Trapping of atoms by resonance radiation pressure. Phys Rev Lett (1978) 40:729–32. doi:10.1103/PhysRevLett.40.729

CrossRef Full Text | Google Scholar

2. Hänsch T, Schawlow A. Cooling of gases by laser radiation. Opt Commun (1975) 13:68–9. doi:10.1016/0030-4018(75)90159-5

CrossRef Full Text | Google Scholar

3. Wineland D, Dehmelt H. Proposed 1014δν/ν laser fluorescence spectroscopy on tl+ mono-ion oscillator iii (side band cooling). Bull Am Phys Soc (1975) 20:637.

Google Scholar

4. Palomaki TA, Teufel JD, Simmonds RW, Lehnert KW. Entangling mechanical motion with microwave fields. Science (2013) 342:710–3. doi:10.1126/science.1244563

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Riedinger R, Hong S, Norte RA, Slater JA, Shang J, Krause AG, et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature (2016) 530:313–6. doi:10.1038/nature16536

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hong S, Riedinger R, Marinković I, Wallucks A, Hofer SG, Norte RA, et al. Hanbury brown and twiss interferometry of single phonons from an optomechanical resonator. Science (2017) 358:203–6. doi:10.1126/science.aan7939

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Forsch M, Stockill R, Wallucks A, Marinković I, Gärtner C, Norte RA, et al. Microwave-to-optics conversion using a mechanical oscillator in its quantum ground state. Nat Phys (2020) 16:69–74. doi:10.1038/s41567-019-0673-7

CrossRef Full Text | Google Scholar

8. Mirhosseini M, Sipahigil A, Kalaee M, Painter O. Superconducting qubit to optical photon transduction. Nature (2020) 588:599–603. doi:10.1038/s41586-020-3038-6

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Mason D, Chen J, Rossi M, Tsaturyan Y, Schliesser A. Continuous force and displacement measurement below the standard quantum limit. Nat Phys (2019) 15:745–9. doi:10.1038/s41567-019-0533-5

CrossRef Full Text | Google Scholar

10. Kampel NS, Peterson RW, Fischer R, Yu P-L, Cicak K, Simmonds RW, et al. Improving broadband displacement detection with quantum correlations. Phys Rev X (2017) 7:021008. doi:10.1103/PhysRevX.7.021008

CrossRef Full Text | Google Scholar

11. Braginski V, Manukin A. Ponderomotive effects of electromagnetic radiation. Sov Phys JETP (1967) 25:653–5.

Google Scholar

12. Braginsky V, Manukin A, Tikhonov M. Investigation of dissipative ponderomotive effects of electromagnetic radiation. Soviet J Exp Theor Phys (1970) 31:829.

Google Scholar

13. Purdy TP, Peterson RW, Yu P-L, Regal CA. Cavity optomechanics with si3n4 membranes at cryogenic temperatures. New J Phys (2012) 14:115021. doi:10.1088/1367-2630/14/11/115021

CrossRef Full Text | Google Scholar

14. Zhang J, Peng B, Kim S, Monifi F, Jiang X, Li Y, et al. Optomechanical dissipative solitons. Nature (2021) 600:75–80. doi:10.1038/s41586-021-04012-1

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Eichenfield M, Camacho R, Chan J, Vahala KJ, Painter O. A picogram- and nanometre-scale photonic-crystal optomechanical cavity. Nature (2009) 459:550–5. doi:10.1038/nature08061

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bernier NR, Tóth LD, Koottandavida A, Ioannou MA, Malz D, Nunnenkamp A, et al. Nonreciprocal reconfigurable microwave optomechanical circuit. Nat Commun (2017) 8:604. doi:10.1038/s41467-017-00447-1

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Jayich AM, Sankey JC, Zwickl BM, Yang C, Thompson JD, Girvin SM, et al. Dispersive optomechanics: a membrane inside a cavity. New J Phys (2008) 10:095008. doi:10.1088/1367-2630/10/9/095008

CrossRef Full Text | Google Scholar

18. Millen J, Monteiro TS, Pettit R, Vamivakas AN. Optomechanics with levitated particles. Rep Prog Phys (2020) 83:026401. doi:10.1088/1361-6633/ab6100

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Kippenberg TJ, Vahala KJ. Cavity optomechanics: back-action at the mesoscale. Science (2008) 321:1172–6. doi:10.1126/science.1156032

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/RevModPhys.86.1391

CrossRef Full Text | Google Scholar

21. Metcalfe M. Applications of cavity optomechanics. Appl Phys Rev (2014) 1:031105. doi:10.1063/1.4896029

CrossRef Full Text | Google Scholar

22. Meystre P. A short walk through quantum optomechanics. Annalen der Physik (2013) 525:215–33. doi:10.1002/andp.201200226

CrossRef Full Text | Google Scholar

23. Barzanjeh S, Xuereb A, Gröblacher S, Paternostro M, Regal CA, Weig EM. Optomechanics for quantum technologies. Nat Phys (2022) 18:15–24. doi:10.1038/s41567-021-01402-0

CrossRef Full Text | Google Scholar

24. Liu Y-C, Hu Y-W, Wong CW, Xiao Y-F. Review of cavity optomechanical cooling. Chin Phys B (2013) 22:114213. doi:10.1088/1674-1056/22/11/114213

CrossRef Full Text | Google Scholar

25. Marquardt F, Chen JP, Clerk AA, Girvin SM. Quantum theory of cavity-assisted sideband cooling of mechanical motion. Phys Rev Lett (2007) 99:093902. doi:10.1103/PhysRevLett.99.093902

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wilson-Rae I, Nooshi N, Zwerger W, Kippenberg TJ. Theory of ground state cooling of a mechanical oscillator using dynamical backaction. Phys Rev Lett (2007) 99:093901. doi:10.1103/PhysRevLett.99.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Marquardt F, Clerk A, Girvin S. Quantum theory of optomechanical cooling. J Mod Opt (2008) 55:3329–38. doi:10.1080/09500340802454971

CrossRef Full Text | Google Scholar

28. Mancini S, Vitali D, Tombesi P. Optomechanical cooling of a macroscopic oscillator by homodyne feedback. Phys Rev Lett (1998) 80:688–91. doi:10.1103/PhysRevLett.80.688

CrossRef Full Text | Google Scholar

29. Cohadon PF, Heidmann A, Pinard M. Cooling of a mirror by radiation pressure. Phys Rev Lett (1999) 83:3174–7. doi:10.1103/PhysRevLett.83.3174

CrossRef Full Text | Google Scholar

30. Arcizet O, Cohadon P-F, Briant T, Pinard M, Heidmann A, Mackowski J-M, et al. High-sensitivity optical monitoring of a micromechanical resonator with a quantum-limited optomechanical sensor. Phys Rev Lett (2006) 97:133601. doi:10.1103/PhysRevLett.97.133601

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kleckner D, Bouwmeester D. Sub-kelvin optical cooling of a micromechanical resonator. Nature (2006) 444:75–8. doi:10.1038/nature05231

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Poggio M, Degen CL, Mamin HJ, Rugar D. Feedback cooling of a cantilever’s fundamental mode below 5 mk. Phys Rev Lett (2007) 99:017201. doi:10.1103/PhysRevLett.99.017201

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Guo J, Norte R, Gröblacher S. Feedback cooling of a room temperature mechanical oscillator close to its motional ground state. Phys Rev Lett (2019) 123:223602. doi:10.1103/PhysRevLett.123.223602

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Saarinen SA, Kralj N, Langman EC, Tsaturyan Y, Schliesser A. Laser cooling a membrane-in-the-middle system close to the quantum ground state from room temperature. Optica (2023) 10:364–72. doi:10.1364/OPTICA.468590

CrossRef Full Text | Google Scholar

35. Rossi M, Mason D, Chen J, Tsaturyan Y, Schliesser A. Measurement-based quantum control of mechanical motion. Nature (2018) 563:53–8. doi:10.1038/s41586-018-0643-8

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Schliesser A, Del’Haye P, Nooshi N, Vahala KJ, Kippenberg TJ. Radiation pressure cooling of a micromechanical oscillator using dynamical backaction. Phys Rev Lett (2006) 97:243905. doi:10.1103/PhysRevLett.97.243905

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Arcizet O, Cohadon PF, Briant T, Pinard M, Heidmann A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature (2006) 444:71–4. doi:10.1038/nature05244

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Gigan S, Böhm HR, Paternostro M, Blaser F, Langer G, Hertzberg JB, et al. Self-cooling of a micromirror by radiation pressure. Nature (2006) 444:67–70. doi:10.1038/nature05273

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Kippenberg T, Vahala K. Cavity opto-mechanics. Opt Express (2007) 15:17172–205. doi:10.1364/OE.15.017172

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Schliesser A, Rivière R, Anetsberger G, Arcizet O, Kippenberg TJ. Resolved-sideband cooling of a micromechanical oscillator. Nat Phys (2008) 4:415–9. doi:10.1038/nphys939

CrossRef Full Text | Google Scholar

41. Lin Q, Rosenberg J, Jiang X, Vahala KJ, Painter O. Mechanical oscillation and cooling actuated by the optical gradient force. Phys Rev Lett (2009) 103:103601. doi:10.1103/PhysRevLett.103.103601

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Thompson JD, Zwickl BM, Jayich AM, Marquardt F, Girvin SM, Harris JGE. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature (2008) 452:72–5. doi:10.1038/nature06715

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Teufel JD, Harlow JW, Regal CA, Lehnert KW. Dynamical backaction of microwave fields on a nanomechanical oscillator. Phys Rev Lett (2008) 101:197203. doi:10.1103/PhysRevLett.101.197203

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Gröblacher S, Hertzberg JB, Vanner MR, Cole GD, Gigan S, Schwab KC, et al. Demonstration of an ultracold micro-optomechanical oscillator in a cryogenic cavity. Nat Phys (2009) 5:485–8. doi:10.1038/nphys1301

CrossRef Full Text | Google Scholar

45. Park Y-S, Wang H. Resolved-sideband and cryogenic cooling of an optomechanical resonator. Nat Phys (2009) 5:489–93. doi:10.1038/nphys1303

CrossRef Full Text | Google Scholar

46. Schliesser A, Arcizet O, Rivière R, Anetsberger G, Kippenberg TJ. Resolved-sideband cooling and position measurement of a micromechanical oscillator close to the heisenberg uncertainty limit. Nat Phys (2009) 5:509–14. doi:10.1038/nphys1304

CrossRef Full Text | Google Scholar

47. Rocheleau T, Ndukum T, Macklin C, Hertzberg JB, Clerk AA, Schwab KC. Preparation and detection of a mechanical resonator near the ground state of motion. Nature (2010) 463:72–5. doi:10.1038/nature08681

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Rivière R, Deléglise S, Weis S, Gavartin E, Arcizet O, Schliesser A, et al. Optomechanical sideband cooling of a micromechanical oscillator close to the quantum ground state. Phys Rev A (2011) 83:063835. doi:10.1103/PhysRevA.83.063835

CrossRef Full Text | Google Scholar

49. Teufel JD, Donner T, Li D, Harlow JW, Allman MS, Cicak K, et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature (2011) 475:359–63. doi:10.1038/nature10261

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Chan J, Alegre TPM, Safavi-Naeini AH, Hill JT, Krause A, Gröblacher S, et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature (2011) 478:89–92. doi:10.1038/nature10461

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Brubaker BM, Kindem JM, Urmey MD, Mittal S, Delaney RD, Burns PS, et al. Optomechanical ground-state cooling in a continuous and efficient electro-optic transducer. Phys Rev X (2022) 12:021062. doi:10.1103/PhysRevX.12.021062

CrossRef Full Text | Google Scholar

52. Meenehan SM, Cohen JD, MacCabe GS, Marsili F, Shaw MD, Painter O. Pulsed excitation dynamics of an optomechanical crystal resonator near its quantum ground state of motion. Phys Rev X (2015) 5:041002. doi:10.1103/PhysRevX.5.041002

CrossRef Full Text | Google Scholar

53. Massel F, Cho SU, Pirkkalainen J-M, Hakonen PJ, Heikkilä TT, Sillanpää MA. Multimode circuit optomechanics near the quantum limit. Nat Commun (2012) 3:987. doi:10.1038/ncomms1993

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Clark JB, Lecocq F, Simmonds RW, Aumentado J, Teufel JD. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature (2017) 541:191–5. doi:10.1038/nature20604

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Elste F, Girvin SM, Clerk AA. Quantum noise interference and backaction cooling in cavity nanomechanics. Phys Rev Lett (2009) 102:207209. doi:10.1103/PhysRevLett.102.207209

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Weiss T, Bruder C, Nunnenkamp A. Strong-coupling effects in dissipatively coupled optomechanical systems. New J Phys (2013) 15:045017. doi:10.1088/1367-2630/15/4/045017

CrossRef Full Text | Google Scholar

57. Weiss T, Nunnenkamp A. Quantum limit of laser cooling in dispersively and dissipatively coupled optomechanical systems. Phys Rev A (2013) 88:023850. doi:10.1103/PhysRevA.88.023850

CrossRef Full Text | Google Scholar

58. Liu Y-C, Xiao Y-F, Luan X, Wong CW. Dynamic dissipative cooling of a mechanical resonator in strong coupling optomechanics. Phys Rev Lett (2013) 110:153606. doi:10.1103/PhysRevLett.110.153606

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Xia K, Evers J. Ground state cooling of a nanomechanical resonator in the nonresolved regime via quantum interference. Phys Rev Lett (2009) 103:227203. doi:10.1103/PhysRevLett.103.227203

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Ojanen T, Børkje K. Ground-state cooling of mechanical motion in the unresolved sideband regime by use of optomechanically induced transparency. Phys Rev A (2014) 90:013824. doi:10.1103/PhysRevA.90.013824

CrossRef Full Text | Google Scholar

61. Guo Y, Li K, Nie W, Li Y. Electromagnetically-induced-transparency-like ground-state cooling in a double-cavity optomechanical system. Phys Rev A (2014) 90:053841. doi:10.1103/PhysRevA.90.053841

CrossRef Full Text | Google Scholar

62. Liu Y-C, Xiao Y-F, Luan X, Gong Q, Wong CW. Coupled cavities for motional ground-state cooling and strong optomechanical coupling. Phys Rev A (2015) 91:033818. doi:10.1103/PhysRevA.91.033818

CrossRef Full Text | Google Scholar

63. Genes C, Ritsch H, Vitali D. Micromechanical oscillator ground-state cooling via resonant intracavity optical gain or absorption. Phys Rev A (2009) 80:061803. doi:10.1103/PhysRevA.80.061803

CrossRef Full Text | Google Scholar

64. Sarma B, Sarma AK. Ground-state cooling of micromechanical oscillators in the unresolved-sideband regime induced by a quantum well. Phys Rev A (2016) 93:033845. doi:10.1103/PhysRevA.93.033845

CrossRef Full Text | Google Scholar

65. Vanner MR, Pikovski I, Cole GD, Kim M, Brukner Č, Hammerer K, et al. Pulsed quantum optomechanics. Proc Natl Acad Sci (2011) 108:16182–7. doi:10.1073/pnas.1105098108

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Wang X, Vinjanampathy S, Strauch FW, Jacobs K. Ultraefficient cooling of resonators: beating sideband cooling with quantum control. Phys Rev Lett (2011) 107:177204. doi:10.1103/PhysRevLett.107.177204

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Machnes S, Cerrillo J, Aspelmeyer M, Wieczorek W, Plenio MB, Retzker A. Pulsed laser cooling for cavity optomechanical resonators. Phys Rev Lett (2012) 108:153601. doi:10.1103/PhysRevLett.108.153601

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Li Y, Wu L-A, Wang ZD. Fast ground-state cooling of mechanical resonators with time-dependent optical cavities. Phys Rev A (2011) 83:043804. doi:10.1103/PhysRevA.83.043804

CrossRef Full Text | Google Scholar

69. Farace A, Giovannetti V. Enhancing quantum effects via periodic modulations in optomechanical systems. Phys Rev A (2012) 86:013820. doi:10.1103/PhysRevA.86.013820

CrossRef Full Text | Google Scholar

70. Wang D-Y, Bai C-H, Liu S, Zhang S, Wang H-F. Optomechanical cooling beyond the quantum backaction limit with frequency modulation. Phys Rev A (2018) 98:023816. doi:10.1103/PhysRevA.98.023816

CrossRef Full Text | Google Scholar

71. Huang S, Agarwal GS. Enhancement of cavity cooling of a micromechanical mirror using parametric interactions. Phys Rev A (2009) 79:013821. doi:10.1103/PhysRevA.79.013821

CrossRef Full Text | Google Scholar

72. Huang S, Chen A. Improving the cooling of a mechanical oscillator in a dissipative optomechanical system with an optical parametric amplifier. Phys Rev A (2018) 98:063818. doi:10.1103/PhysRevA.98.063818

CrossRef Full Text | Google Scholar

73. Gan J-H, Liu Y-C, Lu C, Wang X, Tey MK, You L. Intracavity-squeezed optomechanical cooling. Laser Photon Rev (2019) 13:1900120. doi:10.1002/lpor.201900120

CrossRef Full Text | Google Scholar

74. Asjad M, Li J, Zhu S-Y, You J. Magnon squeezing enhanced ground-state cooling in cavity magnomechanics. Fundam Res (2023) 3:3–7. doi:10.1016/j.fmre.2022.07.006

CrossRef Full Text | Google Scholar

75. Lau H-K, Clerk AA. Ground-state cooling and high-fidelity quantum transduction via parametrically driven bad-cavity optomechanics. Phys Rev Lett (2020) 124:103602. doi:10.1103/PhysRevLett.124.103602

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Genes C, Vitali D, Tombesi P. Simultaneous cooling and entanglement of mechanical modes of a micromirror in an optical cavity. New J Phys (2008) 10:095009. doi:10.1088/1367-2630/10/9/095009

CrossRef Full Text | Google Scholar

77. Shkarin AB, Flowers-Jacobs NE, Hoch SW, Kashkanova AD, Deutsch C, Reichel J, et al. Optically mediated hybridization between two mechanical modes. Phys Rev Lett (2014) 112:013602. doi:10.1103/PhysRevLett.112.013602

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Ockeloen-Korppi CF, Gely MF, Damskägg E, Jenkins M, Steele GA, Sillanpää MA. Sideband cooling of nearly degenerate micromechanical oscillators in a multimode optomechanical system. Phys Rev A (2019) 99:023826. doi:10.1103/PhysRevA.99.023826

CrossRef Full Text | Google Scholar

79. Sommer C, Genes C. Partial optomechanical refrigeration via multimode cold-damping feedback. Phys Rev Lett (2019) 123:203605. doi:10.1103/PhysRevLett.123.203605

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Lai D-G, Huang J-F, Yin X-L, Hou B-P, Li W, Vitali D, et al. Nonreciprocal ground-state cooling of multiple mechanical resonators. Phys Rev A (2020) 102:011502. doi:10.1103/PhysRevA.102.011502

CrossRef Full Text | Google Scholar

81. Naseem MT, Müstecaplıoğlu ÖE. Ground-state cooling of mechanical resonators by quantum reservoir engineering. Commun Phys (2021) 4:95. doi:10.1038/s42005-021-00599-z

CrossRef Full Text | Google Scholar

82. Liu J-Y, Liu W, Xu D, Shi J-C, Xu H, Gong Q, et al. Ground-state cooling of multiple near-degenerate mechanical modes. Phys Rev A (2022) 105:053518. doi:10.1103/PhysRevA.105.053518

CrossRef Full Text | Google Scholar

83. Huang J, Lai D-G, Liu C, Huang J-F, Nori F, Liao J-Q. Multimode optomechanical cooling via general dark-mode control. Phys Rev A (2022) 106:013526. doi:10.1103/PhysRevA.106.013526

CrossRef Full Text | Google Scholar

84. Wen P, Mao X, Wang M, Wang C, Li G-Q, Long G-L. Simultaneous ground-state cooling of multiple degenerate mechanical modes through the cross-kerr effect. Opt Lett (2022) 47:5529–32. doi:10.1364/OL.473885

PubMed Abstract | CrossRef Full Text | Google Scholar