
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 01 August 2023
Sec. Quantum Engineering and Technology
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1215468
A device called the qubit energy tuner (QET), based on single flux quantum (SFQ) circuits, has been proposed for Z control of superconducting qubits. The QET is created by improving flux digital-to-analog converters (flux DACs). It can set the energy levels or frequencies of qubits, particularly flux-tunable transmons, and perform gate operations requiring Z control. The circuit structure of the QET is elucidated, consisting of an inductor loop and flux bias units for coarse or fine-tuning. The key feature of the QET is analyzed to understand how SFQ pulses change the inductor loop current, which provides external flux for qubits. Three simulations were performed to verify QET functionality. The first simulation verified the responses of the inductor loop current to SFQ pulses, showing a relative deviation of approximately 4.259% between the analytical solutions of the inductor loop current and the solutions from the WRSpice time-domain simulation. The second and third simulations, using QuTip, demonstrated how to perform a Z gate and an iSWAP gate using the QET, respectively, with corresponding fidelities of 99.99884% and 99.93906% for only one gate operation to specific initial states. These simulations indicate that the SFQ-based QET could act as an efficient component of SFQ-based quantum–classical interfaces for digital Z control of large-scale superconducting quantum computers.
Josephson qubits with gate and measurement fidelities surpassing the threshold of fault-tolerant quantum computing are attractive candidates for manufacturing scalable quantum computers. Microwave electronics, as a traditional way for qubit control and readout, have succeeded in obtaining gate fidelities beyond 99.9% [1] and realizing quantum supremacy [2]. However, the bottleneck of interconnection becomes significant when the number of qubits increases beyond a thousand due to quantitative restrictions on the input and output ports of the quantum processor and cryogenic transmission lines. It is desirable to introduce single flux quantum (SFQ) digital logic circuits [3] for control and readout [4]to overcome this bottleneck. Digital coherent XY control based on SFQ pulses to transmon qubits was proposed [5], and the fidelities of digital single-qubit gates were measured to be about 95% [6]. Methods of optimization of SFQ pulse sequences for single- [7–9] and two-qubit gates, such as cross-resonance and controlled phase (CZ) gates [10–13], have also been studied.
In order to control qubits with flexibility, SFQ-based devices for Z control have become a frontier that requires further research. McDermott et al. [4] proposed an SFQ-based coprocessor that operates at 3 K for controlling and measuring a quantum processor. This coprocessor requires SFQ-based flux digital-to-analog converters (flux DACs) [14] for Z control, which is an inspiring idea for creating a scalable superconducting quantum processor. Recently, Mohammad et al. [10] proposed an SFQ-based digital controller called DigiQ for superconducting qubits. In DigiQ, the Z control of qubits is performed with bias currents generated by an array of SFQ/DCs. These SFQ/DCs in DigiQ are placed at the 4 K plate of the dilution refrigerator, and bias currents need to be transmitted in superconducting microstrip flex lines to the 10-mK plate where the quantum processor works, which is similar to the approach used in [4].
To further advance the integration of qubits, it is crucial to integrate superconducting SFQ logic circuits for the control and measurement of qubits with quantum processors using 3D integration technologies in future developments [15,16]. Consequently, there is a need to research and design SFQ-based devices for on-chip Z control and ensure that the devices are as simple as possible for scalable quantum processors. These lean devices should be capable of converting SFQ pulse signals into flux signals. The circuits for Z control in DigiQ may be slightly more complex than flux DACs. Therefore, it is intuitive to consider flux DACs as the base for developing SFQ-based devices for Z control. However, the employment of a single flux DAC, as defined in [14], presents challenges in providing flux bias and completing a high-precision Z-control gate simultaneously because of the following reasons: 1) the resetting of a flux DAC at the end of a Z control operation will eliminate not only the flux performing the gate but also the bias flux setting the idle frequency of the controlled qubit and 2) the resetting is achieved by applying Φ0/2 (half of a flux quantum) to the two-junction reset superconducting quantum interference device (SQUID) loop, which may necessitate another flux DAC, an SFQ/DC, or a coprocessor pin for an external current source. This ultimately increases the physical footprint and complexity of the coprocessor or exacerbates the interconnection bottleneck situation.
Here, we introduce a novel SFQ-based device for Z control, which stems from the improvement of flux DACs. The primary function of the qubit energy tuner (QET) is to adjust the energy levels of qubits. By supplying flux from a QET, the energy levels or frequency of a flux-tunable transmon qubit can be precisely set to specific values. Concurrently, QET enables the execution of gate operations that require flux bias, such as a Z gate or an iSWAP gate. Following a gate operation, the QET can seamlessly return the qubit frequency to its idle state.
The circuit structure of QETs is first presented in Section 2. Then, the key features of a specific QET are analyzed, and a formula is derived to calculate its inductor loop current responsible for providing flux. Section 3 describes the ideal Z control method, which employs square-wave-like currents for flux-tunable transmon. Subsequently, in Section 4, simulations are performed to demonstrate the variation in the inductor loop current of a QET providing flux due to SFQ pulses, as well as the performance of a QET in executing Z and iSWAP gates. Finally, in Section 5, the work is concluded, and the challenges and opportunities associated with QETs in the future are discussed.
QET comprises an inductor loop and several flux bias units, which can be either positive or negative, as illustrated in Figure 1. The inductor loop is weakly coupled to the SQUID of a flux-tunable transmon, supplying flux for tuning its energy levels. Each flux bias unit includes a Josephson junction shunted with an inductor coupled to the inductor loop. The Josephson junction can be made of an intrinsic Josephson junction in parallel with a resistor to be an overdamped Josephson junction. The node connected to the Josephson junction and the inductor is treated as an input port of QET for the SFQ pulse signal. After receiving an SFQ pulse, a positive flux bias unit increases the external flux through the SQUID by a specific amount, whereas a negative flux bias unit increases it in the opposite direction or decreases it by the same specific amount. This is realized by making the direction of dotted terminals of positive flux bias units the same as that of the corresponding inductor in the inductor loop but making the direction of dotted terminals of negative flux bias units opposite to that of the corresponding inductor in the inductor loop.
A QET should have at least a pair of flux bias units, one positive and the other negative. In order to tune the energy levels of a transmon more precisely, QET can be designed to have two or more pairs of flux bias units, among which some pairs are used for coarse tuning and others are used for fine-tuning. Inductors in different flux bias units can be coupled. The inspiration for the QET is from the design of the flux DAC proposed in [14] and [17]. Therefore, its circuits have similar but simpler structures compared with those of flux DACs.
The QET shown in Figure 2 is an example of the following analysis. It has a pair of flux bias units for coarse tuning and another pair for fine-tuning. The parameters of elements in the example are listed in Table 2. The symbol for QET in Figure 2 is drawn as in Figure 3. This kind of QET with two pairs of flux bias units is chosen to be analyzed because it combines accuracy, simplicity, and speed better than other cases with only one or over two pairs of flux bias units. On one hand, the QET with only a pair of flux bias units has only one precision, which causes a low speed of high-precision tuning or a low precision of high-speed tuning. On the other hand, the QET with three or more pairs of flux bias units has more ports and circuit elements, which means more complicated control, reduced reliability, and a larger footprint.
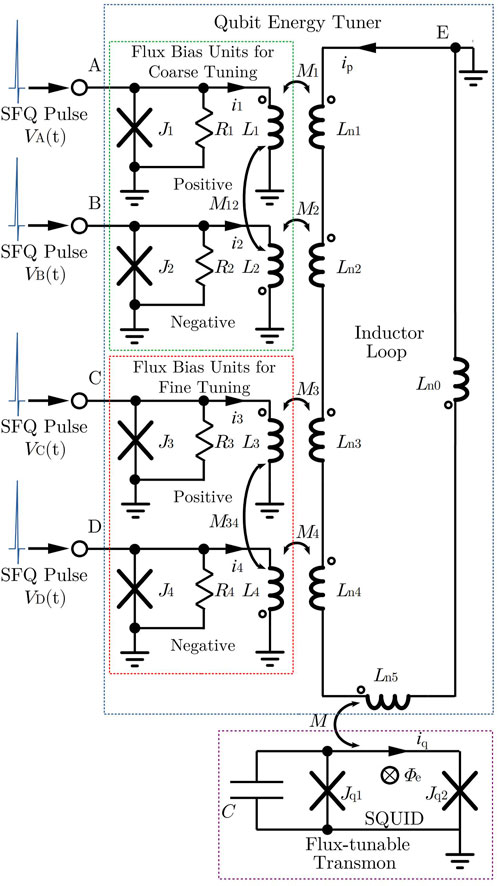
FIGURE 2. Schematic representation of a qubit energy tuner with two pairs of flux bias units for coarse tuning and fine-tuning.
According to Kirchhoff’s voltage law, the electric potentials of nodes A, B, C, D, and E in Figure 2 are
where
is the total inductance of the inductor loop obtained by summing self-inductances of all parts of the inductor loop. L1, L2, L3, and L4 are self-inductances of inductors in flux bias units. M1, M2, M3, and M4 are mutual inductances of flux bias units and the inductor loop, as shown in Figure 2. M is the mutual inductance between the inductor loop and the SQUID of flux-tunable transmon. i1 (t′), i2 (t′), i3 (t′), and i4 (t′) are currents of inductors in flux bias units at the moment t′. ip (t′) and iq (t′) are the currents of the inductor loop and the SQUID at the moment t′.
Under the zero initial condition, integrating both sides of Eqs 1–5 with 0 as the lower bound and time t as the upper bound yields
The mutual inductance M is designed to be much smaller than the total inductance of the inductor loop LΣ and other mutual inductances like M1 for weak coupling to the SQUID of the qubit. Additionally, the ring current of the SQUID iq(t) should be less than the critical current of its Josephson junctions, which is about tens of nA for Al/AlOx/Al junctions and smaller than the current in the inductance loop ip(t) (about several or tens of mA) by two or more orders of magnitude. Therefore, the influence of the SQUID on the inductance loop, Miq, can be ignored in Eq. 11, and the electric potential of node E is rewritten as
Then, let
and we get
where
and
Then, to get i(t), we have
where
The elements aij (i, j = 1, 2, 3, 4, 5) of A are
Therefore, we have
that is,
Because node E is connected to the ground, ΦE should always be zero. In order to make the flux bias units of coarse tuning be able to increase or decrease the external flux through the SQUID by the same amount, the following requirements should be met:
Similarly, for the flux bias units of fine-tuning, we have
Therefore, ip(t) becomes
where ΦA, ΦB, ΦC, and ΦD are the integral of the voltage at nodes A, B, C, and D over time t, respectively. Because the input signal to these nodes is SFQ, ΦA, ΦB, ΦC, and ΦD are multiples of flux quantum Φ0. F becomes
Hence, the relationship between the current of the inductor loop ip(t) and the external flux through the SQUID Φe is
Denoting
yields
Eqs 42–44 mean that the flux provided by QET can be divided into two parts, ncΦec and nfΦef, which are, respectively, created by coarse tuning and fine-tuning. Φec can be regarded as the flux unit of coarse tuning, and Φef can be regarded as the flux unit of fine-tuning. If nc (or nf) SFQ pulses are inputted to port A (or C) of the QET, then the external flux through the SQUID will increase by nc times of Φec (or nf times of Φef). Subsequently, if this external flux needs to be eliminated, nc (or nf) SFQ pulses should be inputted to port B (or D). Usually, for fine-tuning, rf is smaller than rc. If
then the ratio of the flux unit of coarse tuning to the flux unit of fine-tuning can be defined as
where the coupling coefficients are
The parameter rcf indicates the ratio of the flux precision of coarse tuning to that of fine-tuning. It should have an appropriate value greater than 1, like 10, to distinguish the two precisions. The parameter rf is the ratio of the smallest variation of the flux Φe, Φef, to flux quantum Φ0; it determines the flux precision of fine-tuning. The parameter rc is the ratio of Φec to flux quantum Φ0 and can be set by rc = rcf ⋅ rf.
The parameters rcf, rf, and rc are the main concerns and should be first determined to design a QET. Then, with constraints including Eqs 35, 36, 45, 46, 48 ∼Eq. 52, all parameter values of circuit elements should be tried and iterated to meet the requirements from the higher-level design; for example, the footprint of the QET on the chip is matched with the footprint of the qubit.
A QET has almost zero static power dissipation in theory because no current will flow through its resistors when Josephson junctions are not switched. Assuming that a QET is used for a gate operation per 20 ns and about 20 SFQ pulses are required for each gate operation, the average switching frequency of Josephson junctions in the QET, fs, is about 1 GHz. With the critical current IC = 160 μA and a flux quantum Φ0 ≈ 2.06783385 × 10−15Wb, the dynamic power dissipation PD of a QET can be estimated to be 0.33 nW according to the following formula [18]:
In order to simplify the analysis and understand the main factors affecting the results of Z control, the square-wave-like waveforms of currents producing external flux Φe are considered as the ideal cases for a flux-tunable transmon. This section reviewed and discussed how the ideal Z control is performed.
The Hamiltonian of a flux-tunable transmon [19] is
where
is the effective Josephson energy of the SQUID of the transmon with a total Josephson coupling energy of two junctions
an asymmetry coefficient
and a reduced external flux
EC is the charging energy of the transmon. ng is the effective offset charge.
The solution for the kth eigen energy of Eq. 54 with the first-order approximation of perturbation theory [19] is
Usually, the external flux Φe(t) at the moment t for Z control is provided by a conductor line beside the SQUID with its current, iz(t), and a mutual inductance between the line and the SQUID, M. Because the current in the SQUID is much smaller than iz(t), its influence on iz(t) can be ignored. There is
Therefore, EJS (φe) can be written as
By changing iz(t), EJS (iz(t)) can be set to a target value. Then, the energy level Ek, especially E0 and E1, can be tuned so that the qubit frequency is set to the corresponding target value. When EJS (iz(t)) is set, the condition EJS (iz(t))/EC ≫ 1 should be guaranteed to make sure that the qubit is a transmon. According to Eq. 59, we have
Therefore, the differences of energy levels are
and the anharmonicity of the qubit is
Without losing generality, iz(t) has a square-wave-like waveform and is set as
where iw and ii are the currents for setting working frequency ωqw and idle frequency ωqi of a transmon, respectively. ωqw is the qubit frequency used for Z control. ωqi is the qubit frequency when it is idle and is determined to be the frequency of the rotating frame [20]. ts and te are the moments when a gate operation starts and ends, respectively. Then, the qubit frequency becomes
where
Here, we denote
For an idle qubit, its Hamiltonian is
Actually, the time-dependent Hamiltonian of the qubit is
where a† and a are the creation and annihilation operators, respectively, and Δω(t) is defined by
ωq(t) is the actual frequency of the qubit. We denote
as the drive Hamiltonian for Z control. Therefore, there is
In the rotating frame, the drive Hamiltonian for Z control becomes
and the corresponding evolution operator in the rotating frame is
where
In the ideal situation in which iw and ii are constants, when the qubit is working (ts⩽t⩽te), there is ωq(t) = ωqw, so Δω(t) becomes the constant Δωq:
and the Hamiltonian H becomes
We define
as the phase shift realized by Z control, and define
as the gate operation time for Z control. With Eqs 73, 82, 84, 85, we have
According to Eq. 81, the corresponding evolution operator for the qubit becomes
To realize on-chip Z control by SFQ, instead of choosing the Z control line, ii and iw can be produced by the inductor loop current ip(t) of a QET, which means making iz(t) = ip(t).
In order to show how the inductor loop current ip(t) of a QET is controlled by the SFQ signal, a simulation with superconducting circuit simulation software WRSpice for the circuits in the blue-dashed-line box in Figure 4 is performed. The SFQ pulses sent to the input ports of QET, A, B, C, and D, are generated by four DC/SFQs, each of which is driven by a time-dependent current source. Here, the DC/SFQ is used only for generating SFQ pulses to verify the functionality of the QET. In practical engineering, the QET can also be driven by SFQ pulses from other SFQ digital circuits. The existence and influence of two qubits in Figure 4 are ignored temporarily. The circuits of DC/SFQ and QET for simulation are shown in Figures 5, 6, and the corresponding parameters of their elements are listed in Table 1 and Table 2, which are based on the SFQ circuit design data from [21]. In these two tables, the parameters whose names start with the letter “J” are the critical currents of the corresponding Josephson junctions. The circuit of the QET in Figure 6 is slightly different from Figure 2 for consideration of the parasitic inductances, but the functions of the QET will not change essentially. Figure 7 shows the simulation results, including the waveforms of (A) the drive currents for DC/SFQ, ISA, ISB, ISC, and ISD mentioned in Figure 6; (B) the node voltages for QET input ports, VA, VB, VC, and VD, which are SFQ pulses with time interval 2 ns; and (C) the inductor loop current ip.
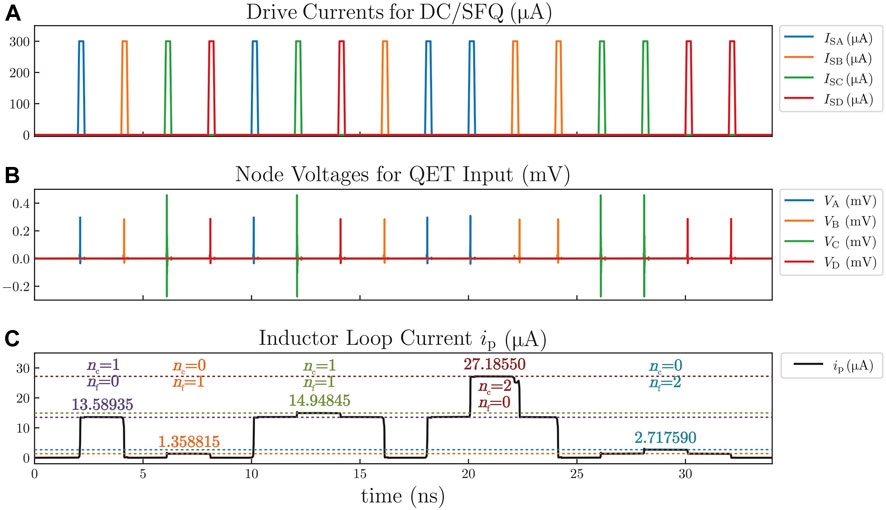
FIGURE 7. Time-domain responses of QET to SFQ pulses produced by DC/SFQ. (A) Drive currents for DC/SFQ, including ISA, ISB, ISC, and ISD. (B) Node voltages for QET input, including VA, VB, VC, and VD. (C) Inductor loop current ip.
To change the inductor loop current ip(t), which provides external flux Φe = Mip(t), nc and nf can be set by the SFQ pulse sequence from DC/SFQ. The simulation and analytical values of the inductor loop current with different nc and nf are compared in Table 3. First, by setting nc = 1 and nf = 0 with SFQ pulses sent to ports A and B (coarse tuning), Δipc can be extracted from the height of the leftmost lug boss of the inductor loop current curve in Figure 7C. The extraction value of Δipc is 13.58935 μA, which is close to the value 13.03599 μA, calculated by Eq. 37 with a relative deviation of 4.245%. Similarly, by setting nc = 0 and nf = 1 with SFQ pulses sent to ports C and D (fine-tuning), Δipf can also be extracted as 1.358815 μA from the second left current lug boss, which is also close to analytical solution 1.303599 μA from Eq. 37 with relative deviation 4.236%. Therefore, rcf from this simulation is 10.00088 according to Eq. 48, almost the same as 10.0, the theory value from analytical solutions.
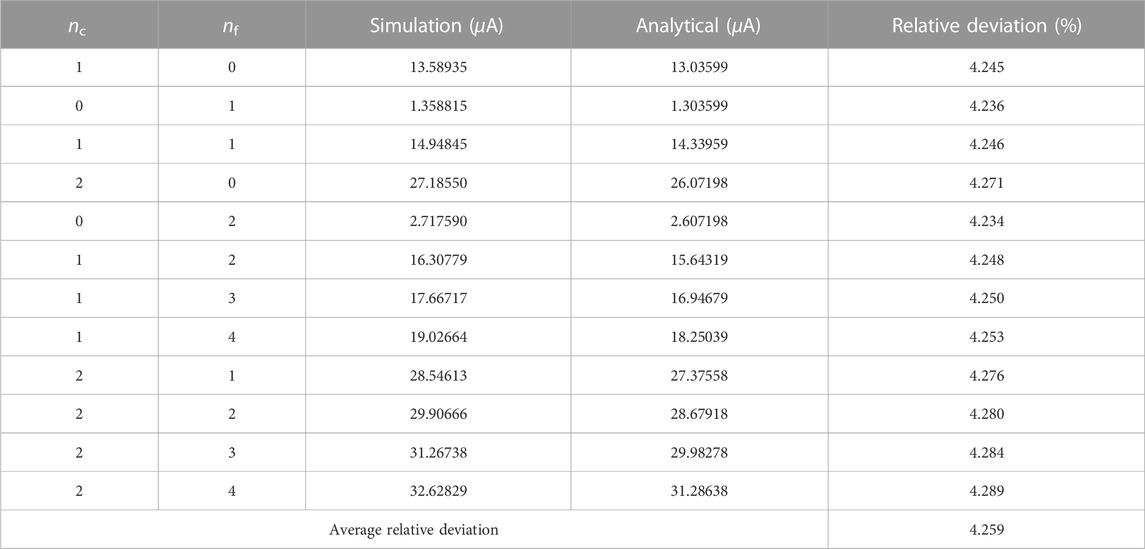
TABLE 3. Simulation and analytical values of the inductor loop current ip with different nc and nf in the simulation for a single QET.
By setting nc = 1 and nf = 1, the two parts of the inductor loop current correspondingly made by coarse tuning and fine-tuning can be accumulated, as shown in the third left lug boss in Figure 7C. By setting nc = 2 and nf = 0, the inductor loop current can be double times Δipc. Similarly, by setting nc = 0 and nf = 2, the inductor loop current can also be double times Δipf. Generally, if the inductor loop current is required to be Nc times Δipc plus Nf times Δipf, then nc should be set as Nc and nf should be set as Nf according to Eq 41. The relative deviations between analytical solutions and simulation solutions of ip for other cases (nc = 1 when nf = 2, 3, 4 and nc = 2 when nf = 1, 2, 3, 4) are also calculated, and the average relative deviation is 4.259%, as shown in Table 3.
The waveform of the inductor loop current is similar to composited square waves on the whole. Their rising and falling edges are steep, which helps avoid crosstalk when the qubit frequency is changing across frequencies of other qubits or resonators because the qubit frequency is changed quickly enough within time (several picoseconds) much shorter than a gate operation time (several nanoseconds).
The simulation in this subsection shows how a QET can perform a Z gate. The circuit for simulation is defined as the circuit in the purple-dashed-line box of Figure 4, which is based on the circuit of the former simulation in the blue-dashed-line box. The controlled qubit, Qubit 1, is a symmetric flux-tunable transmon connected to the former circuit, so we set d = 0 and EJ1 = EJ2 = EJ. Qubit 2 is ignored temporarily. By controlling the time interval of two SFQ pulses inputted to ports A and B of the QET, the phase of a flux-tunable transmon can be adjusted. Qubit 1 is driven only by coarse tuning with nc = 1, so we set ii = 0 and iw = Δipc. Then, Δω(t) can be approximately treated as the constant Δωq when ts⩽t⩽te; that is,
and
Then, with Eqs 86, 89, we have
The evolution operator
By designing the qubit and QET, the parameters EC, EJ, M, and Δipc can be determined properly to make tz in a range easy to realize. Then, for more precise control, the value of tz should be optimized in practical experiments. Fine-tuning can also be performed to compensate for gate errors. In this simulation as a simple case, there are EJ/ℏ = 2π ⋅ (11.147 GHz), EC/ℏ = 2π ⋅ (148.628 MHz), M = 0.02 nH, and Δipc = 13.58935 μA. Moreover, to realize a Z gate, tz should be 2.261 ns by solving the equation φ = π with Eq 90. The initial state of Qubit 1 is set as
The data on ip(t) are first extracted from its time-domain simulation in WRSpice, similar to the former simulation of a single QET without the qubit. Then, it is imported into the Z gate simulation program using QuTip [22,23] to calculate the time-domain data on the drive Hamiltonian for Z control. By calling the function solving master equation or Schrödinger equation of QuTip, like qutip.mesolve() or qutip.sesolve(), the time evolution of the qubit state changed by a Z gate operated by the QET can be figured out with a total Hamiltonian H consisting of drive Hamiltonian Hdz and idle qubit Hamiltonian H0, which is expressed by Eqs 75–78. The anharmonicity of the qubit is also considered in the simulation. Therefore, the creation operator a† and annihilation operator a are treated as 3 × 3 matrices, and the state vectors are all 3-dimensional. The state vectors in the simulation results are projected onto the computational basis to obtain the qubit states in the 2-dimension computational space.
The simulation results for a Z gate by the QET in the rotating frame are presented in Figure 8. In addition to the waveforms, including (A) drive currents for DC/SFQ, (B) node voltages for the QET input, and (C) inductor loop current, (D) the frequencies of the qubit eigenenergies and (E) the qubit frequency are also plotted in Figure 8. The black trajectory of the point representing the qubit state on the surface of the Bloch sphere is drawn in Figure 9. In this simulation, the gate operation time of 2.261 ns is actually controlled by setting the time interval of the rising edges of two square-wave pulses in Figure 8A. During the period of gate operation (in the lug boss of the inductor loop current curve), the qubit frequency is kept at 4.779 GHz with EJS/EC = 137.5, changed from 5.0 GHz with EJS/EC = 150. The end state of the qubit becomes
which is close to the ideal end state
The Z gate fidelity for only this time of operation is
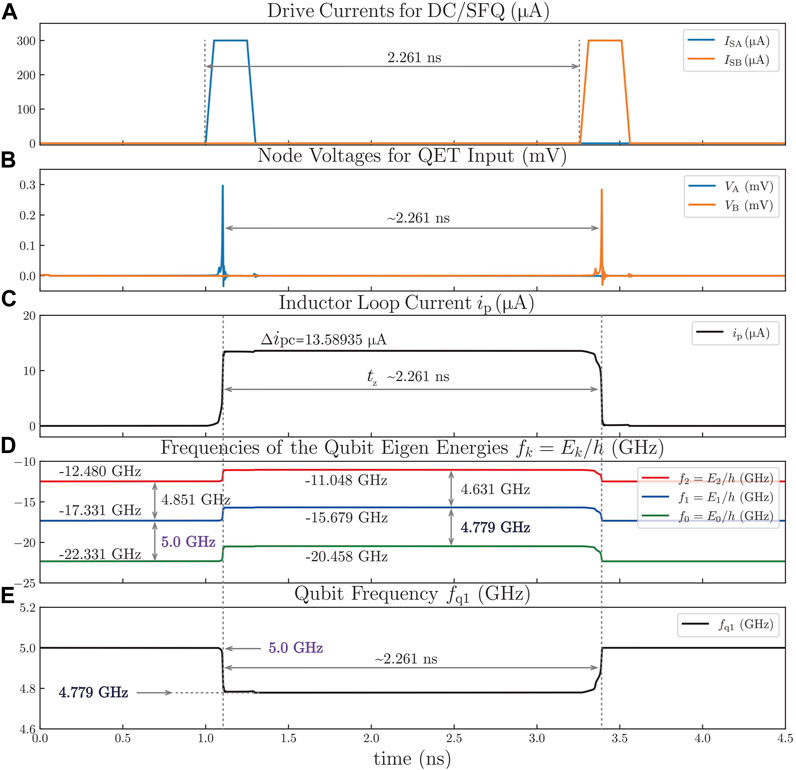
FIGURE 8. Z gate time-domain simulation results. (A) Drive currents for DC/SFQ, including ISA, ISB, ISC, and ISD. (B) Node voltages for QET input, including VA, VB, VC, and VD. (C) Inductor loop current ip. (D) Frequencies of the qubit eigenenergies fk. (E) Qubit frequency fq1.
If relaxation and dephasing are considered, then the simulation should obey the master equation describing the time evolution of a transmon coupled to the environment [24]:
where γ is the relaxation rate and γφ is the pure dephasing rate. H is the Hamiltonian described by Eq 75. ρ is the density matrix of the qubit. With approximation [24,25], the relationships of the two rates, T1 and T2, are
For transmon based on Al/AlOx/Al Josephson junctions, the typical range of T1 is 10 ∼ 110 μs, and the typical range of T2 is 2 ∼ 18 µs [26–28]. In the simulation, T1 is set as 50 µs, and T2 is set as 10 μs. The density matrix of the initial state is
The simulation results for a Z gate with relaxation and dephasing show that the density matrix of the end state is
Additionally, the density matrix of the ideal end state is
Therefore, the fidelity of the Z gate with relaxation and dephasing for only this time is
The simulation in this subsection shows how a QET can perform an iSWAP gate by making the frequency of Qubit 1 the same as that of Qubit 2. The corresponding Hamiltonian (considering rotating wave approximation (RWA) [20]) is
Here, the two qubits have the same anharmonicity α but different idle frequencies ωq1 and ωq2. The creation and annihilation operators are defined as follows:
where Δω is the frequency variation of Qubit 1 caused by the QET. I is a 3 × 3 identity matrix. As defined in the last Section 4.2, a† and a are 3 × 3 matrices as the creation operator and the annihilation operator for a single qubit, respectively. Therefore, the state vectors of qubits in the iSWAP gate simulations are 9-dimensional, and their density matrices are 9 × 9 matrices. Compared with the former simulation for the Z gate, the method of this simulation with WRSpice and QuTip remains unchanged, but the simulation circuit is enlarged, as shown in the green-dashed-line box in Figure 4. The coupling strength between Qubit 1 and Qubit 2 is g = 2π ⋅ (5 MHz). The results are presented in Figure 10. Figure 10A shows the drive currents for DC/SFQ, including ISA and ISB. Figure 10B presents the node voltages for the QET input, including VA and VB. Figure 10C shows the curve of the inductor loop current ip. Figure 10D shows the curve of frequencies of Qubit 1 and Qubit 2 (fq1 and fq2). Figure 10E shows the probability of the qubit state |ψ⟩ populating on |01⟩ or |10⟩.
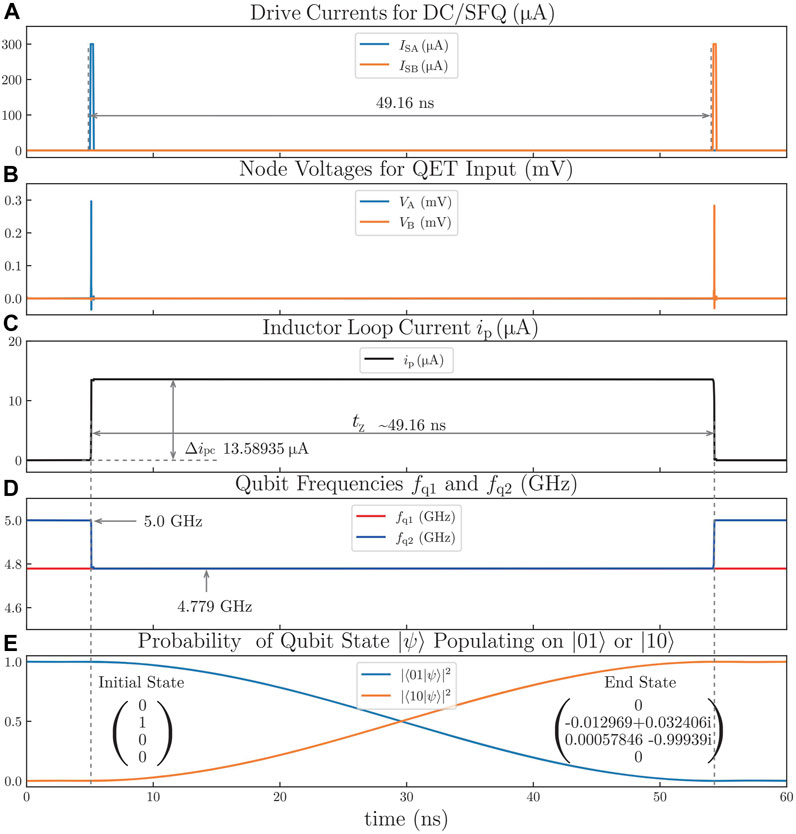
FIGURE 10. iSWAP gate time-domain simulation results. (A) Drive currents for DC/SFQ, including ISA and ISB. (B) Node voltage for QET input. (C) Inductor loop current. (D) Qubit frequencies. (E) Probability of the qubit state |ψ⟩ populating on |01⟩ or |10⟩.
The frequency of Qubit 1 (5.0 GHz) is tuned to the same level as the frequency of Qubit 2 (4.779 GHz) with ip = Δipc = 13.58935 μA by inputting an SFQ pulse to port A of the QET. Then, the QET does nothing for tz = 49.16 ns to wait for state swapping between Qubit 1 and Qubit 2 with the initial state:
When they finish swapping the qubit state, the second SFQ pulse is inputted to port B of the QET, which makes Qubit 1 back to its idle frequency. With the ideal end state,
and the actual end state
in the simulation, the fidelity of the iSWAP gate (49.16 ns) for only this time of operation is
Usually, for two qubits coupling with g = 2π ⋅ (5 MHz), the iSWAP gate needs 50 ns. However, here the gate operation time is optimized as 49.16 ns to eliminate the extra phase shift of Qubit 1 caused by changing its frequency and to ensure that the fidelity of the iSWAP gate is high enough at the same time. The optimal gate operation time can be found by performing the simulation with the same other parameters but different values of gate operation time around 50 ns. As shown in Figure 11, the point at 49.16 ns has almost 0 extra phase shift (0.00058 rad) with a high enough fidelity of 99.93906%, which is a little smaller than the maximum value of 99.95724% at 50.35 ns.
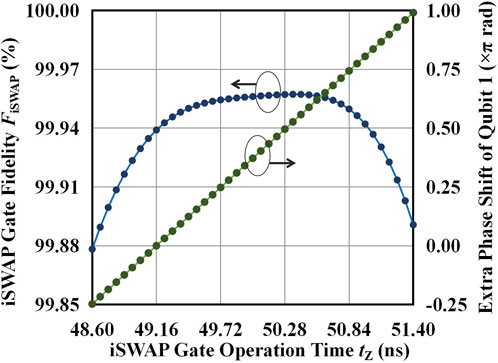
FIGURE 11. Fidelity
Similar to the simulation of the Z gate in the last Section 4.2, the simulation of the iSWAP gate considering the relaxation and dephasing is also performed. For the two-qubit system in the simulation, assuming that both qubits have the same relaxation time T1 and dephasing time T2, the master equation is
where H is the Hamiltonian described by Eq 101. ρ is the 9 × 9 density matrix of the two-qubit system. With the initial state,
the density matrix of the initial state is
Moreover, the density matrix of the end state is
The density matrix of the ideal end state is
The fidelity of the iSWAP gate by QET considering relaxation and dephasing is
In conclusion, we have proposed the QET device with the description of its circuit structure and theory for its SFQ-based digital Z control to a flux-tunable transmon. A QET can convert SFQ pulses to external flux for qubits. Therefore, it can set the idle frequency of a flux-tunable transmon and, at the same time, perform gate operations involving Z control, such as Z gates and iSWAP gates, thus paving an approach for digital Z control of an SFQ-based quantum-classical interface, which is highly desirable for the research and development of a large-scale superconducting quantum computer.
For integrating with flux-tunable transmons and avoiding noise from SFQ circuits simultaneously, the parts of QETs consisting of flux bias units can be fabricated on another substrate, which is electrically connected to the qubit chip with through silicon vias (TSVs) and indium bumps of a silicon interposer [15,16]. In order to realize mutual inductances between transmon SQUIDs and inductor loops of QETs, TSVs and indium bumps should be parts of inductor loops so that the piece of the inductor line of an inductor loop for flux bias can be fabricated on the qubit chip or the surface of the silicon interposer faced to qubits. To eliminate the electrical loss of inductor loops, the material of TSVs should be superconductive (e.g., TiN). QETs may also be used in other application scenarios requiring flux tuning, such as CZ gates [29], flux-tunable couplers [30,31], and qubit readout with a Josephson photomultiplier [32]. Further research should design and fabricate this device for experiments about SFQ-based digital control of qubits, especially flux-tunable transmons.
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Conceptualization, formula derivation, simulation, and writing: XG; formula derivation, revision: KH; validation and investigation: RH; review and editing: JL; resources: WC. All authors contributed to the article and approved the submitted version.
This work was partially supported by the key R&D program of Guangdong province (grant no. 2019B010143002).
XG acknowledges the discussion with Yongcheng He, Genting Dai, Liangliang Yang, Xinyu Wu, Qing Yu, Mingjun Cheng, and Guodong Chen about the methodology of the article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature (2014) 508:500–3. doi:10.1038/nature13171
2. Arute F, Arya K, Babbush R, Bacon D, Bardin JC, Barends R, et al. Quantum supremacy using a programmable superconducting processor. Nature (2019) 574:505–10. doi:10.1038/s41586-019-1666-5
3. Likharev K, Semenov V. Rsfq logic/memory family: A new josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans Appl Superconductivity (1991) 1:3–28. doi:10.1109/77.80745
4. McDermott R, Vavilov M, Plourde B, Wilhelm F, Liebermann P, Mukhanov O, et al. Quantum–classical interface based on single flux quantum digital logic. Quan Sci Technol (2018) 3:024004. doi:10.1088/2058-9565/aaa3a0
5. McDermott R, Vavilov M. Accurate qubit control with single flux quantum pulses. Phys Rev Appl (2014) 2:014007. doi:10.1103/physrevapplied.2.014007
6. Leonard E, Beck MA, Nelson J, Christensen BG, Thorbeck T, Howington C, et al. Digital coherent control of a superconducting qubit. Phys Rev Appl (2019) 11:014009. doi:10.1103/physrevapplied.11.014009
7. Liebermann PJ, Wilhelm FK. Optimal qubit control using single-flux quantum pulses. Phys Rev Appl (2016) 6:024022. doi:10.1103/physrevapplied.6.024022
8. Li K, McDermott R, Vavilov MG. Hardware-efficient qubit control with single-flux-quantum pulse sequences. Phys Rev Appl (2019) 12:014044. doi:10.1103/physrevapplied.12.014044
9. Vozhakov V, Bastrakova MV, Klenov NV, Satanin A, Soloviev II. Speeding up qubit control with bipolar single-flux-quantum pulse sequences. Quan Sci Technol (2023) 8:035024. doi:10.1088/2058-9565/acd9e6
10. Jokar MR, Rines R, Pasandi G, Cong H, Holmes A, Shi Y, et al. Digiq: A scalable digital controller for quantum computers using sfq logic. In: Proceedings of the 2022 IEEE International Symposium on High-Performance Computer Architecture (HPCA); April 2022; Seoul, Korea (2022). p. 400–14. doi:10.1109/HPCA53966.2022.00037
11. Dalgaard M, Motzoi F, Sørensen JJ, Sherson J. Global optimization of quantum dynamics with alphazero deep exploration. npj Quan Inf (2020) 6:6–9. doi:10.1038/s41534-019-0241-0
12. Jokar MR, Rines R, Chong FT. Practical implications of sfq-based two-qubit gates. In: Proceedings of the 2021 IEEE International Conference on Quantum Computing and Engineering (QCE); October 2021; Broomfield, CO, USA (2021). p. 402–12. doi:10.1109/QCE52317.2021.00061
13. Wang Y, Gao W, Liu K, Ji B, Wang Z, Lin Z. Single-flux-quantum-activated controlled-z gate for transmon qubits. Phys Rev Appl (2023) 19:044031. doi:10.1103/physrevapplied.19.044031
14. Johnson M, Bunyk P, Maibaum F, Tolkacheva E, Berkley A, Chapple E, et al. A scalable control system for a superconducting adiabatic quantum optimization processor. Superconductor Sci Technol (2010) 23:065004. doi:10.1088/0953-2048/23/6/065004
15. Rosenberg D, Kim D, Das R, Yost D, Gustavsson S, Hover D, et al. 3d integrated superconducting qubits. npj Quan Inf (2017) 3:42–5. doi:10.1038/s41534-017-0044-0
16. Rosenberg D, Weber SJ, Conway D, Yost D-RW, Mallek J, Calusine G, et al. Solid-state qubits: 3d integration and packaging. IEEE Microwave Mag (2020) 21:72–85. doi:10.1109/mmm.2020.2993478
17. Bunyk PI, Hoskinson EM, Johnson MW, Tolkacheva E, Altomare F, Berkley AJ, et al. Architectural considerations in the design of a superconducting quantum annealing processor. IEEE Trans Appl Superconductivity (2014) 24:1–10. doi:10.1109/tasc.2014.2318294
18. Narayana S, Semenov V. Energy dissipation minimization in superconducting circuits. In: AM Luiz, editor. Superconductivity. Rijeka: IntechOpen (2011). chap. 5. doi:10.5772/16285
19. Koch J, Terri MY, Gambetta J, Houck AA, Schuster DI, Majer J, et al. Charge-insensitive qubit design derived from the cooper pair box. Phys Rev A (2007) 76:042319. doi:10.1103/physreva.76.042319
20. Krantz P, Kjaergaard M, Yan F, Orlando TP, Gustavsson S, Oliver WD. A quantum engineer’s guide to superconducting qubits. Appl Phys Rev (2019) 6:021318. doi:10.1063/1.5089550
21. Li G. Research on superconducting RSFQ circuit for qubit control. Ph.D. thesis. Tsinghua: Tsinghua University (2018).
22. Johansson J, Nation P, Nori F. Qutip: An open-source python framework for the dynamics of open quantum systems. Comput Phys Commun (2012) 183:1760–72. doi:10.1016/j.cpc.2012.02.021
23. Johansson J, Nation P, Nori F. Qutip 2: A python framework for the dynamics of open quantum systems. Comput Phys Commun (2013) 184:1234–40. doi:10.1016/j.cpc.2012.11.019
24. Blais A, Grimsmo AL, Girvin SM, Wallraff A. Circuit quantum electrodynamics. Rev Mod Phys (2021) 93:025005. doi:10.1103/revmodphys.93.025005
25. Schoelkopf R, Clerk A, Girvin S, Lehnert K, Devoret M. Qubits as spectrometers of quantum noise Quantum noise in mesoscopic physics (2003). Available at: https://arxiv.org/abs/cond-mat/0210247 (Accessed June 28, 2023).
26. Xu S, Sun Z-Z, Wang K, Xiang L, Bao Z, Zhu Z, et al. Digital simulation of non-abelian anyons with 68 programmable superconducting qubits (2022). Available at: https://arxiv.org/abs/2211.09802 (Accessed June 29, 2023).
27. Shi Y-H, Liu Y, Zhang Y-R, Xiang Z, Huang K, Liu T, et al. Observing topological zero modes on a 41-qubit superconducting processor (2022). Available at: https://arxiv.org/abs/2211.05341 (Accessed June 29, 2023).
28. Wu Y, Bao W-S, Cao S, Chen F, Chen M-C, Chen X, et al. Strong quantum computational advantage using a superconducting quantum processor. Phys Rev Lett (2021) 127:180501. doi:10.1103/physrevlett.127.180501
29. Xu Y, Chu J, Yuan J, Qiu J, Zhou Y, Zhang L, et al. High-fidelity, high-scalability two-qubit gate scheme for superconducting qubits. Phys Rev Lett (2020) 125:240503. doi:10.1103/physrevlett.125.240503
30. Chen Y, Neill C, Roushan P, Leung N, Fang M, Barends R, et al. Qubit architecture with high coherence and fast tunable coupling. Phys Rev Lett (2014) 113:220502. doi:10.1103/physrevlett.113.220502
31. Yan F, Krantz P, Sung Y, Kjaergaard M, Campbell DL, Orlando TP, et al. Tunable coupling scheme for implementing high-fidelity two-qubit gates. Phys Rev Appl (2018) 10:054062. doi:10.1103/physrevapplied.10.054062
Keywords: qubit, quantum control, superconducting quantum computing, RSFQ, superconducting electronics
Citation: Geng X, He K, Huang R, Liu J and Chen W (2023) Qubit energy tuner based on single flux quantum circuits. Front. Phys. 11:1215468. doi: 10.3389/fphy.2023.1215468
Received: 02 May 2023; Accepted: 17 July 2023;
Published: 01 August 2023.
Edited by:
Weilong Wang, State Key Laboratory of Mathematical Engineering and Advanced Computing, ChinaReviewed by:
Ma Hongyang, Qingdao University of Technology, ChinaCopyright © 2023 Geng, He, Huang, Liu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiao Geng, Z2VuZ3gxOUBtYWlscy50c2luZ2h1YS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.