Abstract
In this paper, we construct a new model based on the coupling of thermoelasticity, plasma, and microelongation effect under volumetric absorption of laser pulse. Three different thermoelasticity theories are applied to construct the new model in a 2D thermoelastic semiconducting medium whose properties are temperature-dependent. The medium surface is exposed to laser radiation having spatial and temporal Gaussian distributions; in addition, the surface is considered traction-free. The general solutions were obtained analytically via Laplace and Fourier transformations; for Laplace inverse, we use the well-known Riemann sum approximation. As an application and consistency validation, silicon material is used.
1 Introduction
Biot is credited by developing the coupling between temperature and strain in his formulation of the classical coupled theory of thermoelasticity (CTE) in 1956 [1]. However, a flaw in this theory gave rise to the concept of generalized thermoelasticity; see, for instance, [2]. The first generalization was proposed by Lord and Shulman (LS) [3]; instead of relying on Fourier’s law, LS’s theory relies on another heat conduction law involving relaxation time [4, 5]. Hence, the produced thermal waves are physically accepted; see [6]. Due to its application in thermoelasticity, this theory has been widely used in many studies [7, 8]. Green and Lindsay (GL) [9] followed LS’s theory with a generalization with two relaxation times that considered temperature–rate dependence. This theory has been applied in many problems of thermoelasticity, making it an essential part of its development; see [10, 11].
Semiconductor materials, which have a wide range of applications in physics and engineering, are among the most significant materials that have directly influenced technological advancement [12, 13]. Thermoelasticity (TE) and the deformation of electrons DE are the two basic mechanisms that are produced when a semiconductor surface is subjected to a laser beam; for further information, see [14]. Recently, the relationship involving TE and DE has become necessary, which increases the viability of using generalized theories to study wave propagation in a semiconductor medium [15]. Various generalizations were used by Lotfy and Lotfy et al. [16–18] to examine the photothermal illumination phenomenon in various results. Ezzat [19] used a novel model within the context of time-fractional derivatives to examine the impacts of combined plasma and thermal waves in a viscoelastic material. In semi-infinite semiconductor materials with such a cylindrical cavity exposed to thermal shock under a simulated model considering variable thermal conductivity, for the investigation of photothermoelastic consequences, we refer to [20]. Youssef and El-Bary [21] addressed a two-dimensional semiconductor material cylinder driven by ramp-type heat through the use of the LS framework to discuss photothermoelastic coupling. More recently, Tayel and Lotfy [22] and Mohammed and Tayel [23] studied the photothermal effects induced by a laser pulse under the new modification of Green and Lindsay (MGL).
Due to the numerous uses of thermoelasticity, the study of materials whose characteristics are temperature-dependent has become increasingly important. The overwhelming majority of results now available on thermoelasticity are achieved for temperature-independent material, despite the fact that components fluctuate at high temperatures; for examples, see [24, 25] and the references within. In terms of the generalized thermoelasticity, some valuable works with significant results for understanding the effect of the influences of temperature-dependent features could be seen in [26–29].
Many applications have been introduced in the fields of science and engineering based on special features of lasers. In material processing various fields such as cutting, drilling of holes, glazing of materials, and spot welding, high-power lasers are utilized [30, 31]. In semiconductor material, excitation caused by laser radiation generates three different waves: thermal, elastic, and plasma waves. Several papers have discussed the transportation processes induced by the laser pulse in semiconductor materials; see [32–36].
Microelongated materials can be found in many branches of material science; some examples of microelongated media involve solid–liquid crystals, structural materials reinforced with crushed elastic fibers, and porous materials having pores stuffed to the gills with gases or non-viscous fluid. It should be noted that numerous effects on microelongated thermoelasticity, such as initial stress, and also comparing relaxation times including their effects on all physical parameters, have not received much attention; see [37–41].
In this paper, we shall discuss the volumetric absorption of laser radiation in a 2D thermoelastic microelongated semiconducting half space whose properties are temperature-dependent. We introduce a novel model based on the coupling of TE, plasma, and microelongation waves by means of three different theories of thermoelasticity, namely, CTE, LS, and GL. Moreover, the temperature-dependent properties are investigated through all the aforementioned waves.
2 Problem setting and basic equations
In what follows, we introduce the system of governing equations that consider the microelongation effect coupled with plasma and TE response. We start by
Energy is represented as follows [38]:The plasma wave equation, which depicts the interaction between plasma and temperature, is as follows [13]:
The equation of motion is given as follows [18, 42]:Microelongation is represented as follows [18, 42]:The microelongation constitutive equation is as follows [43–45]:
where , γ1 = (3λ + 2 μ)αt1, δn = (3λ + 2μ)dn, and γ2 = (3λ + 2 μ)αt2. For a volumetric technique of heating, we let
The aforementioned system of equations can be classified according to the values of
n0and
n1as follows:
1. The classical coupled theory of thermoelasticity (CTE), when n1 = 1, n0 = 0, τ0 =, and v0 = 0.
2. Lord and Shulman theory (LS) when n1 = n0 = 1, v0 = 0, and τ0 > 0.
3. Green and Lindsay theory (GL), when n1 = 1, n0 = 0, and v0 > τ0 > 0.
Consider a TE isotropic and homogeneous microelongated semiconducting 2D half space to be at a reference temperature T0. The medium surface x = 0 is subjected to a laser pulse and considered traction-free.
Due to the two-dimensional effect of ED and TE deformations, we assume that our primary fields depend on (x, z, t). In this setting, the scalar microelongational function in the xz-plane and displacement tensor ui will be written as follows:Thus, the cubic dilatation is expressed as follows:Let us assume the following parameters to be temperature-dependent; see [28, 46]:where f(T0), a given linear dimensionless function, takes the formand ζ is an empirical parameter.
Consequently, our system becomes (2)–(1):andwhere θ = T − T0 is the increment of the temperature.
We now introduce the initial and boundary conditions for the considered problem as follows:The initial conditions areand the boundary conditions becomewhere s0 is the surface recombination velocity.It is possible to use dimensionless variables to make the computations simpler, such asIn computations, the primary governing equations are simplified using Eq. 18, which results in the following:andThe constitutive relations according to Eq. 5 can be written as follows:and the boundary conditions becomeHere, we combine Eqs. 22, 23 to become
where
3 Problem solution
The method of integral transformation will be applied using the first Laplace transform for the variable of t and then the Fourier transform for the coordinate z.Now, introduce Laplace transformThen, Fourier transformApplying Fourier and Laplace transformations for Eqs. 19–21 and Eq. 22, this gives the following system:where is Q(z, t) in the transformed domain, and
Eliminating and from Eqs. 32–35, we obtain the following:and
Eliminating from (36) and (37), we getwhereandFactoring Eq. 38, we obtainwhere are the roots of the characteristic equation.
Eq. 39 has the following solution:where
The solution in terms of is obtained in a similar manner; we havewhereEq. 41 is solved as follows:wherewhereUsing Eq. 33, we havewhere
In a similar way, we getwhereandAs for the displacement, Eq. 22 can be written as follows:where , , and a7 = a6ϵ1.
Using Laplace and Fourier transformation to the last equation, one getsThe solution of the non-homogeneous ordinary differential Eq. 50 giveswhereandTo get the other components, namely, , we will use Eq. 7 in the transformed domain; we have
Here, we consider the stresses related to the boundary conditions only, so we have
whereandNow, to attain the constants Bi, (i = 1, …, 4) and R, we use (28) to obtain the following system:From this, we complete the solution.
4 Inverse of the transformation
In this section, we obtain the inverse of the solutions derived in the aforementioned section; we start by applying the inverse Fourier transform using the following formula:where is understood in the sense of Laplace transform. After that, an inverse by means of Laplace is needed; for this, we use the well-known Riemann sum approximation:For a faster convergence, we let ϕ = 4.7/t; see [47].
5 Special case
In order to increase the visibility of our results, we shall consider a special case when obtaining the numerical results. In particular, we neglect the effect of microelongation, i.e., we take .
6 Application
Consider a silicon material’s half-space being subjected to a laser beam with a Gaussian profile aswhere and .
The following constants, which are based on [48], will be used to calculate the surface temperature θ(0, t), temperature θ, carrier density N displacement u, and stresses σxx and σxz.
7 Numerical investigation
The computational results are divided into two groups. Group A shows the effect of the temperature-dependent properties for LS theory, while group B describes the consistency of the results through three different models. Through this, all the calculations are carried out for t = 4 × 10−3 and z = 0.0001.
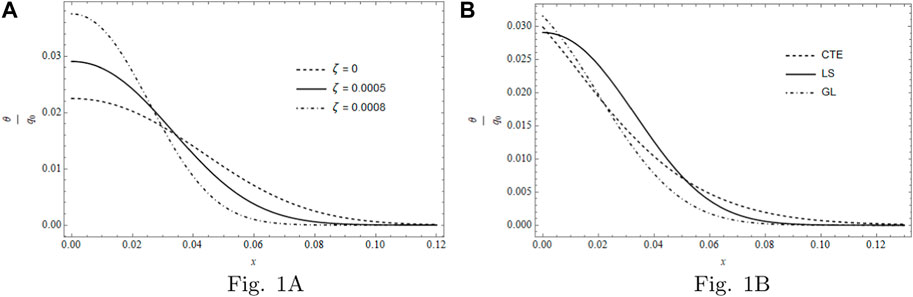
Figure 1 is combined of two sub-graphs. Figure 1A represents θ/q0 at t = 4 × 10−3 for different ζ values, namely, ζ = 0, ζ = 5 × 10−4 and ζ = 8 × 10−4 for LS theory. Figure 1B depicts θ/q0 at t = 4 × 10−3 for a fixed ζ value, that is, ζ = 5 × 10−4 by taking into account three different models: LS, CTE, and GL. From the two sub-figures, we note that the temperature reached its maximum at the irradiated surface and then declined inside the medium until it totally vanishes. Figure 1A shows that the temperature increases as ζ increases, and the penetration inside the medium decreases as ζ increases. Figure 1B shows the GL model possessing the maximum temperature at the surface with lower penetration and that CTE has the maximum penetration into the medium; it is also noted that the LS model has a weak slope near the surface.
FIGURE 1
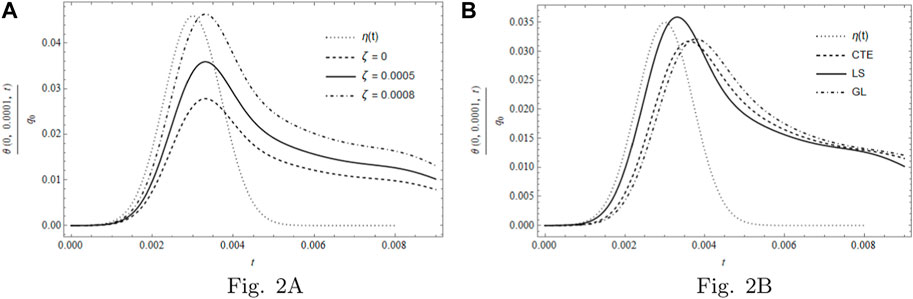
Figure 2 contains two sub-figures, these are as follows: Figure 2A, which displays the temporal surface temperature θ(0, 0.0001, t) per q0 for different ζ values, namely, ζ = 0, ζ = 5 × 10−4 and ζ = 8 × 10−4 for LS theory, and Figure 1B, which describes the temporal surface temperature θ(0, 0.0001, t) per q0 for a fixed ζ value, that is, ζ = 5 × 10−4 considering the three models. The general behavior of the two sub-figures could be stated in the following statement“ The temperature increases until it achieves its maximum with a notably shift from the maximum of laser pulse; after that decreases but it will not be totally eliminated, see [30] for more explanation”. From Figure 2A, we note that the temperature achieves its peak at a longer time when ζ is small enough, which makes the peak value increase with ζ. We also note that the peak gets closer to the profile with greater ζ. At the same time, the curves preserve their behavior even after the laser turns off. In Figure 2B, we see that the LS model gets its peak at a time closer to the maximum of η(t). In addition, this model has the greatest maximum temperature compared with other two models.
FIGURE 2
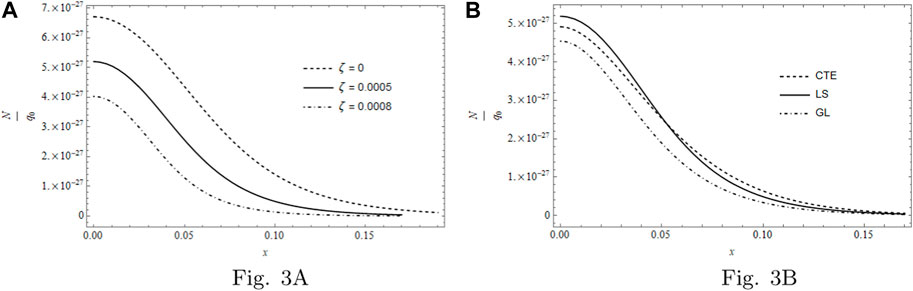
The spatial carrier density distribution N represented in Figure 3, as the previous sub-Figure 3A, outlines the carrier distribution N for ζ = 0, ζ = 5 × 10−4 and ζ = 8 × 10−4 at time t = 4 × 10−3, and sub-Figure 3B describes the carrier density distribution N for a fixed ζ value, that is, ζ = 5 × 10−4, considering the three models. The effect that took place by the parameter ζ can be clearly seen in Figure 3A that it is inversely proportional to the plasma. In Figure 3B, the model of LS possesses the greatest carrier density at the surface, while the GL model possesses the lower carrier density. Moreover, it is noted that penetration is approximately the same for the three models.
FIGURE 3
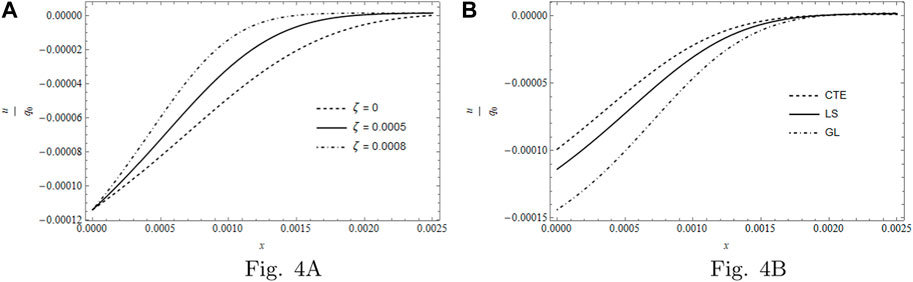
The spatial displacement u represented by Figure 4, as the previous sub-Figure 4A outlines the displacement distribution u for ζ = 0, ζ = 5 × 10−4 and ζ = 8 × 10−4 at time t = 4 × 10−3 and sub-Figure 4B describes the displacement distributions u for a fixed ζ value, that is, ζ = 5 × 10−4, considering the three models. The displacement appears in a region close to the surface and attains negative values; from Figure 4A that represents the effect of ζ, it is clearly seen that the displacement has the same value for all values of ζ at the surface and different penetration inside the medium. Figure 4B describes the case of the three mentioned models; it is noted that the GL model possesses the greatest displacement at the surface, while the CTE possesses the smallest displacement, and the penetration of the three models is slightly the same.
FIGURE 4
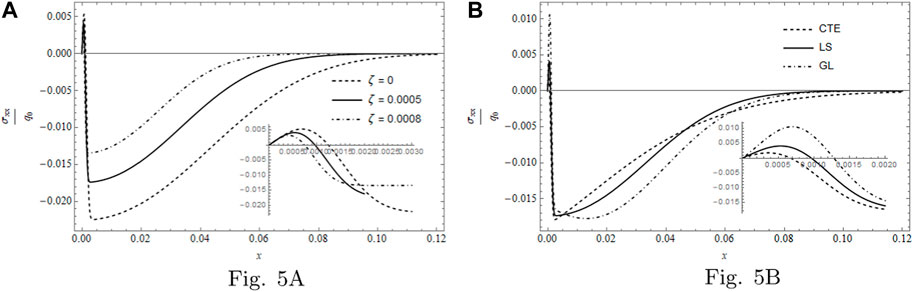
Figure 5 contains two sub-figures; these are as follows: Figure 5A, which displays the stress σxx per q0 for ζ = 0, ζ = 5 × 10−4 and ζ = 8 × 10−4 for LS theory, and Figure 5B, which describes the stress σxx per q0 for a fixed ζ = 5 × 10−4, considering the three models. In both cases, the figure contains a small sub-figure representing the stress distribution in a region close to the surface; this figure shows that the stress obeys the given boundary condition. As for Figure 5A, we see that the positive peak getting smaller as ζ increases. We note that all curves matched together on the illuminated surface until the positive peak is achieved; after that, for a larger ζ, the gradient gets steeper. We can also see that when ζ = 0, the penetration takes the largest value. In Figure 5B, the curve behavior is preserved as in Figure 5A, and the positive peak of the GL model is the greatest, while that of the CTE is the smallest; moreover, the penetration of the CTE is the greatest.
FIGURE 5
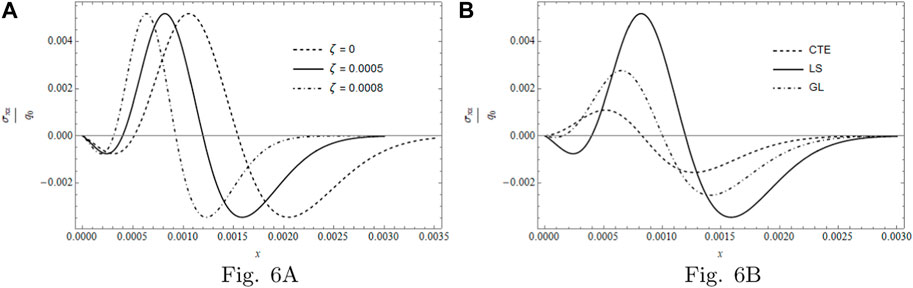
Figure 6 contains two sub-figures; these are as follows: Figure 6A, which displays the stress σxz per q0 for ζ = 0, ζ = 5 × 10−4 and ζ = 8 × 10−4 for LS theory, and Figure 6B, which describes the stress σxz per q0 for a fixed ζ = 5 × 10−4, considering the three models. Figure 6A shows that the increment of ζ caused a delay in both negative and positive peaks. Figure 6B shows that the only model with a negative peak near to the surface is that of LS, and also, LS possesses the highest peaks in both cases (negative and positive peaks).
FIGURE 6
8 Conclusion
In this paper, we introduced a fully coupled system of equations that represents thermal, plasma, elastic, and microelongation effects, and the novel system based on three different theories of thermoelasticity. This system has been applied to 2D TE microelongated semiconducting half space whose properties are temperature-dependent, considering the volumetric absorption illumination induced by a pulsed laser. From the forgoing discussions, we can conclude that
• The obtained results are in line with the physical interpretations.
• A clear effect for the temperature-dependent properties on all variables.
• The GL and CTE models consume more energy and take longer time than the LS model to achieve their peaks.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
KL: conceptualization and methodology. MM: software and data curation. IT: writing—original manuscript preparation. KL: supervision. JA: visualization and investigation. AE-B: software, validation, and writing—reviewing and editing. All authors contributed to the article and approved the submitted version.
Funding
The authors extend their appreciation to the deputyship for research and innovation, the Ministry of Education in Saudi Arabia, for funding this research work through the project number (IFP-2022-47).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Glossary
| λandμ | Lamé’s constants |
| Deformation potential difference | |
| dn | Electronic deformation coefficient |
| T | Absolute temperature |
| N | Carrier density |
| T0 | Reference temperature |
| Volume thermal expansion | |
| Linear thermal expansion | |
| σij | Microelongation stress |
| Ρ | Density |
| K | Thermal conductivity |
| CE | Specific heat at constant strain |
| n0 | Equilibrium-free carrier at temperature T |
| DE | Carrier diffusion coefficient |
| Ρ | Density |
| CE | Specific heat at constant strain |
| Τ | Photo-generated carrier lifetime |
| Eg | Energy gap |
| ei,j | Strain tensor component |
| j0 | Microinertia of the microelement |
| λ1, λ2.α | Microelongational material constants |
| τ0, ν0 | Thermal relaxation times |
| Φ | Scalar microelongational function |
| mk | Microstretch component |
| s = sii | Stress tensor component |
References
1.
BiotMA. Thermoelasticity and irreversible thermodynamics. J Appl Phys (1956) 27(3):240–53. 10.1063/1.1722351
2.
SheriefHEl-SayedAMAAbd El-LatiefAM. Fractional order theory of thermoelasticity. Int J Sol Struct (2010) 47(2):269–75. 10.1016/j.ijsolstr.2009.09.034
3.
LordHWShulmanY. A generalized dynamical theory of thermoelasticity. J Mech Phys Sol (1967) 15(5):299–309. 10.1016/0022-5096(67)90024-5
4.
AwadEFayikMEl-DhabaAR. A comparative numerical study of a semi-infinite heat conductor subject to double strip heating under non-Fourier models. Eur Phys J Plus (2022) 137:1303. 10.1140/epjp/s13360-022-03488-8
5.
FayikMAlhazmiSEAbdouMAAwadE. Transient finite-speed heat transfer influence on deformation of a nanoplate with ultrafast circular ring heating. Mathematics (2023) 11:1099. 10.3390/math11051099
6.
SheriefHHElmisieryAEMElhagaryMA. Generalized thermoelastic problem for an infinitely long hollow cylinder for short times. J Therm Stresses (2004) 27(10):885–902. 10.1080/01495730490498331
7.
SheriefHH. On uniqueness and stability in generalized thermoelasticity. Q Appl Math (1987) 44:773–8.
8.
HenainEFHassanAFMegahedFTayelIM. Thermo-elastic half space under illumination of a laser beam using Lord and Shulman theory. J Therm Stresses (2014) 37(1):51–72. 10.1080/01495739.2013.839431
9.
GreenAELindsayKA. Thermoelasticity. J Elast (1972) 2(1):1–7. 10.1007/BF00045689
10.
SheriefAHH. State space approach to thermoelasticity with two relaxation times. Int J Eng Sci (1993) 31(8):1177–89. 10.1016/0020-7225(93)90091-8
11.
SheriefHHHusseinEM. Fundamental solution of thermoelasticity with two relaxation times for an infinite spherically symmetric space. J App Math Phys (2017) 68(2):1–14. 10.1007/s00033-017-0794-8
12.
MahdyAMSLotfyKEl-BaryATayelIM. Variable thermal conductivity and hyperbolic two-temperature theory during magneto-photothermal theory of semiconductor induced by laser pulses. Eur Phys J Plus (2021) 136:651.
13.
SongYQBaiJTRenZY. Study on the reflection of photothermal waves in a semiconducting medium under generalized thermoelastic theory. Acta Mech (2012) 223:1545–57. 10.1007/s00707-012-0677-1
14.
TrodovicDMNikolicPMBojicicAI. Photoacoustic frecuency transmissin technique: Electronic deformation mechanism in semiconductors. J Appl Phys (1999) 85:7716. 10.1063/1.370576
15.
TrodovicDM. Plasma, thermal and elastic waves in semeconductors. Rev Sci Instrum (2003) 74(1):528. 10.1063/1.1523133
16.
LotfyK. Effect of variable thermal conductivity during the photothermal diffusion process of semiconductor medium. Silicon (2019) 11:1863–73. 10.1007/s12633-018-0005-z
17.
LotfyKEl-BaryAA. Thomson effect in thermo-electro-magneto semiconductor medium during photothermal excitation process. In: Waves random complex media (2020). 10.1080/17455030.2020.1838665
18.
SaeedAMLotfyKEl-BaryAA. Effect of variable thermal conductivity and magnetic field for the generated photo-thermal waves on microelongated semiconductor. Mathematics (2022) 10:4270. 10.3390/math10224270
19.
EzzatM. A novel model of fractional thermal and plasma transfer within a non-metallic plate. Smart Struct Syst (2021) 27(1):73–87. 10.12989/sss.2021.27.1.073
20.
AbbasIHobinyAMarinM. Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J Taibah Univ Sci (2020) 14(1):1369–76. 10.1080/16583655.2020.1824465
21.
El-BaryAAYoussefHM. Characterization of the photothermal interaction due to ramp-type heat on a semiconducting two-dimensional solid cylinder based on the Lord–Shulman model by using double Laplace transform. Mech Based Des Struct Mach (2021). 10.1080/15397734.2020.1833740
22.
TayelIMLotfyK. Photothermal effects in semiconductors induced by surface absorption of a uniform laser radiation under modified Green–Lindsay theory. Eur Phys J Plus (2021) 136:932. 10.1140/epjp/s13360-021-01941-8
23.
MohammedMAYTayelIM. Photothermal influences in semiconductors with temperature-dependent properties generated by laser radiation using strain–temperature rate-dependent theory. Eur Phys J Plus (2022) 137:703. 10.1140/epjp/s13360-022-02910-5
24.
LomakinVA. Theory of nonhomogeneous elastic bodies. Moscow (1976).
25.
EzzatMAOthmanMIEl-KaramanyAS. The Dependence of the Modulus of elasticity on the reference temperature in generalized thermoelasticity. J Thermoelast (2001) 24:1159–76.
26.
YoussefHM. Dependence of modulus of elasticity and thermal conductivity on reference temperature in generalized thermoelasticity for an innite material with a spherical cavity. Appl Math Mech (2005) 26:470–5. 10.1007/BF02465386
27.
AllamMNElsibaiKAAboudlregalAE. Magneto-thermoelasticity for an innite body with a spherical cavity and variable properties without energy dissipation. Int J Sol Struct. (2010) 47:2631–8. 10.1016/j.ijsolstr.2010.04.021
28.
OthmanMIATantawiRSErakiEEM. Effect of initial stress on a semiconductor material with temperature dependent properties under DPL model. Microsyst Technol (2017) 23:5587–98. 10.1007/s00542-017-3326-8
29.
TayelIMMohamedM. Surface absorption illumination in a generalized thermoelastic layer under temperature-dependent properties using MGL model. In: Waves in random and complex media (2021). 10.1080/17455030.2021.1974120
30.
TayelIM. Generalized functionally graded thermoelastic layer under the effect of volumetric absorption of laser radiation. Mech Based Des Struct Mach (2022) 50(10). 10.1080/15397734.2020.1814155
31.
TayelIMHassanAF. Heating a thermoelastic half space with surface absorption pulsed laser using fractional order theory of thermoelasticity. J Theor Appl Mech (2019) 57(2):489–500. 10.15632/jtam-pl/105469.
32.
LotfyKHassanWEl-BaryAKadryM. Response of electromagnetic and Thomson effect of semiconductor mediumdue to laser pulses and thermal memories during photothermal excitation. Resu Phys (2020) 16:102877. 10.1016/j.rinp.2019.102877
33.
KhamisAKEl-BaryAALotfyKBakaliA. Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alex Eng J (2020) 59(1):1–9. 10.1016/j.aej.2019.11.016
34.
AlzahraniFSAbbasIA. Photo-thermal interactions in a semiconducting media with a spherical cavity under hyperbolic two-temperature model. Mathematics (2020) 8(4):585. 10.3390/math8040585
35.
HobinyA. Effect of the hyperbolic two-temperature model without dissipation on photo-thermal interaction in a semi-conducting medium. Results Phys (2020) 18:103167. 10.1016/j.rinp.2020.103167
36.
AbbasISaeedTAlhothualiM. Hyperbolic two-temperature photo-thermal interaction in a semiconductor medium with a cylindrical cavity. Silicon (2020) 13:1871–8. 10.1007/s12633-020-00570-7
37.
ShawSMukhopadhyayB. Moving heat source response in a thermoelastic microelongated solid. J Eng Phys Thermophys (2013) 86:716–22.
38.
AilawaliaPSachdevaSKPathaniaDS. Internal heat source in thermoelastic microelongated solid under green lindsay theory. J Theor Appl Mech (2016) 46:65–82. 10.1515/jtam-2016-0011
39.
AilawaliaPSinglaA. A thermoelastic microelongated layer immersed in an infinite fluid and subjected to laser pulse heating. Mech Mech Eng (2019) 23:233–40. 10.2478/mme-2019-0031
40.
OthmanMIAAtwaSYErakiEEIsmailMF. A thermoelasticmicro-elongated layer under the effect of gravity in the context of the dual-phase lag model. J Appl Math Mech (2021) 101(12):e202100109. 10.1002/zamm.202100109
41.
OthmanMIAIsmailMF. The gravitational field effect on a micro-elongated thermoelastic layer under the fluid load, using the lord-shulman theory and dual-phase-lag model. Multidis Model Mater Struct (2022) 18(5):757–71.
42.
CiccoDNappaL. On the theory of thermomicrostretch elastic solids. J Therm Stress (1999) 22:565–80.
43.
EringenAC. Microcontinuum field theories. In: Foundations and solids, 1. New York, NY, USA: Springer (1999).
44.
EringenAC. Linear theory of micropolar elasticity. J Math Mech (1966) 15:909–23.
45.
EringenAC. Theory of thermo-microstretch elastic solids. Int J Eng Sci (1990) 28:1291–301.
46.
OthmanMIAJahangirANadiaA. Microstretch thermoelastic solid with temperature-dependent elastic properties under the influence of magnetic and gravitational field. J Braz Soc Mech Sci Eng (2018) 40:332. 10.1007/s40430-018-1204-7
47.
TzouDY. Experimental support for the lagging behavior in heat propagation. J Thermophys Heat Transfer (1995) 9(4):686–93. 10.2514/3.725
48.
TayelIMLotfyKEl-BaryAAAlebraheemJMohammedMAY. Microelongated thermo-elastodiffusive waves of excited semiconductor material under laser pulses impact. Mathematics (2023) 11:1627. 10.3390/math11071627
Summary
Keywords
volumetric absorption, microelongation, semiconductors, photogeneration process, generalized thermoelasticity
Citation
Tayel IM, Alebraheem J, Mohammed M, Lotfy K and El-Bary AA (2023) Volumetric absorption illumination induced by laser radiation in a 2D thermoelastic microelongated semiconductor body with temperature-dependent properties. Front. Phys. 11:1213440. doi: 10.3389/fphy.2023.1213440
Received
27 April 2023
Accepted
16 May 2023
Published
01 June 2023
Volume
11 - 2023
Edited by
Mahmoud Abdelrahman, Mansoura University, Egypt
Reviewed by
Hamdy M. Youssef, Umm Al-Qura University, Saudi Arabia
Emad Awad, Alexandria University, Egypt
Updates
Copyright
© 2023 Tayel, Alebraheem, Mohammed, Lotfy and El-Bary.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ismail M. Tayel, i.tayel@mu.edu.sa; Jawdat Alebraheem, j.alebraheem@mu.edu.sa; Mogtaba Mohammed, mogtaba.m@mu.edu.sa; Khaled Lotfy, khlotfy_1@yahoo.com; Alaa A. El-Bary, aaelbary@aast.edu
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.