- 1Institute of High Pressure Physics, Ningbo University, Ningbo, China
- 2School of Physical Science and Technology, Ningbo University, Ningbo, China
- 3School of Physics and Astronomy, Cardiff University, Cardiff, Wales, United Kingdom
- 4Department of Nanotechnology for Sustainable Energy, School of Science and Technology, Kwansei Gakuin University, Sanda, Japan
- 5Center for Spintronics Research Network (CSRN), Osaka University, Toyonaka, Japan
Focusing on the two-dimensional (2D) Su-Schrieffer-Heeger (SSH) model, we propose an additive rule between the real-space topological invariant s of disclinations (related to the Burgers vector B) and the reciprocal-space topological invariant p of bulk wave functions (the vectored Zak phase). The disclination-induced bound states in the 2D SSH model appear only if (s + p/2π) is nonzero modulo the lattice constant. These disclination-bound states are robust against perturbations respecting C4 point group symmetry and other perturbations within an amplitude determined by p. Besides the disclination-bound states, the proposed additive rule also suggests that a half-bound state extends over only half of a sample and a hybrid-bound state, which always have a nonvanishing component of s + p/2π.
1 Introduction
Topology studies the properties of a geometric or physical system under continuous transformations in parameter spaces. Its application in condensed matter physics has, in the past few years, renewed our understanding of energy band structures of crystalline systems [1–4]. As a cornerstone, the so-called bulk-edge correspondence principle [5–9] requires that robust quantum states appear at the boundaries of samples possessing topologically nontrivial band structures [10–13]. This principle links the reciprocal-space topology (i.e., energy band structure) to real-space profiles of quantum states. It provides a foundation for potentially transformative applications in spintronics and other practical areas. Recently [14–22], the bulk-edge correspondence has been extended to higher-order topological phases, culminating in the discovery of topologically protected corner states [23–28]. Applications such as laser cavity and quantum computation have been proposed based on these corner states [29, 30].
Unlike edge states, topological corner states usually appear as bound states in the continuum of bulk spectra, which complicates their experimental detection [31–34]. However, at a disclination center of crystallographic defects, nontrivial higher-order topology induces bound states accompanied by fractional charges, which have been experimentally observed in artificial crystalline systems recently [35–38].
The correlation between the appearance of fractional charges carried by bound states at disclination centers and the reciprocal topological invariant of bulk wave functions is framed as the bulk-disclination correspondence, which offers us a general principle of detecting higher-order topological phases [39–45]. Inspired by these observations of bulk-disclination correspondence, we look into the correlation between these anomalous bound states and the real-space topology of disclinations. Focusing on a typical higher-order topological model–the two-dimensional (2D) Su-Schrieffer-Heeger (SSH) model, we propose an additive rule between the real-space topological invariant s and the reciprocal topological invariant p. The SSH model is one fundemental model of topological insulators, and its extension to higher dimensions has resulted higher-order topological insulators. Especially, because the SSH model is spinless, it is suitable for the realization of the 2D SSH model and its higher-dimensional counterparts in various artifical crystalline systems, which leads to fruitiful experimental observations of topological corner states and accompanying fractional charges. These higher-order topological states are useful in fields such as laser cavity and quantum computation [46–53]. Thus, focusing on the 2D SSH model as an example, it would be helpful for understanding the general relation between the real-space topological defects and the reciprocal topological invariant. Furthermore, our proposal gives a possible explanation for the emergence of disclination-bound states, which may fertilize interesting physical phenomena and applications in the interdisciplinary field of the classical real-space topology of crystallographic defects and the reciprocal-space topology of wave functions, especially in designing disclination-induced bound states in artificial crystalline systems, such as photonic, phononic crystals, and metamaterials [54].
The remaining parts of the paper are organized as follows. In Sec. 2.1, we introduce the topological defect–disclination, the 2D SSH model, and their topological invariants s and p. In Sec.2.2 we explain the proposed additive rule in terms of s and p. In Sec. 2.3, we numerically show that when s + p/2π is nontrivial, bound states appear at centers of disclinations and discuss the specific symmetry protecting them for the 2D SSH model. In Secs. 2.4 and 2.5, we show that half-bound states and hybrid-bound states appear in the centers of disclinations that have s = (0, 1/2) and s = (1/2, 0). In Sec. 3, we discuss the generalization of the additive rule to other lattices and give conclusions of our study.
2 Results
2.1 Disclinations and 2D SSH model
Being global crystallographic defects, local operations cannot remove disclinations [55]. One may use the Volterra method [56] to construct a disclination. An example is depicted in Figure 1A, where a sample is cut into a few identical wedge portions, and one (marked in yellow) is removed to form a disclination after gluing the remaining sections without lattice mismatch. According to the homotopy theory, a disclination is characterized by two parameters (Ω, B). Here Ω is the Frank angle, whose magnitude is the wedge angle and whose sign indicates adding or removing a wedge, and B is the Burgers vector, which measures the lattice distortion induced by the defect [57, 58]. Choosing a start point, B can be evaluated by comparing the loop path around the disclination core and the loop path in a defect-free sample. For more details of the calculation of the Buregers vector, please refer to the Supplementary Material. For a square lattice respecting C4 point group symmetry, Ω can only be a multiple of π/2. The group of non-equivalent classes of B is isomorphic to the discrete group Z2 and Z2 ⊗ Z2 for Ω = ±π/2 and ± π, respectively [42]. The details of equivalenece classes of B is discussed in the Supplementary Material.
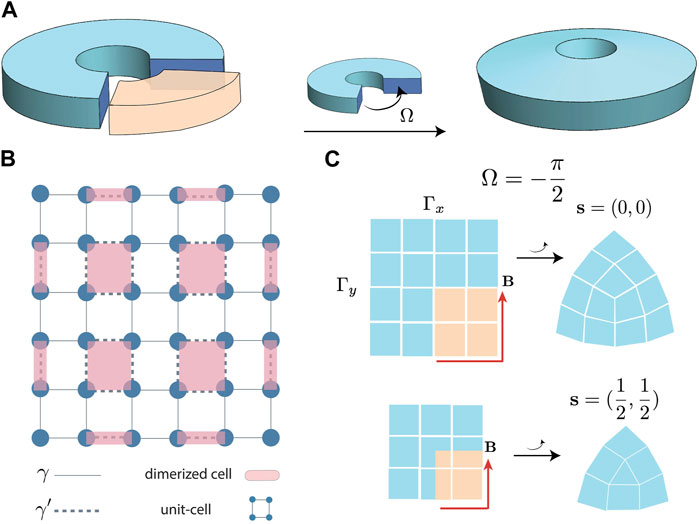
FIGURE 1. Construction and characteristic of a disclination. (A). Schematic of Volterra process for constructing a disclination. A wedge part spanning angle |Ω| is cut off from a symmetric sample, and the remaining sections are glued without any lattice mismatch. The wedge center is located at the point of rotation symmetry of the sample. The resulting disclination has a negative Frank angle Ω =−|Ω|. Alternatively, one may insert an extra wedge instead of removing the wedge, resulting in a disclination with positive Ω =|Ω|. (B). Sample of the 2D SSH model in the case of |γ|<|γ′| that respects C4 point group symmetry, where solid/dashed line indicates the intra/inter-cell hopping of strength γ/γ′, and square/shade indicates the unit/dimerized cell. (C). Two types of disclinations with Ω =−π/2 allowed for samples with C4-point group symmetry characterized by s. Each square represents a unit cell, and the lighter ones are the wedges being removed. s is determined by the parity of the numbers of unit cells on the x- and y-boundaries as
To concrete our study, we consider the 2D SSH model [59, 60], one of the typical models that admit topological corner states [26, 27, 60–62]. A sample of the 2D SSH model is depicted in Figure 1B, where the unit cell consists of four sub-lattices forming a square Bravais lattice. There are two types of hopping, namely, the intra-cell hopping γ and the inter-cell hopping γ′. Depending on the ratio of |γ/γ′|, the 2D SSH model can be in the atomic insulator phase or the atomic-obstructed phase. For the atomic insulator phase, its Wannier center coincides with the atomic lattice, for the atomic-obstructed phase, its Wannier center locates at the middle of two unit-cells. It is noted that for the atomic-obstructed phase, the Wannier center cannot be changed untill the band gaps close. For the detials of the band structure and fractional charge of the 2D SSH model, please refer to the Supplementary Material. For |γ| < |γ′| as in Figure 1B, the lowest energy band is inverted at (π/a, 0) and (0, π/a) in the reciprocal-space (with a the lattice constant) and becomes topologically nontrivial accompanying with corner states [59]. The appearance of topological corner states in the 2D SSH model is owing to the shift of dimerized cells as displayed by the light magenta square in Figure 1B, whose centers are related to the vectored Zak’s phase p = (px, py) by a factor of
Figure 1C displays two distinct disclinations with Ω = −π/2 for the 2D SSH model, where the square represents the unit cell, and the intra-cell and inter-cell hoppings are omitted. Depending on the unfolded Burgers vector B in undistorted space (indicated by red vectors in Figure 1C), the disclinations of Ω = −π/2 are classified into two topologically distinct types as labeled by s = (0, 0) and s = (1/2, 1/2), respectively. The relation between B and s is given as
2.2 Proposed additive rule
Considering that the removal or addition of the wedge part resolves the filling anomaly at the disclination center, we expect a concurrent action of the real-space topological invariant s and the reciprocal topological invariant p, which we propose as an additive rule between them. In Table 1, s is tabulated for all possible values of Ω for the 2D SSH model. The integers inside Table 1 are the numbers of bound states at the different types of disclination centers for both trivial and nontrivial reciprocal topologies. From Table 1, we see that even for the trivial reciprocal topology, bound states exist as s + p/2π is nontrivial, whereas for the nontrivial p bound state is missing if s + p/2π is trivial. We define the net topology of real-space and reciprocal topology as
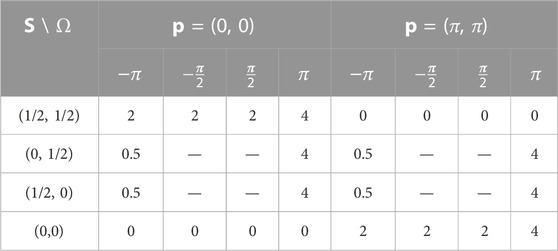
TABLE 1. Number of bound states for different disclination types and reciprocal topology. The disclination is characterized by the real space topological invariant s and the Frank angle Ω. Ω takes the value of −π,
Previous studies suggest that the relationship between real and reciprocal spaces should be multiplicative [21, 36, 67, 68]. We obtain the additive rule because we focus on the bound states rather than the fractional charge. As discussed in Ref. [36], the fractional charge at the disclination core is given by the formula
2.3 Bound states and fractional charges
The first phenomenon of the proposed additive rule is the dissociation of fractional charges from bound states. The construction of disclination lattices and the caculation of fractional charge is discussed in the Methods section. We consider the samples with
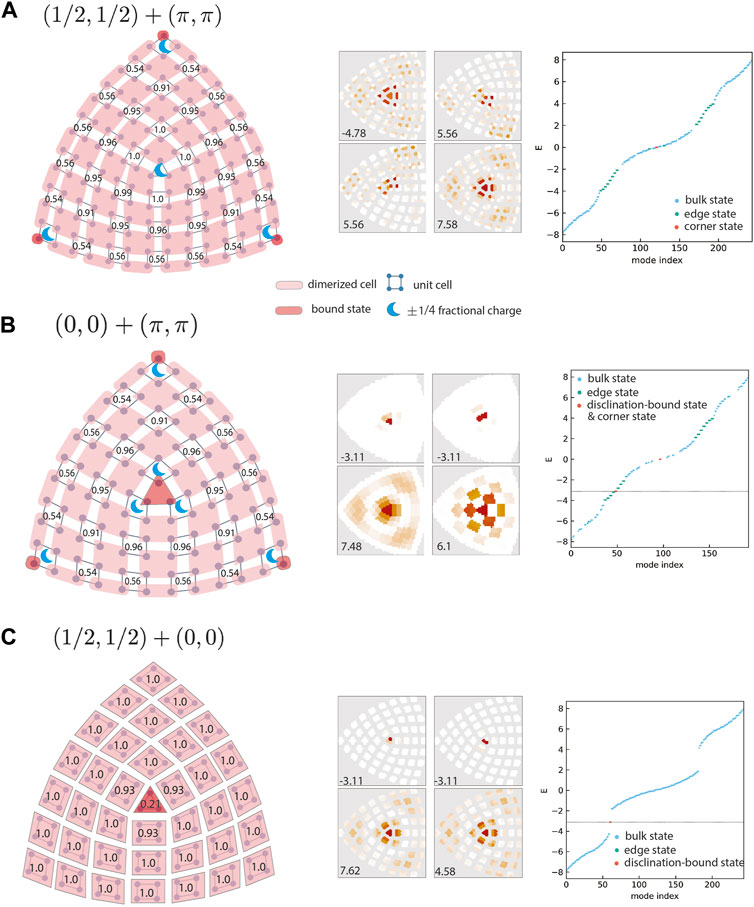
FIGURE 2. Fractional charge and bound state dissociation for
As can be seen in the left panel of Figure 2A, fractional charges appear at the disclination center and the sample corners, but bound states are absent at the center (see also the right panel of Figure 2A) even with the nontrivial reciprocal topology p. This result can be intuitively understood using the dimerization of sites as shown by lighter magenta squares in the left panel of Figure 2A. As explained earlier, the corner state accompanying with 1/4 fractional charge appears due to dimerized cells shifting from the original Bravais lattice and the resulting filling anomaly. However, here in Figure 2A, the filling anomaly at the disclination center that is supposed to be induced by nontrivial p is canceled out by the nontrivial real-space topological invariant s. As a result, no fractionally filled dimerized cell is isolated from the bulk states, as suggested by the additive rule between s and p.
Figure 2B shows the disclination with trivial s = (0, 0) but non-trivial p = (π, π). Since the additive rule gives nontrivial
As the emergence of disclination-bound states is due to the dimerization at the disclination core, it is worth discussing the robustness of these bound states. Here we consider two types of perturbations. One is the perturbation without respecting the C4 point group symmetry, and another is the perturbation respecting the C4 point group symmetry. For the first type of perturbation, we consider three possibilities: onsite potential on the disclination center sites, a dangling bond in the disclination center, and inter-cell hopping connecting sites belonging to the same sub-lattice. As detailed in the Supplementary Material, for the perturbations without C4 point group symmetry, the amplitude of perturbations cannot go beyond |γ − γ′|; otherwise, the disclination-bound states disappear. For the second type of perturbations respecting C4 point group symmetry, the amplitude of perturbations can go beyond |γ − γ′|. This is because of the unique real-space structure in the disclination core, where one sublattice is missing in the central dimer of disclinations that disclination-bound states cannot mix with bulk states respecting C4 point group symmetry. It is noted that the disclination-bound states are not located at zero energy, which suggests the absence of chiral symmetry in the formation of disclination-bound states [45, 69, 70].
2.4 Half-bound states
The second phenomenon of the proposed additive rule is the formation of half-bound states, which decay on one side of the sample but extend over the other. Here we consider a disclination structure with a unsymmetric s index, i.e., (sx, sy) = (0, 1/2) for Ω = −π as displayed in Figure 3. A bound state can be viewed as a wave function with a purely imaginary wavenumber for all independent real-space directions. Because of the unsymmetric disclination structure between kx and ky directions, a half-bound state can be expected. As displayed in Figures 3A, B, we find such half-bound states in our numerical calculations. Interestingly, the decaying direction for the half-bound states depends on the summation value of s + p/2π. As displayed in Figure 3A, when sy + py/2π is nontrivial, the half-bound state decays along the x side. While sx + px/2π is nontrivial, the half-bound state decays along the y side, as displayed in Figure 3B. This is perhaps because of the spatial distortion induced by the disclination structure.
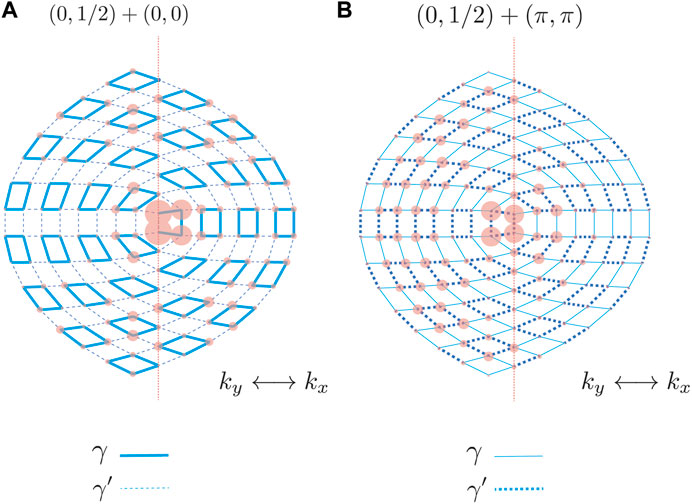
FIGURE 3. Existence of half-bound states. The disclinations have Ω =−π and s =(0,1/2). (A). p =(0,0), the state decays on the x-side but extends over the y-side. (B). p =(π, π), it decays on the y-side but extends over the x-side on the other hand. A dashed line passes through the center of the disclination, which divides the sample into x- (perpendicular to ky direction of the reciprocal space) and y- (perpendicular to kx direction of the reciprocal space) parts.
It is noted that the formation of half-bound states seems analogous to edge states due to the second-order topology. In the 2D SSH model, if the systems have pxpy = 0 but px + py ≠ 0, only edge states exist but no corner state. In the present case, this may be paraphrased: For two-sided systems with sxsy = 0 but sx + sy ≠ 0, only a half-bound state exists but not a bound state. This half-bound state can potentially control wave propagation using artificial crystalline structures such as photonic crystals. These states are impervious to the system size as shown in the Supplemntal Material. For the practical realization of the half-bound state, the hopping amplitude should depend on the distance between the two sites. In this case, the lattice distortion induced by the disclination cannot be ignored. The site’s position should be carefully tuned to achieve a situation similar to the tight-binding model.
2.5 Hybrid-bound states
The third phenomenon of the proposed additive rule is the hybrid-bound state, which can be numerically observed in any disclination with Ω ≥ π and sx ≠ sy. Figure 4A shows a disclination with Ω = π and s = (1/2, 0). This disclination is formed by inserting two extra π/2 blocks into the sample. Considering there are only two-independent directions in two dimensions, we can regard there are three x-parts and three y-parts arranged alternately in Figure 4A. For the sample of Figure 4A, we only observe bound states rather than half-bound states. This is because there are multiple x-parts, unlike the case in Figure 3, which only has one x-part. Furthermore,
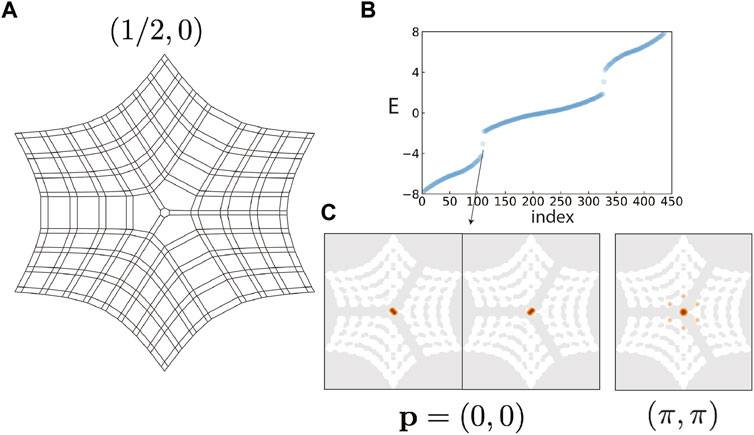
FIGURE 4. Real-space topology protected bound states and reciprocal-space topology protected ones. (A). The disclination has Ω = π and s =(1/2,0), and hence a nontrivial s + p/2π irrespective of p. (B)–(C), Topologically stable bound states invariably emerge at the disclination center. The energy levels are displayed for p =(0,0) in (B), where doubly degenerate in-gap bound states to appear. However, for p =(π, π), a symmetric charge distribution appears inside the bulk band gaps, as shown in (C).
3 Discussion
Finally, we discuss the generalization of the additive rule to other lattices. As the real-space topological invariant s is injective to nonequivalent disclination centers, and the reciprocal space topological invariant p/2π yields the Wannier center, it is intuitive to regard the additive rule as a result of the combination of disclination centers and Wannier centers. For example, for the C4-symmetric lattice, there are two and four non-equivalent disclination centers for Ω = ±π/2 and Ω = ±π, respectively, and two possible Wannier centers. Their combinations give the afore-discussed dissociation of fractional charges from bound states, half-bound states, and hybrid-bound states in the 2D SSH model. Generalizing the additive rule to other C4-symmetric is possible, which we remain as a future study.
To summarize, we proposed an additive rule between the real space and the reciprocal space topology by observing the cancellation of charge filling anomaly at the disclination core indicated by Burgers vector and the Zak phase. To support our proposal, we consider a typical higher-order topological model, the 2D SSH model, and show three pieces of evidence by numerical calculations: the dissociation of fractional charges from bound states, half-bound states, and hybrid-bound states. All those numerical calculations demonstrate the applicability of the proposed additive rule for the typical 2D SSH model.
4 Methods
For the disclination of −π/2, it can be constructed by removing the quarter of the 2D SSH lattice that is spanned by θ ∈ [0, π/2], and then changing the position of the remaining lattices according to θ → 4/3θ. The topological invariant s determines the center of the removing section and the corresponding 2D SSH model sample as displayed in Figure 1C, For other Ω, the construction of disclinations can be done following a similar process, i.e., for Ω = −π, the removing section should be half of the 2D SSH lattice, and the remaining lattices change position according to θ → 2θ. The fractional charge is calculated by solving the tight-binding model of the corresponding disclination lattice and integrating the charge density |ψ|2 up to the first band gap and summing up in each unit cell. The Python package KWANT does this numerical simulation of tight-binding [71].
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
FL conceived the idea and conducted the research project. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by the Research Starting Funding of Ningbo University, NSFC Grant No. 12074205, and NSFZP Grant No. LQ21A040004. KW acknowledges the financial support by JSPS KAKENHI (Grant Nos. 22H05473, JP21H01019, JP18H01154) and JST CREST (Grant No. JPMJCR19T1).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1213158/full#supplementary-material
References
1. Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045
2. Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057
3. Ando Y. Topological insulator materials. J Phys Soc Jpn (2013) 82:102001. doi:10.7566/JPSJ.82.102001
4. Bansil A, Lin H, Das T. Colloquium: Topological band theory. Rev Mod Phys (2016) 88:021004. doi:10.1103/RevModPhys.88.021004
5. Hatsugai Y. Chern number and edge states in the integer quantum hall effect. Phys Rev Lett (1993) 71:3697–700. doi:10.1103/PhysRevLett.71.3697
6. Fu L, Kane CL. Time reversal polarization and a Z2 adiabatic spin pump. Phys Rev B (2006) 74:195312. doi:10.1103/PhysRevB.74.195312
7. Hwang Y, Ahn J, Yang BJ. Fragile topology protected by inversion symmetry: Diagnosis, bulk-boundary correspondence, and Wilson loop. Phys Rev B (2019) 100:205126. doi:10.1103/PhysRevB.100.205126
8. Bouhon A, Black-Schaffer AM, Slager RJ. Wilson loop approach to fragile topology of split elementary band representations and topological crystalline insulators with time-reversal symmetry. Phys Rev B (2019) 100:195135. doi:10.1103/PhysRevB.100.195135
9. Wang Z, Dong L, Xiao C, Niu Q. Berry curvature effects on quasiparticle dynamics in superconductors. Phys Rev Lett (2021) 126:187001. doi:10.1103/PhysRevLett.126.187001
10. Fujita M, Wakabayashi K, Nakada K, Kusakabe K. Peculiar localized state at zigzag graphite edge. J Phys Soc Jpn (1996) 65:1920–3. doi:10.1143/JPSJ.65.1920
11. Delplace P, Ullmo D, Montambaux G. Zak phase and the existence of edge states in graphene. Phys Rev B (2011) 84:195452. doi:10.1103/PhysRevB.84.195452
12. Kane CL, Lubensky TC. Topological boundary modes in isostatic lattices. Nat Phys (2013) 10:39–45. doi:10.1038/nphys2835
13. Hafezi M, Mittal S, Fan J, Migdall A, Taylor JM. Imaging topological edge states in silicon photonics. Nat Photon (2013) 7:1001–5. doi:10.1038/nphoton.2013.274
14. Fu L. Topological crystalline insulators. Phys Rev Lett (2011) 106:106802. doi:10.1103/PhysRevLett.106.106802
15. Slager RJ, Mesaros A, Juričić V, Zaanen J. The space group classification of topological band-insulators. Nat Phys (2013) 9:98–102. doi:10.1038/nphys2513
16. Shiozaki K, Sato M. Topology of crystalline insulators and superconductors. Phys Rev B (2014) 90:165114. doi:10.1103/PhysRevB.90.165114
17. Benalcazar WA, Bernevig BA, Hughes TL. Quantized electric multipole insulators. Science (2017) 357:61–6. doi:10.1126/science.aah6442
18. Langbehn J, Peng Y, Trifunovic L, von Oppen F, Brouwer PW. Reflection-symmetric second-order topological insulators and superconductors. Phys Rev Lett (2017) 119:246401. doi:10.1103/PhysRevLett.119.246401
19. Song Z, Fang Z, Fang C. (d − 2)-dimensional edge states of rotation symmetry protected topological states. Phys Rev Lett (2017) 119:246402. doi:10.1103/PhysRevLett.119.246402
20. Qian S, Liu CC, Yao Y. Second-order topological insulator state in hexagonal lattices and its abundant material candidates. Phys Rev B (2021) 104:245427. doi:10.1103/PhysRevB.104.245427
21. Takahashi R, Zhang T, Murakami S. General corner charge formula in two-dimensional Cn-symmetric higher-order topological insulators. Phys Rev B (2021) 103:205123. doi:10.1103/PhysRevB.103.205123
22. Tan Y, Huang ZH, Liu XJ. Two-particle berry phase mechanism for Dirac and majorana kramers pairs of corner modes. Phys Rev B (2022) 105:L041105. doi:10.1103/PhysRevB.105.L041105
23. Peterson CW, Benalcazar WA, Hughes TL, Bahl G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature (2018) 555:346–50. doi:10.1038/nature25777
24. Imhof S, Berger C, Bayer F, Brehm J, Molenkamp LW, Kiessling T, et al. Topolectrical-circuit realization of topological corner modes. Nat Phys (2018) 14:925–9. doi:10.1038/s41567-018-0246-1
25. Serra-Garcia M, Peri V, Süsstrunk R, Bilal OR, Larsen T, Villanueva LG, et al. Observation of a phononic quadrupole topological insulator. Nature (2018) 555:342–5. doi:10.1038/nature25156
26. Ota Y, Liu F, Katsumi R, Watanabe K, Wakabayashi K, Arakawa Y, et al. Photonic crystal nanocavity based on a topological corner state. Optica (2019) 6:786–9. doi:10.1364/OPTICA.6.000786
27. Xie BY, Su GX, Wang HF, Su H, Shen XP, Zhan P, et al. Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals. Phys Rev Lett (2019) 122:233903. doi:10.1103/PhysRevLett.122.233903
28. Xue H, Ge Y, Sun HX, Wang Q, Jia D, Guan YJ, et al. Observation of an acoustic octupole topological insulator. Nat Commun (2020) 11:2442. doi:10.1038/s41467-020-16350-1
29. Harari G, Bandres MA, Lumer Y, Rechtsman MC, Chong YD, Khajavikhan M, et al. Topological insulator laser: Theory. Science (2018) 359:eaar4003. doi:10.1126/science.aar4003
30. Wu Y, Jiang H, Liu J, Liu H, Xie XC. Non-abelian braiding of Dirac fermionic modes using topological corner states in higher-order topological insulator. Phys Rev Lett (2020) 125:036801. doi:10.1103/PhysRevLett.125.036801
31. Hsu CW, Zhen B, Stone AD, Joannopoulos JD, Soljačić M. Bound states in the continuum. Nat Rev Mater (2016) 1:16048. doi:10.1038/natrevmats.2016.48
32. Benalcazar WA, Cerjan A. Bound states in the continuum of higher-order topological insulators. Phys Rev B (2020) 101:161116. doi:10.1103/PhysRevB.101.161116
33. Cerjan A, Jürgensen M, Benalcazar WA, Mukherjee S, Rechtsman MC. Observation of a higher-order topological bound state in the continuum. Phys Rev Lett (2020) 125:213901. doi:10.1103/PhysRevLett.125.213901
34. Liu F, Wakabayashi K. Higher-order topology and fractional charge in monolayer graphene. Phys Rev Res (2021) 3:023121. doi:10.1103/PhysRevResearch.3.023121
35. Benalcazar WA, Li T, Hughes TL. Quantization of fractional corner charge in Cn-symmetric higher-order topological crystalline insulators. Phys Rev B (2019) 99:245151. doi:10.1103/PhysRevB.99.245151
36. Li T, Zhu P, Benalcazar WA, Hughes TL. Fractional disclination charge in two-dimensional Cn-symmetric topological crystalline insulators. Phys Rev B (2020) 101:115115. doi:10.1103/PhysRevB.101.115115
37. Peterson CW, Li T, Jiang W, Hughes TL, Bahl G. Trapped fractional charges at bulk defects in topological insulators. Nature (2021) 589:376–80. doi:10.1038/s41586-020-03117-3
38. Liu Y, Leung S, Li FF, Lin ZK, Tao X, Poo Y, et al. Bulk–disclination correspondence in topological crystalline insulators. Nature (2021) 589:381–5. doi:10.1038/s41586-020-03125-3
39. Rüegg A, Coh S, Moore JE. Corner states of topological fullerenes. Phys Rev B (2013) 88:155127. doi:10.1103/PhysRevB.88.155127
40. de Juan F, Rüegg A, Lee DH. Bulk-defect correspondence in particle-hole symmetric insulators and semimetals. Phys Rev B (2014) 89:161117. doi:10.1103/PhysRevB.89.161117
41. Slager RJ, Mesaros A, Juričić V, Zaanen J. Interplay between electronic topology and crystal symmetry: Dislocation-line modes in topological band insulators. Phys Rev B (2014) 90:241403. doi:10.1103/PhysRevB.90.241403
42. Teo JC, Hughes TL. Topological defects in symmetry-protected topological phases. Annu Rev Condens Matter Phys (2017) 8:211–37. doi:10.1146/annurev-conmatphys-031016-025154
43. Slager RJ. The translational side of topological band insulators. J Phys Chem Sol (2019) 128:24–38. doi:10.1016/j.jpcs.2018.01.023
44. Roy B, Juričić V. Dislocation as a bulk probe of higher-order topological insulators. Phys Rev Res (2021) 3:033107. doi:10.1103/PhysRevResearch.3.033107
45. Geier M, Fulga IC, Lau A. Bulk-boundary-defect correspondence at disclinations in rotation-symmetric topological insulators and superconductors. Scipost Phys (2021) 10:092. doi:10.21468/SciPostPhys.10.4.092
46. Watanabe H, Po HC. Fractional corner charge of sodium chloride. Phys Rev X (2021) 11:041064. doi:10.1103/PhysRevX.11.041064
47. Jung M, Yu Y, Shvets G. Exact higher-order bulk-boundary correspondence of corner-localized states. Phys Rev B (2021) 104:195437. doi:10.1103/PhysRevB.104.195437
48. Zhang SB, Rui WB, Calzona A, Choi SJ, Schnyder AP, Trauzettel B. Topological and holonomic quantum computation based on second-order topological superconductors. Phys Rev Res (2020) 2:043025. doi:10.1103/PhysRevResearch.2.043025
49. Zhang SB, Calzona A, Trauzettel B. All-electrically tunable networks of majorana bound states. Phys Rev B (2020) 102(R):100503. doi:10.1103/PhysRevB.102.100503
50. Pahomi TE, Sigrist M, Soluyanov AA. Braiding majorana corner modes in a second-order topological superconductor. Phys Rev Res (2020) 2:032068. doi:10.1103/PhysRevResearch.2.032068
51. Li L, Zhu W, Gong J. Direct dynamical characterization of higher-order topological phases with nested band inversion surfaces. Sci Bull (2021) 66:1502–10. doi:10.1016/j.scib.2021.04.006
52. Pan XH, Luo XJ, Gao JH, Liu X. Detecting and braiding higher-order majorana corner states through their spin degree of freedom. Phys Rev B (2022) 105:195106. doi:10.1103/PhysRevB.105.195106
53. Wu J, Wang Z, Biao Y, Fei F, Zhang S, Yin Z, et al. Non-abelian gauge fields in circuit systems. Nat Electron (2022) 5:635–42. doi:10.1038/s41928-022-00833-8
54. Deng Y, Benalcazar WA, Chen ZG, Oudich M, Ma G, Jing Y. Observation of degenerate zero-energy topological states at disclinations in an acoustic lattice. Phys Rev Lett (2022) 128:174301. doi:10.1103/PhysRevLett.128.174301
55. Gopalakrishnan S, Teo JCY, Hughes TL. Disclination classes, fractional excitations, and the melting of quantum liquid crystals. Phys Rev Lett (2013) 111:025304. doi:10.1103/PhysRevLett.111.025304
56. Kleman M, Friedel J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev Mod Phys (2008) 80:61–115. doi:10.1103/RevModPhys.80.61
57. Azevedo S, Moraes F. Topological aharonov-bohm effect around a disclination. Phys Lett A (1998) 246:374–6. doi:10.1016/S0375-9601(98)00527-1
58. Alexander GP, Chen BGG, Matsumoto EA, Kamien RD. Colloquium: Disclination loops, point defects, and all that in nematic liquid crystals. Rev Mod Phys (2012) 84:497–514. doi:10.1103/RevModPhys.84.497
59. Liu F, Wakabayashi K. Novel topological phase with a zero berry curvature. Phys Rev Lett (2017) 118:076803. doi:10.1103/PhysRevLett.118.076803
60. Liu F, Deng HY, Wakabayashi K. Helical topological edge states in a quadrupole phase. Phys Rev Lett (2019) 122:086804. doi:10.1103/PhysRevLett.122.086804
61. Xu K, Zhang X, Luo K, Yu R, Li D, Zhang H. Coexistence of topological edge states and skin effects in the non-hermitian su-schrieffer-heeger model with long-range nonreciprocal hopping in topoelectric realizations. Phys Rev B (2021) 103:125411. doi:10.1103/PhysRevB.103.125411
62. Tang S, Xu Y, Ding F, Liu F. Continuously tunable topological defects and topological edge states in dielectric photonic crystals. Phys Rev B (2023) 107:L041403. doi:10.1103/PhysRevB.107.L041403
63. Zak J. Berry’s phase for energy bands in solids. Phys Rev Lett (1989) 62:2747–50. doi:10.1103/PhysRevLett.62.2747
64. Vanderbilt D, King-Smith RD. Electric polarization as a bulk quantity and its relation to surface charge. Phys Rev B (1993) 48:4442–55. doi:10.1103/PhysRevB.48.4442
65. Resta R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev Mod Phys (1994) 66:899–915. doi:10.1103/RevModPhys.66.899
66. Fang C, Gilbert MJ, Bernevig BA. Bulk topological invariants in noninteracting point group symmetric insulators. Phys Rev B (2012) 86:115112. doi:10.1103/PhysRevB.86.115112
67. Teo JCY, Hughes TL. Existence of majorana-fermion bound states on disclinations and the classification of topological crystalline superconductors in two dimensions. Phys Rev Lett (2013) 111:047006. doi:10.1103/PhysRevLett.111.047006
68. Benalcazar WA, Teo JCY, Hughes TL. Classification of two-dimensional topological crystalline superconductors and majorana bound states at disclinations. Phys Rev B (2014) 89:224503. doi:10.1103/PhysRevB.89.224503
69. Geier M, Trifunovic L, Hoskam M, Brouwer PW. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys Rev B (2018) 97:205135. doi:10.1103/PhysRevB.97.205135
70. Day IA, Akhmerov AR, Varjas D. Topological defects in a double-mirror quadrupole insulator displace diverging charge. Scipost Phys Core (2022) 5:053. doi:10.21468/SciPostPhysCore.5.4.053
Keywords: topological defects, disclination, SSH model, bound states, Zak phase
Citation: He Q, Sun J, Deng H-Y, Wakabayashi K and Liu F (2023) Bound states at disclinations: an additive rule of real and reciprocal space topology. Front. Phys. 11:1213158. doi: 10.3389/fphy.2023.1213158
Received: 27 April 2023; Accepted: 30 May 2023;
Published: 09 June 2023.
Edited by:
Birabar Ranjit Kumar Nanda, Indian Institute of Technology Madras, IndiaReviewed by:
Jianbao Zhao, Canadian Light Source (Canada), CanadaBaizhan Xia, Hunan University, China
Copyright © 2023 He, Sun, Deng, Wakabayashi and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Feng Liu, bGl1ZmVuZ0BuYnUuZWR1LmNu
 Qinghua He1,2
Qinghua He1,2 Katsunori Wakabayashi
Katsunori Wakabayashi Feng Liu
Feng Liu