Exploring the formation dynamics of affective polarization by considering coupled feedback

Polarization issues are generally subject to ideological and affective polarization. Particularly, affective polarization generally accelerates the polarization process. Yet, a wide array of the existing literature has not provided valid ways to make distinctions between them. Therefore, the mechanism contributing to the rise of affective polarization still remains unclear, along with its unique emergent dynamics. To address this issue, we introduces the coupled feedback between opinions and response susceptibility to an attraction–repulsion model which takes into account three parameters: interaction strength, response susceptibility, and tolerance to others. The model features phase diagrams of global consensus, affective polarization, and “harmony with diversity” states. Subsequently, we proceed simulations on time-varying and static social networks, showing that intermediate parameter ranges yield a global consensus as one integrated cluster collapsing and converging toward an uncertain moderate position after long-term persistence. The feedback essentially offers a counterforce to establish an inversion between the global consensus and “harmony with diversity”. Remarkably, strengthening feedback may facilitate polarization by driving the system to first self-organize into one integrated cluster, which then gradually approaches polarization, especially for low tolerance and strong interactions, whereby the step-like dynamic behaviors of opinion entropy suggest the occurrence of a dynamic equilibrium. In summary, the aforementioned phenomena have never been unearthed before and can be regarded as unique dynamics features of affective polarization. Finally, this study attempts to offer a useful approach to the micro foundations of affective polarization for the first time, and the results guide us on how to avoid the dilemmas of this polarization.

1 Introduction

Polarization is, here, conceived as a process of growing constraints in people’s viewpoints and further emergence of alignments along multiple or even opposite lines of potential disagreement [1–3]. Nowadays, the world is being perplexed by the growth of polarization [4,5]. It is, thus, increasingly a concern to understand the nature and causes of polarization and how to prevent the public from reaching dangerous degrees of polarization [6–11].

There exist at least two kinds of polarization that can be easily carried to extremes and undermine the foundation of social order: ideological polarization (IP) [12], which indicates an opposite political view among elites, and affective polarization (AP), whereby individuals develop negative attitudes toward members of the opposing party and become entrenched [13–18]. IP and AP have been rising during the last decade [16,19]. Furthermore, IP refers to the fact that political views are widely dispersed and heterogeneous, or bimodal, among elites. Unlike IP, which is largely driven by rational self-interest motivations [12,20–23], AP itself generally suggests strong affective decision-making with a coupling relationship between individuals’ opinions and their subsequent responses [15]. This coupling relationship essentially creates a negative feedback mechanism, which has been widely observed in empirical cases [15]. For example, individuals with higher levels of out-party animosity report taking a more strong stand against those from the other party (for example, they would not even receive any suggestions from those from the other party) [12] and having more difficulty in repositioning, which is regardless of economic self-interest. The adverse effects of AP can spill over from the political area to other issues such as COVID-19 vaccines [24], gun-control [25], and abortion [26], which is much more harmful than IP. Therefore, AP might have unique dynamics, behind which the mentioned micro negative feedback can naturally be a potential responsible mechanism.

Up to now, a large body of existing studies has explored various mechanisms which are responsible for clustering of beliefs and polarization, especially IP, in complex social systems [2,9,20,27–32], and the mutually reinforcing relation between IP and AP has also been identified. For example, Americans increasingly dislike those of the other party because of intense struggles between Democrats and Republicans [15,33,34], which conversely gives rise to an increasing IP among the US public, rising social inequality, and conflicts [35]. Furthermore, polarization among elites has become mainly affective rather than ideological. The aforementioned realistic problem suggests a call for further explorations to identify the unique dynamic features of AP so as to develop more effective preventing measures to slow or even stop the accelerating polarization process, which has nevertheless received very little attention in the growing literature. Due to the positive feedback, however, the growth of AP seems to have multiple contributing factors, including economic adversity, racial animus, cultural values, religions, gender polarization, and a range of other socioeconomic factors [34,36–38], making the exploration of the unique features of AP arduous. Since the general micro foundation of AP dynamics remains unclear. It leads to the following questions to be addressed: what are the micro foundation of AP dynamics and the unique dynamic features of AP? How does the micro mechanism govern the AP dynamics, together with other potential factors such as interaction strength, response susceptibility, and tolerance level?

In order to address these questions arising from the lack of micro foundation in AP, we adopt a novel attraction–repulsion model (ARM) that captures the coupled feedback between individuals’ opinions and their responses, which essentially belongs to the negative feedback class. The proposed model constructs an adaptive-system perspective on the effects of the rules on emergent dynamics of not only AP and global census (GC) but also the “harmony with diversity” (HD) state, which has been recently identified [39]. It should be noted that the opinion updating rules in our model paradigm are based on a simple assumption that an individual’s attraction to or repulsion from others is only governed by the opinion dissimilarity between them, rather than the positions themselves. In addition, interaction strength, response susceptibility, and individual tolerance have been viewed as vital regulation factors to be considered. We are concerned with how the negative feedback mechanism governs the emergent dynamics of AP, together with the three vital regulation factors.

The discoveries of this study include the following: 1) the identification of conditions under which a population approaches convergence into a moderate position; 2) the identification of the conditions under which the population becomes highly polarized with asymmetric opposite camps or even extremely polarized with symmetric opposite extreme camps, and under which it enters a desired HD state with a stable integrated opinion cluster centering on a neutral point; 3) the transitions between the three states and the triple point; 4) opinions of the majority may first self-organize into one integrated cluster, which then approaches the boundary of an ideological space because of the counterforce exerted by the negative coupled feedback arising from frequent opinion exchange within the cluster; 5) the system collapses into a global consensus with a moderate position after the long-time persistence of one integrated opinion cluster; 6) the remark that strengthening feedback can undoubtedly increase the likelihood of AP. For the first time, our study proposes a basic model framework to explore the unique dynamic features of AP.

The paper is organized as follows: in Section 2, we formally define our opinion evolution model, along with the method to identify the regions of different states; in Section 3, we simulate our model and give results, as well as descriptions and attempts to identify the unique dynamics features of AP. We conclude with a summary of the results and an outlook for future studies in Section 4.

2 Model

The model considers a population of size N where each individual is typified by an opinion x_i(t) at time t, which is a real number in the interval x_i(t) ∈ [−10, + 10]. We adopt the opinion model proposed by [39], where the updating rules of an individual’s opinion x_i(t) are formulated by the following equations:

${\dot{x}}_i\left(t\right)=\left\{\begin{array}{c}A\tanh \left({\alpha }_i{D}_{ji}\left(t\right)\right)\text{if}|D_{ji}\left(t\right)|<T_i;\hfill \\ A\tanh \left({\alpha }_i\sigma \left(D_{ji}\left(t\right)\right)\left(T_i-|D_{ji}\left(t\right)|\right)\right)\text{if}|D_{ji}\left(t\right)|\ge T_i.\hfill \end{array}\right.(1)$

D_ji(t) = x_j(t) − x_i(t) denotes the opinion distance between i and j at time t. T_i is the tolerance threshold of an individual i. α_i can be interpreted as the response susceptibility of the individual. In more detail, α_i positively associates with the extent to which an individual i is passionate or sensitive, i.e., response susceptible to being socially influenced. It is obvious that the nonlinear shape of the influence function tanh(x) is controlled by α, while A quantifies the interaction strength, which is actually the upper bound of the opinion shift driven by each interaction, implying that the influence exerted by individuals on others is capped. σ(D_ji(t)) extracts the sign of D_ji(t).

We first consider a population where the connections of each individual are dynamic and formulated by the activity-driven (AD) model [40–43]. In more detail, k_i(t) denotes the number of interactions an individual i has at time t. It, thus, generates a temporal network formulated by the temporal adjacency matrix A_ij(t), where A_ij(t) = 1 if an individual i owns one connection with an individual j; otherwise, A_ij(t) = 0. Within the AD model framework, each individual i randomly connects k_i individuals from the population at each time step. $k_i={\sum }_j^N{A}_{ij}(t)$ is thus satisfied throughout the simulation. The evolution of opinions is actually coupled to an underlying temporal network. In reality, the empirical statistics show that the interaction activities of people are generally heterogeneous [29,41,42,44]. We, thus, further assume the interactions are extracted from a power-law distribution p(k) ∼ k^−γ.

The proposed model incorporates the micronegative feedback mechanism by which individuals with more extreme opinions become more stubborn and less sensitive, making it more difficult to reposition. The micro feedback mechanism with regards to affective decision-making is based on the individual level and related to intrinsic preferences. On the basis of the basic model defined by Eq. 1, we additionally assume the following feedback function regarding either interaction susceptibility α, using the individual opinion as the variable:

${\alpha }_i\left(t\right)=\eta x_i^{-\beta }\left(t\right),(2)$

where β quantifies the strength of the negative feedback. The larger β, the stronger the feedback becomes, and as a consequence, even moderate individuals will not change their position easily. The feedback function captures the coupled relationship between individuals’ opinions and their preferences. This means that the present model includes intrinsic preferences for a specific opinion. Varying β may generate different evolution dynamics, facilitating an understanding of the effects of the micro feedback on the emergent dynamics of global polarization, global consensus, and “harmony with diversity” (HD) states.

Next, we extend the proposed model from the AD network to the static network where the interactions among individuals are fixed, such as the parts of the online social network Facebook. In such a case, k_i corresponds to the number of edges that the individual i stretches to its neighbors, and the individual is represented by a node in the networks. Therefore, the ones with which each individual interacts remain unchanged.

In numerical simulations, the size of the used time-varying network is N = 1000, where γ = 2.1. The control parameters of the present model are A, β, and T_i, where we assume that individuals have uniform attributes α_i = α, T_i = T, and A_i = A. For simplicity, we set η = 1.0. The final results are obtained from N_r = 100–500 independent realizations, after at least 500 time steps. Before starting each realization, the initial opinion of each individual is independently and randomly sampled from the interval [−1.0, 1.0]. Then, at each time step t, opinion evolves as follows: i) in a random order, each individual i randomly chooses k_i new neighbors out of all individuals, while the neighbors of i remain unchanged in the static social media network. ii) Then, i compares its opinion with each neighbor, attempting to update its opinion according to Eq. 1, with adaptive response susceptibility α(x_i (t − 1)) defined by Eq. 2.

We exhibit the polarization dynamics through the polarization degree of a population, which is measured by the standard deviation (SD) in opinions SD (x₀, … , x_N). We measure the opinion diversity by calculating the opinion entropy S) of the population Cui [39], $S={\sum }_{x_{\mathit{min}}}^{x_{\mathit{max}}}x{\rho }_x$, so as to capture the emergence of the HD state. ${\rho }_x=\frac{N_x}{N}$ is the density of the individual owning opinion x, and N_x denotes the population of the opinion x. Therefore, x_min = −10 and x_max = 10 in our model. A larger SD indicates an increased degree of polarization. For example, the minimum of the polarization is zero, i.e., SD_min = 0, corresponding to the GC state. Otherwise, the system will get extremely polarized if SD is large or equal to SD_max = 10.

Inspired by the phase-identification method developed in [39], we still numerically estimate the boundaries between different states by means of the susceptibility of not only S but also SD.

$\chi \left(S\right)=\frac{\sqrt{⟨S^2⟩-{⟨S⟩}^2}}{⟨S⟩},(3)$

$\chi \left(SD\right)=\frac{\sqrt{⟨{SD}^2⟩-{⟨SD⟩}^2}}{⟨SD⟩},(4)$

where ⟨S⟩ (⟨ SD ⟩) is the ensemble average of S (SD), which can be obtained by averaging S (SD) from N_r independent realizations. ⟨S²⟩ (⟨ SD²⟩) is the secondary moment of the ensemble distribution. One can further identify the boundaries between GC, HD, and AP states according to the principle that χ(S) and χ(SD) exhibit a peak value at the boundary.

3 Results

Figures 1, 2 present the temporal evolution of the individuals’ opinions, polarization degree SD, and opinion entropy S for six different parameter conditions, respectively. Corresponding final opinion distributions are illustrated in Figure 3. We can observe that as the interaction strength A increases, the system first shifts from HD to GC, then from GC to the AP state. More in detail, the presence of opinion-based feedback can facilitate stable integrated opinion cluster centering on a neutral point (see Figure 1A), along with stable considerable S and low-level SD (see Figure 2A). Since individuals are allowed to remain greatly sensitive to the diverse views of others in spite of their opinion distance being slight (see Supplementary Figure S1A), this occurs in frequent opinion exchanges because of both being rather sensitive and have weak mutual attraction [39], further leading to persisting violently oscillating average susceptibility (see Supplementary Figure S1A). In such cases, the system does not easily get trapped in a monotonous state such as GC or AP. Moreover, this cluster exhibits a much more stable trajectory in comparison with Figure 1 in [39], in which the coupled feedback is not considered, showing one advantage of this feedback.

FIGURE 1

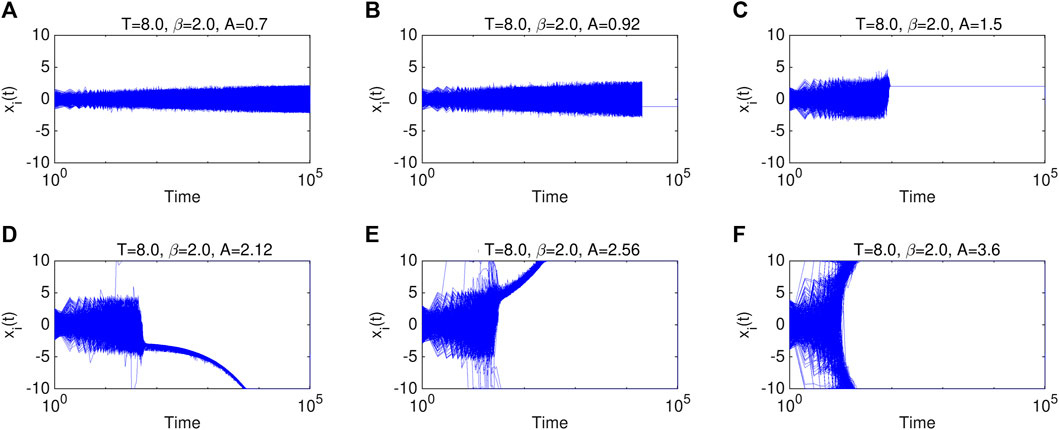
FIGURE 1. Temporal evolution of the individuals’ opinions for six different representative values of A are presented in (A–F), respectively. They are also indicated by the dark green dots in Figures 4A1, A2, for a more explicit presentation. The values of the parameters are listed in the titles of the subplots.

FIGURE 2

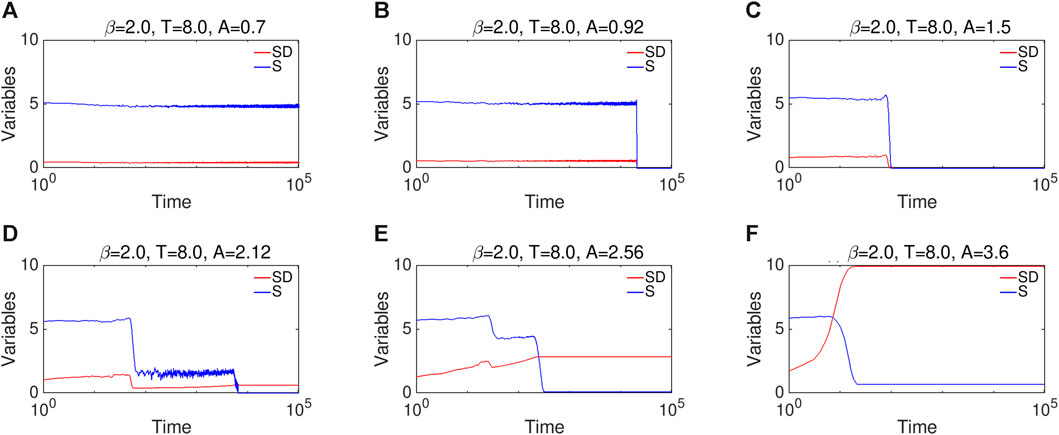
FIGURE 2. Temporal evolution of SD and S for six different representative values of A are presented in (A–F), respectively. The six representative cases are also indicated by the dark green dots in Figures 4A1, A2, for a more explicit presentation. The values of the parameters are the same, as considered in Figure 1.

FIGURE 3

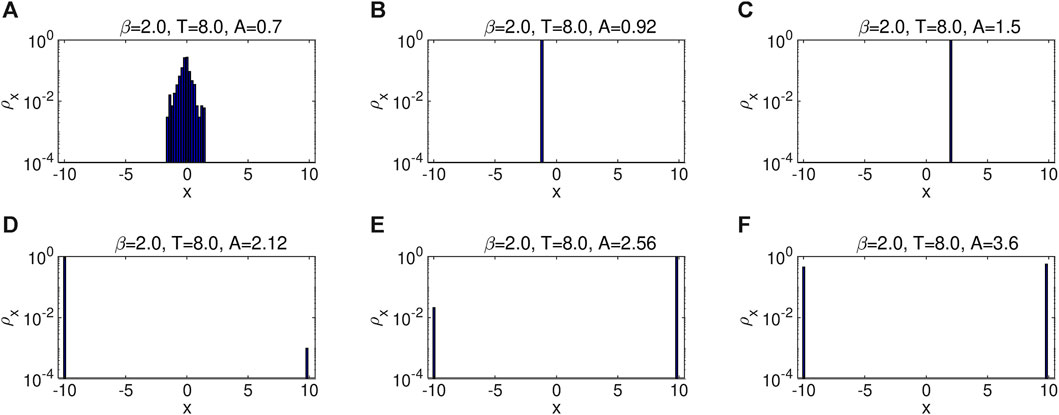
FIGURE 3. Final opinion distributions of the population for six different representative values of A are presented in (A–F), respectively. The values of parameters are listed in the titles of the subfigures, corresponding to the six cases illustrated in Figures 1, 2.

However, the intermediate A instead gives rise to the GC state, in which the integrated cluster collapses and converges into a single moderate position from which it would never move (see Figures 1B, C), exhibiting sudden drops of S and SD (see Figures 2B, C). Intermediate interaction strength brings about a wider opinion spectrum and, thus, more insensitive and insistent individuals in the presence of the feedback, who can hold a more stable position. In addition, at the stage of the opinion cluster, the opinion distances between individuals are mostly within T before the collapse. The aforementioned two factors contribute to a global consensus as sharply as possible. It is, thus, also evidence for the existence of the dynamic equilibrium. Attributing to rather small $\overline{\alpha (t)}$ (see Supplementary Figures S1B, C), individuals become rather slow as the population achieves a high degree of consensus. Remarkably, we can see in Figures 3B, C that the convergence point is not always neutral where all individuals maintain perfect neutrality. The system is definitely initial condition-dependent, which may result from the initial unequal distribution of individuals with opinions on different signs. In such cases, the convergence direction is uncertain. It is hard to achieve a global consensus with a neutral point when coupled feedback is present.

As A gets larger, individuals will not keep an open attitude toward distant ones due to strong repulsive forces caused by strong interaction. The population may get polarized with large SD, which is, however, less than SD_max (i.e., high-level AP rather than extreme AP). In such cases, the population evolves into two opposite camps of different sizes (see asymmetric opinion distributions illustrated in Figures 3D, E), which, thus, belongs to an asymmetric class [45,46]. The opinions of the majority population may first self-organize into one integrated cluster to confront the repulsive force, which can leave the moderates within the tolerance range. However, the repulsion from the opposing stubborn extremists caused by the feedback is superior to their mutual attraction, which will reinforce and shift the cluster until the opinion boundaries absorb it (see Figures 1D, E). As another result, we observe a three-step trajectory of S (see Figures 2D, E and a slowly decreasing $\overline{\alpha (t)}$ after an intensive drop (see Supplementary Figures S1D, E), indicating the occurrence of a dynamic equilibrium. The system actually enters a transient stage. The occurrence of the dynamic equilibrium has never been uncovered in previous studies, especially those considering interactions based on bounded confidence. With increasing A, high-level polarization would be replaced by symmetric extreme polarization with SD ≈ SD_max (see Figures 1F, 2F, 3F). The cluster can be symmetrically torn apart within a short time (see Figure 1F), due to the strong repulsive forces arising from the strong interaction [39]. This makes the prior self-organization into one majority cluster impossible, and individuals become quickly insensitive (see Supplementary Figure S1F) for $\overline{\alpha (t)}\approx 0$).

Figure 4 presents a more clear dependence of SD, S, and χ(S) on interaction strength A and tolerance threshold T. It is obvious in Figures 4A1, A2 that increasing A has an obvious nonlinear effect on both the polarization degree SD and opinion diversity, i.e., opinion entropy S. The range of weak interactions A < A_c1 is for the emergence of HD states, showing small SD and highland of S. We have also checked that the spectrum width of the cluster is positively related to the value of S, while the system governed by the intermediate range A_c1 < A < A_c2 provides sufficient evidence for a GC state with SD = 0 and S = 0. This is definitely in contrast to the emergent properties generated by the attraction–repulsion model without consideration of feedback [39], in which a dynamic balance is responsible for the emergence of HD states. Similar behaviors can be observed in Figures 4B1, B2, while Figures 4C1, C2 reveal that the system undergoes a shift from AP to the HD state with increasing tolerance threshold T. This is largely in accordance with the empirical evidence [47,48] and the social moral rules requiring a high-level of tolerance, essentially attempting to achieve an HD state. In addition, it should be noticed that the peaks of χ(S) correspond rightly to the critical points between these phases, which further validate the phase-identification method developed in [39].

FIGURE 4

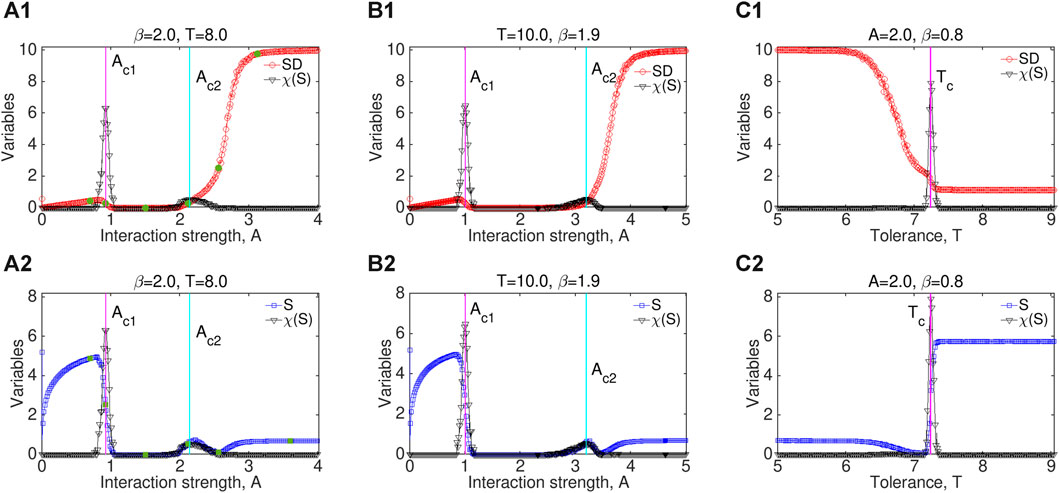
FIGURE 4. In time-varying networks, dependence of SD (red circles) and χ(S) (black triangles) on A are presented in (A1, B1), while dependence of S (blue squares) and χ(S) (black triangles) on A are presented in (A2, B2). In (C1, C2), we plot the dependence of dependence of SD (red circles) and χ(S) (black triangles) on T, and the dependence of dependence of S (blue squares) and χ(S) (black triangles) on T, respectively. In (A1, A2), the six dark green dots correspond to the subplots of six parameter combinations in Figures 1–3. In (A) and (B), pink vertical lines label the positions of A_c1 at which the GC state begins to appear, while light blue vertical lines indicate the positions of A_c2 at which the GC state starts to vanish and shift to the AP state. However, we can observe in (C1) and (C2) that the threshold T_c that denotes a shift from AP to HD. The values of parameters are correspondingly listed in the titles of subfigures.

We next extend the simulations to (A, T) space, as shown in Figure 5, where the color encodes the values of SD for four different representative values of feedback strength β. The system finally evolves into either HD or AP state when β is small such that there is only one transition from HD to AP. When β increases to some extent (β = 2.0), the intermediate range of A can additionally lead to the emergence of the GC state for sufficient tolerance and the triple points (see the blue or black pentagrams illustrated in Figures 5B, D). Therefore, we can observe three different transitions by increasing A: from HD to GC, which is largely dependent on A, from GC to AP and from HD to AP when β is larger than a certain value. For all strong feedback, GC is promoted to erode the regions of HD, and in turn, AP occupies the regions of GC, leading to the shrinkage of HD regions. However, both increasing T and decreasing A can prevent the population from being polarized as much as possible for a given β. However, we find that strong feedback is responsible for the decreasing polarization degree, such that extreme AP is widely replaced by high-level AP (see Figure 5D). The strong stubbornness of individuals (small α_i), as well as the strengthening interactions bringing about intense struggles between individuals of different signs, contribute to the self-organization into one integrated cluster which gradually approaches the boundary (see Figures 1D, E), i.e., the dynamic equilibrium.

FIGURE 5

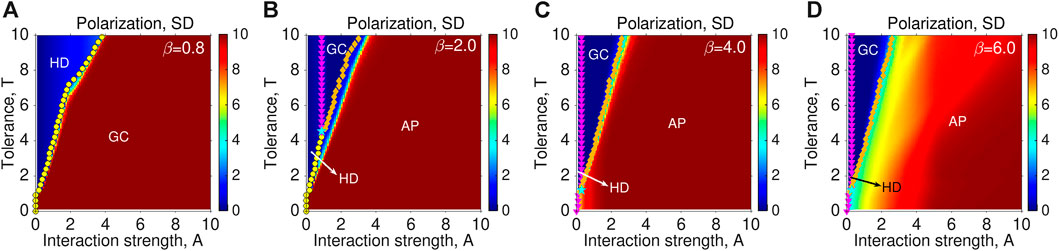
FIGURE 5. Phase diagrams in terms of SD are presented in (A, T) space for four different values of β: (A) β = 0.8, (B) β = 2.0, (C) β = 4.0 and (D) β = 6.0. The lines consisting of pink triangles separate the regions of HD and GC phases, while the lines consisting of yellow circles depict the boundaries indicated by the second threshold A_c2, separating the regions of the HD and P phases, as given by our method. The lines consisting of brown diamonds separate the regions of the GC and P phases. The regions belonging to different states are labeled in the subplots. In particular, the light blue pentagrams illustrated in (B–D) indicate the triple points.

Figure 6 depicts the phase diagrams in (A, β) space. By increasing A, there still occur three transitions when individuals are sufficiently tolerant (see Figures 6B, D): the transition from HD to AP occurs with weak feedback, whereas strong feedback is favorable for the other two transitions: from GC to AP and from HD to GC. It suggests that the interaction strength A plays a decisive role, while larger light red regions of AP (see Figure 6) further confirm that strong feedback may prevent the system from getting extremely polarized and facilitate GC by suppressing HD, which, however, becomes dominant for small β and A, but large T.

FIGURE 6

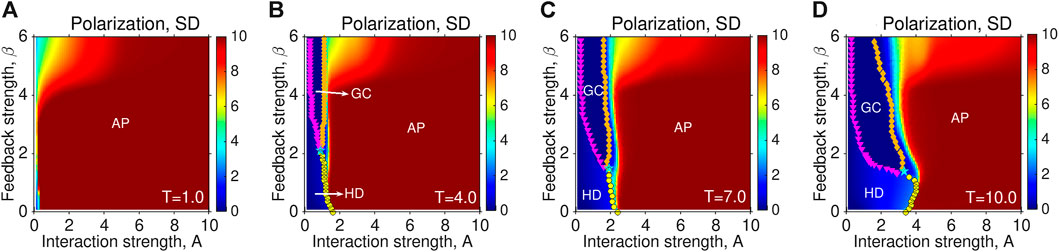
FIGURE 6. Phase diagrams in terms of SD are presented in (A, β) space for four different values of T: (A) T = 1.0, (B) T = 4.0, (C) T = 7.0 and (D) T = 10.0. The lines consisting of pink triangles separate the regions of GC and HD phases, while the lines consisting of yellow circles depict the boundaries indicated by the second threshold A_c2, separating the regions of HD and P phases, as given by our method. The lines consisting of brown diamonds separate the regions of the GC and P phases. The regions belonging to different states are labeled in the subplots. In particular, the light blue pentagram illustrated in (B) indicates one triple point. The four dots correspond to the subplots of the six parameter combinations in Figure 1.

Figure 7 offers a comprehensive view of the effects of individuals’ tolerance on opinion dynamics for different levels of feedback. There is not only one transition from HD to GC with increasing β but also two novel transitions with increasing T: from AP to HD and from AP to GC. We find that, if A is not small, AP is likely to emerge for small T, whose regions expand with A, along with decreasing likelihood of HD and GC, while increasing both T and β is responsible for the GC state. In addition, sufficiently tolerant individuals and weak interactions are essential to easily achieving the HD state. Still, the system can generate triple points in such a parameter space.

FIGURE 7

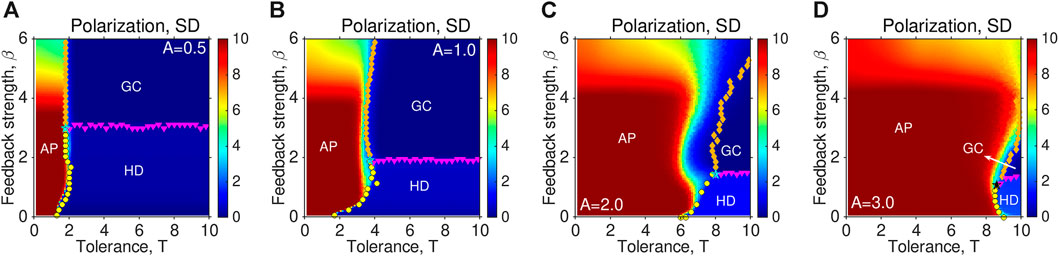
FIGURE 7. Phase diagrams in terms of SD are presented in (T, β) space for four different values of A: (A) A = 0.5, (B) A = 1.0, (C) A = 2.0 and (D) A = 3.0. The lines consisting of pink triangles separate the regions of the GC and HD phases, while the lines consisting of yellow circles depict the boundaries indicated by the second threshold A_c2, separating the regions of HD and P phases, as given by our method. The lines consisting of brown diamonds separate the regions of GC and P phases. The regions belonging to different states are labeled in the subplots, while the light blue pentagrams indicate the existence of triple points.

Overall, Figures 5–7 further confirm that AP may increase with strengthening feedback, particularly with low tolerance and strong interaction. It supports the researchers’ worry that political polarization among the US public may increase due to the AP and the coupled relationship between people’s views and their response sensitivity [15,33–35]. In addition, the phase-identification method allows us to build phase diagrams and locate where the triple points are, by identifying the boundaries between different phases.

Online social networks are increasingly used to access the formation dynamics of opinions with respect to COVID-19 vaccines, gun-control, and abortion [29,30,49,50]. These platforms can reduce barriers and costs to information and, further, allow individuals to freely voice their viewpoints, consequently improving the rate of opinion exchanges. We, thus, subsequently embed our model into the social networks where individuals interact through fixed connections so as to explore whether the topology of fixed connections can result in changes in opinion evolution dynamics. Still, similar phase diagrams are presented in Figure 8 in three different parameter spaces, (A, T), (A, β) and (T, β), suggesting that evolution outcomes are mainly dominated by the model rules rather than the structure of used networks. At the same time, a comparison between Figures 5–8 reveals that the introduction of fixed interactions can remarkably give rise to much larger high-level AP, which is actually attributed to the existence of cluster-level self-reinforced mechanisms (see Supplementary Figure S2) [39]. As another result, both weak feedback and high-level tolerance promote GC regions to erode the regions of HD and to split them into two parts (see Figures 8A1, B2–B4). In such cases, individuals are generally within the stable clusters and moderately sensitive. However, the existence of these clusters can prevent them from contacting and struggling with those of dissimilar opinions, and, in turn, exert a persistent neutralizing influence on the prejudiced opinions on the boundaries because they are highly tolerant, regardless of the fact that they are relatively insensitive. Consequently, opinion exchanges are less frequent to maintain more stable opinions, and the GC state can be more easily achieved.

FIGURE 8

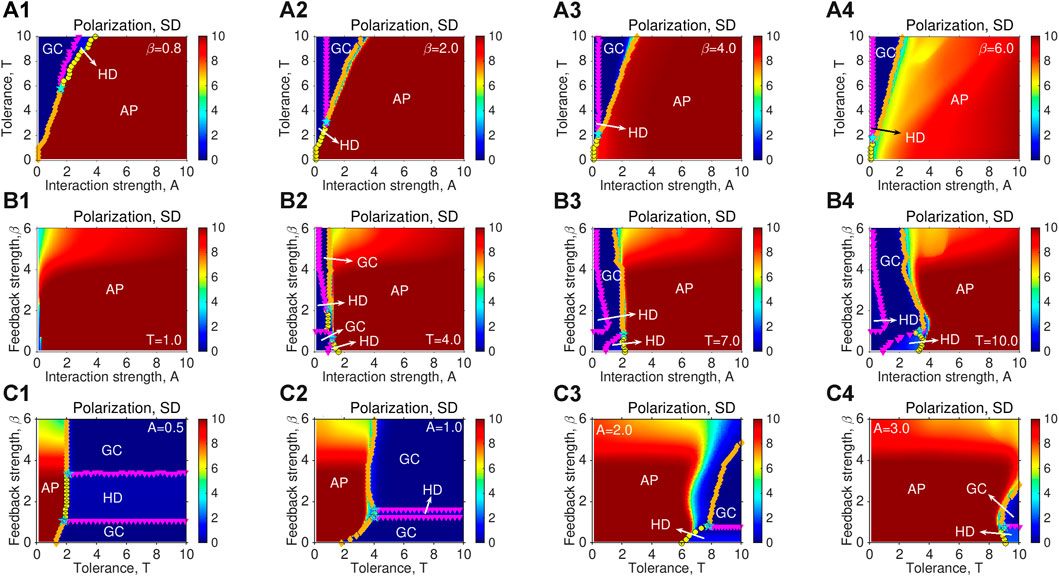
FIGURE 8. Phase diagram for the population embedded on the part of Facebook network, where interactions among individuals are fixed. (A1–A3) Phase diagrams in (A, T) space for four different values of β. (B1–B4) Phase diagram in (A, β) space for four different values of T. (C1–C4) Phase diagram in (T, β) space for four different values of A. We run simulations with SD in all subplots. The lines consisting of different markers denote the boundaries between different phases, which are the same as those presented in Figure 5. The regions of the three phases are correspondingly labeled in the subplots. The light blue pentagrams indicate the triple points, which are more frequent. The degree distribution of the used network is p_k ∼ k^−γ with γ =−3.22. The other structural parameters are: N =43,952, mean degree ⟨k⟩=8.30, ⟨k²⟩=205.36, maximum degree k_max =223, minimum degree k_min =1, modularity is 0.59, clustering coefficient c =0.12, and degree correlation coefficient r ≳0.

4 Discussions and conclusion

For the first time, this study introduced feedback to capture the coupled relationship between individuals’ opinions and their susceptibilities to the views of others, which has been verified to be a useful approach to the micro foundations of AP dynamics. This assumption allows us to explore the unique dynamic features of AP for the first time. The simulations on both time-varying and static social networks show that strong coupled feedback between individuals’ opinions and susceptibility, and strong interaction among narrow minded individuals facilitate the emergence of the AP state. Extreme views easily arise from strong interactions between intolerant individuals. Since strong stubbornness is responsible for the existence of considerable extremists who can exert persistent influence on the moderate interactions in the population. In contrast, weak interaction, high tolerance, and weak coupled feedback are favorable for HD states, which actually guide us on how to avoid the dilemmas caused by AP. Otherwise, strong stubbornness caused by extreme positions makes individuals stand out together to face the opposite of them. In addition, the simulations further confirm that the peak of entropy susceptibility is indeed a sign of transition between GC, HD, and AP states [39].

However, intermediate ranges of parameters yield the GC state, which emerges along with that one integrated cluster, always collapses, and converges toward a moderate position after a long-time persistence, leading to sudden drops in both S and SD. It is the first remark. Moreover, the aforementioned results highlight the second remark that the negative coupled feedback actually offers a counterforce to establish an inversion of the regions between GC and HD, in comparison with the results presented in Figures 4A1–A4, which do not consider this feedback [39]. As the third remark suggests, stronger feedback measuring more emotional response can yield a high likelihood of polarization, which is in accordance with empirical investigations of affective polarization in the US [13,15,33,34]. Still, fixed connections can bring about cluster-level self-reinforced mechanisms which can enlarge the regions of high-level AP.

Moreover, as the fourth remark suggests coupled feedback with a large intermediate A may promote fast self-organization into one opinion cluster toward GC or even high-level AP. This cluster that does not remain robust against time is also responsible for the step-like dynamic behaviors of opinion entropy. In such cases, the system enters a transient stage, suggesting the existence of a dynamic equilibrium. In summary, the aforementioned four remarks cannot be identified by previous studies involving polarization issues; they are novel, unique dynamic features of AP within our model framework.

Our model is based on the simple assumption that interactions among similar actors will reduce their differences and that the opposite is true for interactions among distant actors. It is significant that future studies should take into account some empirical characteristics of individuals which might generate different scenarios, such as heterogeneous duration time of interactions, heterogeneous feedback strength, or different social positions. Moreover, the existence of prior self-organization into one integrated cluster before reaching the AP state may highlight a golden time window, in which regulation measures may most effectively prevent the public from reaching dangerous degrees of AP, which is also worth leaving this investigation to future research. Furthermore, empirical evidence to verify the conclusion of the present study is required. Moreover, this study opens up one interesting issue to identify the difference between AP and IP with respect to their emergent dynamics.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

P-BC designed the model, proceeded with simulations and analysis, and wrote and edited the original manuscript.

Funding

This work was supported by the Key Program of the National Natural Science Foundation of China (Grant No. 71731002) and by the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2021A1515011975).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1213044/full#supplementary-material

References

1. Axelrod R. The dissemination of culture: A model with local convergence and global polarization. J conflict resolution (1997) 41:203–26. doi:10.1177/0022002797041002001

CrossRef Full Text | Google Scholar

2. Bramson A, Grim P, Singer DJ, Berger WJ, Sack G, Fisher S, et al. Understanding polarization: Meanings, measures, and model evaluation. Philos Sci (2017) 84:115–59. doi:10.1086/688938

CrossRef Full Text | Google Scholar

3. Galam S. Unanimity, coexistence, and rigidity: Three sides of polarization. Entropy (2023) 25:622. doi:10.3390/e25040622

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Guilbeault D, Becker J, Centola D. Social learning and partisan bias in the interpretation of climate trends. Proc Natl Acad Sci (2018) 115:9714–9. doi:10.1073/pnas.172266411

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Allcott H, Boxell L, Conway J, Gentzkow M, Thaler M, Yang D. Polarization and public health: Partisan differences in social distancing during the coronavirus pandemic. J Public Econ (2020) 191:104254. doi:10.1016/j.jpubeco.2020.104254

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Krause U. A discrete nonlinear and non-autonomous model of consensus formation. In: S Elyadi, G Ladas, J Popenda, and J Rakowski, editors. Communications in difference equations. Amsterdam: Gordon and Breach Pub. (2000). p. 227–36.

Google Scholar

7. Rainer H, Krause U. Opinion dynamics and bounded confidence: Models, analysis and simulation. J Artifical Societies Soc Simulation (2002) 5:9714–9. doi:10.1073/pnas.172266411

CrossRef Full Text | Google Scholar

8. Hegselmann R, Krause U. Opinion dynamics driven by various ways of averaging. Comput Econ (2005) 25:381–405. doi:10.1007/s10614-005-6296-3

CrossRef Full Text | Google Scholar

9. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys (2009) 81:591. doi:10.1103/RevModPhys.81.591

CrossRef Full Text | Google Scholar

10. Sobkowicz P, Kaschesky M, Bouchard G. Opinion mining in social media: Modeling, simulating, and forecasting political opinions in the web. Government Inf Q (2012) 29:470–9. doi:10.1016/j.giq.2012.06.005

CrossRef Full Text | Google Scholar

11. Moe WW, Schweidel DA. Online product opinions: Incidence, evaluation, and evolution. Marketing Sci (2012) 31:372–86. doi:10.1287/mksc.1110.0662

CrossRef Full Text | Google Scholar

12. Lelkes Y. Mass polarization: Manifestations and measurements. Public Opin Q (2016) 80:392–410. doi:10.1093/poq/nfw005

CrossRef Full Text | Google Scholar

13. Iyengar S, Sood G, Lelkes Y. Affect, not ideologya social identity perspective on polarization. Public Opin Q (2012) 76:405–31. doi:10.1093/poq/nfs038

CrossRef Full Text | Google Scholar

14. Lauka A, McCoy J, Firat RB. Mass partisan polarization: Measuring a relational concept. Am Behav Scientist (2018) 62:107–26. doi:10.1177/0002764218759581

CrossRef Full Text | Google Scholar

15. Iyengar S, Lelkes Y, Levendusky M, Malhotra N, Westwood SJ. The origins and consequences of affective polarization in the United States. Am Behav Scientist (2019) 22:129–46. doi:10.1146/annurev-polisci-051117-073034

CrossRef Full Text | Google Scholar

16. Boxell L, Gentzkow M, Shapiro JM. Cross-country trends in affective polarization. Rev Econ Stat (2022) 1–60. doi:10.1162/rest_a_01160

CrossRef Full Text | Google Scholar

17. Reiljan A. ‘fear and loathing across party lines’(also) in Europe: Affective polarisation in European party systems. Eur J Polit Res (2020) 59:376–96. doi:10.1111/1475-6765.12351

CrossRef Full Text | Google Scholar

18. Wagner M. Affective polarization in multiparty systems. Eur J Polit Res (2020) 69:102199. doi:10.1016/j.electstud.2020.102199

CrossRef Full Text | Google Scholar

19. Abramowitz AI, Saunders KL. Is polarization a myth? J Polit (2008) 70:542–55. doi:10.1017/S0022381608080493

CrossRef Full Text | Google Scholar

20. Axelrod R, Daymude JJ, Forrest S. Preventing extreme polarization of political attitudes. Proc Natl Acad Sci (2021) 118:e2102139118. doi:10.1073/pnas.2102139118

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Grossman GM, Helpman E. Identity politics and trade policy. Rev Econ Stud (2021) 88:1101–26. doi:10.1093/restud/rdaa031

CrossRef Full Text | Google Scholar

22. Perrings C, Hechter M, Mamada R. National polarization and international agreements. Proc Natl Acad Sci (2021) 118:e2102145118. doi:10.1073/pnas.2102145118

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Vasconcelos VV, Constantino SM, Dannenberg A, Lumkowsky M, Weber E, Levin S. Segregation and clustering of preferences erode socially beneficial coordination. Proc Natl Acad Sci (2021) 118:e2102145118. doi:10.1073/pnas.2102153118

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Woolhandler S, Himmelstein DU, Ahmed S, Bailey Z, Bassett MT, Bird M, et al. Public policy and health in the trump era. The Lancet (2021) 397:705–53. doi:10.1016/S0140-6736(20)32545-9

CrossRef Full Text | Google Scholar

25. Sunstein CR. The law of group polarization. University of Chicago Law School, John M. Olin Law and Economics Working Paper (1999). doi:10.2139/ssrn.199668

CrossRef Full Text | Google Scholar

26. DiMaggio P, Evans J, Bryson B. Have american’s social attitudes become more polarized? Am J Sociol (1996) 102:690–755. doi:10.1086/230995

CrossRef Full Text | Google Scholar

27. Kossinets G, Watts DJ. Origins of homophily in an evolving social network. Am J Sociol (2009) 115:405–50. doi:10.1086/599247

CrossRef Full Text | Google Scholar

28. Vasconcelos VV, Levin SA, Pinheiro FL. Consensus and polarization in competing complex contagion processes. J R Soc Interf (2019) 16:20190196. doi:10.1098/rsif.2019.0196

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Baumann F, Lorenz-Spreen P, Sokolov IM, Starnini M. Modeling echo chambers and polarization dynamics in social networks. Phys Rev Lett (2020) 124:048301. doi:10.1103/PhysRevLett.124.048301

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Santos FP, Lelkes Y, Levin SA. Link recommendation algorithms and dynamics of polarization in online social networks. Proc Natl Acad Sci (2021) 118:e2102141118. doi:10.1073/pnas.2102141118

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Chu OJ, Donges JF, Robertson GB, Pop-Eleches G. The microdynamics of spatial polarization: A model and an application to survey data from Ukraine. Proc Natl Acad Sci (2021) 118:e2102141118. doi:10.1073/pnas.2104194118

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Jusup M, Holme P, Kanazawa K, Takayasu M, Romić I, Wang Z, et al. Social physics. Phys Rep (2022) 948:1–148. doi:10.1016/j.physrep.2021.10.005

CrossRef Full Text | Google Scholar

33. Mason L. A cross-cutting calm: How social sorting drives affective polarization. Public Opin Q (2016) 80:351–77. doi:10.1093/poq/nfw001

CrossRef Full Text | Google Scholar

34. Luttig MD, Federico CM, Lavine H. Supporters and opponents of donald trump respond differently to racial cues: An experimental analysis. Res Polit (2017) 4:1–8. doi:10.1177/2053168017737411

CrossRef Full Text | Google Scholar

35. DellaPosta D. Pluralistic collapse: The “oil spill” model of mass opinion polarization. Am Sociological Rev (2020) 85:507–36. doi:10.1177/0003122420922989

CrossRef Full Text | Google Scholar

36. Schaffner BF, MacWilliams M, Nteta T. Understanding white polarization in the 2016 vote for president: The sobering role of racism and sexism. Polit Sci Q (2018) 133:9–34. doi:10.1002/polq.12737

CrossRef Full Text | Google Scholar

37. Sides J, Tesler M, Vavreck L. The 2016 us election: How trump lost and won. J Democracy (2017) 28:34–44. doi:10.1353/jod.2017.0022

CrossRef Full Text | Google Scholar

38. Mitrea EC, Mühlböck M, Warmuth J. Extreme pessimists? Expected socioeconomic downward mobility and the political attitudes of young adults. Polit Behav (2021) 43:785–811. doi:10.1007/s11109-020-09593-7

CrossRef Full Text | Google Scholar

39. Cui PB. Exploring the foundation of social diversity and coherence with a novel attraction–repulsion model framework. Physica A: Stat Mech its Appl (2023) 618:128714. doi:10.1016/j.physa.2023.128714

CrossRef Full Text | Google Scholar

40. Liu S, Perra N, Karsai M, Vespignani A. Controlling contagion processes in activity driven networks. Phys Rev Lett (2014) 112:118702. doi:10.1103/PhysRevLett.112.118702

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Perra N, Gonçalves B, Pastor-Satorras R, Vespignani A. Activity driven modeling of time varying networks. Scientific Rep (2012) 2:1–7. doi:10.1038/srep00469

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Moinet A, Starnini M, Pastor-Satorras R. Burstiness and aging in social temporal networks. Phys Rev Lett (2015) 114:108701. doi:10.1103/PhysRevLett.114.108701

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Baumann F, Lorenz-Spreen P, Sokolov IM, Starnini M. Emergence of polarized ideological opinions in multidimensional topic spaces. Phys Rev X (2021) 11:011012. doi:10.1103/PhysRevX.11.011012

CrossRef Full Text | Google Scholar

44. Cai S-M, Liu P-C, Huang P. Temporal propagating network approach to long-term evolutionary process of public opinion. Int J Mod Phys C (2021) 32:2150048. doi:10.1142/S0129183121500480

CrossRef Full Text | Google Scholar

45. Pierson P, Schickler E. Madison’s constitution under stress: A developmental analysis of political polarization. Annu Rev Polit Sci (2020) 23:37–58. doi:10.1146/annurev-polisci-050718-033629

CrossRef Full Text | Google Scholar

46. Leonard NE, Lipsitz K, Bizyaeva A, Franci A, Lelkes Y. The nonlinear feedback dynamics of asymmetric political polarization. Proc Natl Acad Sci (2021) 118:e2102149118. doi:10.1073/pnas.2102149118

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Spencer-Rodgers J, Williams MJ, Peng K. Cultural differences in expectations of change and tolerance for contradiction: A decade of empirical research. Personal Soc Psychol Rev (2010) 14:296–312. doi:10.1177/1088868310362982

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Noorazar H. Recent advances in opinion propagation dynamics: A 2020 survey. Eur Phys J Plus (2020) 135:1–20. doi:10.1140/epjp/s13360-020-00541-2

CrossRef Full Text | Google Scholar

49. Wang X, Sirianni AD, Tang S, Zheng Z, Fu F. Public discourse and social network echo chambers driven by socio-cognitive biases. Phys Rev X (2020) 10:041042. doi:10.1103/PhysRevX.10.041042

CrossRef Full Text | Google Scholar

50. Johnson NF, Velásquez N, Restrepo NJ, Leahy R, Gabriel N, El Oud S, et al. The online competition between pro-and anti-vaccination views. Nature (2020) 582:230–3. doi:10.1038/s41586-020-2281-1

PubMed Abstract | CrossRef Full Text | Google Scholar