Mitigating transverse mode instability in fiber laser oscillator by employing direct pump modulation

The transverse mode instability (TMI) is a thermal-optical effect, inducing a sudden deterioration of beam quality and average power. This non-linear effect will greatly limit the power scaling of fiber lasers. We demonstrate a direct pump modulation to mitigate TMI in a 30 μm-core-diameter all-fiber laser oscillator. It only relies on function generator and pump drivers without the need of feedback control units. The groups of pump LDs and pump drivers and the phase difference between the channels of function generator have a great impact on the beam stability. Compared with the TMI threshold 180 W in continuous wave (CW) mode, the maximum average output power of a stabilized beam is increased up to 310 W via a multi-parameter-based direct pump modulation.

1 Introduction

Fiber laser is remarkable for its high-power applications due to high conversion efficiency, excellent beam quality, compact structure and low maintenance operation [1–3]. The output powers of monolithic fiber lasers have dramatically advanced over the past decades [4–6]. However, the power scaling in fiber lasers has been hindered by the onset of transverse mode instability (TMI) [7–9]. TMI is a thermally induced non-linear effect generated from the amplification process, leading to the change of refractive index [10, 11]. TMI can cause an unstable energy transfer between different transverse modes, thus inducing a sudden loss of the beam quality and stability in a fiber laser system [12, 13].

A few promising mitigation strategies have been demonstrated to date, which can be classified in two general categories: passive and active [14–19]. However, most of the schemes are not universally applicable. The majority of the passive methods require specially designed optical fiber, while active methods include external control mechanisms. This is no doubt to reduce the attractiveness of these methods when considering the cost and complexity. Pump modulation scheme is relatively simple which was originally proposed by the University of Jena in 2018 [20]. It weakens the modal coupling and stabilizes the output beam via modulating the amplitude and operating frequency of pump LDs, and has been realized in rod-type fiber space coupled laser systems [20]. Through this method, quasi continuous wave laser was obtained. The TMI threshold was increased via appropriate pump parameters catering to the deployed optical fibers [21, 22].

In recent years, fiber lasers based on large-mode-field fibers have developed rapidly. Most high-power fiber lasers are realized by a master oscillator power amplification (MOPA) structure. Compared with MOPA structure, fiber laser oscillators are attracting due to their simple structure and no return light. In 2012, an output power of ∼1 kW was realized by a monolithic fiber laser oscillator based on ytterbium-doped fiber (YDF) with core/inner-cladding diameters of 20/400 μm [23]. In the same year, a nearly diffraction-limited laser based on 10 m passive fiber was constructed with an output power of 2 kW and no stimulated Raman scattering (SRS) effect [24]. In 2017, the monolithic fiber laser oscillator realized an output power of 3 kW with a side lobe suppression ratio of ∼30 dB [25]. In 2018, a 5.2 kW monolithic fiber laser oscillator was achieved by a bidirectional-pumped structure with a Raman stokes intensity of ∼22 dB below the signal [26]. In 2020, the average power of the publicity reported fiber laser oscillator was up to 8 kW. The power of the SRS light was 22 dB smaller than the basic laser power [9]. Thus, it is desirable to apply the pump modulation scheme to the fiber laser oscillator. In this work, we present a direct pump modulation in an all-fiber laser oscillator. This method refers to a multi-parameter-based direct pump modulation, including adjusting the groups of pump LDs with drivers, modulation frequency, current depth and phase difference between two channels of function generator. We have been able to stabilize the beam fluctuations up to 310 W, which is about a factor of 1.72 above the TMI threshold in continuous wave (CW) mode.

This paper has three main sections. Section 2 is dedicated to describing the constructed experimental system. In Section 3, the mitigation of TMI using direct pump modulation is discussed and its performance is evaluated. Section 4 summarizes the main experimental results.

2 Experimental setup

As illustrated in Figure 1, the direct pump modulation is carried out in an all-fiber laser oscillator. In addition to the all-fiber laser oscillator and equipment for laser diagnosis, only function generator and pump drivers are added to the system.

FIGURE 1

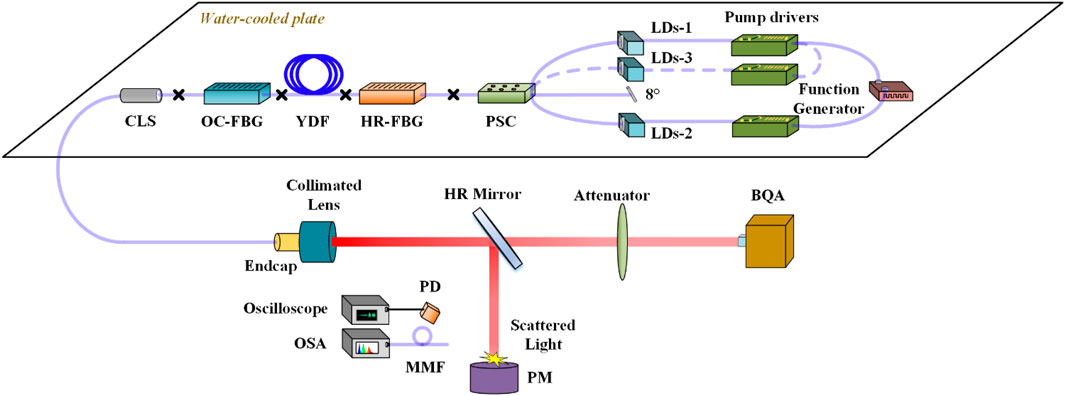
FIGURE 1. Experimental setup including an all-fiber laser oscillator and pump modulation devices. (LDs: Laser diodes; PSC: Pump-signal combiner; HR: High reflection; FBG: Fiber Bragg grating; OC: Output coupler; YDF: Ytterbium-doped fiber; CLS: Cladding light stripper; PD: Photodiode; OSA: Optical spectrum analyzer; MMF: Multimode fiber; PM: Power meter; BQA: Beam quality analyzer).

The fiber laser oscillator is a co-pumped configuration. It is pumped by multiple fiber-coupled LDs with a stabilized emission wavelength of 976 nm. A forward (6 + 1)×1 pump-signal combiner (PSC) can assemble multiple groups of LDs with pump drivers. Two or three pump ports of the PSC are used in our experiment. The central pump port of the PSC is angle cleaved to avoid facet reflection. The light emitted from the combiner injects into the laser oscillation cavity via a high-reflection fiber Bragg grating (HR-FBG). The HR-FBG provides a reflectivity of ∼99.9% with a 3 dB bandwidth of ∼4 nm at the central wavelength of ∼1,080 nm. It is inscribed on the end of YDF. The YDF has a length of ∼20 m with 30/400 μm core/cladding diameters (NA_core = 0.064) and it is coiled in a figure-8 shape with a minimum bend diameter of 85 mm. An output coupler fiber Bragg grating (OC-FBG) provides a reflectivity of ∼10% with a 3 dB bandwidth of ∼1.7 nm at the central wavelength of ∼1,080 nm. A length of 3 m 30/400 μm delivery fiber is spliced after the OC-FBG. A cladding light stripper (CLS) with a length of 100 mm is realized by removing the polymer cladding of delivery fiber and coating the inner cladding with high refractive index ointment. A quartz endcap is employed to output the laser. The whole fiber laser oscillator and pump modulation devices are placed on a water-cooled plate. The photodiode, oscilloscope, optical spectrum analyzer and beam quality analyzer are used to characterize the output beam.

3 Results and discussion

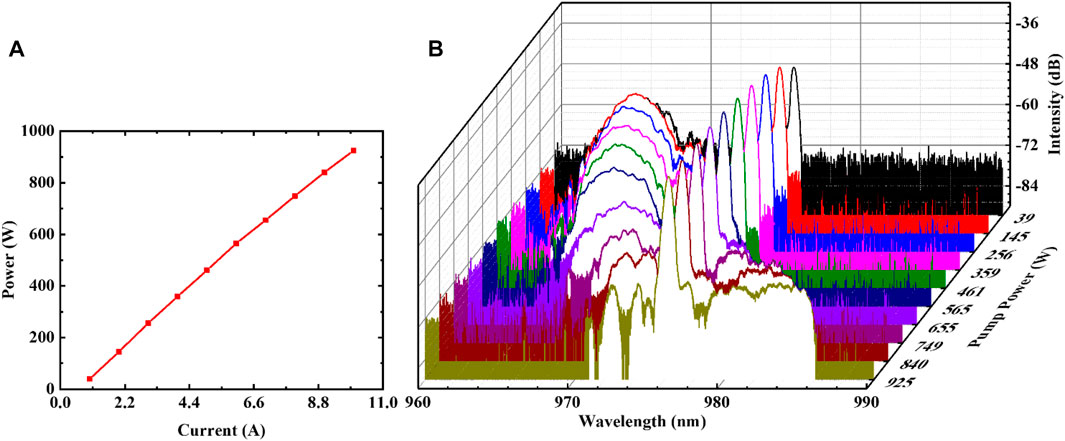
We first test the output characteristics of the all-fiber laser oscillator in the CW mode. Figure 2 shows the power and spectral response of the pump LDs. As depicted in Figure 2A, The total power of pump LDs grows linearly with the increase of current. Figure 2B shows the spectral response of LDs as the power increases. It can be clearly seen that the central wavelength of the main absorption peak is stable around 976 nm. However, there is also a secondary absorption peak that we refer to as the sub-absorption peak. When pump LDs begins to work with a power of 39 W, the maximum intensity of the sub-absorption peak is 14 dB lower than that of the main absorption peak. As the pump power increases, the position of the sub-absorption peak gradually shifts from ∼965 nm to ∼985 nm and the intensity of the sub-absorption becomes even weaker. The side lobe suppression ratio is about 31 dB.

FIGURE 2

FIGURE 2. The power (A) and spectral response (B) of the pump LDs.

The curves of output power and the standard deviation versus pump powers are shown in Figure 3A. The fiber laser oscillator shows a rollover output power of 180 W, along with a sharp increase of standard deviation. This indicates that a distinct temporal instability occurs around the rollover output power. Figures 3B,C depict the beam quality and spectrum of output laser at 180 W. The beam quality is about 1.81 (M²_x = 1.84, M²_y = 1.79) at 180 W. The central wavelength is around 1,080 nm, and there is no SRS and amplified spontaneous emission (ASE) in the spectrum. Figure 3D depicts that the fluctuation of the output laser is similar to a periodic sinusoidal wave, and the main oscillation frequency is about 100 Hz. Compared to fiber laser amplifiers, the fiber laser oscillator has a relatively low characteristic frequency, which is consistent with the report in Ref. [27]. The main frequency of the TMI may be greatly affected by the structure of the laser.

FIGURE 3

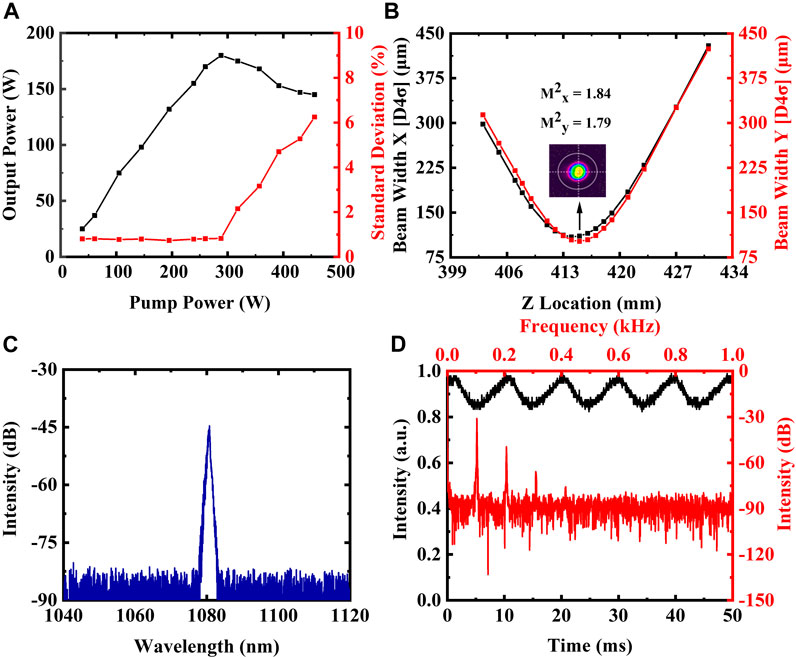
FIGURE 3. The output characteristics of fiber laser oscillator with a TMI threshold of 180 W. (A) The curves of output power and standard deviation versus pump powers. (B, C) The beam quality and output laser spectrum at 180 W. (D) The temporal signals with Fourier spectrum at the onset of TMI.

With the appearance of TMI, modal interference pattern is created via the beating of transverse modes. According to Ref. [28], the increase (decrease) of pump power causes the higher (lower) heat-load in the active fiber, and the modal interference pattern will be compressed (stretched). The change of heat-load alters the transverse refractive index profile of the fiber via the thermo-optic effect. The modal interference pattern is modified due to the variations of the propagation constants of the transverse modes. If there is an appropriate frequency and amplitude of the pump current, the thermally index grating in the longitudinal direction will be washed out. Then, the modal coupling can be weakened, thus leading to a significant reduction of beam fluctuations. According to the control theory and Nyquist-Shannon sampling theory, the signal can be analyzed and stabilized only when the sampling speed and control speed are over ten times of the rate of signal change [29, 30]. The sinusoidal wave with a modulation frequency above 1 kHz is assumed to wash the thermally index grating out in laser systems [20].

We use a dual channel function generator to modulate the pump drivers connected with two groups of pump LDs. The output laser is a sinusoidal wave and is stable in time, which is controlled by the sinusoidal modulation of pump current. When TMI occurs, the beam fluctuations are characterized as amplitude noise in the output laser. In order to analyze the temporal stability of the beam, the amplitude noise is calculated via filtering the main frequency and harmonics of the raw signals (since the input signals are not perfect sinusoidal waves), as depicted in Figure 4A. The standard deviation is used to quantify the magnitude of the amplitude noise, and to judge the TMI threshold. After repeated experiments, we find that the appropriate modulation frequency is 1.67 kHz. The optimal variation range of amplitude is Channel 1: 580 mV–980 mV, Channel 2: 560 mV–960 mV, corresponding to the total pump current of LDs is from 4.3 A to 16.1 A (average pump power: 452 W), i.e., the modulation depth of the current is about 57.8%. Then, the TMI threshold is increased to 195 W (Figure 4B). In addition to the modulation frequency and amplitude, we find that the phase difference between the two channels of the function generator has a great impact on the TMI mitigation effect. Figures 4C–E show that multiple phase differences can increase the TMI threshold, including 28°, 30.3° and 30.4°. When the phase difference is 30.4°, the maximum average output power of a stabilized beam can reach 221 W, which is about 1.23 times of the TMI threshold in CW mode. The beam quality is about 1.55 at around the threshold.

FIGURE 4

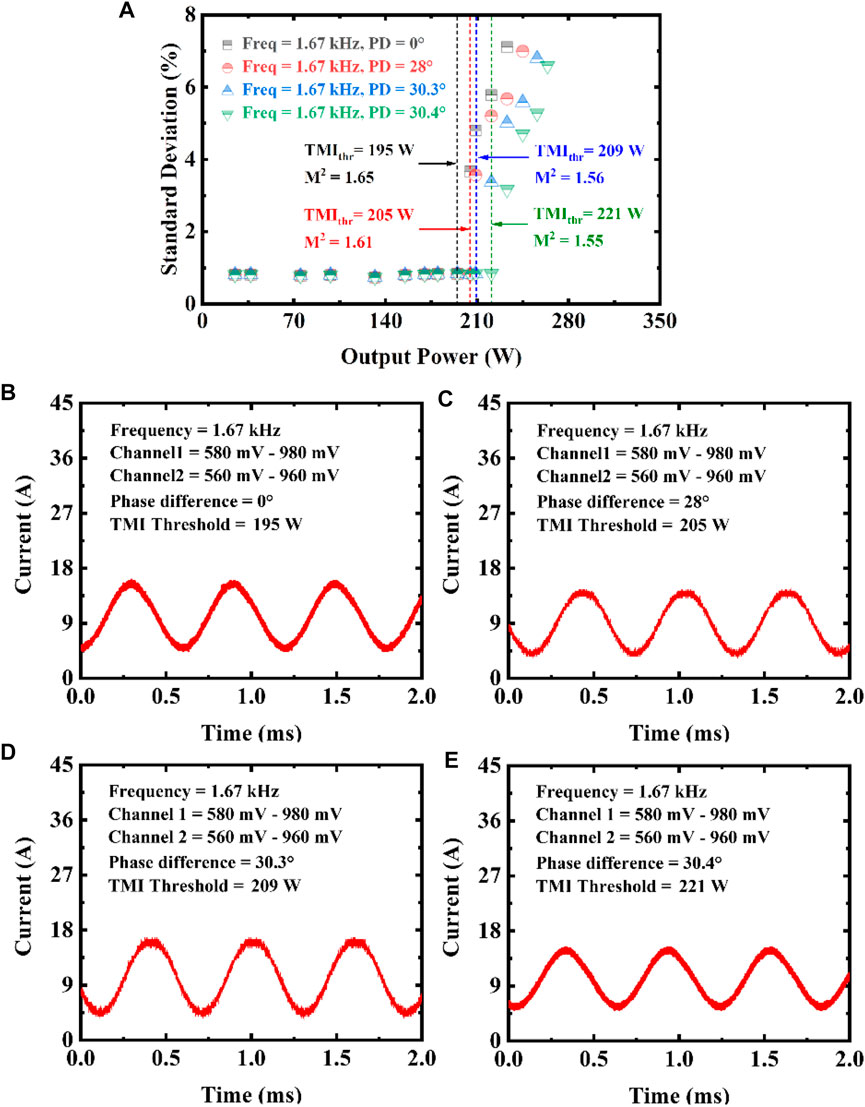
FIGURE 4. (A) The evolution of the standard deviation of the beam fluctuations with the output power under the pump modulation based on two groups of pump LDs (The modulation frequency and its harmonics of raw signals have been filtered out to calculate the temporal stability). (B–E) The actual current of pump LDs at TMI threshold. After the optimal modulation frequency and current depth (which relies on the amplitudes of the two channels of the function generator) are determined, the TMI threshold can be further increased by adjusting the phase difference between the two signal channels. Freq: frequency. PD: Phase Difference.

To investigate the influence of the groups of pump LDs with drivers on the TMI, we increase the two groups of pump LDs to three groups and connect them to three pump ports of laser system. The signal from channel 1 of the function generator injects in two series connection pump drivers, while the channel 2 connects the remaining pump driver. Then, the range of amplitude to reach TMI threshold is Channel 1: 560 mV–960 mV, Channel 2: 580 mV–930 mV, corresponding to the total pump current of LDs is from 2 A to 24.8 A (average pump power: 632 W), i.e., the modulation depth of the current is 85.1%. Compared with the pump modulation with two groups LDs, the TMI threshold is further increased since it can provide a larger power modulation range. The variation of standard deviation with output power is shown in Figure 5A (the amplitude noise is calculated via filtering the main frequency and harmonics of the raw signals). When the current depth is fixed, the maximum average output power of the stabilized beam can be further increased by changing the modulation frequency and phase difference. Figure 5B- Figure 5E shows that multiple combinations can increase the TMI threshold (1.3 kHz 25°, 1.66 kHz 28°, 1.6 kHz 33° and 1.55 kHz 34°). When the modulation frequency and phase difference are 1.55 kHz and 34° respectively, the maximum average output power of a stabilized beam increases to 310 W with a beam quality of 1.5. This output power is about 1.72 times of the TMI threshold in the CW mode.

FIGURE 5

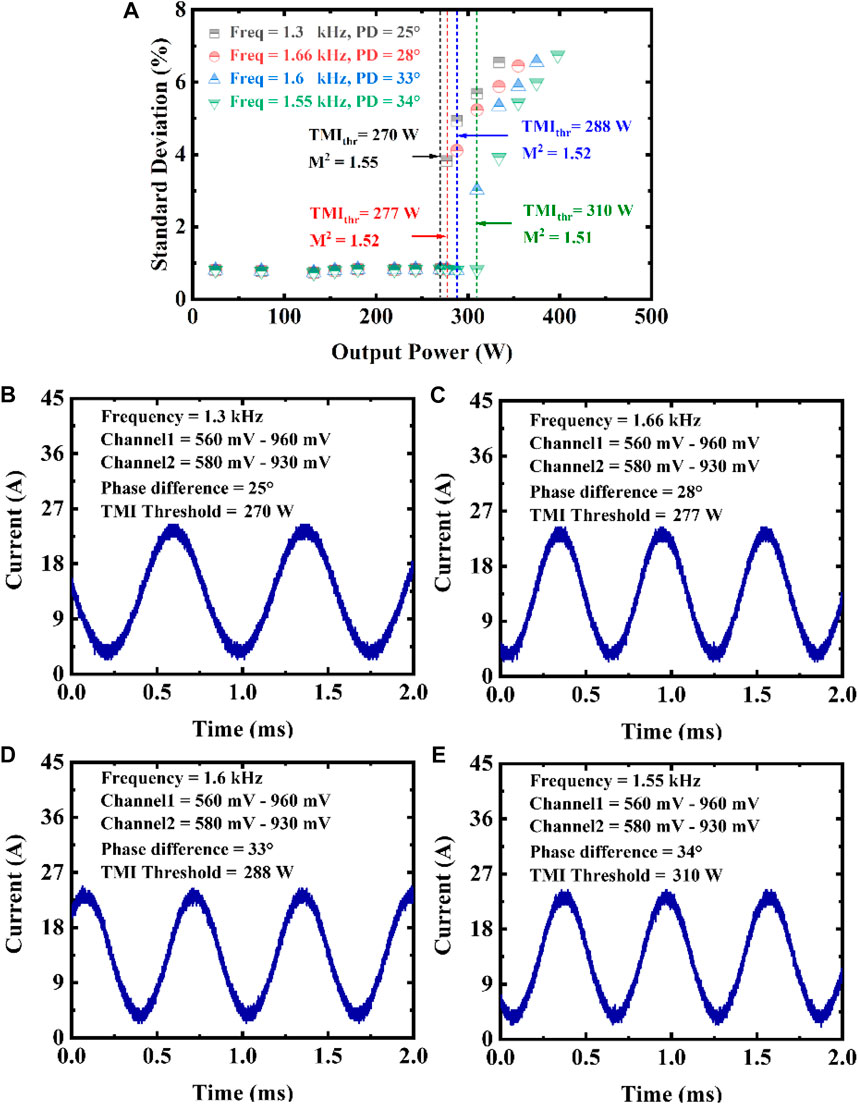
FIGURE 5. (A) The evolution of the standard deviation of the beam fluctuations with the output power under the pump modulation based on three groups of pump LDs (The modulation frequency and its harmonics of raw signals have been filtered out to calculate the temporal stability). (B–E) The actual pump LD current at TMI threshold. Two groups of LDs and their pump drivers are connected in series with channel 1 of the dual channel function generator, and the remaining group is connected with channel 2. Compared with the pump modulation with two groups LDs, the total current of three groups of LDs increases. After the current depth is determined, the maximum average output power of the stabilized beam can be increased by changing the modulation frequency and phase difference between the two channels. Freq: frequency. PD: Phase Difference.

In order to research the spectral characteristics under pump modulation, the spectra of output laser and the spectra of pump LDs at TMI threshold are recorded, respectively. Figures 6A,B show these two items under the modulation of two groups of LDs with drivers. The central wavelength of output laser keeps around 1,080 nm. The main absorption peak of the pump LDs is still around 976 nm. With the change of phase difference, the sub-absorption peak shift towards long wavelength and the maximum absorption intensity is reduced from −65 dB to −70 dB. However, the spectral integral proportion near the central wavelength 976 nm only varies from 53% to 50%, which is almost unchanged. It should be emphasized here that the large difference of the absorption intensity between the spectra of output laser and pump LDs is caused by the two inconsistent sampling positions. Figures 6C,D depict the spectra under the modulation of three groups of LDs with drivers. The central wavelength of the output laser and the main absorption peak of the LDs remain unchanged. The maximum intensity of the sub-absorption peak is similar with that of a same pump power in CW mode (Figure 2B). The position and intensity of the sub absorption peak both only have slight shifts with the modification of modulation frequency and phase difference. The spectral response of the direct pump modulation confirms that the increase of the TMI threshold of the all-fiber laser oscillator is not resulted from the change of pump absorption spectrum, but the power variation caused by multi-parameter current modulation.

FIGURE 6

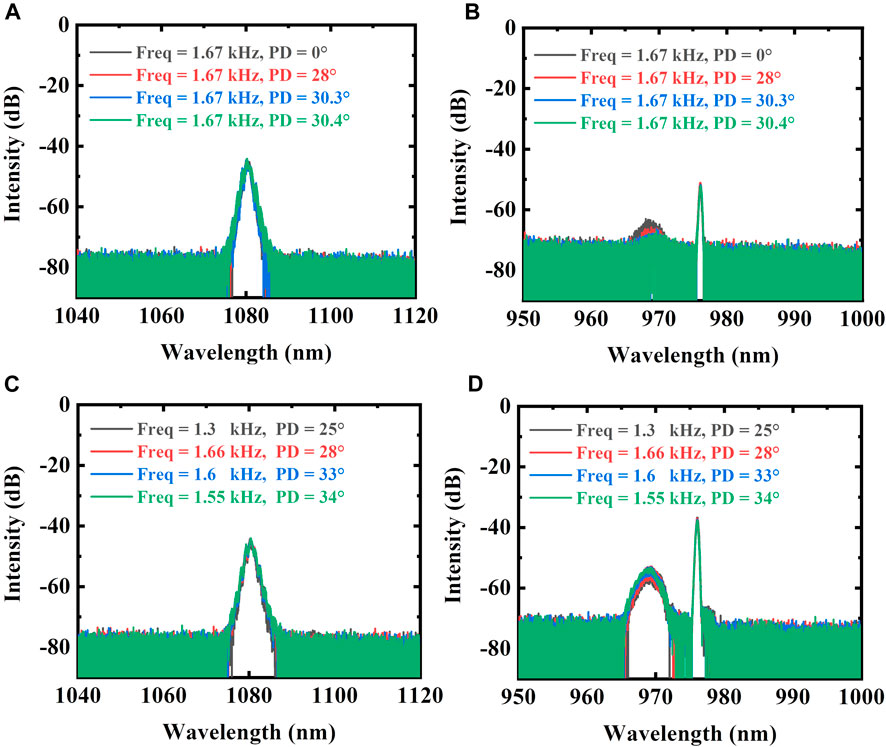
FIGURE 6. The spectra of laser output and LD output at TMI threshold under the pump modulation based on (A, B) two groups of LDs with drivers and (C,D) three groups of LDs with drivers. Freq: Frequency. PD: Phase Difference.

Table 1 summarizes the main results in our experiment. The average output power of a stabilized beam is effectively increased by the modulation of three groups of pump LDs with drivers. It can be inferred that the more groups of LDs with drivers for a laser system (i.e., the more freedom of pump power modulation) within a certain range, the better the TMI suppression effect. We find that the adjustment of phase difference between the channels of the function generator play a key role in the beam stabilization. Besides, multiple combinations of modulation frequency and phase difference can further increase the TMI threshold and improve the beam quality. The direct pump modulation scheme is promising since it caters to not only rod fibers but also LMA fibers. Besides, there is no need of close-loop unit, which can be easier integration with existing fiber laser systems. The drawback of this method is that the output power is modulated, which limits its application. However, for some special applications, such as the needs to use strong and weak alternating laser such as sine waveform, this strategy can greatly improve the output performance of the laser.

TABLE 1

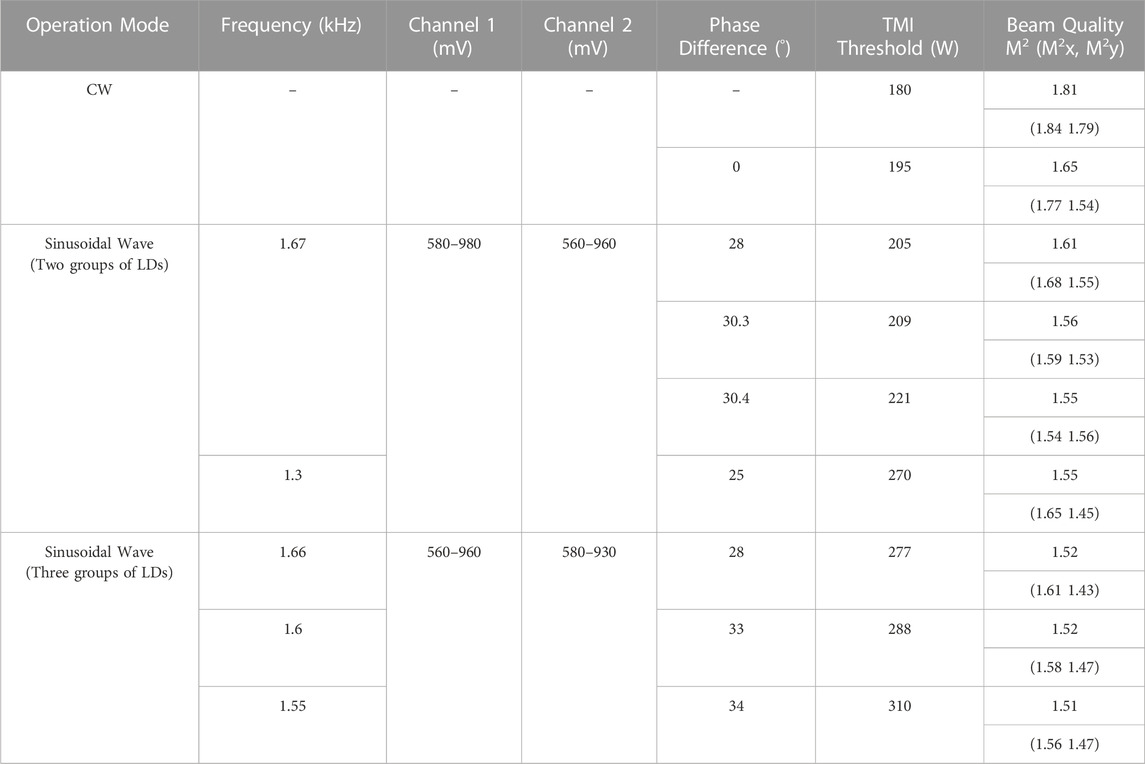
TABLE 1. The TMI threshold and beam quality under CW and pump modulation based on two and three groups of pump LDs.

4 Conclusion

Compared with other TMI mitigation schemes based on pump modulation, we first focus on the LMA fibers lasers and consider more degrees of freedom for modulation parameters in a 30 μm-core-diameter all-fiber laser oscillator. We demonstrate the adjustment of pump LDs groups and the phase difference between the signal channels of the function generator influence the TMI threshold, calling for more attention on the pump modulation. The maximum average power of a stabilized beam is increased up to 310 W via a multi-parameter-based direct pump modulation in our laser system, which is about a factor of 1.72 above the TMI threshold in CW mode.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

Investigation, JC, WL, and XW; resources, QZ, JZ, PL, HZ, DZ, YL and ZJ; writing—original draft preparation, JC; writing—review and editing, JC, WL and XW; supervision, WL, XW and GZ. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Natural Science Foundation of China (12074432, 12204540); Science and Technology Innovation Program of Hunan Province (2021RC3038).

Acknowledgments

The authors would like to thank Xiaoyong Xu and Penglin Zhong for their assistance in the whole experiment.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Shiner B The impact of fiber laser technology on the world wide material processing market. In: Cleo: Applications and Technology 2013. California, USA: San Jose (2013). p. 9–14. doi:10.1364/CLEO_SI.2013.AF2J.1

CrossRef Full Text | Google Scholar

2. Richardson DJ, Nilsson J, Clarkson WA High power fiber lasers: Current status and future perspectives. J Opt Soc Am B (2010) 27(11):B63–B92. doi:10.1364/JOSAB.27.000B63

CrossRef Full Text | Google Scholar

3. Wang Y, Chen G, Li J, “Development and prospect of high-power doped fibers. High Power Laser Sci Eng (2018) 6(3):e40. doi:10.1017/hpl.2018.30

CrossRef Full Text | Google Scholar

4. Jauregui C, Limpert J, Tünnermann A High-power fibre lasers. Nat Photon (2013) 7(11):861–7. doi:10.1038/nphoton.2013.273

CrossRef Full Text | Google Scholar

5. Smith AV, Smith JJ Mode instability in high power fiber amplifiers. Opt Express (2011) 19(11):10180–92. doi:10.1364/OE.19.010180

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zervas MN, Codemard CA High power fiber lasers: A review. IEEE J Sel Top Quan Electron. (2014) 20(5):0904123. doi:10.1109/JSTQE.2014.2321279

CrossRef Full Text | Google Scholar

7. Jauregui C, Eidam T, Otto H-J, Stutzki F, Jansen F, Limpert J, et al. Physical origin of mode instabilities in high-power fiber laser systems. Opt Express (2012) 20(12):12912–25. doi:10.1364/OE.20.012912

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zervas MN Power scaling limits in high power fiber amplifiers due to transverse mode instability, thermal lensing, and fiber mechanical reliability. Proc SPIE (2018) 1051205. doi:10.1117/12.2289792

CrossRef Full Text | Google Scholar

9. Wang Y, Kitahara R, Kiyoyama W, Shirakura Y, Kurihara T, Nakanishi Y, et al. San Francisco, California, USA (2020). p. 1126022. doi:10.1117/12.25458328-kW single-stage all-fiber Yb-doped fiber laser with a BPP of 0.50 mm-mradProc SPIE

CrossRef Full Text | Google Scholar

10. Jauregui C, Eidam T, Limpert J, Tünnermann A Impact of modal interference on the beam quality of high-power fiber amplifiers. Opt Express (2011) 19(4):3258–71. doi:10.1364/OE.19.003258

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ward B, Robin C, Dajani I Origin of thermal modal instabilities in large mode area fiber amplifiers. Opt Express (2012) 20(10):11407–22. doi:10.1364/OE.20.011407

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hansen KR, Alkeskjold TT, Broeng J, Lægsgaard J, “Theoretical analysis of mode instability in high-power fiber amplifiers,” Opt Express (2013) 21(2):1944–71. doi:10.1364/OE.21.001944

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Liu Y, Zhang F, Zhao N, Lin X, Liao L, Wang Y, et al. Single transverse mode laser in a center-sunken and cladding-trenched Yb-doped fiber. Opt Express (2018) 26(3):3421–6. doi:10.1364/OE.26.003421

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Eidam T, Wirth C, Jauregui C, Stutzki F, Jansen F, Otto H-J, et al. Experimental observations of the threshold-like onset of mode instabilities in high power fiber amplifiers. Opt Express (2011) 19(14):13218–24. doi:10.1364/OE.19.013218

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Jauregui C, Otto H-J, Stutzki F, Jansen F, Limpert J, Tünnermann A Passive mitigation strategies for mode instabilities in high-power fiber laser systems. Opt Express (2013) 21(16):19375–86. doi:10.1364/OE.21.019375

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Otto HJ, Stutzki F, Jansen F, Eidam T, Jauregui C, Limpert J, et al. Temporal dynamics of mode instabilities in high-power fiber lasers and amplifiers. Opt Express (2012) 20(14):15710–22. doi:10.1364/OE.20.015710

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Tao R, Ma P, Wang X, Zhou P, Liu Z Mitigating of modal instabilities in linearly-polarized fiber amplifiers by shifting pump wavelength. J Opt (2015) 17(4):45504. doi:10.1088/2040-8978/17/4/045504

CrossRef Full Text | Google Scholar

18. Stutzki F, Jansen F, Eidam T, Steinmetz A, Jauregui C, Limpert J, et al. High average power large-pitch fiber amplifier with robust single-mode operation. Opt Lett (2011) 36(5):689–91. doi:10.1364/OL.36.000689

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Jauregui C, Stihler C, Limpert J, Tünnermann A Transverse mode instabilities in burst operation of high-power fiber laser systems. Proc SPIE (2018) 1051207. doi:10.1117/12.2290021

CrossRef Full Text | Google Scholar

20. Jauregui C, Stihler C, Tünnermann A, Limpert J Pump-modulation-induced beam stabilization in highpower fiber laser systems above the mode instability threshold. Opt Express (2018) 26(8):10691–704. doi:10.1364/OE.26.010691

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Stihler C, Jauregui C, Tünnermann A, Limpert J Phase-shift evolution of the thermally-induced refractive index grating in high-power fiber laser systems induced by pump-power variations. Opt Express (2018) 26(15):19489–97. doi:10.1364/OE.26.019489

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Stihler C, Jauregui C, Tünnermann A, Limpert J Modal energy transfer by thermally induced refractive index gratings in Yb-doped fibers. Light Sci Appl (2018) 7(59):563–74. doi:10.1038/s41377-018-0061-6

CrossRef Full Text | Google Scholar

23. Xiao Y, Brunet F, Kanskar M, Faucher M, Wetter A, Holehouse N 1-kilowatt CW all-fiber laser oscillator pumped with wavelength-beam-combined diode stacks. Opt Express (2012) 20(3):3296–301. doi:10.1364/OE.20.003296

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ruppik S, Becker F, Grundmann FP, Rath W, Hefter U High-power disk and fiber lasers: A performance comparison. Proc SPIE (2012) 149–63. doi:10.1117/12.913286

CrossRef Full Text | Google Scholar

25. Ikoma S, Nguyen HK, Kashiwagi M, Uchiyama K, Shima K, Tanaka D 3 kW single stage all-fiber Yb-doped single-mode fiber laser for highly reflective and highly thermal conductive materials processing. Proc SPIE (2017) 10083. doi:10.1117/12.2250294

CrossRef Full Text | Google Scholar

26. Yang B, Shi C, Zhang H, Ye Q, Pi H, Tao R, et al. Monolithic fiber laser oscillator with record high power. Laser Phys Lett (2018) 15(7):075106. doi:10.1088/1612-202X/aac19

CrossRef Full Text | Google Scholar

27. Yang B, Zhang H, Shi C, Wang X, Zhou P, Xu X, et al. Mitigating transverse mode instability in all-fiber laser oscillator and scaling power up to 2.5 kW employing bidirectional-pump scheme. Opt Express (2016) 24(24):27828–35. doi:10.1364/oe.24.027828

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Jauregui C, Stihler C, Limpert J Transverse mode instability. Adv Opt Photon (2020) 12(2):429–84. doi:10.1364/AOP.385184

CrossRef Full Text | Google Scholar

29. Glad T, Ljung L Control theory. CRC Press (2000).

Google Scholar

30. Doyle JC, Francis BA, Tannenbaum AR Feedback control theory. Courier Corporation (2013).

Google Scholar