Heat transfer in MHD flow of Carreau ternary-hybrid nanofluid over a curved surface stretched exponentially

This investigation aims to study Magnetohydrodynamics (MHD)two-dimensional incompressible boundary layer performing non-Newtonian Carreau ternary-hybrid nanofluid flow with heat transfer through an exponential stretching curved surface. The ternary-hybrid nanofluid has been synthesized with titanium oxide, aluminum oxide, and silver dispersionin the base fluid water. TheNavier Stokes equation and Carreau ternary-hybrid nanofluid model govern the partial differential equations (PDEs), and appropriate similarity transformations are utilized to transfer these PDEs into ordinary differential equations (ODEs). The effects of the pertinent parameters on the dimensionless velocity and temperature profiles are analyzed withfigures. This study provides new insights and solutions to previously unsolved problems related to heat transfer in the MHD flow of a Carreau Ternary-Hybrid Nanofluid over a curved surface stretched exponentially, or it could contribute to the existing knowledge and literature by refining existing models or methods. The surface drag force and Nusselt numbers are studied for the different values of the governing parameters throughgraphs. It is demonstrated that the heat transfer rate and skin friction increase from base fluid to mono, hybrid, and ternary nanofluids. Both heat transfer rate and skin friction increase with the addition of nanoparticles.

1 Introduction

Nanotechnology is a rapidly growing field that studies and manipulates materials at the nanoscale level, typically between 1 and 100 nm. This field has seen a significant increase in research and development over the past few decades, with numerous applications emerging in electronics, medicine, energy, and materials science. One promising application of nanotechnology is developingnanofluids, engineered fluids containing nanoparticles dispersed in a base fluid. These fluids have been shown to have unique thermal and transport properties, such as enhanced thermal conductivity, convective heat transfer, and viscosity. Choi [1] investigated the thermal properties of nanoparticles dispersed in water and other fluids. His work showed that adding nanoparticles to the base fluid could significantly enhance the thermal conductivity of the fluid, which could have critical applications in various thermal systems, including heat exchangers, electronics cooling, and power generation.

Since the publication of Choi’s work, numerous studies have been conducted on applyingnanofluids in various thermal systems. These studies have shown that nanofluids can significantly improve thermal performance and efficiency, making them a promising technology for various applications. However, challenges in developing and implementing nanofluids, such as nanoparticle stability, toxicity, and cost, must be addressed to realize their potential.

Many researchers investigated the radiator’s performance using nanofluid as a coolant theoretically and experimentally [2, 3]. Samantaray et al. [4] studied the impact of several physical phenomena on radiativenanofluid flow, like the second-order slip phenomenon. Researchers [5, 6] have provided insights into the importance of heat transfer mechanisms through nanofluids in industrial applications.

The significant challenges for studying the thermophysical properties of hybrid nanofluids are investigating the improvements for its various applications, especially those related to cooling systems such as electronic cooling, heat exchangers, and automotive cooling systems, as shown in [7]. According to Makishima [8], a hybrid nanofluid is a compound of two or more different types of nanoparticles mixed into a single base liquid. Rif et al. [9] investigated thermal transport analysis using the applications of hybrid nanofluid flow with heat transfer in an oscillating cylinder. Benkhedda et al. [10] explored heat transfer using hybrid nanofluids considering differently shaped nanoparticles in the water-based fluid. Sarkar et al. [11] studiedthe thermal transport properties and analyzed that hybrid nanofluids performed better with thermal performance and pressure drop characteristics than unitary nanofluids. Wakif et al. [12] studied the influence of thermal radiation and roughness of the surface using the applications of alumina–copper oxide hybrid nanofluids using the generalized Buongiorno’snanofluid model. Many engineers and researchers are involved in studying various articles aboutnanofluid in References. [13–18].

However, using ternary-hybrid nanofluids is an emerging area of research in nanofluids. Ternary-hybrid nanofluids refer to suspensions of three different types of nanoparticles in a single base fluid. These nanofluids can have complex particle-particle and particle-fluid interactions, resulting in unique thermal properties. Recent studies have explored using ternary-hybrid nanofluids with differently shaped nanoparticles in various fields of science, including electronics cooling, power generation, and biomedical applications. These studies have shown that the use of ternary-hybrid nanofluids can lead to a significant improvement in heat transfer rates compared to traditional heat transfer fluids. The use of differently shaped nanoparticles in ternary-hybrid nanofluids can also lead to improvements in thermal conductivity and convective heat transfer. For example, the use of platelet-shaped nanoparticles in ternary-hybrid nanofluids has been shown to significantly enhance the thermal conductivity of the fluid, leading to improved heat transfer rates. However, as with any new technology, several challenges are addressed in developing and implementing ternary-hybrid nanofluids, such as particle stability, toxicity, and cost.

Further research is needed to fully understand these complex fluids’ behavior and optimize their properties for various applications.

Elnaqeeb et al. [19] discussed the dynamics of ternary hybrid nanofluids best fit for the description of Newtonian fluids because the density of ternary hybrid nanofluids decreases linearly with the temperature rise. Sahoo and Kumar [20] studied the viscosity of ternary hybrid nanofluids with applications. Recently, Xuan et al. [21] explored some experimental results, thermal performance, and sensitivity analysis of ternary hybrid nanofluids. Currently, non-Newtonian fluid flows interest many researchers due to their increasing industrial and technical applications due to various applications in industries-non-Newtonian liquids such as ketchup, spray, honey lubrication, starch, etc., Carreau [22] introduced the Carreau model given as:

$\mathit{\tau }=\left[{\mu }_{\infty }+\left({\mu }_o-{\mu }_{\infty }\right){\left(1+{\left(\mathrm{\Gamma }\dot{\gamma }\right)}^2\right)}^{\frac{m-1}{2}}\right]{\dot{\gamma }}_{ij}.$

Where $\mathit{\tau }$, $\dot{\gamma }$ represent the extra stress tensor and generalized shear rate, respectively, $\mathrm{\Gamma }$ is the material time, ${\mu }_o$ is the zero-shear rate viscosity, ${\mu }_{\infty }$ is the infinite shear rate viscosity. In terms of the second invariant tensor $\mathrm{\Pi }$, the generalized shear rate can be given by:

$\dot{\gamma }=\sqrt{\frac{1}{2}{\mathrm{\Sigma }\mathrm{\Sigma }\dot{\gamma }}_{ij}{\dot{\gamma }}_{ij}}=\sqrt{\frac{1}{2}}\mathrm{\Pi },$

where $\mathrm{\Pi }=trace\left(\nabla U+{∆U}^{Ť}\right)$ here, we consider the case for which ${\mu }_o=0.$ In the following form, the extra stress tensor is given:

$\mathit{\tau }=\left[{\mu }_0{\left(1+{\left(\mathrm{\Gamma }\dot{\gamma }\right)}^2\right)}^{\frac{m-1}{2}}\right]{\dot{\gamma }}_{ij}.$

Olajuwon [23] numericallystudied the non-Newtonian Carreau fluid onto a porous plate. Heat transfer characteristics are explored, including thermal diffusion and radiation. Shadid and Eckert [24] investigated the Carreau fluid induced by a stretched cylinder with viscous dissipation heating. Geogios [25] discussed the unsteady compressible flow of Carreau fluid with consideration of the slip effect. Hayat et al. [26] carried out the mathematical analysis using a homotopic approach on boundary-driven Carreau fluid flow induced by a stretched heated sheet with permeability. Shehzad et al. [27] examined the non-Newtonian three–dimensional (3D) flow of Jeffery fluid going past a stretched surface with convective boundary conditions. Khan and Hashima [28] investigated the flow field and heat transfer analysis generated by a nonlinear stretching sheet. Akbar et al. [29] studiedtheCarreau fluid boundary-driven problem of shrinking permeable sheets. Abbas et al. [30] explored the behavior of Carreau fluid on a stretching permeability sheet in the presence of variable viscosity and thermal conductivity. Bilal et al. [31] probed the flow features of Carreau fluid caused by a linearly stretching surface in the fact of thermal stratification and magnetic field. Machireddy and Naramgari [32] scrutinized the heat mass transfer characteristics in Carreau fluid flow due to a stretched sheet. Shah et al. [33] studiedthe analysis of MHD Carreau fluid by considering variable thermal conductivity and viscous dissipation heating. Santhosh et al. [34] documented the flow features of Carreau fluid generated by an exponential stretchable surface and partial slip at the wall. Megahed [35] pointed out the Carreau fluid flow prompted by a nonlinearly stretching wall under consideration of heat flux, thermal radiation effects, and variable conductivity. Ramzan et al. [36] reveal that using Carreau ternary-hybrid nanofluids is a relatively new research area, and only a limited number of studies are available in the literature. This is because the behavior of ternary-hybrid nanofluids is more complex than binary or single-nanoparticle systems due to the interactions between the different types of nanoparticles. Some articles about non-Newtonian nanofluid flow are highlighted in References [37–42]. The limited number of studies related to Carreau ternary-hybrid nanofluids highlights the need for further research. This can lead to the development of new theoretical models and frameworks for predicting the behavior of complex fluids.

However, there are still many gaps in our understanding of their behavior and properties.

1. Lack of comprehensive experimental data: Due to the complex nature of ternary-hybrid nanofluids, there is a lack of extensive experimental data related to their thermal, electrical, and mechanical properties.

2. Need for theoretical models: There is a need to develop new theoretical models and frameworks for predicting the behavior of Carreau ternary-hybrid nanofluids under various flow conditions and geometries.

3. Effect of nanoparticle size and concentration: The effect of nanoparticle size and concentration on the behavior and properties of ternary-hybrid nanofluids is not well understood and requires further investigation.

4. Limited application-specific research: There is a lack of application-specific research on their use in various engineering applications such as heat exchangers, cooling systems, and energy generation systems.

Identifying and addressing these research gaps in the literature can help advance our understanding of Carreau ternary-hybrid nanofluids and their potential applications. This study focuses on heat transfer over a curved surface stretched exponentially to fill these gaps. The use of an exponentially stretched surface allows for a more general case compared to previous studies, which have typically focused on linear or power-law stretching.

By combining other factors, the study aims to investigate the heat transfer properties of a complex fluid system under unique conditions. This can provide new insights and understanding of the behavior of such systems, which can be useful in various engineering applications such as heat exchangers, cooling systems, and energy generation systems.

2 Mathematical modeling

This study considers an incompressible two-dimensional MHD flow of a Carreau ternary-hybrid nanofluid over an exponentially stretching curved surface. The nanofluid is composed of TiO₂, Ag, and Al₂O₃ nanoparticles in a water-based fluid. The heat transfer mechanism is studied with thermal radiation and viscous dissipation effects. Two coordinates, r and s, define the model coordinate system. The s-axis is taken along the flow direction, and the r-axis is taken orthogonal. The sheet is assumed to stretch along the s-direction with velocity u_w = $u_w=c{e}^{\frac{s}{L}}$, where c is a constant, and L is a characteristic length. An exponential varying magnetic field B = B₀ e^(s/2L) is applied in the radial direction, where B₀ is a constant. The surface is assumed to be curved with radius R, and the temperature is defined as T_w at the surface and T_∞ far away from the surface, where T_w > T_∞, as shown in Figure 1. This temperature difference drives the heat transfer process.

FIGURE 1

FIGURE 1. Geometry of curved sheet mass conservation equation.

Considering the above assumptions, the continuity, moment, and energy equations [43-45] are as follows:

$v+\left(r+R\right){\partial }_{r}v+R{\partial }_{s}u=0,(1)$

$\frac{u^2}{r+R}=\frac{1}{{\rho }_{thnf}}{\partial }_{r}p,(2)$

$\begin{array}{c}v{\partial }_{r}u+\frac{Ru}{r+R}{\partial }_{s}u+\frac{uv}{r+R}=-\frac{1}{{\rho }_{thnf}}\frac{R}{r+R}{\partial }_{s}p+\frac{{\mu }_{thnf}}{{\rho }_{thnf}}{\left\{1+{\mathrm{\Gamma }}^2{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2\right\}}^{\frac{m-1}{2}}\left\{{\partial }_{rr}u+\frac{1}{r+R}{\partial }_{r}u-\frac{u}{{\left(r+R\right)}^2}\right\}+\frac{{\mu }_{thnf}}{{\rho }_{thnf}}{\mathrm{\Gamma }}^2\left(m-1\right)\\ {\left\{1+{\mathrm{\Gamma }}^2{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2\right\}}^{\frac{m-3}{2}}{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2\left\{{\partial }_{rr}u+\frac{1}{r+R}{\partial }_{r}u-\frac{u}{{\left(r+R\right)}^2}\right\}-\frac{{\sigma }_{thnf}}{{\rho }_{thnf}}{B}_0^{2}u,\end{array}(3)$

${\left(\rho c_p\right)}_{thnf}\left(v{\partial }_{r}T+\frac{Ru}{r+R}{\partial }_{s}T\right)=k_{thnf}\left({\partial }_{rr}T+\frac{1}{r+R}{\partial }_{r}T\right)+{\mu }_{thnf}{\left\{1+{\mathrm{\Gamma }}^2{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2\right\}}^{\frac{m-1}{2}}{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2-\frac{q}{r+R}-{\partial }_{r}q.(4)$

$u$ and $v$ are the velocities in the curvilinear directions $s-$ and $r-,$ respectively. $k_{thnf},{\rho }_{thnf}$ and ${\left(c_P\right)}_{thnf}are$ the ternary-hybrid nanofluid thermal conductivity, ternary-hybrid nanofluiddensity, and ternary-hybrid nanofluidspecific heat, respectively, ${\mathrm{\sigma }}_{\mathrm{t}\mathrm{h}\mathrm{n}\mathrm{f}}$ is the ternary hybrid nanofluid electrical conductivity, ${\mathrm{B}}_0$ symbolizes the magnetic field, p is the dimensional pressure, $\mathrm{\Gamma }$ is a favorable time constant, T is the fluid temperature, $q$ is the radiative heat flux

Boundary conditions are given by:

$u=u_w=c{e}^{\frac{s}{L}},v=0,h_f\left(T_w-T\right)=-k_{thnf}{\partial }_{r}Tatr=0,(5)$

$u\to 0,{\partial }_{r}u\to 0,T\to T_{\infty }asr\to \infty .(6)$

Using Rosseland’s approximation.

$q=-\frac{4\check{\sigma }}{3ǩ}{\partial }_r{T}^4,(7)$

where $\sigma$ is the Stefan-Boltzmann constant, $q$ represents the radiative heat flux and $k$ indicates the mean absorption coefficient.

Employing Taylor’s seriesfor the temperature variation $\left(T^4\right)$ expansion about $T_{\infty }$.

$T^4\approx 4T_{\infty }^{3}T-3T_{\infty }^4,(8)$

Substituting Eq. 8 into Eq. 7, one can have

$q=-\frac{{16\check{\sigma }T}_{\infty }^3}{3ǩ}{\partial }_{rr}T,(9)$

Using Eq. 7, the energy Eq. 4 is given in the following form:

$\left(v{\partial }_{r}T+\frac{Ru}{r+R}{\partial }_{s}T\right)=\frac{k_{thnf}}{{\left(\rho c_p\right)}_{thnf}}\left(1+\frac{{16\check{\sigma }T}_{\infty }^3}{3ǩk_0}\right)\left({\partial }_{rr}T+\frac{1}{r+R}{\partial }_{r}T\right)+\frac{{\mu }_{thnf}}{{\left(\rho c_p\right)}_{thnf}}{\left\{1+{\mathrm{\Gamma }}^2{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2\right\}}^{\frac{m-1}{2}}{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2.(10)$

The similarity variables $\xi ,\delta$ are given as follows:

$\xi =r{\left(\frac{c}{2\nu L}\right)}^{0.5}{e}^{\frac{s}{2L}},\delta =R{\left(\frac{c}{2\nu L}\right)}^{0.5}{e}^{\frac{s}{2L}}(11)$

In terms of similarity variables, the expressions $u$, $v$, $p,$ and $T$ are defined as follows:

Defining the following dimensionless variable transformations, see [44–46].

$u=c{e}^{\frac{s}{L}}{f}^{\prime }\left(\xi \right),v=-\frac{R}{r+R}{\left(\frac{c\nu }{2L}\right)}^{0.5}{e}^{\frac{s}{2L}}\left[f\left(\xi \right)+\xi f^{\prime \left(\xi \right)}\right],(12)$

$p=\rho c^2{e}^{\frac{2s}{L}}P\left(\xi \right),\theta =\frac{T-T_{\infty }}{T_w-T_{\infty }}.(13)$

The correlations for ternary hybrid nanoparticles given by [47]:

${\left({\rho c}_p\right)}_{Thnf}={\varphi }_1{\left({\rho c}_p\right)}_1+{\varphi }_2{\left({\rho c}_p\right)}_2+{\varphi }_3{\left({\rho c}_p\right)}_3+\left(1-{\varphi }_1-{\varphi }_2-{\varphi }_3\right){\left({\rho c}_p\right)}_f(14)$

${\left(\rho \right)}_{Thnf}=\left(1-{\varphi }_1-{\varphi }_2-{\varphi }_3\right){\rho }_f+{\varphi }_1{\rho }_1+{\varphi }_2{\rho }_2+{\varphi }_3{\rho }_3(15)$

${\mu }_{Thnf}=\frac{{\mu }_f}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}{\left(1-{\varphi }_3\right)}^{2.5}}(16)$

$\frac{{\left(k\right)}_{Thnf}}{{\left(k\right)}_{hnf}}=\frac{k_1+2k_{hnf}-2{\varphi }_1\left(k_{hnf}-k_1\right)}{k_1+2k_{hnf}+{\varphi }_1\left(k_{hnf}-k_1\right)},\frac{{\left(k\right)}_{hnf}}{{\left(k\right)}_{nf}}=\frac{k_2+2k_{nf}-2{\varphi }_2\left(k_{nf}-k_2\right)}{k_2+2k_{nf}+{\varphi }_2\left(k_{nf}-k_2\right)},\frac{{\left(k\right)}_{nf}}{{\left(k\right)}_f}=\frac{k_3+2k_f-2{\varphi }_3\left(k_f-k_3\right)}{k_3+2k_f+{\varphi }_3\left(k_f-k_3\right)},(17)$

$\frac{{\left(\sigma \right)}_{Thnf}}{{\left(\sigma \right)}_{hnf}}=\frac{{\sigma }_1\left(1+{2\varphi }_1\right)+{\varphi }_{hnf}\left(1-{2\varphi }_1\right)}{{\sigma }_1\left(1-{\varphi }_1\right)+{\sigma }_{hnf}\left(1+{\varphi }_1\right)},\frac{{\left(\sigma \right)}_{hnf}}{{\left(\sigma \right)}_{nf}}=\frac{{\sigma }_2\left(1+{2\varphi }_2\right)+{\varphi }_{nf}\left(1-{2\varphi }_2\right)}{{\sigma }_2\left(1-{\varphi }_2\right)+{\sigma }_{nf}\left(1+{\varphi }_2\right)},\frac{{\left(\sigma \right)}_{nf}}{{\left(\sigma \right)}_f}=\frac{{\sigma }_3\left(1+{2\varphi }_3\right)+{\varphi }_f\left(1-{2\varphi }_3\right)}{{\sigma }_3\left(1-{\varphi }_3\right)+{\sigma }_f\left(1+{\varphi }_3\right)},(18)$

The thermophysical constants with respect to the nanoparticles and base fluid are given in Table 1.

TABLE 1

TABLE 1. Thermal properties of the nanoparticles and base fluid [47].

Using Eqs 11–13, the requirement of the continuity equation is automatically satisfied. Eqs 2, 3, 10 given by:

$\frac{f^{\prime 2}}{\xi +\delta }=\frac{{\rho }_f}{{\rho }_{thnf}}{P}^{\prime }(19)$

$\begin{array}{c}\frac{{\rho }_f}{{\rho }_{thnf}}\left(\frac{4\delta }{\xi +\delta }P+\frac{\delta \xi }{\xi +\delta }{P}^{\prime }\right)=\frac{{\mu }_{thnf}}{{\mu }_f}\frac{{\rho }_f}{{\rho }_{thnf}}\\ \times \left[{\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\right\}}^{\frac{m-1}{2}}\left(f^{‴}+\frac{f^{″}}{\xi +\delta }-\frac{f^{\prime }}{{\left(\xi +\delta \right)}^2}\right)+\left(m-1\right)We\times {\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\right\}}^{\frac{m-3}{2}}\left(f^{‴}+\frac{f^{″}}{\xi +\delta }-\frac{f^{\prime }}{{\left(\xi +\delta \right)}^2}\right){\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2]\right]\\ +\frac{\delta }{{\left(\xi +\delta \right)}^2}f{f}^{\prime }+\frac{\delta }{\xi +\delta }f{f}^{″}-\frac{\left(\xi +2\delta \right)}{{\left(\xi +\delta \right)}^2}\delta {f^{\prime }}^2-\frac{{\sigma }_{thnf}}{{\rho }_{thnf}}M{f}^{\prime },\end{array}(20)$

$\frac{k_{thnf}}{k_f}\frac{{\left(\rho c_p\right)}_f}{{\left(\rho c_p\right)}_{thnf}}\left({\theta }^{″}+\frac{{\theta }^{\prime }}{\xi +\delta }\right)+\frac{{\left(\rho c_p\right)}_f}{{\left(\rho c_p\right)}_{thnf}}Rd\left({\theta }^{″}+\frac{{\theta }^{\prime }}{\xi +\delta }\right)+\frac{\delta \mathit{Pr}}{\xi +\delta }\left(f{\theta }^{\prime }-2f^{\prime }\theta \right)+\frac{{\mu }_{thnf}}{{\mu }_f}\frac{{\left(\rho c_p\right)}_f}{{\left(\rho c_p\right)}_{thnf}}PrEc{\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\right\}}^{\frac{m-1}{2}}{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right),}^2=0,(21)$

Using Eqs 19, 20, one can eliminate pressure

$\begin{array}{ll}\hfill \frac{{\mu }_{thnf}}{{\mu }_f}\frac{{\rho }_f}{{\rho }_{thnf}}& \left[\left(m-1\right)\left(m-3\right)W{e}^2{\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\right\}}^{\frac{m-5}{2}}{\times \left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^3{\left(f^{‴}-\frac{f^{″}}{\xi +\delta }+\frac{f^{\prime }}{{\left(\xi +\delta \right)}^2}\right)}^2+\left(m-1\right)We{\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\right\}}^{\frac{m-3}{2}}\right.\hfill \\ \hfill & {\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\times \left(f^{iv}+\frac{f^{″}}{{\left(\xi +\delta \right)}^2}-\frac{f^{\prime }}{{\left(\xi +\delta \right)}^3}\right)+\left(m-1\right)We{\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\right\}}^{\frac{m-3}{2}}\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)\hfill \\ \hfill & \times \left(f^{‴}-\frac{f^{″}}{\xi +\delta }+\frac{f^{\prime }}{{\left(\xi +\delta \right)}^2}\right)\left({3f}^{‴}-\frac{f^{″}}{\xi +\delta }+\frac{f^{\prime }}{{\left(\xi +\delta \right)}^2}\right)+{\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\xi +\delta }\right)}^2\right\}}^{\frac{m-1}{2}}\left[f^{iv}+\frac{2f^{‴}}{\xi +\delta }+\frac{f^{″}}{{\left(\xi +\delta \right)}^2}-\frac{f^{\prime }}{{\left(\xi +\delta \right)}^3}\right]]\hfill \\ \hfill & -\frac{3\delta f^{\prime 2}}{{\left(\xi +\delta \right)}^2}-\frac{3\delta f^{\prime }{f}^{″}}{\xi +\delta }-\frac{\delta f{f}^{\prime }}{{\left(\xi +\delta \right)}^3}+\frac{\delta f{f}^{″}}{{\left(\xi +\delta \right)}^2}+\frac{\delta f{f}^{‴}}{\xi +\delta }-\frac{{\sigma }_{thnf}}{{\rho }_{thnf}}M{f}^{″}=0.\hfill \end{array}(22)$

The transformed boundary conditions are

$f\left(0\right)=0,f^{\prime }\left(0\right)=1,{\theta }^{\prime }\left(0\right)=-\frac{k_{thnf}}{k_f}Bi\left(1-\theta \left(0\right)\right)at\xi =0,f^{\prime }\left(\xi \right)=0,f^{″\left(\xi \right)}=0,\theta \left(\xi \right)=0as\xi \to \infty .(23)$

The emerging non-dimensional physical parameters in the model are given by:

$\begin{array}{c}\mathrm{M}=\frac{2l{\mathrm{\sigma }}_{\mathrm{f}}{\mathrm{B}}_0^2}{u_w{\mathrm{\rho }}_{\mathrm{f}}}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{f}\mathrm{i}\mathrm{e}\mathrm{l}\mathrm{d}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r},\mathit{pr}=\frac{{\mu }_f{\left(c_p\right)}_f}{k_f}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{P}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{t}\mathrm{l}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r},\hfill \\ We=\frac{{\mathrm{\Gamma }}^2{u}_w^3}{2l{\upsilon }_f}\mathrm{W}\mathrm{e}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r},Rd=\frac{{16\stackrel{\mathrm{ˇ}}{\sigma }T}_{\infty }^3}{3\stackrel{\mathrm{ˇ}}{k}{k}_0}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r},\hfill \\ Ec=\frac{u_w^2}{{\left(c_p\right)}_f\left(T_w-T_{\infty }\right)}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{E}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r},\mathrm{a}\mathrm{n}\mathrm{d}Bi=\left(\frac{h}{k_f}\right)\sqrt{\frac{{2l\upsilon }_f}{c}}{e}^{\frac{-s}{2L}}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{B}\mathrm{i}\mathrm{o}\mathrm{t}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\hfill \end{array}(24)$

The skin friction $c_{fs}$ and Nusselt number $N{u}_s$ for our problem are given as

$c_{fs}=\frac{{\tau }_{rs}}{{\rho }_f{u}_w^2},{Nu}_s=\frac{s{q}_w}{k_f\left(T_w-T_{\infty }\right)},(25)$

where ${\tau }_{rs}$ implies the wall shear stress and $q_w$ indicates the wall heat flux. These are given by.

${\tau }_{rs}={\mu }_{thnf}{\left[{\left\{1+{\mathrm{\Gamma }}^2{\left({\partial }_{r}u-\frac{u}{r+R}\right)}^2\right\}}^{\frac{m-1}{2}}\left({\partial }_{r}u-\frac{u}{r+R}\right)\right]}_{r=0},q_w=-k_{thnf}{\left({\partial }_{r}T\right)}_{r=0}.(26)$

Equations 25, 26 give

${Re}_s^{0.5}{C}_{fs}=\frac{{\mu }_{thnf}}{{\mu }_f}{\left\{1+We{\left(f^{″}-\frac{f^{\prime }}{\delta }\right)}^2\right\}}^{\frac{m-1}{2}}\left(f^{″}\left(0\right)-\frac{f^{\prime }\left(0\right)}{\delta }\right),(27)$

$5.5\times {10}^6,(28)$

3 Solution methodology

To solve the set of differential Eqs 20–22 with boundary conditions (24), MATLABsoftware was employed. To utilize MATLAB’s bvp4c function, the general steps would involve the following.

1. Define the boundary value problem (BVP.

2. Set up the problem in the form required by bvp4c.

3. Create a function file.

4. Call the bvp4c function.

5. Retrieve and analyze the solution.

Ensuring the methodology is accurately described in the paper to avoid any confusion or misinterpretation is crucial. Also, Table 2 shows how the finding was validated by comparing it to the literature, [48].

TABLE 2

TABLE 2. Comparison of $-{\mathrm{R}\mathrm{e}}_s^{1/2}{C}_{fs}$ values for different radius of curvature.

4 Results and discussion

This study investigates the MHD two-dimensional incompressible boundary layer flow of non-Newtonian Carreau ternary-hybrid nanofluid through an exponential stretching curved surface. The current nanofluid model can be used to improve the.

• Heat transfer efficiency in microelectronics cooling,

• Efficiency of drug delivery systems,

• Mixing and reaction efficiency in chemical processing,

• The efficiency of energy conversion devices, such as microturbines and microfuel cells.

In this study, the ternary-hybrid nanofluid has been synthesized with the dispersion of titanium oxide, aluminum oxide, and silver nanoparticles in the base fluid water. The governing momentum and energy equations, along with Carreau ternary-hybrid nanofluid models, are employed, and appropriate similarity transformations are utilized to transfer these PDEs into ordinary differential equations (ODEs). The “bvp4c” function is used through MATLAB to solve the nonlinear ODEs system that arises in BVPs. It is a robust and efficient numerical method that is suitable for a wide range of problems, including those with highly nonlinear behavior. Theeffects of the pertinent parameters on dimensionless velocity and temperature profiles and physical quantities of interest are analyzed with figures.

In Figures 2A–D, the dimensionless velocity is shown as a function of the power-law index and curvature parameter for different types of fluids: base fluid, nanofluid, hybrid nanofluid, and ternary hybrid nanofluid. The power-law index characterizes the non-Newtonian behavior of the fluid and represents how its viscosity changes with shear rate. A higher power-law index indicates a more shear-thinning fluid, where the viscosity decreases with increasing shear rate, resulting in a higher velocity. Conversely, a lower power-law index indicates a more shear-thickening fluid, where viscosity increases with the shear rate, resulting in a lower velocity.

FIGURE 2

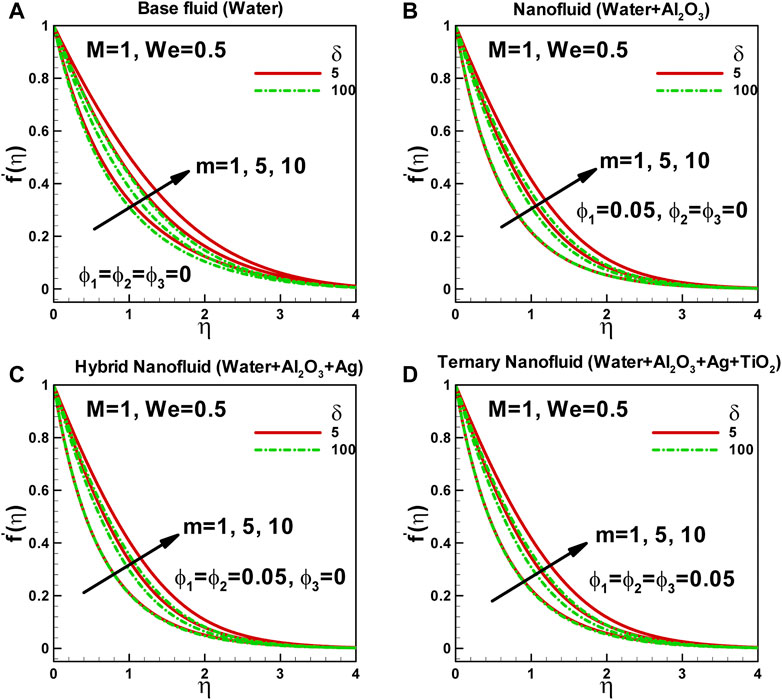
FIGURE 2. Effects of power-law index and curvature parameter on dimensionless velocity along curved surface stretched exponentially.

On the other hand, the curvature parameter describes the curvature of the surface along which the fluid flows. A positive curvature parameter represents a surface that is curved conclusively, while a negative curvature parameter represents a surface that is curved convexly. The curvature parameter affects the fluid velocity by altering the pressure gradient along the curved surface. Positive curvature leads to a higher velocity, while negative curvature leads to a lower velocity. It is observed that, in each case, the dimensionless velocity increases with an increase in the power-law index. However, the curvature parameter tends to reduce the velocity within the boundary layer. As a result, the boundary layer thickness decreases with an increasing nanoparticle volume fraction.

These figures provide valuable insights into the intricate relationship between fluid properties and external factors such as surface curvature. The power-law index quantifies the non-Newtonian behavior of the fluid, while the curvature parameter influences fluid velocity by affecting the pressure gradient along the curved surface. The specific combination of nanoparticles and base fluid used in the Carreau ternary-hybrid nanofluid would determine its power-law index. The geometry of the surface, characterized by the curvature parameter, can introduce velocity gradients along the surface, with greater curvature resulting in more significant velocity variations. The fact that non-Newtonian behavior and surface geometry can have different effects on different types of fluids emphasizes the importance of understanding the specific properties of a fluid to model its behavior accurately. This knowledge is crucial for optimizing the performance of cooling systems and other applications involving heat transfer in fluids.

In Figures 3A–D, the influence of the magnetic field and Weissenberg number on the dimensionless velocity of a non-Newtonian Carreau ternary-hybrid nanofluid is depicted. It is observed that both the magnetic field and the Weissenberg number impact the dimensionless velocity in each case. The magnetic field can affect the motion of charged particles and induce flow in a conducting fluid. In the case of non-Newtonian fluids, the magnetic field also influences the rheological properties of the fluid, including its viscosity and elasticity. The magnitude and orientation of the magnetic field can significantly alter the flow characteristics of the nanofluid, such as the velocity profile and the thickness of the boundary layer.

FIGURE 3

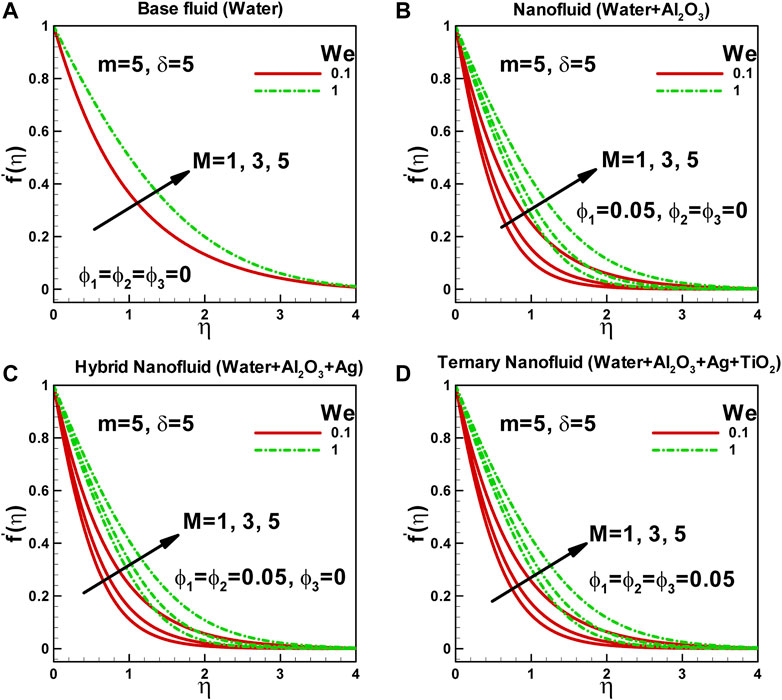
FIGURE 3. Effects of magnetic field and Weissenberg number on dimensionless velocity along curved surface stretched exponentially.

On the other hand, the Weissenberg number quantifies the elastic effects present in non-Newtonian fluids. It represents the ratio of elastic forces to viscous forces and determines the extent of shear-induced deformation and relaxation of the fluid. A higher Weissenberg number indicates a more elastic fluid, while a lower Weissenberg number indicates a more viscous fluid.

The specific effects of the magnetic field and Weissenberg number on the dimensionless velocity of the fluid flowing along an exponentially stretched curved surface will depend on the particular details of the system and the governing equations that describe the flow. Generally, the magnetic field can increase the velocity of the nanofluid, depending on the field’s direction and the fluid flow’s orientation. Moreover, a higher Weissenberg number can enhance the elastic effects within the fluid, resulting in a higher velocity, whereas a lower Weissenberg number can lead to a lower velocity. The specific behavior will depend on the particular conditions and characteristics of the fluid and the system being studied.

In Figures 4A–D, the influence of the power-law index and curvature parameter on the dimensionless temperature of a non-Newtonian Carreau fluid flowing along an exponentially stretched curved surface is presented. The power-law index is a parameter that characterizes the viscosity behavior of non-Newtonian fluids. Unlike Newtonian fluids, non-Newtonian fluids exhibit more complex flow behavior, and their thermal boundary layer thickness is affected by various physical properties. The power-law index specifically affects the shear stress and viscosity of the fluid, which in turn impacts the velocity and temperature profiles of the flow. As the power-law index increases, the fluid’s viscosity also increases, resulting in changes in the velocity profile. Consequently, the surface temperature and the thermal boundary layer thickness also increase. This variation in temperature and thickness can significantly influence the heat transfer characteristics of the flow. On the other hand, the curvature parameter plays a role in determining the dimensionless temperature of the fluid. When the fluid flows over a curved surface, centrifugal forces are induced, which affect the fluid flow and temperature distribution. For instance, on a concave surface, the increased velocity near the surface due to the centrifugal forces leads to a higher fluid temperature. Conversely, on a convex surface, the reduced velocity results in a lower fluid temperature.

FIGURE 4

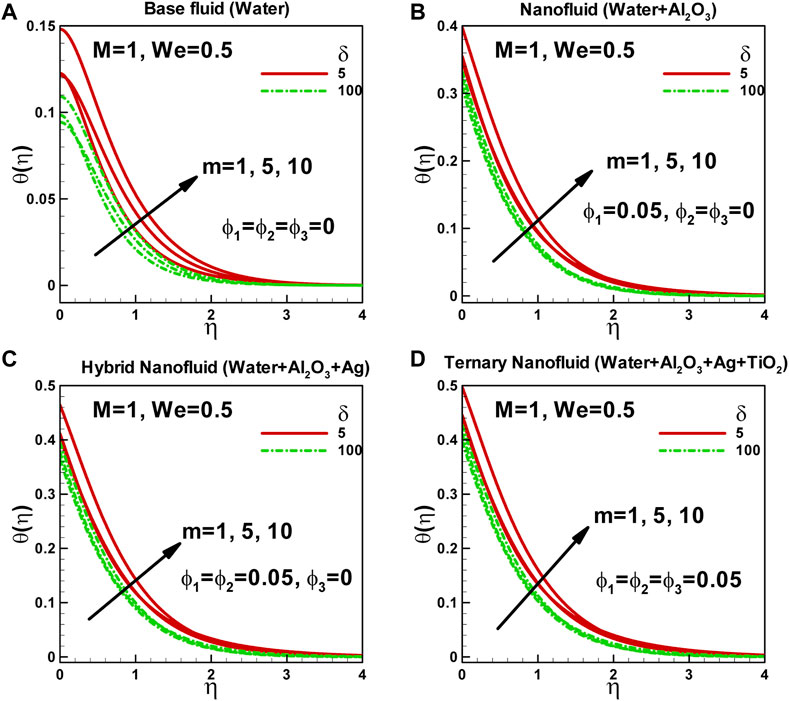
FIGURE 4. Effects of power-law index and curvature parameter on dimensionless temperaturealong curved surface stretched exponentially.

The curvature of the surface causes the fluid to experience centrifugal forces, which in turn generate secondary flows perpendicular to the main flow direction. These secondary flows contribute to the increased mixing of the fluid, creating a zigzag motion. Consequently, the curvature of the surface influences the thickness of the thermal boundary layer. As the curvature increases, the thickness of the thermal boundary layer also increases due to the presence of these secondary flows. Overall, the power-law index and curvature parameter significantly affect the dimensionless temperature of the non-Newtonian Carreau fluid flowing along a curved surface. These parameters impact the fluid’s viscosity, velocity profile, temperature distribution, and thermal boundary layer thickness, ultimately influencing the heat transfer characteristics of the flow.

In Figures 5A–D, the effects of radiation and viscous dissipation parameters on the dimensionless temperature of a fluid are illustrated for four selected types of fluids. Radiation significantly affects energy transfer within and between the fluid and its surroundings. The curvature can further impact the radiation effects when considering a curved surface. The radiation parameter quantifies the importance of radiation in heat transfer. A higher radiation parameter indicates a greater significance of radiation effects, resulting in a higher heat transfer rate and temperature distribution. As the radiation parameter increases, the surface temperature also increases. Consequently, the thermal boundary layer thickness and thermal resistance also increase. The presence of radiation can alter the temperature distribution, affecting the heat transfer characteristics of the fluid.

FIGURE 5

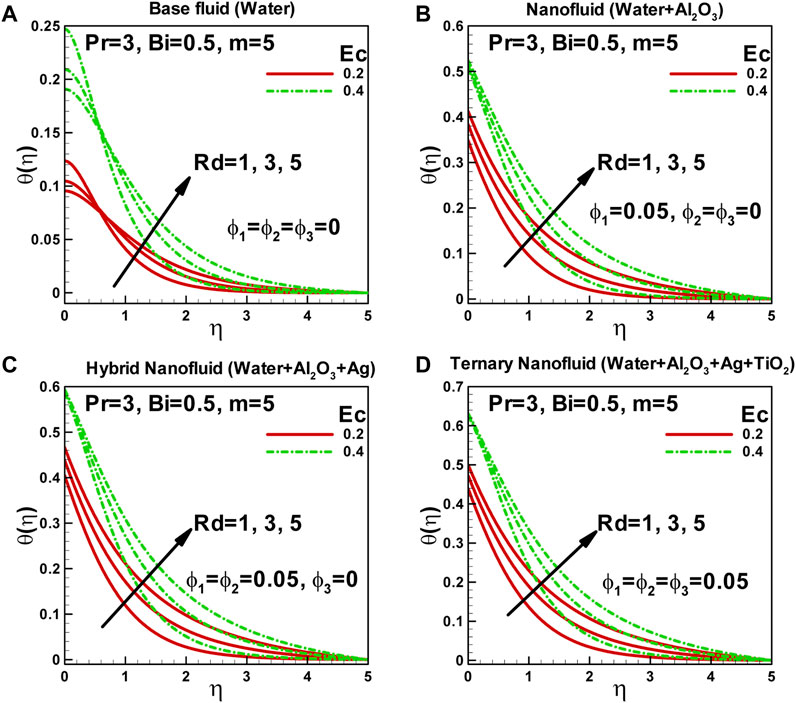
FIGURE 5. Effects of radiation and viscous dissipation parameters on dimensionless temperaturealong curved surface stretched exponentially.

Viscous dissipation refers to the energy the fluid dissipates due to internal frictional forces. It is closely related to the viscosity and velocity gradient of the fluid. The viscous dissipation parameter describes the significance of this energy dissipation in heat transfer. A higher viscous dissipation parameter implies a greater energy dissipation and heating within the fluid. As a result, the temperature distribution increases. The viscous dissipation effects can be particularly pronounced when the fluid experiences significant internal friction. In general, both radiation and viscous dissipation parameters tend to enhance the fluid’s temperature distribution. Increased radiation parameter increases heat transfer rates and surface temperatures, consequently affecting the thermal boundary layer thickness and resistance. A higher viscous dissipation parameter increases energy dissipation and heating within the fluid, leading to a higher temperature distribution.

Understanding the influence of radiation and viscous dissipation parameters on the temperature distribution is crucial for accurately predicting and analyzing heat transfer in various fluid systems. Considering these parameters, one can optimize heat transfer processes and design more efficient thermal systems.

In Figures 6A–D, the relationship between skin friction along a curved surface stretched exponentially, and various parameters, including the power-law index, curvature parameter, and Weissenberg number, are depicted. The skin friction coefficient measures the resistance to fluid flow along a surface. It quantifies the force exerted by the fluid on the surface, indicating the amount of friction experienced by the fluid. Several factors, such as the power-law index, curvature parameter, and Weissenberg number, can influence skin friction. The Weissenberg number characterizes the viscoelastic behavior of the fluid and represents the ratio of the relaxation time to the shear rate. As observed in Figures 6A–D, the Weissenberg number positively influences skin friction. In the presence of nanoparticles, the fluid’s viscosity increases, making it more flow-resistant. This improved viscosity results in higher skin friction as the fluid require more force to overcome the resistance and move over the surface. Additionally, the presence of nanoparticles can cause the boundary layer to thicken, further increasing the contact between the fluid and the surface, leading to higher skin friction.

FIGURE 6

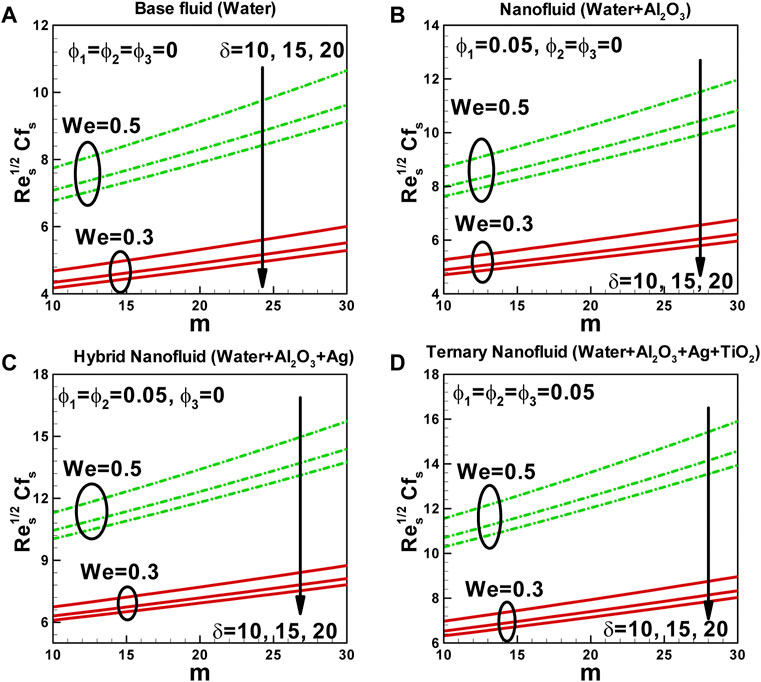
FIGURE 6. Variation of skin friction with power-law index for different values of curvature parameter and Weissenberg numberalong curved surface stretched exponentially.

The power-law index also affects the viscosity of the fluid. As the power-law index increases, indicating a more non-Newtonian behavior, the viscosity of the fluid increases. This increase in viscosity contributes to a higher skin friction coefficient. The curvature parameter, on the other hand, influences skin friction by altering the surface area, pressure gradient, and boundary layer thickness. A curved surface can generally reduce skin friction compared to a flat surface due to decreased surface area and pressure gradient. It is worth noting that the solid volume fraction of nanoparticles also plays a role in skin friction. As the volume fraction of nanoparticles increases, the interaction between the fluid and the surface intensifies, increasing skin friction.

Understanding the relationship between the power-law index, curvature parameter, Weissenberg number, and skin friction is important for predicting and optimizing fluid flow behavior and frictional losses in various applications. Considering these parameters, one can design surfaces and systems that minimize skin friction and improve fluid flow efficiency.

In Figures 7A–D, the variation of the Nusselt number with the power-law index for different values of the curvature parameter and Weissenberg number is illustrated. The Nusselt number represents the heat transfer between a fluid and a solid surface. It quantifies the convective heat transfer rate, indicating how efficiently heat is transferred from the surface to the fluid. Several factors, including the power-law index, curvature parameter, and Weissenberg number, influence the Nusselt number.

FIGURE 7

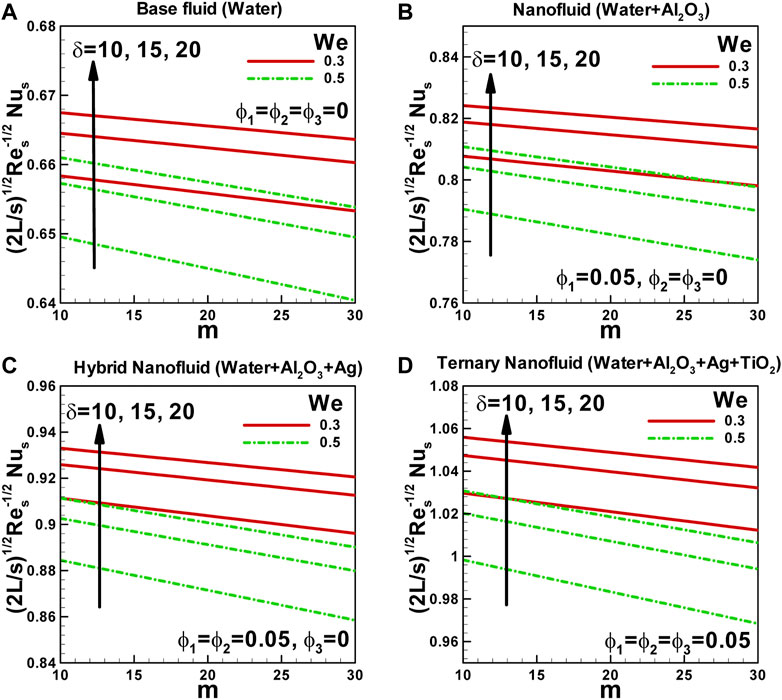
FIGURE 7. Variation of Nusselt number with power-law index for different values of curvature parameter and Weissenberg numberalong curved surface stretched exponentially.

The Weissenberg number characterizes the viscoelastic behavior of the fluid and is determined by the product of the relaxation time and the shear rate. As observed in Figure 7, the Weissenberg number decreases the Nusselt number in a viscoelastic fluid. This is attributed to various factors, such as the thinning of the boundary layer, delayed vortex shedding, changes in flow patterns, and alterations in the thermal boundary layer. These effects collectively lead to a reduction in the heat transfer rate and, consequently, a decrease in the Nusselt number.

The power-law index describes the rheological behavior of a non-Newtonian fluid. An increase in the power-law index generally leads to a decrease in the Nusselt number. A higher power-law index corresponds to a steeper velocity profile near the solid surface than a lower power-law index. This steeper velocity profile results in a thinner thermal boundary layer and reduced heat transfer rate, leading to a lower Nusselt number. Additionally, an increase in the power-law index increases the apparent viscosity of the non-Newtonian fluid. The higher viscosity near the solid surface reduces the fluid velocity, decreasing the heat transfer rate and the Nusselt number.

The curvature parameter influences the heat transfer characteristics of a fluid flowing over a curved surface. The curvature parameter generally enhances the Nusselt number along a curved surface stretched exponentially. This is due to several factors, including increased surface area, flow pattern changes, boundary layer thickness reduction, and turbulence. These effects collectively promote a higher heat transfer rate and, consequently, an increase in the Nusselt number.

It is important to note that the Nusselt number increases from the base fluid to the ternary hybrid nanofluid as the solid volume fraction of nanoparticles increases. This suggests that nanoparticles can enhance the heat transfer rate and, consequently, the Nusselt number. The increased surface area and improved thermal conductivity associated with the presence of nanoparticles contribute to this enhancement. Understanding the influence of the power-law index, curvature parameter, Weissenberg number, and nanoparticle volume fraction on the Nusselt number are crucial for optimizing heat transfer in various applications. Considering these factors, one can design surfaces, fluids, and systems that maximize heat transfer efficiency and improve overall performance.

The variation of the Nusselt number with magnetic field for different values of the Biot number and radiation along a curved surface stretched exponentially is presented in Figures 8A–D for various nanofluids. The Nusselt number indicates how efficiently heat is transferred from the surface to the fluid. Several factors, including the magnetic field, radiation parameter, and Biot number, influence the Nusselt number in this scenario.

FIGURE 8

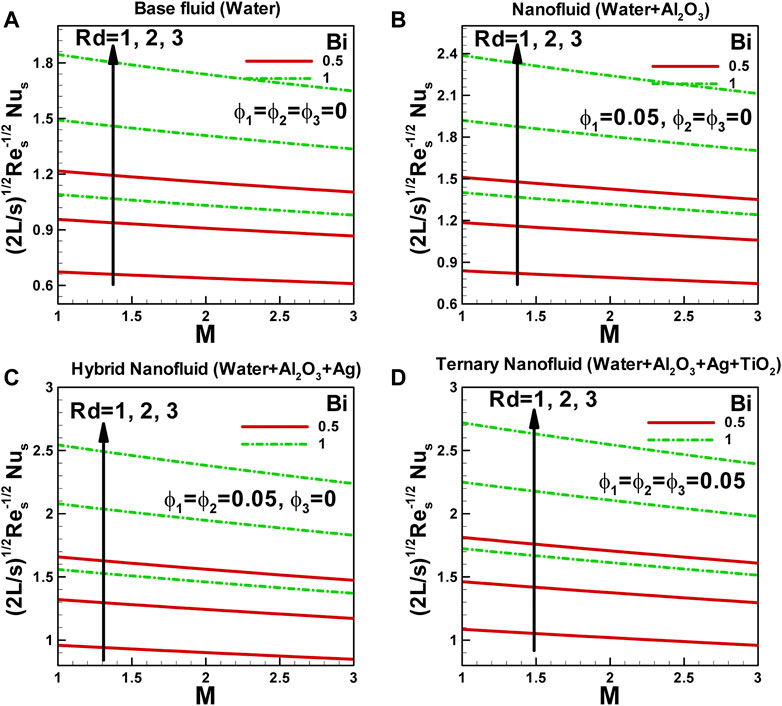
FIGURE 8. Variation of Nusselt number with magnetic field for different values of Biot number and radiation along curved surface stretched exponentially.

Firstly, let’s consider the effect of the magnetic field on the Nusselt number. When a magnetic field is applied, it can alter the fluid’s flow behavior and heat transfer characteristics. A magnetic field influences the motion of charged particles and induces flow in conducting fluids, which can affect convective heat transfer. In general, an increase in the magnetic field strength leads to a decrease in the Nusselt number. The magnetic field can suppress fluid motion, inhibit mixing near the surface, and reduce the heat transfer rate. The magnetic field exerts a restraining force on the fluid, making it more flow-resistant and reducing the convective heat transfer. Hence, the Nusselt number decreases with an increasing magnetic field.

Next, let’s discuss the influence of the radiation parameter on the Nusselt number. Radiation refers to the transfer of heat energy through electromagnetic waves, independent of any physical medium. The radiation parameter represents the importance of radiation effects in heat transfer. As the radiation parameter increases, the heat transfer rate through radiation becomes more significant, increasing the Nusselt number. This is because radiation can directly transfer heat energy from the surface to the fluid, bypassing the convective heat transfer mechanism. Therefore, a higher radiation parameter leads to enhanced heat transfer and increasedNusselt number. The Biot number characterizes the relative significance of conduction heat transfer within the solid to the convective heat transfer at the solid-fluid interface. A higher Biot number indicates that conduction within the solid is more dominant than convection at the surface. In general, an increase in the Biot number leads to an increase in the Nusselt number. This is because a higher Biot number implies a more conductive solid, which enhances heat transfer through the solid-fluid interface. Consequently, the convective heat transfer rate increases, resulting in a higher Nusselt number.

Regarding the influence of the nanofluids or solid volume fraction of nanoparticles on the Nusselt number, it is observed that the Nusselt number is minimum for the base fluid and increases with an increasing number of nanofluids or solid volume fraction of nanoparticles. The presence of nanoparticles in the fluid can enhance the convective heat transfer by increasing the effective thermal conductivity and providing additional surface area for heat transfer. As a result, the heat transfer rate improves, leading to a higher Nusselt number. Moreover, the ternary nanofluids, which consist of a combination of nanoparticles and base fluid, exhibit the highest Nusselt number among the different nanofluid configurations. This can be attributed to the synergistic effects of the nanoparticles and base fluid, which further enhance heat transfer through improved thermal conductivity and altered flow patterns.

Understanding the variations of the Nusselt number with the magnetic field, radiation parameter, Biot number, and nanoparticle concentration is crucial for optimizing heat transfer in applications involving curved surfaces. Considering these factors, one can design systems that maximize heat transfer efficiency, improve cooling performance, and ensure effective thermal management.

5 Conclusion

The novelty of this paper lies in the combination of heat transfer, MHD flow, Carreauternary-hybrid nanofluid, curved surface, and exponential stretching. The study of this scenario has the potential to provide new insights and contribute to the development of new technologies. This study analyzes the heat transfer phenomenon for a two-dimensional MHD heat transfer of Carreau ternary-hybrid nanofluid over an exponential stretching of a curve surface. The effects of radiation and viscous dissipation are introduced through governing equations. These equations are reduced to a highly nonlinear coupled ODEs system, which is solved using MATLAB software. The influences of relevant parameters are investigated to examine the behavior of dimensionless velocity, temperature, skin friction, and Nusselt number for base fluid, mono, hybrid, and ternary nanofluids. The results of the study are presented in graphical forms. From the comprehensive exploration, the following conclusions can be drawn.

• The power-law index, magnetic field, and Weissenberg number boost the dimensionless velocity, whereas the curvature parameter tends to reduce the velocity inside the boundary layer.

• The power-law index, radiation, viscous dissipation, and curvature parameters enhance the surface temperature.

• The Weissenberg number helps in increasing skin friction, which increases with the addition of nanoparticles.

• The power-law index leads to an increase in the skin friction coefficient, whereas the curvature parameter reduces the skin friction over a curved surface.

• The power-law index and Weissenberg number reduce the Nusselt number.

• The curvature parameter boosts the Nusselt number along a curved surface.

• The Nusselt number increases from base fluid to mono, hybrid, and ternary nanofluids.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2023/01/21942).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Choi S. Enhancing thermal conductivity of fluids with nanoparticles. In: DA Siginer, and HP Wang, editors. Developments applications of non-Newtonian flows. New York: ASME (1995). p. 99–105. vol FED-vol 231/MD-vol 66.

Google Scholar

2. Elias MM, Miqdad M, Mahbubul IM, Saidur R, Kamalisarvestani M, Sohel MR, et al. Effect of nanoparticle shape on the heat transfer and thermodynamic performance of a shell and tube heat exchanger. Int Commun Heat Mass Transfer (2013) 44:93–9. doi:10.1016/j.icheatmasstransfer.2013.03.014

CrossRef Full Text | Google Scholar

3. Esfahani JA, Akbarzadeh M, Rashidi S, Rosen MA. Influences of wavy wall and nanoparticles on entropy generation over heat exchanger plat. Int J Heat Mass Transf (2017) 109:1162–71. doi:10.1016/j.ijheatmasstransfer.2017.03.006

CrossRef Full Text | Google Scholar

4. Samantaray SS, Shaw S, Misra A, Nayak MK, Prakash J. Darcy-Forchheimer up/downflow of entropy optimized radiativenanofluids with second-order slip, nonuniform source/sink, and shape effects. Heat Transfer (2022) 51:2318–42. doi:10.1002/htj.22403

CrossRef Full Text | Google Scholar

5. Patel HR, Mittal AS, Darji RR. MHD flow of micropolarnanofluid over a stretching/shrinking sheet considering radiation. Int Commun Heat Mass Transf (2019) 108:104322. doi:10.1016/j.icheatmasstransfer.2019.104322

CrossRef Full Text | Google Scholar

6. Alotaibi H, Althubiti S, Eid MR, Mahny KL. Numerical treatment of MHD flow of Cassonnanofluid via convectively heated nonlinear extending surface with viscous dissipation and suction/injection effects. Comput Mater Continua (2021) 66:229–45. doi:10.32604/cmc.2020.012234

CrossRef Full Text | Google Scholar

7. Sarkar J, Ghosh P, Adil A. A review on hybrid nanofluids: Recent research, development, and applications. Renew Sustenerg Rev (2015) 43:164–77. doi:10.1016/j.rser.2014.11.023

CrossRef Full Text | Google Scholar

8. Makishima A. Possibility of hybrid materials. Ceram Jap (2004) 39(2):90–91.

Google Scholar

9. Arif M, Kumam P, Khan D, Watthayu W. Thermal performance of GO-MoS2/engine oil as Maxwell hybrid nanofluid flow with heat transfer in oscillating vertical cylinder. Case Stud Therm Eng (2021) 27:101290. doi:10.1016/j.csite.2021.101290

CrossRef Full Text | Google Scholar

10. Benkhedda M, Boufendi T, Tayebi T, Chamkha AJ. Convective heat transfer performance of hybrid nanofluid in a horizontal pipe considering nanoparticles shapes effect. J Therm Anal Calorim (2020) 140(1):411–25. doi:10.1007/s10973-019-08836-y

CrossRef Full Text | Google Scholar

11. Sarkar J, Ghosh P, Adil A. A review on hybrid nanofluids: Recent research, development, and applications. Renew Sustain Energ Rev. (2015) 43:164–77. doi:10.1016/j.rser.2014.11.023

CrossRef Full Text | Google Scholar

12. Wakif A, Chamkha A, Thumma R, Animasaun IL, Sehaqui R. Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina-copper oxide hybrid nanofluids utilizing the generalized Buongiorno'snanofluid model. J Therm Anal Calorim (2021) 143(2):1201–20. doi:10.1007/s10973-020-09488-z

CrossRef Full Text | Google Scholar

13. Roy NC, Hossain A, Pop I. Flow and heat transfer of MHD dusty hybrid nanofluids over a shrinking sheet. Chin J Phys (2022) 77(2022):1342–56. doi:10.1016/j.cjph.2021.12.012

CrossRef Full Text | Google Scholar

14. Roy NC, Pop I. Unsteady magnetohydrodynamic stagnation point flow of a nanofluid past a permeable shrinking sheet. Chin J Phys (2022) 75(2022):109–19. doi:10.1016/j.cjph.2021.12.018

CrossRef Full Text | Google Scholar

15. Roy NC, Pop I. Heat and mass transfer of a hybrid nanofluid flow with binary chemical reaction over a permeable shrinking surface. Chin J Phys (2022) 76(2022):283–98. ‏doi:10.1016/j.cjph.2021.10.041

CrossRef Full Text | Google Scholar

16. Hamzah H, Canpolat C, Jasim LM, &Sahin B. Hydrothermal index and entropy generation of a heated cylinder placed between two oppositely rotating cylinders in a vented cavity. Int J Mech Sci (2021) 201:106465. doi:10.1016/j.ijmecsci.2021.106465

CrossRef Full Text | Google Scholar

17. Mehrizi AA, Farhadi M, Afroozi HH, Sedighi K, Darz AR. Mixed convection heat transfer in a ventilated cavity with hot obstacle: Effect of nanofluid and outlet port location. Int Commun Heat Mass Transfer (2012) 39(7):1000–8. doi:10.1016/j.icheatmasstransfer.2012.04.002

CrossRef Full Text | Google Scholar

18. Jasim LM, Hamzah H, Canpolat C, Sahin B. Mixed convection flow of hybrid nanofluid through a vented enclosure with an inner rotating cylinder. Int Commun Heat Mass Transfer (2021) 121:105086. doi:10.1016/j.icheatmasstransfer.2020.105086

CrossRef Full Text | Google Scholar

19. Elnaqeeb T, Animasaun IL, Shah NA. Ternary-hybrid nanofluids: Significance of suction and dual-stretching on three-dimensional flow of water conveying nanoparticles with various shapes and densities. Z Naturforsch (2021) 76(3):231–43. doi:10.1515/zna-2020-0317

CrossRef Full Text | Google Scholar

20. Sahoo RR, Kumar V. Development of a new correlation to determine the viscosity of ternary hybrid nanofluid. Int Commun Heat Mass Tran (2020) 111:104451. doi:10.1016/j.icheatmasstransfer.2019.104451

CrossRef Full Text | Google Scholar

21. Xuan Z, Zhai Y, Ma M, Li Y, Wang H. Thermo-economic performance and sensitivity analysis of ternary hybrid nanofluids. J Mol Liq (2021) 323:114889. doi:10.1016/j.molliq.2020.114889

CrossRef Full Text | Google Scholar

22. Carreau PJ. Rheological equations from molecular network theories. Trans Soc Rheol (1972) 16:99–127. doi:10.1122/1.549276

CrossRef Full Text | Google Scholar

23. Olajuwon BI. Convection heat and mass transfer in a hydromagnetic Carreau fluid past a vertical porous plate in presence of thermal radiation and thermal diffusion. Therm Sci (2011) 15:241–52. doi:10.2298/tsci101026060o

CrossRef Full Text | Google Scholar

24. Shadid JN, Eckert ERG. Viscous heating of a cylinder with finite length by a high viscosity fluid in steady longitudinal flow-II. Non-Newtonian Carreau model fluids. Int J Heat Mass Transfer (1992) 35:2739–49. doi:10.1016/0017-9310(92)90114-8

CrossRef Full Text | Google Scholar

25. Georgiou GC. The time-dependent, compressible Poiseuille and extrudate-swell flows of a Carreau fluid with slip at the wall. J Non-newtonain Fluid Mech (2003) 109:93–114. doi:10.1016/s0377-0257(02)00164-7

CrossRef Full Text | Google Scholar

26. Hayat T, Asad S, Mustafa M, Alsaedi A. Boundary layer flow of Carreau fluid over a convectively heated stretching sheet. Appl Math Comput (2014) 246:12–22. doi:10.1016/j.amc.2014.07.083

CrossRef Full Text | Google Scholar

27. Shehzad SA, Alsaedi A, Hayat T. Three-dimensional flow of Jeffery fluid with convective surface boundary conditions. Int J Heat Mass Transfer (2012) 55:3971–6. doi:10.1016/j.ijheatmasstransfer.2012.03.027

CrossRef Full Text | Google Scholar

28. Khan M, Hashima A. Boundary layer flow and heat transfer to Carreau fluid over a nonlinear stretching sheet. AIP Adv (2015) 5:107203–14. doi:10.1063/1.4932627

CrossRef Full Text | Google Scholar

29. Akbar NS, Nadeem S, Haq RU, Ye S. MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: Dual solutions. Ain Shams Eng J (2014) 5:1233–9. doi:10.1016/j.asej.2014.05.006

CrossRef Full Text | Google Scholar

30. Abbas T, Rehman S, Shah RA, Idrees M, Qayyum M. Analysis of MHD Carreau fluid flow over a stretching permeable sheet with variable viscosity and thermal conductivity. Phys A (2020) 551:124225. doi:10.1016/j.physa.2020.124225

CrossRef Full Text | Google Scholar

31. Bilal S, Shafqatullah Alshomrani AS, Malik MY, Kausar N, Khan F, et al. Analysis of Carreau fluid in the presence of thermal stratification and magnetic field effect. Results Phys (2018) 10:118–25. doi:10.1016/j.rinp.2018.05.005

CrossRef Full Text | Google Scholar

32. Machireddy GR, Naramgari S. Heat and mass transfer in radiative MHD Carreau fluid with cross-diffusion. Ain Shams Eng J (2018) 9:1189–204. doi:10.1016/j.asej.2016.06.012

CrossRef Full Text | Google Scholar

33. Shah RA, Abbas T, Idrees M, Ullah M. MHD Carreau fluid slip flow over a porous stretching sheet with viscous dissipation and variable thermal conductivity. Bound Value Probl (2017) 1-17:94. doi:10.1186/s13661-017-0827-4

CrossRef Full Text | Google Scholar

34. Santosh HB, Raju CS, Makinde OD. The flow of radiated Carreau dusty fluid over exponentially stretching sheet with partial slip at the wall. Diffusion Foundations (2018) 16:96–108. doi:10.4028/www.scientific.net/df.16.96

CrossRef Full Text | Google Scholar

35. Megahed M. Carreau fluid flow due to nonlinearly stretching sheet with thermal radiation, heat flux, and variable conductivity. Appl Math Mech (English Ed (2019) 40:1615–24. doi:10.1007/s10483-019-2534-6

CrossRef Full Text | Google Scholar

36. Ramzan M, Ali F, Akkurt N, Saeed A, Kumam P, Galal AM. Computational assesment of Carreau ternary hybrid nanofluid influenced by MHD flow for entropy generation. J Magnetism Magn Mater (2023) 567:170353. doi:10.1016/j.jmmm.2023.170353

CrossRef Full Text | Google Scholar

37. Roy NC, Saha G. Heat and mass transfer of dusty Casson fluid over a stretching sheet. Arabian J Sci Eng (2022) 47:16091–101. doi:10.1007/s13369-022-06854-x

CrossRef Full Text | Google Scholar

38. Roy NC, Pop I. Dual solutions of a nanofluid flow past a convectively heated nonlinearly shrinking sheet. Chin J Phys (2023) 82(2023):31–40. doi:10.1016/j.cjph.2022.12.008

CrossRef Full Text | Google Scholar

39. Roy NC, Pop I. Dual solutions of magnetohydrodynamic mixed convection flow of an Oldroyd-B nanofluid over a shrinking sheet with heat source/sink. Alexandria Eng J (2022) 61(8):5939–48. doi:10.1016/j.aej.2021.11.021

CrossRef Full Text | Google Scholar

40. Roy NC, Pop I. Exact solutions of Stokes' second problem for hybrid nanofluid flow with a heat source. Phys Fluids (2021) 33(6):063603. ‏doi:10.1063/5.0054576

CrossRef Full Text | Google Scholar

41. Selimefendigil F, Hakan F. Effects of an inner stationary cylinder having an elastic rod-like extension on the mixed convection of CNT-water nanofluid in a three dimensional vented cavity. Int J Heat Mass Transfer (2019) 137:650–68. doi:10.1016/j.ijheatmasstransfer.2019.03.093

CrossRef Full Text | Google Scholar

42. Zontul H, Hamzah H, Kurtulmuş N, Şahin B. Investigation of convective heat transfer and flow hydrodynamics in rectangular grooved channels. Int Commun Heat Mass Transfer (2021) 126:105366. doi:10.1016/j.icheatmasstransfer.2021.105366

CrossRef Full Text | Google Scholar

43. Kumar KA, Reddy JVR, Sugunamma V, Sandeep N. Simultaneous solutions for MHD flow of Williamson fluid over a curved sheet with nonuniform heat source/sink. Heat Tran Res (2019) 50:581–603. doi:10.1615/heattransres.2018025939

CrossRef Full Text | Google Scholar

44. Ahmed K, Khan WA, Akbar T, Rasool G, Alharbi SO, Khan I. Numerical investigation of mixed convective Williamson fluid flow over an exponentially stretching permeable curved surface. Fluid (2021) 6(7):260. doi:10.3390/fluids6070260

CrossRef Full Text | Google Scholar

45. Hayat T, Aziz A, Muhammad T, Alsaedi A. Numerical study for nanofluid flow due to a nonlinear curved stretching surface with convective heat and mass conditions. Results Phys (2017) 7:3100–6. doi:10.1016/j.rinp.2017.08.030

CrossRef Full Text | Google Scholar

46. Zehra I, Abbas N, Amjad M, Nadeem A, Saleem S, Issakhov A. Cassonnanoliquid flow with Cattaneo-Christov flux analysis over a curved stretching/shrinking channel. Case Stud Therm Eng (2021) 27:101146. doi:10.1016/j.csite.2021.101146

CrossRef Full Text | Google Scholar

47. Elnaqeeb T, LareAnimasaun I, Shah NA. Ternary-hybrid nanofluids: Significance of suction and dual-stretching on three-dimensional flow of water conveying nanoparticles with variousshapes and densities. Z Naturforsch (2021) 76(3):231–43. doi:10.1515/zna-2020-0317

CrossRef Full Text | Google Scholar

48. Okechi NF, Jalil M, Asghar S. Flow of viscous fluid along an exponentially stretching curved surface. Results Phys (2017) 7:2851–4. doi:10.1016/j.rinp.2017.07.059

CrossRef Full Text | Google Scholar