Deuterium–deuterium fusion in nanowire plasma driven with a nanosecond high-energy laser

Investigating the enhancement of the interaction between laser and plasma is crucial for fundamental and applied physics research studies based on laser-induced acceleration and nuclear reactions. The improvement of energy conversion efficiency resulting in increasing reaction yields has been extensively studied by the interaction of femtosecond (fs) or picosecond (ps) lasers with nanowire targets. However, the effects of nanosecond (ns) lasers interacting with nanowire targets on energy absorption and production yield remain unknown. To address this issue, we conducted a deuterium–deuterium fusion experiment based on the collision of two plasmas induced by the interaction of the kilo-Joule-level nanosecond laser with nanowire targets. The experimental results of neutron detection indicate that the yields of nanowire targets remain at the same level as those of planar targets. We have used the counter-streaming collisionless plasma model to perform a numerical analysis of the output of nuclear reaction products at the center-of-mass energy (E_c.m.) values between 10 and 30 keV, and the calculation results are in good agreement with the experimental results. In addition, a magneto-hydrodynamic numerical simulation was also performed. It shows that the critical density of the target’s surface, which forms on the picosecond time scale, blocks the absorption of laser energy with nanosecond pulse length. Consequently, both our experimental and simulation results indicate that the enhancement factor is limited when a target with a spatial period less than µm is used in conjunction with a ns laser. Therefore, additional research is highly desirable to develop a target structure that can improve the efficiency of energy conversion between the laser and the target.

1 Introduction

The integration of laser, plasma, and nuclear physics has been widely explored [1–7] in recent years due to the rapid advances in laser technology [8–11]. For example, high-power lasers are currently an important tool for creating extreme plasma environments for studies in nuclear astrophysics and laboratory astrophysics [12–14]. The particles generated through high-intensity-laser-driven plasma, as well as the induced secondary beams, hold significant importance for fundamental research and practical applications in a variety of fields, including laboratory astrophysics, nuclear physics, inertial confinement, and thermonuclear fusion [15–26]. Therefore, these innovative cross-disciplinary studies are actively seeking to explore and utilize the properties of these particles.

One of the primary objectives in laser-driven plasma is to accelerate a maximum number of particles or produce more secondary particles for both fundamental and applied physics research, which include photonuclear physics, photonuclear transmutation, and radiography (involving electrons, protons, X/γ rays, and neutrons). Several methods have been proposed and demonstrated to significantly improve the energy conversion efficiency in laser-driven plasma, such as near-critical density plasma targets, plasma waveguides, grating targets, T-shaped targets, nanowire targets, and others [3,27–38]. The use of the relativistic femtosecond (fs) laser to irradiate nanowire targets has been demonstrated through both theoretical models and experiments to significantly enhance energy conversion efficiency. In addition, the abovementioned schemes have also been applied to enhance electron acceleration, ion acceleration, and secondary radiation and produce ultra-high-energy density states. In 2013, Purvis et al. from Colorado State University in the United States used a relativistic fs laser to interact with a nanowire target to generate hot electrons with a density 100 times higher than the critical density and a temperature of several keV, which opened up a new era for creating an extreme environment of high-energy-density physics [38]. After that, with more improvement, they used the fs laser to interact with the nanowire target to generate a 0.35 Tbar extremely high-pressure plasma environment in 2017 [39]. The extreme light infrastructure (ELI) also uses a microstructure target in the proton acceleration experiment and enhances the conversion efficiency of laser energy by placing a single layer of plastic nanospheres in front of the target [40]. Furthermore, the latest research from Colorado State University shows that the neutron yield from deuterium–deuterium (D–D) fusion reaction based on the interaction between the fs laser and the deuterated polyethylene nanowire target is 500 times higher than that of the planar target [41], which is also confirmed by our collaboration using a Joule-class femtosecond laser system [42]. In addition to the fs laser, recent experimental results have demonstrated that when the picosecond (ps) laser is incident on the nanowire target [43], the energy coupling efficiency between them can also be improved. Compared with the case of the planar target, the intensity of the He-like line in the nanowire target is enhanced by three times.

It is well known that in nuclear astrophysics, especially in the Gamow window, the energies of the ions of interest range from a few keV to hundreds of keV. Therefore, the interaction of nanosecond (ns) lasers with solid targets is well suited to generate extreme plasma environments at energy levels higher than the normal range. At the LENS laboratory in Catania, Italy, nanowire targets made of different materials are irradiated by using an infrared laser with an intensity of 10¹² W/cm², a pulse duration of 6 ns, and an energy of 2 J [44,45]. It was found that, in the nanowire form, nanostructures on the surface of the target can absorb laser energy with very high efficiency. The nanowire target can generate an extreme plasma environment that is an order of magnitude higher in temperature and has a higher density than the planar target, and theoretical calculations indicate that the neutron yield is expected to be improved when a ns laser interacts with nanowire targets. However, the effect of the interaction between kJ-level ns lasers and nanowire targets on energy absorption and neutron yield is still unclear.

In this work, based on the collision of two plasma streams, we first carry out the experimental study of kJ-level ns laser irradiation on the CD₂ nanowire target by the colliding plasma method [46,47] and evaluate their energy conversion efficiency by measuring the yield of nuclear reaction products. Our results show that the nanowire target cannot significantly enhance the energy absorption of such a high-energy ns laser compared with the results of the planar target. Combining the experimental results with the magneto-hydrodynamic numerical simulation results, the main reason is that the nanowire target only works within the duration of the first few ps in the whole process. Then, with the formation of plasma higher than the critical density on the surface of the nanowire target, the laser is reflected instead of absorbed. This paper is organized as follows. Section 2 outlines the experimental setup. Section 3 presents the reaction results of the experimental detection and the numerical calculation for the neutron yield. Furthermore, the magneto-hydrodynamic numerical simulation is also analyzed and discussed. A brief summary is given in Section 4.

2 Experimental setup

The experiment was carried out at the ShenGuang-II Laser Facility of the National Laboratory on High-Power Lasers and Physics in Shanghai, China. Figure 1 shows a schematic diagram of the experimental setup [48–50].

FIGURE 1

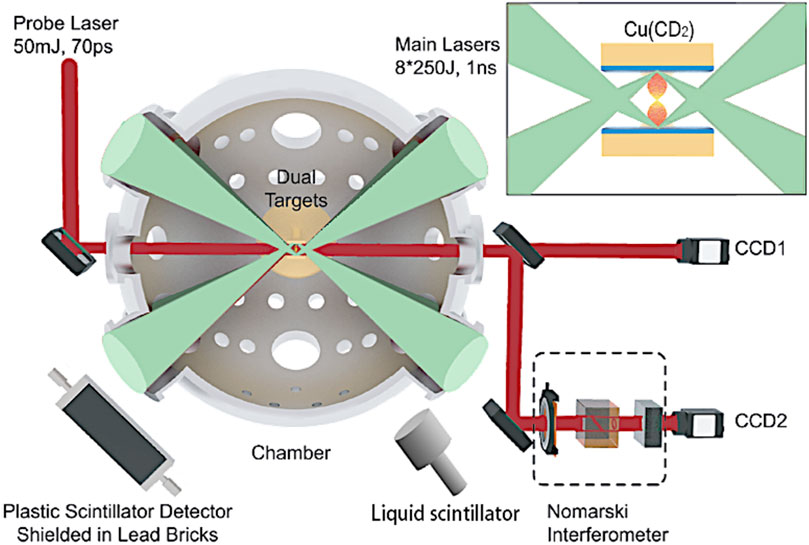
FIGURE 1. Schematic layout of the experimental setup. Four laser beams were tuned to focus on the target on one side and another four on the opposite side. The densities of the plasmas were recorded using the probe laser and a Nomarski interferometer. Neutron signals were characterized by scintillation detectors at different distances.

There were eight laser beams aimed at the center of the target chamber, and each beam could deliver an energy of approximately 250 J with a pulse width of 1 ns at a wavelength of 351 nm (3ω). A dual target was located at the center of the chamber. Both of the targets had 2.0 × 2.0 mm²-sized copper bases, which were coated with 200–500 μm-thick deuterated hydrocarbon (CD_1.96H_0.04)_n layers from Sigma-Aldrich Trading Co., Ltd., and contained 98 atom% D. The opposing layers on the target were separated by a 4 mm distance between each other. The nanosecond lasers were arranged as two sets (4 + 4), and each set had four lasers focusing on one side of the dual target. The diameter of the focal spots was approximately 150 μm, and the corresponding intensity was approximately 6 × 10¹⁵ W/cm². The counter-streaming plasma flows were generated under such symmetric ablation conditions. The center-of-mass energy of the nuclei increases accordingly, and therefore, the reaction rate can be significantly enhanced, especially in the sub-Coulomb barrier ranges. In the collider mechanism, around 100 neutrons can be received by the detector for one laser shot. So, we used a TOF detection system with scintillation detectors and oscilloscopes to record these neutrons arriving at the detectors at the same time and avoid the strong electromagnetic pulse (EMP) impact on the shooting time.

The interaction between the counter-streaming plasma flows was measured with optical diagnostics, including Nomarski interferometry and shadow graphics, by a 9th probe laser with a duration of 70 ps and a wavelength of 526 nm. The probe laser passed through the plasma interaction zone generated by the main laser beams and achieved interference images. Meanwhile, snapshots of the plasma at different times could be taken by changing the delay time between the probe laser and the main lasers.

The scintillation detectors were coupled with photo-multiplier tubes (PMTs) used for detecting neutrons. A liquid scintillation detector EJ301 with a volume of (π/4) × 12.7² × 12.7 cm³ with PMT ET9330B and a plastic scintillation detector BC420 with a volume of 40 × 10 × 10 cm³ with an ET9427B PMTs were placed on each side of the scintillator. The two types of PMTs were manufactured by ET Enterprises Ltd., of the United Kingdom. The scintillation detectors were located outside the laser target chamber at different distances (4.8 m for EJ301 and 4.5 m for BC420) and shielded by lead bricks with a thickness of about 2 cm. The data of gamma and neutron signals were recorded by using several oscilloscopes. With a start signal from the main lasers, the neutrons’ time-of-fight (TOF) spectra were recorded by oscilloscopes with bandwidths of 1 GHz. Each scintillator was set at a different distance from the shooting target. For the calibration of a laser-driven neutron source, we developed a direct calibration method with a gated fission neutron source ²⁵² [51]. Using the “PSD-TOF window” function, which has the highest background-γ-rejection, we improved the confidence level of the final results for both liquid and plastic scintillators. After comparing with the result of the Compton edge method and neutron beam method, the gated fusion neutron source method achieves much cleaner neutron signals and avoids some interference caused by the modeling accuracy of the neutron detectors. This approach can be widely used in laser-driven nuclear physics experiments with higher accuracy for neutron detection.

3 Results and discussion

The delayed time of 1 ns when the plasma collides can be determined from the shadow images. The plasma stream front’s expanding velocity for this period was calculated to be v_p ≃ 8.4 × 10⁵ m/s. It is possible to measure the deuterium ion motion at the plasma’s front. Deuterium atoms have a kinetic energy of roughly 10 keV. As a result, the Gamow window of relevance in nuclear astrophysics is not far from the center-of-mass energy of deuterium ions in the laser–plasma collision. According to the nuclear reaction theory, the neutrons generated by deuterium–deuterium fusion at this low energy are quasi-monoenergetic and have an angular distribution that is very near to isotropic.

3.1 Neutron yields

The typical TOF spectra from one of the liquid scintillators are shown in Figure 2. The first peak at around 300 ns represents the photon signal generated when the main laser pulse irradiates the targets. These photons usually contain different frequency bands, including radio frequency, visible light, X-ray, and gamma-ray, generated when the main lasers hit the targets. Since most X-ray and gamma-ray emissions in atoms or nuclei have a duration time of less than 1 ns, these photons are expected to arrive at the detectors as a ns-width pulse, which is same as that of the original driving laser. The second peak represents the neutron products. The neutron from the D(d, n)³He reaction has an energy of E_n = 2.45 MeV, corresponding to a speed of 2.16 cm/ns, which is much smaller than that of the photons (30 cm/ns). In a non-relativistic case, the time for a neutron with energy E_n and mass m_n to travel the distance L is

$t=\frac{L}{v}=\frac{L}{\sqrt{\frac{2E_{\text{n}}}{m_{\text{n}}}}},(1)$

where v is the speed of neutron flight. Once time t is measured experimentally, the energy of the neutron can be calculated as

$E_{\text{n}}=\frac{m_{\text{n}}}{2}{\left(\frac{L}{t}\right)}^2.(2)$

FIGURE 2

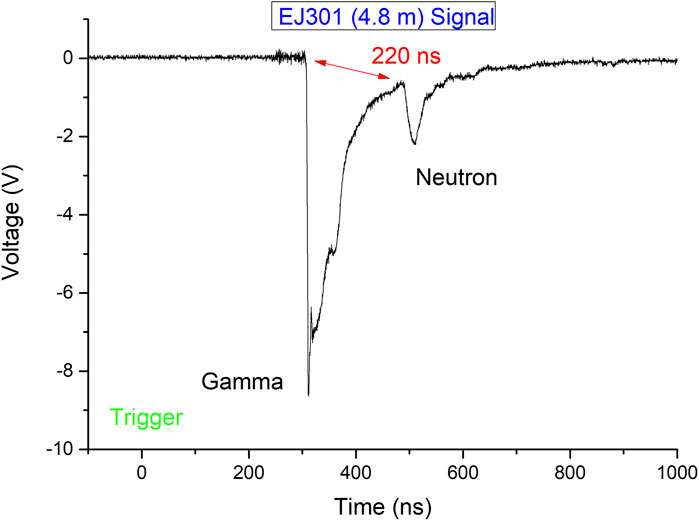
FIGURE 2. Typical TOF spectra come from the liquid scintillation detector 4.8 m away from the target.

In laser–plasma experiments, it is convenient to use the bremsstrahlung γ-ray pulses emitted instantaneously at the target to determine the precise take-off time and arrival signal. Thus, we have

$E_{\text{n}}=\frac{m_{\text{n}}}{2}{\left(\frac{1}{\frac{t^{\prime }}{L}+\frac{1}{c}}\right)}^2,(3)$

where t′ is the time between the γ-ray signal and the neutron arrival signal and c is the speed of light. There is excellent agreement between the measured neutron speed and the known 2.45 MeV neutron speed at various detector locations.

Because it immediately affects the accuracy of the experimental results, the scintillator detector system’s neutron signal calibration accuracy is crucial. As stated in Section 2, the detection system was calibrated using three different techniques: the direct calibration method using a neutron beam, the indirect calibration method using a Compton edge, and the direct calibration method using a gated fission neutron source ²⁵²Cf. We calibrate the TOF neutron detection for this experiment using the data on neutron signals captured by several oscilloscopes using the gated fusion neutron source technique. The calibration findings of EJ301 and BC420 detectors are shown in Table 1, along with their uncertainty percentages of 46% and 50%, respectively.

TABLE 1

TABLE 1. Calibration with different methods for deuterium–deuterium neutron detectors.

The neutron results of the high-energy ns laser-driven D–D fusion reaction experiment with nanowire targets were originally obtained after data sampling correction, solid angle correction, efficiency correction, shielding correction, and simulation correction. The transmittance of a 2.45 MeV neutron incident on a 2 cm lead shielding thickness is simulated by the GEANT4 codes 10. 2. p01 as 84.9% percent. Additionally, the 2.45 MeV neutron incident effectiveness for the BC420 and EJ301 detectors was 87.3% and 24.5%, respectively. The simulation error, which is connected to the cross-section database’s uncertainty, is estimated within 5%. The precise time, or the precise distance of the neutron traveling from the target to the detectors, can be determined from the delay between the initial gamma and neutron signals. Hence, the solid angles for EJ301 and BC420 are 4.4 × 10⁻⁵ and 1.6 × 10⁻⁵, respectively. Because of the shocks at the starting point, there may be a 1 percent margin of error when determining the starting position of the gamma and neutron peak. One percent of the flying distance’s uncertainty will be transferred to the solid angle.

The uncertainty in the neutron area sampling (due to the shocks at the starting position and accounting for the duration of the tailing of the neutron peak) is around 10%. The total systematical uncertainty of the neutron yield in this experiment was calculated using the error transfer formula to be 47% for EJ301 and 51% for BC420, respectively. It is also important to note that in the experiment, a single sandwich target (with a nanowire inside) and a single side target were also used. The fact that the detectors in both situations were unable to produce the appearance of neutron peaks, however, shows that the majority of the neutron yields measured in the experiment come from the nuclear reaction when expanding plasma streams from both sides collide at the center of the dual targets in the vacuum chamber. Table 2 displays the overall average neutron yields for each shot with the statistical uncertainty.

TABLE 2

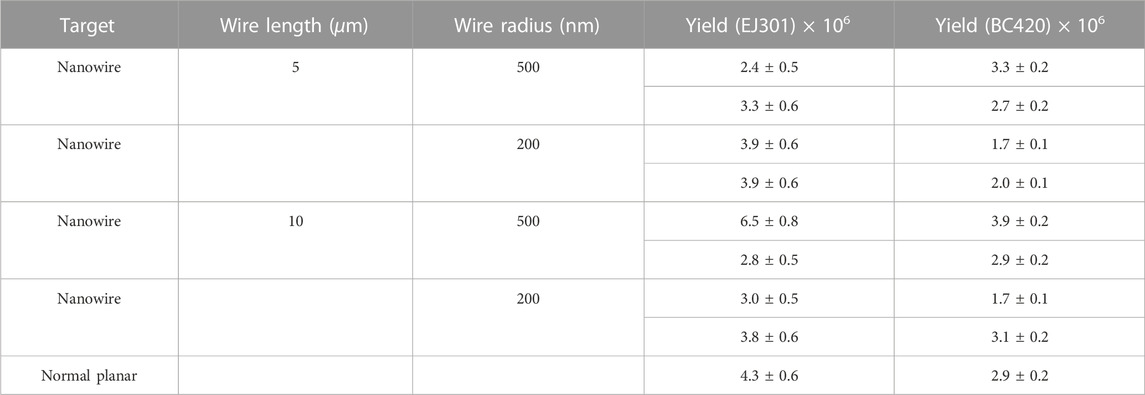
TABLE 2. Results of average neutron yields for deuterium–deuterium fusion reaction with EJ301 and BC420 detection. The fourth and fifth columns provide the statistical uncertainty of neutron detection of EJ301 and BC420. The systematical uncertainty is 47% for EJ301 and 51% for BC420, respectively.

The neutron yield for various target specifications is displayed in Figure 3 at the same order of 10⁶ per shot. Except for the fluctuations in the results of the fifth shot run, all other data points are at the same level of approximately 3 × 10⁶/shot, which indicates that the efficiency of laser coupling to plasma is practically the same for planar targets and nanowire targets with various parameters. The results of EJ301 and BC420 at the same laser shot, however, differ slightly because the plastic scintillator’s neutron signal peak falls more quickly than EJ301, causing the γ and neutron signals to be separated so that the error in the region beneath the neutron signal peak is negligible. Meanwhile, the luminescent substance in the liquid scintillator EJ301 has three different main components for mean decay times, so the longest component causes the γ signal to form a tail to a large extent. The neutron signal, which is influenced by the electronics of the significant γ signal, is typically at the tail of the strong γ peak. Since the response signal of liquid one is less stable than that of the plastic scintillator BC420, there is uncertainty in identifying the region beneath the peak of the neutron signal. To suppress the γ signal in the experiment, the target substrate material and lead shielding must be taken into account. When the γ signal is easily distinguished from the neutron signal, the electronic deviation can be minimized.

FIGURE 3

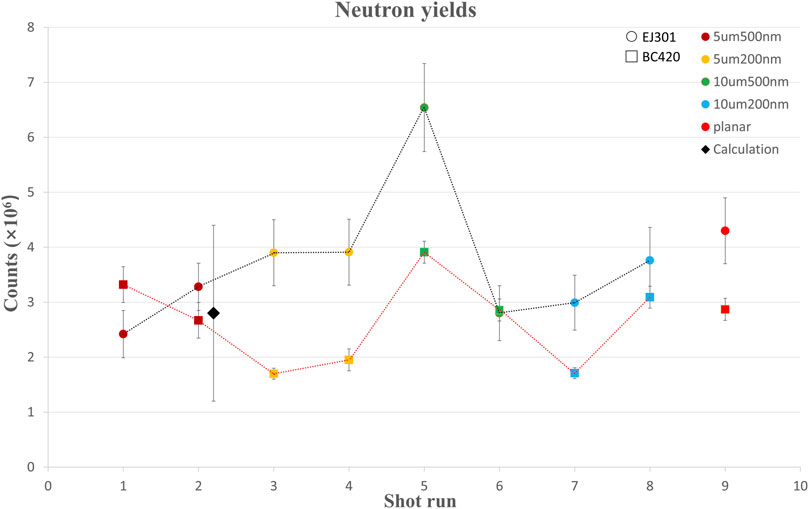
FIGURE 3. Neutron yields with the statistical uncertainty from EJ301 and BC420 detection and different target parameters. The circle represents the result of EJ301 detection, and the square represents that of BC420. The black diamond represents the results of the numerical calculation with an optical diagnostics approach for the second shot run. Different colors correspond to different target parameters.

The detected neutrons contain three sources: the initial laser-induced plasma (N_p), the beam-target (cold) reaction (N_b), and the center region where two plasma streams meet (N_c). The aggregate of the three sources represents the overall fusion yield: N_total = N_p + N_b + N_c. The N_p can be accomplished with the experiment of dual targets setup as one side target with a CD layer and the opposite one without a CD layer, and N_b with a single side target setup with a CD layer while maintaining laser parameters. The experimental results show that N_p and N_b can both be ignored. Moreover, the quantity of neutron yields decreased by nearly two orders of magnitude when a target surface was rotated by 5° on one side compared to that of the 180° collision target. A conclusion can be drawn: most of the fusion yields are produced by impacts between opposing plasma streams. So, N_total is mostly from the N_c, that is the plasma stream collision. In the experimental energy range, both the carbon and deuteron atoms were completely energized (approximately 10 keV). With the deuterated hydrocarbon layer material having 98 atom% D, the ratio of C and D atoms in the CD material is 1: 1.96. Considering that the plasma is electrically neutral on the um scale and that C ions and D ions are almost completely ionized, the density of deuterons in the plasma can be estimated to be

$n_D=\frac{1.96}{6+1.96}{n}_e,(4)$

where n_e is the density of electrons in the plasma. From the data of density, the D–D collision frequency can be estimated. The D–D mean free path, λ_DD, can be written as follows [52]:

${\lambda }_{DD}=\frac{m_D^2{\nu }_{12}^4}{4\pi Z^4{e}^4{n}_D\ln {\mathrm{\Lambda }}_{12}},(5)$

where m_D is the mass of the deuteron, ν₁₂ is the relative velocity of the deuteron, Z is the deuteron’s charge, e is the elementary electric charge, and ln Λ₁₂ = 10 is the Coulomb logarithm of plasma [53].

From the plasma front edge of the shadow imaging, the relative deuteron velocity ν₁₂ is estimated as 2 × 8.4 × 10⁵ m/s (corresponding to E_cm of 14.7 keV). From Figure 4B, an upper limit value of the electron density is chosen as 1 × 10²⁰ cm⁻³. The result of λ_DD calculated is larger than 26.4 mm, which is much larger than the 4 mm distance between the two planes of the dual target.

FIGURE 4

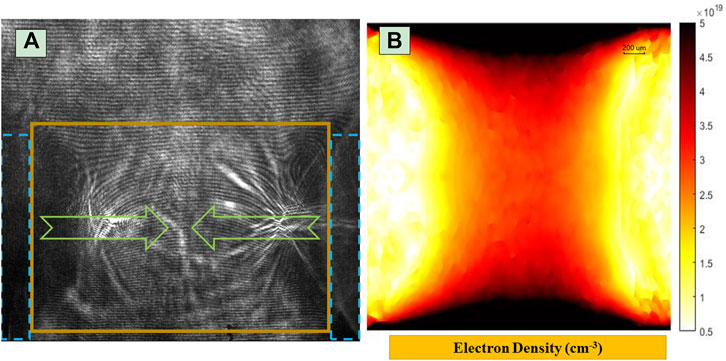
FIGURE 4. (A) Typical Nomarski interferogram of the plasma streams (green arrows) from one shot run calculation. The original position of the dual target is displayed by two blue dashed lines. (B) The corresponding electron density distribution from the area is marked with a yellow box of the interferogram, derived by the Abel inversion approach.

For fusion center-of-mass energies greater than 14.7 keV in this experiment configuration, the plasma is, therefore, collisionless. The interference pictures captured by the Nomarski interferometer are displayed in Figure 4. For this shot for calculation, a planar dual target with a thickness of 500 μm CD layers (5 um length and 500 nm radius) on either side and a probing laser delay time of 1 ns in relation to the main laser was made. The dark area surrounds the dual target on either side, indicating that the plasma density in this area surpasses the threshold for probe laser propagation in the plasma. The left and right plasma flow velocity vectors are also indicated by green arrows. The yellow box region in Figure 4A was subjected to the Abel inversion approach [54] to obtain the plasma density distribution, which is shown in Figure 4B.

The front portion of the expanding plasma can be thought of as a thin target with a quasi-thermal equilibrium of ions acting as a collisionless plasma, as was already stated earlier. Additionally, almost all neutrons can be thought of as the result of the nuclear reaction between two colliding plasma streams, in which there is a “relatively small” possibility that two deuterons will collide. With these assumptions, a numerical calculation using the simplified plasma dynamic model was performed to estimate the neutron yields. We assume that the deuterons from one target can only interact with those from the opposing side as two colliding deuterium ions with velocities of ν₁ and ν₂ do so in the laboratory system. The fusion yield can be written as follows [55]:

$Y=\int \int \int n_1\left(\overrightarrow{r_1}\right)n_2\left(\overrightarrow{r_2}\right)\sigma \left({\nu }_1,{\nu }_2\right)d\overrightarrow{r_1}d\overrightarrow{r_2}dA,(6)$

where $\overrightarrow{r_1}$ and $\overrightarrow{r_2}$ are vectors pointing to the integrated element from the left and right target points, respectively. n₁ and n₂ are the deuteron densities of the left and right sides, respectively. σ is the deuterium–deuterium reaction cross section. A is the section area of the colliding streams. The cross section is related to the center-of-mass energy of the two colliding deuterium ions:

$\sigma \left(E_{cm}\right)=S\left(E_{cm}\right)\exp \left(-2\pi \eta \right)/\left(E_{cm}\right),(7)$

where $E_{cm}=m{({\nu }_1+{\nu }_2)}^2/4$ is the center-of-mass energy, S(E_cm) is the astrophysical S-factor, and $\eta =\frac{Z_1{Z}_2{e}^2}{\hslash ({\nu }_1+{\nu }_2)}$ is the Sommerfeld parameter. A parameterized expression that takes the S factor in numerical calculations [56] is shown as

$\sigma \left(E_{cm}\right)=\frac{1}{E_{cm}}S\left(E_{cm}\right)\exp \frac{-B_G}{\sqrt{E_{cm}}},(8)$

where $B_G=31.397\sqrt{keV}$ is the Gamow constant. The electron density distribution is derived from an experimental interferogram by the Abel inversion approach. The deuteron density, as a function of time and position, is calculated from electron density according to Eq. 4. The ion speed ν is simplified as a constant in the collisionless regime, i.e., ν = z/t₀, where t₀ is the delayed time (2 ns in this case) of the probe laser and z is the distance to the target.

As a result, the entire plasma plane was integrated, as shown in Eq. 6, to produce the complete reaction yield. The neutron yield from the D–D reaction at various speeds in the plasma environment is shown in Figure 5, given the presumptions mentioned earlier. It is discovered that as E_cm increases, the cross section grows, while the number of ions (N) increases and drops. Thus, as seen by the solid blue line in Figure 5, the majority of the neutron yields come from the E_cm energy range of 10–30 keV. Thus, it provides a useful experimental method for nuclear reactions in plasma environments with energy regions of interest in nuclear astrophysics.

FIGURE 5

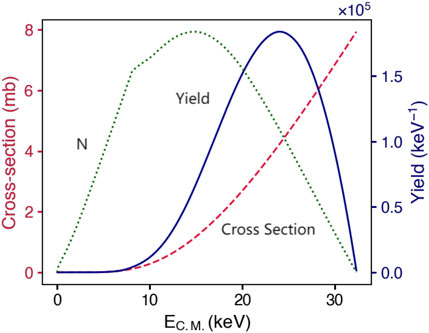
FIGURE 5. Neutron yield contributed by deuterium ions with different E_cm energies. Three data lines are shown in this chart: the number of the ions from the experimental diagnostic (the dotted green line), the D(d, n)³He cross section (the dashed red line), and the calculated neutron yield (the solid blue line).

The distance between the dual target’s two surfaces is the main source of computation uncertainty. The information regarding target distance will be crucial when determining the plasma expansion velocity and ion energy. The target rods’ bending deformation will result in a shorter distance than the intended standard distance of 4 mm. The distance is predicted to be between 2.5 and 3 mm because the nanowire layers on one side of the shot are 500 um thick. As a result, the neutron yield is computed at intervals of 0.1 mm for targets that are 2.5–3 mm away. In addition, the average value of the calculated neutron yield with standard deviation for this shot run is (2.8 ± 1.6) × 10⁶, which agrees well with the experimental detection results shown in Table 2 and Figure 3.

The process of resolving interference images shown in Figure 4A, carrying out Abel inversion and getting the two-dimensional density distribution of plasma, may result in a substantial amount of uncertainty due to the inadequacies of interference diagnosis techniques for plasma at present. The offset of the interference fringes is modest when the probe laser passes over the center reaction area between the dual targets, but speckle noise in the interference image is rather high, and thus, the computed density will have a large uncertainty. The neutron yield will be significantly affected by even small changes in the plasma density. Additionally, the physical model used in the article is still uncomplicated. Even though the primary physical properties of collisionless plasma are taken into account, some physical processes, including convection and filamentation function, may have some influence on the density distribution of the plasma. In addition, the computation does not take into account the plasma’s own magnetic field. A circular magnetic field created by two colliding plasma streams has already been seen and described [57] under circumstances that are comparable to our experiment, and the magnetic field can be as strong as 10 T. Deuterium ions having energies of several keV will be deflected under such a magnetic field intensity, adding to the difference between the reaction yield and the expected value.

3.2 Discussion

The aforestated experimental findings demonstrate that little difference exists between the nanowire targets used in these experiments and planar targets. The nanowire’s influence is less obvious in the experimental results of using a ns laser than in the performance variation resulting from using a ps/fs laser. Within a few ps, the nanowire’s high-density and -temperature regions dissipate into the background plasma. Thus, this advantage is not maintained under a longer time scale.

The MHD code FLASH [58] was used to simulate the evolution of planar and nanowire targets’ plasma parameters of ions’ density and temperature at the initial moment and 0.1 ns. The simulation result is shown in Figure 6. The velocity, temperature, and density profiles of the nanowire target compared with those of the planar target at 0.1 and 1.0 ns are shown in Figure 7. When the ns laser irradiates the wire target with our experiment parameters, the long pulse laser causes the expansion of the target so that the target surface reaches the critical density before the end of the laser pulse. The laser cannot directly interact with the depth of the wire target at 10 ps after the shooting time. When the time reaches 0.1 ns, the distribution of density, velocity, and temperature of plasma electrons almost kept the same. Only within the early dynamics of laser target interaction, around 10 ps, the energy absorption efficiency of the nanowire target was superior to that of the planar target. However, this tiny fraction would be smeared and negligible in the following long-term laser–plasma interaction, around ns.

FIGURE 6

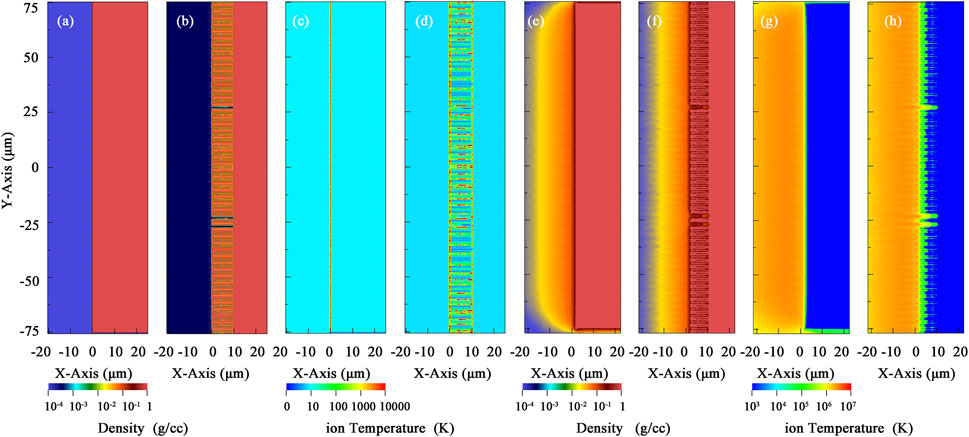
FIGURE 6. The velocity and density distributions of the ions in the plasma, as well as the evolution of the plasma over time, have a significant impact on the numerical calculation of nuclear reaction yields. By precisely determining the number of ions involved in nuclear reactions and their reaction cross sections, higher calculation accuracy can be attained. This can be achieved by increasing the quality of diagnostic data, such as by upgrading the energy and contrast of the probe laser or collecting multiple interference images continuously for one shot. In addition, the ability to reconstruct the physical process of plasma collisions will be substantially enhanced if more diagnostic techniques can be developed, such as monitoring the interior temperature and magnetic field of the plasma. Evolution of planar (A, C, E, G) and nanowire (B, D, F, H) targets’ plasma parameters of ions’ density (A, B, E, F) and temperature (C, D, G, H) at the initial moment (A–D) and 0.1 ns (E–H).

FIGURE 7

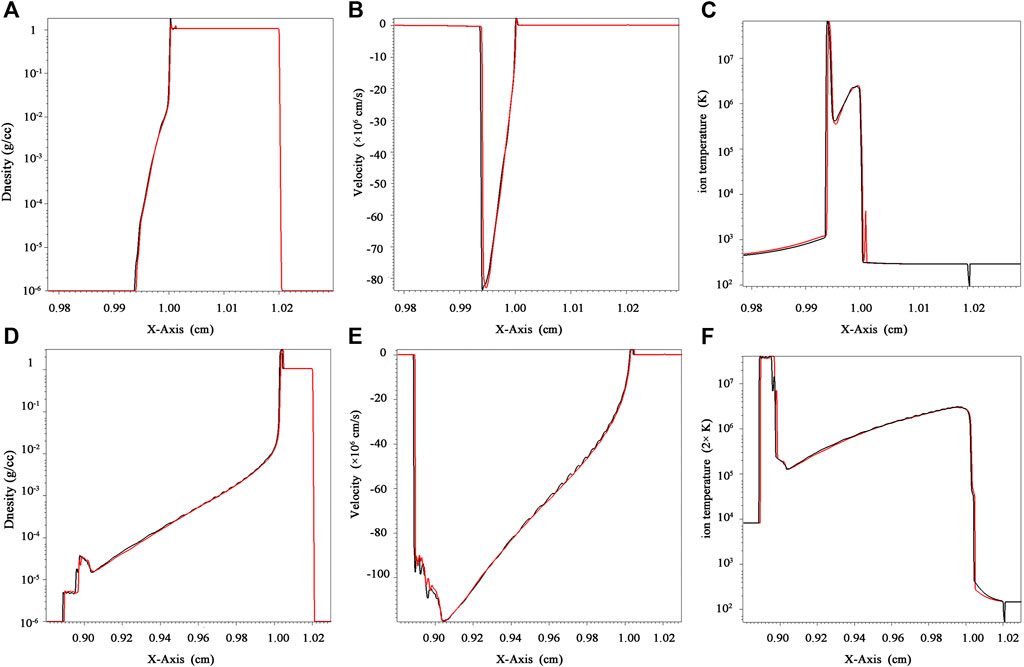
FIGURE 7. Velocity, temperature, and density profiles of the nanowire target were compared with those of the planar target at 0.1 ns (A–C) and 1.0 ns (D–F), respectively.

When an ultra-short intense laser pulse is applied, the electrons are quickly expelled away, while the deuterium ions mainly remain in place and maintain their structure without being scattered. Deuterium ions experience a Coulomb explosion in a matter of nanoseconds, colliding with other deuterium ions created by other nearby nanowires to produce a significant number of nuclear reaction events. In contrast, for long-term and moderate intense laser pulses, the electrons are slowly driven away and, as a result, the space between nearby nanowires gradually fills with plasma. Deuterium ions are released in the 4π-direction. Additionally, the production of plasma in the first few picoseconds reflects the remainder of the laser pulse, transforming the nanowire target into a target with circumstances comparable to a planar target under fs or ps laser irradiation. As such, in contrast with ultra-short pulse lasers, the efficiency of using ordinary nanowire targets in improving the energy conversion efficiency between the laser and plasma is not significant.

This experiment’s neutron yield amounted to 10⁶ per shot. The temperature density augmentation of the plasma under the ns laser is not sufficiently maintained by the nanowire, and the nanowire has no impact on the outcome of the nuclear reaction on the ns scale. It is necessary to conduct more research on the electronic impact of the significant γ signal on the liquid scintillation neutron signal amplitude. The most crucial step is to model the processes of laser targeting and plasma collisions using a hydrodynamic program that incorporates equation of state parameters and experimental data for physical analysis. We are developing the program in the hope of obtaining semi-quantitative information on the cross section of deuterium–deuterium-related reactions in harsh conditions. Further simulation is required to investigate the possibility of designing a microstructured target with a “burning” time scale on the order of ns, which is likely to produce outcomes that are distinct from those of conventional targets.

4 Summary

In summary, the experiment, based on the nanosecond laser with an energy of 2 kJ irradiation on a nanowire target to generate two colliding plasma jets and then induce nuclear reactions, was carried out for the first time. From the perspective of nuclear reaction products, the effect of the interaction between the ns laser and nanowire target on energy conversion efficiency was investigated. The experimental detection and numerical calculation results agree well and show that whether it is a nanowire target or a normal planar target, the neutron yields are at the same order of 10⁶ per shot. This means that the use of ns lasers cannot enhance the energy conversion efficiency between the laser and the target by interacting with nanowire targets, as is the case with the use of fs or ps lasers. Combining the experimental results and the magneto-hydrodynamic numerical simulation results, we suspect that the nanowire target only absorbs laser efficiently during the first few picoseconds during the whole process. Then, with the formation of plasma surpassing the critical density on the surface of the nanowire target, the laser is reflected instead of being absorbed. Using micrometer or even millimeter scale structure targets may be more suitable for the kJ-ns laser system to improve the laser absorption efficiency. Artificial nanowire structures should be investigated further to improve the targets’ laser-absorbing efficiency. We are currently studying this possibility. It is well known that in nuclear astrophysics, the interaction of ns lasers with solid targets is well suited to generate extreme plasma environments with energies ranging from a few keV to hundreds of keV, especially the Gamow window. According to the previous discussion, further improvement of plasma diagnostic technology is the key to a more accurate understanding of the process and mechanism of laser-driven nuclear reaction and to obtain a more accurate cross section of laser-driven nuclear reactions in plasma. Our experimental results and numerical simulations can serve as a reference to establish better such experimental conditions in the future.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XX and CL contributed to the work equally and should be regarded as co-first authors. BG and CF provided overall leadership and oversight for the experiment. XX and CL conceived the study, conducted the experiments, performed analysis, and prepared the manuscript. DK and WM contributed to the development of the nanowire targets. The experiments were performed by FL, GZ, WS, CH, XD, ZM, and JZ. XZ, GZ, and WS carried out the calculation simulations. BG, CF, and WM helped with writing, proofreading, and reforming the structure of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This study was funded by the National Science Fund for Distinguished Young Scholars (No. 12125509), National Natural Science Foundation of China (Nos 11961141003, 1197050502, 11775321, 11975316, 12005305, U2267204, U2241281, and 11875191), President’s Foundation of China Institute of Atomic Energy (Nos YZ222402000401, YC212212000301, and 18YC212212000201), Young Talents Fund of China National Nuclear Corporation (Nos FY222506000201, FC232412000201, and FY212406000901), and Continuous Basic Research Project (Nos BJ19002211 and WDJC-2019-02).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer AB is currently organizing a Research Topic with the authors CF & BG at the time of the review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Matinyan S. Lasers as a bridge between atomic and nuclear physics. Phys Rep (1998) 298:199–249. doi:10.1016/S0370-1573(97)00084-7

CrossRef Full Text | Google Scholar

2. Ditmire T, Zweiback J, Yanovsky V, Cowan T, Hays G, Wharton K. Nuclear fusion from explosions of femtosecond-laser heated deuterium clusters. Nature (1999) 398:489–92. doi:10.1038/19037

CrossRef Full Text | Google Scholar

3. Schwoerer H, Beleites B, Magill J. Lasers and nuclei: Applications of ultrahigh intensity lasers in nuclear science. Lecture Notes Phys (2006). doi:10.1007/b11559214

CrossRef Full Text | Google Scholar

4. Esarey E, Schroeder C, Leemans W. Physics of laser-driven plasma-based electron accelerators. Rev Mod Phys (2009) 81:1229–85. doi:10.1103/RevModPhys.81.1229

CrossRef Full Text | Google Scholar

5. Macchi A, Borghesi M, Passoni M. Ion acceleration by superintense laser-plasma interaction. Rev Mod Phys (2013) 85:751–93. doi:10.1103/RevModPhys.85.751

CrossRef Full Text | Google Scholar

6. Corde S, Phuoc KT, Lambert G, Fitour R, Malka V, Rousse A, et al. Femtosecond x rays from laser-plasma accelerators. Rev Mod Phys (2013) 85:1–48. doi:10.1103/RevModPhys.85.1

CrossRef Full Text | Google Scholar

7. Labaune C, Baccou C, Depierreux S, Goyon C, Loisel G, Yahia V, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun (2013) 4:2506. doi:10.1038/ncomms3506

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Strickland D, Mourou G. Compression of amplified chirped optical pulses. Opt Commun (1985) 55:447–9. doi:10.1016/0030-4018(85)90151-8

CrossRef Full Text | Google Scholar

9. Mourou G, Fisch N, Malkin V, Toroker Z, Khazanov E, Sergeev A, et al. Exawatt-zettawatt pulse generation and applications. Opt Commun (2012) 285:720–4. doi:10.1016/J.OPTCOM.2011.10.089

CrossRef Full Text | Google Scholar

10. Danson C, Haefner C, Bromage J, Butcher T, Chanteloup J, Chowdhury E, et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci Eng (2019) 7:54. doi:10.1017/hpl.2019.36

CrossRef Full Text | Google Scholar

11. Li Z, Kawanaka J. Laser technique improvement for Exawatt-class peak-power in Japan. Rev. Laser. Eng. (2021) 49, 101.

Google Scholar

12. Remington B, Arnett D, Paul R, Drake N, Takabe H. Modeling astrophysical phenomena in the laboratory with intense lasers. Science (1999) 284:1488–93. doi:10.1126/science.284.5419.1488

CrossRef Full Text | Google Scholar

13. Zhang J, Zhao G. Introduction to laboratory astrophysics. Physics (2000) 29:4. doi:10.3321/j.issn:0379-4148.2000.07.003

CrossRef Full Text | Google Scholar

14. Huang M, Quevedo HJ, Zhang G, Bonasera A. Nuclear astrophysics with lasers. Nucl Phys News (2019) 29:9–13. doi:10.1080/10619127.2019.1603555

CrossRef Full Text | Google Scholar

15. Malka V, Fritzler S, Lefebvre E, Aleonard M, Burgy F, Chambaret J, et al. Electron acceleration by a wake field forced by an intense ultrashort laser pulse. Science (2002) 298:1596–600. doi:10.1126/science.1076782

PubMed Abstract | CrossRef Full Text | Google Scholar

16. McKenna P, Ledingham K, McCanny T, Singhal R, Spencer I, Santala M, et al. Demonstration of fusion-evaporation and direct-interaction nuclear reactions using high-intensity laser-plasma-accelerated ion beams. Phys Rev Lett (2003) 91:075006. doi:10.1103/PhysRevLett.91.075006

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Roth M, Brambrink E, Audebert P, Blazevic A, Clarke R, Cobble J, et al. Laser accelerated ions and electron transport in ultra-intense laser matter interaction. Laser Part Beams (2005) 23:95–100. doi:10.1017/S0263034605050160

CrossRef Full Text | Google Scholar

18. Robson L, Simpson P, Clarke R, Ledingham KWD, Lindau F, Lundh O, et al. Scaling of proton acceleration driven by petawatt-laser–plasma interactions. Nat Phys (2007) 3:58–62. doi:10.1038/nphys476

CrossRef Full Text | Google Scholar

19. Robinson APL, Neely D, McKenna P, Evans RG. Spectral control in proton acceleration with multiple laser pulses. Plasma Phys Controlled Fusion (2007) 49:373–84. doi:10.1088/0741-3335/49/4/002

CrossRef Full Text | Google Scholar

20. Fujioka S, Takabe H, Yamamoto N, Salzmann D, Wang F, Nishimura H, et al. X-ray astronomy in the laboratory with a miniature compact object produced by laser-driven implosion. Nat Phys (2009) 5:821–5. doi:10.1038/nphys1402

CrossRef Full Text | Google Scholar

21. Bulanov S, Esirkepov T, Habs D, Pegoraro F, Tajima T. Relativistic laser-matter interaction and relativistic laboratory astrophysics. The Eur Phys J D (2008) 55:483–507. doi:10.1140/epjd/e2009-00138-1

CrossRef Full Text | Google Scholar

22. Meinecke J, Doyle H, Miniati F, Bell A, Bingham R, Crowston R, et al. Turbulent amplification of magnetic fields in laboratory laser-produced shock waves. Nat Phys (2014) 10:520–4. doi:10.1038/nphys2978

CrossRef Full Text | Google Scholar

23. Blackburn T, Ridgers C, Kirk J, Bell A. Quantum radiation reaction in laser–electron-beam collisions. Phys Rev Lett (2014) 112:015001. doi:10.1103/PhysRevLett.112.015001

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bailey J, Nagayama T, Loisel G, Rochau G, Blancard C, Colgan J, et al. A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature (2015) 517:56–9. doi:10.1038/nature14048

PubMed Abstract | CrossRef Full Text | Google Scholar

25. King B, Heinzl T. Measuring vacuum polarization with high-power lasers. High Power Laser Sci Eng (2016) 4:e5. doi:10.1017/hpl.2016.1

CrossRef Full Text | Google Scholar

26. Fu C, Zhang G, Ma Y. New opportunities for nuclear and atomic physics on the femto-to nanometer scale with ultra-high-intensity lasers. Matter Radiat Extremes (2022) 7:024201. doi:10.1063/5.0059405

CrossRef Full Text | Google Scholar

27. Green JS, Robinson A, Booth N, Carroll DC, Dance RJ, Gray RJ, et al. High efficiency proton beam generation through target thickness control in femtosecond laser-plasma interactions. Appl Phys Lett (2014) 104:214101. doi:10.1063/1.4879641

CrossRef Full Text | Google Scholar

28. Back CA, Grun J, Decker C, Suter LJ, Davis J, Landen LO, et al. Efficient multi-kev underdense laser-produced plasma radiators. Phys Rev Lett (2001) 87:275003. doi:10.1103/PhysRevLett.87.275003

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Oubrerie K, Leblanc A, Kononenko O, Lahaye R, Andriyash A. I., et al. Controlled acceleration of gev electron beams in an all-optical plasma waveguide. Light: Sci Appl (2022) 11:180. doi:10.1038/s41377-022-00862-0

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wang W, Sheng Z, Zhang J. A model for the efficient coupling between intense lasers and subwavelength grating targets. Phys Plasmas (2008) 15:030702. doi:10.1063/1.2898456

CrossRef Full Text | Google Scholar

31. Kulcsar G, AlMawlawi D, Budnik FW, Herman PR, Moskovits M, Zhao L, et al. Intense picosecond x-ray pulses from laser plasmas by use of nanostructured velvet targets. Phys Rev Lett (2000) 84:5149–52. doi:10.1103/PhysRevLett.84.5149

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Vallières S, Salvadori M, Permogorov A, Cantono G, Svendsen K, Chen Z, et al. Enhanced laser-driven proton acceleration using nanowire targets. Scientific Rep (2021) 11:2226. doi:10.1038/s41598-020-80392-0

CrossRef Full Text | Google Scholar

33. Dimitri K, Mathieu L, Bjrn B, Burr L, Gärtner F, Gremillet L, et al. Enhancing laser-driven proton acceleration by using micro-pillar arrays at high drive energy. Scientific Rep (2017) 7:11366. doi:10.1038/s41598-017-11589-z

CrossRef Full Text | Google Scholar

34. Humphries OS, Allan P, Brown C, Hobbs L, James SF, Ramsay MG, et al. Time evolution of transient plasma states from nanowire arrays irradiated at relativistic intensities. Commun Phys (2020) 3:170. doi:10.1038/s42005-020-00438-7

CrossRef Full Text | Google Scholar

35. Bochkarev SG, Brantov AB, Gozhev DA, Bychenkov VY. Neutron production from structured targets irradiated by an ultrashort laser pulse. J Russ Laser Res (2021) 42:292–303. doi:10.1007/s10946-021-09962-5

CrossRef Full Text | Google Scholar

36. Cantono G, Permogorov A, Ferri J, Smetanina E, Dmitriev A, Persson A, et al. Laser-driven proton acceleration from ultrathin foils with nanoholes. Scientific Rep (2021) 11:5006. doi:10.1038/s41598-021-84264-z

CrossRef Full Text | Google Scholar

37. Qin C, Zhang H, Li S, Wang N, Li A, Fan L, et al. High efficiency laser-driven proton sources using 3d-printed micro-structure. Commun Phys (2022) 5:124. doi:10.1038/s42005-022-00900-8

CrossRef Full Text | Google Scholar

38. Purvis MA, Shlyaptsev VN, Hollinger R, Bargsten C, Pukhov A, Prieto A, et al. Relativistic plasma nanophotonics for ultrahigh energy density physics. Nat Photon (2013) 7:796–800. doi:10.1038/nphoton.2013.217

CrossRef Full Text | Google Scholar

39. Bargsten C, Hollinger R, Capeluto MG, Kaymak V, Pukhov A, Wang S, et al. Energy penetration into arrays of aligned nanowires irradiated with relativistic intensities: Scaling to terabar pressures. Sci Adv (2017) 3:e1601558. doi:10.1126/sciadv.1601558

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Margarone D, Klimo O, Kim IJ, Prokůpek J, Limpouch J, Jeong TM, et al. Laser-driven proton acceleration enhancement by nanostructured foils. Phys Rev Lett (2012) 109:234801. doi:10.1103/PhysRevLett.109.234801

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Curtis A, Calvi C, Tinsley J, Hollinger R, Kaymak V, Pukhov A, et al. Micro-scale fusion in dense relativistic nanowire array plasmas. Nat Commun (2018) 9:1077. doi:10.1038/s41467-018-03445-z

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Kong D, Zhang G, Shou Y, Xu S, Mei Z, Cao Z, et al. High-energy-density plasma in femtosecond-laser-irradiated nanowire-array targets for nuclear reactions. Matter Radiat Extremes (2022) 7:064403. doi:10.1063/5.0120845

CrossRef Full Text | Google Scholar

43. Hill MP, Humphries O, Royle R, Williams B, Ramsay MG, Miscampbell A, et al. (2020)Volumetric heating of nanowire arrays to kev temperatures using kilojoule-scale petawatt laser interactions, Available at: https://arxiv.org/abs/2007.10410

Google Scholar

44. Altana C, Amaru V, Castro G, Tudisco S, Lanzalone G, Malferrari L, et al. Nanostructured surfaces for nuclear astrophysics studies in laser-plasmas. The Eur Phys J Conferences (2017) 165:01002. doi:10.1051/epjconf/201716501002

CrossRef Full Text | Google Scholar

45. Muoio A, Altana C, Frassetto M, Lanzalone G, Malferrari L, Mascali D, et al. Nanostructured targets irradiation by ns-laser for nuclear astrophysics applications: First results. J Instrumentation (2017) 12:C03076. doi:10.1088/1748-0221/12/03/C03076

CrossRef Full Text | Google Scholar

46. Mascali D, Tudisco S, Bonanno A, Gambino N, Ivanovski S, Anzalone A, et al. Colliding laser-produced plasmas: A new tool for nuclear astrophysics studies. Radiat Effects Defects Sol (2010) 165:730–6. doi:10.1080/10420151003729847

CrossRef Full Text | Google Scholar

47. Fu C, Bao J, Chen L, He J, Hou L, Li L, et al. Laser-driven plasma collider for nuclear studies. Sci Bull (2015) 60:1211–3. doi:10.1007/s11434-015-0821-0

CrossRef Full Text | Google Scholar

48. Zhao JR, Zhang P. X., Yuan DW, Chen LM, Li T, et al. Neutron yield enhancement in laser-induced deuterium-deuterium fusion using a novel shaped target. Rev Scientific Instr (2015) 86:063505. doi:10.1063/1.4922912

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Zhao JR, Zhang XP, Yuan DW, Li YT, Li DZ, Rhee YJ, et al. A novel laser-collider used to produce monoenergetic 13.3 MeV (7)Li (d, n) neutrons. Scientific Rep (2016) 6:27363. doi:10.1038/srep27363

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Zhang X, Zhao J, Yuan D, Fu C, Bao J, Chen L, et al. Deuteron-deuteron fusion in laser-driven counter-streaming collisionless plasmas. Phys Rev C (2017) 96:055801. doi:10.1103/PhysRevC.96.055801

CrossRef Full Text | Google Scholar

51. Xi X, Zhang G, Liu F, Fu G, He C, Chen H, et al. Direct calibration of neutron detectors for laser-driven nuclear reaction experiments with a gated neutron source. Rev Scientific Instr (2023) 94:013301. doi:10.1063/5.0127101

CrossRef Full Text | Google Scholar

52. Chenais-Popovics C, Renaudin P, Rancu O, Gilleron F, Gauthier JC, Larroche O, et al. Kinetic to thermal energy transfer and interpenetration in the collision of laser-produced plasmas. Phys Plasmas (1997) 4:190–208. doi:10.1063/1.872132

CrossRef Full Text | Google Scholar

53. Ramazanov TS, Kodanova SK. Coulomb logarithm of a nonideal plasma. Phys Plasmas (2001) 8:5049–50. doi:10.1063/1.1407820

CrossRef Full Text | Google Scholar

54. Yasutomo Y, Miyata K, Himeno S-I, Enoto T, Ozawa Y. A new numerical method for asymmetrical abel inversion. IEEE Trans Plasma Sci (1981) 9:18–21. doi:10.1109/TPS.1981.4317374

CrossRef Full Text | Google Scholar

55. Rolfs CE, Rodney S. W., Clayton D. D. Cauldrons in the cosmos. Am J Phys (1989) 57:188–9. doi:10.1119/1.16074

CrossRef Full Text | Google Scholar

56. Bosch H, Hale G. Improved formulas for fusion cross-sections and thermal reactivities. Nucl fusion (1992) 32:611–31. doi:10.1088/0029-5515/32/4/I07

CrossRef Full Text | Google Scholar

57. Li CK, Ryutov DD, Hu SX, Rosenberg MJ, Zylstra AB, Séguin FH, et al. Structure and dynamics of colliding plasma jets. Phys Rev Lett (2013) 111:235003. doi:10.1103/PhysRevLett.111.235003

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Fryxell B, Olson K, Ricker P, Timmes F, Zingale M, Lamb D, et al. An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophys. J. Suppl. Ser. (2000) 131 (1):273.

CrossRef Full Text | Google Scholar