An innovative approach based on meta-learning for real-time modal fault diagnosis with small sample learning

The actual multimodal process data usually exhibit non-linear time correlation and non-Gaussian distribution accompanied by new modes. Existing fault diagnosis methods have difficulty adapting to the complex nature of new modalities and are unable to train models based on small samples. Therefore, this paper proposes a new modal fault diagnosis method based on meta-learning (ML) and neural architecture search (NAS), MetaNAS. Specifically, the best performing network model of the existing modal is first automatically obtained using NAS, and then, the fault diagnosis model design is learned from the NAS of the existing model using ML. Finally, when generating new modalities, the gradient is updated based on the learned design experience, i.e., new modal fault diagnosis models are quickly generated under small sample conditions. The effectiveness and feasibility of the proposed method are fully verified by the numerical system and simulation experiments of the Tennessee Eastman (TE) chemical process.

1 Introduction

With the development of many sensors and industrial networks, modern chemical industry is moving toward large-scale, hierarchical, information integration and strong interaction, leading to frequent failures and unstable product quality in chemical production processes, and chemical process troubleshooting is one of the effective techniques to ensure product quality and efficient production operation [1, 2]. In the actual chemical production process, the adjustment of the product grade or index, the fluctuation of material quality, and the imbalance of feed ratio all lead to the multimodal characteristics of the chemical process [3]. Therefore, multimodal characteristics are widely present in modern manufacturing industries [4, 5]. Compared with unimodal processes, the multimodal process data are more complex, usually manifested as non-linear time correlation and non-Gaussian distribution accompanied by new modes [6]. If deep learning is directly applied to multimodal chemical processes, it will be difficult to adapt to complex characteristics such as new modes and to construct accurate fault diagnosis models under small samples [7, 8]. Therefore, the deep learning-based fault diagnosis method for new modes in small samples is of research value.

Existing multimodal chemical process fault diagnosis methods can be classified into statistical learning, machine learning, and deep learning methods, among which statistical learning and machine learning methods have been studied previously. For example, Zhao et al. studied a local modal fault diagnosis method using multiple local PCA statistical models [9], but the method requires the use of accurate modal information in the offline modeling stage. To address the problem of incomplete modal prior knowledge, Tan et al. applied the clustering method to the multimodal chemical process and effectively improved the accuracy of fault diagnosis [10]. Wang et al. proposed a stable and transitional modal fault diagnosis method based on the transition probabilities between different modes [11]. Natarajan et al. gave the minimum distance from the test data to the training data center by calculating the selection of the locally optimal PCA model criterion [12]. Deep learning has made important progress in many fields in recent years, but there are relatively few studies on deep learning for multimodal chemical process fault diagnosis. In addition, the training of deep learning fault diagnosis models usually requires a large amount of labeled data, but new modes often have only a small amount of data [13–16]. How to make full use of multimodal process characteristics and model design experience of the existing modes under small-sample conditions to rapidly construct new modal fault diagnosis models based on deep learning is of great importance to ensure the safety and product quality of the actual chemical processes.

Existing small-sample data learning methods can be divided into three categories: data augmentation-based methods, model improvement-based methods, and algorithm optimization-based methods [17, 18]. Data augmentation-based methods achieve the purpose of expanding the dataset by generating new data [19], but the manipulation of data is not universal and requires the designer to have sufficient knowledge of the relevant domain. Model improvement-based approaches model small data by limiting the model complexity, reducing the hypothesis space, and reducing VC dimension [20] but require a priori knowledge and extensive experience of the designer, and the aforementioned two approaches cannot effectively utilize the design experience of existing modes. Algorithm-based optimization methods search for suitable solutions faster by improving the optimization algorithm [21, 22], and meta-learning is an improved optimization algorithm. The proposed meta-learning method provides research ideas to solve the problems such as inadequate utilization of model design experience of the existing modes and small samples [23]. For example, Finn et al. proposed the model-agnostic meta-learning (MAML) method, which first trains a set of initialization parameters and then performs one or more steps of gradient adjustment to achieve rapid adaptation to new tasks with only a small amount of data [24, 25]. However, MAML is very sensitive to the neural network structure and requires time-consuming hyperparameter search to stabilize the training and improve the model generalization power [26]. To address these problems, Antoniou et al. optimized MAML in terms of robustness, training stability, automatic learning of inner-loop hyperparameters, and computational efficiency during inference and training, which significantly improved the generalization performance of MAML [27] but at the expense of computation and memory. Nichol et al. replaced the process of computing second-order differentiation in MAML with the one in which each task is performed using the stochastic gradient descent (SGD) in a standard form without expanding the computational graph or computing arbitrary second-order derivatives, reducing the amount of computation and memory required by MAML [28]. However, the aforementioned methods have a single network structure and cannot transform the network structure as the task changes, and meta-learning faces problems such as cumbersome network structure design and time-consuming parameter search.

In the field of machine learning and artificial intelligence, several state-of-the-art (SOTA) algorithms have been developed to tackle various tasks. Although these algorithms have their own advantages, they also come with certain limitations. Here is a summary of the advantages and limitations to the existing SOTA algorithms in this area. The advantages are as follows: high accuracy: SOTA algorithms often achieve remarkable accuracy in solving complex problems; robustness: many SOTA algorithms exhibit robustness in handling noisy or incomplete data; generalization: SOTA algorithms often possess excellent generalization capabilities; and scalability: several SOTA algorithms are designed to handle large-scale datasets efficiently. The limitations are as follows: computational complexity: many SOTA algorithms, particularly those based on deep learning architecture, require significant computational resources to train and deploy; interpretability: while SOTA algorithms often achieve impressive performance, they can be black-box models, meaning they lack interpretability; data dependency: SOTA algorithms heavily rely on large and diverse datasets for training; and overfitting: some SOTA algorithms are susceptible to overfitting, especially when dealing with small datasets.

To solve the aforementioned problems, this paper proposes a new modal fault diagnosis method, MetaNAS, which uses meta-learning to find the optimal initial parameters, and the new modal can find the network structure with optimal performance by only a few steps of gradient update based on the optimal initial parameters. The optimal initial parameters are to be learned so that the fault diagnosis model is obtained by performing a few steps of updates based on the optimal initial parameters under a small sample of the new mode. MetaNAS solves the limitations to fault diagnosis by NAS, such as underutilization of the existing modal design experience and difficulty in training models under small samples.

The main contributions of this paper are as follows [1]: the proposed MetaNAS method can automatically design fault diagnosis network models and realize automatic fault diagnosis under small samples of new modes [2]. To address the problems of underutilization of the existing modal design experience and difficulty in training models under small samples, meta-learning is used to learn the model design experience of existing models and obtain the optimal initial parameters so that the new modal can obtain the fault diagnosis model with only a few steps of gradient update under small samples [3]. Continuous relaxation optimization converts the discrete channel selection process into a continuous optimization process, making NAS more efficient and convenient.

2 Manuscript formatting

2.1 Model-agnostic meta-learning

The entire dataset, training set, and test set are denoted by $D$, $D_{meta-train}$, and $D_{meta-test}$, respectively, and in meta-learning, a series of tasks $T$ is sampled according to the distribution $p\left(T\right)$ of $D_{meta-train}$, where there are N categories in the $i_{th}$ task, and each category has K samples, calling the problem an N-class K-sample problem [19]. The data in each N-class K-sample problem are further divided into a training set and a test set, and in order not to be confused, the training set in $T_i$ is called the support set and the test set is called the query set, denoted as $T_i^s$ and $T_i^q$, respectively. The core idea of MAML is to learn an optimal initial parameter $\stackrel{\sim }{\omega }$ in all tasks $T$ such that $D_{meta-test}$ to perform one or more steps of gradient adjustment based on $\stackrel{\sim }{\omega }$ to achieve the goal of fast adaptation to new tasks and good performance with only a small amount of data. The optimal initial parameters are learned according to the following rules:

${\omega }_i^{m+1}={\omega }_i^m-{\chi }_{inner}\frac{\partial L\left(T_i^s;{\omega }_i^m\right)}{\partial {\omega }_i^{m+1}},(1)$

where ${\chi }_{inner}$ is the internal learning rate of parameter $\omega$, $m$ is the update step in each task $T$, $f$ is the parameterization function of the network weight $\omega$, and $L$ is the loss function. During the internal learning process, $T_i^s$ is used to calculate the loss of task $T_i$ and let the parameter $\omega$ be updated from ${\omega }_i^m$ to ${\omega }_i^{m+1}$, where ${\omega }_i^0=\omega$. After M steps, $L(f\left(T_i^q;{\omega }_i^M\right)$ in $T_i^q$ is used to update the optimal initial parameters, which can be expressed as follows:

$\stackrel{\sim }{\omega }=\stackrel{\sim }{\omega }-{\chi }_{outer}\frac{\partial {{\displaystyle \sum }}_{T_i^q\sim p\left(T\right)}L\left(f\left(T_i^q;{\omega }_i^M\right)\right)}{\partial \stackrel{\sim }{\omega }},(2)$

where ${\chi }_{outer}$ is the external learning rate of parameter $\stackrel{\sim }{\omega },$ and eventually, when the model converges, the optimal initial parameter $\stackrel{\sim }{\omega }$ is obtained. This makes the initial parameters so sensitive that a better model can be obtained in only a few steps of updating on $D_{meta-test}$.

2.2 Automatic fault diagnosis

The core idea of the automatic fault diagnosis (AutoFD) method is to continue the discrete network search process by continuous relaxation optimization, assigning weights to all candidate operations separately, then optimizing the operation weights and network parameters by gradient descent, and then using the operation weight parameters to select the corresponding operations to form the final network model [29, 30].

Let $O$ be the candidate operation set, each candidate operation is denoted as $o$; given the input $x$, the operation output $\overline{o}\left(x\right)$ after continuous relaxation optimization is as follows:

$\overline{o}\left(x\right)={\displaystyle \sum }_{o\in O}\frac{\exp \left({\alpha }_o\right)}{{\sum }_{o^{\prime }\in O}\exp \left({\alpha }_{o^{\prime }}\right)}o\left(x\right),(3)$

where $\alpha$ represents the operation weight vector, which represents the importance of different candidate operations in the corresponding edge. After the training is completed, the operation corresponding to the largest weight is selected according to the operation weight parameter as the final result.

Through continuous relaxation optimization, the NAS problem is transformed into a double optimization problem, which can be solved by using the two-step update algorithm.

$\alpha =\alpha -\delta \frac{\partial L\left(\omega -\xi \frac{\partial L\left(\omega ,\alpha \right)}{\partial \omega }\right)}{\partial \alpha },(4)$

$\omega =\omega -\chi \frac{\partial L\left(\omega ,\alpha \right)}{\partial \omega },(5)$

where $L$ denotes the loss function and $\xi$ means the internal learning rate.

3 The proposed method

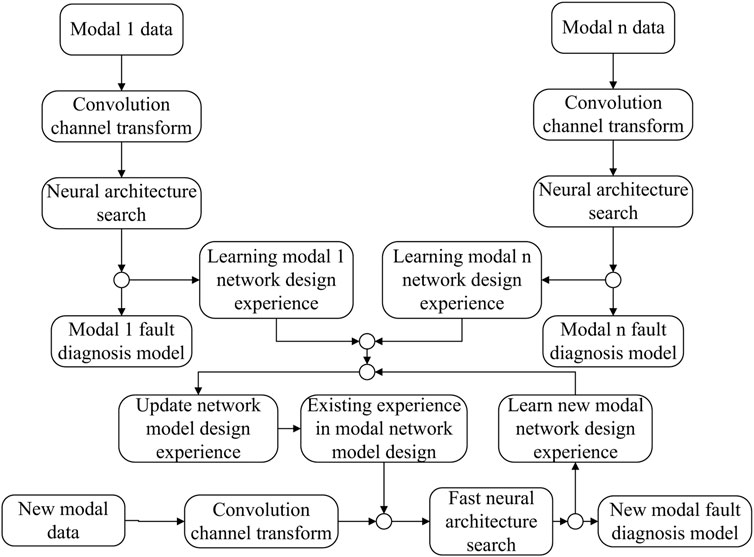
The MetaNAS method is proposed to address the problems of existing methods that do not fully utilize the model design experience of the previous modes and require a large amount of feature data, and the overall flow chart of the method is shown in Figure 1. MetaNAS first assigns weights to the candidate channels and transforms the discrete channel selection process into a continuous optimization process by optimizing the continuous weights instead of the channel selection process. Then, MAML is used to learn the optimal initial parameters of the required learning parameters in NAS, and when a new mode appears, a better fault diagnosis model for the new mode is obtained with only a few steps of updates based on the optimal initial parameters when only a small amount of data is available for the new mode.

FIGURE 1

FIGURE 1. Flowchart of the proposed MetaNAS method.

3.1 Channel weight parameters

AutoFD uses multi-channel convolution to enhance the performance of the network, but the selection of convolutional channels is very time-consuming. In order to make NAS more efficient, this paper uses continuous relaxation optimization to make the discrete convolutional channel selection process continuous. The candidate channels are denoted by $C=\left\{C_1,C_2,\cdots ,C_n\right\}$ to denote the set of candidate channels, which are used as the candidate input channels of the network, i.e., $I=\left\{I_1,I_2,\cdots ,I_n\right\}$, the selection process of these candidate input channels is discrete, the channels are assigned weights $\beta =\left\{{\beta }_1,{\beta }_2,\cdots ,{\beta }_n\right\}$, and these weights are transformed by the Softmax function to mix all the channels in the candidate channel set to obtain a mixed input.

$\mathrm{I}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}=\sum \frac{{\exp }^{\left(\beta \right)}}{{{\displaystyle \sum }}_{i^{\prime }\in I}{\exp }^{\left({\beta }_i^{\prime }\right)}}i.(6)$

Thus, each channel $C$ is associated with a weight coefficient $\beta$ corresponding to it, and continuous relaxation optimization uses a continuous weight coefficient to represent the discrete candidate channels. This continuous weight coefficient indicates the importance of the corresponding channel in the network input, so the performance of the network on the validation set can be updated quickly by using gradient descent for each operation, effectively avoiding the time-consuming process of training all network inputs and selecting the well-performing inputs. After the search is completed, the channel corresponding to the top three values of the weight coefficient is selected as the final operation convolution channel. By the aforementioned method, the NAS problem is transformed into a two-layer optimization problem of learning the smallest values of operation weight ${\alpha }^{*}$, network weight ${\omega }^{*}$, and channel weight ${\beta }^{*}$ with the loss function.

$\mathrm{L}\mathrm{v}\mathrm{a}\mathrm{l}\left({\omega }^{*},{\alpha }^{*},{\beta }^{*}\right),(7)$

$\underset{\alpha }{\min }\mathrm{L}\mathrm{v}\mathrm{a}\mathrm{l}\left({\omega }^{*}|(\alpha ,\beta ),\alpha ,\beta \right),(8)$

$\mathrm{s}.\mathrm{t}.{\omega }^{*}\left(\alpha \right)=\arg \underset{\omega }{\min }\mathrm{L}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\left(\omega ,\alpha \right),(9)$

${\omega }^{*}\left(\beta \right)=\arg \underset{\omega }{\min }\mathrm{L}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\left(\omega ,\beta \right).(10)$

3.2 The proposed method

In order to make the NAS process of the new modal fault diagnosis more efficient, this paper uses MAML to learn the design experience of previous modes and NAS, the new modal chemical process based on the learned design experience. In Subsection 3.1, MAML is trained on the training set to obtain the optimal initial parameters $\stackrel{\sim }{\omega }$ for fast adaptation in the new task. Similarly, the optimal network initial parameter $\stackrel{\sim }{\omega }$, operation weight initial parameter $\stackrel{\sim }{\alpha }$, and channel weight initial parameter $\stackrel{\sim }{\beta }$ are learned using the training set data in MetaNAS, which enables MetaNAS to quickly obtain a better model with a few steps of the gradient update on the new task, where the parameters $\stackrel{\sim }{\omega }$, $\stackrel{\sim }{\alpha }$, and $\stackrel{\sim }{\beta }$ are the NAS parameters defined in Subsection 2.1 and Subsection 3.1.

In order to learn the previous modal NAS design experience, this paper is based on the MAML strategy to learn the optimal NAS initial parameters $\stackrel{\sim }{\omega }$, $\stackrel{\sim }{\alpha }$, and $\stackrel{\sim }{\beta }$. Similar to AutoFD, the operation weight parameter $\alpha$, network parameter $\omega$, and channel weight parameter $\beta$ cannot be trained independently, so the initial parameters $\stackrel{\sim }{\omega }$, $\stackrel{\sim }{\alpha }$, and $\stackrel{\sim }{\beta }$ also need to be jointly optimized. In MetaNAS, the initial parameters $\stackrel{\sim }{\omega }$, $\stackrel{\sim }{\alpha }$, and $\stackrel{\sim }{\beta }$ are also solved by joint optimization. Eqs 1, 2 are used in subsection 2.1 to update the optimal initial parameters $\stackrel{\sim }{\omega }$, where Eq. 1 is used to update the internal parameters and Eq. 2 is used to update the external initial parameters, and similarly, MetaNAS contains two parts: internal parameter update and external initial parameter update. In the internal parameter update part, the NAS parameters $\omega$, $\alpha$, and $\beta$ are jointly optimized in a specific task $T_i^s$ according to the following equations:

${\omega }_i^{m+1}={\omega }_i^m-{\chi }_{inner}\frac{\partial L\left(g\left(T_i^s;{\alpha }_i^m,{\beta }_i^m,{\omega }_i^m\right)\right)}{\partial {\omega }_i^m},(11)$

${\alpha }_i^{m+1}={\alpha }_i^m-{\delta }_{inner}\frac{\partial L\left(g\left(T_i^s;{\alpha }_i^m,{\beta }_i^m,{\omega }_i^m\right)\right)}{\partial {\alpha }_i^m},(12)$

${\beta }_i^{m+1}={\beta }_i^m-{\epsilon }_{inner}\frac{\partial L\left(g\left(T_i^s;{\alpha }_i^m,{\beta }_i^m,{\omega }_i^m\right)\right)}{\partial {\beta }_i^m},(13)$

where ${\chi }_{inner}$ is the internal learning rate of the network parameter $\omega$, ${\delta }_{inner}$ is the internal learning rate of the operational weight parameter $\alpha$, ${\epsilon }_{inner}$ is the internal learning rate of the channel weight parameter $\beta$, and $g$ is the parameterization function of $\omega$, $\alpha$, and $\beta$; initially, $\left({\omega }_i^0=\stackrel{\sim }{\omega },{\alpha }_i^0=\stackrel{\sim }{\alpha },{\beta }_i^0=\stackrel{\sim }{\beta }\right)$. In the external parameter update, in order to obtain an optimal initial point, after M steps, the loss function $L\left(g\left(T_i^s;{\alpha }_i^m,{\beta }_i^m,{\omega }_i^m\right)\right)$ in task $T_i^q$ is calculated to jointly optimize the parameters $\stackrel{\sim }{\omega }$, $\stackrel{\sim }{\alpha }$, and $\stackrel{\sim }{\beta }$ according to the following equation:

$\stackrel{\sim }{\omega }=\stackrel{\sim }{\omega }-{\chi }_{outer}\frac{\partial {{\displaystyle \sum }}_{T_i^q\sim p\left(T\right)}L\left(g\left(T_i^q;{\alpha }_i^M,{\beta }_i^M,{\omega }_i^M\right)\right)}{\partial \stackrel{\sim }{\omega }},(14)$

$\stackrel{\sim }{\alpha }=\stackrel{\sim }{\alpha }-{\delta }_{outer}\frac{\partial {{\displaystyle \sum }}_{T_i^q\sim p\left(T\right)}L\left(g\left(T_i^q;{\alpha }_i^M,{\beta }_i^M,{\omega }_i^M\right)\right)}{\partial \stackrel{\sim }{\alpha }},(15)$

$\stackrel{\sim }{\beta }=\stackrel{\sim }{\beta }-{\epsilon }_{outer}\frac{\partial {{\displaystyle \sum }}_{T_i^q\sim p\left(T\right)}L\left(g\left(T_i^q;{\alpha }_i^M,{\beta }_i^M,{\omega }_i^M\right)\right)}{\partial \stackrel{\sim }{\beta }},(16)$

where ${\chi }_{outer}$ is the external learning rate of the network parameter $\stackrel{\sim }{\omega }$, ${\delta }_{outer}$ is the external learning rate of the operational weight parameter $\stackrel{\sim }{\alpha }$, and ${\epsilon }_{outer}$ is the external learning rate of the channel weight parameter $\stackrel{\sim }{\beta }$. When the results converge, the optimal initial parameters $\stackrel{\sim }{\omega }$, $\stackrel{\sim }{\alpha }$, and $\stackrel{\sim }{\beta }$ are obtained, and the new task is updated on the basis of the parameters $\stackrel{\sim }{\omega }$, $\stackrel{\sim }{\alpha }$, and $\stackrel{\sim }{\beta }$ to obtain better results quickly.

3.3 New modal fault online diagnosis steps

The new modal chemical process fault diagnosis algorithm proposed in this paper can be divided into four steps, namely, model construction, search phase, training and optimization phase, and real-time diagnosis, which are as follows:

Step 1. Model construction. The network model is a two-way branch linked by several convolutional neural network units, the network units within the branch and between the branches are linked by edge operations, the data to be processed are input at the beginning of the two branches, the fully connected layer for outputting fault diagnosis results is also connected at the end of the two branches, the said network units also include edge operations and nodes, the input within the unit is also divided into two ways, and the output is one way, the same as the network model in the AutoFD method.

Step 2. Search phase.

Step 2.1. The raw chemical production process data on multiple modes are normalized and dimensionally preprocessed to make data dimensions that satisfy the structural search of the meta-learning network.

Step 2.2. The pre-processed data are manipulated to form candidate channels for multi-channel convolution and are stitched with the preprocessed data to generate inputs for the network search phase.

Step 2.3. The candidate input channels are individually assigned weights to further obtain the mixed inputs.

Step 2.4. The set of candidate operations are defined, and a weight is assigned to each operation.

Step 2.5. Iterating steps 2.3 and 2.4 repeatedly, the Adam/SGD optimizer is chosen to adjust the network parameters, channel weight parameters, and operation weight parameters by using the cross-entropy loss function and backpropagation so as to obtain the optimal network initial parameters, channel optimal initial parameters, and operation optimal initial parameters as the initial parameters of the new mode.

Step 3. Training and optimization phase.

Step 3.1. Normalization and dimensional preprocessing are performed for the new modal chemical production process data so that the input data dimensions satisfy the meta-learning network structure search.

Step 3.2. The optimal network initial parameter $\stackrel{\sim }{\omega }$, optimal channel weight initial parameter $\stackrel{\sim }{\beta }$, and optimal operation weight initial parameter $\stackrel{\sim }{\alpha }$ are used as initial parameters to train the new modal chemical production process data into the network, and the optimized network parameter ${\omega }^{*}$, channel weight parameter ${\beta }^{*}$, and operation weight parameter ${\alpha }^{*}$ are obtained after training.

Step 3.3. The channel weight parameter ${\beta }^{*}$ and operation weight parameter ${\alpha }^{*}$ obtained by the aforementioned optimization are used to filter the selected convolutional channels and convolutional operations in the network, and obtain the fault diagnosis network model corresponding to the new mode.

Step 4. Real-time diagnosis. The data obtained in real time are normalized and preprocessed so that the input data dimensions of the network are satisfied. Then, the data are input into the obtained diagnosis network for real-time diagnosis.

4 Experimental verifications

For all datasets, in the network search phase, the same candidate operations, candidate convolution channels, and the structure of the network are used as in AutoFD, with candidate convolution channels. The network in the empirical phase of the learning design is determined by the operation weight parameter $\stackrel{\sim }{\alpha }$ and the channel weight parameter $\stackrel{\sim }{\beta }$. The candidate operations are as follows: 3 × 3 separable convolution, 5 × 5 separable convolution, 3 × 3 null convolution, 5 × 5 null convolution, 3 × 3 maximum pooling, 3 × 3 average pooling, keep the original input, and clear the original input. When there is a new task, the optimal network structures ${\alpha }_i^{*}$ and ${\beta }_i^{*}$ can be obtained by updating on the basis of the original network structure parameters.

The dataset is first divided into validation and test sets, and then, the training set is subdivided into training and validation sets, and the test set is subdivided into training and test sets, and the aforementioned four sets are noted as the training set in the training phase, validation set in the training phase, training set in the test phase, and test set in the test phase for easy distinction [31, 32].

First, in the training set of the training phase, K data are randomly selected from the selected N class samples as a task T. Then, in the validation set of the training phase, 10 data are randomly selected from each category sample as the test data in the training phase, so there should be N*(K+10) data in task T. In the NAS process, let the network training epoch be E1, and each time, first, S1 independent tasks are randomly selected, and then, the search training of the network is performed with these S1 tasks. In the internal search phase, the ordinary SGD is chosen to optimize the parameters of the network, the operation weight parameters, and the channel weight parameters, and the internal learning rates are set to ${\chi }_{inner}$, ${\delta }_{inner}$, and ${\epsilon }_{inner}$ in the internal sojourn phase, and the accuracy and efficiency of the network are weighed by adjusting the internal step size M. In the external search phase, the Adam optimizer is chosen to optimize the initial parameters of the network, the initial parameters of the operation weights, and the initial parameters of the channel weights, and the external learning rates are set to ${\chi }_{outer}$, ${\delta }_{outer}$, and ${\epsilon }_{outer}$. In the validation phase, first, K data are randomly selected from the samples of N classes as task T in the training set of the testing phase, so there should be N*(K + Q) data in task T. Let the network training epoch be E2 times, and each time, S2 independent tasks are randomly selected first, and the final accuracy is the average diagnostic accuracy of S2 independent tasks.

All training and verification experiments are completed on a PC equipped with Inteli7-10875H 2.30 GHz, 16 GB DDR4, WDC PCSN730, and NVIDIA GeForce RTX 2060. All Python codes are completed under the PyTorch framework, using the parallel acceleration capabilities provided by CUDA and cuDNN to achieve fast training and diagnostic tasks.

4.1 New modal fault online diagnosis steps

In this paper, a typical multimodal numerical simulation model proposed by Ge et al. [25] is taken for testing, which has been adopted by many scholars to verify the effectiveness of multimodal algorithms, and the specific structure of the model is denoted as follows:

$\begin{array}{l}{x}_1=0.5678s_1+0.3766s_2+e_1,\\ x_2=0.7382s_1+0.0566s_2+e_2,\\ x_3=0.8291s_1+0.4009s_2+e_3,\\ x_4=0.6519s_1+0.2070s_2+e_4,\\ x_5=0.3792s_1+0.8045s_2+e_5,\end{array}(17)$

where five variables $x_1$, $x_2$, $x_3$, $x_4$, and $x_5$ have different distributions of $s_1$ and $s_2$. $e_1$, $e_2$, $e_3$, $e_4$, and $e_5$ are five mutually independent noises that obey the Gaussian distribution with mean 0 and standard deviation 0.01. According to the two different distributions of $s_1$ and $s_2$, the model has two different modes, mode 1 (mode1) and mode 2 (mode2), which are represented as follows [26]:

$\begin{array}{l}\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}1s_1:U\left(-\mathrm{10,7}\right),s_2:N\left(-\mathrm{15,1}\right),\\ \mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}1s_1:U\left(\mathrm{2,5}\right),s_2:N\left(\mathrm{7,1}\right),\end{array}(18)$

where $U$ denotes uniform distribution and $N$ denotes Gaussian distribution; each measured data contain five moments of data $\left[d_1,d_2,d_3,d_4,d_5\right]$, and $d_i$ is $\left[x_1,x_2,x_3,x_4,x_5\right]$ for each moment; each data have 25 features; for each mode, first 1,000 normal samples are generated, followed by the next 1,000 samples generated as fault data, and the fault data are generated according to the following rules.

Fault 1: Addition of a step signal of amplitude 4 at the beginning of the 1001st sample.

Fault 2: Adding a ramp signal of 0.02 (i-400) at the beginning of the 1001st sample.

Fault 3: A sinusoidal signal with amplitude, offset, and frequency of 1 is added at the beginning of the 1001st sample.

Here, 1,000 data were generated for each mode of normal and fault 1, 2, and 3, respectively, where 4,000 data of mode1 were used as the training set and the data were divided into training and validation sets in the ratio of 7:3 to learn the optimal initial parameters. mode2 also contained 4,000 data, and the data were divided into training and test sets in the ratio of 7:3.

The dataset is divided according to the category $N=4$; the number of data items $K=10,50,100,\mathrm{a}\mathrm{n}\mathrm{d}150$; the network training epoch is $E_1=10$; the number of randomly selected independent tasks $S_1=100$; the internal learning rate ${\chi }_{innner}=0.05$, ${\delta }_{innner}=15$, and ${\epsilon }_{innner}=15$; the internal step size $M=4$; the external learning rate ${\chi }_{outer}={10}^{-3}$, ${\delta }_{outer}={10}^{-3}$, and ${\epsilon }_{outer}={10}^{-3}$; test data size $Q=150$ for the validation phase; $E_2=5$ for the network training epoch; and the number of randomly selected independent tasks $S_2=80$. The results of the numerical system multi-fault experiments are shown in Table 1 and Figure 2.

TABLE 1

TABLE 1. Multi-fault diagnosis accuracy of numerical simulation with different training set sizes.

FIGURE 2

FIGURE 2. Multi-fault diagnosis accuracy of numerical simulation with different training set sizes.

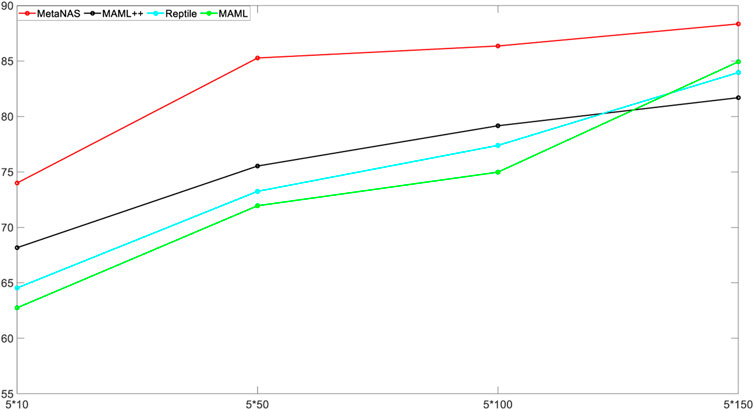
It can be seen that as the training set size increases on mode2 data, the amount of knowledge learned by each method from the data increases accordingly and the diagnostic accuracy of MetaNAS, MAML++ [21], Reptile [22], and MAML [19] also increases. The diagnostic accuracy of MetaNAS with a training set size of 3 × 10 was as high as 74%, while the highest of the compared methods was 68.17% for MAML++. The diagnostic accuracy of MetaNAS with a training set size of 3 × 50 was 85.27%, and none of the compared methods exceeded 76%. The diagnostic accuracy of MetaNAS with a training set size of 3 × 100 was 86.35%, and all the compared methods exceeded 80%. At a training set size of 3 × 150, the diagnostic accuracy of MetaNAS was 88.34%, and all the compared methods exceeded 84%. MetaNAS achieved the highest diagnostic accuracy in each category of the training set size.

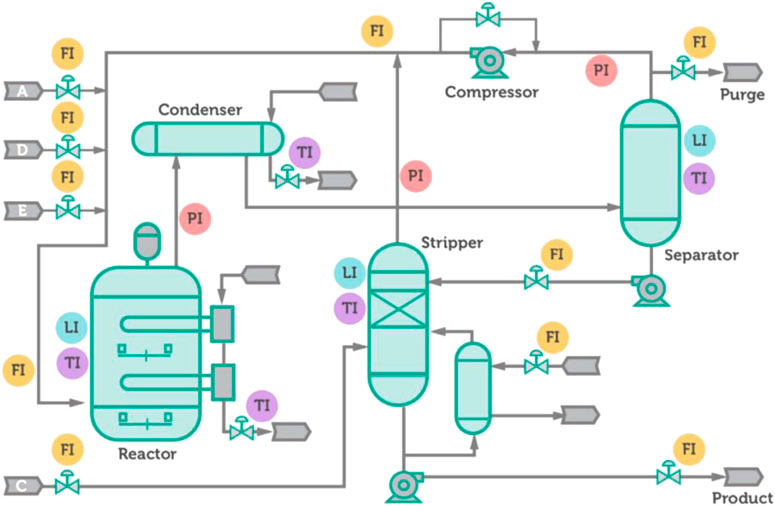
4.2 TE multi-modal simulation

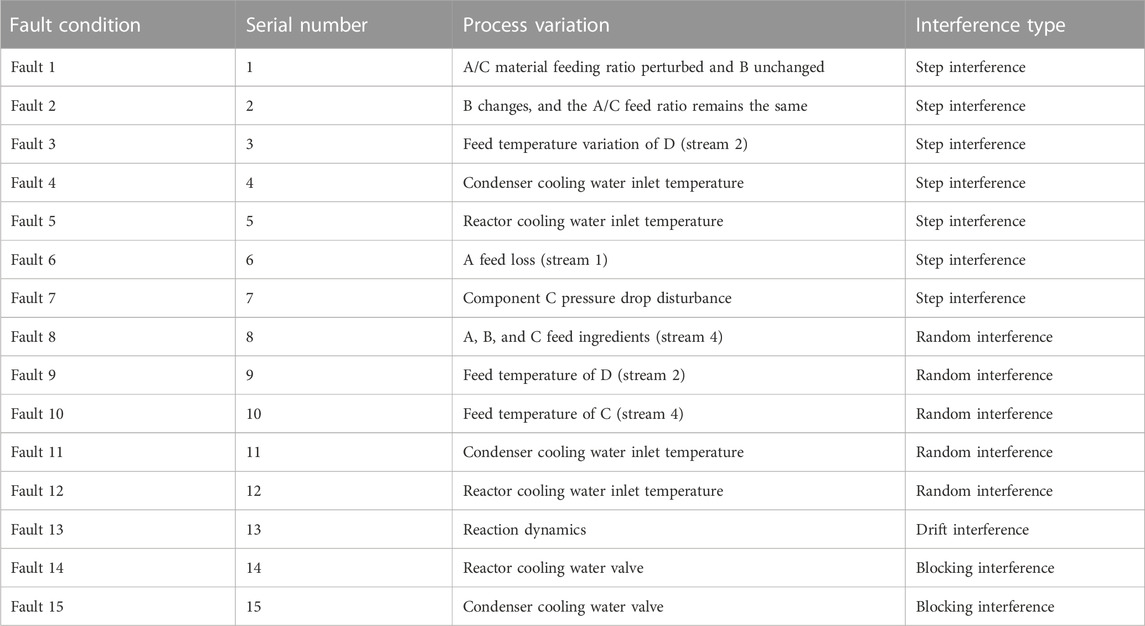
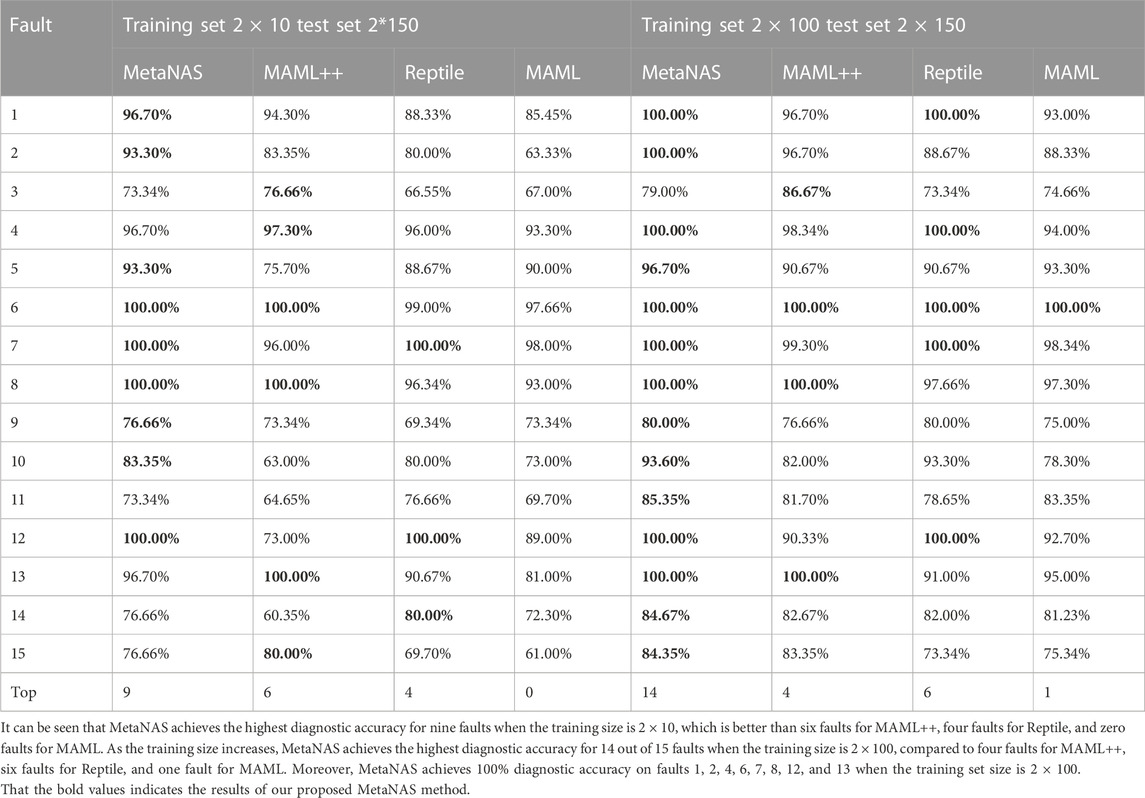
The TE chemical process is a standard experimental simulation platform. This paper adopts the TE simulation platform provided by http://depts.washington.edu/control/LARRY/TE/download.html. The TE process is presented in Figure 3. In the multimodal process fault diagnosis experimental study, the TE process simulation platform is set up with six G/H product ratios to obtain the process data under normal and fault conditions in six modes as mentioned in Table 2 and verify the performance of MetaNAS through multimodal TE process fault diagnosis experiments. In each mode normal operating condition, simulation for 72 h with a sampling interval of 3 min, 1,440 normal samples were obtained. In total, 15 kinds of faults were set when collecting fault samples, including seven step change faults (faults 1–7), five random change faults (faults 8–12), one slow drift fault (fault 13), and two blockage faults (faults 14 and 15); faults were introduced after 10 h of simulation in the normal operating condition, and the simulation was continued for 62 h with a sampling interval of 3 min, i.e., 200 normal samples and 1,220 fault samples were collected each time during the simulation of collecting fault samples.

FIGURE 3

FIGURE 3. Tennessee Eastman process.

TABLE 2

TABLE 2. TE operation mode single-fault description.

In the multimodal process fault diagnosis experiment, for the six modal process data obtained, 1,000 normal samples (6,000 normal samples) and 1,000 samples for each fault (i.e., 6,000 samples for each fault) are selected to form the dataset to be used; each data contains 12 operational variables and 41 process variables, and the variable dimension of each data is 53, which is filled with 0 at the end of the data and then converted into an 8 × 8 two-dimensional matrix as the candidate input of the network.

The data on modes 1, 2, 3, 4, and 5 were used as the training set, and the data on mode 6 were used as the test set. First, single-fault diagnosis experiments are performed on the multimodal dataset with the division N = 2; the number of data entries K = 10, 50, 100, and 150; $E_1=12$ for the network training epoch; the number of randomly selected independent tasks $S_1=200$; the internal learning rate ${\chi }_{inner}=0.05$, ${\delta }_{inner}=15$, and ${\epsilon }_{inner}=15$; the internal step size M = 4; the external learning rate ${\chi }_{outer}={10}^{-3}$, ${\delta }_{outer}={10}^{-3}$, and ${\epsilon }_{outer}={10}^{-3}$; the test data size Q = 150 in the validation phase; $E_2=6$ in the network training epoch, and the number of randomly selected independent tasks $S_2=90$; the results of the single-fault diagnosis are shown in Table 3.

TABLE 3

TABLE 3. TE single-fault diagnosis accuracy with different training set sizes.

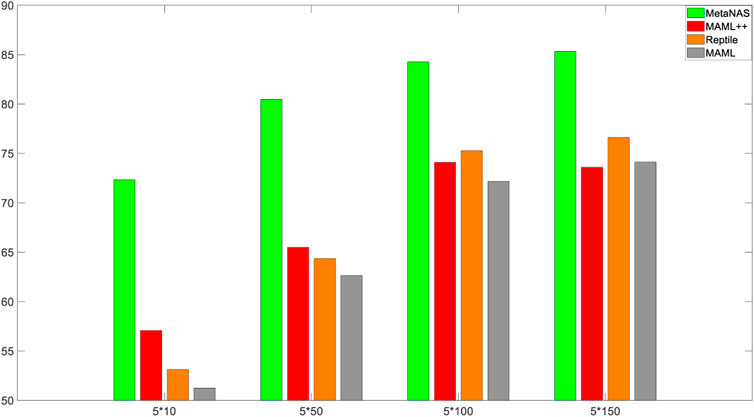
Then, the multimodal dataset is subjected to multiple fault diagnosis experiments, and a total of five operating conditions, normal 0, fault 1, fault 8, fault 13, and fault 15, are selected as the study objects, covering common step disturbances, random disturbances, drift disturbances, blocking disturbances, and other faults. The division of the dataset N = 5; the number of data entries K = 10, 50, 100, and 150; the training epoch $E_1=10$; the number of randomly selected independent tasks $S_1=500$; the internal learning rate ${\chi }_{inner}=0.1$, ${\delta }_{inner}=30$, and ${\epsilon }_{inner}=30$; the internal step size M = 5; the external learning rate ${\chi }_{outer}={10}^{-3}$, ${\delta }_{outer}={10}^{-3}$, and ${\epsilon }_{outer}={10}^{-3}$; the test data size Q = 150 in the validation phase; the training epoch $E_2=10$; and the number of randomly selected independent tasks $S_2=100$; the multi-fault diagnosis results are shown in Table 4 and Figure 4.

TABLE 4

TABLE 4. TE multi-fault diagnosis accuracy with different training set sizes.

FIGURE 4

FIGURE 4. TE multi-fault diagnosis accuracy with different training set sizes.

It can be seen that the diagnostic accuracy of MetaNAS, MAML++, Reptile, and MAML increases as the size of the mode6 training set increases. The diagnostic accuracy of MetaNAS with a training set size of 5 × 10 is 72.35%, while the highest diagnostic accuracy of the comparison method is 57.07% for MAML++. The diagnostic accuracy of MetaNAS with a training set size of 5 × 50 is 80.47%, while the comparison method does not exceed 66%. The diagnostic accuracy of MetaNAS with a training set size of 5 × 100 is 84.29%, and the comparison methods are all over 76%. The diagnostic accuracy of MetaNAS with a training set size of 5 × 150 is 85.34%, and all the comparison methods exceed 77%. MetaNAS achieves the highest diagnostic accuracy in each category of the training set size.

Because MetaNAS has the advantage of using design experience to design a unique network structure for new modes, unlike MAML++, Reptile, and MAML, which use fixed network models, it usually requires additional time overhead for network model generation. During TE multi-fault experiments, the number of model parameters of MetaNAS, MAML, MAML++, and Reptile are 2.4 megabytes, 3.2 megabytes, 3.2 megabytes, 3.2 megabytes, and 3.2 megabytes, respectively, and MetaNAS takes about 1.5 s more than MAML for network model generation in each batch during the validation phase, where the number of model parameters is calculated by the thop.profile () function and the model runtime is calculated by the time.time () function.

Summarizing the aforementioned three experiments, it can be concluded that the diagnostic accuracy of MetaNAS is higher than that of the compared MAML++, Reptile, and MAML methods in most faults. MetaNAS uses AutoFD for NAS based on MAML, which provides a rich candidate network structure for MAML and solves the problem of a single meta-learning network structure, and MetaNAS’s network model does not require a complex and time-consuming design process. Comparing the results of MetaNAS and MAML in the three experimental results, we can see that the diagnostic results of MetaNAS are higher than those of the base method MAML in the case of different training set sizes of the same dataset, which indicates that MetaNAS can obtain better fault diagnosis capability after adding AutoFD because the network model structure can be learned, and the fault diagnosis results of MetaNAS in many faults are better than those of MAML++ and the Reptile algorithm, which are improved on the basis of MAML, proving the effectiveness of the MetaNAS method.

5 Conclusion

The MetaNAS method is proposed to find the optimal initial parameters to be learned in NAS by meta-learning, and the new mode can find the best performing network structure with only a few gradient updates based on the optimal initial parameters. MetaNAS uses NAS to provide a rich learnable network architecture for meta-learning method so that the network structure of meta-learning is no single. It also automates the network design, making it possible to quickly obtain fault diagnosis models with better performance even for new modes with small samples. MetaNAS solves the limitations to fault diagnosis through NAS, such as underutilization of the existing modal design experience and difficulty in training models with small samples. The effectiveness and superiority of the proposed method in fault diagnosis under the small samples of new models are demonstrated by numerical system and TE process simulations. However, the existing model design experiences are obtained from different modes of the same chemical process, and the learning of different industrial process model design experiences is lacking. The next work will focus on the study of learning algorithms about different industrial process model design experiences and NAS algorithms on unbalanced datasets.

Moving forward, there are several potential avenues for future research and improvement. First, expanding the application of MetaNAS to different fault diagnosis domains and datasets would provide a broader evaluation of its effectiveness and generalizability. Second, investigating the integration of additional data sources or modalities could enhance the diagnostic capabilities of MetaNAS. Furthermore, exploring the interpretability of the MetaNAS approach is an important direction for future research. Last, considering the scalability of the MetaNAS approach to handle larger and more complex fault diagnosis tasks would be valuable. By pursuing these future research directions, we can further advance the field of real-time fault diagnosis with small sample learning and continue to improve the performance, applicability, and interpretability of the MetaNAS approach.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

Conceptualization, TL; software, JH; methodology, SR. All authors contributed to the article and approved the submitted version.

Funding

The study was supported by Shaanxi Provincial Science and Technology Department: 2023-JC-YB-547.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhao K, Hu J, Shao H, Hu J. Federated multi-source domain adversarial adaptation framework for machinery fault diagnosis with data privacy. Reliability Eng Syst Saf (2023) 236:109246. doi:10.1016/j.ress.2023.109246

CrossRef Full Text | Google Scholar

2. Liu Y, Zeng J, Bao J, Xie L. A unified probabilistic monitoring framework for multimode processes based on probabilistic linear discriminant analysis. IEEE Trans Ind Inform (2020) 16(10):6291–300. doi:10.1109/tii.2020.2966707

CrossRef Full Text | Google Scholar

3. Zhang J, Zhou D, Chen M. Monitoring multimode processes: A modified PCA algorithm with continual learning ability. J Process Control (2021) 103:76–86. doi:10.1016/j.jprocont.2021.05.007

CrossRef Full Text | Google Scholar

4. Dong J, Zhang C, Peng K. A new multimode process monitoring method based on a hierarchical Dirichlet process—hidden semi-markov model with application to the hot steel strip mill process. Control Eng Pract (2021) 110:104767. doi:10.1016/j.conengprac.2021.104767

CrossRef Full Text | Google Scholar

5. Jin B, Cruz L, Gonçalves N. Pseudo RGB-D face recognition. IEEE Sensors J (2022) 22(22):21780–94. doi:10.1109/jsen.2022.3197235

CrossRef Full Text | Google Scholar

6. Jiang Q, Yan X. Multimode process monitoring using variational Bayesian inference and canonical correlation analysis. IEEE Trans Automation Sci Eng (2019) 16(4):1814–24. doi:10.1109/tase.2019.2897477

CrossRef Full Text | Google Scholar

7. Yang C, Zhou L, Huang K, Ji H, Long C, Chen X, et al. Multimode process monitoring based on robust dictionary learning with application to aluminium electrolysis process. Neurocomputing (2019) 332:305–19. doi:10.1016/j.neucom.2018.12.024

CrossRef Full Text | Google Scholar

8. Zhao K, Jiang H, Wang K, Pei Z. Joint distribution adaptation network with adversarial learning for rolling bearing fault diagnosis. Knowledge-Based Syst (2021) 222:106974. doi:10.1016/j.knosys.2021.106974

CrossRef Full Text | Google Scholar

9. Zhao SJ, Zhang J, Xu YM. Performance monitoring of processes with multiple operating modes through multiple PLS models. J process Control (2006) 16(7):763–72. doi:10.1016/j.jprocont.2005.12.002

CrossRef Full Text | Google Scholar

10. Jin B, Cruz L, Gonçalves N. Deep facial diagnosis: Deep transfer learning from face recognition to facial diagnosis. IEEE Access (2020) 8:123649–61. doi:10.1109/access.2020.3005687

CrossRef Full Text | Google Scholar

11. Wang F, Tan S, Peng J, Chang Y. Process monitoring based on mode identification for multi-mode process with transitions. Chemometrics Intell Lab Syst (2012) 110(1):144–55. doi:10.1016/j.chemolab.2011.10.013

CrossRef Full Text | Google Scholar

12. Zhao K, Jiang H, Liu C, Wang Y, Zhu K. A new data generation approach with modified Wasserstein auto-encoder for rotating machinery fault diagnosis with limited fault data. Knowledge-Based Syst (2022) 238:107892. doi:10.1016/j.knosys.2021.107892

CrossRef Full Text | Google Scholar

13. Yao R, Jiang H, Li X, Cao J. Bearing incipient fault feature extraction using adaptive period matching enhanced sparse representation. Mech Syst Signal Process (2022) 166:108467. doi:10.1016/j.ymssp.2021.108467

CrossRef Full Text | Google Scholar

14. Wang Y, Yao Q, Kwok JT, Ni LM. Generalizing from a few examples: A survey on few-shot learning. ACM Comput Surv (Csur) (2020) 53(3):1–34. doi:10.1145/3386252

CrossRef Full Text | Google Scholar

15. Benaim S, Wolf L. One-shot unsupervised cross domain translation. Adv Neural Inf Process Syst (2018) 31. doi:10.48550/arXiv.1806.06029

CrossRef Full Text | Google Scholar

16. Riaz S, Qi R, Tutsoy O, Iqbal J. A novel adaptive PD-type iterative learning control of the PMSM servo system with the friction uncertainty in low speeds. PloS one (2023) 18(1):e0279253. doi:10.1371/journal.pone.0279253

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bertinetto L, Henriques JF, Valmadre J, Torr P, Vedaldi A. Learning feed-forward one-shot learners. Adv Neural Inf Process Syst (2016) 29. doi:10.48550/arXiv.1606.05233

CrossRef Full Text | Google Scholar

18. Riaz S, Lin H, Waqas M, Afzal F, Wang K, Saeed N. An accelerated error convergence design criterion and implementation of lebesgue-p norm ILC control topology for linear position control systems. Math Probl Eng (2021) 2021:1–12. doi:10.1155/2021/5975158

CrossRef Full Text | Google Scholar

19. Zhao K, Jia F, Shao H. A novel conditional weighting transfer Wasserstein auto-encoder for rolling bearing fault diagnosis with multi-source domains. Knowledge-Based Syst (2023) 262:110203. doi:10.1016/j.knosys.2022.110203

CrossRef Full Text | Google Scholar

20. Hariharan B, Girshick R. Low-shot visual recognition by shrinking and hallucinating features. In: Proceedings of the IEEE international conference on computer vision; 22-29 Oct. 2017; Venice, Italy (2017).

CrossRef Full Text | Google Scholar

21. Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks. In: International conference on machine learning; August 6th to August 11th, 2017; Sydney, Australia (2017).

Google Scholar

22. Riaz S, Lin H, Elahi H. A novel fast error convergence approach for an optimal iterative learning controller. Integrated Ferroelectrics (2020) 213(1):103–15. doi:10.1080/10584587.2020.1859828

CrossRef Full Text | Google Scholar

23. Al-Shedivat M, Bansal T, Burda Y, Sutskever I, Mordatch I, Abbeel P. Continuous adaptation via meta-learning in nonstationary and competitive environments. (2017) arXiv preprint arXiv:171003641 2017.

Google Scholar

24. Antoniou A, Storkey AJ. Learning to learn by self-critique. Adv Neural Inf Process Syst (2019) 32. doi:10.48550/arXiv.1905.10295

CrossRef Full Text | Google Scholar

25. Riaz S, Lin H, Mahsud M, Afzal D, Alsinai A, Cancan M. An improved fast error convergence topology for PDα-type fractional-order ILC. J Interdiscip Math (2021) 24(7):2005–19. doi:10.1080/09720502.2021.1984567

CrossRef Full Text | Google Scholar

26. Nichol A, Achiam J, Schulman J. On first-order meta-learning algorithms. (2018) arXiv preprint arXiv:180302999 2018.

Google Scholar

27. Yan K, Ji Z, Shen W. Online fault detection methods for chillers combining extended kalman filter and recursive one-class SVM. Neurocomputing (2017) 228:205–12. doi:10.1016/j.neucom.2016.09.076

CrossRef Full Text | Google Scholar

28. Yan K, Ji Z, Lu H, Huang J, Shen W, Xue Y. Fast and accurate classification of time series data using extended ELM: Application in fault diagnosis of air handling units. IEEE Trans Syst Man, Cybernetics: Syst (2017) 49(7):1349–56. doi:10.1109/tsmc.2017.2691774

CrossRef Full Text | Google Scholar

29. Yan C, Chang X, Li Z, Guan W, Ge Z, Zhu L, et al. Zeronas: Differentiable generative adversarial networks search for zero-shot learning. IEEE Trans pattern Anal machine intelligence (2021) 44(12):9733–40. doi:10.1109/tpami.2021.3127346

CrossRef Full Text | Google Scholar

30. Li M, Huang P-Y, Chang X, Hu J, Yang Y, Hauptmann A. Video pivoting unsupervised multi-modal machine translation. IEEE Trans Pattern Anal Machine Intelligence (2022) 45:3918. doi:10.1109/TPAMI.2022.3181116

CrossRef Full Text | Google Scholar

31. Zhang L, Chang X, Liu J, Luo M, Li Z, Yao L, et al. TN-ZSTAD: Transferable network for zero-shot temporal activity detection. IEEE Trans Pattern Anal Machine Intelligence (2022) 45:3848–61. doi:10.1109/tpami.2022.3183586

CrossRef Full Text | Google Scholar

32. Chang X, Ren P, Xu P, Li Z, Chen X, Hauptmann A. A comprehensive survey of scene graphs: Generation and application. IEEE Trans Pattern Anal Machine Intelligence (2021) 45(1):1–26. doi:10.1109/tpami.2021.3137605

CrossRef Full Text | Google Scholar