Photonic crystal fiber with double-layer rings for the transmission of orbital angular momentum

In this paper, we propose a novel photonic crystal fiber (PCF) with double-layer rings for transmitting orbital angular momentum (OAM). The substrate of PCF is a pure silicon base. The inner circle is doped with Fluoride to reduce the refractive index (RI), and the transmission domain is doped with Germanium dioxide to increase the RI. On the outer side of the transmission ring, air holes are regularly arranged to restrict the beam transmission within the transmission layer. After calculation, the proposed OAM fiber can effectively support 118 OAM modes in the range of 1.3–1.75 μm with excellent characteristics. In addition, we also found that proposed fiber has “bandgap-like” mode field characteristics.

1 Introduction

Optical communication is one of the important communication methods, and is highly favored with its high capacity and high speed. In recent years, conventional optical communication technology is getting closer to Shannon’s limit. Therefore, wavelength division multiplexing (WDM) [1], mode division multiplexing (MDM) [2] and other multiplexing technologies have become the primary directions of optical communication. Among them, orbital angular momentum (OAM) beam is an excellent carrier beam [3–5]. OAM was proposed by Allen [6] in 1992 and has made a big splash in the field of optical communication. The vortex beam has the phase factor of e^ilφ and the phase distribution is vortex-shaped. Most importantly, OAM theoretically has infinite orthogonal modes in Hilbert space, which provides a very ideal transmission channel for optical communication.

In recent years, the research of OAM transmission fibers has focused on ring core fibers (RCFs) and photonic crystal fibers (PCFs).OAM-RCFs include step index RCF [7], graded index RCF [8], refractive index modulated (RI- modulated) RCF [9], etc. OAM-RCFs improve the characteristics by making corresponding changes of transmission layer rings to make them more compatible with OAM transmission. The design principle of OAM-PCF is that the periodic arrangement of air holes restricts the beam propagating in the fiber core. By adjusting the number [10], arrangement [11], shape [12] of air holes, the supported OAM number by the fiber is greatly increased. There are also some studies on setting transmission rings in PCF, which are RI-modulated. The transmission layer works with the air holes to confine the beam. The fiber combining RCF and PCF has good characteristics for transmitting OAM. In addition, some special rotating fibers [13] also have unique advantages in transmitting OAM.

In this paper, we propose a PCF containing a double layer of rings. The inner ring is doped with Fluoride to reduce the RI, and the transmission layer is doped with Germanium dioxide to increase the RI. Air holes are regularly arranged on the outside of the transmission layer to restrict the beam within the transmission layer. After calculation, our proposed fiber can support 118 OAM modes in the range of 1.3 μm–1.75 μm and has excellent features such as large mode field and flat dispersion. In addition, proposed fiber also shows characteristics of “bandgap-like PCF".

2 Structure of the designed PCF with double-layer rings

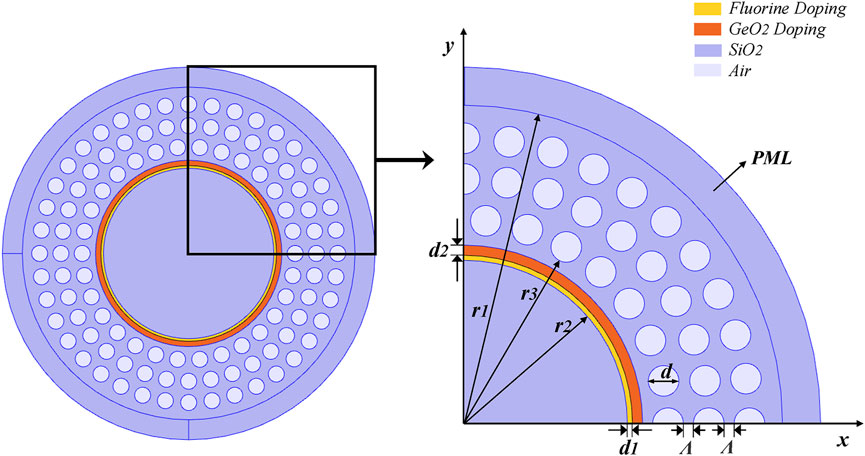
The schematic diagram of our proposed OAM fiber with double layer rings is shown in Figure 1. We dope two layers of rings in the silicon-based PCF. The inner ring is fluoride doped to reduce the RI, and the outer ring is germaniμm dioxide doped to improve the RI. The double-layer circular structure fiber effectively improves the RI difference between the transmission layer and the substrate. The radius of the fiber cladding r1 is 62.5 μm r2 is 32 μm, and the thickness of the fluoride doped layer is d1 = 1 μm with a RI of 1.43. The thickness of the high refractive index layer (HRIL) of the germanium dioxide doped layer is d2 = 2 μm with a RI of 1.48.

FIGURE 1

FIGURE 1. The schematic diagram of proposed OAM fiber with double-layer rings.

Outside the HRIL we set the air holes arranged periodically. r3 is 37 μm, and the diameter of the air holes d is 6 μm. The air hole spacing Λ is 2 μm. The number of air holes from the inner layer to the outer layer is 30, 36, and 40. In the outermost layer, we set the perfect match layer (PML) with a thickness of 7.5 μm. PML acts as a near-ideal absorber or radiator domain. Therefore, PML reduces the influence of beam reflection and improves the calculation accuracy.

3 Characteristics of PCF with double-layer rings

3.1 Number of OAM modes

According to the fiber coupling mode theory, OAM can be formed by coupling the even and the odd mode of the same vector mode in the fiber [14]:

$\left\{\begin{array}{c}{\sigma }^{\pm }OA{M}_{\pm l}=H{E}_{l+\mathrm{1,1}}^{even}\pm jH{E}_{l+\mathrm{1,1}}^{odd}\\ {\sigma }^{\mp }OA{M}_{\pm l}=E{H}_{l-\mathrm{1,1}}^{even}\pm jE{H}_{l-\mathrm{1,1}}^{odd}\end{array}\right.(1)$

where l represents the order of the OAM and vector modes. The positive and negative of σ represents the spin direction. even and odd denote the even and odd modes of the vector modes, respectively. The imaginary number j represents the phase difference of π/2.

In the field of optical communication, increasing the communication capacity is very important. And using OAM as a transmission carrier, the number of modes determines the communication capacity. For OAM transmission fibers, increasing the RI of the transmission layer will increase the OAM numbers. But this results in higher losses. For example, Sulfur-based doping is chosen as the HRIL. Although this increases the number of supported OAM modes, it raises the confinement loss (CL), which is not conducive to the long-distance transmission of the beam.

The purpose of our design is to reduce the RI difference between the transmission layer and the substrate as much as possible if the loss caused by the doped HRIL is acceptable. This will result in a significant improvement in the number of transmission modes. The outer ring is doped with Germanium dioxide and HRILis doped with Fluoride. On the outside of the HRIL, air holes are periodically arranged, which can reduce the RI of the substrate. Figure 2 shows the mode field distribution of higher order modes. After calculation, the OAM fiber can effectively support 118 modes in range of 1.3 μm–1.75 μm.

FIGURE 2

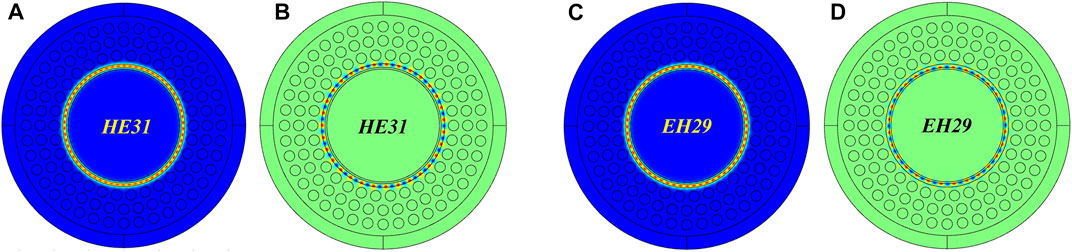
FIGURE 2. (A) Mode field distribution of HE_31,1. (B) Z-direction electric field of HE_31,1. (C) Mode field distribution of EH_29,1. (D) Z-direction electric field of EH_29,1.

3.2 Effective refractive index and its differences

We analyzed the supported modes from 1,300 nm to 1750 nm. The effective refractive index (ERI) is defined as:

$n_{eff}=\frac{\beta }{k_0}(2)$

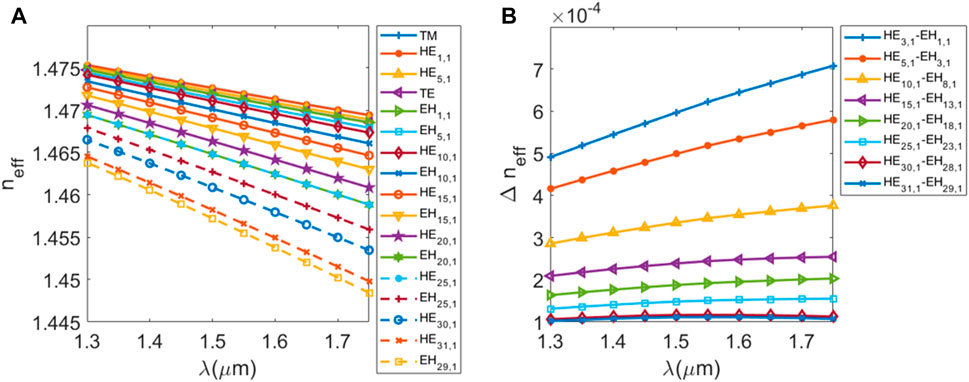
where β is the propagation constant, k₀ is the wave number in a vacuum. Figure 3A shows the variation of the ERI with wavelength for some vector modes. As the wavelength increases, the ERI of the vector modes all decrease. Among them, the ERI of the higher-order mode EH_29,1 is the lowest, and the ERI is 1.44832 at 1.75 μm. In addition, the ERI’s variation between different wavelengths of the same mode increases gradually as the mode order rises.

FIGURE 3

FIGURE 3. (A) n_eff of the some vector modes. (B) Δn_eff of some vector modes.

ERID reflects the quality of the OAM formed by vector mode coupling. According to the fiber degeneracy mode theory, HE_l+1,1 and EH_l-1,1 will degenerate when the ERI is close to forming the LP mode. This is unfavorable for the formation of OAM because we prefer the coupling of odd and even modes of the same vector mode. It is generally believed that when the ERID of HE_l+1,1 and EH_l-1,1 is above 10^–4, the formation of LP mode will be avoided. Figure 3B shows the variation of ERID with wavelength. The ERID decreases as the mode order increases. Among them, the ERID between HE_31,1 and EH_29,1 is the lowest to 0.000102. Although the model we designed can also support higher-order vector modes, we discarded them because they do not satisfy the ERID condition for forming OAM.

3.2.1 Confinement loss

The CL reflects the loss of the light propagating through the fiber. The CL is defined as [15, 16]:

$CL=-\frac{2\pi }{\lambda }\frac{20}{\ln \left(10\right)}{10}^{6}Im\left(n_{eff}\right)\left(dB/m\right)(3)$

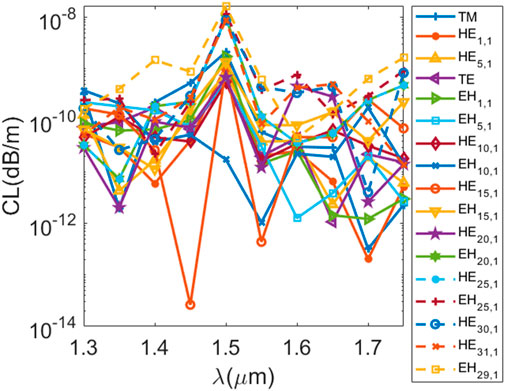
where λ is wavelength, and Im(n_eff) is the imaginary part of the n_eff. Figure 4 shows the CL’s variation of some vector modes over wavelength. For wavelength from 1.3 μm to 1.75 μm, the CL of most vector modes oscillates in the range of 10^–11–10^–9 dB/m. The lower transmission loss can ensure more effective transmission of information. Table 1 shows the number of OAM modes and CL of other OAM fibers. It indicates that the number of OAM modes supported by designed OAM fiber is higher, and the CL is smaller.

FIGURE 4

FIGURE 4. CL of some vector modes.

TABLE 1

TABLE 1. The number of OAM modes and CL of the recently proposed OAM fiber.

Theoretically, light is confined inside transmission layer owe to the HRIL [17, 18], but it will also be leaked out inevitably because the outer layer of the HRIL is a silicon-based substrate with higher RI than the inner low refractive index layer (LRIL), and the leakage from the outer layer will be more serious. Air holes outside the HRIL can effectively prevent the leakage of light waves and thus reduce CL.

3.3 Effective mode area and nonlinear coefficient

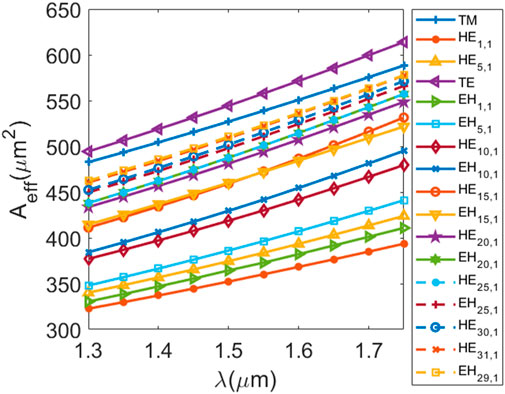
The effective mode area (EMA) and nonlinear coefficient are important parameters to evaluate the beam propagation quality [19]. The EMA represents the energy concentration, and the nonlinear coefficient is used to characterize the nonlinear effect of the fiber [20]. Since the effective mode field area is inversely proportional to the nonlinear coefficient, we need to increase the effective mode field area in optical communication. The higher effective mode field area and the lower nonlinear coefficient improve the optical signal-to-noise ratio. The EMA is given by [21, 22]:

$A_{eff}=\frac{{\left(\iint {\left|E\left(x,y\right)\right|}^{2}dxdy\right)}^2}{{\iint \left|E\left(x,y\right)\right|}^{4}dxdy}(4)$

where $E\left(x,y\right)$ is the field distribution of the transverse electric field. The nonlinear coefficient is defined as [21]:

$\gamma =\frac{2\pi n_2}{\lambda A_{eff}}(5)$

where n₂ is the nonlinear index for fused silica, and n₂ = $2.6\times {10}^{-20}{m}^2{W}^{-1}$. Figure 5 shows the variation of the EMA with wavelength for some modes. The EMA becomes larger with the increase of mode order. The EMA of all vector modes is above 320 μm², and the EMA of HE_31,1 reaches 577.763 μm² at 1.75 μm. The greater EMA reflects the higher energy concentration and smaller nonlinear coefficient.

FIGURE 5

FIGURE 5. EMA of some vector modes.

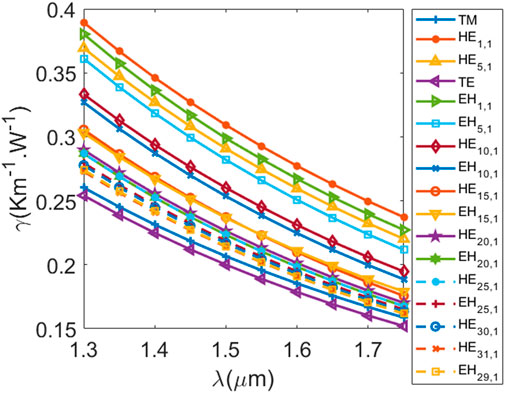
Figure 6 shows the nonlinear coefficient variation of some modes over wavelength. As the wavelength increases, the nonlinear coefficient decreases. In addition, the nonlinear coefficient decreases with the mode order, which indicates that the nonlinear effect of the higher-order mode is weaker and more conducive to transmission. The nonlinear coefficients are all below 0.4 km^-1 W⁻¹, which indicates the OAM mode supported by proposed fiber has good transmission characteristics.

FIGURE 6

FIGURE 6. Nonlinear coefficient of some vector modes.

3.3.1 Dispersion

In optical communications, dispersion has a significant effect on the efficiency of information transmission. A large dispersion causes a high delay. The definition of dispersion is [23]:

$D=-\frac{\lambda }{c}\frac{{\partial }^2{n}_{eff}}{\partial {\lambda }^2}(6)$

Where $\lambda$ is the wavelength, and $c$ is the speed of light in a vacuum. Figure 7 shows the variation of partial vector mode dispersion with wavelength. When the mode’s order is below HE_16,1 and EH_14,1, the dispersion is negative. When the order is higher than these two modes, the dispersion value is positive. And the absolute value of dispersion increases with the wavelength. The positive and negative distribution of dispersion is beneficial to the dispersion compensation of optical communication network and can improve the accuracy of information transmission.

FIGURE 7

FIGURE 7. Dispersion of some vector modes.

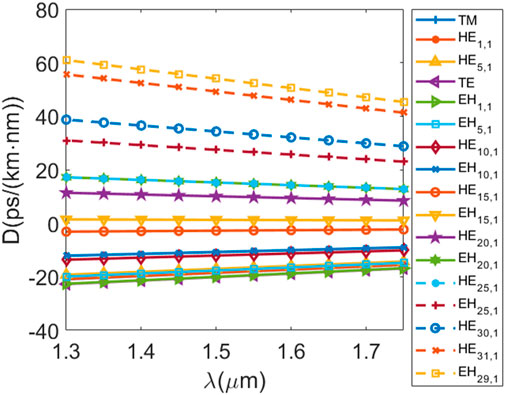
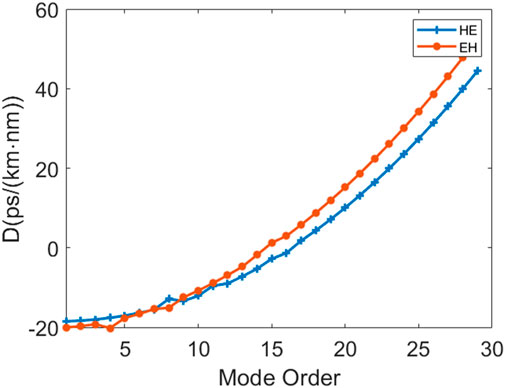
In addition, the vector mode has a smaller dispersion and a flat variation. In the calculated band, the HE_31,1 mode has the highest absolute dispersion value of 60.962 ps/(km·nm) at 1.75 μm and a flat dispersion curve slope of 0.00348 ps/(km·nm²). Figure 8 shows the variation of dispersion value with mode order for all vector modes at 1.55 μm. The dispersion values show a monotonic increase with the increase of mode order.

FIGURE 8

FIGURE 8. Dispersion values for all vector modes at 1550 nm.

4 “Bandgap-like” properties of OAM fiber

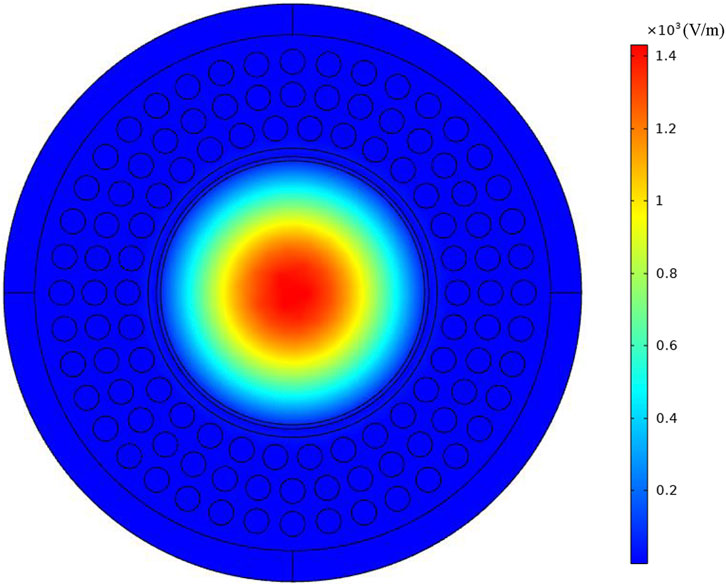
Due to the LRIL in proposed fiber, the fiber exhibits the characteristics of a bandgap-PCF. We call this property “bandgap-like”. Figure 9 shows the fundamental mode of the bandgap-like mode field. The main feature is that the beam propagates on a pure silicon-based substrate with a LRIL doped with fluoride in its outer layer. Intuitively, the beam appears to be confined by the LRIL, like light propagating through air in a bandgap PCF. The ERI of the bandgap-like mode is lower than the normal vector mode. The fundamental mode of the bandgap-like mode starts to appear at 1,550 nm when the ERI is 1.44389.

FIGURE 9

FIGURE 9. Base-mode of bandgap-like fiber.

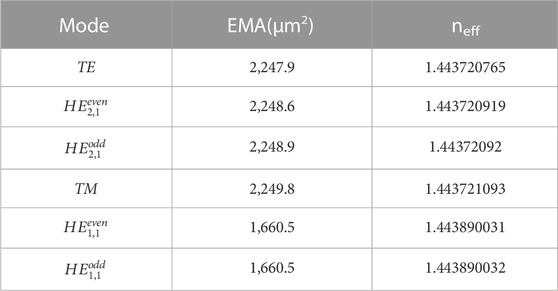
These bandgap-like modes propagate at the central base with a large EMA. Table 2 shows the EMA and ERI of some bandgap-like modes. Furthermore, these modes are highly degenerate. According to fiber mode theory, the ERI of vector modes that degenerate to form the same LP mode are very close. Figure 10 shows the mode field distribution of the “bandgap-like” vector modes and their polarization direction. The white arrow shows the polarization direction of the electric field. Combined with the optical fiber mode theory, we can analyze the beam mode by the polarization of the electric field. The bandgap-like mode ${\mathrm{H}\mathrm{E}}_{\mathrm{2,1}}^{\mathrm{o}\mathrm{d}\mathrm{d}}$, ${\mathrm{H}\mathrm{E}}_{\mathrm{2,1}}^{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}$, TM and TE have a very low difference in ERI, which is consistent with this feature. Although this “bandgap-like” mode cannot be used to form OAM mode, its large EMA and highly degenerate properties make it unique. “Bandgap-like” mode of proposed fiber can be used for optical communication because of its large field area.

TABLE 2

TABLE 2. The EMA and ERI of some of the bandgap-like modes.

FIGURE 10

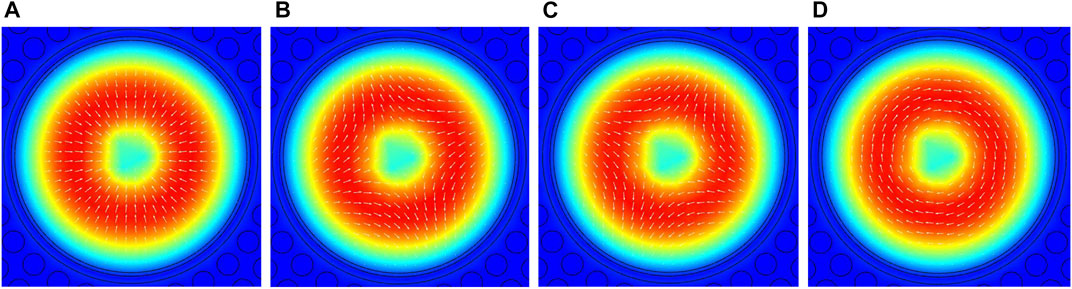
FIGURE 10. Mode field distribution of the bandgap-like vector mode and its polarization direction. (A) TM (B) ${\mathrm{H}\mathrm{E}}_{\mathrm{2,1}}^{\mathrm{o}\mathrm{d}\mathrm{d}}$ (C) ${\mathrm{H}\mathrm{E}}_{\mathrm{2,1}}^{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}$ (D) TE.

5 Conclusion

In this paper, we propose a PCF fiber with double-layer rings for transmitting OAM. The RI is modulated by different doping of the rings. This increases the RI difference between the transmission layer and the substrate, increasing the supported OAM numbers. The regular arrangement of air holes also restricts the light beam. After calculation, the fiber can support 118 OAM modes in the range of 1.3–1.75 μm. The CL of most vector modes oscillates in the range of 10^–11–10^–9 dB/m. The EMA of all vector modes is above 320μm², and the nonlinear coefficients of all modes are below 0.4 km^-1 W⁻¹. The dispersion value is small and changes gently. In addition, the “bandgap-like” mode field appears in the optical fiber, which is characterized by large EMA and high degeneracy.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XQ proposed the idea and wrote this manuscript, YL revised the manuscript. All authors contributed to the article and approved the submitted version.

Acknowledgments

We are grateful to the people in the laboratory who have helped us. The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (61905062).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1207182/full#supplementary-material

References

1. Zhu L, Zhu G, Wang A, Wang L, Ai J, Chen S. 18 km low-crosstalk OAM + WDM transmission with 224 individual channels enabled by a ring-core fiber with large high-order mode group separation. Opt Lett (2018) 43(8):1890–3. doi:10.1364/OL.43.001890

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhu J, Zuo M, Yang Y, Ge D, Shen L, Chen Z, et al. Multiple-ring-core FM-EDF for weakly-coupled MDM amplification with low differential modal gain. IEEE Photon J (2021) 13(1):7100511. doi:10.1109/JPHOT.2021.3051455

CrossRef Full Text | Google Scholar

3. Lian Y, Qi X, Wang Y, Bai Z, Wang Y, Lu Z. OAM beam generation in space and its application. Opt Lasers Eng (2022) 151:106923. doi:10.1016/j.optlaseng.2021.106923

CrossRef Full Text | Google Scholar

4. Ma M, Lian Y, Wang Y, Lu Z. Generation, transmission and application of orbital angular momentum in optical fiber: A review. Front Phys (2021) 9:773505. doi:10.3389/fphy.2021.773505

CrossRef Full Text | Google Scholar

5. Lian Y, Yu Y, Han S, Luan N, Wang Y, Lu Z. IEEE Sensors J (2022) 22(5):3828–43. doi:10.1109/JSEN.2022.3145833

CrossRef Full Text

6. Allen L, Beijersbergen MW, Spreeuw RJ, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45(11):8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wang H, Liang Y, Zhang X, Chen S, Shen L, Zhang L. Low-loss orbital angular momentum ring-core fiber: Design, fabrication and characterization. J Lightwave Technol (2020) 38(22):6327–33. doi:10.1109/jlt.2020.3012285

CrossRef Full Text | Google Scholar

8. Zhu G, Hu Z, Wu X, Du C, Luo W, Chen Y. Scalable mode division multiplexed transmission over a 10-km ring-core fiber using high-order orbital angular momentum modes. Opt Express (2018) 26(2):594–604. doi:10.1364/OE.26.000594

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang J, Liu J, Shen L, Zhang L, Luo J, Liu J. Mode-division multiplexed transmission of wavelength-division multiplexing signals over a 100-km single-span orbital angular momentum fiber. Photon Res (2020) 8(7):1236–42. doi:10.1364/prj.394864

CrossRef Full Text | Google Scholar

10. Jia C, Jia H, Wang N, Chai J, Xu X, Lei Y. Theoretical analysis of a 750-nm bandwidth hollow-core ring photonic crystal fiber with a graded structure for transporting 38 orbital angular momentum modes. IEEE Access (2018) 6:20291–7. doi:10.1109/access.2018.2817577

CrossRef Full Text | Google Scholar

11. Nandam A, Shin W. Spiral photonic crystal fiber structure for supporting orbital angular momentum modes. Optik (2018) 169:361–7. doi:10.1016/j.ijleo.2018.05.055

CrossRef Full Text | Google Scholar

12. Kabir MA, Hassan MM, Hossain MN, Paul BK, Ahmed K. Design and performance evaluation of photonic crystal fibers of supporting orbital angular momentum states in optical transmission. Opt Commun (2020) 467:125731. doi:10.1016/j.optcom.2020.125731

CrossRef Full Text | Google Scholar

13. Zhang Z, Liu X, Wei W, Ding L, Tang L, Li Y. The simulation of vortex modes in twisted few-mode fiber with inverse-parabolic index profile. IEEE Photon J (2020) 12(3):1–8. doi:10.1109/jphot.2020.2994819

CrossRef Full Text | Google Scholar

14. Kuiri B, Dutta B, Sarkar N, Santra S, Mandal P, Mallick K, et al. Design and optimization of photonic crystal fiber with low confinement loss guiding 98 OAM modes in THz band. Opt Fiber Technol (2022) 68:102752. doi:10.1016/j.yofte.2021.102752

CrossRef Full Text | Google Scholar

15. Kuiri B, Dutta B, Sarkar N, Santra S, Atta R, Patra AS. Development of photonic crystal fiber supporting 124 OAM modes with flat dispersion and low confinement loss. Opt Quan Electron (2022) 54:527. doi:10.1007/s11082-022-03942-y

CrossRef Full Text | Google Scholar

16. She Y, Zhou D, Chen X, Ni J. Bend-resistant low bending loss and large mode area single-mode fiber with low NA. Opt Fiber Technol (2019) 51:101–6. doi:10.1016/j.yofte.2019.05.006

CrossRef Full Text | Google Scholar

17. Wang W, Wang N, Li K, Geng Z, Jia H. A novel dual guided modes regions photonic crystal fiber with low crosstalk supporting 56 OAM modes and 4 LP modes. Opt Fiber Technol (2020) 57:102213. doi:10.1016/j.yofte.2020.102213

CrossRef Full Text | Google Scholar

18. Zhang L, Meng Y. Design and analysis of a photonic crystal fiber supporting stable transmission of 30 OAM modes. Opt Fiber Technol (2021) 61:102423. doi:10.1016/j.yofte.2020.102423

CrossRef Full Text | Google Scholar

19. Wang W, Sun C, Wang N, Jia H. A design of nested photonic crystal fiber with low nonlinear and flat dispersion supporting 30+50 OAM modes. Opt Commun (2020) 471:125823. doi:10.1016/j.optcom.2020.125823

CrossRef Full Text | Google Scholar

20. Lei Y, Xu X, Wang N, Jia H. Numerical analysis of a photonic crystal fiber for supporting 76 orbital angular momentum modes. J Opt (2018) 20(10):105701. doi:10.1088/2040-8986/aaddb8

CrossRef Full Text | Google Scholar

21. Zhang L, Zhang K, Peng J, Deng J, Yang Y, Ma J. Circular photonic crystal fiber supporting 110 OAM modes. Opt Commun (2018) 429:189–93. doi:10.1016/j.optcom.2018.07.014

CrossRef Full Text | Google Scholar

22. She Y, Zhang W, Tu S, Liang G. Large mode area single mode photonic crystal fiber with ultra-low bending loss. Optik (2021) 229:165556. doi:10.1016/j.ijleo.2020.165556

CrossRef Full Text | Google Scholar

23. Hassan MM, Kabir MA, Hossain MN, Nguyen TK, Paul BK, Ahmed K. Numerical analysis of circular core shaped photonic crystal fiber for orbital angular momentum with efficient transmission. Appl Phys B (2020) 126(9):145. doi:10.1007/s00340-020-07497-2

CrossRef Full Text | Google Scholar