Numerical study of the effect of a magnetic field on Rayleigh-Taylor instability with different density disturbances

Rayleigh-Taylor instability (RTI) is a fundamental physical process in fluids and plasmas. RTI is ubiquitous and must be considered in the field of high-energy-density physics, such as in space physics, astrophysics, and inertial confinement fusion. In this work, two-dimensional numerical simulations of laser-driven RTI with different density perturbations are performed using a radiation magnetohydrodynamic simulation program (FLASH). The effect of the applied magnetic field on the evolution of RTI at different Atwood numbers is systematically discussed. The results show that RTI evolves freely without an external magnetic field, and it is accompanied by the generation of secondary Kelvin–Helmholtz instability. Reducing the Atwood number weakens the mixing of fluids and has a strong stabilizing effect on the RTI. Introducing an external magnetic field parallel to the perturbation wave vector further inhibits the development of RTI and Kelvin–Helmholtz instability, with magnetic pressure playing a dominant role. The study results are important to gaining an in-depth understanding of the mixing of magnetic fluids and the magnetic field evolution at the instability interface and provide a reference for subsequent experimental studies on the related magnetization RTI.

1 Introduction

Rayleigh-Taylor instability (RTI) is the phenomenon of turbulent mixing due to the gradual growth of interfacial disturbances when the scalar product of the density gradient and the pressure gradient acting on the interface reference system is negative [1–4]. RTI generally evolves in three stages, namely, stages of linear growth, nonlinear growth, and turbulent mixing. The typical characteristics of RTI are bubble and mushroom-shaped spike structures. RTI, as a fundamental physical phenomena of fluids, exists widely in environments such as the Earth’s oceans, atmosphere, and mantle [5,6]. In space physics, magnetic RTI is observed during the eruption of solar prominences and thus plays an essential role in the formation of the solar wind [7,8]. In astrophysics, RTI is commonly found in supernova remnants, galactic media, and other environments. Hester et al. found that magnetic RTI explains the filamentary structures observed in the Crab Nebula [9]. In inertial confinement fusion (ICF), owing to the unevenness of the target surface and the non-uniformity of the laser focal spot, RTI and Kelvin–Helmholtz instability (KHI) inevitably occur at the target interface, which is an obstacle to achieving central ignition [10]. Although the National Ignition Facility of the United States achieved ignition (i.e., fusion energy greater than the laser input energy) for the first time in December 2022, it remains necessary to find methods that are more effective in suppressing fluid instability and thus steadily improve the ignition gain.

In theory, Chandrasekhar gave the linear growth rate of RTI in ideal magnetohydrodynamics (MHD). Chandrasekhar showed that the magnetic field parallel to the k direction of the perturbation wave vector has a particular stabilizing effect on RTI. The direct effect is seen from the critical wavelength λ_c obtained [11–13]. Using Layzer’s theoretical model of potential flow, Li et al. found that the development of RTI in ideal MHD is constrained by the magnetic pressure brought about by transverse magnetic fields [14]. Prajapati studied RTI in incompressible strongly coupled viscoelastic fluids by establishing generalized hydrodynamic equations. The equations considered the effects of an inhomogeneous magnetic field, density gradient, and uniform rotation, and the calculation results showed that the magnetic field and viscoelastic effect play an important role in suppressing RTI [15].

The present work focuses on ICF, where an in-depth understanding of RTI is essential for fusion ignition and a high gain. One option for achieving efficient ICF ignition is to use a strong preset seed magnetic field. Samulski et al. investigated the effect of an external magnetic field on RTI during deceleration using a radiant MHD simulation program (FLASH). Their results showed that the development of RTI could be inhibited by an appropriate seed magnetic field and sufficient magnetic field amplification effect [16]. Perkins et al.’s simulations suggested that the compression of imposed seed magnetic fields of tens of Tesla to more than 10⁴ T (T) under implosion may reduce the hotspot conditions required for ignition and propagating burn in indirectly driven ICF [17]. Barbeau et al. proposed an experimental scheme based on the National Ignition Facility and analyzed the RTI generated by the modulation layer with different densities by simulating the applied magnetic field with different horizontal flow directions [18]. Their results showed that a strong applied magnetic field (80 T) had a stronger stabilizing effect on the low-density material (20 mg/cm³). In high-energy density fluids, strong shock waves, strong magnetic fields, steep density gradients, non-ideal equations of state, and the nonlocalized energy transfer of particles and radiation all generate RTI and KHI [19]. Lugmer et al. studied the RTI spike merging process under multimode perturbations using Gaussian-like laser pulses [20]. Gao et al. carried out RTI experiments adopting the OMEGA-EP device in the United States, using ultrafast proton imaging technology to measure the distribution of the Biermann spontaneous magnetic field near the RTI spike [21]. Sun et al. conducted a two-dimensional simulation of RTI generated by a laser-driven CH-modulated target using FLASH code. They analyzed the effect of external magnetic fields having different directions and initial strengths on the evolution of the RTI. Their results showed that external magnetic fields in parallel wave vector directions restrained the RTI, and a stabilizing effect resulted from the competing magnetic pressure, magnetic tension, and thermal pressure gradient forces [3,4]. Although many RTI studies have adopted intense lasers, further research on RTI needs to be conducted at different density ratios (i.e., different Atwood numbers) and for coupled external magnetic fields.

This paper proposes an experimental scheme for generating magnetic RTI. We conduct a two-dimensional numerical study of RTI generated from polystyrene (CH) modulated targets driven by the Chinese Shenguang-II laser facility [22] and systematically discuss the effects of the external magnetic field on the evolution of RTI at different Atwood numbers. The results of the study are essential to understanding the mixing of magnetic fluids and the evolution of magnetic fields at unstable interfaces. The remainder of the paper is organized as follows. Section 2 presents the numerical simulation model, Section 3 gives the Rayleigh-Taylor instability experimental scheme, Section 4 presents the results of numerical simulation, and Section 5 summarizes the results of the paper.

2 Numerical simulation model

We use FLASH to conduct a numerical study of two-dimensional (2D) compressible MHD. Specifically, we discuss the evolution of RTI for different density perturbations. FLASH is an open-source, modular, and parallel multi-physical simulation program with an adaptive mesh refinement function [23]. The three-temperature radiation MHD solver calculates the laser energy deposition, multi-group radiation diffusion, and equilibrium electron, ion, and radiation temperatures and is suitable for high-energy density physical modeling. The equation of state and opacity of the target material (CH, Au) are calculated using the codes BADGER and IONMIX, respectively [24,25]. The main control equations used in this paper are as follows.

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \vec{u}\right)=0(1)$

$\frac{\partial \rho \vec{u}}{\partial t}+\vec{\nabla }\cdot \left(\rho \vec{u}\vec{u}-\frac{1}{4\pi }\vec{B}\vec{B}\right)+\vec{\nabla }{P}_{tot}=0(2)$

$\frac{\partial \rho E_{\text{tot\hspace{0.17em}}}}{\partial t}=-\vec{\nabla }\cdot \left[\vec{u}\left(\rho E_{\text{tot\hspace{0.17em}}}+P_{tot}\right)+\frac{1}{4\pi }\vec{B}\left(\vec{u}\cdot \vec{B}\right)\right](3)$

$\frac{\partial \vec{B}}{\partial t}=-\vec{\nabla }\cdot \left(\vec{u}\vec{B}-\vec{B}\vec{u}\right)+\frac{c}{e}\vec{\nabla }\times \frac{\vec{\nabla }{P}_e}{n_e}(4)$

$\vec{\nabla }\times \vec{B}=\frac{4\pi }{\mathrm{c}}\vec{j}(5)$

$\vec{\nabla }\cdot \vec{B}=0(6)$

$P_{\text{tot\hspace{0.17em}}}=P+\frac{B^2}{8\pi }=P_{\text{ele\hspace{0.17em}}}+P_{\text{ion\hspace{0.17em}}}+P_{\text{rad\hspace{0.17em}}}+\frac{B^2}{8\pi }(7)$

$E_{\text{tot\hspace{0.17em}}}=ϵ+\frac{\vec{u}\cdot \vec{u}}{2}+\frac{B^2}{8\pi }={ϵ}_{\text{ele\hspace{0.17em}}}+{ϵ}_{ion}+{ϵ}_{rad}+\frac{\vec{u}\cdot \vec{u}}{2}+\frac{B^2}{8\pi }(8)$

Eqs 1–3 are respectively continuity, momentum, and energy equations, where ρ is the density of the magnetized fluid, u is the velocity of the fluid, B is the magnetic field, E_tot is the total energy, and ϵ is the specific internal energy. P_tot is the total pressure, where P_ele, P_ion, and P_rad are respectively the ion, electron, and radiation pressure,. Eqs 4–6 are Maxwell’s equations, where j is the current density.

3 RTI experimental scheme

Figure 1 is a schematic of the initial simulation setup. The simulation domain is a two-dimensional x − −y plane with dimensions L_x × L_y = 2000 μm × 1,200 μm. An adaptive mesh having a maximum resolution of 5 μm is used. The laser has total energy E_L of 2000 J and a wavelength λ_L of 0.351 μm. The focal spot radius R_L is 100 μm. A Gaussian beam is injected from directly below the simulation domain upward at the position (1,000 μm, −200 μm). The laser has a pulse width τ_L of approximately 2 ns) and intensity of approximately 3.2 × 10¹⁵ W/cm². The target structure shown in Figure 1 is divided into three layers of Au, CH, and low-density foam. The low-density foam layer has a width of 880 μm. The CH layer has a mass density of ρ₂ = 1.0 g/cc and an area of L_x × L_y = 2000 μm × 100 μm. As the shielding layer, the Au layer prevents the CH and low-density foam layers from being ablated by the laser and plasma stray light before the RTI is generated. The Au layer has a width of 20 μm and a mass density ρ_Au = 19.32 g/cc. An initial single-mode sinusoidal disturbance with λ = 60 μm and a peak–valley amplitude of A₀ = 20 μm (y = 20 cos(2πx/60)) is introduced to the substrate interface between the CH and foam layers. Low-density helium (He) background plasma is set elsewhere in the simulation domain (ρ = 10^–5 g/cc), with the initial temperature set at room temperature (290 K). The initial density of the low-density foam layer ρ₁ is varied to adjust the density ratio within the CH perturbation layer. In addition, our previous work demonstrated that the Biermann self-generated magnetic field does not affect the interface dynamics of RTI and KHI. Therefore, the present work does not consider the Biermann self-generated magnetic field effect [4].

FIGURE 1

FIGURE 1. Initial simulation setup for laser-driven RTI.

The simulation is conducted for the six cases listed in Table 1. Cases 1–3 have a density ratio ρ₁/ρ₂ = 0.2, where the Atwood number A_t = 2/3. Case 1 has no external magnetic field, and Cases 2 and 3 respectively have initial magnetic fields of 1 T and 5 T applied in the x-direction. Cases 4–6 have a density ratio ρ₁/ρ₂ = 0.4, where the Atwood number A_t = 3/7. Case 4 has no external magnetic field, and cases 5 and 6 respectively have an initial magnetic field of 1 T and 5 T in the x-direction.

TABLE 1

TABLE 1. Simulation parameters under different initial conditions.

The introduction of an external magnetic field may lead to amplification of the environmental magnetic field and suppression of the RTI. The external magnetic field must be strong enough to suppress the development of the RTI. Sano et al. indicated that there is a critical magnetic field that suppresses the RTI [26]; i.e., the development of the RTI is suppressed only when the strength of the initial applied magnetic field is higher than the critical magnetic field. This phenomenon is characterized by comparing the values of the dimensionless Alfvén number R_A (R_A = u/v_A) (where u is the average velocity of the interface RTI and $v_A=\sqrt{\frac{B^2}{4\pi \rho }}$ is the Alfvén velocity). When R_A < 1, the Lorentz force acting on the fluid firmly stabilizes the interface instability. Here, the initial intensity of the applied magnetic field B₀ is far above the critical magnetic field intensity B_cri ∼ 0.56 T. In addition, we change the foam density, affecting both the initial Atwood number across the interface and the variation in the interface velocity. Concerning the RTI growth, we note that the perturbation grows more rapidly for a low-density foam. In this work, we study the effect of the external magnetic field on the RTI evolution under different Atwood numbers.

4 Simulation results and analysis

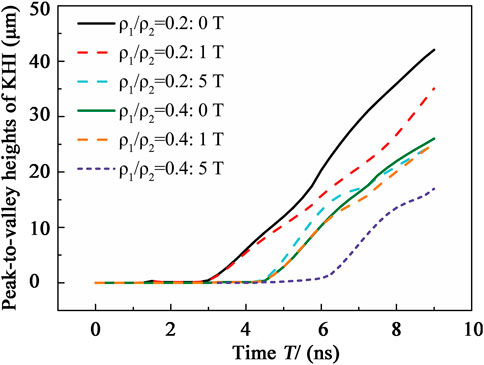
Figure 2 shows the electron density distribution at 0 ns, 3 ns, 6 ns, and 9 ns, respectively, for a density ratio ρ₁/ρ₂ = 0.2 and no external magnetic field. The timing starts at the moment of incidence of the laser pulse. As the laser light enters the Au layer, a forward shock wave is generated and gradually propagated through the CH-disturbed layer and toward the low-density foam. When the impact reaches the interface between CH and foam, a Richtmyer–Meshkov instability forms under the impact pressure, resulting in a phase reversal of the disturbance and subsequently increasing the amplitude of the disturbance. When the laser pulse ends, the system slows down, triggering RTI in the reference frame of the interface [12,27]. Generally, the evolution of RTI can be divided into three stages of linear growth, nonlinear growth, and turbulent mixing. The electron density distribution shows intuitively the evolution of the RTI in the different stages. During the linear growth stage (0–3 ns), there is continuous fluid mixing and vorticity deposition between layers with different densities, and the interface disturbance increases exponentially. At 3 ns, interface disturbance A is approximately 60 μm and the wavelength λ of the initial disturbance is equivalent to that of the RTI. As the RTI enters the second stage, a typical bubble and mushrooming spiky structure appears, as shown in Figure 2C. In addition, there is a rolling phenomenon at the tail of the RTI spikes. A cat’s eye vortex structure then develops, resulting in secondary KHI, as shown in Figure 2D. Strictly speaking, macroscopic MHD instability usually develops along with other interfacial instability in the evolutionary process, and turbulent mixing processes induced by RTI and KHI appear later.

FIGURE 2

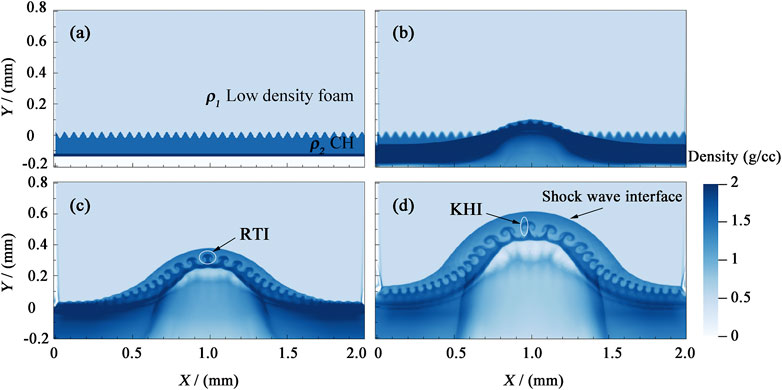
FIGURE 2. Density ratio ρ₁/ρ₂ = 0.2 and electron density distribution without an external magnetic field: (A–D) electron density at 0, 3, 6, and 9 ns, respectively.

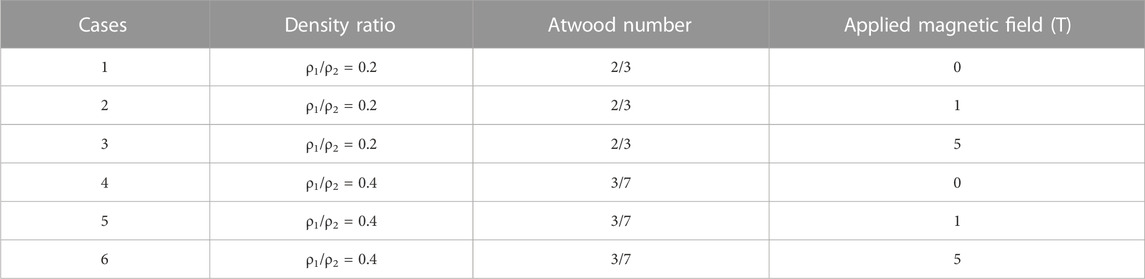
Figure 3 shows electron density distributions at 9 ns under four conditions of different density ratios and applied magnetic fields. Figures 3A, C shows the distributions for a density ratio ρ₁/ρ₂ = 0.2, Figures 3B,D those for a density ratio ρ₁/ρ₂ = 0.4; Figures 3A, B those no applied magnetic field, and Figures 3C, D those for an initial magnetic field of 1 T applied in the x-direction. Figure 3 shows that in all four cases, the RTI enters a nonlinear growth stage, which means that the typical bubble and spike structures appear, although their details differ. Here, we briefly describe the mixing zone height MZ and interface height P of the RTI, as shown in Figure 3A. In Figure 3A, the interface height p = 550 μm. The average evolution speed is ${\bar{u}}_P=61.1\mathrm{k}\mathrm{m}/\mathrm{s}$, the instantaneous velocity of the interface u_P = 66 km/s, and the RTI mixing zone height MZ is 115 μm. The average speed is ${\bar{u}}_M=12.8\mathrm{k}\mathrm{m}/\mathrm{s}$. At this time, the plasma sound velocity is $c_s=\sqrt{\left(\bar{z}{k}_B{T}_e+\gamma k_B{T}_i\right)/m_i}=55.6\mathrm{k}\mathrm{m}/\mathrm{s}$, indicating that during the nonlinear growth stage of the RTI, the RTI interface evolves at supersonic speeds. In Figure 3B, the RTI interface height P and MZ are 520 μm and 110 μm, respectively. A comparison of Figures 3A, C shows that the application of a magnetic field of 1 T in the x-direction hardly affects the RTI interface dynamics. However, the development of the KHI vortex at the tail of the spike is partially suppressed. A similar finding is obtained by comparing Figures 3B, D, for which a detailed quantitative analysis is conducted later. In summary, A_t controls the development of the RTI spike interface and mixing region to some extent, and the external magnetic field mainly controls the evolution of the secondary KHI in the spiked tail.

FIGURE 3

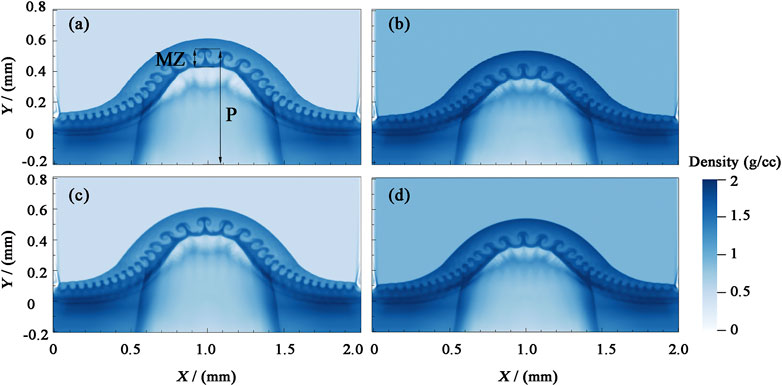
FIGURE 3. Electron density distributions during RTI evolution at 9 ns. Panels (A) and (C) show results for a density ratio of 0.2, panels (B) and (D) show results for a density ratio of 0.4, panels (A) and (B) show results for no applied magnetic field, and panels (C) and (D) show results for an initial magnetic field of 1 T applied in the x-direction.

Figure 4 shows the vorticity distributions at 9 ns to further describe the evolution of the RTI and KHI under different density disturbances and applied magnetic fields. Figures 4A,C,E shows the distributions for a density ratio ρ₁/ρ₂ = 0.2, Figures 4B,F those for a density ratio ρ₁/ρ₂ = 0.4, Figures 4A,B those for no applied magnetic field, Figures 4C,D those for an initial applied magnetic field of 1 T in the x direction and Figures 4E,F those for an initial magnetic field of 5 T applied in the x direction. Vorticity ω(ω = ∇ × u) is the degree of rotation of the fluid, which characterizes the degree of mixing of the fluids on the two sides of the interface during the evolution of the magnetic fluid instability. On the x − y two-dimensional plane, only the z component perpendicular to the plane of the paper $({\omega }_z=\frac{\partial u_y}{\partial x}-\frac{\partial u_x}{\partial y})$ is displayed, with the unit ns⁻¹. We enlarge the RTI in the black frame of Figure 4A to clearly show the RTI spike and KHI vortex structure. In Figure 4, the vorticity of the KHI vortex on the two sides of the tail of the spike is opposing and gradually decreases from the inside out. The modulus of the vorticity is a maximum of approximately 3 ns⁻¹, at the center of the vortex. A comparison of Figures 4A,B shows that reducing A_t weakens the mixing of fluids to a maximum modulus of vorticity of approximately 1.5 ns⁻¹. A comparison of Figures 4A,C,E shows that the applied magnetic field has no appreciable effect on the development of the shock wave interface and RTI interface. However, an increase in the intensity of the applied magnetic field has a strong stabilizing effect on the KHI vortex. As shown in Figure 4E, when an initial magnetic field of 5 T is applied in the x-direction, the tail of the RTI spike forms only a finger-like structure, which seriously affects the evolution of the KHI vortex. This indicates that the magnetic lines of the force and the fluid at the spike interface compress and fold with each other, destroying the spiral arm of the vortex and inhibiting the formation of the KHI vortex. Similar inferences are made by comparing Figures 4B,D,F.

FIGURE 4

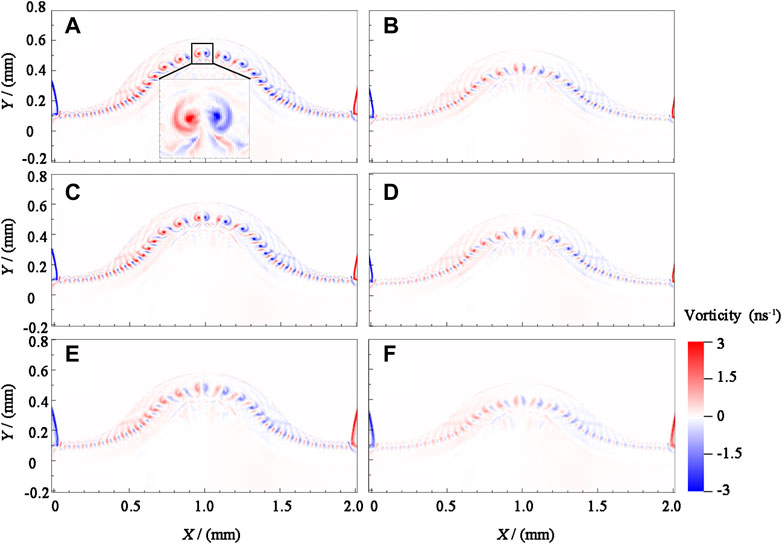
FIGURE 4. Vorticity distributions during RTI evolution at 9 ns. Panels (A), (C), and (E) show results for a density ratio of 0.2, panels (B), (D), and (F) show results for a density ratio of and 0.4, panels (A) and (B) show results for no applied magnetic field, panels (C) and (D) show results for an initial magnetic field of 1 T applied in the x-direction, and panels (D) and (F) show results for an initial magnetic field of 5 T applied in the x-direction.

The above analysis reveals that the external magnetic field in the x-direction affects the evolution of the RTI spikes. Figure 5 shows the magnetic field intensity distributions under different density ratios and an initial magnetic field of 5 T applied in the x-direction to allow an in-depth discussion of the mechanism of magnetic field stabilization. Figures 5A,C shows the distributions for a density ratio ρ₁/ρ₂ = 0.2, Figures 5B,D those for a density ratio ρ₁/ρ₂ = 0.4, Figures 5A,C those at 3 ns, and Figures 5B,D those at 9 ns. Figure 5A shows that at 3 ns, the RTI behind the target has not yet formed, and the shock wave carrying plasma outflow gradually propagates into the CH perturbation layer. At this time, the plasma outflow continuously compresses the magnetic field lines, such that they continuously fold, twist, and deform. Finally, at 9 ns, the magnetic field lines are amplified by a factor of 20 (B_max ∼ 100 T). Similarly, at a density ratio ρ₁/ρ₂ = 0.4, the external magnetic field is compressed by a factor of approximately 12 (B_max ∼ 60 T). It is inferred that reducing the Atwood number weakens the interaction between the fluid and external magnetic field. The vital magnetic field region is mainly distributed at the tip of the RTI spike, mostly because the kinetic energy of the fluid near the RTI interface is partially converted into magnetic energy. We determine the efficiency of converting kinetic energy into magnetic energy using the dimensionless parameter σ$\sigma =B_{\max }^2/8\pi Z{m}_i{n}_i{v}_i$, where B_max is the maximum magnetic field strength and m_i and n_i are respectively the ion mass and number density [28,29]. As shown in Figure 5B, at 9 ns, the ratio of the magnetic energy to interfacial fluid kinetic energy σ = 40%.

FIGURE 5

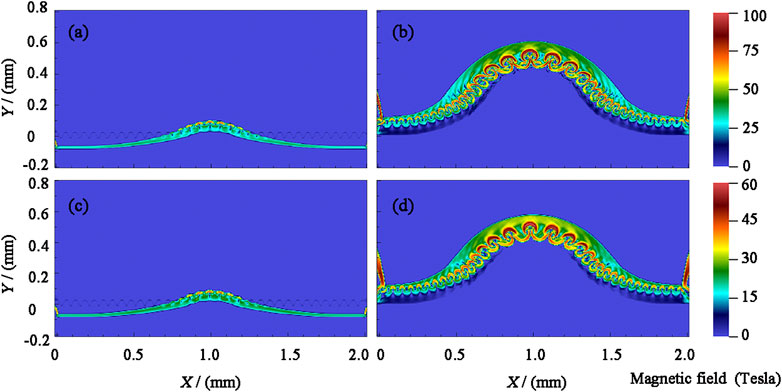
FIGURE 5. Distributions of the magnetic field strength at different times. Panels (A) and (B) show results for a density ratio of 0.2 and magnetic field strengths at 3 and 9 ns, respectively. Panels (C) and (D) show results for a density ratio of 0.4 and magnetic field strengths at 3 and 9 ns, respectively. All panels show results for an initial magnetic field of 5 T applied in the x direction.

Our previous work confirmed that the stabilizing effect of an external magnetic field in the x-direction on RTI and KHI is mainly due to the Lorentz force generated by the amplified magnetic field, with the magnetic pressure gradient force being dominant [4]. The present work further analyzes the evolution of RTI under different density ratios. Figure 6 shows the vector distributions of the thermal and magnetic pressure gradient forces under the initially applied 5-T magnetic field in the x-direction at 9 ns, with different density ratios and conditions. Figures 6A,B show results for a density ratio ρ₁/ρ₂ = 0.2, Figures 6C,D show those for a density ratio ρ₁/ρ₂ = 0.4, Figures 6A,C shows the vector distributions of the thermal pressure gradient force and Figures 6B,D shows the vector distribution of the magnetic pressure gradient force. When there is no external magnetic field, the RTI and KHI develop freely under thermal pressure gradient forces. When there is an external magnetic field parallel to the perturbation wave vector, the development of RTI and KHI at the fluid interface is affected by the combined effects of thermal and magnetic pressure gradient forces. Figures 6A,C shows that the thermal pressure gradient force is distributed throughout the RTI evolution region, and the forces on the two sides of the spike are oppositely directed. The accumulation promotes the further development of the RTI, with a maximum value of approximately 5 ×10¹⁴ Dyne/cm³. The magnetic pressure gradient force is mainly distributed in the tip region, mostly owing to the coupling between the plasma flow at the tip and the applied magnetic field being most robust, resulting in a large magnetic energy gradient, with a maximum value of approximately 3 ×10¹⁴ Dyne/cm³. Figures 6B,D shows that reducing the Atwood number weakens the interaction between the fluid and applied magnetic field, and the magnetic energy gradients at the tip of the spike decreases, resulting in a weaker magnetic pressure gradient force of $(\sim 1.4\times \mathrm{1}{\mathrm{0}}^{\mathrm{14}}\mathrm{D}\mathrm{y}\mathrm{n}\mathrm{e}/\mathrm{c}{\mathrm{m}}^{\mathrm{3}})$.

FIGURE 6

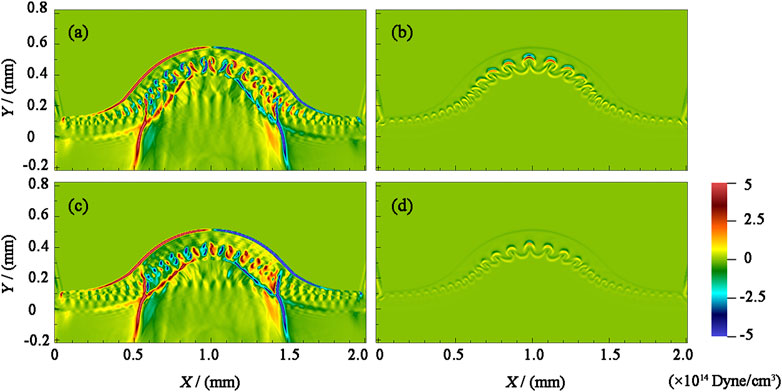
FIGURE 6. Vector distributions of the thermal and magnetic pressure gradient forces at 9 ns. Panels (A) and (C) show results for the thermal pressure gradient force, panels (B) and (D) those for the magnetic pressure gradient force, panels (A) and (B) those for a density ratio of 0.2, and panels (C) and (D) those for a density ratio of 0.4.

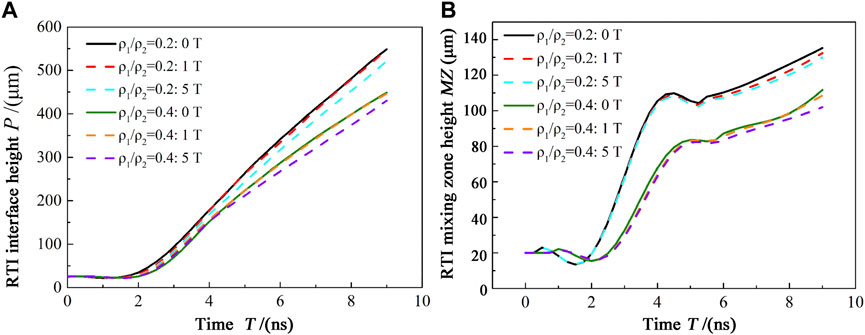
The evolution of the RTI and KHI at the tip tail under different density ratios and external magnetic fields was qualitatively demonstrated above. The results showed that decreasing the Atwood number weakens the mixing of fluids and effectively inhibits the development of RTI. In contrast, an external magnetic field parallel to the direction of the disturbance wave vector effectively suppresses the development of the KHI vortices at the tail of the RTI spike. Figures 7A,B quantitatively presents the temporal variations in the RTI interface height P and RTI mixing zone height MZ, respectively. Figure 8 quantitatively presents the temporal change in the KHI vortex height at the spike’s tail. The solid lines in Figures 7, 8 show results for the absence of an external magnetic field, with the solid black line presenting results for a density ratio ρ₁/ρ₂ = 0.2 and the solid green line presenting those for a density ratio ρ₁/ρ₂ = 0.4. The dotted lines show results for an external magnetic field. Figure 7 shows that reducing A_t inhibits the development of the RTI interface and RTI mixing region. In the case of an external magnetic field, the development of the RTI interface and mixing region follows a growth rule similar to that in the case of no magnetic field. In addition, the external magnetic field parallel to the disturbance wave vector stabilizes the development of the RTI interface and mixing region. A stronger initial magnetic field is required if it is necessary to more substantially suppress the RTI. Figure 8 shows that the initial density ratio and applied magnetic field in the simulation do not completely suppress the KHI at the tail of the RTI spike, and the KHI vortices are in a linear growth stage in all six cases. A comparison of results reveals that lower A_t inhibits the development of KHI vortices, whereas an external magnetic field parallel to the disturbance wave vector has a strong inhibitory effect on the KHI vortices. At 9 ns, the density ratio ρ₁/ρ₂ = 0.2, and the KHI vortex height for a 5-T magnetic field is 40% times less than that without a magnetic field.

FIGURE 7

FIGURE 7. Temporal variations in (A) the RTI interface height and (B) the RTI mixing zone height.

FIGURE 8

FIGURE 8. Temporal variation in the peak-to-valley height of the KHI.

On the basis of ideal MHD theory [11,27,28], in the absence of a magnetic field, the linear growth rate of RTI is ${\gamma }_{RTI}=\sqrt{A_{t}kg}$. Taking the case of ρ₁/ρ₂ = 0.2 as an example, the equivalent acceleration, p = 550 μm is the RTI interface height, g = 6.79 × 10¹² m/s², A_t = 0.67, calculated by wave vector k = 2π/λ, and calculate ${\gamma }_{RTI}^{-1}=1.45\mathrm{n}\mathrm{s}$. The corresponding KHI linear growth rate at the tail of the RTI spike is ${\gamma }_{KHI}=\frac{k\mathrm{\Delta }u}{2}\frac{\sqrt{{\rho }_1{\rho }_2}}{{\rho }_1+{\rho }_2}$ [27], where Δu is the shear velocity difference at the KHI vortex, obtained Δu ∼ 50 km/s. For density ratio ρ₁/ρ₂ = 0.2, when the initial magnetic field of 5 T is applied in the x-direction, the linear growth rate of RTI is expressed as ${\gamma }_{RTI}^{-1}={\left(\sqrt{A_{t}kg-\frac{2\left(B^2{\cos }^2\theta \cdot k^2\right)}{\left({\rho }_2-{\rho }_1\right)}}\right)}^{-1}\approx 1.51\mathrm{n}\mathrm{s}$, where θ is the angle between the magnetic field and the wave vector, and the linear growth rate of the KHI at the tail of the corresponding spike meets ${\gamma }_{KHI}^{-1}={\left(\frac{k}{\left({\rho }_1+{\rho }_2\right)}\sqrt{{\rho }_1{\rho }_2{(\mathrm{\Delta }u)}^2-\frac{1}{{\mu }_0}\left({\rho }_1+{\rho }_2\right)\left(B_1^2+B_2^2\right)}\right)}^{-1}\approx 2.78\mathrm{n}\mathrm{s}$, indicating that the presence of an external magnetic field reduces the evolution rate of the KHI while having a limited stabilizing effect on the RTI. A stronger initial external magnetic field is required to completely suppress the RTI. A comprehensive comparison reveals that the linear evolution time for the simulation results is approximately 3 ns, which is in good agreement with the theoretical value $(\sim 1.51\mathrm{n}\mathrm{s})$. A more detailed analysis may require consideration of the effects of non-ideal MHD, such as the effects of viscosity and magnetic diffusivity.

5 Summary

In this paper, a two-dimensional numerical simulation of laser-driven RTI under different density perturbations is conducted based on FLASH. The effect of different applied magnetic fields on the evolution of RTI at different Atwood numbers is systematically discussed. The results show that RTI can evolve freely without an external magnetic field, and accompanied by the secondary instability (KHI) occurs at the tip tail. Continuously decreasing the Atwood numbers will significantly weaken the mixing between fluids and have a strong stabilizing effect on RTI, with the RTI interface development significantly reduced by 18% and the spike height in the RTI mixing zone decreased by 60%. When an applied magnetic field of 1 T is introduced in the x-direction, the applied magnetic field has no significant impact on the development of the shock wave interface and RTI interface. However, with the increased intensity of the applied magnetic field (initial application of 5 T), it strongly stabilizes the KHI vortex. The plasma outflow continuously compresses and amplifies the magnetic field, which eventually amplifies by 20 times at 9 ns (B_max ∼ 100 T)at ρ₁/ρ₂ = 0.2. The combination of thermal and magnetic pressure gradient forces affects the development of RTI and KHI at the fluid interface.

Hence, the introduction of the external magnetic field may lead to two results: amplifying the environmental magnetic field and suppressing the RTI by the external magnetic field. The external magnetic field must be strong enough to ensure that the development of the RTI is suppressed. Only when the strength of the initial applied magnetic field is higher than the critical magnetic field, The development of RTI is suppressed. And the suppression effect is positively correlated with the intensity of the introduced external magnetic field. The introduced applied magnetic field mode may be an appropriate or potential candidates for fusion yield enhancement and ignition. Effective suppression of RTI may permit ignition recovery or at least increased fusion yields of ICF. We have previously used visible light optical diagnostics to measure the evolution of KHI vortex structures [30]. But the resolution limit of optical diagnosis, the fine structure of KHI cannot be captured in higher plasma density, and we cannot observe the later evolution. Currently, using the x-ray backlighting technique to diagnose the evolution of RTI and KHI, generally [31]. Those radiographs were performed by point projection, with an x-ray source produced by the Ultrashort pulse laser (picosecond beam) focused on high Z metal foil (Kα x-ray emission line: $\sim 4.5keV$) and an imaging plate detector. This diagnostic presents a static tens of micrometers resolution. It allows us to distinguish the fine structure in RTI and KHI. The research results are of great significance for an in-depth understanding of the mixing and magnetic field evolution at the unstable interface between magnetic fluids and also provide a reference for subsequent research on magnetization RTI experiments. The research results are of great significance for an in-depth understanding of the mixing and magnetic field evolution at the unstable interface between magnetic fluids.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

WS proposed this study and led the simulations, data analysis, and the interpretation of the results. WS carried out the FLASH simulations. CL, LF, JW, ZW, and CH contributed to discussion and helped to improve the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12205382, 12005305, U2267204, and U2241281), Young Talents Cultivation Fund of China Institute of Atomic Energy (Grant No. YC222412000901).

Acknowledgments

The simulations were carried out on the Beijing super cloud computing center in Beijing. The authors were particularly grateful to Flash Center for Computational Science at the University of Chicago for allowing us to use the FLASH code.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rigon G, Albertazzi B, Mabey P, Michel T, Falize E, Bouffetier V, et al. Exploring the atwood-number dependence of the highly nonlinear Rayleigh-Taylor instability regime in high-energy-density conditions. Phys Rev E (2021) 104:045213. doi:10.1103/physreve.104.045213

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Kull H-J. Theory of the Rayleigh-Taylor instability. Phys Rep (1991) 206:197–325. doi:10.1016/0370-1573(91)90153-d

CrossRef Full Text | Google Scholar

3. Sun W. Numerical study of the effect of magnetic field on laser-driven Rayleigh–Taylor instability under multi-mode disturbance. In: Sixth International Symposium on Laser Interaction with Matter; Held 10-12 August 2022; Ningbo, China (2022). p. 144–8.

Google Scholar

4. Wei S, Chong L, Zhu L, Jia-Yong Z. Numerical study of effect of magnetic field on laser-driven Rayleigh-Taylor instability. Acta Physica Sinica (2022) 71:154701. doi:10.7498/aps.71.20220362

CrossRef Full Text | Google Scholar

5. Kelley M, Haerendel G, Kappler H, Valenzuela A, Balsley B, Carter DA, et al. Evidence for a Rayleigh-Taylor type instability and upwelling of depleted density regions during equatorial spread f. Geophys Res Lett (1976) 3:448–50. doi:10.1029/gl003i008p00448

CrossRef Full Text | Google Scholar

6. Conrad CP, Molnar P. The growth of Rayleigh—Taylor-Type instabilities in the lithosphere for various rheological and density structures. Geophys J Int (1997) 129:95–112. doi:10.1111/j.1365-246x.1997.tb00939.x

CrossRef Full Text | Google Scholar

7. Mishra SK, Singh T, Kayshap P, Srivastava A. Evolution of magnetic Rayleigh–Taylor instability into the outer solar corona and low interplanetary space. Astrophysical J (2018) 856:86. doi:10.3847/1538-4357/aaae03

CrossRef Full Text | Google Scholar

8. Hillier A. The magnetic Rayleigh–Taylor instability in solar prominences. Rev Mod Plasma Phys (2018) 2:1–47. doi:10.1007/s41614-017-0013-2

CrossRef Full Text | Google Scholar

9. Hester JJ, Stone JM, Scowen PA, Jun B-I, Gallagher JS, Norman ML, et al. Wfpc2 studies of the crab nebula. iii. magnetic Rayleigh-Taylor instabilities and the origin of the filaments. Astrophysical J (1996) 456:225–33. doi:10.1086/176643

CrossRef Full Text | Google Scholar

10. Casner A, Mailliet C, Rigon G, Khan S, Martinez D, Albertazzi B, et al. From icf to laboratory astrophysics: Ablative and classical Rayleigh–Taylor instability experiments in turbulent-like regimes. Nucl Fusion (2018) 59:032002. doi:10.1088/1741-4326/aae598

CrossRef Full Text | Google Scholar

11. Chandrasekhar A. Hydrodynamic and hydromagnetic stability. Oxford: Clarendon Press: International Series of Monographs on Physics (1961).

Google Scholar

12. Manuel M-E, Khiar B, Rigon G, Albertazzi B, Klein S, Kroll F, et al. On the study of hydrodynamic instabilities in the presence of background magnetic fields in high-energy-density plasmas. Matter Radiat Extremes (2021) 6:026904. doi:10.1063/5.0025374

CrossRef Full Text | Google Scholar

13. Shivamoggi BK. Rayleigh-Taylor instability of a compressible plasma in a horizontal magnetic field. Z für Angew Mathematik Physik ZAMP (1982) 33:693–7. doi:10.1007/bf00944951

CrossRef Full Text | Google Scholar

14. Li Y, Luo X-S. Theoretical analysis of effects of viscosity, surface tension, and magnetic field on the bubble evolution of Rayleigh-Taylor instability. Acta Phys Sin (2014) 63:085203. doi:10.7498/aps.63.085203

CrossRef Full Text | Google Scholar

15. Prajapati R. Rayleigh-Taylor instability in non-uniform magnetized rotating strongly coupled viscoelastic fluid. Phys Plasmas (2016) 23:022106. doi:10.1063/1.4941593

CrossRef Full Text | Google Scholar

16. Samulski C, Srinivasan B, Manuel M-E, Masti R, Sauppe J, Kline J. Erratum:“deceleration-stage RRayleightTaylorgrowth in a background magnetic field studied in cylindrical and cartesian geometries”[matter radiat. extremes 7, 026902 (2022)]. Matter Radiat Extremes (2022) 7:069901. doi:10.1063/5.0125513

CrossRef Full Text | Google Scholar

17. Perkins L, Ho D-M, Logan B, Zimmerman G, Rhodes M, Strozzi D, et al. The potential of imposed magnetic fields for enhancing ignition probability and fusion energy yield in indirect-drive inertial confinement fusion. Phys Plasmas (2017) 24:062708. doi:10.1063/1.4985150

CrossRef Full Text | Google Scholar

18. Barbeau Z, Raman K, Manuel M, Nagel S, Shivamoggi B. Design of a high energy density experiment to measure the suppression of hydrodynamic instability in an applied magnetic field. Phys Plasmas (2022) 29:012306. doi:10.1063/5.0067124

CrossRef Full Text | Google Scholar

19. Casner A, Rigon G, Albertazzi B, Michel T, Pikuz T, Faenov A, et al. Turbulent hydrodynamics experiments in high energy density plasmas: Scientific case and preliminary results of the turbohedp project. High Power Laser Sci Eng (2018) 6:e44. doi:10.1017/hpl.2018.34

CrossRef Full Text | Google Scholar

20. Lugomer S. Laser–matter interactions: Inhomogeneous richtmyer–meshkov and Rayleigh–Taylor instabilities. Laser Part Beams (2016) 34:123–36. doi:10.1017/s0263034615000956

CrossRef Full Text | Google Scholar

21. Gao L, Nilson P, Igumenschev I, Fiksel G, Yan R, Davies J, et al. Observation of self-similarity in the magnetic fields generated by the ablative nonlinear Rayleigh-Taylor instability. Phys Rev Lett (2013) 110:185003. doi:10.1103/physrevlett.110.185003

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhu JQ, Zheng YX, Chen SH. Shenguang-ii laser facility developed invited. China laser (2019) 46:0100002. doi:10.3788/CJL201946.0100002

CrossRef Full Text | Google Scholar

23. Fryxell B, Olson K, Ricker P, Timmes F, Zingale M, Lamb D, et al. Flash: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophysical J Suppl Ser (2000) 131:273–334. doi:10.1086/317361

CrossRef Full Text | Google Scholar

24. Heltemes T, Moses G. Badger v1. 0: A fortran equation of state library. Comp Phys Commun (2012) 183:2629–46. doi:10.1016/j.cpc.2012.07.010

CrossRef Full Text | Google Scholar

25. MacFarlane J. Ionmix-a code for computing the equation of state and radiative properties of lte and non-lte plasmas. Comp Phys Commun (1989) 56:259–78. doi:10.1016/0010-4655(89)90023-4

CrossRef Full Text | Google Scholar

26. Sano T, Tamatani S, Matsuo K, Law KFF, Morita T, Egashira S, et al. Laser astrophysics experiment on the amplification of magnetic fields by shock-induced interfacial instabilities. Phys Rev E (2021) 104:035206. doi:10.1103/physreve.104.035206

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Huntington C, Shimony A, Trantham M, Kuranz C, Shvarts D, Di Stefano C, et al. Ablative stabilization of Rayleigh-Taylor instabilities resulting from a laser-driven radiative shock. Phys Plasmas (2018) 25:052118. doi:10.1063/1.5022179

CrossRef Full Text | Google Scholar

28. Huntington CM, Fiuza F, Ross JS, Zylstra AB, Drake RP, Froula DH, et al. Observation of magnetic field generation via the weibel instability in interpenetrating plasma flows. Nat Phys (2015) 21:173–6. doi:10.1038/nphys3178

CrossRef Full Text | Google Scholar

29. Sun W, Lei Z, Lv C, Zhong J. Effect of an applied magnetic field on kelvin–helmholtz instability driven by a laser under multi-mode disturbance. Phys Plasmas (2022) 29:052110. doi:10.1063/5.0090063

CrossRef Full Text | Google Scholar

30. Sun W, Zhong J, Lei Z, Zhang S, Wang L, Zhao K, et al. Suppressing kelvin–helmholtz instability with an external magnetic field. Plasma Phys Controlled Fusion (2020) 62:065007. doi:10.1088/1361-6587/ab84ad

CrossRef Full Text | Google Scholar

31. Harding E, Hansen J, Hurricane O, Drake R, Robey H, Kuranz C, et al. Observation of a kelvin-helmholtz instability in a high-energy-density plasma on the omega laser. Phys Rev Lett (2009) 103:045005. doi:10.1103/physrevlett.103.045005

PubMed Abstract | CrossRef Full Text | Google Scholar