Robustness of consensus in m-rose networks

The consensus of deterministic networks investigates the relationships between consensus and network topology, which can be measured by network coherence. The m-rose networks are composed of m circles, which share a common node. Recently, scholars have obtained the first-order coherence of 5-rose networks. This paper takes the more general m-rose networks as the research object, firstly, the m-rose networks are introduced. Secondly, the relationships between Laplacian eigenvalues and polynomial coefficients are used to obtain the first-order and second-order coherence of the m-rose networks. Finally, the effects of topology parameters such as the number of petals m and the length of a cycle n on the robustness of network consensus are discussed, and the validity of the conclusion is verified by numerical simulation.

1 Introduction

With the development of network science, the study of network dynamics has become a hot spot. There are many networks in the real world, such as social networks [1], supply chain networks, and ecological networks [2–4]. The study of networks can solve practical problems in computer science, mathematical science, control science, and many other disciplines. With the deepening of research, network research has made new progress in many aspects, such as network synchronization [5–8], node containment control [9], network consensus, and robustness [10–13].

The problem of network consensus studies how multiple individuals in the network achieve consensus in direction, and location, which has potential applications in sensor networks, communication control, and other aspects [14, 15]. The consensus of the network can be measured by the network coherence, which can be quantified by the Laplacian spectrum of the network [16]. Reference [17] investigated the first-order coherence of three types of symmetric star networks and found that the increase in branch length and the number of branches of star networks will weaken the consensus of three types of networks. Reference [18] studied the consensus of scale-free networks with noise and found that the average degree of node dynamics has a great impact on the network consensus. Reference [19] deduced the consensus problems for a group of agents with heterophyllous dynamics, which can arouse future research in synchronization processes over heterophyllous multiagent networks.

The advantage of a deterministic network is that the coherence can be solved, so it can promote the in-depth study of practical network models. Reference [20] studied the consensus in a deterministic network model given the initial state of the leader points. As a kind of deterministic network, the m-rose networks have attracted the attention of scholars. Reference [21] proved that the 3-rose networks are determined by the Laplacian spectrum by calculating the quadratic coefficients of the Laplacian polynomial corresponding to the 3-rose networks. Reference [22] obtained the first-order coherence of the 5-rose networks by using the Laplacian spectrum and investigated the effect of the number of petals on the consensus.

Inspired by the above literature, this paper analyzes the robustness of consensus of the m-rose networks, which is more applicable. The first and second-order coherence of the m-rose networks is obtained by computing the Laplacian polynomials. It was found that the topological structure parameters have a significant impact on the robustness of the consensus of the m-rose networks. The main innovation is as follows.

1. Compared with Ref. [22], this paper extends the 5-rose networks to more general m-rose networks, eliminating the limitation of network cycles and expanding its practical application range.

2. Due to the difficulty in solving the Laplacian spectrum of the m-rose networks, we apply the Laplacian theorem and iterative methods to obtain the Laplacian polynomial of the m-rose networks, and then get the coherence of the m-rose networks.

3. The effect of the number of petals m and the length of a cycle n on the consensus of the m-rose networks was considered, and it was found that the smaller the topological parameters m and n, the better the consensus of the networks.

2 Preliminaries

2.1 The Laplacian eigenvalues of network The Laplacian matrix of network

G with S nodes is defined as L(G) = M(G) − A(G), where M(G) = diag (m₁, m₂, m₃, … , m_S−1, m_S), m_i denotes the degree of node i. $A(G)={(a_{ij})}_{S\times S}$ is the adjacency matrix, if i and j are connected, a_ij = 1, otherwise, a_ij = 0. Let the roots of equation |λI − L| = 0 be the Laplacian eigenvalues of the network.

2.2 network coherence

In reality, the network will inevitably be disturbed by noise, and the state of the network nodes will deviate from the consistent state. At this time, network coherence is used to measure the network consensus. To investigate how noise affects network consensus, the first-order consensus dynamic model under noise interference is described as follows [18]:

$\dot{x}=-Lx\left(t\right)+\rho \left(t\right),(1)$

x(t) ∈ R^S is the state vector, L represents the Laplacian matrix, ρ(t) ∈ R^S denotes the Gaussian white noise interference of S nodes at time t. The first-order network coherence is defined as:

$H^1=\frac{1}{S}\sum _{i=1}^S\underset{t\to \infty }{\lim }\mathrm{v}\mathrm{a}\mathrm{r}\left\{x_i\left(t\right)-\frac{1}{S}\sum _{j=1}^S{x}_j\left(t\right)\right\},(2)$

where var represents variance.

Define the output of system (1) as:

$y=Mx,(3)$

where $M=I-\frac{1}{S}\mathit{1}{\mathit{1}}^{\mathit{T}}$, 1 is S-vector of all ones.

Combined with (1) and (2), H¹ can be expressed as

$H^1=\frac{1}{S}\mathrm{t}\mathrm{r}\left({\int }_0^{\infty }{e}^{-L^{T}tQ{e}^{-Lt}}dt\right),(4)$

where tr represents the trace of the matrix.

From [18], the relationships between the first-order network coherence and the Laplacian eigenvalues are described as follows:

$H^1=\frac{1}{2S}\sum _{i=2}^S\frac{1}{{\lambda }_i}.(5)$

Meanwhile, let x₁(t), x₂(t) be the velocity vector and the position vector, respectively. The second-order consensus dynamic model under noise interference is described as follows [10]:

$\left[\begin{array}{c}\hfill \dot{x_1}\left(t\right)\hfill \\ \hfill \dot{x_2}\left(t\right)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 0\hfill & \hfill I\hfill \\ \hfill -L\hfill & \hfill -L\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_1\left(t\right)\hfill \\ \hfill x_2\left(t\right)\hfill \end{array}\right]+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill I\left(t\right)\hfill \end{array}\right]\rho \left(t\right).(6)$

From [10], the relationships between the second-order network coherence and the Laplacian eigenvalues are described as follows:

$H^2=\frac{1}{2S}\sum _{i=2}^S\frac{1}{{\lambda }_i^2}.(7)$

The network coherence H¹ and H² measures the robustness of the system subject to the noise. Lower H¹ and H² means that nodes reach better consensus at the average of their current states.

2.3 The m-rose networks

The m-rose networks are a generalization of friendship networks, which are composed of m circles, and m circles have a common node [23]. In this paper, we study m-rose networks R (m, n) with the length of the cycle n, which have mn − m + 1 nodes and mn edges. R (6, 10) is shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of 6-rose network R (6, 10).

3 The coherence of m-rose networks R (m, n)

To obtain the coherence of R (m, n), this paper first obtains the Laplacian polynomial of 6-rose networks R (6, n), and gets the Laplacian polynomial of m-rose networks R (m, n) through a similar method. According to the relationships between polynomial coefficients and eigenvalues, the coherence of R (m, n) is further calculated.

Let the Laplacian matrix corresponding to R (6, n) be L, combined with the definition of the Laplacian matrix and the topological structure of R (6, n). The Laplacian polynomial of R (6, n) is Q₁(λ) = |λI − L|, Q₁(λ)

$=\left|\begin{array}{ccccccccccccccccc}\hfill \lambda -12\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill \end{array}\right|$

then,

$Q_1\left(\lambda \right)=|\lambda I-L|=M_{6n-5}\left(\lambda \right)+{\left(-1\right)}^{n+1}{P}_{n-1}^5\left(\lambda \right)\left[2+{\left(-1\right)}^n{P}_{n-2}\left(\lambda \right)\right]+$

$\left[{\left(-1\right)}^{2n}+{\left(-1\right)}^{6n-2}+{\left(-1\right)}^{8n-4}+{\left(-1\right)}^{10n-6}+{\left(-1\right)}^{12n-8}\right]P_{n-1}^4\left(\lambda \right)\left(U_{2n-2}\left(\lambda \right)+O_{2n-2}\left(\lambda \right)\right)$

$=\left(\lambda -12\right)P_{n-1}^6\left(\lambda \right)-12P_{n-1}^5\left(\lambda \right)P_{n-2}\left(\lambda \right)+{\left(-1\right)}^{n+1}12P_{n-1}^5\left(\lambda \right).(8)$

Where M_6n−5(λ) =

$\left|\begin{array}{ccccccccccccccccc}\hfill \lambda -12\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \cdots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill \end{array}\right|$

$U_{2n-2}\left(\lambda \right)=\left|\begin{array}{cccccccccccccccc}\hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right|$

$O_{2n-2}\left(\lambda \right)=\left|\begin{array}{cccccccccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill ⋮\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill \end{array}\right|$

$P_n\left(\lambda \right)=\left|\begin{array}{ccccccc}\hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -2\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill \lambda -2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \lambda -2\hfill \end{array}\right|$

Let the Laplacian matrix of R (m, n) be L^*, similar to solving the Laplacian polynomial of R (6, n), the Laplacian polynomial of R (m, n) is Q₂(λ) = |λI − L^*|,

$Q_2\left(\lambda \right)=|\lambda I-L^{*}|=M_{mn-m+1}\left(\lambda \right)+{\left(-1\right)}^{n+1}{P}_{n-1}^{m-1}\left(\lambda \right)\left[2+{\left(-1\right)}^n{P}_{n-2}\left(\lambda \right)\right]+$

$\left[{\left(-1\right)}^{2n}+{\left(-1\right)}^{6n-2}+\cdots +{\left(-1\right)}^{2mn-2m+4}\right]P_{n-1}^{m-2}\left(\lambda \right)\left(U_{2n-2}\left(\lambda \right)+O_{2n-2}\left(\lambda \right)\right)$

$=\left(\lambda -2m\right)P_{n-1}^m\left(\lambda \right)-2m{P}_{n-1}^{m-1}\left(\lambda \right)P_{n-2}\left(\lambda \right)+{\left(-1\right)}^{n+1}2m{P}_{n-1}^{m-1}\left(\lambda \right)$

$=P_{n-1}^{m-1}\left(\lambda \right)\left[\left(\lambda -2m\right)P_{n-1}\left(\lambda \right)-2m{P}_{n-2}\left(\lambda \right)+{\left(-1\right)}^{n+1}2m\right].$

Theorem 1. The first-order coherence of m-rose networks R(m, n) is

$H^1=\frac{n^2-1}{2\left(mn-m+1\right)}\left(\frac{m-1}{6}+\frac{2+m\left(n-2\right)}{12+12m\left(n-1\right)}\right).$

Proof. Let 0 < α₁ ≤ α₂ ≤ ⋯ ≤ α_n−1 be the Laplacian eigenvalues of P_n−1(λ), P_n−1(λ) = a_n−1λⁿ⁻¹+ a_n−2λⁿ⁻² + ⋯ + a₁λ + a₀, 0 = β₁ < β₂ ≤ β₃ ≤ ⋯ ≤ β_n be the Laplacian eigenvalues of K_n(λ), K_n(λ) = (λ − 2m)P_n−1(λ) − 2mP_n−2(λ) + (−1)ⁿ⁺¹2m = b_nλⁿ + b_n−1λⁿ⁻¹ + ⋯ + b₁λ.According to preliminaries,

$H^1=\frac{1}{2\left(mn-m+1\right)}\left[\left(m-1\right)\sum _{i=1}^{n-1}\frac{1}{{\alpha }_i}+\sum _{i=2}^n\frac{1}{{\beta }_i}\right].(10)$

According to [17] and the Vieta theorem,

$\sum _{i=1}^{n-1}\frac{1}{{\alpha }_i}=-\frac{a_1}{a_0}=\frac{n^2-1}{6},(11)$

$\sum _{i=2}^n\frac{1}{{\beta }_i}=-\frac{b_2}{b_1}=-\frac{a_1-2m{a}_2-2m{P}_{n-2}\left(2\right)}{a_0-2m{a}_1-2m{P}_{n-2}\left(1\right)}$

$=\frac{\left(n-1\right)\left(n+1\right)\left[2+m\left(n-2\right)\right]}{12+12m\left(n-1\right)}.(12)$

$a_0={(-1)}^{n-1}n,a_1={(-1)}^{n-2}\frac{(n-1)n(n+1)}{6},a_2={(-1)}^{n-3}\frac{(n-2)(n-1)n(n+1)(n+2)}{120}$. P_n−2 (1), P_n−2 (2) are the first-order coefficient and quadratic coefficient of P_n−2(λ),

$P_{n-2}\left(1\right)={\left(-1\right)}^{n-3}\frac{\left(n-2\right)\left(n-1\right)n}{6},P_{n-2}\left(2\right)={\left(-1\right)}^{n-4}\frac{\left(n-3\right)\left(n-2\right)\left(n-1\right)n\left(n+1\right)}{120}.$

By Eqs 10–12, we obtain,

$H^1=\frac{n^2-1}{2\left(mn-m+1\right)}\left(\frac{m-1}{6}+\frac{2+m\left(n-2\right)}{12+12m\left(n-1\right)}\right).$

Theorem 2. The second-order coherence of m-rose networks R(m, n) is $H^2=\frac{1}{2(mn-m+1)}\{\frac{(m-1)(n^2-1)}{6}(\frac{n^2}{15}+\frac{7}{30})+{[\frac{(n^2-1)(mn-2m+2)}{12mn-12m+12}]}^2-\frac{(n^2-4)(n^2-1)(mn-3m+3)}{180mn-180m+180}\}$.

Proof. According to preliminaries,

$H^2=\frac{1}{2\left(mn-m+1\right)}\left[\left(m-1\right)\sum _{i=1}^{n-1}\frac{1}{{\alpha }_i^2}+\sum _{i=2}^n\frac{1}{{\beta }_i^2}\right].(13)$

According to [20] and the Vieta theorem,

$\sum _{i=1}^{n-1}\frac{1}{{\alpha }_i^2}={\left(\frac{a_1}{a_0}\right)}^2-\frac{2a_2}{a_0}=\frac{n^2-1}{6}\left(\frac{n^2}{15}+\frac{7}{30}\right),(14)$

$\sum _{i=2}^n\frac{1}{{\beta }_i^2}={\left(\frac{b_2}{b_1}\right)}^2-\frac{2b_3}{b_2}={\left[\frac{\left(n^2-1\right)\left(mn-2m+2\right)}{12mn-12m+12}\right]}^2-2\frac{a_2-2m{a}_3-2m{P}_{n-2}\left(3\right)}{a_0-2m{a}_1-2m{P}_{n-2}\left(1\right)}$

$={\left[\frac{\left(n^2-1\right)\left(mn-2m+2\right)}{12mn-12m+12}\right]}^2-\frac{\left(n^2-4\right)\left(n^2-1\right)\left(mn-3m+3\right)}{180mn-180m+180}.(15)$

$a_3={(-1)}^{n-4}\frac{(n-3)(n-2)(n-1)n(n+1)(n+2)(n+3)}{5040}$. P_n−2 (3) is the third term coefficient of P_n−2(λ), $P_{n-2}(3)={(-1)}^{n-5}\frac{(n-4)(n-3)(n-2)(n-1)n(n+1)(n+2)}{5040}$.By Eqs 13–15, Theorem 2 is proved.

4 Numerical simulation

Figures 2A, 3A) shows the relationships between H¹(H²) and the number of petals m. When n is fixed, H¹(H²) is positively correlated with the number of petals m and increases at a decreasing rate. The smaller the length of the cycle n is, the smaller H¹(H²) is. The consensus of the network is inversely proportional to the coherence, so as the number of petals of the m-rose networks increases, the first-order (second-order) consensus of the network decreases. If the number of petals m is sufficiently large, H¹(H²) will tend to a constant value and the consensus reaches its weakest.

FIGURE 2

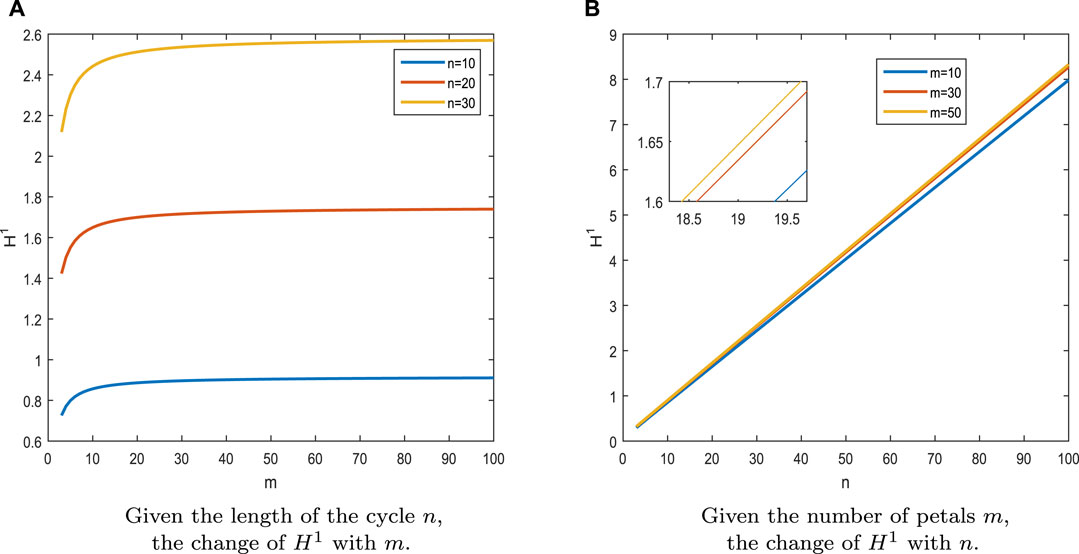
FIGURE 2. (A) Given the length of the cycle n, the change of H¹ with m (B) Given the number of petals m, the change of H¹ with n.

FIGURE 3

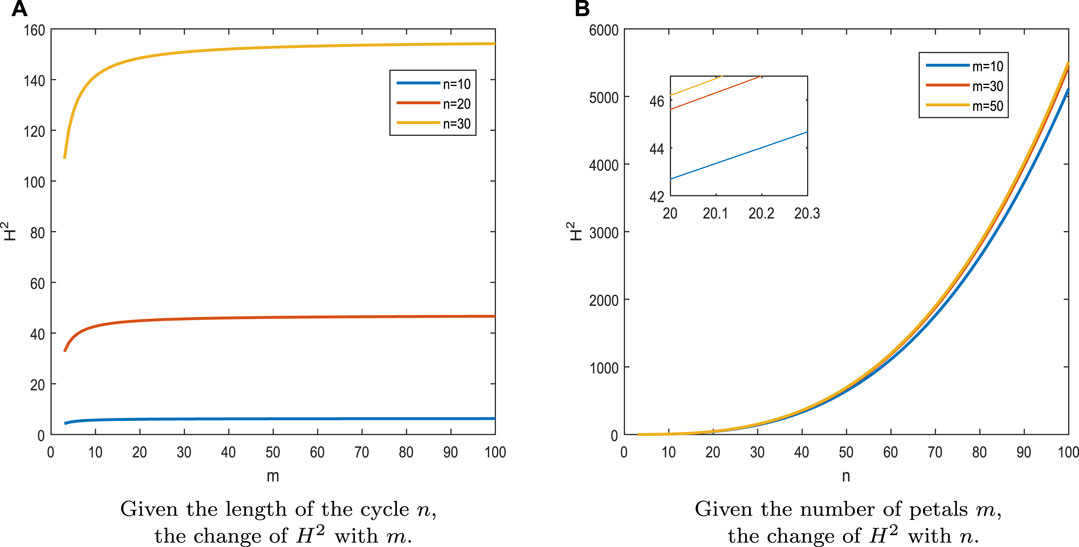
FIGURE 3. (A) Given the length of the cycle n, the change of H² with m. (B) Given the number of petals m, the change of H² with n.

Figures 2B, 3B shows the relationships between H¹(H²) and the length of the cycle n. When m is fixed, H¹(H²) is positively correlated with the length of the cycle n. The smaller the number of petals m is, the smaller H¹(H²) is. Therefore, when the length of the cycle of m-rose networks increases, the first-order (second-order) consensus of the network decreases.

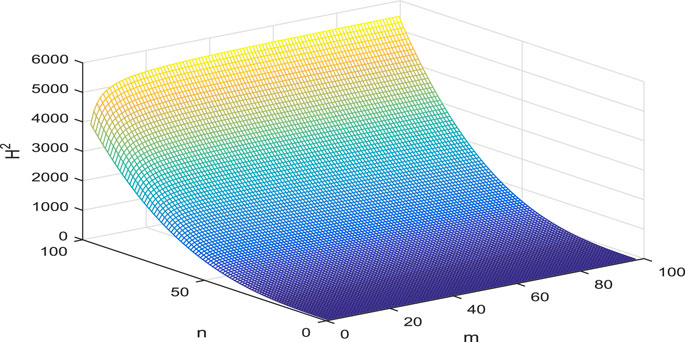
Figure 4 shows the relationships between H² and the number of petals m and the length of the cycle n. It is found that the influence of the length of the cycle n on the coherence is stronger than the number of petals m. A similar conclusion is drawn for the first-order consensus of the m-rose networks.

FIGURE 4

FIGURE 4. The change of H² with the number of petals m and the length of the cycle n.

5 Conclusion

In this paper, the robustness of the consensus of m-rose networks is studied. Using the Laplacian theorem and determinant properties, the concrete analytical expressions of the first-order and second-order coherence of m-rose networks are obtained. Based on the analytical formula, the effects of the number of petals m and the length of the cycle n of the network on the consensus are simulated experimentally. When the length of the cycle n is fixed, the consensus of the m-rose networks will weaken with the increase of the number of petals m. The smaller the length of the cycle n, the stronger the robustness of consensus. When the number of petals m is fixed, the consensus of the m-rose network will weaken with the increase of the length of the cycle n. The smaller the number of petals m, the stronger the robustness of consensus. When the number of petals m and the length of the cycle n both increase, the consensus decreases, and the impact of the length of the cycle n on the consensus is stronger than the number of petals m.

In this paper, we consider the consensus of single-layer m-rose networks. How to get the consensus of multi-layer m-rose networks and the consensus of m-rose weighted networks are worthy of further study.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, WD and JZ; methodology, WD and JZ; software, XL; validation, HG and JZ; formal analysis, XL and HG; writing—original draft preparation, HG and WD; writing—review and editing, JZ; supervision, XL; and project administration, HG. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (No. 2022D01A246, No. 2022D01A247) and the project of Key Laboratory of New Energy and Materials Research of Xinjiang Institute of Engineering, Xinjiang Uygur Autonomous Region University Basic Research Business Fund Research Project (No. XJEDU2022P129), National innovation and entrepreneurship training program for College Students (No. 202210994014), School level project of Xinjiang institute of Light industry Technology (No. XJQG2023S94).

Acknowledgments

We express our sincere gratitude to the persons who gave us valuable comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Cozzo E, Banos R, Meloni S, Moreno Y. Contact-based social contagion in multiplex networks. Phys Rev E (2013) 88(5):050801. doi:10.1103/physreve.88.050801

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhen L, Huang L, Wang W. Green and sustainable closed-loop supply chain network design under uncertainty. J Clean Prod (2019) 227:1195–209. doi:10.1016/j.jclepro.2019.04.098

CrossRef Full Text | Google Scholar

3. Strydom T, Dalla V, Poisot T. SVD entropy reveals the high complexity of ecological networks. Front Ecol Evol (2021) 9:623141. doi:10.3389/fevo.2021.623141

CrossRef Full Text | Google Scholar

4. Yuan M, Guo X, Wu L, Zhang Y, Xiao N, Ning D, et al. Climate warming enhances microbial network complexity and stability. Nat Clim Change (2021) 11(4):343–8. doi:10.1038/s41558-021-00989-9

CrossRef Full Text | Google Scholar

5. Zhang J, Ma Z, Li X, Qiu J. Cluster synchronization in delayed networks with adaptive coupling strength via pinning control. Front Phys (2020) 8:235. doi:10.3389/fphy.2020.00235

CrossRef Full Text | Google Scholar

6. Berner R, Yanchuk S. Synchronization in networks with heterogeneous adaptation rules and applications to distance-dependent synaptic plasticity. Front Appl Math Stat (2021) 47:714978. doi:10.3389/fams.2021.714978

CrossRef Full Text | Google Scholar

7. Zhu J, Huang D, Jiang H, Bian J, Yu Z. Synchronizability of multilayer variable coupling windmill-type networks. Mathematics (2021) 9:2721. doi:10.3390/math9212721

CrossRef Full Text | Google Scholar

8. Rao P, Guo X. Finite-time synchronization of Kuramoto-oscillator networks with a pacemaker based on cyber-physical system. Front Phys (2022) 10:1208. doi:10.3389/fphy.2022.1077045

CrossRef Full Text | Google Scholar

9. Liu L, Zhou W, Li X, Sun Y. Dynamic event-triggered approach for cluster synchronization of complex dynamical networks with switching via pinning control. Neurocomputing (2019) 340:32–41. doi:10.1016/j.neucom.2019.02.044

CrossRef Full Text | Google Scholar

10. Liu J, Bao Y, Zheng W, Hayat S. Network coherence analysis on a family of nested weighted n-polygon networks. Fractals (2021) 29(8):2150260. doi:10.1142/s0218348x21502601

CrossRef Full Text | Google Scholar

11. Shang Y. Consensus and clustering of expressed and private opinions in dynamical networks against attacks. IEEE Syst J (2022) 14(2):2078–84. doi:10.1109/jsyst.2019.2956116

CrossRef Full Text | Google Scholar

12. Xu Y, Deng Y, Ma C, Zhang K. The enfigram: A robust method for extracting repetitive transients in rolling bearing fault diagnosis. Mech Syst Signal Process (2021) 158:107779. doi:10.1016/j.ymssp.2021.107779

CrossRef Full Text | Google Scholar

13. Du W, Zhu J, Gao H, Li X. Consensus analysis of the weighted corona networks. Front Phys (2022) 10:948247. doi:10.3389/fphy.2022.948247

CrossRef Full Text | Google Scholar

14. Muniraju G, Tepedelenlioglu C, Spanias A. Analysis and design of robust max consensus for wireless sensor networks. IEEE Trans Signal Inf Process over Networks (2019) 5(4):779–91. doi:10.1109/tsipn.2019.2945639

CrossRef Full Text | Google Scholar

15. Li X, Chen X, Yang Y, Mo L. Consensus analysis for high-order heterogeneous networks with communication delays and dynamically changing digraphs. Int J Control Automation Syst (2018) 16(2):550–8. doi:10.1007/s12555-016-0453-4

CrossRef Full Text | Google Scholar

16. Patterson S, Bamieh B. Consensus and coherence in fractal networks. IEEE Trans Control Netw Syst (2014) 1(4):338–48. doi:10.1109/tcns.2014.2357552

CrossRef Full Text | Google Scholar

17. Gao H, Zhu J, Chen X, Zhang L, Li X. Coherence analysis of symmetric star topology networks. Front Phys (2022) 10:876994. doi:10.3389/fphy.2022.876994

CrossRef Full Text | Google Scholar

18. Sun W, Sun M, Guan J, Jia Q. Robustness of coherence in noisy scale-free networks and applications to identification of influential spreaders. IEEE Trans Circuits Syst Express Briefs (2020) 37:1274–8. doi:10.1109/tcsii.2019.2929139

CrossRef Full Text | Google Scholar

19. Shang Y. Practical consensus for heterophilous multiagent networks with constrained states. J Franklin Inst (2022) 359(18):10931–48. doi:10.1016/j.jfranklin.2022.04.037

CrossRef Full Text | Google Scholar

20. Sun W, Hong M, Liu S, Fan K. Leader-follower coherence in noisy ring-trees networks. Nonlinear Dyn (2020) 102(3):1657–65. doi:10.1007/s11071-020-06011-9

CrossRef Full Text | Google Scholar

21. Liu F, Huang Q. Laplacian spectral characterization of 3-rose graphs. Linear Algebra its Appl (2013) 439(10):2914–20. doi:10.1016/j.laa.2013.07.029

CrossRef Full Text | Google Scholar

22. Wang X, Xu H, Dai M. First-order network coherence in 5-rose graphs. Physica A: Stat Mech its Appl (2019) 527:121129. doi:10.1016/j.physa.2019.121129

CrossRef Full Text | Google Scholar

23. Wang J, Huang Q, Belardo F, Huang Y. Comparison of expression of growth hormone-releasing hormone and its receptor splice variant 1 in different stages of endometriosis. Utilitas Mathematica (2013) 91:33–8.

PubMed Abstract | Google Scholar