Analysis on propagation law of shallow underground chemical explosion seismic waves

Introduction: Seismic waves generated by shallow underground explosions propagate differently from those generated by surface explosions. Thus, an accurate understanding of the propagation laws of seismic waves generated by explosions at various burial depths and TNT equivalent amounts is significant in assessing the destructive power of munitions and establishing guidelines for their application.

Methods: In this study, we conducted several ground vibration velocity tests of shallow underground chemical explosion seismic waves for various TNT equivalent amounts and burial depths in a shooting range and analyzed the propagation of the seismic waves. Using the explosion similarity theory and dimensional analysis, we derived an equation for the estimation of the particle vibration velocity of shallow underground chemical explosion seismic waves. This equation calculation results have a very high degree of agreement with the measured data, measured data verify that the accuracy of the calculation model is better than 90.2%.

Results and discussion: This equation calculation results have a very high degree of agreement with the measured data, measured data verify that the accuracy of the calculation model is better than 90.2%, which greatly improves the calculation accuracy of the shallow underground chemical explosion seismic wave particle vibration velocity, and thus provide effective theoretical support for analyzing explosion seismic waves in engineering tests.

1 Introduction

One of the main parameters in the evaluation of the destructive power of munitions is the propagation of the explosion-generated seismic waves. Seismic waves can propagate through various media such as soil, sand, and concrete, and their energy decays gradually during propagation. Thus, seismic waves exhibit favorable characteristics for long-distance transmission and lasting damage [1–3]. The depths at which explosives are buried have a significant effect on the propagation law of the generated seismic waves. The commonly used formula for calculating peak ground vibration velocity of surface explosions of ammunition cannot well reflect the propagation attenuation law of seismic waves caused by shallow underground explosions. The theoretical calculation results are of low accuracy and poor usability, and thus lack practical value. Therefore, it is necessary to conduct research on the propagation attenuation law of seismic waves caused by shallow underground explosions, and establish a calculation function with higher accuracy for peak ground vibration velocity of seismic waves caused by shallow underground explosions. This is of great significance for accurately evaluating the destructive power of ammunition explosions, guiding ammunition design and use, and seismic protection of targets.

In recent years, research on shallow underground chemical explosions has mainly focused on the analysis of the explosion shock wave pressure and size of the explosion crater. Studies on the analysis of seismic wave propagation are relatively fewer and have particularly focused on the propagation law of seismic waves concerning surface and air explosions. [4] designed and optimized the overall procedure of a test network for the sensing of explosion-generated seismic wave distribution and obtained accurate information on the seismic wave signals caused by surface explosions. Furthermore, using the time difference of the arrival localization principle, they obtained accurate information on the locations of explosion points. [5] detected seismic waves generated by ground explosions and subsequently analyzed their spatiotemporal evolution and frequency characteristics to identify their dominant frequency bands. [6] conducted surface explosion tests under various charge amounts and detonation conditions and obtained an attenuation law of propagating explosion-generated seismic waves via theoretical analysis, on-site monitoring, digital signal processing, and other methods. [7] estimated the vibration intensity of cloud bomb explosion-generated seismic waves and established their attenuation law. Furthermore, based on the existing particle vibration velocity equation, they derived an equation for the determination of the particle vibration velocity of cloud bomb explosion-generated seismic waves and reported good consistency between calculated and measured data. [8] examined the propagation characteristics, particularly the dominant frequency distribution, of explosion-generated seismic waves in square-shaped, V-shaped, and U-shaped depressions using a three-dimensional finite element numerical simulation to investigate the influence of local depression topography on the propagation of explosion-generated seismic waves. [9] analyzed the effects of explosion vibration velocity field and frequency on the seismic wave propagation and investigated the correlation between the explosion vibration velocity and the explosion equivalent and propagation distance of the seismic wave. Furthermore, they determined the band dominant frequency, duration, near-field initial motion, and propagation law of rock and soil explosion-generated seismic waves. [10] analyzed the time-domain and frequency-domain characteristics of seismic wave signals generated by thermobaric warhead air explosions and reported a method for the evaluation of the damage power of the seismic waves. To study the fluctuation of rocks and soil under the action of shallow buried underground explosions, [11] established a theoretical model based on the free surface motion of seismic waves in a semi-infinite medium, and the results indicated a negative correlation between the explosion seismic wave displacement and the explosion source burial depth. Based on the conservation of seismic energy and experiential relation, [12] proposed a model for the envelope function of the power spectral density and acceleration amplitude of explosion-generated seismic waves that considered the influence of charge volume and burst distance. They used measured explosion test data to calibrate the model parameters and thus provided a method for the practical simulation of single-point, two-point (slight difference) and multi-point (micro-difference) explosion seismic waves. [13] investigated the irregular changes occurring in the particle vibration time history of seismic waves during the strong seismic stage and reported that the characteristics of strong seismic pulses could not be described using a Fourier spectrum. Furthermore, their results provided vital information for analyzing the impact characteristics of explosion-generated seismic waves. [8] established a physical similarity model of an open pit slope and conducted blast tests to study the propagation of explosion seismic waves through various filling media and structural surface inclination angles.

To calculate ground vibration velocity of explosion-induced seismic waves more accurately, domestic and foreign researchers have conducted relevant research based on Sadowski’s formula. [14] investigated the vibration attenuation law of deep-buried small clearance tunnels based on scale analysis and established an expanded Sadowski expansion formula that considers the resistance line and the free surface. The experimental results show that the extended Sadowski formula can better predict the vibration attenuation caused by explosions in deep-buried small clearance tunnel engineering. [15] used regression analysis based on on-site monitoring data of blasting to compare the relative errors between the traditional Sadowski formula and the improved formula that considers dimension analysis and altitude. The improved formula has higher calculation accuracy. The research results are of certain significance for the safety evaluation of blasting. [16] analyzed the collected vibration data and fit reasonable K and alpha values using the linear regression method. They provided Sadowski formula coefficients suitable for the experimental geological conditions and determined the safety range of blasting vibration control for the applicable geological conditions. [17] considered the influence of the errors of the distance from the measuring point to the center of the seismic source and the pressure of the air shock wave (ASW) frontal pressure on the calculation of the equivalent TNT mass obtained by the Sadowski empirical formula. They evaluated the external factors affecting the calculation results of the equivalent TNT mass when explosives explode in the air. [18] established a source energy calculation model for underground explosions under different terrain conditions based on a modified Sadowski formula that reflects the elevation difference factor. Compared with the traditional source energy model, the proposed modified source model greatly improved the calculation accuracy. The research results provide a reliable method for calculating the explosive energy of penetrating weapons. [19] converted and sorted the blasting vibration velocity monitored on-site based on the Sadowski formula, and performed linear regression on the monitoring data of the slowest velocity decay to obtain the Sadowski formula with the slowest velocity decay. Based on this formula and the vibration control value, they used the linear regression control method to calculate the blasting amount for subsequent construction. This calculation method provides a reference for designing the blasting amount in subsequent engineering projects. [20] conducted regression analysis on the blasting vibration velocity of different elevation points through on-site small-scale tests and verified the applicability of the Sadowski formula for small-scale blasting while considering the elevation effect. In practical engineering applications, the relevant coefficient values should be determined based on the geological conditions of the project, and then the Sadowski formula or modified formula should be used to obtain more accurate calculation results.

From the above analysis, it can be seen that the analysis of the propagation law of explosive seismic waves mainly focuses on the seismic effects caused by surface explosions of ammunition and the regression analysis of the Sadowski formula using acquired data. However, there is currently no accurate and comprehensive research on the propagation attenuation law of seismic waves caused by shallow underground explosions and the construction of a calculation formula for ground vibration velocity of explosive seismic waves with clear physical significance. Therefore, it is necessary to carry out research on the propagation and evolution law and vibration calculation formula of seismic waves caused by shallow underground explosions.

In this study, the vibration velocity signals of seismic waves under various TNT charge amounts and burial depths were measured using a ground vibration velocity measurement system and subsequently analyzed to establish an evolution law for seismic waves generated by shallow underground explosions. An equation for calculating seismic wave-particle vibration velocity was derived based on the explosion similarity theory using dimensional analysis, which provides a highly precise theoretical method for the data acquisition of shallow underground chemical explosion seismic waves.

2 Propagation characteristics of explosion seismic waves

Seismic waves are elastic waves and can be divided into two basic types: body waves and surface waves. Body waves can be further classified into longitudinal waves and shear waves. Longitudinal waves (P wave) are waves whose propagation direction is consistent with the particle vibration direction in the medium. They cause the medium to compress or expand and are also known as compression, tensile, or density waves. Longitudinal waves exhibit the lowest energy, lowest amplitude, and highest propagation speed and are generally the earliest to reach a measurement point [21,22]. Shear waves (S waves) propagate in a direction perpendicular to that of the particle vibration resulting in shear deformation of the medium. Shear waves exhibit higher energy, higher amplitude, and lower propagation speed than longitudinal waves.

To study the propagation of body waves in a media, the influence of a physical force is generally ignored. The equations of motion is shown in Eq. 1

$\rho \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}=\left(\lambda +G\right)\nabla \left(\nabla •u\right)+G{\nabla }^{2}u(1)$

where $\rho$ is the medium density, $\lambda$ is the Lame constant, G is the shear or stiffness modulus, $u$ is the displacement vector, and $\nabla$ is the Laplace operator.

Surface waves are waves that propagated along a surface or a medium interface formed due to a discontinuous surface in the medium. Rayleigh and Loew waves are examples of surface waves; Loew waves are only generated when a thin layer of different media is present on a half-space surface [23,24], while Rayleigh waves are formed by the superposition of longitudinal waves and shear waves with a particle displacement perpendicular to a free surface. Using an explosion equivalent load model, in which the blast source is simplified to a spherical cavity, the motion law of explosion seismic waves on the free surface of a semi-infinite medium can be analyzed according to the elastic dynamics classical Lame problem solution. If the horizontal and vertical displacements of a free surface are represented as $w_r$ and $w_z$, respectively, the displacement of surface particles under any pulse can be expressed as Eq. 2 [25,26]

$w\left(r,z,t\right)={\int }_0^t{f}_1\left(t-\tau \right)w_{\epsilon }\left(r,z,t\right)d\tau (2)$

$w\left(r,z,t\right)$ is the central source perturbation solution which varies according to the unit transition function $\epsilon \left(t\right)$ and $f\left(t-\tau \right)$ represents the transition from the basic central source to other sources and is calculated using Eq. 3

$f\left(\tau \right)=f\left(\tau \right)-{\int }_0^{\tau }f\left(s\right)\exp \left[-\left(\tau -s\right)\right]ds(3)$

Assuming $\gamma =\frac{C_S}{C_P}$ and $a=\frac{1}{C_P}$, the specific form of the $w_r$ component can be expressed as Eq. 4

$w_r=-\frac{4}{\pi {\xi }_1}{\int }_1^{\frac{1}{r}}\frac{{\left(2-{\lambda }^2\right)}^2\sqrt{{\lambda }^2-1}}{{\left(2-{\lambda }^2\right)}^4+16\left({\lambda }^2-1\right)\left(1-{\lambda }^2{\gamma }^2\right)}(\eta \sqrt{1-{\gamma }^2{\lambda }^2}\sin \frac{{\phi }_1}{2}+\gamma \lambda \cos \frac{{\phi }_1}{2})\frac{d\lambda }{\sqrt{{\rho }_1}}(4)$

The specific form of the $w_z$ component as Eq. 5

$w_z=-\frac{8}{\pi }{\int }_1^{\frac{1}{r}}\frac{{\left(2-{\lambda }^2\right)}^2\sqrt{{\lambda }^2-1}\sqrt{1-{\lambda }^2{\gamma }^2}}{{\left(2-{\lambda }^2\right)}^4+16\left({\lambda }^2-1\right)\left(1-{\lambda }^2{\gamma }^2\right)}\sin \frac{\phi }{2}\frac{d\lambda }{\sqrt{{\rho }_1}}(5)$

In the above equations,

${\rho }_1=\sqrt{\left[{\xi }^2+{\eta }^2\left(1-{\lambda }^2{\gamma }^2\right)-{\left(\lambda C_S\right)}^2{a}^2\right]+4{\left(\lambda C_S\right)}^2{a}^2{\xi }^2\left(1-{\lambda }^2{\gamma }^2\right)}(6)$

$\varphi =\arctan \theta \left[\frac{2\left(\lambda C_S\right)a\eta \sqrt{1-{\lambda }^2{\gamma }^2}}{{\left(\lambda C_S\right)}^2{a}^2-{\xi }^2-{\eta }^2\left(1-{\lambda }^2{\gamma }^2\right)}+\frac{\pi }{2}\right](7)$

The above equations can be used to evaluate the horizontal and vertical displacement as well as the particle vibration velocity of explosion seismic waves and consequently describe the model of the particle vibration displacement in a semi-free space.

3 Composition and principle of explosion seismic wave testing system

As the seismic wave produced at an explosion site are short-duration non-stationary random signals that exhibit rapid mutation [27], the response time of the seismic wave sensor should be as short as possible with a favorable response rate. In general, the frequency range of the explosion seismic wave is between 30 and 300 Hz [28], and the working bandwidth of the sensor needs to meet this range. Because the test site environment is bad and there are many uncertain factors, the test system needs to have good reliability to ensure the test normal conduct.

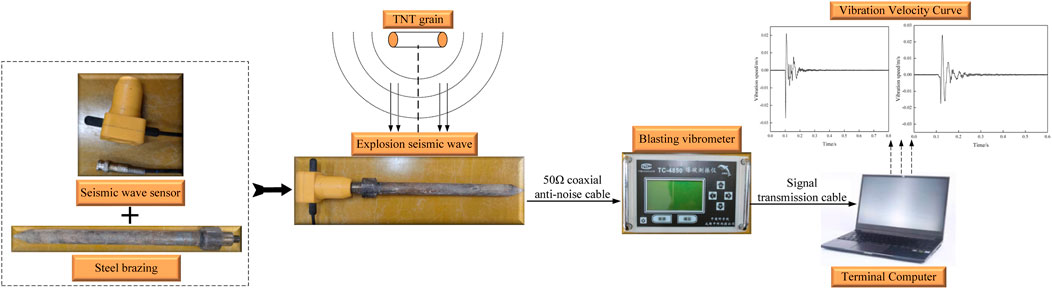
Seismic waves propagate such that in a near-field region, transverse waves and longitudinal waves arrive at virtually the same time, whereas, in a far-field region, longitudinal waves arrive earlier. Far-field seismic waves are mainly Rayleigh waves. Rayleigh wave on the tangential, radial and vertical vibration direction there is a certain relationship, so it can choose a direction to measure the explosion seismic wave ground vibration velocity [29]. However, in an actual explosion text, the longitudinal vibration velocity is generally measured for explosion seismic wave. Based on the frequency range of explosion seismic wave vibration signals, a single magnetoelectric speed sensor of the inertial type was selected. The sensor is installed such that its upper surface is 20 cm above the ground. Furthermore, to ensure that the sensor and the Earth are connected as one, it is fastened on a steel structure using a thread and the structure is then buried into the soil and tamped. After an ammunition explosion, the resulting vibrations travel along the NovoLog ground, soil, and rocks and cause the sensor shell to vibrate. However, owing to inertia, the core rod, coil, and damping ring of the sensor do not vibrate, which leads to relative motion between these components and the shell. Consequently, an electromotive force proportional to the vibration velocity is induced owing to the magnetic field in the air gap in the coil.

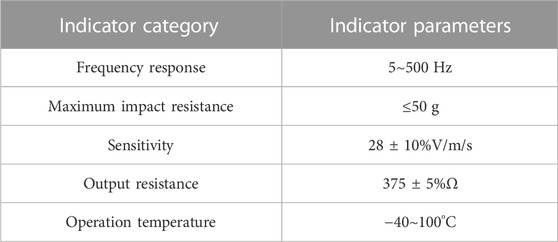
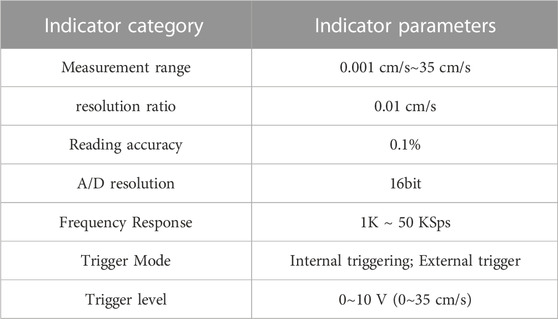
The seismic wave measurement system for the explosion site consists of a single magnetoelectric velocity sensor, a TC-4850 blasting vibration meter, a data acquisition/processing terminal, and a 50 Ω coaxial anti noise cable. The main technical parameters of a single magnetoelectric speed sensor and a blasting vibration meter are shown in Tables 1, 2.

TABLE 1

TABLE 1. Main technical specifications of single item magnetoelectric speed sensor.

TABLE 2

TABLE 2. Main technical specifications of TC-4850 blasting vibration tester.

Due to the formation of high-speed flying fragments caused by the shell rupture during the ammunition explosion process, the impact of fragments on the vibration meter can directly cause damage to the measurement system and prevent data acquisition. Therefore, in actual testing, the vibration meter is usually placed inside a steel box, and then the vibration meter and protective box are buried underground by digging a pit. To ensure accurate acquisition of ground vibration signals during the explosion process, the triggering method of the vibration meter is set to internal triggering, with a triggering level of 0.1 cm/s and a negative delay collection time of 1 s, to ensure accurate acquisition of the variation law of velocity with time during the ground vibration process.

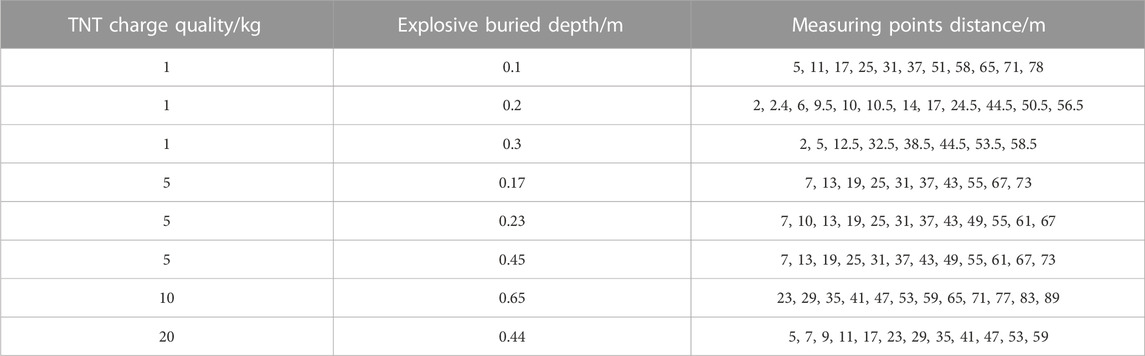
Figure 1 shows the structure of the explosion seismic wave measurement system, and Table 3 shows the values of the TNT charge, charge burial depth, and measurement point layout distance used in this study. The selection of TNT explosive mass and burial depth is based on relevant experiments conducted in the early stage. The selection of measurement point positions is mainly based on the estimated peak ground vibration velocity caused by TNT explosive mass explosion and the measurement point positions that will be focused on in the subsequent research process.

FIGURE 1

FIGURE 1. Explosion seismic wave measurement system.

TABLE 3

TABLE 3. Explosion test parameters and measuring points location.

4 Seismic wave test results analysis

The seismic wave data of the shallow underground chemical explosion tests were extracted, and the ground vibration velocity curves for the various TNT charges, different explosive burial depth and different measuring point distances were obtained as shown in Figure 2. As numerous tests were conducted, it will be tedious and futile to report all the ground vibration velocity curves. As shown in Figure 2, we have chosen to report the vibration velocity curves generated under four explosion conditions; TNT equivalent of 1 kg and burial depth of 0.1 m and 0.3 m, TNT equivalent of 5 kg and burial depth of 0.23 m, and TNT equivalent of 20 kg and burial depth of 0.44 m. The peak ground vibration velocities for the four explosion conditions were estimated from the respective curves and are shown in Table 4.

FIGURE 2

FIGURE 2. Explosion seismic wave ground vibration velocity curve for (A) TNT equivalent 1 kg, burial depth 0.1 m, and measurement point distances of 5, 11, 17, 25, and 31 m (B) TNT equivalent 1 kg, burial depth 0.3 m, and measurement point distances of 38.5, 44.5, 53.5, 58.5 and 65.5 m (C) TNT equivalent 5 kg, burial depth 0.23 m, and measurement point distances 43, 49, 55, 61 and 67 m (D) TNT equivalent 20 kg, burial depth 0.23 m, and measurement point distances of 43, 49, 55, 61 and 67 m.

TABLE 4

TABLE 4. Peak ground vibration velocity values of the explosion seismic waves (cm/s).

It can be seen from the ground vibration velocity curve in Figure 2 that the seismic wave signal generated during the explosion of the ammunition has only one peak. After the peak, the ground vibration velocity gradually attenuates and tends to 0 m/s. The ground vibration velocity curves at different measuring points have a high degree of similarity in the changing trends. This is because among the components of the explosion seismic wave, the Rayleigh wave has the largest amplitude on the free surface. Therefore, from the ground vibration velocity curve of the explosion seismic wave, the ground vibration velocity peak caused by the Rayleigh wave is the most significant, which is essentially different from natural seismic waves. Combined with the peak ground vibration velocity data in Table 4, the basic propagation law of explosive seismic waves in the soil medium can be obtained for different explosive TNT masses, different measuring point positions and different explosive burial depths. To more clearly analyze the relationship between the peak value and attenuation rate of explosive seismic wave ground vibration velocity and TNT charge and explosive buried depth, plot and analyze the peak value data of seismic wave ground vibration velocity in the above 8 different explosion environments. Taking the measurement point distance as the independent variable x and the ground vibration velocity peak value as the dependent variable y, the peak change curve of seismic waves ground vibration velocity is plotted, such as Figure 3 shown.

FIGURE 3

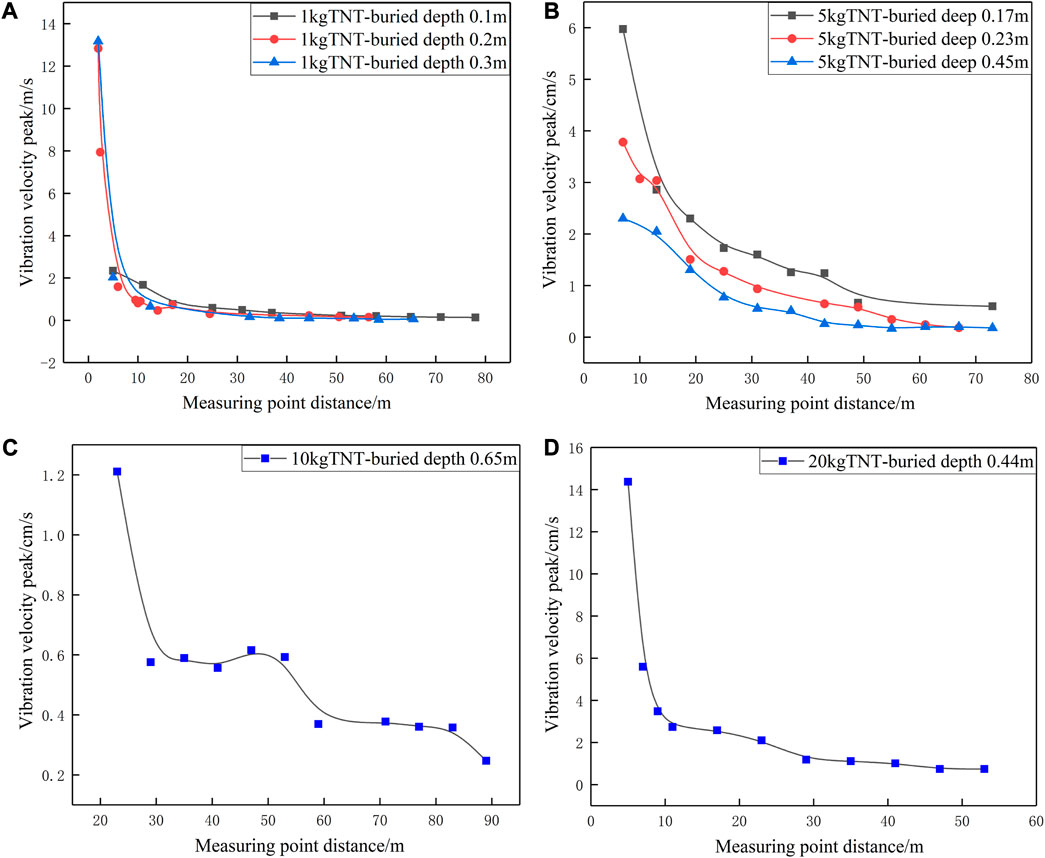
FIGURE 3. Peak ground vibration velocity curves for (A) 1 kg TNT and burial depths 0.1, 0.2, and 0.3 m (B) 5 kg TNT and burial depths 0.17, 0.23, and 0.45 m (C) 10 kg TNT and burial depth 0.65 m (D) 20 kg TNT and burial depth 0.44 m.

The results indicate that although the peak ground vibration velocity exhibits a negative correlation with the measuring point distance, the attenuation rate is not constant. As indicated by the tendency of the slope of the peak ground vibration velocity peak attenuation curve, the peak value decays faster at a measurement point closer to the burst center, and the duration of the ground vibration at a particular speed is longer at a measurement point away from the burst center. Furthermore, the propagation distance of the seismic wave is larger and damage to the target is more intense. For example, the attenuation rate of the peak ground vibration velocity from 2 to 2.4 m for the explosion of a 1 kg TNT equivalent buried at a depth of 0.2 m is 12.2585 cm/s/m. As the measurement point distance increased, the attenuation rate gradually decreased from 12.2585 cm/s/m to 1.7619 cm/s/m 2.4–6 m), 0.1809 cm/s/m (6–9.5 m), 0.1698 cm/s/m (10–10.5 m), 0.087 cm/s/m (14–17 m), and 0.0562 cm/s/m (17–24.5 m), which indicates that the ground vibration velocity of the explosion seismic wave gradually weakens. Furthermore, the results showed that the attenuation law of the vibration velocity changed abruptly at certain measurement points and did not exhibit acceptable consistency from the first to the last measuring point. In Figure 3, the peak ground vibration velocity for an explosion of 10 kg TNT buried at a depth of 0.65 m, measured at a point 47 m from the burst center (0.6154 cm/s) was higher than that measured at a point 41 m from the burst center (0.5565 cm/s), which was not consistent with the law of seismic wave propagation attenuation. This abnormality in the results was attributed to an error in the sensor installation process. The sensors in question were buried at different depths which resulted in a higher value of the vibration velocity at a distance away from the burst center. After disregarding the incorrect data, the measured results generally met the propagation law of explosion seismic waves in a soil medium. Therefore, to obtain accurate data and make reliable comparisons, the velocity sensors must be installed at the same burial depth.

At a constant TNT equivalent value, the peak ground vibration velocity of the explosion seismic waves decreased as the burial depth increased, which indicated a negative correlation. The change in the peak ground vibration velocity with the burial depth for TNT equivalent charges of 1 kg and 5 kg is shown in Figure 4.

FIGURE 4

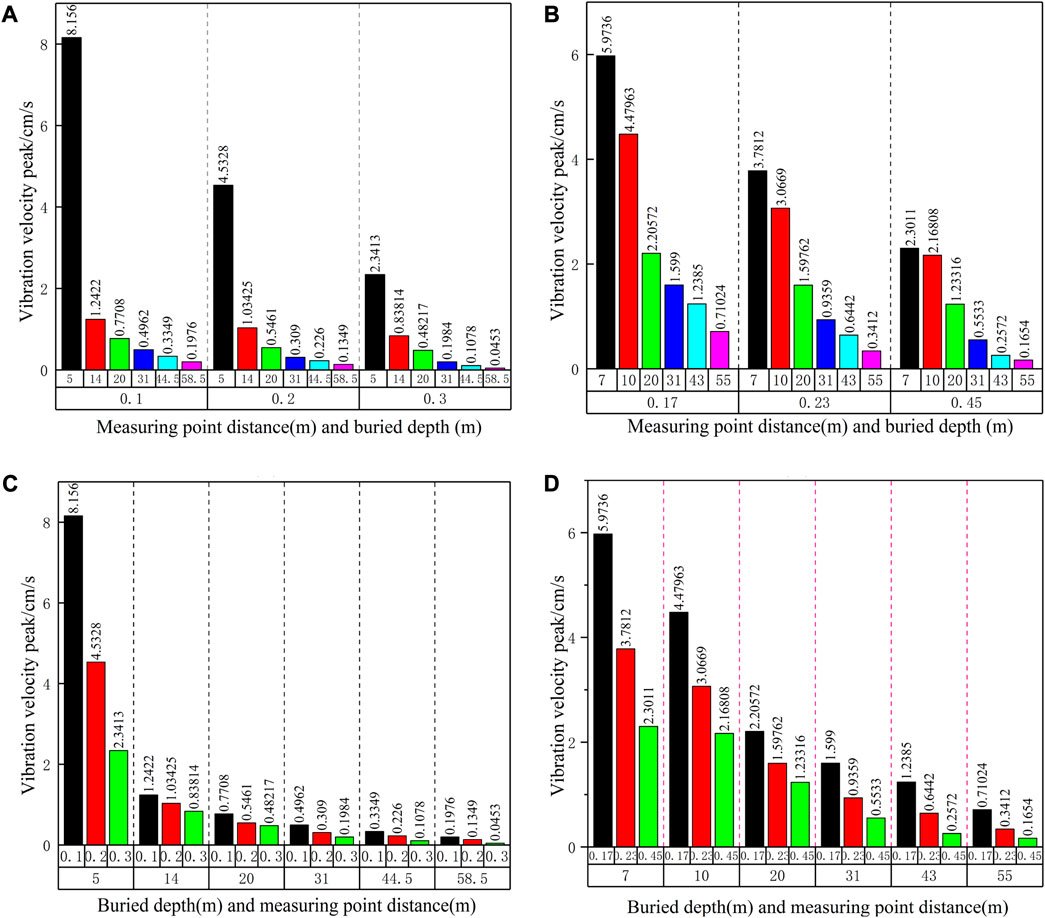
FIGURE 4. Correlation between the peak ground vibration velocity and explosive burial depth (A) and (C) 1 kg TNT and burial depths 0.1, 0.2, and 0.3 m at various measurement point distances, (B) and (D) 5 kg TNT and burial depths 0.17, 0.23, and 0.45 m at various measurement point distances.

As shown in Figure 4, the peak vibration velocity decreases exponentially (quadratic function) with an increase in the explosion distance and burial depth. The peak ground vibration velocity, measured at a distance of 19 m from the explosion center, for a TNT equivalent of 5 kg decreased from 2.2987 cm/s to 1.5071 and 1.3047 cm/s as the burial depth was increased from 0.17 m to 0.23 and 0.47 m, respectively. and closer to the explosion center. At a measurement point distance of 7 m from the explosion center, decreased from 5.9736 cm/s to 3.7812 and 2.3011 cm/s as the burial depth was increased from 0.17 m to 0.23 and 0.47 m, respectively, indicating that the attenuation rate of the peak vibration velocity (9.9018 cm/s/m) is more significantly affected by the burial depth closer to the explosion center. For a constant burial depth, the attenuation rate of the peak vibration velocity for an increase in the measurement point distance from 7 to 55 m was 0.1097 cm/s/m. This indicated that the change in the burial depth exhibited a more significant effect than the change in the measuring point distance on the peak ground vibration velocity of the explosion seismic waves.

The correlation between the explosive burial depth and peak vibration velocity was further analyzed based on the mechanism of the generation of explosion seismic waves. When an explosive explodes in air, the explosive products expand significantly, collide with the ground, and consequently, owing to the compressibility of the surface propagation medium, partly convert to seismic waves manifested as vibrations on the ground. The vibration velocity is directly related to the energy transformation in the collision process, and the higher the compressibility of the ground propagation medium, the higher the conversion of the energy of the explosive products into seismic waves, and consequently the higher the peak ground vibration velocity. According to the density distribution law for a surface propagation medium, as the burial depth increases, the soil medium becomes denser. Thus, soil closer to the surface is more readily compressed, which increases the proportion of explosion products converted to seismic waves, and consequently a higher peak ground vibration velocity. Whereas, the soil compressibility decreases with depth, and thus the peak ground vibration velocity of the explosion seismic waves decreases.

5 Particle vibration velocity calculation model

The ground vibration velocity curves generated under various TNT charges and burial depths indicated that the propagation law of explosion seismic waves for a shallow underground chemical explosion is closely related to the burial depth [30]. However, at present, the existing equation for the estimation of the particle vibration velocity is only applicable for air explosions and thus provides unreliable results for ground explosions, particularly for certain burial depths. Therefore, to solve this issue, along with the measuring point distance and TNT charge, the burial depth must also be considered in the formulation of an equation for the ground vibration velocity of seismic waves generated by shallow underground explosions.

Several studies have reported that the ground vibration velocity of explosion seismic waves is directly related to the compressibility and energy conversion ratio of the propagation medium. As the propagation medium compressibility is mainly related to the material density $\rho$, and the material sound velocity $C$ also affects the seismic waves travel speed [28], based on the similarity law of explosion, the peak ground vibration velocity of explosion seismic waves can be expressed in terms of the equivalent TNT charge $Q$, unit of TNT explosive release quality chemical energy $E_0$, measuring point distance $R$, material density $\rho$, and sound velocity $C$ (Eq. 8).

$V=f\left(Q,E_0,R,\rho ,C\right)(8)$

According to the dimensional homogeneity principle and comprehensively considering the form and physical meaning of the independent variable dimension, the equivalent TNT charge $Q$, measuring point distance $R$, and speed of sound $C$ are selected as reference physical quantities, and the dimensional power exponent is sorted based on the Π theorem [31,32]. Thus, three dimensionless physical quantities can be expressed as Eq. 9

$\left\{\begin{array}{l}{\mathrm{\Pi }}_1=\frac{E_0}{C^2}\\ {\mathrm{\Pi }}_2=\frac{\rho R^3}{Q}\\ {\mathrm{\Pi }}^{\prime }=\frac{V}{C}\end{array}\right.(9)$

Eq. 8 can be rewritten as Eq. 10

$\frac{V}{C}=f\left(\frac{E_0}{C^2},\frac{\rho R^3}{Q}\right)(10)$

In an actual explosion test, the energy $E_0$ released by an equivalent TNT charge $Q$ is calculated as a product, and thus, Eq. 10 can be rewritten accordingly as Eq. 11

$\frac{V}{C}=f\left(\frac{Q{E}_0}{\rho C^2{R}^3}\right)(11)$

From the perspective of stress wave theory, for a specific surface propagation medium, $\rho C^2$ represents a certain elastic parameter of the material [33]. For linear elastic materials, $\rho C^2$ is the material elastic modulus, and its dimension is consistent with those of stress and pressure. It can be represented as a dimensionless quantity, for a propagation medium pressure $P_0$ and charge burial depth $H$ using Eq. 8, and the functional relationship of the particle vibration velocity V can be expressed as Eq. 12

$V=f\left(Q,E_0,R,\rho ,C,P_0\right)(12)$

Furthermore, its dimensionless function can be expressed as Eq. 13

$\frac{V}{C}=f\left(\frac{Q{E}_0}{\rho C^2{R}^3},\frac{P_0}{\rho C^2}\right)(13)$

For a specific medium, there exists a functional relationship between the dimensionless peak particle vibration velocity $V$ and the dimensionless charge Q, and thus, Eq. 13 can be further rewritten as Eq. 14

$\frac{V}{C}=f_1\left(\frac{Q{E}_0}{\rho C^2{R}^3}\right)f_2\left(\frac{P_0}{\rho C^2}\right)(14)$

Based on the results of previous experiments, the functional relationship represented in Eq. 14 is concretized, and the materialized functional relationship is represented as Eq. 15

$\frac{V}{C}\sqrt{\frac{P_0}{\rho C^2}}=f\left(\frac{Q{E}_0}{\rho C^2{R}^3}\right)(15)$

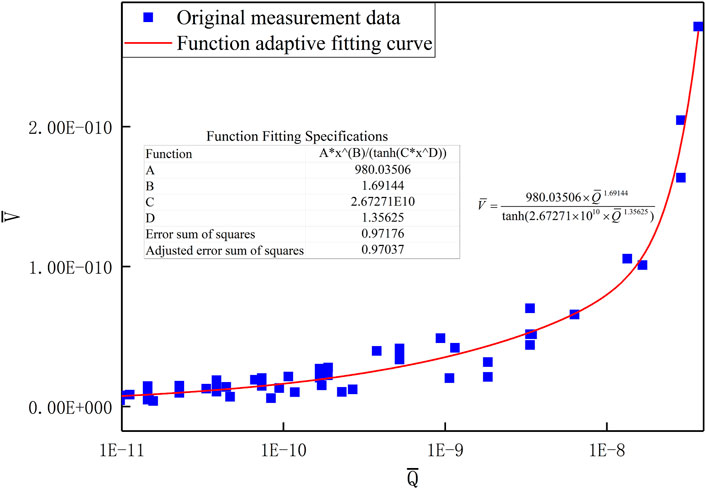
To obtain a quantitative expression of the functional relationship of the particle vibration velocity, the explosion seismic wave test data performed in this study were organized according to Eq. 15 During data sorting, $\overline{V}=\frac{V}{C}\sqrt{\frac{P_0}{\rho C^2}}$, and $\overline{Q}=\frac{Q{E}_0}{\rho C^2{R}^3}$ were defined, the data sorting result is shown in Figure 5.

FIGURE 5

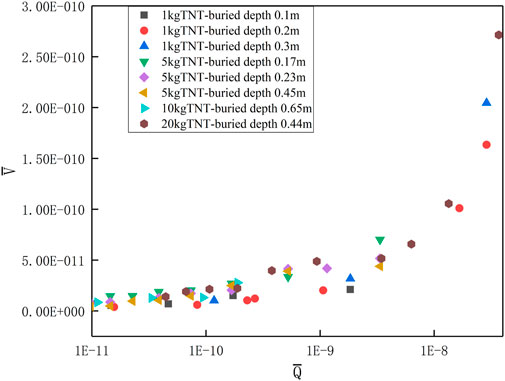
FIGURE 5. Dimensionless particle vibration velocity peaks produced by different TNT charges and different explosive burial depths.

The results in Figure 5 indicate that the general trend of the sorted data satisfies the consistent variation law. Therefore, to obtain a quantitative formula for calculating the particle vibration velocity of explosive seismic waves, using a nonlinear adaptive fitting method to fit the functional relationship of the above test data, the functional relationship consistent with the above-mentioned data trend is as Eq. 16

$\overline{V}=\frac{980.03506\times {\overline{Q}}^{1.69144}}{\tanh \left(2.67271\times {10}^{10}\times {\overline{Q}}^{1.35625}\right)}(16)$

The above functional relationship fitting results and the existing measured data and the function fitting technical indicators are shown in the following Figure 6.

FIGURE 6

FIGURE 6. The fitting effect of the functional relationship and the measured data.

The results of the curve fitting in Figure 6 indicate that the established fitting curve is consistent with the peak ground vibration velocity of the explosion seismic waves measured at various distances for various TNT charges and burial depths. Furthermore, the error sum of the functional relationship fitting curve for the measured seismic wave data is 0.97176 (the closer the sum of squares of errors is to 1, the better the fitting effect of the function and the more significant the fitting model), which indicates a high fitting accuracy.

We use the measured seismic wave data of shallow chemical explosion with the mass of TNT explosive of 5 kg and 10 kg and the buried depth of explosive of 0.2 m and 0.65 m respectively to verify the calculation accuracy of the model. The relative error between the calculated value and the measured value is shown in Figure 7. The calculation formula of relative error is shown in Eq. 17

$\phi =\left|\frac{\mathrm{C}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}-\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}\right|\times 100\%(17)$

FIGURE 7

FIGURE 7. Relative error diagram of measured value and calculated value.

It can be seen from the relative error results between the above measured values and calculated values that the maximum relative error occurs when the TNT explosive mass is 5 kg, and the distance between the measuring point and the detonation center is 15 m, 9.8%; the minimum relative error occurs when the TNT explosive mass is 10 kg, and the distance between the measuring point and the detonation center is 7 m, 0.4%; the relative error at other measuring points is between the two. It can be concluded that the calculation accuracy of the above equation for calculating the vibration velocity of shallow underground chemical explosion seismic wave is better than 90.2%. Therefore, the particle vibration velocity formula of explosive seismic wave established by the method of explosion similarity law and dimensional analysis in this study can reflect the propagation attenuation law of shallow chemical explosion seismic wave, and can provide theoretical support for the calculation of ground vibration velocity of shallow chemical explosion seismic wave in engineering testing. Therefore, the equation for the estimation of particle vibration velocity of explosion seismic waves established in this study using the explosion similarity law and dimensional analysis method can accurately reflect the propagation and attenuation law of shallow underground chemical explosion seismic waves. Consequently, it provides theoretical support for the calculation of the ground vibration velocity of seismic waves generated by shallow underground chemical explosions in engineering tests.

6 Conclusion

Due to the fact that the propagation attenuation law of seismic waves caused by surface explosions of ammunition and the existing theoretical models for calculating ground vibration velocity cannot well reflect the propagation characteristics of explosive materials caused by shallow underground explosions, a measurement system for seismic waves caused by shallow underground explosions was established. A research study was carried out to investigate the ground vibration velocity of explosive seismic waves with different TNT explosive masses at different depths. The analysis of the test results shows that:

(1) In the process of shallow underground explosions, the ground vibration velocity of explosive seismic waves decreases gradually with the increase of the distance from the epicenter of the explosion. However, the attenuation rate is not consistent. Specifically, in areas close to the epicenter, the vibration velocity attenuates rapidly, while in areas far from the epicenter, the vibration velocity attenuates slowly. Moreover, the duration of the seismic waves is longer. Therefore, the destructive range of the explosive seismic waves is greater and the destructive effect lasts longer.

(2) The size of the ground vibration velocity peak of explosive seismic waves caused by shallow underground explosions is significantly affected by the depth of the explosive material. When the TNT charge mass is constant, the ground vibration velocity peak of the explosive seismic waves gradually decreases with the increase of the depth of the explosive material, and the size of the vibration velocity peak is negatively correlated with the depth of the explosive material. Moreover, the influence of the depth of the explosive material on the vibration velocity peak is much greater than the influence brought by changes in distance from the measurement point.

(3) A calculation formula for the ground vibration velocity of explosive seismic waves caused by shallow underground explosions was established based on the explosion similarity theory and dimensional analysis. By using the measured data and nonlinear adaptive fitting, a quantitative functional relationship expression was obtained. The calculation results of this functional relationship formula are in very good agreement with the measured data, and the calculation accuracy of the functional relationship formula is better than 90.2%.

The research results clarify the relationship between the propagation attenuation law of seismic waves caused by shallow underground explosions and the depth of explosive materials. The calculation formula for the ground vibration velocity peak of explosive seismic waves established using dimensional analysis methods has higher accuracy than the traditional Sadovsky formula calculations. It can better reflect the propagation and distribution characteristics of shallow underground explosive seismic waves, and provides theoretical support for the calculation of ground vibration velocity peaks caused by shallow underground explosions and the seismic performance structure design of targets. It has significant engineering application value.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LW: Conceptualization; data curation; formal analysis; methodology; software; writing–original draft; DK: Project administration; writing—review and editing; resources. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by National Foundation Strengthening Program Key Research Project and National Equipment Program of China, project numbers 2021-JCJQ-ZD-360-11 and 14021001050206.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer CZ declared a shared affiliation with the authors to the handling editor at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chen H, Kong DR, Tong X, Yang F, Li LP. Research on measuring methods on explosion seismic waves. APPL MECH MATE (2014) 670-671:1188–93. doi:10.4028/www.scientific.net/AMM.670-671.1188

CrossRef Full Text | Google Scholar

2. Hamama I, Yamamoto MY, Eigabry MN, Medhat NI, Elbehiri HS, Othman AS, et al. Investigation of near-surface chemical explosions effects using seismo-acoustic and synthetic aperture radar analyses. J ACOUST SOC Am (2022) 151(3):1575–92. doi:10.1121/10.0009406

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yang JH, Wu ZN, Sun WB, Yao C, Wang Q. Numerical simulation on radiation and energy of blast-induced seismic waves in deep rock masses. J Cent South Univ (2022) 29(2):645–62. doi:10.1007/s11771-022-4908-x

CrossRef Full Text | Google Scholar

4. Zhu YJ. Analysis and processing of seismic wave signals in explosion point location. Taiyuan, China: North University of China (2021). doi:10.27470/d.cnki.ghbgc.2021.001143

CrossRef Full Text | Google Scholar

5. Chen YH, Ma K, Chen J. Evolution and frequency characteristics of ground explosion seismic waves. Ind Saf Environ Prot (2021) 47(05):13–5.

Google Scholar

6. Ma K. Research on the measurement and propagation law of surface explosion seismic waves. Minneapolis, Minnesota: North Central University (2021). doi:10.27470/d.cnki.ghbgc.2021.000642

CrossRef Full Text | Google Scholar

7. Wang LQ, Shang F, Kong DR. Research on the seismic wave test method of a certain type of cloud bomb explosion. J Test Tech (2020) 34(05):376–80. doi:10.3969/j.issn.1671-7449.2020.05.002

CrossRef Full Text | Google Scholar

8. Li WT, Zhao K, Xu CY. Research on the influence of local depression topography on the propagation law of explosion seismic waves. Mod Mining (2019) 35(09):56–60. doi:10.3969/j.issn.1674-6082.2019.09.016

CrossRef Full Text | Google Scholar

9. Yang L, Han Y, Tang Q. Mechanism and site effect analysis of explosion earthquakes. Gansu Sci Tech (2014) 33(18):37–41.`

Google Scholar

10. Zhang MM. Research on the seismic wave test method in the explosion field of the thermobaric warhead. Nanjing, Xuanwu: Nanjing University of Science and Technology (2017).

Google Scholar

11. Liu HQ, Yang HD. Motion law of explosion seismic waves on free surface of semi-infinite medium. J Liaoning Univ Eng Tech (Natural Sci Edition) (2015) 34(02):186–91. doi:10.11956/j.issn.1008-0562.2015.02.009

CrossRef Full Text | Google Scholar

12. Guo SB, Pan YF, Gao PZ. Simulation of explosion seismic waves. Explosion and Shock (2005) 04:335–40.

Google Scholar

13. Hao ZH, Lin DC, Bai CH. Analysis of shock characteristics of explosion seismic waves. J Fire Explosives (2004) 01:30–2. doi:10.14077/j.issn.1007-7812.2004.01.009

CrossRef Full Text | Google Scholar

14. Shi JJ, Guo SC, Zhang W. Expansion of blast vibration attenuation equations for deeply buried small clearance tunnels based on dimensional analysis. Front Earth Sci (2022) 10. doi:10.3389/feart.2022.889504

CrossRef Full Text | Google Scholar

15. Dai SH, An ZK, Wang XC, Han RJ. Research on the calculation formula of blasting vibration velocity in open pit coal mines. J Liaoning Univ Eng Tech (Natural Sci Edition) (2022) 41(01):41–6. doi:10.11956/j.issn.1008-0562.2022.01.007

CrossRef Full Text | Google Scholar

16. Xue ZX, Zhao X. Parameter determination and safety range evaluation of Sadovsky formula under hard rock geological conditions. Low temperature building Technol (2021) 43(04):124–7. doi:10.13905/j.cnki.dwjz.2021.04.030

CrossRef Full Text | Google Scholar

17. Tochilin SN, Komissarov PV, Basakina SS. Assessment of errors in determining the TNT equivalency of air explosions. Russ J Phys Chem B (2020) 14(4):631–5. doi:10.1134/S1990793120040259

CrossRef Full Text | Google Scholar

18. Guo JH, Fan JB. Numerical calculation method for earth penetrating weapon explosion energy based on vibration. J Vibration Shock (2020) 39(10):180–4. doi:10.13465/j.cnki.jvs.2020.10.024

CrossRef Full Text | Google Scholar

19. Xia CH, Liu ZF, Shan GY, Shen SW. Calculation method of blasting charge based on blasting vibration velocity attenuation and control values. Mod Tunnel Tech (2018) 55(04):163–70. doi:10.13807/j.cnki.mtt.2018.04.022

CrossRef Full Text | Google Scholar

20. Yang MS, Fu YG, Liu ZJ, Rao YZ. Exploration of the elevation effect of small charge close range blasting in open-pit mines. Mining Res Dev (2017) 37(07):19–22. doi:10.13827/j.cnki.kyyk.2017.07.005

CrossRef Full Text | Google Scholar

21. Li Z, Li Z, Li J. Effect of concave terrain on explosion-induced ground motion. INT J ROCK MECH MIN (2021) 148:104948. doi:10.1016/j.ijrmms.2021.104948

CrossRef Full Text | Google Scholar

22. Simonenko VA, Shishkin NI, Shishkina GA. Movement of the ground in Rayleigh waves produced by underground explosions. PRIKL MEKH TEKHN FIZ (2006) 4:461–71. doi:10.1007/s10808-006-0078-0

CrossRef Full Text | Google Scholar

23. Hai Z, Zhao TY, Dai W. Wave scattering by crack under shock P-wave in an elastic half-space. J VIB ENG TECHNOL (2022) 10(1):425–43. doi:10.1007/s42417-021-00385-9

CrossRef Full Text | Google Scholar

24. Lu Q, Ding Y, Liu YZ. Evolution of seismic wave energy radiated from underground explosions in viscoelastic solids. Explosion and Shock (2021) 41(9):51–9. doi:10.11883/bzycj-2021-0058

CrossRef Full Text | Google Scholar

25. Tugelbayeva GK. Mathematical models for numerical solution of nonstationary problems of geomechanics. AIP Conf Proc (2020) 2312(1):050024.

CrossRef Full Text | Google Scholar

26. Novoselov A, Fuchs F, Bokelmann G. Acoustic-to-seismic ground coupling: Coupling efficiency and inferring near-surface properties. GEOPHYS J INT (2020) 223(1):144–60. doi:10.1093/gji/ggaa304

CrossRef Full Text | Google Scholar

27. Zhang MM, Kong DR, Chen WZ. Testing of detonation seismic effect of thermobaric explosive and analysis of its attenuation characteristics. J Test Tech (2016) 30(06):540–4.

Google Scholar

28. Gómez S, Sanchidrián JA, Segarra P. Near-field vibration from blasting and rock damage prediction with a full-field solution. INT J ROCK MECH MIN (2020) 134:104357. doi:10.1016/j.ijrmms.2020.104357

CrossRef Full Text | Google Scholar

29. Zhang YL, Wang SQ, Yuan JF. Experimental study on similarity law of shock wave parameters of different levels of TNT explosion. J Projectile, Arrow Guidance (2016) 36(06):53–6. doi:10.15892/j.cnki.djzdxb.2016.06.014

CrossRef Full Text | Google Scholar

30. Zohuri GI. Dimensional analysis beyond the pi theorem. Berlin: Spring (2017).

Google Scholar

31. Gao GF. Dimensional analysis:theories and applications[M]. Beijing: Science Press (2021).

Google Scholar

32. Chao HX, Hu H, Lei Q. Experimental study on shock wave of warhead dynamic explosion based on seismic wave triggering. Explosion and Shock (2021) 41(08):105–13. doi:10.11883/bzycj-2020-0196

CrossRef Full Text | Google Scholar

33. Li S. Propagation law of blasting seismic waves at structural surfaces with different filling media. Ganzhou, China: Jiangxi University of Science and Technology (2019).

Google Scholar