- 1Department of Physics, Faculty of Science, Kyoto Sangyo University, Kyoto, Japan
- 2Multi-Scale Mechanics, Thermal and Fluids Engineering, Faculty of Engineering Technology, University of Twente, Enschede, Netherlands
- 3Institute of Applied Mechanics (CE), University of Stuttgart, Stuttgart, Germany
We investigate numerically the sound properties of disordered dense granular packings in two dimensions. Employing linear equations of motion and excluding contact changes from our simulations, we demonstrate time evolution of sinusoidal standing waves of granular disks. We varied the strength of normal and tangential viscous forces between the disks in contact to explore the dependence of sound characteristics such as dispersion relations, attenuation coefficients, and sound speeds on the contact damping. For small wave numbers, the dispersion relations and sound speeds of acoustic modes are quite insensitive to the damping. However, a small dip in the phase speed of the transverse mode decreases as the viscous force in normal direction increases. In addition, the dispersion relation of the rotational mode differs qualitatively from the theoretical prediction for granular crystals. Therefore, disordered configurations with energy dissipation play a prominent role in sound properties of granular materials. Furthermore, we report how attenuation coefficients depend on the contact damping and quantify how they differ from the prediction of lattice theory. These improved relations, based on our numerical results, can in future be compared to advanced theories and experiments.
1 Introduction
Granular materials have important sound characteristics for materials research and engineering [1], including measuring elastic moduli [2–4], geotechnical soil investigation, oil and gas exploration, and understanding seismic waves and earthquakes [5, 6].
For a better understanding of the sound in granular media, theoretical models incorporating the rotational degrees of freedom in the microstructure are crucial [7], e.g., the model of one-dimensional granular chains [8, 9]. In two or three dimensions, theoretical models of granular crystals have been extensively developed [7, 10–13]. The theory of granular crystals is based on micromechanics of granular particles on lattice and well explains the dispersion relations of acoustic sound modes as well as characteristic “optical-like” dispersion relations of rotational modes. The optical-like dispersion relations represent wave propagation of micropolar rotations of granular particles, which have been widely tested by experiments [11] and numerical simulations [10, 12]. Moreover, special attention has been paid to the influence of material properties of granular particles, such as the stiffness and viscosity for normal/tangential relative motions between the particles in contact [13].
Compared to lattice models, research on sound in amorphous solids has primarily focused on glass and jamming transitions [14–21]. Prior studies have investigated the impact of disorder on sound properties, revealing several anomalies. For instance, the acoustic sound speeds of amorphous solids are typically at their lowest at intermediate frequencies (wave numbers) [14–21]. Additionally, sound attenuation, as described by the theory of Rayleigh scattering [22–25], shows disorder-induced broadening at high frequencies (wave numbers) [26–35].
Because granular materials in nature are mostly disordered, the studies of amorphous solids are relevant to the sound in disordered granular media. However, most of the studies assume that constituent particles are “frictionless”, where rotational modes are not considered [14–20]. Recently, we had numerically studied sound in disordered granular media in two dimensions [36]. We focused on the influence of tangential stiffness on the dispersion relations and found that the optical-like dispersion relation deviates from the prediction of lattice theory [10–12] if the wave number of the initial standing wave exceeds a critical value. In addition to the influence of tangential stiffness, the theory of granular crystals predicts how the viscous forces between the particles in contact affect sound characteristics [13], which we have not yet examined in our disordered granular media.
In this paper, we introduce a numerical model of two-dimensional disordered granular materials to investigate how the contact damping, i.e., the viscous forces between the particles in contact, affects the sound characteristics. As the ordinary discrete element method (DEM) simulations of granular materials [37], the contact force consists of elastic and viscous forces. The elastic force includes normal and tangential components, where both are modeled by linear springs with different spring constants [36]. The viscous force is also decomposed into normal and tangential components which are characterized by two viscosity coefficients. In contrast to the theory of granular crystals [10–13], our numerical model is based on disordered configurations of the particles. Furthermore, in order to compare our results with the studies of granular crystals [10–13], we only demonstrate small oscillations of the particles around their equilibrium positions, where any plastic deformations due to opening/closing contacts [38, 39] and the microscopic friction do not occur.
In the following, we explain our numerical method in Section 2 and summarize all the details of our model in Supplementary Material S1 (SM). We show our numerical results in Section 3 and provide additional data in SM. Lastly, we discuss and conclude our findings in Section 4.
2 Numerical method
In this section, we explain our numerical method for the analysis of sound in disordered granular media. First, we introduce our numerical model and define dimensionless parameters to represent the strength of forces between the granular particles in contact (Section 2.1). Next, we show how to prepare disordered configurations of the particles by numerical simulations (Section 2.2). To examine sound in the prepared granular media, we introduce linear equations of motion (Section 2.3). Then, we numerically solve the linear equations of motion with initial velocities (Section 2.4).
2.1 Contact model
Our numerical model of granular materials is the aggregate of two-dimensional disks. We introduce the force between the two disks, i and j, in contact as the sum of elastic and viscous forces. The elastic force consists of normal and tangential parts as knξij and
In our numerical model, the strength of contact forces is determined by the microscopic stiffness and viscosity, i.e., kn, kt, ηn, and ηt. To control the strength of contact forces, we introduce the following dimensionless parameters [13],
Here, the stiffness ratio ρK quantifies the strength of tangential elastic forces, while the damping ratio ρD represents the relative magnitude of tangential viscous forces. In addition, the damping factor ϵn, together with ρD, controls the strength of energy dissipation.
The dimensionless parameters, Eq. 1, were suggested by Kruyt [13] to quantify the influence of microscopic properties on the sound in granular crystals. In Ref. [36], we have studied the role of ρK in the sound characteristics of two-dimensional “disordered” granular disks, where the contact damping was absent, i.e., ρD = ϵn = 0. In this paper, we will focus on the effects of ρD and ϵn on the sound properties of disordered granular disks. Note that we do not introduce the tangential elastic force and viscous forces, i.e., ρK = ρD = ϵn = 0, when we prepare disordered configurations of the disks (Section 2.2). However, we introduce these forces when we simulate small oscillations of the disks around their equilibrium positions, where ρK is fixed to unity (Section 2.3).
2.2 Disordered configurations
We prepare disordered configurations of granular disks by the same method as in Refs. [36, 40]. Our system is a 50:50 binary mixture of N = 32,768 disks, where every disk has the same mass m and different diameters, dS and dL = 1.4dS. A repulsive force between the disks, i and j, in contact is given by the elastic force in normal direction, fij = knξij. We randomly distribute the N disks in a L × L square periodic box and fully minimize elastic energy of the system with the FIRE algorithm [41]. We stop the energy minimization if the maximum acceleration of the disks becomes less than
2.3 Linear equations of motion
To simulate sound in the disordered granular media, we introduce linear equations of motion of the granular disks [45, 46]. Now, we introduce the tangential elastic force and viscous forces between the disks in contact. Because the disordered configurations, {ri (0)} (Section 2.2), are mechanically stable, we describe small oscillations of the disks around {ri (0)} by the following equation [36, 40, 47],
Here, t denotes time and
is a 3N-dimensional displacement vector which consists of translational displacement in the xy-plane, ui(t) ≡ ri(t) − ri (0), and angular displacement of each disk, θi(t). In the linear equations of motion (Eq. 2),
In Eq. 2, the elastic forces between the disks in contact are given by
is the time derivative of the 3N-dimensional displacement vector, q(t). Each element of
The linear equations of motion (Eq. 2) are equivalent to the so-called “spring-dashpot model”, i.e., a canonical model of granular materials for DEM simulations [36]. However, the matrices,
2.4 Initial velocities
To examine sound properties of the granular disks, we employ a similar method as in Refs. [36, 40, 47]. We numerically integrate the linear equations of motion, Eq. 2, under periodic boundary conditions. Initial velocities of the disks are given by a sinusoidal standing wave,
where A and k are amplitude and wave vectors, respectively [37, 40, 47]. As shown in SM, we use different amplitude and wave vectors to demonstrate three different types of elastic wave, i.e., longitudinal (L), transverse (T), and rotational (R) modes. The latter (R mode) represents micropolar rotations of the disks [36], which are not relevant in frictionless systems [40, 47].
3 Results
In this section, we show our numerical results of sound in disordered granular media. First, we explain time evolution of sinusoidal standing waves (Section 3.1) and analyze velocity auto-correlation functions (VAFs) of the granular disks (Section 3.2). We extract sound characteristics, i.e., dispersion relations (Section 3.3) and attenuation coefficients (Section 3.4), from numerical data of VAFs. We also examine how sound speeds are affected by the strength of contact damping (Section 3.5). Lastly, we compare our numerical results with theoretical predictions of granular crystals (Section 3.6) to figure out the influence of disordered configurations.
3.1 Time evolution of standing waves
By using numerical solutions of the linear equations of motion (Eq. 2), we visualize time evolution of the sinusoidal standing wave. Figure 1 displays snapshots of our numerical simulation at t/t0 = (A) 0, (B) 2, (C) 4, and (D) 6. Each disk (circle) is colored according to its angular velocity,
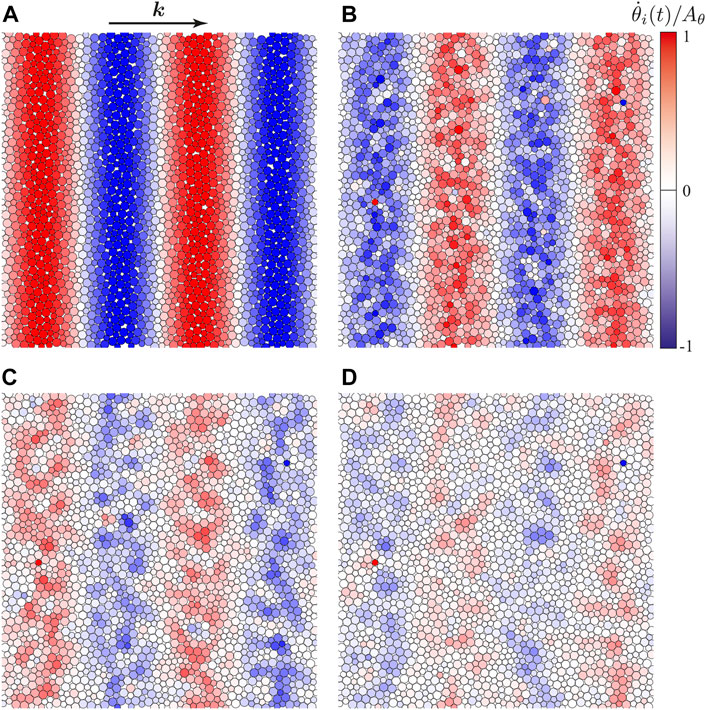
FIGURE 1. Time evolution of a standing wave of which wave vector k (kd0≃0.29) is indicated by the horizontal arrow. The angular velocities,
3.2 Velocity auto-correlation functions
From numerical solutions of Eq. 2, we obtain the data of disk velocities,
with the imaginary unit I, where the disk position ri(t) is also obtained from the numerical solutions of Eq. 2. Then, we introduce the L and T modes as
respectively, where
The normalized VAFs of L, T, and R modes are defined as
respectively. Figure 2 shows the time evolution of (A) CL (k, t), (B) CT (k, t), and (C) CR (k, t), where the dimensionless parameters, ρK, ρD, and ϵn, are as in Figure 1. To calculate each VAF, we use two different wave vectors (as listed in Table 1 in the SM) and average each VAF over the two samples (wave vectors). As can be seen, the oscillation of L mode is faster than that of T mode (Figures 2A, B). Furthermore, the oscillation of R mode is much faster than those of L and T modes (note the different horizontal scale in Figure 2C), meaning that the sound speed of micropolar rotations of the disks is much larger than acoustic sound speeds. In addition, the R mode decays much faster than the acoustic L and T modes, implying stronger scattering and energy dissipation of rotational motions. Notice that the VAFs are entirely damped (“overdamped”) without oscillations if the parameters, ρD and ϵn, are sufficiently large.
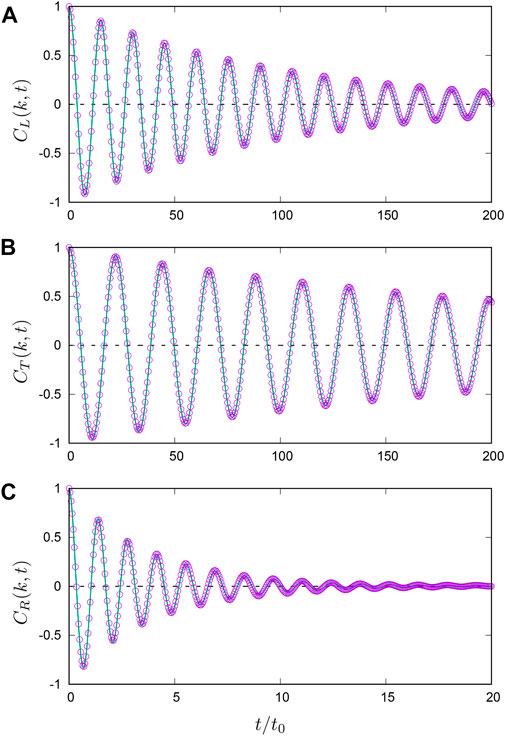
FIGURE 2. Normalized VAFs of (A) L, (B) T, and (C) R modes as functions of the scaled time t/t0, where the scaled wave number is kd0≃0.40 and dimensionless parameters, ρK, ρD, and ϵn, are as in Figure 1. The solid lines are the damped oscillations (Eq. 12) fitted to the numerical results (circles). Note that the horizontal scale in (C) is an order smaller than those in (A, B).
To extract sound characteristics of the granular disks, we fit a damped oscillation,
to the data of normalized VAFs (α = L, T, R) [36, 40, 47]. In Eq. 12, the frequency ωα(k) represents the dispersion relation, while the coefficient γα(k) quantifies the sound attenuation of each mode. For each wave number k, we adjust the fitting parameters, ωα(k) and γα(k), to see perfect agreement between the data of normalized VAFs and damped oscillations. The solid lines in Figure 2 are the damped oscillations; Eq. 12, fitted to the data of normalized VAFs (circles). We also confirm perfect agreement between the data and Eq. 12 for all the dimensionless parameters, ρK, ρD, and ϵn, used in simulations (data are not shown).
When the VAFs are overdamped, the data of normalized VAFs cannot be described by the damped oscillation, Eq 12. Therefore, there is a need to introduce a criterion for the fitting parameters, ωα(k) and γα(k). Here, we employ the Ioffe-Regel (IR) limit for the criterion, where Eq. 12 is meaningful only if the condition
is satisfied [18]. The ratio πγα(k)/ωα(k) is a monotonically increasing function of the wave number k. Hence Eq. 13 is equivalent to
3.3 Dispersion relations
We analyze the dispersion relation of each mode, ωα(k) (α = L, T, R), extracted from the data of VAFs and clarify its dependence on the contact damping. Figure 3A displays ωα(k) as functions of the scaled wave number kd0, where we control the damping ratio ρD as listed in the legend (see SM for their dependence on the damping factor ϵn). In this figure, the dispersion relations of L and T modes exhibit ordinary acoustic branches, where ωL(k) and ωT(k) increase from zero with the wave number. The dispersion relation of L mode is larger than that of T mode, i.e., ωL(k) > ωT(k), over the whole range of k. This means that the oscillation of the VAF of L mode is always faster than that of T mode (as shown in Figures 2A, B). In addition, these dispersion relations are quite insensitive to ρD (Figure 3A) and ϵn (SM). This trend is consistent with the theoretical prediction of granular crystals [13] though ωT(k) is cut-off at the limit wave number
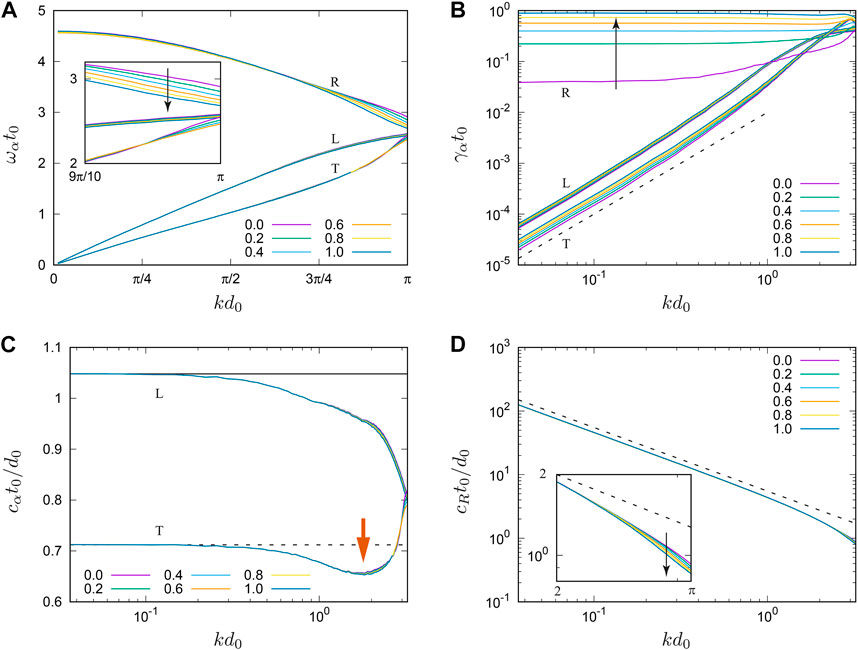
FIGURE 3. (A) Dispersion relations, ωα(k) (α = L, T, R), as functions of the scaled wave number, kd0. The inset shows a zoom-in to the range between 9π/10≤ kd0≤ π. (B) Double logarithmic plots of attenuation coefficients, γα(k) (α = L, T, R), and kd0, where the dashed line has the slope 2. (C) Semi-logarithmic plots of the phase speeds, cα(k) (α = L, T), and kd0, where the horizontal lines represent macroscopic speeds of sound (in the limit, k →0). The orange arrow indicates a small dip in cT(k). (D) Double logarithmic plots of the phase speed, cR(k), and kd0, where the dashed lines have the slope −1. The inset shows a zoom-in to the range between 2≤ kd0≤ π. In (A–D), the damping factor is given by ϵn =0.08, whereas the damping ratio ρD increases as listed in the legends and indicated by the black arrows.
In contrast to the acoustic dispersion relations, the dispersion relation of the R mode exhibits a characteristic optical-like branch (Figure 3A) [7]. The influence of contact damping is significant at large wave number, where ωR(k) dramatically decreases if we increase either ρD (inset to Figure 3A) or ϵn (SM). It is interesting that the viscous forces in normal and tangential directions, characterized by ϵn and ρD, respectively, have a similar effect on ωR(k) because micropolar rotations of the disks are driven only by tangential forces. In addition, ωR(k) in Figure 3A is not cut-off though ωT(k) is at
3.4 Attenuation coefficients
We examine sound attenuation of each mode by the attenuation coefficients, γα(k) (α = L, T, R), extracted from the data of VAFs. Figure 3B displays γα(k) as functions of the scaled wave number, where we vary ρD as listed in the legend (see SM for the effect of ϵn on γα(k)). In the continuum limit, k → 0, the attenuation coefficients of the L and T modes are quadratic in the wave number, i.e., γL(k), γT(k) ∼ k2, as indicated by the dashed line. The quadratic growth of the attenuation coefficients is typical of viscoelastic media [40] and is also predicted by the lattice theory of granular crystals [13]. In addition, regardless of the wave number, both γL(k) and γT(k) increase with the increase of strength of contact damping (see also SM).
In contrast, the attenuation coefficient of the R mode remains constant, γR(k) ∼const., in the continuum limit and is much larger than those of acoustic modes, i.e., γR(k) ≫ γL(k), γT(k), for small wave numbers. Therefore, the decay of the normalized VAF of R mode is much faster than those of L and T modes (as shown in Figure 2). However, if the damping ratio is relatively small (ρD < 0.4), the attenuation coefficient of the R mode becomes smaller than those of acoustic modes, i.e., γR(k) < γL(k), γT(k), at large wave number. We also observe this phenomenon if the damping factor ϵn is small enough (SM). Because the lattice theory of granular crystals implies that the attenuation of R mode is always stronger than those of acoustic modes [13], our results suggest that the weak attenuation of R mode at large wave number is specific to disordered granular disks. Similar to the acoustic modes, γR(k) significantly increases with the increase of strength of contact damping regardless of the wave number (see also SM).
3.5 Phase speeds
We quantify sound speed of each mode by phase speed defined as cα(k) ≡ ωα(k)/k (α = L, T, R). Figure 3C shows cL(k) and cT(k) as functions of the scaled wave number, where we vary the parameter ρD as listed in the legend (see SM for different values of ϵn). As can be seen, the phase speeds of acoustic L and T modes converge to constants (horizontal lines) in the continuum limit, k → 0. The continuum limit, cα(0) (α = L, T), is insensitive to the strength of contact damping, ρD and ϵn. Therefore, the viscous forces between the disks in contact do not affect macroscopic speeds of sound [40].
The phase speed of L mode, cL(k), is a monotonically decreasing function of the wave number, meaning that the dispersion relation, ωL(k), becomes sub-linear at large wave number (see Figure 3A). The phase speed of T mode, cT(k), also decreases from the continuum limit, cT (0), when the wave number k increases from zero. However, further increasing k, we observe that cT(k) starts increasing and generates a small “dip” at intermediate wave number (as indicated by the arrow in Figure 3C). Such a small dip in the phase speed is characteristic of (energy conserving) disordered media [47, 53] and has been considered to be a sign of the boson peak in vibrational density of states [54–58]. It is believed that the boson peak is a consequence of elastic heterogeneities in disordered materials [59–61]. Therefore, the small dip in cT(k) is unique to our study on disordered granular disks, i.e., is not expected to exist in cT(k) of granular crystals [7, 10–13]. Note that cL(k) exhibits no dip, which is in sharp contrast with the results of disordered frictionless disks [40]. Moreover, cL(k) is relatively insensitive to the strength of contact damping, ρD and ϵn. Similarly, cT(k) is not affected by the damping ratio ρD, though it is cut-off at
As shown in Figure 3D, the phase speed of the R mode, cR(k), exhibits asymptotic behavior, i.e., cR(k) ∼ k−1 (dashed lines), in the continuum limit, k → 0. Thus, the optical-like branch in the dispersion relations becomes flat, ωR(k) ∼const., when the wave number is small enough, Figure 3A. The influence of contact damping is significant at large wave number, where cR(k) is lowered with the increase of contact damping (see the inset).
3.6 Comparison with lattice theory
We compare our numerical results with theoretical predictions of granular crystals. In particular, we focus on the dependence of sound characteristics on the strength of contact damping, ρD and ϵn.
The lattice theory of granular crystals [13] predicts that, in the continuum limit, k → 0, the dispersion relations of the L and T modes depend on the stiffness ratio as
The lattice theory also predicts that, in the continuum limit, the dispersion relation of the R mode is controlled by the dimensionless parameters according to
where a0 is a dimensionless constant [13]. To examine the theoretical prediction, we plot our numerical results of the dispersion relation at the smallest wave number, ωR (Δk), as a function of the damping ratio ρD in Figure 4A. In this figure, the dashed line is the theoretical prediction; Eq. 14, approximated to the data of ωR (Δk) for ϵn = 0.02 (where a0 ≃ 1.3 × 10−2 with a prefactor, 4.59). It is apparent that our results are qualitatively different from the theoretical prediction; Eq. 14 is convex upward, while the data are convex downward. Our findings suggest that the influence of disordered disk configurations on the R mode cannot be neglected even in the continuum limit.
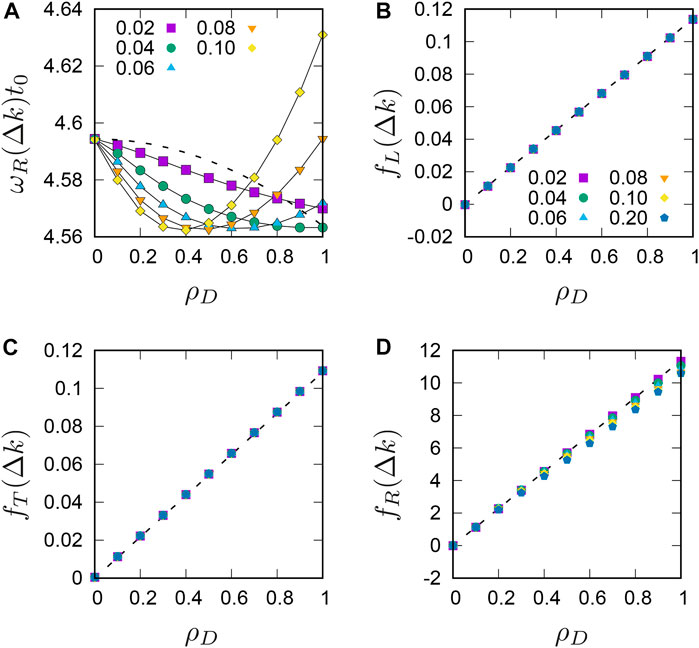
FIGURE 4. (A) Continuum limits of the dispersion relation of the R mode, ωR (Δk), as functions of the damping ratio ρD, where the damping factor ϵn increases as listed in the legend. The dashed line is a prediction by the lattice theory of granular crystals. (B–D): Continuum limits of the dimensionless functions, fα(Δk), of (B) α = L, (C) T, and (D) R modes as functions of ρD, where ϵn increases as listed in the legend of (B). The dashed lines indicate Eqs 15–17.
In the continuum limit, the attenuation coefficients of the L and T modes are predicted to be quadratic in the wave number as
where
Adjusting the parameters, we see good agreements between Eqs. 15–17 and numerical results. Figures 4B–D show dimensionless functions, (B)
4 Discussion
In this study, we conducted numerical simulations to investigate sound in disordered granular media in two dimensions. Our aim is to clarify the difference between granular crystals and disordered granular packings, where the special attention has been paid to the influence of viscous forces between the particles in contact. Our main findings are summarized as follows.
1. At large wave number, the dispersion relation of the rotational (R) mode is more sensitive to the contact damping than those of the acoustic longitudinal (L) and transverse (T) modes.
2. In the continuum limit, the dependence of the dispersion relation of the R mode on the strength of contact damping qualitatively differs from the theoretical prediction of granular crystals.
3. The attenuation coefficients in disordered granular packings are described by Eqs. 15–17 in the continuum limit, which are totally different from the theoretical predictions of granular crystals.
4. The small dip in the phase speed of the T mode is typical of disordered systems (does not exist in granular crystals), where its magnitude decreases with the increase of damping factor.
5. Different from disordered “frictionless” systems, there is no dip in the phase speed of the L mode in disordered granular disks, where the elastic and viscous forces are introduced in the tangential direction.
Because we found qualitative differences between granular crystals and disordered granular packings even in the continuum limit (where microstructures are entirely coarse-grained), our results suggest that advanced new theory is necessary for describing sound properties of disordered granular materials.To compare our results with the previous ones [36, 40], we have prepared the initial disordered configurations with the packing fraction, 0.9. However, the packing fraction or confining pressure strongly affects sound properties [53] and more systematic studies are needed in future. The eigenmodes are another important aspect of vibrational properties of disordered particle packings [62]. The relation between eigenmodes, contact damping or the damping matrix, dispersion relations, and attenuation coefficients needs to be clarified. Moreover, the low frequency eigenmodes are directly related to the elastic moduli [62], which could pave the way to develop advanced theories for sound in disordered media. In addition to studying the response of the disordered disk systems to an imposed standing wave, the response of the system to more general perturbations or initial conditions will lead to a better understanding and possibly to fluctuation-dissipation relations for disordered disk systems. In our numerical model, we used harmonic potentials for the elastic energy but more realistic non-linear elastic forces, e.g., the Hertz-Mindlin contact, have not been examined. In addition, we did not take plastic deformations of the system into account. In reality, however, contact changes and the Coulomb friction play an important role in mechanical responses of granular materials [63]. To implement these plastic deformations, we need to generalize our numerical model as left to future work. It is also interesting to examine other contact models, e.g., the rolling resistance or cohesive interaction due to capillary bridges. Furthermore, the influence of microstructure such as size distributions and polydispersity is also important. For practical purposes, numerical simulations in three dimensions are crucial as an additional degree of freedom, i.e., the twisting motion of spheres in contact, induces a pure decoupled rotational mode, which we left for future work.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material further inquiries can be directed to the corresponding author.
Author contributions
KS, KT, and SL designed the research and wrote the article. KS performed the research. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by JSPS KAKENHI Grant Numbers 20H01868, 21H01006, and 22K03459. This work was also financially supported by 2021 Inamori Research Grants and the Information Center of Particle Technology. SL and KT acknowledge funding from the German Science Foundation (DFG) through the project STE-969/16-1 within the SPP 1897 “Calm, Smooth and Smart”.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1192270/full#supplementary-material
References
1. Sheng P. Introduction to wave scattering, localization and mesoscopic phenomena. Verlag Berlin Heidelberg: Springer (2006).
2. Taghizadeh K, Steeb H, Luding S, Magnanimo V. Elastic waves in particulate glass-rubber mixtures. Proc R Soc A (2021) 477:20200834. doi:10.1098/rspa.2020.0834
3. Taghizadeh K, Steeb H, Magnanimo V, Luding S. Elastic waves in particulate glass-rubber mixture: Experimental and numerical investigations/studies. EPJ Web Conf (2017) 140:12019. doi:10.1051/epjconf/201714012019
4. Cheng H, Luding S, Saitoh K, Magnanimo V. Elastic wave propagation in dry granular media: Effects of probing characteristics and stress history. Int J Sol Struct. (2020) 187:85–99. doi:10.1016/j.ijsolstr.2019.03.030
5. Hennino R, Trégourès N, Shapiro NM, Margerin L, Campillo M, van Tiggelen BA, et al. Observation of equipartition of seismic waves. Phys Rev Lett (2001) 86:3447–50. doi:10.1103/physrevlett.86.3447
6. Sato H, Fehler MC, Maeda T. Seismic wave propagation and scattering in the heterogeneous earth. Verlag Berlin Heidelberg: Springer (2012).
7. Schwartz LM, Johnson DL, Feng S. Vibrational modes in granular materials. Phys Rev Lett (1984) 52:831–4. doi:10.1103/physrevlett.52.831
8. Taghizadeh K, Shrivastava RK, Luding S. Stochastic model for energy propagation in disordered granular chains. Materials (2021) 14:1815. doi:10.3390/ma14071815
9. Taghizadeh K, Steeb H, Luding S. Energy propagation in 1D granular soft-stiff chain. EPJ Web Conf (2021) 249:02002. doi:10.1051/epjconf/202124902002
10. Merkel A, Tournat V, Gusev V. Dispersion of elastic waves in three-dimensional noncohesive granular phononic crystals: Properties of rotational modes. Phys Rev E (2010) 82:031305. doi:10.1103/physreve.82.031305
11. Merkel A, Tournat V, Gusev V. Experimental evidence of rotational elastic waves in granular phononic crystals. Phys Rev Lett (2011) 107:225502. doi:10.1103/physrevlett.107.225502
12. Merkel A, Luding S. Enhanced micropolar model for wave propagation in ordered granular materials. Int J Sol Struct. (2017) 106-107:91–105. doi:10.1016/j.ijsolstr.2016.11.029
13. Kruyt NP. Micromechanical study of dispersion and damping characteristics of granular materials. J Mech Mater Struct (2012) 7:347–61. doi:10.2140/jomms.2012.7.347
14. Ruocco G, Sette F, DiLeonardo R, Monaco G, Sampoli M, Scopigno T, et al. Relaxation processes in harmonic glasses? Phys Rev Lett (2000) 84:5788–91. doi:10.1103/physrevlett.84.5788
15. Monaco G, Mossa S. Anomalous properties of the acoustic excitations in glasses on the mesoscopic length scale. PNAS (2009) 106:16907–12. doi:10.1073/pnas.0903922106
16. Mizuno H, Yamamoto R. General constitutive model for supercooled liquids: Anomalous transverse wave propagation. Phys Rev Lett (2013) 110:095901. doi:10.1103/physrevlett.110.095901
17. Marruzzo A, Schirmacher W, Fratalocchi A, Ruocco G. Heterogeneous shear elasticity of glasses: The origin of the boson peak. Sci Rep (2013) 3:1407. doi:10.1038/srep01407
18. Mizuno H, Mossa S, Barrat J-L. Acoustic excitations and elastic heterogeneities in disordered solids. PNAS (2014) 111:11949–54. doi:10.1073/pnas.1409490111
19. Baldi G, Giordano VM, Monaco G, Ruta B. Sound attenuation at terahertz frequencies and the boson peak of vitreous silica. Phys Rev Lett (2010) 104:195501. doi:10.1103/physrevlett.104.195501
20. Baldi G, Giordano VM, Ruta B, DalMaschio R, Fontana A, Monaco G. Anharmonic damping of terahertz acoustic waves in a network glass and its effect on the density of vibrational states. Phys Rev Lett (2014) 112:125502. doi:10.1103/physrevlett.112.125502
21. Caroli C, Lemaître A. Fluctuating elasticity fails to capture anomalous sound scattering in amorphous solids. Phys Rev Lett (2019) 123:055501. doi:10.1103/physrevlett.123.055501
22. Matic A, Engberg D, Masciovecchio C, Börjesson L. Sound wave scattering in network glasses. Phys Rev Lett (2001) 86:3803–6. doi:10.1103/physrevlett.86.3803
23. Rufflé B, Foret M, Courtens E, Vacher R, Monaco G. Observation of the onset of strong scattering on high frequency acoustic phonons in densified silica glass. Phys Rev Lett (2003) 90:095502. doi:10.1103/physrevlett.90.095502
24. Moriel A, Kapteijns G, Rainone C, Zylberg J, Lerner E, Bouchbinder E. Wave attenuation in glasses: Rayleigh and generalized-Rayleigh scattering scaling. J Chem Phys (2019) 151:104503. doi:10.1063/1.5111192
25. Wang L, Berthier L, Flenner E, Guan P, Szamel G. Sound attenuation in stable glasses. Soft Matter (2019) 15:7018–25. doi:10.1039/c9sm01092k
26. Sette F, Krisch MH, Masciovecchio C, Ruocco G, Monaco G. Dynamics of glasses and glass-forming liquids studied by inelastic X-ray scattering. Science (1998) 280:1550–5. doi:10.1126/science.280.5369.1550
27. Masciovecchio C, Ruocco G, Sette F, Krisch M, Verbeni R, Bergmann U, et al. Observation of large momentum phononlike modes in glasses. Phys Rev Lett (1996) 76:3356–9. doi:10.1103/physrevlett.76.3356
28. Benassi P, Krisch M, Masciovecchio C, Mazzacurati V, Monaco G, Ruocco G, et al. Evidence of high frequency propagating modes in vitreous silica. Phys Rev Lett (1996) 77:3835–8. doi:10.1103/physrevlett.77.3835
29. Ruocco G, Sette F, DiLeonardo R, Fioretto D, Krisch M, Lorenzen M, et al. Nondynamic origin of the high-frequency acoustic attenuation in glasses. Phys Rev Lett (1999) 83:5583–6. doi:10.1103/physrevlett.83.5583
30. Masciovecchio C, Mermet A, Ruocco G, Sette F. Experimental evidence of the acousticlike character of the high frequency excitations in glasses. Phys Rev Lett (2000) 85:1266–9. doi:10.1103/physrevlett.85.1266
31. Masciovecchio C, Baldi G, Caponi S, Comez L, DiFonzo S, Fioretto D, et al. Evidence for a crossover in the frequency dependence of the acoustic attenuation in vitreous silica. Phys Rev Lett (2006) 97:035501. doi:10.1103/physrevlett.97.035501
32. Scopigno T, DiLeonardo R, Ruocco G, Baron AQR, Tsutsui S, Bossard F, et al. High frequency dynamics in a monatomic glass. Phys Rev Lett (2004) 92:025503. doi:10.1103/physrevlett.92.025503
33. Devos A, Foret M, Ayrinhac S, Emery P, Rufflé B. Hypersound damping in vitreous silica measured by picosecond acoustics. Phys Rev B (2008) 77(R):100201. doi:10.1103/physrevb.77.100201
34. Baldi G, Zanatta M, Gilioli E, Milman V, Refson K, Wehinger B, et al. Emergence of crystal-like atomic dynamics in glasses at the nanometer scale. Phys Rev Lett (2013) 110:185503. doi:10.1103/physrevlett.110.185503
35. Bouchbinder E, Lerner E. Universal disorder-induced broadening of phonon bands: From disordered lattices to glasses. New J Phys (2018) 20:073022. doi:10.1088/1367-2630/aacef4
36. Saitoh K, Shrivastava RK, Luding S. Rotational sound in disordered granular materials. Phys Rev E (2019) 99:012906. doi:10.1103/physreve.99.012906
37. Luding S. Anisotropy in cohesive, frictional granular media. J Phys Condens Matter (2005) 17:S2623–40. doi:10.1088/0953-8984/17/24/017
38. Schreck CF, Bertrand T, O’Hern CS, Shattuck MD. Repulsive contact interactions make jammed particulate systems inherently nonharmonic. Phys Rev Lett (2011) 107:078301. doi:10.1103/physrevlett.107.078301
39. Saitoh K, Magnanimo V, Luding S. A Master equation for the probability distribution functions of forces in soft particle packings. Soft Matter (2015) 11:1253–8. doi:10.1039/c4sm02452d
40. Saitoh K, Mizuno H. Sound damping in soft particle packings: The interplay between configurational disorder and inelasticity. Soft Matter (2021) 17:4204–12. doi:10.1039/d0sm02018d
41. Bitzek E, Koskinen P, Gähler F, Moseler M, Gumbsch P. Structural relaxation made simple. Phys Rev Lett (2006) 97:170201. doi:10.1103/physrevlett.97.170201
42. O’Hern CS, Silbert LE, Liu AJ, Nagel SR. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys Rev E (2003) 68:011306. doi:10.1103/physreve.68.011306
43. van Hecke M. Jamming of soft particles: Geometry, mechanics, scaling and isostaticity. J Phys Condens Matter (2010) 22:033101. doi:10.1088/0953-8984/22/3/033101
44. Liu AJ, Nagel SR. The jamming transition and the marginally jammed solid. Annu Rev Condens Matter Phys (2010) 1:347–69. doi:10.1146/annurev-conmatphys-070909-104045
45. Goldstein H, Poole C, Safko J. Classical mechanics. 3rd ed. London, United Kingdom: Pearson Education Limited (2014).
47. Gelin S, Tanaka H, Lemaître A. Anomalous phonon scattering and elastic correlations in amorphous solids. Nat Mat (2016) 15:1177–81. doi:10.1038/nmat4736
48. Silbert LE, Liu AJ, Nagel SR. Vibrations and diverging length scales near the unjamming transition. Phys Rev Lett (2005) 95:098301. doi:10.1103/physrevlett.95.098301
49. Wyart M, Silbert LE, Nagel SR, Witten TA. Effects of compression on the vibrational modes of marginally jammed solids. Phys Rev E (2005) 72:051306. doi:10.1103/physreve.72.051306
50. Wyart M, Nagel SR, Witten TA. Geometric origin of excess low-frequency vibrational modes in weakly connected amorphous solids. Europhys Lett (2005) 72(3):486–92. doi:10.1209/epl/i2005-10245-5
51. Silbert LE, Liu AJ, Nagel SR. Normal modes in model jammed systems in three dimensions. Phys Rev E (2009) 79:021308. doi:10.1103/physreve.79.021308
52. Tighe BP. Relaxations and rheology near jamming. Phys Rev Lett (2011) 107:158303. doi:10.1103/physrevlett.107.158303
53. Mizuno H, Ikeda A. Phonon transport and vibrational excitations in amorphous solids. Phys Rev E (2018) 98:062612. doi:10.1103/physreve.98.062612
54. Monaco G, Giordano VM. Breakdown of the Debye approximation for the acoustic modes with nanometric wavelengths in glasses. PNAS (2009) 106:3659–63. doi:10.1073/pnas.0808965106
55. Lubchenko V, Wolynes PG. The origin of the boson peak and thermal conductivity plateau in low-temperature glasses. PNAS (2003) 100:1515–8. doi:10.1073/pnas.252786999
56. Grigera TS, Martin-Mayor V, Parisi G, Verrocchio P. Phonon interpretation of the ‘boson peak’ in supercooled liquids. Nature (2003) 422:289–92. doi:10.1038/nature01475
57. Schirmacher W, Ruocco G, Scopigno T. Acoustic attenuation in glasses and its relation with the boson peak. Phys Rev Lett (2007) 98:025501. doi:10.1103/physrevlett.98.025501
58. Mizuno H, Shiba H, Ikeda A. Continuum limit of the vibrational properties of amorphous solids. Proc Natl Acad Sci U S A (2017) 114:E9767.
59. Schirmacher W. Thermal conductivity of glassy materials and the “boson peak. Europhys Lett (2006) 73:892–8. doi:10.1209/epl/i2005-10471-9
60. Marruzzo A, Köhler S, Fratalocchi A, Ruocco G, Schirmacher W. Vibrational anomalies and marginal stability of glasses. Eur Phys J Spec Top (2013) 216:83–93. doi:10.1140/epjst/e2013-01731-5
61. Ferrante C, Pontecorvo E, Cerullo G, Chiasera A, Ruocco G, Schirmacher W, et al. Acoustic dynamics of network-forming glasses at mesoscopic wavelengths. Nat Commun (2013) 4:1793. doi:10.1038/ncomms2826
62. Mizuno H, Saitoh K, Silbert LE. Elastic moduli and vibrational modes in jammed particulate packings. Phys Rev E (2016) 93:062905. doi:10.1103/physreve.93.062905
Keywords: granular material, acoustic sound, disorder, molecular dynamics simulation, soft matter
Citation: Saitoh K, Taghizadeh K and Luding S (2023) Sound characteristics of disordered granular disks: effects of contact damping. Front. Phys. 11:1192270. doi: 10.3389/fphy.2023.1192270
Received: 23 March 2023; Accepted: 10 May 2023;
Published: 22 May 2023.
Edited by:
Marco Laurati, University of Florence, ItalyReviewed by:
Dong Wang, Yale University, United StatesAlessandro Sarracino, University of Campania Luigi Vanvitelli, Italy
Copyright © 2023 Saitoh, Taghizadeh and Luding. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kuniyasu Saitoh, ay5zYWl0b2hAY2Mua3lvdG8tc3UuYWMuanA=
 Kuniyasu Saitoh
Kuniyasu Saitoh Kianoosh Taghizadeh
Kianoosh Taghizadeh Stefan Luding
Stefan Luding