- 1School of Biological Science and Medical Engineering, Southeast University, Nanjing, China
- 2School of Biomedical Engineering and Informatics, Nanjing Medical University, Nanjing, China
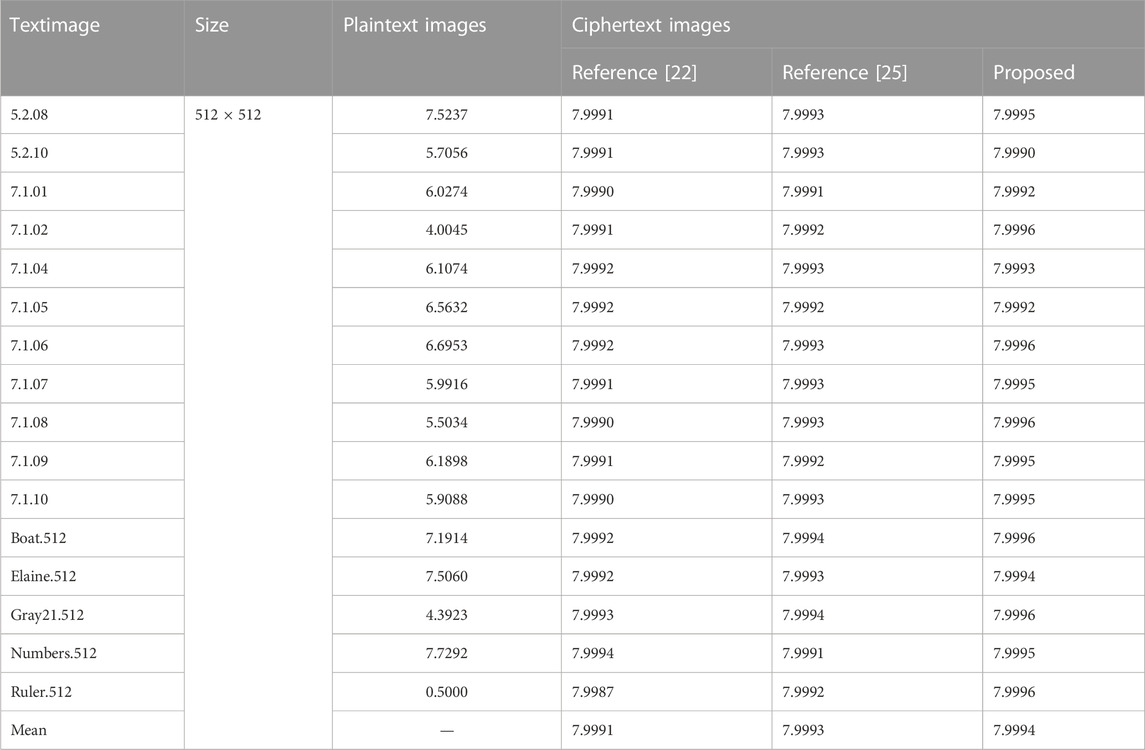
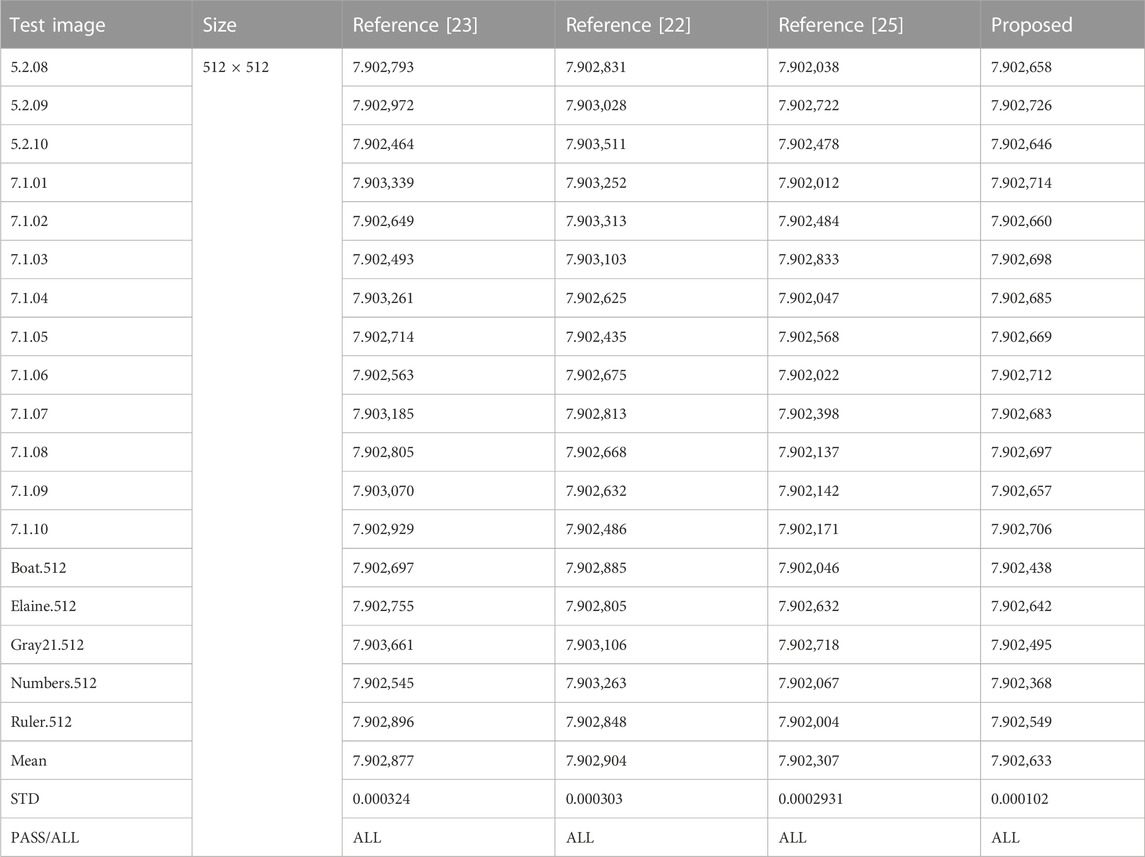
Digital images are characterized by high redundancy and strong interpixel correlation. Breaking the correlation between data and improving sensitivity are crucial to protecting image information. To effectively achieve this goal, a chaotic encryption algorithm based on Josephus cycle scrambling diffusion is proposed in this paper. First, the adaptive key is generated by the Hash function to generate the initial value of the chaotic system, which is highly related to the plaintext image. The generation of the adaptive key can effectively resist plaintext attacks. Second, the pseudorandom sequence generated by the two-difference chaotic mapping is applied as the step sequence and direction sequence of Josephus traversal and optimizes Josephus traversal via variable steps and directions; the ranks of plain-text images are scrambled by the Josephus cycle to break the strong correlation between pixels. Finally, the initial cipher-text is divided into blocks to complete the Josephus cycle scrambling diffusion of image blocks, intrablock pixel bits and bit planes. The double permutations at the pixel level and bit level break the high correlation between pixels. Compared with the previous studies, our algorithm’s average entropy of encrypted images is 7.9994, which has slightly improved. The correlation coefficient of the cryptographic image fluctuates up and down by approximately 0. In addition, the algorithm has the advantages of a large key space, high key sensitivity, anti-robust attack, and feasible encryption efficiency.
1 Introduction
Due to the epidemic, increasing interpersonal communications have been moved to the internet. As a result, users' demands for privacy protection and information security are gradually becoming urgent. Unlike text data, digital images, as a kind of two-dimensional information commonly used online, possess considerable data volume, high redundancy and strong interpixel correlations. Therefore, traditional encryption methods are not applicable for encrypting images, while the existing encryption algorithms for digital images generally have the disadvantages of complicated encryption processes and long time consumption, which no longer satisfy the demands of image encryption.
Chaos theory was first introduced by mathematician Matthews [1] into the field of cryptography; however, it was not until 1998 that Fridrich [2] proposed an image encryption algorithm based on chaotic mapping, which opened a new era of this particular algorithm’s rapid development. American mathematician Claude Shannon [3] suggested the classical structure of image encryption based on a chaotic system to be scrambling-diffusion. In the scrambling phase, the positions of image pixels are varied so that their distribution is as random as possible, destroying the similarity between neighboring pixels in the plain-text image. In the diffusion phase, the pixel values interact with each other and change randomly to hide the plain-text image information [4–6]. The security of the encryption effect of this algorithm based on chaotic systems is mainly determined by the structure of this encryption algorithm and the performance of the adopted chaotic systems [7].
According to the confusion system used for encryption, chaotic encryption algorithms can be classified into two types: continuous chaotic encryption algorithms and discrete chaotic encryption algorithms. Continuous chaotic systems consist of one-dimensional higher-order nonlinear differential equations or multivariate first-order differential equations, while discrete chaotic systems comprise iterative mappings, i.e., difference equations. Low-dimensional continuous chaotic systems were previously applied to cryptography in chaos theory because of their simple structure and easy implementation. For example, Gao et al. [8] proposed an image encryption algorithm based on the typical Lorenz and Chen systems.
Due to its small or discontinuous chaotic range, resulting in an uneven distribution of the output chaotic sequence, C. Pak [9], R.A. Elmanfaloty [10] improved the structures of different one-dimensional chaotic systems to effectively increase the chaotic range of chaotic systems and improve the uniformity of chaotic system distribution and the key space of encryption algorithms. Wang et al. [11] proposed a chaotic image encryption algorithm with a perceptual model based on a high-dimensional Loranz chaotic system and a perceptual model of a neural network. Cheng et al. [12], based on a five-dimensional super multiwing chaotic system, designed a chunkwise scrambling algorithm with mixed R, G, and B components to enhance the dependency among the components and improve the scrambling efficiency. Discrete chaotic systems include one-dimensional chaotic mappings and high-dimensional chaotic mappings. One-dimensional chaotic mappings such as logistic mappings, segmented linear chaotic mappings, and Tent are used for image encryption because of their simple structure and fast calculation, such as those of the digital image encryption algorithm based on logistic mapping proposed by Wang et al. [13]. However, their one-dimensional discrete chaotic mapping interval is narrow, multiple period windows will lead to a small cipher space, and the attacker can analyze and attack the chaotic mapping used, which is proven to be insecure [14]. To overcome the shortcomings of one-dimensional chaotic mappings, researchers have proposed many different methods to construct chaotic mappings. Hua et al. [15] proposed a two-dimensional logic-based tuned sinusoidal mapping and used it for image encryption. Due to truncation and rounding errors, the chaotic trajectory can be trapped in a cycle when the device is operated with finite accuracy [16]. [17] proposed extending the time for chaotic mappings to enter a cycle with extended accuracy, which is also limited in its effectiveness since the accuracy cannot be scaled up infinitely. Another approach is to combine multiple mappings together by cascading or switching [12]. Both cascading and switching ignore the interactions between multiple mappings, and their combination’s effect depends on the superiority of the strategy. Chai et al. [38] proposed an image encryption scheme based on multiobjective optimization and block compressed sensing. However, those methods based on chaotic systems only scramble the plaint image pixel position, which does not change the entropy and histogram values of the plaintext. This means that the capacity to defend against statistical attacks is poor.
Additionally, some nonchaotic encryption schemes have been used for image encryption at the bit level. The Arnold transform, geometry transform, and E curve transform are classical image scrambling algorithms that are nonchaotic. Hua et al. [28] proposed a two-dimensional plane scrambling algorithm based on Josephus travel. Yu and Yang [35] proposed a symmetric algorithm applied in remote sensing images, which improved encryption security. A dynamic bit-flipping diffusion encryption algorithm is proposed in the literature. Zhu et al. [36] proposed a three-dimensional bit-level image encryption algorithm using Rubik’s cube method.
Inspired by the above literature, we combine image bit-level and bit-level encryption and propose an image encryption method with high security and sensitivity by combining a new two-dimensional differential chaotic map and an improved Joseph cycle. In this paper, we propose an image encryption method with high security and sensitivity by combining a new two-dimensional differential chaos mapping and an improved Josephus cycle. The image chunking strategy is utilized to enhance the algorithm scrambling efficiency; the improved Josephus cycle enables dynamic variable-step and variable-direction Josephus scrambling diffusion. The scrambling-diffusion of encrypted images is carried out in two dimensions: pixel bits within a block and pixel bit planes within a block, which can effectively reduce the correlation between adjacent data, and the scrambling effect of encrypted images is more random and effective [18]. Also used the adaptive key, which came from the sum and average of the plain-text image, while the method in this paper adopted the hash value of the plain-text image as the adaptive key, which is more sensitive to plain-text changes.
In this paper, the security of the algorithm is verified and compared with related algorithms in terms of correlation and information entropy. The experimental results show that the algorithm in this paper encrypts images with uniform pixel distribution and low interpixel correlation and can effectively resist common attacks with high security.
2 Basic theory
2.1 Chaotic systems
2.1.1 Two-dimensional differential chaotic map
A chaotic system is a nonlinear dynamic system. It has randomness, sensitivity to initial conditions, nonperiodicity and long-term unpredictability. It is suitable for image encryption with a large amount of data and high correlation. Two-dimensional chaotic mapping contains fewer periodic windows in branching graphs, a larger range of chaotic parameters, and faster operation compared to one-dimensional chaotic mapping, and these properties are consistent with cryptographic characteristics, so two-dimensional chaotic mapping is often used in key generators. Combined with the Nicholson-Bailey model [40] in the study of biological populations, the two-dimensional difference equation to be studied in this paper is proposed as follows, which is a variation of Nicholson-Bailey model [41].
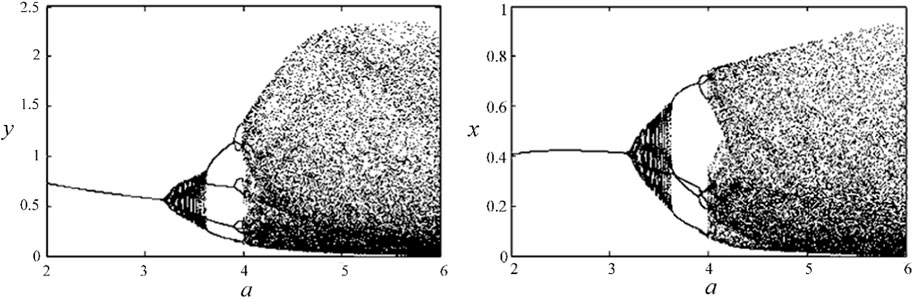
The r is chosen as 3, the initial point is arbitrarily set between [0, 1], and Eq. 1 is iterated 1,000 times. Figure 1 shows the bifurcation diagram of parameter a about x and y in the interval [2, 6]. From the figure, we can see that it is a curve at [2, 3.22], so the equation converges at this stage. When a = 3.23, the Hopf branch appears, and periodic motion occurs at [3.23, 3.62]. At [3.63, 3.90], the image contains a 4-terminal curve, which means a motion of 4-cycle. When the equation is greater than 3.91, as a increases, there is no regularity at the beginning, and the equation gradually enters chaos.
2.1.2 Lyapunov exponent
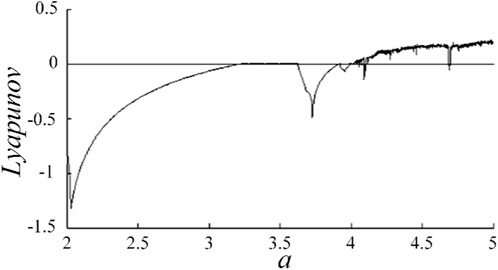
The Lyapunov exponent is an important index to verify the randomness and chaotic characteristics of chaotic sequences. If the Lyapunov exponent of the chaotic system is positive, the chaotic system has chaotic characteristics. The larger the positive value is, the better the chaotic characteristics of the chaotic system are.
It can be seen from Figure 2, when a > 4.04, the Lyapunov exponent is greater than zero, which indicates that the equation enters a chaotic phenomenon. Figure 2 verifies that the Lyapunov exponent diagram of this 2D difference equation agrees with the bifurcation diagram, and the equation shows rich dynamic behavior as the parameter a changes in the interval [2, 6].
2.1.3 Stability analysis of chaotic systems
The immovable points of the nonlinear iterative equations are used as a powerful tool to describe the evolution of the system dynamics. System (1) contains immobile points that satisfy the
The solution is:
Among them:
The positive equilibrium point of Eq. 1 is expressed as
To discuss the stability of the equilibrium point, model (1) is written in the following equations:
Adding a small permutation
To obtain a linear stability analysis, the Taylor expansion of the above equation is given as:
For the equilibrium point
where the characteristic roots are
For positive equilibrium point
Given the matrix:
where the characteristic equation of
Additionally, revised as:
where
Solving the condition for asymptotic stability of the positive equilibrium point as:
2.2 Josephus cycle
Josephus cycle [37] is a classical problem of mathematical application: it is known that individuals (denoted by the numbers 1,2,3,4, n, respectively) are sitting around a round table. Starting with the person numbered 1, the person who has counted to
To increase the diversity of Josephus, this paper introduces the pseudorandom sequence generated by a chaotic system as the dynamic step of the Josephus cycle based on the original rule; using the parity of the pseudorandom sequence as the dynamic direction, the Josephus function is further extended to
2.3 Combined scrambling diffusion of bits and bit planes
The pixels of a grayscale map are generally composed of 8-digit binary, where the amount of binary information varies greatly from position to position. For example, a “1” in the eighth bit represents 128 (
From Eq. 14, it can be seen that as the bits increase, the proportion of information contained in the bits increases. Therefore, the bits of different bit positions are scrambled. Then, the scrambled bit planes are diffused by the bit positions. Finally, 8 bit planes are obtained after bit position diffusion, and these bit planes are reorganized into one pixel plane to obtain the image after bit position diffusion.
3 Image encryption algorithm
3.1 Encryption algorithm
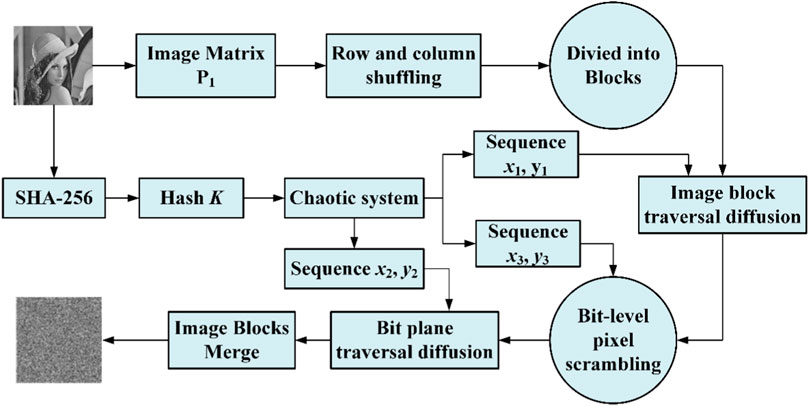
The encryption scheme proposed in this paper mainly consists of five parts: image rank permutation, image block division, image block diffusion, bit-level scrambling diffusion and cipher-text image block combination. The proposed encryption scheme can be represented by a block diagram, as shown in Figure 3. The whole scheme can be divided into pixel diffusion and bit diffusion. First, an adaptive key is generated through a plain-text image for the chaotic system’s initial values, and three pairs of pseudorandom sequences are generated. Second, to diffuse the image via row and column shuffling and divide into blocks, one pair of pseudo random sequences is used for the modified Josephus traversal to finish the block scrambling diffusion. Third, another two pairs of pseudorandom sequences finish shuffling at the bit level for the pixel and bit plane. In combination with a modified Josephus traversal, the image is dislocated and diffused using a production-issue chaotic sequence.
3.2 Key generation
Adaptive keys are an effective method to improve the resistance of encrypted images to known plaintext attacks. As [19] described, independent key streams increase the possibility of selecting plaintext attacks. In contrast, generating adaptive keys from plain-text images can achieve a 1-time 1-classification effect. Of course, the plain-text image has to be highly dispersed into the keystream. For this reason, this paper uses the hash value of the plain-text image to construct the initial value of the chaotic system. Any small change in the image will result in a huge change in the hash value, and the initial value of the chaotic system will also change. Of course, the use of different system parameters and initial values determines the superiority of the cryptographic complexity of this chaotic sequence [20]. Showed that choosing appropriate parameters in the chaotic interval could make the autocorrelation property of the resulting chaotic sequence close to white noise. Therefore, in this paper, the adaptive key is processed and controlled to fall within the chaotic interval.
Read the plain-text image
The initial values generated by Eq. 15 are brought into Eq. 1 to iterate the random sequence of
3.3 Image scrambling encryption
First read in the image
The image block scrambling process can be divided into the following 3 steps.
Step 1 Interblock scrambling. In this paper, we give a cyclic traversal method with variable step length and direction. The method is combined with a chaotic system, in which the chaotic sequence
Step 2Block built-in scrambling protects pixel bit scrambling and bit plane scrambling.
Step 2.1. Pixel bit position scrambling uses the chaotic sequence
Step 2.2. Bit plane scrambling, image blocks are all composed of 8 bit planes, using chaotic sequences
Step 3 Splice the cipher-text image blocks to obtain the cipher-text image.
3.4 Image recovery
The decryption process is the reverse of the encryption process, and the main steps are as follows:
Input: Ciphertext image, SHA-256 cipher-text value H.
Out: Plaintext image.
Step 1The ciphertext image I is converted into a 2-D moment of size M × N array.
Step 2Generated the key sequences {
Step 3Block built-in scrambling protects pixel bit scrambling and bit plane scrambling.
Step 3.1. Joseph traversal with sequence {
Step 3.2. Joseph traversal with sequence {
Step 4. Joseph traversal with sequence {
4 Security analysis
The effectiveness of the proposed encryption algorithm is verified from histogram, correlation, differential attack, key space, information entropy, clipping and noise attacks using data from the USC-SIPI 'Miscellaneous' database.
4.1 Histogram analysis
The more uniform the histogram is, the looser the relationship between the pixel intensity value and the number of pixels, the more random the image is, and the more difficult it is for an attacker to recover the original image through a histogram analysis attack.
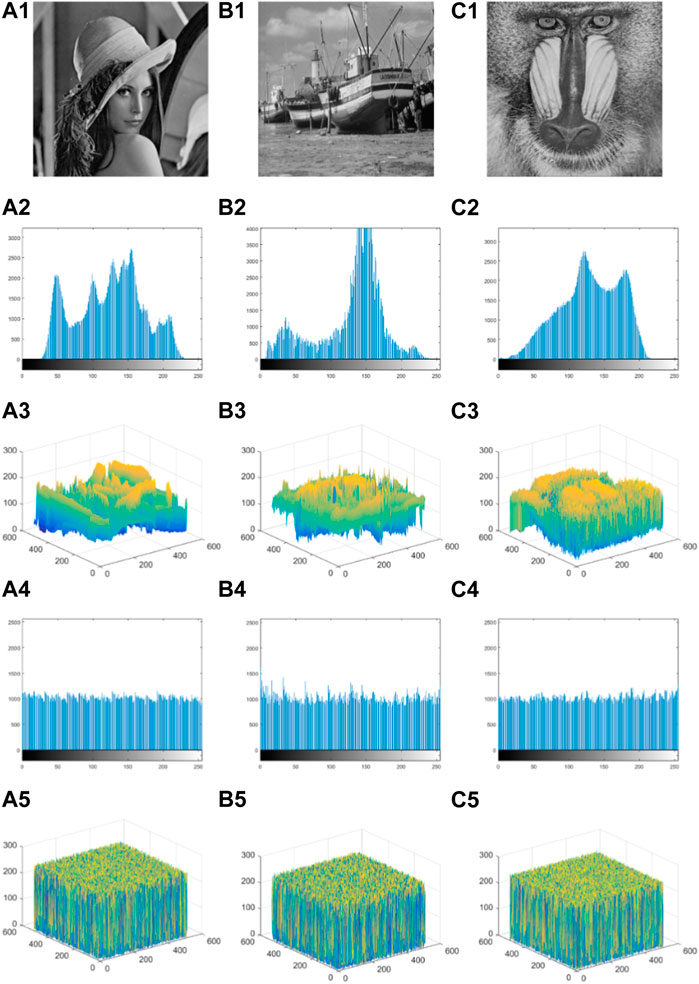
Figure 4 shows the histograms and pixel distributions of the three images of Lena, Boat, and Feifei in the testing database, where the first row is the plain-text image, the second is the histogram of the plain-text image, the third is the pixel distribution of the plain-text image, and the fourth and fifth are the histograms and pixel distributions of the cipher-text obtained from encryption of the corresponding plain-text. Both the histogram and the pixel distribution of the plain-text image present significant differences, i.e., uneven distribution. The difference between the histogram and the pixel distribution of the obtained cipher text is relatively insignificant, and the comparison shows that the pixel distribution of the cipher text is more uniform than that of the plain text. This is because the Josephus cyclic scrambling diffusion of bit positions and bits at the bit level changed the bit values composed of the plain-text image’s bit planes so that the pixel value distribution of the reconstructed pixel planes tends to be uniform. Therefore, the algorithm in this paper was proven to have a good ability to resist statistical analysis.
To test the uniformity of the histogram, a chi-square test was used, which is computed by the following equation.
where
When
4.2 Correlation analysis
The neighboring pixel values of plain-text images are very close to each other and have a strong correlation. Breaking the correlation between pixels is important to resist statistical analysis attacks. Correlation analysis is used to test the strength of the correlation between image pixels. The correlation between ordinary image pixels is usually extremely high, and the correlation coefficient of an image usually tends to be close to 1. If the correlation between adjacent or most pixels can be broken instead, then if the correlation and the correlation coefficient are reduced, it is more resistant to statistical analysis attacks. The correlation coefficient is calculated using the following equation:
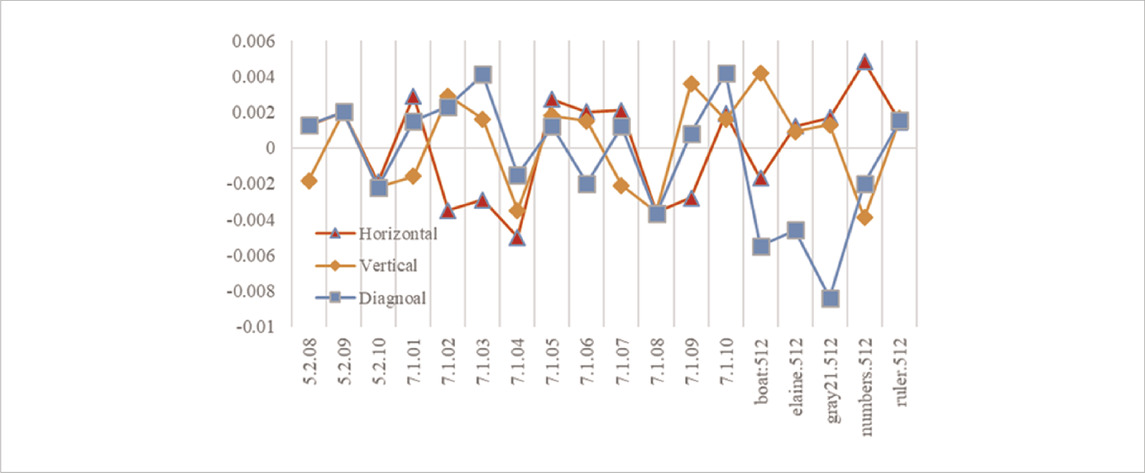
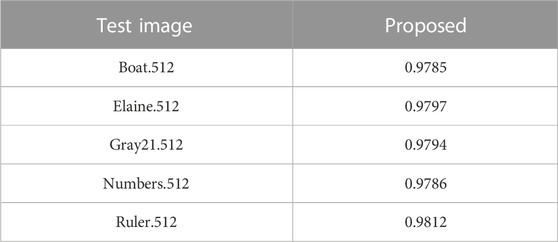
Randomly selected 5,000 pairs of pixel points, the statistical results of the correlation between the horizontal, vertical and diagonal directions of the original image and the cipher-text image in the test database are shown in Table 1, from which it can be seen that the number of prior relationships in the three directions of the cipher-text image fluctuates up and down around x = 0, indicating that the correlation between the pixels of the adjacent images of the plain-text is very low, revealing that the proposed encryption method is reliable and secure.
Figures 5–7 visualizes the correlation results before and after encryption. The plain-text images are strongly correlated in three directions. After the proposed encryption algorithm, the correlation of neighboring pixels is substantially weakened. It is this structure and characteristics of the plain-text image that make it resistant to statistical attacks.
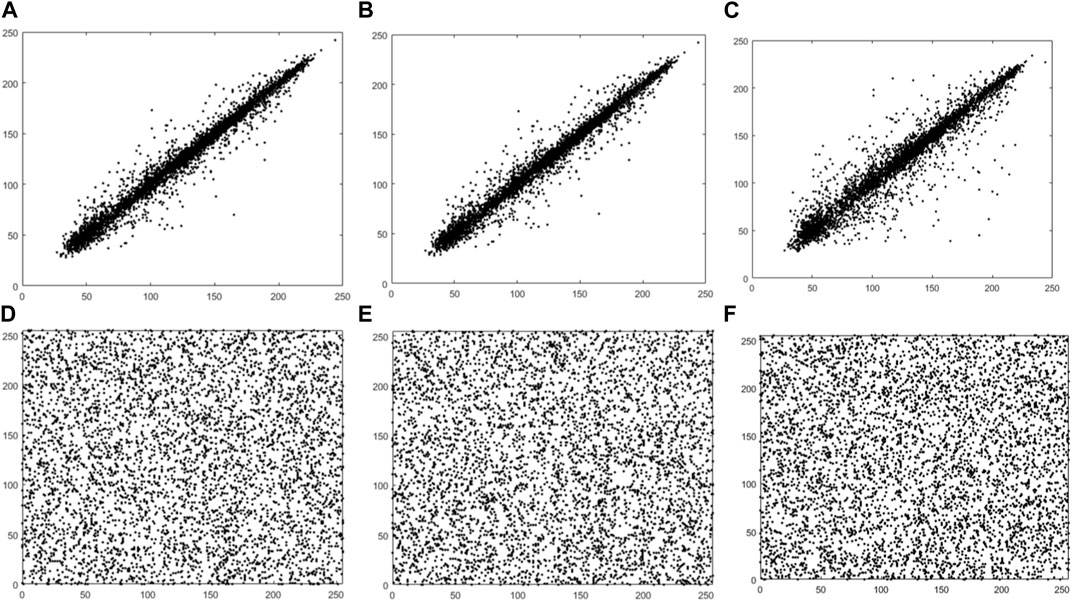
FIGURE 5. Correlations of adjacent pixels in the horizontal (A,D), vertical (B,E), and diagonal (C,F) directions before and after Lena encryption.
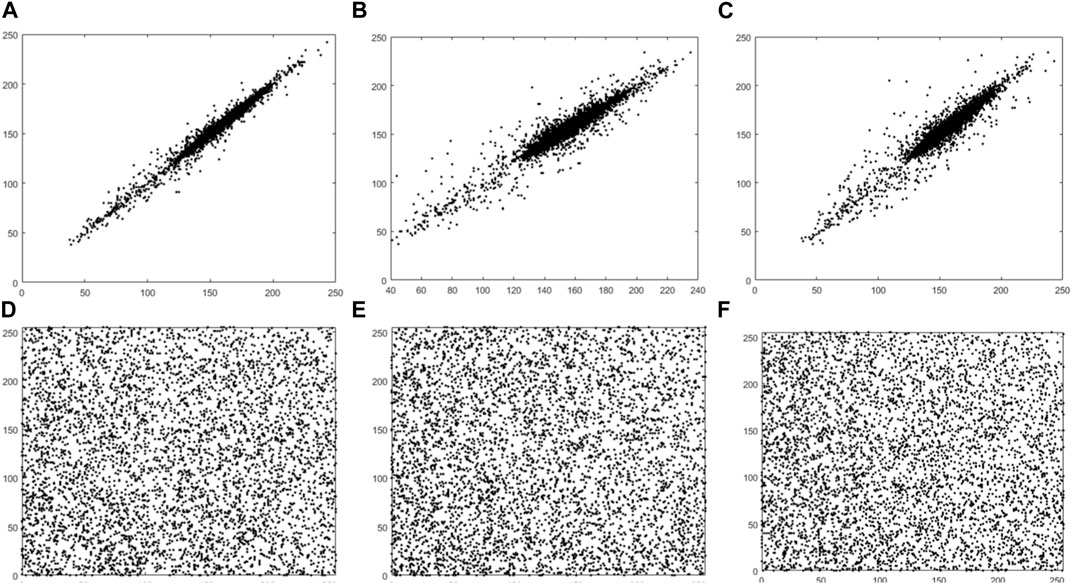
FIGURE 6. Correlations of adjacent pixels in the horizontal (A,D), vertical (B,E), and diagonal (C,F) directions before and after boat encryption.
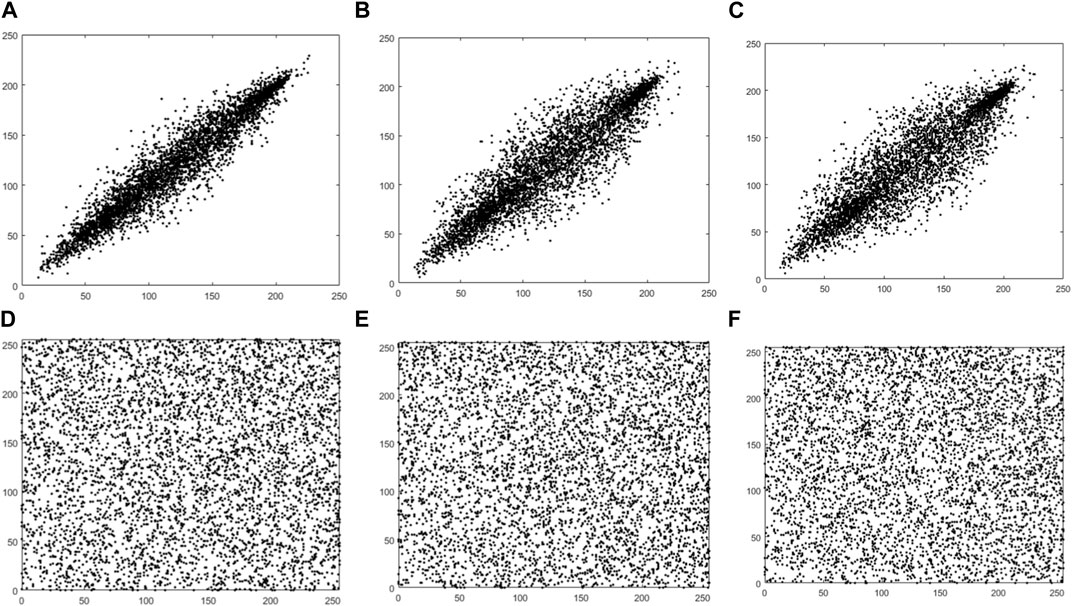
FIGURE 7. Correlations of adjacent pixels in the horizontal (A,D), vertical (B,E), and diagonal (C,F) directions before and after Feifei encryption.
4.3 Differential attack analysis
The differential attack is a deciphering method to attack the encryption algorithm by analyzing the degree of cipher-text change due to the subtle difference in plain-text. To analyze the resistance of the proposed encryption algorithm to the differential attack, this paper observes the degree of difference between the cipher-text images after two encryptions by changing the pixel value at any point in the plain-text image. If the degree of difference is large, the proposed algorithm is able to resist the differential attack effectively. The pixel change rate (NPCR) and the pixel average change intensity (UACI) are usually measured using the expressions of NPCR and UACI as follows:
where
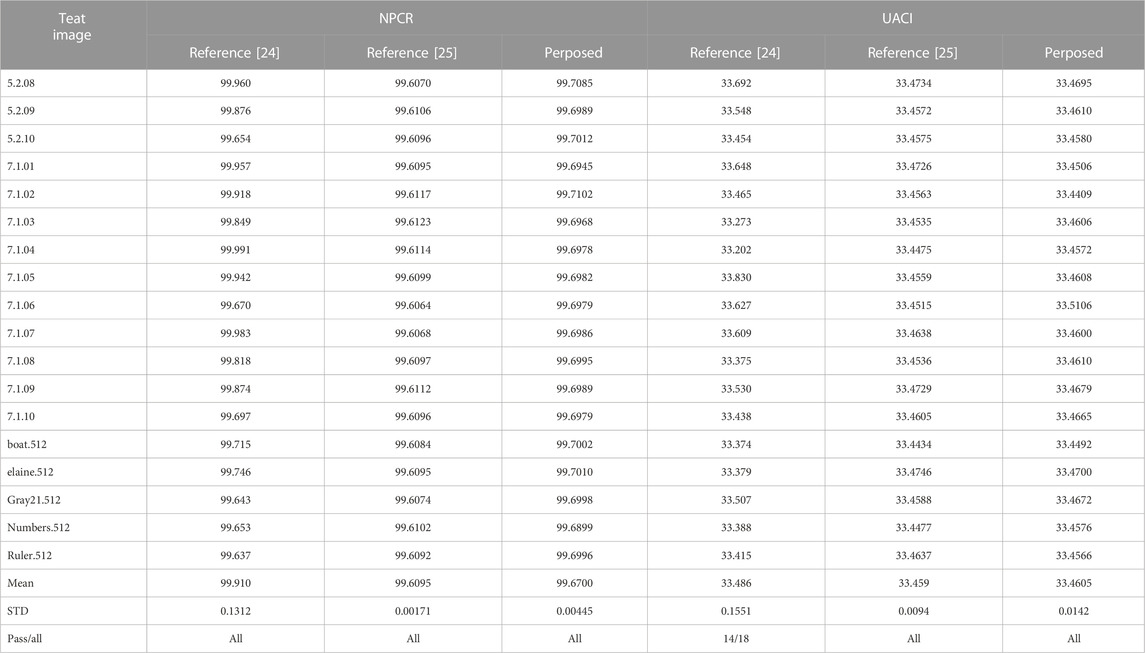
The NPCR and UACI pairwise scores of the test images were analyzed. The mean value of NPCR and the standard deviation of UACI of the proposed method in this paper are 99.6700 and 0.0045, respectively. The mean value and standard deviation of UACI are 33.4605 and 0.0142, respectively. The comparison shows that the NPCR, UACI of the proposed encryption algorithm is very close to the theoretical value, and its labelling difference is the smallest among the compared methods. This indicates that the proposed method has better sensitivity. In addition, the significance level of our images is set to 0.05, and then the critical values of NPCR and UACI corresponding to different sizes are calculated. Compared with the approaches of [22, 23], the proposed method exhibits the same pass rate, but the mean value of the encrypted images in this paper is closer to the theoretical value of 33.4605%, but the standard deviation 0.0142 of the encryption algorithm in this paper fell between the two comparative works, indicating that the encryption algorithm in this paper can better resist the differential attack, but the stability of the ability to resist the split attack is between the two comparative methods.
4.4 Key space analysis
To effectively resist brute force attacks, the key should have a sufficiently large key space in addition to a strong sensitivity. The size of the key space is determined by the number of keys; the larger the number of keys, the larger the key space of the encryption algorithm, and the stronger its ability to resist brute-force attacks.
The security key factors of the encryption algorithm in this paper are five, which are two parameters of the system, two initial values of the chaotic system and the order of chaos taking m. The sensitivity of both chaotic parameters and chaotic initial values is
4.5 Information entropy analysis
Information entropy is a test of uncertainty and is calculated as in Eq. 19.
The information entropy can better reflect the overall randomness of the image, while the local information entropy can better reflect the microscopic randomness of the image. Local information entropy is an improved information algorithm that selects nonoverlapping regions in an image and calculates the evaluation information entropy of these regions, which is calculated as in Eq. 20:
4.6 Clipping attack and noise attack
A clipping attack is an attack method that intercepts and destroys or removes part of the data of a cipher-text image during transmission. Usually, the clipped part is a region in the image with strong interpixel correlation, and the lost information is difficult to recover. Therefore, breaking the interpixel correlation is a measure of the clipping resistance performance of the image encryption algorithm. If the strong interpixel correlation of the image leads to decryption, it may fail when the cipher-text image after the loss of information does not provide enough valid information. In this paper, by combining two-dimensional difference mapping with the Josephus cycle, the image is dislocated using a chunking strategy with uniform pixel distribution, and when the cipher-text image is clipped, the clipped part is not a complete distinction in the original image but is scattered in various regional points so that the clipped image still retains enough information to enable it to recover the corresponding plain-text image. The following test images of Lena et al. shown in Figure 8 are clipped by 1/16, 1/8, and 1/4 (the pixels at the clipped position are all 0, and the clipped sample is shown in Figure 10), and the decrypted image of the clipped cipher-text image is shown in the second row of Figure 8. The algorithm in this paper has certain recovery ability when subjected to clipping attacks, and the encryption algorithm in this paper can resist certain clipping attacks.

FIGURE 8. Encryption results after clipping attack (A) Encryption of Lena’s 1/4 clipping, (B) Encryption of Boat’s 1/8 clipping, (C) Encryption of Feifei’s 1/16 clipping.
Figure 9 shows the effect of Lean reduced by different decryption algorithms at the same degree of clipping, and it can be seen that the proposed encryption algorithm is different from [25]. There is almost no difference between the proposed encryption algorithm and [25], but it is significantly better than the algorithms in [26, 27].

FIGURE 9. Decryption results after noise attack: (A) decryption of “Lena” with noise intensity of 0.25, (B) decryption of “Ship” with noise intensity of 0.10, and (C) Decryption of “Baboon” with noise intensity of 0.05.

FIGURE 10. Comparison of decryption results after clipping attack: (A) 1/4° clipping of the encrypted “Lena”, (B) Decryption by the algorithm proposed in this paper, (C) Decryption by the algorithm proposed in [25], (D) Decryption by the algorithm in [26], (E) Decryption by the algorithm in [27].
Image noise is the unnecessary or redundant interference information that exists in image data. In the process of image acquisition or transmission, due to the influence of image sensor material, working environment, transmission channel, etc., the image may receive noise contamination, which will have a certain impact on the decryption of the terminal image. Therefore, the ability to resist certain noise attacks is an indicator of the performance of image encryption algorithms. In this paper, we use pepper noise to simulate noise contamination in transmission and add different intensities of pepper noise to the cipher image to test the anti-noise ability of the algorithm in this paper.
Figure 10 shows the results obtained by restoring the test cipher-text image after adding pretzel noise with noise densities of 0.25, 0.10, and 0.05. From this, it can be seen that the greater the noise intensity, the deeper the impact on the image and the poorer the quality of the decrypted image, but the algorithm in this paper can still distinguish the main information of the original image from the overall effect, which indicates that the algorithm in this paper can tolerate a certain degree of noise and has a certain anti-interference ability.
Figure 11 shows the individual results of using the encryption algorithms proposed in this paper and [25, 26] for cipher-text image restoration under noise attacks. The first column shows the proposed algorithm in this paper, the second column shows the results of [25], and the third column is the results of [42]. The first row is a 1% noise attack, and the second row is a 5% noise attack. By comparing the decrypted images under the same noise interference, it can be seen that the decryption algorithm in this paper outperforms the other two encryption algorithms.

FIGURE 11. Comparison of decryption results after noise attack: (A) decrypted after a 1% noise attack by the proposed algorithm, (B) decrypted after a 1% noise attack by the algorithm in [25], (C) decrypted after a 1% noise attack by the algorithm in [42], (D) decrypted after a 5% noise attack by the proposed algorithm, (E) decrypted after a 5% noise attack by the algorithm in [25], and (F) decrypted after a 5% noise attack by the algorithm in [42].
4.7 Lossless and perceived encryption analysis
The proposed method is lossless encryption. We use the value of the peak signal measure noise ratio (PSNR) to calculate the difference between the plain and cipher images. When the value of PSNR between the plain image and the cipher image is minimal, the encryption performance is better. In contrast, the PSNR value between plain and decrypted images must be infinity to prove that the encryption is lossless. PSNR can be calculated by Eq. (21)
where I is the plain image, I′ is the image cipher or image decrypt depending on the calculation of the encryption or decryption process and the pixel coordinates are i, j. The result measured by PSNR is presented in Table 3.
We also use structural similarity (SSIM) to measure the quality of the encryption proposed for the cipher image. In addition, SSIM is also used to measure the quality of the decrypted image from the distortion that occurs, which has a value between 0 and 1. A large value means that SSIM is better. The SSIM can be calculated by Eq. 22
where
4.8 Encryption time and encryption complexity analysis
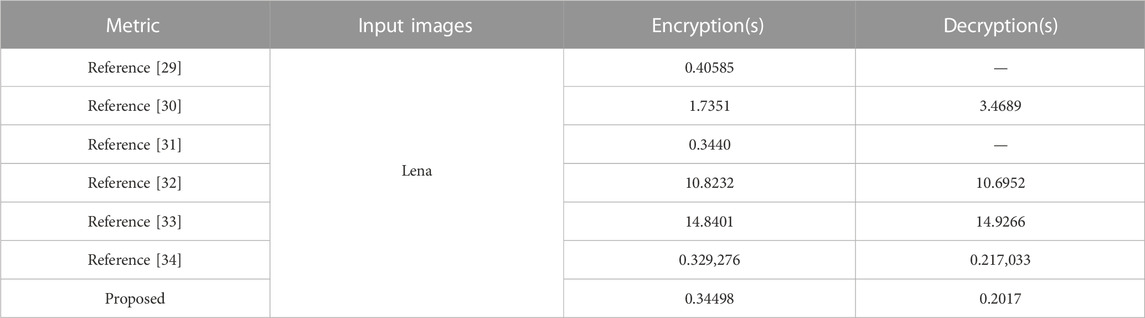
In this section, we chose an image named Lena, which is a representation to compare the encryption time with the other encryption schemes. Table 6 shows different algorithms’ encryption times. Encryption is not the best, but it is the best in decryption since decryption does not need to recive the pseudorandom sequence.
The proposed algorithm’s computational complexity mainly depends on the calculation of the integer data. The proposed encryption method’s computational complexity is
5 Conclusion
To address the problems of weak security of current image encryption algorithms, this paper proposes a Josephus cycle image encryption algorithm based on a two-difference chaotic system. The chunking strategy is used to improve the efficiency of the scrambling diffusion, and the adaptive key generation algorithm is used to break the correlation between neighboring pixels through the scrambling diffusion of bit bits and bit planes by applying the rank transformation method and the Josephus cycle with variable step length and direction. Experimental evidence is conducted using USC-SIPI 'Miscellaneous’ images, which are commonly used in encryption. The results show that the algorithm in this paper can effectively resist common attacks such as information analysis, brute force, noise, and clipping and can be applied to the encryption and transmission of image information. However, the algorithm in this paper also has certain shortcomings, and the bit-level encryption in this paper increases the complexity of the algorithm. To guarantee the security of the algorithm, it is complicated to choose the scrambling method, which affects the encryption speed, and if the algorithm is applied to fast mobile devices, the efficiency of the algorithm needs to be further improved.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: http://sipi.usc.edu/database/.
Author contributions
HZ provided the idea of algorithm. HZ and WS carried out the simulations, arranged the architecture, and drafted the manuscript. LL supervised the work and revised the manuscript. Both authors read and approved the final manuscript.All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Matthews R. On the derivation of a “Chaotic” encryption algorithm. Cryptologic (1989) 13(1):29–42. doi:10.1080/0161-118991863745
2. Fridrich J. Symmetric ciphers based on two-dimensional chaotic maps. Int J Bifurcation chaos (1998) 8(6):1259–84. doi:10.1142/s021812749800098x
3. Shannon CE. Communication theory of secrecy systems. Bell Syst Tech J (1949) 28(4):656–715. doi:10.1002/j.1538-7305.1949.tb00928.x
4. Li CQ, Lin D, Lu JH. Cryptanalyzing an Image-Scrambling encryption algorithm of pixel bits. IEEE Multimedia (2017) 24(3):64–71. doi:10.1109/mmul.2017.3051512
5. Hua ZY, Yi S, Zhou Y. Medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Process. (2018) 144:134–44. doi:10.1016/j.sigpro.2017.10.004
6. Hu J, Han F. A pixel-based scrambling scheme for digital medical images protection. J Netw Comput Appl (2009) 32(4):788–94. doi:10.1016/j.jnca.2009.02.009
7. Zheng J, Luo Z, Zhang Q. An efficient image encryption algorithm based on multi chaotic system and random DAN coding. Multimedia Tools Appl (2020) 79:29901–21. doi:10.1007/s11042-020-09454-9
8. Gao T, Chen Z. Image encryption based on a new total shuffling algorithm. Chaos, solitons and fractals (2008) 38(1):213–20. doi:10.1016/j.chaos.2006.11.009
9. Pak C, An K, Jang P, Kim J. A novel bit-level color image encryption using improved 1D chaotic map. Multimedia Tools Appl (2018) 78(9):12027–42. doi:10.1007/s11042-018-6739-1
10. Elmanfaloty RA, Abou-Bakr E. An image encryption scheme using a 1D chaotic double section skew tent map. Complexity (2020) 2020:7647421–18. doi:10.1155/2020/7647421
11. Wang XY, Yang L, Liu R, Kadir A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn (2010) 62(3):615–21. doi:10.1007/s11071-010-9749-8
12. Cheng G, Wang C, Chen H. A novel color image encryption algorithm based on hyperchaotic system and permutation-diffusion architecture. Int J Bifurcation Chaos (2019) 29(09):1950115. doi:10.1142/s0218127419501153
13. Wang X, Teng L, Qin X. A novel colour image encryption algorithm based on chaos. Signal Process (2012) 92:1101–8. doi:10.1016/j.sigpro.2011.10.023
14. Arroyo D, Diaz J, Rodriguez FB. Cryptanalysis of a one round chaos-based substitution permutation network. Signal Process (2013) 93:1358–64. doi:10.1016/j.sigpro.2012.11.019
15. Hua Z, Zhou Y. Image encryption using 2D logistic-adjusted-sine map. Inf Sci (2016) 339:237–53. doi:10.1016/j.ins.2016.01.017
16. Chen C, Sun K, He S. An improved image encryption algorithm with finite computing precision. Signal Process (2020) 168:107340. doi:10.1016/j.sigpro.2019.107340
17. Flores-Vergara A, Inzunza-Gonzalez E, Garcia-Guerrero E, López-Bonilla O, Rodríguez-Orozco E, Hernández-Ontiveros J, et al. Implementing a chaotic cryptosystem by performing parallel computing on embedded systems with multiprocessors. Entropy (2019) 21:268. doi:10.3390/e21030268
18. Niu Y, Zhang X. An image encryption algorithm based on filling curve and adjacent pixel bit scrambling. J Electro Inf Tech (2022) 44(3):1137–46.
19. Rehman AU, Liao X, Kulsoom A, Ullah S. A modified (Dual) fusion technique for image encryption using SHA-256 hash and multiple chaotic maps. Multimedia Tools Appl (2016) 75(18):11241–66. doi:10.1007/s11042-015-2851-7
20. Lin T, Xu Y. Experimental study of different parameters on chaotic stream ciphers forinformation encryption. Acta Scientiarum Naturalium Universitatis Sunyatseni (2004) 43(S2):101–4. doi:10.3321/j.issn:0529-6579.2004.z2.026
21. Huang L, Han G, Xiang J, Min L. Optimization of chaotic measurement matrix in compressive sensing. In: Proceedings of the 2nd International Conference on Digital Signal Processing; Tokyo (2018).
22. Alawida M, Samsudin A, Alshoura WH. An image encryption scheme based on hybridizing digital chaos and finite state machine. Signal Process (2019) 164:249–66. doi:10.1016/j.sigpro.2019.06.013
23. Himeur Y, Boukabou A. A robust and secure key-frames based video watermarking system using chaotic encryption. Multimedia Tools Appl (2018) 77(7):8603–27. doi:10.1007/s11042-017-4754-2
24. Zhou Y, Bao L, Chen L. Image encryption using a new parametric switching chaotic system. Signal Process (2013) 93(11):3039–52. doi:10.1016/j.sigpro.2013.04.021
25. Xian Y, Wang X. Fractal sorting matrix and its application on chaotic image encryption. Inf Sci (2021) 547:1154–69. doi:10.1016/j.ins.2020.09.055
26. Cun Q, Tong X, Zhu W, Zhang M. Selective image encryption method based on dynamic DNA coding and new chaotic map. Optik (2021) 243:167286. doi:10.1016/j.ijleo.2021.167286
27. Chai X, Chen Y, Broyde L. A novel chaos-based image encryption algorithm using DNA sequence operations,. Opt Lasers Eng (2017) 88:197–213. doi:10.1016/j.optlaseng.2016.08.009
28. Hua Z, Xu B, Jin F, Huang F. Image encryption using Josephus problem and filtering diffusion. IEEE Access (2021) 7:8660–74. doi:10.1109/access.2018.2890116
29. Girdhar A, Kapur H, Kumar V. A novel grayscale image encryption approach based on chaotic maps and image blocks. Appl Phys (2021) 127:39. doi:10.1007/s00340-021-07585-x
30. Yan X, Wang X, Xian Y. Chaotic image encryption algorithm based on arithmetic sequence scrambling model and DNA encoding operation. Multimedia Tools Appl (2021) 80:10949–83. doi:10.1007/s11042-020-10218-8
31. Ping P, Xu F, Mao Y, Wang Z. Designing permutation–substitution image encryption networks with Henon map. Neurocomputing (2018) 283:53–63. doi:10.1016/j.neucom.2017.12.048
32. Chai X, Gan Z, Yuan K, Chen Y, Liu X. A novel image encryption scheme based on DNA sequence operations and chaotic systems. Neural Comput Appl (2019) 31:219–37. doi:10.1007/s00521-017-2993-9
33. Hu T, Liu Y, Gong L, Ouyang C. An image encryption scheme combining chaos with cycle operation for DNA sequences. Nonlinear Dyn (2016) 87:51–66. doi:10.1007/s11071-016-3024-6
34. Sakshi P, Thanikkaiselvan V. Image encryption using a spectrally efficient halton logistics tent (HaLT) Map and DNA encoding for secured. Entropy (2022).
35. Yu Z, Yang Z. Method of remote sensing image detail encryption based on symmetry algorithm. J Ambient Intelligence Humanized Comput (2021). doi:10.1007/s12652-020-02818-x
36. Hua Z, Zhou Y. Design of image cipher using block-based scrambling and image filtering. Inf Sci (2017) 396:97–113. doi:10.1016/j.ins.2017.02.036
37. Park J, Dogan A, TeıxeıraBlock R. Josephus Problem: When the reality is more cruel than the old story. Hacettepe J Math Stat (2021) 50:970–81.
38. Chai X, Fu J, Gan Z, Lu Y, Zhang Y. An image encryption scheme based on multi-objective optimization and block compressed sensing. Nonlinear Dyn (2022) 108:2671–704. doi:10.1007/s11071-022-07328-3
39. Nakano K, Suzuki K. Known-plaintext attack-based analysis of double random phase encoding using multiple known plaintext-ciphertext pairs. Appl Opt (2022) 61:9010–9. doi:10.1364/ao.469244
40. Nicholson A, Bailey V. The balance of animal populations: Part I, in proceedings of the zoological society of landon. Oxford, UK: Blackwell Publishing (1935). p. 551–98.
41. Hassan S, Ahluwalia D, Maddali RK, Manglik M. Computational dynamics of the nicholson-bailey models. Eur Phys J plus (2018) 133(349):2–22.
Keywords: image encryption, chaotic mapping, Josephus cycle, security analysis, attacks
Citation: Zhang H, Sun W and Lu L (2023) Chaotic encryption algorithm with scrambling diffusion based on the Josephus cycle. Front. Phys. 11:1191793. doi: 10.3389/fphy.2023.1191793
Received: 22 March 2023; Accepted: 25 April 2023;
Published: 09 May 2023.
Edited by:
Teddy Craciunescu, National Institute for Laser Plasma and Radiation Physics, RomaniaCopyright © 2023 Zhang, Sun and Lu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ling Lu, bHZsaW5nQG5qbXUuZWR1LmNu
 Huijie Zhang1
Huijie Zhang1 Ling Lu
Ling Lu