Non-local residual symmetry and soliton-cnoidal periodic wave interaction solutions of the KdV6 equation

The residual symmetry of the KdV6 equation is obtained by the Painlevé truncate expansion. Since the residual symmetry is non-local, five field quantities are introduced to localize it into the local one. Besides, the interaction solutions between solitons and cnoidal periodic waves of the KdV6 equation are constructed by making use of the consistent tanh expansion method. As an illustration, a specific interaction solution in the form of tanh function and Jacobian elliptic function is discussed both analytically and graphically.

1 Introduction

Due to the wide applications in explaining physical phenomena, seeking exact solutions of non-linear equations becomes one of the most important tasks in non-linear science. In fact, finding solutions of non-linear evolution equations is not an easy thing, and only in few special cases one may write down the explicit analytical solutions. Despite of this fact, kinds of non-linear excitations such as the solitons, conoidal periodic waves, Painlevé waves have been found. However, although the non-linear waves or even the interactions among solitons have been well studied, the research on the interactions among different types of non-linear waves is still a thorny issue. Recently, Lou discovered that, starting from the non-local symmetries of non-linear equations, the interactions, such as the soliton-Painlevé wave, soliton-cnoidal periodic wave, soliton-KdV wave, etc., can be established [1-6]. Moreover, recent researches have also shown that the interaction solutions between solitons and other non-linear excitations can also be obtained by the consistent tanh expansion (CTE) method, which is evolved from the classical tanh function expansion method [7-9].

In Ref. [10], K²S²T [A. Karasu-Kalkanlı, A. Karasu, A. Sakovich, S. Sakovich, R. Turhan] introduced the Painlevé test for integrability of partial differential equation to the sixth-order non-linear wave equation

$\begin{array}{ll}\hfill & u_{\mathit{xxxxxx}}+{\alpha }_1{u}_x{u}_{\mathit{xxxx}}+{\alpha }_2{u}_{xx}{u}_{\mathit{xxx}}+{\alpha }_3{u}_x^2{u}_{xx}\hfill \\ \hfill & +{\alpha }_4{u}_{tt}+{\alpha }_5{u}_{\mathit{xxxt}}+{\alpha }_6{u}_x{u}_{xt}+{\alpha }_7{u}_t{u}_{xx}=0,\hfill \end{array}(1)$

where α_i (i = 1, 2, … , 7) are arbitrary parameters. They found that there were four cases of relations between the parameters that pass the Painlevé test. Three of those cases correspond to the known integrable equations, the bidirectional Sawada–Kotera equation (11)–(15), the bidirectional Kaup-Kupershmidt equation (11), (12) and (16) and the Drinfeld-Sokolov-Satsuma-Hirota system [17-19], whereas the fourth one

$\left({\partial }_x^2+8u_x{\partial }_x+4u_{xx}\right)\left(u_t+u_{\mathit{xxx}}+6u_x^2\right)=0(2)$

turns out to be new. This new integrable case is associated with the same spectral problem as of the potential KdV equation, so Eq. 2 is also called the KdV6 equation. In Ref. [10], K²S²T also showed the Lax pair, auto-Bäcklund transformation, traveling wave solutions, and third-order generalized symmetries of the KdV6 equation. In fact, since K²S²T first derived the KdV6 equation, there has been a growing interest in finding its exact solutions, conservation laws and various integrable properties [20-24]. However, as far as we know, the research on the interaction solution of this equation is still lacking.

In present paper, we shall focus on investigating the non-local residual symmetry and the interactions between solitons and cnoidal periodic waves for the KdV6 equation. The paper is organized as follows: In Section 2, the non-local residual symmetry of the KdV6 equation is derived. To constitute a local symmetry, five dependent variables are brought in, thus the non-local symmetry is localized into the Lie point symmetry of the enlarged KdV6 system. In Section 3, with the aid of the CTE method, the interaction solutions between solitons and cnoidal periodic waves of the KdV6 equation are acquired. According to these explicit solutions, the dynamical properties of the interaction solutions are investigated. Finally, the main results are summarized in Section 4.

2 Non-local residual symmetry and its localization

By the transformation v = u_x, $w=u_t+u_{\mathit{xxx}}+6u_x^2$, Eq. 2 is equivalent to

$v_t+v_{\mathit{xxx}}+12v{v}_x-w_x=0,w_{\mathit{xxx}}+8v{w}_x+4w{v}_x=0.(3)$

Since the KdV6 Eq. 3 possesses Painlevé property, we formulate the truncated Painlevé expansion as

$v=\frac{p_2}{{\varphi }^2}+\frac{p_1}{\varphi }+p_0,w=\frac{q_2}{{\varphi }^2}+\frac{q_1}{\varphi }+q_0,(4)$

where p₂, p₁, p₀, q₂, q₁ and q₀ are undetermined functions depending on {x, t}. Substituting the expansion 4) into Eq. 3 and collecting the terms with the same power of ϕ, we get the expressions

$\begin{array}{cc}\hfill & p_2=-{\varphi }_x^2,p_1={\varphi }_{xx},p_0=-\frac{1}{4}\frac{{\varphi }_{\mathit{xxx}}}{{\varphi }_x}+\frac{1}{8}\frac{{\varphi }_{xx}^2}{{\varphi }_x^2}+\lambda ,\hfill \\ \hfill & q_2=-12\lambda {\varphi }_x^2-{\varphi }_x{\varphi }_{\mathit{xxx}}+\frac{3}{2}{\varphi }_{xx}^2-{\varphi }_x{\varphi }_t,\hfill \\ \hfill & q_1=12\lambda {\varphi }_{xx}+{\varphi }_{\mathit{xxxx}}+{\varphi }_{xt}-\frac{3{\varphi }_{xx}{\varphi }_{\mathit{xxx}}}{{\varphi }_x}+\frac{3}{2}\frac{{\varphi }_{xx}^3}{{\varphi }_x^2},\hfill \\ \hfill & q_0=\frac{9\lambda {\varphi }_{xx}^2}{{\varphi }_x^2}+\frac{1}{2}\frac{{\varphi }_{xx}{\varphi }_{xt}}{{\varphi }_x^2}-\frac{2\lambda {\varphi }_t}{{\varphi }_x}-\frac{8\lambda {\varphi }_{\mathit{xxx}}}{{\varphi }_x}-\frac{1}{2}\frac{{\varphi }_{\mathit{xxxxx}}}{{\varphi }_x}+\frac{3}{2}\frac{{\varphi }_{\mathit{xxx}}^2}{{\varphi }_x^2}\hfill \end{array}(5)$

with λ being a free integral constant. In this case, Eq. 3 can be represented as its Schwartzian form

$8\lambda {\left(\frac{{\varphi }_t}{{\varphi }_x}\right)}_x+3\left\{\varphi ;x\right\}{\left\{\varphi ;x\right\}}_x+20\lambda {\left\{\varphi ;x\right\}}_x+{\left\{\varphi ;x\right\}}_t+{\left\{\varphi ;x\right\}}_{\mathit{xxx}}=0(6)$

with the Schwartzian derivative $\{\varphi ;x\}=\frac{{\varphi }_{\mathit{xxx}}}{{\varphi }_x}-\frac{3}{2}\frac{{\varphi }_{xx}^2}{{\varphi }_x^2}$. The Schwartzian form (6) is form invariant under the Möbious transformation

$\varphi \to \frac{a+b\varphi }{c+d\varphi },\left(ad\ne bc\right)(7)$

which implies that Eq. 6 possesses the symmetry

${\sigma }^{\varphi }=d_1+d_2\varphi +d_3{\varphi }^2(8)$

with d_i (i = 1, 2, 3) being three random constants.

In view of the expansion 4), it is found that {p₀, q₀} is just the solution of the KdV6 equation, so the following non-auto-Bäcklund transformation theorem is true.

Non-auto-Bäcklund transformation theorem. If ϕ satisfies the Schwartzian Equation 6, then

$\begin{array}{cc}\hfill v& =-\frac{1}{4}\frac{{\varphi }_{\mathit{xxx}}}{{\varphi }_x}+\frac{1}{8}\frac{{\varphi }_{xx}^2}{{\varphi }_x^2}+\lambda ,\hfill \\ \hfill w& =\frac{9\lambda {\varphi }_{xx}^2}{{\varphi }_x^2}+\frac{1}{2}\frac{{\varphi }_{xx}{\varphi }_{xt}}{{\varphi }_x^2}-\frac{2\lambda {\varphi }_t}{{\varphi }_x}-\frac{8\lambda {\varphi }_{\mathit{xxx}}}{{\varphi }_x}-\frac{1}{2}\frac{{\varphi }_{\mathit{xxxxx}}}{{\varphi }_x}+\frac{3}{2}\frac{{\varphi }_{\mathit{xxx}}^2}{{\varphi }_x^2}\hfill \end{array}(9)$

constitutes a solution of the KdV6 Eq. 3.

In addition, the substituting of the expansion 4) into Eq. 3 also tells us that the residues p₁ and q₁, taking the form as Eq. 5, exactly satisfy the symmetry equations of the KdV6 equation, i.e.,

$\begin{array}{cc}\hfill {\sigma }_t^v+{\sigma }_{\mathit{xxx}}^v+12{\sigma }^v{v}_x+12v{\sigma }_x^v-{\sigma }_x^w& =0,\hfill \\ \hfill {\sigma }_{\mathit{xxx}}^w+8{\sigma }^v{w}_x+8v{\sigma }^w+4{\sigma }^w{v}_x+4w{\sigma }_x^v& =0.\hfill \end{array}(10)$

Thus {p₁, q₁} is then named as the residual symmetry of the KdV6 equation. Clearly, seen from Eq. 5, the residual symmetry {p₁, q₁} contains the space and time derivatives of ϕ, which means that this symmetry is non-local. We turn now to the task of localizing it into a local one such that one can use Lie’s first principle to recover the original Bäcklund transformation. To this end, the following five field quantities have to be introduced

${\varphi }_1={\varphi }_x,{\varphi }_2={\varphi }_{1x},g={\varphi }_t,g_1={\varphi }_{1t},h=v_x.(11)$

As a result, the residual symmetry {p₁, q₁} of the KdV6 equation is converted into the Lie point symmetry

$\begin{array}{ll}\hfill & {\left\{{\sigma }^v,{\sigma }^w,{\sigma }^{\varphi },{\sigma }^{{\varphi }_1},{\sigma }^{{\varphi }_2},{\sigma }^g,{\sigma }^{g_1},{\sigma }^h\right\}}^T\hfill \\ \hfill & =\left\{{\varphi }_2,-4{\varphi }_{1}h+4v{\varphi }_2+8\lambda {\varphi }_2+g_1,-{\varphi }^2,-2\varphi {\varphi }_1,-2{\varphi }_1^2-2\varphi {\varphi }_2,\right.\hfill \\ \hfill & -{\left.2\varphi g,-2{\varphi }_{1}g-2\varphi g_1,-\frac{8v{\varphi }_1^2-8\lambda {\varphi }_1^2-{\varphi }_2^2}{2{\varphi }_1}\right\}}^T\hfill \end{array}(12)$

of the enlarged KdV6 system {3), 6), 9), (11)}.

As is known, symmetry reduction [25, 26] is one of the most powerful methods to study exact explicit solutions for non-linear equations. Based on the Lie point symmetry (12), one may continue to explore more abundant symmetry reduction solutions for the KdV6 equation. The details on this topic might be reported in our future research work.

3 CTE solvability of the KdV6 equation and its soliton-cnoidal wave interaction solutions

In this section, we would like to obtain the soliton-cnoidal wave interaction solutions for the KdV6 Eq. 3. In the frame of the CTE method, by balancing the highest order non-linearity and dispersive term of the KdV6 equation, we take v and w in the following generalized truncated tanh function expansion

$\begin{array}{cc}\hfill v& =v_2{\tanh }^{2}f+v_1\tanh f+v_0,\hfill \\ \hfill w& =w_2{\tanh }^{2}f+w_1\tanh f+w_0,\hfill \end{array}(13)$

where v_i, w_i (i = 0, 1, 2), being six real-valued functions of (x, t), are to be determined from the requirement for solutions v and w to satisfy Eq. 3. Inserting Eq. 13 into the KdV6 equation and requiring the coefficients of all powers of tanh f to be zeros yield twelve overdetermined partial differential equations. After a few detail calculations, we can conclude that

$\begin{array}{cc}\hfill v& =-f_x^2{\tanh }^{2}f+f_{xx}\tanh f-\frac{1}{4}\frac{f_{\mathit{xxx}}}{f_x}+\frac{1}{8}\frac{f_{xx}^2}{f_x^2}+\frac{1}{2}{f}_x^2+\lambda ,\hfill \\ \hfill w& =\left(2f_x^4-12\lambda f_x^2-f_x{f}_{\mathit{xxx}}+\frac{3}{2}{f}_{xx}^2-f_x{f}_t\right){\tanh }^{2}f\hfill \\ \hfill & +\left[f_{\mathit{xxxx}}-\frac{3f_{xx}{f}_{\mathit{xxx}}}{f_x}+f_{xt}+\frac{3f_{xx}^3}{2f_x^2}-\left(6f_x^2-12\lambda \right)f_{xx}\right]\tanh f\hfill \\ \hfill & -\frac{1}{2}\frac{f_{\mathit{xxxxx}}}{f_x}+\frac{2f_{xx}{f}_{\mathit{xxxx}}}{f_x^2}-\frac{1}{2}\frac{f_{\mathit{xxt}}}{f_x}+\frac{3}{2}\frac{f_{\mathit{xxx}}^2}{f_x^2}+\frac{1}{2}\frac{f_{xx}{f}_{xt}}{f_x^2}\hfill \\ \hfill & -\left(\frac{21}{4}\frac{f_{xx}^2}{f_x^3}-4f_x+\frac{8\lambda }{f_x}\right)f_{\mathit{xxx}}+\frac{9}{4}\frac{f_{xx}^4}{f_x^4}+\left(\frac{3}{2}+\frac{9\lambda }{f_x^2}\right)f_{xx}^2\hfill \\ \hfill & +\left(f_x-\frac{2\lambda }{f_x}\right)f_t-2f_x^4+16\lambda f_x^2-24{\lambda }^2,\hfill \end{array}(14)$

and the expansion function f is determined by

$\begin{array}{cc}\hfill & \frac{1}{4}\frac{f_{\mathit{xxxxxx}}}{f_x}-\frac{3}{2}\frac{f_{xx}{f}_{\mathit{xxxxx}}}{f_x^2}+\frac{1}{4}\frac{f_{\mathit{xxxt}}}{f_x}-\left(\frac{5}{2}\frac{f_{\mathit{xxx}}}{f_x^2}-\frac{45}{8}\frac{f_{xx}^2}{f_x^3}+\frac{5}{2}{f}_x-\frac{5\lambda }{f_x}\right)f_{\mathit{xxxx}}\hfill \\ \hfill & -\frac{3}{4}\frac{f_{\mathit{xxt}}{f}_{xx}}{f_x^2}+\frac{15}{2}\frac{f_{\mathit{xxx}}^2{f}_{xx}}{f_x^3}-\left(\frac{1}{4}\frac{f_{xt}}{f_x^2}+\frac{15f_{xx}^3}{f_x^4}+\frac{20\lambda f_{xx}}{f_x^2}\right)f_{\mathit{xxx}}+\frac{45}{8}\frac{f_{xx}^5}{f_x^5}\hfill \\ \hfill & +\left(\frac{3}{4}\frac{f_{xx}^2}{f_x^3}-f_x+\frac{2\lambda }{f_x}\right)f_{xt}+\frac{15\lambda f_{xx}^3}{f_x^3}-\left(\frac{2\lambda f_t}{f_x^2}-6f_x^3+20\lambda f_x\right)f_{xx}=0\hfill \end{array}(15)$

with λ being an arbitrary integral constant.

In order to obtain the interaction solutions between solitons and other non-linear excitations for the KdV6 equation, the expansion function in Eq. 15 may be assumed in the form

$f=\frac{x-{\omega }_{1}t}{b_1}+W\left(\frac{x-{\omega }_{0}t}{b_0}\right)\equiv \frac{x-{\omega }_{1}t}{b_1}+W\left(\xi \right),(16)$

where ω₁ and ω₀ describe the velocities of the soliton and its surrounding W-wave, b₁ and b₀ are two quantities referring to the widths of the soliton and W-wave, respectively. Specially, if W(ξ) = 0 is taken, the solution (14) with Eq. 16 reduces to the trivial traveling wave solution.

Inserting the ansatz (16) into Eq. 15 and introducing the abbreviation

$W_{\xi }\left(\xi \right)=W_1,(17)$

it follows that Eq. 15 becomes the equation satisfied by the elliptic function

$W_{1\xi }^2=a_4{W}_1^4+a_3{W}_1^3+a_2{W}_1^2+a_1{W}_1+a_0(18)$

with coefficients a₁, a₄ and ω₁ taking the form

$\begin{array}{cc}\hfill a_1& =\frac{a_0{b}_1}{b_0}+\frac{b_0{a}_2}{b_1}-\frac{a_3{b}_0^2}{b_1^2}+\frac{4b_0^3}{b_1^3},a_4=4,\hfill \\ \hfill {\omega }_1& =\frac{\left(2b_0^2{b}_1^2{\omega }_0+a_2{b}_1^2-3a_3{b}_0{b}_1+24b_0^2\right)\left(a_0{b}_1^4-a_2{b}_0^2{b}_1^2+2a_3{b}_0^3{b}_1-12b_0^4\right)}{16b_0^6{b}_1^4\lambda }\hfill \\ \hfill & +\frac{2b_0^4{b}_1^2{\omega }_0-5a_0{b}_1^4+5a_2{b}_0^2{b}_1^2-10a_3{b}_0^3{b}_1+60b_0^4}{2b_0^4{b}_1^2}.\hfill \end{array}(19)$

Hence, the corresponding relation between the solution of the KdV6 equation and that of Eq. 18 is established. Given any one solution of Eq. 18, the associated interaction solution of the KdV6 system can be realized. According to Ref. [27], Eq. 18 has varieties of solutions in the form of Jacobian elliptic functions, which gives us a chance to look for the physically relevant soliton-cnoidal periodic wave interaction solutions for the KdV6 equation. As a representative example, we suppose now that Eq. 18 owns the solution

$W_1=\frac{c_{0}CD}{1-c_1{S}^2},(20)$

where c₀ and c₁ are two real constants, S ≡ sn (ξ, m), C ≡ cn (ξ, m) and D ≡ dn (ξ, m) represent the Jacobian elliptic sine function, Jacobian elliptic cosine function and Jacobian elliptic function of the third kind, respectively, and m is known as the modulus of the Jacobian elliptic functions. Substituting the solution (20) into Eq. 18 and eliminating the coefficients of different powers of Jacobian elliptic functions, we obtain after a brief calculation

$\begin{array}{cc}\hfill & a_0=m^3+2m^2+m,a_2=-m^2-6m-1,\hfill \\ \hfill & a_3=0,b_0=\frac{1}{2}{b}_1\delta \left(m+1\right),c_0=\delta \sqrt{m},c_1=m,\hfill \\ \hfill & {\omega }_1=\left(1-\frac{{\left(m-1\right)}^2}{b_1^2\lambda {\left(m+1\right)}^2}\right){\omega }_0+\frac{20{\left(m-1\right)}^2}{b_1^2{\left(m+1\right)}^2}-\frac{2\left(5m^2+6m+5\right){\left(m-1\right)}^2}{b_1^4\lambda {\left(m+1\right)}^4}.\hfill \end{array}(21)$

Next integrating the notation (17), the expression for the cnoidal periodic wave can be written as

$W=-\delta \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(m^{1/2}S\right)+c_2(22)$

with an integral constant c₂. Substituting this into Eq. 16, we form now the formula for the expansion function

$f=-\delta \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(m^{1/2}S\right)-\frac{{\omega }_{1}t}{b_1}+\frac{x}{b_1}+c_2.(23)$

Therefore, after inserting Eq. 23 into the solution (14), the soliton-cnoidal periodic wave interaction solution of the KdV6 equation is constructed. Here we omit the lengthy formulas for the sake of simplicity.

As pointed out in our pervious work [2, 7], soliton-cnoidal wave interaction solutions can be regarded as dressed solitons, namely, solitons dressed by cnoidal periodic waves. After taking the limit tanh(f) = ±1 in the solution (14), i.e., removing the soliton cores of v and w, only the cnoidal periodic wave parts remain. To illustrate the soliton-cnoidal periodic wave structure in more detail, it is exhibited in a graphical way with the parameters c₂ = 0, δ = b₁ = λ = 1, ω₀ = 2 and m = 0.01; Figures 1A,B display the profiles of the soliton-cnoidal wave structures at t = 0; Figures 1C,D depict the soliton cores of v and w, where the dashed lines show the left parts of the solitons, i.e., taking tanh(f) = −1 in the solution (14), and the right parts are displayed by the solid lines. Figures 1E,F show the corresponding cnoidal periodic wave structures. As is expected, apart from the soliton cores, the solutions v and w rapidly tend to the cnoidal periodic waves propagating along the x direction.Furthermore, we would like to illustrate how to control the profiles of the soliton-cnoidal periodic waves and analyze their dynamical behaviors. First, the designable of the velocity of the cnoidal periodic wave is to be considered. Figure 2 exhibits the time-space evolutions of the soliton-cnoidal periodic wave solution (14). The overtaking collision processes between solitons and cnoidal waves are shown in Figure 2A, B. Here both the solitons and the cnoidal waves are right-moving, but the velocity of cnoidal waves, selected as ω₀ = 2, is slower than the velocity of solitons ω₁ = 7.96, which is calculated from Eq. 19. As time evolves, the soliton collide with every peak of cnoidal wave, and both the amplitudes and the widths of solitons and cnoidal periodic waves are unchanged except for a phase shift; Figure 2C, D show the interactions between solitons and cnoidal waves with zero velocity. In this situation, the cnoidal waves can be viewed as the standing waves. The right-going solitons collide with the standing periodic waves during their propagations. It is also shown that the collisions between solitons and cnoidal waves are elastic with a slight phase shift. The head-on collision between solitons and cnoidal waves can be observed from Figure 2E, F, which display the right-going solitons colliding with the left-going cnoidal waves (ω₀ = −2). In addition, the straight line that the soliton propagates along is x = ω₁t − b₁c₂, determined by Eq. 23, which is drawn in Figure 2A, B by solid lines.

FIGURE 1

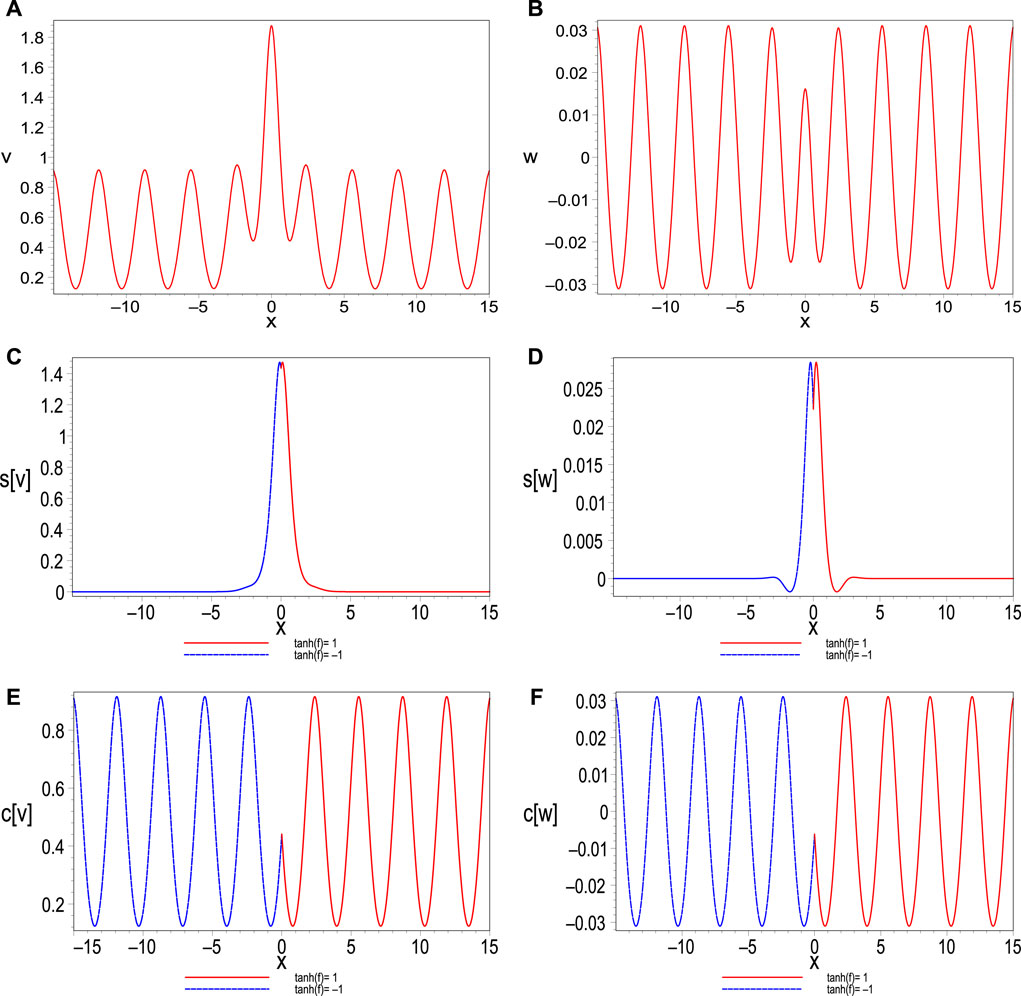
FIGURE 1. (A) and (B): Profiles of the soliton-cnoidal periodic wave interaction solutions with parameters c₂=0, λ = δ = b₁=1, ω₀=2 and m =0.01. (C) and (D): Soliton cores of the interaction solutions. (E) and (F): Background periodic waves of the interaction solutions.

FIGURE 2

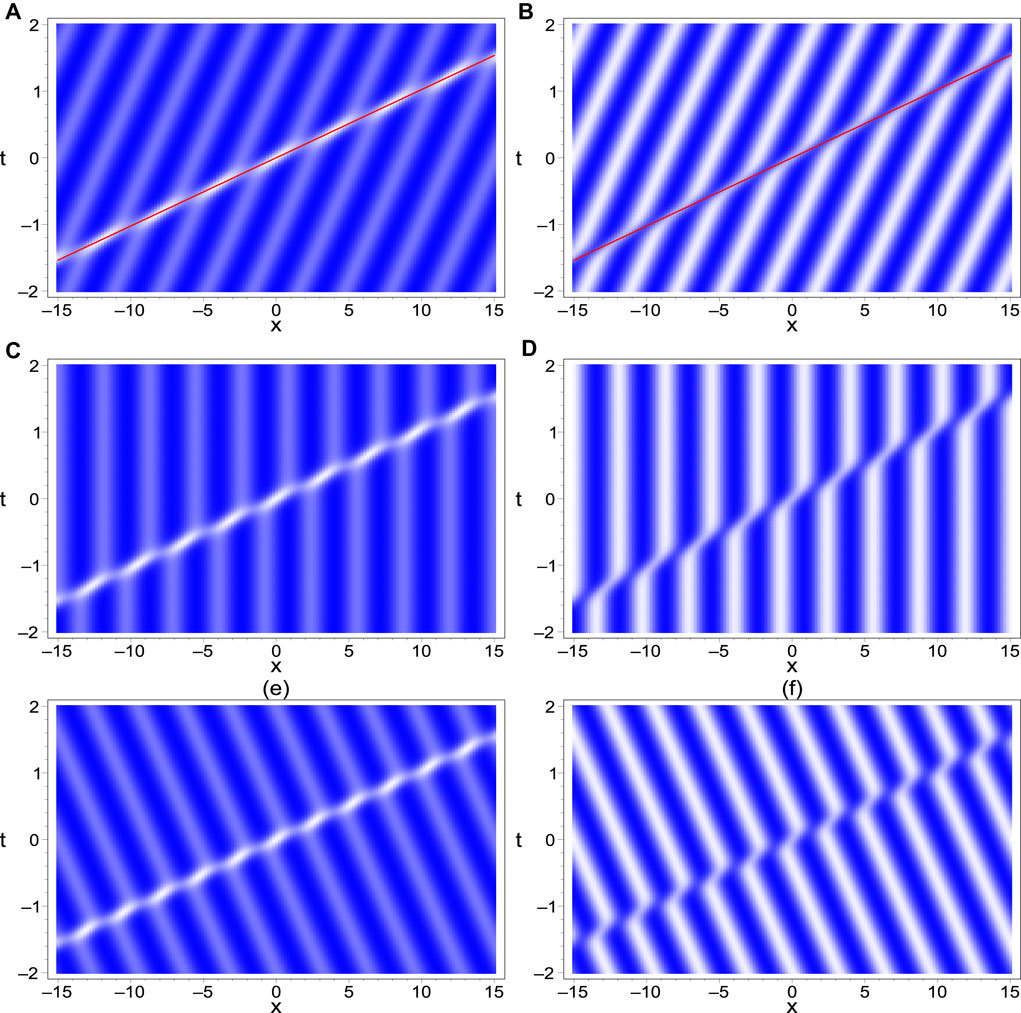
FIGURE 2. Density profiles of the soliton-cnoidal periodic wave with the parameters (A) and (B)ω₀=2; (C) and (D): ω₀=0; (E) and (F): ω₀=−2. Other parameters are the same as those in Figure 1.

As shown in Eq. 21, the wave parameter m indicates not only the modulus of the Jacobian elliptic function, but also the amplitude of Jacobian elliptic function. With the increasing of m, the amplitude of the cnoidal periodic wave trends to decrease. In particular, under the asymptotic condition m → 0, the soliton profiles go to be the classical KdV6 solitons, and the surrounding cnoidal periodic waves are non-zero and with a slight amplitude periodic wave, which is displayed in Figure 3.

FIGURE 3

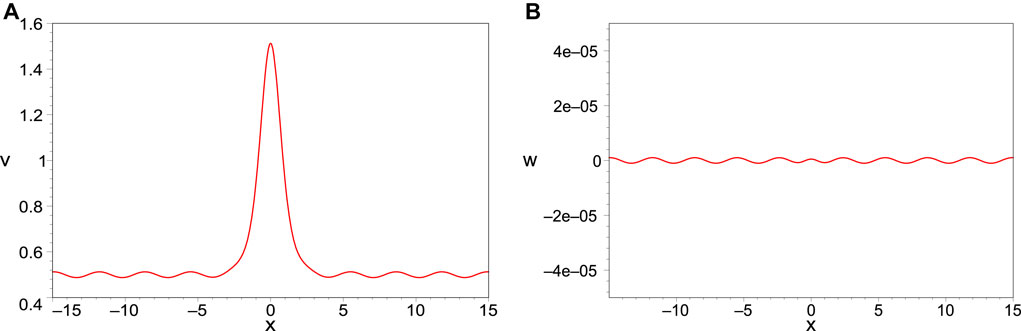
FIGURE 3. 2D plots of the soliton-cnoidal periodic wave interaction solutions (A) v and (B) w with m = 0.00001, and other parameters are chosen as those in Figure 1.

4 Summary and discussion

In this paper, by making use of the truncated Painlevé expansion, the residual symmetry of the KdV6 equation was derived. To eliminate the non-locality of the residual symmetry, we introduced five new field quantities ϕ₁, ϕ₂, g, g₁ and h to localize it into the local Lie point symmetry of the enlarged KdV6 system {(3), (6), (9), (11)}. Besides, the CTE method was applied to the KdV6 equation to get its soliton-cnoidal wave interaction solutions. In the process of solving the equation that the expansion function f satisfies, an intimate connection between this equation and the equation satisfied by the elliptic functions was constructed. By choosing any one elliptic function solution, the corresponding interaction solutions of the KdV6 equation can be acquired. To show the interaction solution more concretely, the Jacobian elliptic wave solution (20) of Eq. 18 was introduced. The results show that the soliton-cnoidal wave interaction solutions of the KdV6 equation can be viewed as the solitons dressed by the cnoidal periodic waves. Once the cnoidal wave backgrounds are taken away, only the soliton cores are left. The results also exhibit that the shapes of the soliton-cnoidal wave interaction solutions of the KdV6 equation are designable by selecting different values of wave parameters. In particular, how to design the velocities and amplitudes of the cnoidal periodic waves were demonstrated, and the dynamical behaviors of the soliton-cnoidal periodic wave interaction solutions were analyzed. In addition, we believe that the method used for getting non-local residual symmetry in this paper can also be applied to complex functional equations, such as the non-linear Schrödinger type equations, and their abundant soliton-nonlinear wave interaction solutions can also be obtained by symmetry reduction method. More studies regarding the soliton-nonlinear wave interaction solutions for other partial differential equations will be reported in our future research work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LZ: Methodology, Software, Formal analysis, Writing–original draft. XC: Conceptualization, Funding acquisition, Resources, Supervision, Writing–review and editing. WY: Investigation, Formal analysis. ZZ: Software, Formal analysis.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11975204 and 12075208), the Project of Zhoushan City Science and Technology Bureau (Grant No. 2021C21015) and the Training Program for Leading Talents in Universities of Zhejiang Province.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hu XR, Lou SY, Chen Y. Explicit solutions from eigenfunction symmetry of the Korteweg-de Vries equation. Phys Rev E (2012) 85:056607. doi:10.1103/physreve.85.056607

CrossRef Full Text | Google Scholar

2. Cheng XP, Chen CL, Lou SY. Interactions among different types of nonlinear waves described by the Kadomtsev-Petviashvili equation. Wave Motion (2014) 51:1298–308. doi:10.1016/j.wavemoti.2014.07.012

CrossRef Full Text | Google Scholar

3. Cheng XP, Yang YQ, Ren B, Wang JY. Interaction behavior between solitons and (2+1)-dimensional CDGKS waves. Wave Motion (2016) 86:150–61. doi:10.1016/j.wavemoti.2018.08.008

CrossRef Full Text | Google Scholar

4. Ren B. Symmetry reduction related with nonlocal symmetry for Gardner equation. Commun Nonlinear Sci Numer Simul (2017) 42:456–63. doi:10.1016/j.cnsns.2016.06.017

CrossRef Full Text | Google Scholar

5. Xia YR, Yao RX, Xin XP. Residual symmetry, Bäcklund transformation, and soliton solutions of the higher-order Broer-Kaup system. Adv Math Phys (2021) 2021:1–10. doi:10.1155/2021/9975303

CrossRef Full Text | Google Scholar

6. Liu XZ, Yu J. Solitons and symmetry reduction solutions of a nonlocal two-mode Korteweg-de Vries equation. Math Method Appl Sci (2022) 45:11423–32. doi:10.1002/mma.8458

CrossRef Full Text | Google Scholar

7. Lou SY, Cheng XP, Tang XY. Dressed dark solitons of the defocusing nonlinear Schrödinger equation. Chin Phys Lett (2014) 31:070201. doi:10.1088/0256-307X/31/7/070201

CrossRef Full Text | Google Scholar

8. Lou SY. Consistent riccati expansion for integrable systems. Stud Appl Math (2015) 134:372–402. doi:10.1111/sapm.12072

CrossRef Full Text | Google Scholar

9. Wu JW, Cai YJ, Lin J. Residual symmetries, consistent Riccati expansion integrability, and interaction solutions of a new (3+1)-dimensional generalized Kadomtsev-Petviashvili equation. Chin Phys B (2022) 31:030201. doi:10.1088/1674-1056/ac1f08

CrossRef Full Text | Google Scholar

10. Karasu-Kalkanl A, Karasu A, Sakovich A, Sakovich S, Turhan R. A new integrable generalization of the Korteweg-de Vries equation. J Math Phys (2008) 49:073516. doi:10.1063/1.2953474

CrossRef Full Text | Google Scholar

11. Dye JM, Parker A. On bidirectional fifth-order nonlinear evolution equations, Lax pairs, and directionally dependent solitary waves. J Math Phys (2001) 42:2567–89. doi:10.1063/1.1354642

CrossRef Full Text | Google Scholar

12. He JS, Cheng Y, Roemer RA. Solving bi-directional soliton equations in the KP hierarchy by gauge transformation. J High Energ Phys. (2006) 2006:103. doi:10.1088/1126-6708/2006/03/103

CrossRef Full Text | Google Scholar

13. Ma YL, Geng XG. Darboux and Bäcklund transformations of the bidirectional Sawada-Kotera equation. Appl Math Comput (2012) 218:6963–5. doi:10.1016/j.amc.2011.12.077

CrossRef Full Text | Google Scholar

14. Lai XJ, Cai XO. Adomian decomposition method for approximating the solutions of the bidirectional Sawada-Kotera equation. Z Naturforsch A (2010) 65:658–64. doi:10.1515/zna-2010-8-906

CrossRef Full Text | Google Scholar

15. Dong JJ, Li B, Yuen MW. Soliton molecules and mixed solutions of the(2+1)-dimensional bidirectional Sawada-Kotera equation. Commun Theor Phys (2020) 72:025002. doi:10.1088/1572-9494/ab6184

CrossRef Full Text | Google Scholar

16. Dye JM, Parker A. A bidirectional Kaup-Kupershmidt equation and directionally dependent solitons. J Math Phys (2002) 43:4921–49. doi:10.1063/1.1503866

CrossRef Full Text | Google Scholar

17. Karasu-Kalkanlı A, Sakovich SY. Bäcklund transformation and special solutions for the Drinfeld-Sokolov-Satsuma-Hirota system of coupled equations. J Phys A: Math Gen (2001) 34:7355–8. doi:10.1088/0305-4470/34/36/315

CrossRef Full Text | Google Scholar

18. Heris JM, Lakestani M. Exact solutions for the integrable sixth-order Drinfeld-Sokolov-Satsuma-Hirota system by the analytical methods. Int Sch Res Notices (2014) 2014:1–8. doi:10.1155/2014/840689

CrossRef Full Text | Google Scholar

19. Huang LL, Chen Y. Nonlocal symmetry and similarity reductions for the Drinfeld-Sokolov-Satsuma-Hirota system. Appl Math Lett (2017) 64:177–84. doi:10.1016/j.aml.2016.09.010

CrossRef Full Text | Google Scholar

20. Li JB, Zhang Y. The geometric property of soliton solutions for the integrable KdV6 equations. J Math Phys (2010) 51:043508–967. doi:10.1063/1.3359002

CrossRef Full Text | Google Scholar

21. Kupershmidt BA. Kdv6: An integrable system. Phys Lett A (2008) 372:2634–9. doi:10.1016/j.physleta.2007.12.019

CrossRef Full Text | Google Scholar

22. Lin RL, Yao HS, Zeng YB. Restricted flows and the soliton equation with self-consistent sources. Symmetry Integr Geom (2006) 2:096. doi:10.3842/SIGMA.2006.096

CrossRef Full Text | Google Scholar

23. Zhao ZL, Chen Y, Han B. On periodic wave solutions of the KdV6 equation via bilinear Bäcklund transformation. Optik (2017) 140:10–7. doi:10.1016/j.ijleo.2017.04.016

CrossRef Full Text | Google Scholar

24. Bruzon MS, Garrido TM. Symmetries and conservation laws of a KdV6 equation. Discrete Contin Dyn Syst (2018) 11:631–41. doi:10.3934/dcdss.2018038

CrossRef Full Text | Google Scholar

25. Yang B, Song YJ, Wang ZG. Lie symmetry analysis and exact solutions of the (3+1)-dimensional generalized shallow water-like equation. Front Phys (2023) 11:1131007. doi:10.3389/fphy.2023.1131007

CrossRef Full Text | Google Scholar

26. Liu N. Invariant solutions and conservation laws of the variable-coefficient Heisenberg ferromagnetic spin chain equation. Front Phys (2020) 8:260. doi:10.3389/fphy.2020.00260

CrossRef Full Text | Google Scholar

27. Liu SK, Liu SD. Nonlinear equations in physics. Beijing: Peking University Press (2000).

Google Scholar