Alpha clustering in nuclear astrophysics and topology

When we think of clustering in nuclear physics, the astrophysical importance within light nuclei and structural manifestations with classical analogs immediately come to mind. ⁴He, also known as the alpha particle, is the most abundant nucleus in the Universe, being quite tightly bound for its mass, with a first excited state of over 20 MeV. The nature of the alpha particle places it in a unique position within nuclear astrophysics and structure (including geometry). The plurality of energy release from stellar hydrogen fusion—whether quiescent or explosive—comes from the conversion of hydrogen to helium. Within more complex nuclei, the alpha particles are continuously arranged, leading to fascinating phenomena such as excited rotational bands, Borromean ring ground states, and linear structures. Nuclei with an equal and even number of protons and neutrons are colloquially referred to as “alpha conjugate nuclei,” where such special properties are the most pronounced and easiest to spot. However, when a single nucleon or a pair of nucleons is added to the system, alpha clustering not only remains evident but it may also be enhanced. Excited states with large alpha partial widths are a signature of clustering behavior, and these states can have a profound effect on the reaction rates in astrophysical systems when the excitation energy aligns with the so-called Gamow energy—the preferential thermal energy to statistically overcome the Coulomb barrier. In this article, we will consider in detail the specific ramifications of alpha clustering in selected scenarios for both nuclear astrophysics and topology. In particular, we discussed the astrophysical reactions of ⁷Li (α, γ), ⁷Be+α, ¹¹C (α, p), and ³⁰S (α, p), where α-clusters may increase the reaction rates from 10% to an order of magnitude; large α resonances make the astrophysical rate of ¹⁸F (p, α) quite uncertain. We also focused on the α rotational bands of both positive and negative parities of ¹¹B and ¹¹C, and finally on the strongest evidence for the linear-chain cluster state observed in ¹⁴C.

1 Introduction

The clustering of α particles in nuclei plays a critical role in both nuclear astrophysics and nuclear structure. Before delving into the topic, we will review the synthesis of several elements in the light and medium mass regions as they pertain to α clusters. We will then discuss by what empirical measurements and which types of experiments are most suitable to discuss α-clusterization. Once the groundwork is laid, we will review works published over the last dozen years on α-clusterization in the following nuclei: ¹¹B, ¹¹C, ¹⁴C, ¹⁵O, ¹⁹Ne, and ³⁴Ar.

Most of the aforementioned nuclei are radioactive, which often requires rare isotope beams (RIBs). However, clusterization has a long history even in stable isotopes. In particular, during the quiescent phases of stellar evolution of a massive star leading to an iron core in pre-collapse Type II supernovae, clusterization may not be limited to α-clusters, as shown in the Cluster Nucleosynthesis Diagram Figure 1, inspired by the Ikeda diagram [1]. In a massive star (10 M_⊙) according to one model, the core burning temperature, density, and lifetime are as follows: hydrogen, 37 × 10⁶ K, 3.8 g/cm³, and 7.3 × 10⁶ years; helium, 1.80 × 10⁸ K, 620 g/cm³, and 0.72 × 10⁶ years; carbon, 7.20 × 10⁸ K, 6.4 × 10⁵ g/cm³, and 320 years; neon, 1.9 × 10⁹ K, $>10^6$ g/cm³, and $<10$ years; oxygen, 1.8 × 10⁹ K, 1.3 × 10⁷ g/cm³, and 0.5 years; silicon, 3.4 × 10⁹ K, 1.1 × 10⁸ g/cm³, and $<1$ day; and collapse, 8.3 × 10⁹ K, $>3.4\times 10^9$ g/cm³, and 0.45 s [2]. From this example, it can be seen that α-clusters shape the evolution of stars more than any other clusterization burning, e.g., the Hoyle state is responsible for the nucleosynthesis of all heavier elements and helps set the timescale [3]. Although we will mainly discuss the ν-process, νp-process, hot carbon–nitrogen–oxygen (HCNO) cycles, and the αp process, the aforementioned stellar nucleosynthesis shows us that α clusters generally play an important role in such scenarios.

FIGURE 1

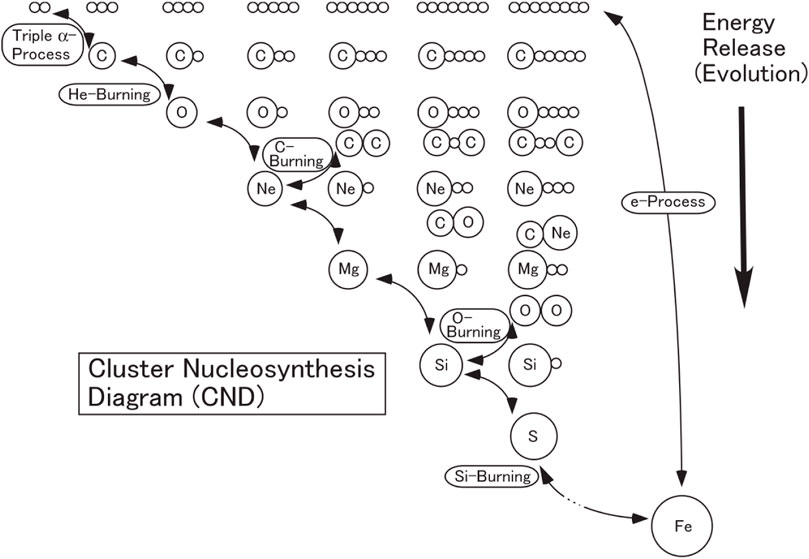
FIGURE 1. Cluster Nucleosynthesis Diagram (CND) [83] for nucleosynthesis during the evolution of a massive star. The small open circles are α-clusters. As the chart starts on the upper left with the lightest elements, energy generation is produced going down, shown on the right side. The image shows in a simple way which nuclei may have clusters. ^© 1994 Elsevier. Reprinted with permission.

The Wigner limit, W, is frequently encountered in the literature, although it is strongly dependent on the radius, R, without any specific structural information, and there are several definitions. In this article, the maximum width of a resonance can be estimated as follows:

${\mathrm{\Gamma }}_{W_i}=\frac{2{\hslash }^2}{{\mu }_i{R}_i^2}{P}_{{\ell }_i},(1)$

where μ is the reduced mass of the channel, R is the channel radius, and P_ℓ is the channel penetrability for channel i [4,5]. The penetrability is calculated as $P_{\ell }=\frac{\rho }{F_{\ell }^2+G_{\ell }^2}$ where $\rho =\frac{kR}{\hslash }$ includes the phase space factor k, and F_ℓ and G_ℓ are the regular and irregular Coulomb functions, respectively. The dimensionless partial width is then ${\theta }_i^2={\mathrm{\Gamma }}_i/{\mathrm{\Gamma }}_{W_i}$, which can be used like a spectroscopic factor for a single-particle state. A typical radius can be calculated as $R_i=R_0(A_1^{1/3}+A_2^{1/3})$, where R₀ is typically chosen from 1.2 to 1.6 fm and A is the atomic mass number. A more refined concept of α-clusterization can instead be calculated with the asymptotic normalization coefficient (ANC), but for basic discussions, the Wigner limit is sufficient. Although the Wigner limit is model-dependent, it is not widely agreed upon which θ² defines an α cluster (e.g., it might be 10%, 25%, or 50%). The basic idea is to obtain Γ_α from an experiment and simply compare it to Γ_W.

There are several experiments for determining Γ_α. Elastic α-scattering has a large cross section, although owing to the Coulomb barrier, elastic scattering of a charged particle rarely shows a resonant structure near the α separation energy, S_α, because of the Rutherford peak. The Trojan horse method is able to measure two-body reactions with extremely low cross sections via a two-to-three-body reaction in a quasi-free kinematics condition [6–8]. α-transfer reactions, such as (⁶Li, d) or (⁷Li, t), are also quite good near S_α and even below it for sub-threshold energies to obtain the ANCs of peripheral reactions [9]. Photodisintegration is useful to study the radiative capture on an unstable species when the recoil is stable (Utsunomiya et al. [10]), and moreover, the type and origin of the background differ from those of the radiative capture (Smith et al. [11]). Coulomb dissociation (Baur et al. [12]) and time reversal studies have sizable cross sections and can be used at higher beam energies. In the case when Γ_α is smaller than another competing partial width, say (α, p) or (α, n) direct measurements, application of the isolated, narrow-resonance condition for the reaction A (i, j)B as

$\gamma \equiv \frac{{\mathrm{\Gamma }}_i\cdot {\mathrm{\Gamma }}_j}{{\mathrm{\Gamma }}_i+{\mathrm{\Gamma }}_j}\approx {\mathrm{\Gamma }}_j\iff {\mathrm{\Gamma }}_j\ll {\mathrm{\Gamma }}_i,(2)$

where γ is the reduced width [5] and the smaller partial width controls the contribution to the reaction rate.

Most of the experiments discussed in this paper use an RIB on gaseous helium targets using the thick target in the inverse kinematics (TTIK) technique [13], which has several advantages. First, the intensity of short-lived RIBs is several orders of magnitude less than the primary beam, so the statistics would be very poor using a thin target of implanted helium (Lennard et al. [14]). One way to increase the total yield is obviously using a thicker target. Second, the impinging beam loses significant energy within the target (often times being stopped entirely), and using the kinematic equations, the measured energy of the reaction point and, hence, the beam energy at that point can be deduced if the energy loss functions and the specific reaction are known. Because the reaction of interest is measured over a large range of energy, it, moreover, prevents the time-consuming retuning of the RIB. In this manuscript, all reactions are written in the astrophysical, normal kinematics nomenclature for convenience despite the fact that most of the experiments were performed in inverse kinematics.

2 Rotational bands and astrophysics of ¹¹B and ¹¹C

Lithium, beryllium, and boron are relatively less abundant than other light and medium mass nuclei, and the astrophysical sites of their production and destruction continue to pose challenges today, for example, the cosmological lithium problem (Hou et al. [15]; Hayakawa et al. [16] and references therein). The nuclei ¹¹B and ¹¹C are mirror nuclei, and some excited states show a dilute form of alpha-clusterization as either 2α + t or 2α +³He, respectively [17–19]. Furthermore, both have been observed to have positive- and negative-spin rotational bands, represented as α-clusterization (Yamaguchi et al. [20], Yamaguchi et al. [21] and references therein). These α-clusters can play an essential role in many explosive environments: ν-process, pp-V, rap (II, III, and IV), and the νp-process. The aforementioned processes may be found in a number of stellar environments: supermassive stars with low metallicity, novae, big-bang nucleosynthesis, and core-collapse supernovae. Considering the number of theoretical and experimental studies, the diverse manifestation of α-clusters, and a large range of astrophysical impact, the present review will mainly focus on ⁷Li (α, α) and ⁷Be (α, α).

The ν-process occurs in core-collapse supernovae where neutrinos are emitted from the proto–neutron star [22]. In the ν-process, ¹¹B is mainly produced via ⁴He (ν, ν′p)³H (α, γ)⁷Li (α, γ)¹¹B, although it can be enhanced by (anti-)neutrino inelastic and breakup reactions on ¹²C as well. Therefore, a precise measurement of ⁷Li (α, γ)¹¹B at $>1$ GK can provide valuable information to reactions and oscillations of neutrinos. The ⁷Be (α, γ) reaction can either take place in the pp-V chain as ⁷Be (α, γ)¹¹C (β⁺ν)¹¹B (p, 2α)⁴He or in a number of the rap-processes and also the νp-process [23–25] (Section 4). Except in the case where ¹¹C decays ($\sim 20$ min), this reaction can bridge the gap from the pp region to the CNO region, similar to the triple-α process. Although the (α, γ) reactions at high temperature are important on ⁷Li and ⁷Be, looking at Eq. 2, it is mainly Γ_γ (typically on order eV), spin-parity, and energy which dominate the analytic reaction rate from these alpha-clusters, not Γ_α. Experiments on α-scattering can determine or constrain the energy and spin-parity but not Γ_γ. The dominance of Γ_γ was recently confirmed by a direct measurement of ⁷Be (α, γ) [26, 27] when compared with the evaluation by Kelley et al. [28]. However, in converse to α scattering, no information was obtained on Γ_α and hence the cluster structure of ¹¹C.

An experiment on ⁷Li+α in inverse kinematics showed only ground-state transitions [20], and the total cross section of ⁷Li (α, p) was comparable to a normal kinematics experiment [29]. The best-fit R-Matrix parameters are shown in Table 1, although a major enhancement in the reaction rate compared to the Nuclear Astrophysics Compilation of REaction rates (NACRE) was not found [30]. Conversely, in the ⁷Be+α inverse kinematic experiment, several channels were seen, (α, α₀), (α, α₁), (α, p₀), and (α, p₁), measuring the charged particles and gamma rays in coincidence [21]. Freer et al. [31] also carried out a similar experiment, except not separating out the inelastic component. Although the two spectra show a basic similarity of the peak shape and relative location, Freer et al. [31] showed a factor of two to three lower cross sections, and the centroids of the peak structure were shifted down by approximately 500 keV. Yamaguchi et al. [21] were able to explain nearly all the resonances with known peaks rather than introducing new resonances. A factor of approximately 10% enhancement in the reaction rate over NACRE could be expected between 1.5 and 3 GK [30]. Although the experiments do not agree on the exact quantum values, it is clear alpha-clusterization is prominent in both sets of experiments, with the best-fit R-Matrix parameters shown in Table 2. Most recently, Psaltis et al. confirmed the astrophysical reaction rate for ⁷Be (α, γ) suggested in NACRE II [26, 27, 32] with a significantly improved precision.

TABLE 1

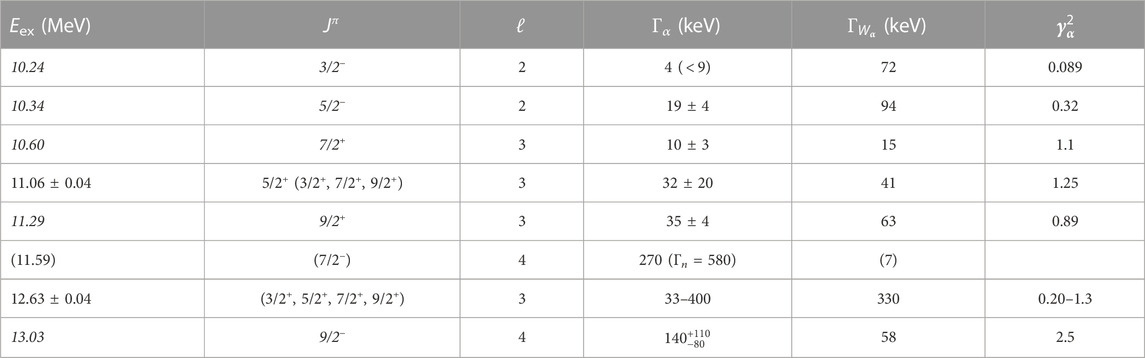
TABLE 1. Best-fit resonance parameters of ¹¹B determined by Yamaguchi et al. [20]. Values in italics were fixed to those found in the literature [85,86]. The penetrability limit, ${\gamma }_{\alpha }^2$, was calculated by ${\mathrm{\Gamma }}_{\alpha }/2P_{{\ell }_{\alpha }}$. R₀ was initially set to 1.15 fm, but the R-Matrix fit could not reproduce the valleys; thus, R₀ was set to 0.9 fm for the R-Matrix fit and ${\mathrm{\Gamma }}_{W_{\alpha }}$.

TABLE 2

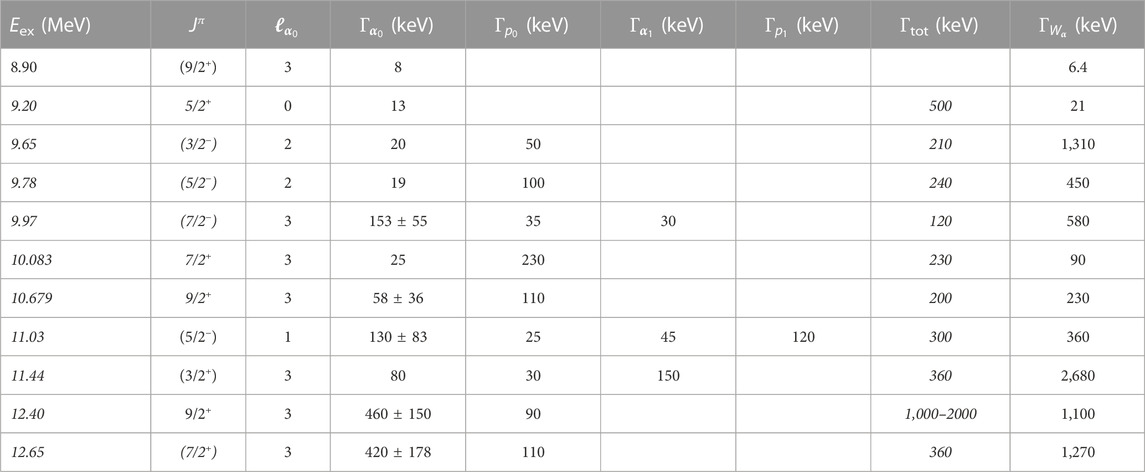
TABLE 2. Best-fit resonance parameters of ¹¹C determined by Yamaguchi et al. [21]. Values in italics were fixed to those found in the literature [85,86]. Other J^π values are possible but are omitted here. R₀ was set to 1.2 fm for ${\mathrm{\Gamma }}_{W_{\alpha }}$.

Although the astrophysical reaction rate was not significantly changed by any of these measurements, the rotational bands in ¹¹B and ¹¹C are interesting from a structure perspective. Previously known rotational bands, as well as those found by Yamaguchi et al. are shown in Figures 2, 3. Both the K = 5/2⁺ and K = 3/2⁺ bands show a linear dependence of E_ex on J (J + 1) and may be related to their oblate, multi-centered α-cluster structure (Soić et al. [33] and references therein). Inspection of the figures indicates mirror levels offset by approximately 500 keV, which diminishes at a higher excitation energy, possibly from a phase transition from the shell model to cluster states (Freer et al. [31] and references therein). It might be strange that the ground state of ¹¹B, which is 3/2⁻, appears above the 1/2⁻ state, but Ragnarsson et al. [34] found a similar energy of the two states, suggesting the 3/2⁻ state is lower than expected. As the figures show, the negative parity bands in both ¹¹B and ¹¹C do not show a perfect linear correlation, and there is a commonality that the energies of two of the bandheads are lower than expected. A calculation using antisymmetrized molecular dynamics (AMD) qualitatively reproduced these findings, attributing this difference to a weaker interaction between the three-center cluster bandhead compared to a more rigid structure of higher-energy states [35]. Finally, the 9/2⁺, 12.4-MeV state in ¹¹C observed may be a missing member of the K = 3/2⁺ band.

FIGURE 2

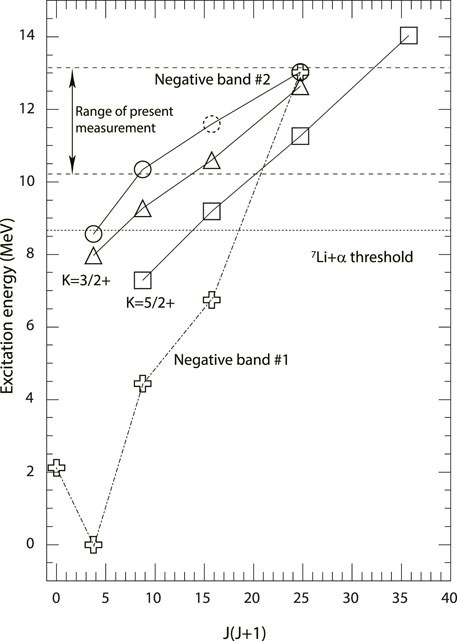
FIGURE 2. Rotational bands in ¹¹B from Yamaguchi et al. [20]. The positive parity bands show very good linearity, whereas the proposed negative parity bands demonstrate some deviance, as described in the text. ^© 2011 American Physical Society. Reprinted with permission.

FIGURE 3

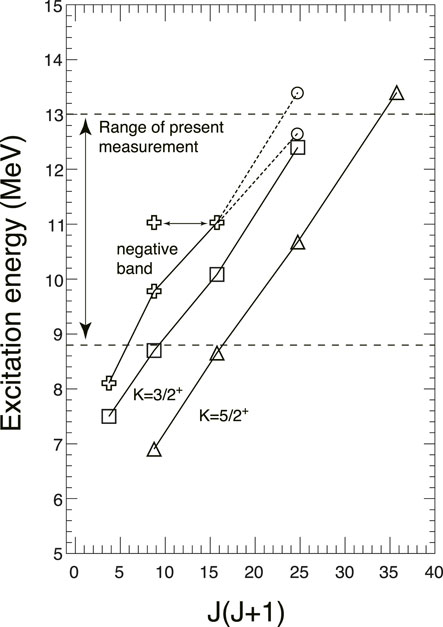
FIGURE 3. Rotational bands in ¹¹C from Yamaguchi et al. [21]. The positive parity bands have excellent linearity, but the proposed negative band shows a non-linear behavior similar to the second negative parity band in ¹¹B in Figure 2. ^© 2013 American Physical Society. Adapted with permission.

3 Linear state and rotation in ¹⁴C

Cluster states where all the clusters fall in a line—the linear-chain cluster state (LCCS)—have been of theoretical interest since the 1950s [36]. Linear clusters are seen in other quantum mechanical systems, such as chemistry. Carbon dioxide (CO₂) shows a linear geometry with an atom of carbon covalently double-bonded between two oxygen atoms at 180°; the molecule can rotate and/or vibrate, which are also observed in the nuclear structure. The shapes of nuclei and their excited states have been frequently studied (and even used to explain certain shape isomers), but until the last several years, no experiment had found strong evidence to verify the LCCS in nuclei. From an intuitive perspective, we may think of modeling the nucleus as a pair of atoms, where most of them are joined into one of the clusters and only a small number of nucleons are used to bond them together. Efforts in the cluster shell model of adding a single nucleon to α-conjugate nuclei may, in the future, add multiple nucleons to gain better understanding of this phenomenon [37]. Initial theories on the LCCS looked at α-nuclei like ¹²C and ¹⁶O with no bonding nucleons, but other theoretical topologies better fit the experimental data. For example, the Hoyle state in ¹²C was found to be either a molecular-like state of ⁸Be+α or a weak coupling of three α-particles [38], and the 0⁺ state just above the four-α threshold in ¹⁶O showed quenching of the moment of inertia consistent with a superfluid state [39]. Until now, ¹⁴C is the only species where the experimental work shows a strong indication of a theoretical LCCS.

Suhara and Kanada-En’Yo [40] proposed a prolate band starting a few MeV above the α threshold of ¹⁴C as an LCCS using the AMD method. The wavefunction dominating the LCCS and an intuitive cartoon are shown in Figure 4. The LCCS was demonstrated to be stabilized by orthogonality to underlying states, and it has a nature of J^π = 0⁺, 2⁺, and 4⁺. Independently, several groups around the world began looking for this LCCS using a ¹⁰Be beam on a helium target for elastic scattering [41–43]. Similar to the ⁷Be case mentioned previously, Freer et al. [41] and Yamaguchi et al. [43] had a reasonable agreement in the spectral shape but the absolute cross sections did not agree. Unlike the case of ⁷Be, Freer et al. [41] found a cross section about a factor of four higher than Yamaguchi et al. [43]. As Freer et al. [41] used a normalization factor for the absolute cross section and Yamaguchi et al. [43] only relied on the experimental parameters, the latter might be considered more reliable. Similar to ⁷Be, the peak structure showed less consistency toward the lower energy side, where the energy loss function plays an important role. Although Freer et al. [41] did not find evidence for a prolate rotational band, Yamaguchi et al. [43] found striking similarity in the energy and spin for the LCCS of Suhara and Kanada-En’Yo [40], as shown in Figure 5. Fritsch et al. [42] used an active target but showed deviation from these results, such as much smaller absolute cross sections (even than Rutherford scattering), no goodness of fit between their theoretical and measured J^π, and a sharp E_{c. m.} locus for inelastic scattering.

FIGURE 4

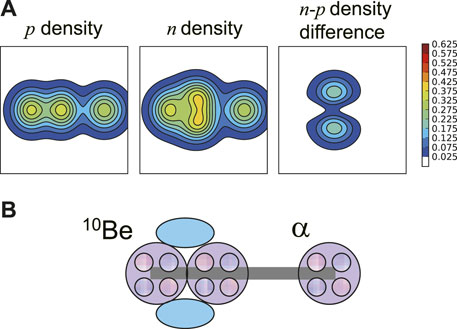
FIGURE 4. Wavefunction of the predominated LCCS determined by the AMD method [40, 84]. (A) Proton density, neutron density, and their difference. (B) Intuitive image of the wavefunction. ^© 2016 Yamaguchi et al. [43] under the CC BY license.

FIGURE 5

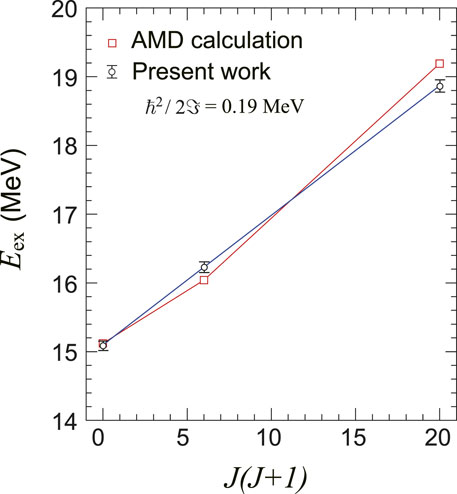
FIGURE 5. Rotational band of the LCCS comparing the AMD calculation [40] to the experimental data [43]. The best R-Matrix fit did not take any guidance from the theory. The agreement between the two is excellent and is strong evidence of an LCCS. ^© 2016 Yamaguchi et al. [43] under the CC BY license.

Table 3 shows a strong indication of an LCCS, only plotting the relevant states. Although the widths show some differences, their average downward trend is the same. Moreover, it is not straightforward to ascertain ${\theta }_{\alpha }^2$ from the AMD calculation, and so, the theoretical width was extracted by an overlap of the AMD and Brink wavefunctions [44]. The cause of this disagreement is an open question, which could be an experimental issue, a theoretical ambiguity, the physical states themselves, or some combination of the aforementioned issues. As the 4⁺ state is in a doublet with a 5⁻ state, it is possible that the 4⁺ component is actually stronger due to limited orthogonality between these two resonances. As Γ_α(5⁺) = 9.4% was measured experimentally, the maximum limit of this effect was evaluated as ${\theta }_{\alpha }^2(4^{+})=7\%$. Another possibility is that the 4⁺ resonance has a large Γ_n ≥ 300 keV, resulting in ${\theta }_{\alpha }^2\ge 5\%$—although there are no predictions available, nearby resonances having Γ_n of a similar order. The AMD calculation also did not include several factors such as the rotational motion of ¹⁰Be, the radial motion of the α particle, and the possible fragmentation of the state; the first point is most relevant for the 0⁺ state, while the second aspect may explain the 2⁺ and 4⁺ widths. More work should be carried out to determine the values both experimentally and theoretically to determine if it is a true LCCS.

TABLE 3

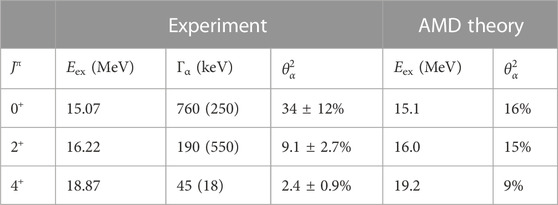
TABLE 3. Selected experimental data on ¹⁴C [43] and an AMD calculation predicting an LCCS [40]. R₀ was set to 1.34 fm for the experimental ${\mathrm{\Gamma }}_{W_{\alpha }}$.

4 Astrophysics of the compound nucleus ¹⁵O

The νp-process occurs in the neutrino-driven wind of core-collapse supernovae [24, 25, 45], where owing to the neutrino interactions, the material is actually proton rich similar to the rp-process (Section 6). Light p-nuclei such as ^92,94Mo and ^96,98Ru, which cannot be explained by other astrophysical sites, might originate from this process. Because of the environment, a sequence like ⁷Be (α, γ)¹¹C (α, p) can compete with the triple-alpha process to bridge the gap between the pp-chains and the CNO region. In this case, it begins the αp-process, which can increase the energy generation by two or three orders of magnitude in less than one second. However, unlike the rp-process, some longer-lived species such as ⁵⁶Ni and ⁶⁴Ge can be bypassed by (n, p) reactions as a small amount of protons are turned into neutrons by neutrino interactions. The amount of the material to be processed depends on bridging the A = 5, 8 mass gaps, requiring knowledge of the ¹¹C (α, p) reaction. Most recently, the ¹¹C (α, p) reaction was found to be one of the two most important processes in the ν-process in core-collapse supernovae Yao et al. [46], as described in Section 2.

Prior to the work on a direct measurement, the compilations relied on the time-reversed reaction ¹⁴N (p, α)¹¹C via the activation method [30, 47]. The method is quite successful and determines the ¹¹C (α, p₀) rate at all angles, but it does not give any information on excited-state transitions. With a fairly simple setup (Figure 6), Hayakawa et al. [48] measured the (α, p₀), (α, p₁), and (α, p₂) reactions on ¹¹C without gamma-detectors (such as used to separate states in Section 2). The experiment used beam tracking monitors to get a system time-of-flight (TOF) for each incoming beam that coincided with the proton detected using a silicon strip detector. Using the TTIK method, the depth of the beam’s interaction in the target gas determines E_cm, which can be measured by the system TOF. The events are shown in Figure 7 for both high and low energies, where the difference in beam energy is from the energy loss in the second beamline monitor used (multi-channel plate or parallel plate avalanche counter). Protons show loci and the correct gradient along the calculated lines for p₀₋₂, except for broadening toward lower energy, owing to the resolution of the silicon detector.

FIGURE 6

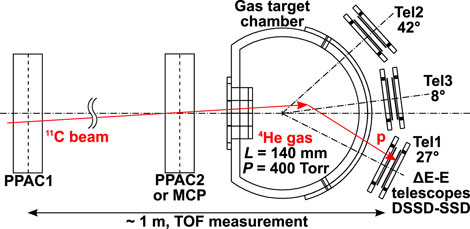
FIGURE 6. Experimental setup for ¹¹C (α, p) using an extended, thick gas cell to allow a measurable time-of-flight (TOF) between the ¹¹C-beam ions and outgoing protons [48], as shown in Figure 7 for Tel1. Two beam monitors and segmented silicon detectors enable a calculation of the precise depth of each interaction. ^© 2016 American Physical Society. Reprinted with permission.

FIGURE 7

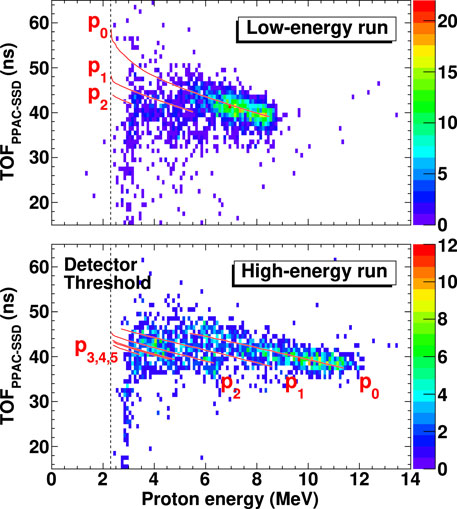
FIGURE 7. Detected energy of protons vs. the relative time-of-flight (TOF) for ¹¹C (α, p) measurement [48] for Tel1 (Figure 6). Simulations for different transitions are shown in red and reproduce the centroids of the loci. ^© 2016 American Physical Society. Reprinted with permission.

The results show that the (α, p₁₋₂) cross sections were about an order of magnitude lower (maximum 20%) than the (α, p₀) rate. The summed reaction rate was higher than compilations as much as 40% [30, 47], specifically due to resonances at 0.9 and 1.35 MeV which were not considered. Conversely, the Hauser–Feshbach statistical rate over-estimates the total experimental rate at low energies but begins to match at higher temperatures [49]. As the Hauser–Feshbach rate suggests only a small difference between (α, p₀₋₂) and the total rate (α_all, p_all), the experiment has likely measured the main transitions.

No Γ_α partial widths were previously known. However, the statistics, resolution, and overlapping widths suggested that a new R-Matrix fit to the data was unlikely to bring new information. Some α-elastic scattering was observed at rather high energies but not reported since it was well over the three GK region of known astrophysical importance. Approximately 50 years ago, the α-cluster structure of ¹⁵O was studied up to 8 MeV over the α-threshold via the ¹²C (³He, α)¹¹C and ¹⁴N (p, α)¹¹C reactions (Weller [50], Weller [51]; Huttlin and Rollefson [52], and references therein). Weller assumed an α-particle of ℓ = 1 orbital angular momentum couples to one of the states in the ¹¹C core. The lowest-lying cluster states in ¹⁵O would have an excitation associated with the α-decay threshold, while higher-lying states are based on excitations of the ¹¹C core and different couplings of the α-particle with the core’s intrinsic angular momenta. To test this theory, Huttlin and Rollefson made higher-energy measurements of ¹⁴N (p, α)¹¹C and found some similarities with ¹²C (³He, α); the study was ultimately inconclusive as definitive spin-parity assignments were unavailable for many states, which began to overlap. Unfortunately, further investigation seems to have waned in both theoretical and experimental work on the α-cluster structure of ¹⁵O in the intervening years. Considering the continued astrophysical attention to the ¹¹C (α, p) reaction since the mid-2000s, additional studies of the α-cluster structure of ¹⁵O—including reanalysis of old data with modern methods—may be warranted.

5 Subthreshold alpha states in ¹⁹Ne

Typically, when a given channel has a significantly smaller width than its competing astrophysical channel, the smaller width dominates the analytic reaction rate, as shown in Eq. 2. However, when a nearby resonance has the same J^π, these resonances can interfere depending on the widths and sometimes drastically change the reaction probability. In general, it requires a direct measurement as the interference sign cannot otherwise be deduced, but measurements of the widths, spin-parity, and energy can reduce the uncertainty. Such resonances are often outside the Gamow window and can also be the subthreshold. A key example of this case is the α-cluster structure of ¹⁹Ne which affects the ¹⁸F (p, α) reaction, where the proton threshold is above the α-threshold, but the ℓ = 0 resonances interfere with each other (J^π = 1/2⁺, 3/2⁺) for temperatures below 0.3 GK [53, 54].

Classical novae occur in explosive binary star systems, typically with recurrence times greater than a thousand years. One partner is a white dwarf which accretes matter from a low-mass, less-evolved companion until the accreted material builds up enough pressure to induce thermonuclear runaway in the compact object’s envelope. In addition to supernovae and neutron star mergers, novae are the most powerful thermonuclear explosions in the universe. The ¹⁸F (p, α) reaction is one of the few remaining nuclear structure cases where the uncertainty is large enough to influence the outcome of classical novae simulations; the other two cases are ²⁵Al (p, γ) and ³⁰P (p, γ). The 2-h half-life of ¹⁸F is comparable to the timescale for the nova ejecta to become transparent to γ radiation, making it an ideal radiotracer of the explosion. Its decay to ¹⁸O emits a neutrino and positron, the latter of which annihilates with an electron to form a pair of γ-rays, and is thought to be the main source of 511-keV γ-rays from a nova explosion. However, thus far, no such signal from nearby novae has been detected by a satellite telescope.

From a nuclear physics perspective, it is difficult to calculate the maximum distance to a nova to determine the expected 511-keV flux because the ¹⁸F (p, α) rate remains quite uncertain despite nearly three decades of research since ¹⁸F was produced as a radioactive beam. Interference between ℓ = 0 states (J^π = 1/2⁺, 3/2⁺) near the proton threshold with higher-lying states is a major source of this uncertainty. There is a well-known 3/2⁺ resonance at E_r = 664.7 keV (E_ex = 7.0747 MeV) with Γ_p = 15.2 keV and Γ_α = 23.8 keV [55]. A broad 1/2⁺ state was predicted [56] and also observed by several works near E_r ≈ 1.5 MeV but not resolved [53, 57, 58]. A state with ℓ = 0 was resolved at E_r = 1.38 (3) with a smaller total width Γ = 130 (10) keV, as shown in Figure 8 [59]. The partial widths of the 1/2⁺ state remain uncertain, but it was shown that as long as the width is broad, the partial widths of Γ_p and Γ_α do not affect the interference pattern [60]. The uncertainty of 30 keV of the state also does influence the magnitude or location of the interference [60]. Enough information on the higher-lying states in ¹⁹Ne to constrain the experiment is extant, and so the focus of the community is looking at ℓ = 0 states nearby the proton threshold in addition to pushing the direct measurement to lower energies. According to mirror symmetry, there are two 3/2⁺ states and one 1/2⁺ state near the proton separation energy of ¹⁹Ne in ¹⁹F.

FIGURE 8

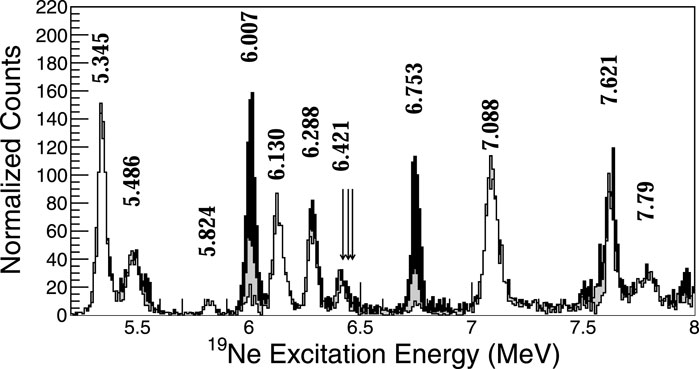
FIGURE 8. Focal plane data from Grand RAIDEN for the ¹⁹F (³He, t)¹⁹Ne measurement at 420 MeV [59]. Peaks are labeled and shown overlaid from the lowest to the highest angle: Θ = 0.0° − 0.5° (white), Θ = 0.8° − 1.2° (gray), and Θ = 1.6° − 2.0° (black). Peaks at different angles are normalized to the 1/2⁺, 5.345-MeV state. Δℓ = 0 (J^π = 1/2⁺ and 3/2⁺) states are forward focused and appear white, Δℓ = 1 states appear at larger angles and are black, and a mixture indicates another angular momentum transfer or overlapping states.

Several experiments were published in the last several years [59, 61, 62], which were analyzed by Kahl et al. [60]. Since then, new experiments [63, 64] and further analysis of the existing data were also presented [65, 66]. The subthreshold state at 6.132 (5) MeV was unambiguously identified as an ℓ = 0 transition by a model-independent method, as shown in Figure 8 [59], and its spin-parity in combination with that of Kahl et al. was determined as 3/2⁺ [64]. Another subthreshold state is approximately 6.29 MeV and was measured to be 1/2⁺ [67], which is now confirmed as a doublet [59, 61, 64, 68, 69]. It is noted that for low-spin states in this region, the calculated mirror energy displacement (MED) is 70 ± 50 keV [64], and pairing the 6.13 MeV state with a known 3/2⁺ state in ¹⁹F requires an MED of over 350 keV; this may suggest an unknown 3/2⁺ state in ¹⁹F. The final 3/2⁺ state(s) in this region should be above the proton separation energy, and two such states with tentative assignments were provided by Hall et al. [61] at 6.423 (3) and 6.441 (3) MeV.

The clusters in ¹⁹F and ¹⁹Ne have been described in terms of oscillator shells including s, p, and sd harmonics [56, 66]. The ℓ = 1 α cluster states (J^π = 1/2⁺, 3/2⁺) are interesting in a comparison with ²⁰Ne, where n = 3 nodes are Pauli-blocked in ¹⁶O+α but not in the A = 19 mirror case [66]. A broad 1/2⁺ state was paired with the 5.94-MeV state in ¹⁹F by the generator coordinate method (GCM) [56], and experiments looking for a broad state near 6 MeV in ¹⁹Ne have been reported [63]. Twenty years ago, Descouvemont and Baye [70] used the GCM and paired the same state with a resonance at 5.34 MeV in ¹⁹F rather than the 5.94-MeV state as they found the energies were up to 1 MeV smaller in experiment vs. theory. If one takes the experiments from Di Leva et al. [71] on ¹⁹F and Torresi et al. [72] for ¹⁹Ne, it can be seen there may be no missing state from GCM studies, as shown in Table 4. These $1/2_2^{+}$ and $3/2_4^{+}$ theoretical states are strongly coupled to the n = 4 node α channel, which were also assigned to the experimental energies shown here [66]. Assuming the aforementioned analysis is correct, the “missing,” broad, 1/2⁺ state in ¹⁹Ne has no significant interference effect on ¹⁸F (p, α), being shielded by another resonance, having significantly smaller Γ_α, and being far from the proton threshold.

TABLE 4

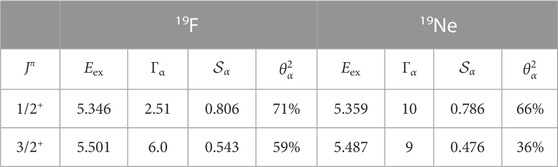
TABLE 4. Second GCM states from Dufour and Descouvemont [56] with the spectroscopic factors ${\mathcal{S}}_{\alpha }$, experimental excitation energies and Γ_α from ¹⁹F [71] and ¹⁹Ne [72], and the Wigner limit of Eq. 1 with R₀ = 1.4 fm. It should be noted that for the ¹⁹F 1/2⁺ state, we have assigned it to 5.34 MeV [70] rather than 5.94 MeV [56]. The cluster pairing between the theory and experiment proposed here is supported by Volya et al. [66].

The ¹⁸F (p, α) reaction requires not only knowledge of ¹⁹Ne but also further investigation of its mirror ¹⁹F.

6 Astrophysics of the compound nucleus ³⁴Ar

Type I X-ray bursts (XRBs) are similar to classical novae, except the compact object is a neutron star rather than a white dwarf. As such, XRBs are a class of astronomical phenomena where in a binary pair, a low mass star accretes matter onto a neutron star and regular explosions take place. Indeed, there are over 100 known XRBs within our galaxy. Characteristic bursting behavior shows a very sharp rise time (one to 10 s) and then a thermal decline. The energy output is around 10³⁹–10⁴⁰ ergs for 10–100 s, and the bursts repeat much more frequently than in classical novae, in the order of hours to days, owing to the compactness of the neutron star. The amount of the accreted material per time, $\dot{M}$, is inversely proportional to the luminosity and time between bursts because the HCNO cycle can operate longer between bursts and increase the amount of helium. The sharp rise time and maximum luminosity are modeled as coming from a series of (α, p) (p, γ) reactions [73], for example, starting from ¹⁴O and going to around ³⁸Ca. Schematically, this is pure helium burning without waiting for β-decays as the hydrogen content is not changed.

³⁴Ar is, like ¹⁴O, an $\frac{N-Z}{2}=-1$ nucleus and important for X-ray bursts in the αp-process as the compound reaction for ³⁰S+α. The species is an α nucleus (²⁸Si) with two additional protons. The ³⁰S (α, p) reaction is identified as a potentially important reaction, contributing more than 5% to the total energy generation (Parikh et al. [74]), influencing the elemental abundances in the burst ashes (Parikh et al. [74]) relevant to compositional inertia (Taam [75] for a description of this phenomenon), moving the material away from the ³⁰S waiting point (Iliadis et al. [76]), and possibly accounting for double peaked XRBs (Fisker et al. [77]). Another study found the ³⁰S (α, p) reaction sensitivity in XRBs among the top four in a single-zone model (Cyburt et al. [78]), as well as having a prominent (but unquantified) impact on the burst light curve in a multizone model.

The only experimental paper to measure Γ_α in ³⁴Ar is by Kahl et al. [79] using an active target. The center-of-mass energies of that study are near 3 GK, being rather higher than the peak XRB temperature of 1.3–2.0 GK. There have been several theoretical works to determine ³⁰S (α, p), but here, we focus mainly on the experimentally determined values for Γ_α. Three states with the proposed α-cluster structure were observed between approximately 4.3 and 5.5 MeV, which had ${\theta }_{\alpha }^2$ ranging from 8% to 100%, as shown in Table 5. The dip-like structures are shown in Figure 9 along with χ². It may be unusual if all the strong resonances have J^π = 2⁺, and if the first resonance observed is 4⁺, the order is the opposite for a rotational band. However, a measurement of ³⁶Ar (⁶Li, d)⁴⁰Ca showed several resonances of the same spin-parity emerged at similar energies with large spectroscopic factors (Yamaya et al. [80]), including two multiplets with 2⁺ each, and ⁴⁰Ca is nearby in mass to ³⁴Ar.

TABLE 5

TABLE 5. Best fit level parameters of ³⁴Ar determined by Kahl et al. [79]. The proton width was controlled by the reduced dimensionless partial widths $\xi \equiv {\theta }_{\mathrm{p}}^2/{\theta }_{\alpha }^2$ as α elastic scattering is much less sensitive to Γ_p (as shown by the errors); it turns out ⟨ξ⟩ = 3%, the same as found in a measurement of ²¹Na (α, α) [87]. The 12.08-MeV level is shown in italics as there is a large systematic uncertainty associated with it. R₀ was set to 1.45 fm for ${\mathrm{\Gamma }}_{W_{\alpha }}$.

FIGURE 9

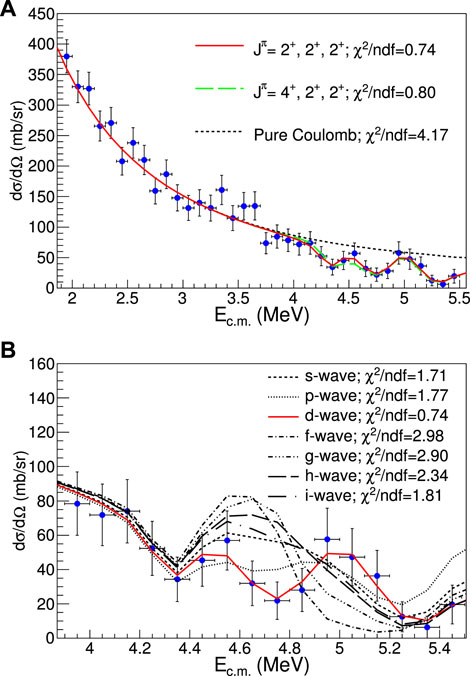
FIGURE 9. ³⁰S+α elastic scattering excitation function including fits from Table 5 [79]. (A) Energy of the entire spectrum; bumps near 3.5 MeV are background-induced. Two R-Matrix fits are compared against pure Coulomb scattering. (B) All physically allowed ℓ_α values for the E_r = 4.78 MeV resonance, showing the unambiguous assignment of ℓ = 2. ^© 2018 American Physical Society. Reprinted with permission.

The ³³Cl (p, α) time-reversal reaction was measured previously to constrain the ³⁰S (α, p) reaction around 3 GK [81]. They found a comparable cross section from the NON-SMOKER code, whereas Kahl et al. [79] found a factor of 10 times increase in the reaction rate compared to the statistical model [49]. The difference could be attributed to Deibel et al [81] measuring the ³⁰S (α₀, p₀) rate, similar to the case of ¹¹C (α, p). These rates are, as mentioned previously, outside the astrophysical region of interest for XRBs. However, Long et al. [82] performed an ³⁶Ar (p, t) spectroscopy experiment over the XRB Gamow window with 30-keV resolution. No ³⁴Ar states were observed with a width larger than the resolution. Therefore, they estimated Γ_α for the levels they observed from a shell-model calculation and found a cross section in the astrophysical region of interest significantly lower than that of the NON-SMOKER statistical model. Unfortunately, as the experiment did not overlap with the other two studies, a comparison between their results at different energies is not possible. More experiments to measure Γ_α in ³⁴Ar and also ³⁰S (α, p) at astrophysical energies are certainly warranted. According to the data in Table 5, Γ_α either dominates or contributes strongly to the ³⁰S (α, p) resonant reaction rate (at least at higher temperatures). A confirmation of the total widths of these states would be helpful to rule out contributions from Γ_p.

7 Conclusion

We presented studies on several nuclei both from a nuclear astrophysics and/or structural perspective. Alpha-clusters are found in a variety of lighter-mass species on both sides of the valley of stability. Although most of the works call for future studies, we emphasize that it is not necessarily finding alpha-clusters in the atomic nuclei but why. It is hard to imagine that alpha-clusters do not play an essential role in the nuclear structure, particularly in light nuclei. Yet, simply identifying them without an overarching framework would likely lead to a preponderance of data, looking for a good model or scenario to justify. We showed that the application of alpha-clusters in the selected nuclei spread over a large, somewhat mutually exclusive, domain.

For high-temperature astrophysical reactions like (α, γ), α, clusters may be involved, but typically, Γ_γ has the smallest width and thus, dominates the rate. On the other hand, for (α, p) reactions, despite clusterization, which leads to large Γ_α values, these reduced widths may be quite important even if Γ_p is just a few percentage of the Wigner limit. We infer a similar situation is true with (α, n) reactions but did not review them. Sometimes, from the interference between states of the same J^π, often from the α-width, it can have a huge impact on the lower energy rate like ¹⁸F (p, α), and the interference sign cannot be predicted by theory. We found that positive parity, α-cluster rotational bands show an excellent linearity, whereas negative parity bands require deeper understanding for the non-linear structure. Finally, we reviewed the strongest experimental evidence for an experimental linear-chain cluster state in ¹⁴C.

Author contributions

DK came up with the conception and design of the study at the suggestion of HY. DK wrote the manuscript draft. DK, HY, and SH commented on the draft and are responsible for revisions to the submitted version. All authors contributed to the article and approved the submitted version.

Funding

This work was carried out under the contract PN 23.21.01.06 sponsored by the Romanian Ministry of Research, Innovation and Digitalization and JSPS KAKENHI (nos 19K03883 and 23H01181), and the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ikeda K, Takigawa N, Horiuchi H. The systematic structure-change into the molecule-like structures in the self-conjugate $4n$ nuclei. Prog Theor Phys Supp (1968) 68:464–75. doi:10.1143/ptps.e68.464

CrossRef Full Text | Google Scholar

2. Chiosi C. Stellar nucleosynthesis and chemical evolution of galaxies. EAS Publications Ser (2007) 27:25–39. doi:10.1051/eas:200714225C

CrossRef Full Text | Google Scholar

3. Hoyle F. On nuclear reactions occuring in very hot stars. I. The synthesis of elements from carbon to nickel. Astrophys J Supp (1954) 1:121–46. doi:10.1086/190005

CrossRef Full Text | Google Scholar

4. Blatt JM, Weisskopf VF. Theoretical nuclear physics. New York: Wiley (1962).

Google Scholar

5. Rolfs C, Rodney WS. Cauldrons in the cosmos. Chicago: The University of Chicago Press (1988).

Google Scholar

6. Baur G. Breakup reactions as an indirect method to investigate low-energy charged-particle reactions relevant for nuclear astrophysics. Phys Lett B (1986) 178:135–8. doi:10.1016/0370-2693(86)91483-8

CrossRef Full Text | Google Scholar

7. Tribble RE, Bertulani CA, La Cognata M, Mukhamedzhanov AM, Spitaleri C. Indirect techniques in nuclear astrophysics: A review. Rep Prog Phys (2014) 77:106901. doi:10.1088/0034-4885/77/10/106901

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Spitaleri C, La Cognata M, Lamia L, Mukhamedzhanov AM, Pizzone RG. Nuclear astrophysics and the Trojan horse method. Eur Phys J A (2016) 52:77. doi:10.1140/epja/i2016-16077-2

CrossRef Full Text | Google Scholar

9. Mukhamedzhanov AM, Tribble RE. Connection between asymptotic normalization coefficients, subthreshold bound states, and resonances. Phys Rev C (1999) 59:3418–24. doi:10.1103/PhysRevC.59.3418

CrossRef Full Text | Google Scholar

10. Utsunomiya H, Katayama S, Gheorghe I, Imai S, Yamaguchi H, Kahl D, et al. Photodisintegration of ⁹Be through the 1/2⁺ state and cluster dipole resonance. Phys Rev C (2015) 92:064323. doi:10.1103/PhysRevC.92.064323

CrossRef Full Text | Google Scholar

11. Smith R, Gai M, Stern SR, Schweitzer DK, Ahmed MW. Precision measurements on oxygen formation in stellar helium burning with gamma-ray beams and a Time Projection Chamber. Nat Comm (2021) 12:5920. doi:10.1038/s41467-021-26179-x

CrossRef Full Text | Google Scholar

12. Baur G, Bertulani CA, Rebel H. Coulomb dissociation as a source of information on radiative capture processes of astrophysical interest. Nucl Phys A (1986) 458:188–204. doi:10.1016/0375-9474(86)90290-3

CrossRef Full Text | Google Scholar

13. Artemov KP, Belyanin OP, Vetoshkin AL, Wolskj R, Golovkov MS, Gol’dberg VZ, et al. Effective method of study of alpha-cluster states. Sov J Nucl Phys (1990) 52:408–11.

Google Scholar

14. Lennard WN, Geissel H, Alexander TK, Hill R, Jackson DP, Lone MA, et al. Depth profiles of 35 keV ³He ions in metals. Nucl Instr Meth Phys Res B (1985) 10:592–5. doi:10.1016/0168-583X(85)90315-5

CrossRef Full Text | Google Scholar

15. Hou SQ, He JJ, Parikh A, Kahl D, Bertulani CA, Kajino T, et al. Non-extensive statistics to the cosmological lithium problem. Astrophys J (2017) 834:165. doi:10.3847/1538-4357/834/2/165

CrossRef Full Text | Google Scholar

16. Hayakawa S, La Cognata M, Lamia L, Yamaguchi H, Kahl D, Abe K, et al. Constraining the primordial lithium abundance: New cross section measurement of the ⁷Be + n reactions updates the total ⁷Be destruction rate. Astrophys J (2021) 915:L13. doi:10.3847/2041-8213/ac061f

CrossRef Full Text | Google Scholar

17. Tohsaki A, Horiuchi H, Schuck P, Röpke G. Alpha cluster condensation in ¹²C and ¹⁶O. Phys Rev Lett (2001) 87:192501. doi:10.1103/PhysRevLett.87.192501

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kawabata T, Akimune H, Fujimura H, Fujita H, Fujita Y, Fujiwara M, et al. Isovector and isoscalar spin-flip M1 strengths in ¹¹B. Phys Rev C (2004) 70:034318. doi:10.1103/PhysRevC.70.034318

CrossRef Full Text | Google Scholar

19. Kawabata T, Akimune H, Fujita H, Fujita Y, Fujiwara M, Hara K, et al. 2 α + t cluster structure in ¹¹B. Phys Lett B (2007) 646:6–11. doi:10.1016/j.physletb.2006.11.079

CrossRef Full Text | Google Scholar

20. Yamaguchi H, Hashimoto T, Hayakawa S, Binh DN, Kahl D, Kubono S, et al. α resonance structure in ¹¹B studied via resonant scattering of ⁷Li+α. Phys Rev C (2011) 83:034306. doi:10.1103/PhysRevC.83.034306

CrossRef Full Text | Google Scholar

21. Yamaguchi H, Kahl D, Wakabayashi Y, Kubono S, Hashimoto T, Hayakawa S, et al. α-resonance structure in ¹¹C studied via resonant scattering of ⁷Be+α and with the ⁷Be(α,p) reaction. Phys Rev C (2013) 87:034303. doi:10.1103/PhysRevC.87.034303

CrossRef Full Text | Google Scholar

22. Yoshida T, Kajino T, Yokomakura H, Kimura K, Takamura A, Hartmann DH. Supernova neutrino nucleosynthesis of light elements with neutrino oscillations. Phys Rev Lett (2006) 96:091101. doi:10.1103/PhysRevLett.96.091101

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wiescher M, Gorres J, Graff S, Buchmann L, Thielemann F-K. The hot proton-proton chains in low-metallicity objects. Astrophys J (1989) 343:352–64. doi:10.1086/167709

CrossRef Full Text | Google Scholar

24. Fröhlich C, Martínez-Pinedo G, Liebendörfer M, Thielemann F-K, Bravo E, Hix WR, et al. Neutrino-Induced nucleosynthesis of A>64 nuclei: The νp process. Phys .Rev Lett (2006) 96:142502. doi:10.1103/PhysRevLett.96.142502

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wanajo S. The rp-process in neutrino-driven winds. Astrophys J (2006) 647:1323–40. doi:10.1086/505483

CrossRef Full Text | Google Scholar

26. Psaltis A, Chen AA, Longland R, Connolly DS, Brune CR, Davids B, et al. Direct measurement of resonances in ⁷Be(α,γ)¹¹C relevant to ν p -process nucleosynthesis. Phys Rev Lett (2022) 129:162701. doi:10.1103/PhysRevLett.129.162701

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Psaltis A, Chen AA, Longland R, Connolly DS, Brune CR, Davids B, et al. First inverse kinematics measurement of resonances in ⁷Be(α,γ)¹¹C relevant to neutrino-driven wind nucleosynthesis using DRAGON. Phys Rev C (2022) 106:045805. doi:10.1103/PhysRevC.106.045805

CrossRef Full Text | Google Scholar

28. Kelley JH, Kwan E, Purcell JE, Sheu CG, Weller HR. Energy levels of light nuclei. Nuc Phys A (2012) 880:88–195. doi:10.1016/j.nuclphysa.2012.01.010

CrossRef Full Text | Google Scholar

29. Konstantinova MP, Myakinin EV, Petrov AM, Romanov AN. Sov J Exp Theor Phys (1963) 16:278.

30. Angulo C, Arnould M, Rayet M, Descouvemont P, Baye D, Leclercq-Willain C, et al. A compilation of charged-particle induced thermonuclear reaction rates. Nucl Phys A (1999) 656:3–183. doi:10.1016/S0375-9474(99)00030-5

CrossRef Full Text | Google Scholar

31. Freer M, Achouri NL, Angulo C, Ashwood NI, Bardayan DW, Brown S, et al. Resonances in ¹¹C observed in the ⁴He(⁷Be,α)⁷Be and ⁴He(⁷Be,p)¹⁰B reactions. Phys Rev C (2012) 85:014304. doi:10.1103/PhysRevC.85.014304

CrossRef Full Text | Google Scholar

32. Xu Y, Takahashi K, Goriely S, Arnould M, Ohta M, Utsunomiya H. NACRE II: An update of the NACRE compilation of charged-particle-induced thermonuclear reaction rates for nuclei with mass number A<16. Nuc Phys A (2013) 918:61–169. doi:10.1016/j.nuclphysa.2013.09.007

CrossRef Full Text | Google Scholar

33. Soić N, Freer M, Donadille L, Clarke NM, Leask PJ, Catford WN, et al. α-decay of excited states in ¹¹C and ¹¹B. Nucl Phys A (2004) 742:271–90. doi:10.1016/j.nuclphysa.2004.06.027

CrossRef Full Text | Google Scholar

34. Ragnarsson I, Åberg S, Hakansson HB, Sheline RK. Application of the cranked Nilsson model in some light nuclei: The super backbend in ¹¹B and ¹¹C? Nucl Phys A (1981) 361:1–22. doi:10.1016/0375-9474(81)90468-1

CrossRef Full Text | Google Scholar

35. Suhara T, Kanada-En’yo Y. Cluster structures in ¹¹B. Phys Rev C (2012) 85:054320. doi:10.1103/PhysRevC.85.054320

CrossRef Full Text | Google Scholar

36. Morinaga H. Interpretation of some of the excited states of 4n self-conjugate nuclei. Phys Rev (1956) 101:254–8. doi:10.1103/PhysRev.101.254

CrossRef Full Text | Google Scholar

37. Della Rocca V, Iachello F. Cluster shell model: I. Structure of ⁹Be. ⁹B Nucl Phys A (2018) 973:1–32. doi:10.1016/j.nuclphysa.2018.02.003

CrossRef Full Text | Google Scholar

38. Horiuchi H. Many-cluster problem by the orthogonality condition model –general discussion and ¹²C problem. Prog Theor Phys (1975) 53:447–60. doi:10.1143/PTP.53.447

CrossRef Full Text | Google Scholar

39. Ohkubo S, Hirabayashi Y. α-particle condensate states in ¹⁶O. Phys Lett B (2010) 684:127–31. doi:10.1016/j.physletb.2009.12.066

CrossRef Full Text | Google Scholar

40. Suhara T, Kanada-En’Yo Y. Cluster structures of excited states in ¹⁴C. Phys Rev C (2010) 82:044301. doi:10.1103/PhysRevC.82.044301

CrossRef Full Text | Google Scholar

41. Freer M, Malcolm JD, Achouri NL, Ashwood NI, Bardayan DW, Brown SM, et al. Resonances in ¹⁴C observed in the ⁴He(¹⁰Be,α)¹⁰Be reaction. Phys Rev C (2014) 90:054324. doi:10.1103/PhysRevC.90.054324

CrossRef Full Text | Google Scholar

42. Fritsch A, Beceiro-Novo S, Suzuki D, Mittig W, Kolata JJ, Ahn T, et al. One-dimensionality in atomic nuclei: A candidate for linear-chain α clustering in ¹⁴C. Phys Rev C (2016) 93:014321. doi:10.1103/PhysRevC.93.014321

CrossRef Full Text | Google Scholar

43. Yamaguchi H, Kahl D, Hayakawa S, Sakaguchi Y, Abe K, Nakao T, et al. Experimental investigation of a linear-chain structure in the nucleus ¹⁴C. Phys Lett B (2017) 766:11–6. doi:10.1016/j.physletb.2016.12.050

CrossRef Full Text | Google Scholar

44. Kanada-En’yo Y, Suhara T, Taniguchi Y. Approximation of reduced width amplitude and application to cluster decay width. Prog Theor Exp Phys (2014) 2014:073D02. doi:10.1093/ptep/ptu095

CrossRef Full Text | Google Scholar

45. Pruet J, Hoffman RD, Woosley SE, Janka H-T, Buras R. Nucleosynthesis in early supernova winds. II. The role of neutrinos. Astrophys J (2006) 644:1028–39. doi:10.1086/503891

CrossRef Full Text | Google Scholar

46. Yao X, Kusakabe M, Kajino T, Cherubini S, Hayakawa S, Yamaguchi H. Supernova nucleosynthesis, radioactive nuclear reactions and neutrino-mass hierarchy. Eur Phys J W Conf (2022) 260:01007. doi:10.1051/epjconf/202226001007

CrossRef Full Text | Google Scholar

47. Caughlan GR, Fowler WA. Thermonuclear reaction rates V. Atom Data Nucl Data Tab (1988) 40:283–334. doi:10.1016/0092-640X(88)90009-5

CrossRef Full Text | Google Scholar

48. Hayakawa S, Kubono S, Kahl D, Yamaguchi H, Binh DN, Hashimoto T, et al. First direct measurement of the ¹¹C(α, p)¹⁴N stellar reaction by an extended thick-target method. Phys Rev C (2016) 93:065802. doi:10.1103/PhysRevC.93.065802

CrossRef Full Text | Google Scholar

49. Rauscher T, Thielemann F-K. Astrophysical reaction rates from statistical model calculations. Atom Data Nucl Data Tab (2000) 75:1–351. doi:10.1006/adnd.2000.0834

CrossRef Full Text | Google Scholar

50. Weller HR. Observation of alpha-particle core-excited threshold states in ¹⁵O. Phys Lett B (1969) 30:409–11. doi:10.1016/0370-2693(69)90474-2

CrossRef Full Text | Google Scholar

51. Weller HR. Observation of α-particle core-excited threshold states in light nuclei. Phys Rev Lett (1972) 28:247–9. doi:10.1103/PhysRevLett.28.247

CrossRef Full Text | Google Scholar

52. Huttlin GA, Rollefson AA. Alpha-cluster levels in ¹⁵O as seen in the reaction ¹⁴N(p,α₀)¹¹C. Phys Rev C (1974) 9:576–80. doi:10.1103/physrevc.9.576

CrossRef Full Text | Google Scholar

53. Dalouzy JC, Achouri L, Aliotta M, Angulo C, Benhabiles H, Borcea C, et al. Discovery of a new broad resonance in ¹⁹Ne: Implications for the destruction of the cosmic γ-ray emitter ¹⁸F. Phys Rev Lett (2009) 102:162503. doi:10.1103/PhysRevLett.102.162503

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Chae KY, Bardayan DW, Blackmon JC, Gregory D, Guidry MW, Johnson MS, et al. First experimental constraints on the interference of 3/2⁺ resonances in the ¹⁸F(p, α)¹⁵O reaction. Phys Rev C (2006) 74:012801. doi:10.1103/PhysRevC.74.012801

CrossRef Full Text | Google Scholar

55. Bardayan DW, Blackmon JC, Bradfield-Smith W, Brune CR, Champagne AE, Davinson T, et al. Destruction of ¹⁸F via ¹⁸F(p,α)¹⁵O burning through the E_c.m.=665 keV resonance. Phys Rev C (2001) 63:065802. doi:10.1103/PhysRevC.63.065802

CrossRef Full Text | Google Scholar

56. Dufour M, Descouvemont P. The ¹⁸F(p, α) ¹⁵O low-energy S-factor: A microscopic approach. Nucl Phys A (2007) 785:381–94. doi:10.1016/j.nuclphysa.2006.12.101

CrossRef Full Text | Google Scholar

57. Adekola AS, Brune CR, Bardayan DW, Blackmon JC, Chae KY, Cizewski JA, et al. ¹⁹Ne levels studied with the ¹⁸F(d,n)¹⁹Ne*(¹⁸F+p) reaction. Phys Rev C (2012) 85:037601. doi:10.1103/PhysRevC.85.037601

CrossRef Full Text | Google Scholar

58. Mountford DJ, Murphy ASJ, Achouri NL, Angulo C, Brown JR, Davinson T, et al. Resonances in ¹⁹Ne with relevance to the astrophysically important ¹⁸F(p,α)¹⁵O reaction. Phys Rev C (2012) 85:022801. doi:10.1103/PhysRevC.85.022801

CrossRef Full Text | Google Scholar

59. Kahl D, Woods PJ, Fujita Y, Fujita H, Abe K, Adachi T, et al. s-wave resonances for the ¹⁸F(p, α)¹⁵O reaction in novae. Eur Phys J A (2019) 55:4. doi:10.1140/epja/i2019-12682-9

CrossRef Full Text | Google Scholar

60. Kahl D, José J, Woods PJ. Uncertainties in the ¹⁸F(p, α)¹⁵O reaction rate in classical novae. Astron Astrophys (2021) 653:A64. doi:10.1051/0004-6361/202140339

CrossRef Full Text | Google Scholar

61. Hall MR, Bardayan DW, Baugher T, Lepailleur A, Pain SD, Ratkiewicz A, et al. Key ¹⁹Ne states identified affecting γ-ray emission from ¹⁸F in novae. Phys Rev Lett (2019) 122:052701. doi:10.1103/PhysRevLett.122.052701

PubMed Abstract | CrossRef Full Text | Google Scholar

62. La Cognata M, Fisichella M, Pietro Di A, Figuera P, Goldberg VZ, Cherubini S, et al. Observation of ¹⁵N+α resonant structures in ¹⁹F using the thick target in inverse kinematics scattering method. Phys Rev C (2019) 99:034301. doi:10.1103/PhysRevC.99.034301

CrossRef Full Text | Google Scholar

63. Riley JE, Laird AM, de Séréville N, Parikh A, Fox SP, Hammache F, et al. Sub-threshold states in ¹⁹Ne relevant to ¹⁸F(p,α)¹⁵O. Phys Rev C (2021) 103:015807. doi:10.1103/PhysRevC.103.015807

CrossRef Full Text | Google Scholar

64. Portillo F, Longland R, Cooper AL, Hunt S, Laird AM, Marshall C, et al. Spin-parities of subthreshold resonances in the ¹⁸F(p,α)¹⁵O reaction. Phys Rev C (2023) 107:035809. doi:10.1103/PhysRevC.107.035809

CrossRef Full Text | Google Scholar

65. Goldberg VZ, Nurmukhanbetova AK, Volya A, Nauruzbayev DK, Serikbayeva GE, Rogachev GV. α -cluster structure in ¹⁹F and ¹⁹Ne in resonant scattering. Phys Rev C (2022) 105:014615. doi:10.1103/PhysRevC.105.014615

CrossRef Full Text | Google Scholar

66. Volya A, Goldberg VZ, Nurmukhanbetova AK, Nauruzbayev DK, Rogachev GV. Lowest-energy broad α -cluster resonances in ¹⁹F. Phys Rev C (2022) 105:014614. doi:10.1103/PhysRevC.105.014614

CrossRef Full Text | Google Scholar

67. Bardayan DW, Chipps KA, Ahn S, Blackmon JC, deBoer RJ, Greife U, et al. The first science result with the JENSA gas-jet target: Confirmation and study of a strong subthreshold ¹⁸F(p, α)¹⁵O resonance. Phys Lett B (2015) 751:311–5. doi:10.1016/j.physletb.2015.10.073

CrossRef Full Text | Google Scholar

68. Laird AM, Parikh A, Murphy ASJ, Wimmer K, Chen AA, Deibel CM, et al. Is γ-ray emission from novae affected by interference effects in the ¹⁸F(p,α)¹⁵O reaction? Phys Rev Lett (2013) 110:032502. doi:10.1103/PhysRevLett.110.032502

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Parikh A, Laird AM, de Séréville N, Wimmer K, Faestermann T, Hertenberger R, et al. Spectroscopy of ¹⁹Ne for the thermonuclear ¹⁵O(α, γ)¹⁹Ne and ¹⁸F(p, α)¹⁵O reaction rates. Phys Rev C (2015) 92:055806. doi:10.1103/PhysRevC.92.055806

CrossRef Full Text | Google Scholar

70. Descouvemont P, Baye D. Microscopic study of α+¹⁵N cluster structure in ¹⁹F. Nucl Phys A (1987) 463:629–43. doi:10.1016/0375-9474(87)90635-X

CrossRef Full Text | Google Scholar

71. Di Leva A, Imbriani G, Buompane R, Gialanella L, Best A, Cristallo S, et al. Measurement of 1323 and 1487 keV resonances in ¹⁵N(α,γ)¹⁹F with the recoil separator ERNA. Phys Rev C (2017) 95:045803. doi:10.1103/PhysRevC.95.045803

CrossRef Full Text | Google Scholar

72. Torresi D, Wheldon C, Kokalova T, Bailey S, Boiano A, Boiano C, et al. Evidence for ¹⁵O+α resonance structures in ¹⁹Ne via direct measurement. Phys Rev C (2017) 96:044317. doi:10.1103/PhysRevC.96.044317

CrossRef Full Text | Google Scholar

73. Wallace RK, Woosley SE. Explosive hydrogen burning. Astrophys J Supp (1981) 45:389–420. doi:10.1086/190717

CrossRef Full Text | Google Scholar

74. Parikh A, José J, Moreno F, Iliadis C. The effects of variations in nuclear processes on type I X-ray burst nucleosynthesis. Astrophys J Supp (2008) 178:110–36. doi:10.1086/589879

CrossRef Full Text | Google Scholar

75. Taam RE. X-ray bursts from thermonuclear runaways on accreting neutron stars. Astrophys J (1980) 241:358–66. doi:10.1086/158348

CrossRef Full Text | Google Scholar

76. Iliadis C, Endt PM, Prantzos N, Thompson WJ. Explosive hydrogen burning of ²⁷Si, ³¹S, ³⁵Ar, and ³⁹Ca in novae and X-ray bursts. Astrophys J (1999) 524:434–53. doi:10.1086/307778

CrossRef Full Text | Google Scholar

77. Fisker JL, Thielemann F-K, Wiescher M. The nuclear reaction waiting points: ²²Mg, ²⁶Si, ³⁰S, and ³⁴Ar and bolometrically double-peaked type I X-ray bursts. Astrophys J (2004) 608:L61–4. doi:10.1086/422215

CrossRef Full Text | Google Scholar

78. Cyburt RH, Amthor AM, Heger A, Johnson E, Keek L, Meisel Z, et al. Dependence of X-ray burst models on nuclear reaction rates. Astrophys J (2016) 830:55. doi:10.3847/0004-637x/830/2/55

CrossRef Full Text | Google Scholar

79. Kahl D, Yamaguchi H, Kubono S, Chen AA, Parikh A, Binh DN, et al. First measurement of ³⁰S+α resonant elastic scattering for the ³⁰S(α,p) reaction rate. Phys Rev C (2018) 97:015802. doi:10.1103/PhysRevC.97.015802

CrossRef Full Text | Google Scholar

80. Yamaya T, Saitoh M, Fujiwara M, Itahashi T, Katori K, Suehiro T, et al. Cluster structure in ⁴⁰Ca via the α-transfer reaction. Nucl Phys A (1994) 573:154–72. doi:10.1016/0375-9474(94)90019-1

CrossRef Full Text | Google Scholar

81. Deibel CM, Rehm KE, Figueira JM, Greene JP, Jiang CL, Kay BP, et al. First measurement of the ³³Cl(p,α)³⁰S reaction. Phys Rev C (2011) 84:1–6. doi:10.1103/PhysRevC.84.045802

CrossRef Full Text | Google Scholar

82. Long AM, Adachi T, Beard M, Berg GPA, Couder M, deBoer RJ, et al. α-unbound levels in ³⁴Ar from ³⁶Ar(p,t)³⁴Ar reaction measurements and implications for the astrophysical ³⁰S(α,p)³³Cl reaction rate. Phys Rev C (2018) 97:054613. doi:10.1103/PhysRevC.97.054613

CrossRef Full Text | Google Scholar

83. Kubono S. Nuclear clustering aspects in astrophysics. Zeit Phys A (1994) 349:237–40. doi:10.1007/BF01288966

CrossRef Full Text | Google Scholar

84. Suhara T, Kanada-En’yo Y. Be-α correlations in the linear-chain structure of C isotopes. Phys Rev C (2011) 84:024328. doi:10.1103/PhysRevC.84.024328

CrossRef Full Text | Google Scholar

85. Ajzenberg-Selove F. Energy levels of light nuclei A = 11-12. Nucl Phys A (1990) 506:1–158. doi:10.1016/0375-9474(90)90271-M

CrossRef Full Text | Google Scholar

86. Tilley DR, Kelley JH, Godwin JL, Millener DJ, Purcell JE, Sheu CG, et al. Energy levels of light nuclei. Nucl Phys A (2004) 745:155–362. doi:10.1016/j.nuclphysa.2004.09.059

CrossRef Full Text | Google Scholar

87. Binh DN. Study of the ²¹Na(α, p)²⁴Mg stellar reaction by α-scattering and (α, p) measurements in inverse kinematics. Ph.D. thesis. Tokyo, Japan: The University of Tokyo (2010).

Google Scholar