Matter-antimatter rearrangements using the R-matrix method

Antihydrogen atoms, $\bar{\text{H}}$, are now routinely created and can be stored for long enough to allow comparison with ordinary matter. A major goal of these efforts is to test potential physics beyond the Standard Model. This will require further developments in the experiments including the accumulation of more antihydrogen atoms and their storage over longer times. The latter is limited by the unavoidable presence of normal hydrogen molecules. Interactions of $\bar{\text{H}}$ with H₂ lead to the destruction of the hard-won antimatter. Little is known about these interactions but quantitative information will be crucial in guiding experimental developments. Physically realistic modelling of rearrangement scattering of “heavy” antimatter particles (antiprotons, $\bar{\text{p}}$, and antihydrogen atoms) by normal matter molecules, such as H₂ + ${\displaystyle \bar{\text{H}}}\to$ Pn + Ps + H (where Pn represents protonium and Ps positronium), requires the development of new theoretical and computational methodologies. R-matrix theory offers a strong prospect for tackling such problems having proved itself in atomic, molecular and optical physics. It divides the problem into a computationally demanding but energy-independent inner region and simpler energy-dependent outer regions. We propose to adapt the new RmatReact ultracold chemistry approach for the more complex molecular matter-antimatter problems. Here, developments required for the inner region, the boundary and outer regions are outlined. We also report some preliminary bound-state calculations on the {p,p,$\bar{\text{p}}$} system and a study of the required mixed coordinate systems for the general effective 3-body case and their transformations at the R-matrix boundary surfaces.

1 Introduction

Antihydrogen atoms, ${\displaystyle \bar{\text{H}}}$, can now be created and stored for long enough to allow very precise tests of their properties for comparison with ordinary matter [1–3] for example to test fundamental symmetries, such a charge-parity-time (CPT) and the weak equivalence principle (WEP) and other potential physics beyond the Standard Model, via spectroscopy experiments and gravitational measurements. This will require further developments in the experiments over the next few years including in the accumulation of more antihydrogen atoms and their storage over longer times (days or weeks). The latter is limited by the unavoidable presence of normal hydrogen molecules in the apparatus. Interactions of ${\displaystyle \bar{\text{H}}}$ with H₂ lead to destruction of the hard-won antimatter. Little is known about these interactions, which include elastic and rotationally inelastic collisions, particle rearrangement processes, as well as in-flight proton-antiproton and electron-positron annihilation, and quantitative information will be crucial in guiding the experimental developments. Realistic modelling of rearrangement scattering of “heavy” antimatter particles (antiprotons, ${\displaystyle \bar{\text{p}}}$, and antihydrogen atoms) by normal matter molecules, such as H₂ + ${\displaystyle \bar{\text{H}}}\to$ Pn + Ps + H (where Pn represents protonium and Ps positronium), requires the development of new theoretical and computational methodologies. R-matrix theory [4] offers a strong prospect for tackling matter-antimatter rearrangement scattering having proved itself in many problems in atomic, molecular and optical physics. It divides the problem into a computationally demanding but energy-independent inner region and simpler energy-dependent outer regions. Indeed, ${\displaystyle \bar{\text{p}}}$ capture by He⁺ and H with emission of an electron has been investigated using the R-matrix formalism [5–7]. We propose to adapt the new RmatReact ultracold chemistry approach [8] for the more complex molecular matter-antimatter problems. Techniques used for normal chemical reactions will have to be redesigned to deal with the new interactions between particles associated with the mixed matter-antimatter collisions, in particular the nuclei-antinuclei Coulomb attractions, strong electron-positron correlations and particle-antiparticle annihilations.

In Section 2, developments required for the inner region, the boundary and outer regions of the R-matrix method are outlined. In Section 3 an initial study of the required mixed coordinate systems for the general effective 3-body case and their transformations at the R-matrix boundary surfaces is reported. These systems, which combine coordinates from each arrangement, are needed in the R-matrix inner region with associated links to the separate coordinate systems for each collisional and reactive arrangement outer region on the boundary hypersurface. In Section 4, we report some preliminary bound-state calculations on the {p,p,${\displaystyle \bar{\text{p}}}$} system (protonium plus proton—relevant to the inner region).

2 R-matrix approach

We propose to overcome a major bottleneck in understanding matter-antimatter collisions by developing the capability to calculate in full dimension and fully quantum mechanically, the scattering cross sections for molecular matter-antimatter rearrangements. Theory and simulation of antimatter formation and trapping are crucial in designing and interpreting experiments [9] but the necessary accurate scattering cross sections are lacking. We will make use of recent R-matrix developments [8] in the EPSRC High-End Computing (HEC) Consortium UK-AMOR [10], combined with recent variational approaches to solving matter-antimatter collision problems [5–7, 11].

Our early objectives are to adapt existing codes for the inner region, the boundary and outer regions of the R-matrix method for the adiabatic treatment of molecular matter-antimatter problems We will validate this work with test calculations on Pn + p which we can compare with mass-scaled literature Ps + e⁻ results, then apply the methods and codes to calculate rearrangement cross sections for a system of high priority for experiments: ${{\mathrm{H}}_2}^{+}$+ ${\displaystyle \bar{\text{p}}}\to$ Pn + H [12] (${{\mathrm{H}}_2}^{+}$ may be produced and captured alongside positrons in the production of ${\displaystyle \bar{\text{H}}}$).

Our later objectives are to further adapt the inner region, boundary and outer region codes for non-adiabatic processes, such as Ps formation and apply the methods and codes to calculate rearrangement cross sections for other systems of high priority for experimentalists, in particular H₂ + ${\displaystyle \bar{\text{H}}}\to$ Pn + Ps + H, together with some investigations of ${{\mathrm{H}}_2}^{+}$ + $\bar{\text{H}}\to$ Pn + H + e⁺, as a relevant and related process of intermediate complexity.

Our general approach to tackle the heavy-projectile/molecular-target systems of interest will be to adapt and combine existing R-matrix methodologies from three areas: normal chemical reactions, light-particle (electron/positron/positronium) collisions with atoms and molecules; and antiproton-atom collisions. We will adapt the new UK-AMOR RmatReact code package [8]. Initially, the adiabatic approach will be adopted but this will be adaptable to the later non-adiabatic treatments. This will be essential as collisions involving excited states of ${\displaystyle \bar{\text{H}}}$ are of experimental relevance and rearrangement channels involving separation of an electron, a positron or Ps are open even at zero collision energy for most of the systems considered. Non-adiabatic effects and processes will be incorporated by applying approaches used in light-particle-atom/molecule collisions [4]. We will solve the non-relativistic scattering problem. Ultra-short-range effects, and nuclear annihilation cross-sections, can be determined from the scattering wavefunctions using a delta function pseudo potential approach [13] which uses the zero range approximation of the strong force. This gives good results for H-${\displaystyle \bar{\text{H}}}$, but a more sophisticated approach based on the Coulomb-corrected strong-force scattering length is available [14, 15]–see also the Supplementary Material. This may be required for systems such as H₂ + ${\displaystyle \bar{\text{H}}}$ when the three nuclei approach the same point in space—the Coulomb attractions between the protons and the antiproton make this energetically feasible, unlike the case of normal nuclei.

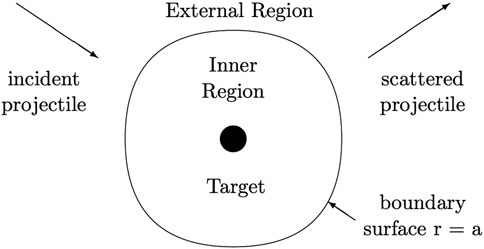
In R-matrix theory the inner region contains the interacting systems at close range and a full ab initio approach accounts for all interactions. As developed for electron atom/molecule scattering with excitation, the inner region boundary is a sphere centred on the nuclear centre of mass with radius r = a such that the “target” atomic or molecular states are contained within the sphere and the colliding electron is the only particle which crosses the boundary—see Figure 1.

FIGURE 1

FIGURE 1. Schematic separation of configuration space in the R-matrix method.

The outer region Schrödinger equation is a set of multichannel coupled differential equations and the R-matrix is the inverse log-derivative matrix of the wavefunction at the boundary radius. At larger distances (the asymptotic region) the propagated solutions are matched to known forms consistent with non-vanishing potential interactions and the scattering parameters are calculated.

For low-energy atom-molecule collisions without rearrangement, the theory is applied in the centre of mass frame, using Jacobi coordinates for the three-body nuclear problem, or internal molecular coordinates and a collision vector between the atom and the molecular centre of mass in the N-body case. The boundary radius is determined by the requirement that the colliding bodies are distinguishable from the boundary outwards, that is, their component electronic and rovibrational states have negligible overlap. The outer region interaction is made up of inverse power potentials in the collision vector, R, for |R| > A. This defines the inner region for non-reactive collisions, with the intramolecular coordinates taken either over all space or to a radial value at which the included molecular wavefunctions effectively vanish. The inner region requires electronic and nuclear states for the all-body system (in practice expanded in bases of target state wavefunctions).

For reactive scattering the boundary definition is extended to a mixed coordinate system which includes R_α for each arrangement α. The inner region part of the solution is a bound-state problem for all the interacting particles with modified finite-range boundary conditions to allow non-zero probability amplitudes associated with the R_α in the initial and final arrangements.

The calculations in the outer regions for the different arrangements may be considered separately, linked together by the full R-matrix defined on the multidimensional boundary surface. This is chosen such that the pre- and post-reaction components are distinct entities outside the corresponding parts of the boundary surface, with no overlap between probability amplitudes for different arrangements [4, 8, 16]. The divisions of configuration space for the ${{\mathrm{H}}_2}^{+}$ + ${\displaystyle \bar{\text{p}}}\to$ Pn + H rearrangement are given in Figure 2.

FIGURE 2

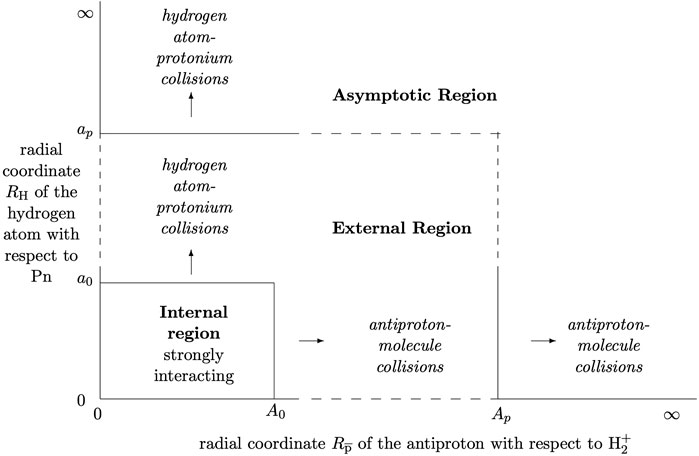
FIGURE 2. Separation of R-matrix configuration space for the ${{\mathrm{H}}_2}^{+}$ + $\bar{\text{p}}\to$ Pn + H rearrangement (A₀ and a₀ are the inner region boundary values for $\bar{\text{p}}$ and H radial coordinates respectively).

Our non-adiabatic treatment will make use of and expand established theories. Burke [4] details an R-matrix formalism for dissociative attachment and vibrational excitation in electron molecule collisions: the treatment of Le Dourneuf et al [17], extended by Gillan et al [18] allows for Born-Oppenheimer electronic calculations on a grid of nuclear configurations to be combined non-adiabatically with motion of the nuclei. Alternatively, R-matrix calculations using the “energy balance adiabatic nuclei” method of Stibbe and Tennyson [19] include impact dissociation for electron collisions with H₂ (see also Scarlett et al [20]). For antimatter interactions, Sakimoto [5–7] has investigated $\bar{\text{p}}$ capture by He⁺ and H with emission of an electron using the R-matrix formalism, with simultaneous grid-based treatment of the electron and the nuclei. We will adapt this approach and also use the Le Dourneuf et al treatment as seems necessary.

2.1 Adiabatic theory

The first task would be to adapt the bound-state code DVR3D [21] to tackle, adiabatically, closely interacting matter-antimatter atoms (with positively and negatively charged nuclei). The strongly attractive potentials will require large well-designed basis sets. The extension to rearrangement collisions will use theory for mixed coordinate systems [16, 22, 23]. DVR3D can use Lobatto shape functions and quadrature for the inner region basis functions of the R_α, as utilized by Manolopoulos et al. [16], which (as do B-splines) have particularly useful properties to treat both bound-state and continuum basis requirements and which have been applied as a discrete variable representation (DVR) to the atom-atom code DUO in RmatReact ([8] and references). Burke [4] includes a rearrangement formalism for positronium formation in positron atom collisions, and an early calculation [24] includes explicit formulation of the “Bloch operators”, added to the inner region Hamiltonian in R-matrix and log-derivative Kohn [16] calculations to ensure Hermiticity with non-vanishing continuum functions at the boundary, for the mixed coordinate systems.

We will generate the multiple-arrangement boundary surface as indicated in ([4, 8, 16]), given in terms of the chosen magnitudes R_α = A_α of the collision vectors R_α for each arrangement. We have studied the mixed coordinate systems and their transformations at the boundary surfaces for our requirements, guided by related work with Jacobi and hyperspherical coordinates [22, 25, 26]–see Section 3 below. For the different arrangements to be treated as uncoupled outside the inner region, while linked by the boundary R-matrix [4], the values of A_α are constrained by the kinematics. For example, for ${{\mathrm{H}}_2}^{+}$ + ${\displaystyle \bar{\text{p}}}$, Pn can be produced in states with principal quantum number up to 68 [12], with associated expected value radius 7.6 Bohr, or an extent of ∼10 Bohr.

The outer region RmatReact codes PFARM ([8, 27, 28] form asymptotic solutions for charged and neutral collision products and when needed, can propagate R-matrices to suitable matching distances (A_p and a_p in Figure 2). Minor adaptations are needed for propagation with two or more arrangement matrix blocks [4]. PFARM can already propagate two uncoupled sets of states linked only by off-diagonal block terms.

Following initial test calculations on Pn + p scattering, elastic, inelastic, rearrangement and (in-flight) annihilation cross-sections for ${{\mathrm{H}}_2}^{+}$ + $\bar{\text{p}}$ collisions would be determined. The reaction of ${{\mathrm{H}}_2}^{+}$ + $\bar{\text{p}}$ to give Pn + H is the most amenable to an adiabatic treatment [29] and has been observed experimentally [12] but so far observations are not explained by theory [30, 31]. Modifications for taking account of the strong interaction at short range will be made as needed and their effects examined. Interactions of H₂ with $\bar{\text{H}}$ are of the greatest interest for predicting the lifetime of stored antimatter, but this system is arguably the most challenging of those considered here. Cross sections for H₂ + ${\displaystyle \bar{\text{H}}}\to$ Pn + PsH would be computed, adiabatically as a first step.

2.2 Non-adiabatic theory

For our treatment of non-adiabatic processes and additional rearrangements such as {Pn + Ps} + H, we aim to incorporate Sakimoto’s DVR grid methods into our mixed Jacobi-type bases for all particles. Our experience with adiabatic applications will act as a guide to the feasibility of this approach. The sizes of basis set required will determine how many further dimensions for the light particles can be included explicitly.

Following Sakimoto’s approach [5–7], we will further adapt DVR3D to include electronic/positronic basis functions and matrix elements. The inner region boundary and outer region treatment for two-body break up channels would be defined as for the adiabatic cases but three-body break up, including ${{\mathrm{H}}_2}^{+}$ + ${\displaystyle \bar{\text{H}}}\to$ Pn + H + e⁺, will be considered by analogy with existing double-ionisation theory [32]. It seems likely that a full-dimensional inner-region treatment of the six-particle H₂/${\displaystyle \bar{\text{H}}}$ system may be impractical. Thus we will also implement the theory of Le Dourneuf et al and Gillan et al. For 3-body break-up, light and heavy particles will have to be treated equivalently in the boundary surface and R-matrix.

3 Coordinate systems and transformations

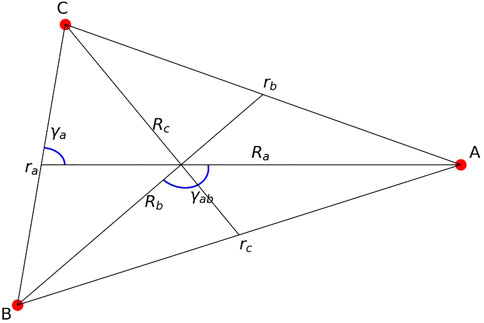
While [8] considers various approaches, bases and coordinates for the RmatReact inner region in useful detail for many-particle (atom-molecule) interacting systems, it does not give explicit details of how the boundary requirements for rearrangement affect the physical shape of the inner region shown in Figure 1. The [8] discussions build on [4] chapters 7 (positron atom collisions with positronium formation) and 11 (non-adiabatic electron molecule collisions with dissociation) which set out details of internal region basis expansions in both arrangements, and transformations at the boundaries chosen so that the one relevant expansion has non-zero surface amplitudes at each boundary. However it is assumed that the inner region integrals over the mixed coordinate hypervolume can be carried out without undue difficulty. Sakimoto’s atomic rearrangement calculations [5–7] are able to use the product channel Jacobi coordinates to describe both arrangements in the inner region and boundary definitions by taking advantage of the lightness of the electron. Reference [16] gives a general description of the mixed-coordinate approach. We may briefly illustrate the kind of necessary coordinate changes and make-up of the R-matrix inner region hypervolume and boundary transformations between internal and external regions using the example of three spinless (for ease of notation) interacting particles A, B, and C, with an initial arrangement of A colliding with molecular (ionic) structure BC and an additional final arrangement B + CA. The standard Jacobi coordinate structure is shown in Figure 3, which also establishes notation.

FIGURE 3

FIGURE 3. Jacobi coordinates.

In the centre of mass frame, as described by Miller [22] the six coordinates R_a, r_a describe the system in arrangement a (A + BC), while R_b, r_b describe the system in arrangement b (B + CA). In arrangement a, it is convenient [22] to use the revised coordinates {R_a, r_a, γ_a} and {θ_a, ϕ_a, ψ_a} where θ_a and ϕ_a are the spherical polar angle coordinates of R_a and ψ_a (0-2π) is the orientation of the ABC triangle about R_a. The inner region basis functions of {r_a, γ_a} and {θ_a, ϕ_a, ψ_a}, in R-matrix terms the target states combined with the colliding particle angular coordinate functions, with label i and angular quantum numbers {J, M_J, l_i} can be summarized as products of rotation matrix angular momentum functions ${D_{m{M}_J}}^{J*}({\psi }_a,{\theta }_a,{\varphi }_a)$ [33] with spherical harmonic functions $Y_{j_{i}m}({\gamma }_a,0)$, multiplied by a function U_ai (r_a) and summed over m as in equation (13) of [22]: J and j_i combine to give l_i. These basis states are used with basis functions of R_a to form a wavefunction expansion of the scattering system in arrangement a. Equation (14) of [22] is an example of this with a wavefunction including expansions in more than one arrangement.

[22] and its successor papers perform integrals over all space, whereas in the R-matrix method all three particles interact in a finite volume which must interface with two (to begin with) exit arrangements, a and b. This finite volume is bounded by a hypersurface defined by R_a = A_a and R_b = A_b, thus both of these conditions must be included in the coordinates defining the inner region. That this approach is feasible can be illustrated by our ABC example. The coordinates {r_a, γ_a} may be replaced by {R_b, γ_ab}, with γ_ab (0-π) as shown in Figure 3. The relation between the volume elements is given in [22] (equation between (25) and (26)), or in [23] equation (2.18d).

$\begin{array}{ll}\hfill d\tau & =r_a^2{R}_a^2\sin {\gamma }_{a}d{r}_{a}d{R}_{a}d{\gamma }_a\hfill \\ \hfill & ={\left(\frac{{\mu }_a{\mu }_b}{m_a{m}_b}\right)}^{3/2}{R}_a^2{R}_b^2\sin {\gamma }_{ab}d{R}_{a}d{R}_{b}d{\gamma }_{ab}\hfill \end{array}$

We note the reduced mass factors can be removed by switching to mass-scaled Jacobi coordinates: details are given in our Supplementary Material along with the full set of transformations from the a coordinates to the b coordinates ([22] Appendix A). With (for example) particle A having mass M_A and total mass M, the B − C reduced mass m_a = M_BM_C/(M_B + M_C) and the A plus BC collisional reduced mass μ_a = M_AM_BM_C/(m_aM) with cyclic permutation for the b and c arrangements.

There is no problem in performing the transformed integrals over all space, however we are interested in the transformation at the R-matrix boundaries from the mixed coordinate system to the a and b systems. We note that for the orientation coordinates the transformation of the rotation matrices of {θ_a, ϕ_a, ψ_a} to corresponding rotation matrices of coordinates {θ_b, ϕ_b, ψ_b}, dependent on angle γ_ab, given by equation (24) in [22], is standard angular momentum theory [33].

At the R_a = A_a boundary, the {R_a, R_b, γ_ab} mixed coordinates need to be related to arrangement a coordinates:

${\int }_0^{A_a}d{R}_a{R}_a^2{\int }_0^{A_b}d{R}_b{R}_b^2{\int }_0^{{\theta }_{ab}}d{\gamma }_{ab}\sin {\gamma }_{ab}={\left(\frac{{\mu }_a{\mu }_b}{m_a{m}_b}\right)}^{-3/2}{\int }_0^{A_a}d{R}_a{R}_a^2{\int }_0^{a_a}d{r}_a{r}_a^2{\int }_{{\theta }_{a,\mathit{min}}}^{{\theta }_{a,\mathit{max}}}d{\gamma }_a\sin {\gamma }_a$

where we may take θ_ab = π and (R_a dependent) a_a can be no larger than

$a_a={\mu }_a\left(\frac{R_a}{M_c}+\frac{A_b}{m_b}\right)$

([22] Appendix A). Our Supplementary Material gives expressions for θ_a, max and θ_a, min. As preliminary work, programs have been written to evaluate test integrals over a mixed Jacobi coordinate inner region volume using single arrangement coordinates: the single arrangement limits for a given hypervolume can be found for given numerical quadrature grid sizes on the fly.

The relevance of this work for the larger project with full description of the colliding atoms and molecules is that values of A_a and A_b must be chosen not only so that the reactants are separated at the boundary for a particular arrangement, but also so that the limits placed on r_a and r_b by the mixed coordinate system do not affect the surface transformations to the external regions. In practice this means that for initial calculations the wavefunctions decribing the target (or product) states should be effectively zero outside of the range indicated in the integral transformation to be fully consistent with the inner region, as the external region R-matrix formulation assumes all coordinates apart from R_a (or R_b) have been fully integrated over at the boundary. Thus the choice of A_a and A_b needs to take into account more factors than in standard R-matrix calculations. Example figures demonstrating geometrical constraints on coordinate limits are included in the Supplementary Material. The transformation of surface amplitudes from mixed coordinates to single arrangement coordinates is in principle sraightforward. The preliminary test work and programs on the 3-particle Jacobi coordinates included transformations of test function amplitudes at fixed boundary values.

The work summarized in the Supplementary Material also studied alternatives to the mixed coordinate systems, such as Delves coordinates and tangent sphere coordinates, and principal axis hyperspherical coordinates (see, for example [25, 26, 34]), which are formulated for composite systems. These can be employed in the antimatter work if the mixed coordinate inner region and boundary transformations prove to be problematic. However, in real problems, when combined with additional bases and states describing the component particles of the composite colliding systems, the mixed Jacobi-type coordinate system seems so far to be the most straightforward and natural extension to the existing R-matrix packages.

4 Bound-state calculations

The RmatReact project [8] plans to modify existing nuclear motion programs [21, 35] to solve the inner region problem. Here we have used the unmodified Triatom code [36] (a finite basis representation code related to DVR3D) to conduct some preliminary bound-state calculations on {p,p,${\displaystyle \bar{\text{p}}}$} (or Pn + p) - a system of heavy particles common to the inner region problems for a number of interesting matter/antimatter interactions (such as H₂/$\bar{\text{H}}$, ${{\mathrm{H}}_2}^{+}$/${\displaystyle \bar{\text{p}}}$ and ${{\mathrm{H}}_2}^{+}$/${\displaystyle \bar{\text{H}}}$). The (bound-state) energies (and wavefunctions) can be compared with mass-scaled literature {e⁻, e⁻, e⁺} results [37] (that is Ps⁻ or Ps + e⁻). We consider the non-relativistic problem - that is only taking into account the Coulomb force proton-proton repulsion and proton-antiproton attractions. Details of the calculations are given in the Supplementary Material.

Pn + p has only one bound state (by analogy with Ps⁻) so to make a more demanding test of the dynamics of this mixed matter-antimatter system that a code designed for normal molecules can reproduce, we have investigated the lowest-lying s-wave resonance states using a simple stabilization method [38, 39]. The radial basis functions consist of products of a Gaussian and associated Laguerre polynomials, all defined in terms of the quantity y = βr² (where r is a p-${\displaystyle \bar{\text{p}}}$ distance). Thus varying β changes the length scale of the basis set. The energy of a resonance is expected to remain nearly constant over a range of scaling parameter values. Here we use β^−1/2 which has dimension of length.

4.1 Results

We report calculations here where β^−1/2 is varied from 0.000859 to 0.008125 a₀ - see Figure 4 and Supplementary Figure S4 in the Supplementary Material. The latter also includes a tabulation of the plotted data.

FIGURE 4

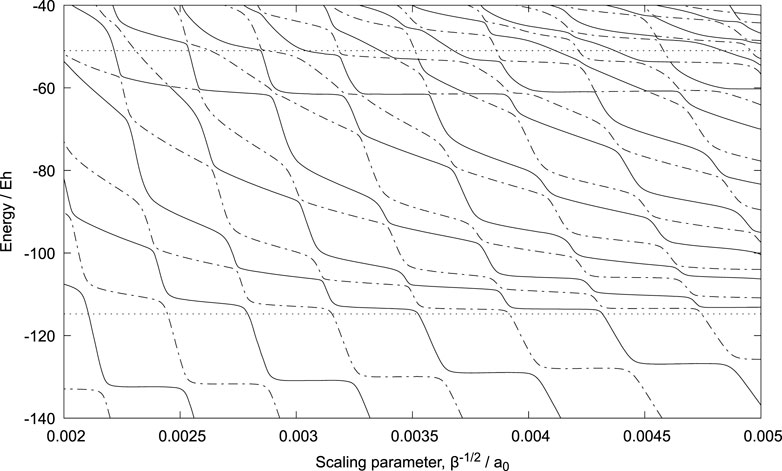
FIGURE 4. Stabilization diagram for the {p,p,$\bar{\text{p}}$} system. The (near) horizontal regions at approximately −130, −113, −62 and −54 E_h represent resonance states—in every case they are higher in energy than expected from mass scaling of accurate calculations on Ps⁻ (−139.6, −116.9, −64.9 and −54.8 E_h). The horizontal dotted lines represent the protonium n = 2 (−114.7 E_h) and n = 3 (−51.0 E_h) states (non-relativistic values for consistency).

The energy of the bound state of Pn + p is minimised with respect to β at −483.1 E_h, that is below the expected −481.0 E_h. (E_h represents Hartree, the atomic unit of energy.) This discrepancy is due to inaccuracy in the numerical quadratures required for the Coulomb potential energy integrals. In the case of the integrals involving the proton-antiproton distances, Triatom uses Gauss-Laguerre quadrature and numerical problems were encountered when large numbers of quadrature points were used (that is greater than the 103 used for the reported results).

In spite of this issue, we pursued the exploration of Pn + p resonances to see if the chosen basis set could reproduce, at least qualitatively, the main features. Indeed the stabilization diagram, Figure 4, does show (near) horizontal regions, representing resonance states, at approximately −130, −113, −62 and −54 E_h. In every case they are higher in energy than expected from mass scaling of accurate calculations on Ps⁻ (−139.6, −116.9, −64.9 and −54.8 E_h). Note also that the second lowest resonance should be below the protonium n = 2 energy (represented by the horizontal dotted line at −114.7 E_h). The mean energies of the horizontal regions vary with β and the values obtained for the largest β, giving a horizonal and stable region, are −132.5, −113.4, −61.5 and −53.5 E_h. See also Supplementary Table S1 where the present calculated energies of the {p,p,$\bar{\text{p}}$} bound state and lowest-lying s-wave resonances are compared with the literature results (mass-scaled from Ps⁻/Ps + e⁻); the β^−1/2 values corresponding to each energy are also given. We attribute the discrepancies in the energies, in the case of lower resonance states especially, to the inability of the chosen basis set to simultaneously represent both long- and short-range effects (in addition to the quadrature error already noted). This must be taken into account in forthcoming calculations.

5 Conclusion

We have set out a road-map for treatment of matter-antimatter scattering processes including rearrangement using the R-matrix method. We have described the complexities involved and set out an approach to solve these problems. This will be extendable to larger systems including for example molecular antimatter. We note that spectroscopic investigation of the antihydrogen molecular anion ${{{\displaystyle \bar{\mathrm{H}}}}_2}^{-}$ (the antimatter equivalent of ${{\mathrm{H}}_2}^{+}$) may allow much more sensitive tests of CPT [40, 41]. We have also reported an initial study of the required mixed coordinate systems and some preliminary bound-state calculations on {p,p,${\displaystyle \bar{\text{p}}}$}.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

MP and ML conceived and designed the study and developed the overall theoretical approach. The coordinate transformation studies were conducted by EK (with input from MP and ML), whilst the bound-state studies were conducted by LV (with input from ML). MP and ML wrote the manuscript with input from EK and LV. All authors contributed to the article and approved the submitted version.

Funding

The contribution of EK was supported by the Ada Lovelace Centre, UK Science and Technology Facilities Council. MP’s work made use of support by CoSeC, the Computational Science Centre for Research Communities, through Collaborative Computational Project Q and High-End-Consortium (HEC) UK-AMOR.

Acknowledgments

We are grateful for helpful discussions with Jonathan Tennyson and Mike Charlton. The bound-state calculations were performed using the Maxwell High Performance Computing Cluster of the University of Aberdeen IT Service.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1187537/full#supplementary-material

References

1. Ahmadi M, Alves BXR, Baker CJ, Bertsche W, Capra A, Carruth C, et al. Investigation of the fine structure of antihydrogen. Nature (2020) 578:375–80. doi:10.1038/s41586-020-2006-5

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Baker CJ, Bertsche W, Capra A, Carruth C, Cesar CL, Charlton M, et al. Laser cooling of antihydrogen atoms. Nature (2021) 592:35–42. doi:10.1038/s41586-021-03289-6

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kolbinger B, Amsler C, Cuendis SA, Breuker H, Capon A, Costantini G, et al. Measurement of the principal quantum number distribution in a beam of antihydrogen atoms. Europ Phys J D (2021) 75:91. doi:10.1140/epjd/s10053-021-00101-y

CrossRef Full Text | Google Scholar

4. Burke PG. R-Matrix theory of atomic collisions. Springer (2011).

Google Scholar

5. Sakimoto K. R-matrix calculation of antiproton capture by helium ions. Phys Rev A (2007) 76:042513. doi:10.1103/physreva.76.042513

CrossRef Full Text | Google Scholar

6. Sakimoto K. Cross sections for antiproton capture by helium ions. Phys Rev A (2010) 82:012501. doi:10.1103/physreva.82.012501

CrossRef Full Text | Google Scholar

7. Sakimoto K. Unified treatment of hadronic annihilation and protonium formation in slow collisions of antiprotons with hydrogen atoms. Phys Rev A (2013) 88:012507. doi:10.1103/physreva.88.012507

CrossRef Full Text | Google Scholar

8. McKemmish LK, Tennyson J. General mathematical formulation of scattering processes in atom–diatomic collisions in the RmatReact methodoogy. Phil Trans R Soc A (2019) 377:20180409. doi:10.1098/rsta.2018.0409

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Jonsell S, Charlton M. On the binding energies of antihydrogen formed by the interactions of antiprotons in cold positron plasmas. J Phys B (2021) 54:025001. doi:10.1088/1361-6455/abcded

CrossRef Full Text | Google Scholar

10.Available at: https://www.ukamor.com (Accessed May 16, 2023).

11. Mant BP, Law MM, Strasburger K. Hydrogen molecule-antihydrogen atom potential energy surface and scattering calculations. J Phys B (2019) 52:185201. doi:10.1088/1361-6455/ab312e

CrossRef Full Text | Google Scholar

12. Lodi Rizzini E, Venturelli L, Zurlo N, Charlton M, Amsler C, Bonomi G, et al. Further evidence for low-energy protonium production in vacuum. E Phys J Plus (2012) 127:124. doi:10.1140/epjp/i2012-12124-9

CrossRef Full Text | Google Scholar

13. Jonsell S, Saenz A, Froelich P, Zygelman B, Dalgarno A. Stability of hydrogen-antihydrogen mixtures at low energies. Phys Rev A (2001) 64:052712. doi:10.1103/physreva.64.052712

CrossRef Full Text | Google Scholar

14. Jonsell S. Rearrangement and annihilation in antihydrogen-atom scattering. AIP Conf Proc (2008) 1037:347–357. doi:10.1063/1.2977853

CrossRef Full Text | Google Scholar

15. Jonsell S, Armour EAG, Plummer M, Liu Y, Todd AC. Helium–antihydrogen scattering at low energies. New J Phys (2012) 14:035013. doi:10.1088/1367-2630/14/3/035013

CrossRef Full Text | Google Scholar

16. Manolopoulos DE, D’Mello M, Wyatt RE. Quantum reactive scattering via the log derivative version of the Kohn variational principle: General theory for bimolecular chemical reactions. J Chem Phys (1989) 91:6096–102. doi:10.1063/1.457428

CrossRef Full Text | Google Scholar

17. Le Dourneuf M, Schneider BI, Burke PG. Theory of vibrational excitation and dissociative attachment: An R-matrix approach. J Phys B (1979) 12:L365–9. doi:10.1088/0022-3700/12/12/008

CrossRef Full Text | Google Scholar

18. Gillan CJ, Nagy O, Burke PG, Morgan LA, Noble CJ. Electron scattering by nitrogen molecules. J Phys B (1987) 20:4585–603. doi:10.1088/0022-3700/20/17/032

CrossRef Full Text | Google Scholar

19. Stibbe DT, Tennyson J. Near-threshold electron impact dissociation of H₂ within the adiabatic nuclei approximation. N J Phys (1998) 1:2. doi:10.1088/1367-2630/1/1/002

CrossRef Full Text | Google Scholar

20. Scarlett LH, Fursa DV, Knol J, Zammit MC, Bray I. Isotopic and vibrational-level dependence of H₂ dissociation by electron impact. Phys Rev A (2021) 103:L020801. doi:10.1103/physreva.103.l020801

CrossRef Full Text | Google Scholar

21. Tennyson J, Kostin MA, Barletta P, Harris GJ, Polyansky OL, Ramanlal J, et al. DVR3D: A program suite for the calculation of rotation–vibration spectra of triatomic molecules. Comput Phys Commun (2004) 163:85–116. doi:10.1016/j.cpc.2003.10.003

CrossRef Full Text | Google Scholar

22. Miller WH. Coupled equations and the minimum principle for collisions of an atom and a diatomic molecule, including rearrangements. J Chem Phys (1969) 50:407–18. doi:10.1063/1.1670812

CrossRef Full Text | Google Scholar

23. Zhang JZH, Miller WH. Quantum reactive scattering via the S-mstrix version of the Kohn variational principle: Differential and integral cross sections for D + H₂ → HD + H. J Chem Phys (1989) 91:1528–47. doi:10.1063/1.457650

CrossRef Full Text | Google Scholar

24. Higgins K, Burke PG. Positron scattering by atomic hydrogen including positronium formation. J Phys B (1993) 26:4269–88. doi:10.1088/0953-4075/26/22/029

CrossRef Full Text | Google Scholar

25. Carter S, Meyer W. A variational method for the calculation of vibrational energy levels of triatomic molecules using a Hamiltonian in hyperspherical coordinates. J Chem Phys (1990) 93:8902–14. doi:10.1063/1.459229

CrossRef Full Text | Google Scholar

26. Parker GA, Keil M, Morrison MA, Crocchianti S. Quantum reactive scattering in three dimensions: Using tangent-sphere coordinates to smoothly transform from hyperspherical to Jacobi regions. J Chem Phys (2000) 113:957–70. doi:10.1063/1.481876

CrossRef Full Text | Google Scholar

27. Sunderland AG, Noble CJ, Burke VM, Burke PG. A parallel R-matrix program PRMAT for electron–atom and electron–ion scattering calculations. Comp Phys Commun (2002) 145:311–40. doi:10.1016/s0010-4655(02)00140-6

CrossRef Full Text | Google Scholar

28. Brigg WJ, Tennyson J, Plummer M. R-matrix calculations of low-energy electron collisions with methane. J Phys B (2014) 47:185203. doi:10.1088/0953-4075/47/18/185203

CrossRef Full Text | Google Scholar

29. Cohen JS. Dissociation and ionization in capture of antiprotons and negative muons by the hydrogen molecular ion. J Phys B (2005) 38:441–56. doi:10.1088/0953-4075/38/4/011

CrossRef Full Text | Google Scholar

30. Sakimoto K. Protonium formation in collisions of antiprotons with hydrogen molecular ions. J Phys B (2004) 37:2255–76. doi:10.1088/0953-4075/37/11/004

CrossRef Full Text | Google Scholar

31. Cohen JS. Reactive collisions of atomic antihydrogen with the H₂ and ${\mathrm{H}}_2^{+}$ molecules. J Phys B (2006) 39, 3561–74. doi:10.1088/0953-4075/39/17/013

CrossRef Full Text | Google Scholar

32.UK engineering and physical science research Council Grant EP/T019530/1, Available at: https://gow.epsrc.ukri.org/NGBOViewGrant.aspx?GrantRef=EP/T019530/1 (Accessed May 16, 2023).

Google Scholar

33. Rose ME. Elementary theory of angular momentum. Wiley (1967).

Google Scholar

34. Pack RT, Parker GA. Quantum reactive scattering in three dimensions using hyperspherical (APH) coordinates. Theory. J Chem Phys (1987) 87:3888–921. doi:10.1063/1.452944

CrossRef Full Text | Google Scholar

35. Kozin IN, Law MM, Tennyson J, Hutson JM. New vibration–rotation code for tetraatomic molecules exhibiting wide-amplitude motion: WAVR4. Comput Phys Commun (2004) 163:117–31. doi:10.1016/j.cpc.2004.07.005

CrossRef Full Text | Google Scholar

36. Tennyson J, Miller S, Le Sueur CR. Triatom: Programs for the calculation of ro-vibrational spectra of triatomic molecules. Comp.Phys Commun (1993) 75:339–64. doi:10.1016/0010-4655(93)90048-h

CrossRef Full Text | Google Scholar

37. Zhou Y, Lin CD. Comparative Studies of Excitations and Resonances in H⁻, Ps⁻, and e⁺ + H Systems. Phys Rev Lett (1995) 75:2296–9. doi:10.1103/physrevlett.75.2296

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Hazi AU, Taylor HS. Stabilization method of calculating resonance energies: Model problem. Phys Rev A (1970) 1:1109–20. doi:10.1103/physreva.1.1109

CrossRef Full Text | Google Scholar

39. Mandelshtam VA, Ravuri TR, Taylor HS. Calculation of the density of resonance states using the stabilization method. Phys Rev Lett (1993) 70:1932–5. doi:10.1103/physrevlett.70.1932

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Myers EG. CPT tests with the antihydrogen molecular ion. Phys Rev A (2018) 98:010101(R). doi:10.1103/physreva.98.010101

CrossRef Full Text | Google Scholar

41. Zammit MC, Charlton M, Jonsell S, Colgan J, Savage JS, Fursa DV, et al. Laser driven production of the antihydrogen molecular ion. Phys Rev A (2019) 100:042709. doi:10.1103/physreva.100.042709

CrossRef Full Text | Google Scholar