QCD sum rule study on the fully strange tetraquark states of JPC = 2++

We apply the QCD sum rule method to systematically study the fully strange tetraquark states with the quantum number J^PC = 2⁺⁺. We construct both the diquark–antidiquark and mesonic–mesonic currents and calculate both their diagonal and off-diagonal correlation functions. Based on the obtained results, we further construct three mixing currents that are nearly non-correlated. We use one mixing current to extract the mass of the lowest-lying state to be $2.03_{-0.15}^{+0.16}$ GeV, which can be used to explain f₂(2010) as a fully strange tetraquark state of J^PC = 2⁺⁺. This state was observed by BESIII in the ϕϕ channel, and we propose to confirm it in the η⁽′⁾η⁽′⁾ channel.

1 Introduction

Many exotic hadrons were observed in particle experiments during the past 20 years [1], some of which are good candidates for the fully strange tetraquark states [2–22]. Especially the BESIII collaboration performed a partial wave analysis of the J/ψ → γϕϕ decay in 2016 [23]. They observed three tensor resonances, namely, f₂(2010), f₂(2300), and f₂(2340) in the ϕϕ invariant mass spectrum, whose masses and widths were measured to be

$f_2\left(2010\right):M\approx 2011\mathrm{M}\mathrm{e}\mathrm{V},(1)$

$\mathrm{\Gamma }\approx 202\mathrm{M}\mathrm{e}\mathrm{V};$

$f_2\left(2300\right):M\approx 2297\mathrm{M}\mathrm{e}\mathrm{V},(2)$

$\mathrm{\Gamma }\approx 149\mathrm{M}\mathrm{e}\mathrm{V};$

$f_2\left(2340\right):M\approx 2339\mathrm{M}\mathrm{e}\mathrm{V},(3)$

$\mathrm{\Gamma }\approx 319\mathrm{M}\mathrm{e}\mathrm{V}.$

These three resonances contain many strangeness components, so they are possible fully strange tetraquark states of J^PC = 2⁺⁺. With a large amount of the J/ψ sample, BESIII collaborations are still examining the physics happening in this energy region, and more rich-strangeness signals are expected in the coming future. Similar experiments can also be performed by Belle-II, COMPASS, GlueX, and PANDA, etc.

The fully strange tetraquark states are interesting from two aspects. Experimentally, their widths are possibly not very broad [possibly at the order of $\mathcal{O}$(100 MeV)], so they are capable of being observed. Theoretically, their internal structures are simpler than other tetraquark states due to the Pauli principle’s restriction on identical strangeness quarks and antiquarks, which limits their potential number and makes them easier to be observed. In the past 15 years, we have applied the QCD sum rule method to study the fully strange tetraquark states with quantum numbers J^PC = 0⁻⁺/1^±±/4⁺⁻ [24–32]. More theoretical studies can be found in [33–42].

In this paper, we shall study the fully strange tetraquark states with the quantum number J^PC = 2⁺⁺. We shall systematically construct both the diquark–antidiquark and mesonic–mesonic currents. We shall apply the method of QCD sum rules to study these currents as a whole, and extract the mass of the lowest-lying state to be $2.03_{-0.15}^{+0.16}$ GeV. Our results suggest that the f₂(2010) can be explained as the fully strange tetraquark state of J^PC = 2⁺⁺, while it is not easy to interpret the f₂(2300) and f₂(2340) as such states.

This paper is organized as follows. In Section 2, we systematically construct the fully strange tetraquark states with the quantum number J^PC = 2⁺⁺. We use these currents to perform QCD sum rule analyses in Section 3, where we calculate both their diagonal and off-diagonal correlation functions. Based on the obtained results, we use the diquark–antidiquark currents to perform numerical analyses in Section 4, and we use their mixing currents to perform numerical analyses in Section 5. The obtained results are summarized and discussed in Section 6.

2 Interpolating currents

The fully strange tetraquark currents with quantum numbers J^PC = 0⁻⁺/1^±±/4⁺⁻ have been systematically constructed in [24–30, 43]. In this section, we follow the same approach to construct the fully strange tetraquark currents with the quantum number J^PC = 2⁺⁺. We observe three independent diquark–antidiquark currents.

${\eta }_1^{\mu \nu }=\mathcal{S}\left[s_a^{T}C{\gamma }^{\mu }{s}_b{\bar{s}}_a{\gamma }^{\nu }C{\bar{s}}_b^T\right],(4)$

${\eta }_2^{\mu \nu }=\mathcal{S}\left[s_a^{T}C{\gamma }^{\mu }{\gamma }_5{s}_b{\bar{s}}_a{\gamma }^{\nu }{\gamma }_{5}C{\bar{s}}_b^T\right],(5)$

${\eta }_3^{\mu \nu }=g_{\rho \sigma }\mathcal{S}\left[s_a^{T}C{\sigma }^{\mu \rho }{s}_b{\bar{s}}_a{\sigma }^{\nu \sigma }C{\bar{s}}_b^T\right],(6)$

where a and b are color indices, C = iγ₂γ₀ is the charge-conjugation operator, and the symbol $\mathcal{S}$ represents symmetrizing and subtracting trace terms in the set {μν}. Among these currents, ${\eta }_1^{\mu \nu }$ and ${\eta }_3^{\mu \nu }$ have the antisymmetric color structure ${[ss]}_{{\bar{\mathbf{3}}}_C}{[\bar{s}\bar{s}]}_{{\mathbf{3}}_C}$, and ${\eta }_2^{\mu \nu }$ has the symmetric color structure ${[ss]}_{{\mathbf{6}}_C}{[\bar{s}\bar{s}]}_{{\bar{\mathbf{6}}}_C}$, so the internal structure of ${\eta }_1^{\mu \nu }$ and ${\eta }_3^{\mu \nu }$ is more stable than that of ${\eta }_2^{\mu \nu }$. Moreover, the first current ${\eta }_1^{\mu \nu }$ only contains the S-wave diquark field $s_a^{T}C{\gamma }^{\mu }{s}_b$ and the S-wave antidiquark field ${\bar{s}}_a{\gamma }^{\nu }C{\bar{s}}_b^T$, so it has a more stable internal structure that may lead to a better sum rule result. In addition, the diquark field $s_a^{T}C{\sigma }^{\mu \nu }{s}_b$ of J^P = 1^± contains both S- and P-wave components, so the third current ${\eta }_3^{\mu \nu }$ may also lead to a good sum rule result; the second current ${\eta }_2^{\mu \nu }$ contains the P-wave diquark field $s_a^{T}C{\gamma }^{\mu }{\gamma }_5{s}_b$, so its predicted mass is probably larger. In the present study, we only consider tetraquark currents without derivatives, and more J^PC = 2⁺⁺ currents can be constructed when using derivatives. However, their internal structures are not so stable, and their predicted masses are probably also larger.

In addition to the aforementioned diquark–antidiquark currents, we find six mesonic–mesonic currents.

${\xi }_1^{\mu \nu }=\mathcal{S}\left[{\bar{s}}_a{\gamma }^{\mu }{s}_a{\bar{s}}_b{\gamma }^{\nu }{s}_b\right],(7)$

${\xi }_2^{\mu \nu }=\mathcal{S}\left[{\bar{s}}_a{\gamma }^{\mu }{\gamma }_5{s}_a{\bar{s}}_b{\gamma }^{\nu }{\gamma }_5{s}_b\right],(8)$

${\xi }_3^{\mu \nu }=g_{\rho \sigma }\mathcal{S}\left[{\bar{s}}_a{\sigma }^{\mu \rho }{s}_a{\bar{s}}_b{\sigma }^{\nu \sigma }{s}_b\right],(9)$

${\xi }_4^{\mu \nu }={\lambda }_n^{ab}{\lambda }_n^{cd}\mathcal{S}\left[{\bar{s}}_a{\gamma }^{\mu }{s}_b{\bar{s}}_c{\gamma }^{\nu }{s}_d\right],(10)$

${\xi }_5^{\mu \nu }={\lambda }_n^{ab}{\lambda }_n^{cd}\mathcal{S}\left[{\bar{s}}_a{\gamma }^{\mu }{\gamma }_5{s}_b{\bar{s}}_c{\gamma }^{\nu }{\gamma }_5{s}_d\right],(11)$

${\xi }_6^{\mu \nu }={\lambda }_n^{ab}{\lambda }_n^{cd}{g}_{\rho \sigma }\mathcal{S}\left[{\bar{s}}_a{\sigma }^{\mu \rho }{s}_b{\bar{s}}_c{\sigma }^{\nu \sigma }{s}_d\right].(12)$

We can verify the following relations through the Fierz rearrangement, so the number of independent mesonic–mesonic currents is also three.

$\left(\begin{array}{c}\hfill {\xi }_4^{\mu \nu }\hfill \\ \hfill {\xi }_5^{\mu \nu }\hfill \\ \hfill {\xi }_6^{\mu \nu }\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill -\frac{5}{3}\hfill & \hfill -1\hfill & \hfill +1\hfill \\ \hfill -1\hfill & \hfill -\frac{5}{3}\hfill & \hfill -1\hfill \\ \hfill +2\hfill & \hfill -2\hfill & \hfill -\frac{2}{3}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\xi }_1^{\mu \nu }\hfill \\ \hfill {\xi }_2^{\mu \nu }\hfill \\ \hfill {\xi }_3^{\mu \nu }\hfill \end{array}\right).(13)$

Moreover, we can use the Fierz rearrangement to relate the diquark–antidiquark and mesonic–mesonic currents.

$\left(\begin{array}{c}\hfill {\eta }_1^{\mu \nu }\hfill \\ \hfill {\eta }_2^{\mu \nu }\hfill \\ \hfill {\eta }_3^{\mu \nu }\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill -\frac{1}{2}\hfill & \hfill +\frac{1}{2}\hfill & \hfill +\frac{1}{2}\hfill \\ \hfill +\frac{1}{2}\hfill & \hfill -\frac{1}{2}\hfill & \hfill +\frac{1}{2}\hfill \\ \hfill +1\hfill & \hfill +1\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\xi }_1^{\mu \nu }\hfill \\ \hfill {\xi }_2^{\mu \nu }\hfill \\ \hfill {\xi }_3^{\mu \nu }\hfill \end{array}\right).(14)$

Therefore, the diquark–antidiquark and mesonic–mesonic constructions are equivalent to each other, when the local currents are investigated. We shall use this Fierz identity to study the decay behaviors at the end of this paper.

3 QCD sum rule analysis

The QCD sum rule method is a powerful and successful non-perturbative method [44, 45]. In this section, we apply it to study the currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ and calculate their two-point correlation functions

$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{ij}^{\mu \nu ,{\mu }^{\prime }{\nu }^{\prime }}\left(q^2\right)& \equiv \hfill & i\int d^{4}x{e}^{\mathit{iqx}}⟨0|\mathbf{T}\left[{\eta }_i^{\mu \nu }\left(x\right){\eta }_j^{{\mu }^{\prime }{\nu }^{\prime },†}\left(0\right)\right]|0⟩\hfill \\ \hfill & =\hfill & {\mathrm{\Pi }}_{ij}\left(q^2\right)\times {\mathcal{S}}^{\prime }\left[{\tilde{g}}^{\mu {\mu }^{\prime }}{\tilde{g}}^{\nu {\nu }^{\prime }}\right],\hfill \end{array}(15)$

at both the hadron and quark–gluon levels. Here, ${\tilde{g}}^{\mu \nu }=g^{\mu \nu }-q^{\mu }{q}^{\nu }/q^2$, and the symbol ${\mathcal{S}}^{\prime }$ denotes symmetrizing and subtracting trace terms in the two sets {μν} and {μ′ν′}, respectively.

At the hadron level, we generally assume that the currents ${\eta }_i^{\mu \nu }$ (i = 1⋯3) couple to the states X_n (n = 1⋯N) through

$⟨0|{\eta }_i^{\mu \nu }|X_n⟩=f_{in}{ϵ}^{\mu \nu },(16)$

where f_in is the decay constant and ϵ^μν is the symmetric and traceless polarization tensor. Then, we use the dispersion relation to express Π_ij(q²) as

${\mathrm{\Pi }}_{ij}\left(q^2\right)={\int }_{s_{<}}^{\infty }\frac{{\rho }_{ij}^{\text{phen}}\left(s\right)}{s-q^2-i\epsilon }ds,(17)$

where $s_{<}=16m_s^2$ is the physical threshold and ${\rho }_{ij}^{\text{phen}}(s)$ is the phenomenological spectral density. We parameterize it for the states X_n and a continuum contribution as

$\begin{array}{ccc}\hfill & \hfill & {\rho }_{ij}^{\text{phen}}\left(s\right)\times {\mathcal{S}}^{\prime }\left[{\tilde{g}}^{\mu {\mu }^{\prime }}{\tilde{g}}^{\nu {\nu }^{\prime }}\right]\hfill \\ \hfill & =\hfill & \sum _n\delta \left(s-M_n^2\right)\langle 0|{\eta }_i^{\mu \nu }|X_n\rangle \langle X_n|{\eta }_j^{{\mu }^{\prime }{\nu }^{\prime },†}|0\rangle +\cdots \hfill \\ \hfill & =\hfill & \sum _n{f}_{in}{f}_{jn}\delta \left(s-M_n^2\right)\times {\mathcal{S}}^{\prime }\left[{\tilde{g}}^{\mu {\mu }^{\prime }}{\tilde{g}}^{\nu {\nu }^{\prime }}\right]+\cdots ,\hfill \end{array}(18)$

where M_n is the mass of X_n and ⋯ is contributed by the continuum. It should be noted that the widths of X_n are not taken into account in the present study, and the two-meson thresholds are also not taken into account, such as the ϕϕ threshold. The Fierz rearrangement given in Eq. 13 indicates that the tetraquark currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ can easily couple to two mesons, which causes some difficulties in extracting the correct information about the resonance when the two-meson thresholds contribute significantly. The authors of [46] suggest that the four-quark diagrams with no singularity at $s={({\sum }_{i=1}^4{m}_i)}^2$ (m_i is the quark mass) are relevant to two free mesons but not relevant to the four-quark state. However, the validity of this criterion is still not clear.

At the quark–gluon level, we apply the method of the operator product expansion (OPE) to calculate Eq. 15 and extract the OPE spectral density ${\rho }_{ij}(s)\equiv {\rho }_{ij}^{\text{OPE}}(s)$. In this study, we take into account the Feynman diagrams shown in Figure 1 and perform the calculations up to the twelfth dimension, where we consider the perturbative term, the strange quark mass m_s, the quark condensate $⟨\bar{s}s⟩$, the double-gluon condensate $⟨g_s^{2}GG⟩$, the quark–gluon mixed condensate $⟨g_s\bar{s}\sigma Gs⟩$, and their combinations. We do not consider some other condensates, such as $⟨g_s\bar{s}{D}_{\mu }{G}^{\mu \nu }{\gamma }_{\nu }s⟩$ and the diagrams with up/down quark loops, since their calculations are difficult. The vacuum saturation is assumed for higher-dimensional operators, i.e., $⟨\bar{s}s\bar{s}s⟩\approx {⟨\bar{s}s⟩}^2$ and $⟨\bar{s}s{g}_s\bar{s}\sigma Gs⟩\approx ⟨\bar{s}s⟩⟨g_s\bar{s}\sigma Gs⟩$. We calculate all the diagrams proportional to $g_s^{N=0}$ and $g_s^{N=1}$, where we find the D = 6 term ${⟨\bar{s}s⟩}^2$ and the D = 8 term $⟨\bar{s}s⟩⟨g_s\bar{s}\sigma Gs⟩$ to be important. We partly calculate the diagrams proportional to $g_s^{N\ge 2}$, and we find their contributions to be small.

FIGURE 1

FIGURE 1. Feynman diagrams for the fully strange tetraquark currents of J^PC =2⁺⁺.

Finally, we perform the Borel transformation at both the hadron and quark–gluon levels. After approximating the continuum using ρ_ij(s) above the threshold value s₀, we arrive at the sum rule equation

$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{ij}\left(s_0,M_B^2\right)& =\hfill & \sum _n{f}_{in}{f}_{jn}{e}^{-M_n^2/M_B^2}\hfill \\ \hfill & =\hfill & {\int }_{s_{<}}^{s_0}{e}^{-s/M_B^2}{\rho }_{ij}\left(s\right)ds.\hfill \end{array}(19)$

The explicit sum rule equations extracted from the currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ are as follows:

$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{11}& =\hfill & {\int }_{16m_s^2}^{s_0}{e}^{-s/M_B^2}ds\times \left[\frac{s^4}{86016{\pi }^6}-\frac{m_s^2{s}^3}{2880{\pi }^6}+\left(-\frac{11⟨g_s^{2}GG⟩}{122880{\pi }^6}-\frac{3m_s⟨\bar{s}s⟩}{320{\pi }^4}\right)s^2\right.\hfill \\ \hfill & \hfill & +\left(\frac{5⟨g_s^{2}GG⟩m_s^2}{9216{\pi }^6}-\frac{7m_s⟨g_s\bar{s}\sigma Gs⟩}{288{\pi }^4}+\frac{{⟨\bar{s}s⟩}^2}{18{\pi }^2}\right)s\hfill \\ \hfill & \hfill & \left.+\frac{11⟨g_s^{2}GG⟩m_s⟨\bar{s}s⟩}{6912{\pi }^4}+\frac{5m_s^2{⟨\bar{s}s⟩}^2}{24{\pi }^2}+\frac{7⟨\bar{s}s⟩⟨g_s\bar{s}\sigma Gs⟩}{144{\pi }^2}\right]\hfill \\ \hfill & \hfill & +\left(-\frac{⟨g_s^{2}GG⟩{⟨\bar{s}s⟩}^2}{432{\pi }^2}-\frac{4m_s{⟨\bar{s}s⟩}^3}{9}+\frac{⟨g_s^{2}GG⟩m_s⟨g_s\bar{s}\sigma Gs⟩}{1152{\pi }^4}+\frac{m_s^2⟨\bar{s}s⟩⟨g_s\bar{s}\sigma Gs⟩}{4{\pi }^2}\right)\hfill \\ \hfill & \hfill & +\frac{1}{M_B^2}\left(\frac{5⟨g_s^{2}GG⟩m_s^2{⟨\bar{s}s⟩}^2}{3456{\pi }^2}+\frac{5m_s^2{⟨g_s\bar{s}\sigma Gs⟩}^2}{288{\pi }^2}+\frac{5m_s{⟨\bar{s}s⟩}^2⟨g_s\bar{s}\sigma Gs⟩}{54}\right),\hfill \end{array}(20)$

$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{22}& =\hfill & {\int }_{16m_s^2}^{s_0}{e}^{-s/M_B^2}ds\times \left[\frac{s^4}{43008{\pi }^6}-\frac{m_s^2{s}^3}{360{\pi }^6}+\left(-\frac{19⟨g_s^{2}GG⟩}{122880{\pi }^6}+\frac{7m_s⟨\bar{s}s⟩}{160{\pi }^4}\right)s^2\right.\hfill \\ \hfill & \hfill & +\left(-\frac{{⟨\bar{s}s⟩}^2}{9{\pi }^2}+\frac{17m_s⟨g_s\bar{s}\sigma Gs⟩}{288{\pi }^4}+\frac{11⟨g_s^{2}GG⟩m_s^2}{9216{\pi }^6}\right)s\hfill \\ \hfill & \hfill & \left.-\frac{17⟨\bar{s}s⟩⟨g_s\bar{s}\sigma Gs⟩}{144{\pi }^2}+\frac{7⟨g_s^{2}GG⟩m_s⟨\bar{s}s⟩}{6912{\pi }^4}+\frac{7m_s^2{⟨\bar{s}s⟩}^2}{4{\pi }^2}\right]\hfill \\ \hfill & \hfill & +(\frac{m_s^2⟨\bar{s}s⟩{⟨g_s\bar{s}\sigma Gs⟩}^2}{2{\pi }^2}-\frac{⟨g_s^{2}GG⟩{⟨\bar{s}s⟩}^2}{432{\pi }^2}+\frac{⟨g_s^{2}GG⟩m_s⟨g_s\bar{s}\sigma Gs⟩}{1152{\pi }^4}-\frac{8m_s{⟨\bar{s}s⟩}^3}{9})\hfill \\ \hfill & \hfill & +\frac{1}{M_B^2}\left(\frac{7⟨g_s^{2}GG⟩m_s^2{⟨\bar{s}s⟩}^2}{3456{\pi }^2}+\frac{65m_s{⟨\bar{s}s⟩}^2⟨g_s\bar{s}\sigma Gs⟩}{54}-\frac{13m_s^2{⟨g_s\bar{s}\sigma Gs⟩}^2}{72{\pi }^2}\right),\hfill \end{array}(21)$

$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{33}& =\hfill & {\int }_{16m_s^2}^{s_0}{e}^{-s/M_B^2}ds\times \left[\frac{s^4}{43008{\pi }^6}-\frac{m_s^2{s}^3}{576{\pi }^6}+\left(\frac{m_s⟨\bar{s}s⟩}{80{\pi }^4}-\frac{⟨g_s^{2}GG⟩}{6144{\pi }^6}\right)s^2+\frac{m_s^2⟨g_s^{2}GG⟩}{576{\pi }^6}s\right.\hfill \\ \hfill & \hfill & \left.+\frac{13m_s^2{⟨\bar{s}s⟩}^2}{12{\pi }^2}-\frac{⟨g_s^{2}GG⟩m_s⟨\bar{s}s⟩}{576{\pi }^4}\right]+\left(\frac{m_s^2⟨\bar{s}s⟩{⟨g_s\bar{s}\sigma Gs⟩}^2}{2{\pi }^2}-\frac{8m_s{⟨\bar{s}s⟩}^3}{9}\right)\hfill \\ \hfill & \hfill & +\frac{1}{M_B^2}\left(\frac{⟨g_s^{2}GG⟩m_s^2{⟨\bar{s}s⟩}^2}{432{\pi }^2}+\frac{2m_s{⟨\bar{s}s⟩}^2⟨g_s\bar{s}\sigma Gs⟩}{3}-\frac{m_s^2{⟨g_s\bar{s}\sigma Gs⟩}^2}{16{\pi }^2}\right),\hfill \end{array}(22)$

$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{12}& =\hfill & {\int }_{16m_s^2}^{s_0}{e}^{-s/M_B^2}ds\times \left[\frac{⟨g_s^{2}GG⟩}{40960{\pi }^6}{s}^2-\frac{m_s^2⟨g_s^{2}GG⟩}{3072{\pi }^6}s+\frac{⟨g_s^{2}GG⟩m_s⟨\bar{s}s⟩}{2304{\pi }^4}\right]\hfill \\ \hfill & \hfill & +\frac{1}{M_B^2}\left(-\frac{⟨g_s^{2}GG⟩m_s^2{⟨\bar{s}s⟩}^2}{1152{\pi }^2}\right),\hfill \end{array}(23)$

$\begin{array}{ll}\hfill {\mathrm{\Pi }}_{13}& ={\int }_{16m_s^2}^{s_0}{e}^{-s/M_B^2}ds\times \left[-\frac{m_s^2}{960{\pi }^6}{s}^3+\frac{m_s⟨\bar{s}s⟩}{32{\pi }^4}{s}^2+\left(\frac{5m_s⟨g_s\bar{s}\sigma Gs⟩}{96{\pi }^4}+\frac{⟨g_s^{2}GG⟩m_s^2}{2304{\pi }^6}-\frac{{⟨\bar{s}s⟩}^2}{9{\pi }^2}\right)s\right.\hfill \\ \hfill & \left.-\frac{⟨g_s^{2}GG⟩m_s⟨\bar{s}s⟩}{384{\pi }^4}+\frac{2m_s^2{⟨\bar{s}s⟩}^2}{3{\pi }^2}-\frac{5⟨\bar{s}s⟩⟨g_s\bar{s}\sigma Gs⟩}{48{\pi }^2}\right],\hfill \\ \hfill & +\left(\frac{⟨g_s^{2}GG⟩{⟨\bar{s}s⟩}^2}{432{\pi }^2}-\frac{⟨g_s^{2}GG⟩m_s⟨g_s\bar{s}\sigma Gs⟩}{1152{\pi }^4}\right)+\frac{1}{M_B^2}\left(\frac{{⟨\bar{s}s⟩}^2{m}_s⟨g_s\bar{s}\sigma Gs⟩}{2}-\frac{5m_s^2{⟨g_s\bar{s}\sigma Gs⟩}^2}{48{\pi }^2}\right),\hfill \end{array}(24)$

$\begin{array}{ll}\hfill {\mathrm{\Pi }}_{23}& ={\int }_{16m_s^2}^{s_0}{e}^{-s/M_B^2}ds\times [\left(\frac{m_s⟨g_s\bar{s}\sigma Gs⟩}{96{\pi }^4}-\frac{⟨g_s^{2}GG⟩m_s^2}{768{\pi }^6}\right)s+\frac{⟨g_s^{2}GG⟩m_s⟨\bar{s}s⟩}{128{\pi }^4}-\frac{⟨\bar{s}s⟩⟨g_s\bar{s}\sigma Gs⟩}{48{\pi }^2}]\hfill \\ \hfill & +\left(\frac{⟨g_s^{2}GG⟩m_s⟨g_s\bar{s}\sigma Gs⟩}{384{\pi }^4}-\frac{⟨g_s^{2}GG⟩{⟨\bar{s}s⟩}^2}{144{\pi }^2}\right)+\frac{1}{M_B^2}\left(\frac{{⟨\bar{s}s⟩}^2{m}_s⟨g_s\bar{s}\sigma Gs⟩}{18}-\frac{m_s^2{⟨g_s\bar{s}\sigma Gs⟩}^2}{48{\pi }^2}\right).\hfill \end{array}(25)$

For completeness, we have calculated both the diagonal and off-diagonal correlation functions. We shall investigate them using two steps, the single-channel analysis and the multi-channel analysis, in the following sections.

4 Single-channel analysis

In this section, we perform the single-channel analysis. To perform this, we simply neglect the off-diagonal correlation functions; i.e., we assume ρ_ij(s)|_i≠j = 0 so that only ρ_ii(s) ≠ 0. Under this assumption, any two of the three currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ cannot mainly couple to the same state X; otherwise,

$\begin{array}{ll}\hfill {\rho }_{ij}\left(s\right)& \times {\mathcal{S}}^{\prime }\left[{\tilde{g}}^{\mu {\mu }^{\prime }}{\tilde{g}}^{\nu {\nu }^{\prime }}\right]\hfill \\ \hfill & =\sum _n\delta \left(s-M_n^2\right)\langle 0|{\eta }_i^{\mu \nu }|X_n\rangle \langle X_n|{\eta }_j^{{\mu }^{\prime }{\nu }^{\prime },†}|0\rangle +\cdots \hfill \\ \hfill & \approx \delta \left(s-M_X^2\right)\langle 0|{\eta }_i^{\mu \nu }|X\rangle \langle X|{\eta }_j^{{\mu }^{\prime }{\nu }^{\prime },†}|0\rangle +\cdots \hfill \\ \hfill & \ne 0.\hfill \end{array}(26)$

This allows us to further assume that the three currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ couple separately to the three states X_1,2,3 through

$⟨0|{\eta }_i^{\mu \nu }|X_j⟩=f_{ij}{ϵ}^{\mu \nu },(27)$

with f_ii ≠ 0 and f_ij = 0 for i, j = 1⋯3 and i ≠ j.

Now, we can parameterize the diagonal spectral density ρ_ii(s) as one-pole dominance for the state X_i and a continuum contribution. This simplifies Eq. 19 to be

${\mathrm{\Pi }}_{ii}\left(s_0,M_B^2\right)=f_{ii}^2{e}^{-M_i^2/M_B^2}={\int }_{s_{<}}^{s_0}{e}^{-s/M_B^2}{\rho }_{ii}\left(s\right)ds.(28)$

It can be used to calculate M_i through

$M_i^2\left(s_0,M_B\right)=\frac{{\int }_{s_{<}}^{s_0}{e}^{-s/M_B^2}s{\rho }_{ii}\left(s\right)ds}{{\int }_{s_{<}}^{s_0}{e}^{-s/M_B^2}{\rho }_{ii}\left(s\right)ds}.(29)$

We use the spectral density ρ₁₁(s) given in Eq. 20 as an example to perform the single-channel numerical analysis. We take the following values for various sum rule parameters [1, 47–53]:

$\begin{array}{ccc}\hfill m_s\left(2\mathrm{G}\mathrm{e}\mathrm{V}\right)& =\hfill & 93_{-5}^{+11}\mathrm{M}\mathrm{e}\mathrm{V},\hfill \\ \hfill ⟨g_s^{2}GG⟩& =\hfill & \left(0.48\pm 0.14\right){\mathrm{G}\mathrm{e}\mathrm{V}}^4,\hfill \\ \hfill \langle \bar{s}s\rangle & =\hfill & -\left(0.8\pm 0.1\right)\times {\left(0.240\text{\hspace{0.17em}GeV}\right)}^3,\hfill \\ \hfill ⟨g_s\bar{s}\sigma Gs⟩& =\hfill & -M_0^2\times \langle \bar{s}s\rangle ,\hfill \\ \hfill M_0^2& =\hfill & \left(0.8\pm 0.2\right){\mathrm{G}\mathrm{e}\mathrm{V}}^2.\hfill \end{array}(30)$

Equation 29 states that mass M₁ depends on two free parameters, the threshold value s₀, and the Borel mass M_B. We consider three aspects to determine their working regions: a) the convergence of OPE, b) the sufficient amount of pole contribution, and c) the stability of the mass dependence on these two parameters.

First, we investigate the convergence of OPE, which is the cornerstone of a reliable QCD sum rule analysis. We require the D = 12/10/8 terms to be less than 5%/10%/20%, respectively.

${\text{CVG}}_{12}=\left|\frac{{\mathrm{\Pi }}_{11}^{D=12}\left(\infty ,M_B^2\right)}{{\mathrm{\Pi }}_{11}\left(\infty ,M_B^2\right)}\right|\le 5\%,(31)$

${\text{CVG}}_{10}=\left|\frac{{\mathrm{\Pi }}_{11}^{D=10}\left(\infty ,M_B^2\right)}{{\mathrm{\Pi }}_{11}\left(\infty ,M_B^2\right)}\right|\le 10\%,(32)$

${\text{CVG}}_8=\left|\frac{{\mathrm{\Pi }}_{11}^{D=8}\left(\infty ,M_B^2\right)}{{\mathrm{\Pi }}_{11}\left(\infty ,M_B^2\right)}\right|\le 20\%.(33)$

Figure 2 shows that through the dashed curves, the lower bound of the Borel mass is determined to be $M_B^2\ge 1.53$ GeV².

FIGURE 2

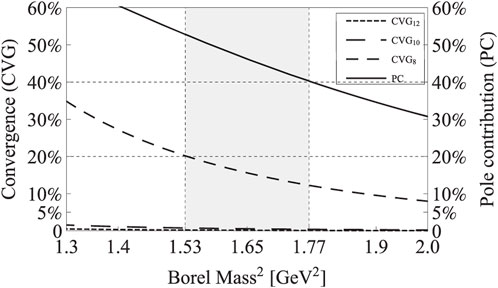
FIGURE 2. CVG_12/10/8 and PC with respect to the Borel mass M_B. These curves are obtained using the spectral density ρ₁₁(s) given in Eq. 20, when setting s₀=6.5 GeV².

Second, we investigate the one-pole-dominance assumption by requiring the pole contribution to be larger than 40%:

$\text{Pole\hspace{0.17em}Contribution\hspace{0.17em}}\left(\text{PC}\right)=\left|\frac{{\mathrm{\Pi }}_{11}\left(s_0,M_B^2\right)}{{\mathrm{\Pi }}_{11}\left(\infty ,M_B^2\right)}\right|\ge 40\%.(34)$

Figure 2 shows that through the solid curve, the upper bound of the Borel mass is determined to be $M_B^2\le 1.77$ GeV² when setting s₀ = 6.5 GeV². Altogether, we determine the Borel window to be 1.53 ${\mathrm{G}\mathrm{e}\mathrm{V}}^2\le M_B^2\le 1.77$ GeV² for s₀ = 6.5 GeV². We redo the same procedures and find that there are non-vanishing Borel windows when $s_0\ge s_0^{\text{min}}=5.4$ GeV².

Third, we investigate the stability of the mass dependence on s₀ and M_B. As shown in Figure 3, we find a mass minimum around s₀ ≈ 3 GeV², and the mass dependence on s₀ is moderate inside the region 5.5 GeV² ≤ s₀ ≤ 7.5 GeV². As shown in Figure 4, the mass dependence on M_B is rather weak inside the Borel window 1.53 ${\mathrm{G}\mathrm{e}\mathrm{V}}^2\le M_B^2\le 1.77$ GeV².

FIGURE 3

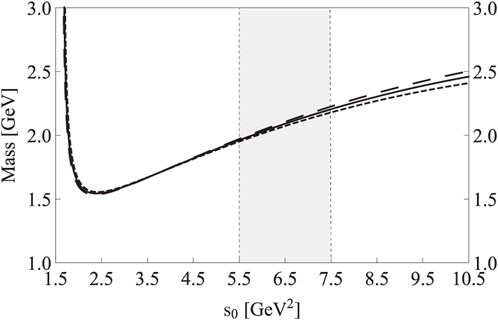
FIGURE 3. Mass M₁ of the state X₁ with respect to the threshold value s₀. Short-dashed/solid/long-dashed curves are obtained by setting $M_B^2=1.53/1.65/1.77$ GeV², respectively. These curves are obtained using the spectral density ρ₁₁(s) given in Eq. 20.

FIGURE 4

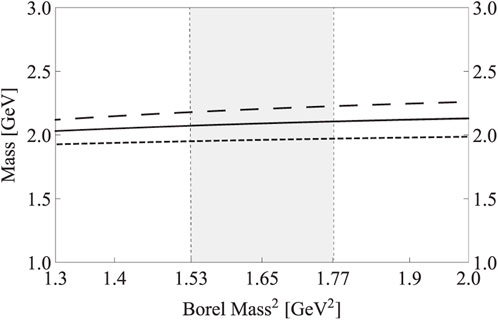
FIGURE 4. Mass M₁ of the state X₁ with respect to the Borel mass M_B. Short-dashed/solid/long-dashed curves are obtained by setting s₀=5.5/6.5/7.5 GeV², respectively. These curves are obtained using the spectral density ρ₁₁(s) given in Eq. 20.

Altogether, we determine our working regions to be 5.5 GeV² ≤ s₀ ≤ 7.5 GeV² and 1.53 ${\mathrm{G}\mathrm{e}\mathrm{V}}^2\le M_B^2\le 1.77$ GeV², where the mass of X₁ is calculated to be

$M_1=2.09_{-0.22}^{+0.19}\mathrm{G}\mathrm{e}\mathrm{V}.(35)$

Its central value is obtained by setting s₀ = 6.5 GeV² and $M_B^2=1.65$ GeV², and its uncertainty is due to the Borel mass M_B, the threshold value s₀, and various sum rule parameters listed in Eq. 30.

We follow the same procedures to study the other two currents, ${\eta }_2^{\mu \nu }$ and ${\eta }_3^{\mu \nu }$, separately. The obtained results are shown in Table 1. We shall further study the three currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ as a whole and perform the multi-channel analysis in the next section.

TABLE 1

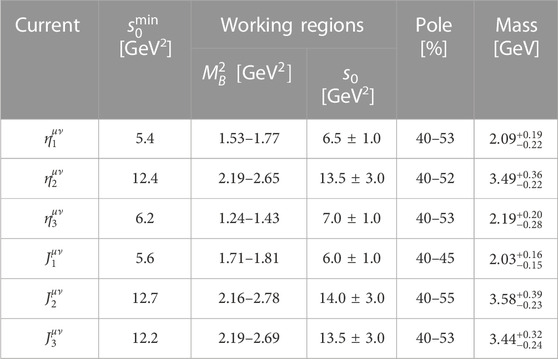
TABLE 1. QCD sum rule results for the fully strange tetraquark states with the quantum number J^PC =2⁺⁺, extracted from the diquark–antidiquark currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ and their mixing currents $J_{\mathrm{1,2,3}}^{\mu \nu }$.

5 Multi-channel analyses

In this section, we perform the multi-channel analyses. To perform this, we do not neglect the off-diagonal correlation functions any more, i.e., ρ_ij(s)|_i≠j ≠ 0. When setting s₀ = 6.0 GeV² and $M_B^2=1.76$ GeV², the 3 × 3 matrix ${\mathrm{\Pi }}_{ij}(s_0,M_B^2)$ becomes

${\mathrm{\Pi }}_{ij}\left(s_0,M_B^2\right)=\left(\begin{array}{ccc}\hfill 2.16\hfill & \hfill 0.08\hfill & \hfill -3.20\hfill \\ \hfill 0.08\hfill & \hfill -1.85\hfill & \hfill 0.45\hfill \\ \hfill -3.20\hfill & \hfill 0.45\hfill & \hfill 1.02\hfill \end{array}\right)\times 10^{-6}{\mathrm{G}\mathrm{e}\mathrm{V}}^{14}.(36)$

Therefore, ${\eta }_1^{\mu \nu }$ and ${\eta }_3^{\mu \nu }$ are strongly correlated with each other, and the off-diagonal terms are indeed non-negligible.

In order to diagonalize the 3 × 3 matrix ${\mathrm{\Pi }}_{ij}(s_0,M_B^2)$, we construct three mixing currents $J_{\mathrm{1,2,3}}^{\mu \nu }$

$\left(\begin{array}{c}\hfill J_1^{\mu \nu }\hfill \\ \hfill J_2^{\mu \nu }\hfill \\ \hfill J_3^{\mu \nu }\hfill \end{array}\right)={\mathbb{T}}_{3\times 3}\left(\begin{array}{c}\hfill {\eta }_1^{\mu \nu }\hfill \\ \hfill {\eta }_2^{\mu \nu }\hfill \\ \hfill {\eta }_3^{\mu \nu }\hfill \end{array}\right),(37)$

where ${\mathbb{T}}_{3\times 3}$ is the transition matrix.

We use ${\mathrm{\Pi }}_{ij}^{\prime }(s_0,M_B^2)$ to denote the correlation functions extracted from the mixing currents $J_{\mathrm{1,2,3}}^{\mu \nu }$. This 3 × 3 matrix becomes

${\mathrm{\Pi }}_{ij}^{\prime }\left(s_0,M_B^2\right)=\left(\begin{array}{ccc}\hfill 4.85\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -2.17\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1.35\hfill \end{array}\right)\times 10^{-6}{\mathrm{G}\mathrm{e}\mathrm{V}}^{14},(38)$

when setting

${\mathbb{T}}_{3\times 3}=\left(\begin{array}{ccc}\hfill 0.76\hfill & \hfill -0.03\hfill & \hfill -0.64\hfill \\ \hfill -0.38\hfill & \hfill 0.79\hfill & \hfill -0.49\hfill \\ \hfill 0.52\hfill & \hfill 0.61\hfill & \hfill 0.59\hfill \end{array}\right),(39)$

as well as s₀ = 6.0 GeV² and $M_B^2=1.76$ GeV². Therefore, the off-diagonal terms of ${\mathrm{\Pi }}_{ij}^{\prime }(s_0,M_B^2)$ are negligible, and the three mixing currents $J_{\mathrm{1,2,3}}^{\mu \nu }$ are nearly non-correlated around here. Moreover, the two correlation functions, ${\mathrm{\Pi }}_{22}^{\prime }(s_0,M_B^2)$ and ${\mathrm{\Pi }}_{33}^{\prime }(s_0,M_B^2)$, are both negative around s ≈ 6.0 GeV². This suggests that they are both non-physical around here, and the masses extracted from them should be significantly larger than $\sqrt{6.0}$ GeV $\approx 2.5$ GeV.

Now, we can use the procedures applied in the previous section on the currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ to study their mixing currents $J_{\mathrm{1,2,3}}^{\mu \nu }$. The obtained results are shown in Table 1. Particularly, the mass extracted from the current $J_1^{\mu \nu }$ is

$M_1^{\prime }=2.03_{-0.15}^{+0.16}\mathrm{G}\mathrm{e}\mathrm{V},(40)$

as shown in Figures 5, 6 with respect to the threshold value s₀ and the Borel mass M_B.

FIGURE 5

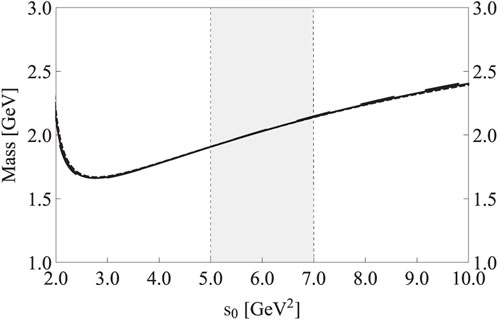
FIGURE 5. Mass $M_1^{\prime }$ of the state $X_1^{\prime }$ with respect to the threshold value s₀. Short-dashed/solid/long-dashed curves are obtained by setting $M_B^2=1.71/1.76/1.81$ GeV², respectively. These curves are obtained using the spectral density ${\rho }_{11}^{\prime }(s)$ extracted from the mixing current $J_1^{\mu \nu }$.

FIGURE 6

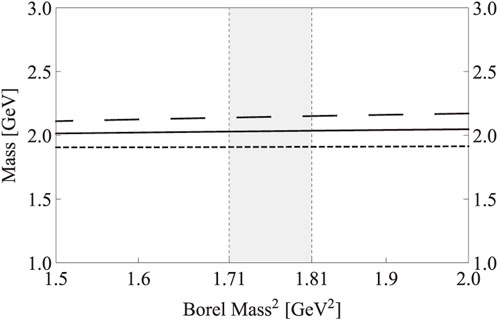
FIGURE 6. Mass $M_1^{\prime }$ of the state $X_1^{\prime }$ with respect to the Borel mass M_B. Short-dashed/solid/long-dashed curves are obtained by setting s₀=5.0/6.0/7.0 GeV², respectively. These curves are obtained using the spectral density ${\rho }_{11}^{\prime }(s)$ extracted from the mixing current $J_1^{\mu \nu }$.

6 Summary and discussions

In this paper, we use the QCD sum rule method to study the fully strange tetraquark states with the quantum number J^PC = 2⁺⁺. We systematically construct their interpolating currents and find three independent diquark–antidiquark currents, denoted as ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$. We calculate both their diagonal and off-diagonal correlation functions. Based on the obtained results, we construct three mixing currents that are nearly non-correlated and denoted as $J_{\mathrm{1,2,3}}^{\mu \nu }$. We use both the diquark–antidiquark currents ${\eta }_{\mathrm{1,2,3}}^{\mu \nu }$ and the mixing currents $J_{\mathrm{1,2,3}}^{\mu \nu }$ to perform QCD sum rule analyses. The obtained results are shown in Table 1.

Particularly, we use the mixing current $J_1^{\mu \nu }$ to evaluate the mass of the lowest-lying state to be $2.03_{-0.15}^{+0.16}$ GeV, while the masses extracted from the other two mixing currents, $J_2^{\mu \nu }$ and $J_3^{\mu \nu }$, are significantly larger than 3.0 GeV. The fully strange tetraquark states of J^PC = 2⁺⁺ naturally decay into the ϕϕ channel, where the BESIII collaboration observed three tensor resonances, namely, f₂(2010), f₂(2300), and f₂(2340) [23]. Accordingly, our results suggest that the f₂(2010) can be explained as the fully strange tetraquark state of J^PC = 2⁺⁺, while it is not easy to interpret the f₂(2300) and f₂(2340) as such states.

In this paper, we also systematically construct the fully strange mesonic–mesonic currents of J^PC = 2⁺⁺, which can be related to the diquark–antidiquark currents through the Fierz rearrangement. In particular, we can apply Eqs. 37 and 39, and Eq. 14 to transform the mixing current $J_1^{\mu \nu }$ to be

$J_1^{\mu \nu }=-1.04{\xi }_1^{\mu \nu }-0.25{\xi }_2^{\mu \nu }+0.37{\xi }_3^{\mu \nu }.(41)$

This Fierz identity suggests that the lowest-lying state dominantly decays into the S-wave ϕ(1020)ϕ(1020) channel through the mesonic–mesonic current ${\xi }_1^{\mu \nu }$, while it can also decay into the D-wave η⁽′⁾η⁽′⁾ channel through ${\xi }_2^{\mu \nu }$. Accordingly, we propose to confirm the f₂(2010) in the η⁽′⁾η⁽′⁾ channel in the future Belle-II, BESIII, COMPASS, GlueX, and PANDA experiments. In addition, more possible decay patterns can be obtained by annihilating an $s\bar{s}$ pair into a gluon, which then transits into the final states with a pair of strange mesons, such as $K\bar{K}$.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This project was supported by the National Natural Science Foundation of China under grant no. 12075019, the Jiangsu Provincial Double-Innovation Program under grant no. JSSCRC2021488, and the Fundamental Research Funds for the Central Universities.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zyla PA, Barnett RM, Beringer J, Dahl O, Dwyer DA, Groom DE, et al. Review of particle physics. PTEP (2020) 2020(8):083C01. doi:10.1093/ptep/ptaa104

CrossRef Full Text | Google Scholar

2. Chen H-X, Chen W, Liu X, Zhu S-L. The hidden-charm pentaquark and tetraquark states. Phys Rept (2016) 639:1–121. doi:10.1016/j.physrep.2016.05.004

CrossRef Full Text | Google Scholar

3. Liu Y-R, Chen H-X, Chen W, Liu X, Zhu S-L. Pentaquark and tetraquark states. Prog Part Nucl Phys (2019) 107:237–320. doi:10.1016/j.ppnp.2019.04.003

CrossRef Full Text | Google Scholar

4. Chen H-X, Chen W, Liu X, Liu Y-R, Zhu S-L. An updated review of the new hadron states. Rept Prog Phys (2023) 86(2):026201. doi:10.1088/1361-6633/aca3b6

CrossRef Full Text | Google Scholar

5. Lebed RF, Mitchell RE, Swanson ES. Heavy-quark QCD exotica. Prog Part Nucl Phys (2017) 93:143–94. doi:10.1016/j.ppnp.2016.11.003

CrossRef Full Text | Google Scholar

6. Esposito A, Pilloni A, Polosa AD. Multiquark resonances. Phys Rept (2017) 668:1–97. doi:10.1016/j.physrep.2016.11.002

CrossRef Full Text | Google Scholar

7. Hosaka A, Iijima T, Miyabayashi K, Sakai Y, Yasui S. Exotic hadrons with heavy flavors: X, Y, Z, and related states. PTEP (2016) 2016(6):062C01. doi:10.1093/ptep/ptw045

CrossRef Full Text | Google Scholar

8. Guo F-K, Hanhart C, Meißner U-G, Wang Q, Zhao Q, Zou B-S. Hadronic molecules. Rev Mod Phys (2018) 90(1):015004. doi:10.1103/RevModPhys.90.015004

CrossRef Full Text | Google Scholar

9. Ali A, Lange JS, Stone S. Exotics: Heavy pentaquarks and tetraquarks. Prog Part Nucl Phys (2017) 97:123–98. doi:10.1016/j.ppnp.2017.08.003

CrossRef Full Text | Google Scholar

10. Olsen SL, Skwarnicki T, Zieminska D. Nonstandard heavy mesons and baryons: Experimental evidence. Rev Mod Phys (2018) 90(1):015003. doi:10.1103/RevModPhys.90.015003

CrossRef Full Text | Google Scholar

11. Karliner M, Rosner JL, Skwarnicki T. Multiquark states. Ann Rev Nucl Part Sci (2018) 68:17–44. doi:10.1146/annurev-nucl-101917-020902

CrossRef Full Text | Google Scholar

12. Bass SD, Moskal P. η′ and η mesons with connection to anomalous glue. Rev Mod Phys (2019) 91(1):015003. doi:10.1103/RevModPhys.91.015003

CrossRef Full Text | Google Scholar

13. Brambilla N, Eidelman S, Hanhart C, Nefediev A, Shen C-P, Thomas CE, et al. The XYZ states: Experimental and theoretical status and perspectives. Phys Rept (2020) 873:1–154. doi:10.1016/j.physrep.2020.05.001

CrossRef Full Text | Google Scholar

14. Guo F-K, Liu X-H, Sakai S. Threshold cusps and triangle singularities in hadronic reactions. Prog Part Nucl Phys (2020) 112:103757. doi:10.1016/j.ppnp.2020.103757

CrossRef Full Text | Google Scholar

15. Ketzer B, Grube B, Ryabchikov D. Light-meson spectroscopy with COMPASS. Prog Part Nucl Phys (2020) 113:103755. doi:10.1016/j.ppnp.2020.103755

CrossRef Full Text | Google Scholar

16. Yang G, Ping J, Segovia J. Tetra- and penta-quark structures in the constituent quark model. Symmetry (2020) 12(11):1869. doi:10.3390/sym12111869

CrossRef Full Text | Google Scholar

17. Roberts CD, Richards DG, Horn T, Chang L. Insights into the emergence of mass from studies of pion and kaon structure. Prog Part Nucl Phys (2021) 120:103883. doi:10.1016/j.ppnp.2021.103883

CrossRef Full Text | Google Scholar

18. Fang S-S, Kubis B, Kupść A. What can we learn about light-meson interactions at electron-positron colliders? Prog Part Nucl Phys (2021) 120:103884. doi:10.1016/j.ppnp.2021.103884

CrossRef Full Text | Google Scholar

19. Jin S, Shen X. Highlights of light meson spectroscopy at the BESIII experiment. Natl Sci Rev (2021) 8(11):nwab198. doi:10.1093/nsr/nwab198

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Albaladejo M, Bibrzycki L, Dawid SM, Fernandez-Ramirez C, Gonzalez-Solis S, Hiller Blin AN, et al. Novel approaches in hadron spectroscopy (2021). Available at: https://arxiv.org/abs/2112.13436 (Accessed December 26, 2021).

Google Scholar

21. Meng L, Wang B, Wang G-J, Zhu S-L. Chiral perturbation theory for heavy hadrons and chiral effective field theory for heavy hadronic molecules. Available at: https://arxiv.org/abs/2204.08716 (Accessed April 19, 2022).

Google Scholar

22. Brambilla N, Chen H-X, Esposito A, Ferretti J, Francis A, Guo F-K, et al. Substructure of multiquark hadrons (snowmass 2021 white paper). Available at:https://arxiv.org/abs/2203.16583 (Accessed March 30, 2022).

Google Scholar

23. Ablikim M, Achasov M, Ai X, Albayrak O, Albrecht M, Ambrose D, et al. Observation of pseudoscalar and tensor resonances in J/ψ → γϕϕ. Phys Rev D (2016) 93(11):112011. doi:10.1103/PhysRevD.93.112011

CrossRef Full Text | Google Scholar

24. Chen H-X, Liu X, Hosaka A, Zhu S-L. Y(2175) state in the QCD sum rule. Phys Rev D (2008) 78:034012. doi:10.1103/PhysRevD.78.034012

CrossRef Full Text | Google Scholar

25. Chen H-X, Hosaka A, Zhu S-L. I^GJ^PC = 1⁻1⁻⁺ tetraquark states. Phys Rev D (2008) 78:054017. doi:10.1103/PhysRevD.78.054017

CrossRef Full Text | Google Scholar

26. Chen H-X, Hosaka A, Zhu S-L. I^GJ^PC = 0⁺1⁻⁺ tetraquark states. Phys Rev D (2008) 78:117502. doi:10.1103/PhysRevD.78.117502

CrossRef Full Text | Google Scholar

27. Chen H-X, Shen C-P, Zhu S-L. Possible partner state of the Y(2175). Phys Rev D (2018) 98(1):014011. doi:10.1103/PhysRevD.98.014011

CrossRef Full Text | Google Scholar

28. Cui E-L, Yang H-M, Chen H-X, Chen W, Shen C-P. QCD sum rule studies of $$s s {\bar{s}} {\bar{s}}$$ s s s ¯ s ¯ tetraquark states with $$J^{PC} = 1^{+-}$$ J PC = 1 + -s s {\bar{s}} {\bar{s}} tetraquark states with J^PC = 1⁺⁻. Eur Phys J C (2019) 79(3):232. doi:10.1140/epjc/s10052-019-6755-y

CrossRef Full Text | Google Scholar

29. Dong R-R, Su N, Chen H-X, Cui E-L, Zhou Z-Y. QCD sum rule studies on the $$s s {\bar{s}} {\bar{s}}$$ tetraquark states of $$J^{PC} = 0^{-+}$$s s \bar{s} \bar{s} tetraquark states of J^PC = 0⁻⁺. Eur Phys J C (2020) 80(8):749. doi:10.1140/epjc/s10052-020-8340-9

CrossRef Full Text | Google Scholar

30. Dong R-R, Su N, Chen H-X. Highly excited and exotic fully-strange tetraquark states. Eur Phys J C (2022) 82(11):983. doi:10.1140/epjc/s10052-022-10955-0

CrossRef Full Text | Google Scholar

31. Chen H-X, Chen W, Liu X, Liu X-H. Establishing the first hidden-charm pentaquark with strangeness. Eur Phys J C (2021) 81(5):409. doi:10.1140/epjc/s10052-021-09196-4

CrossRef Full Text | Google Scholar

32. Chen H-X. Hadronic molecules in B decays. Phys Rev D (2022) 105(9):094003. doi:10.1103/PhysRevD.105.094003

CrossRef Full Text | Google Scholar

33. Wang Z-G. Analysis of as a tetraquark state with QCD sum rules. Nucl Phys A (2007) 791:106–16. doi:10.1016/j.nuclphysa.2007.04.012

CrossRef Full Text | Google Scholar

34. Wang Z-G. Light tetraquark state candidates. Adv High Energ Phys. (2020) 2020:1–7. doi:10.1155/2020/6438730

CrossRef Full Text | Google Scholar

35. Agaev SS, Azizi K, Sundu H. Nature of the vector resonance Y(2175). Phys Rev D (2020) 101(7):074012. doi:10.1103/PhysRevD.101.074012

CrossRef Full Text | Google Scholar

36. Azizi K, Agaev SS, Sundu H. Light axial-vector and vector resonances X(2100) and X(2239. Nucl Phys B (2019) 948:114789. doi:10.1016/j.nuclphysb.2019.114789

CrossRef Full Text | Google Scholar

37. Pimikov AV. Nonlocal gluon condensates in QCD sum rules. Phys Rev D (2022) 106(5):056011. doi:10.1103/PhysRevD.106.056011

CrossRef Full Text | Google Scholar

38. Liu F-X, Liu M-S, Zhong X-H, Zhao Q. Fully-strange tetraquark ss\bar{s}\bar{s} spectrum and possible experimental evidence. Phys Rev D (2021) 103(1):016016. doi:10.1103/PhysRevD.103.016016

CrossRef Full Text | Google Scholar

39. Lü Q-F, Wang K-L, Dong Y-B. The tetraquark states and the structure of X(2239) observed by the BESIII collaboration *ss \bar{s} \bar{s} tetraquark states and the newly observed structure X(2239) by BESIII Collaboration. Chin Phys C (2020) 44(2):024101. doi:10.1088/1674-1137/44/2/024101

CrossRef Full Text | Google Scholar

40. Deng C, Ping J, Wang F, Goldman T. Tetraquark state and multibody interaction. Phys Rev D (2010) 82:074001. doi:10.1103/PhysRevD.82.074001

CrossRef Full Text | Google Scholar

41. Drenska NV, Faccini R, Polosa AD. Higher tetraquark particles. Phys Lett B (2008) 669:160–6. doi:10.1016/j.physletb.2008.09.038

CrossRef Full Text | Google Scholar

42. Ebert D, Faustov RN, Galkin VO. Masses of light tetraquarks and scalar mesons in the relativistic quark model. Eur Phys J C (2009) 60:273–8. doi:10.1140/epjc/s10052-009-0925-2

CrossRef Full Text | Google Scholar

43. Su N, Chen H-X. S- and P-wave fully strange tetraquark states from QCD sum rules. Phys Rev D (2022) 106(1):014023. doi:10.1103/PhysRevD.106.014023

CrossRef Full Text | Google Scholar

44. Shifman MA, Vainshtein AI, Zakharov VI. QCD and resonance physics. theoretical foundations. Nucl Phys B (1979) 147:385–447. doi:10.1016/0550-3213(79)90022-1

CrossRef Full Text | Google Scholar

45. Reinders LJ, Rubinstein H, Yazaki S. Hadron properties from QCD sum rules. Phys Rept (1985) 127:1–97. doi:10.1016/0370-1573(85)90065-1

CrossRef Full Text | Google Scholar

46. Lucha W, Melikhov D, Sazdjian H. Tetraquark-adequate formulation of QCD sum rules. Phys Rev D (2019) 100(1):014010. doi:10.1103/PhysRevD.100.014010

CrossRef Full Text | Google Scholar

47. Yang K-C, Hwang WYP, Henley EM, Kisslinger LS. QCD sum rules and neutron-proton mass difference. Phys Rev D (1993) 47:3001–12. doi:10.1103/PhysRevD.47.3001

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Narison S. QCD as a theory of hadrons: From partons to confinement. Oxford, UK: Oxford University Press (2005).

Google Scholar

49. Gimenez V, Lubicz V, Mescia F, Porretti V, Reyes J. Operator product expansion and quark condensate from lattice QCD in coordinate space. Eur Phys J C (2005) 41:535–44. doi:10.1140/epjc/s2005-02250-9

CrossRef Full Text | Google Scholar

50. Jamin M. Flavour-symmetry breaking of the quark condensate and chiral corrections to the Gell-Mann–Oakes–Renner relation. Phys Lett B (2002) 538:71–6. doi:10.1016/S0370-2693(02)01951-2

CrossRef Full Text | Google Scholar

51. Ioffe BL, Zyablyuk KN. Gluon condensate in charmonium sum rules with three-loop corrections. Eur Phys J C (2003) 27:229–41. doi:10.1140/epjc/s2002-01099-8

CrossRef Full Text | Google Scholar

52. Ovchinnikov AA, Pivovarov AA. QCD sum rule calculation of the quark gluon condensate. Sov J Nucl Phys (1988) 48:721–3.

Google Scholar

53. Ellis JR, Gardi E, Karliner M, Samuel MA. Renormalization-scheme dependence of Padé summation in QCD. Phys Rev D (1996) 54:6986–96. doi:10.1103/PhysRevD.54.6986

PubMed Abstract | CrossRef Full Text | Google Scholar