The simulation of terahertz waves transmission in the arc plasma

The diagnostic of high-density hot plasma is a challenging task due to its high temperature and electron density. Arc plasma is one of the typical hot density plasmas, and its diagnosis is the key to develop its new applications. In this paper, the temperature and density distributions of welding plasmas with different discharge currents are numerically simulated based on a Tungsten Inert Gas Arc Welding model, and the electron density distributions are calculated. Then propagation properties of broadband terahertz (THz) waves in the modeling arc jets are calculated by the finite difference time domain method. These results not only provide a preliminary theoretical guidance for in-depth understanding the problems of blackout in re-entry communication, but also develop a new idea for the terahertz diagnostic of plasma with high density.

1 Introduction

There is increasing attention to arc discharge due to its wide range of applications, including arc welding [1, 2], spray coating [3, 4], materials processing [5], arc lamp [6], and some emerging applications: synthesis of graphene [7, 8] and other Nano-Materials [9]. In order to make better use of arc discharge to develop new applications, it is important to learn the plasma properties, especially the electron density and temperature [10, 11]. Generally, the electron density of arc discharge ranges from 10¹³ to 10¹⁸ cm⁻³, and the gas temperature exceeds 1000 K [12, 13], which makes it difficult to measure the electron density and temperature. The most frequently used techniques for determining the electron density are optical diagnostics, including Thomson scattering method, continuum radiation, atomic line Stark broadening, and so on [12, 14, 15]. Microwave diagnostic [16–21] is an effective method to measure various plasmas with plasma density below 10¹³ cm⁻³, however, it is invalid to measure the plasma of higher density due to the limited frequency of microwave [22].

In the past two decades, researchers have made significant efforts in the generation and detection of terahertz radiation [23], which has made it widely used in various scenarios: material characterization, terahertz imaging, terahertz microscopy for biological and medical applications, terahertz communication, and so on [24–27]. Among these applications, THz spectroscopy is a versatile technique that can also be employed in the characterization of chemistry and its evolution in plasma processing systems [28]. And some studies about THz waves in plasmas have been performed by a few groups. Yuan et al. studied the propagation characteristics of broadband THz waves in atmospheric pressure microplasma [29, 30], magnetized plasma [31], and thermal plasma [32] by theoretical analysis and numerical simulation. Zheng et al. studied the propagation properties of THz wave in unmagnetized plasma with the ZT-FDTD (Z-Transform Finite Difference Time Domain) method and experimental method [33]. Tian investigated the absorption spectra of THz wave in plasma with inhomogeneous collision frequency [34]. Wang and Cao discussed the propagation properties of THz waves through a dusty plasma slab, respectively [35, 36]. Zhao investigated the THz wave absorption by a preformed plasma created by a laser pulse [37]. Jiang employed the terahertz time-domain spectroscopy to characterize the electron density of inductively-coupled argon plasmas [38]. Guo theoretically analyzed the propagation properties of THz wave in a magnetized plasma with inhomogeneous electron density and collision frequency [39]. Curcio performed the experiment of laser-produced plasma diagnostics with wideband terahertz pulses [40]. Ouaras used a broadband CW-terahertz spectroscopy to characterize reactive plasmas [28]. In conclusion, more and more research work is trying to study the propagation properties and applications of THz waves in various plasmas.

In this paper, Tungsten Inert Gas (TIG) Arc Welding, an arc discharge plasma model is established, and the temperature and density distributions are simulated. Then the propagation properties of broadband THz wave in this plasma are studied by finite difference time domain method.

2 Numerical model

2.1 Governing equations

Tungsten Inert Gas Arc Welding is an arc discharge device using pure tungsten or activated tungsten (such as thorium tungsten) as a non-melting electrode and an inert gas such as argon or helium as a shielding gas. In this paper, the cathode is made of tungsten, the anode is made of copper and high purity argon is used as the shielding gas. In order to make the problem simple and straightforward, only the firstly ionized argon ions are considered here, and the following particles exist in the arc system: Ar, Ar⁺, and e.

The governing equations for simulating the arc column region of the argon arc plasmas can be expressed as follows [41, 42]:

(1) Mass continuity equation:

$\frac{\partial }{\partial z}\left(\rho v_{\mathrm{z}}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r\rho v_{\mathrm{r}}\right)=0(1)$

where ρ is the total mass density of argon plasmas, v_z and v_r are the axial and radial components of the plasma velocity.

(2) Momentum conservation equations:

$\frac{\partial }{\partial z}\left(\rho v_{\mathrm{z}}^2\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r\rho v_{\mathrm{r}}{v}_{\mathrm{z}}\right)=-\frac{\partial p}{\partial z}+\frac{\partial }{\partial z}\left(2\mu \frac{\partial v_{\mathrm{z}}}{\partial z}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left[\mu r\left(\frac{\partial v_z}{\partial r}+\frac{\partial v_{\mathrm{r}}}{\partial z}\right)\right]+j_{\mathrm{r}}{B}_{\mathrm{\theta }}$

$\frac{\partial }{\partial z}\left(\rho v_{\mathrm{z}}{v}_{\mathrm{r}}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r\rho v_{\mathrm{r}}^2\right)=-\frac{\partial p}{\partial r}+\frac{\partial }{\partial z}\left[\mu \left(\frac{\partial v_{\mathrm{r}}}{\partial z}+\frac{\partial v_{\mathrm{z}}}{\partial r}\right)\right]+\frac{1}{r}\frac{\partial }{\partial r}\left(2\mu r\frac{\partial v_{\mathrm{r}}}{\partial r}\right)-\frac{2\mu v_{\mathrm{r}}}{r^2}-j_{\mathrm{z}}{B}_{\mathrm{\theta }}(2)$

where p is the operating pressure, ρ and μ are the mass density and viscosity of argon plasmas, B_θ is the circumferential component of the self-induced magnetic induction intensity, while j_z and j_r are the axial and radial components of the total current density.

(3) Energy conservation equation:

$\frac{\partial }{\partial z}\left(\rho h{v}_{\mathrm{z}}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r\rho h{v}_{\mathrm{r}}\right)=\frac{\partial }{\partial z}\left(\lambda \frac{\partial T}{\partial z}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(\lambda r\frac{\partial T}{\partial r}\right)+\overrightarrow{j}\cdot \stackrel{\rightharpoonup }{E}(3)$

Where h is the specific enthalpy of the plasma and λ is the thermal conductivity, $\stackrel{\rightharpoonup }{j}$ is the total current density vector, and $\overrightarrow{E}$ is the electric field.

(4) Poisson equation:

$\frac{\partial }{\partial z}\left(\sigma \frac{\partial \phi }{\partial x}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(\sigma r\frac{\partial \phi }{\partial r}\right)=0(4)$

Where $\sigma$ is the electric conductivity and φ is the electric potential of the plasma.

The number densities of each species are calculated based on the charge neutrality condition (i.e., n_e = $n_{{\mathrm{A}\mathrm{r}}^{+}}$) and the Saha equation [43]:

$\frac{n_{\mathrm{e}}{n}_{{\mathrm{A}\mathrm{r}}^{+}}}{n_{\mathrm{A}\mathrm{r}}}=\frac{2Z_{{\mathrm{A}\mathrm{r}}^{+}}\left(T\right)}{Z_{\mathrm{A}\mathrm{r}}\left(T\right)}{\left(\frac{2\pi mkT}{h^2}\right)}^{3/2}\exp \left(-\frac{E_1}{kT}\right)(5)$

where, $n_{\mathrm{e}}$, $n_{\mathrm{A}\mathrm{r}}$ and $n_{{\mathrm{A}\mathrm{r}}^{+}}$ are the number densities of electron, Ar and Ar⁺, $E_1$ is the first-order ionization energy of $\mathrm{A}\mathrm{r}$, h and k are Planck constant and Boltzmann constant, respectively. And the values of the constants are: E₁ = 1,1523  kJ/mol, k = 1.38 × 10⁻²³  J/K and h = 6.626 × 10⁻³⁴ J ·s. $Z_{\mathrm{A}\mathrm{r}}\left(T\right)$ and $Z_{{\mathrm{A}\mathrm{r}}^{+}}\left(T\right)$ are the partition functions of Ar and Ar⁺, respectively:

$Z_{\mathrm{A}\mathrm{r}}\left(T\right)=1+60\exp \left(-\frac{162500}{T}\right)+\cdots (6)$

$Z_{{\mathrm{A}\mathrm{r}}^{+}}\left(T\right)=4+2\exp \left(-\frac{2062}{T}\right)+2\exp \left(-\frac{156560}{T}\right)+\cdots (7)$

The pressure of the particles in the arc obeys the Dalton partial pressure equation:

$p={\displaystyle \sum }_j{n}_{j}kT-\Delta p=\left(n_{\mathrm{A}\mathrm{r}}+2n_e\right)kT-\Delta p(8)$

here, n_j—is the density of particle j. And then

$\begin{array}{l}{n}_e^2{Z}_{\mathrm{A}\mathrm{r}}\left(T\right)kT+4Z_{{\mathrm{A}\mathrm{r}}^{+}}\left(T\right)kT{\left(\frac{2\pi mkT}{h^2}\right)}^{3/2}\times \exp \left(-\frac{E_1}{kT}\right)\times n_e\\ =2Z_{{\mathrm{A}\mathrm{r}}^{+}}\left(T\right)p\times {\left(\frac{2\pi mkT}{h^2}\right)}^{3/2}\times \exp \left(-\frac{E_1}{kT}\right)\end{array}(9)$

2.2 Computational domain and simulation results

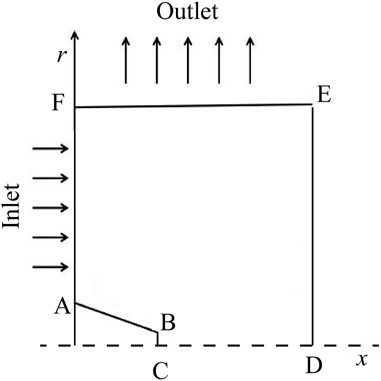
During the arc discharge process, the shielding gas argon is in a flowing state and is at a constant speed 15 L/min. At present, the mainstream software for simulating arc discharge is ANSYS FLUENT. The temperature field distribution, pressure field distribution, velocity field distribution, radiation field distribution, electromagnetic vector distribution and other data can be obtained through simulation. Since the arc discharge plasma is in a local thermodynamic equilibrium state [44–46], the electron temperature, the argon atom temperature, and the argon ion temperature are all the same, and the absolute temperature is in K, and the pressure unit of is in Pa. The schematic diagram of the calculation domain used for the simulation is shown in Figure 1, AF is the inlet and EF is the outlet. CD is the axis of axisymmetry, ABC and DE are the cathode and anode, respectively. The tip radius of the Tungsten electrode is 0.5 mm, and the lengths of the calculation domain along the direction of r and x are both 10 mm.

FIGURE 1

FIGURE 1. The schematic diagram of the numerical simulation.

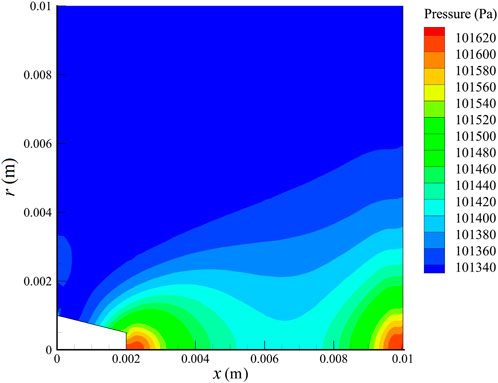
The pressure field distributions under the discharge current of 100 A are shown in Figure 2. As can be seen from Figure 2, the pressure of the arc near the anode and cathode regions is large, and the pressure at a position away from the two regions is reduced. However, the pressure difference is in 0.01 standard atmospheres (<0.01 atm), so the change in pressure gradient will be ignored in the subsequent calculation of electron density.

FIGURE 2

FIGURE 2. 2D distribution of arc pressure under an operating pressure of 1 atm.

The arc temperature distributions of the discharge currents of 100, 150, and 200 A are shown in Figure 3, respectively. From the result, one can see that the arc temperature increases as the discharge current increases, and there is a maximum gradient near the cathode. At 1 mm below the cathode, the arc temperature can reach up to 20,000 K. The arc temperature distribution along the radial direction at 1 mm below the cathode at three different discharge currents is shown in Figure 4. The arc temperature distribution is in good agreement with the experimental results as in Refs. [47, 48].

FIGURE 3

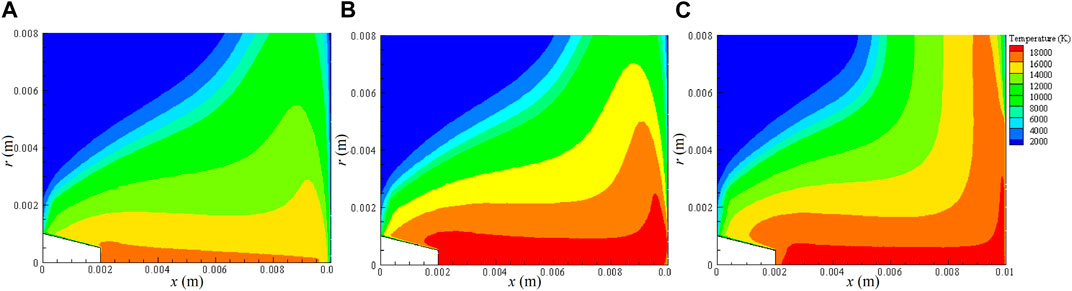
FIGURE 3. The contour plot of arc plasma temperature distribution at discharge current of (A) 100 A, (B) 150 A, and (C) 200 A.

FIGURE 4

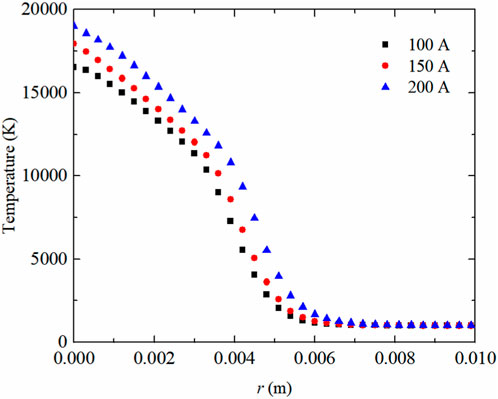
FIGURE 4. Temperature distribution of the arc plasma at the cross section of 1 mm below the cathode at different discharge currents.

According to the results of pressure and temperature distribution, the electron density distribution can be obtained. And the electron density distributions under different currents are shown in Figure 5. The peak value density of plasma reaches the order of 10²³ m⁻³, which is closer to the experimental data [49].

FIGURE 5

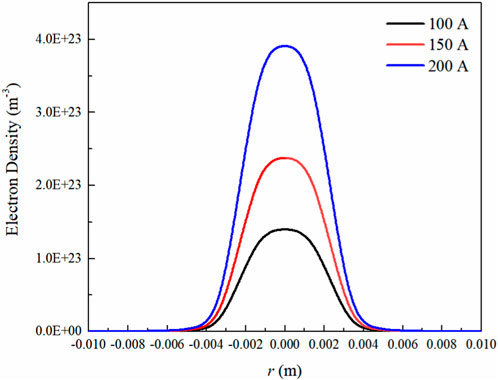
FIGURE 5. Density distribution of arc section at 1 mm below the cathode under different discharge currents.

2.3 The calculation model of THz wave transmission

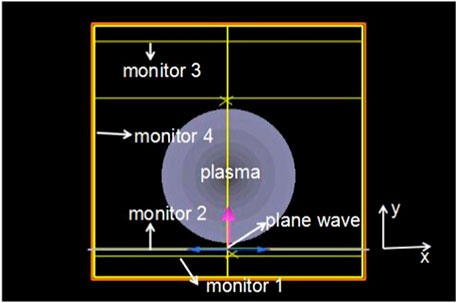
Figure 6 shows the transmission characteristics of terahertz waves in arc plasma simulated by the FDTD method, which is based on a two-dimensional axisymmetric calculation model on the X-Y plane. The plasma region is divided into 11 layers from the center to the outer layer, corresponding to the electron density gradient at 1 mm below the arc tungsten, the outer diameter is 10 mm. The x-direction boundary of the FDTD calculation region is periodic, ensuring that the incident wave is a plane wave, and the y-direction boundary is PML; the mesh is divided into 0.2 μm × 0.2 μm. Then, the THz wave transmission characteristics can be obtained by solving the electromagnetic field equations:

$\left\{\begin{array}{l}\nabla \times \overrightarrow{\mathrm{H}}=\frac{-i\omega }{c}\epsilon \overrightarrow{\mathrm{E}}\\ \nabla \times \overrightarrow{\mathrm{E}}=\frac{i\omega }{c}\mu \overrightarrow{\mathrm{H}}\end{array}\right.(10)$

where the THz wave is assumed to be harmonic, linearly polarized and uniform electromagnetic wave incidents into the plasma, $\epsilon$ and $\mu$ are the permeability and permittivity of the medium. According to the Drude model, the complex permittivity of the plasma is

$\epsilon \left(\omega \right)={\epsilon }_0\left(1-\frac{{\omega }_{\mathrm{p}\mathrm{e}}^2}{\omega \left(\omega -i{\nu }_{\mathrm{m}}\right)}\right)={\epsilon }_0\left(1+\chi \left(\omega \right)\right)(11)$

here, $\chi \left(\omega \right)$ is the susceptibility, ${\nu }_{\mathrm{m}}$ is the collision frequency, and ${\omega }_{\mathrm{p}\mathrm{e}}={\left(e^2{n}_e/{\epsilon }_0{m}_e\right)}^{1/2}$ is the plasma frequency. Then, we can obtain the transmission characteristics of the THz wave in arc plasma by applying permittivity of the plasma described by Eq. 11 in the FDTD method.

FIGURE 6

FIGURE 6. Arc plasma calculation model for FDTD-Solutions.

The collision frequency between electrons and neutrals simply scales with discharge pressure (number density): ${\nu }_{\mathrm{m}}$ = const × p₀ (p in Torr), and here the const for argon can be found in Ref. [50]. By the result of Figure 1, the pressure p₀ is about 760 Torr, so the collision frequency is about 1.5 × 10¹² Hz by computation.

To diagnose plasma by electromagnetic wave method, it is generally assumed that the plasma is flat or the transverse dimension of the plasma is much larger than a wavelength. Therefore, firstly, in the simulation process, the plasma is assumed to be a flat with a one-dimensional non-uniform density distribution, and the incident frequency of the THz wave is chosen to 0.01–10 THz and its interaction with electromagnetic waves is obtained.

3 Results and discussion

Figures 7A–C show the transmission, reflection, and absorption of broadband THz wave (0.01–10 THz) in the plasmas with different discharge currents. From Figure 7A, it can be seen, with the current increasing, the “cut frequency” increases. This is because of the increasing of plasma density with the increasing of the current. Based on this phenomenon, the plasma frequency can be roughly obtained, which may be used as the method for flat distributed arc plasma diagnostic with THz wave. That is, the size of the arc plasma is so much larger compared to the incident terahertz wavelength that the effect of its dimension on terahertz transmission can be neglected.

FIGURE 7

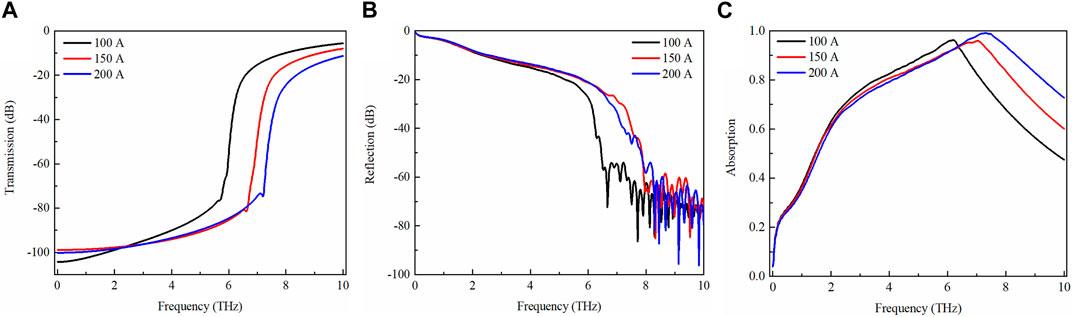
FIGURE 7. The transmission of THz wave in flat distribution plasma with different currents. (A) Transmission. (B) Reflection. (C) Absorption.

From Figure 7B, it can be seen that the most energy of low frequency THz wave is reflected by the plasma, and almost no change with increasing current because of the incident wave frequency is much lower than the plasma frequency. For the high frequency THz wave, the reflection not only depends on the plasma density but also the spatial distribution of plasma density [51]. As shown in Figure 7C, with the increasing of current, the absorbing bandwidth increases, and absorption peak moves to high frequency. The primary causes of these results are the resonance absorption peak moving to high frequency with the increasing of the plasma density.

In the above, it is supposed that the plasma is one-dimension flat distribution, however, the arc plasma is usually of finite volume and the cross-section shows a circular shape in actual situations. Then, the collisionless plasma with uniform and nonuniform density distribution of circular cross-sections are applied to simulate the electromagnetic wave transmission, and the results are shown in Figures 8A, B respectively. The dashed lines in Figure 8A are the corresponding plasma frequencies for mean electron density of different discharge current according to Figure 5. From the transmission results, the corresponding plasma frequencies can be easily obtained for the uniform plasma density distribution, as shown in Figure 8A. However, in case the plasma density distribution is nonuniform, as shown in Figure 5, we can find it difficult to obtain the plasma frequency directly from the transmission results shown in Figure 8B. Therefore, the plasma density distribution has significant influence on the plasma frequency obtained through the electromagnetic wave transmission properties.

FIGURE 8

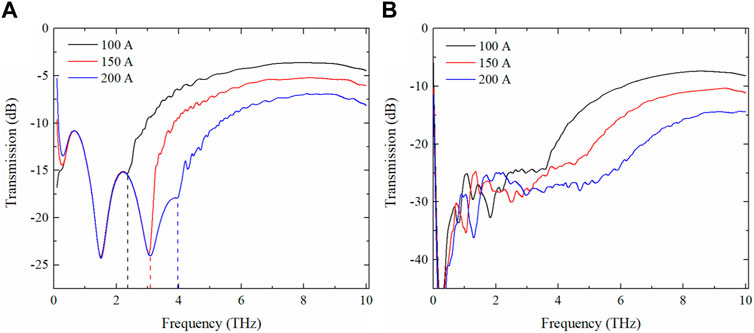
FIGURE 8. The transmission characteristics of THz wave in circular distribution plasma. (A) Uniform density distribution. (B) Nonuniform density distribution shown in Figure 5.

In addition, the plasma collision frequency can also influence the transmission characteristics of THz waves in the arc plasma. In order to discuss the influence of collision frequency, we assume that the arc plasma has a uniform cylindrical distribution, and the collision frequencies are set as 0.1, 0.5, and 1.5 THz respectively. The corresponding transmission results are shown in Figure 9A–C. From the results, we can find that when the collision frequency is small, for example, 0.1 THz, the plasma frequency still can be obtained by the transmission results. As the collision frequency increases, the plasma cutoff frequency becomes more difficult to obtain and eventually completely indistinguishable as shown in Figure 9C.

FIGURE 9

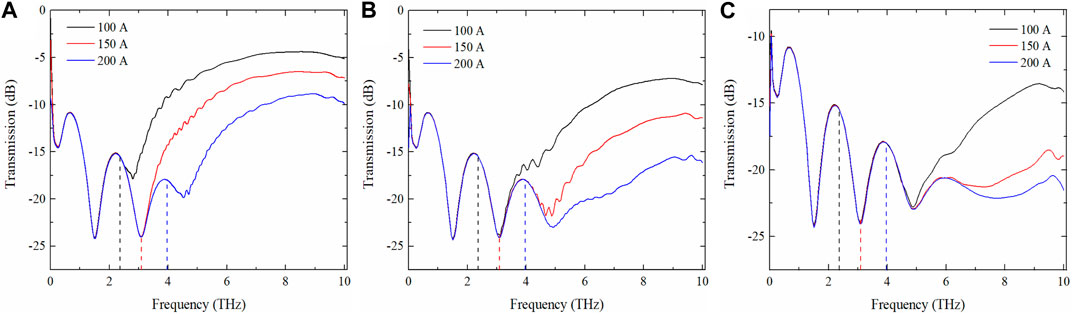
FIGURE 9. The transmission characteristics of THz wave in arc plasma with different collision frequencies: (A) 0.1 THz, (B) 0.5 THz, and (C) 1.5 THz.

Therefore, based on the above research, it can be seen that for arc plasmas with dimensions much larger than the wavelength of the incident THz wave, the THz technique can be used to achieve diagnosis of the large size arc plasmas. However, for cases where the cross-sectional size of the arc plasma has a non-negligible effect on the THz wave transmission, the plasma density distribution as well as the collision frequency can then have an important effect on the THz diagnosis results. Consequently, for small size arc plasma, it may lead to the technology only applicable to diagnose collisionless plasmas with a uniform density distribution.

4 Conclusion

In this work, the arc welding plasma is simulated by using ANSYS FLUENT, and the pressure and temperature distribution of the plasma are simulated based on the TIG arc plasma model. According to the simulation results, the electron density distribution is obtained by combining the conditions of the local thermodynamic equilibrium state of the arc discharge plasma. Then the propagation of THz waves is calculated by FDTD method. These results show that the reflection, transmission and absorption of the THz wave change with the discharge currents, and exhibit abundant phenomena. Additionally, the electron density distribution and collision frequency can have significant influence on the transmission characteristics of THz wave in arc plasma. From the results, it is found that for high-density plasma such as arc discharge, we can use the THz wave with appropriate frequency for diagnosis under the appropriate circumstances that the collision is infrequent and plasma density distribution is almost uniform or the size of arc plasma is much larger compared to the incident THz wavelength.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The research has been financially supported by National Natural Science Foundation of China (No. 12205067).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Acherjee B. Hybrid laser arc welding: State-of-art review. Opt Laser Technol (2018) 99:60–71. doi:10.1016/j.optlastec.2017.09.038

CrossRef Full Text | Google Scholar

2. Baeva M. Non-equilibrium modeling of tungsten-inert gas arcs. Plasma Chem Plasma Process (2017) 37:341–70. doi:10.1007/s11090-017-9785-y

CrossRef Full Text | Google Scholar

3. Cheng J, Wang B, Liu Q, Liang X. In-situ synthesis of novel Al-Fe-Si metallic glass coating by arc spraying. J Alloys Compd (2017) 716:88–95. doi:10.1016/j.jallcom.2017.05.032

CrossRef Full Text | Google Scholar

4. Gedzevicius I, Valiulis AV. Analysis of wire arc spraying process variables on coatings properties. J Mater Process Technol (2006) 175:206–11. doi:10.1016/j.jmatprotec.2005.04.019

CrossRef Full Text | Google Scholar

5. Bendavid A, Martin PJ. Review of thin film materials deposition by the filtered cathodic vacuum arc process at CSIRO. J Aust Ceram Soc (2014) 50 (1):86–101.

Google Scholar

6. Chan SY, Yang TH, Chang YN. Design of electronic ballast for short-arc xenon lamp with interleaved half-wave rectifier. IEEE Trans Power Electr (2015) 31 (7):5102–5112. doi:10.1109/TPEL.2015.2480860

CrossRef Full Text | Google Scholar

7. Lux H, Edling M, Siemroth P, Schrader S. Fast and cost-effective synthesis of high-quality graphene on copper foils using high-current arc evaporation. Materials (2018) 11:804. doi:10.3390/ma11050804

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Li N, Wang Z, Zhao K, Shi Z, Gu Z, Xu S. Large scale synthesis of N-doped multi-layered graphene sheets by simple arc-discharge method. Carbon (2010) 48:255–9. doi:10.1016/j.carbon.2009.09.013

CrossRef Full Text | Google Scholar

9. Xing G, Jia S, Shi Z. The production of carbon nano-materials by arc discharge under water or liquid nitrogen. New Carbon Mater (2007) 22:337–41. doi:10.1016/s1872-5805(08)60005-0

CrossRef Full Text | Google Scholar

10. Inada Y, Matsuoka S, Kumada A, Ikeda H, Hidaka K. Multi-time electron density imaging over arc discharges around the current zero point. J Phys D: Appl Phys (2014) 47:175201. doi:10.1088/0022-3727/47/17/175201

CrossRef Full Text | Google Scholar

11. Inada Y, Kumada A, Ikeda H, Hidaka K, Nakano T, Murai K, et al. Comparative study on extinction process of gas-blasted air and CO2arc discharge using two-dimensional electron density imaging sensor. J Phys D: Appl Phys (2017) 50:175202. doi:10.1088/1361-6463/aa652b

CrossRef Full Text | Google Scholar

12. Wang Y, Li J, Shi X, Wu H, Ding H. Measurement of electron density and electron temperature of a cascaded arc plasma using laser Thomson scattering compared to an optical emission spectroscopic approach. Plasma Sci Technol (2017) 19:115403. doi:10.1088/2058-6272/aa861d

CrossRef Full Text | Google Scholar

13. Bussière W. Influence of sand granulometry on electrical characteristics, temperature and electron density during high-voltage fuse arc extinction. J Phys D: Appl Phys (2001) 34:925–35. doi:10.1088/0022-3727/34/6/314

CrossRef Full Text | Google Scholar

14. Park S, Choe W, Youn Moon S, Park J. Electron density and temperature measurement by continuum radiation emitted from weakly ionized atmospheric pressure plasmas. Appl Phys Lett (2014) 104:084103. doi:10.1063/1.4866804

CrossRef Full Text | Google Scholar

15. Tomita K, Yoshitake S, Uchino K, Takenaka D, Toda H, Hikita M, et al. Measurements of electron density and electron temperature of arc discharge plasmas containing metallic vapors using laser thomson scattering. Electr Eng Jap (2014) 188 (4):1–8. doi:10.1002/eej.22635

CrossRef Full Text | Google Scholar

16. Gurchenko AD, Gusakov EZ. The possibility of measuring radial-velocity fluctuations in a tokamak plasma with the aid of enhanced microwave-scattering diagnostics. Tech Phys Lett (2018) 44:337–40. doi:10.1134/s1063785018040193

CrossRef Full Text | Google Scholar

17. Hu J, Liu A, Zhou C, Zhang X, Wang M, Zhang J, et al. An accurate automated technique for quasi-optics measurement of the microwave diagnostics for fusion plasma. Plasma Sci Technol (2017) 19:084002. doi:10.1088/2058-6272/aa6794

CrossRef Full Text | Google Scholar

18. Godyak V. Comments on plasma diagnostics with microwave probes. Phys Plasmas (2017) 24:060702. doi:10.1063/1.4984781

CrossRef Full Text | Google Scholar

19. Yanin DV, Kostrov AV, Smirnov AI, Gushchin ME, Korobkov SV, Strikovskii AV, et al. Diagnostics of the atmospheric-pressure plasma parameters using the method of near-field microwave sounding. Tech Phys (2012) 57:468–77. doi:10.1134/s1063784212040251

CrossRef Full Text | Google Scholar

20. Papeer J, Mitchell C, Penano J, Ehrlich Y, Sprangle P, Zigler A. Microwave diagnostics of femtosecond laser-generated plasma filaments. Appl Phys Lett (2011) 99:141503. doi:10.1063/1.3643478

CrossRef Full Text | Google Scholar

21. Lei L, Tobias B, Domier CW, Luhmann NC, Kramer GJ, Valeo EJ, et al. A synthetic diagnostic for the evaluation of new microwave imaging reflectometry diagnostics for DIII-D and KSTAR. Rev Scientific Instr (2010) 81:10D904. doi:10.1063/1.3464461

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Godyak V, Demidov V. Probe measurements of electron-energy distributions in plasmas: What can we measure and how can we achieve reliable results? J Phys D: Appl Phys (2011) 44:233001. doi:10.1088/0022-3727/44/23/233001

CrossRef Full Text | Google Scholar

23. Kumar M, Tripathi VK, Jeong Y. Laser driven terahertz generation in hot plasma with step density profile. Phys Plasmas (2015) 22:063106. doi:10.1063/1.4922675

CrossRef Full Text | Google Scholar

24. Dhillon SS, Vitiello MS, Linfield EH, Davies AG, Hoffmann MC, Booske J, et al. The 2017 terahertz science and technology roadmap. J Phys D: Appl Phys (2017) 50 (4):043001. doi:10.1088/1361-6463/50/4/043001

CrossRef Full Text | Google Scholar

25. Nijdam S, Desai KV, Park S-J, Sun PP, Sakai O, Lister G, et al. Foundations of plasma photonics: Lamps, lasers, and electromagnetic devices. Plasma Sourc Sci. Technol. (2023) 31:123001. doi:10.1088/1361-6595/ac8448

CrossRef Full Text | Google Scholar

26. Chiang WH, Mariotti D, Sankaran RM, Eden JG, Ostrikov K. Microplasmas for advanced materials and devices. Adv Mater (2020) 32:1905508. doi:10.1002/adma.201905508

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Houriez LS, Mehrpour Bernety H, Rodríguez JA, et al. Experimental study of electromagnetic wave scattering from a gyrotropic gaseous plasma column. Appl Phys Lett (2022) 120:223101. doi:10.1063/5.0095038

CrossRef Full Text | Google Scholar

28. Ouaras K, Righetti F, Cappelli MA. Broadband cw-terahertz spectroscopy for characterizing reactive plasmas. J Phys D: Appl Phys (2019) 52:195202. doi:10.1088/1361-6463/ab085e

CrossRef Full Text | Google Scholar

29. Yuan C, Zhou Z, W. Zhang J, Xiang X, Sun H, Wang H, et al. Propagation of terahertz waves in an atmospheric pressure microplasma with Epstein electron density profile. J Appl Phys (2011) 109:063305. doi:10.1063/1.3561834

CrossRef Full Text | Google Scholar

30. Gao R, Yuan C, Wang Y, Zhou Z, Gong D, Fang Y, et al. The terahertz characteristics of a sandwich type microplasma structure. J Appl Phys (2013) 114:123302. doi:10.1063/1.4822170

CrossRef Full Text | Google Scholar

31. Yuan C, Zhou Z, Xiang X, Sun H, Pu S. Propagation of broadband terahertz pulses through a dense-magnetized-collisional-bounded plasma layer. Phys Plasmas (2010) 17 (11):113304. doi:10.1063/1.3515895

CrossRef Full Text | Google Scholar

32. Yuan C, Zhou Z, Xiang X, Sun H, Wang H, Xing M, et al. Propagation properties of broadband terahertz pulses through a bounded magnetized thermal plasma. Nucl Instrum Methods Phys Res Sec B: Beam Interact Mater At (2011) 269 (1):23–29. doi:10.1016/j.nimb.2010.10.003

CrossRef Full Text | Google Scholar

33. Zheng L, Zhao Q, Liu S, Xing X, Chen Y. Theoretical and experimental studies of terahertz wave propagation in unmagnetized plasma. J Infrared Milli Terahz Waves (2013) 35:187–97. doi:10.1007/s10762-013-0035-y

CrossRef Full Text | Google Scholar

34. Tian Y, Han Y, Ling Y, Ai X. Propagation of terahertz electromagnetic wave in plasma with inhomogeneous collision frequency. Phys Plasmas (2014) 21 (2):023301. doi:10.1063/1.4864072

CrossRef Full Text | Google Scholar

35. Wang M, Xu Z, Dong Y, Xu J, Zhang M. The interaction of terahertz waves and a dusty plasma slab with Epstein distribution. Frequenz (2016) 70 (1–2):39–45. doi:10.1515/freq-2015-0161

CrossRef Full Text | Google Scholar

36. Cao Y, Li H, Wang Z, Wu Z. Propagation characteristics of oblique incident terahertz wave in nonuniform dusty plasma. Int J Antenn Propag (2016). doi:10.1155/2016/9454730

CrossRef Full Text | Google Scholar

37. Zhao J, Zhang L, Wu T, Zhang C, Zhao Y. Wavelength scaling of terahertz wave absorption via preformed air plasma. IEEE Trans Thz Sci Technol (2016) 6:846–50. doi:10.1109/tthz.2016.2607022

CrossRef Full Text | Google Scholar

38. Jang D, Uhm HS, Jang D, Hur MS, Suk H. Electron density characterization of inductively-coupled argon plasmas by the terahertz time-domain spectroscopy. Plasma Sourc Sci. Technol. (2016) 25:065008. doi:10.1088/0963-0252/25/6/065008

CrossRef Full Text | Google Scholar

39. Guo L, Guo L, Li J. Propagation of terahertz electromagnetic waves in a magnetized plasma with inhomogeneous electron density and collision frequency. Phys Plasmas (2017) 24:022108. doi:10.1063/1.4973654

CrossRef Full Text | Google Scholar

40. Curcio A, Petrarca M. Diagnosing plasmas with wideband terahertz pulses. Opt Lett (2019) 44:1011. doi:10.1364/ol.44.001011

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Choo RTC, Szekely J, David S. On the calculation of the free surface temperature of gas-tungsten-arc weld pools from first principles: Part II. Modeling the weld pool and comparison with experiments. Metall Trans B (1992) 23:371–84. doi:10.1007/bf02656292

CrossRef Full Text | Google Scholar

42. Fan HG, Shi YW, Na S. Numerical analysis of the arc in pulsed current gas tungsten arc welding using a boundary-fitted coordinate. J Mater Process Technol (1997) 72:437–45. doi:10.1016/s0924-0136(97)00208-2

CrossRef Full Text | Google Scholar

43. Chen X, Han P. On the thermodynamic derivation of the Saha equation modified to a two-temperature plasma. J Phys D: Appl Phys (1999) 32:1711–8. doi:10.1088/0022-3727/32/14/324

CrossRef Full Text | Google Scholar

44. Ribic B, Burgardt P, DebRoy T. Optical emission spectroscopy of metal vapor dominated laser-arc hybrid welding plasma. J Appl Phys (2011) 109:083301. doi:10.1063/1.3552307

CrossRef Full Text | Google Scholar

45. Boselli M, Colombo V, Ghedini E, Gherardi M, Sanibondi P. Two-temperature modelling and optical emission spectroscopy of a constant current plasma arc welding process. J Phys D: Appl Phys (2013) 46:224009. doi:10.1088/0022-3727/46/22/224009

CrossRef Full Text | Google Scholar

46. Yi W, Mingzhe R, Xingwen L, Murphy AB, Xiaohua W, Fei Y, et al. Numerical analysis of the effect of the chamber width and outlet area on the motion of an air arc plasma. IEEE Trans Plasma Sci (2008) 36:2831–7. doi:10.1109/tps.2008.2004040

CrossRef Full Text | Google Scholar

47. Haddad GN, Farmer AJD. Welding J (1985) 64:339.

48. Zhou X, Zhang Y, Zhai G. IEEE holm conference on electrical contacts (2017). p. 8085.

Google Scholar

49. Minghua Chen MH, Liming Liu LM. Study on attraction of laser to arc plasma in laser-TIG hybrid welding on magnesium alloy. IEEE Trans Plasma Sci (2011) 39:1104–9. doi:10.1109/tps.2011.2109739

CrossRef Full Text | Google Scholar

50. Franz G. Low pressure plasmas and microstructuring technology. Springer-Verlag Berlin Heidelberg (2009).

Google Scholar

51. Yao JF, Yu Z, Yuan CX, Zhou Z, Wang X, Kudryavtsev AA. The influence of plasma distribution on microwave reflection in a plasma-metal model. IEEE Trans Plasma Sci (2020) 48:359–63. doi:10.1109/tps.2019.2943519

CrossRef Full Text | Google Scholar