Marilena Avrigeanu
Vlad Avrigeanu- Horia Hulubei National Institute for Physics and Nuclear Engineering (IFIN-HH), Măgurele, Romania
The nuclear data evaluation for deuteron-induced reactions and α-particle emission by neutron interactions is addressed within “Nuclear data for fusion technology, from basic research to full-scale applications.” The status and open questions related to these subjects in the area of nuclear data for fusion technology, specifically for the nuclear design of the ITER fusion device, the European DEMO fusion reactor, and the IFMIF-DONES Irradiation Facility, are briefly reviewed. A firm demand for accurate cross-sections of reactions induced by neutrons and deuterons exists, in this respect, within a more enlarged energy range up to 50 MeV than for fission applications. The current requirements are closely met by the TENDL Evaluated Nuclear Data Library, settled using the TALYS nuclear model code, which is one of the most widely used codes in basic research and applications including nuclear fusion technology. However, further improvement of this data library has recently been suggested, while, with respect to fission applications, not only the aforementioned energy range but also the diversity of nuclear data for fusion technologies is plainly stretched. Consequently, the progress of nuclear data activities conducted more recently on deuteron-induced reactions and α-emission by neutron interactions, throughout the European Fusion Program and subsequent to previous achievements within F4E and EUROfusion programs, is wholly summarized.
1 Introduction
Demand for accurate cross-sections of reactions induced by neutrons and deuterons is highly relevant to the nuclear design of the ITER fusion device [1], European DEMO fusion reactor [2], and International Fusion Materials Irradiation Facility (IFMIF) [3]. Particularly, the concern is for an enlarged energy range rather than for fission applications, i.e., up to 50 MeV ([4, 5] and Refs. therein). Related activities [6] are also being conducted within the Fusion Technology Program of the EUROfusion Consortium [7], subsequent to a previous partnership agreement of Fusion for Energy (F4E) [8] with the Consortium on Nuclear Data Development and Analysis [9].
The current requirements in this respect are closely met by the Evaluated Nuclear Data Library (TENDL) [10], settled by using the output of the TALYS nuclear model code system [11], which is one of the most widely used systems in basic research and applications including nuclear fusion technology. However, a need for its further improvement has recently been referred [6], while, with respect to fission applications, not only the aforementioned energy range but also the diversity of nuclear data for fusion technologies is plainly stretched. On the other hand, a sub-library of the latest version 3.2 [12] of the Fusion Evaluated Nuclear Data Library (FENDL) [13], developed at IAEA/NDS, will include the most recent corresponding results for direct use in both basic research and applications.
So far, theoretical models are not (yet) capable of accurately predicting unmeasured cross-sections for an arbitrary nucleus and extended energy range. Instead, actual evaluations triggered by current requirements still rely on high-quality experimental data, in particular for making proper choices of the models’ free parameters [14, 15]. Consequently, specific nuclear data evaluations are requested to improve the TENDL files based, to a large extent, on automated calculations with the TALYS code using default nuclear models, assumptions, and parameters [16]. Improving charged-particle emission, within (n, α) reactions, and (α, n) nuclear data evaluations is also important [17].
This mini-review is structured as follows: the progress of nuclear data activities conducted more recently on deuteron-induced reactions is explored in Section 2, and α-emission by neutron interactions is explored in Section 3, throughout the European Fusion Program and subsequent to previous achievements within F4E and EUROfusion programs. The conclusion is given in Section 4.
2 Deuteron reaction cross-section evaluation
2.1 Role of specific deuteron reaction mechanisms
The accurate nuclear data of deuteron-induced reactions are most important for selecting and validating the structural materials and the major technologies to be taken into consideration within the nuclear design of ITER, DEMO, and IFMIF. Requested deuteron activation cross-sections are of significant interest for shielding design as well as the radiation damage estimation including the hydrogen, tritium, and helium emission. They are related to “gas bubble accumulation,” which goes through the surface swelling effects and finally deteriorates the properties of the material [18].
However, the systematics of deuteron activation cross-sections related to gas accumulation, e.g., (d, p), (d, 2p), (d, t), and (d, α), is modest compared to the case of neutrons. At the same time, evident discrepancies have been found even between the newest evaluation predictions, e.g., TENDL-2021 [10], in respect to the existing data. They pointed out neglected peculiarities of the deuteron interaction process, as well as the need to complete the theoretical frame of deuteron–nucleus interaction analysis. Thus, the non-compound processes of direct interactions (DIs), namely, breakup (BU) and direct reactions (DRs), should be considered in addition to the pre-equilibrium emission (PE) and evaporation from the compound nucleus (CN). Neglect of these reaction-mechanism contributions to the deuteron activation cross-section estimation triggers the current discrepancies of the evaluation predictions.
2.2 Deuteron breakup outcome
The distinct reaction mechanism of the deuteron interactions is the deuteron breakup into its nucleon constituents, the so-called breakup nucleons. Its complexity is increased by the addition to the primary deuteron–target nucleus interaction of the nuclear reactions induced by the breakup nucleons ([19] and Refs. therein). Moreover, the larger the target nucleus mass and charge, the higher the importance of the deuteron BU, which becomes dominant for heavy target nuclei at deuteron incident energies, particularly around the Coulomb barrier [20].
The physical picture of deuteron breakup in the Coulomb and nuclear fields of the target nucleus concerns (i) the elastic breakup (EB), in which the target nucleus remains in its ground state and none of the deuteron nucleons interacts with it, and (ii) the inelastic breakup or breakup fusion (BF), where one of these deuteron constituents interacts non-elastically with this nucleus. On the other hand, the deuteron breakup processes have two opposite effects on the deuteron activation cross-sections that should be considered equally.
First, the deuteron total-reaction cross-section σR, which is shared among different outgoing channels, is reduced by the value of the total (EB+BF) breakup cross-section σBU. On the other hand, the BF component contributes to different reaction channels through breakup-nucleon interactions with the target nucleus. Thus, the absorbed proton or neutron following the deuteron breakup contributes to the enhancement of the corresponding (d, xn) or (d, xp) reaction cross-sections, respectively. The importance of the BF enhancement has been particularly found for the case of the second and third chance-emitted particle channels [19–23].
Empirical parametrization ([19] and Refs. therein) of both the total breakup-nucleon emission
Thus, improvements in the nuclear model code capabilities to extend the evaluated deuteron-induced reaction cross-sections of Mn [22] and all stable isotopes of Zr [21] and 95−98,100Mo [23], in view of a final work concerning natural Mo, have been considered by analyzing all data up to 50 MeV. A sample case is shown in Figure 1 for deuterons on the heaviest 100Mo isotope. One should note that DI and PE+CN fractions oscillate around half of σR (gray-shaded area). Thus, the key role of the direct interactions [19, 21, 22], neglected so far, is emphasized.
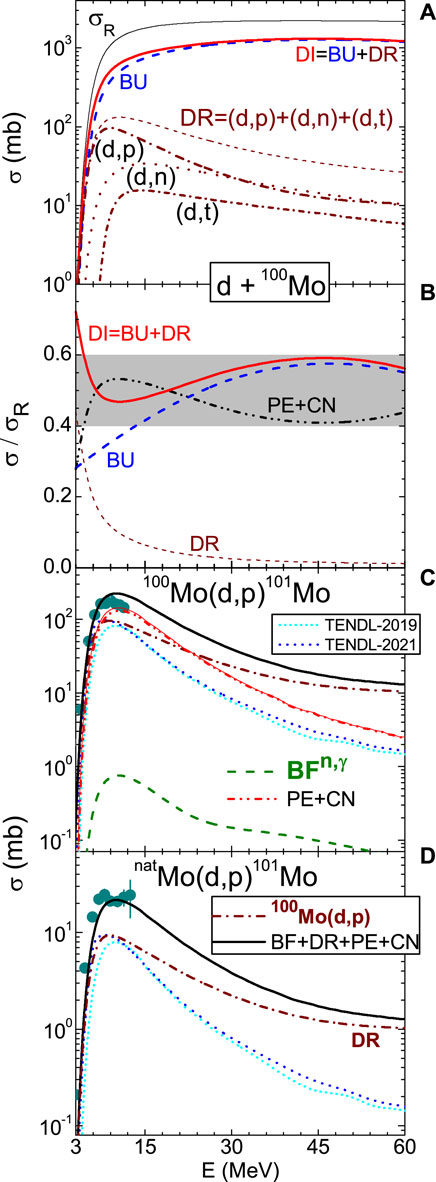
FIGURE 1. Energy dependence of (A) n+100Mo total reaction σR (thin solid curve), DI (thick solid) components of BU (dashed), DR (thin-dashed), stripping (d, p) (dash–dotted) and (d, n) (dotted), and pickup (d, t) (short dash–dotted) cross-sections, (B) ratios of them and PE+CN (dash–dot–dotted) to σR, and (C,D) measured [24], evaluated [10] (short-dashed and short-dotted), and calculations (solid) for the (d, p) reaction on 100Mo and natMo along (n, γ)-BF enhancement (dashed), (d, p) reaction, and PE+CN components.
2.3 Deuteron-induced direct reactions
The deuteron interaction with low- and medium-mass target nuclei, at incident energies below and around the Coulomb barrier, proceeds largely through stripping (d, p) and (d, n), pickup (d, t), and (d, α) DR mechanisms. Then, PE and CN become important at higher energies ([21] and Refs. therein). The assessment of the (d, p) and other direct reactions’ contributions not included within TALYS output is carried out using the distorted-wave Born approximation (DWBA) method within the code FRESCO [25] and available data for spectroscopic factor establishment. There have been involved, in this respect, the post/prior form distorted-wave transition amplitudes for stripping and pickup reactions, respectively, as well as the finite-range interaction. Moreover, the population of the discrete levels available within the ENSDF library [26] was considered, while the analysis of the available proton angular distributions provided the corresponding spectroscopic factors ([19] and Refs. therein).
The DR contributions are essential for describing the measured excitation functions corresponding to the first chance-emitted particles. A comparative analysis of the experimental (d, p) and (d, 2p) excitation functions, the model calculations, and the evaluation predictions has emphasized the role of deuteron BU and stripping reactions for the hydrogen gas accumulation process [23]. Thus, the deuteron-related enhanced version TALYS-1.96, along with this continuous code development (see [27], pag. 20 for the most important updates), could be used to obtain deuteron reaction data of increased accuracy [19]. Furthermore, requirements within the corresponding validation activities at ENS/EUROfusion [7, 28] could be also met. However, an additional increase due to the stripping, (d, p) and (d, n), pickup, (d, t) and (d, α), direct reactions should be carried out using FRESCO, anymore [27].
Nevertheless, a specific point of consistent model calculations is the involvement of the same model parameters within different reaction mechanisms, e.g., the same OMP parameters for the calculation of breakup cross-sections, distorted waves in the ingoing/outgoing channels of DR, PE transition rates, and transmission coefficients of various ingoing/outgoing CN channels. The overall agreement between the measured data and model calculations [19] sustains the theoretical frame of reaction mechanisms taken into account for the deuteron–nucleus interaction, emphasizing the key role of direct interactions, i.e., the breakup and direct reactions. Finally, the best point of the consistent theoretical frame associated with the analysis of the deuteron–nucleus interactions through advanced codes is the improved predictability where no data exist. On the other hand, requirements for new measurements for the completion of the large gaps of (d, 2p) data on specific nuclei along the priority list of candidate materials for ITER/IFMIF [1] are obvious.
3 Validation of α-particle optical potential for α-emission
3.1 Common issues of α-particle-induced reactions and α-emission analysis
The α-particle optical model potential (OMP) that was obtained previously by analyzing α-particle elastic scattering and induced reactions on A ≈ 45–209 nuclei, at energies ≤50 MeV [29], received another confirmation [30] by considering the α-induced reaction data published within the last decade. The use of consistent parameter sets, i.e., already validated by the analysis of other independent data that are distinct from α-induced reaction or α-emission cross-sections, has made possible the suitable data account in terms of the CN and PE models. An obvious correlation exists, however, between the accuracy of the independent data, the input parameters determined by their fit, and final uncertainties of the calculated reaction cross-sections.
On the other hand, no further empirical rescaling factors of the γ and nucleon widths have been used, in order to avoid compensation effects of less-accurate model parameters, while the former are still mandatory within large-scale nuclear data evaluations. Moreover, a suitable description of all competitive reaction channels, in addition to the α-emission of interest, should also be aimed at the validation of consistent parameter sets. At the same time, the analysis should also concern the available data not only for one of the stable isotopes of the elements other than the mono-isotopic ones in nature but also for whole isotopic chains and neighboring elements.
Then, the α-emission from excited nuclei in nucleon-induced reactions on A ∼60 [31, 32] and A ∼90 [33] nuclei has also been described by the same α-particle OMP. Similar usage of consistent parameter sets, considering all competitive reaction channels, and eventually isotopic chains of neighboring elements, has been considered for the α-emission and for α-particle-induced reaction analysis. The main drawback that had to be overcome was the underestimation of the α-emission cross-sections [34, 35] by taking into account OMPs settled by the suitable account of α-particle elastic scattering and induced reactions [29, 36–38].
3.2 Specific α-emission contributions
The additional consideration that should be given to the pickup DR, leading to an increase in the α-emission beyond the CN+PE predictions, has been shown more recently [31, 32], while its suitable account at the Giant Quadrupole Resonance (GQR) energies of 55,57,58Fe and 59,61,62,65Ni (Figures 2A–C) has been attributed to a like-GQR component. An alternate solution has been, thus, provided to the so-called α-potential mystery [39] to describe the absorption and emission of α-particles of large interest for astrophysics and fusion technology.
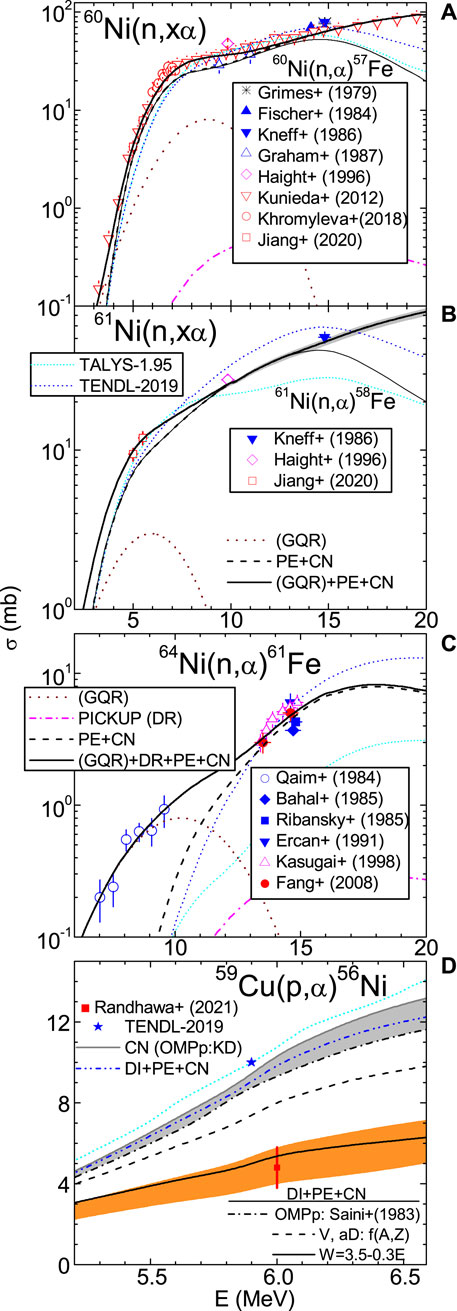
FIGURE 2. Same as Figure 1D except (A–C) 60,61,64Ni(n, xα) components of PE+CN (dashed curves and thin solid for (n, α) reactions), DR pickup (dash–dotted), like-GQR (dotted), and their sum (solid) [32]; (D) 59Cu(p,α)56Ni reaction [50] and various proton OMPs, including (N-Z)/A dependence (dashed) and anomalous depth W(E) (solid and orange band).
The same analysis for the stable isotopes of Zr, Nb, and Mo becomes challenging, with Zr nuclei within both incident and emergent reaction channels. Actually, the α-emission in neutron-induced reactions on stable Mo isotopes made the object of an earlier systematic investigation up to 20 MeV [40] using α-particle OMP [41] describing A ∼60 compound-nuclei α-particle decay. A significant underestimation at incident energies around ≤10 MeV for 92,98Mo was obtained at that time. This OMP makes predictions that differ significantly from potentials for incident α particles [42] including a double-folding model (DFM) of microscopic real potential [29, 34, 36–38]. The discrepancy in the results corresponding to OMPs [36, 41] even led to the assumption that nuclear density distribution is dependent on nuclear temperature [34, 35].
The α-emission cross-sections larger than CN+PE predictions, distinct from the data error bars, have finally been described using additional pickup DR and like-GQR decay of excited nuclei by neutrons on Zr, Nb, and Mo stable isotopes [33]. The pickup contributions to (n, α) reactions have been calculated through the DWBA method using the code FRESCO [25]. The one-step reaction takes place through the pickup of the 3He cluster, while the “spectator model” [43] for the two transferred protons in the (n, α) reaction has been taken into account. However, the lack of a measured α-particle angular distribution for the (n, α) reactions within this work made only straightforward DWBA calculations of related pickup cross-sections possible. Thus, the spectroscopic factors (SFs) of Glendenning [44] have been used for the spectator proton pair [43], in addition to SFs for the picked neutron. Thus, the latter become responsible for the angular momentum transfer. They were obtained through the analysis of α-particle angular distributions of one-nucleon pickup reactions
A description of both the absorption and emission of α particles, thus, becomes possible by the same potential [29], in support of its use for large-scale nuclear data evaluations as the TALYS corresponding default option. In fact, this conclusion could be found within the previous analysis for Zr [35] and Mo [34], before DR and like-GQR decay consideration, due to outstanding cross-section measurements for 91Zr(n,nα)87Srm [45] and 95Mo(n,α)92Zr [46, 47] reactions. At the same time, it is suggested that the simple OMP [41] could include, beyond the CN contribution, the additional ones that only now receive full consideration. Nonetheless, further measurements at incident energies corresponding to GQR energies of excited nuclei, as well as heavier isotopes of elements, may shed light on the eventual like-GQR α-emission.
3.3 Account of α-emission off the line of stability
In the meantime, a former assumed overestimation of a first direct measurement for 59Cu(p,α)56Ni reaction cross-sections by a factor of 2 at an energy of ∼6 MeV [48] was also solved. Due consideration of proton OMP anomalies at sub-Coulomb energies for medium-weight nuclei has been shown to be critical for the analysis of this unprecedented measurement [49]. So, the usefulness of using consistent parameter sets established by a former analysis of independent data has been shown once more.
Thus, we have shown [50] that variation in predicted cross-sections from standard statistical model calculations and cross-section range related to the anomalous proton imaginary potential depth, for target nuclei off the line of stability, is distinct and well separated (Figure 2D). Consequently, the new measurement [48] provides, under unique conditions, tests of proton isoscalar and isovector real-potential components, the anomalous imaginary potential, and the alpha-particle OMP [29], for nuclei off the line of stability. Moreover, it has, thus, been completed for the similar α-emission account by this OMP [29] for Cu stable isotopes [31] at once with all α-induced reactions on Ni stable isotopes [51].
4 Conclusion
The major role of direct interactions, namely, breakup, stripping, and pickup processes, is emphasized by the overall agreement between the measured data and model calculations related to the deuteron–nucleus interaction for significant structural material elements (Al, V, Fe, Ni, Co, Cu, Zr, Nb, and Mo). These so far neglected reaction mechanism contributions to the deuteron activation cross-section estimation are responsible for the discrepancies still shown by the current evaluation predictions. On the other hand, an accurate assessment of these contributions to hydrogen, tritium, and helium gas accumulation, which is responsible for structural material damage, is strongly requested for the improvement of shielding design and radiation effect analysis. Nevertheless, the comparative analysis of experimental data, evaluation, and model calculations emphasized the uncertainties within the actual evaluations and, consequently, the requirement for the upgrade of the latter. Actually, the strongest point of the consistent theoretical frame associated with the analysis of the deuteron–nucleus interactions, using advanced codes, is the improved predictability where no data exist.
At the same time, it could be essential the more recent interest in the microscopic analysis of inclusive breakup and direct reactions [52–55]. Although they are still being investigated numerically, further progress may also eventually contribute to increased accuracy of the phenomenological evaluation of the deuteron activation. Suitable distinction among the breakup mechanism and the stripping direct reaction within microscopic deuteron breakup will be most beneficial in this respect. The correct assessment of the inelastic breakup enhancement, being triggered by the maximum energy of the breakup nucleon that differs significantly from that of the outgoing stripping nucleons, is, thus, a prerequisite for semi-classical and quantum theories. Their validation demands an overall increase of the deuteron data basis and complementary measurements of either (d, px) and (n, x) or (d, nx) and (p, x) reaction data within corresponding incident-energy ranges. Although the actual scarce data are mainly available for natural elements of structural materials, similar measurements on their distinct isotopes would be most useful for model endorsement. Recent programs at strong new facilities [56, 57] seem really promising.
On the other hand, a suitable description of the available data for competitive reaction channels has prevented compensation effects of less-accurate model parameters for the analysis of either α-particle-induced reactions or α-emission on/from key structural material elements (Fe, Co, Ni, Cu, Zn, Zr, Nb, and Mo). Detailed analyses based on consistent input parameter sets are important for eventually improving the global parameters to then be involved within large-scale evaluations. However, the correlation of the measured error bars of the primary data providing the consistent input parameters, the corresponding limits of these parameters, and the final uncertainty bands of the calculated results has to be carefully considered. Thus, matching of the experimental and calculated cross-section uncertainties could be obtained as well as its correspondence to the limits of the distinct data formerly involved within the consistent parameter assessment.
Remaining questions emphasize the need for additional measurements. Thus, further data at incident energies corresponding to GQR energies of excited nuclei, as well as heavier isotopes of elements (e.g., Ni and Mo), may definitely shed light on the question of possible like-GQR α-emission. At the same time, consideration of additional pickup direct reaction contribution to (n, α) reactions, within the DWBA method, using accurate spectroscopic factors obtained through analysis of α-particle angular distributions would unequivocally support it. Moreover, of particular interest would be further isomeric state activation data in order to better understand the nuclear-level density angular momentum dependence determined by the nuclear momentum of inertia ([58, 59] and Refs. therein).
Author contributions
MA and VA conceived this mini-review together. All authors contributed to the article and approved the submitted version.
Funding
This work was carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Program (Grant Agreement No. 101052200—EUROfusion). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Acknowledgments
The authors acknowledge key guidance and work together with Arjan Koning and Dimitri Rochman, helpful and fruitful coordination by Ulrich Fischer and Dieter Leichtle within EUROfusion ND undertaking, and support from the Nuclear Energy Agency (NEA) Data Bank, Paris, by providing their services for the data file assembly and maintenance and hosting the progress meetings.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.ITER Organization. ITER organization (2007). Available at: http://www.iter.org/ (Accessed January 31, 2023).
2. Federici G, Bachmann C, Biel W, Boccaccini L, Cismondi F, Ciattaglia S, et al. Overview of the design approach and prioritization of R&D activities towards an EU DEMO. Fusion Eng Des 109-111 (2016) 1464–74. doi:10.1016/j.fusengdes.2015.11.050
3. Moeslang A, Heinzel V, Matsui H, Sugimoto M. The IFMIF test facilities design. Fusion Eng Des (2006) 81:863–71. doi:10.1016/j.fusengdes.2005.07.044
4. Ledoux X, Aïche M, Avrigeanu M, Avrigeanu V, Balanzat E, Ban-d’Etat B, et al. The neutrons for science facility at SPIRAL-2. Radiat Prot Dosimetry (2017) 180:115–9. doi:10.1093/rpd/ncx257
5. Mardor I, Aviv O, Avrigeanu M, Berkovits D, Dahan A, Dickel T, et al. The soreq applied research accelerator facility (SARAF): Overview, research programs and future plans. Eur Phys J A (2018) 54:91. doi:10.1140/epja/i2018-12526-2
6. Fischer U, Avrigeanu M, Avrigeanu V, Konobeyev A, Kodeli I, Leeb H, et al. Nuclear data activities of the EUROfusion consortium. EPJ Web Conf (2020) 239:21001. doi:10.1051/epjconf/202023921001
7.EURO. EUROfusion programme (2014). Available at: https://users.euro-fusion.org/ (Accessed January 31, 2023).
8.EURO. Fusion for energy (2007). Available at: https://fusionforenergy.europa.eu/ (Accessed January 31, 2023).
9. Fischer U, Avrigeanu M, Avrigeanu V, Cabellos O, Dzysiuk N, Koning A, et al. Nuclear data for fusion technology - the European approach. EPJ Web Conf (2017) 146:09003. doi:10.1051/epjconf/201714609003
10. Koning A, Rochman D, Sublet JC, Dzysiuk N, Fleming M, van der Marck S. Tendl: Complete nuclear data library for innovative nuclear science and technology. Nucl Data Sheets (2019) 155 1–55. doi:10.1016/j.nds.2019.01.002
11. Koning AJ, Hilaire S, Duijvestijn MC. ND 2007. In: Proceedings of the International Conference on Nuclear Data for Science and Technology - ND2007; April 22-27, 2007; Nice, France (2008). p. 211–4. Lastly, available at nds.iaea.org/talys.
12. Leichtle D, Trkov A. FENDL library for fusion neutronics calculations. In: Summary report from the Technical Meeting; 2-5 Sept 2019; Vienna, Austria. Tech rep IAEA (2019).
13. Forrest RA, Capote R, Otsuka N, Kawano T, Koning AJ, Kunieda S, et al. FENDL-3 library – summary documentation. (2012) Vienna, Austria: Tech. rep IAEA.
14. Hermanne A, Ignatyuk AV, Capote R, Carlson BV, Engle JW, Kellett MA, et al. Reference cross sections for charged-particle monitor reactions. Nucl Data Sheets (2018) 148:338–82. doi:10.1016/j.nds.2018.02.009
15. Engle JW, Ignatyuk AV, Capote R, Carlson BV, Hermanne A, Kellett MA, et al. Recommended nuclear data for the production of selected therapeutic radionuclides. Nucl Data Sheets (2019) 155:56–74. doi:10.1016/j.nds.2019.01.003
16. Fischer U, Angelone M, Avrigeanu M, Avrigeanu V, Bachmann C, Dzysiuk N, et al. The role of nuclear data for fusion nuclear technology. Fusion Eng Des (2018) 136:162–7. Proceedings of the 13th International Symposium on Fusion Nuclear Technology (ISFNT-13). doi:10.1016/j.fusengdes.2018.01.036
17. Westerdale SS, Junghans A, deBoer RJ, Pigni M, Dimitriou P. (α, n) nuclear data evaluations and data needs. Summary Report of the Technical Meeting (2022), 8-12 November 2021, Vienna, Austria, Report INDC(NDS)-0836. Tech. rep.
18. Rubel M. Fusion neutrons: Tritium breeding and impact on wall materials and components of diagnostic systems. J Fusion Energ (2019) 38:315–29. doi:10.1007/s10894-018-0182-1
19. Avrigeanu M, Rochman D, Koning AJ, Fischer U, Leichtle D, Costache C, et al. Advanced breakup-nucleon enhancement of deuteron-induced reaction cross sections. Eur Phys J A (2022) 58:3. doi:10.1140/epja/s10050-021-00659-6
20. Avrigeanu M, Avrigeanu V, Koning AJ. Investigation of deuteron breakup and deuteron-induced fission on actinide nuclei at low incident energies. Phys Rev C (2012) 85:034603. doi:10.1103/PhysRevC.85.034603
21. Šimečková E, Avrigeanu M, Mrázek J, Novak J, Štefánik M, Costache C, et al. Deuteron-induced reactions on natZr up to 60 mev. Phys Rev C (2021) 104:044615. doi:10.1103/PhysRevC.104.044615
22. Avrigeanu M, Šimečková E, Fischer U, Mrázek J, Novak J, Štefánik M, et al. Deuteron-induced reactions on manganese at low energies. Phys Rev C (2020) 101:024605. doi:10.1103/PhysRevC.101.024605
23. Avrigeanu M, Avrigeanu V. Role of direct interactions in (d,p) and (d,2p) reactions. In: Int. Conf. on Nucl. Data for Sci. and Tech. (ND2022); July 25−29; Sacramento, California, US (2022). 2022. https://indico.frib.msu.edu/event/52/contributions/971/ (Accessed January 31, 2023).
24. Otuka N, Dupont E, Semkova V, Pritychenko B, Blokhin A, Aikawa M, et al. Towards a more complete and accurate experimental nuclear reaction data library (EXFOR): International collaboration between nuclear reaction data centres (NRDC). Nucl Data Sheets (2014) 120:272–6. doi:10.1016/j.nds.2014.07.065
25. Thompson IJ. Coupled reaction channels calculations in nuclear physics. Comp Phys Rep (1988) 7:167–212. doi:10.1016/0167-7977(88)90005-6
26. [Dataset] . Evaluated nuclear structure data file (ENSDF) (2022). Available at https://www.nndc.bnl.gov/ensdf/ (Accessed January 31, 2023)
27. Koning A, Hilaire S, Goriely S. Talys-1.96/2.0. simulation of nuclear reactions. Tech. rep: Vienna (2021). Available at: https://www-nds.iaea.org/talys/tutorials/talys_v1.96.pdf (Accessed January 15, 2022).
28. Leichtle D, Leichtle D, Trkov A. Considerations on V&V needs for FENDL data and application. In: FENDL Library for Fusion Neutronics Calculations. Summary report from the Technical Meeting; 2-5 Sept. 2019; Vienna, Austria. IAEA, Vienna (2019). p. 15. Report INDC(NDS)-0797.
29. Avrigeanu V, Avrigeanu M, Mănăilescu C. Further explorations of the α-particle optical model potential at low energies for the mass range a ≈ 45–209. Phys Rev C (2014) 90:044612. doi:10.1103/PhysRevC.90.044612
30. Avrigeanu V, Avrigeanu M. Role of consistent parameter sets in an assessment of the α-particle optical potential below the coulomb barrier. Phys Rev C (2019) 99:044613. doi:10.1103/PhysRevC.99.044613
31. Avrigeanu V, Avrigeanu M. Validation of an optical potential for incident and emitted low-energy α-particles in the A ≈ 60 mass range. Eur Phys J A (2021) 57:54. doi:10.1140/epja/s10050-020-00336-0
32. Avrigeanu V, Avrigeanu M. Validation of an optical potential for incident and emitted low-energy α-particles in the A ≈ 60 mass range. II. Neutron–induced reactions on Ni isotopes. Eur Phys J A (2022) 58:189. doi:10.1140/epja/s10050-022-00831-6
33. Avrigeanu M, Avrigeanu V. Consistent optical potential for incident and emitted low-energy α particles. iii. nonstatistical processes induced by neutrons on zr, nb, and mo nuclei. Phys Rev C (2023) 107:034613. doi:10.1103/PhysRevC.107.034613
34. Avrigeanu M, von Oertzen W, Avrigeanu V. On temperature dependence of the optical potential for alpha-particles at low energies. Nucl Phys A (2006) 764:246–60. doi:10.1016/j.nuclphysa.2005.10.001
35. Avrigeanu V, Avrigeanu M. Consistent optical potential for incident and emitted low-energy α particles. II. α emission in fast-neutron-induced reactions on Zr isotopes. Phys Rev C (2017) 96:044610. doi:10.1103/PhysRevC.96.044610
36. Avrigeanu M, von Oertzen W, Plompen AJM, Avrigeanu V. Optical model potentials for α-particles scattering around the coulomb barrier on a ∼100 nuclei. Nucl Phys A (2003) 723:104–26. doi:10.1016/S0375-9474(03)01159-X
37. Avrigeanu M, Obreja AC, Roman FL, Avrigeanu V, von Oertzen W. Complementary optical-potential analysis of α-particle elastic scattering and induced reactions at low energies. At Data Nucl Data Tables (2009) 95:501–32. doi:10.1016/j.adt.2009.02.001
38. Avrigeanu M, Avrigeanu V. α-particle nuclear surface absorption below the Coulomb barrier in heavy nuclei. Phys Rev C (2010) 82:014606. doi:10.1103/PhysRevC.82.014606
39. Rauscher T. Solution of the α-potential mystery in the γ process and its impact on the Nd/Sm ratio in meteorites. Phys Rev Lett (2013) 111:061104. doi:10.1103/PhysRevLett.111.061104
40. Reimer P, Avrigeanu V, Chuvaev SV, Filatenkov AA, Glodariu T, Koning A, et al. Reaction mechanisms of fast neutrons on stable Mo isotopes below 21 MeV. Phys Rev C (2005) 71:044617. doi:10.1103/PhysRevC.71.044617
41. Avrigeanu V, Hodgson PE, Avrigeanu M. Global optical potentials for emitted α-particles. Phys Rev C (1994) 49:2136–41. doi:10.1103/PhysRevC.49.2136
42. McFadden L, Satchler GR. Optical-model analysis of the scattering of 24.7 mev alpha particles. Nucl Phys (1966) 84:177–200. doi:10.1016/0029-5582(66)90441-X
43. Smits J, Siemssen R, Van Der Werf S, Van Der Woude A. The 58,60,62,64Ni(p,α)55,57,59,61Co reactions and their description by the semi-microscopic model for three-nucleon transfer. Nucl Phys A (1979) 319:29–49. doi:10.1016/0375-9474(79)90169-6
44. Glendenning NK. Tables of nuclear structure amplitudes for two-nucleon transfer involving light projectiles (a ≤ 4). At Data Nucl Data Tables (1975) 16:1–134. doi:10.1016/0092-640X(75)90031-5
45. Semkova V, Bauge E, Plompen A, Smith D. Neutron activation cross sections for zirconium isotopes. Nucl Phys A (2010) 832:149–69. doi:10.1016/j.nuclphysa.2009.10.133
46. Rapp W, Koehler PE, Käppeler F, Raman S. 95Mo(n, α) cross section from 1 eV to 500 keV: A test of the α + nucleus optical potential used in calculating reaction rates for explosive nucleosynthesis. Phys Rev C (2003) 68:015802. doi:10.1103/PhysRevC.68.015802
47. Zhang G, Wu H, Zhang J, Liu J, Yin Y, Chen J, et al. Cross section measurement for the 95Mo(n,α)92Zr reaction at 4.0, 5.0 and 6.0MeV. Appl Radiat Isot (2010) 68:180–3. doi:10.1016/j.apradiso.2009.09.013
48. Randhawa JS, Kanungo R, Refsgaard J, Mohr P, Ahn T, Alcorta M, et al. First direct measurement of 59Cu(p,α)56Ni: A step towards constraining the Ni-Cu cycle in the cosmos. Phys Rev C (2021) 104:L042801. doi:10.1103/PhysRevC.104.L042801
49. Avrigeanu V, Avrigeanu M. Charged-particle optical potentials tested by first direct measurement of the 59Cu(p,α)56Ni reaction. Phys Rev C (2022) 106:024615. doi:10.1103/PhysRevC.106.024615
50. Avrigeanu V, Avrigeanu M. Charged–particle optical potentials proved by first direct measurement of 59Cu(p,α)56Ni reaction (2021). Report arXiv:2111.09775 [nucl-th]Available at: http://arxiv.org/abs/2111.09775v1 (Accessed November 30, 2022).
51. Avrigeanu V, Avrigeanu M. Analysis of uncertainties in α-particle optical-potential assessment below the Coulomb barrier. Phys Rev C (2016) 94:024621. doi:10.1103/PhysRevC.94.024621
52. Lei J, Moro AM. Reexamining closed-form formulae for inclusive breakup: Application to deuteron- and 6Li-induced reactions. Phys Rev C (2015) 92:044616. doi:10.1103/PhysRevC.92.044616
53. Ogata K, Yoshida K. Applicability of the continuum-discretized coupled-channels method to the deuteron breakup at low energies. Phys Rev C (2016) 94:051603. doi:10.1103/PhysRevC.94.051603
54. Potel G, Perdikakis G, Carlson BV, Atkinson MC, Dickhoff WH, Escher JE, et al. Toward a complete theory for predicting inclusive deuteron breakup away from stability. Eur Phys J A (2017) 53:178. doi:10.1140/epja/i2017-12371-9
55. Lei J, Moro AM. Post-prior equivalence for transfer reactions with complex potentials. Phys Rev C (2018) 97:011601. doi:10.1103/PhysRevC.97.011601
56. Kreisel A, Weissman L, Cohen A, Hirsh T, Shor A, Aviv O, et al. Measurements of 59Co(d,p)60m,gCo,51V(d,p)52V, and natV(d,xn)51Cr cross sections in the 2.7 − −5.4 − MeV energy range. Phys Rev C (2019) 99:034611. doi:10.1103/PhysRevC.99.034611
57. Ledoux X, Foy JC, Ducret JE, Frelin AM, Ramos D, Mrázek J, et al. First beams at neutrons for science. Eur Phys J A (2021) 57:257. doi:10.1140/epja/s10050-021-00565-x
58. Avrigeanu V, Glodariu T, Plompen AJM, Weigmann H. On consistent description of nuclear level density. J Nucl Sci Tech (2002) 39:746–9. doi:10.1080/00223131.2002.10875205
Keywords: nuclear reactions, cross-sections, deuteron breakup, alpha-particle emission, radiation effects
Citation: Avrigeanu M and Avrigeanu V (2023) Structural material nuclear data basic research. Front. Phys. 11:1172697. doi: 10.3389/fphy.2023.1172697
Received: 23 February 2023; Accepted: 12 May 2023;
Published: 26 May 2023.
Edited by:
Marco La Cognata, Laboratori Nazionali del Sud (INFN), ItalyReviewed by:
Pareshkumar Prajapati, Manipal Academy of Higher Education, IndiaCopyright © 2023 Avrigeanu and Avrigeanu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marilena Avrigeanu, bWFyaWxlbmEuYXZyaWdlYW51QG5pcG5lLnJv