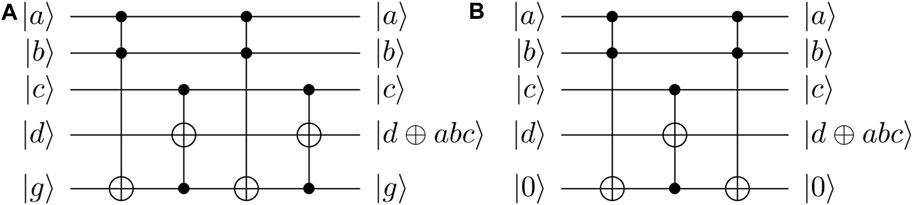New record in the number of qubits for a quantum implementation of AES

Optimizing the quantum circuit for implementing Advanced Encryption Standard (AES) is crucial for estimating the necessary resources in attacking AES by the Grover algorithm. Previous studies have reduced the number of qubits required for the quantum circuits of AES-128/-192/-256 from 984/1112/1336 to 270/334/398, which is close to the optimal value of 256/320/384. It becomes a challenging task to further optimize them. AimTaking aim at this task, we find a method for how the quantum circuit of AES S-box can be designed with the help of the automation tool LIGHTER-R. Particularly, the multiplicative inversion in $F_{2^8}$, which is the main part of the S-box, is converted into the multiplicative inversion (and multiplication) in $F_{2^4}$, then the latter can be implemented by LIGHTER-R because its search space is small enough. By this method, we construct the quantum circuits of S-box for mapping |a⟩|0⟩ to |a⟩|S(a)⟩ and |a⟩|b⟩ to |a⟩|b ⊕ S(a)⟩ with 20 qubits instead of 22 in the previous studies. In addition, we introduce new techniques to reduce the number of qubits required by the S-box circuit for mapping |a⟩ to |S(a)⟩ from 22 in the previous studies to 16. Accordingly, we synthesize the quantum circuits of AES-128/-192/-256 with 264/328/392 qubits, which implies a new record.

1 Introduction

The parallelism of quantum computing makes quantum computers have significant speed-up compared with classical computers in certain specific problems, such as solving linear systems [1–3], classification [4–8], dimensionality reduction [9–12], linear regression [13–15], association rule mining [16], anomaly detection [17,18] and so on. Quantum algorithms, such as Shor [19], Grover [20], and Simon [21], seriously threaten the security of modern cryptography. Although the scale of quantum computers is not enough to break through the cryptographic primitives so far, with the development of technology, these quantum algorithms will be realized in the future. Thus, accurately estimating the actual arrival time of quantum threats is the key to ensuring the steady renewal of the cryptosystem. With the steady development of quantum computing hardware, evaluating the minimum quantum resources required to realize Shor, Grover, Simon, and other cryptanalysis quantum algorithms has become one of the main factors affecting the actual arrival time of quantum threats. For example, because T-depth and number of qubits realized by current quantum computers are limited, they are regarded as the main optimization goal in most previous studies about the quantum circuit implementations of the above algorithms.

It is significant to estimate the cost of the Grover algorithm attacking Advanced Encryption Standard (AES) [22]. On the one hand, AES is one of the most studied and popular symmetric ciphers in the world. On the other hand, the cost was used as the benchmark to define different security levels of post-quantum public-key schemes when the National Institute of Standards and Technology (NIST) [23] called for proposals for the standardization of post-quantum cryptography. In the implementation, the quantum circuit of AES is the core of Grover oracle, which is the most complicated part of the whole algorithm. For this reason, optimizing the quantum circuit of AES becomes an important method of reducing the quantum resources required for Grover-algorithm-attacking AES. Among the tasks necessary to optimize the quantum circuit for AES, how to use fewer resources to realize the AES S-box, the only non-linear component, is one of the main influencing factors.

Some quantum circuits of AES were designed to reduce the T-depth. In 2020, Jaques et al. [24] constructed a quantum circuit of S-box for |a⟩|b⟩ → |a⟩|b ⊕ S(a)⟩ (a, b and S(a) are 8-bit vectors) with T-depth 6, and then synthesized the quantum circuit of AES-128 with a T-depth of 120. In 2022, Li et al. [25] proposed the S-box circuits for |a⟩|0⟩ → |a⟩|S(a)⟩ and |a⟩|b⟩ → |a⟩|b ⊕ S(a)⟩ with T-depth 4, and then reduced the T-depth required for the quantum circuit of AES-128 to 80. Huang et al. [26] gave the circuit for |a⟩|b⟩ → |a⟩|b ⊕ S(a)⟩ with a T-depth of 3, and then further reduced the T-depth required for the quantum circuit of AES-128 to 60. Jang et al. [27] synthesized the quantum circuit of AES-128 with a T-depth of 30 by introducing an improved pipeline method for round function iteration.

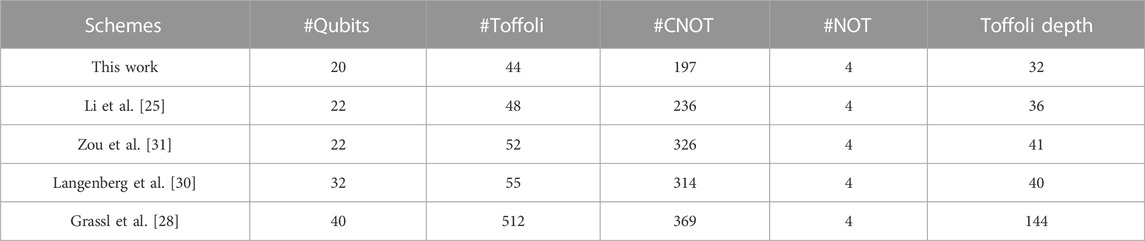
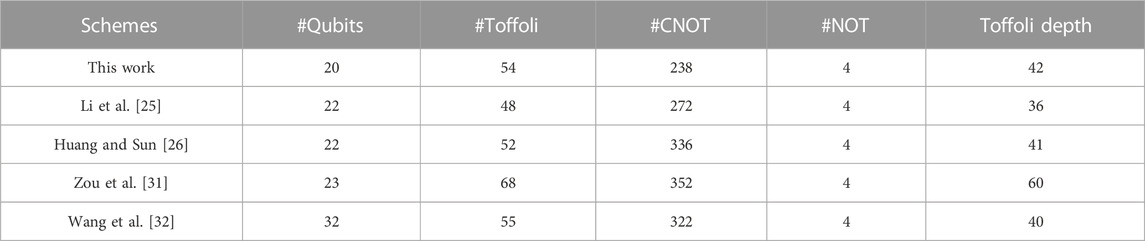
At the same time, quite a few quantum circuits of AES were designed to reduce the number of qubits (see Table 1). In 2016, Grassl et al. [28] implemented the quantum circuit of AES-128 with 984 qubits by presenting the 40 qubits quantum circuit of S-box for ${\mathcal{C}}_1:|\mathit{a}\rangle |\mathbf{0}\rangle \to |\mathit{a}\rangle |S(\mathit{a})\rangle$ and introducing zig-zag method for round function iteration. In 2018, Almazrooie et al. [29] reduced the number of qubits required for the quantum circuit of AES-128 to 976 by finding an improved key expansion iteration method. In 2020, Langenberg et al., [30] constructed the S-box circuit for ${\mathcal{C}}_1$ with 32 qubits and completed key expansion iteration by zig-zag method, then realized the quantum circuit of AES-128 with 864 qubits. Zou et al., [31] proposed a circuit for ${\mathcal{C}}_1$ with 22 qubits and gave an improved zig-zag method for round function iteration and key expansion iteration by introducing the 23 qubits quantum circuits of S-box and its inverse for ${\mathcal{C}}_2:|\mathit{a}\rangle |\mathit{b}\rangle \to |\mathit{a}\rangle |\mathit{b}\oplus S(\mathit{a})\rangle$ and ${\mathcal{C}}_3:|\mathit{a}\rangle |S(\mathit{a})\rangle \to |\mathbf{0}\rangle |S(\mathit{a})\rangle$, then used 512 qubits to construct the quantum circuit of AES-128. In 2022, Wang et al. [32] synthesized the 400 qubits quantum circuit of AES-128 by giving a straight-line method for key expansion iteration. Huang et al., [26] proposed the S-box circuit for ${\mathcal{C}}_2$ with 22 qubits, and introduced a straight-line method for round function iteration by giving the 22 qubits quantum circuit of S-box for ${\mathcal{C}}_4:|\mathit{a}\rangle \to |S(\mathit{a})\rangle$, then implemented the quantum circuit of AES-128 with 374 qubits. In the same period as Huang et al., Li et al. [25] synthesized the quantum circuit of AES-128 with 270 qubits by presenting the 22 qubits quantum circuits of S-box for ${\mathcal{C}}_1$, ${\mathcal{C}}_2$ and ${\mathcal{C}}_4$ as well as adopting the straight-line method for round function iteration.

TABLE 1

TABLE 1. Summary of the number of qubits required for implementing AES-128. “RFIM” and “KSIM” represent the round function iteration method and key expansion iteration method respectively.

It can be seen that the number of qubits required for the quantum circuit of AES has been greatly improved through the efforts of scholars, approaching the optimal value of 256/320/384. It seems that further reducing them has become a challenging task. In this work, we study how the AES S-box can be constructed with fewer qubits, thereby reducing the number of qubits required for the quantum circuit of AES. Note that any mention of qubits in this work refers to logical qubits. Our contributions are as follows:

• We find a method to construct the quantum circuit of AES S-box with the help of automation tool LIGHTER-R, which can reduce the number of qubits required by ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ from 22 in the previous studies [25, 26, 31] to 20. Particularly, the quantum circuit of the multiplicative inversion in $F_{2^8}$ is the main factor affecting the number of qubits required by the quantum circuit of the S-box. But there is no automatic tool to optimize it. Dasu et al. [33] presented an automatic tool, namely, LIGHTER-R, that can generate the quantum circuit of effectively implementing the multiplicative inversion in $F_{2^4}$. Unfortunately, the tool LIGHTER-R cannot give the quantum circuit for implementing the multiplicative inversion in $F_{2^8}$ since it requires greater search space. We find that the multiplicative inversion in $F_{2^8}$ can be computed through multiplicative inversion (and multiplication) in $F_{2^4}$, and the latter can be realized by the tool LIGHTER-R.

• We introduce a new technique to construct the quantum circuit of S-box for ${\mathcal{C}}_4:|\mathit{a}\rangle \to |S(\mathit{a})\rangle$ with only 16 qubits instead of 22 in the previous studies [25, 26]. Different from connecting ${\mathcal{C}}_1:|\mathit{a}\rangle |\mathbf{0}\rangle \to |\mathit{a}\rangle |S(\mathit{a})\rangle$ and ${\mathcal{C}}_3:|\mathit{a}\rangle |S(\mathit{a})\rangle \to |\mathbf{0}\rangle |S(\mathit{a})\rangle$ to obtain ${\mathcal{C}}_4$, we synthesize it in a direct way.

• We find that uncomputation for removing ancilla qubits (i.e., reinstate the initial state |0⟩) in some cases can be completed with fewer Toffoli and CNOT gates (without adding additional qubits). Therefore, our S-box circuit for ${\mathcal{C}}_1$ also requires fewer Toffoli and CNOT gates than the previous studies [25, 31]. Note that the number of Toffoli and CNOT gates is often regarded as a secondary optimization goal.

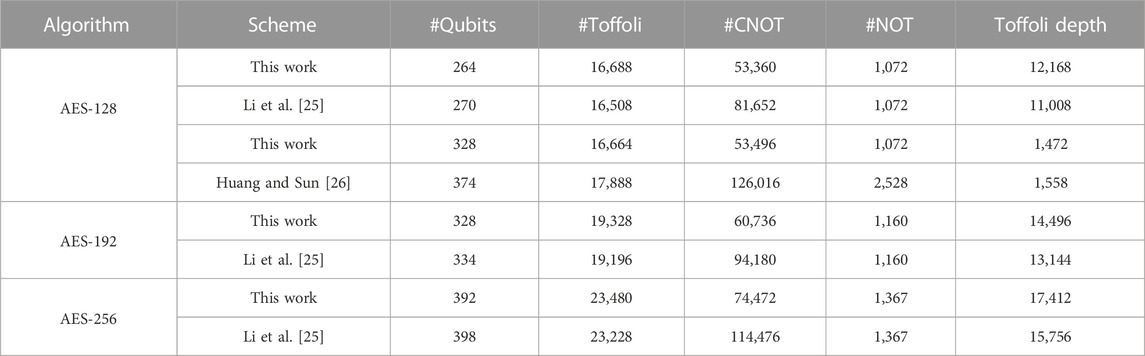
• By employing the above quantum circuits of S-box, we synthesize the quantum circuit of AES-128 with 264 qubits instead of 270 in a previous study [25], which implies a new record. Similarly, we also synthesize the quantum circuits of AES-192/-256 with 328/392 qubits instead of 334/398 in a previous study [25].

The rest of this paper is organized as follows. In Section 2, we briefly review the S-box of AES. In Section 3, we use the tool LIGHTER-R to obtain the quantum circuit of implementing the multiplicative inversion in $F_{2^4}$. In Section 4, our quantum circuits of the S-box are given. In Section 5, we synthesize the quantum circuit of AES. In Section 6, we conclude the paper.

2 Preliminaries

2.1 The S-box of AES

2.1.1 Algebraic structure of S-box

The non-linear transformation S-box first takes a byte input $\mathit{a}\in F_{2^8}=F_2[x]/(x^8+x^4+x^3+x+1)$, then replaces a with its multiplicative inversion a⁻¹ (when a = 0, set a⁻¹ = 0), and finally performs an affine transformation which is composed of multiplication by an invertible matrix and the addition of a constant vector. Specifically, the S-box transformation is expressed as

$S\left(\mathit{a}\right)=A{\mathit{a}}^{-1}\oplus \mathit{c},(1)$

where

$A=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right),\mathit{c}=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right).$

The computation of the S-box can be divided into two steps, i.e., computing the multiplicative inversion a⁻¹ and performing the affine transformation. The affine transformation can be implemented with CNOT and NOT gates only. Thus, how to realize the quantum circuit of finding a⁻¹ with low costs becomes one of the main factors optimizing the quantum circuit of the S-box.

2.1.2 A decomposition of S-box

In Ref. [34], Wolkerstorfer et al. constructed the following composite field $F_{{(2^4)}^2}$ isomorphic to $F_{2^8}$,

• The field polynomial of $F_{2^4}$ is x⁴ + x + 1;

• The field polynomial of $F_{{(2^4)}^2}$ is x² + x + λ, where $\lambda ≔x^3+x^2+x\in F_{2^4}$.

Due to isomorphism, the mapping matrix $M:F_{2^8}\to F_{{(2^4)}^2}$ and its inverse matrix $M^{-1}:F_{{(2^4)}^2}\to F_{2^8}$ are determined as

$M=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),M^{-1}=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).(2)$

Based on the composite field $F_{{(2^4)}^2}$, AES’s S-box can be rewritten as

$S\left(\mathit{a}\right)=A{M}^{-1}{\left(M\mathit{a}\right)}^{-1}\oplus \mathit{c},\mathit{a}\in F_{2^8}.(3)$

The multiplication by invertible matrices M, AM⁻¹ (merging of matrices A and M⁻¹) and the addition of a constant vector c can be implemented with CNOT and NOT gates only. Thus, the key to optimizing the S-box circuit becomes how the quantum circuit of finding (Ma)⁻¹ $(M\mathit{a}\in F_{{(2^4)}^2})$ can be implemented with low costs.

As pointed out in Ref. [34], any element $\mathit{p}\in F_{{(2^4)}^2}$ can be represented as a linear polynomial with coefficients in $F_{2^4}$, i.e., p = p₀ + p₁x, $p_0,p_1\in F_{2^4}$, and its multiplicative inversion p⁻¹ can be expressed as

$\begin{array}{cc}\hfill {\mathit{p}}^{-1}& ={\left({\mathit{p}}^{17}\right)}^{-1}\left(p_0+p_1\right)+{\left({\mathit{p}}^{17}\right)}^{-1}{p}_{1}x≔n_0+n_{1}x,\hfill \\ \hfill {\mathit{p}}^{17}& =p_1^2\times \lambda +\left(p_0+p_1\right)p_0\in F_{2^4}.\hfill \end{array}(4)$

where $\lambda ≔x^3+x^2+x\in F_{2^4}$. It is necessary for finding p⁻¹ to compute (p₀ + p₁)p₀, $p_1^2\times \lambda$, ${({\mathit{p}}^{17})}^{-1}(p_0+p_1)$ and ${({\mathit{p}}^{17})}^{-1}{p}_1$, which mainly involve the multiplication (including constant multiplication $p_1^2\times \lambda$) and multiplicative inversion operations in $F_{2^4}$.

It can be seen that the implementation of the S-box can be divided into three modules, i.e., the multiplication in $F_{2^4}$, the multiplicative inversion in $F_{2^4}$, the multiplication by invertible matrices M, AM⁻¹ and the addition of a constant vector c.

3 Quantum circuit of implementing the multiplicative inversion in $F_{2^4}$

Some quantum circuits of implementing the multiplicative inversion in $F_{2^4}$ have been proposed. Almazrooie et al. [35] constructed it by employing the quantum circuit of implementing the multiplication in $F_{2^4}$ many times. Saravanan et al. [36], Chung et al. [37] and Wang et al. [32] implemented it respectively based on a composite field $F_{{(2^2)}^2}$. Recently, Li et al. [25] constructed it by converting its classical circuit in Ref. [38] into a quantum version. See Table 3 for specific resource estimates.

In Ref. [33], Dasu et al. presented an automation tool, namely, LIGHTER-R¹, which can give the quantum circuit implementation of any 4-bit S-box based on a lookup table. The quantum circuit given by LIGHTER-R requires the optimal number of qubits. Recently, the tool has been widely applied in the quantum circuit implementation of other cryptography, such as Present and Gift [39], RECTANGLE and KNOT [40], DEFAULT [41] and so on.

We found that the multiplicative inversion in $F_{2^4}$ can be seen as a 4-bit S-box, whose lookup table is shown in Table 2. Thus, to obtain the quantum circuit of implementing the multiplicative inversion in $F_{2^4}$, we employ the tool LIGHTER-R directly. The resulting circuit is shown in Figure 1.

TABLE 2

TABLE 2. Lookup table of the multiplicative inversion in ${\mathit{F}}_{{\mathbf{2}}^{\mathbf{4}}}$.

FIGURE 1

FIGURE 1. Quantum circuit of implementing the multiplicative inversion in $F_{2^4}$. Here, b = (b₀, b₁, b₂, b₃) and its inverse ${\mathit{b}}^{-1}=(b_0^{-1},b_1^{-1},b_2^{-1},b_3^{-1})$ are the input vector and output vector, respectively. Note that b corresponds to an element in $F_{2^4}$. Swap operation only changes the index of qubits and does not require quantum gates.

The Tof₄/C³(X)/CCCNOT gate² in the dashed box of Figure 2 realizes the function of |a⟩|b⟩|c⟩|d⟩ → |a⟩|b⟩|c⟩|d ⊕ abc⟩ and can be decomposed by some Toffoli gates with an ancilla qubit (see Figure 2). Specifically, if the ancilla qubit is an unknown quantum state |g⟩, the CCCNOT gate can be decomposed by using the circuit in Figure 2A. If the state of |g⟩ is known to be |0⟩, the last Toffoli gate in Figure 2A is unnecessary which corresponds to Figure 2B. Thus, according to Figures 1, 2, we can obtain two quantum circuits of implementing the multiplicative inversion in $F_{2^4}$ for $F_{2^4}in{v}_0:|\mathit{b}\rangle |0\rangle \to |{\mathit{b}}^{-\mathit{1}}\rangle |0\rangle$ and $F_{2^4}in{v}_1:|\mathit{b}\rangle |g\rangle \to |{\mathit{b}}^{-\mathit{1}}\rangle |g\rangle$. These two quantum circuits will be used to implement the quantum circuit of the AES (8-bit) S-box. In the process, if there is an idle quantum state |0⟩, we use $F_{2^4}in{v}_0$. Otherwise, we use $F_{2^4}in{v}_1$.

FIGURE 2

FIGURE 2. Quantum circuits of CCCNOT.

The resource estimates of these two quantum circuits for $F_{2^4}in{v}_0$ and $F_{2^4}in{v}_1$ are given in Table 3. Compared with the previous studies, our quantum circuits require fewer qubits.

TABLE 3

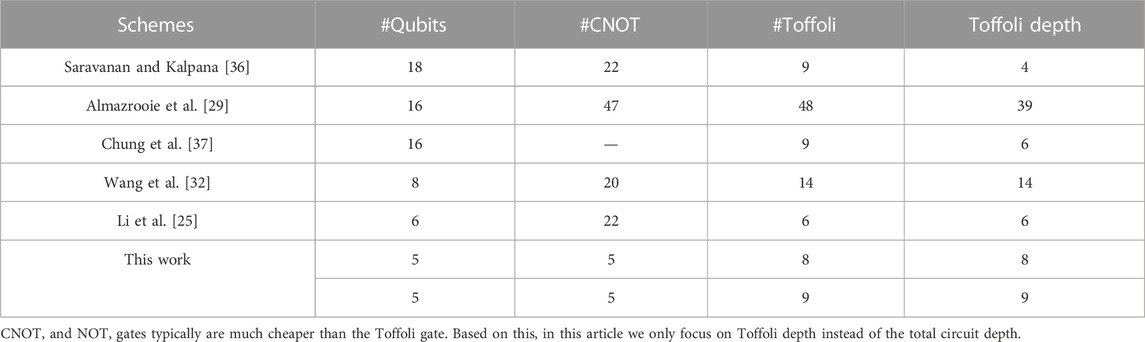
TABLE 3. Quantum resource estimates for the implementation of the multiplicative inversion in ${\mathbf{F}}_{{\mathbf{2}}^{\mathbf{4}}}$. #Toffoli/CNOT means the number of Toffoli and CNOT gates. #qubits means the number of qubits.

4 Quantum circuits of S-box

In the section, we propose three quantum circuits of S-box for ${\mathcal{C}}_1:|\mathit{a}\rangle |\mathbf{0}\rangle \to |\mathit{a}\rangle |S(\mathit{a})\rangle$, ${\mathcal{C}}_2:|\mathit{a}\rangle |\mathit{b}\rangle \to |\mathit{a}\rangle |\mathit{b}\oplus S(\mathit{a})\rangle$ and ${\mathcal{C}}_4:|\mathit{a}\rangle \to |S(\mathit{a})\rangle$ respectively³. Along the way, we directly adopt Li et al.’s [25] quantum circuits, including U_M, $U_{A{M}^{-1}}$, Mul, B₋Mul and $U_{q^2\lambda }$.

• U_M: |x⟩ → |Mx⟩ requires 8 qubits, 15 CNOT gates, and a total depth of 8; $U_{A{M}^{-1}}:|\mathit{x}\rangle \to |A{M}^{-1}\mathit{x}\rangle$ requires 8 qubits, 26 CNOT gates and a total depth of 10. Here, $\mathit{x}\in F_{2^8}$. Matrices A and M are referred in Eqs 1, 2 respectively.

• Mul: |f⟩|g⟩|0⁴⟩ → |f⟩|g⟩|f ⋅ g⟩ requires 12 qubits, 9 Toffoli gates, 23 CNOT gates and a Toffoli depth of 6; B₋Mul: |f⟩|g⟩|h⟩ → |f⟩|g⟩|h ⊕f ⋅ g⟩ requires 12 qubits, 9 Toffoli gates, 28 CNOT gates and Toffoli depth 6. Here, $\mathit{f},\mathit{g},\mathit{h}\in F_{2^4}$;

• $U_{q^2\lambda }:|q\rangle \to |q^2\times \lambda \rangle$ requires 4 qubits, 3 CNOT gates, and a total depth of 3. Here $\lambda ≔x^3+x^2+x\in F_{2^4}$, q is an arbitrary element in $F_{2^4}$.

4.1 Quantum circuit of S-box for ${\mathcal{C}}_1$

In order to implement the quantum circuit of S-box for ${\mathcal{C}}_1$, we first propose a quantum circuit of finding p⁻¹ for |p⟩|0⟩ → |p⟩|p⁻¹⟩. Here $\mathit{p}=p_0+p_{1}x\in F_{{(2^4)}^2}$ and its multiplicative inversion is ${\mathit{p}}^{-1}={({\mathit{p}}^{17})}^{-1}(p_0+p_1)+{({\mathit{p}}^{17})}^{-1}{p}_{1}x≔n_0+n_{1}x$.

We divide into four steps, i.e., computing p¹⁷, calculating the multiplicative inversion ${({\mathit{p}}^{17})}^{-1}$ of p¹⁷, obtaining p⁻¹ and uncomputation (i.e., clear up ancilla qubits), to construct the quantum circuit for |p⟩|0⟩ → |p⟩|p⁻¹⟩. Specifically, we first give the quantum circuit for $U_{p^{17}}:|\mathit{p}\rangle |0^4\rangle =|{\mathit{p}}_0\rangle |{\mathit{p}}_1\rangle |0^4\rangle \to |\mathit{p}\rangle |{\mathit{p}}^{17}\rangle$. According to ${\mathit{p}}^{17}=p_1^2\times \lambda +(p_0+p_1)p_0\in F_{2^4}$, $U_{p^{17}}$ can be realized by performing Mul, $U_{p_1^2\lambda }$ (take q≔p₁) and some CNOT gates (see the red box in Figure 3). Then $|{({\mathit{p}}^{17})}^{-1}\rangle$ is obtained by performing $F_{2^4}in{v}_0$ on |p¹⁷⟩|0⟩. Here, instead of adding a new qubit, we use an idle quantum state |0⟩ from output qubits as an ancilla qubit. Next $|{\mathit{p}}^{-1}\rangle =|{({\mathit{p}}^{17})}^{-1}(p_0+p_1)\rangle |{({\mathit{p}}^{17})}^{-1}{p}_1\rangle ≔|{\mathit{n}}_0\rangle |{\mathit{n}}_1\rangle$ is obtained in output qubits by performing Mul two times. At this time, the circuit is in state $|\mathit{p}\rangle |{({\mathit{p}}^{17})}^{-1}\rangle |{\mathit{p}}^{-1}\rangle$. In the end, $|{({\mathit{p}}^{17})}^{-1}\rangle$ in ancilla qubits has to be removed for reuse, i.e., completing uncomputation. As mentioned in Ref. [25], the general idea of completing the uncomputation is to perform $F_{2^4}in{v}_1^{†}$ (since there is no idle quantum state |0⟩) and $U_{p^{17}}^{†}$ on $|\mathit{p}\rangle |{({\mathit{p}}^{17})}^{-1}\rangle$. However, due to ${({\mathit{p}}^{17})}^{-1}={({\mathit{p}}^{-1})}^{17}$, ${({\mathit{p}}^{17})}^{-1}$ can also be expressed as $n_1^2\times \lambda +(n_1+n_0)n_0$. Therefore, we only apply $U_{p^{17}}^{†}$ (the inverse circuit of $U_{p^{17}}$) to implement $U_{{(p^{-1})}^{17}}^{†}:|{\mathit{p}}^{-1}\rangle |{({\mathit{p}}^{17})}^{-1}\rangle =|{\mathit{p}}^{-1}\rangle |{({\mathit{p}}^{-1})}^{17}\rangle \to |{\mathit{p}}^{-1}\rangle |\mathbf{0}\rangle$. The resulting quantum circuit, as shown in Figure 3, requires 20 qubits instead of 22 in a previous study [25].

FIGURE 3

FIGURE 3. Quantum circuit for |p⟩|0¹²⟩ → |p⟩|p⁻¹⟩|0⁴⟩. p = (p₀, p₁) and p⁻¹ = (n₀, n₁) are 8-bit input and output vectors respectively. CNOT gates between four qubit-sized wires should be read as multiple parallel CNOT gates applied bitwise. Dashed lines indicate wires that are not used in the corresponding circuit of the square box. Using $U_{q^2\lambda }$ to implement $U_{p_1^2\lambda }^{†}$ due to $p_1\in F_{2^4}$. $U_{p_1^2\lambda }^{†}$ is implemented by the inverse circuit of $U_{p_1^2\lambda }$. A quantum state |0⟩ from output qubits is used as ancilla qubit of $F_{2^4}in{v}_0$.

By combining the quantum circuit in Figure 3 with U_M and $U_{A{M}^{-1}}$, we obtain the quantum circuit of S-box for ${\mathcal{C}}_1$ in Figure 4, which requires 20 qubits.

FIGURE 4

FIGURE 4. Quantum circuit of the S-box for ${\mathcal{C}}_1:|\mathit{a}\rangle |0^{12}\rangle \to |\mathit{a}\rangle |S(\mathit{a})\rangle |0^4\rangle$. The input is one element $\mathit{a}\in F_{2^8}$. The output is S(a). $U_{out{(M\mathit{a})}^{-1}}:|M\mathit{a}\rangle |\mathbf{0}\rangle \to |M\mathit{a}\rangle |{(M\mathit{a})}^{-1}\rangle$ is implemented by the quantum circuit in Figure 3 since Ma is contained in $F_{{(2^4)}^2}$. $U_{M^{-1}}$ is implemented by the inverse circuit of U_M. ⊕ represents that the constant vector c is added by flipping four qubits with four NOT gates.

The quantum resource estimates of ${\mathcal{C}}_1$ are shown in Table 4. Compared with the previous studies, our S-box circuit for ${\mathcal{C}}_1$ requires fewer quantum resources including the number of qubits.

TABLE 4

TABLE 4. Comparison of our S-box circuit for ${\mathbf{C}}_{\mathbf{1}}$ with previous works.

Remark 1. Compared with the circuit outlined by Li et al., our circuit is different in two aspects. First, we take an idle qubit from output qubits as ancilla qubits and then compute ${(p^{-1})}^{17}$ by $F_{2^4}in{v}_0$. Second, we find that uncomputation can be completed only by performing circuit $U_{p^{17}}^{†}$ without $F_{2^4}in{v}_1^{†}$. As a result, our S-box circuit for ${\mathcal{C}}_1$ requires not only fewer qubits but also fewer Toffoli gates and lower Toffoli depth. Cost estimates can be found in Table 4.

Our results show that uncomputation for removing ancilla qubits (i.e., reinstate the initial state |0⟩) can be optimized when the algebraic relationship between the value in ancilla qubits and f(x) is simpler than that between x and the value in ancilla qubits. Here, assume that f(x) is an arbitrary invertible non-linear transformation, the goal circuit U_f: |x⟩|0⟩ → |x⟩|f(x)⟩ is implemented by introducing some ancilla qubits. For example, in Figure 4, x≔p, f(x)≔p⁻¹, after getting the output information p⁻¹, as analyzed above, the value ${({\mathit{p}}^{17})}^{-1}$ in ancilla qubits has simpler algebraic relationship with p⁻¹ than with p.

4.2 Quantum circuit of S-box for ${\mathcal{C}}_2$

In order to implement the quantum circuit of S-box for ${\mathcal{C}}_2$, we first proposed an improved quantum circuit for |p⟩|h⟩ → |p⟩|h ⊕p⁻¹⟩.

Similar to Figure 3, we divide into four steps to implement |p⟩|h⟩ → |p⟩|h ⊕p⁻¹⟩. First, |p¹⁷⟩ is obtained by performing $U_{p^{17}}$ on |p⟩|0⁴⟩. However, unlike Figure 3, we only use $F_{2^4}in{v}_1$ to compute $|{({\mathit{p}}^{17})}^{-1}\rangle$ since there is no idle quantum state |0⟩. The input state in output qubits is |h⟩ = |h₀⟩|h₁⟩ instead of |0⁸⟩. Next, |h ⊕p⁻¹⟩ = |h₀ ⊕n₀⟩|h₁ ⊕n₁⟩ is obtained by using B₋Mul twice instead of Mul. In the end, we need to clean up $|{({\mathit{p}}^{17})}^{-1}\rangle$. Unfortunately, the removal has to be completed by $F_{2^4}in{v}_1$ and $U_{p^{17}}^{†}$ because the output qubits are in state |h ⊕p⁻¹⟩ instead of |p⟩. Note that because of the same function, we only use $F_{2^4}in{v}_1$ instead of $F_{2^4}in{v}_1^{†}$ (i.e., |b⁻¹⟩|g⟩ → |b⟩|g⟩, ${({\mathit{b}}^{-1})}^{-1}=\mathit{b}$). The resulting quantum circuit, as shown in Figure 5, requires 20 qubits instead of 22 in a previous study [25].

FIGURE 5

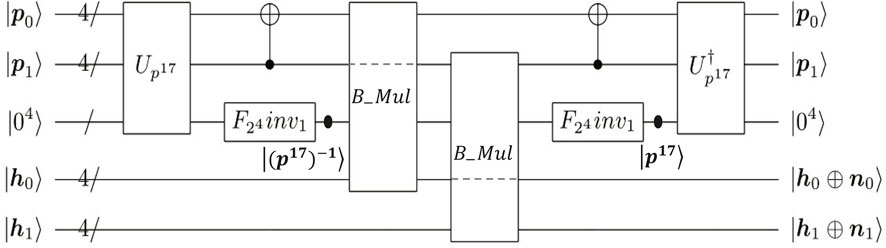
FIGURE 5. Quantum circuit for |p⟩|h⟩|0⁴⟩ → |p⟩|h ⊕p⁻¹⟩|0⁴⟩. h = (h₀, h₁) is an arbitrary 8-bit vector. $F_{2^4}in{v}_1$ applies an unknown quantum state |g⟩ from output qubits as its ancilla qubit, which is returned to the same state at the end of the circuit.

By combining the quantum circuit in Figure 5 with U_M and $U_{A{M}^{-1}}$, we construct the quantum circuit of S-box for ${\mathcal{C}}_2:|\mathit{a}\rangle |\mathit{b}\rangle |0^4\rangle \to |\mathit{a}\rangle |\mathit{b}\oplus S(\mathit{a})\rangle |0^4\rangle$ in Figure 6, whose number of qubits is 20.

FIGURE 6

FIGURE 6. Quantum circuit for ${\mathcal{C}}_2:|\mathit{a}\rangle |\mathit{b}\rangle |0^4\rangle \to |\mathit{a}\rangle |\mathit{b}\oplus S(\mathit{a})\rangle |0^4\rangle$.
$U_{M{A}^{-1}\mathit{b}\oplus {(M\mathit{a})}^{-1}}:|M\mathit{a}\rangle |M{A}^{-1}\mathit{b}\rangle$$\to |M\mathit{a}\rangle |M{A}^{-1}\mathit{b}\oplus {(M\mathit{a})}^{-1}\rangle$
is implemented by the quantum circuit in
Figure 5 because MA⁻¹b and Ma
are contained in $F_{{(2^4)}^2}$. $U_{M{A}^{-1}}$ is
implemented by the inverse circuit of $U_{A{M}^{-1}}$.

Table 5 summarizes the quantum resources needed to realize ${\mathcal{C}}_2$. Compared with previous studies, our S-box circuit for ${\mathcal{C}}_2$ requires fewer qubits.

TABLE 5

TABLE 5. Comparison of our S-box circuit for ${\mathbf{C}}_{\mathbf{2}}$ with previous works.

Remark 2. Compared with the circuit described by Li et al., we take an idle qubit from output qubits as ancilla qubits and then compute ${(p^{-1})}^{17}$ by $F_{2^4}in{v}_1$, resulting in a reduction in the number of qubits. Cost estimates can be found in Table 5.

4.3 Quantum circuit of S-box for ${\mathcal{C}}_4$

Based on the idea mentioned in Ref. [42], Li et al [25] and Huang et al. [26] realized the goal by connecting two quantum circuits for |a⟩|0⟩ → |a⟩|S(a)⟩ and |a⟩|S(a)⟩ → |0⟩|S(a)⟩. Here, different from the previous method, we realize the goal by proposing a quantum circuit for |p⟩ → |p⁻¹⟩.

Similar to Figure 3, we first obtain |p¹⁷⟩ by performing $U_{p^{17}}$ on |p⟩|0⁴⟩, and then compute $|{({\mathit{p}}^{17})}^{-1}\rangle$ by performing $F_{2^4}in{v}_0$ on |p¹⁷⟩|0⟩ (since there is idle quantum state |0⟩). Next, we perform the circuit In₋Mul in Eq. 5 of Observation 1 twice to obtain |n₀⟩ and |n₁⟩ respectively, i.e., the circuit is in state $|{\mathit{n}}_1\rangle |0^4\rangle |{({\mathit{p}}^{17})}^{-1}\rangle |{\mathit{n}}_0\rangle$. Along the way, instead of adding additional qubits, |p₀⟩ is removed for gaining storage space to place n₁ after obtaining |n₀⟩. In the end, $|{({\mathit{p}}^{17})}^{-1}\rangle$ is removed by executing $U_{{(p^{-1})}^{17}}^{†}$ on $|{\mathit{n}}_0\rangle |{\mathit{n}}_1\rangle |{({\mathit{p}}^{17})}^{-1}\rangle =|{\mathit{p}}^{-1}\rangle |{({\mathit{p}}^{17})}^{-1}\rangle$. The resulting quantum circuit, as shown in Figure 7, requires 16 qubits.

FIGURE 7

FIGURE 7. Quantum circuit for |p⟩|0⁸⟩ → |p⁻¹⟩|0⁸⟩.

Observation 1. The quantum circuit for In₋Mul: |f⟩|g⟩|0⟩ → |0⟩|g⟩|f ⋅ g⟩ can not only get f ⋅ g, but also release storage space to place other values if f is useless in subsequent operations. In₋Mul can be implemented as follows

$|\mathit{f}\rangle |\mathit{g}\rangle |0^4\rangle \stackrel{F_{2^{4}in{v}_1}\cdot Mul}{\to }|\mathit{f}\rangle |{\mathit{g}}^{-1}\rangle |\mathit{f}\cdot \mathit{g}\rangle \stackrel{F_{2^{4}in{v}_0}\cdot Mu{l}^{†}}{\to }|0^4\rangle |\mathit{g}\rangle |\mathit{f}\cdot \mathit{g}\rangle (5)$

Due to (f ⋅ g) ⋅g⁻¹ = f, the circuit Mul^† (|f⟩|g⟩|f ⋅ g⟩ → |f⟩|g⟩|0⟩) is used to convert |f⟩|g⁻¹⟩|f ⋅ g⟩ into |0⟩|g⁻¹⟩|f ⋅ g⟩. At this moment, there exist an idle quantum state |0⟩, so |g⁻¹⟩ is converted back into |g⟩ by $F_{2^4}in{v}_0$.

By combining the quantum circuit in Figure 7 with U_M and $U_{A{M}^{-1}}$, we obtain the S-box circuit for ${\mathcal{C}}_4$: |a⟩|0⁸⟩ → |S(a)⟩|0⁸⟩ in Figure 8, which requires 16 qubits.

FIGURE 8

FIGURE 8. Quantum circuit for ${\mathcal{C}}_4:|\mathit{a}\rangle |0^8\rangle \to |S(\mathit{a})\rangle |0^8\rangle$. $U_{in{(Ma)}^{-1}}:|\mathit{a}\rangle \to |{(M\mathit{a})}^{-1}\rangle$ is implemented by the quantum circuit in Figure 7 because Ma is contained in $F_{{(2^4)}^2}$.

Table 6 summarizes the quantum resources needed to implement the S-box circuit for ${\mathcal{C}}_4$. Compared with previous studies, our S-box circuit for ${\mathcal{C}}_4$ requires fewer qubits.

TABLE 6

TABLE 6. Comparison of our S-box circuit for ${\mathbf{C}}_{\mathbf{4}}$ with previous works.

In order to reduce the number of qubits, we often would like to compute f(x) with an in-place circuit, i.e., |x⟩ → |f(x)⟩. For example, we directly obtain the in-place quantum circuit $F_{2^4}in{v}_0$ by the tool LIGHTER-R. However, for some complex functions f(x) (e.g., the multiplicative inversion in $F_{2^8}$), directly designing an in-place quantum circuit is difficult. As mentioned in Ref. (Huang and Sun, 2022), a natural idea is to construct an in-place circuit based on out-of-place sub-circuits. Huang et al. (Huang and Sun, 2022) proposed an in-place quantum circuit for |x⟩ → |f(x)⟩ by connecting two out-of-place circuit |x⟩|0⟩ → |x⟩|f(x)⟩ and |f⁻¹(y)⟩|y⟩ → |0⟩|y⟩ (f⁻¹ is invertible function of f). Thus, their in-place circuit requires at least 4n qubits if f(x): {0,1}²ⁿ → {0,1}²ⁿ is an arbitrary invertible non-linear transformation. By connecting |a⟩|0⟩ → |a⟩|S(a)⟩ and |a⟩|S(a)⟩ → |0⟩|S(a)⟩, Huang et al. (Huang and Sun, 2022) and Li et al. (Li et al., 2022b) gave the quantum circuit of S-box for ${\mathcal{C}}_4$, whose cost estimates can be found in Table 6.

Observation 2. |x⟩ → |f(x)⟩ can be constructed with at least 3n qubits. If f(x) can be expressed as f(x) = f₀(x₀)‖f₁(x₁) (f₀(x₀), f₁(x₁): {0,1}ⁿ → {0,1}ⁿ are invertible non-linear transformation) when x is divided into x₀ and x₁, i.e., x≔x₀‖x₁, |x⟩ → |f(x)⟩ is implemented as followed

$|{\mathit{x}}_{\mathbf{0}}\rangle |{\mathit{x}}_1\rangle |0^n\rangle \stackrel{U_{f_0}}{\to }|0^n\rangle |{\mathit{x}}_1\rangle |{\mathit{f}}_{\mathit{0}}\left({\mathit{x}}_{\mathit{0}}\right)\rangle \stackrel{SWAP\cdot U_{f_1}}{\to }|{\mathit{f}}_{\mathit{0}}\left({\mathit{x}}_{\mathit{0}}\right)\rangle |{\mathit{f}}_{\mathit{1}}\left({\mathit{x}}_{\mathit{1}}\right)\rangle |0^n\rangle (6)$

|x₀⟩ is removed to gain storage space to place f₁ (x₁) only when it is useless in subsequent operations. In our circuit for |p⟩ → |p⁻¹⟩, x≔p = p₀‖p₁ and f(x)≔p⁻¹ = f₀ (x₀)‖f₁ (x₁) (note $f_0(x_0)≔{({\mathit{p}}^{17})}^{-1}(p_0+p_1),f_1(x_1)≔{({\mathit{p}}^{17})}^{-1}{p}_1$), $U_{f_0}$ and $U_{f_1}$ are implemented with the circuit in eq. (5) (${({\mathit{p}}^{17})}^{-1}$ is computed in ancilla qubits which is regarded as constant in f₀ (x₀) and f₁ (x₁)).

5 Quantum circuit implementations of AES

AES is a family of iterative block ciphers, which encrypts 16 bytes (i.e., 128 bits) of plaintexts and consists of a round function and key expansion. The subroutines of the round function include SubBytes, ShiftRows, MixColumns, and AddRoundKey (note the last round does not perform the MixColumns). The subroutines of key expansion include SubWord, RotWord, and Rcon. AES’s three instances AES-128 (10 iterations), AES-192 (12 iterations), and AES-256 (14 iterations) correspond to the key lengths of 128, 192, and 256 bits respectively. The full specification of AES can be found in Ref. [22].

In the present study, we implement the SubBytes (applying 16 S-box substitutions) and SubWord (applying 4 S-box substitutions) by the S-box circuits in Section 4. For other linear operations, the ShiftRows and Rotword can be implemented by appropriate rewiring. The MixColumns can be implemented with 368 CNOT gates [43]. The AddRoundKey is implemented with 128 CNOT gates. The Rcon is implemented by applying NOT gates.

In the following, we introduce the methods of round function iteration and key expansion iteration, then synthesize the quantum circuit of AES.

5.1 Method of round function iteration

As shown in Table 1, quite a few round function iteration methods were introduced. Grassl et al. [28] proposed the zig-zag method, which requires 512 + 24 = 536 qubits (24 is the number of ancilla qubits required by their S-box circuit for ${\mathcal{C}}_1$), to implement the round function iteration of AES-128. Almazrooie et al. [29] and Langenberg et al., [30] employed the zig-zag method to complete the iteration. Zou et al., [31] proposed an improved zig-zag method that requires at least 256 qubits. Wang et al., [32] realized the iteration by the improved zig-zag method. Recently, Li et al., [25] presented a straight-line method, which requires 128 + 14 = 142 qubits (14 is the number of ancilla qubits required by their S-box circuit for ${\mathcal{C}}_4$). To make a tradeoff between the number of qubits and Toffoli depth, Huang et al. [26] completed the iteration by the straight-line method with 128 + 8 × 14 = 240 qubits (i.e., running S-box circuit for ${\mathcal{C}}_4$ eight-time simultaneously in constructing the SubBytes of ith iteration R_i).

We also apply Li et al.’s straight-line method to realize the round function iteration of AES-128. From Figure 8, we can see that our S-box circuit for ${\mathcal{C}}_4$ reduces the number of ancilla qubits from 14 in the previous studies [25, 26] to 8. As a result, the number of qubits required to implement the round function iteration of AES-128 becomes 128 + 8 = 136. Similarly, the round function iteration of AES-192/-256 can also be implemented with 136/136 qubits.

Remark 3. We can also make a trade-off between the number of qubits and Toffoli depth by adding the number of S-box circuits for ${\mathcal{C}}_4$ in parallel. That is, if we implement k S-box circuits for ${\mathcal{C}}_4$ in parallel (k divided by 16) each time in constructing the SubBytes of R_i, the number of qubits required for the round function iteration of AES-128/-192/-256 becomes 128 + 8k.

5.2 Method of key expansion iteration

Some key expansion iteration methods were proposed. Grassl et al. [28] proposed the pipeline method, which requires at least 448 + 24 = 472 qubits (24 is the number of ancilla qubits required by their S-box circuit for ${\mathcal{C}}_1$), to implement the key expansion iteration of AES-128. Then Almazrooie et al. [29] presented an improved pipeline method that requires at least 416 + 48 = 464 qubits. Langenberg et al., [30] found that the zig-zag method can be used to complete the key expansion iteration, which requires 352 + 16 = 368 qubits. Zou et al., [31] proposed an improved zig-zag method to realize the iteration, which requires 256 + 7 = 263 (7 is the number of ancilla qubits required by Zou et al.’s S-box circuit for ${\mathcal{C}}_2$). Wang et al. [32] presented a straight-line method to implement the key expansion iteration, which requires 128 + 16 qubits. To make a tradeoff between the number of qubits and Toffoli depth, Jaques et al. [24] completed the iteration by the straight-line method with 128 + 4 × 121 = 612 qubits (i.e., running S-box circuit for ${\mathcal{C}}_2$ four-time simultaneously in constructing the SubWord of key K_i in the ith iteration). Li et al. [25] and Huang et al. [26] adopted the straight-line method to complete the iteration.

Here, we apply the straight-line method to implement the key expansion iteration of AES-128. Because our S-box circuit for ${\mathcal{C}}_2$ requires 4 ancilla qubits (see Figure 6), the key expansion iteration of AES-128 can be realized with 128 + 4 = 132 qubits. Similarly, we perform the key expansion iteration of AES-192/-256 with 196/260 qubits. Of course, as a trade-off between the number of qubits and Toffoli depth, the number of qubits can also be 128 + 4h/192 + 4h/256 + 4h for the key expansion iteration of AES-128/-192/-256 (h is the number of running S-box circuit for ${\mathcal{C}}_2$ in parallel when the SubWord is constructed).

Remark 4. In synthesizing the quantum circuit of the AES, if the SubBytes in R_i and SubWord in the key expansion are not constructed simultaneously, we can reuse idle qubits, which is applied to implement the round function iteration, to construct the SubWord. Thus, as the previous studies Grassl et al. [28]; Almazrooie et al. [29]; Langenberg et al. [30]; Wang et al. [32]; Li et al. [25]; Zou et al. [31], they implement the key expansion without adding additional ancilla (see Table 1). Otherwise, as a trade-off between the number of qubits and Toffoli depth, it is necessary to add new qubits as the previous studies [24,26].

5.3 Quantum circuits for implementing AES

Based on the straight-line method above, we synthesize the quantum circuit of AES-128 with 264 qubits, where 136 qubits and 128 qubits are used to complete the round function iteration and key expansion iteration. Note that 8 ancilla qubits in round function iteration are reused to implement the key expansion iteration.

First, as mentioned in the previous studies [25, 26, 28, 31], to save qubits, R₀ which adds the key K₀ on plaintext m (whitening step) is implemented by apply NOT gates on some specific qubits of |K₀⟩ (at most 128 NOT gates). Then when |R₀⟩ is used to compute the SubBytes in R₁ later, |R₀⟩ is reinstated |K₀⟩ by applying NOT gates (at most 128 NOT gates). Particularly, the SubBytes in R₁ are constructed by running our S-box circuit for ${\mathcal{C}}_1$ sixteen times. The depth of ${\mathcal{C}}_1$ is 3. The SubWord in K₁ is constructed by running the S-box circuit for ${\mathcal{C}}_2$ four times. The depth of ${\mathcal{C}}_2$ is 2. After realizing the SubWord, we perform the Rotword and Rcon to obtain K₁ while ShiftRows and MixColumns are implemented. At last, the AddRoundKey is implemented by performing 128 CNOT in parallel. Therefore, realizing R₀ and R₁ require Toffoli depth 3 × 32 + 2 × 42 = 180. Besides, these two rounds require 16 × 44 + 4 × 54 = 920 Toffoli gates, 197 × 16 + 238 × 4 + 96 + 368 + 128 = 4696 CNOT gates, and 256 + 4 × 20 + 1 = 337 NOT gates.

Then, we implement R_i (i > 1). Because ${\mathcal{C}}_4$ requires 8 ancilla qubits (see Figure 8), we run the S-box circuit for ${\mathcal{C}}_4$ sixteen times in order to construct the SubBytes. The depth of ${\mathcal{C}}_4$ is 16, i.e., the Toffoli-depth is 78 × 16 = 1,248. Similarly, because ${\mathcal{C}}_2$ requires 4 ancilla qubits (see Figure 6), two S-box transformations in SubWord of K_i can be implemented in parallel. Thus, the depth of ${\mathcal{C}}_2$ required for constructing the SubWord is 2, i.e., the Toffoli-depth is 42 × 2 = 84. After realizing the SubWord, we perform the Rotword and Rcon to obtain K_i while ShiftRows and MixColumns are implemented. The AddRoundKey is implemented last, by performing 128 CNOT in parallel. As a result, R_i can be constructed with Toffoli depth 1,248 + 84 = 1,332 since the SubBytes and SubWord cannot be implemented in parallel. Besides, R_i requires 16 × 96 + 4 × 54 = 1752 Toffoli gates, 244 × 16 + 238 × 4 + 96 + 368 + 128 = 5448 CNOT gates (R₁₀ does not perform the MixColumns and requires 244 × 16 + 238 × 4 + 96 + 128 = 5080 CNOT gates) and 4 × 20 + 1 = 81 NOT gates (R₉ and R₁₀ require 4 × 20 + 4 = 84 NOT gates).

At last, by combining these quantum circuits above, we can obtain the quantum circuit for implementing AES-128. Similarly, the quantum circuit of AES-192/-256 can be implemented with 334/398 qubits, respectively. Table 7 gives the quantum resources required for implementing AES. Obviously, our improved quantum circuits of S-box result in a reduction of the number of qubits.

TABLE 7

TABLE 7. Quantum resources for implementing AES.

Remark 5. We can make a trade-off between the number of qubits and Toffoli-depth. From Figures 6, 8, it can be seen that the number of ancilla qubits required for two S-box circuits for ${\mathcal{C}}_2$ is the same as the number of ancilla qubits required for one S-box circuit for ${\mathcal{C}}_4$. We regard two parallel circuits for ${\mathcal{C}}_2$ as a whole circuit and call such circuit and ${\mathcal{C}}_4$ double-width S-box circuits. In this case, 18 double-width S-box circuits in total are required in constructing the SubBytes and SubWord of R_i (i > 1). If p double-width S-box circuits is implemented in parallel (p divided by 18, i.e., p = 1, 2, 3, 6, 9, 18), the number of qubits required for AES-128 will be 256 + 8p.

• When p = 1, circuit costs for implementing AES-128 is given in Table 7;

• When p > 1, the Toffoli-depth of constructing the SubBytes and SubWord in R_i (i > 1) becomes 78 × 18/p = 1,404/p.

• When p = 2, the depth of S-box circuit for ${\mathcal{C}}_1$ in constructing the SubBytes of R₁ is 3, i.e., the Toffoli-depth is 32 × 3 = 96. And the depth of the S-box circuit for ${\mathcal{C}}_2$ in constructing the SubWord of round key K₁ becomes 1, i.e., the Toffoli-depth is 42. Thus, R₁ is implemented with a Toffoli-depth of 138;

• When p = 3 or 6, the Toffoli-depth of SubBytes in constructing R₁ is 32 × 2 = 64, and the Toffoli-depth of SubWord in constructing the round key K₁ becomes 36. Thus, R₁ is implemented with a Toffoli depth of 100. Here, the SubWord is constructed with the S-box circuit for ${\mathcal{C}}_2$ in Ref.[25] because it requires lower Toffoli-depth and the ancilla qubits are also sufficient at this time;

• When p = 9 or 18, the Toffoli-depth of SubBytes in constructing R₁ is 32, and the Toffoli-depth of SubWord in constructing the round key K₁ becomes 36. Thus, R₁ is implemented with a Toffoli depth of 68. Table 7 also gives the quantum resources required for implementing AES-128 when p = 9.

6 Conclusion

In this study, we set a new record of the number of qubits required to synthesize the quantum circuit of AES. First, we find a method to realize the quantum circuit of the AES S-box with the help of the automation tool LIGHTER-R. Specifically, the main part of the S-box, i.e., the multiplicative inversion in $F_{2^8}$, is computed through the multiplicative inversion (and multiplication) in $F_{2^4}$, then the quantum circuit implementation of the latter is obtained by the tool LIGHTER-R. Based on this, the quantum circuits of S-box for ${\mathcal{C}}_1:|\mathit{a}\rangle |\mathbf{0}\rangle \to |\mathit{a}\rangle |S(\mathit{a})\rangle$ and ${\mathcal{C}}_2:|\mathit{a}\rangle |\mathit{b}\rangle \to |\mathit{a}\rangle |\mathit{b}\oplus S(\mathit{a})\rangle$ are constructed with 20 qubits instead of 22 in the previous studies respectively. Second, by introducing new techniques, we reduce the number of qubits required by the S-box circuit for ${\mathcal{C}}_4:|\mathit{a}\rangle \to |S(\mathit{a})\rangle$ from 22 in the previous studies to 16. At last, by applying these S-box circuits for ${\mathcal{C}}_1$, ${\mathcal{C}}_2$ and ${\mathcal{C}}_4$, we synthesize the quantum circuits of AES-128/-192/-256 with 264/328/392 qubits instead of 270/334/398 in the previous studies.

Some inspirations can be drawn from our results. On the one hand, automated tools, for example, the LIGHTER-R, should be fully utilized. On the other hand, similar to our circuit for |a⟩ → |S(a)⟩, we should design the goal circuit directly as far as possible instead of using the previous trivial method, i.e., connecting two circuits. Particularly, since other symmetric ciphers (such as SM4 and Camellia) also use a similar S-box, their quantum circuits might be optimized by our methods.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos 61972048, 62272056, and 61976024) and Henan Key Laboratory of Network Cryptography Technology (LNCT2021-A10).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1171753/full#supplementary-material

Footnotes

¹The source code of LIGHTER-R is available at https://github.com/vdasu/lighter-r.

²They refer to the same quantum gate. Only CCCNOT is mentioned below.

³The code that verifies the correctness of these S-box circuits is available at https://github.com/lzq192921/quantum-circuit-implementation-of-AES.git.

References

1. Harrow AW, Hassidim A, Lloyd S. Quantum algorithm for linear systems of equations. Phys Rev Lett (2009) 103:150502. doi:10.1103/physrevlett.103.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wan L, Yu C, Pan S, Gao F, Wen Q, Qin S. Asymptotic quantum algorithm for the toeplitz systems. Phys Rev A (2018) 97:062322. doi:10.1103/physreva.97.062322

CrossRef Full Text | Google Scholar

3. Liu H, Wu Y, Wan L, Pan S, Qin S, Gao F, et al. Variational quantum algorithm for the Poisson equation. Phys Rev A (2021) 104:022418. doi:10.1103/physreva.104.022418

CrossRef Full Text | Google Scholar

4. Lloyd S, Mohseni M, Rebentrost P. Quantum algorithms for supervised and unsupervised machine learning (2013). arXiv preprint arXiv:1307.0411.

Google Scholar

5. Wiebe N, Braun D, Lloyd S. Quantum algorithm for data fitting. Phys Rev Lett (2012) 109:050505. doi:10.1103/physrevlett.109.050505

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Rebentrost P, Mohseni M, Lloyd S. Quantum support vector machine for big data classification. Phys Rev Lett (2014) 113:130503. doi:10.1103/physrevlett.113.130503

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ye Z, Li L, Situ H, Wang Y. Quantum speedup for twin support vector machines (2019). arXiv preprint arXiv:1902.08907.

Google Scholar

8. Li Q, Huang Y, Jin S, Hou X, Wang X. Quantum spectral clustering algorithm for unsupervised learning (2022). arXiv preprint arXiv:2203.03132.

Google Scholar

9. Lloyd S, Mohseni M, Rebentrost P. Quantum principal component analysis. Nat Phys (2014) 10:631–3. doi:10.1038/nphys3029

CrossRef Full Text | Google Scholar

10. Cong I, Duan L. Quantum discriminant analysis for dimensionality reduction and classification. New J Phys (2016) 18:073011. doi:10.1088/1367-2630/18/7/073011

CrossRef Full Text | Google Scholar

11. Pan S, Wan L, Liu H, Wang Q, Qin S, Wen Q, et al. Improved quantum algorithm for a-optimal projection. Phys Rev A (2020) 102:052402. doi:10.1103/physreva.102.052402

CrossRef Full Text | Google Scholar

12. Yu C, Gao F, Lin S, Wang J. Quantum data compression by principal component analysis. Quan Inf Process (2019) 18:249–20. doi:10.1007/s11128-019-2364-9

CrossRef Full Text | Google Scholar

13. Wang G. Quantum algorithm for linear regression. Phys Rev A (2017) 96:012335. doi:10.1103/physreva.96.012335

CrossRef Full Text | Google Scholar

14. Yu C, Gao F, Wen Q. An improved quantum algorithm for ridge regression. IEEE Trans Knowledge Data Eng (2019) 33:1–866. doi:10.1109/tkde.2019.2937491

CrossRef Full Text | Google Scholar

15. Yu C, Gao F, Liu C, Huynh D, Reynolds M, Wang J. Quantum algorithm for visual tracking. Phys Rev A (2019) 99:022301. doi:10.1103/physreva.99.022301

CrossRef Full Text | Google Scholar

16. Yu C, Gao F, Wang Q, Wen Q. Quantum algorithm for association rules mining. Phys Rev A (2016) 94:042311. doi:10.1103/physreva.94.042311

CrossRef Full Text | Google Scholar

17. Liu N, Rebentrost P. Quantum machine learning for quantum anomaly detection. Phys Rev A (2018) 97:042315. doi:10.1103/physreva.97.042315

CrossRef Full Text | Google Scholar

18. Guo M, Liu H, Li Y, Li W, Gao F, Qin S, et al. Quantum algorithms for anomaly detection using amplitude estimation. Physica A: Stat Mech its Appl (2022) 604:127936. doi:10.1016/j.physa.2022.127936

CrossRef Full Text | Google Scholar

19. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J Comput (1997) 26:1484–509. doi:10.1137/s0097539795293172

CrossRef Full Text | Google Scholar

20. Grover LK. A fast quantum mechanical algorithm for database search. In: GL Miller, editor. Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. New York, NY, USA: ACM (1996). p. 212–9.

CrossRef Full Text | Google Scholar

21. Simon DR. On the power of quantum computation. SIAM J Comput (1997) 26:1474–83. doi:10.1137/s0097539796298637

CrossRef Full Text | Google Scholar

22. Joan D, Vincent R. Specification for the advanced encryption standard (aes). Springfield: FIPS 197 (2001).

Google Scholar

23.NIST. Submission requirements and evaluation criteria for the post-quantum cryptography standardization process (2016).

Google Scholar

24. Jaques S, Naehrig M, Roetteler M, Virdia F. Implementing grover oracles for quantum key search on aes and lowmc. In: A Canteaut,, and Y Ishai, editors. Advances in cryptology – eurocrypt 2020. Cham: Springer (2020). p. 280–310.

CrossRef Full Text | Google Scholar

25. Li Z, Cai B, Sun H, Liu H, Wan L, Qin S, et al. Novel quantum circuit implementation of advanced encryption standard with low costs. Sci China Phys Mech Astron (2022) 65:290311. doi:10.1007/s11433-022-1921-y

CrossRef Full Text | Google Scholar

26. Huang Z, Sun S. Synthesizing quantum circuits of aes with lower t-depth and less qubits (2022). Cryptology ePrint Archive, Paper 2022/620.

Google Scholar

27. Jang K, Baksi A, Kim H, Song G, Seo H, Chattopadhyay A. Quantum analysis of aes (2022). Cryptology ePrint Archive, Paper 2022/683.

Google Scholar

28. Grassl M, Langenberg B, Roetteler M, Steinwandt R. Applying grover’s algorithm to aes: Quantum resource estimates. In: T Takagi, editor. Post-quantum cryptography. Cham: Springer (2016). p. 29–43.

CrossRef Full Text | Google Scholar

29. Almazrooie M, Samsudin A, Abdullah R, Mutter KN. Quantum reversible circuit of aes-128. Quan Inf Process (2018) 17:112–30. doi:10.1007/s11128-018-1864-3

CrossRef Full Text | Google Scholar

30. Langenberg B, Pham H, Steinwandt R. Reducing the cost of implementing the advanced encryption standard as a quantum circuit. IEEE Trans Quan Eng (2020) 1:1–12. doi:10.1109/tqe.2020.2965697

CrossRef Full Text | Google Scholar

31. Zou J, Wei Z, Sun S, Liu X, Wu W. Quantum circuit implementations of aes with fewer qubits. In: S Moriai,, and H Wang, editors. Advances in cryptology – asiacrypt 2020. Cham: Springer (2020). p. 697–726.

CrossRef Full Text | Google Scholar

32. Wang Z, Wei S, Long G. A quantum circuit design of aes requiring fewer quantum qubits and gate operations. Front Phys (2022) 17:41501–7. doi:10.1007/s11467-021-1141-2

CrossRef Full Text | Google Scholar

33. Dasu VA, Baksi A, Sarkar S, Chattopadhyay A. Lighter-r: Optimized reversible circuit implementation for sboxes. In: 2019 32nd IEEE International System-on-Chip Conference (SOCC). Singapore: IEEE (2019). p. 260–5. doi:10.1109/SOCC46988.2019.1570548320

CrossRef Full Text | Google Scholar

34. Wolkerstorfer J, Oswald E, Lamberger M. An asic implementation of the aes sboxes. In: B Preneel, editor. Topics in cryptology - CT-RSA 2002. Berlin, Heidelberg: Springer (2002). p. 67–78.

Google Scholar

35. Almazrooie M, Abdullah R, Samsudin A, Mutter KN. Quantum grover attack on the simplified-aes. In: Proceedings of the 2018 7th International Conference on Software and Computer Applications. New York, NY, USA: ACM (2018). p. 204–11. doi:10.1145/3185089.3185122

CrossRef Full Text | Google Scholar

36. Saravanan P, Kalpana P. Novel reversible design of advanced encryption standard cryptographic algorithm for wireless sensor networks. Wireless Personal Commun (2018) 100:1427–58. doi:10.1007/s11277-018-5647-z

CrossRef Full Text | Google Scholar

37. Chung D, Lee S, Choi D, Lee J. Alternative tower field construction for quantum implementation of the aes s-box. IEEE Trans Comput (2022) 71:2553–64. doi:10.1109/tc.2021.3135759

CrossRef Full Text | Google Scholar

38. Boyar J, Peralta R. A new combinational logic minimization technique with applications to cryptology. In: P Festa, editor. Experimental algorithms. Berlin, Heidelberg: Springer (2010). p. 178–89.

CrossRef Full Text | Google Scholar

39. Jang K, Song G, Kim H, Kwon H, Kim H, Seo H. Efficient implementation of present and gift on quantum computers. Appl Sci (2021) 11:4776. doi:10.3390/app11114776

CrossRef Full Text | Google Scholar

40. Baksi A, Jang K, Song G, Seo H, Xiang Z. Quantum implementation and resource estimates for rectangle and knot. Quan Inf Process (2021) 20:395–24. doi:10.1007/s11128-021-03307-6

CrossRef Full Text | Google Scholar

41. Jang K, Baksi A, Breier J, Seo H, Chattopadhyay A. Quantum implementation and analysis of default (2022). Cryptology ePrint Archive.

Google Scholar

42. Amy M, Di Matteo O, Gheorghiu V, Mosca M, Parent A, Schanck J. Estimating the cost of generic quantum pre-image attacks on sha-2 and sha-3. In: R Avanzi,, and H Heys, editors. Selected areas in cryptography – SAC 2016. Cham: Springer (2017). p. 317–37.

CrossRef Full Text | Google Scholar

43. Xiang Z, Zeng X, Lin D, Bao Z, Zhang S. Optimizing implementations of linear layers. IACR Trans Symmetric Cryptology (2020) 2020:120–45. doi:10.46586/tosc.v2020.i2.120-145

CrossRef Full Text | Google Scholar