Tailed skyrmions—An obscure branch of magnetic solitons

We report tailed skyrmions—a new class of stable soliton solutions of the 2D chiral magnet model. Tailed skyrmions have elongated shapes and emerge in a narrow range of fields near the transition between the spin spirals and the saturated state. We analyze the stability range of these solutions in terms of external magnetic field and magnetocrystalline anisotropy. We calculate minimum energy paths and homotopies (continuous transitions) between tailed skyrmions of the same topological charge. The discovery of tailed skyrmions extends the diversity of already known solutions. This is illustrated by solitons with complex morphology, such as tailed skyrmion bags with and without chiral kinks.

1 Introduction

Chiral magnets represent a unique class of materials where the competition between local interaction, in particular, Heisenberg exchange and Dzyaloshinskii-Moriya interaction [1, 2] (DMI), gives rise to a vast variety of topological magnetic solitons such as kπ-skyrmions [3–6], skyrmion bags [7, 8], skyrmions at the Bogomolny point [9], and skyrmions with chiral kinks [10]. Note that the physical systems that exhibit such diversity of solitons possessing arbitrary topological charges and morphology are very rare in nature.

The primary parameter that distinguishes magnetic solitons is the topological charge, which defines the homotopy class of a particular solution:

$Q=\frac{1}{4\pi }\int \mathbf{n}\cdot \left({\partial }_{\text{x}}\mathbf{n}\times {\partial }_{\text{y}}\mathbf{n}\right)\mathrm{d}x\mathrm{d}y,(1)$

where n is the magnetization unit vector field.

The solutions with identical Q can be continuously (without the appearance of magnetic singularities) transformed into each other [7]. We refer to such transformations as homotopies, which can be defined as follows. For two magnetic textures n₁(r) and n₂(r) with identical Q, there is a unity parametric vector field n(r; τ), τ ∈ [0, 1], which is continuous with respect to r and τ, and obeys the boundary conditions n(r; 0) = n₁(r), n(r; 1) = n₁(r). Homotopy between any two configurations n₁(r) and n₂(r) is not defined uniquely as there are infinitely many ways to introduce the parameter τ. A constraint can be introduced by considering only those homotopies that represent minimum energy paths (MEPs), i.e., the paths lying lowermost on the energy surface of the system. In this case, the path parameter τ can be associated with the reaction coordinate—the displacement along the MEP—which we normalize to ensure that the reaction coordinate is also defined on the interval [0,1]. Homotopies satisfying the MEP condition are also physically relevant as they define thermal stability of the magnetic configurations within harmonic rate theories [11–15]. Homotopies are, by definition, impossible for solitons with different Q.

The representative and the most well-studied soliton in chiral magnets—π-skyrmion with Q = −1 is shown in Figures 1A, B. π-skyrmions were theoretically predicted more than 30 years ago by Bogdanov and Yablonskii [3–5]. Nowadays, there is a long list of magnetic materials where π-skyrmions were observed experimentally [16].

FIGURE 1

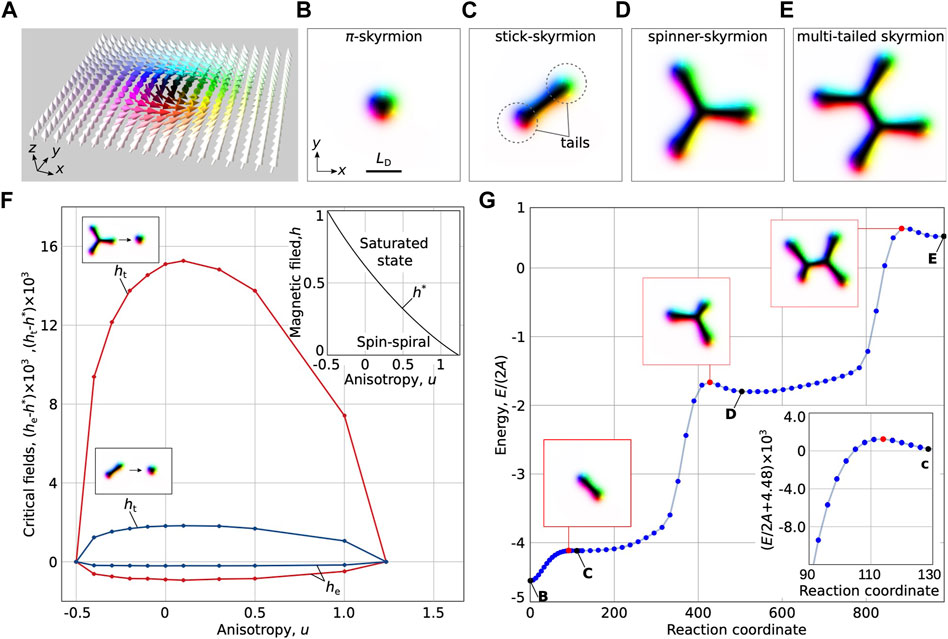
FIGURE 1. Tailed skyrmions. (A) The magnetization vector field of the π-skyrmion. (B) Top view of a π-skyrmion, where colors encode the magnetization direction. (C–E) Color-coded spin texture of tailed skyrmions with Q = −1. (F) Stability diagram of tailed skyrmions in terms of the magnetic field, h, and magnetocrystalline anisotropy, u. (G) Minimum energy path between skyrmions depicted in (B–E). All simulations were performed on the 4L_D × 4L_D domain.

Another type of axially symmetric solitons referred to as kπ-skyrmions (k > 1) was theoretically predicted by Bogdanov and Hubert [6]. Despite the morphological diversity of kπ-skyrmions, they all belong to only two homotopy classes, with Q = 0 and Q = −1 for even and odd k, respectively.

The non-axially symmetric solutions with arbitrary topological charge, also known as skyrmion bags [7, 8] and skyrmions with chiral kinks [9, 10] were found only recently. The skyrmion bags with positive topological charge have recently been observed in FeGe plates using transmission electron microscopy [17]. Co-existing skyrmion and its antiparticle (antiskyrmion) were observed experimentally in FeGe thin platelet [18].

In this article, we introduce a new class of chiral magnetic skyrmions we refer to as tailed skyrmions. We demonstrate rich diversity of tailed skyrmions and present a comprehensive study of their static properties, stability and finite-temperature dynamics. Tailed skyrmions can be thought of as various elongated skyrmions stabilized in the narrow range of external magnetic fields close to the elliptical instability field of an ordinary π-skyrmion. Some examples of tailed skyrmions are shown in Figure 1. To our knowledge, this type of solitons has not been reported in the literature.

2 Model

We consider the two-dimensional (2D) micromagnetic model of a chiral magnet containing three energy terms:

$\mathcal{E}=\int \left\{w_{\text{ex}}\left(\mathbf{n}\right)+w_{\text{D}}\left(\mathbf{n}\right)+w_{\text{U}}\left(\mathbf{n}\right)\right\}l\mathrm{d}x\mathrm{d}y,(2)$

where n = M/M_s is the magnetization unit vector field which is uniform across the film thickness l, M_s is the saturation magnetization, $w_{\text{ex}}(\mathbf{n})=\mathcal{A}{\left|\nabla \mathbf{n}\right|}^2$ is the Heisenberg exchange interaction and $w_{\text{U}}(\mathbf{n})=M_{\text{s}}{B}_{\text{ext}}\left(1-n_{\text{z}}\right)+\mathcal{K}\left(1-n_{\text{z}}^2\right)$ is the potential term containing the Zeeman interaction and the easy-axis/easy-plane anisotropy. The external magnetic field is perpendicular to the plane of the film, B_ext‖e_z.

The DMI term $w_{\text{D}}(\mathbf{n})=\mathcal{D}w(\mathbf{n})$ is defined by combinations of Lifshitz invariants [3], ${\mathrm{\Lambda }}_{ij}^{(k)}=n_i{\partial }_k{n}_j-n_j{\partial }_k{n}_i$. The results presented below are valid for systems with Bloch-type modulations [19], Néel-type modulations [20–22] as well as for crystals with D_2d or S₄ point group symmetry [3]. Without loss of generality, we assume Bloch-type DMI, $w(\mathbf{n})={\mathrm{\Lambda }}_{\text{zy}}^{(\mathrm{x})}+{\mathrm{\Lambda }}_{\text{xz}}^{(\mathrm{y})}$, in our calculations. By introducing the characteristic size of chiral modulations $L_{\text{D}}=4\pi \mathcal{A}/\mathcal{D}$ and the characteristic magnetic field $B_{\text{D}}={\mathcal{D}}^2/(2M_{\text{s}}\mathcal{A})$, we reduce the number of independent parameters to two, namely, the dimensionless external magnetic field h = B_ext/B_D and anisotropy parameter $u=\mathcal{K}/(M_{\text{s}}{B}_{\text{D}})$. As follows from the rigorous analysis on the Γ-convergence of the corresponding micromagnetic Hamiltonians (see Refs. [19, 23, 24]), the effective anisotropy constant, $\mathcal{K}$, includes leading contribution of both the dipole-dipole interaction and the ${\mathrm{\Lambda }}_{\text{yx}}^{(\mathrm{z})}$ Lifshitz invariant in the thin sample limit, l → 0.

3 Methods

This work involves several numerical methods. Stable magnetic configurations are obtained via direct energy minimization using the conjugate gradient method with stereographic projections of the n-field. For details, see Supplementary Materials in Ref. [25]. MEPs between the stable states are calculated using the geodesic nudged elastic band (GNEB) method [26, 27]. Dynamical properties of tailed skyrmions are investigated via the numerical integration of the Landau-Lifshitz-Gilbert (LLG) equation [28] using the well-established semi-implicit method from Ref. [29].

The calculations were performed and double-checked with various software. In particular, we used Excalibur [30] and Mumax3 [31] for energy minimization and calculation of stability ranges. MEPs were calculated using the Spirit code [32]. We used high-accuracy finite difference schemes in the energy minimization to remove numerical artifacts in the calculation of derivatives in Eq. 2. A typical mesh density in our simulations is 64 nodes per L_D. The details can be found in Refs. [7], [10].

For the MEP calculations and stochastic LLG simulations, we used an effective spin-lattice model of nearest neighbors. All calculations were performed with periodic boundary conditions in the film plane. For visualization of the magnetization, we use the standard color code as explained in Figures 1A, B.

4 Initial guesses

To obtain statically stable solutions for tailed skyrmions in Mumax3, we constructed initial guesses for the n-field by placing domains with magnetization antiparallel to the field, n = (0, 0, − 1), into the state with magnetization pointing along the field, n = (0, 0, 1). In the case of axially symmetric skyrmions, e.g., π-skyrmion in Figures 1A, B, we use a circular shape domain with magnetization down. For tailed skyrmions shown in Figures 1C–E, the domains with down magnetization should approximately mimic the shape of the skyrmion, which can be achieved by placing circular domains in a chain. For details, see the Supplementary Materials with the corresponding Mumax script.

In the simulation with Excalibur and Spirit, we used the built-in options allowing one to drag and invert the magnetization field interactively, as illustrated in Supplementary Movie S1. Notably, the interactive modification of the magnetization field with the drag tool permits for examining whether the skyrmion has reached the optimal shape and size.

5 Results

5.1 Stability diagram

Figures 1C–E shows elementary tailed skyrmions. The two solutions with two and three tails can be referred to as a stick-skyrmion and a spinner-skyrmion, respectively. We use these solutions to illustrate the range of tailed skyrmion existence. In Figure 1F, the critical fields for stick-skyrmion and spinner-skyrmion are shown with blue and red curves, respectively. The field range corresponding to stable tailed skyrmions is bound from above by the transition field into axially symmetric π-skyrmion, h_t, and from below by elliptic instability field, h_e. Note that Figure 1F shows the deviation of h_t and h_e from h*—the critical field corresponding to the transition between the spin-spiral state and the ferromagnetic phase—so as to emphasize the difference between the critical fields which are quite close to each other. The dependence h*(u) is the solution of the well-known equation [5]:

$2\pi -4\sqrt{h+2u}-\frac{\sqrt{2}h}{\sqrt{u}}\ln \frac{\sqrt{h+2u}+\sqrt{2u}}{\sqrt{h+2u}-\sqrt{2u}}=0,(3)$

which is derived from the criterion that the energy of the isolated spiral (2π-domain wall) equals the energy of the saturated ferromagnetic state. The functional dependence h*(u) is shown in the inset of Figure 1F.

The critical fields for any tailed skyrmion solutions always meet at two points: 1) the Bogomolnyi point h = 1, u = −0.5 and 2) the phase transition point between the spin spiral and ferromagnetic phases h = 0, u = π²/8. Thus, the stability range of tailed skyrmions includes both in-plane and strong out-of-plane anisotropy systems.

The range of the external magnetic field corresponding to stable spinner-skyrmion (see the domain bound by the red lines in Figure 1F) is roughly eight times larger than that for the stick-skyrmion (see the domain bound by the blue lines). The stability range for most of the other tailed-skyrmion solutions considered in this work was found to coincide with high precision with the stability range of the spinner-skyrmion. In particular, at zero anisotropy the spinner-skyrmion transforms to the π-skyrmion at the field h = 0.63185, while for the multi-tailed skyrmion shown in Figure 1E, the transition field is h = 0.63115. The reason for all other multi-tailed skyrmions to have a similar critical field is their structure. All multi-tailed skyrmions have threefold branching parts that the stick-skyrmion does not have. The transformation of any multi-tailed skyrmion into the π-skyrmion starts with the collapse of the branching part. The saddle point configurations shown in the insets of Figure 1G illustrate this effect. The MEP in Figure 1G demonstrates that the energy barrier associated with the collapse of the threefold branching part is higher than the barrier protecting the stick-skyrmion from collapsing. This makes the stability range for multi-tailed skyrmions wider than that for stick-skyrmions. Therefore, the area bound by the red curves in Figure 1F can be considered as a good estimate for the stability range of all tailed-skyrmions.

5.2 Homotopies and minimum energy paths

Figure 1G shows the MEP connecting the π-skyrmion, stick-skyrmion, spinner-skyrmion and four-tailed skyrmion (see Figures 1B–E). The calculated MEP turns out to be a homotopy as the topological charge of the system remains the same, Q = −1, at every point of the MEP. Some other examples of homotopy MEPs have already been presented in Ref. [33], reporting the method for finding exotic three-dimensional hybrid skyrmion tubes.

Starting from the π-skyrmion solution and following the MEP we observe a sequential increase in the number of tails in the magnetic texture. The growth of a new tail requires overcoming an energy barrier that turns out to be significantly larger than that for the reverse process, i.e., removal of the tail. The latter defines the stability of the tailed states, and can also be written in the form of inequality, ${\mathcal{E}}_{BC}-{\mathcal{E}}_B>{\mathcal{E}}_{BC}-{\mathcal{E}}_C$, where ${\mathcal{E}}_B$ and ${\mathcal{E}}_C$ are energies of skyrmions shown in (B) and (C), ${\mathcal{E}}_{BC}$ is the energy at the saddle point between them. With an increasing external magnetic field, the barriers corresponding to the tail contraction decrease and eventually disappear, leading to the transition of the tailed skyrmions into the axially symmetric π-skyrmion state.

As follows from the MEP calculations, the energy of the tailed skyrmions increases with the number of tails, meaning that tailed skyrmions represent higher energy metastable states. The latter is consistent with the previous study [34].

The question about the second lowest energy soliton with Q = −1 remains open. For instance, 3π-skyrmion and some of the skyrmion bags seem to be promising candidates. However, comparing the energies of tailed skyrmions, we found that the stick skyrmion may certainly compete with these solutions. In particular, at h = 0.617 and u = 0, the energy of stick-skyrmion is only 8.4% higher than that of the π-skyrmion, while the energy of 3π-skyrmion for these parameters is 11% higher. Moreover, the 3π-skyrmion is significantly bigger than the π-skyrmion and has a diameter of $\sim 8L_{\text{D}}$. The size of other skyrmion bags with Q = −1 is even larger. This means that the stick-skyrmion is not only lower in energy than other solutions but also has the shortest distance to the π-skyrmion in the configuration space.

5.3 Thermally activated transition from π-skyrmion to stick-skyrmion

Since the tailed stick-skyrmion solution is the closest local minimum to the π-skyrmion state, excitation of a π-skyrmion by external stimuli such as thermal fluctuations can induce a nucleation of the stick-skyrmion. To demonstrate this, we performed finite-temperature spin dynamics simulations for h = 0.617 and u = 0. We used the LLG time step $\mathrm{\Delta }t=0.01J\gamma {\mu }_{\text{s}}^{-1}$, and damping parameter α = 0.1. The system was simulated at the temperature of T = 0.2J/k_B, i.e., significantly lower than the critical temperature for spin spiral ordering, which was estimated to be T_c = 0.7J/k_B for chosen parameters [35].

The initial magnetic texture of axially symmetric π-skyrmion is shown in Figure 2A. The thermal fluctuations result in skyrmion deformation, as seen in Figures 2B–D. After turning off the temperature and performing cooling with the LLG simulation at T = 0, the deformed skyrmion quickly turned into a stick-skyrmion, as shown in Figures 2E, F and in Supplementary Movie S2. A longer heating of the system, in principle, can also give rise to the appearance of spinner-skyrmion and other multi-tailed skyrmions. However, such events have a much lower probability because of the large distance between corresponding minima in the parameter space and higher energy barriers, Figure 1G. Nevertheless, our results suggest a simple approach to the experimental observation of tailed skyrmions.

FIGURE 2

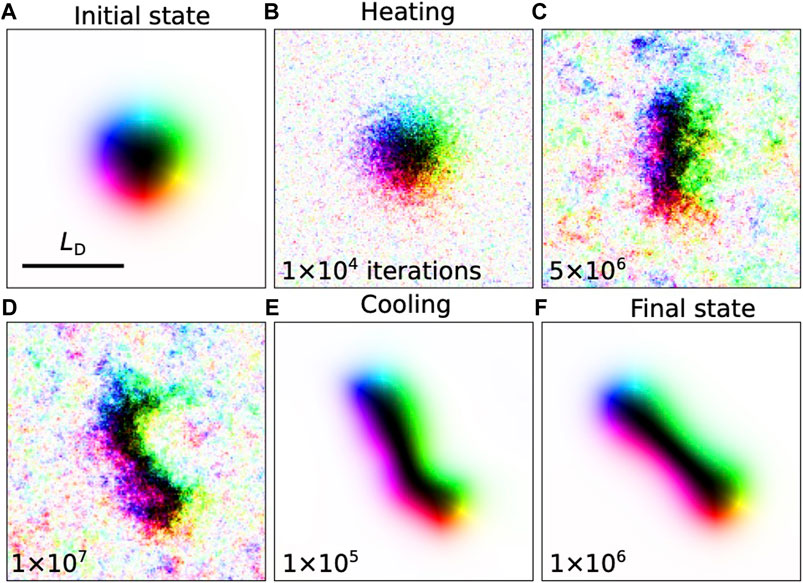
FIGURE 2. Snapshots of the system during the heating-cooling protocol of stochastic LLG simulations. (A) The initial configuration of π-skyrmion. (B–D) Snapshots of the system after 10⁴, 5⋅10⁶ and 10⁷ iterations of stochastic LLG simulations with fixed temperature of T = 0.2J/k_B. (E,F) Snapshots after 10⁵ and 10⁶ LLG time steps with T = 0. Simulations are performed on the 8L_D × 8L_D computational domain for h = 0.617, u = 0.

The current-induced dynamic of tailed skyrmions is quite rich and demonstrates various types of motion, including the breathing mode and the rotational motion. Moreover, one can induce switching between tailed skyrmions by applying sufficient current density. Detailed investigation of these effects goes beyond the scope of this study and will be presented elsewhere. Nevertheless, to prove the stability of the tailed skyrmions under translational motion we provide a movie (see the Supplementary Material) that illustrates the dynamics of four skyrmions shown in Figure 1: ordinary π-skyrmion (Figure 1B), stick-skyrmion (Figure 1C), spinner-skyrmion (Figure 1D), and multitailed skyrmion (Figure 1E). In this simulations, we used the following material parameters: $\mathcal{A}=4$ pJ/m, $\mathcal{D}=0.718$ mJ/m² (L_D = 70 nm), $\mathcal{K}=0$, the electric current density j = 10⁹ A/m, the parameter of non-adiabaticity ξ = 0.1 and the damping parameter α = 0.01. The simulation domain size is 6L_D × 6L_D. The total time of simulations is 2 microseconds. The script that can be used to reproduce these results is provided in the supplementary material. The simulations demonstrate that the shape of the tailed skyrmions does not change during the motion induced by relatively low current. Since all the skyrmions have identical Q = −1, they move with the positive deflection angle. The absolute values of the deflection angle are different for all skyrmions and depend on their symmetry, which agrees with the previous study of skyrmion dynamics [36].

5.4 Tailed skyrmions with arbitrary topological charge

So far, we have only discussed solutions with Q = −1. However, the tails can, in principle, be added to any soliton with an arbitrary topological charge. Adding a tail creates a new soliton, but does not change the topological charge of the system. This section provides examples of such skyrmions. All solutions presented in the following were obtained on a square simulation domain of size L_x = L_y = 8L_D for parameters h = 0.617 and u = 0.

In Figure 3, we show topologically trivial solitons—skyrmionium with tails. Note that all solitons shown in Figure 3 are homotopically equivalent despite a different number of tails and their position on the inner or outer contour of the solitons. Noticeably, the skyrmionium with more than three tails on the outer contour, see, e.g., Figures 3G–I, has rotational symmetry of order equal to the number of tails.

FIGURE 3

FIGURE 3. Tailed skyrmions with Q = 0. Skyrmionium with tails on the inner contour only (A,B), on both contours (C), and on the outer contour only (D–I). The scale bar is the same for all images.

Figure 4 provides examples of tailed skyrmion bags of various topological charges and demonstrates diversity of tailed skyrmions. For example, Figures 4C–E shows three skyrmion configurations with the same topological charge Q = −1 but different symmetry and different number of tails. Figures 4G, H demonstrates two different skyrmion bags with the same positive topological charge, Q = +3.

FIGURE 4

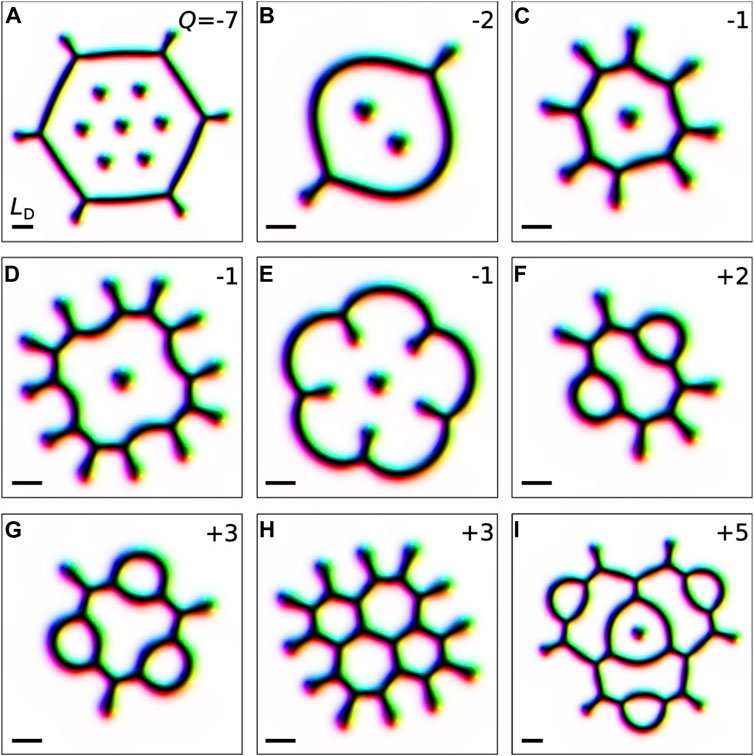
FIGURE 4. Skyrmion bags with tails stabilized for u = 0 and h = 0.617. Each image in (A–I) shows a tailed skyrmion bag with the topological charge indicated in the top right corner and varying from Q=−7 to Q=+5.

Another qualitatively new feature appears in the case of skyrmions with chiral kinks and tails. Figure 5 provides several examples of such skyrmions having various topological charges. Note that the chiral kink on the outer contour of the skyrmion carries the topological charge Q = +1. Because of this, the topological charge of skyrmions in Figures 5A, B equals zero and does not depend on the number of tails. The skyrmions with antikinks of topological charge Q = −1 are only stable at strong out-of-plane anisotropy [10].

FIGURE 5

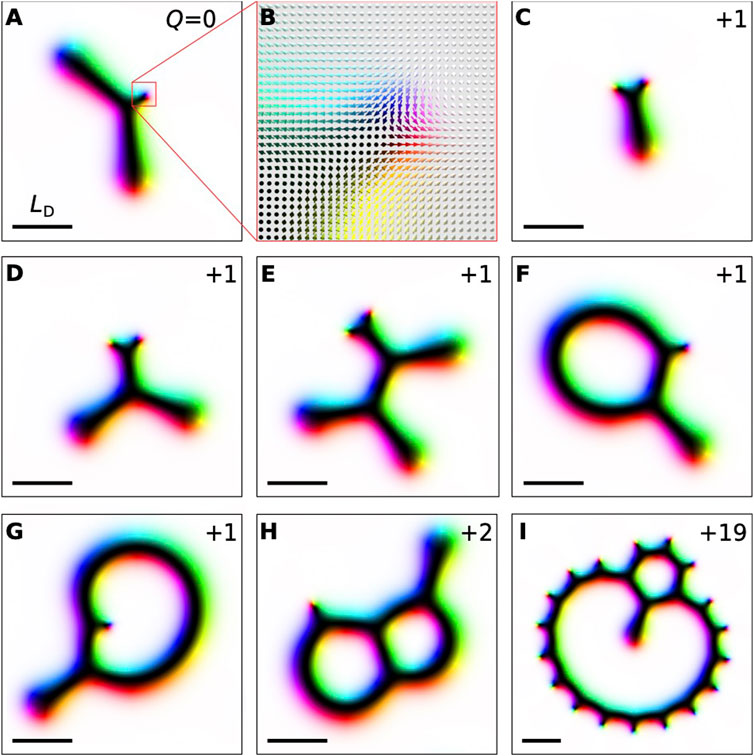
FIGURE 5. Skyrmions with tails and chiral kinks stabilized for h = 0.617 and u = 0. Each image in (A–I) shows a tailed skyrmion with one or a few chiral kinks and different topological charge Q indicated in the top right corner. The image in (B) is a detailed view of the spin texture near the chiral kink of the skyrmion shown in (A).

Figures 5C–E illustrate that the chiral kinks form coupled pairs in the presence of tails. A similar phenomenon was observed for chiral kinks on the 2π-domain wall [10]. Generally, the chiral kinks on a straight domain wall repel each other at large distances and attract each other only at small distances [10]. Similarly, a pair of kinks can form a coupled state on tailed skyrmions, with finite distance between the kinks on the order of 0.1L_D. With increasing field, the solutions with Q = +1 shown in Figures 5C–E collapse to an antiskyrmion [37]. Figures 5F–I show skyrmion bags with positive topological charges hosting chiral kinks and tails simultaneously.

5.5 Effect of strong perpendicular anisotropy on tailed skyrmions

So far, the diversity of tailed skyrmions has been demonstrated for the u = 0 case. However, all tailed skyrmion solutions can also be obtained for any value of u in the range from −1/2 to π²/8 (see the diagram in Figure 1F). Moreover, for strong perpendicular anisotropy, u ≲ π²/8, we found distinct co-existing solutions representing tailed skyrmions of different lengths. In Figures 6B,C, we show several examples of stick-skyrmions of different lengths, which coexist for a given u, h, with ordinary π-skyrmion shown in Figure 6A and are separated by small energy barriers. The energy of the stick-skyrmion increases with its length. Note that such tailed skyrmions of different lengths are observed only at strong anisotropy. As Figure 6G shows, the magnetic structure of such stick-skyrmions is non-trivial. In particular, the y component of magnetization is modulated along the skyrmion symmetry axis giving an energy gain sufficient for the skyrmion stabilization. The number of zeros of n_y increases with the length of a stick-skyrmion.

FIGURE 6

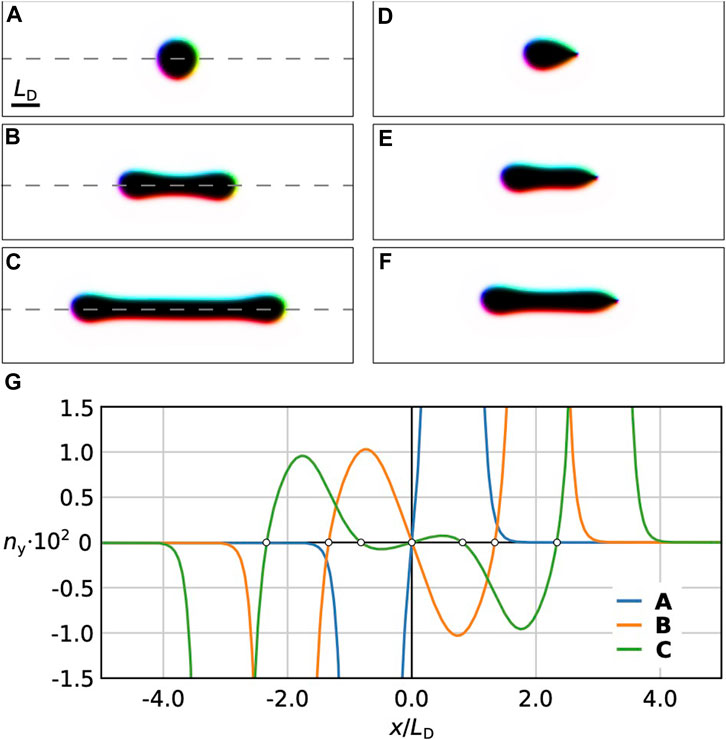
FIGURE 6. (A) axially symmetric π-skyrmion. (B,C) stick-skyrmions of different lengths. (D) chiral droplet soliton. (E,F) stick-skyrmion with one tail and one chiral kink. All solutions co-exist for u = 1.194 and h = 0.01. The energy minimization was performed on a large size domain, L_y = 4L_D and L_x = 16L_D, to avoid the influence of periodic boundary conditions. All images have identical scale, as marked in (A). (G) y-component of magnetization along the dashed symmetry line of the skyrmions (A–C). Hollow circles denote the zeros of n_y(x).

Interestingly, the stick-skyrmion with one tail and one chiral kink (see Figures 6D–F) also exhibits multiple minima corresponding to the solutions of different lengths.

6 Conclusion

In conclusion, we presented in this work a new class of chiral skyrmions—tailed skyrmions. We identified the range of uniaxial anisotropy and perpendicular magnetic field where the tailed skyrmions remain statically stable. We show a wide diversity of tailed skyrmions with arbitrary topological charges. The presence of tails changes only the soliton’s symmetry but does not change its topological charge. Thus, the transitions between tailed and tail-free solutions are homotopies. We demonstrated that such transitions can be identified using the GNEB method. The energy barriers involved in the homotopies tend to be smaller than what needs to be overcome to change the topological charge of the system [38]. As a result, tailed skyrmions can be obtained from a regular π-skyrmion by applying weak thermal fluctuations, as demonstrated by the stochastic LLG simulations.

Our results contribute to the development of a complete picture of the diversity of statically stable magnetic solitons in chiral magnets. After submission of the paper, we became aware of structurally similar solutions discovered in a superconducting system [39].

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

VK performed calculations, NK and PB supervised. FR originally discovered the tailed skyrmion configuration. VK wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors acknowledge financial support from the Icelandic Research Fund (Grant No. 217750), the University of Iceland Research Fund (Grant No. 15673), the Swedish Research Council (including Grant No. 2020-05110), and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant No. 856538, project “3D MAGiC”).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1171079/full#supplementary-material

SUPPLEMENTARY MOVIE S1 | Movie 1 demonstrates the process of constructing initial guesses for tailed skyrmions in Excalibur code.

SUPPLEMENTARY MOVIE S2 | Movie 2 demonstrates the process of stick-skyrmion nucleation from the π-skyrmion by means of temperature fluctuations. It shows the stochastic LLG simulations followed by cooling of the system.

SUPPLEMENTARY MOVIE S3 | Movie 3 illustrates the current-induced dynamics of the π-skyrmion, stick-skyrmion, spinner-skyrmion, and multi-tailed skyrmion (see Figures 1B–D).

SUPPLEMENTARY DATA SHEET S1 | Mumax script “initial_state.mx3” contains code for creating initial guesses for stick-, spinner- and multi-tailed skyrmions.

SUPPLEMENTARY DATA SHEET S2 | Mumax script “tailed_sk_dynamics.mx3” contains code for simulating current-induced dynamics of tailed skyrmions.

References

1. Dzyaloshinsky I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3

CrossRef Full Text | Google Scholar

2. Moriya T. Anisotropic superexchange interaction and weak ferromagnetism. Phys Rev (1960) 120:91–8. doi:10.1103/PhysRev.120.91

CrossRef Full Text | Google Scholar

3. Bogdanov AN, Yablonskii DA. Thermodynamically stable “vortices” in magnetically ordered crystals. the mixed state of magnets. Sov Phys JETP (1989) 68.

Google Scholar

4. Bogdanov A, Hubert A. The properties of isolated magnetic vortices. physica status solidi (b) (1994) 186:527–43. doi:10.1002/pssb.2221860223

CrossRef Full Text | Google Scholar

5. Bogdanov A, Hubert A. Thermodynamically stable magnetic vortex states in magnetic crystals. J Magnetism Magn Mater (1994) 138:255–69. doi:10.1016/0304-8853(94)90046-9

CrossRef Full Text | Google Scholar

6. Bogdanov A, Hubert A. The stability of vortex-like structures in uniaxial ferromagnets. J Magnetism Magn Mater (1999) 195:182–92. doi:10.1016/S0304-8853(98)01038-5

CrossRef Full Text | Google Scholar

7. Rybakov FN, Kiselev NS. Chiral magnetic skyrmions with arbitrary topological charge. Phys Rev B (2019) 99:064437. doi:10.1103/PhysRevB.99.064437

CrossRef Full Text | Google Scholar

8. Foster D, Kind C, Ackerman PJ, Tai J-SB, Dennis MR, Smalyukh II. Two-dimensional skyrmion bags in liquid crystals and ferromagnets. Nat Phys (2019) 15:655–9. doi:10.1038/s41567-019-0476-x

CrossRef Full Text | Google Scholar

9. Barton-Singer B, Ross C, Schroers BJ. Magnetic skyrmions at critical coupling. Commun Math Phys (2020) 375:2259–80. doi:10.1007/s00220-019-03676-1

CrossRef Full Text | Google Scholar

10. Kuchkin VM, Barton-Singer B, Rybakov FN, Blügel S, Schroers BJ, Kiselev NS. Magnetic skyrmions, chiral kinks, and holomorphic functions. Phys Rev B (2020) 102:144422. doi:10.1103/PhysRevB.102.144422

CrossRef Full Text | Google Scholar

11. Vineyard GH. Frequency factors and isotope effects in solid state rate processes. J Phys Chem Sol (1957) 3:121–7. doi:10.1016/0022-3697(57)90059-8

CrossRef Full Text | Google Scholar

12. Brown W. Thermal fluctuation of fine ferromagnetic particles. IEEE Trans Magnetics (1979) 15:1196–208. doi:10.1109/TMAG.1979.1060329

CrossRef Full Text | Google Scholar

13. Braun H-B. Thermally activated magnetization reversal in elongated ferromagnetic particles. Phys Rev Lett (1993) 71:3557–60. doi:10.1103/PhysRevLett.71.3557

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Fiedler G, Fidler J, Lee J, Schrefl T, Stamps RL, Braun HB, et al. Direct calculation of the attempt frequency of magnetic structures using the finite element method. J Appl Phys (2012) 111:093917. doi:10.1063/1.4712033

CrossRef Full Text | Google Scholar

15. Bessarab PF, Uzdin VM, Jónsson H. Harmonic transition-state theory of thermal spin transitions. Phys Rev B (2012) 85:184409. doi:10.1103/PhysRevB.85.184409

CrossRef Full Text | Google Scholar

16. Tokura Y, Kanazawa N. Magnetic skyrmion materials. Chem Rev (2020) 121:2857–97. doi:10.1021/acs.chemrev.0c00297

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Tang J, Wu Y, Wang W, Kong L, Lv B, Wei W, et al. Magnetic skyrmion bundles and their current-driven dynamics. Nat Nanotechnology (2021) 16:1086–91. doi:10.1038/s41565-021-00954-9

CrossRef Full Text | Google Scholar

18. Zheng F, Kiselev NS, Yang L, Kuchkin VM, Rybakov FN, Blügel S, et al. Skyrmion–antiskyrmion pair creation and annihilation in a cubic chiral magnet. Nat Phys (2022) 18:863–8. doi:10.1038/s41567-022-01638-4

CrossRef Full Text | Google Scholar

19. Davoli E, Di Fratta G, Praetorius D, Ruggeri M. Micromagnetics of thin films in the presence of Dzyaloshinskii–Moriya interaction. Math Models Methods Appl Sci (2022) 32:911–39. doi:10.1142/S0218202522500208

CrossRef Full Text | Google Scholar

20. Romming N, Hanneken C, Menzel M, Bickel JE, Wolter B, von Bergmann K, et al. Writing and deleting single magnetic skyrmions. Science (2013) 341:636–9. doi:10.1126/science.1240573

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kézsmárki I, Bordács S, Milde P, Neuber E, Eng L, White J, et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor gav 4 s 8. Nat Mater (2015) 14:1116–22. doi:10.1038/nmat4402

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Romming N, Kubetzka A, Hanneken C, von Bergmann K, Wiesendanger R. Field-dependent size and shape of single magnetic skyrmions. Phys Rev Lett (2015) 114:177203. doi:10.1103/physrevlett.114.177203

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gioia G, James RD. Micromagnetics of very thin films. Proc R Soc Lond Ser A: Math Phys Eng Sci (1997) 453:213–23. doi:10.1098/rspa.1997.0013

CrossRef Full Text | Google Scholar

24. Muratov CB, Slastikov VV. Domain structure of ultrathin ferromagnetic elements in the presence of dzyaloshinskii–moriya interaction. Proc R Soc A: Math Phys Eng Sci (2017) 473:20160666. doi:10.1098/rspa.2016.0666

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Rybakov FN, Borisov AB, Blügel S, Kiselev NS. New type of stable particlelike states in chiral magnets. Phys Rev Lett (2015) 115:117201. doi:10.1103/PhysRevLett.115.117201

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Bessarab P, Uzdin V, Jónsson H. Method for finding mechanism and activation energy of magnetic transitions, applied to skyrmion and antivortex annihilation. Comput Phys Commun (2015) 196:335–47. doi:10.1016/j.cpc.2015.07.001

CrossRef Full Text | Google Scholar

27. Bessarab PF. Comment on “path to collapse for an isolated néel skyrmion”. Phys Rev B (2017) 95:136401. doi:10.1103/PhysRevB.95.136401

CrossRef Full Text | Google Scholar

28. ter Haar D. In: Collected Papers of L.D. Landau (pergamon). chap. 18 - On the Theory of the Dispersion of Magnetic Permeability in Ferromagnetic bodies. 101–114 (1965). doi:10.1016/B978-0-08-010586-4.50023-7

CrossRef Full Text | Google Scholar

29. Mentink JH, Tretyakov MV, Fasolino A, Katsnelson MI, Rasing T. Stable and fast semi-implicit integration of the stochastic landau–lifshitz equation. J Phys Condensed Matter (2010) 22:176001. doi:10.1088/0953-8984/22/17/176001

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Rybakov FN, Babaev E (2020). Excalibur software. Available at: http://quantumandclassical.com/excalibur/.

Google Scholar

31. Vansteenkiste A, Leliaert J, Dvornik M, Helsen M, Garcia-Sanchez F, Van Waeyenberge B. The design and verification of mumax3. AIP Adv (2014) 4:107133. doi:10.1063/1.4899186

CrossRef Full Text | Google Scholar

32. Müller GP, Hoffmann M, Dißelkamp C, Schürhoff D, Mavros S, Sallermann M, et al. Spirit: Multifunctional framework for atomistic spin simulations. Phys Rev B (2019) 99:224414. doi:10.1103/PhysRevB.99.224414

CrossRef Full Text | Google Scholar

33. Kuchkin VM, Kiselev NS. Homotopy transitions and 3d magnetic solitons. APL Mater (2022) 10:071102. doi:10.1063/5.0097559

CrossRef Full Text | Google Scholar

34. Melcher C. Chiral skyrmions in the plane. Proc R Soc A: Math Phys Eng Sci (2014) 470:20140394. doi:10.1098/rspa.2014.0394

CrossRef Full Text | Google Scholar

35. Kuchkin VM, Bessarab PF, Kiselev NS. Thermal generation of droplet soliton in chiral magnet. Phys Rev B (2022) 105:184403. doi:10.1103/PhysRevB.105.184403

CrossRef Full Text | Google Scholar

36. Kuchkin VM, Chichay K, Barton-Singer B, Rybakov FN, Blügel S, Schroers BJ, et al. Geometry and symmetry in skyrmion dynamics. Phys Rev B (2021) 104:165116. doi:10.1103/physrevb.104.165116

CrossRef Full Text | Google Scholar

37. Kuchkin VM, Kiselev NS. Turning a chiral skyrmion inside out. Phys Rev B (2020) 101:064408. doi:10.1103/PhysRevB.101.064408

CrossRef Full Text | Google Scholar

38. Bessarab PF, Müller GP, Lobanov IS, Rybakov FN, Kiselev NS, Jónsson H, et al. Lifetime of racetrack skyrmions. Scientific Rep (2018) 8:3433. doi:10.1038/s41598-018-21623-3

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Barkman M, Babaev E. private communication (2023)

Google Scholar