Thermal geometries and the Joule–Thomson expansion of modified charged and slowly rotating black holes

Thermodynamics of charged and slowly rotating black holes in 4D Gauss–Bonnet gravity has attracted a great deal of attention due to its intrinsic complications and rich phase structures. In this paper, we revisit the thermodynamics of charged and slowly rotating black holes and provide the correct thermodynamic volume and entropy. Thermodynamic geometries are a powerful tool to study the microstructure of black holes. Based on the Hessian matrix of the black hole mass, we introduce thermodynamic geometric methods and give its scalar curvature (Ruppeiner and Weinhold). Furthermore, we investigate the Joule–Thomson expansion of slowly rotating black hole in 4D Gauss–Bonnet gravity in this research study. Interestingly, we explicitly state that the expression of the Joule–Thomson coefficient is obtained from the basic formulas of enthalpy and temperature. Then, we obtain the isenthalpic curve in the T − P graph and demonstrate the cooling–heating region by the inversion curve. The inversion temperature and inversion curves are obtained, and we investigate the similarities and differences between van der Waals fluids and charged fluids.

1 Introduction

According to the classical view, black holes (BHs) are compact objects and can absorb matter and energy of all natures without skipping anything out. These bald objects [1, 2] basically were defined on the basis of very few criteria such as mass, angular momentum, and electromagnetic charges. In visitation of quantum field theory, specifically in the background of the curved spacetime, the fundamental link between the BH area, its entropy [3], and the occupied temperature related to the gravity on its surface [4] was discussed. Moreover, it was depicted that the radiation emission is similar to the BH body’s spectrum. All these hypotheses direct toward the evolution of BH thermodynamics, developing the pioneer semiclassical interpretation of gravitational hypotheses and a deepest view in the apprehension of a feasible quantum explanation of gravitational interactions [5–10].

The motivation behind the derivation of a well-defined D → 4 limit for 4D Gauss–Bonnet gravity is based on the interest to test the alternative of Einstein’s general theory of relativity. Slowly rotating black hole (SRBH) solutions have been constructed in 4D Gauss–Bonnet gravity via asymptotically flat, de Sitter, and anti-de Sitter spacetime [11, 12]. Furthermore, a charged rotating BH has been developed in 4D Einstein–Gauss–Bonnet (EGB) gravity using the complex co-ordinate transformations. Among the higher-curvature gravities, the so-called EGB gravity is a broadly studied theory, whose Lagrangian includes Einstein’s terms with the the Gauss–Bonnet concoction of quadratic curvature terms. On the other hand, the Gauss–Bonnet term yields the non-trivial gravitational dynamics in the D ≥ 5 dimension. A common class of reconstructions of GR is directed at the higher-curvature theories, in which it is assumed that a sum of powers of the curvature tensor is proportional to stress energy and extended to obtain the linear relationship between spacetime curvature (the Einstein tensor) and stress energy in GR [13–16]. We study the null geodesics to examine the shape of the shadow cast by a rotating charged BH in 4D EGB gravity [17, 18] and also discuss their horizon properties and casted shadows. The phenomenon of BH shadows along the emission energy, and the horizon structure has been investigated to see the influence of the Gauss–Bonnet term and BH charge on the event horizon, effective potential, shadow, and energy emission rate, and the results are compared to the non-rotating counterpart. In contrast to Einstein’s theory, 4D EGB gravity is the causal structure, which deviates from its parallel, and the region around the singularity becomes time-like, whereas it is space-like for Einstein’s gravity [19, 20]. Finally, it is worth mentioning that taking α → 0, GR results in 4D are recovered. In addition, one can observe from the complete graphic analysis that GR provides a more compact and stable model in distinction with EGB. Nevertheless, the same can be reached in the arena of EGB gravity taking smaller values of the coupling constant α.

While studying the thermodynamic features of AdS BHs, it became known that the cosmological constant could be treated as thermodynamic pressure, whereas conjugate variables as the thermodynamic volumes can further be utilized to harmonize the charged AdS BHs with the van der Waals gas–liquid systems [21]. At this time, the inclusion of the cosmological constant in the BH thermodynamics takes place [22–25], which is used in the formation of the first law of BH thermodynamics, having homogeneity with the Smarr relation. In the first law of thermodynamics, if the cosmological constant is treated as the thermodynamics pressure, then the mass of the BH is elaborated as the enthalpy. These hypotheses provide the basis for the detailed discussion of thermodynamic features of BHs in the enhanced version of phase space through its expanded designation of thermodynamic phase space [26–29].

Ökcü and Aydyner [30, 31] creatively extended the study on the Joule–Thomson expansion for charged AdS BHs. In view of the classical thermodynamics, the Joule–Thomson expansion attributes to the gas expansion process from high temperature to low temperature via penetrable plugs, which may be named as an isenthalpic process [32–34]. Therefore, this inventive research was enhanced for all types of BH geometries; for more details, one can consult the research in [35–39]. Since the origination of work by Gibbs and Caratheodory, the study of thermodynamic geometries remained a topic of hot research up till now. The outcomes are approached by two dissimilar ways [33]. The first one consists of the inauguration of metric formations on the space of thermodynamic equilibrium states, while the second one is based on the use of contact formation of the thermodynamic phase space. Weinhold, in his work, instigated a timely equilibrium state on a metric elaborated as the Hessian of the inner thermodynamic energy, while derivatives are calculated relative to the important thermodynamic variables. Ruppeiner [40] inaugurated a metric with conformal equivalence to Weinhold’s metric, having the inversion temperature as a conformal factor. The outcomes resulted in the application of the Ruppeiner geometry and have been disclosed in [41, 42]. The applications of this approach in the BH thermodynamics are found in [43, 44]. Hermann [45] and Mrugala [46–48], while developing the second approach, incorporated the natural contact formation of the phase space. All the thermodynamic variables (extensive and intensive) are selected with the accumulation of thermodynamic potential to develop the understandable co-ordinates in phase space. The space of thermodynamic equilibrium state is a subspace of phase space developed by the smooth embedding mapping, say ϕ (ϕ: equilibrium state → phase space). This statement directly shows that each system is equipped with its own space (equilibrium state). Alternatively, in phase space, it is applicable to introduce the basic Gibbs 1-form, which, when forecasted upon the equilibrium state with the withdrawal of φ, produces the first law of thermodynamics and the conditions for thermodynamic equilibrium [49, 50].

This paper is organized as follows: In Section 2, we explain the charged four-dimensional Gauss–Bonnet BH geometry, and further discussion is divided in two sections. In Section 2.1, we discuss the thermal stability of geometries, and in Section 2.2, we explore the thermal geometries. In Section 3, we study slowly rotating BHs in 4D Guass–Bonnect gravity. In Section 4, we study the Joule–Thomson expansion for the SRBH in 4D Guass–Bonnet gravity. In Section 5, we summarize our study.

2 Charged four-dimensional Gauss–Bonnet black holes

The Einstein–Hilbert action for the GBT is formulated as [51]

$\mathcal{I}=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}\left[R+\alpha \left(R_{\gamma \delta \zeta \xi }{R}^{\gamma \delta \zeta \xi }-4R_{\gamma \delta }{R}^{\gamma \delta }+R^2\right)\right],(1)$

where R is a curvature scalar. By re-scaling the GB coupling constant α, i.e., α/D − 4, and taking the limit D → 4 in the GB term, one can obtain the solution of four-dimensional GBBH [52–54], and the metric element is given by

$d{s}^2=-f\left(r\right)d{t}^2+\frac{d{r}^2}{f\left(r\right)}+r^{2}d{\theta }^2+r^{2}si{n}^2\theta d{\varphi }^2,(2)$

with the metric function f(r) that can be written as

$f\left(r\right)=1+\frac{r^2\left(1-\sqrt{4\alpha \left(\frac{a}{r^2}-\frac{8M\sqrt{\varphi }}{\sqrt{\pi }{r}^4}+\frac{2M}{r^3}-\frac{Q}{r^2}\right)+1}\right)}{2\alpha }.(3)$

The BH solution in Eq. 3 contains the Gauss–Bonnet mass M, charge Q, cloud of string parameter a, and coupling constant α, which are considered to be positive. In the Lorentzian distribution, the mass–density relation of a static and spherically symmetric gravitational source is ${\rho }_{\varphi }=\frac{\sqrt{\varphi }M}{{\pi }^{3/2}{\left(\pi \varphi +r^2\right)}^2}$, in which ϕ represents the strength of the non-commutative parameter in the Lorentzian distribution. Analytical quantities in this case were also discussed, and we noted that the SRBH metric in 4D Gauss–Bonnet gravity is regular everywhere except r = 0, where a > 0. In [53, 54], it was shown that in de Sitter spacetimes, the examined BH horizon is directly analogous to the charged Nariai models (derived from the Reissner–Nordstrom–de Sitter metric). For large values of the 4D Gauss–Bonnet coupling constant α, de Sitter consequences did not overlap in the permitted mass with the GR results. Finally, it is worth mentioning that taking α → 0, GR results in 4D are recovered. In addition, one can observe the complete graphic analysis where GR provides a more compact and stable model in contrast with EBG. Nevertheless, the same can be reached in the arena of EGB gravity taking smaller values of the coupling constant α. We will have a discussion about the roots of f(r) in order to study the effects of parameters α and ϕ on our solutions. We can analyze about some other physical quantities such as mass, temperature, and heat capacity. First of all, we discuss the conserved thermodynamic features of the BH. Then, we calculate mass, temperature, and some other thermodynamic amounts as a function of entropy. From Eq. 3, we can obtain the mass M by taking f(r) = 0 as

$M=\frac{\sqrt{\pi }\left(-a{r_h}^2+\alpha +Q{r_h}^2+{r_h}^2\right)}{2\left(\sqrt{\pi }{r}_h-4\sqrt{\varphi }\right)},(4)$

where r₀ notions are the event horizon of the BH. The thermal property (temperature) of BHs can be determined as

$T=\frac{8\sqrt{\pi }{r}_h\sqrt{\varphi }\left(a-Q-1\right)+\pi {r_h}^2\left(-a+Q+1\right)-\pi \alpha }{4\pi r_h{\left(\sqrt{\pi }{r}_h-4\sqrt{\varphi }\right)}^2},(5)$

where a and α are constants. The entropy of the BH is given by

$s=\pi r_h^2.(6)$

We could find the mass of the BH in terms of its entropy s and the radius of curvature related to the cosmological constant, obtained as

$M\left(s,\alpha ,Q\right)=\frac{s\left(-a+Q+1\right)+\pi \alpha }{2\sqrt{\pi }\left(\sqrt{s}-4\sqrt{\varphi }\right)}.(7)$

Using the well-known expression $T=\frac{\partial M}{\partial s}$, one can deduce the temperature of the slowly rotating BH as

$T\left(s,\alpha ,Q\right)=\frac{8\sqrt{s}\sqrt{\varphi }\left(a-Q-1\right)+s\left(-a+Q+1\right)-\pi \alpha }{4\sqrt{\pi }\sqrt{s}{\left(\sqrt{s}-4\sqrt{\varphi }\right)}^2}.(8)$

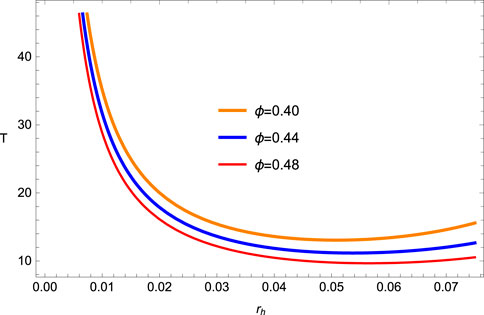
Equation (8) will be next used to obtain better results regarding the BH solution. From Figure 1, one can see that the temperature in terms of horizon radius remains positive and provides a stable solution for the fixed values a and α.

FIGURE 1

FIGURE 1. Plot of temperature in terms of horizon radius with different values of ϕ.

2.1 Thermal stability

The thermal stability of the BH can be analyzed by finding the heat capacity and divergence that provide the positive and negative roots. The positive sign shows the stability, and the negative sign shows the instability of BHs disregarding the values of involved parameters. We extract another useful feature of the heat capacity relation in the scenario of phase transition interpretations through its divergence [55–57]. The heat capacity expression can be calculated as

$C=\frac{T}{\frac{{\partial }^{2}M}{{\partial }^{2}S}}=\frac{2s\left(4\sqrt{\varphi }-\sqrt{s}\right)\left(8\sqrt{s}\sqrt{\varphi }\left(-a+Q+1\right)+s\left(a-Q-1\right)+\pi \alpha \right)}{s^{3/2}\left(a-Q-1\right)-12s\sqrt{\varphi }\left(a-Q-1\right)-4\pi \alpha \sqrt{\varphi }+3\pi \alpha \sqrt{s}},(9)$

where

$\frac{{\partial }^{2}M}{\partial S^2}=\frac{s^{3/2}\left(a-Q-1\right)-12s\sqrt{\varphi }\left(a-Q-1\right)-4\pi \alpha \sqrt{\varphi }+3\pi \alpha \sqrt{s}}{8\sqrt{\pi }{s}^{3/2}{\left(\sqrt{s}-4\sqrt{\varphi }\right)}^3}.(10)$

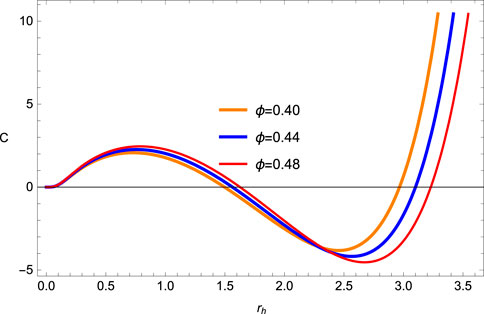
Moreover, the physical and non-physical solutions of BHs can be discussed by analyzing the roots of temperature. Concerning the aforementioned discussion, one may wish to have an analysis of the roots and divergence of heat capacity. From Figure 2, one can observe that the heat capacity in terms of horizon radius is positive within the range 0≤ r_h ≤ 1.5 (give stable region) but remains negative in the range 1.5≤ r_h ≤ 3.30 (give unstable region). Furthermore, the value of r_h = 3.30 provides the stable solution for the fixed parameters a and α. We calculate the roots of heat capacity termed as bound points, as follows:

$\begin{array}{cc}\hfill r_{h,BP\left(+\right)}& ={(\pi \alpha \left(-a+Q+1\right)-8\left(\sqrt{\varphi \left(-{\left(a-Q-1\right)}^3\right)\left(16\varphi \left(-a+Q+1\right)+\pi \alpha \right)}-4\varphi {\left(-a+Q+1\right)}^2\right))}^{\frac{1}{2}}/\sqrt{\pi }\left(-a+Q+1\right),\hfill \\ \hfill r_{h,BP\left(-\right)}& =-{(\pi \alpha \left(-a+Q+1\right)-8\left(\sqrt{\varphi \left(-{\left(a-Q-1\right)}^3\right)\left(16\varphi \left(-a+Q+1\right)+\pi \alpha \right)}-4\varphi {\left(-a+Q+1\right)}^2\right))}^{\frac{1}{2}}/\sqrt{\pi }\left(-a+Q+1\right).\hfill \end{array}(11)$

FIGURE 2

FIGURE 2. Plot of heat capacity in terms of horizon radius with different values of ϕ.

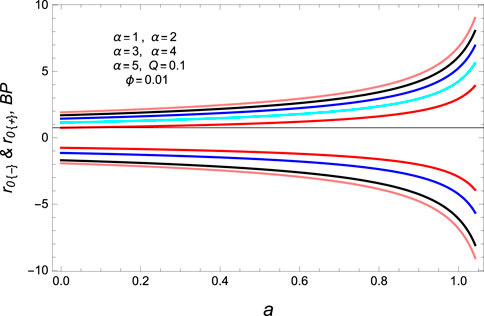
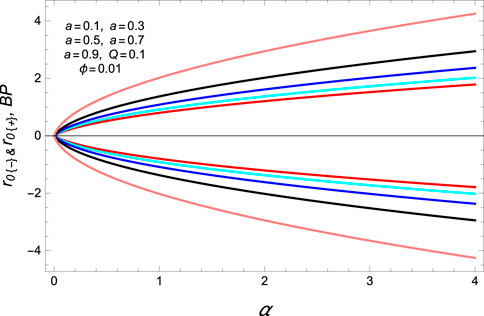
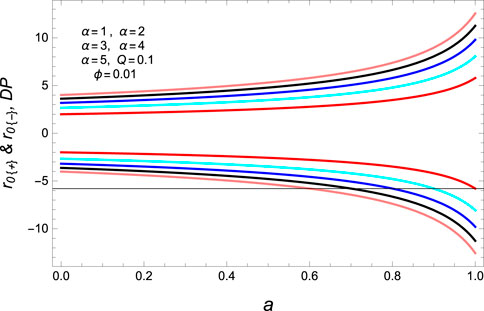
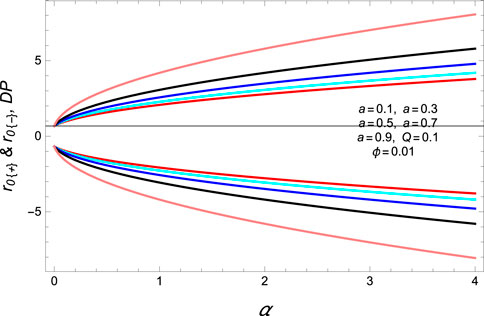
Here, the subscript B.P shows the bound point. As specified bounds, depending on the metric parameters, we introduce an admissible domain for the event horizon radius. After the investigation of geometric quantities of the extracted solutions, we examine the thermal stability of the SRBH, which is thermally stable in the mentioned range. We obtain the two real possible roots of heat capacity. For real roots, they must satisfy the condition α > 0 and a > 0. Interestingly, in Figures 3, 4), bound points are increasing and decreasing functions of the fixed parameters, i.e., α > 0 and a > 0. These points provide the information of the stable solution in the given range 0≤ r_h ≤ 10 and 0≤ r_h ≤ 4, respectively. Furthermore, one can find the divergent points calculated as

$\begin{array}{ll}\hfill r_{h,DP\left(+\right)}& =\frac{1}{\sqrt{\pi }}\left[\left(\frac{1}{{\left(-a+Q+1\right)}^2}\right)-2\left(a-Q-1\right)\left(24\varphi \left(-a+Q+1\right)+\pi \alpha \right)\right.\hfill \\ \hfill & +\left({\left(-a+Q+1\right)}^2\left({\pi }^2{\alpha }^2-160\pi \alpha \varphi \left(a-Q-1\right)+2304{\varphi }^2{\left(-a+Q+1\right)}^2\right)\right)/\hfill \\ \hfill & \left({\pi }^3{\alpha }^3{\left(a-Q-1\right)}^3+272{\pi }^2{\alpha }^2\varphi {\left(-a+Q+1\right)}^4-11520\pi \alpha {\varphi }^2{\left(a-Q-1\right)}^5\right.\hfill \\ \hfill & +{\left.110592{\varphi }^3{\left(-a+Q+1\right)}^6+32{\pi }^{3/2}\sqrt{{\alpha }^3\varphi {\left(a-Q-1\right)}^7{\left(16\varphi \left(-a+Q+1\right)+\pi \alpha \right)}^2}\right)}^{\frac{1}{3}}\hfill \\ \hfill & +\left({\pi }^3{\alpha }^3{\left(a-Q-1\right)}^3+272{\pi }^2{\alpha }^2\varphi {\left(-a+Q+1\right)}^4-11520\pi \alpha {\varphi }^2{\left(a-Q-1\right)}^5\right.\hfill \\ \hfill & +{\left.{\left.110592{\varphi }^3{\left(-a+Q+1\right)}^6+32{\pi }^{3/2}\sqrt{{\alpha }^3\varphi {\left(a-Q-1\right)}^7{\left(16\varphi \left(-a+Q+1\right)+\pi \alpha \right)}^2}\right)}^{\frac{1}{3}}\right]}^{\frac{1}{2}},\hfill \\ \hfill r_{h,DP\left(-\right)}& =-\frac{1}{\sqrt{\pi }}\left[\left(\frac{1}{{\left(-a+Q+1\right)}^2}\right)-2\left(a-Q-1\right)\left(24\varphi \left(-a+Q+1\right)+\pi \alpha \right)\right.\hfill \\ \hfill & +\left({\left(-a+Q+1\right)}^2\left({\pi }^2{\alpha }^2-160\pi \alpha \varphi \left(a-Q-1\right)+2304{\varphi }^2{\left(-a+Q+1\right)}^2\right)\right)/\hfill \\ \hfill & \left({\pi }^3{\alpha }^3{\left(a-Q-1\right)}^3+272{\pi }^2{\alpha }^2\varphi {\left(-a+Q+1\right)}^4-11520\pi \alpha {\varphi }^2{\left(a-Q-1\right)}^5\right.\hfill \\ \hfill & +{\left.110592{\varphi }^3{\left(-a+Q+1\right)}^6+32{\pi }^{3/2}\sqrt{{\alpha }^3\varphi {\left(a-Q-1\right)}^7{\left(16\varphi \left(-a+Q+1\right)+\pi \alpha \right)}^2}\right)}^{\frac{1}{3}}\hfill \\ \hfill & +\left({\pi }^3{\alpha }^3{\left(a-Q-1\right)}^3+272{\pi }^2{\alpha }^2\varphi {\left(-a+Q+1\right)}^4-11520\pi \alpha {\varphi }^2{\left(a-Q-1\right)}^5\right.\hfill \\ \hfill & +{\left.{\left.110592{\varphi }^3{\left(-a+Q+1\right)}^6+32{\pi }^{3/2}\sqrt{{\alpha }^3\varphi {\left(a-Q-1\right)}^7{\left(16\varphi \left(-a+Q+1\right)+\pi \alpha \right)}^2}\right)}^{\frac{1}{3}}\right]}^{\frac{1}{2}}.\hfill \end{array}(12)$

FIGURE 3

FIGURE 3. Plot of bound points in terms of a with different values of α.

FIGURE 4

FIGURE 4. Plot of bound points in terms of a with different values of α.

We discuss the divergent points in Figures 5, 6), and there are also increasing and decreasing functions for different ranges of the fixed parameters a and α. Divergence points provide the information about the stable solution in left and right panels within range 0≤ r_h ≤ 10.

FIGURE 5

FIGURE 5. Plot of divergent points in terms of a with different values of α.

FIGURE 6

FIGURE 6. Plot of divergent points in terms of α with different values of a.

2.2 Thermal geometries

In this section, we study the thermodynamic geometries developed by Ruppeiner and Weinhold for BHs [40–42]. We calculate the thermodynamic geometries such as Ruppeiner and Weinhold [58] for charged BHs in 4D Gauss–Bonnet gravity. In spite of all the numerous works in BH thermodynamics, a detailed microstructure of BHs was still missing. Here, we explore and study the general quantities of thermodynamic geometry for the considered BH. Weinhold’s and Ruppeiner’s formalisms are used in order to justify the phase transition for the charged BH in 4D Gauss–Bonnet gravity [59–63]. Furthermore, based on the Hessian matrix of the BH mass, we introduce thermodynamic geometric methods and give its scalar curvatures (Ruppeiner and Weinhold). Furthermore, the graphical behaviors of these scalar curvatures with the horizon radius are investigated. The illustration of the Weinhold geometry can be written as

${g_{ij}}^W={\partial }_i{\partial }_{j}M\left(S,\alpha ,\varphi \right).(13)$

Metric in terms of mass function can be expressed as

$d{s}_W^2=M_{SS}{dS}^2+M_{\alpha \alpha }d{\alpha }^2+M_{\varphi \varphi }d{\varphi }^2+2M_{S\alpha }dSd\alpha +2M_{S\varphi }dSd\varphi +2M_{\alpha \varphi }d\alpha d\varphi ,(14)$

whose matrix form is given by

$\left(\begin{array}{ccc}\hfill M_{SS}\hfill & \hfill M_{S\alpha }\hfill & \hfill M_{S\varphi }\hfill \\ \hfill M_{\alpha S}\hfill & \hfill M_{\alpha \alpha }\hfill & \hfill 0\hfill \\ \hfill M_{\varphi S}\hfill & \hfill 0\hfill & \hfill M_{\varphi \varphi }\hfill \end{array}\right).$

We calculate the Weinhold scalar curvature (R^W) using the aforementioned equations. The mathematical expression can be written as

$R^W=\frac{4\sqrt{\pi }\left(4\sqrt{\varphi }-\sqrt{\pi }\sqrt{{r_h}^2}\right)\left(4\sqrt{\pi }\sqrt{{r_h}^2\varphi }+\pi {r_h}^2-96\varphi \right)}{{\left(12\sqrt{\varphi }-\sqrt{\pi }\sqrt{{r_h}^2}\right)}^2\left(-\pi a{r_h}^2+\pi \alpha +\pi Q{r_h}^2+\pi {r_h}^2\right)}.(15)$

One can observe in Figure 7 that the curvature scalar of the Weinhold geometry for the charged BH provides the stable region in the given range 0.22≤ r_h ≤ 0.44. Furthermore, we consider the Ruppeiner geometry that is conformal to the Weinhold geometry. The Ruppeiner curvature scalar is determined as

$d{s}_R^2=\frac{d{s}_W^2}{T}.(16)$

FIGURE 7

FIGURE 7. Plot of the Weinhold geometry in terms of horizon radius with fixed values α and a.

The mathematical expression for the Ruppeiner geometry is as follows:

$\begin{array}{ll}\hfill R^{\left(RUP\right)}& =16{\pi }^{3/2}{r}_h{\left(\sqrt{\pi }{r}_h-4\sqrt{\varphi }\right)}^2\left(4\sqrt{\varphi }-\sqrt{\pi }\sqrt{{r_h}^2}\right)\left(4\sqrt{\pi }\sqrt{{r_h}^2\varphi }+\pi {r_h}^2-96\varphi \right)/\hfill \\ \hfill & {\left(12\sqrt{\varphi }-\sqrt{\pi }\sqrt{{r_h}^2}\right)}^2\left(-\pi a{r_h}^2+\pi \alpha +\pi Q{r_h}^2+\pi {r_h}^2\right)\left(\pi {r_h}^2\left(-a+Q+1\right)+8\sqrt{\pi }{r}_h\sqrt{\varphi }\left(a-Q-1\right)-\pi \alpha \right).\hfill \end{array}(17)$

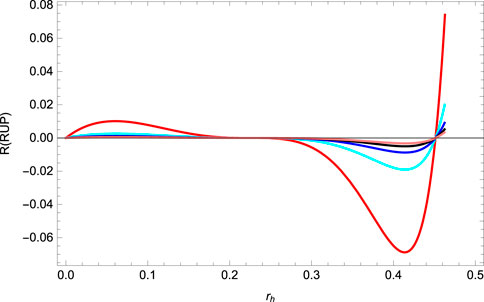
Obtaining the analytical solution of Eq. 14 with respect to r_h is not easy. In order to investigate the horizons, we plot the graph for the Ruppeiner geometry in Figure 8. Furthermore, for studying the effects of the metric function versus radial co-ordinates, it is observed that (Figure 8) for the small values of the geometrical mass, the metric function has only one root. Furthermore, the effects of the mass on the horizon could be divided into three regions such as 0≤ r_h ≤ 0.30, 0.30≤ r_h ≤ 0.44, and 0.44≤ r_h ≤ 0.50. After that, point r₀ = 0.44 will have an increasing function, and it will provide the stable solution of the geometrical mass.

FIGURE 8

FIGURE 8. Plot of the Ruppeiner geometry in terms of horizon radius with fixed values α and a.

3 Slowly rotating BHs in 4D Gauss–Bonnet gravity

The 4D GBT has an interesting and phenomenological match with the GR [62]. The conformal metric with g_μν → e^−2ϕg_μν, yielding the 4D Gauss–Bonnet action, reads to be [63]

$S_4^G=\alpha \int d^{4}x\sqrt{-g}\left[\frac{1}{2}\varphi \mathcal{G}-G^{\mu \nu }{\nabla }_{\mu }\varphi {\nabla }_{\nu }\varphi -\frac{1}{8}{\left({\left(\nabla \varphi \right)}^2\right)}^2-\frac{1}{2}{\left(\nabla \varphi \right)}^2\square \varphi \right].(18)$

No further conjectures regarding specific solutions to higher-dimensional background spacetimes are necessary. We develop the slowly rotating BH models in the 4D GBT as

$d{s}^2=-f\left(r\right)d{t}^2+\frac{d{r}^2}{h\left(r\right)}+2a{r}^{2}p\left(r\right){\sin }^2\theta dtd\varphi +r^2\left[d{\theta }^2+{\sin }^2\theta d{\varphi }^2\right].(19)$

In this development, we are interested in developing Schwarzschild-like solutions, where h(r) = f(r). By setting x = cos(θ), our line element can be written as [61]

$d{s}^2=-f\left(r\right)d{t}^2+\frac{d{r}^2}{f\left(r\right)}+2a{r}^{2}p\left(r\right)\left(1-x^2\right)dtd\varphi +r^2\left[\frac{d{x}^2}{1-x^2}+\left(1-x^2\right)d{\varphi }^2\right].(20)$

Utilizing the aforementioned metric, we can solve the metric function for f(r) through the geometric expression [61]:

$f\left(r\right)=1+\frac{r^2\left(1+\sqrt{1+\frac{4\alpha \mathrm{\Lambda }}{3}+\frac{8\alpha M}{r^3}}\right)}{2\alpha }.(21)$

4 Joule–Thomson expansion for the SRBH in 4D Gauss–Bonnet gravity

A classical physical quantity Joule–Thomson expansion is one of the well-known processes to discuss the temperature change of gas from the high-pressure region to the low-pressure region through a porous plug [64, 65]. It mainly explores the process of gas expansion that expresses the temperature decrease (cold effect) and temperature increase (heat effect); during the whole expansion, enthalpy is kept constant. This change depends on the Joule–Thomson coefficient, which is given by [32–34]

${\mu }_{JT}={\left(\frac{\partial T}{\partial P}\right)}_H=\frac{1}{C_p}\left[T{\left(\frac{\partial V}{\partial T}\right)}_p-V\right],(22)$

where the heat capacity at constant pressure can be written as

$c_P={\left(\frac{\partial S}{\partial T}\right)}_P.(23)$

The entropy is obtained at event horizon by the area law as follows [34–37]:

$S=\pi r_0^2,(24)$

and

$P=-\frac{\mathrm{\Lambda }}{8\pi }=\frac{3}{8\pi L^2}.(25)$

At this stage, it is straightforward to see that the aforementioned BH properties satisfy the following Smarr relation:

$dM=TdS+VdP+\phi d\alpha .$

From the aforementioned relation, thermodynamic parameters can be defined as

$T={\left(\frac{\partial M}{\partial S}\right)}_{P,\alpha },V={\left(\frac{\partial M}{\partial P}\right)}_{S,\alpha }and\phi ={\left(\frac{\partial M}{\partial \alpha }\right)}_{S,P}.(26)$

Using f(r) = 0, the mass of the BH can be written as

$M=\frac{3\alpha +8\pi P{r}_0^4+3r_0^2}{6r_0}.(27)$

Here, r₀ denotes the event horizon, which we will discuss in further calculations. From Eq. 21, one can obtain the Hawking temperature in terms of horizon radius as

$T=\frac{r_0\left(1+\sqrt{1+\frac{8\alpha M}{r_0^3}-\frac{32\pi \alpha P}{3}}\right)}{4\pi \alpha }-\frac{3M}{2\pi r_0^2\sqrt{1+\frac{8\alpha M}{r_0^3}-\frac{32\pi \alpha P}{3}}}.(28)$

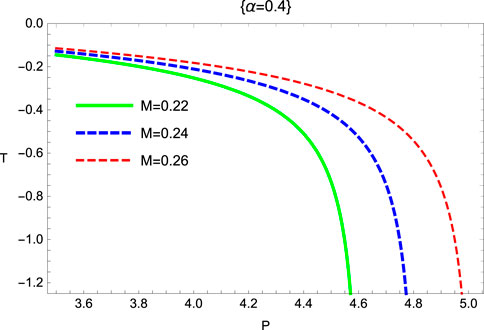
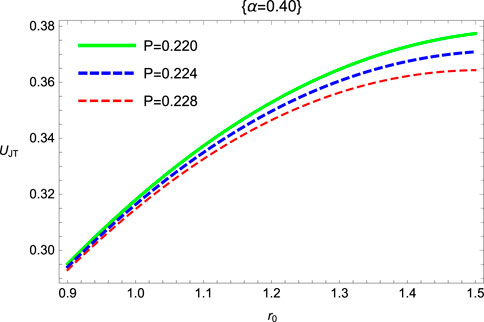
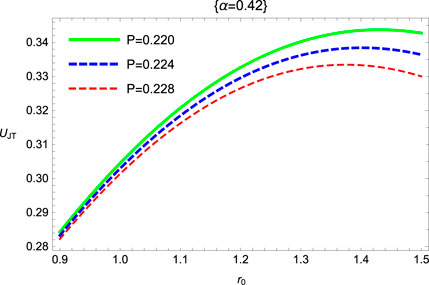
One can analyze the behavior of isenthalpic curves (thermodynamic property) from Figures 9, 10 for fixed values α = 0.4 and α = 0.6 in the case of the SRBH in 4D Gauss–Bonnet gravity. The isenthalpic curves shift to the cooling region as we increase the value of α. We observed that the converging values of M along r₀ isenthalpic curves shrink to zero in the SRBH in 4D Gauss–Bonnet gravity. Furthermore, the inversion curves separate and distinguish the plane of isenthalpic curves into two regions, namely, cooling and heating regions. Analogy between the cosmological constant Λ and the thermodynamics pressure is associated with the conjugate property recognized as volume. This relation can be expressed as

$V=\frac{4\pi r_0^3}{3}.(29)$

FIGURE 9

FIGURE 9. Plot of isenthalpic curves with fixed value α =0.4.

FIGURE 10

FIGURE 10. Plot of isenthalpic curves with fixed value α =0.6.

The potential of BHs is shown as

$\phi =\frac{1}{2r_0}.(30)$

The pressure reads are shown as

$P=\frac{3\left(-\alpha +2M{r}_0-r_0^2\right)}{8\pi r_0^4}.(31)$

From the temperature relation, one can calculate the horizon radius as

$r_0=\frac{1}{2}\sqrt[3]{\frac{3}{2}}{\left[-\frac{3\sqrt{M^2\left(32\pi \alpha P+1\right)}}{\pi \left(32\pi \alpha P^2-3P\right)}+\frac{32\alpha MP}{32\pi \alpha P^2-3P}+\frac{3M}{\pi \left(32\pi \alpha P^2-3P\right)}\right]}^{\frac{1}{3}}.(32)$

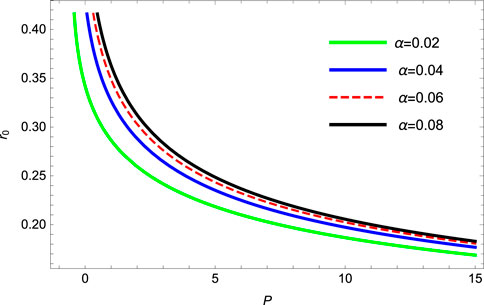
The inversion curves related to the horizon radius shown in Figure 11 show the positive behavior and satisfy the μ_JT condition for fixed α = 0.02, 0.04, 0.06, & 0.08. We observe that the inversion curves via the horizon radius are both positive. From Eqs 22, 23, the Joule–Thomson expansion coefficient is determined as

${\mu }_{JT}=\frac{4{\alpha }^3+r_0^6\left(2-8\pi \alpha P\right)+6\alpha r_0^4+9{\alpha }^2{r}_0^2}{3\pi \alpha {\left(2\alpha +r_0^2\right)}^2}.(33)$

FIGURE 11

FIGURE 11. Plot of horizon radius in terms of pressure.

The cooling–heating regions are deduced by the sign of Eq. 33 in Figures 12, 13. Because pressure always falls during expansion, temperature changes the sign of coefficient μ_JT, which means that a positive temperature change results in a cooling region and a negative temperature change results in a heating region. As shown previously, both the numerator and the denominator are always positive if p > 0. So, there will be no singular or divergent point for μ_JT. We have confirmed in our discussion that the expansion is always positive and provides the regime of the cooling process. From the definition of the Joule–Thomson expansion, we can extract the inversion temperature as

$T_i=\frac{-2{\alpha }^3+r_0^6\left(2-8\pi \alpha P\right)+3\alpha r_0^4\left(3-16\pi \alpha P\right)+3{\alpha }^2{r}_0^2}{12\pi \alpha r_0{\left(2\alpha +r_0^2\right)}^2}.(34)$

FIGURE 12

FIGURE 12. Plot of the Joule–Thomson coefficient in terms of horizon radius.

FIGURE 13

FIGURE 13. Plot of the Joule–Thomson coefficient in terms of horizon radius.

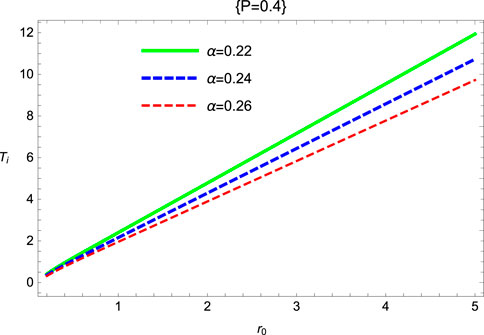
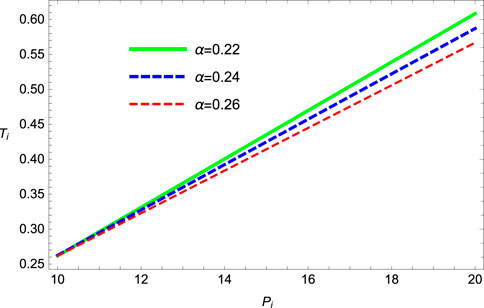
Figure 14 shows the behavior of inversion temperature with increasing values of α and setting p = 0.4 and p = 0.8 for the SRBH in 4D Gauss–Bonnet gravity. The temperature increases under the region 0 ≤ r₀ ≤ 5, which provides the thermodynamically stable region. Figure 15 represents the T_i − P_i plane; in this figure, we investigated that the curves are not closed along the minimum inversion curves and are comparable to the van der Waals fluids. The inversion temperature is inversely proportional to the value of α in the SRBH, and it is habituated to separate the cooling and heating regions. In three trajectories, the position of the inversion point (Ti − Pi) shifts to the higher values with the increase in parameter α.

FIGURE 14

FIGURE 14. Plot of inversion temperature in terms of r₀ with the fixed value of pressure P.

FIGURE 15

FIGURE 15. Plot of inversion temperature in terms of inversion pressure P_i.

5 Conclusion

In this work, we study the fact that the modified charged and slowly rotating BHs contain some required thermodynamic characteristics, such as entropy and temperature. Factually, BH is a thermodynamic system containing Hawking temperature proportional to its surface gravity on the horizon area. Thermal stability of the BH system is a major characteristic, which may directly be related to the heat capacity [64, 65]. In this paper, we considered two cases for BHs, the first one is thermal geometry and the second is the Joule–Thomson expansion. In Figures 1, 2, we graphed the temperature and heat capacity, and these results behaviorally depict the local stability of the BH systems.

We compare how physical quantities of the solutions modified by varying coupling strengths of the 4D Gauss–Bonnet theory (GBT) relate to standard Einstein’s gravity results. We considered a negative cosmological constant in the 4D Gauss–bonnet theory, which necessarily leads to the minimum mass of the BH solution. The leading order in the rotation parameter is used to develop the BH solutions; here, we analyzed the thermodynamic properties of this BH solution. We also observed that, for a large value of the 4D Gauss–Bonnet coupling constant, the de Sitter solution did not overlap the recognized mass of the GR case. However, the new 4D EGB theory as an alternative to Einstein’s theory is attracting strong attention. In this structure, there are extensive works to support the dedication and perspicacity of the nature of the new 4D EGB theory.

We studied the bound and divergent points in Figures 3–6, which are increasing and decreasing functions. With the increasing values of α, a, the BH system turns more stable, whereas the divergence takes place at smaller values of α. So, the instability of BHs increases for smaller values of α. Thermodynamic geometries named as Weinhold and Ruppeiner for the compact system are graphed in Figures 7, 8. Curvature scalars of Weinhold and Ruppeiner geometries for charged BHs exhibit singularity and a stable region with different values of α and a; in this view, we investigated and depicted the thermodynamic phase transition. Recently, we carried out a similar work by discussing the thermal stability of BTZ-like BHs [66]. By comparing these works, we concluded that charged BHs in 4D Gauss–Bonnet are thermally stable and fulfill the thermodynamic geometrical quantities. Moreover, this work may be beneficial for future research studies.

In the second part of our work, we have investigated the Joule–Thomson expansion for the SRBH in 4D Gauss–Bonnet gravity, where cosmological constant Λ is considered as pressure and the BH mass as enthalpy. Furthermore, we have explored the thermodynamic quantities of the SRBH in 4D Gauss–Bonnet gravity in the extended phase space and obtained the equation of state [64]. We have plotted the isenthalpic and inversion curves in the T − P plane and deduced the cooling and heating regions for different values of α and mass M. It shows that, in contrast to van der Waals fluids, the inversion curves are closed, and there is only one inversion curve.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This project was supported by the National Natural Science Foundation of China (Grant Nos. 11901379 and 12171305). The authors thank the reviewers for their comments on this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ruffini R, Wheeler JA. Introducing the black hole. Phys Today (1971) 24:30–41. doi:10.1063/1.3022513

CrossRef Full Text | Google Scholar

2. Bekenstein JD. Black holes: Classical properties, thermodynamics and heuristic quantization. arXiv:gr-qc/9808028 (1998).

Google Scholar

3. Bekenstein JD. Black holes and entropy. Phys Rev D (1973) 8:2333–46. doi:10.1103/physrevd.7.2333

CrossRef Full Text | Google Scholar

4. Hawking SW. Particle creation by black holes. New York: Springer (1975).

Google Scholar

5. Bardeen JM, Carter B, Hawking SW. The four laws of black hole mechanics. Commun Math Phys (1973) 31:161–70. doi:10.1007/bf01645742

CrossRef Full Text | Google Scholar

6. Klebanov IR, Witten E. AdS/CFT correspondence and symmetry breaking. Nucl Phys B (1999) 556:89–114. doi:10.1016/s0550-3213(99)00387-9

CrossRef Full Text | Google Scholar

7. Kubiznk D, Mann RB. P- V criticality of charged AdS black holes. JHEP (2012) 1207:33. doi:10.1007/jhep07(2012)033

CrossRef Full Text | Google Scholar

8. Bueno P, Cano PA, Moreno J, van der Velde G. Regular black holes in three dimensions. Phys Rev D (2021) 104:L021501. doi:10.1103/physrevd.104.l021501

CrossRef Full Text | Google Scholar

9. Mann RB, Solodukhin SN. Universality of quantum entropy for extreme black holes. Nucl Phys B (1998) 523:293–307. doi:10.1016/s0550-3213(98)00094-7

CrossRef Full Text | Google Scholar

10. Medved AJ, Kunstatter G. Quantum corrections to the thermodynamics of charged 2D black holes. Phys Rev D (1992) 60:104029. doi:10.1103/physrevd.60.104029

CrossRef Full Text | Google Scholar

11. Papnoi U, Farruh A. Rotating charged black hole in 4D Einstein–Gauss–Bonnet gravity: Photon motion and its shadow. Phys Dark Univ (2022) 35:100916. doi:10.1016/j.dark.2021.100916

CrossRef Full Text | Google Scholar

12. Farruh A, Sanjar S, Pankaj S, Siwach S. Charged black hole in 4D einstein-gauss-bonnet gravity: Particle motion, plasma effect on weak gravitational lensing and centre-of-mass energy. J Cosm Astro Part Phys (2021) 2021:045. doi:10.1088/1475-7516/2021/08/045

CrossRef Full Text | Google Scholar

13. Cano PA, Murcia A. Electromagnetic quasitopological gravities. JHEP (2020) 10:125. doi:10.1007/jhep10(2020)125

CrossRef Full Text | Google Scholar

14. Podolský J, Ortaggio M. Robinson–Trautman spacetimes in higher dimensions. Class Quant Grav (2006) 23:5785. doi:10.1088/0264-9381/23/20/002

CrossRef Full Text | Google Scholar

15. Jacobson T. When is g_ttg_rr = −1. Class Quant Grav (2007) 24:5717–9. doi:10.1088/0264-9381/24/22/n02

CrossRef Full Text | Google Scholar

16. Hervik S, Ortaggio M. Universal black holes. JHEP (2020) 2:47. doi:10.1007/jhep02(2020)047

CrossRef Full Text | Google Scholar

17. Babar GZ, Farruh A, Abdullah ZB. Gravitational lensing in 4D EinsteinGaussBonnet gravity in the presence of plasma. Phys Dark Univ (2021) 32:100798. doi:10.1016/j.dark.2021.100798

CrossRef Full Text | Google Scholar

18. Kumar R, Shafqat UI, Sushant G. Gravitational lensing by charged black hole in regularized 4D Einstein Gauss Bonnet gravity. EPJC (2020) 80:1128. doi:10.1140/epjc/s10052-020-08606-3

CrossRef Full Text | Google Scholar

19. Övgün A. Black hole with confining electric potential in scalar-tensor description of regularized 4-dimensional Einstein Gauss Bonnet gravity. Phys Lett B (2021) 820:136517. doi:10.1016/j.physletb.2021.136517

CrossRef Full Text | Google Scholar

20. Bousder M, Bourakadi KE, Bennai M. Charged 4D Einstein-Gauss-Bonnet black hole: Vacuum solutions, Cauchy horizon, thermodynamics. Phys Dark Univ (2021) 32:100839. doi:10.1016/j.dark.2021.100839

CrossRef Full Text | Google Scholar

21. Dolan BP. Pressure and volume in the first law of black hole thermodynamics. Class Quant Grav (2011) 28:235017. doi:10.1088/0264-9381/28/23/235017

CrossRef Full Text | Google Scholar

22. Kastor D, Ray S, Traschen J. Enthalpy and the mechanics of AdS black holes. Class Quant Grav (2009) 26:195011. doi:10.1088/0264-9381/26/19/195011

CrossRef Full Text | Google Scholar

23. Dolan BP. Compressibility of rotating black holes. Phys Rev D (2011) 84:127503. doi:10.1103/physrevd.84.127503

CrossRef Full Text | Google Scholar

24. Cvetic M, Gibbons GW, Kubiznk D, Pope CN. Black hole enthalpy and an entropy inequality for the thermodynamic volume. Phys Rev D (2011) 84:024037. doi:10.1103/physrevd.84.024037

CrossRef Full Text | Google Scholar

25. L ü H, Pang Y, Pope CN, Vazquez-Poritz JF. AdS and Lifshitz black holes in conformal and Einstein-Weyl gravities. Phys Rev D (2012) 86:044011. doi:10.1103/physrevd.86.044011

CrossRef Full Text | Google Scholar

26. Bhattacharya K, Majhi BR, Samanta SV. van der Waals criticality in AdS black holes: A phenomenological study. Phys Rev D (2017) 96:084037. doi:10.1103/physrevd.96.084037

CrossRef Full Text | Google Scholar

27. Miao YG, Wu YM. Thermodynamics of the Schwarzschild-AdS black hole with a minimal length. Adv High Energ Phys. (2017) 2017:1–14. doi:10.1155/2017/1095217

CrossRef Full Text | Google Scholar

28. Hendi SH, Sheykhi A, Panahiyan S, Eslam Panah B. Phase transition and thermodynamic geometry of Einstein-Maxwell-dilaton black holes. Phys Rev D (2016) 92:064028. doi:10.1103/physrevd.92.064028

CrossRef Full Text | Google Scholar

29. Kuang XM, Miskovic O. Thermal phase transitions of dimensionally continued AdS black holes. Phys Rev D (2017) 95:046009. doi:10.1103/physrevd.95.046009

CrossRef Full Text | Google Scholar

30. Ökcü Ö, Aydiner E. JouleThomson expansion of the charged AdS black holes. EPJC (2017) 77:24. doi:10.1140/epjc/s10052-017-4598-y

CrossRef Full Text | Google Scholar

31. Ökcü Ö, Aydiner E. JouleThomson expansion of KerrAdS black holes. EPJC (2018) 78:123. doi:10.1140/epjc/s10052-018-5602-x

CrossRef Full Text | Google Scholar

32. Ghaffarnejad H, Yaraie E, Farsam M. Quintessence reissner nordström anti de Sitter black holes and Joule thomson effect. Theo Phys (2018) 57:1671–82. doi:10.1007/s10773-018-3693-7

CrossRef Full Text | Google Scholar

33. Cisterna A, Hu SQ, Kuang XM. Joule Thomson expansion in AdS black holes with momentum relaxation. Phys Lett B (2019) 797:134883. doi:10.1016/j.physletb.2019.134883

CrossRef Full Text | Google Scholar

34. Guo S, Han Y, Li GP. Joule–Thomson expansion of a specific black hole in f (R) gravity coupled with Yang–Mills field. Class Quant Grav (2020) 37:085016. doi:10.1088/1361-6382/ab77ec

CrossRef Full Text | Google Scholar

35. Barrow JD. The area of a rough black hole. Phys Lett B (2020) 808:135643. doi:10.1016/j.physletb.2020.135643

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Alemany PA, Zanette DH. Fractal random walks from a variational formalism for Tsallis entropies. Phys Rev D (1994) 49:956–8. doi:10.1103/physreve.49.r956

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Saridakis EN. Barrow holographic dark energy. Phys Rev D (2020) 102:123525. doi:10.1103/physrevd.102.123525

CrossRef Full Text | Google Scholar

38. Cano PA, Murcia A. Resolution of Reissner–Nordström singularities by higher-derivative corrections. Class Quant Grav (2021) 38:075014. doi:10.1088/1361-6382/abd923

CrossRef Full Text | Google Scholar

39. Lan SQ. Joule-Thomson expansion of charged Gauss-Bonnet black holes in AdS space. Phys Rev D (2018) 98:084014. doi:10.1103/physrevd.98.084014

CrossRef Full Text | Google Scholar

40. Ruppeiner G. Thermodynamics: A riemannian geometric model. Phys Rev A (1979) 20:1608–13. doi:10.1103/physreva.20.1608

CrossRef Full Text | Google Scholar

41. Ruppeiner G. Riemannian geometry in thermodynamic fluctuation theory. Rev Mod Phys (1995) 67:605–59. doi:10.1103/revmodphys.67.605

CrossRef Full Text | Google Scholar

42. Ruppeiner G. Erratum: Riemannian geometry in thermodynamic fluctuation theory. Rev Mod Phys (1996) 68:313. doi:10.1103/revmodphys.68.313

CrossRef Full Text | Google Scholar

43. Cai R, Cho J. Thermodynamic curvature of the BTZ black hole. Phys Rev D (1999) 60:067502. doi:10.1103/physrevd.60.067502

CrossRef Full Text | Google Scholar

44. Shen J. Thermodynamic geometry and critical behavior of black holes. arXiv: gr-qc/0512035 (2005).

Google Scholar

45. Sarkar G, Sengupta T, Tiwari BN. On the thermodynamic geometry of BTZ black holes. JHEP (2006) 611:15. doi:10.1088/1126-6708/2006/11/015

CrossRef Full Text | Google Scholar

46. Hermann R. Physics and systems. New York: Marcel Dekker (1973).

Google Scholar

47. Mrugala R. Geometrical formulation of equilibrium phenomenological thermodynamics. Rep Math Phys (1978) 14:419–27. doi:10.1016/0034-4877(78)90010-1

CrossRef Full Text | Google Scholar

48. Mrugala R. Submanifolds in the thermodynamic phase space. Rep Math Phys (1985) 21:197–203. doi:10.1016/0034-4877(85)90059-x

CrossRef Full Text | Google Scholar

49. Castillo GFT, Velasquez MM. Riemannian structure of the thermodynamic phase space. Rev Mex F (1993) 39:194.

Google Scholar

50. Hernandez G, Lacomba EA. Contact Riemannian geometry and ther-modynamics. Diff Geom Appl (1998) 8:205–16. doi:10.1016/s0926-2245(98)00006-0

CrossRef Full Text | Google Scholar

51. Zeng XX, Zhang HQ, Zhang H. Shadows and photon spheres with spherical accretions in the four-dimensional GaussBonnet black hole. EPJC (2020) 80:872. doi:10.1140/epjc/s10052-020-08449-y

CrossRef Full Text | Google Scholar

52. Glavan D, Lin C. Einstein-Gauss-Bonnet gravity in four-dimensional spacetime. Phys Rev Lett (2020) 124:081301. doi:10.1103/physrevlett.124.081301

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Singh DV, Ghosh SG, Maharaj SD. Clouds of strings in 4D einstein–gauss–bonnet black holes. Phys Dark Univ (2020) 30:100730. doi:10.1016/j.dark.2020.100730

CrossRef Full Text | Google Scholar

54. Anacleto MA, Brito F, Campos J, Passos E. Absorption and scattering of a noncommutative black hole. Phys Lett B (2020) 803:135334. doi:10.1016/j.physletb.2020.135334

CrossRef Full Text | Google Scholar

55. Cai RG, Hu YP, Pan QY, Zhang YL. Thermodynamics of black holes in massive gravity. Phys Rev D (2015) 91:024032. doi:10.1103/physrevd.91.024032

CrossRef Full Text | Google Scholar

56. Azreg-Anou M. Black hole thermodynamics: No inconsistency via the inclusion of the missingP−Vterms. Phys Rev D (2015) 91:064049. doi:10.1103/physrevd.91.064049

CrossRef Full Text | Google Scholar

57. Sadeghi J, Pourhassan B, Rostami M. P−Vcriticality of logarithm-corrected dyonic charged AdS black holes. Phys Rev D (2016) 94:064006. doi:10.1103/physrevd.94.064006

CrossRef Full Text | Google Scholar

58. Soroushfar S, Saffari R, Kamvar N. Thermodynamic geometry of black holes in f (R) gravity. EPJC (2016) 76:476. doi:10.1140/epjc/s10052-016-4311-6

CrossRef Full Text | Google Scholar

59. Hawking SW. Black holes and thermodynamics. Phys Rev D (1976) 13:191–7. doi:10.1103/physrevd.13.191

CrossRef Full Text | Google Scholar

60. Hawking SW, Page DN. Thermodynamics of black holes in anti-de Sitter space. Commun Math Phys (1983) 87:577–88. doi:10.1007/bf01208266

CrossRef Full Text | Google Scholar

61. Gammon M, Mann R. Slowly rotating black holes in 4D gauss-bonnet gravity. arXiv preprint arXiv:2210.01909 (2022).

Google Scholar

62. Clifton T, Carrilho P, Fernandes PG, Mulryne DJ. Observational constraints on the regularized 4D Einstein-Gauss-Bonnet theory of gravity. Phys Rev D (2020) 102:084005. doi:10.1103/physrevd.102.084005

CrossRef Full Text | Google Scholar

63. Hennigar RA, Kubizňák D, Mann RB, Pollack C. On taking the 4D limit of gauss-bonnet gravity: Theory and solutions. J High Energ Phys. (2020) 7:18. doi:10.1007/JHEP07(2020)027

CrossRef Full Text | Google Scholar

64. Ökcü Ö, Aydiner E. JouleThomson expansion of KerrAdS black holes. Eur Phys C (2018) 78:123. doi:10.1140/epjc/s10052-018-5602-x

CrossRef Full Text | Google Scholar

65. Haldar A, Biswas R. Joule-Thomson expansion of five-dimensional Einstein-Maxwell-Gauss-Bonnet-AdS black holes. EPL (2018) 123:40005. doi:10.1209/0295-5075/123/40005

CrossRef Full Text | Google Scholar

66. Ditta A, Tiecheng X, Mustafa G, Yasir M, Atamurotov F. Thermal stability with emission energy and Joule Thomson expansion of regular BTZ-like black hole. EPJC (2022) 82:756. doi:10.1140/epjc/s10052-022-10708-z

CrossRef Full Text | Google Scholar