A review of the Kondo insulator materials class of strongly correlated electron systems: Selected systems and anomalous behavior

Studies of strongly correlated electron systems have been at the forefront of research in condensed matter physics ever since the discovery of the co-existence of strong Pauli-paramagnetism and superconductivity in the archetypal heavy-fermion compound CeCu₂Si₂ in 1979. The construct of correlated electron physics typifies the behavior of thermal and electronic properties of a material when the Coulomb interaction between conduction electrons exceeds the electron kinetic energy at a given thermal energy and redefines in remarkable ways our understanding of the behavior of a metal near its ground state. While correlated electron behavior has by now been demonstrated in a variety of different types of materials, Kondo systems in particular are arguably the most intensively studied among these. The Kondo interaction is used to describe the effect that a spin-magnetic ion has on its environment when immersed in the conduction electron sea of a metal. The localized spin of the Kondo ion polarizes nearby conduction electrons to form a so-called Kondo cloud, which acts to screen and magnetically (partially) neutralize the localized spin. In Kondo systems, the low-temperature behavior is prone to the formation of heavy fermions, which is the term given to quasiparticle excitations that define the emergence of effective electron masses that can be up to three orders of magnitude greater than that of a free electron. The Kondo effect presents itself in three guises: first, the single-ion Kondo state which is found in a metal having only a small amount of magnetic ions dissolved into it; second, the incoherent Kondo state in materials where there is a Kondo ion in every crystallographic unit cell of the material, but the Kondo ions remain incoherent or uncoupled from each other; and third, the coherent Kondo lattice state which manifests itself toward low temperatures where the interaction between Kondo ions becomes comparable to the thermal energy of conduction electrons that mediate magnetic exchange between Kondo ions. In a small number of cases, the outcome of a material condensing into the Kondo state turns out to be the peculiar formation of a very narrow energy band gap at the metallic Fermi energy. Such a band gap has significant consequences in practically all of the physical properties of a material that stem from the behavior of conduction electrons in proximity of the Fermi energy. This is most readily seen in electrical resistivity, heat capacity, and magnetic susceptibility. The band gapping gives cause to the term Kondo insulator (also referred to as Kondo semimetal or heavy-fermion semiconductor) that is used to describe this exceptional variety of Kondo systems. The term Kondo insulator is in general use although most Kondo insulators have a small but finite electrical conduction in the low-temperature limit where Kondo screening may be accomplished to its full extent. While the Kondo lattice ground state is exemplified by a very high density of electronic states at the Fermi energy, Kondo insulators, on the other hand, have, by virtue of narrow band gapping, a low density of electronic states. It remains a counter-intuitive observation, therefore, that despite their low density of states, Kondo insulators have curiously strong spin polarization energy scales and accompanying high values of their Kondo temperature, being the defining quantity which acts as an organizing principle in their temperature-dependent physical properties. In this article, we review the fundamentals of the Kondo insulating state, and we discuss the theoretical principles of what is presently understood about the formation of a Kondo insulator. The experimental results of a selected number of examples that have gained prominence in this class of materials are compared to each other in order to seek out similarities that may help deepen our understanding of the Kondo insulating state.

1 Introduction

A long-standing and multi-faceted problem in condensed matter physics is posed by the introduction of a magnetic impurity in a metal. Considering the very successfully adopted non-interacting or “free-electron” approach of our understanding of ordinary metals, it appears to be rather counter-intuitive that a magnetic moment may survive on the impurity at all when the impurity is immersed into the environment of a sea of degenerate conduction electrons. This question was the subject of much debate [[1,2], see, e.g., M. B. Maple in Part I] that accompanied the development of the related subject of Kondo physics from the late 1960s. When a magnetic ion with spin and charge residing in an unfilled d − or f − electron shell is inserted into a metal, charge neutrality and spin parity result in conduction electrons nearby to the impurity spin screening or compensating the spin in an antiferromagnetic coupling, with characteristic energy k_BT_K, where k_B is Boltzmann’s constant and T_K is the Kondo temperature. The formation of the Kondo cloud leads essentially to a gain in energy per magnetic impurity which is customarily written as follows:

$k_{\text{B}}{T}_{\text{K}}\sim E_{\text{F}}{e}^{-1/\mathbb{N}\left(E_{\text{F}}\right)J_{\text{ex}}}\propto D^{*}{e}^{-1/\mathbb{N}\left(E_{\text{F}}\right)J_{\text{ex}}},(1)$

where J_ex measures the exchange coupling between the f − electrons and conducting electrons that gives rise to a hybridized band between these two types of electrons, of width D*. This expression then connects the Sommerfeld coefficient γ (see discussion below and Eq. 2), the electronic density of states at the Fermi energy $\mathbb{N}\left(E_{\text{F}}\right)$, and the electron mass m in a straightforward but very consequential manner. The heat capacity attributable to the electrons in a metal follows $C_{\text{el}}\left(T\right)=\gamma T$, with an enhancement in the heat capacity that directly tracks the electronic density of states at the Fermi energy.

The screening of a magnetic moment by the “Kondo cloud” is a many-body problem; it takes place gradually as a function of temperature and in the T → 0 limit with complete screening when a non-magnetic singlet state is achieved. The theoretical treatment of the spin-only case was a convenient and adequate yet simplified treatment of the problem dealing with, for example, Fe impurities dissolved in a metal such as Cu or Au, but a more embracive approach that includes spin-orbit effects and crystal-electric field splitting is demanded when dealing with orbitally active ℓ > 0 rare-earth magnetism [3]. It is insightful to consider the two main theoretical approaches with which moment formation in solids was treated in the years leading up to the era of strongly correlated electron physics in 1979 [4]. The first of these was the Friedel-Anderson model [5,6]. Here, the proximity of the unfilled magnetic d − or f − shell to the metallic Fermi energy is considered to lead to quantum-mechanical hybridization of the magnetic orbital with the conduction electrons and, in effect, the washing out of the magnetic moment. In the Kondo model [2, see Part II], on the other hand, the formation of a singlet is the outcome of screening of the impurity spin by conduction electrons. The full or partial demise of a magnetic moment on an atom in a metal is, thus, a matter of comparing energies: the prevailing thermal energy, the bandwidth and location in energy with respect to the Fermi energy, and the magnitude of the exchange between the magnetic moment and its surroundings.

The study of Kondo physics has a strong foundation in the magnetism of rare-earth-based compounds, and especially so for the elements Ce, Sm, and Yb with orbital angular momentum L = 3 when their predisposition toward the trivalent ionic state leads to the spin $S=\frac{1}{2}$ and total angular momentum $J=\frac{5}{2}$ quantum-mechanical states. Having an odd number of electrons in their unfilled f − shells means that these elements are known as Kramers ions in which the ground multiplet retains at least a two-fold degeneracy (Kramer’s rule [7] states that the time-degeneracy of the $(J+\frac{1}{2})$ components of the crystal-field multiplet cannot be lifted by an electric field). The exchange between the f − electron shell and conduction electrons is not negligible; however, this results for the most part in polarization of the conduction electrons, while the magnetic moment of the ion remains the same as the Hund’s rule magnetic moment in free space or in insulators, for example. On the one hand, the localized magnetic moments of these elements provide exemplary cases of the moment being conserved in the solid state, but at the same time, they are known for many examples where the f − electron shell lies below but close to the metallic Fermi energy. This means that the conduction electrons, −and by extension the material’s physical properties, acquire a measure of f − electron character.

A particularly useful property with which we inspect how the electronic density of states at the Fermi energy ${\left[\partial \mathbb{N}\left(ϵ\right)/\partial ϵ\right]}_{ϵ=E_{\text{F}}}=\mathbb{N}(E_{\text{F}})$ affects the behavior of electrons in a metal is the heat capacity C(T). To understand this, let us introduce a few salient concepts. We first assume that in a metallic solid, the electronic and lattice degrees of freedom under a prevailing finite thermal energy are decoupled to a good approximation. By virtue of the Pauli principle, we also assume that low-energy orbitals occupied by the electrons may not be multiply occupied, and thus, also electron–electron interactions are non-existent for practical purposes. This is just the fundamental picture of the non-interacting Fermi liquid, which provides a basis to treat the electrons in a metal as a free-electron gas. In momentum space, the Fermi momentum p_F = ℏk_F separates the occupied |k| ≤ |k_F| states from the unoccupied |k| > |k_F| ones. The Fermi energy is related to the Fermi wavevector k_F through the dispersion relation ${ϵ}_{k=k_{\mathrm{F}}}\equiv E_{\mathrm{F}}={\left(\hslash {\mathbf{k}}_{\mathrm{F}}\right)}^2/2m$. In momentum space, the occupied states lie within a sphere of radius |p_F| with the associated Fermi energy chosen by the principle that summation over all the accessible states of particles within the Fermi sphere must yield precisely the number of particles in the system.

The matter of adiabaticity and interactions of particles across the boundary p_F is important. In the Landau Fermi liquid phenomenological treatment of electrons in metals, the following fundamental principles hold: spin and momentum remain good quantum numbers with which we describe non-interacting particles and interacting (quasi)particles, the latter which derives from excitations across p_F at T > 0, and the interacting system may be assimilated by adiabatically turning on interactions over time t, which measures the lifetime of the resulting excitations or quasiparticles. Through the theorem of adiabaticity, the ground state of the non-interacting Fermi gas transforms into the ground state of the interacting system which is known as a Fermi liquid. In this process, the dynamical properties such as mass and magnetic moment become renormalized to a new set of numbers, while spin, charge, and momentum of the fermionic electrons remain invariant [8]. We write for the particle density of N number of non-interacting particles per unit volume V, n = N/V, and it may be shown that the density of states $\mathbb{N}(ϵ)=\left(3/2\right)\left(n/E_{\mathrm{F}}\right)\sqrt{ϵ/E_{\mathrm{F}}}$, or at the Fermi energy, $\mathbb{N}\left(E_{\mathrm{F}}\right)=\left(3/2\right)\left(n/E_{\mathrm{F}}\right)$. For electron momenta at |p_F|, we have for the electron mass m of the electron; m = p_F/v (p = p_F) in terms of the Fermi velocity |v_F|. At the Fermi surface, the quasiparticle density of states may be written as $\mathbb{N}\left(E_{\mathrm{F}}\right)=m|{\mathbf{p}}_{\mathrm{F}}|/{\pi }^2{\hslash }^3$. We now turn to the interacting case. We consider a filled Fermi sphere plus a single particle of momentum |p| such that p > p_F, but p − p_F ≪ p_F. For the energy of this particle, $ϵ-E_{\mathrm{F}}=p^2/2m-E_{\mathrm{F}}\approx \left(p_{\mathrm{F}}/m^{*}\right)\left(p-p_{\mathrm{F}}\right)$ where the effective mass m* now accounts for the interaction-dressed fermion instead of the bare electron mass m for the non-interacting case.

The aforementioned introduced concepts are brought together by the Sommerfeld coefficient γ [[9] and references within].

$\gamma =\frac{{\pi }^2}{3}{k}_{\mathrm{F}}^2\mathbb{N}\left(E_{\mathrm{F}}\right)=\frac{k_{\mathrm{B}}^2}{3{\hslash }^2}{k}_{\mathrm{F}}{m}^{*}.(2)$

Here, we see the implication that a high effective mass has on the heat capacity of a metal, since the Sommerfeld coefficient describes the electronic heat capacity through $C_{\text{el}}\left(T\right)=\gamma T$. The problem may also be described by approaching Eq. 2 from the density of states. A so-called f − electron many-body Kondo resonance (also referred to as the Abrikosov–Suhl resonance) forms in the electronic density of states near the Fermi energy as a result of the virtual bound state consisting of conduction electrons that screen the local moment. The existence of this resonance has been amply illustrated by using model calculations and by a variety of spectroscopic experiments, [1, 10]

An important consequence of the Kondo resonance is the prediction that the conduction-electron/f − electron (c − f) hybridization leads to the formation of an (indirect or pseudo-) energy gap at the Fermi energy [[11], and references within], of width ϵ_i ∼ T_K and which, in turn, is governed by the effective mass enhancement factor through $\left(m^{*}/m\right)\simeq {\left({ϵ}_{\mathrm{i}}/T_{\text{K}}\right)}^2$ [11]. This is a common feature of Kondo systems, with correspondence between the single-ion Kondo effect in a dilute impurity system and the Kondo lattice case, on the other hand, that has a Kondo ion in every unit cell of the lattice [12]. In a small number of known Kondo materials, however, −all of which are characterized by a strong c − f hybridization, gapping, which we refer to as ϵ_d, takes places at the Fermi energy, which produces a marked loss of charge carriers. The hybridization is temperature driven, and so is the gapping. In panel (a) of Figure 1, the unperturbed case of a |k|² dispersed wavevector is compared with the situation where strong band hybridization produces a direct energy gap ϵ_d and a small, indirect energy gap ϵ_i. The shape of the gap within the renormalized density of states, − see panel (b) of Figure 1, is a matter of the strength of the hybridization.

FIGURE 1

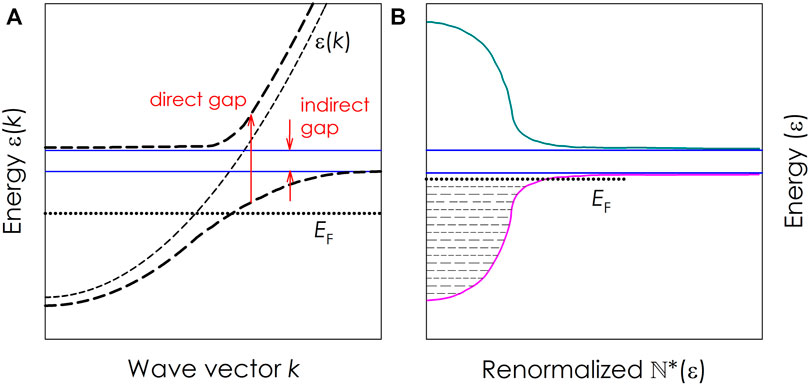
FIGURE 1. (A) Wavevector dispersion for the unperturbed case (thin dashed line) near the Fermi energy (dotted line) and the hybridized case (pair of thick dashed lines) shown to produce energy gapping (schematic adapted from [40]). (B) Density of renormalized band states ${\mathbb{N}}^{*}\left(ϵ\right)$ alongside the indirect gap.

While theoretical development of our understanding of the formation of the Kondo insulating state remains an ongoing pursuit [13–15], the subject has recently gained attention [[16,17], and references within] on account of the contemporary physics of topology having relation to the formation of the heavy-fermion Kondo insulating state. We consider an electron situated at the edge of the valence band. A combination of an appropriate change in k together with an excitation in energy k_BT ≳ ϵ_i would accomplish a transfer into the conduction band. The viability of this process has an obvious temperature dependence and, thus, produces electrical conduction that is dependent on temperature by the rate at which the conduction band is populated. At high temperature, T ≫ T_K, the electrical resistivity of a Kondo insulator may resemble that of a metal, and the magnetic susceptibility would pick up a Pauli-like spin response of the free electrons above the Fermi energy, in the conduction band. As the temperature is lowered, bridging the energy gap becomes less and less feasible, and the conduction band slowly becomes depleted. The magnetic susceptibility diminishes or, at most, becomes constant in temperature in the event of spin pairing in the lower band, and the electrical conductivity likewise diminishes, contrary to what happens in an ordinary metal. Whether and to what extent the electrical resistivity ρ(T) of a Kondo insulator remains finite or not at low temperatures has been a matter of considerable debate. We discuss salient points in what follows. We refer to the so-called “impurity Kondo” effect as the single-ion Kondo problem, which for most practical purposes is relevant for the incoherent temperature region of a Kondo lattice where the Kondo ions act independently (or incoherent) from each other. Starting from the single-ion Kondo problem, the progressive screening or formation of the virtual bound state as temperature is lowered enhances the effectiveness of the Kondo ion as a scattering center of charge carriers. The interaction strength J_ex grows logarithmically, which was first demonstrated by Kondo [18] in a perturbation calculation beyond first order: $J\to J\left(T\right)=J+2J^2{\mathbb{N}}_{\text{F}}\ln \left(D^{*}/T\right)$. The electrical resistivity in turn corresponds with a logarithmic correction [19].

${\rho }_{\text{imp}}\left(T\right)=\frac{3\pi m{J}^{2}S\left(S+1\right)}{2e^2\hslash E_{\text{F}}}\left[1-J_{\text{ex}}{\mathbb{N}}_{\text{F}}\ln \left(\frac{k_{\text{B}}T}{D^{*}}\right)+\mathcal{O}\left(J_{\text{ex}}^3\right)\right].(3)$

Here, D* is the hybridized bandwidth, e is the electron charge, and S represents the spin on the Kondo ion.

As it stands, Eq. 3 presents a resistivity that increases without bound as T → 0. For this question, one has to be mindful of the limit of validity of the aforementioned equation. The temperature scaling of the resistivity posed by Eq. 3 breaks down when the hybridized bandwidth approaches D* ≃ T_K from the T > T_K side. Instead of continuing to diverge, experimentally the resistivity of a single-ion Kondo system is frequently observed to saturate at low temperatures. This behavior augurs well with the prediction when describing the scattering process of a conduction electron by the static potential of an isolated Kondo ion from a phase shift point of view [20], namely, that a complete phase shift π/2 is accomplished in the T → 0 limit; the scattering can be no greater and it, therefore, saturates at the unitarity limit. Apart from these considerations, it is instructive to look into the nature of the energy gap in real materials a little closer. From the shape of the gap in the normalized density of states ${\mathbb{N}}^{*}\left(ϵ\right)$ posed in Figure 1, if the Fermi energy lies within the gap, or when charge carriers at low temperatures become unable to get excited into the conduction band, then the material would be an insulator. However, it was recognized early on [21] that spin degeneracy alone cannot account for real types of f − electron systems that have orbital degrees of freedom in addition. Furthermore, a particular behavior in the specific heat and its magnetic field dependence of the well-studied Kondo insulator CeNiSn [22] was modeled not by an energy gap structure as simple as is portrayed in Figure 1 but by a V− shape gap instead, having a residual density of states within the gap. This picture was born out by band-structure calculations [23], as well as by nuclear magnetic resonance studies on various 4f − and 5f − electron Kondo insulators [24–27]. It is worthwhile to note that the physics of materials having residual densities of states need to be treated with caution. With the procurement of higher and higher purity sample material of CeNiSn, the divergence in resistivity at low temperatures was found to be an artifact of impurities, and CeNiSn is possibly best described as a “failed Kondo insulator” [28].

In the last part of this discussion, we refer to the recent work carried out to develop the concept of topological Kondo insulators. Topological insulators as such represent a new state of matter, and the field is barely more than a decade in the making [29]. Topological insulators are similar to more traditional electrical insulators in that an energy gap separates the top of the occupied electronic band from the lowest energy of the empty band. In a non-interacting system such as a non-ordered magnetic material, surface states are protected by symmetry (importantly, time-reversal symmetry) which means that at the boundary or edge of a topological insulator with the surrounding vacuum, metallic surface states are formed by virtue of being gapless. In practice, this means that a bulk insulator is in effect short-circuited by the finite electrical conductivity on its surface(s). The reader is referred to the insightful demonstration of the involvement of surface states in the electrical conduction of the archetypal Kondo insulator SmB₆ [30]. Resistivity saturation at low temperatures in Kondo insulators is ubiquitous, but the theoretical foundation for this phenomenon in correlated semiconductors remains the subject of debate. A very recent study [15] searched for the source of this behavior in the charge carrier scattering rate itself operating as the relevant energy scale, with the finite lifetime of carriers being responsible for resistivity that saturates in the low-temperature quantum regime. Topological surface conductivity [31] and a non-trivial metallic state [32] were likewise found in the face-centered cubic Kondo insulator YbB₁₂.

In the paragraphs that follow, we review the physical properties of a selection of Kondo insulators. We highlight certain experimental commonalities among these systems but also focus on those aspects of these selected ones which challenge our understanding beyond the standard pattern of behavior of this materials class.

2 Experimental properties

2.1 CeRu₄Sn₆—a non-centrosymmetric Kondo insulator

Following exploratory studies [33] of the physical properties of CeRu₄Sn₆, the electrical resistivity of this compound was connected with that of typical Kondo insulating behavior [34], and interestingly, the specific heat C_p(T)/T ∼ − log T was shown to diverge in a logarithmic manner below T ≈ 6 K (with measurements that extended down to 0.35 K). Studies of nuclear magnetic resonance, specific heat [35], and muon-spin relaxation [36] confirmed that this compound escapes any kind of magnetic order down to 0.05 K.

The fact that CeRu₄Sn₆ forms in a non-centrosymmetric and tetragonal crystal structure (space group $I\bar{4}2m$) was rather atypical for contemporary Kondo insulators: all known Kondo insulators at the time were known to be of cubic crystal symmetry [37,38]. A second notable exception with a non-centrosymmetric crystal structure is that of the archetypal Kondo insulator Ce₃Bi₄Pt₃. Here, the tunability between the Kondo insulating state and the semimetal state was aptly demonstrated by doping with the lighter metal Pd in place of Pt [39]. It is instructive to consider this aspect of crystal symmetry a little deeper. First, a structure as simple as a cubic environment is more approachable theoretically for understanding the Kondo insulating state: following the reasoning given by Alexandrov et al. [38], this portrays a scenario in which the Γ₈ quartet of f states hybridizes with a d state quartet that involves a Kramers doublet plus orbital degeneracy and produces the Kondo insulating state. This situation was also discussed in an early study of Kondo insulators [40]. The requirement of just one conduction band at the Fermi energy may readily be achievable in cubic structures, taking the view that hybridization gap compounds are fundamentally conventional semiconductors but with a large Coulomb repulsion. This links to the strongly correlated state that is ubiquitous in Kondo insulators, as was demonstrated [35] for the case of CeRu₄Sn₆.

Notwithstanding its tetragonal crystal structure, it was noted [41] that the diagonal $c^{\prime }=\sqrt{2}a$ in the basal plane of the tetragonal structure of CeRu₄Sn₆ differs in length from the c − axis by less than 0.2%, which portrays a quasi-cubic view of its crystal structure. Moreover, a cubic crystal structure for Kondo insulators has paved the way for one avenue of understanding the formation of the Kondo insulating state: in a cubic environment, the J = 5/2 assigned orbitals of a trivalent Ce ion splits into a Γ₇ doublet and a Γ₈ quartet. Raman experiments (see references in [38]) have demonstrated that it is the Kondo screening of the quartet that is responsible for the insulating state—hence the Kondo insulating phenomenon in these materials. At the same time, the fourfold symmetry of this same multiplet protects the formation of topological states in this materials class [38].

On the other hand, certain aspects directly attributable to the tetragonal crystal structure of CeRu₄Sn₆ were brought to bear in the finding of anisotropy in single crystals, in the magnetization and specific heat measured in applied fields [41] as well as in the electrical and optical conductivity [42]. This anisotropy and its origin were firmly grounded in experiments and calculations [43] of resonant inelastic X-ray scattering, which assigned the ground state as a Γ₆ doublet, and the expected (for $S=\frac{1}{2},J=\frac{5}{2}$ of the trivalent Ce³⁺ state) two excited Γ₇ doublets lying at 30 meV and 85 meV, respectively. In contrast to the anticipated behavior of a so-called electrical insulator, an intriguing property of the electrical resistivity ρ(T) of CeRu₄Sn₆ is its robust metallicity in the T → 0 limit as conveyed by saturation in ρ, even under applied pressure [44].

In the first report [30] of experiments that elegantly demonstrated the presence of surface electrical conduction in what is arguably the most intensively studied Kondo insulator SmB₆, this phenomenon was shortly afterward associated with a non-trivial topology in SmB₆ [45]. CeRu₄Sn₆ was the next Kondo insulator to be identified with this type of topology [16], and theoretical studies of density functional plus dynamical mean field [46] found that both band crossing and an indirect Kondo gap were at play in CeRu₄Sn₆, either of which would suffice to explain the remnant metallicity at low temperature. The calculations in the local density approximation plus Gutzwiller method [47] showed that CeRu₄Sn₆ was the first Weyl semimetal in the heavy-fermion class of materials, which opens up an interesting new connection between strong electronic correlations and topology. A practical approach to navigate the observation of resistivity saturation in CeRu₄Sn₆ was mapped out by the treatment of fitting the temperature dependence of the spin-lattice relaxation rate, the specific heat, and the magnetic susceptibility, using putative in-gap states inside a V-shape gap [35]. Whether or not impurities are at play in this type of material and whether the level of (accidental) impurities in a putative Kondo insulator drives the balance between the Kondo insulating state and a semimetal were proposed [38] to make surface states robust against deviations from ideal purity of the bulk. Finally, we refer the reader also to the treatment of the residual conduction of CeRu₄Sn₆ and similar systems as a bulk property of a many-body problem in the quantum regime [15].

A consistent formulation of the electronic ground state of CeRu₄Sn₆ remains elusive. The pathological influence of impurity states in semimetals is problematic and divides opinion on whether the compound CeRu₄Sn₆ should be classified as a Kondo insulator or as a semimetal—see, for instance, the discussion on cubic topological Kondo insulators [38]. In very recent work [48], evidence was forwarded for CeRu₄Sn₆ being quantum critical without tuning, −in particular on account of a divergence that was found in the Grüneisen ratio at low temperatures. This observation solidified the notion of quantum criticality in CeRu₄Sn₆ that was mooted in earlier studies [34]. Bar very few exceptions, magnetic quantum critical systems require some form of tuning—using pressure, applied magnetic field, or chemical doping, in order to reach the quantum critical state.

2.2 U₂Ru₂Sn—a tetragonal 5f − electron Kondo insulator

In uranium metallic compounds, the 5f − orbital that is generally responsible for magnetism and for correlated electron effects is more delocalized in spatial extent than what is the case for the 4f − orbital in rare-earth compounds. On the one hand, the inherently more extended nature of the partly filled 5f orbital is more susceptible to details of other elements in its neighboring crystal environment, and at the same time, orbital polarization and magnetocrystalline anisotropy arising from strong spin-orbit coupling is a defining feature of uranium compounds. Possibly, the most remarkable prototype of the multi-faceted behavior and a confounding array of properties associated with 5f − electron magnetism is the compound URu₂Si₂. The so-called hidden order found at 17.5 K has escaped a quantitative understanding ever since its discovery in the mid-eighties [(49,50), and references within]. The reader is referred to the case made in favor of hastatic order [51], which occurs as a result of quasiparticle hybridization of half-integer-spin conduction electrons in URu₂Si₂ with the integer-spin non-Kramers doublet of the 5f² ground state.

Here, we turn attention to the Kondo insulator U₂Ru₂Sn, the first report of which classified it as a weak paramagnet [52]. This compound belongs to a series of ternary intermetallic actinide compounds that adopt a crystal structure arrangement with space group P4/mbm. A single-site symmetry is provided for the U atom in the crystal structure [53,54].

A closer look at the temperature dependence of the electrical resistivity ρ(T) [55] showed a behavior that typifies the electrical transport of a Kondo insulator: starting from ρ ≃ 500 μΩ cm at room temperature which is high compared to ordinary metals, ρ increases on cooling below room temperature in a ρ(T) ∝ − ln(T) manner which signifies the incoherent Kondo state. A very broad peak is traced out across most of the temperature range below room temperature (reaching a maximum at $\sim 100$ K), and after a minimum at $\sim 20$ K, ρ(T) increases again as T → 0. The thermo-electric power S(T), Hall coefficient R_H(T), specific heat C_p(T), and magnetic susceptibility χ(T) against temperature gave compelling evidence [27] for the characteristic feature in U₂Ru₂Sn in the range $\sim 100-200$ K, consistently interpreted as the consequence of the opening of an energy gap in the conduction band. In terms of χ(T), instead of proceeding in a Curie–Weiss-like manner as one would expect for magnetic moments that are more or less localized, here the downturn in χ(T) below the broad maximum is associated with demagnetizing of Kondo spins as a result of screening, in concert with energy gap formation in strongly renormalized bands in the correlated electron state. As with the case in the previous section of CeRu₄Sn₆, U₂Ru₂Sn is also of tetragonal crystal structure and likewise challenged the notional concept of Kondo insulators being cubic. In single-crystal material, it was found that the non-cubic symmetry in U₂Ru₂Sn produces a remarkable anisotropy in the electrical resistivity [56] and the Knight shift [26]. It is important to note that in both cases, the non−f electron counterpart Th₂Ru₂Sn [27] (for U₂Ru₂Sn) and LaRu₄Sn₆ [33] (for CeRu₄Sn₆) have overall metallic resistivity, which means that the semiconducting behavior and energy gap formation are entirely attributable to the involvement of f − electrons from unfilled shells with the conduction electrons.

Anisotropy in the Knight shift of U₂Ru₂Sn and the temperature dependence of its magnetic susceptibility [26] were connected to the anisotropy of the energy gap forming in this compound, and by virtue of Eq. 1, this means that the Kondo energy scale would be different between the in-plane and out-of-plane directions. Taking the point of departure of a V − shape gap in the density of states together with a finite bandwidth, the temperature dependence of the relaxation rate $1/T_1\left(T\right)$ of ¹¹⁹Sn − NMR on U₂Ru₂Sn was modeled [26] over $\sim 2$ orders of magnitude in temperature. The appearance of anisotropy in the energy gap in a tetragonal crystal structure of the Kondo insulator U₂Ru₂Sn, thus, resonates well with the situation in CeRu₄Sn₆ described in Section 2.1.

2.3 CeRu₂Al₁₀—Magnetic order in a Kondo semimetal

Originally studied in the context of developing correlated semimetals [57], the orthorhombic structure compound CeRu₂Al₁₀ was portrayed [58] as having its cerium atom located inside an oversized atomic cage composed of Ru and Al atoms. This type of crystal structure promotes lattice vibrations in the form of optical phonons (quantized lattice vibrations) or Einstein modes in addition to the more common acoustic or Debye modes that are thermally excited in a periodic crystal lattice. Many defining properties of CeRu₂Al₁₀ are shared by its iso-electronic counterpart CeOs₂Al₁₀, as discussed further below. Like the case of CeRu₄Sn₆, the Ce site in CeRu₂Al₁₀ also lacks spatial inversion symmetry.

CeRu₂Al₁₀ belongs to a series of isostructural rare-earth aluminides [59], also subsequently shown to be amenable to the actinide element U [60], but this cerium compound in particular was singled out for certain peculiarities in the Ce−Ru and Ce−Al bonding [61]. At first, an anomaly at T₀ ≃ 30 K that was consistently found in several physical properties including electrical transport and magnetization was associated with a putative insulator-to-metal transition in studies on polycrystalline samples [58]. The location of the transition was shown to be magnetic field insensitive up to 14 T [62], but the electrical resistivity, for example, showed a marked increase below T₀ upon applying fields. The T₀ transition was eventually shown [63] to be pliable to very high magnetic fields and to shift down in temperature at fields upward of $\sim 28$ T and become fully suppressed at 50 T. The positive magnetoresistance below T₀ results in the dismantling of the metallic state in this temperature region, regardless apparently of the symmetry parameter that gets broken at T₀. Long-range magnetic order in a stoichiometric compound with cerium as the magnetic species at as high as 30 K was completely unexpected, and arguments to the contrary were discussed by Nishioka et al. [64]. Instead, a charge–density wave transition was proposed [65,66] as a more plausible cause for the opening of a gap over parts of the Fermi surface at T₀. Other alternative possibilities for the nature of the mysterious T₀ transition were forwarded, such as a Peierls (dimerization) transition [(67), and references within] with non-magnetic singlet pair formation [68] and a resonating valence bond state [69].

Interestingly, both the isostructural compounds CeRu₂Al₁₀ and CeOs₂Al₁₀ were found to show near-identical anomalies at 30 K [64], and both were shown, by virtue of the temperature dependence of their magnetic susceptibility χ(T) plus their semimetal-like transport ρ(T) behavior above T₀, to belong to the Kondo insulator class of materials. In these two compounds, the b − direction was found to produce the characteristic broad peak in χ(T) around 200 K, which signals the demagnetization accompanying the Kondo insulating state. Similar behavior in χ(T) and ρ(T), with pronounced hybridization gap formation, was identified also in the third one of the three-member cerium-based family, namely, CeFe₂Al₁₀ [70], but there was no 30 K feature in CeFe₂Al₁₀ and no ordering of any parameter down to 1 K [64].

The initial report on CeRu₂Al₁₀ [58] drew considerable interest in this compound and was followed shortly afterward when two groups working independently identified the 30 K feature unequivocally through neutron scattering and muon-spin relaxation as the mark of a long-range paramagnetic-to-antiferromagnetic phase transition [71,72]. This turned out likewise to be the case for CeOs₂Al₁₀ [73]. The finding of a magnetically ordered state emerging within the Kondo insulating phase stood in stark contrast to the conventional understanding [74] that Kondo insulators become demagnetized at temperatures below the energy gap formation. This is because strong hybridization strips the localized 4f − electron spin of much of its magnetic character as the spin-magnetic moment is washed away into the degenerate conduction band upon quantum-mechanical mixing of bands. However, a further perplexing finding had to be explained additionally, namely, the strong magnetocrystalline anisotropy that was reported in all three compounds, including the magnetic ordered CeRu₂Al₁₀ and CeOs₂Al₁₀ [64] and the non-ordered CeFe₂Al₁₀ [75]. It is known that the magnitude of the magnetic susceptibility decreases by only about 10% below T₀ in the two ordered compounds (by contrast to what would be expected in a conventional antiferromagnet), and χ(T) furthermore decreases for all three principal directions of the applied field below T₀. Here, the orbital magnetic moment of Ce³⁺ has to be accounted for as well to explain the ordering and the anisotropy.

The anisotropy in the Kondo insulator CeFe₂Al₁₀ was pointed out [76] to be a rare occurrence among this materials class since Kondo insulators commonly adopt a cubic crystal structure. It is of interest, therefore, that the other two non-cubic Kondo insulators dealt with in this paper also exhibit similar anisotropy, notably in the electric [77] and thermal transport [78] of CeRu₄Sn₆ and in the case of U₂Ru₂Sn, in χ(T) and ρ(T) [79], as well as in the Knight shift [26]. An important advancement toward understanding the physics of CeRu₂Al₁₀ was realized by calculating the crystal-electric field levels using single-crystal magnetic susceptibility [80]. Acting as a Kramers ion, trivalent cerium, here, has its 6 − fold ground multiplet split into three doublets, and importantly, the first excited state is situated at 326 K, which leaves the magnetic ground doublet well isolated. The experimental studies [80] concluded strong 4f − orbital hybridization with the 3p orbitals of Al (i.e., inter-site mixing). The theoretical study of Hanzawa [81], however, pointed to the importance of intra-site 4f − 5d orbital mixing, and these two types of hybridization competing for the 4f − electron of cerium need to be contextualized in the frame of the anomalous magnetic order.

On the realization of single-crystal studies on CeRu₂Al₁₀ [80], it became evident that the easy axis (a) of magnetization in the paramagnetic state is, surprisingly, not the direction of the ordered moment (c − axis) below T₀. A study using polarization-dependent soft x-ray spectroscopy [82] found that the crystal-electric field moment can entirely account for the unusually small ordered moment (0.38 μ_B) in CeRu₂Al₁₀. Magnetic ordering involving reduced magnetic moments of this type (the saturated Russel–Saunders moment value is M_z = g_J ⋅ J = 2.14 μ_B for the Ce f^5/2 manifold) is common in Kondo lattice heavy-fermion compounds in which the Kondo effect at higher temperatures degenerates part of the Ce magnetic moment, leaving only a reduced moment toward lower temperature when a magnetic ordered ground state might be achieved within the RKKY−Kondo competing effects.

An inelastic neutron scattering study [83] proved an intrinsic connection between Kondo insulating or semimetal behavior in CeRu₂Al₁₀ and its magnetic order. The existence of spin gaps, localized in the wavevector space, was found at 116 K and 145 K. These are both situated well inside the paramagnetic range of temperature, which points to an anisotropic energy gap forming on small parts of the Fermi surface and that persists to enter the magnetic ordered region. The spin gap is very sensitive to electron doping and perhaps not surprisingly, electron doping in the form of Rh in the place of Ru [84] rapidly collapses the energy gap. However, electron doping provided a further hint about the complex ground state, namely, that as the energy gap is closed, it achieves at the same time a change in the ordered magnetic structure [85]. Hole doping of CeRu₂Al₁₀, using Re in the place of Ru [86], revealed compelling insights into the complex and multi-parameter ground state of this compound. In the weakly doped compound CeRu_1.94Re_0.06Al₁₀, it was established that the ordered moment was reduced by nearly 50% but equally significant was the finding that here the ordered moment had swung to the b − direction, as opposed to the c − direction for undoped CeRu₂Al₁₀. Hole doping has achieved primarily to weaken the crystal-electric field-derived ordered moment (the spin gap in the doped compound remained, at 93 K, nearly unchanged). Furthermore, it placed the competition between anisotropic hybridization causing spin gapping (which persists into the magnetic ordered phase, contrary to what is the case with electron doping [84]) and anisotropy of the crystal-electric field effect at the center of the anomalous magnetic order and accompanying phenomena in CeRu₂Al₁₀.

3 Summary

In the broad and well-studied subject of metal physics, strongly correlated electron systems form one of the most important developments in condensed matter physics in recent times. When the mixing of local-moment electron orbitals with the conduction band becomes very strong, the Kondo semimetal or insulating state forms at the boundaries between metal/semimetal and magnetic/non-magnetic phases. These phase boundaries are not crossed in the usual manner of a phase transition; instead, they are connected adiabatically and accessed by varying the material temperature. In this review, we have highlighted the foundation features of Kondo insulators but with emphasis on what makes the selected three compounds stand out from their otherwise more conventional counterparts.

The compounds discussed here deviate from the rule that Kondo insulators have a cubic crystal structure. This is shown to produce magnetocrystalline anisotropy in all three compounds, an attribute for which they occupy a niche in this materials class. CeRu₄Sn₆ has been shown to possess non-trivial topology [16] and is, thus, a candidate for the topological insulating state [17,29,38]. Initially identified with signatures of quantum criticality [34] by its electronic specific heat that diverges in a logarithmic fashion at low temperatures, a recent multi-parameter study [48] provided compelling evidence that CeRu₄Sn₆ is in close proximity to a quantum critical point. This finding places the compound CeRu₄Sn₆ at the confluence of quantum criticality and the topological Kondo insulating state, a situation that is probably unique.

U₂Ru₂Sn is a tetragonal Kondo insulator with pronounced anisotropy among several of its physical properties [26]. Anisotropy might intuitively be associated with the symmetry of a tetragonal crystal structure, but it should be remembered that the magnetic (5f) electrons in uranium compounds are known to be much more delocalized than what is the case in 4f-electron compounds of rare earths. Despite the dual nature of 5f − electrons having been confirmed by the electronic band-structure calculations and x-ray photoemission studies in U₂Ru₂Sn [87], the anisotropy in this Kondo insulator, nevertheless, points to magnetism that derives from a sufficient measure of non-spherical electronic orbitals.

In the case of CeRu₂Al₁₀, the semi-metallicity that is characterized by anisotropic gapping of electron states on the Fermi surface occurs already toward higher temperatures in the paramagnetic state far above the ground state, in the range where the first excited crystal-field doublet becomes depopulated upon cooling down. At the unusually high temperature (among cerium compounds) of 30 K, CeRu₂Al₁₀ orders in a long-range antiferromagnet state where competing crystal fields and anisotropic hybridization achieves to turn the ordered magnetic moment away from the crystal-electric field determined direction or “easy” axis.

The CeT₂Al₁₀ (T = Fe, Ru, and Os) series of compounds offers the rare opportunity to study the systematics of a trio of Kondo insulators.

Author contributions

AS was responsible for conceptualizing this manuscript, and is fully accountable for the content of this manuscript, although the cited publications are the work of many groups working on subject matter related to this review.

Funding

This study has benefited from grants from the South African National Research Foundation and funding assistance from the Science Faculty Research Committee and the University Research Committee of the University of Johannesburg.

Acknowledgments

The author is grateful for many insightful discussions and fruitful collaborations with Devashibhai Adroja at the ISIS Pulsed Neutron and Muon Facility, Michael Baenitz and coworkers at the MPI-CPfS in Dresden, Silke Paschen at TU-Vienna, and Pascale Deen at the ESS in Lund, Sweden.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. In:W Buyers, editor. Moment Formation in solids. New York: Plenum Press (1984). p. 1–21. chap. 1.

Google Scholar

2. In:H Suhl, editor. A treatise on modern theory and materials, magnetism, V. Academic Press (1973). Available at: https://doi.org/10.1016/B978-0-12-575305-0.50004-1.

Google Scholar

3. Hirst LL. Theory of the coupling between conduction electrons and moments of 3d and 4f ions in metals. Adv Phys (1978) 27:231–85. doi:10.1080/00018737800101374

CrossRef Full Text | Google Scholar

4. Steglich F, Aarts J, Bredl CD, Lieke W, Meschede D, Franz W, et al. Superconductivity in the presence of strong Pauli paramagnetism: CeCu₂Si₂. Phys Rev Lett (1979) 43:1892–6. doi:10.1103/physrevlett.43.1892

CrossRef Full Text | Google Scholar

5. Friedel J. Metallic alloys. Nuovo Cimento Suppl (1958) 7:287–311. doi:10.1007/bf02751483

CrossRef Full Text | Google Scholar

6. Anderson PW. Localized magnetic states in metals. Phys Rev (1961) 124:41–53. doi:10.1103/physrev.124.41

CrossRef Full Text | Google Scholar

7. Kramers HA. Zur ableitung der quantenmechanischen intensitätsformeln. Proc R Acad Sci Amsterdam (1930) 33:953–8.

Google Scholar

8. Coleman P. Introduction to many-body physics. Cambridge University Press (2015). doi:10.1017/CBO9781139020916

CrossRef Full Text | Google Scholar

9. Degiorgi L. The electrodynamic response of heavy-electron compounds. Rev Mod Phys (1999) 71:687–734. doi:10.1103/revmodphys.71.687

CrossRef Full Text | Google Scholar

10. Gunnarsson O, Schönhammer K. Photoemission from Ce compounds: Exact model calculation in the limit of large degeneracy. Phys Rev Lett (1983) 50:604–7. doi:10.1103/physrevlett.50.604

CrossRef Full Text | Google Scholar

11. Dordevic SV, Basov DN, Dilley NR, Bauer ED, Maple MB. Hybridization gap in heavy fermion compounds. Phys Rev Lett (2001) 86:684–7. doi:10.1103/physrevlett.86.684

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Coleman P. Heavy fermions: Electrons at the edge of magnetism. John Wiley & Sons, Ltd) (2007). Available at: https://doi.org/10.1002/9780470022184.hmm105.

Google Scholar

13. Chowdhury D, Sodemann I, Senthil T. Mixed-valence insulators with neutral Fermi surfaces. Nat Commun (2018) 9:1766–7. doi:10.1038/s41467-018-04163-2

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Li L, Sun K, Kurdak C, Allen JW. Emergent mystery in the Kondo insulator samarium hexaboride. Nat Rev Phys (2020) 2:463–79. doi:10.1038/s42254-020-0210-8

CrossRef Full Text | Google Scholar

15. Pickem M, Maggio E, Tomczak JM. Resistivity saturation in Kondo insulators. Commun Phys (2021) 4:226–1. –8. doi:10.1038/s42005-021-00723-z

CrossRef Full Text | Google Scholar

16. Sundermann M, Strigari F, Willers T, Winkler H, Prokofiev A, Ablett JM, et al. CeRu₄Sn₆: A strongly correlated material with nontrivial topology. Scientific Rep (2016) 5:17937. doi:10.1038/srep17937/1–9

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Dzero M, Xia J, Galitski V, Coleman P. Topological Kondo insulators. Annu Rev Condensed Matter Phys (2016) 7:249–80. doi:10.1146/annurev-conmatphys-031214-014749

CrossRef Full Text | Google Scholar

18. Kondo J. Resistance minimum in dilute magnetic alloys. Prog Theor Phys (1964) 32:37–49. doi:10.1143/ptp.32.37

CrossRef Full Text | Google Scholar

19. Hewson AC. The Kondo problem to heavy fermions. Cambridge: Cambridge University Press (1993).

Google Scholar

20. Barnes SE. Derivation of exact results for the single-ion Kondo problem with the use of diagrammatic methods. Phys Rev B (1986) 33:3209–46. doi:10.1103/physrevb.33.3209

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Sasao T, Harima H. Formation mechanism of hybridization gap in Kondo insulators based on a realistic band model and application to YbB₁₂. J Phys Soc Jpn (2003) 72:1131–7. doi:10.1143/jpsj.72.1131

CrossRef Full Text | Google Scholar

22. Izawa K, Suzuki T, Kitamura M, Fujita T, Takabatake T, Nakamoto G, et al. The origin of magnetic field dependence of specific heat in single-crystalline CeNiSn. J Phys Soc Jpn (1996) 65:3119–22. doi:10.1143/jpsj.65.3119

CrossRef Full Text | Google Scholar

23. Ślebarski A, Jezierski A, Mähl S, Neumann M, Borstel G. Influence of the Kondo-hole impurities on the electronic structure of CeNiSn and CeRhSb. Phys Rev B (1998) 58:4367–71. doi:10.1103/physrevb.58.4367

CrossRef Full Text | Google Scholar

24. Nakamura K, Kitaoka Y, Asayama K, Takabatake T, Nakamoto G, Tanaka H, et al. Impurity and doping effects on the pseudoenergy gap in CeNiSn: A Sn NMR study. Phys Rev B (1996) 53:6385–92. doi:10.1103/physrevb.53.6385

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Nakamura K, Kitaoka Y, Asayama K, Takabatake T, Nakamoto G, Fujii H. Effective carrier doping by magnetic field into a pseudogapped state in CeNiSn: A Sn NMR study. Phys Rev B (1996) 54:6062–4. doi:10.1103/physrevb.54.6062

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Rajarajan AK, Rabis A, Baenitz M, Gippius AA, Morozowa EN, Mydosh JA, et al. NMR investigations of U₂Ru₂Sn: A possible Kondo insulator. Phys Rev B (2007) 76:024424. doi:10.1103/physrevb.76.0244241–5

CrossRef Full Text | Google Scholar

27. Tran VH, Paschen S, Rabis A, Senthilkumaran N, Baenitz M, Steglich F, et al. Magnetic, thermodynamic, NMR, and transport properties of the heavy-fermion semiconductor U₂Ru₂Sn. Phys Rev B (2003) 67:075111. 1–7. doi:10.1103/physrevb.67.075111

CrossRef Full Text | Google Scholar

28. Bareille C, Nam TS, Takabatake T, Kuroda K, Yajima T, NakayamaM , et al. Strongly anisotropic high-temperature Fermi surface of the Kondo semimetal CeNiSn revealed by angle-resolved photoemission spectroscopy. Phys Rev B (2019) 100:045133./1–9. doi:10.1103/physrevb.100.045133

CrossRef Full Text | Google Scholar

29. Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/revmodphys.82.3045

CrossRef Full Text | Google Scholar

30. Kim DJ, Thomas S, Grant T, Botimer J, Fisk Z, Xia J. Surface Hall effect and nonlocal transport in SmB₆: Evidence for surface conduction. Scientific Rep 3 (2013) 3150–4. doi:10.1038/srep03150

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sato Y, Xiang Z, Kasahara Y, Kasahara S, Chen L, Tinsman C, et al. Topological surface conduction in Kondo insulator YbB₁₂. J Phys D: Appl Phys (2021) 54:404002./1–6. doi:10.1088/1361-6463/ac10d9

CrossRef Full Text | Google Scholar

32. Hagiwara K, Ohtsubo Y, Matsunami M, ichiro Ideta S, Tanaka K, Miyazaki H, et al. Surface kondo effect and non-trivial metallic state of the Kondo insulator YbB₁₂. Nat Commun (2016) 7:12690–7. doi:10.1038/ncomms12690

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Das I, Sampathkumaran E. Electrical-resistance anomalies in a Ce-Ru-Sn phase. Phys Rev B (1992) 46:4250–2. Available at: https://10.1103/PhysRevB.46.4250.

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Strydom A, Guo Z, Paschen S, Viennois R, Steglich F. Electronic properties of semiconducting CeRu₄Sn₆. Physica B (2005) 293:359–61.

Google Scholar

35. Brüning EM, Brando M, Baenitz M, Bentien A, Strydom AM, Walstedt RE, et al. Low-temperature properties of CeRu₄Sn₆ from NMR and specific heat measurements: Heavy fermions emerging from a Kondo-insulating state. Phys Rev B (2010) 82:125115./1–10. doi:10.1103/physrevb.82.125115

CrossRef Full Text | Google Scholar

36. Strydom A, Hillier A, Adroja D, Paschen S, Steglich F. Low-temperature muon spin relaxation measurements on CeRu₄Sn₆. J Magnetism Magn Mater (2007) 310:377–9. doi:10.1016/j.jmmm.2006.10.084

CrossRef Full Text | Google Scholar

37. Riseborough PS. Heavy fermion semiconductors. Adv Phys (2000) 49:257–320. doi:10.1080/000187300243345

CrossRef Full Text | Google Scholar

38. Alexandrov V, Dzero M, Coleman P. Cubic topological Kondo insulators. Phys Rev Lett (2013) 111:226403./1–5. doi:10.1103/physrevlett.111.226403

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Dzsaber S, Prochaska L, Sidorenko A, Eguchi G, Svagera R, Waas M, et al. Kondo insulator to semimetal transformation tuned by spin-orbit coupling. Phys Rev Lett (2017) 118:246601. 1–6. doi:10.1103/physrevlett.118.246601

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Aeppli G, Fisk Z. Kondo insulators. Comments Condensed Matter Phys (1992) 16:155–65.

Google Scholar

41. Paschen S, Winkler H, Nezu T, Kriegisch M, Hilscher G, Custers J, et al. Anisotropy of the Kondo insulator CeRu₄Sn₆. J Phys Conf Ser (2010) 200:012156. doi:10.1088/1742-6596/200/1/012156

CrossRef Full Text | Google Scholar

42. Guritanu V, Wissgott P, Weig T, Winkler H, Sichelschmidt J, Scheffler M, et al. Anisotropic optical conductivity of the putative Kondo insulator CeRu₄Sn₆. Phys Rev B (2013) 87:115129–1. –5. doi:10.1103/physrevb.87.115129

CrossRef Full Text | Google Scholar

43. Amorese A, Kummer K, Brookes N, Stockert O, Adroja D, Strydom A, et al. Determining the local low-energy excitations in the Kondo semimetal CeRu₄Sn₆ using resonant inelastic x-ray scattering. Phys Rev B (2018) 98:081116. doi:10.1103/physrevb.98.081116(R)/1–6

CrossRef Full Text | Google Scholar

44. Zhang J, Zhang S, Lv ZCM, Zhao H, Yang Y, Chen G, et al. Pressure effect in the Kondo semimetal CeRu₄Sn₆ with nontrivial topology. Chin Phys B (2018) 27:097103097103. 1–5. doi:10.1088/1674-1056/27/9/097103

CrossRef Full Text | Google Scholar

45. Ohtsubo Y, Yamashita Y, Hagiwara K, i Ideta S, Tanaka K, Yukawa R, et al. Non-trivial surface states of samarium hexaboride at the (111) surface. Nat Commun (2019) 10:2298–1–7. doi:10.1038/s41467-019-10353-3

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wissgott P, Held K. Electronic structure of CeRu₄Sn₆: A density functional plus dynamical mean field theory study. Eur Phys J B (2016) 89:5–7. doi:10.1140/epjb/e2015-60753-5

CrossRef Full Text | Google Scholar

47. Xu Y, Yue C, Weng H, Dai X. Heavy Weyl fermion state in CeRu₄Sn₆. Phys Rev X (2017) 7:011027. doi:10.1103/physrevx.7.011027

CrossRef Full Text | Google Scholar

48. Fuhrman W, Sidorenko A, Hänel J, Winkler H, Prokofiev A, Rodriguez-Rivera J, et al. Pristine quantum criticality in a Kondo semimetal. Sci Adv (2021) 7:eabf9134. eabf9134/1–4. doi:10.1126/sciadv.abf9134

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Palstra T, Menovsky A, van den Berg J, Dirkmaat A, Kes P, Nieuwenhuys G, et al. Superconducting and magnetic transitions in the heavy-fermion system URu₂Si₂. Phys Rev Lett (1985) 55:2727–30. doi:10.1103/physrevlett.55.2727

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Schlabitz W, Baumann J, Pollit B, Rauchschwalbe U, Mayer H, Ahlheim U, et al. Superconductivity and magnetic order in a strongly interacting Fermi-system: URu₂Si₂. Z für Physik B (1986) 62:171–7. doi:10.1007/bf01323427

CrossRef Full Text | Google Scholar

51. Chandra P, Coleman P, Flint R. Hastatic order in the heavy-fermion compound URu₂Si₂. Nature (2013) 493:621–6. doi:10.1038/nature11820

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Havela L, Sechovský V, Svoboda P, Nakotte H, Prokeš K, de Boer F, et al. Magnetism in U₂T₂X compounds. J Magnetism Magn Mater (1995) 140–144:1367–8. doi:10.1016/0304-8853(94)00934-1

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Mirambet F, Gravereau P, Chevalier B, Trut L, Etourneau J. Crystal structure of the new ternary stannides U₂M₂Sn with M ≡ Fe or Rh. J Alloys Compd (1993) 191:L1–3. –L3. doi:10.1016/0925-8388(93)90052-o

CrossRef Full Text | Google Scholar

54. Peron M, Kergadallan Y, Rebizant J, Meyer D, Winand J, Zwirner S, et al. A new family of actinide ternary intermetallic compounds. J Alloys Compd (1993) 201:203–8. doi:10.1016/0925-8388(93)90885-q

CrossRef Full Text | Google Scholar

55. Menon L, de V du Plessis P, Strydom A. Possible Kondo insulating behaviour in U₂Ru₂Sn. Solid State Commun (1998) 106:519–21. doi:10.1016/s0038-1098(98)00071-4

CrossRef Full Text | Google Scholar

56. Strydom A, Troć R. Single-crystal magnetoresistivity and magnetic susceptibility of the Kondo semimetal U₂Ru₂Sn. Solid State Commun (2003) 126:207–12. doi:10.1016/s0038-1098(03)00064-4

CrossRef Full Text | Google Scholar

57. Paschen S, Baenitz M, Tran V, Rabis A, Steglich F, Carrillo-Cabrera W, et al. Towards strongly correlated semimetals: U₂Ru₂Sn and Eu₈Ga₁₆Ge₃₀. J Phys Chem Sol (2002) 63:1183–8. doi:10.1016/s0022-3697(02)00160-9

CrossRef Full Text | Google Scholar

58. Strydom A. Thermal and electronic transport in CeRu₂Al₁₀: Evidence for a metal–insulator transition. Physica B: Condensed Matter (2009) 404:2981–4. doi:10.1016/j.physb.2009.07.044

CrossRef Full Text | Google Scholar

59. Thiede VMT, Ebel T, Jeitschko W. Ternary aluminides LnT₂Al₁₀ (Ln=Y, La–Nd, Sm, Gd–Lu and T=Fe, Ru, Os) with YbFe₂Al₁₀ type structure and magnetic properties of the iron-containing series. J Mater Chem (1998) 8:125–30. doi:10.1039/a705854c

CrossRef Full Text | Google Scholar

60. Troć R, Pasturel M, Tougait O, Potel M, Noël H. Crystal structure and physical properties of a new intermetallic compound URu₂Al₁₀. Intermetallics (2011) 19:913–8. doi:10.1016/j.intermet.2011.02.008

CrossRef Full Text | Google Scholar

61. Tursina AI, Nesterenko SN, Murashova EV, Chernyshev IV, Noël H, Seropegin YD. CeRu₂Al₁₀ with the YbFe₂Al₁₀ structure type. Acta Crystallogr Section E (2005) E61:i12–4. i12–i14. doi:10.1107/s1600536805000310

CrossRef Full Text | Google Scholar

62. Strydom A. CeRu₂Al₁₀: Anomalous magnetic ordering and its field stability. J Low Temperature Phys (2010) 159:160–3. doi:10.1007/s10909-009-0121-7

CrossRef Full Text | Google Scholar

63. Kondo A, Wang J, Kindo K, Takesaka T, Kawamura Y, Nishioka T, et al. High-field magnetization of CeRu₂Al₁₀. J Phys Soc Jpn (2010) 79:073709073709. –4. doi:10.1143/jpsj.79.073709

CrossRef Full Text | Google Scholar

64. Nishioka T, Kawamura Y, Takesaka T, Kobayashi R, Kato H, Matsumara M, et al. Novel phase transition and the pressure effect in YbFe₂Al₁₀-type CeT₂Al₁₀ (T= Fe, Ru, Os). J Phys Soc Jpn (2009) 78:123705. 1–4. doi:10.1143/jpsj.78.123705

CrossRef Full Text | Google Scholar

65. Kimura S, Iizuka T, Miyazaki H, Irizawa A, Muro Y, Takabatake T. Electronic-structure-driven magnetic ordering in a Kondo semiconductor CeOs₂Al₁₀. Phys Rev Lett (2011) 106:056404056404. doi:10.1103/PhysRevLett.106.0564041–4

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Kimura S, Iizuka T, Miyazaki H, Hajiri T, Matsunami M, Mori T, et al. Optical study of charge instability in CeRu₂Al₁₀ in comparison with CeOs₂Al₁₀ and CeFe₂Al₁₀. Phys Rev B (2011) 84:165125./1–7. doi:10.1103/physrevb.84.165125

CrossRef Full Text | Google Scholar

67. Hanzawa K. Lattice distortion for stabilizing the spin-Peierls state in CeRu₂Al₁₀. J Phys Soc Jpn (2010) 79:084704084704. 1–4. doi:10.1143/jpsj.79.084704

CrossRef Full Text | Google Scholar

68. Tanida H, Tanaka D, Sera M, Moriyoshi C, Kuroiwa Y, Takesaka T, et al. Possible long-range order with singlet ground state in CeRu₂Al₁₀. J Phys Soc Jpn (2010) 79:043708043708. 1–4. doi:10.1143/jpsj.79.043708

CrossRef Full Text | Google Scholar

69. Hanzawa K. Resonating valence bond state with antiferromagnetic order in Ce compounds. J Phys Soc Jpn (2011) 80:113701–4. doi:10.1143/JPSJ.80.113701

CrossRef Full Text | Google Scholar

70. Muro Y, Motoya K, Saiga Y, Takabatake T. Formation of a hybridization gap in a cage-like compound CeFe₂Al₁₀. J Phys Soc Jpn (2009) 78:083707083707. 1–3. doi:10.1143/jpsj.78.083707

CrossRef Full Text | Google Scholar

71. Robert J, Mignot JM, André G, Nishioka T, Kobayashi R, Matsumura M, et al. Long-range order and low-energy magnetic excitations in CeRu₂Al₁₀ studied via neutron scattering. Phys Rev B (2010) 82:100404. doi:10.1103/physrevb.82.100404

CrossRef Full Text | Google Scholar

72. Khalyavin DD, Hillier AD, Adroja DT, Strydom AM, Manuel P, Chapon LC, et al. Long-range magnetic order in CeRu₂Al₁₀ studied via muon spin relaxation and neutron diffraction. Phys Rev B (2010) 82:100405. doi:10.1103/physrevb.82.100405

CrossRef Full Text | Google Scholar

73. Adroja DT, Hillier AD, Deen PP, Strydom AM, Muro Y, Kajino J, et al. Long-range ordering of reduced magnetic moments in the spin-gap compound CeOs₂Al₁₀ as seen via muon spin relaxation and neutron scattering. Phys Rev B (2010) 82:104405./1–9. doi:10.1103/physrevb.82.104405

CrossRef Full Text | Google Scholar

74. Mignot JM, Alekseev PA, Robert J, Petit S, Nishioka T, Matsumara M, et al. Dispersive magnetic-resonance mode in the Kondo semiconductor CeFe₂Al₁₀. Phys Rev B (2014) 89:161103./1–5. doi:10.1103/physrevb.89.161103

CrossRef Full Text | Google Scholar

75. Muro Y, Yutani K, Kajino J, Onimaru T, Takabatake T. Anisotropic c-f hybridization in the Kondo semiconductor CeFe₂Al₁₀. J Korean Phys Soc (2013) 63:508–11. doi:10.3938/jkps.63.508

CrossRef Full Text | Google Scholar

76. Adroja DT, Hillier AD, Muro Y, Takabatake T, Strydom AM, Bhattacharyya A, et al. Muon-spin-relaxation and inelastic neutron scattering investigations of the caged-type Kondo semimetals: CeT₂Al₁₀ (T = Fe, Ru and Os). Physica Scripta (2013) 88:068505068505–22. doi:10.1088/0031-8949/88/06/068505

CrossRef Full Text | Google Scholar

77. Winkler H, Lorenzer K, Prokofiev A, Paschen S. Anisotropic electrical resistivity of the Kondo insulator CeRu₄Sn₆. J Phys Conf Ser (2012) 391:012077–4. doi:10.1088/1742-6596/391/1/012077

CrossRef Full Text | Google Scholar

78. Hänel J, Winkler H, Ikeda M, Jl J, Martelli V, Prokofiev A, et al. Anisotropic thermopower of the Kondo insulator CeRu₄Sn₆. J Electron Mater (2014) 43:2440–3. doi:10.1007/s11664-014-3139-9

CrossRef Full Text | Google Scholar

79. Paschen S, Tran V, Senthilkumaran N, Baenitz M, Steglich F, Strydom A, et al. First results on U₂Ru₂Sn single crystals. Physica B (2003) 329–333:549–50. doi:10.1016/s0921-4526(02)02396-7

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Yutani K, Muro Y, Kajino J, Sato T, Takabatake T. Crystal-field effect on anisotropic magnetic properties of CeT₂Al₁₀ (T = Ru and Os). J Phys Conf Ser (2012) 391:012070–4. doi:10.1088/1742-6596/391/1/012070

CrossRef Full Text | Google Scholar

81. Hanzawa K. Crystalline electric field effects in CeT₂Al₁₀ (T = Ru, Os). J Phys Soc Jpn (2011) 80:023707–4. doi:10.1143/JPSJ.80.023707

CrossRef Full Text | Google Scholar

82. Strigari F, Willers T, Muro Y, Yutani K, Takabatake T, Hu Z, et al. Crystal-field ground state of the orthorhombic Kondo insulator CeRu₂Al₁₀. Phys Rev B (2012) 86:081105./1–5. doi:10.1103/PhysRevB.86.081105

CrossRef Full Text | Google Scholar

83. Adroja D, Hillier A, Muro Y, Kajino J, Takabatake T, Peratheepan P, et al. Competing 4f − electron dynamics in Ce(Ru_1−xFe_x)₂Al₁₀ (0 ≤ x ≤ 1.0): Magnetic ordering emerging from the Kondo semiconducting state. Phys Rev B (2013) 87:224415./1–14. doi:10.1103/physrevb.87.224415

CrossRef Full Text | Google Scholar

84. Tanida H, Nohara H, Nakagawa F, Yoshida K, Sera M, Nishioka T. Drastic changes in electronic properties of Kondo semiconductor CeRu₂Al₁₀ induced by Rh doping: Anisotropic transport properties in the antiferromagnetic ordered state. Phys Rev B (2016) 94:165137./1–10. doi:10.1103/physrevb.94.165137

CrossRef Full Text | Google Scholar

85. Guo H, Tanida H, Kobayashi R, Kawasaki I, Sera M, Nishioka T, et al. Magnetic instability induced by Rh doping in the Kondo semiconductor CeRu₂Al₁₀. Phys Rev B (2013) 88:115206./1–8. doi:10.1103/physrevb.88.115206

CrossRef Full Text | Google Scholar

86. Bhattacharyya A, Khalyavin D, Adroja D, Strydom A, Hillier A, Manuel P, et al. Anomalous change of the magnetic moment direction by hole doping in CeRu₂Al₁₀. Phys Rev B (2014) 90:174412./1–9. doi:10.1103/physrevb.90.174412

CrossRef Full Text | Google Scholar

87. Chełkowska G, Morkowski J, Szajek A, Stȩpień-Damm J, Troć R. Electronic structure and photoemission studies on Kondo semimetal U₂Ru₂Sn. Eur Phys J B (2003) 35:349–55. doi:10.1140/epjb/e2003-00287-y

CrossRef Full Text | Google Scholar