Fuzzy response to SH guided-wave scattering by semicircular depressions on the boundary of a ribbon-shaped elastic plate

In this paper, the fuzzy scattering problem with semicircular depressions on the boundary of a band-shaped elastic plate with steady SH guided wave incident is studied and an analytical solution is given. First, the SH guided wave is constructed by the guided wave expansion method, and then the scattered wave satisfying the free condition of the boundary stress of the strip domain is constructed by the cumulative mirror method. Finally, a definite solution equation is obtained based on the fact that the shear stress at the edge of the semi-circular recessed hole is zero. In this paper, the ambiguity of the number of waves and the width of the bands is taken into account. In order to avoid the irreversibility of interval algorithm and the difficulty of solving non-linear equations, the membership function of fuzzy quantity is segmented to make the membership degree and fuzzy quantity correspond respectively. A deterministic problem that translates into piecewise processing. Two numerical examples are given to examine the changes in fuzzy response of different numbers of fuzzy waves and fuzzy thicknesses to the dynamic stress concentration factor of the hoop at the collapse limit.

1 Introduction

The scattering theory of elastic waves is widely used in the fields of earthquake engineering, ocean engineering and geological exploration. The research and application of elastic wave scattering are very extensive, and rich results have been achieved. For the study of elastic wave scattering problems, several parameters are uncertain. This is due to the ambiguity of its own objective attributes, the approximate processing of mathematical modeling, and the use of random parameters as deterministic parameters. Since the American cybernetics expert Professor Zadeh proposed fuzzy sets in 1965, the research direction of fuzzy mathematics has become more extensive, such as fuzzy reliability, fuzzy control, fuzzy optimization, fuzzy calculus equations and so on. Tong et al. [1] investigated the adaptive fuzzy output-feedback backstepping control design problem for uncertain strict-feedback non-linear systems in the presence of unknown virtual and actual control gain functions and immeasurable states. Shi et al. [2] proposed the issue of the reliable asynchronous sampled-data filtering of Takagi-Sugeno (T-S) fuzzy delayed neural networks with stochastic intermittent faults, randomly occurring time-varying parameter uncertainties and controller gain fluctuation. Zhao et al. [3] solved the problem of asymptotic tracking control for a class of uncertain switched non-linear systems under fuzzy approximation framework. Shi et al. [4] dealt with the non-fragile memory filtering issue of T-S fuzzy delayed neural networks with randomly occurring time-varying parameter uncertainties and variable sampling rates. Liu et al. [5] proposed the concept of q-rung orthopair fuzzy sets (q-ROFSs) to be able to describe more complex fuzzy uncertainty information effectively. Sun et al. [6] researched the issue of fuzzy adaptive control for a class of strict-feedback non-linear systems with non-affine nonlinear faults. Hu et al. [7] explored the performance of fuzzy system-based medical image processing for predicting the brain disease. Zhu et al. [8] investigated the event-triggered control problem for stochastic non-linear systems with unmeasured states and unknown backlash-like hysteresis. Lin et al. [9] proposed a novel picture fuzzy multi-criteria decision making (MCDM) model to solve the site selection problem for car sharing stations. Zhang et al. [10] studied the fault detection problem for continuous-time fuzzy semi-Markov jump systems (FSMJSs) by employing an interval type-2 (IT2) fuzzy approach. Wang et al. [11] presented a fault-tolerant tracking control strategy for Takagi-Sugeno fuzzy model-based non-linear systems which combines integral sliding mode control with adaptive control technique. Garg H et al. [12] introduced a novel multi-attribute decision making (MADM) method under interval-valued intuitionistic fuzzy (IVIF) set environment by integrating a Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method. Pan et al. [13] developed a novel risk analysis approach by merging interval-valued fuzzy sets (IVFSs), improved Dempster-Shafer (D-S) evidence theory, and fuzzy Bayesian networks (BNs), acting as a systematic decision support approach for safety insurance for the entire life cycle of a complex system under uncertainty. In other numerical applications, spectral elemental methods are also effectively applied by researchers [14-15]. Mahariq I et al. [16] explored the on-resonance and off-resonance optical response of dielectric cylinders excited by normal incident plane waves. Mahariq I et al. [17] also studied photonic nanojets resulting from corrugated cylinders (with irregular boundaries) under normally incident plane-wave illumination.

SH waves are the most fundamental elastic waves, propagating in a direction perpendicular to the direction of vibration. The SH wave has only one inverse plane vibration displacement (out-of-plane displacement). Compared to P and SV waves, SH waves have the simplest elastodynamic behaviour. For elastic dynamics problems with complex initial boundary conditions, P and SV waves can be difficult to find solutions for. For SH waves, however, such problems can be easily solved to obtain further analytical solutions. There are a lot of ambiguity factors in the elastic wave scattering problem, such as seismic intensity, wave speed, medium shear modulus, medium density, amplitude and frequency of incident waves, etc., all of which are typical ambiguities with randomness and ambiguity. In this paper, the ambiguity of the number of waves and plate thickness ambiguity of SH guided wave scattering are studied for the semicircular depression on the boundary of the band-shaped elastic plate, and the membership function is segmented so that the ambiguity and the membership function correspond respectively. This method can avoid the appearance of interval numbers and combine the decomposition theorem of fuzzy numbers well. In this paper, a new theoretical method is given to deal with fuzzy dynamics knowledge, and the curve of dynamic stress concentration factor of semicircular sag boundary with membership degree of fuzzy quantity is discussed in detail, and a valuable reference conclusion for practical engineering is obtained.

2 Theoretical model and analysis

2.1 Theoretical model

In this paper, the classical model in the reference [18] is used as an example to further illustrate the use of fuzzy mathematics in solving the scattering problem for defects in thin plates. As shown in Figure 1, the thickness of the infinitely long strip-shaped domain is h, the upper boundary is $B_U$, the lower boundary is $B_L$, the center of the depression is $o$, and the radius is $r$. The shear modulus and density of the medium are $\mu$ and $\rho$, respectively. The right-hand plane rectangular coordinate system $\left(o,x,y\right)$ is established with the center of a circle $o$ as the origin, where the X-axis is parallel to the length direction of the belt shape domain, and the Y-axis is parallel to the thickness direction. At the same time, taking the center of the circle as the pole, a plane polar coordinate system (O, r, θ) is established. Introduce complex variables $z=x+iy=r{e}^{i\theta }$; $\overline{z}=x-iy=r{e}^{-i\theta }$, of which $i=\sqrt{-1}$, and establish complex plane $\left(z,\overline{z}\right)$. When the SH wave propagates in the plate, the out-of-plane direction is the vibration direction of the particle, and the amplitude w is only a function of the coordinates (x, y, t) or (r, θ, t).

FIGURE 1

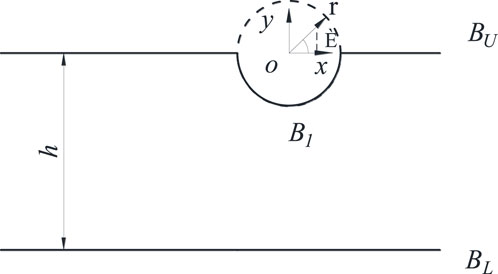
FIGURE 1. Theoretical model of steady-state scattering of SH waves by semi-cylindrical depressions in elastic ribbon domains.

2.2 Control equation

According to the theoretical model shown in Figure 1, the control equations satisfying the upper and lower boundary stress freedom can be obtained. According to reference [19], the control equation for the anti-plane dynamics problem can be obtained. The governing equation of the elasto-dynamic inverse plane problem is the scalar wave Eq. 1:

$\mu \Delta w=\rho \frac{{\partial }^{2}w}{\partial t^2}(1)$

In the formula: $\Delta$ is the two-dimensional Laplace operator. In this chapter, the steady-state SH wave is analyzed. According to the separation variable method, after separating the space variable and the time variable, the time harmonic factor $e^{-i\omega t}$ is omitted, and the Helmholtz equation, which is the governing equation of Eq. 2 is obtained:

$\Delta w+k^{2}w=0(2)$

Where: $k=\omega /c_s$ is the wave number of the anti-plane shear wave, $\omega$ is the circular frequency, and $c_s=\sqrt{\mu /\rho }$ is the phase velocity. In the complex plane, the Helmholtz equation and the stress-strain relationship can be expressed as:

$4\frac{\partial w}{\partial z\partial \overline{z}}+k^{2}w=0(3)$

$\left\{\begin{array}{l}{\tau }_{xz}=\mu \left(\frac{\partial w\left(z,\overline{z}\right)}{\partial z}+\frac{\partial w\left(z,\overline{z}\right)}{\partial \overline{z}}\right)\\ \\ {\tau }_{yz}=\mu i\left(\frac{\partial w\left(z,\overline{z}\right)}{\partial z}-\frac{\partial w\left(z,\overline{z}\right)}{\partial \overline{z}}\right)\end{array}\right.(4)$

$\left\{\begin{array}{l}{\tau }_{rz}=\mu \left[\frac{\partial w\left(z,\overline{z}\right)}{\partial z}{e}^{i\theta }+\frac{\partial w\left(z,\overline{z}\right)}{\partial \overline{z}}{e}^{-i\theta }\right]\\ \\ {\tau }_{\theta z}=\mu i\left[\frac{\partial w\left(z,\overline{z}\right)}{\partial z}{e}^{i\theta }-\frac{\partial w\left(z,\overline{z}\right)}{\partial \overline{z}}{e}^{-i\theta }\right]\end{array}\right.(5)$

2.3 Incident wave

Establish a global coordinate system at any point of the upper boundary $B_U$ of the belt domain, and satisfy the stress freedom condition (6) of the upper and lower boundaries of the belt domain. The SH guided wave expression is Eq. 7, where $\exp \left[i\left(k_{m}x-\omega t\right)\right]$ is the propagation term in the x-direction. m is the guided wave order and its physical meaning is the number of nodes of the interference term in the y-axis direction. $w_m^1$ and $w_m^2$ are the amplitudes of the corresponding propagating guided waves. When m is an even number $w_m^1=0$. When m is an odd number $w_m^2=0$.

$q_m$ satisfies Eq. 8, $k_m$ is the apparent wave-number in the x-axis direction, and $q_m$ satisfies Eq. 9. Only when $k_m$ is a real number, $\exp \left[i\left(k_{m}x-wt\right)\right]$ can represent a propagating traveling wave in the direction of the x-axis. Considering the issues discussed in this chapter, the study of non-propagating waves has no meaning. Therefore, when the m-order SH guided wave is incident, the wave number is required to satisfy $k>m\pi /h$.

$\mu {\left.\frac{\partial w}{\partial y}\right|}_{y=-h,0}=0(6)$

$w_m=w_m^1\sin \left[q_m\left(y+\frac{h}{2}\right)\right]+w_m^2\cos \left[q_m\left(y+\frac{h}{2}\right)\right]\exp \left[i\left(k_{m}x-\omega t\right)\right](7)$

$q_m=\frac{m\pi }{h}(8)$

$q_m^2=k^2-k_m^2(9)$

Using the superposition method to superimpose the guided waves of each order, all the displacement waves in the strip-shaped medium satisfying the stress freedom of the upper and lower boundaries can be obtained:

$w^i={\displaystyle \sum _{m=0}^{+\infty }}{w}_m={\displaystyle \sum _{m=0}^{+\infty }}{f}_m\left(\mathrm{y}\right)\exp \left[i\left(k_{m}x-\omega t\right)\right](10)$

In this chapter, the steady-state SH wave is discussed, and the time harmonic factor $e^{-i\omega t}$ is omitted. When the incident guided wave is of order m, the expressions of displacement and stress are as follows:

$w^{\left(i\right)}=\left\{w_m^1\cdot \sin \left[q_m\left(y+\frac{h}{2}\right)\right]+w_m^2\cdot \cos \left[q_m\left(y+\frac{h}{2}\right)\right]\right\}\cdot \exp \left(i{k}_{m}x\right)(11)$

$\left\{\begin{array}{l}\begin{array}{l}{\tau }_{xz}^{\left(i\right)}=i\mu k_m\cdot \left\{w_m^1\cdot \sin \left[q_m\left(y+\frac{h}{2}\right)\right]+w_m^2\cdot \cos \left[q_m\left(y+\frac{h}{2}\right)\right]\right\}\cdot \exp \left(i{k}_{m}x\right)\\ \end{array}\\ {\tau }_{yz}^{\left(i\right)}=q_m\left\{w_m^1\cdot \cos \left[q_m\left(y+\frac{h}{2}\right)\right]-w_m^2\cdot \sin \left[q_m\left(y+\frac{h}{2}\right)\right]\right\}\cdot \exp \left(i{k}_{m}x\right)\end{array}\right.(12)$

$\left\{\begin{array}{l}\begin{array}{l}{\tau }_{rz}^{\left(i\right)}={\tau }_{xz}^{\left(i\right)}\cos \left(\theta \right)+{\tau }_{yz}^{\left(i\right)}\sin \left(\theta \right)\\ \end{array}\\ {\tau }_{\theta z}^{\left(i\right)}=-{\tau }_{xz}^{\left(i\right)}\sin \left(\theta \right)+{\tau }_{yz}^{\left(i\right)}\cos \left(\theta \right)\end{array}\right.(13)$

2.4 Scattered waves

Under the action of incident SH waves, the concave will produce scattered waves. By using the method of repeated mirror image, the semi-cylindrical depression $B_1$ is extended to the medium into a whole circle, which is named as the circular hole $\overline{B_1}$. According to the wave function expansion method, the displacement and stress of all-space scattered waves generated by the boundary of a circular hole satisfy:

${w^{\left(s\right)}}_0^0\left(z\right)=w_0{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n{H}_n^{\left(1\right)}\left(k\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^n(14)$

${{\tau }_{rz}^{\left(s\right)}}_0^0\left(z\right)=\frac{k\mu }{2}{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z\right|\right)\cdot {\left(\frac{z}{\left|z\right|}\right)}^{\left(\mathrm{n}-1\right)}{e}^{i\theta }-H_{n+1}^{\left(1\right)}\left(k\left|z\right|\right)\cdot {\left(\frac{z}{\left|z\right|}\right)}^{\left(\mathrm{n}+1\right)}{e}^{-i\theta }](15)$

${{\tau }_{\theta z}^{\left(s\right)}}_0^0\left(z\right)=\frac{ik\mu }{2}{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z\right|\right)\cdot {\left(\frac{z}{\left|z\right|}\right)}^{\left(\mathrm{n}-1\right)}{e}^{i\theta }+H_{n+1}^{\left(1\right)}\left(k\left|z\right|\right)\cdot {\left(\frac{z}{\left|z\right|}\right)}^{\left(\mathrm{n}+1\right)}{e}^{-i\theta }](16)$

The scattered wave ${w^{\left(s\right)}}_0^0$ generated by the circular hole $\overline{B}$ is reflected for the first time at the boundaries $B_U$ and $B_L$ of the band domain, respectively. This reflected wave can be represented by the mirror images ${w^{\left(s\right)}}_1^1$ and ${w^{\left(s\right)}}_2^1$ of the scattered wave ${w^{\left(s\right)}}_0^0$ to the boundaries $B_U$ and $B_L$, which is called the first mirror scattered wave. The first reflected wave will have a second reflection on the boundaries $B_U$ and $B_L$ of the strip domain, respectively. The reflected wave can be represented by the mirror images ${w^{\left(s\right)}}_1^2$ and ${w^{\left(s\right)}}_2^2$ of the first mirror scattered waves ${w^{\left(s\right)}}_1^1$ and ${w^{\left(s\right)}}_2^1$ on the boundaries $B_U$ and $B_L$, known as the secondary mirror scattering wave.

Repeating this, the displacements of the P-th mirror scattered waves are ${w^{\left(s\right)}}_1^P$ and ${w^{\left(s\right)}}_2^P$, and the corresponding stresses are ${{\tau }_{rz}^{\left(s\right)}}_1^p$, ${{\tau }_{\theta z}^{\left(s\right)}}_1^p$, ${{\tau }_{rz}^{\left(s\right)}}_2^p$ and ${{\tau }_{\theta z}^{\left(s\right)}}_2^p$. Among them, P is the number of mirror images and the subscripts 1 and 2 represent the mirror faces of $B_U$ and $B_L$, respectively.

${w^{\left(s\right)}}_1^p\left(z\right)=w_0{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n{H}_n^{\left(1\right)}\left(k\left|z_1^p\right|\right){\left(\frac{z_1^p}{\left|z_1^p\right|}\right)}^{{\left(-1\right)}^{p}n}(17)$

${{\tau }_{rz}^{\left(s\right)}}_1^p\left(z\right)=\frac{k\mu }{2}{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z_1^p\right|\right)\cdot {\left(\frac{z_1^p}{\left|z_1^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}-1\right)}{e}^{{\left(-1\right)}^{p}i\theta }-H_{n+1}^{\left(1\right)}\left(k\left|z_1^p\right|\right)\cdot {\left(\frac{z_1^p}{\left|z_1^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}+1\right)}{e}^{{\left(-1\right)}^{\left(p+1\right)}i\theta }](18)$

$\begin{array}{l}{{\tau }_{\theta z}^{\left(s\right)}}_1^p\left(z\right)={\left(-1\right)}^P\frac{ik\mu }{2}{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z_1^p\right|\right)\cdot {\left(\frac{z_1^p}{\left|z_1^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}-1\right)}{e}^{{\left(-1\right)}^{p}i\theta }+\\ \left.H_{n+1}^{\left(1\right)}\left(k\left|z_1^p\right|\right)\cdot {\left(\frac{z_1^p}{\left|z_1^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}+1\right)}{e}^{{\left(-1\right)}^{\left(p+1\right)}i\theta }\right]\end{array}(19)$

${w^{\left(s\right)}}_2^p\left(z\right)=w_0{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n{H}_n^{\left(1\right)}\left(k\left|z_2^p\right|\right){\left(\frac{z_2^p}{\left|z_2^p\right|}\right)}^{{\left(-1\right)}^{p}n}(20)$

$\begin{array}{l}{{\tau }_{rz}^{\left(s\right)}}_2^p\left(z\right)=\frac{k\mu }{2}{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z_2^p\right|\right)\cdot {\left(\frac{z_2^p}{\left|z_2^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}-1\right)}{e}^{{\left(-1\right)}^{p}i\theta }-\\ \left.H_{n+1}^{\left(1\right)}\left(k\left|z_2^p\right|\right)\cdot {\left(\frac{z_2^p}{\left|z_2^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}+1\right)}{e}^{{\left(-1\right)}^{\left(p+1\right)}i\theta }\right]\end{array}(21)$

$\begin{array}{l}{{\tau }_{\theta z}^{\left(s\right)}}_2^p\left(z\right)={\left(-1\right)}^P\frac{ik\mu }{2}{\displaystyle \sum _{n=-\infty }^{+\infty }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z_2^p\right|\right)\cdot {\left(\frac{z_2^p}{\left|z_2^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}-1\right)}{e}^{{\left(-1\right)}^{p}i\theta }+\\ \left.H_{n+1}^{\left(1\right)}\left(k\left|z_2^p\right|\right)\cdot {\left(\frac{z_2^p}{\left|z_2^p\right|}\right)}^{{\left(-1\right)}^p\left(\mathrm{n}+1\right)}{e}^{{\left(-1\right)}^{\left(p+1\right)}i\theta }\right]\end{array}(22)$

In the above formula:

$z_1^p=z-i\left[\frac{{\left(-1\right)}^{p}h+h}{2}+\left(p-1\right)h\right](23)$

$z_2^p=z+i\left[h+\frac{{\left(-1\right)}^{p+1}h+h}{2}+\left(p-1\right)h\right](24)$

Using the superposition method, the scattered waves obtained by each mirror image are accumulated together, and the displacement of the scattered waves generated by the circular hole $\overline{B}$ that can satisfy the stress freedom of the upper and lower boundaries of the strip domain can be obtained as Eq. 25, and the stress is expressed as Eq. 26 and 27.

$w^{\left(s\right)}\left(z\right)={w^{\left(s\right)}}_0^0\left(z\right)+{\displaystyle \sum _{P=1}^{+\infty }}\left({w^{\left(s\right)}}_1^P\left(z\right)+{w^{\left(s\right)}}_2^P\left(z\right)\right)(25)$

${\tau }_{rz}^{\left(s\right)}\left(z\right)={{\tau }_{rz}^{\left(s\right)}}_0^0\left(z\right)+{\displaystyle \sum _{P=1}^{+\infty }}\left({{\tau }_{rz}^{\left(s\right)}}_1^P\left(z\right)+{{\tau }_{rz}^{\left(s\right)}}_2^P\left(z\right)\right)(26)$

${\tau }_{\theta z}^{\left(s\right)}\left(z\right)={{\tau }_{\theta z}^{\left(s\right)}}_0^0\left(z\right)+{\displaystyle \sum _{P=1}^{+\infty }}\left({{\tau }_{\theta z}^{\left(s\right)}}_1^P\left(z\right)+{{\tau }_{\theta z}^{\left(s\right)}}_2^P\left(z\right)\right)(27)$

2.5 Definite solution conditions

The incident wave and scattered wave constructed according to the above method have already satisfied the condition that the shear stress at the boundary $B_U$ and $B_L$ is zero, so that the condition of stress freedom at the concave boundary $B_1$ becomes the definite solution condition of the whole problem. The resulting coefficients A_n on the scattered wave function level are the set of Eq. 28. Firstly, the coordinate translation technique is used to translate the stress expressions solved in other coordinate systems into the complex plane $\left(z,\overline{z}\right)$. Then, the Fourier expansion method is used, and both ends of the formula are multiplied by $e^{-im{\theta }_j}$ at the same time, and then the infinite algebraic equations with coefficient A_n are integrated on the interval $\left(-\pi ,0\right)$. Finally, the truncated finite terms are solved.

${\tau }_{rz}^{\left(i\right)}\left(z\right)+{\tau }_{rz}^{\left(s\right)}\left(z\right)=0,z\in B(28)$

2.6 Dynamic stress concentration factor

Under the action of steady-state SH wave, the dynamic stress concentration factor characterizes the degree of dynamic stress concentration. Define Eq. 29 as the dynamic stress concentration factor of the recessed edge.

$\gamma =\frac{\left|{\tau }_{\theta z}\right|}{\left|{\tau }_0\right|}(29)$

Where: ${\tau }_{\theta z}$ is the angular stress on the edge of the depression and ${\tau }_0=\mu k{w}_0$ is the maximum amplitude of the incident stress.

3 Examples and analysis

3.1 Analysis of fuzzy example 1

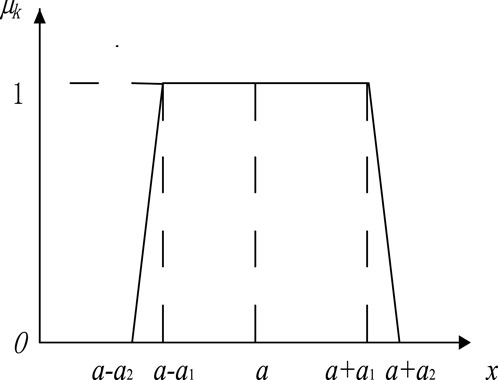
There are several fuzzy parameters in this problem including wave amplitude, frequency, and wave speed in the plane of perturbation which may all be fuzzy numbers. As can be seen from reference [20], the different affiliation curves are treated according to trapezoidal segments. It is assumed that the ambiguity membership function of the wavenumber is ${\mu }_k\left(x\right)$ and the trapezoidal distribution is shown in Figure 2. According to the method of fuzzy cut set, the interval under a certain degree of membership is obtained. The points in this interval actually have different degrees of membership, so that the fuzzy cutest set is not exactly the same as the general interval number. Since the subtraction and division of the four arithmetic operations of interval numbers are not reversible, it is difficult to deal with fuzzy numbers, and at most an enlarged interval solution can be obtained. According to the corresponding relationship between points and membership degrees, different membership degree curves are processed in segments.

FIGURE 2

FIGURE 2. Trapezoidal distribution.

The related membership relationship can be expressed as:

${\mu }_{\mathrm{k}}\left(x\right)=\left\{\begin{array}{l}0;x\le a-a_2\\ \frac{a_2+x-a}{a_2-a_1};a-a_2<x\le a-a_1\\ 1;a-a_1<x<a+a_1\\ \frac{a_2-x+a}{a_2-a_1};a+a_1\le x<a+a_2\\ 0;x\ge a+a_2\end{array}\right.$

The analysis only needs to consider a range of $a-a_2<x\le a+a_2$ divided into three segments. Order ${\mu }_{\mathrm{k}}\left(x\right)=\lambda$.

When $x=k\in \left(a-a_2,a-a_1\right)$, $k=\left(a_2-a_1\right)\lambda +a-a_2$ ;

When $x=k\in \left(a-a_1,a+a_1\right)$, $\lambda \equiv 1$;

When $x=k\in \left(a+a_1,a+a_2\right),k=a_2+a-\lambda \left(a_2-a_1\right)$;

Let a = 2, a₂ = 1.5, a₁ = 1, r = 1. By considering the different thicknesses $h=3$, $h=6$, $h=10$ and $h=20$ in the strip domain and substituting different affiliation relations, the cyclic dynamic stress concentration factor at the semi-circular depression are further obtained at different levels of affiliation.

Figure 3 shows the distribution of the hoop dynamic stress concentration factor of the semicircular depression in different sections when the thickness of the belt domain is $h=3$. The left transition region of the membership function curve is the low wave number region, and the dynamic stress concentration factor is significantly higher than that of the core region and the right transition region (high wave number region). The angle of the left transition zone is 180⁰–270⁰ for the front wave and 270⁰-360⁰ for the back wave. The front wave front in the left transition region oscillates more obviously than the back wave front, because the front wave first arrives when the incident wave hits the inside of the band. The core area is a non-empty and non-single element interval. Although the membership degree of points in the core area is $\lambda =1$, due to the difference in the numerical value of specific points, the dynamic stress concentration factor of the core area exhibits irregular oscillations, which is caused by fuzzy uncertainty.

FIGURE 3

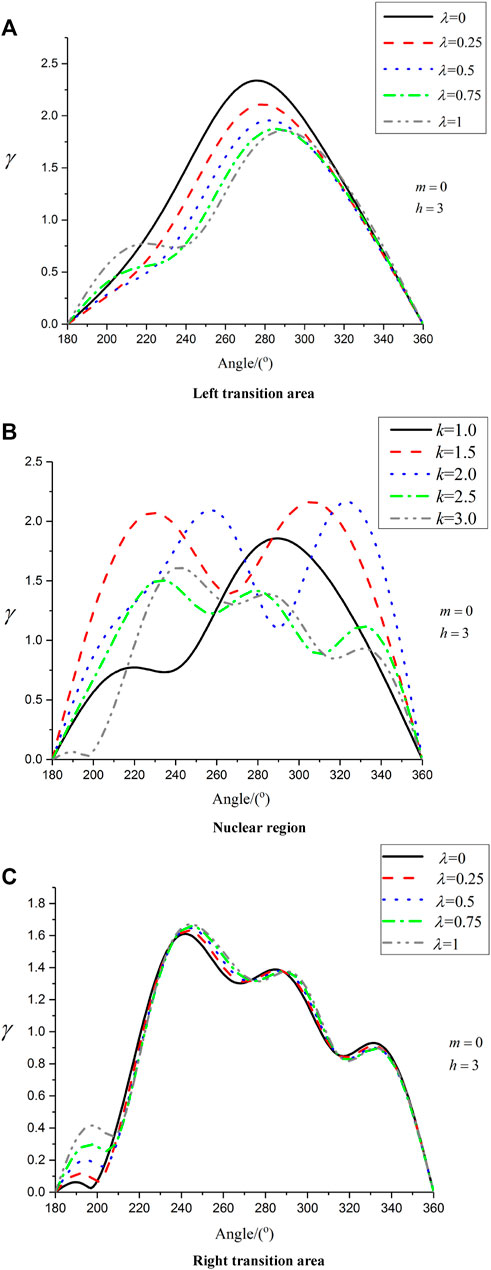
FIGURE 3. Distribution of hoop dynamic stress concentration factor of semi-circular depression when the thickness of the ribbon domain is $h=3$. (A–C) represent the results of these three subsets: Left transition area, Nuclear region and Right transition area.

As can be seen from Figure 4, the left transition area of the membership function curve is a low wave number area, the maximum value of dynamic stress concentration factor appears on the membership degree $\lambda =1$ curve, and the peak value of the core area appears on the membership degree $k=2.0$ curve, while the peak value of the right transition area appears on the membership degree $\lambda =0.5$ curve. The peaks of membership degrees appear on the curves of different membership degrees, which is obviously caused by fuzzy uncertainty. The change of the stress concentration factor curve in the right transition region is more complicated than that in the left transition region, which indicates that the high wave number region has a more serious influence than the low wave number region.

FIGURE 4

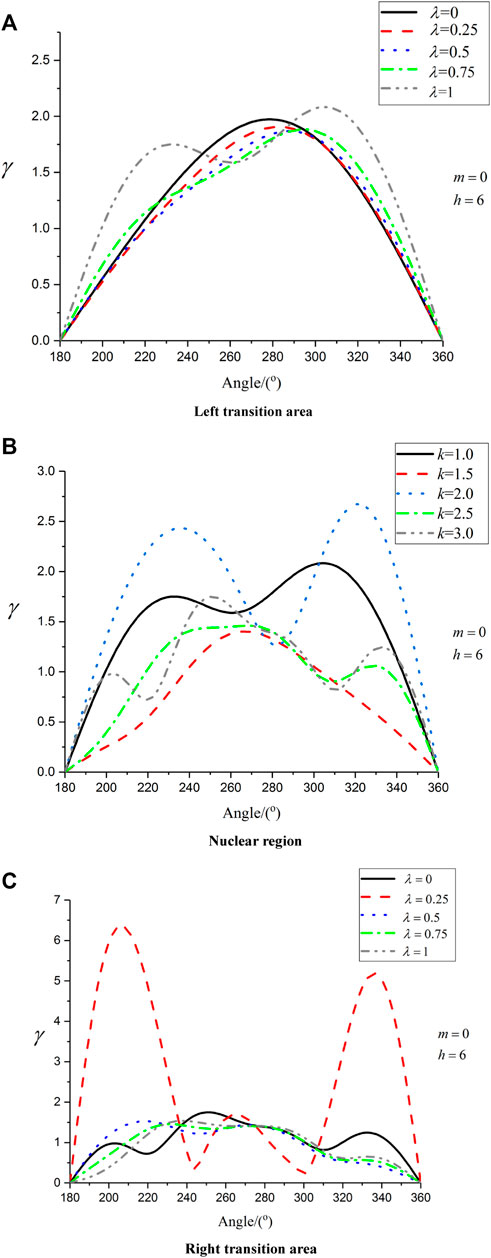
FIGURE 4. Distribution of hoop dynamic stress concentration factor of semi-circular depression when the thickness of the ribbon domain is $h=6$. (A–C) represent the results of these three subsets: Left transition area, Nuclear region and Right transition area.

From Figure 5, the thickness $h=10$ of the band-shaped domain shows the distribution of the hoop dynamic stress concentration factor of the semicircular depression. The left transition area of the membership function curve is the low wave number area, and the dynamic stress concentration factor curve is not obviously oscillated, and the core area and the right transition area are the medium wave number area and the high wave number area, respectively. When the membership degree of the left transition zone is $\lambda =0.25$, the maximum value of the peak appears. The membership degrees of the core area are all $\lambda =1$, but the maximum value of the wave peak appears at $\mathrm{k}=1.0$, and the maximum value of the peak of the dynamic stress concentration factor in the right transition area appears at $\lambda =0.25$. Due to the influence of fuzzy and uncertain factors, the positions of the peaks in different sections of the membership curve are different. It can be seen from the figure that the number of wave peaks in the right transition area is significantly more than that in the nuclear area and the left transition area, and the right transition area oscillates more violently.

FIGURE 5

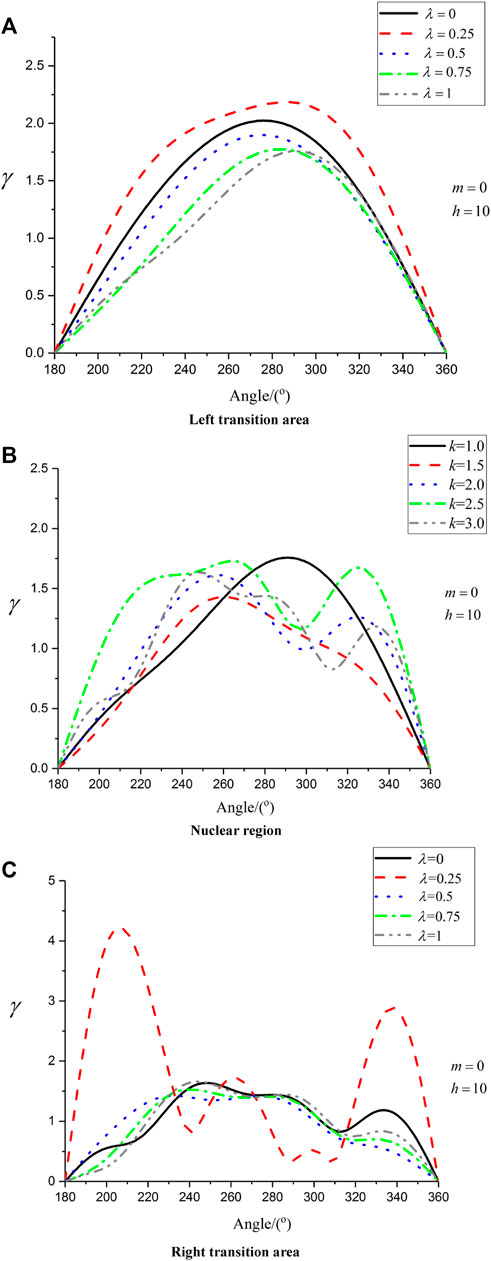
FIGURE 5. Distribution of hoop dynamic stress concentration factor of semi-circular depression when the thickness of the ribbon domain is $h=10$. (A–C) represent the results of these three subsets: Left transition area, Nuclear region and Right transition area.

It can be seen from Figure 6 that the dynamic stress concentration factor in the left transition area of the membership function curve is significantly higher than that in the core area and the right transition area, and the curve of the stress concentration factor in the left transition area changes gently. With the increase of wave number, the curve has obvious oscillation, and the change is more obvious in the right transition region (high wave number region). The maximum value of the wave crest in the left transition area appears at the position of membership degree $\lambda =0.25$, and although the membership degree of the core area is $\lambda =1$, the maximum value of the wave crest appears at $k=2.5$. The peak value of the right transition area appears at $\lambda =0.25$. The transition regions of different segments show different correlations, which also lead to the maximum value of the peaks appearing on the curves of different membership degrees.

FIGURE 6

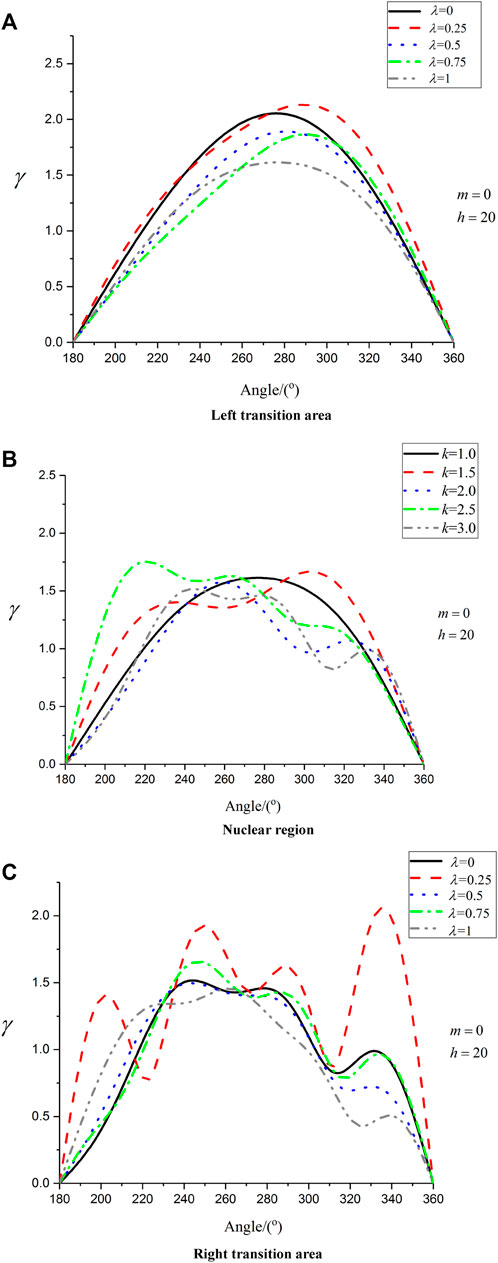
FIGURE 6. Distribution of hoop dynamic stress concentration factor of semi-circular depression when the thickness of the ribbon domain is $h=20$. (A–C) represent the results of these three subsets: Left transition area, Nuclear region and Right transition area.

3.2 Analysis of fuzzy example 2

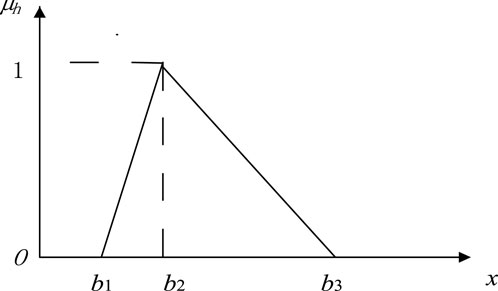
As can be seen from reference [21], the different affiliation curves are treated according to triangular segments. Assuming that the fuzzy membership function of the thickness h of the elastic plate in the belt domain is ${\mu }_h\left(x\right)$, it is a triangular distribution as shown in Figure 7. According to the method of fuzzy cut set, the interval under a certain degree of membership is obtained. The points in this interval actually have different degrees of membership, so that the fuzzy cut set is not exactly the same as the general interval number. Since the subtraction and division of the four arithmetic operations of interval numbers are not reversible, it is difficult to deal with fuzzy numbers, and at most an enlarged interval solution can be obtained. According to the corresponding relationship between points and membership degrees, different membership degree curves are processed in segments.

${\mu }_{\mathrm{h}}\left(x\right)=\left\{\begin{array}{l}0;x<b_1\\ \frac{1}{b_2-b_1}x-\frac{b_1}{b_2-b_1};b_1\le x<b_2\\ -\frac{1}{b_3-b_2}x+\frac{b_3}{b_3-b_2};b_2\le x<b_3\\ 0;b_3\le x\end{array}\right.$

FIGURE 7

FIGURE 7. Triangular distribution.

In this analysis, only $b_1<x\le b_3$ is considered and divided into two sections. Order ${\mu }_{\mathrm{h}}\left(x\right)={\lambda }_1$. When $x=h\in \left(b_1,b_2\right)$, $h=\left(b_2-b_1\right){\lambda }_1+b_1$. When $x=h\in \left(b_2,b_3\right)$, $h=b_3-{\lambda }_1\left(b_3-b_2\right)$. Let b₁ = 1, b₂ = 2, b₃ = 5, r = 0.8 and consider the hoop dynamic stress concentration factor curve at the semicircular depression under different membership levels under the condition of $k=0.1$, $k=1$ and $k=2$.

It can be seen from Figure 8 that when $m=0$, $\mathrm{k}=0.1$ is a phenomenon of low-frequency quasi-static incidence of SH guided waves. Whether it is the left transition region or the right transition region, the dynamic stress concentration factor curve exhibits a position symmetry about 270⁰. The variation law of the dynamic stress concentration factor of the membership function is very similar, and when the membership degree is $\lambda =0$, the peak of the dynamic stress concentration factor is the largest. The changing law of the dynamic stress concentration factor in the right transition zone is also very similar in the case of different membership relationships, but the maximum value of the wave peak appears at the position of $\lambda =1$. Due to the uncertainty of the fuzzy wave number, the positions of the peaks in the left and right transition regions are different.

FIGURE 8

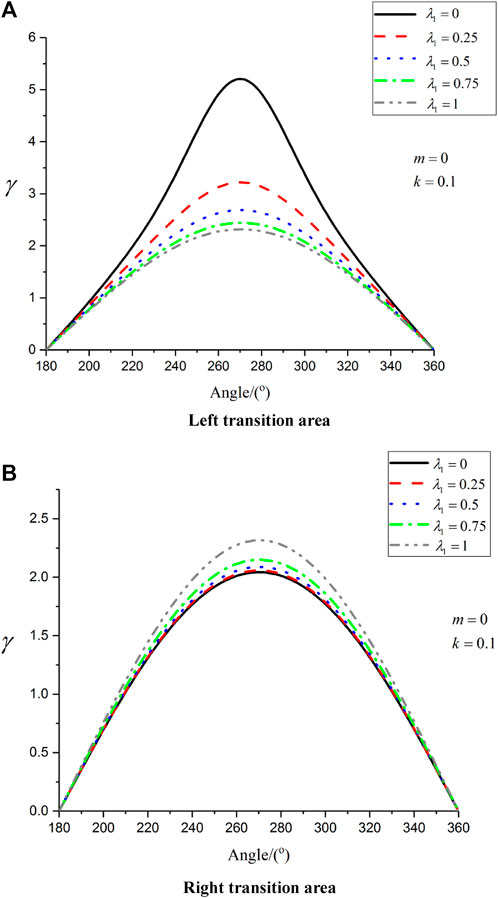
FIGURE 8. Distribution of hoop dynamic stress concentration factor with $k=0.1$ at semicircular depressions. (A,B) represent the results of these two subsets: Left transition area and Right transition area.

It can be seen from Figure 9 that when $k=1$ corresponds to the incident situation of the intermediate frequency SH guided wave. From the curves of the left and right transition regions, it can be seen that the dynamic stress concentration factor of the front wave surface is more obvious than the fluctuation stress concentration factor of the back side. The maximum value of the wave crest in the left transition area appears at the position of membership degree $\lambda =0$, while the maximum value of the wave peak in the right transition area appears at the position of membership degree $\lambda =0.75$. The values of different membership degrees are different, and the changes of the dynamic stress concentration factor in the left and right transition regions are also different.

FIGURE 9

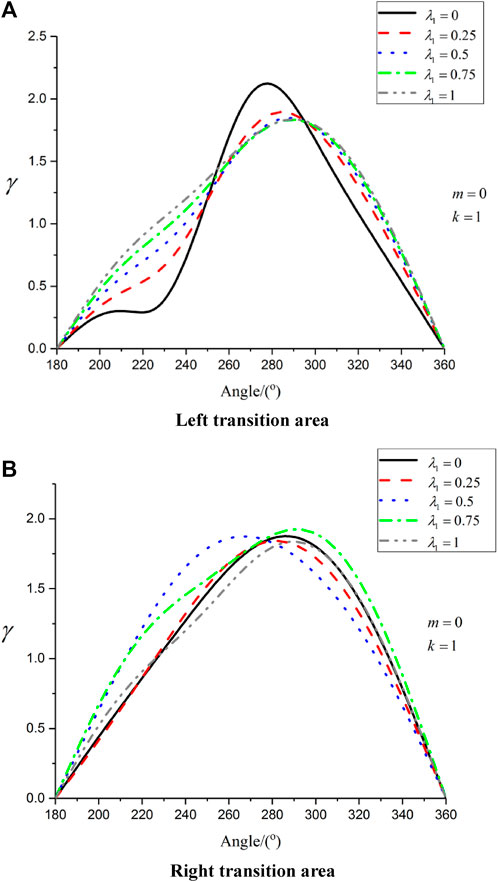
FIGURE 9. Distribution of hoop dynamic stress concentration factor with $k=1$ at semicircular depressions. (A,B) represent the results of these two subsets: Left transition area and Right transition area.

It can be seen from Figure 10 that when $k=2$ corresponds to the incident case of high-frequency SH guided waves. The values of different membership degrees in the left and right transition regions are different, and the variant rules of the dynamic stress concentration factor are also different. However, it can be clearly seen that the variation law of the dynamic stress concentration factor curve in the left and right transition zones basically appears in the form of two peaks. The peak maximum value in the left transition area appears on the $\lambda =0$ curve, while the peak maximum value in the right transition area appears on the $\lambda =0.75$ curve. From this, it can be concluded that the fuzzy relationship is uncertain, and different fuzzy membership relationships lead to different positions of wave crests.

FIGURE 10

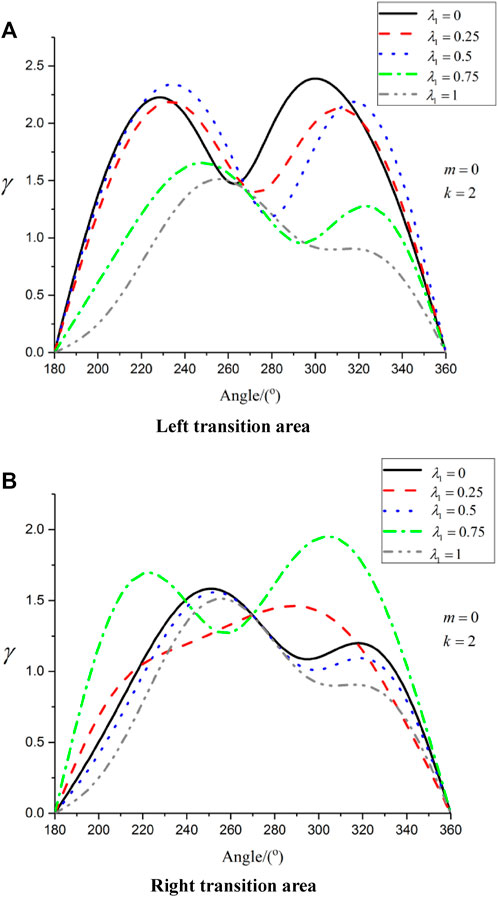
FIGURE 10. Distribution of hoop dynamic stress concentration factor with $k=2$ at semicircular depressions. (A,B) represent the results of these two subsets: Left transition area and Right transition area.

4 Conclusion

The solution to the elastic wave scattering problem is often a non-linear function of various parameters, and there is no mature and unified method to obtain the explicit expression of the fuzzy parameters. Even if the inverse function is reached, it is mostly a multi-valued function. Various parameters are often ambiguous, and the membership function of fuzzy response is not always solved by using the membership function of known fuzzy parameters, and the irreversibility of interval algorithm also brings many difficulties in solving fuzzy response problem. In this paper, the correspondence between the subordinate function and the fuzzy quantity pairs is exploited to segment the subordinate function so that each segment corresponds to the fuzzy quantity. This method can effectively avoid the process of interval calculation and does not violate the decomposition process of fuzzy numbers. Two different affiliation curves are given for the trapezoidal and triangular distributions. We solve the multi-source fuzzy scattering problem for wave number and band shape domain thickness, respectively. The calculation example results show the feasibility of the algorithm, and provide theoretical basis and reference value for the application of fuzzy mathematics to earthquake engineering.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

EQ and HQ contributed to the conception and design of the study. EQ performed the statistical analysis and wrote the first draft of the manuscript. JG wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the Heilongjiang Provincial Undergraduate Universities Basic Scientific Research Business Young Innovative Talents Project (145209209).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tong S, Min X, Li Y. Observer-based adaptive fuzzy tracking control for strict-feedback nonlinear systems with unknown control gain functions. IEEE Trans Cybernetics (2020) 50(9):3903–13. doi:10.1109/TCYB.2020.2977175

CrossRef Full Text | Google Scholar

2. Shi K, Wang J, Tang Y, Zhong S. Reliable asynchronous sampled-data filtering of T–S fuzzy uncertain delayed neural networks with stochastic switched topologies. Fuzzy Sets Syst (2020) 381:1–25. doi:10.1016/j.fss.2018.11.017

CrossRef Full Text | Google Scholar

3. Zhao X, Wang X, Ma L, Zong G. Fuzzy approximation based asymptotic tracking control for a class of uncertain switched nonlinear systems. IEEE Trans Fuzzy Syst (2019) 28(4):632–44. doi:10.1109/TFUZZ.2019.2912138

CrossRef Full Text | Google Scholar

4. Shi K, Wang J, Zhong S, Tang Y, Cheng J. Non-fragile memory filtering of T-S fuzzy delayed neural networks based on switched fuzzy sampled-data control. Fuzzy Sets Syst (2020) 394:40–64. https://doi .org/10.1016/j.fss.2019.09.001.

CrossRef Full Text | Google Scholar

5. Liu P, Chen SM, Wang P. Multiple-attribute group decision-making based on q-rung orthopair fuzzy power maclaurin symmetric mean operators. IEEE Trans Syst Man, Cybernetics: Syst (2018) 50(10):3741–16. doi:10.1109/TSMC.2018.2852948

CrossRef Full Text | Google Scholar

6. Sun K, Liu L, Qiu J, et al. Fuzzy adaptive finite-time fault-tolerant control for strict-feedback nonlinear systems[J]. IEEE Trans Fuzzy Syst (2020) 29(4):786–96. doi:10.11009/TFUZZ.2020.2965890

CrossRef Full Text | Google Scholar

7. Hu M, Zhong Y, Xie S, Lv H, Lv Z. Fuzzy system based medical image processing for brain disease prediction. Front Neurosci (2021) 15:714318. doi:10.3389/fnins.2021.714318

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhu Z, Pan Y, Zhou Q, Lu C. Event-triggered adaptive fuzzy control for stochastic nonlinear systems with unmeasured states and unknown backlash-like hysteresis. IEEE Trans Fuzzy Syst (2020) 29(5):1273–83. doi:10.1109/TFUZZ.2020.2973950

CrossRef Full Text | Google Scholar

9. Lin M, Huang C, Xu Z. MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustain cities Soc (2020) 53:101873. doi:10.1016/j.scs.2019.101873

CrossRef Full Text | Google Scholar

10. Zhang L, Lam HK, Sun Y, Liang H. fault detection for fuzzy semi-markov jump systems based on interval type-2 fuzzy approach. IEEE Trans Fuzzy Syst (2019) 28(10):2375–88. doi:10.1109/TFUZZ.2019.2936333

CrossRef Full Text | Google Scholar

11. Wang Y, Jiang B, Wu ZG, Xie S, Peng Y. Adaptive sliding mode fault-tolerant fuzzy tracking control with application to unmanned marine vehicles. IEEE Trans Syst Man, Cybernetics: Syst (2020) 51(11):6691–700. doi:10.1109/TSMC.2020.2964808

CrossRef Full Text | Google Scholar

12. Garg H, Kumar K. A novel exponential distance and its based TOPSIS method for interval-valued intuitionistic fuzzy sets using connection number of SPA theory. Artif Intelligence Rev (2020) 53(1):595–624. doi:10.1007/s10462-018-9668-5

CrossRef Full Text | Google Scholar

13. Pan Y, Zhang L, Li ZW, Ding L. Improved fuzzy bayesian network-based risk analysis with interval-valued fuzzy sets and D–S evidence theory. IEEE Trans Fuzzy Syst (2019) 28(9):2063–77. doi:10.1109/TFUZZ.2019.2929024

CrossRef Full Text | Google Scholar

14. Mahariq I, Giden IH, Alboon S, Fouad Aly WH, Youssef A, Kurt H. Investigation and analysis of acoustojets by spectral element method[J]. Mathematics (2022) 10(17):3415. https://www.mdpi.com/2227-7390/10/23/4516.

Google Scholar

15. Mahariq I, Kuzuoğlu M, Tarman IH, Kurt H. Photonic nanojet analysis by spectral element method[J]. IEEE Photonics J. (2014) 6(5):1–14. doi:10.1109/JPHOT.2014.2361615

CrossRef Full Text | Google Scholar

16. Mahariq I, Kurt H. On-and off-optical-resonance dynamics of dielectric microcylinders under plane wave illumination[J]. JOSA B (2015) 32(6):1022–1030. doi:10.1364/JOSAB.32.001022

CrossRef Full Text | Google Scholar

17. Mahariq I, Astratov VN, Kurt H. Persistence of photonic nanojet formation under the deformation of circular boundary[J]. JOSA B (2016) 33(4):535–542. doi:10.1364/JOSAB.33.000535

CrossRef Full Text | Google Scholar

18. Qu EX, Qi H, Guo J, Wang L. Dynamic response analysis of SH-guided waves in a strip-shaped elastic medium for a semi-cylindrical depression[J]. Arch. Appl. Mech. (2023) 93(3):1241–1258. doi:10.1007/s00419-022-02325-9

CrossRef Full Text | Google Scholar

19. Liu D, Gai B, Tao G. Applications of the method of complex functions to dynamic stress concentrations[J]. Wave motion (1982) 4(3):293–304. doi:10.1016/0165-2125(82)90025-7

CrossRef Full Text | Google Scholar

20. Shi WP, Fang SJ, Zhang CP, Yang HL. Fuzzy response of semicircular concave boundaries in half space to SH wave scattering [J]. Mech. strength (2011) 33(03):373–378. doi:10.16579/j.issn.1001.9669.2011.03.012

CrossRef Full Text | Google Scholar

21. Liu YW, Shi WP. Fuzzy scattering of steady-state incident plane SH waves by circular elastic inclusions in a right-angle plane[J]. Mech. strength (2012) 34(03):371–378. doi:10.16579/j.issn.1001.9669.2012.03.003

CrossRef Full Text | Google Scholar