Energy conservation theory for second language acquisition (ECT-L2A): a partial validation of kinetic energy–aptitude and motivation

While language aptitude and motivation are important contributors to second language (L2) attainment, two major gaps in the past research have been 1) a lack of non-linear models stemming from a naïve and tacit assumption that learning outcomes are linearly related to their predictors, and 2) a lack of unified and integrative understanding of key individual differences (ID) variables. This study aims to explore the relationship between motivation and aptitude in the context of second language acquisition using ideas from physics. This is done by seeking to validate several theoretical claims put forth by the energy conservation theory for second language acquisition (ECT-L2A) while attempting to integrate key ID variables into a unified model. In this study, 203 adult Spanish-speaking learners of L2 English were recruited. The participants encompassed a wide range of proficiency levels. To assess their language aptitude, the LLAMA_F test was administered, while motivation was measured using the Attitude Motivation Test Battery. Attainment was gauged through a grammaticality judgment test. Data analysis included correlation assessments, R-squared measures, and orthogonal regression employing the total least-squares method. The correlation analyses and regression findings were consistent with the predictions derived from ECT-L2A. Aptitude exhibited a positive relationship with attainment, but this effect diminished as proficiency increased. Conversely, while all participants displayed motivation to learn, motivation decreased as attainment levels advanced throughout L2 development. The effect of motivation on achievement followed an asymptotic pattern, with its contribution to target language (TL) mastery diminishing. Combining aptitude and motivation as a single unit, the learning trajectory mirrored the curve envisioned by ECT-L2A. The results of this study offer two key interpretations regarding motivation and aptitude in the context of second language acquisition. Firstly, both motivation and aptitude undergo changes in relation to attainment, with their effects varying as learners progress. Secondly, their efficacy in achieving native-like proficiency during L2 development differs significantly. These findings underscore the importance of considering the non-linear and interconnected nature of language aptitude and motivation in understanding their role in L2 acquisition. The implications of these findings for language teaching and learning strategies warrant further exploration.

Introduction

In second language acquisition (SLA), the crossover into physics for theoretical inspiration has been, for the most part, nonexistent until Larsen-Freeman [1] introduced the notion of complexity theory and de Bot [2] followed with dynamic systems theory. Both complexity/chaos theory and dynamic systems theory have their origins in the principles of non-linearity, uncertainty, and unpredictability found in mathematics and quantum physics. However, neither feature mathematical models of their interdisciplinary source but instead draw on the conceptual models of complexity, non-linearity, dynamicity, self-organizing, adaptive, and emergent system, adopted as analogous metaphor under the SLA context. As a result, crossing the boundary of SLA proper and venturing into the “hard” sciences has led to appropriating the language of those disciplines as a metaphorical device to introduce novel ideas in SLA contexts without its mathematical complements. Energy Conservation Theory of Second Language Acquisition (ECT-L2A) is the first SLA theory to not only draw inspiration from physics but also to use the mathematical equation to explain a significant L2 phenomenon, inter-learner variability on ultimate attainment. ECT-L2A’s contribution is trailblazing in that though conceptual models abound in SLA, mathematical models are rare, if not nonexistent.

In physics, the law of energy conservation states that the total energy of an isolated system remains conserved, and energy can only be transformed or transferred from one form to another within a system. It is a bounded and closed system in which the total energy does not grow indefinitely; instead, it reaches an equilibrium after transforming from one state to another while the object involved does work. One application of this law is the motion of an object in a central force field moving toward a fixed point without reaching the center. A central force is an attractive (negative) force that points from the particle towards the center point whose magnitude only depends on the distance of the object to the center. There are three component energies that explain this process: 1) the kinetic energy of the particle in motion, 2) the attractive potential energy of the central force, and 3) the repulsive centrifugal energy due to angular momentum which prevents the object from reaching the center. The total energy E of the central force motion in physics is given below, where U(r) = potential energy, m = mass, v = velocity, and L = angular momentum¹: $\frac{1}{2}m{v}^2+\left(\frac{L^2}{2m{r}^2}+U\left(r\right)\right)=E$. The effective potential U_eff(r) is defined as the sum of the opposing centrifugal energy with the central force potential energy: $U_{eff}\left(\mathrm{r}\right)=\left(\frac{L^2}{2m{r}^2}+U\left(r\right)\right)$. An alternative form is the following: $U_{eff}\left(\mathrm{r}\right)=\left(\frac{L^2}{2m{r}^2}-\frac{\alpha }{r}\right)$. Kinetic energy can be defined as the difference between the total energy and the effective potential. The effective potential is useful for visualizing orbital mechanics widely used to describe the trajectory of a particle in central force motion. This is because given the angular momentum, one can plot the effective potential and predict stable circular orbits and see how the centrifugal barrier prevents the approaching object from overtaking the central mass [3].

When L2 development is represented as a process in which the learner is drawn to the target language; we can equally attribute learning as a process that involves transformation of energies that are kinetic, potential and centrifugal. The learner and the target language are two gravitating masses separated by a distance r_0, which by extension of the same analogy is the distance between the learner’s position in the learning process relative to the target language (TL). In physics, kinetic energy is the energy of an object headed towards the central force due to its velocity and mass, defined as 1/2mv². Outfitting this algorithm in SLA, the particle is, analogously speaking, the L2 learner approaching the target language (central force) with two properties of aptitude and motivation that are positive in value². Potential energy, on the other hand, is defined as the stored energy of an object due to its position relative to other objects in the system. It is a function of distance r with a boundary condition that the potential energy is zero when the distance between the two objects is at infinity. In SLA, there is an attractive pull of the TL input that draws the learner closer to his/her ultimate attainment in the L2 acquisition process from a distance of nonexistent L2 knowledge, (distance of “infinity”) to complete L2 knowledge of being native-like (distance of “zero”). The role played by input is theorized to act as the potential energy of the system consumed by the kinetic energy (aptitude and motivation) to reach the target language goal. Lastly, the centrifugal energy provides outward force that prevents the object from reaching the center. The potential energy related to the central force is attractive, but if there is angular momentum, a centrifugal barrier arises. With angular momentum, it becomes very difficult to reach the central force because it requires ever faster speed towards the center with greater kinetic energy. This phenomenon is similar to a well-attested observation in SLA that adult L2 learners inevitably reach an end state of ultimate attainment characterized by asymptotic progression towards the TL without ever reaching native-likeness. The repulsive barrier that counteracts kinetic energy (motivation and aptitude) and potential energy (TL input traction) prevents the learner from attaining native-like proficiency. This is defined as the centrifugal energy. In SLA, the source of centrifugal energy is the role played by the typological distance between the TL and the L1 of the learner, similar to the role played by angular momentum in physics.

Based on the mathematic formulae of central force motion in physics and the noted parallel with L2 ultimate attainment in SLA, a mathematical model of L2 ultimate attainment can be outfitted with comparable variables. The conservation of energy in SLA is expressed as the following equation based on the mathematic formulae of central force motion and conservation of energy in physics:

$\in =\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }+\frac{{\mathrm{\eta }}^2}{r^2}-\frac{\mathrm{\rho }}{r}(1)$

Due to space constraints, a comprehensive derivation of ECT-L2A will not be provided here. Interested readers are encouraged to refer to Han et al. [4,5] for a detailed explanation. The three energies from Eq. 1 and their analogous counterparts in SLA are summarized in Table 1 below [4,5].

TABLE 1

TABLE 1. Operationalization of central force energies in SLA.

The kinetic energy is motivation (as a function of distance towards native-likeness) and aptitude. It represents the learners’ inner drive and cognitive resources. The potential energy is the role played by target language input. As the distance towards native-likeness narrows, the role of L2 input grows. Lastly, the centrifugal energy is the typological distance between the L2 learner’s native language and the target language. This represents the barrier that prevents learners from reaching L2 native-likeness. In ECT-L2A, the outcome in question is L2 ultimate attainment that is variable, asymptotic, and bounded, and the predictors are aptitude, motivation, L2 input, and L1-TL deviance. Though there are certainly other important aspects of L2 learning not considered here, these four are theorized as indispensable conditions of L2 development and its end-state product. Aptitude, motivation and L2 input are the essential conditions minimally necessary for any learning to take place. That is, if at least one of these conditions are numerically measured as “zero” or absent in the learner’s initial state, learning cannot possibly proceed regardless of other factors being present, however favorable they may be. Minimally, there must be an ability to learn, a desire to learn, and an opportunity to learn, all of which varies from one individual to another. Still, individual differences in aptitude, motivation and L2 input alone cannot account for variable end-state if all three are allowed to contribute indefinitely to the ultimate outcome. If left unchecked, there is nothing that would seemingly prevent the indefinite growth of the TL until all learners converge at native-likeness regardless of their variable initial conditions–a most unlikely outcome in the case of adult learners based on years of SLA research. The final variable, L1-TL deviance, then acts as the counter, reactive force pushing back against the progress made by the combined effect of aptitude, motivation, and input. In reality, learners do not progress towards the TL indefinitely and the L1-TL deviance effectively functions as the barrier.

The presence of barriers in language learning can be likened to the effect of centrifugal force. Just as centrifugal force acts as a barrier preventing objects from reaching the center, the first language acts as a barrier that hinders adult learners from achieving native-like proficiency. The decline in motivation is specifically related to the pursuit of native-like proficiency. Once learners reach the point of ultimate attainment, there is no longer a strong drive to achieve native-like proficiency. Consequently, while the expansion of language cognition can continue beyond what is commonly shared by native speakers, encompassing areas such as academic discourse, literary/poetic language, or other genre-specific domains and their lexicon, fundamental aspects of language cognition such as pronunciation, fluency, intonation, and spontaneous speech are expected to reach a state of ultimate attainment, where significant progress is no longer made. The initial stages of learning are often characterized by a heightened enthusiasm for the new language and culture, leading to an increase in motivation. However, as learning progresses and reaches a plateau, motivation to attain native-like proficiency tends to diminish.

The role of L1-TL deviance is intended to represent the point of diminishing returns in achieving native-like fluency for adult learners as their proficiency increases. While the impact of L1-TL deviance is evident even for beginners, significant progress towards native-like fluency is observed during the early stages of learning. It is important to note that the effect of L1-TL deviance is not confined to the later stages of acquisition but rather manifests throughout the entire learning process. The concept of L1-TL deviance is invoked to explain the existence of differential gaps among adult L2 learners. It hypothesizes that as the L1-TL deviance increases, the ultimate attainment of adult learners is likely to be further away from native proficiency. For instance, an English learner whose first language is Dutch is generally expected to come closer to sounding like a native English speaker compared to someone whose first language is Japanese (all things being equal). This is because the L1-TL deviance between English and Japanese is greater than the L1-TL deviance between English and Dutch. In short, the role of L1-TL deviance helps explain the variations in ultimate attainment among adult L2 learners based on the magnitude of L1-TL deviance between their native language and the target language.

Given the three variables that contribute positively to learning and one variable that opposes them, the four are theorized to interact and transform under one system. What emerges is an end-state of learning, the L2 ultimate attainment of the adult learner. For the current study, the focus was on aptitude and motivation only. The role of kinetic energy as a combination of aptitude and motivation in second language acquisition under the theory of ECT-L2A deserves a closer look.

Kinetic Energy: Aptitude and Motivation. Aptitude and motivation, as learner-internal factors, have an additive effect on the overall L2 learning outcome. Aptitude is operationalized as a constant Λ, defined as an innate trait of the learner that specializes in learning an additional language other than the native language. Regardless of where the learner stands in the L2 developmental trajectory, their aptitude is not expected to vary but remain constant. Motivation on the other hand, is a function denoted as ζ(r) of the learner’s position (simply denoted as r) in the learning process relative to the target language.

In the context of mechanics, “r” represents the distance between an object and a central body, while “η” (eta) represents the centrifugal force. Admittedly, it may initially seem like a stretch to apply concepts from mechanical physics to language learning. However, this paper aims to employ the principles of a conserved system in physics, where different energies interact and transform to achieve a state of equilibrium. These energies are analogously linked to the key variables of motivation and aptitude in language learning, with the ultimate attainment of learning outcomes representing the state of equilibrium. As proficiency increases, the role of input becomes more prominent since previously inaccessible L2 input becomes accessible due to improved proficiency. Consequently, learners are able to process a greater amount and wider variety of input. For instance, a reader at the graduate level can handle more diverse genres and texts compared to a pre-school reader. Nonetheless, the reason why learners cannot approach a state close to the target language (TL) is due to the conservation of resources in the system. In reality, motivation and aptitude do not contribute indefinitely or linearly to language learning. Otherwise, given sufficient time, all adult learners would converge to native-like proficiency.

The domain of the learner’s position, i.e., the possible range of r is from r = ∼0 to r = ∼∞, defined as the distance from the reference point of the central object, the target language. Value of r = ∼0 means that the distance to the target language is approximately zero³, which is interpreted as a situation where the learner’s ultimate attainment has reached the full measure of the target language at the native-like level. When r = ∼∞ the L2 learner’s level is a true beginner who comes into the central force field with no knowledge of the target language from an “infinite” distance away from the target language norm. Relatedly, motivation ζ(r), is a function of r and it is indicative of the changes in learner’s motivation based on his/her relative position to the target language during the learning process. The sum of two terms aptitude and motivation [Λ + ζ(r)] is equal to the kinetic energy of the learner. Although this form is different from physics, much like the physics formula, kinetic energy of the learner requires both positive values of motivation and aptitude. Intuitively, this means that if either motivation or aptitude (or both) is zero, kinetic energy becomes zero and learning is essentially impossible. From the physics perspective, this is equivalent to the condition that permits the particle to travel when $U_{eff}\left(\mathrm{r}\right)$ < ∈ (see Eq. 2 below), or equivalently when the kinetic energy is positive. In SLA, the kinetic energy is what the individual learner brings to the L2 learning process, and it represents the largest overall variability attributed to L2 learning outcome at the level of the individual. An L2 learner with a higher combination of aptitude and motivation has greater kinetic energy towards the TL. Based on Eq. 1 the effective potential is the sum of potential and centrifugal energy.

$U_{eff}\left(\mathrm{r}\right)=\frac{{\mathrm{\eta }}^2}{r^2}-\frac{\mathrm{\rho }}{r}(2)$

Given that the total energy ε is conserved for each learner in a closed system, higher ∈ means higher levels of ultimate attainment because r can only decrease as far as the total energy ∈ allows. Alternatively, the ultimate attainment of individuals can be derived by solving for r in $\in =\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }+\frac{{\mathrm{\eta }}^2}{r^2}-\frac{\mathrm{\rho }}{r}$. At the point of ultimate attainment (r₀), motivation $\mathrm{\zeta }\left(\mathrm{r}\right)$ becomes zero and solving for r leads to Eq. 3 below [6]:

$r_0=\frac{{2\mathrm{\eta }}^2}{\mathrm{\rho }+\sqrt{{4\mathrm{\epsilon }\mathrm{\eta }}^2+{\mathrm{\rho }}^2}}(3)$

Note that because $\mathrm{\zeta }\left(\mathrm{r}\right)$ = 0, ε = ∈−Λ. Another important point is that the above solution is true when r is equal to r⁻¹ or 1/r. Therefore, Eq. 3 can relate aptitude to attainment without the role of motivation. The equation above also relates attainment as a function of ε which is linked to aptitude as ∈−Λ.

For a true beginner in the absence of L2 input, when learning begins at r = ∼∞, centrifugal energy (η²/r²) and potential energy (−ρ/r) are approximately zero and the only terms left are ζ(r) + Λ. At the onset of learning, the only forces that propel the learner towards the TL are his/her own motivation for learning the TL and FL aptitude. As previously discussed, Λ ≠ 0, and ζ(r) ≠ 0, motivation or aptitude cannot be zero and kinetic energy must be some positive value of aptitude plus motivation. Learning commences when L2 input is present in the environment and r becomes smaller, getting closer to the TL as in ε = ζ(r) + Λ−ρ/r. In L2 acquisition, centrifugal energy exists because η has a positive value. The L2 learner is prevented from reaching native-likeness (r = ∼0) because r will decrease to a value until the kinetic energy of ζ(r) + Λ = ∼0 and learning ceases. As the learner develops L2 competence, motivation ζ(r) (consequently kinetic energy) increases due to the minus value of the traction provided by the input (−ρ/r). Concurrently, the centrifugal energy (η²/r²) slowly starts to build up, until the r² value nears zero, which overtakes the values of all other terms and dominates the equation. At this point, due to the conservation of energy, the kinetic energy decreases, eventually becoming zero, and the system reaches an equilibrium of stable end-state, the ultimate attainment of the learner’s L2. The L2 ultimate attainment is the lowest possible r value due to the conservation of energy.

Most importantly, L2 ultimate attainment of the learner is predicted based on the lower bound of r in the learner’s central force system. This point is called the turning point, where the total energy of the system is equal to its effective potential. At this juncture, the kinetic energy is zero and the rate of learning slows down to zero; effectively, learning reaches its end-state. Mathematically, this happens when:

$U_{eff}\left(\mathrm{r}\right)=\in (4)$

Figure 1 below represents the graph of U_eff with different η values, three different scenarios of the total energy, and corresponding turning points r₀ at which the rate of learning halts and one scenario in which ∈ = 0.

FIGURE 1

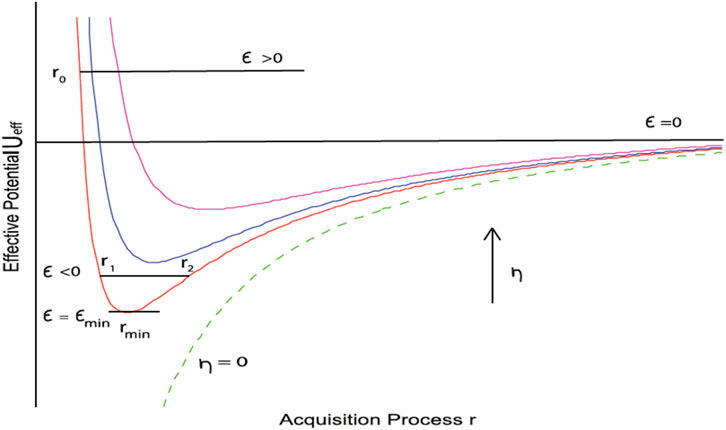
FIGURE 1. Effective potential vs. acquisition process. U_eff with different values of η: Three scenarios of asymptotic attainment in SLA based on the total energy [4,5].

The curved colored lines show U_eff under four different values of η. The dotted green line is for when η = 0 (L1 acquisition) and the acquisition process r approaches zero as U_eff approaches infinity. An increase in η causes the U_eff curve to flatten out more and the turning point r₀ (where the rate of acquisition process r becomes zero) occurs at an earlier point along r. This means that an increase in L1-TL deviance leads to an L2 ultimate attainment that is farther away from the TL native-norm. The total energy is positive (∈ > 0). For vast majority of adult L2 acquisition, the kinetic energy is positive and learning starts from r = ∼∞. The traction of the input increases the learner’s kinetic energy as the learner progresses towards the TL until the learner’s kinetic energy depletes due to the centrifugal force of the L1 and learning slows to a halt. Depending on η, ζ(r), and Λ, learning becomes asymptotic at different points in the acquisition process, eventually coming to an end-state at r₀.

In summary, ECT-L2A can be interpreted, inter alia, to have the following implications regarding language acquisition:

(1) Kinetic energy (aptitude + motivation) must be present (positive) under the target linguistic environment for language learning (either L1 or L2) to take place. Aptitude, motivation, and input are necessary and sufficient conditions that contribute positively to language acquisition and its ultimate outcome.

(2) In L2 acquisition, L1-TL deviance prevents aptitude, motivation, and language input from contributing indefinitely to L2 attainment by decelerating the rate of learning until it reaches a plateau. In general, greater typological distance leads to greater non-conformity to the target language.

(3) In L2 acquisition, kinetic energy increases with increase in proficiency due to the rise in the traction of the input until it reaches a maximum value⁴. At this point the learner must “pay” the linguistic barrier created by the L1-TL deviance which penalizes the kinetic energy until the rate of learning slows down, effectively rendering the learner’s aptitude and motivation to be ineffective.

(4) Most optimal learning condition occurs when motivation and aptitude are high, L1-TL deviance is low, and L2 input is optimal. Under these parameters the rate of learning is fast and the learner’s ultimate attainment is closest to native-likeness. The opposite conditions represent the lowest level of L2 ultimate attainment and the slowest rate of learning for an individual learner: motivation and aptitude are low, L1-TL deviance is high, and L2 input is poor.

Limiting the scope to motivation and aptitude, the following predictions were made about these two constructs and their effect on L2 success: 1) ECT-L2A predicts that the motivation of a true beginner with no knowledge of the TL increases as the learner interacts with the TL input. However, as the learner’s proficiency increases, the typological distance between the TL and L1 acts as a centrifugal barrier and further gains towards native-like competence becomes asymptotic. This in turn reduces motivation to a level that is lower than when the learner was a true beginner. 2) Aptitude, as a constant, is expected to remain the same throughout the learning process at the individual level; however, the effect of aptitude will wane as the learner approaches native-likeness due to the centrifugal effect of L1-TL deviance. 3) As for the kinetic energy, the combined value of motivation and aptitude is expected to contribute positively but decrease with increase in L2 proficiency.

Research questions and hypotheses

The research questions in the present study were motivated by the predictions made by ECT-L2A with regards to aptitude and motivation. The primary aim of this study was to test these hypotheses.

Hypothesis 1. (H1): The participants in this study will show a positive correlation between language proficiency and aptitude since high values of Λ will lead to smaller r and Λ remains constant at the individual level. However, the variability in language proficiency explained by aptitude will decrease as language proficiency increases because as r gets smaller, the influence of aptitude Λ is overshadowed by the role played by L1-T1 deviance.

Hypothesis 2. (H2): ETC-L2A model can be used to explain both global measure of proficiency as the sum of all items as well as local measure of each individual grammar rule.

Hypothesis 3. (H3): Overall, the participants in this study will show a negative correlation between performance on language proficiency and motivation since motivation ζ(r) diminishes as r → 0. However, motivation may increase and show positive correlation for beginners due to the effect of potential energy $-\frac{\mathrm{\rho }}{\mathrm{r}}$ on the conservation of total energy. In addition, the variability in language proficiency explained by motivation will decrease as language proficiency increases. This is because as r gets smaller, the influence of ζ(r) is overshadowed by the role played by L1-TL deviance.

Hypothesis 4. (H4): Different components of motivation will show different correlations with language proficiency; not all structures are equally sensitive to the effect of motivation.

Hypothesis 5. (H5): The combined effect of motivation and aptitude will have a positive relationship with language proficiency, per ζ(r) + Λ. However, with increasing language proficiency, ζ(r) + Λ (kinetic energy) will decrease due to the decrease in ζ(r) (motivation) caused by L1-TL deviance.

Participants

A total of four hundred and one (N = 401) volunteers signed the informed consent to participate in the study. Two hundred and three (N = 203) adult English learners (L1 Spanish) were selected based on specific selection criteria. There were three inclusion criteria for selection based on the study’s domain of generalizability. First, English was the participants’ second language because the domain to generalize was for second language acquisition. Second, the participants’ first language was Spanish because the study aimed to control for the effect of the participants’ first language by only sampling from the same L1 population. The third desideratum was age of arrival (AOA) in United States after twelve in order to eliminate the risk of confounding age effect (critical period hypothesis) with performance on GJT. The average age was 30 years (SD = 8.28); average age of arrival was 26.24 years (SD = 8.17) and the average length of studying English was 3.366 years (SD = 4.22).

Instruments

Measure of aptitude

LLAMA is a free aptitude test that is available to researchers, and its popularity has been increasing in recent years due to its accessibility [7]. The LLAMA test is comprised of four subtests (called LLAMA_B, LLAMA_D LLAMA_E and LLAMA_F) that measure phonetic coding ability, grammar sensitivity, rote learning ability and inductive learning ability. For the current study, LLAMA_F was used to measure language analytic ability of the participants [31]. First, the examinees were given a series of pictures with a short sentence in an artificial language that described each picture. There were 20 images in total and participants had 15 s to study the unknown language that described each image for a total of 5 min. Then they were asked to match new picture prompts with sentences in the artificial language that correctly described them. The participants had unlimited time to finish the test but their response time for each item was recorded.

Measure of motivation

Gardner’s Attitude/Motivation Test Battery (AMTB) based on Gardner’s socio-educational model was used to measure the participants’ motivation [8]. Gardner’s model predicts that by and large motivation is positively correlated with L2 achievement, which has been supported by empirical studies. For instance, Gardner’s AMTB has shown overall correlation from 0.08 (for instrumental orientation and objective measures of achievement) to 0.39 (between motivation and self-ratings of achievement) based on a meta-analysis involving 10,489 participants [9]. AMTB has also been thoroughly validated for its content and construct (both convergent and discriminant) as well as internal reliability with the reported median Cronbach alpha coefficient of 0.85 (for a full report see [10]).

The present study employed sections of AMTB that measured three major constructs of motivation, integrativeness, and instrumentality. They were further divided into six components of 1) interest in foreign language, 2) motivational intensity, 3) attitudes toward learning, 4) integrative orientation, 5) desire to learn English, and 6) instrumental orientation. Each item asked the participants to rate how much they agreed with a statement that expressed various opinions about learning English. The items were rated on a 6-point Likert scale that ranged from “strongly disagree” to “strongly agree.”

Measure of L2 attainment

A grammaticality judgement test (GJT) was used to measure the participants’ morphosyntactic⁵ knowledge of English. Specifically, DeKeyser [11] GJT was used which was adapted from [12] study. The GJT was comprised of 11 major categories of morphology and syntax: 1) Past tense; 2) Plurality; 3) Third-person singular; 4) Present progressive; 5) Determiners; 6) Pronominalization; 7) Yes-no questions; 8) Wh-questions; 9) Word order; 10) Particle movement; 11) Subcategorization. There were exactly 100 grammatical and 100 ungrammatical items. In the original study, DeKeyser [11] reported reliability coefficient of 0.91 for grammatical items and 0.97 for ungrammatical items on his instrument. Sentences were constructed with high frequency words of one or two syllables in length, and only one violation of rule type was tested in ungrammatical/grammatical pairs. All items were randomized in order to ensure that they did not appear consecutively as a paired set of the same rule type. Scoring was done dichotomously with a point value of 0 for the wrong answer and 1 for the correct answer. The raw score for each participant was calculated as the total number of correctly marked items. The maximum total point possible was 200. A background survey was used to obtain demographic information. The aptitude test, motivation survey, and background questionnaire were all translated to Spanish. Directions for each instrument was also written in Spanish.

Scoring

AMTB was scored as a tally of its components of attitude and motivation by adding the Likert scale ratings for each item. Numerically, 6 points were assigned to “strongly agree”; 5 for “moderately agree”; 4 for “slightly agree”; 3 for “slightly disagree”; 2 for “moderately disagree”; and 1 for “strongly disagree” for positively worded items. For negatively worded items, the numeric scoring was reserved. Daily English use was likewise scored as 6; “always” as 5; “very frequently” as 4; “sometimes” as 3; “rarely” as 2; “very rarely”, and “never” as 1. According to AMTB, motivation is defined by three components of motivational intensity (10 items), desire to learn the language (10 items) and attitude towards learning (10 items). Therefore, motivation was estimated by aggregating the Likert rating scores of these 30 items.

For GJT and LLAMA_F, speed (response time) and accuracy were combined into a single holistic score. This was done to account for the participants’ knowledge and processing speed. This was accomplished by calculating Rate Correct Score or RCS, defined as the following:

$RCS=\frac{c}{\sum RT}(5)$

In the formula above, c is the number of correct responses scored dichotomously as 0 or 1 for each item on the test. In the case of GJT, a single tally was recorded with a possible range of 0–200. The denominator is the sum of all reaction times (RT) in the set of trials under consideration [13]. By using RCS in the study, the two dimensions of speed and accuracy were given equal weight. RCS, therefore, sheds light on both the level of morphosyntactic knowledge and the retrieval speed or automaticity. Similarly, when aptitude was measured by RCS, both the processing speed and the ability to infer grammatical rules were given equal importance.

General method of analysis

To test the correlational relationship between GJT and aptitude and between GJT and motivation, three different types of correlations were analyzed. First, Pearson product-moment correlation (PPMC), which measures the direction and strength of linear relationship between two variables measured on interval or ratio scale, was performed on GJT with LLAMA_F then GJT with motivation. Next, a partial correlation was performed controlling for the effect of age of arrival and length of English study. A partial correlation removes the confounding effect of a set of controlling random variables [14]. Lastly, according to Bandalos [15] the correlational relationship between two variables will be attenuated to the extent that both instruments are not measuring reliably. Because correlation between two scores is restricted by their reliabilities, correction for attenuation (or dis-attenuated correlation) was used to estimates how well the given instrument would predict the criterion score despite having less than perfect reliability [15]. Based on the reliabilities obtained from the current study, dis-attenuated correlations were calculated for aptitude, motivation and GJT.

The variability in GJT explained by independent variables of aptitude and motivation was investigated by computing R² (coefficient of determination)—the proportion of variance in the dependent variable (GJT) that is predicted or explained by the independent variable. This was accomplished by noting the changes in variability and R² among three major proficiency groups: first quartile group (lowest 25% on GJT) interquartile group (middle 50% on GJT) and fourth quartile group (the highest 25%) based on GJT scores labeled as low, intermediate and advanced, respectively. For the test of Hypothesis 3 and 6 in which componential relationships are examined, correlation between GJT and 11 rule types were calculated and compared for analysis, followed by correlations between GJT and motivation components according to AMTB.

Finally, for the test of Hypothesis 5, aptitude and motivation scores were summed to create an estimate of the participants’ kinetic energy. Adding two different variables (aptitude and motivation) measured in different scales requires feature scaling in which both independent variables are on equivalent scales [16]. In the current study, normalization was chosen instead of standardization because standardization or mean-centering results in negative values. Motivation, aptitude and attainment values cannot be negative in ECT-L2A formula. A min-max normalization rescaled the data to values between 0 and 1. Each value was subtracted from its minimum then divided by the difference of maximum and minimum scores. Aptitude and motivation scores were normalized before the two values were added to create a new variable, kinetic energy. Kinetic energy was subsequently correlated with GJT, and a plot of kinetic energy by GJT was produced.

One major drawback to correlational analysis is its underlying assumption of linearity. According to ECT-L2A the relationship between aptitude, motivation and attainment follow non-linear curves as expressed by $\in =\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }+\frac{{\mathrm{\eta }}^2}{r^2}-\frac{\mathrm{\rho }}{r}$. Attainment is described by its asymptotic curvilinear relationship with individual difference variables. To directly test the validity of ECT-L2A formula, a regression model expressed as Eq. 1 was used to fit the data. However, modeling ECT-L2A presents a difficult challenge using classical regression methods because the asymptotic relationships are vertical (parallel to the y-axis) as can be seen in Figure 5 when attainment is on the x-axis as r, the distance away from nativelikeness. Instead of using linear regression with ordinary least squares (OLS) method, orthogonal distance regression via total least squares (TLS) was used to fit the hypothesized models to the data. The method is based on finding points on fitted curve orthogonal to the data by minimizing the Euclidean distance to each point (x_i, y_i) on the line. It uses total least-squares to account for errors in both the response variable and the explanatory variables [17].

Results

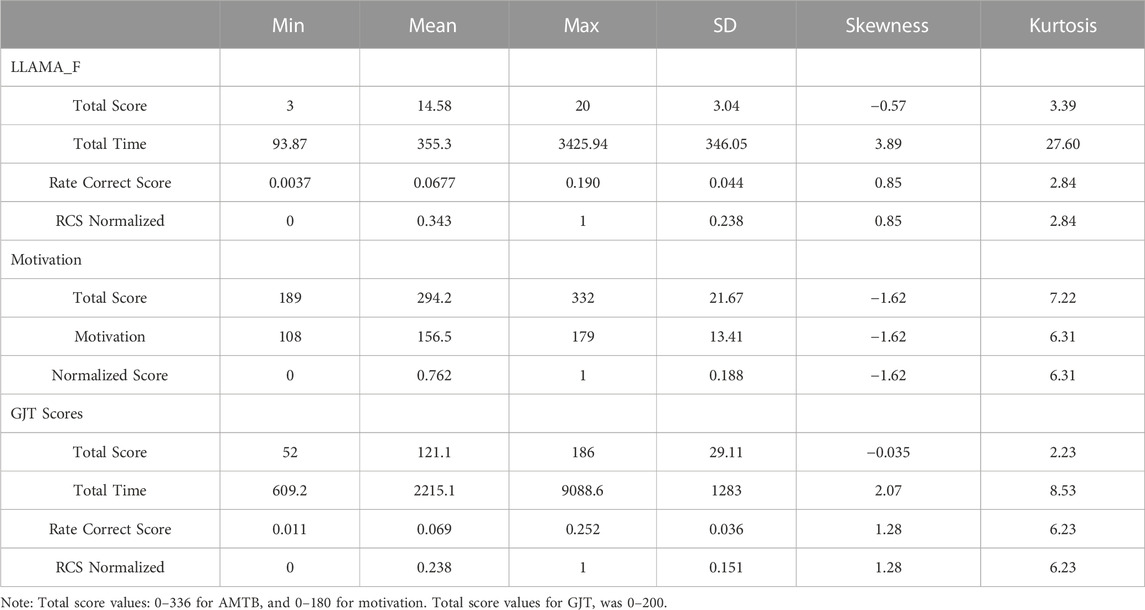
The mean raw score for LLAMA_F was 14.58 which was equivalent to getting 73% correct out of 20 items. The standard deviation was rather large with 3, and on average, it took 17 s to answer each question. Few participants were able to get the perfect score of 20 which limited the upper range with a possible ceiling effect. When the raw score was adjusted for time (RCS), any possibility of ceiling effect was eliminated (Table 2). The total scores for AMTB and motivation showed that participants were highly motivated to learn English, each receiving 88% and 87% of the total points respectively. For comparison, an apathetic response (neutral for all items) would have resulted in a score of 168 for AMTB and 90 for motivation. Any scores below those values would have indicated aversion towards learning English. The minimum values found in the data showed that even for the lowest scoring participant (189 for AMTB and 108 for motivation), they were still positively oriented in motivation and attitude towards learning English (Table 2).

TABLE 2

TABLE 2. Descriptive statistics.

The mean raw score on GJT for all 203 participants was 121.1 or about 60.5%. This was better than the expected value of guessing on all items with a 50% probability. However, not one participant was able to answer all items correctly or perform at the native-like standard of 97%. According to Johnson and Newport’s [12] study, native speakers scored a mean of 97% which would have been equivalent to a score of 195 or better on the instrument. The highest score was 186 (Table 2). This meant that no one was proficient enough to be identified as having native-like morphosyntactic knowledge.

Aptitude and attainment

Hypothesis 1

H1. The participants will show a positive correlation between performance on GJT and aptitude; however, variability in GJT explained by aptitude will decrease as GJT increases. This is because as r gets smaller, the influence of aptitude Λ is overshadowed by the role played by L1-T1 deviance.

The positive relationship between aptitude and attainment was corroborated based on correlation analysis. For PPMC, there was a positive correlation between the two variables, r = 0.498, p = 3.65e−14, R² = 0.249. Partial correlation showed positive relationship r = 0.506, p = 1.66e−14, R² = 0.256 as well as dis-attenuated correlation r = 0.645, R² = 0.416. The correlation between aptitude and attainment was estimated to range from 0.498 to 0.645, highly significant and accounting for variance in attainment by 25–41 percent. Individuals with higher grammatical inferencing abilities or aptitude, performed better at grammaticality judgment tests (L2 attainment), even after age of arrival and length of residence were taken into consideration for adult learners past the age of puberty. Accounting for these factors and the instrument’s reliability increased the overall strength of the relationship between aptitude and achievement as expected.

What is lost in a correlation analysis is a nuanced understanding on the specific rate of increase in attainment vis-à-vis aptitude, afforded by the ECT-L2A equation. ECT-L2A predicts a square root relationship $\sqrt{\mathrm{\Lambda }}$—a specific kind of non-linear relationship rather than linear–with attainment (GJT_RCS) when attainment is scaled in the positive direction. This claim was tested by fitting an orthogonal regression model to $\mathrm{\Lambda }={\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)}^2$. In orthogonal regression form this is simply: y = b₁x₁, where the independent variable is GJT² and the outcome variable is LLAMA_F. The results of orthogonal regression model revealed a satisfactory fit, (β = 4.403, p < 0.001, SE = 0.578). Graphically, the fit of ECT-L2A predicted outcome was overlaid with GJT vs. aptitude data (Figure 2).

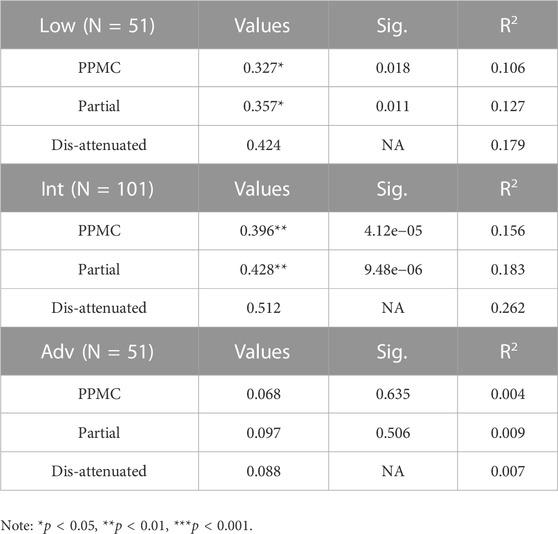
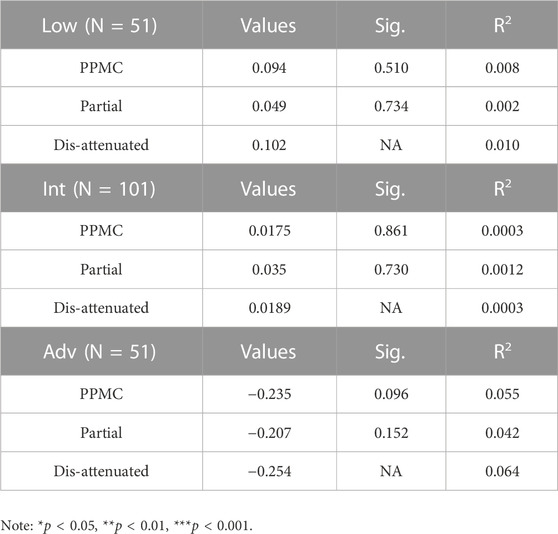
Correlation analyses between aptitude and attainment split by first quartile group (low proficiency), interquartile group (intermediate proficiency), and fourth quartile (advanced) supported the hypothesis. Partial correlation controlled for the effects of age of arrival and length of residence in United States, while dis-attenuated correlation adjusted for the less than perfect reliability of each instrument. The strength of the correlational relationship was significant and strong for the low and intermediate groups but dropped below 0.1 and became non-significant for the advanced group (Table 3). Interestingly, the correlation and its related R² increased from low to intermediate then dropped for the advanced group. The initial increase in correlation followed by a steep decline can be explained under the ECT-L2A framework. From a longitudinal perspective, Equation 1 implies that as attainment increases, deviation energy overwhelms all other energies including kinetic in which aptitude is a component. As the learner gains proficiency in second language, the role of aptitude changes relative to effective potential $\frac{{\mathrm{\eta }}^2}{r^2}-\frac{\mathrm{\rho }}{r}$. In fact, the role of aptitude increases (note the negative sign in front of potential) but starts to drastically decrease as the centrifugal overtakes all other energies. Because the total energy is constant, the change in aptitude’s influence over an individual must be equal but opposite in sign to the effective potential or approximately $\frac{{-\mathrm{\eta }}^2}{r^2}+\frac{\mathrm{\rho }}{r}$.

FIGURE 2

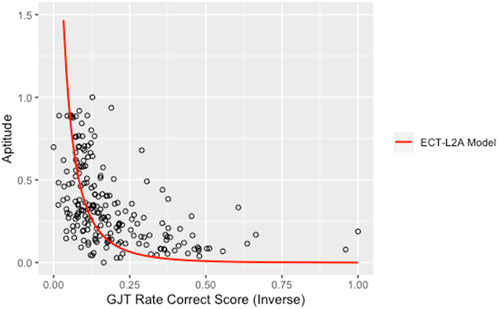
FIGURE 2. Regression Model of Aptitude and GJT_RCS. Note: The figure on the right is the same model with GJT_RCS with inverse axis in which the score increases from 1 (min) to 0 (max).

TABLE 3

TABLE 3. Aptitude correlations by proficiency.

Hypothesis 2

H2. ETC-L2A model can be used to explain both global measure of proficiency as the sum of all items as well as local measure of each individual grammar rule.

Hypothesis 2 was first tested by correlating 11 rule types (each as RCS) with LLAMA_F_RCS.

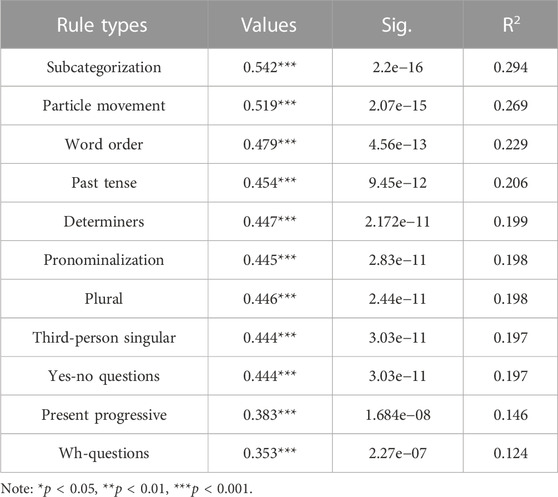
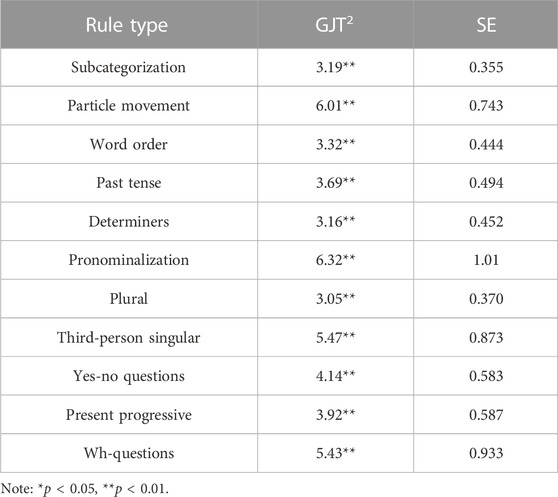
For the test of Hypothesis 3, more salient features of morphosyntax such as pronoun gender, subject-verb inversion and do-support were expected to show greater sensitivity with aptitude. The strongest relationships were found for subcategorization (r = 0.542), participle movement (r = 0.519) and word order (r = 0.479). Although the strength of the correlations varied, all 11 rule types were statistically significant (Table 4).

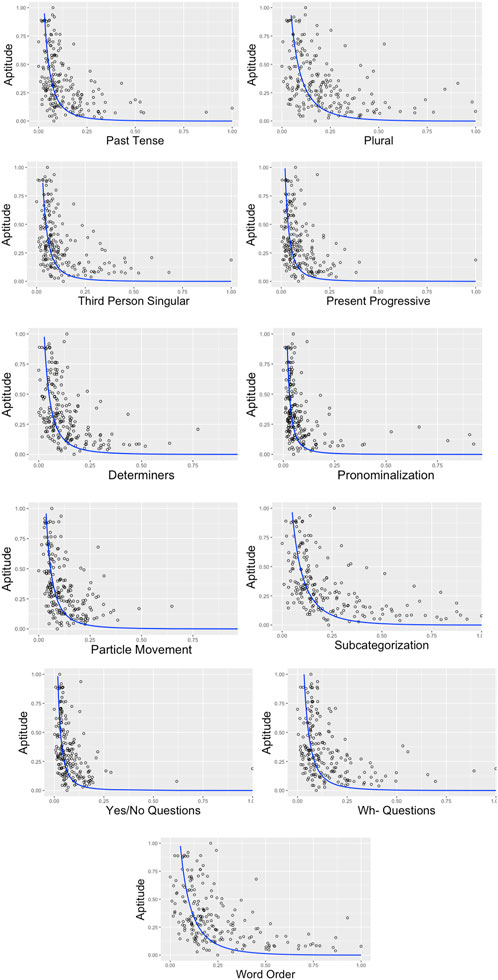
Next, the model used to fit the composite GJT score with aptitude was tested on each grammar rule. First aptitude scores were plotted alongside each rule type. This was followed by fitting $\mathrm{\Lambda }={\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}}\right)}^2$ for all rule types separately. Figure 3 below showed that for all 11 rules, an upward curve in the direction of r → 0 was observed.

Figure 3 shows that the square of the score by rule type appears to be a good approximation of the pattern exhibited by the scatterplot. This was confirmed by the orthogonal regression results in which for all 11 rule types, the betas of GJT² were positive and significant at 0.01 level (Table 5). The blue lines in Figure 3 represent the orthogonal regression fit, $\mathrm{\Lambda }={\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}}\right)}^2$.

TABLE 4

TABLE 4. Correlations between rule types and aptitude.

FIGURE 3

FIGURE 3. Aptitude by eleven rule types.

TABLE 5

TABLE 5. Regression fit for $\mathrm{\Lambda }={\left({\mathbf{G}\mathbf{J}\mathbf{T}}_{\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e}\mathbf{T}\mathbf{y}\mathbf{p}\mathbf{e}}\right)}^{\mathbf{2}}$

Motivation and attainment

Hypothesis 3

H3. Overall, the participants in this study will show a negative correlation between performance on GJT and motivation since the influence of motivation ζ(r) diminishes as r → 0. However, motivation may increase and show positive correlation for beginners because of potential energy $-\frac{\rho }{r}$ on the conservation of total energy.

As predicted, the correlation between motivation and attainment was negative and significant at 0.05 level: for PPMC, there was a negative correlation, r = −0.173, p = 0.013, R² = 0.30. Partial correlation showed negative relationship r = −0.163, p = 0.020, R² = 0.26 as well as dis-attenuated correlation r = −0.187, R² = 0.035, though its effect and proportion of variance explained were rather small compared to aptitude. While aptitude is theorized to be constant for the individual learner, motivation is a function of r and therefore varies dependent on their distance to nativelikeness. Equation 1 was transformed into an intrinsically linear regression model by substituting GJT_RCS for r⁻¹ and equating motivation with the negative of effective potential: $\mathrm{\zeta }\left(\mathrm{r}\right)=-\frac{{\mathrm{\eta }}^2}{r^2}+\frac{\mathrm{\rho }}{r}$.

$\mathrm{\zeta }\left(\mathrm{r}\right)=-{\mathrm{\eta }}^2{\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)}^2+\mathrm{\rho }\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)(6)$

In this model, the independent variable was GJT_RCS (normalized) and the outcome variable was motivation (normalized). The overlay of the orthogonal regression model predicted by ECT-L2A can be seen in Figure 4 below. Motivation increased as proficiency (GJT_RCS inverse) progressed from low (normalized score of 1) to about 0.25. Afterwards, there was a significant vertical drop as the score neared zero.

The red curve is the overlay of the predicted outcome. It shows that the model underestimates motivation for low proficiency learners. The curve does not appear to fit as well as the aptitude model (Figure 2); nonetheless, the model’s betas have the correct sign per Equation 6 (negative for GJT² and positive for GJT) and they are all significant at 0.001 level (GJT²: β = −10.498, p < 0.001, SE = 2.808; GJT: β = 6.865, p < 0.001, SE = 0.865). Lastly, ECT-L2A predicts increase in motivation due to the rise of potential energy $-\frac{\mathrm{\rho }}{r}$ which, as r → 0, decreases due to the overwhelming influence of L1 to target language distance in $\frac{{\mathrm{\eta }}^2}{r^2}$.

As r → 0 from ∞, the effective potential decreases while motivation increases to maintain the conservation of energy. However, at the minimum point, the curve changes, and the effective potential increases (here $\frac{{\mathrm{\eta }}^2}{r^2}$ takes over), at which point motivation must decrease until learning reaches an asymptote. Figure 4 show that as r moves towards 0, there is a slight increase⁶ in the slope until it reaches a peak, followed by a steep (almost vertical) decline in slope. Correlation analyses between motivation and attainment split by GJT proficiency supported these predictions.

In Table 6, the correlation between motivation and GJT was positive for the low and intermediate proficiency group but became negative for the advanced proficiency group. The findings support the positive relationship between motivation and attainment in the beginning followed by decrease and negative relationship afterwards. However, in all three groups, the correlations were not significant.

FIGURE 4

FIGURE 4. ECT-L2A regression model of motivation and GJT_RCS (Inverse). Note: GJT_RCS (Inverse) means that the score increases from 1 (min) to 0 (max).

TABLE 6

TABLE 6. Motivation correlations by proficiency.

Hypothesis 4

H4. Different components of motivation will show different correlations with GJT; not all motivation types are equally sensitive to the learning outcome.

Hypothesis 4 was tested by correlating each component of AMTB with GJT_RCS.

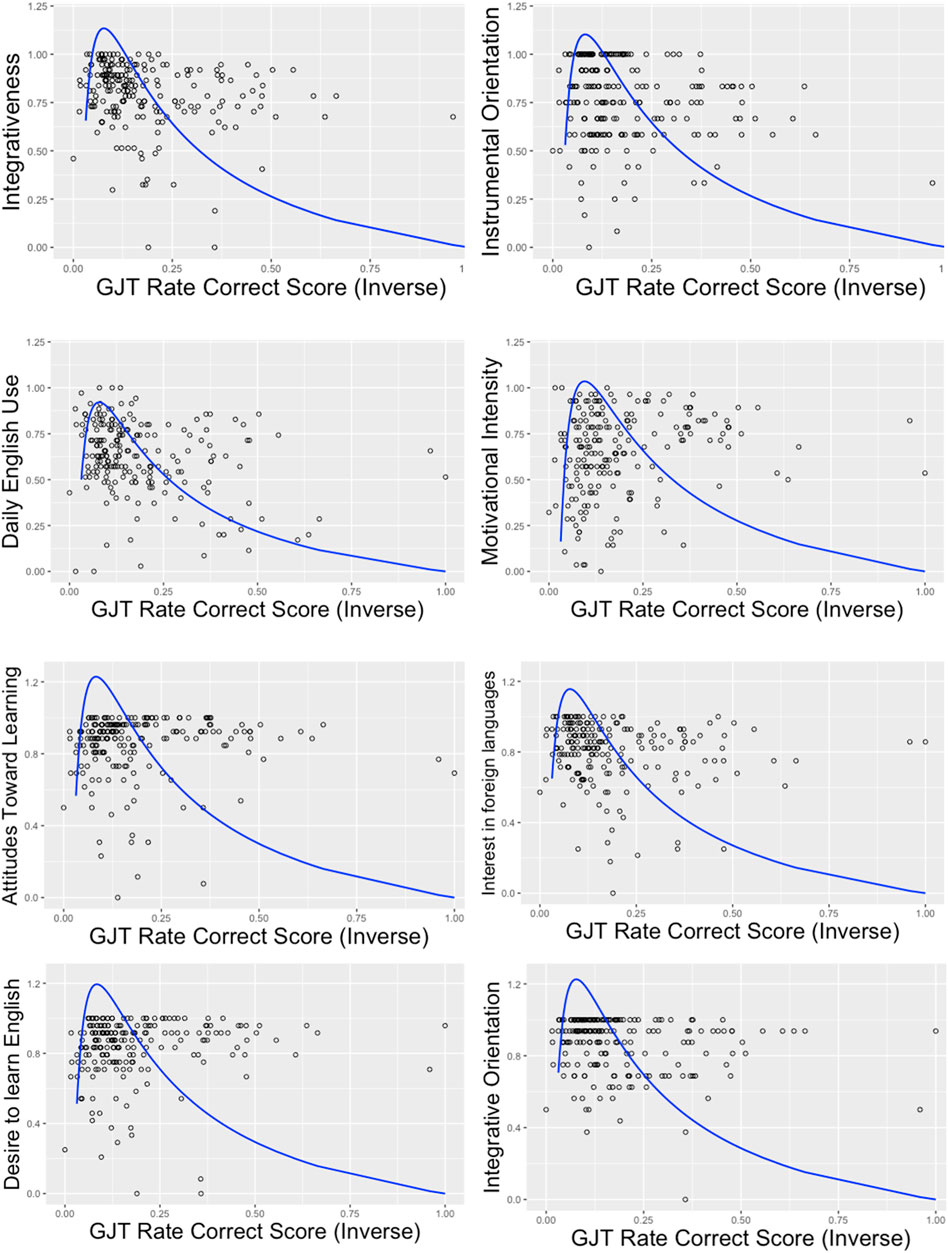
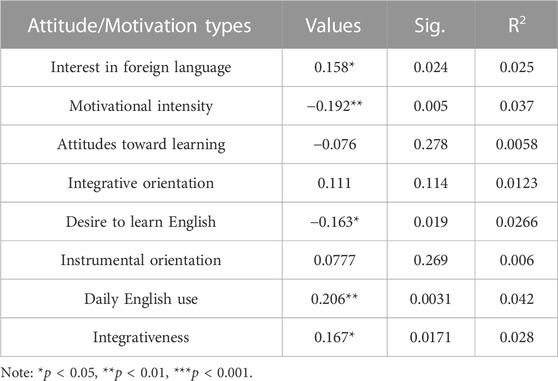
The correlation analysis revealed a mix of positive, negative, significant, and non-significant relationships. Certain aspects of motivation and attitude such as interest in foreign language, integrative orientation, instrumental orientation, daily English use, and integrativeness were found to be positively correlated with GJT. Others (motivational intensity, attitudes towards learning, and desire to learn English) were negatively correlated with attainment. Furthermore, about half were statistically significant: interest in foreign language, motivational intensity, desire to learn English, daily English use, and integrativeness (Table 7). To test whether the same relationship for GJT and motivation was also found for each motivation and attitude component, AMTB components were plotted alongside the inverse of GJT_RCS. This was followed by fitting $\mathrm{\zeta }\left(\mathrm{r}\right)=-{\mathrm{\eta }}^2{\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)}^2+\mathrm{\rho }\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)$ for each motivation/attitude component separately, in place of the composite $\mathrm{\zeta }\left(\mathrm{r}\right)$. Figure 5 below shows that for all 8 components of AMTB, identical patterns emerged as r → 0: different components of AMTB followed the curve of $-\frac{{\mathrm{\eta }}^2}{r^2}+\frac{\mathrm{\rho }}{r}$ indicated by the blue line.

The effective potential (Equation 7) does appear to be a good approximation of the patterns exhibited by the scatterplot, although not as well as the fit between aptitude and attainment (Figure 5). For all components of motivation and attitude, the model’s betas had the correct sign per Equation 6 (negative for GJT² and positive for GJT) and they were all significant at 0.01 level (Table 8).

FIGURE 5

FIGURE 5. Motivation by eight attitude/motivation types.

TABLE 7

TABLE 7. Correlations between attitude/motivation types and GJT.

TABLE 8

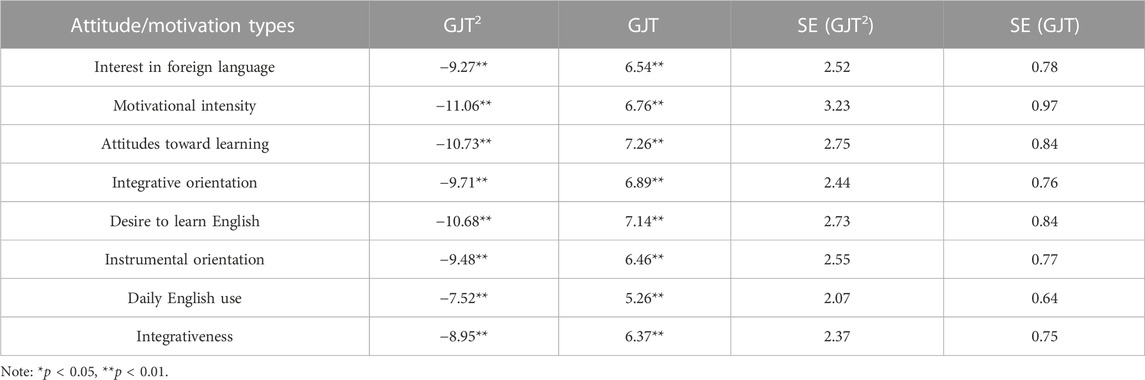
TABLE 8. Regression fit for Equation 7 by attitude/motivation types.

Kinetic energy and attainment

H5. The combined effect of motivation and aptitude will have a positive correlation with GJT, per ζ(r) + Λ. However, with increasing GJT, ζ(r) + Λ will decrease due to the decrease in ζ(r) caused by L1-TL deviance.

The correlation between the sum of aptitude and motivation with attainment was estimated to range from 0.306 to 0.396 (dependent on the type of correlation), highly significant and accounting for variance in attainment from 9 to 16 percent. For PPMC, there was a positive correlation, r = 0.306, p = 8.65e−06, R² = 0.093. Partial correlation showed positive relationship r = 0.296, p = 1.88e−05, R² = 0.088 as well as dis-attenuated correlation r = 0.396, R² = 0.157. In general, individuals with higher grammatical inferencing abilities or aptitude plus motivation for second language performed better on grammaticality judgment tests (L2 attainment), even after age of arrival and length of study were taken into consideration.

Like motivation, the curve of change represented by the effective potential is the same as the change expressed by $\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }$ but in the opposite direction due to the negative sign of effective potential. This means that changes in kinetic energy should resemble effective potential reflected by the x-axis (Figure 1). Because kinetic energy is the sum of motivation and aptitude, and aptitude is a constant whereas motivation is a function with respect to r, the overall change and effectiveness of kinetic energy in learning outcome should resemble the patterns exhibited by motivation. Alternatively, if the relationship between kinetic and attainment as described by ECT-L2A is valid, the data should reflect the curve of Figure 1 flipped upside down around the x-axis. This can be shown by solving for the kinetic energy in Equation 1: $\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }=-\frac{{\mathrm{\eta }}^2}{r^2}+\frac{\mathrm{\rho }}{r}+\in$. Kinetic energy is essentially the negative of the effective potential $-\left(\frac{{\mathrm{\eta }}^2}{r^2}-\frac{\mathrm{\rho }}{r}\right)$ plus a constant ($\in$). Figure 6 below is the scatterplot of kinetic energy (sum of aptitude and motivation after normalization) and GJT (normalized inverse). The scatterplot in Figure 6 showed promising resemblance to the theoretical model shown in Figure 1, rotated around the x-axis. To formally test whether the scatterplot fit the ECT-L2A equation, $\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }=-\frac{{\mathrm{\eta }}^2}{r^2}+\frac{\mathrm{\rho }}{r}+\in$ was transformed to reflect an intrinsically linear regression model by substituting GJT_RCS for r⁻¹ and solving for the kinetic energy which is $\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }$.

$\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }=-{\mathrm{\eta }}^2{\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)}^2+\mathrm{\rho }\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)+\in (7)$

Once again this allowed the above equation to be stated in a regression form, y = b₁x₁ + b₂x₂ + c, where the independent variable was GJT and the outcome variable was the sum of motivation and aptitude, normalized. Equation 7 was subsequently fitted with the data using orthogonal regression. The visual fit of the model can be seen in Figure 6.

The orthogonal regression model based on ECT-L2A (red curve) does appear to support the model and provide a reasonable fit of the curve found in the scatterplot (Figure 6). The orthogonal regression showed satisfactory fit (GJT²: β = −6.051, p < 0.001, SE = 1.677; GJT: β = 4.366, p < 0.001, SE = 0.520). Betas for GJT_RCS squared and GJT_RCS were both significant at 0.001 level. The negative sign in front of GJT² beta and the positive sign for GJT beta also confirmed Eq. 7 in which the second-order term is negative and the first-order term is positive.

Although kinetic energy is generally expected to have a positive correlation with attainment, kinetic energy is also expected to decrease in the process due to the decrease in motivation as r approaches zero. Correlation analyses between kinetic energy and attainment split by first quartile group (low proficiency), interquartile group (intermediate proficiency), and fourth quartile (advanced) of GJT scores supported this prediction (Table 9).

The strength of the correlational relationship was significant and strong for the low and intermediate groups but became negative and non-significant for the advanced group (Table 9). R-squared consistently decreased from low to advanced group. From a longitudinal perspective, Equation 1 implies that as attainment increases, deviation energy overwhelms all other energies including kinetic energy. As the learner gains proficiency in their second language, the role of aptitude and motivation changes relative to the effective potential $\frac{{\mathrm{\eta }}^2}{r^2}-\frac{\mathrm{\rho }}{r}$. Because the total energy is constant, the change in kinetic energy’s influence over an individual must be equal but opposite in sign of the effective potential or approximately $\frac{{-\mathrm{\eta }}^2}{r^2}+\frac{\mathrm{\rho }}{r}$. In other words, as the effective potential changes, the role of kinetic energy must also change correspondingly but in the opposite direction in order to maintain the conservation of the total energy.

FIGURE 6

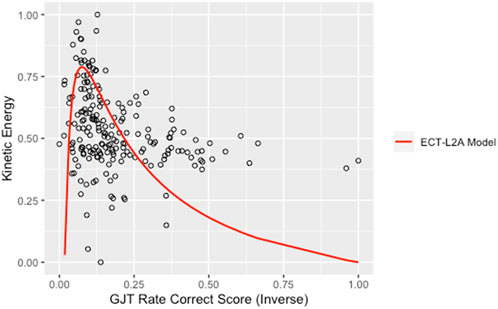
FIGURE 6. ECT-L2A Model Fit of Kinetic Energy vs. GJT_RCS (Inverse). Note: GJT_RCS (Inverse) means that the score increases from 1 (min) to 0 (max).

TABLE 9

TABLE 9. Kinetic energy correlations by proficiency.

Discussion

Relationship between aptitude and attainment

In the current study, Hypothesis 1 posited that the correlation between performance on GJT and aptitude would be positive since high values of Λ lead to smaller r but Λ remains constant at the individual level. To reiterate, language aptitude was indeed positively correlated with second language attainment. At face value, this is not only intuitively plausible, but for all intents and purposes, a necessary outcome for aptitude (or measures thereof) to have construct validity. Aptitude is defined as an ability or a set of abilities that predicts faster and better learning outcomes relative to those who have less. A positive correlation, therefore, is not surprising but expected. Yet, what has been lacking in the past research is the specificity of the type of positive relationship expected between aptitude and attainment. A positive correlation between two covariates implies an underlying assumption that the relationship is strictly linear and indefinite. In contrast, while ECT-L2A likewise predicts a positive association between aptitude and attainment, the relationship is described by Eq. 1 to be curvilinear and asymptotic.

Energy conservation theory from a longitudinal perspective predicted that the variability in GJT explained by aptitude would decrease as GJT increases because as r gets smaller, the influence of aptitude Λ is overshadowed by the role played by L1-TL deviance. In the current study, the asymptotic relationship and the subsequent decrease in variance explained by aptitude gave support to this hypothesis. And beyond what was reported in the previous chapter, the role of aptitude diminishing with increase in proficiency warrants further discussion. In a meta-analysis on aptitude by Li [18], it was reported that aptitude was only predicative in the initial stages of L2 grammar acquisition and less so during the latter stages of learning. This was assumed to be associated with explicit learning conditions during the initial stages which later yields to implicit learning in advanced stages [18]. Regardless of whether implicit or explicit learning is implicated, ECT-L2A argues that aptitude’s influence on learning outcome is overwhelmed by the centrifugal effect of the L1 to TL deviance. This does not suggest that as learning progresses, one’s aptitude attenuates and weakens. What Eq. 1 implies is that the distance traversed by the learner’s journey towards nativelikeness (the r term) is significantly shorter when the learner’s proficiency is advanced compared to when they were beginners. It is much more difficult to make significant improvements as an advanced user than it is to make the same amount of improvement as a beginner. For any given level of aptitude, the gain in proficiency (or a decrease in r) is much larger for beginners, but for the same level of aptitude, the gain in proficiency (or a decrease in r) is much smaller when the same learner reaches more advanced proficiency. It is therefore more challenging to make the same amount of progress as an advanced learner than it is for beginners. That is, there is a large aptitude gap between distinguishing oneself among peers during the initial stages of learning compared to advanced stages of learning.

Finally, according to Hypothesis 2, different grammatical structures showed different degrees of correlations with aptitude. In DeKeyser’s [11] study, present progressives, determiners, wh-questions, plurals and subcategorization were highly correlated with age of arrival whereas word order, yes-no questions and pronoun gender did not show differential proficiency. DeKeyser explained the discrepancies in correlational significance by alluding to respective structures’ perceptual salience and their interaction with implicit/explicit learning mechanisms. In contrast, all 11 structures in the present study were found to be significantly correlated with mid to high effect sizes (Table 4). Small effect sizes were found for yes-no questions, present progressives and wh-questions while the strongest relationships were found for subcategorization, participle movement and word order (Table 4). This may have been due to the fact that in LLAMA_F, subcategorization, participle movement and word order types were represented, but neither interrogatives of any kind nor progressives were exemplified in the artificial language of LLAMA_F.

Granted, in DeKeyser’s [11] study, the correlation was with age of arrival not aptitude, but the argument presented by DeKeyser was that adults rely on explicit learning, and consequently structures more amenable to explicit instruction showed larger correlations. Regarding this claim, there are two methodologically motivated reasons to cast doubt on the differential correlations reported in DeKeyser’s study. First, in DeKeyser’s study the sample size was only 57. Small-scale studies have low statistical power and the results are not replicable. Second, although the GJT used was timed, individual’s reaction time was not recorded. Two individuals with the same score could not be differentiated beyond their accuracy score. In the current study, however, all individuals were differentiable beyond their total scores–thus mitigating any ceiling or floor effect–by incorporating their total reaction time as RCS. Methodological shortcomings aside, ECT-L2A was able to provide a unifying theory that linked all 11 grammar rules and their behaviors under a single mathematical formula without having to rely on speculations of explicit versus implicit learning distinctions. Thus, ECT-L2A was able to provide a more parsimonious explanation to the phenomena of aptitude’s diminishing role in attainment compared to the ones suggested by Li [18] or DeKeyser [11].

Relationship between motivation and attainment

Hypothesis 3 predicted that there would be a negative correlation between performance on GJT and motivation since motivation ζ(r) diminishes as r → 0. However, motivation may increase and show positive correlation for beginners due to the effect of potential energy on the conservation of total energy. Overall, the correlation between motivation and attainment was negative because as proficiency increased motivation decreased. This was a surprising finding but not unprecedented. A small number of studies have reported negative or non-significant correlation between motivation and learning outcomes [19, 20]. In the meta-analysis by Al-Hoorie [21] on Dörnyei’s L2 Motivational Self System, all three components of ideal self, ought-to self, and L2 experience had non-significant correlations with L2 achievement when the analysis was adjusted for low quality studies that could bias the results and publication bias was also taken into consideration. In other words, the 95% confidence interval included negative correlations when these adjustments were made. Because such findings are counterintuitive, the curious case of inverse relationship between motivation and attainment deserves a deeper discussion. Based on conventional wisdom, a motivated learner is expected to display greater intensity, focus, and perseverance towards the language acquisition process; consequently, the student is expected to learn better, learn more, and retain more information than those who are less motivated. ECT-L2A does predict motivation to contribute positively towards learning outcome. All things being equal, those who are more motivated should achieve more than those who are not as motivated because high values of ζ(r) will lead to smaller r. However, under the conservation of energy theory, motivation decreases with progression towards native-likeness due to the centrifugal force of L1 to TL distance. A natural consequence of this is that relative to beginners, more advanced learners are marked by lower motivation levels (see Table 6).

The source of negative correlation, therefore, is not due to the effect of motivation causing reduced levels of attainment. Contrarily, it is that once learners reach a certain level of high proficiency, their motivation is overshadowed by the deviation energy. This does not mean that advanced learners are no longer motivated to learn the target language. Unlike aptitude or grammatically judgment scores, motivation data was negatively skewed and all participants including the advanced proficiency learners indicated that they were motivated to learn English. Because everyone was motivated and willing to learn, separation based on motivation among the participants was not as wide as other measures. Comparison of coefficient of variation⁷ (CV), a measure of dispersion around the mean, revealed that motivation was the smallest at 0.0856, while aptitude and GJT showed similar CVs at 0.2085 and 0.240, respectively, almost three times more dispersed than motivation (these numbers can be easily calculated based on Table 2). Even when motivation was lower for advanced participants, they were still interested in learning English. This begs the question: if the source of negative correlation was not due to the effect of motivation causing reduced levels of attainment, how are we to explain the decrease in motivation with concurrent increase in proficiency?

According to ECT-L2A, there is a simple mathematical reason why motivation behaves the way it does. Based on Equation 7, $\mathrm{\zeta }\left(\mathrm{r}\right)=-{\mathrm{\eta }}^2{\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)}^2+\mathrm{\rho }\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)$, motivation will be positive as long as the second term with input mass is greater than the first term in which attainment is squared and multiplied by the negative of eta squared. When the effect of the L1-TL term becomes greater than the impact of the input (the second part of the equation), motivation $\mathrm{\zeta }\left(\mathrm{r}\right)$ is negative, i.e., it decreases. Beyond the mathematical explanation, there are two possible reasons why motivation may diminish with progression towards nativelikeness. First, variability in GJT explained by motivation decreased as GJT increased as the learners advanced from beginner to intermediate (Table 6). This is because as r gets smaller, the influence of ζ(r) is overshadowed by the role played by L1-TL deviance. Motivation for L2 does not have the same impact on outcome for higher proficiency learners as it once did when they were beginners. Eventually, learning becomes asymptotic and learners are not making progress towards native-likeness as they were used to during the initial stages of L2 acquisition. At this point, the asymptotic “wall” due to L1 to TL deviance that prevents full native-like proficiency could become a crucial demotivating factor. In L2 motivation literature, self-efficacy theory and expectancy-value theory share the common belief that a learner’s motivation is predicated on his/her own view of the expectancy of success, values attached to the objective, and self-assessment of their abilities to carry out the task. These theories place importance on the role of the learner’s past L2 learning experience and argue that whether L2 learners are highly motivated or not may hinge on how they have attributed their past success or failure. This is also related to their self-confidence, or the linguistic self-confidence and the level of anxiety one might have towards learning a new language [22]. How learners attribute their past failures or success will significantly affect their motivation towards future L2 endeavors [23]. Notice that according to Eq. 1, motivation is expected to increase as long as the attractive pull of the input mass multiplied by proficiency is smaller than the effect of the centrifugal energy. In the early stages of L2 development, learners are expected to experience noticeable growth. However, the L1 to TL distance presents a difficult wall to climb during the late stages of L2 development, which would dampen learners’ expectations of further success, linguistic self-confidence and their self-assessment of their abilities. All of which may lead adult learners to temper their motivation and attitude towards learning the target language with more realistic expectations as learning outcomes approach an asymptotic end-state. Concurrently, their linguistic development is likely to stop and fossilization may set in [24]. Successful learners, therefore, remain motivated even when they have reached advanced stages.

A second reason why motivation may decrease is that once learners have acquired enough of the target language to fulfill their basic communicative needs, the drive to continue the effort towards L2 mastery may diminish. In other words, when learners acquire enough language for basic communicative needs, learning more is not as important or valuable. This type of phenomena is known as the law of diminishing utility [25]. In SLA terms, it suggests that as the L2 learners’ proficiency increases, the marginal utility derived from learning declines in value; for example, it provides more value for the learner to go from a beginner to an intermediate user of TL than it is to go from an intermediate to an advanced user. Given that mastering a second language requires a lot of time, effort, and resources, it is difficult to maintain one’s motivation as it was in the beginning when learners’ needs are subject to such changes [26]. Although motivation waxes and wanes throughout the learning trajectory, exceptionally motivated learners still have higher level of motivation relative to others even when it wanes due to energy conservation. By the same token, the longitudinal drain on motivation means that those who can maintain a high level of motivation despite experiencing the asymptotic wall will eventually become successful learners.

In Hypothesis 4, different components of motivation were predicted to show different correlations with GJT because not all motivation types are equally sensitive to the learning outcome. The results confirmed that while some constructs were positively correlated, others were not (see Table 7). Past findings seem to lend some support to the notion that a wide range of correlations between motivation and achievement indeed exists. Dörnyei’s L2MSS was negatively correlated with GJT in the pilot study [20]. And according to a meta-analysis on L2MSS, motivation showed positive correlation with achievement albeit weakly (rs = 0.20), but the same relationship became non-significant when the meta-analysis was adjusted for quality and publication bias [21]. Other studies have shown motivation to have no significant relationship with GJT [19], poor predicator of proficiency levels [27], or have outright claimed that motivation was not a predictor of foreign language learning [28]. More relevant to the current studies’ operationalization of motivation was Masgoret and Gardner’s meta-analysis of AMTB [29]. Attitude toward learning, integrativeness, motivation, and integrative orientation were all positively correlated with achievement: strongest for self-ratings but weakest for objective measures. Still, a small number of constructs such as instrumental orientation and integrative orientation were found to be non-significant in second language contexts (as opposed to foreign language) and at secondary education levels. Despite the wide range of constructs and their uniquely complex interaction with students under less-than-optimal conditions specified by different motivation theories, conservation of energy was able to unify them all. While correlations between motivation constructs and GJT produced multiple outcomes: negative, positive, significant, and non-significant (Table 7), a single ECT-L2A derived model explained their behavior as following Equation 7 (Figure 5). Thus, the incredible parsimony afforded by ECT-L2A was able to explain, predict, and unify various constructs of motivation. Regardless of the specific manner or type in which learners are motivated, if the motivation in question provides an impetus and a drive towards target language acquisition, its relationship to attainment can be assumed to follow Eq. 1. This is no small feat considering the diversity of theoretical constructs and the dynamicity of motivation under different conditions: a singular unifying theory that can model all motivation types.

Relationship between kinetic energy and attainment

To explore how the combined effects of motivation and aptitude operate together vis-à-vis attainment, Hypothesis 5 in the present study predicted that kinetic energy would have a positive correlation with GJT, per ζ(r) + Λ. However, with increasing GJT, kinetic energy was also expected to decrease due to the decrease in motivation caused by L1-TL deviance or the centrifugal energy. Results from the current study showed that the sum of aptitude and motivation was positively correlated with GJT, but the strength of the correlation and variance explained diminished with increase in proficiency.

Perhaps not surprisingly, adult L2 learners who possess high aptitude and motivation performed better than those who did not, as evidenced by the positive correlation. In the current study, participant ID #22, for example, had one of the top five scores on GJT (181 raw score) despite having studied English for only 2 years. As expected, participant #22 had above average aptitude score (raw score of 16) and well above average motivation (raw score of 171) that put him at 84th percentile. Similarly, participant ID #66 had a top ten GJT raw score of 167 with only 1 year of studying English. Again, his motivation score was one standard deviation above the mean at 177, and his aptitude score was also one standard deviation above the mean at 17, putting this participant at 84th percentile on both variables. When both motivation and aptitude were below the mean, a high GJT score was still attainable, but it came at the cost of years of studying English. For example, participant #122 who had the highest GJT score of 185, had both below average motivation (151) and aptitude (9). However, #122 had spent 15 years studying English, well above the mean of 3.36 years in the sample. Compared to participant #22 who took only 2 years to reach a GJT score of 171, it took participant #122 15 years to obtain a similar score, which speaks volumes about the importance of motivation and aptitude.

Based on ECT-L2A, a low measure in either of the two variables may be compensated by a high measure in the other because kinetic energy is defined as the sum of the two terms. A high level of motivation is seemingly able to overcome low aptitude while low motivation can be balanced by high aptitude. This was also reflected in the data. For example, participant #188 had an above average GJT score of 157 (one SD above the mean) despite having a poor aptitude score of 10 (no better than guessing) with less than 2 years of studying English. What may have compensated for poor aptitude was the participant’s high motivation score of 175, which was near the total maximum score of 180. On the other hand, participant #140 had well below the average motivation score of 130 but was able to obtain a high GJT score of 163 (one SD above the mean) with only 2 years of studying English. This participant had a high aptitude score of 16. In summary, it seems that a highly motivated learner with less than extraordinary aptitude can still make great progress on par with those with high aptitude.

Per ECT-L2A, aptitude and motivation are given equal weight in the formation of kinetic energy. The empirical evidence regarding their contribution to learning outcome, however, suggests that aptitude carries greater weight than motivation. The variance in GJT explained by aptitude ranged from 25 to 41 percent (Table 3), easily surpassing motivation’s share of about 2–3 percent in the variance explained (Table 6). Does this mean that talent for foreign languages matters more than motivated effort? The results of Tables 3, 6 do not categorically favor one or the other. As previously discussed, the coefficient of variation for motivation was three times smaller than aptitude. Plus, all participants were motivated to learn English; consequently, the separation in motivation needed to discriminate one learner from another was rather small. When the range of motivation is restricted (i.e., everyone is motivated) correlation coefficient goes down [15]. Due to this attenuation effect on correlation, direct comparison between aptitude and motivation vis-à-vis outcome warrants cautious interpretation and further research.

In essence, the relationship between attainment and kinetic energy (aptitude and motivation combined) can be described by the Equation: $\mathrm{\zeta }\left(\mathrm{r}\right)+\mathrm{\Lambda }=-{\mathrm{\eta }}^2{\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)}^2+\mathrm{\rho }\left({\mathrm{G}\mathrm{J}\mathrm{T}}_{\mathrm{R}\mathrm{C}\mathrm{S}}\right)+\in$. Since kinetic energy cannot be negative, the right side of the equation will remain positive as long as the second terms with the input mass is greater than the first term in which attainment is squared and multiplied by the negative of eta squared. When the effect of L1-TL deviance becomes greater than the positive contributions made by the input (the second part of the equation), the learning outcome reaches an asymptote. As a result, the strength of the correlation and variance explained diminishes with increase in proficiency, as demonstrated in the current study (Table 9). For most adult learners, no matter how much aptitude and motivation they have for learning the target language, it gets progressively more difficult to make advances towards native likeness. The hill gets steeper, so to speak. To attain near-native proficiency, exceptional motivation and aptitude are required because of the squared term attached to the multiplicative effect of eta–the overwhelming influence of the L1-TL deviance. From a longitudinal perspective, regardless of one’s relative standing in motivation and aptitude, the learner may continue to gain proficiency in the target language but never reach native likeness. While small changes (due to L2 input, learner motivation) in the learning environment can have a striking impact on attainment when the TL proficiency is low, environmental stimulation in the form of instruction or motivation will not likely lead to drastic changes in the system’s behavior during the later stages. In sum, the behavior of kinetic energy can be characterized as being positively related to achievement in the initial stages of learning, but the rate of improvement accelerates negatively during advanced proficiency, ultimately becoming asymptotic as further gains become negligible. In fact, this type of non-linear and asymptotic relationship between a learning outcome and its predictor has been universally recognized in cognitive psychology as a common phenomenon.

Conclusion

Perhaps it is no coincidence that it has taken the field of SLA over five decades to officially theorize language acquisition as a non-linear process via CDST and subsequently two more decades for ECT-L2A to express it as a mathematical model. To fully embrace non-linearity, mathematical models must continue to accompany future SLA research. The history of science teaches us that treading uncharted waters is the hallmark of progress and breakthroughs. Isaac Newton once recognized that in order to understand the law of gravity, a new method of doing math was needed to describe celestial motion. He was said to have thus invented differential calculus to explain the law of gravitation [30]. Theory construction is often limited by the methods available and the framework in which theories are expressed. The field of SLA may still be young, but it is also in danger of being trapped in a perpetual asymptotic growth, replete with incremental findings that contribute local, situated, atomistic and mostly observational understanding but provides no major theoretical breakthroughs. What is needed more than ever are fresh new perspectives and interdisciplinary partnerships, however unconventional they may be [5]. In this regard, the social-physics approach of outfitting conservation of energy for second language acquisition provides a unique perspective that is missing in most other SLA theories.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving human participants were reviewed and approved by the Teachers College Institutional Review Board. The patients/participants provided their written informed consent to participate in this study.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The ECT-L2A model uses different Greek letters for the variables (compare Eqs 1–4).

²It should be noted here that a conceptual parallel is drawn between kinetic energy in SLA and mv²/2 in physics.

³Since division by zero is undefined, r cannot be exactly zero; it can only be asymptotically zero.

⁴Technically, this is the minimum point in the effective potential graph (Figure 1).

⁵While GJT is a common measure of morphosyntactic knowledge in L2 research, it admittedly provides a limited window on the scope of such knowledge.

⁶Because r is marked by its inverse relationship to attainment, the slope is positive from this perspective (as r goes to zero), not negative (as r goes to positive infinity).

⁷Coefficient of variation is defined as the standard deviation divided by the mean.

References

1. Larsen-Freeman D. Chaos/complexity science and second language acquisition. Appl Linguistics (1997) 18:141–65. doi:10.1093/applin/18.2.141

CrossRef Full Text | Google Scholar

2. de Bot K. Introduction: Second language development as a dynamic process. Mod Lang J (2008) 79:166–78. doi:10.1111/j.1540-4781.2008.00712.x

CrossRef Full Text | Google Scholar

3. Goldstein H. Classical mechanics. 2nd ed. MA Addison-Wesley (1980).

Google Scholar

4. Han Z-H, Bao G, Wiita P. Energy conservation: A theory of L2 ultimate attainment. Int Rev Appl Linguistics (2017) 50 (2):133–64. doi:10.1515/iral-2016-0034

CrossRef Full Text | Google Scholar

5. Han Z-H, Bao G, Wiita P. Energy conservation in SLA: The simplicity of a complex adaptive system. In: L Ortega, and Z-H Han, editors. Complexity theory and language development. In celebration of Diane Larsen-Freeman. John Benjamins (2017). p. 210–31.

Google Scholar

6. Han Z, Bao G. Is there a critical period for second language acquisition? A theoretical social physics approach. Preprints (2021):2021030540. doi:10.20944/preprints202103.0540.v1

CrossRef Full Text | Google Scholar

7. Rogers V, Meara P, Barnett-Legh T, Curry C, Davie E. Examining the LLAMA aptitude tests. J Eur Second Lang Assoc (2017) 1(1):49–60. doi:10.22599/jesla.24

CrossRef Full Text | Google Scholar

8. Gardner RC. Attitude/motivation test battery. Canada: The University of Western Ontario (2004).

Google Scholar

9. Masgoret AM, Gardner RC. Attitudes, motivation, and second language learning: a meta-analysis of studies conducted by gardner and associates. Lang Learn (2003) 53:123–63. doi:10.1111/1467-9922.00212

CrossRef Full Text | Google Scholar

10. Gardner RC, Smythe PC. On the development of the attitude/motivation test Battery. Can Mod Lang Rev (1981) 37:510–25. doi:10.3138/cmlr.37.3.510

CrossRef Full Text | Google Scholar

11. DeKeyser R. The robustness of critical period effects in second language acquisition. Stud Second Lang Acquisition (2000) 22(4):499–533. doi:10.1017/S0272263100004022

CrossRef Full Text | Google Scholar

12. Johnson JS, Newport EL. Critical period effects in second language learning: The influence of maturational state on the acquisition of English as a second language. Cogn Psychol (1989) 21(1):60–99. doi:10.1016/0010-0285(89)90003-0

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Woltz DJ, Was CA. Availability of related long-term memory during and after attention focus in working memory. Mem Cogn (2006) 34(3):668–84. doi:10.3758/bf03193587

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Baba K, Shibata R, Sibuya M. Partial correlation and conditional correlation as measures of conditional independence. Aust N Z J Stat (2004) 46:657–64. doi:10.1111/j.1467-842X.2004.00360.x

CrossRef Full Text | Google Scholar

15. Bandalos DL. Measurement theory and applications for the social sciences. New York: Guilford Publications (2018).

Google Scholar

16. S-M Chow, E Ferrer, and F Hsieh, editors. The Notre Dame series on quantitative methodology. Statistical methods for modeling human dynamics: An interdisciplinary dialogue. Routledge/Taylor & Francis Group (2010).

Google Scholar

17. Markovsky I, Van Huffel S. Overview of total least-squares methods. Signal Process. (2007) 87(10):2283–302. doi:10.1016/j.sigpro.2007.04.004

CrossRef Full Text | Google Scholar

18. Li S. The associations between language aptitude and second language grammar acquisition: A meta-analytic review of five decades of research. Appl Linguistics (2015) 363:385–408. doi:10.1093/applin/amu054

CrossRef Full Text | Google Scholar

19. Binalet CB, Guerra JM. A Study on the relationship between motivation and language learning achievement among tertiary students. Int J Appl Linguistics English Lit (2014) 3(5):251–60. doi:10.7575/aiac.ijalel.v.3n.5p.251

CrossRef Full Text | Google Scholar

20. Kim P. Motivation and aptitude: A partial validation of ECT-l2a. Stud Appl Linguistics TESOL (2019) 19(2):19–38. doi:10.7916/salt.v19i2.3414

CrossRef Full Text | Google Scholar

21. Al-Hoorie AH. The L2 motivational self-system: A meta-analysis. Stud Second Lang Learn Teach (2018) 8:721–54. doi:10.14746/ssllt.2018.8.4.2

CrossRef Full Text | Google Scholar

22. Dörnyei Z. Motivation in second and foreign language learning. Lang Teach (1998) 31:117–35. doi:10.1017/S026144480001315X

CrossRef Full Text | Google Scholar

23. Erler L, Macaro E. Decoding ability in French as a foreign language and language learning motivation. Mod Lang J (2011) 95(4):496–518. doi:10.1111/j.1540-4781.2011.01238.x

CrossRef Full Text | Google Scholar

24. Han Z-H. Fossilization in adult second language acquisition. Bristol, United Kingdom. Multilingual Matters (2004).

Google Scholar

25. Kauder E. Genesis of the marginal utility theory from Aristotle to the end of the eighteenth century. Econ J (1953) 63(251):638–50. doi:10.2307/2226451

CrossRef Full Text | Google Scholar

26. Busse V, Walter C. Foreign language learning motivation in higher education: A longitudinal study of motivational changes and their causes. Mod Lang J (2013) 97:435–56. doi:10.1111/j.1540-4781.2013.12004.x

CrossRef Full Text | Google Scholar

27. Matsumoto M. Second language learners’ motivation and their perception of their teachers as an affecting factor. New Zealand Stud Appl Linguistics (2011) 17(2):37–52. doi:10.3316/informit.808628981621588

CrossRef Full Text | Google Scholar

28. Taguchi K. Is motivation a predictor of foreign language learning? Int Edu J (2006) 7(4):560–9.

Google Scholar

29. AMTB. International AMTB research project (2003). Retrieved from: http://publish.uwo.ca/∼gardner/docs/englishamtb.pdf (Accessed October, 2015).

Google Scholar

30. Smith G. In: EN Zalta, editor. “Isaac Newton”, the stanford Encyclopedia of philosophy (2007). URL = <https://plato.stanford.edu/entries/newton/>.

Google Scholar

31. Meara P. LLAMA language aptitude test manual (2005). Retrieved from: http://www.lognostics.co.uk/tools/llama/llama_manual.pdf (Accessed October, 2015).

Google Scholar