Photo-thermoelastic wave propagation with changing thermal conductivity on excited pulsed laser nanoscale microelongated semiconductor material

Indroduction: The novel model of a non-local elastic semiconductor material that is microelongated is created. The process of photothermal transfer is responsible for the stimulation of the material. Photo-thermoelastic theories are used when the thermal conductivity is changed for the non-local medium. Under the influence of laser pulses, the effective framework describes the nanoscale microelongation instance as well as the interference between the photo-thermoelastic propagation waves in the non-local medium. It is possible to think of thermal conductivity as a linear function of temperature when electronic and thermoelastic deformation mechanisms are described. Two-dimensional deformation (2D) is used to extract the main fields, which obtained in non-dimension.

Methods: Harmonic wave analysis, which is described by the normal mode, has been used to convert the basic equations into non-homogeneous higher-order ordinary differential equations. Applying a small subset of the possible non-local semiconductor surface conditions leads to exhaustive solutions.

Result and Discussion: The outcomes of numerical simulations for silicon (Si) are graphically shown. There are comparisons made and explanations given for the investigated physical factors like their thermal conductivity, laser pulses and microelongation parameters.

1 Introduction

Recent developments in the generalized thermoelastic theory have allowed its benefits to be applied to a wider range of fields of research, including as nuclear reactors, rocket and missile technologies, shipbuilding, and massive steam turbine systems. Silicon (Si) and other elastic semiconducting materials found new applications in many branches of engineering and materials science as a consequence of technological developments. Semiconductors play an essential role in modern industry across the board, but especially in the electronics industry. Semiconductor materials are crucial to the development of solar cells and other clean energy technologies. This is why semiconductor physics, and especially semiconductor internal structure, has been a popular topic of study in recent years. Electronic deformation occurs when excited electrons are pushed to the surface through absorption due to the temperature influence of light (ED). Yet, the internal particle collisions lead to thermoelastic (TE) deformations in the non-local semiconductor owing to the depths of the semiconductor. This is why we focus on the microinertia processes of the microelements, also called the kinetics of internal particles. We all know that the electrical resistance of semiconductors decreases with increasing temperature, and that the degree of conduction varies with both temperature and distance from the surface. This suggests that thermal conductivity could change with distance, as suggested by Eringen [1, 2]. Hence, several factors, such as thermal conductivity, internal structure (microelements), and light energy absorbed, must be taken into account while studying semiconductors (photothermal excitation).

The models utilized to describe the semiconductor material might be developed using the micropolar elastic solid body and microstretch thermoelasticity continuum theory. Researchers around the turn of the last century looked into the relationship between micropolar processes (micro-deformation) and the physical characteristics of semiconductors [1]. Eringen [2, 3] considered the microstructure of an elastic body as part of his examination of the micropolar theory. Microstretch thermoelasticity is used as a unifying concept in a new model created by Eringen [3]. Using microstretch effects, numerous writers [4–7] developed the generalized thermoelasticity theories. Lotfy et al. [8, 9] presented a many problem of how the generalized microstretch thermoelasticity theory may be put to use. Ramesh et al. [10] introduced the microstretch theory, which has inspired the study of fluid mechanics models for viscoelastic porous media. Ezzat and Abd-Elaal [11] studied the porous medium according to viscoelastic boundary layer flow with free convection effects with one relaxation time. When waves inside the medium are examined using functionally graded circumstances, the microelongated medium is created as a result of the influence of varying internal heat sources [12, 13]. Ailawalia et al. [14–16] studied the thermoelastic microelongated elastic material under plane strain deformation in accordance with different thermal memories by relocating internal heat sources. Using the twofold porosity phenomenon, Marin [17] studied the structure of elastic materials when subjected to micropolar influences.

It is well known that the rules of classical continuum mechanics (CCM) remain the same regardless of the size of the system under investigation. Due to the equations in its system, it cannot predict a large influence. As a result, it may not work in contexts where elements like size dependence and the scaling of mechanical phenomena play a substantial role. Discrete models provide a solution to all of the above problems, but doing so requires a lot of computational power. This has prompted efforts to develop models of modified continuum mechanics that include intrinsic lengths and so account for size effects. According to the principles of classical continuum mechanics, all matter is made up of an endless number of points, including particles, which can only move with regard to their immediate neighbours. As classical mechanics does not show many tiny phenomena like microdeformation and microdislocation, it has limited practical applicability and is thus seldom used. With this new information in hand, it was clear that a unified viewpoint was required to inculcate the idea that a material particle is a volume element that would deform and rotate, and that the material is, in general, a multiscale material. The particle’s nonlocal interactions with other particles in the medium must also be included into the calculation of its equilibrium. From this, it is clear that the material model is a nonlocal micro-continuum theory. Nonlocal elasticity was initially proposed by Eringen [18]. Eringen investigated the theory of nonlocal thermoelasticity [18]. While discussing nonlocal elasticity, he went through the following: constitutive relations; governing equations; balancing laws in continuum mechanics; and equations of displacement and temperature. The lattice building theory and the classical continuum theory are connected by the non-local thermoelastic theory, which acts as a bridge between the two. Tzou [19, 20] later proposed the dual-phase-lag heat conduction theory, which incorporates two phase-lags related to the heat flow and the temperature gradient. Gupta and Mukhopadhyay [21] have recently done work on extended thermoelastic theory using non-local theory of heat conduction. A novel theory on the energy equation was established by Tzou and Guo [22], which depicts the lagging response in space as the later in time. Phase-lagging captures the ultrafast response in the femtosecond domain, while non-local provides light on the underlying nanoscale physical process [23]. According to nonlocal theories, matter particles are immobile in space and can only move in one direction (without spinning or rotating). Attenuation functions are developed to illustrate how the strength of long-range interactions between particles decreases with increasing distance [24]. Using these functions, constitutive equations have been developed, and the equilibrium equations in continuum theory are defined by the integral functions for kinematic variables. This was very close to the classical mechanics theories. To broaden the scope of local mechanics, nonlocal continuum mechanics at tiny scales was developed [25].

Applications in semiconductors, magnetometers, solar panels, nuclear fields, geophysics, and other related domains have boosted the profile of the study of plane wave propagation in a photo-thermo-elastic solid. The photothermal phenomena are studied when multiple laser beams impact a semiconductor sample during an ED deformation [26]. Photothermal methods with ultrasensitive laser spectroscopy have been used to evaluate several physical properties while analyzing the waves’ propagation through a semiconductor using photoacoustic spectroscopy [27–30]. Hobiny and Abbas [31] used two-dimensional deformation of semiconductors to investigate the interplay between photothermal and thermoelastic theories. Todorovic et al. [32, 33] used the photoacoustic transmission technique to get the optical properties of the stimulated semiconductor from microcantilevers during the ED deformation. Nevertheless, Lotfy et al. [34–40] presented other uses when the photo-thermoelasticity strategy was applied to the semiconductor silicon elastic medium of present day technology. The dual phase-lags model is used in the photo-thermoelasticity theory for excitation semiconductor materials [41, 42]. When the semiconductor medium is excited, its thermal conductivity may be chosen as a function of distance [43, 44]. Ezzat [45, 46] created a unique fractional heat order model that defines the non-metallic organic semiconductor medium for the study of thermal-plasma-elastic waves. Ismail et al. [47] looked at how excited microelongated semiconductors with varying thermal conductivity affected thermal-optical-elastic waves. Hall current’s effect on non-Local semiconductor material’s Optical-Elastic-Thermal-Diffusive waves was studied by Chteoui et al. [48]. Thermo-diffusion waves for nonlocal semiconductor were studied by Almoneef et al. [49] utilizing the fractional calculus and the laser short-pulse effect. Using an improved multi-phase-lag theory and thermal activation with diffusion and gravitational field on a semiconducting material, Zenkour [50–53] investigated several challenges in generalized photo-thermoelasticity.

The plasma transfer process and mechanical thermoelasticity phenomena are investigated using the suggested model in an endlessly deformable semiconductor medium with homogenous, isotropic, and thermoelastic characteristics. Previous studies ignore the fact that nanoscale microelongating a non-local semiconductor material causes a change in thermal conductivity. Based on the photo-thermoelasticity theory, this work explores how the thermal conductivity of a non-local semiconductor medium might change in response to a temperature gradient. Using the nanoscale microelongated non-local semiconductor and the microinertia of the medium, a novel model is constructed in accordance with the 2D (TD and ED) deformation processes under the impact of laser pulse to obtain the transmission of plane waves in a nanoscale medium. Harmonic wave technique with the normal mode analysis is used to locate the linear solution to the dimensionally unconstrained main fields. Elimination technique of simultaneous differential equations has provided the relevant physical quantities: temperature, displacement, carrier density, stresses and microelongation function. In a non-local medium, the fundamental solutions may be obtained when conditional forces are applied to the free surface. The results of numerical simulations of silicon material are shown graphically. The results provide light on the propagation of waves in an energized material. Changes in the thermal relaxation time for the photo-thermoelasticity theory are used to make a number of comparisons when the thermal conductivity is varied owing to the influence of elongation factors, laser pulse and the non-local effect.

2 Mathematical model and main equations

The plasma distribution ($N$) (the phase of carrier density), elastic displacement vector ($u_i$), and microelongational amount ($\varphi$) are three additional main variables other than the thermal wave distribution (variations temperature $T$). The microelongated non-local photo-thermoelasticity theory gives the essential governing equations for 2D deformation in Cartesian coordinates (see Figure 1). Following Eringen [1–3], generalized thermoelasticity [54–56], and Lotfy et al. [47, 48] the basic formulations for non-local thermo-elastic material in the absence of heat source and body forces, the following constitutive equations (the nonlocal stress–strain equations) may be expressed for a nanoscale microelongated semiconductor photo-electronics medium:

$\left.\begin{array}{l}{\sigma }_{iI}^{\prime }=\left({\lambda }_o\varphi +\lambda u_r{,}_r\right){{\delta }_i}_I+2\mu {u_{I,}}_i-\widehat{\gamma }\left(1+v_o\frac{\partial }{\partial t}\right)T{{\delta }_i}_I-\left(\left(3\lambda +2\mu \right)d_{n}N\right){{\delta }_i}_I,\\ m_i=a_0{\varphi }_{,i},\left(1-{\xi }^2{\nabla }^2\right){\sigma }_{iI}={\sigma }_{iI}^{\prime },\\ s-\left(1-{\xi }^2{\nabla }^2\right){\sigma }^{\prime }={\lambda }_o{u}_i{,}_i-{\beta }_1\left(1+v_o\frac{\partial }{\partial t}\right)T+-\left(\left(3\lambda +2\mu \right)d_{n}N\right){{\delta }_2}_i+{\lambda }_1\varphi ,\\ \xi =\frac{a{e}_0}{l}.\end{array}\right\}.(1)$

FIGURE 1

FIGURE 1. Geometry of the problem.

The diffusion equation of plasma (the optoelectronics equation) is given by for the nanostructure medium of semiconductors during the transport process [44]:

$\dot{N}=D_E{N}_{,ii}-\frac{N}{\tau }+\kappa T.(2)$

Where the “comma” before an index suggests space-differentiation, the dot” above a symbol suggests time-differentiation and the thermal activation nanoscale coupling parameter $\kappa =\frac{\partial n_0}{\partial T}\frac{T}{\tau }$ ($n_0$ is equilibrium carrier concentration).

The field equations of motion for non-scale microelongation and microinertia processes may be represented as [1–3, 47], in accordance with the temperature field change and Eringen’s model of nonlocal thermoelastic model:

$\left.\begin{array}{l}{\sigma }_{ij,j}^{\prime }\hspace{0.17em}=\rho \left(1-{\xi }^2{\nabla }^2\right){\ddot{u}}_i\\ \left(\lambda +\mu \right)u_{j,ij}+\mu u_{i,jj}+{\lambda }_o{\varphi }_{,i}-\widehat{\gamma }\left(1+v_o\frac{\partial }{\partial t}\right)T_{,i}-{\delta }_n{N}_{,i}=\rho \left(1-{\xi }^2{\nabla }^2\right){\ddot{u}}_i\end{array}\right\}.(3)$

${\alpha }_o{\varphi }_{,ii}-{\lambda }_1\varphi -{\lambda }_o{u}_{j,j}+{\widehat{\gamma }}_1\left(1+v_o\frac{\partial }{\partial t}\right)T=\frac{1}{2}j\rho \left(1-{\xi }^2{\nabla }^2\right)\ddot{\varphi .}(4)$

When $\xi =0$, the third equation may be reduced to the constitutive equation of classical local photo-thermoelasticity.

The heat equation, also known as the heat transport equation, in a non-local microelongated optical-thermal-elastic field may be stated when the thermal conductivity is variable as follows [47]:

${\left(K{T}_{,i}\right)}_{,i}-\left(\rho C_E\left(n_1+{\tau }_o\frac{\partial }{\partial t}\right)\dot{T}-\widehat{\gamma }{T}_o\left(n_1+n_o{\tau }_o\frac{\partial }{\partial t}\right)\left({\dot{u}}_{i,i}-\rho Q\right)\right)+\frac{E_g}{\tau }N={\widehat{\gamma }}_1{T}_o\dot{\varphi }.(5)$

Where $Q=\frac{I_0{\gamma }^{\prime }t}{2\pi r^2{t}_0^2}\exp \left(-\frac{z^2}{r^2}-\frac{t}{t_0}-{\gamma }^{\prime }x\right)$ (the external heat sources) is the thermal effect of laser pulses which falls on the semiconductor medium, $I_0$ represents the absorbed energy according to the pulse rise time $t_0$, $r$ expresses the radius of the beam and ${\gamma }^{\prime }$ is the heating energy absorption at depth $z$. Take into account the thermal conductivity $K$, which varies and may be chosen as a linear function of temperature. The non-local microelongated semiconductor material’s changing thermal conductivity under the effect of a heat source is represented as a function of temperature as shown in [57]:

$K\left(T\right)=K_0\left(1+\pi T\right).(6)$

When the medium is temperature independent and the small parameter $\pi$ is negative, the constant thermal conductivity (reference) is $K_0$. The integral form of thermal conductivity may be derived using the Kirchhoff transform [57], which is utilized to convert the nonlinear temperature components into linear ones:

$\mathrm{\Theta }=\frac{1}{K_0}{\displaystyle \underset{0}{\overset{T}{\int }}}K\left(\mathfrak{R}\right)d\mathfrak{R}.(7)$

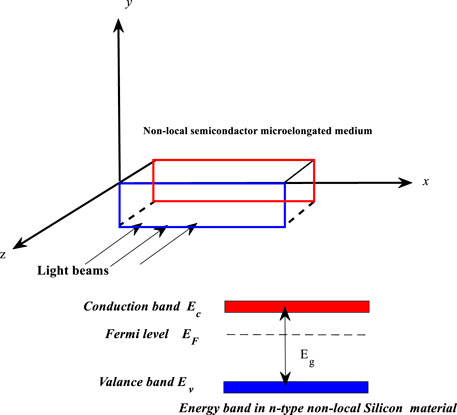
All physical fields and temperature changes will be assumed to take place in the xz-plane with the $t$-time variation throughout this study. As a result, the displacement tensor $u_i$ and the scalar $\varphi$ can be presented as.

$\left.\begin{array}{l}{u}_i=\left(u_1,0,u_3\right);u_1=u\left(x,z,t\right),u_3=w\left(x,z,t\right),\\ \varphi =\varphi \left(x,z,t\right),\\ e=\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}.\end{array}\right\}.(8)$

Parameter ${\widehat{\gamma }}_1=\left(3\lambda +2\mu \right){\alpha }_{t_2}$ reflects a portion of the micro-elongation effects of the non-local semiconductor medium, and its value, ${\alpha }_{t_2}$, is the microelongated thermal expansion coefficient. The following form describes the solution space for the underlying Eqs 2–4:

$\left.\begin{array}{l}\left(\lambda +\mu \right)\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}w}{\partial x\partial z}\right)+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)+\\ {\lambda }_o\frac{\partial \varphi }{\partial x}-\widehat{\gamma }\left(1+v_o\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial x}-{\delta }_n\frac{\partial N}{\partial x}=\rho \left(1-{\xi }^2\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial z^2}\right)\right)\left(\frac{{\partial }^{2}u}{\partial t^2}\right)\end{array}\right\},(9)$

$\left.\begin{array}{l}\left(\lambda +\mu \right)\left(\frac{{\partial }^{2}u}{\partial x\partial z}+\frac{{\partial }^{2}w}{\partial z^2}\right)+\mu \left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)+\\ {\lambda }_o\frac{\partial \varphi }{\partial z}-\widehat{\gamma }\left(1+v_o\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial z}-{\delta }_n\frac{\partial N}{\partial z}=\rho \left(1-{\xi }^2\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial z^2}\right)\right)\left(\frac{{\partial }^{2}w}{\partial t^2}\right)\end{array}\right\},(10)$

${\alpha }_o\left(\frac{{\partial }^2\varphi }{\partial x^2}+\frac{{\partial }^2\varphi }{\partial z^2}\right)-{\lambda }_1\varphi -{\lambda }_{o}e+{\widehat{\gamma }}_1\left(1+v_o\frac{\partial }{\partial t}\right)T=\frac{1}{2}j\rho \left(1-{\xi }^2\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial z^2}\right)\right)\frac{{\partial }^2\varphi }{\partial t^2}.(11)$

Using the various models of non-scale microelongated photo-thermoelasticity theories [coupled-dynamical (CD) model, Lord and Shulman (LS) model, and Green and Lindsay (GL) model] [53, 54, 57], one may calculate the thermal and elastic relaxation times. The thermal conductivity, which is in the variable case in computations, may be taken from the fundamental equations by using the map transform, as shown in Eqs 7, 8:

Operating $\frac{\partial }{\partial x_i}$ on the all terms of Eq. 7, yields:

$\left.\begin{array}{l}{K}_0\frac{\partial \mathrm{\Theta }}{\partial x_i}=K\left(T\right)\frac{\partial T}{\partial x_i}\Rightarrow K_0{\mathrm{\Theta }}_{,i}=K\left(T\right)T_{,i},\\ \left(K_0/K\right){\mathrm{\Theta }}_{,i}=T_{,i}.\end{array}\right\}.(12)$

Again, the non-linear factor was ignored while differentiating Eqs 7, 12:

$\left.\begin{array}{l}{K}_0\frac{{\partial }^2\mathrm{\Theta }}{\partial x_i^2}=\frac{\partial }{\partial x_i}\left(K\left(T\right)\frac{\partial T}{\partial x_i}\right)=\frac{\partial }{\partial x_i}\left(K_0\left(1+\pi T\right)\frac{\partial T}{\partial x_i}\right)\\ =K_0\left(1+\pi T\right)\frac{{\partial }^{2}T}{\partial {x_i}^2}+K_0\pi {\left[\frac{\partial T}{\partial x_i}\right]}^2=K\frac{{\partial }^{2}T}{\partial {x_i}^2},\\ \left(K_0/K\right){\mathrm{\Theta }}_{,ii}=T_{,ii}.\end{array}\right\}.(13)$

The time differentiation of Eq. 7 is:

$K_0\frac{\partial \mathrm{\Theta }}{\partial t}=K\left(T\right)\frac{\partial T}{\partial t}.(14)$

The map transformation applied to Eq. 2, where $\frac{\partial }{\partial x_i}$ may be used on both sides through Eq. 12, produces:

$\left.\begin{array}{l}\frac{\partial }{\partial t}\frac{\partial N}{\partial x_j}=D_E\frac{\partial N_{,ii}}{\partial x_j}-\frac{1}{\tau }\frac{\partial N}{\partial x_j}+\kappa \frac{\partial T}{\partial x_j},\\ \frac{\partial }{\partial t}\frac{\partial N}{\partial x_j}=D_E\frac{\partial N_{,ii}}{\partial x_j}-\frac{1}{\tau }\frac{\partial N}{\partial x_j}+\frac{\kappa K_0}{K}\frac{\partial \mathrm{\Theta }}{\partial x_j},\\ \frac{\partial }{\partial t}\frac{\partial N}{\partial x_j}=D_E\frac{\partial N_{,ii}}{\partial x_j}-\frac{1}{\tau }\frac{\partial N}{\partial x_j}+\kappa \frac{\partial \mathrm{\Theta }}{\partial x_j}.\end{array}\right\}.(15)$

In the preceding Eq. 15, the last term in the first half may be enlarged as follows, ignoring the non-linear elements:

$\begin{array}{l}\frac{\kappa K_0}{K}\frac{\partial \mathrm{\Theta }}{\partial x_j}=\frac{\kappa K_0}{K_0\left(1+\pi T\right)}\frac{\partial \mathrm{\Theta }}{\partial x_j}=\kappa {\left(1+\pi T\right)}^{-1}\frac{\partial \mathrm{\Theta }}{\partial x_j}=\kappa {\left(1-\pi T+\left(\pi T\right)\right.}^2-.......)\frac{\partial \mathrm{\Theta }}{\partial x_j}=\kappa \frac{\partial \mathrm{\Theta }}{\partial x_j}-\kappa \pi T\frac{\partial \mathrm{\Theta }}{\partial x_j}+{\left(\pi T\right)}^2\frac{\partial \mathrm{\Theta }}{\partial x_j}-.......=\kappa \frac{\partial \mathrm{\Theta }}{\partial x_j}\end{array}\}.(16)$

Equation 15 is the result of using the Leibniz integral rule:

$\frac{\partial N}{\partial t}=D_E{N}_{,ii}-\frac{1}{\tau }N+\kappa \mathrm{\Theta }.(17)$

The microelongated heat Eq. 5 may be rewritten as follows after applying the map transform:

${\mathrm{\Theta }}_{,ii}-\left(\frac{1}{k}\left(n_1+{\tau }_o\frac{\partial }{\partial t}\right)\frac{\partial \theta }{\partial t}-\frac{\widehat{\gamma }{T}_o}{K_0}\left(n_1+n_o{\tau }_o\frac{\partial }{\partial t}\right)\left(\frac{\partial u_{i,i}}{\partial t}-\rho Q\right)\right)+\frac{E_g}{K_0\tau }N=\frac{{\widehat{\gamma }}_1{T}_0}{K_0}\dot{\varphi ,}(18)$

where $\frac{1}{k}=\frac{\rho C_E}{K_0}$ represents the thermal diffusivity.

We propose the following non-dimensional quantities to eliminate the complexity of mathematical model:

$\left.\begin{array}{l}\overline{N}=\frac{{\delta }_n}{n_0\widehat{\gamma }}N,\left({\overline{x}}_i,{\overline{\xi }}_1\right)=\frac{{\omega }^{*}\left(x_i,{\xi }_1\right)}{C_T},{\overline{u}}_i=\frac{\rho C_T{\omega }^{*}}{T_o\widehat{\gamma }}{u}_i,\left(\overline{t},{\overline{\tau }}_o,{\overline{\nu }}_o\right)={\omega }^{*}\left(t,{\tau }_o,{\nu }_o\right),\\ C_T^2=\frac{2\mu +\lambda }{\rho },\overline{\theta }=\frac{\theta }{T_o},{{\overline{\sigma }}_i}_j=\frac{{{\sigma }_i}_j}{T_o\widehat{\gamma }},\overline{\varphi }=\frac{\rho C_T^2}{T_o\widehat{\gamma }}\varphi ,{\omega }^{*}=\frac{\rho C_E{C}_T^2}{K_0},C_L^2=\frac{\mu }{\rho },\\ \left({\mathrm{\Pi }}^{\prime },{\psi }^{\prime }\right)=\frac{\rho {{\omega }^{*}}^2\left(\mathrm{\Pi },\psi \right)}{T_0\widehat{\gamma }},Q^{\prime }=\frac{Q}{T_0{C}_E}.\end{array}\right\}.(19)$

The displacements may be further reduced in complexity by representing them as functions into the potential scalar $\mathrm{\Pi }\left(x,z,t\right)$ and $\mathrm{\Psi }\left(x,z,t\right)=\left(0,\psi ,0\right)$ vector space-time, as illustrated below, in accordance with Helmholtz’s theory:

$\overrightarrow{u}=grad\mathrm{\Pi }+curl\mathrm{\Psi }.(20)$

Subtracting the superscripts from Eq. 19, which is the consequence of applying it to Eqs 9, 10, 17, 18, we get:

$\left({\nabla }^2-{\epsilon }_3-{\epsilon }_2\frac{\partial }{\partial t}\right)N+{\epsilon }_4\mathrm{\Theta }=0,(21)$

$\left(\left(1+{\xi }^2\frac{{\partial }^2}{\partial t^2}\right){\nabla }^2-\frac{{\partial }^2}{\partial t^2}\right)\mathrm{\Pi }+\left(1+v_o\frac{\partial }{\partial t}\right)\mathrm{\Theta }+a_1\varphi -N=0,(22)$

$\left(\left(1+{\xi }^2\frac{{\partial }^2}{\partial t^2}\right){\nabla }^2-a_3\frac{{\partial }^2}{\partial t^2}\right)\psi =0,(23)$

$\left(\left(1+\mathbb{C}\frac{{\partial }^2}{\partial t^2}\right){\nabla }^2-C_3-C_4\frac{{\partial }^2}{\partial t^2}\right)\varphi -C_5{\nabla }^2\mathrm{\Pi }+C_6\left(1+v_o\frac{\partial }{\partial t}\right)\mathrm{\Theta }=0,(24)$

${\nabla }^2\mathrm{\Theta }-\left(\left(n_1\frac{\partial }{\partial t}+{\tau }_o\frac{{\partial }^2}{\partial t^2}\right)\mathrm{\Theta }-\epsilon \left(n_1\frac{\partial }{\partial t}+n_o{\tau }_o\frac{{\partial }^2}{\partial t^2}\right){\nabla }^2\mathrm{\Pi }\right)+{\epsilon }_{5}N-{\epsilon }_1\frac{\partial \varphi }{\partial t}={\mathrm{\Theta }}_0{\mathrm{\Theta }}^{*}{e}^{-{\gamma }^{\prime }x}\}.(25)$

Where ${\mathrm{\Theta }}^{*}=\epsilon \left(\frac{1}{t}\left(n_{1}t+n_0{\tau }_0\left\{1-\frac{t}{t_0}\right\}\right)\right)e^{-\left(\frac{z^2}{r^2}+\frac{t}{t_0}\right)}$ and ${\mathrm{\Theta }}_0=\frac{I_0{\gamma }^{\prime }{K}_0}{2\pi a^2{t}_0^2}$.

The constitutive equations for the 2D variation in heat conductivity are as follows:

$\left.\begin{array}{l}\left(1-{\xi }^2{\nabla }^2\right){\sigma }_{xx}=\frac{\partial u}{\partial x}+a_2\frac{\partial w}{\partial z}-\left(1+v_o\frac{\partial }{\partial t}\right)\mathrm{\Theta }-N+a_1\varphi ,\\ \left(1-{\xi }^2{\nabla }^2\right){\sigma }_{zz}=a_2\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}-\left(1+v_o\frac{\partial }{\partial t}\right)\mathrm{\Theta }-N+a_1\varphi ,\\ \left(1-{\xi }^2{\nabla }^2\right){\sigma }_{xz}=a_4\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right).\end{array}\right\},(26)$

where,

$\begin{array}{c}{a}_1=\frac{{\lambda }_o}{\rho c_T^2},a_2=\frac{\lambda }{\rho C_T^2},a_3=\frac{\rho C_T^2}{\mu },\epsilon =\frac{{\widehat{\gamma }}^2{n}_o}{K_0\rho },{\epsilon }_1=\frac{{\widehat{\gamma }}_1\widehat{\gamma }{T}_o}{K_0\rho },{\epsilon }_2=\frac{C_T^2}{D_E{\omega }^{*}},a_4=\frac{\mu }{\rho C_T^2},C_4=\frac{\rho j{{\omega }^{*}}^4}{{\alpha }_0{C}_2^2},\\ {\epsilon }_3=\frac{C_T^2}{\tau D_E{{\omega }^{*}}^2},{\epsilon }_4=\frac{{\delta }_n{C}_T^2}{D_E\widehat{\gamma }{{\omega }^{*}}^2},{\epsilon }_5=\frac{E_g\widehat{\gamma }{C}_T^2}{\tau K_0{\omega }^{*}{\delta }_n},C_3=\frac{{\lambda }_1{{\omega }^{*}}^2}{{\alpha }_0{C}_T^2},C_5=\frac{{\lambda }_o{{\omega }^{*}}^2}{{\alpha }_0{C}_T^2},C_6=\frac{{\widehat{\gamma }}_1\rho {{\omega }^{*}}^2{T}_o}{\widehat{\gamma }{\alpha }_0},\\ {\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial z^2},\mathbb{C}=\frac{\rho j{\xi }^2{{\omega }^{*}}^2}{{\alpha }_0{C}_2^2}.\end{array}$

3 Harmonic wave analysis

Any function $\coprod \left(x,z,t\right)$ whose solutions satisfy Eqs 21–25 may be represented for time-harmonic vibrations with a plane wave propagating in 2D with wave number $b$ in the direction of the positive z-axis [42–46]:

$\coprod \left(x,z,t\right)=\overline{\coprod }\left(x\right)\exp \left(\omega t+ibz\right).(27)$

Non-dimensional complex frequency $\mathrm{\omega }={\omega }_0+i\zeta$ corresponds to the amplitude $\overline{\coprod }\left(x\right)$ of the function $\coprod \left(x,z,t\right)$ fields and $i=\sqrt{-1}$. Using the fundamental Eq. 21–26, and the normal mode analysis Eq. 27, we obtain:

$\left(D^2-{\alpha }_1\right)\overline{N}+{\epsilon }_4\overline{\mathrm{\Theta }}=0,(28)$

$\left(D^2-A_1\right)\overline{\mathrm{\Pi }}+A_2\overline{\mathrm{\Theta }}++a_1^{\prime }\overline{\varphi }-a_2^{\prime }\overline{N}=0,(29)$

$\left(D^2-A_3\right)\overline{\psi }=0,(30)$

$\left(D^2-A_4\right)\overline{\varphi }-C_5^{*}\left(D^2-b^2\right)\overline{\mathrm{\Pi }}+A_5\overline{\mathrm{\Theta }}=0,(31)$

$\left(D^2-A_6\right)\overline{\mathrm{\Theta }}-A_7\left(D^2-b^2\right)\overline{\mathrm{\Pi }}+{\epsilon }_5\overline{N}-A_8\overline{\varphi }={\mathrm{\Theta }}_0\stackrel{\sim }{\mathrm{\Theta }}\exp \left(-{\gamma }^{\prime }x\right),(32)$

$\left.\begin{array}{l}\left(\left(1-b^2\right)-{\xi }^2{D}^2\right){\overline{\sigma }}_{xx}=D\overline{u}+ib{a}_2\overline{w}-A_2\overline{\mathrm{\Theta }}-\overline{N}+a_1\overline{\varphi },\\ \left(\left(1-b^2\right)-{\xi }^2{D}^2\right){\overline{\sigma }}_{zz}=a_{2}D\overline{u}+ib\overline{w}-A_2\overline{\mathrm{\Theta }}-\overline{N}+a_1\overline{\varphi },\\ \left(\left(1-b^2\right)-{\xi }^2{D}^2\right){\overline{\sigma }}_{xz}=a_4\left(ib\overline{u}+D\overline{w}\right).\end{array}\right\}.(33)$

where,

$\left.\begin{array}{l}{a}_2^{\prime }=\frac{1}{\left(1+{\omega }^2{\xi }^2\right)},A_1=b^2+\frac{{\omega }^2}{\left(1+{\omega }^2{\xi }^2\right)},A_2=\frac{1+{\nu }_o\omega }{\left(1+{\omega }^2{\xi }^2\right)},A_3=b^2+\frac{a_3{\omega }^2}{\left(1+{\omega }^2{\xi }^2\right)},\\ D=\frac{d}{d\mathrm{x}},A_4=\frac{b^2+C_3+C_4{\omega }^2}{1+\mathbb{C}{\omega }^2},A_5=\frac{C_6\left(1+{\nu }_o\omega \right)}{1+\mathbb{C}{\omega }^2},C_5^{*}=\frac{C_5}{1+\mathbb{C}{\omega }^2},a_1^{\prime }=\frac{a_1}{\left(1+{\omega }^2{\xi }_1^2\right)},\\ A_6=b^2+\omega \left(n_1+{\tau }_o\omega \right),A_7=\epsilon \left(n_1\omega +n_o{\tau }_o{\omega }^2\right),A_8={\epsilon }_1\omega ,{\alpha }_1=b^2+{\epsilon }_3+{\epsilon }_2\omega ,\\ \stackrel{\sim }{\mathrm{\Theta }}={\mathrm{\Theta }}^{*}\exp \left(-\omega t-ibz\right).\end{array}\right\}.(34)$

The determinant of the coefficient matrix f must for the system of Eqs 28–32 appear for there to be a non-trivial solution for $\overline{\varphi },\overline{N},\overline{\mathrm{\Theta }}$ and $\overline{\mathrm{\Pi }}$ after simplifying we have this result:

$\left\{D^8-{\mathrm{{\rm B}}}_1{D}^6+{\mathrm{{\rm B}}}_2{D}^4-{\mathrm{{\rm B}}}_3{D}^2+{\mathrm{{\rm B}}}_4\right\}\left(\overline{\varphi },\overline{N},\overline{\mathrm{\Theta }},\overline{\mathrm{\Pi }}\right)=g\exp \left(-{\gamma }^{\prime }x\right),(35)$

where,

${\mathrm{{\rm B}}}_1=-\left(-A_2{A}_7+C_5^{*}{a}_1-A_1-A_4-A_6-{\alpha }_1\right),$

$\begin{array}{l}{\mathrm{{\rm B}}}_2=\left(A_2{A}_7-C_5^{*}{a}_1^{\prime }+A_1+A_4+A_6\right){\alpha }_1+\left(A_7-{\epsilon }_3\right){\epsilon }_4{a}_2^{\prime }\\ +\left(b^2{A}_7+A_4{A}_7-A_8\right)A_2-b^2{C}_5^{*}{a}_1^{\prime }-A_5{A}_7{a}_1^{\prime }-A_6{C}_5^{*}{a}_1^{\prime }-A_1{A}_4+A_1{A}_6+A_4{A}_6,\end{array}$

$\begin{array}{c}{\mathrm{{\rm B}}}_3=-\left(\left(-A_2{A}_7+C_5^{*}{a}_1^{\prime }\right)b^2-A_2{A}_4{A}_7+A_5{A}_7{a}_1^{\prime }+A_6{C}_5^{*}{a}_1^{\prime }-A_1{A}_4-A_1{A}_6+A_2{A}_8-A_4{A}_6\right){\alpha }_1\hfill \\ \left(-C_5^{*}{a}_2^{\prime }+A_1+A_4\right){\epsilon }_4{\epsilon }_3+\left(-b^2{A}_7{a}_2^{\prime }-A_4{A}_7{a}_2+A_8\right){\epsilon }_4+\left(-A_2{A}_4{A}_7+\left(A_5{A}_7+A_6{C}_5^{*}\right)a_1^{\prime }\right)b^2\hfill \\ -A_1{A}_4{A}_6+A_2{A}_4{A}_8{a}_2^{\prime }-A_5{A}_8{a}_1^{\prime },\hfill \end{array}$

$\begin{array}{l}{\mathrm{{\rm B}}}_4=\left(\left(b^2{C}_5^{*}{a}_1^{\prime }-A_1{A}_4\right){\epsilon }_3+b^2{A}_4{A}_7-A_4{A}_8\right){\epsilon }_4\\ +\left(\left(A_2{A}_4{A}_7-A_5{A}_7-A_6{C}_5^{*}{a}_1^{\prime }\right)b^2+A_1{A}_4{A}_6{a}_2^{\prime }-A_2{A}_4{A}_8+A_5{A}_8{a}_1^{\prime }\right){\alpha }_1.\end{array}$

$g=\left({{\gamma }^{\prime }}^8-\left(A_2{A}_4-C_5^{*}{a}_1^{\prime }+b^2+A_4\right){{\gamma }^{\prime }}^6+\left(A_2{A}_4{a}_1^{\prime }+A_4{C}_5^{*}{a}_1^{\prime }{b}^2\right){{\gamma }^{\prime }}^4-\left(b^2{C}_5^{*}{a}_1^{\prime }-A_2{A}_4\right){{\gamma }^{\prime }}^2+A_2{A}_4{b}^2{C}_5^{*}{a}^{\prime }\right){\mathrm{\Theta }}_0\stackrel{\sim }{\mathrm{\Theta }}$

Equation 35 may be factored to provide [42]:

$\left(D^2-k_1^2\right)\left(D^2-k_2^2\right)\left(D^2-k_3^2\right)\left(D^2-k_4^2\right)\left\{\overline{\mathrm{\Theta }},\overline{N},\overline{\mathrm{\Pi }},\overline{\varphi }\right\}\left(x\right)=0.(36)$

It has been noted that in order for the roots to satisfy our condition that they have positive real portions, we need them to satisfy the solution of Eq. 36, which is limited as $x\to \infty$. The auxiliary equation with the roots $k_n^2\left(n=1,2,3,4,\mathrm{R}\mathrm{e}\left(k_n\right)>0\right)$ of Eq. 36 is:

$k^8-{\mathrm{{\rm B}}}_1{k}^6+{\mathrm{{\rm B}}}_2{k}^4-{\mathrm{{\rm B}}}_3{k}^2+{\mathrm{{\rm B}}}_4=0.(37)$

Generalized linear solutions to Eq. 35 may be written for the temperature fields as follows:

$\overline{\mathrm{\Theta }}\left(x\right)={\displaystyle \sum _{i=1}^4}{\mathrm{\Lambda }}_i\left(b,\omega \right)e^{-k_{i}x}+L_{1}g\exp \left(-{\gamma }^{\prime }x\right).(38)$

The other physical quantities are:

$\overline{\varphi }\left(x\right)=\left({\displaystyle \sum _{i=1}^4}{\mathrm{\Lambda }}_i^{\prime }\left(b,\omega \right)e^{-k_{i}x}={\displaystyle \sum _{i=1}^4}{h}_{1i}{\mathrm{\Lambda }}_i\left(b,\omega \right)e^{-k_{i}x}\right)+L_{2}g\exp \left(-{\gamma }^{\prime }x\right),(39)$

$\overline{\mathrm{\Pi }}\left(x\right)=\left({\displaystyle \sum _{i=1}^4}{\mathrm{\Lambda }}_i^{″}\left(b,\omega \right)e^{-k_{i}x}={\displaystyle \sum _{i=1}^4}{h}_{2i}{\mathrm{\Lambda }}_i\left(b,\omega \right)e^{-k_{i}x}\right)+L_{3}g\exp \left(-{\gamma }^{\prime }x\right),(40)$

$\overline{N}\left(x\right)=\left({\displaystyle \sum _{i=1}^4}{\mathrm{\Lambda }}_i^{‴}\left(b,\omega \right)e^{-k_{i}x}={\displaystyle \sum _{i=1}^4}{h}_{3i}{\mathrm{\Lambda }}_i\left(b,\omega \right)e^{-k_{i}x}\right)+L_{4}g\exp \left(-{\gamma }^{\prime }x\right).(41)$

The relations between ${\mathrm{\Lambda }}_i$, ${\mathrm{\Lambda }}_i^{\prime }$, ${\mathrm{\Lambda }}_i^{″}$ and ${\mathrm{\Lambda }}_i^{‴}$ (unknown parameters) can be obtained from the above system of Eqs 28–32 as:

$\begin{array}{l}{h}_{1i}=\frac{\left(d_1{k}_i^4+d_2{k}_i^2+d_3\right)}{\left(k_i^6+d_4{k}_i^4+d_5{k}_i^2+d_6\right)},h_{3i}=-\frac{\left({\epsilon }_4\right)}{\left(k_i^2-{\alpha }_1\right)},h_{2i}=\frac{\left(A_2{k}_i^4+d_7{k}_i^2+d_8\right)}{\left(k_i^6+d_4{k}_i^4+d_5{k}_i^2+d_6\right)},\\ d_1=A_2{C}_5^{*}-a_2^{\prime }{A}_5,d_2=-A_2{b}^2{C}_5^{*}-A_2{C}_5^{*}{\alpha }_1-C_5^{*}{a}_2{a}_2^{\prime }{\epsilon }_4+A_1{A}_5+A_5{\alpha }_1,\\ d_3=b^2{A}_2{C}_5^{*}{\alpha }_1+b^2{C}_5^{*}{a}_2{\epsilon }_4-A_1{A}_5{\alpha }_1,d_4=C_5^{*}{a}_1^{\prime }-A_1-a^{\prime }{A}_4-{\alpha }_1,\\ d_5=-b^2{C}_5^{*}{a}_1^{\prime }-C_5^{*}{a}_1^{\prime }{\alpha }_1+A_1{A}_4+A_1{a}_2^{\prime }{\alpha }_1+A_4{a}_2^{\prime }{\alpha }_1,d_6=b^2{\alpha }_1{a}_1^{\prime }{C}_5^{*}-A_1{a}_2^{\prime }{A}_4{\alpha }_1,\\ d_7=-a_2^{\prime }{A}_2{A}_4-A_2{\alpha }_1+A_5{a}_1^{\prime }-a_2{\epsilon }_4,d_8=A_2{A}_4{\alpha }_1+A_4{a}_2{\epsilon }_4-a_1^{\prime }{A}_5{\alpha }_1,\end{array}$

$L_1=-{\left({{\gamma }^{\prime }}^8-B_1{{\gamma }^{\prime }}^6+B_2{{\gamma }^{\prime }}^4-B_3{{\gamma }^{\prime }}^2+B_4\right)}^{-1},$

$L_2=-\frac{\left(d_1{{\gamma }^{\prime }}^4+d_2{{\gamma }^{\prime }}^4+d_3\right)}{\left({{\gamma }^{\prime }}^6+d_4{{\gamma }^{\prime }}^4+d_5{{\gamma }^{\prime }}^4+d_6\right)},$

$L_3=-\frac{\left({\epsilon }_4\right)}{\left({{\gamma }^{\prime }}^2-{\alpha }_1\right)},$

$L_4=\frac{\left(A_2{{\gamma }^{\prime }}^4+d_7{{\gamma }^{\prime }}^2+d_8\right)}{\left({{\gamma }^{\prime }}^6+d_4{{\gamma }^{\prime }}^4+d_5{{\gamma }^{\prime }}^2+d_6\right)}.$

The real root of Eq. 30 is $k_5^2$ which can be obtained from the factorized following form:

$\left(D^2-k_5^2\right)\overline{\psi }\left(x\right)=0.(42)$

The values of the root $k_5^2$ represents as:

$k_5=\pm \sqrt{A_3}=\pm \omega \sqrt{a_3.}(43)$

It is possible to rewrite Eq. 42 so that its linear solution is:

$\overline{\psi }\left(x\right)={\mathrm{\Lambda }}_5\left(b,\omega \right)\exp \left(-k_{5}x\right).(44)$

Where ${\mathrm{\Lambda }}_5$ is the last unknown parameter. With Eq. 20, we can express the displacement components in terms of the free parameters as:

$\left.\begin{array}{l}\overline{u}\left(x\right)=-{\displaystyle \sum _{n=1}^4}{\mathrm{\Lambda }}_n{h}_{2i}{k}_n{e}^{-k_{n}x}-ib{\mathrm{\Lambda }}_5{e}^{-k_{5}x}-L_{3}g{\gamma }^{\prime }\exp \left(-{\gamma }^{\prime }x\right),\\ \overline{w}\left(x\right)={\displaystyle \sum _{n=1}^4}ib\left(h_{2i}{\mathrm{\Lambda }}_n{e}^{-k_{n}x}+L_{3}g{\gamma }^{\prime }{\mathrm{e}}^{-{\gamma }^{\prime }x}\right)-k_5{\mathrm{\Lambda }}_5{e}^{-k_{5}x}.\end{array}\right\}.(45)$

The constitutive relations according to Eq. 33 can be represented as:

$\left.\begin{array}{l}{\overline{\sigma }}_{xx}={\displaystyle \sum _{n=1}^4}\frac{{\mathrm{\Lambda }}_n\left(h_{2i}\left(k_n^2-b^2{a}_2\right)-A_2-h_{3i}+a_1{h}_{1i}\right)e^{-k_{n}x}-ib{k}_5\left(a_2-1\right){\mathrm{\Lambda }}_5{e}^{-k_{5}x}}{\left(\left(1-b^2\right)-{\xi }^2{k}_n^2\right)}-{\varsigma }_{1}g\exp \left(-{\gamma }^{\prime }x\right),\\ {\overline{\sigma }}_{zz}={\displaystyle \sum _{n=1}^4}\frac{{\mathrm{\Lambda }}_n\left(h_{2i}\left(a_2{k}_n^2-b^2\right)-A_2-h_{3i}+a_1{h}_{1i}\right)e^{-k_{n}x}-ib{k}_5\left(1-a_2\right){\mathrm{\Lambda }}_5{e}^{-k_{5}x}}{\left(\left(1-b^2\right)-{\xi }^2{k}_n^2\right)}-{\varsigma }_{2}g\exp \left(-{\gamma }^{\prime }x\right),\\ {\overline{\sigma }}_{xz}={\displaystyle \sum _{n=1}^4}\frac{ib{\mathrm{\Lambda }}_n{k}_n\left(h_{2i}-1\right)e^{-k_{n}x}+\left(1+k_5^2\right){\mathrm{\Lambda }}_5{e}^{-k_{5}x}}{\left(\left(1-b^2\right)-{\xi }^2{k}_n^2\right)}-{\varsigma }_{3}g\exp \left(-{\gamma }^{\prime }x\right),\\ {\varsigma }_1=-A_2{b}^2+a_1\left({{\gamma }^{\prime }}^2-1\right)-2ib-{\gamma }^{\prime }{L}_4+L_2+L_3),\\ {\varsigma }_2=-A_4{b}^2+a_2\left({{\gamma }^{\prime }}^2-1\right)-2ib-{\gamma }^{\prime }{L}_4+L_2+L_3),\\ {\varsigma }_3={{\gamma }^{\prime }}^2{L}_4-{\gamma }^{\prime }{L}_1.\end{array}\right\}.(46)$

4 Photo-thermomechanical conditions

In this part, different boundary restrictions are imposed at the surface of the nanoscale microelongated medium while the thermal conductivity is changing in order to acquire the general parameters ${\mathrm{\Lambda }}_n$ [57].

The mechanical load conditions have a degree of flexibility in their selection and may be expressed as follows [is subjected to a mechanical load in $x$-direction (traction load) and free otherwise (tangent traction is free)] [48]:

$\left.\begin{array}{l}\left.\begin{array}{l}{\sigma }_{xx}=p,\\ {\overline{\sigma }}_{xx}=\overline{p}\left(x\right)\exp \left(\omega t+ibz\right),\end{array}\right\}\\ \left.\begin{array}{l}{\sigma }_{xz}=0,\\ {\overline{\sigma }}_{xz}=0\end{array}\right\}.\end{array}\right\}.(47)$

Because the temperature can rise or fall so rapidly, or at least in such a short time, when pulsed laser stimulation is used, very little heat is lost to the surrounding area. As a consequence of this, the use of pulsed laser excitation can be helpful for absorption measurements. It is also good to know that the illumination of a solid surface by a laser beam may cause a range of different physical reactions, some of which are reliant on the amount of energy present. If a material is subjected to laser radiation, some of the energy will be transformed into heat. This particular kind of heat creation allows heat waves to spread across the material, which has a number of different impacts (e.g., photothermal effects). The fact that the surrounding plane (x = 0) of the material is subjected to laser pulses is another factor that is taken into consideration. In this scenario, the temperature state that may be taken into consideration is as follows:

$T\left(0,z,t\right)=\mathrm{\Phi }\left(z,t\right)=\stackrel{\sim }{H}\lambda –\left(1-\stackrel{\sim }{R}\right)f\left(z\right)g\left(t\right).(48)$

Where $f\left(z\right)=\frac{2\exp \left(-2z^2/R_G\right)}{R_G\sqrt{2\pi }}$ and $g\left(t\right)=\frac{8t^3\exp \left(-2t^2/t_0^2\right)}{t_0^2}$ ($\stackrel{\sim }{H}$ represents the energy of laser pulse per unit length (the maximum amount of light energy that a laser is capable of producing in the course of one of its pulses), $\stackrel{\sim }{R}$ denotes the surface reflectivity, $R_G$ expresses the radius of the Gaussian beam, $t_0$ denotes the laser pulse rise-time and $\lambda –$ is the coefficient of extinction).

The elongation scalar function, which expresses the microelongation situation in normal mode as follows, may be selected at will:

$\overline{\phi }=0.(49)$

Carriers, after diffusing with the recombination speed on the surface $\stackrel{\sim }{S}$, reach the sample’s surface, where they may recombine with a given probability. As a result, the following expression may be used to describe the carrier density border condition:

${\left.\frac{\partial \overline{N}}{\partial x}\right|}_{x=0}=-\frac{\stackrel{\sim }{S}}{D_E}{n}_0.(50)$

Using the above boundary conditions Eqs 47–50 with normal mode analysis, yields:

$\left.\begin{array}{l}{\displaystyle \sum _{n=1}^4}{\mathrm{\Lambda }}_n\left(h_{2i}\left(k_n^2-b^2{a}_2\right)-A_2-h_{3i}+a_1{h}_{1i}\right)-ib{k}_5\left(a_2-1\right){\mathrm{\Lambda }}_5=-\overline{p}\left(x\right)\exp \left(\omega t+ibz\right)+{\varsigma }_{1}g=P_0,\\ {\displaystyle \sum _{n=1}^4}ib{\mathrm{\Lambda }}_n{k}_n\left(h_{2i}-1\right)+\left(1+k_5^2\right){\mathrm{\Lambda }}_5-{\varsigma }_{2}g=0,\\ {\displaystyle \sum _{i=1}^4}{\mathrm{\Lambda }}_i\left(b,\omega \right)=\mathrm{\Theta }\left(z,t\right)\exp \left(\omega t+ibz\right)-L_{1}g={\mathrm{\Phi }}_0,\\ {\displaystyle \sum _{i=1}^4}{h}_{1i}{\mathrm{\Lambda }}_i\left(b,\omega \right)+L_{2}g=0,\\ {\displaystyle \sum _{i=1}^4}{h}_{3i}{k}_i{\mathrm{\Lambda }}_i\left(b,\omega \right)=\frac{\stackrel{\sim }{S}}{D_e}{n}_0-{\gamma }^{\prime }{L}_{4}g=N_0.\end{array}\right\}.(51)$

Five unknown constants ${\mathrm{\Lambda }}_n$, may be solved for by using the matrix inverse approach. Deformations, temperature fields, and all other physical medium variables have solvable solutions.

5 Special cases

There will be a presentation of some appropriate cases in order to put into consideration the influence that different models have on the variable quantities. The material properties of the nanoscale microelongated semiconductor be characterized as follows, according to the values of the parameters that are mentioned below.

5.1 Generalized nanoscale microelongated thermoelasticity theory with variable thermal conductivity

When the plasma wave distribution, which is dependent on the carrier density, is ignored, i.e., $N=0$, the problem is obtained in accordance with the generalized non-scale microelongated thermoelasticity theory under the influence of variable thermal conditions. This occurs when the theory is applied under the influence of variable thermal conditions. In this particular instance, the series of equations has been streamlined in order to conform to past studies [14, 15].

5.2 Non-local photo-thermoelasticity theory with variable thermal conductivity

The non-local photo-thermoelasticity theory with the plasma effect and variable thermal conductivity is shown for the semiconductor medium when the microelongation parameters are ignored (${\alpha }_o={\lambda }_o={\lambda }_1=0$). The equations that control the situation may be written as [42, 43].

5.3 Different models of non-local photo-thermoelasticity theory

Several models of non-local microelongated photo-thermoelasticity theory under the effect of changing thermal conductivity may be constructed [54–56] depending on the values of the parameters $n_1,n_o,{\tau }_o$ and $v_o$. These models can be generated as follows: the CD model: $n_1=1,n_o={\tau }_o=v_o=0$_, the LS model: $v_o=0,{\tau }_o>0$, $n_1=n_o=1$, and the GL model: $n_1=1,n_o=0,v_o\ge {\tau }_o>0$.

5.4 The variable thermal conductivity

If the nanoscale microelongated semiconductor medium is unaffected by the negative parameter and is unaffected by the temperature gradient, then it is said to be independent of both ($\pi =0,K=K_0$). In this particular case, the issue is studied using a thermal conductivity that is held constant [31, 44].

5.5 The nonlocality effect

The issue is addressed in the local semiconductor situation, and the local microelongated photo-thermoelasticity theory is studied [47]. Ignoring the non-local parameter allows for the investigation of the problem in its local form.

Using the equation for the map, which is Eq. 7, we can determine that the relation between $T$ and $\mathrm{\Theta }$:

$\mathrm{\Theta }=\frac{1}{K_0}{\displaystyle \underset{0}{\overset{T}{\int }}}{K}_0\left(1+\pi T\right)dT=T+\frac{\pi }{2}{T}^2=\frac{\pi }{2}{\left(T+\frac{1}{\pi }\right)}^2-\frac{1}{2\pi },\mathrm{o}\mathrm{r}(52)$

$T=\frac{1}{\pi }\left[\sqrt{1+2\pi \mathrm{\Theta }}-1\right]=\frac{1}{\pi }\left[\sqrt{1+2\pi \overline{\mathrm{\Theta }}\exp \left(\omega t+ibz\right)}-1\right].(53)$

6 Numerical results

During the numerical simulation, silicon (Si) is used in the role of the polymer non-local microelongated semiconducting material. In this instance, the main fields and wave propagations are acquired in the form of graphs. The many different input parameters for the physical constants of Si are employed via the use of computer software programming (Matlab 2022a). The following table presents the SI unit representations of the physical constants for non-local silicon (homogeneous, isotropic, thermoelastic from n-type) [32, 58, 59]:

$\lambda =3.64\mathrm{x}{10}^{10}N/m^2,\mu =5.46\times {10}^{10}N/m^2,\rho =2330kg/m^3,T_0=800\mathrm{K},$

$d_n=-9\mathrm{x}{10}^{-31}{m}^3,D_E=2.5\times {10}^{-3}{m}^2/s,E_g=1.11eV,\stackrel{\sim }{s}=2m/s,\tau =5\mathrm{x}{10}^{-5}s,$

${\alpha }_{t_1}=0.04\mathrm{x}{10}^{-3}{K}^{-1},{\alpha }_{t_2}=0.017\mathrm{x}{10}^{-3}{K}^{-1},K=150W{m}^{-1}{K}^{-1},C_e=695J/\left(kgK\right),$

$j=0.2\times {10}^{-19}{m}^2,\gamma =0.779\times {10}^{-9}N,k={10}^{10}N{m}^{-2},t=0.001,{\lambda }_0=0.5\times {10}^{10}N{m}^{-2},$

${\lambda }_1=0.5\times {10}^{10}N{m}^{-2},{\alpha }_0=0.779\times {10}^{-9}N,{\tau }_0=0.00005,{\nu }_0=0.0005,{\stackrel{\sim }{n}}_0={10}^{20}{m}^{-3}.$

The laser parameters which are utilized [46]:

$\stackrel{⌢}{R}=91\%,t_0=10\text{ns},\lambda –=0.001{\mathrm{m}}^{-1},R_G=0.45\text{mm},\stackrel{\sim }{H}=10\mathrm{J},t_0=9ps,r=100\mu m,{\gamma }^{\prime }=0.001m^{-1},I_0={10}^{5}J.$

The wave number is $b=0.5$ when a mechanical stress $\overline{P}=1$ is applied in the closed range $0\le x\le 5$ at $z=-1$ (dimensionless distance). For a limited amount of time $t=0.001$, a graphical representation of the non-dimensional properties of the key quantities in 2D deformation is provided. The results have been represented using the field quantities’ real values for simplicity ($\mathrm{\omega }={\mathrm{\omega }}_0+\mathrm{i}\mathrm{\zeta }$, when $\mathrm{\zeta }=0.05$ and ${\mathrm{\omega }}_0=-2.5$ ).

7 Discussion

Figure 2 displays, in six different subfigures, the primary field distributions of temperature, microelongation, elastic (displacement), plasma (photo-electronic), and two mechanical wave components (${\sigma }_{xx}$ and ${\sigma }_{xz}$) versus the dimensionless distance. The CD, LS, and GL models of nanoscale microelongated photo-thermoelasticity are compared in the figures’ insets in terms of how their thermal and elastic relaxation times differ from one another. All numerical findings are influenced by a non-local parameter when $\pi =-0.04$, indicating that the thermal conductivity is changeable. The free non-local semiconductor surface is compatible with all physical field distributions shown in this group’s overview (Figure 2). In the first subfigure, the boundary condition is met because the mechanical and laser thermal effect conditions cause the temperature rise distribution to be different for each of the three curves when $t\ge t_0$. The endpoint values of the two curves diverge as a result of the impact that is caused by the mechanical relaxation time parameter. When the value of the temperature increment distribution is increased, the mechanical relaxation time and thermal memory parameter both have a negative impact on the value. This highlights how the mechanical relaxation time parameter may have an effect on the temperature increment distribution as well as the thermal wave that is based on thermal memory. The distribution of the carrier density function, also known as the plasma wave, is shown in the fourth subfigure. All three curves have the same starting values at the positive point on the surface according to the carrier concentration. Because of the photo-electronics effect, this meets the boundary criterion since it significantly increases from the beginning owing to the thermal effect of laser pulses in order to reach the maximum point. Because of the influence of the relaxation time parameters, the values at the ends of all three curves are identical to one another. The significance of the relaxation time parameters for the carrier density distribution and photothermal waves is demonstrated by the fact that the value of the carrier density distribution decreases when the mechanical relaxation time parameter is increased. This finding demonstrates the importance of the relaxation time parameters for these two phenomena. In accordance with the photothermal impact, also known as the ED and TE deformation, the thermal wave and plasma wave both increase until they reach their highest point. The temperature and carrier density distributions both experience a decrease in the second range that follows an exponentially decreasing trend as the distance between them increases. This trend continues until the distributions are close to one another, at which point they converge to the zero line and are in agreement with the experimental findings [60]. The nanoscale microelongation function (second subfigure) starts at zero, rises during the course of the three models in line with the photothermal effect, and achieves its maximum value with an increase in distance. The distribution reduces as it moves away from the surface until it approaches the lowest value, then regularly grows and decreases until it achieves the equilibrium state that corresponds to coincide with the zero line. Because of the influence of thermal and elastic relaxation periods, the displacement distributions predicted by the LS and GL models (shown in the third subfigure) behave in the same way as those predicted by the CD model (decreases gradually, minimal). The elastic waves within the medium coincide and converge at the equilibrium state to the zero line. The non-local stress distribution (${\sigma }_{xx}$) starts at the same positive location near the surface of the semiconductor in all three models, and then quickly rises to reach its greatest value close to the surface. This pattern is consistent across all three models. As the distance from the surface increases, the stress distribution takes on the form of a wave, and as the distance continues to increase, the wave eventually vanishes into the material. The non-local tangent stress distributions begin with a value of zero and then rapidly increase until they reach their maximum value for GL model, but take an opposite behavior for CD and LS models. After reaching their lowest position, they begin to rise again and continue to do so until they reach the zero line, which they do when the distance reaches its maximum.

FIGURE 2

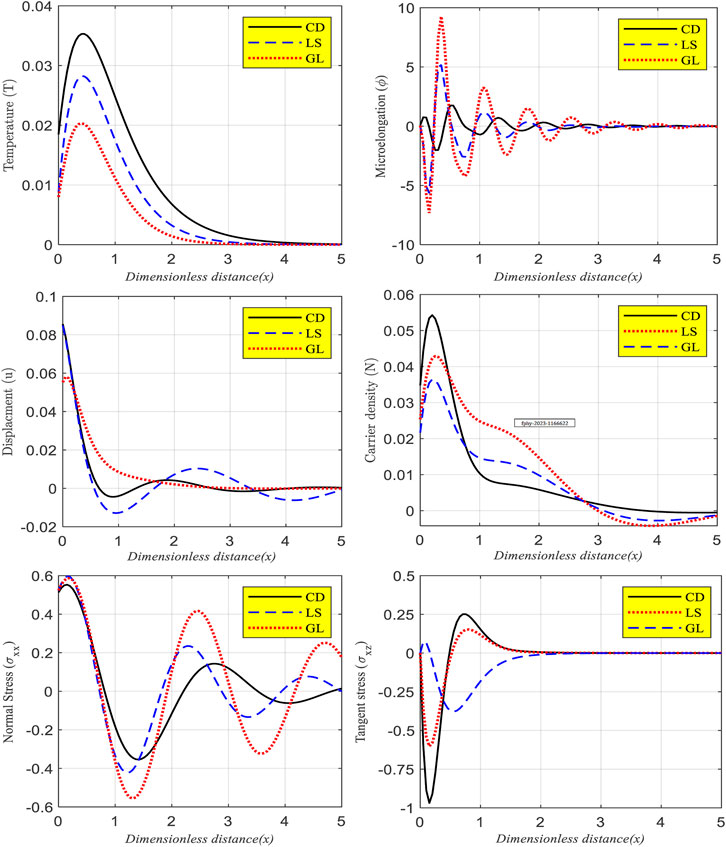
FIGURE 2. The effect of a non-local parameter and laser pulses with varying thermal conductivity on the change of the main fields versus dimensionless distance in different thermal memory.

Figure 3 now includes a total of six subfigures that illustrate the primary field distributions vs. distance for two different scenarios. In each subfigure, there is a comparison between the distributions that take place when the nanoscale material (Si) non-local parameter is present and those that take place when it is absent (local). Calculations are carried out in line with the GL model of the photo-thermoelasticity theory whenever the variable thermal conductivity ($\pi =-0.04$) occurs at the same minuscule dimensionless time. The propagation of the waves generated by distribution fields is substantially impacted by the non-local parameter.

FIGURE 3

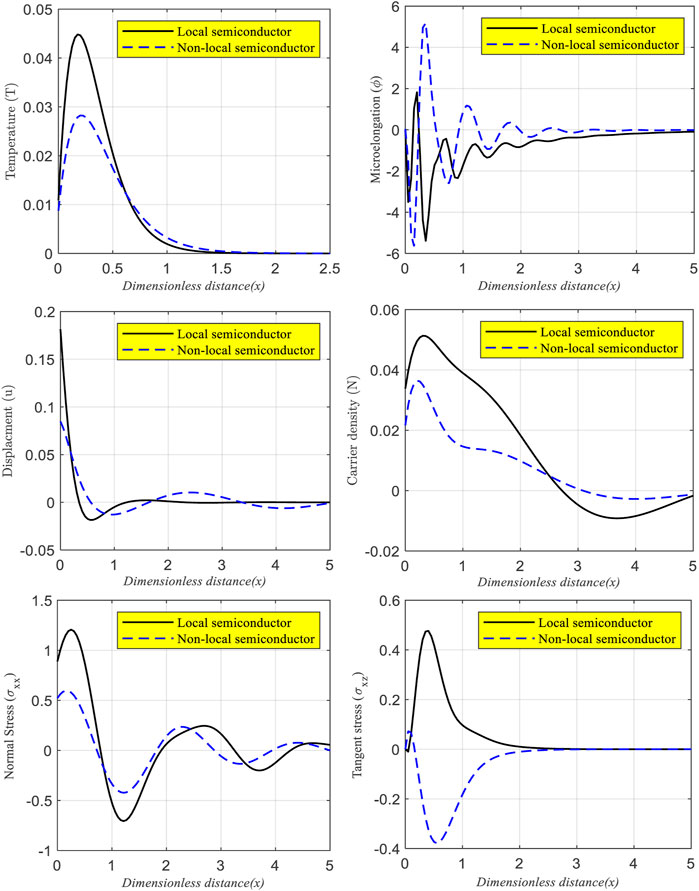
FIGURE 3. The wave propagation of the main fields according to variable thermal conductivity, the GL model, and laser pulses in the presence or absence of non-local parameter.

The examined functions plotted when $\pi =0,\pi =-0.02$ and $\pi =-0.04$ (three different thermal conductivity values) against the dimensionless distance are shown in Figure 4 under the GL model for non-local medium. These functions correspond to each of the three possible outcomes for the thermal conductivity ($\pi =0,\pi =-0.02$ and $\pi =-0.04$). The waves travel in a manner that is identical to that seen in Figure 2, except with unique explored function amplitude values. These values are determined by the several possible values of. The changes in thermal conductivity have a significant impact on the fields that have been investigated.

FIGURE 4

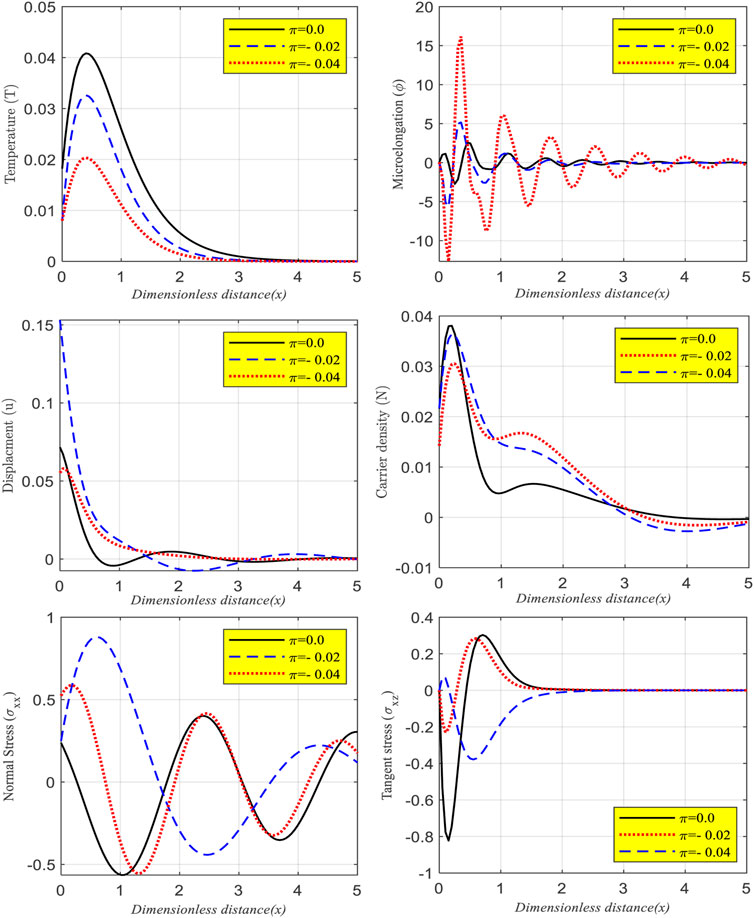
FIGURE 4. The principal fields as a function of horizontal distance over a range of thermal conductivities in a Si medium exhibiting non-local properties and laser pulses as predicted by the GL model.

Figure 5 shows the impact of the laser pulses on the wave propagation of the main physical filed. When the changing thermal conductivity ($\pi =-0.04$) happens at the same microscopic dimensionless time, calculations are carried out in accordance with the GL model of the non-local photo-thermoelasticity theory. During this category, the model was studied under the influence of laser pulses and without the influence of laser pulses. We notice through the propagation of the waves that the laser pulses clearly affect the distribution of the fields under study with the increase of the distance.

FIGURE 5

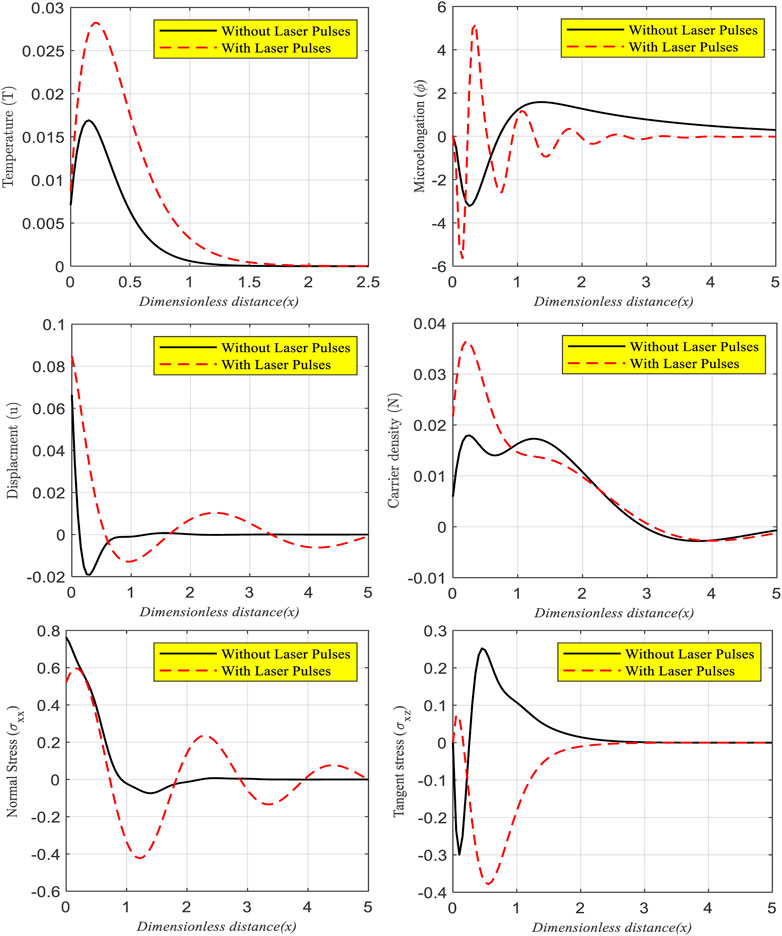
FIGURE 5. The wave propagation of the main fields according to variable thermal conductivity, the GL model, and the nonlocality medium in the presence or absence of laser pulses.

8 The validation of the results

When non-local parameter instances are missing and variable thermal conductivity is present, the present results are consistent with those in [47]. When the nanoscale microelongation parameters are not known and the thermal conductivity is constant ($\pi =0$) across a wide temperature range, the results of the present investigation are consistent with those presented in [46].

9 Conclusion

As a result of applying the nanoscale microelongated photo-thermoelasticity theory to the non-local semiconductor material, a novel model is proposed. In order to get a deeper understanding of how the thermal conductivity parameter influences the model within the context of photoexcitation transport mechanisms, we examine the model in a thermal domain. Graphical representations of the effects of wave propagation are provided for the thermal relaxation durations, changing thermal conductivity, laser pulses, and non-local parameters. In order to account for thermal memory fluctuation, two-dimensional deformation is accounted for utilizing model equations when thermal conductivity changes with temperature. Thermal relaxation durations have a substantial impact on the wave propagations of temperature increment, microelongation function, displacements, carrier density increase, normal stress, and tangential stress (CD, LS, and GL models). In contrast, all physical fields achieve equilibrium and satisfy the boundary conditions. Non-local factor has a significant influence on the distributions of the key fields. Variable thermal conductivity parameter values have a significant role in the propagation of waves. In a numerical study of the non-local semiconducting semiconductor silicon, the thermoelastic and plasma wave equations, together with the necessary boundary conditions, fulfill all physical field variables (n-type). In contrast, the effect of non-local factors and changing thermal conductivity has been extensively studied. The integration of thermal conductivity and non-local parameters has a significant impact on all field values in the half-space, such as temperature, displacements, stresses, carrier density, and chemical potential. The non-local microelongated semiconductor material may be used extensively in the fabrication of semiconductor devices such as integrated circuits, medical equipment, accelerometers, mobile phones, and optical lithography. This article’s study and findings will be essential for understanding how non-local semiconductors, such as diodes and triodes, are used in contemporary electronic devices.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KL: Conceptualization, Methodology, Software, Data curation. SE-S: Writing- Original draft preparation. KL: Supervision, Visualization, Investigation. AE-B: Software, Validation, AF and RC: New Software; Writing- Reviewing and Editing. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors extend their appreciation to Princess Nourah bint Abdulrahman University for fund this research under Researchers Supporting Project number (PNURSP2023R154) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Eringen AC. Microcontinuum field theories, vol. 1, foundations and solids. New York: Springer Verlag (1999).

Google Scholar

2. Eringen AC. Linear theory of micropolar elasticity. J Math Mech (1966) 15:909–23.

Google Scholar

3. Eringen AC. Theory of thermo-microstretch elastic solids. Int J Eng Sci (1990) 28(12), 1291–301. doi:10.1016/0020-7225(90)90076-u

CrossRef Full Text | Google Scholar

4. Sheoran D, Kumar R, Kumar S, Kalkal K. Wave propagation in an initially stressed rotating thermo-diffusive medium with two-temperature and micro-concentrations. Int J Numer Methods Heat Fluid Flow (2021) 31 (4), 1245–67. doi:10.1108/hff-05-2020-0305

CrossRef Full Text | Google Scholar

5. Othman M, Lotfy K. The influence of gravity on 2-D problem of two temperature generalized thermoelastic medium with thermal relaxation. J Comput Theor Nanoscience (2015) 12:2587–600. doi:10.1166/jctn.2015.4067

CrossRef Full Text | Google Scholar

6. De Cicco , Nappa L. On the theory of thermomicrostretch elastic solids. J Therm Stress (1999) 22(6):565–80. doi:10.1080/014957399280751

CrossRef Full Text | Google Scholar

7. Sheoran D, Kumar R, Thakran S, Kalkal K. Thermo-mechanical disturbances in a nonlocal rotating elastic material with temperature dependent properties. Int J Numer Methods Heat Fluid Flow (2021) 31(12):3597–620. doi:10.1108/hff-12-2020-0794

CrossRef Full Text | Google Scholar

8. Lotfy K, Abo-Dahab SM. Two-dimensional problem of two temperature generalized thermoelasticity with normal mode analysis under thermal shock problem. J Comput Theor Nanoscience (2015) 12, 1709–19. doi:10.1166/jctn.2015.3949‏‏‏

CrossRef Full Text | Google Scholar

9. Othman M, Lotfy K. Effect of rotation on plane waves in generalized thermo-microstretch elastic solid with one relaxation time. Multidiscipline Model Mat. Str. (2011) 7(1):43–62. doi:10.1108/15736101111141430

CrossRef Full Text | Google Scholar

10. Ramesh G, Prasannakumara B, Gireesha B, Rashidi M. Casson fluid flow near the stagnation point over a stretching sheet with variable thickness and radiation. J Appl Fluid Mech (2016) 9(3):1115–022. doi:10.18869/acadpub.jafm.68.228.24584

CrossRef Full Text | Google Scholar

11. Ezzat M, Abd-Elaal M. Free convection effects on a viscoelastic boundary layer flow with one relaxation time through a porous medium. J Franklin Inst (1997) 334:685–706. doi:10.1016/S0016-0032(96)00095-6

CrossRef Full Text | Google Scholar

12. Shaw S, Mukhopadhyay B. Periodically varying heat source response in a functionally graded microelongated medium. Appl Math Comput (2012) 218(11):6304–13. doi:10.1016/j.amc.2011.11.109

CrossRef Full Text | Google Scholar

13. Shaw S, Mukhopadhyay B. Moving heat source response in a thermoelastic micro-elongated Solid. J Eng Phys Thermophys (2013) 86(3):716–22. doi:10.1007/s10891-013-0887-y

CrossRef Full Text | Google Scholar

14. Ailawalia P, Sachdeva S, Pathania D. Plane strain deformation in a thermo-elastic microelongated solid with internal heat source. Int J Appl Mech Eng (2015) 20(4):717–31. doi:10.1515/ijame-2015-0047

CrossRef Full Text | Google Scholar

15. Sachdeva S, Ailawalia P. Plane strain deformation in thermoelastic micro-elongated solid. Civil Environ Res (2015) 7(2):92–8.

Google Scholar

16. Ailawalia P, Kumar S, Pathania D. Internal heat source in thermoelastic micro-elongated solid under Green Lindsay theory. J Theor Appl Mech (2016) 46(2):65–82. doi:10.1515/jtam-2016-0011

CrossRef Full Text | Google Scholar

17. Marin M, Vlase S, Paun M. Considerations on double porosity structure for micropolar bodies. AIP Adv (2015) 5(3):037113. doi:10.1063/1.4914912

CrossRef Full Text | Google Scholar

18. Eringen AC. Theory of nonlocal thermoelasticity. Int J Enfineering Sci (1974) 12:1063–77. doi:10.1016/0020-7225(74)90033-0

CrossRef Full Text | Google Scholar

19. Tzou DY. A unified field approach for heat conduction from macro to micro-scales. J Heat Transfer (1995) 117(1):8–16. doi:10.1115/1.2822329

CrossRef Full Text | Google Scholar

20. Tzou DY. The generalized lagging response in small-scale and high-rate heating. Int J Heat Mass Transfer (1995) 38(17):3231–40. doi:10.1016/0017-9310(95)00052-b

CrossRef Full Text | Google Scholar

21. Gupta M, Mukhopadhyay S. A study on generalized thermoelasticity theory based on non-local heat conduction model with dual-phase-lag. J Therm Stresses (2019) 42(9):1123–35. doi:10.1080/01495739.2019.1614503

CrossRef Full Text | Google Scholar

22. Tzou DY, Guo ZY. Nonlocal behavior in thermal lagging. Int J Therm Sci (2010) 49(7):1133–7. doi:10.1016/j.ijthermalsci.2010.01.022

CrossRef Full Text | Google Scholar

23. Choudhuri SKR. On a thermoelastic three-phase-lag model. J Therm Stresses (2007) 30(3):231–8. doi:10.1080/01495730601130919

CrossRef Full Text | Google Scholar

24. Eringen A, Edelen D. On nonlocal elasticity. Int J Eng Sci (1972) 10:233–48. doi:10.1016/0020-7225(72)90039-0

CrossRef Full Text | Google Scholar

25. Eringen A, Wegner J. Nonlocal continuum field theories. Appl Mech Rev (2003) 56(B20–B22):B20–2. doi:10.1115/1.1553434

CrossRef Full Text | Google Scholar

26. Gordon JP, Leite RCC, Moore RS, Porto SPS, Whinnery JR. Long-transient effects in lasers with inserted liquid samples. Bull Am Phys Soc (1964) 119:501–10.

Google Scholar

27. Kreuzer LB. Ultralow gas concentration infrared absorption spectroscopy. J Appl Phys (1971) 42:2934–43. doi:10.1063/1.1660651

CrossRef Full Text | Google Scholar

28. Tam AC. Ultrasensitive laser spectroscopy. New York: Academic Press (1983). p. 1–108.

CrossRef Full Text | Google Scholar

29. Tam AC. Applications of photoacoustic sensing techniques. Rev Mod Phys (1986) 58:381–431. doi:10.1103/revmodphys.58.381

CrossRef Full Text | Google Scholar

30. Tam AC. Photothermal investigations in solids and fluids. Boston: Academic Press (1989). p. 1–33.

Google Scholar

31. Hobinya A, Abbas I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys (2019) 15:102588. doi:10.1016/j.rinp.2019.102588

CrossRef Full Text | Google Scholar

32. Todorovic DM, Nikolic PM, Bojicic AI. Photoacoustic frequency transmission technique: Electronic deformation mechanism in semiconductors. J Appl Phys (1999) 85:7716–26. doi:10.1063/1.370576

CrossRef Full Text | Google Scholar

33. Song YQ, Todorovic DM, Cretin B, Vairac P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int J Sol Struct. (2010) 47:1871–5. doi:10.1016/j.ijsolstr.2010.03.020

CrossRef Full Text | Google Scholar

34. Lotfy K. The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field. Can J Phys (2016) 94:400–9. doi:10.1139/cjp-2015-0782

CrossRef Full Text | Google Scholar

35. Lotfy K. A novel model of photothermal diffusion (PTD) for polymer nano-composite semiconducting of thin circular plate. Physica B- Condenced Matter (2018) 537:320–8. doi:10.1016/j.physb.2018.02.036

CrossRef Full Text | Google Scholar

36. Lotfy K, Kumar R, Hassan W, Gabr M. Thermomagnetic effect with microtemperature in a semiconducting Photothermal excitation medium. Appl Math Mech Engl Ed (2018) 39(6):783–96. doi:10.1007/s10483-018-2339-9

CrossRef Full Text | Google Scholar

37. Mahdy A, Lotfy K, El-Bary A, Sarhan H. Effect of rotation and magnetic field on a numerical-refined heat conduction in a semiconductor medium during photo-excitation processes. The Eur Phys J Plus (2021) 136(5):1–17. doi:10.1140/epjp/s13360-021-01552-3

CrossRef Full Text | Google Scholar

38. Mahdy A, Lotfy K, El-Bary A, Washan W. Analytical solution of magneto-photothermal theory during variable thermal conductivity of a semiconductor material due to pulse heat flux and volumetric heat source. Waves in Random and Complex Media (2021) 31(6):2040–57. doi:10.1080/17455030.2020.1717673

CrossRef Full Text | Google Scholar

39. Lotfy K. A novel model for Photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field. Sci Rep (2019) 9:3319. doi:10.1038/s41598-019-39955-z

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Lotfy K. Effect of variable thermal conductivity during the photothermal diffusion process of semiconductor medium. Silicon (2019) 11:1863–73. doi:10.1007/s12633-018-0005-z

CrossRef Full Text | Google Scholar

41. Abbas I, Alzahranib F, Elaiwb A. A DPL model of photothermal interaction in a semiconductor material. Waves in Random and Complex media (2019) 29:328–43. doi:10.1080/17455030.2018.1433901

CrossRef Full Text | Google Scholar

42. Khamis A, El-Bary A, Lotfy K, Bakali A. Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alex Eng J (2020) 59(1):1–9. doi:10.1016/j.aej.2019.11.016

CrossRef Full Text | Google Scholar

43. Lotfy K, El-Bary A, El-Sharif A. Ramp-type heating micro-temperature for a rotator semiconducting material during photo-excited processes with magnetic field. Results Phys (2020) 19:103338. doi:10.1016/j.rinp.2020.103338

CrossRef Full Text | Google Scholar

44. Mondal S, Sur A. Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Waves in Random and Complex Media (2021) 31(6):1835–58. doi:10.1080/17455030.2019.1705426

CrossRef Full Text | Google Scholar

45. Ezzat M. Hyperbolic thermal-plasma wave propagation in semiconductor of organic material. Waves in Random and complex Media (2022) 32(1):334–58. doi:10.1080/17455030.2020.1772524

CrossRef Full Text | Google Scholar

46. Ezzat M. A novel model of fractional thermal and plasma transfer within a non-metallic plate. Smart Structures Syst (2021) 27(1):73–87.

Google Scholar

47. Ismail G, Gepreel K, Lotfy K, Mahdy A, El-Bary A, Saeed A. Influence of variable thermal conductivity on thermal-plasma-elastic waves of excited microelongated semiconductor. Alexandria Eng J (2022) 61(12):12271–82. doi:10.1016/j.aej.2022.06.024

CrossRef Full Text | Google Scholar

48. Chteoui R, Lotfy K, El-Bary A, Allan M. Hall current effect of magnetic-optical elastic-thermal-diffusive non-local semiconductor model during electrons-holes excitation processes. Crystals (2022) 12:1680. doi:10.3390/cryst12111680

CrossRef Full Text | Google Scholar

49. Almoneef A, El-Sapa S, Lotfy K, El-Bary A, Saeed A. Laser short-pulse effect on thermodiffusion waves of fractional heat order for excited nonlocal semiconductor. Adv Condensed Matter Phys (2022) 2022:1523059. doi:10.1155/2022/1523059

CrossRef Full Text | Google Scholar

50. Zenkour A. On generalized three-phase-lag models in photo-thermoelasticity. Int J Appl Mech (2022) 14:2250005. doi:10.1142/S1758825122500053

CrossRef Full Text | Google Scholar

51. Zenkour A. Exact coupled solution for photothermal semiconducting beams using a refined multi-phase-lag theory. Opt Laser Tech (2020) 128:106233. doi:10.1016/j.optlastec.2020.106233

CrossRef Full Text | Google Scholar

52. Zenkour A. Effect of thermal activation and diffusion on a photothermal semiconducting half-space. J Phys Chem Sol (2019) 132:56–67. doi:10.1016/j.jpcs.2019.04.011

CrossRef Full Text | Google Scholar

53. Zenkour A. Refined multi-phase-lags theory for photothermal waves of a gravitated semiconducting half-space. Compos Structures (2019) 212:346–64. doi:10.1016/j.compstruct.2019.01.015

CrossRef Full Text | Google Scholar

54. Lord H, Shulman Y. A generalized dynamical theory of thermoelasticity. J Mech Phys Solid (1967) 15:299–309. doi:10.1016/0022-5096(67)90024-5

CrossRef Full Text | Google Scholar

55. Green A, Lindsay K. Thermoelasticity. J Elast (1972) 2:1–7. doi:10.1007/bf00045689

CrossRef Full Text | Google Scholar

56. Biot M. Thermoelasticity and irreversible thermodynamics. J Appl Phys (1956) 27:240–53. doi:10.1063/1.1722351

CrossRef Full Text | Google Scholar

57. Youssef H, El-Bary A. Two-temperature generalized thermoelasticity with variable thermal conductivity. J Therm Stresses (2010) 33:187–201. doi:10.1080/01495730903454793

CrossRef Full Text | Google Scholar

58. Mandelis A, Nestoros M, Christofides C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt Eng (1997) 36(2):459–68. doi:10.1117/1.601217

CrossRef Full Text | Google Scholar

59. LotfyHassan KW, El-Bary AA, Kadry MA. Response of electromagnetic and Thomson effect of semiconductor medium due to laser pulses and thermal memories during photothermal excitation. Results Phys (2020) 16:102877. doi:10.1016/j.rinp.2019.102877

CrossRef Full Text | Google Scholar

60. Liu J, Han M, Wang R, Xu S, Wang X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J Appl Phys (2022) 131:065107. doi:10.1063/5.0082014

CrossRef Full Text | Google Scholar

Nomenclature