
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 27 June 2023
Sec. Nuclear Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1166566
This article is part of the Research Topic Advances in Laser-Driven Nuclear Physics View all 19 articles
 Hanxu Zhang
Hanxu Zhang Xu Wang*
Xu Wang*A unified theoretical framework is presented for the isomeric excitation of the 229Th nucleus via electronic processes. These processes include nuclear excitation by electron transition (NEET), nuclear excitation by electron capture (NEEC), and nuclear excitation by inelastic electron scattering (NEIES). Detailed calculation results on the excitation rate and the excitation cross section are presented.
In 1976, Kroger and Reich proposed that 229Th has an isomeric state with energy below 100 eV (denoted as 229mTh) [1]. With the development of experimental techniques, the energy of this isomeric state was estimated to be 1 ± 4 eV [2], 3.5 ± 1.0 eV [3], 7.6 ± 0.5 eV [4], and recently 8.28 ± 0.17 eV [5]. The energy of the second excited state of 229Th is 29 keV. The second lowest nuclear state is the isomeric state of 235U, which has an energy of 76 eV [6–8]. Therefore, 229mTh is the only known nuclear excited state on the 1-eV order of magnitude, and it has attracted much attention in recent years for its potential applications in nuclear optical clocks [9–12], nuclear lasers [13], checking temporal variations of fundamental constants [14–16], etc.
These potential applications make it desirable to prepare the isomeric state in a controllable and efficient way. Currently, 229mTh can be obtained from α decay of 233U or β decay of 229Ac [17]. The efficiency of the former decay is very low with the obtained nuclei having a recoil energy of 84 keV, and the latter decay is subject to low yield of 229Ac. Direct light excitation using vacuum ultraviolet light has been attempted by several groups without success [18–21]. Possible reasons include inaccurate knowledge of the isomeric energy, competing fluorescence signals from the electrons, competition with nonradiative channels, etc. In 2019, Masuda et al. obtained this isomeric state experimentally by an indirect light excitation approach [22]. They used narrowband 29 keV synchrotron radiations to excite the 229Th nuclei from the ground state to the second excited state which then decays preferably into the isomeric state [23]. Excitation processes via coupling to electrons have also been extensively studied, for example, electronic bridge (EB) processes [24–30], inelastic scattering of electrons [31, 32] or muons [33], and laser-driven electron recollision [34–36].
In the current paper we consider nuclear excitation of 229Th by three different but related electronic processes. They include nuclear excitation by electron transition (NEET) [37–41], nuclear excitation by electron capture (NEEC) [42–50], and nuclear excitation by inelastic electron scattering (NEIES) [31, 32, 51, 52]. Figure 1 shows an illustration of these three processes: (a) NEET occurs when the electron transitions from a higher bound state to a lower bound state and excites the nucleus simultaneously. It was first proposed in 1973 in 235U [37] and has been confirmed experimentally with 197Au [38, 40]. (b) NEEC occurs when a free electron is captured by an ion and excites the nucleus with the released energy. It has been proposed and widely discussed for a long time, mostly with 93Mo. At present there are still discrepancies between theoretical calculations and experimental results, and also between different experiments [48–50]. (c) NEIES occurs when the electron transitions from a higher continuum state to a lower continuum state. It is a widely studied process in nuclear physics, almost all with high-energy electrons [52–58]. Tkalya proposes to excite 229Th with low-energy electrons on the order of 10 eV [31]. We have also calculated and analyzed this process in depth in our previous work [32].
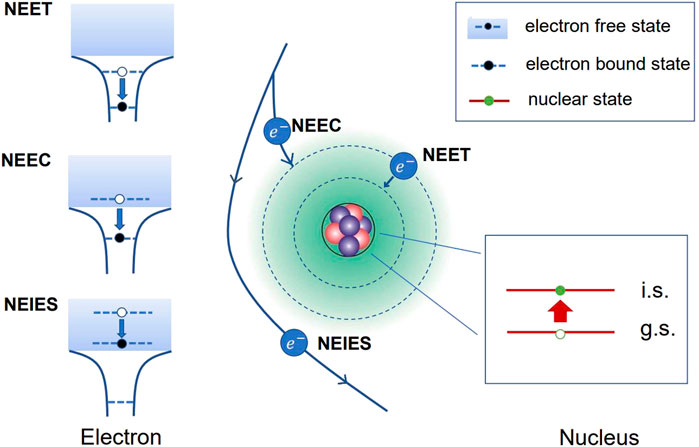
FIGURE 1. Schematic illustration of NEET, NEEC and NEIES processes. NEET is associated with bound-bound electronic transitions, NEEC is associated with free-bound transitions, and NEIES is associated with free-free transitions. The nucleus is excited from the ground state to the isomeric state by the energy released from the electronic process.
The goal of the current work is twofold. One is to provide a unified theoretical framework for the three electronic excitation processes. They are usually studied separately, but they are in fact related with differences only in the type of the initial or the final electronic states. The other goal is to present the NEET, NEEC, and NEIES results for 229mTh. Although the NEIES process has been studied previously [31, 32], results of NEET or NEEC have not been reported for 229Th in the literature, as far as we are aware of. Our results presented here can be directly used for the excitation of 229Th in complex environments, such as plasmas, beam collisions, etc.
The common point of NEET, NEEC, and NEIES is that the electron transitions from a state with higher energy to a state with lower energy, and the nucleus is excited simultaneously with the released energy. No photons are emitted during these processes. The system (consisting of a nucleus, an electron, and a quantized radiation field) transitions from an initial state |i⟩ (t = ti) to a final state |f⟩ (t = tf) under the effect of an interaction Hamiltonian V. The time evolution operator of the system is given as
where
Expand the time evolution operator and assume the following three conditions: (a) |i⟩ ≠ |f⟩; (b) ti = 0, tf = ∞; and (c) the initial and final states have a total dissipation rate Γt, so the time evolution of the wave function is multiplied by
where I is the unit operator. The transition rate can be given as the transition probability divided by the lifetime τ = 1/Γt of the system
where Lt is a normalized Lorenzian function
Consider the on-shell condition of Ei = Ef, and if the dissipation in the system or the subsequent decay process can be ignored, then Γt approaches 0, and the Lorenzian reduces to the Dirac-δ function
Given the interaction operator V and the initial and final states of the system, the interaction matrix element Vfi can be calculated. Then the transition rate can then be obtained with Eq. 4 or Eq. 6.
The system under consideration consists of a nucleus, an electron, and a quantized radiation field. The total Hamiltonian can be written as
where Hn is the Hamiltonian for the nucleus, He for the electron, and Hrad for the radiation field. V is the interaction Hamiltonian. The initial state |i⟩ and the final state |f⟩ are eigenstates of H0.
The state of the total system is written as the product of the states of the nucleus |IM⟩, of the electron |ϕ⟩, and of the radiation field with n optical quanta |n⟩:
Here Ii,f and Mi,f are the total angular momentum and the magnetic quantum number of the initial or the final state of the nucleus.
For the nuclear part, the initial state is the nuclear ground state with energy, Eg = 0 eV and spin parity
The electronic wave functions are eigenstates of the time-independent Dirac equation
where
ρnu/el is the charge density of the nucleus/electron shell.
For the NEET process, |ϕi⟩ and |ϕf⟩ are both Dirac bound states with the form
where gnη(r) and fnη(r) are radial wave functions, n is the principal quantum number, η is a notation determined by the total angular momentum j and the orbital angular momentum l, and m is the magnetic quantum number of j. η is given by
For η < 0, l should be changed to l′ = 2j − l. Ωηm are spherical spinors
where χν is
For the NEIES process, |ϕi⟩ and |ϕf⟩ are both Dirac scattering states, which can be expanded into partial wave series [59, 60]:
The initial state (before scattering) takes the plus sign and the final state (after scattering) takes the minus sign: |ϕi⟩ = |kiνi⟩(+) and |ϕf⟩ = |kfνf⟩(−). k is the wave vector.
For the NEEC process, |ϕi⟩ is a Dirac scattering state and |ϕf⟩ is a Dirac bound state.
The interaction Hamiltonian V is given by
where the first integral is the couplings between the nuclear current density jn and the electron current density je with the vector potential A of the radiation field. The second integral is the Coulomb interaction between the nucleus and the electron, with ρn and ρe being the charge density operator of the nucleus and of the electron, respectively. The vector potential of the radiation field can be expanded in multipole components as
In the above expression, λ, μ, q are the angular momentum quantum number, magnetic quantum number, and wave number, respectively, and
Here R is the radius of the spherical volume under consideration, L is the angular momentum operator, jλ(qr) is a spherical Bessel function, and Yλμ is the spherical harmonics. The expansion coefficient a and its conjugate are the operators for photon annihilation and creation. The matrix elements of these operators are
where |n⟩ represents a number state with n photons.
Using Eq. 8 and Eqs 15–18, the transition matrix element Vfi can be obtained [61]
where
In the above formulas κ = ΔE/c with ΔE = 8.28 eV being the energy of the isomeric state, and
For NEET, the initial and final states of the electron may have spontaneous radiation, and the isomeric state of the nucleus has an internal conversion rate and a radiation decay rate. Thus, Γt in Eq. 5 will be ΓNEET = Γi + Γf + Γn, where Γi/f is the spontaneous emission rate of electronic state, Γn = ΓIC + Γγ is the natural width of the isomeric state, with ΓIC being the internal conversion rate and Γγ being the radiation decay rate.
Introduce reduced nuclear transition probabilities
With Eqs 10, 19, averaging over initial states and summing over final states, the modulus square of the matrix element in Eq. 4 becomes
where
and
For Mλ type transition, one needs to change
With Eq. 4 and Eq. 25, we obtain the transition rate of NEET
Here,
The excitation rate for the NEEC process can also be derived from Eq. 4, except that Γt will be different, since the initial state is now a free state. If the electron is captured into the ionic ground state, then ΓNEEC = Γn. Otherwise ΓNEEC = Γf + Γn. With Eqs. 10, 14, 19, 24, the modulus square of the interaction matrix element becomes
The excitation cross section can be defined through ω = σj, with j being the flux of the initial free state
ΓNEEC is usually very small so the Lorenzian can be approximated as the Dirac-δ function, which has been referred as the isolated resonance approximation [46]. Generally speaking, if the energy of the incoming electron has a certain distribution, it is often necessary to integrate over the energy of the free electron. The so-called resonant strength is defined to simplify the calculation
For NEIES, Fermi’s Golden Rule can be obtained by summing over the final energy states of the electron with Eq. 6
where Ω is the solid angle of the outgoing direction,
With Eq. 14 and 19 and Eq. 24, averaging over initial states and summing over final states, the modulus square of the interaction matrix element becomes
And the total NEIES cross section is
In this section, we present calculation results of 229mTh excited via NEET, NEEC, and NEIES. For the 229Th nucleus, the spin parity of the ground state is 5/2+ and that of the isomeric state is 3/2+, so the transition type is magnetic dipole (M1) or electronic quadrupole (E2). Relevant information about the nuclear transition matrix elements is packed in the reduced nuclear transition probabilities. There are some degree of uncertainties (roughly by a factor of two) with them, because they are obtained from model calculations or experimental analyses with approximations, for example, calculations in the framework of a quasiparticle-phonon model with inclusion of Coriolis couplings [63, 64], or experimental data analyses [65–68] exploiting Alaga rules [69, 70]. Ab initio calculations of B (E2/M1) for a nucleus like 229Th are out of reach in the foreseeable future, and there is no conclusive means to judge which set of values is better than other sets. In this paper, we use the values suggested by Minkov and Pálffy in 2017 [71]
where W.u. stands for Weisskopf units. Note that the direction of nuclear transition has the relation
According to Eq. 28 and 30 and Eq. 34, the calculation of the transition rate or the cross section eventually reduces to the calculation of electron radial wave functions in Eq. 27. In this paper, all calculations involving the electron radial wave functions, including the spontaneous emission rates, are performed using the code RADIAL [72] with the Dirac-Hartree-Fock-Slater method [73, 74] and a Fermi charge distribution for the nucleus.
NEET occurs when the energy difference between two electronic bound states matches the nuclear isomeric energy ΔE = Eis − Eg = 8.28 eV. The finite widths of the initial and final states allow transitions to occur when there is a little mismatch of energy. The bigger the energy mismatch, the smaller the excitation rate. For 229mTh, the half-life is 7 ± 1 μs (ΓIC ≈ 10–11 eV) via internal conversion [75] and about 1880 s (Γγ ≈ 10–19 eV) via γ decay [76], while the half-life of the electronic state is typically on the order of 1–10 ns (Γi/f ≈ 10–8 − 10–7 eV). Therefore, usually Γi/f ≫ΓIC ≫Γγ.
Because ΓNEET ≈ Γi + Γf is on the order of 10–8 eV, the width of the Lorenzian is very narrow. To ensure a nonnegligible excitation rate, we try to find ϕi − ϕf pairs that satisfy: (i) the energy constraint
The first ionization energy of neutral 229Th is 6.3 eV, so NEET can not occur in neutral 229Th. The energy levels of 229Th with different ionic states are also different. As listed in Table 1, for 229Th1+, a single transition 7p3/2 → 5f5/2 is found satisfying both constraints (
The initial electronic state 7p3/2 can decay via spontaneous emission, the rate of which is calculated to be Γi = 3.76 × 10−9 a. u., corresponding to a lifetime of 6.4 ns. The final state 5f5/2 does not have a spontaneous emission channel. For the nuclear part, the IC channel is closed because the energy of the final electronic state 5f5/2 is below −8.28 eV. The γ decay rate Γγ (= 1.28 × 10−20 a. u.) is negligible due to the very long lifetime. Therefore for this NEET channel ΓNEET ≈ Γi = 3.76 × 10−9 a. u., and the rate of NEET is calculated to be
This value is the rate of NEET for a single 229Th+ ion assuming that the ion is prepared in the 7p3/2 initial state.
Similar calculations can be performed for the 229Th2+ ion and the 229Th3+ ion. For the 229Th2+ ion, four NEET channels are found satisfying the above two constraints, as listed in Table 2. For the 229Th3+ ion, more than 20 NEET channels are found satisfying the above two constraints. However, most of them contribute little. Table 3 lists the seven channels with the largest NEET rate.
The NEEC cross sections are calculated with Eq. 30. Figure 2A presents the largest 10 NEEC channels of 229Th1+,2+,3+ ions. The peak values of these dominant channels are on the order of 103 to 109 b. The highest one shown by the inset corresponds to electron capture into the ground state (7s1/2) of the 229Th1+ ion, which has no spontaneous emission channel. In this case, ΓNEEC = ΓIC = 8 × 10−11 eV. It should be pointed out that each line in Figure 2A is actually a Lorenzian with a relatively narrow width, as illustrated by the inset. The peak represents the resonant condition
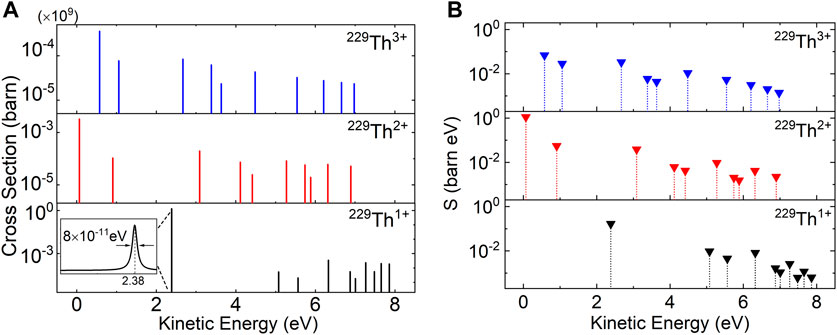
FIGURE 2. (A) Isomeric excitation cross sections of 229Th1+,2+,3+ ions through NEEC. For each ionic state, the largest 10 NEEC channels are shown. The inset zooms in a small energy range around 2.38 eV. (B) The corresponding resonant strengths S.
In real calculations, it is often found that the S values of some channels are several orders of magnitude larger than other channels. Figure 3A shows the resonant strengths of different channels captured into electronic states with different principal quantum numbers and orbital angular momenta. When the principal quantum number increases, the resonant strength decreases. And when the orbital angular momentum increases, the resonant strength decreases exponentially. The reason is that the radial matrix element in Eqs 27 and 31 decreases rapidly with the increase of n and l. Figure 3B shows the radial matrix element Mfi as a function of the integral upper limit r. When the final state is 7s1/2, Mfi is lager than that of 10s1/2 and 7d3/2, and the value of Mfi converges where r is very small (usually smaller than 0.1 a. u.). This means that the wave function close to the nucleus is dominant. These phenomena are caused by the change of the radial wave function with n and l. For the final state of electron, the larger the n and l, the farther away the electron from the nucleus, the smaller the amplitude of the wave function near the nucleus. For the initial state of electron, partial-wave components with small angular momenta are more appreciably distorted [32, 36]. Therefore, the amplitudes of the partial wave with large angular momenta are much smaller than that with l = 0.
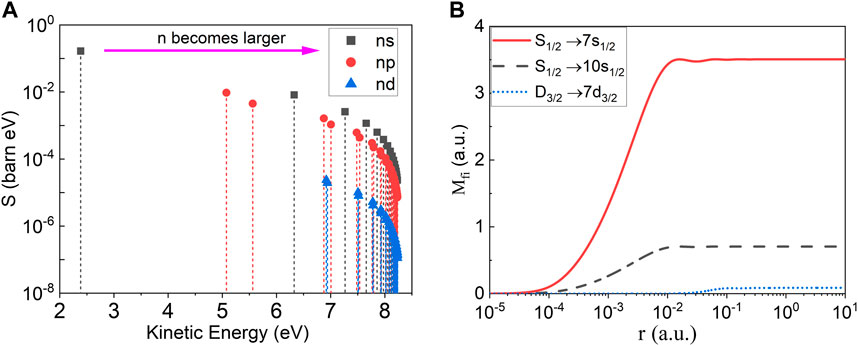
FIGURE 3. (A) NEEC resonant strengths S for captures into ns, np, nd electronic states of the 229Th1+ ion as a function of the free-electron energy. (B) Radial matrix element Mfi of partial wave transition channels when the free electron is captured into different bound states.
The NEIES process has been discussed in detail previously, for 229Th [31, 32] and 235U [51]. Here we just mention it briefly.
Figure 4 displays the NEIES cross sections for different ion-core potentials. Three cases have been shown, namely, the neutral 229Th atom, the bare nucleus 229Th90+, and without the ion-core potential [i.e.,
In this section, we consider isomer excitation via the above-explained electronic processes in plasmas, which are assumed to be in thermal equilibrium. The distribution of ionic states can be estimated using the Saha equation [77, 78]
where
The rate of exciting a single 229Th nucleus in the plasma is
where
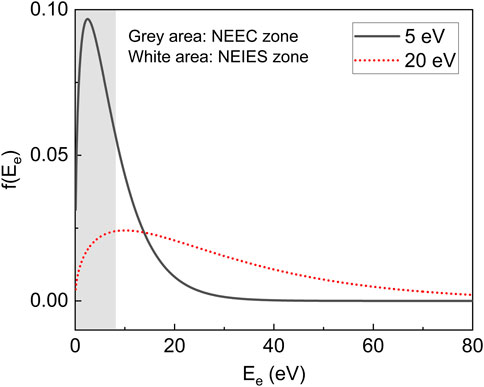
FIGURE 5. The kinetic energy distribution of the electrons for kBT = 5 eV and 20 eV. The gray area (Ee < 8.3 eV) indicates the NEEC zone, and the white area (Ee > 8.3 eV) indicates the NEIES zone.
Example results are shown in Table 4 for two different temperatures (5 eV, 20 eV) and two different electron densities (1016 cm−3, 1020 cm−3). Under these conditions,
In contrast, NEEC and NEIES processes depend more sensitively on the plasma parameters because their initial states are free states. Whether NEEC or NEIES dominates depends on the temperature. For example, at kBT = 5 eV,
(a) Note that the NEET rates given in Sec 3.1 are based on the assumption that the ion has been prepared in the desired excited state ϕi. However, one needs to keep in mind that it may not be an easy task to prepare a specific ionic excited state. As shown in Sec 3.4, in plasma environments NEET is usually less efficient than NEEC or NEIES. An experimental environment that can more precisely control the ion excited state may favor the NEET process, such as an electron beam ion trap [80].
One should also bear in mind that the energy of the 229Th isomer is only known with an uncertainty of 0.17 eV, which may result in an underestimation or overestimation of the calculated NEET rate. This uncertainty may lead to an uncertainty of about 1–4 orders of magnitude in the NEET rate. However, without a more precise determination of the isomeric energy, little can be done further, except for more precise calculations of the electronic structure and listing out possible NEET channels based on the current value of the isomeric energy.
(b) The NEEC process mostly occurs with free-electron energies within the range (0, Eis) because the final state of the electron is a bound state with a negative energy. Rare exceptions might exist if the final state is a bound state within the continuum, for example, a doubly excited state. These exceptions are beyond the scope of the current study, but might worth an investigation.
(c) The NEIES process can be realized more straightforwardly by using an external electron beam with electron energies tuned to values corresponding to the highest excitation cross sections, i.e., around 10 eV from Figure 4.
(d) Parallel to these nuclear-excitation processes are a few atomic processes, including electron-impact ionization, electron-impact atomic excitation, and radiative recombination. The cross section of electron-impact ionization is usually on the order of 10–16 cm2 [81]. The cross section of electron-impact atomic excitation is usually on the order of 10–19 cm2 [81]. And the cross section of radiative recombination is usually between 10–18 to 10–23 cm2 [82]. They are at least several orders of magnitude stronger than the nuclear excitation processes and little interference is expected between the atomic processes and the nuclear-excitation processes [83].
In this paper, we consider nuclear excitation of 229Th from the ground state to the low-lying isomeric state via electronic processes including NEET, NEEC and NEIES. We present a unified theoretical framework for the three processes with formulas for the excitation rate and the excitation cross section. These three processes are usually discussed separately for different nuclei, and we believe that a unified theoretical framework is helpful and useful for the general reader in this community. We emphasize that this is the first time the NEET and NEEC processes of 229Th are investigated, although the accuracy of the NEET rates are limited by the current uncertainty in the isomeric energy. Detailed numerical results are presented which can be used directly in future studies.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
HZ and XW contributed to this work from four aspects. 1) HZ performed the formula derivation. 2) HZ and XW performed the analysis of numerical results. 3) HZ wrote the first draft of the manuscript. 4) XW assisted with the discussion and revised the article. All authors contributed to the article and approved the submitted version.
We acknowledge funding support from NSFC Grant No. 12088101.
The authors acknowledge useful discussions with Mr Boqun Liu.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Kroger LA, Reich CW. Features of the low-energy level scheme of 229Th as observed in the α-decay of 233U. Nucl Phys A (1976) 259:29–60. doi:10.1016/0375-9474(76)90494-2
2. Reich CW, Helmer RG. Energy separation of the doublet of intrinsic states at the ground state of 229Th. Phys Rev Lett (1990) 64:271–3. doi:10.1103/PhysRevLett.64.271
3. Helmer RG, Reich CW. An excited state of 229Th at 3.5 eV. Phys Rev C (1994) 49:1845–58. doi:10.1103/PhysRevC.49.1845
4. Beck BR, Becker JA, Beiersdorfer P, Brown GV, Moody KJ, Wilhelmy JB, et al. Energy splitting of the ground-state doublet in the nucleus 229Th. Phys Rev Lett (2007) 98:142501. doi:10.1103/PhysRevLett.98.142501
5. Seiferle B, von der Wense L, Bilous PV, Amersdorffer I, Lemell C, Libisch F, et al. Energy of the 229Th nuclear clock transition. Nature (2019) 573:243–6. doi:10.1038/s41586-019-1533-4
6. Huizenga J, Rao C, Engelkemeir D. 27-minute isomer of 235U. Phys Rev (1957) 107:319–20. doi:10.1103/PhysRev.107.319
7. Freedman MS, Porter FT, Wagner F, Day P. Transition in 26-min 235mU of less than 23 electronvolts. Phys Rev (1957) 108:836–41. doi:10.1103/PhysRev.108.836
8. Browne E, Tuli J. Nuclear data sheets for A = 235. Nucl Data Sheets (2014) 122:205–92. doi:10.1016/j.nds.2014.11.002
9. Pauli W Zur frage der theoretischen deutung der satelliten einiger spektrallinien und ihrer beeinflussung durch magnetische felder. Naturwissenschaften (1924) 12:741–3. doi:10.1007/BF01504828
10. Peik E, Tamm C. Nuclear laser spectroscopy of the 3.5 eV transition in 229Th. EPL (2003) 61:181–6. doi:10.1209/epl/i2003-00210-x
11. Rellergert WG, DeMille D, Greco RR, Hehlen MP, Torgerson JR, Hudson ER. Constraining the evolution of the fundamental constants with a solid-state optical frequency reference based on the 229Th nucleus. Phys Rev Lett (2010) 104:200802. doi:10.1103/PhysRevLett.104.200802
12. Campbell CJ, Radnaev AG, Kuzmich A, Dzuba VA, Flambaum VV, Derevianko A. Single-ion nuclear clock for metrology at the 19th decimal place. Phys Rev Lett (2012) 108:120802. doi:10.1103/PhysRevLett.108.120802
13. Tkalya EV. Proposal for a nuclear gamma-ray laser of optical range. Phys Rev Lett (2011) 106:162501. doi:10.1103/PhysRevLett.106.162501
14. Flambaum VV. Enhanced effect of temporal variation of the fine structure constant and the strong interaction in 229Th. Phys Rev Lett (2006) 97:092502. doi:10.1103/PhysRevLett.97.092502
15. Berengut JC, Dzuba VA, Flambaum VV, Porsev SG. Proposed experimental method to determine α sensitivity of splitting between ground and 7.6 eV isomeric states in 229Th. Phys Rev Lett (2009) 102:210801. doi:10.1103/PhysRevLett.102.210801
16. Fadeev P, Berengut JC, Flambaum VV. Sensitivity of 229Th nuclear clock transition to variation of the fine-structure constant. Phys Rev A (2020) 102:052833. doi:10.1103/PhysRevA.102.052833
17. Verlinde M, Kraemer S, Moens J, Chrysalidis K, Correia J, Cottenier S, et al. Alternative approach to populate and study the 229Th nuclear clock isomer. Phys Rev C (2019) 100:024315. doi:10.1103/PhysRevC.100.024315
18. Jeet J, Schneider C, Sullivan ST, Rellergert WG, Mirzadeh S, Cassanho A, et al. Results of a direct search using synchrotron radiation for the low-energy 229Th nuclear isomeric transition. Phys Rev Lett (2015) 114:253001. doi:10.1103/PhysRevLett.114.253001
19. Yamaguchi A, Kolbe M, Kaser H, Reichel T, Gottwald A, Peik E. Experimental search for the low-energy nuclear transition in 229Th with undulator radiation. New J Phys (2015) 17:053053. doi:10.1088/1367-2630/17/5/053053
20. Stellmer S, Kazakov G, Schreitl M, Kaser H, Kolbe M, Schumm T. Attempt to optically excite the nuclear isomer in 229Th. Phys Rev A (2018) 97:062506. doi:10.1103/PhysRevA.97.062506
21. von der Wense L, Seiferle B, Stellmer S, Weitenberg J, Kazakov G, Pálffy A, et al. A laser excitation scheme for 229mTh. Phys Rev Lett (2017) 119:132503. doi:10.1103/PhysRevLett.119.132503
22. Masuda T, Yoshimi A, Fujieda A, Fujimoto H, Haba H, Hara H, et al. X-ray pumping of the 229Th nuclear clock isomer. Nature (2019) 573:238–42. doi:10.1038/s41586-019-1542-3
23. Tkalya EV, Zherikhin AN, Zhudov VI. Decay of the low-energy nuclear isomer 229mTh (3/2+, 3.5±1.0 eV) in solids (dielectrics and metals): A new scheme of experimental research. Phys Rev C (2000) 61:064308. doi:10.1103/PhysRevC.61.064308
24. Tkalya EV. Probability of nonradiative excitation of nuclei in transitions of an electron in an atomic shell. Sov Phys JETP (1992) 75:200–9.
25. Porsev SG, Flambaum VV. Electronic bridge process in 229Th+. Phys Rev A (2010) 81:042516. doi:10.1103/PhysRevA.81.042516
26. Porsev SG, Flambaum VV, Peik E, Tamm C. Excitation of the isomeric 229mTh nuclear state via an electronic bridge process in 229Th+. Phys Rev Lett (2010) 105:182501. doi:10.1103/PhysRevLett.105.182501
27. Bilous PV, Peik E, Pálffy A. Laser-induced electronic bridge for characterization of the 229mTh →229gTh nuclear transition with a tunable optical laser. New J Phys (2018) 20:013016. doi:10.1088/1367-2630/aa9cd9
28. Dzyublik AY. Excitation of 229mTh in the electron bridge via continuum, as a scattering process. Phys Rev C (2020) 102:024604. doi:10.1103/PhysRevC.102.024604
29. Bilous PV, Bekker H, Berengut JC, Seiferle B, von der Wense L, Thirolf PG, et al. Electronic bridge excitation in highly charged 229Th ions. Phys Rev Lett (2020) 124:192502. doi:10.1103/PhysRevLett.124.192502
30. Nickerson BS, Pimon M, Bilous PV, Gugler J, Beeks K, Sikorsky T, et al. Nuclear excitation of the 229Th isomer via defect states in doped crystals. Phys Rev Lett (2020) 125:032501. doi:10.1103/PhysRevLett.125.032501
31. Tkalya EV. Excitation of 229mTh at inelastic scattering of low energy electrons. Phys Rev Lett (2020) 124:242501. doi:10.1103/PhysRevLett.124.242501
32. Zhang H, Wang W, Wang X. Nuclear excitation cross section of 229Th via inelastic electron scattering. Phys Rev C (2022) 106:044604. doi:10.1103/PhysRevC.106.044604
33. Tkalya EV Cross section of the coulomb excitation of by low energy muons. Chin Phys C (2021) 45:094102. doi:10.1088/1674-1137/ac0b3a
34. Wang W, Zhou J, Liu B, Wang X. Exciting the isomeric 229Th nuclear state via laser-driven electron recollision. Phys Rev Lett (2021) 127:052501. doi:10.1103/PhysRevLett.127.052501
35. Wang W, Zhang H, Wang X. Strong-field atomic physics meets 229Th nuclear physics. J Phys B: Mol Opt Phys (2022) 54:244001. doi:10.1088/1361-6455/ac45ce
36. Wang X. Nuclear excitation of 229Th induced by laser-driven electron recollision. Phys Rev C (2022) 106:024606. doi:10.1103/PhysRevC.106.024606
37. Morita M. Nuclear excitation by electron transition and its application to uranium 235 separation. Prog Theor Phys (1973) 49:1574–86. doi:10.1143/PTP.49.1574
38. Fujioka H, Ura K. Nanosecond stroboscopic electron spectroscopy for observation of nuclear excitation by electron transition (NEET) in 197Au. Jpn J Appl Phys (1985) 24:1703. doi:10.1143/JJAP.24.1703
39. Tkalya EV. Nuclear excitation in atomic transitions (NEET process analysis). Nucl Phys A (1992) 539:209–22. doi:10.1016/0375-9474(92)90267-N
40. Kishimoto S, Yoda Y, Seto M, Kobayashi Y, Kitao S, Haruki R, et al. Observation of nuclear excitation by electron transition in 197Au with synchrotron X-rays and an avalanche photodiode. Phys Rev Lett (2000) 85:1831–4. doi:10.1103/PhysRevLett.85.1831
41. Sakabe S, Takahashi K, Hashida M, Shimizu S, Iida T. Elements and their transitions feasible for NEET. Data Nucl Data Tables (2005) 91:1–7. doi:10.1016/j.adt.2005.07.002
42. Goldanskii VI, Namiot VA. On the excitation of isomeric nuclear levels by laser radiation through inverse internal electron conversion. Phys Lett B (1976) 62:393–4. doi:10.1016/0370-2693(76)90665-1
43. Cue N. Nuclear excitation by target electron capture. Nucl Instrum Methods Phys Res B (1989) 40:25–7. doi:10.1016/0168-583X(89)90914-2
44. Yuan ZS, Kimball JC. First-principles calculation of the cross sections for nuclear excitation by electron capture of channeled nuclei. Phys Rev C (1993) 47:323–8. doi:10.1103/PhysRevC.47.323
45. Harston M, Chemin J. Mechanisms of nuclear excitation in plasmas. Phys Rev C (1999) 59:2462–73. doi:10.1103/PhysRevC.59.2462
46. Pálffy A, Scheid W, Harman Z. Theory of nuclear excitation by electron capture for heavy ions. Phys Rev A (2006) 73:012715. doi:10.1103/PhysRevA.73.012715
47. Gunst J, Litvinov YA, Keitel CH, Pálffy A. Dominant secondary nuclear photoexcitation with the X-ray free-electron laser. Phys Rev Lett (2014) 112:082501. doi:10.1103/PhysRevLett.112.082501
48. Chiara C, Carroll J, Carpenter M, Greene J, Hartley D, Janssens R, et al. Isomer depletion as experimental evidence of nuclear excitation by electron capture. Nature (2018) 554:216–8. doi:10.1038/nature25483
49. Wu Y, Keitel CH, Pálffy A. 93mMo isomer depletion via beam-based nuclear excitation by electron capture. Phys Rev Lett (2019) 122:212501. doi:10.1103/PhysRevLett.122.212501
50. Guo S, Ding B, Zhou X, Wu Y, Wang J, Xu S, et al. Probing 93mMo isomer depletion with an isomer beam. Phys Rev Lett (2022) 128:242502. doi:10.1103/PhysRevLett.128.242502
51. Liu B, Wang X. Isomeric excitation of 235U by inelastic scattering of low-energy electrons. Phys Rev C (2022) 106:064604. doi:10.1103/PhysRevC.106.064604
52. Hofstadter R, Fechter HR, McIntyre JA. High-energy electron scattering and nuclear structure determinations. Phys Rev (1953) 92:978–87. doi:10.1103/PhysRev.92.978
53. Barber WC. Inelastic electron scattering. Springer Tracts Mod Phys (1962) 12:1–42. doi:10.1146/annurev.ns.12.120162.000245
54. Rosen M, Raphael R, Überall H. Generalized helm model for transverse electroexcitation of nuclear levels. Phys Rev (1967) 163:927–34. doi:10.1103/PhysRev.163.927
55. Theissen H. Spectroscopy of light nuclei by low energy (¡ 70 MeV) inelastic electron scattering. Springer Tracts Mod Phys (1972) 65:1–57. doi:10.1007/BFb0041391
56. Donnelly TW, Walecka JD. Electron scattering and nuclear structure. Annu Rev Nucl Sci (1975) 25:329–405. doi:10.1146/annurev.ns.25.120175.001553
57. Bertrand FE. Excitation of giant multipole resonances through inelastic scattering. Annu Rev Nucl Sci (1976) 26:457–509. doi:10.1146/annurev.ns.26.120176.002325
58. Taylor RE. Deep inelastic scattering: The early years. Rev Mod Phys (1991) 63:573–95. doi:10.1103/RevModPhys.63.573
60. Berestetskii VB, Lifshitz EM, Pitaevskii LP. Quantum electrodynamics, 4. Oxford: Butterworth-Heinemann (1982).
61. Alder K, Bohr A, Huus T, Mottelson B, Winther A. Study of nuclear structure by electromagnetic excitation with accelerated ions. Rev Mod Phys (1956) 28:432–542. doi:10.1103/RevModPhys.28.432
62. Abramowitz M, Stegun IA. Handbook of mathematical functions with formulas, graphs, and mathematical tables, 55. Washington: US Government printing office (1964).
63. Blin-Stoyle R. Theory of complex nuclei. Phys Bull (1977) 28:131. doi:10.1088/0031-9112/28/3/058
64. Aas AJ, Mach H, Borge MJG, Fogelberg B, Grant IS, Gulda K, et al. Enhanced and quenched B(E1) transition rates between parity doublet bands in 227Ra. Nucl Phys A (1996) 611:281–314. doi:10.1016/S0375-9474(96)00312-0
65. Bemis CE, McGowan FK, Ford JLC, Milner WT, Robinson RL, Stelson PH, et al. Coulomb excitation of states in 229Th. Phys Scr (1988) 38:657–63. doi:10.1088/0031-8949/38/5/004
66. Gulda K, Kurcewicz W, Aas AJ, Borge MJG, Burke DG, Fogelberg B, et al. The nuclear structure of 229Th. Nucl Phys A (2002) 703:45–69. doi:10.1016/S0375-9474(01)01456-7
67. Barci V, Ardisson G, Barci-Funel G, Weiss B, El Samad O, Sheline RK. Nuclear structure of 229Th from γ-ray spectroscopy study of 233U α-particle decay. Phys Rev C (2003) 68:034329. doi:10.1103/PhysRevC.68.034329
68. Ruchowska E, Płóciennik W, Źylicz J, Mach H, Kvasil J, Algora A, et al. Nuclear structure of 229Th. Phys Rev C (2006) 73:044326. doi:10.1103/PhysRevC.73.044326
69. Tkalya EV, Schneider C, Jeet J, Hudson ER. Radiative lifetime and energy of the low-energy isomeric level in 229Th. Phys Rev C (2015) 92:054324. doi:10.1103/PhysRevC.92.054324
70. Dykhne AM, Tkalya EV. 229mTh (3/2+, 3.5 eV) and a check of the exponentiality of the decay law. J Exp Theor Phys (1998) 67:549–52. doi:10.1134/1.567724
71. Minkov N, Pálffy A. Reduced transition probabilities for the gamma decay of the 7.8 eV isomer in 229Th. Phys Rev Lett (2017) 118:212501. doi:10.1103/PhysRevLett.118.212501
72. Salvat F, Fernandez-Varea JM. Radial: A fortran subroutine package for the solution of the radial Schrödinger and Dirac wave equations. Comput Phys Commun (2019) 240:165–77. doi:10.1016/j.cpc.2019.02.011
73. Liberman DA, Waber JT, Cromer DT. Self-Consistent-field Dirac-slater wave functions for atoms and ions. I. Comparison with previous calculations. Phys Rev (1965) 137:A27–34. doi:10.1103/PhysRev.137.A27
74. Liberman DA, Cromer DT, Waber JT. Relativistic self-consistent field program for atoms and ions. Comput Phys Commun (1971) 2:107–13. doi:10.1016/0010-4655(71)90020-8
75. Seiferle B, von der Wense L, Thirolf P G Lifetime measurement of the 229Th nuclear isomer. Phys Rev Lett (2017) 118:042501. doi:10.1103/PhysRevLett.118.042501
76. Borisyuk PV, Chubunova EV, Kolachevsky NN, Lebedinskii YY, Vasiliev OS, Tkalya EV. Excitation of 229Th nuclei in laser plasma: The energy and half-life of the low-lying isomeric state. arXiv [Preprint] (2018). Available at: http://arxiv.org/abs/1804.00299v1 (Accessed April 1, 2018).
79. Qi J, Zhang H, Wang X. Isomeric excitation of 229Th in laser-heated clusters. Phys Rev Lett (2023) 130:112501. doi:10.1103/PhysRevLett.130.112501
80. Levine MA, Marrs RE, Henderson JR, Knapp DA, Schneider MB. The electron beam ion trap: A new instrument for atomic physics measurements. Phys Scr (1988) 1988:157–63. doi:10.1088/0031-8949/1988/T22/024
81.National Institute of Standards and Technology Physical Measurement Laboratory. Atomic reference data for electronic structure calculations (2001). Available at: https://physics.nist.gov/PhysRefData/Ionization/atom_index.html.
82. Ichihara A, Eichler J. Cross sections for radiative recombination and the photoelectric effect in the K, L, and M shells of one-electron systems with 1 ≤ Z ≤ 112 calculated within an exact relativistic description. Data Nucl Data Tables (2000) 74:1–121. doi:10.1006/adnd.1999.0825
Keywords: thorium-229, isomer, nuclear excitation, NEET, NEEC, NEIES
Citation: Zhang H and Wang X (2023) Theory of isomeric excitation of 229Th via electronic processes. Front. Phys. 11:1166566. doi: 10.3389/fphy.2023.1166566
Received: 15 February 2023; Accepted: 07 June 2023;
Published: 27 June 2023.
Edited by:
Bing Guo, China Institute of Atomic Energy, ChinaReviewed by:
Mikhail G. Kozlov, Petersburg Nuclear Physics Institute (RAS), RussiaCopyright © 2023 Zhang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xu Wang, eHdhbmdAZ3NjYWVwLmFjLmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.