Investigation of 22Mg levels via resonant scattering of 18Ne + α

The α resonant scattering on ¹⁸Ne was measured in inverse kinematics to understand the α-clustering of proton-rich ²²Mg nucleus, performed at the CNS Radio-Isotope Beam Separator (CRIB) of Center for Nuclear Study, University of Tokyo, located at the RIBF of RIKEN Nishina Center. The excitation function of ²²Mg was obtained for the excitation energies of 10–16 MeV by adopting the thick-target method. Several resonances were evident in the present work, which implies the existence of energy levels with large α widths. Since energy levels were not clearly observed at the astrophysically important energy range, upper limits on the ¹⁸Ne (α, α)¹⁸Ne cross section were set. The astrophysical impact was also investigated by estimating the ¹⁸Ne (α, p)²¹Na cross section.

1 Introduction

The α-cluster structure in atomic nuclei has been one of the most interesting topics in nuclear physics. The α-clusterization of self-conjugate (N = Z) and A = 4n (n = 2, 3, 4, ⋯) nuclei including ⁸Be, ¹²C, ¹⁶O, and ²⁰Ne has been studied extensively for decades [1–3]. The strong evidence for the α-cluster structure was found through the studies. Observations of a series of levels with large α reduced widths that form a rotational band can provide a convincing probe for α-cluster configuration in the nuclei. The development of theoretical models and rare isotope beams has provided significant opportunities to extend our knowledge of the α-cluster structure in exotic nuclei. Experimental investigations on the α-clusterization of neutron-rich nuclei, including ¹⁰Be, ¹²Be, and ¹⁴C, have been performed [4–6]. These studies have substantially improved our understanding of the α-cluster structure in neutron-rich nuclei; however, α-cluster studies of proton-rich (neutron-deficient) nuclei have not been sufficiently established. Considering the isobaric invariance of the nuclear force, the characteristics of the α-cluster structure for a proton-rich nucleus are similar to those for its mirror nucleus. For example, experimental results indicate that some of the observed resonances in ¹¹C may originate from the negative-parity cluster band, which is analogous to its mirror nucleus ¹¹B [7, 8].

The α-cluster structure of neutron-rich ²²Ne has been extensively investigated both experimentally and theoretically [9–13]. Rogachev et al. observed a splitting of 1⁻, 3⁻, 7⁻, and 9⁻ α-cluster states into doublets [10], which could be theoretically explained by the extended two cluster model (ETCM) calculation assuming the α + ¹⁸O two-cluster configuration [11]. Recently, Kimura suggested the presence of two kinds of α-cluster structures in ²²Ne using the hybrid-generator coordinate method (GCM) calculation. The first is the molecular orbital bands with the α + ¹⁶O core and two valence neutrons, which correspond to the observed α-cluster states below the α + ¹⁸O threshold energy reported in [14, 15]. The other is the α + ¹⁸O molecular bands, which correspond to the observed states above the threshold energy reported in Ref. [10].

Studies on the α-cluster structure of proton-rich ²²Mg are still very rare. The GCM calculation predicted the existence of the 1⁻ and 3⁻ doublet states located at excitation energies of 12–13 MeV, assuming the α + ¹⁸Ne two-cluster model [11]. Considering the lower energy level density of proton-rich nuclei than that of neutron-rich nuclei, observing doublets should be easier in the case of the ²²Mg nucleus. However, the experimental data obtained by Goldberg et al. [12] show no clear evidence of the doublets. Although the excitation function of mirror nucleus ²²Ne in [12] show the existence of the strong 1⁻ and 3⁻ doublets originating from the α-clustering, the excitation function of ²²Mg is rather featureless. The authors could not specify the reason for the absence of the doublets since the quality of the ²²Mg data was not sufficient for independent analysis.

A powerful approach for investigating the α-cluster structure in the ²²Mg nucleus is to populate α-cluster states by resonant elastic scattering of ¹⁸Ne and α. Therefore, we measured ¹⁸Ne + α resonant scattering using ¹⁸Ne rare isotope beam to identify predicted 1⁻ and 3⁻ doublets. The excited states of ²²Mg have been extensively investigated by various nuclear reactions, including ¹²C (¹⁶O, ⁶He)²²Mg [16]; ²⁴Mg (p, t)²²Mg [17, 18]; ¹⁸Ne (α, p)²¹Na [19–21]; and ²¹Na (p, p)²¹Na [22–24]. The α partial widths are, however, not known for most levels, which cannot provide a clear evidence of the α-clusterization in the ²²Mg nucleus. In the present study, the excitation function of ²²Mg was obtained for excitation energies of E_x ∼ 10–16 MeV, which can provide important information about the energy level properties including α partial widths.

Investigating the spectroscopic information of ²²Mg also plays a crucial role in understanding the astrophysically important ¹⁸Ne (α, p)²¹ Na reaction because the reaction occurs through the resonances in the compound nucleus. The ¹⁸Ne (α, p)²¹Na reaction is known as one of the possible breakout routes from the hot-CNO cycles, which leads the rapid proton capture (rp) process [25–27]. In a recent sensitivity study by Cyburt et al., the ¹⁸Ne (α, p)²¹Na reaction was identified as one of the most important reactions which impact on the X-ray burst light curve and the composition of burst ashes [28]. Considering the typical X-ray burst temperature of T ∼ 2 GK, the Gamow window corresponds to the excitation energy E_x ∼ 9.56–10.96 MeV. Therefore, it is important to study the energy level properties of ²²Mg in this energy region. The ¹⁸Ne (α, p)²¹Na reaction has been studied by direct measurements [19–21] and time-reversal reaction measurement [29]. The experimental results, however, show a large discrepancy. In the present work, the ¹⁸Ne (α, p)²¹Na reaction cross section was estimated based on the experimental level structure of the ²²Mg nucleus.

2 Experiment

The α resonant elastic scattering of ¹⁸Ne was measured in inverse kinematics at the CNS Radio-Isotope Beam Separator (CRIB) [30, 31] of the Center for Nuclear Study, University of Tokyo, located at the RIBF of RIKEN Nishina Center. A schematic of the experimental setup is shown in Figure 1. The ¹⁸Ne rare isotope beam was produced by using the in-flight (IF) method. A primary ¹⁶O beam with an energy of 8.026 MeV/u from the AVF cyclotron [32] was delivered to the F0 focal plane of CRIB and bombarded a ³He gas target. Then, a secondary ¹⁸Ne beam was produced by the ³He (¹⁶O, ¹⁸Ne)n reaction. The ³He gas was contained in the cell at a pressure of 360 Torr. The ³He gas atoms were isolated from the beam line kept at a high-level vacuum by using 2.5-μm-thick Havar foils as the entrance and exit windows. To increase the density of the ³He gas target and the intensity of the secondary ¹⁸Ne beam, a cryogenic system using liquid nitrogen was used [33]. The areal thickness of the ³He gas target was achieved to be 1.54 mg/cm² by keeping the temperature at T ∼90 K.

FIGURE 1

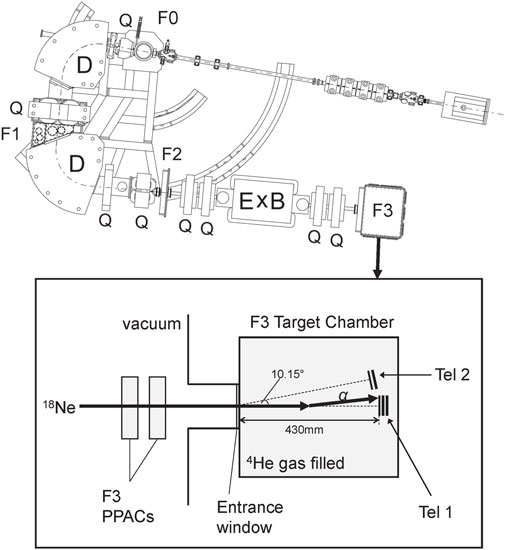
FIGURE 1. Schematic view of the CRIB separator (top) and the experimental setup for the ¹⁸Ne + α resonant scattering measurement at the F3 focal plane (bottom). The ¹⁸Ne beam particles were identified and monitored by two F3 PPACs. ⁴He gas at 470 Torr was filled to the chamber, which was sealed with a 23-μm-thick Mylar foil as a beam entrance window. The energy and position of the recoiling α particle were measured by ΔE-E silicon detector telescopes (Tel 1 and Tel 2).

¹⁸Ne¹⁰⁺ ions were selected by a double achromatic system with a proper magnetic rigidity (Bρ) value of 0.5920 Tm, which is optimized to obtain the maximum ¹⁸Ne beam production rate. A slit of ±15 mm was installed at the momentum dispersive focal plane (F1) to remove the beam contaminations produced due to various nuclear reactions, yielding the momentum dispersion Δp/p ∼ 1%. The secondary beam particles were further purified using the Wien Filter (WF) system by applying a high voltage of ±59.5 kV. Two delay-line-type PPACs [34] were installed downstream of the WF to measure the time and the two-dimensional position information for each secondary beam particle. By using PPACs, the secondary beam identification after the WF was performed. The ¹⁸Ne beam intensity and purity were ∼2.6 × 10⁵ pps and ∼ 65%, respectively. The impurities were ¹⁷F⁹⁺ (∼ 28%) and ¹⁶O⁸⁺ (∼ 4%), respectively. A small amount of other beam species including ¹⁵O⁸⁺, ¹³N⁷⁺, and ⁴He²⁺ was also observed. These contaminants were clearly excluded by the time-of-flight information in the final analysis.

The F3 target chamber was filled with ⁴He gas for α scattering measurement. The ⁴He gas was at a pressure of 470 Torr and was sealed with a 23-μm-thick aluminized Mylar foil as a beam entrance window. The ⁴He target pressure was selected to stop the ¹⁸Ne beam before it reaches the detector. The ¹⁸Ne beam energy after passing through the target entrance window was measured as 45.2 ± 1.1 MeV, which is consistent with an energy loss calculation result considering the Bρ value of 0.5920 Tm and the effective thickness of ∼ 45 μm Mylar foil for the two PPACs and the beam entrance window. By adopting the thick-target method in inverse kinematics [35], a wide range of excitation energies of ²²Mg was investigated with a single ¹⁸Ne beam energy.

The energy and position of the recoiling α particles were obtained using two sets of ΔE-E silicon detector telescopes. The central telescope (Tel 1) was installed at 430 mm downstream from the entrance window of the target chamber along the beam axis. The other telescope (Tel 2) was located at 10.15° off from the beam axis, as viewed from the center of the entrance window. Tel 1 (Tel 2) consisted of 20-μm-, 496-μm-, and 485-μm-thick (20-μm- and 1500-μm-thick) silicon detectors. The most energetic α particles from the ¹⁸Ne (α, α)¹⁸Ne reaction could be entirely stopped under these conditions. Each detector had 16 strips and an active area of 50 × 50 mm². Energy calibration of each strip was carried out by using an α-emitting source composed of ¹⁴⁸Gd (3.148 MeV), ²⁴¹Am (5.462 MeV), and ²⁴⁴Cm (5.771 MeV). Since the energy range of recoiling α particles is much wider (0–27 MeV) than that of the α particles from the source, additional energy calibration was required for the high-energy region. α beams at various energies (13, 15, 20, and 25 MeV) were used for this purpose.

Even after the beam purification using the CRIB spectrometer, beam-like α particles were transported to the F3 reaction target chamber. These beam-like α particles were produced at the upstream of the beam line and selected by the Bρ value which was set for the ¹⁸Ne beam particles of interest. The number of the beam-like α particles was much less than the number of ¹⁸Ne beam particles (≪ 0.01%); however, an amount comparable to that of the reaction products reached the central telescope. Therefore, the argon target was used for the background measurement. The argon gas pressure of about 87 Torr was selected so that the incident particles exhibit energy losses similar to those of ⁴He gas. By comparing the two α spectra obtained with and without the ⁴He gas target, the contribution from beam-like α particles was identified.

3 Data analysis

3.1 Kinematics reconstruction

The particle identification was performed by the standard energy loss techniques. A typical particle identification plot obtained at the central telescope is shown in Figure 2. The total energy deposition of the particles is plotted as a function of energy deposition in the ΔE detector. As shown in the figure, α particles were clearly separated without significant contamination from other charged particle groups. The α particles with E_tot ∼ 13 MeV were observed in the background run with argon gas, as shown in Figure 2B, indicating that those α particles were contaminants in the secondary beams. The beam-like α particles were clearly distinguished by using the time-of-flight information between the PPAC and the second layer of the telescope, as shown in Figure 3.

FIGURE 2

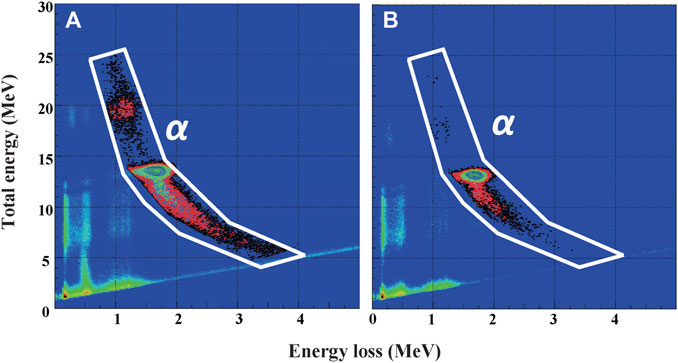
FIGURE 2. A typical particle identification plot is shown. The total energy of a recoiling particle is plotted as a function of the energy deposition in the first layer of the telescope. Events in the region with thick solid lines are identified as α particles from (A) ⁴He and (B) argon gas run.

FIGURE 3

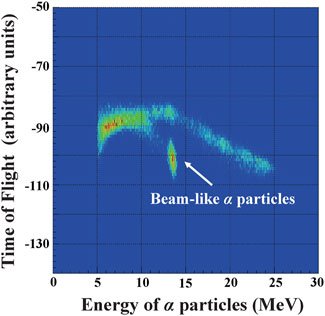
FIGURE 3. The ToF between the F3 PPAC and the second layer of the Tel 1 is plotted as a function of the energy of α particles. The beam-like α particles from the upstream were clearly separated from the recoiling α particles. The slope-like dependence observed at high energies is due to the slewing effect (which is not corrected in this plot).

The α particles in coincidence with the ¹⁸Ne beams incident in the target chamber were selected for further analysis. The measured energy of the α particle (E_α) was converted to the center-of-mass energy of ¹⁸Ne + α system (E_c.m.) by assuming the elastic scattering kinematics using

$E_{\text{c.m.}}=\frac{M_{\text{Ne}}+M_{\alpha }}{4M_{\text{Ne}}{\cos }^2{\theta }_{\text{lab}}}{E}_{\alpha },(1)$

where M_Ne and M_α are the nuclear masses of the ¹⁸Ne and α particle, respectively, and θ_lab is the scattering angle in the laboratory frame. The value of θ_lab was determined using the trajectories of the recoiling α particle and corresponding ¹⁸Ne beam particle at the reaction vertex. The reaction vertex in the extended gas target was reconstructed by considering the energy losses of the ¹⁸Ne beam and recoiling α particle in ⁴He gas. The energy loss functions were obtained using the SRIM code [36]. Direct measurement of the energy loss of the ¹⁸Ne beam at six different target pressures in the present study was in good agreement with the SRIM calculation result.

3.2 Excitation function of ¹⁸Ne + α elastic scattering

The differential cross section of ¹⁸Ne + α resonant elastic scattering in the center-of-mass frame was calculated by

$\begin{array}{cc}\hfill {\left(\frac{d\sigma }{d\mathrm{\Omega }}\right)}_{\text{c.m.}}& =\frac{1}{4\text{cos}{\theta }_{\text{lab}}}{\left(\frac{d\sigma }{d\mathrm{\Omega }}\right)}_{\text{lab}}\hfill \\ \hfill & =\frac{1}{4\text{cos}{\theta }_{\text{lab}}}\frac{Y}{IN\mathrm{\Delta }{\mathrm{\Omega }}_{\text{lab}}},\hfill \end{array}(2)$

where Y is the yield of recoiling α particles, θ_lab is the scattering angle in the laboratory frame, I is the number of ¹⁸Ne beam particles incident on the target, N is the number of ⁴He target atoms, and ΔΩ_lab is the solid angle covered by the detector.

The number of incident ¹⁸Ne beam particles was counted using two F3 PPACs. To obtain the precise number of beam particles entering into the target chamber through the entrance window, an additional cut was applied to the ¹⁸Ne beam events. The positions of the beam particles at the target entrance were reconstructed event-by-event by extrapolating the beam trajectory obtained at two F3 PPACs, and then ¹⁸Ne beam events falling in the diameter of the entrance of the target chamber were selected. A total of ∼ 1.33 × 10¹⁰¹⁸Ne beam ions impinged on the target during the runs.

The excitation function of ¹⁸Ne + α resonant elastic scattering was extracted by selecting α events with an angular range of 0° ≤ θ_lab ≤ 7° (166° ≤ θ_c.m. ≤ 180°). The solid angle was calculated using the known detector geometry and reaction vertex of each event as a function of E_{c. m}. Due to the finite angular range of θ_lab, an average value of solid angle at the reaction vertex (or E_{c. m.}) was used. The areal number density of ⁴He atoms was obtained by considering the effective target thickness as a function of E_{c. m.}. The uncertainty in E_{c. m.} was measured to be approximately 50–100 keV, depending on the energy. The uncertainty originates from the energy resolution of a silicon detector (30–90 keV) and energy straggling of the ¹⁸Ne beam and α particles in the gas (20–60 keV).

3.3 Upper limits on the cross section

The ¹⁸Ne (α, α)¹⁸Ne cross section extracted in the present work is rather smooth in the energy region below E_{c. m.} < 3 MeV. In this region, however, two small bumps were observed at E_{c. m.} ∼2.6 MeV and 2.7 MeV in the cross section spectrum. Several resonances in ²²Mg have been identified in the energy range through the previous ¹⁸Ne (α, p)²¹Na reaction study as reported in [20]. For instance, two energy levels located at the resonance energies of E_r = 2.52 ± 0.14 MeV and E_r = 2.72 ± 0.14 MeV have been reported in the previous direct measurement by Groombridge et al. [20]. However, the existence of these resonances is not obvious in our data, possibly due to the insufficient statistics. Therefore, the upper limits on the cross section were set to indicate the possible maximum resonant cross section that is consistent with our experimental spectrum. Figure 4 shows the obtained upper limits by assuming hypothetical levels located at E_{c. m.} = 2.63 MeV (top) and E_{c. m.} = 2.75 MeV (middle). The upper limit with both hypothetical levels is also plotted in the figure (bottom). The black circles represent the empirical cross sections obtained at 0° ≤ θ_lab ≤ 7°. The blue solid lines represent the best fit curves for the observed bumps. The reduced χ² value of the best fit curve is 0.893. The shape of the resonance was assumed to be Gaussian, as plotted as a red dotted line in the figure, because the broadening by the experimental resolution is expected to dominate the width. The width of the Gaussian was assumed to be 50 keV to fit the observed bumps. The normalization factor of the distribution was then increased until the χ² value decreased to a prescribed amount, resulting in a one-sigma confidence level. The red dashed lines represent the upper limits of the ¹⁸Ne (α, α)¹⁸Ne cross section. A fluctuation of experimental data points was also observed at E_{c. m.} ∼ 2.9 MeV. This bump could be a corresponding resonance at E_r = 2.87 ± 0.14 MeV reported in a previous work [20]; however, it does not fall into the Gamow window at T ∼ 2 GK. Therefore, the upper limit was not evaluated for this resonance.

FIGURE 4

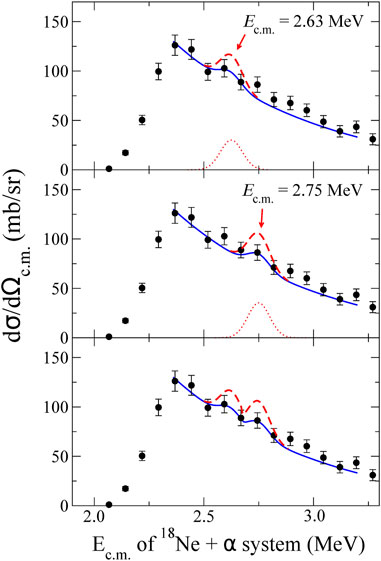
FIGURE 4. The upper limits of the ¹⁸Ne (α, α)¹⁸Ne cross section by assuming hypothetical levels located at E_{c. m.} = 2.63 MeV (top) and E_{c. m.} = 2.75 MeV (middle) are plotted as red dashed lines. The upper limit with both resonances is also plotted (bottom). The one-sigma confidence level was considered to obtain the upper limit. The black circles represent the experimental excitation function obtained at 0° ≤ θ_lab ≤ 7°, the blue solid line represents the best fitting result of it, and the red dotted line represents each hypothetical level.

4 Discussion

4.1 Astrophysical implication

Two small bumps observed in the present work fall within the Gamow window of the astrophysically important ¹⁸Ne (α, p)²¹Na reaction relevant to a temperature of T ∼ 2 GK. The contribution of the observed bumps to the ¹⁸Ne (α, p)²¹Na reaction was then investigated. The cross section of the ¹⁸Ne (α, p)²¹Na reaction was calculated using the Breit–Wigner formula [37].

${\sigma }_{BW}\left(E\right)=\frac{{\lambda }^2}{4\pi }\frac{\left(2J_r+1\right)}{\left(2J_{\text{Ne}}+1\right)\left(2J_{\alpha }+1\right)}\frac{{\mathrm{\Gamma }}_{\alpha }{\mathrm{\Gamma }}_p}{{\left(E-E_r\right)}^2+{\left({\mathrm{\Gamma }}_{\text{tot}}/2\right)}^2},(3)$

where λ is the de Broglie wavelength; E_r is the resonance energy; J, J_Ne, and J_α are the spins of resonance, ¹⁸Ne, and ⁴He, respectively. Γ_α, Γ_p, and Γ_tot are the α partial width, proton partial width, and total width, respectively. Γ_tot = Γ_α + Γ_p was assumed in the calculations. Two hypothetical levels used in the upper limit calculation were considered to be the resonances for the ¹⁸Ne (α, p)²¹Na reaction, where the resonance energies were adopted as E_r = 2.63 and 2.75 MeV. Γ_α values of both resonances were determined by further analyzing with the R-matrix code SAMMY8 [38, 39], where the experimental energy increase of ∼ 50 keV was assumed. The best fit yielded values of Γ_α = 15 keV for both resonances. The spin and parity of both resonances was adopted as J^π = 0⁺ while calculating the cross section. Several J^π values for the resonances located in the astrophysically important energy region have been suggested in the previous direct measurement by Groombridge et al. [20], including J^π = 0⁺. However, the choice of other J^π values such as J^π = 1⁻ or 2⁺ for observed bumps would imply our Γ_α which exceed the Wigner limit. Table 1 summarizes the resonance parameters used in the ¹⁸Ne (α, p)²¹Na cross section calculations.

TABLE 1

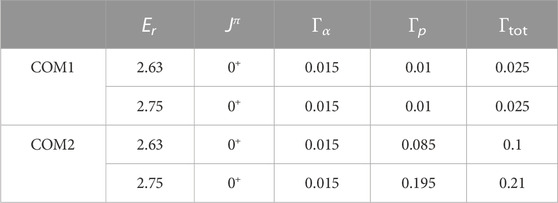
TABLE 1. The resonance parameters used in the ¹⁸Ne (α, p)²¹Na cross section calculation are summarized. Two sets of parameters (“COM1” and “COM2”) are used in the calculation to illustrate the sensitivity of the Γ_p for the reaction cross section. All energies are expressed in MeV.

Although proton resonant scattering on the ²¹Na nucleus has been measured in literatures [22–24], Γ_p in the corresponding energy region has not been reported so far. To approximate Γ_p values for the resonances, the Wigner limit for the proton was calculated by Γ_w = 2ℏ²/μR²P_l, where μ is the reduced mass, R is the interaction radius, and P_l is the penetrability of a given orbital angular momentum l. An interaction radius of R = 1.35 (1 + 21^1/3) fm [24] was adopted in the calculation. By considering the global mean reduced proton width ${\theta }_p^2$ = 0.0045, suggested in [40], Γ_p was estimated to be ∼10 keV for the resonances at E_r = 2.63 and 2.75 MeV, which is summarized as “COM1” in Table 1. To illustrate the sensitivity of the proton widths for the ¹⁸Ne (α, p)²¹Na reaction cross section, another set of Γ_p values for the resonances was approximated by assuming Γ_p = Γ_tot − Γ_α (“COM2” in Table 1). We adopted Γ_tot = 0.1 MeV (Γ_tot = 0.21 MeV) for the resonance at E_r = 2.63 MeV (E_r = 2.75 MeV), as reported in the previous direct measurement by Groombridge et al. [20].

The calculation results for the ¹⁸Ne (α, p)²¹Na reaction cross section are shown in Figure 5, in comparison with the previous experimental results. The cross sections deduced by the Breit–Wigner formula using two sets of Γ_p values are shown as the green dashed and black solid lines, respectively. The blue triangles represent the experimental data obtained by Salter et al. [29], which were determined from the time-reversal reaction measurement. The ¹⁸Ne (α, p₀)²¹Na reaction cross section was inferred by using the principle of the detailed balance theorem [41]; therefore, their data can provide a lower limit for the cross section. The red squares represent the ¹⁸Ne (α, p)²¹Na cross section derived from the resonance parameters reported by Groombridge et al. [20]. The black squares represent the recent direct measurement results by Anastasiou et al. [21], which shows a lower cross section by almost an order of magnitude compared with that of Groombridge et al. As shown in the figure, our calculation results indicate that the ¹⁸Ne (α, p)²¹Na reaction cross section depends critically on the proton widths of the resonances in the astrophysically important energy region. Thus, experimental studies of the Γ_p are highly required for a conclusive understanding of the ¹⁸Ne (α, p)²¹Na reaction cross section.

FIGURE 5

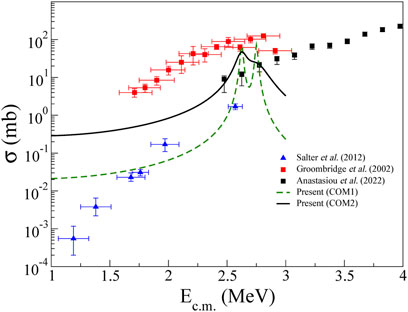
FIGURE 5. Comparison of the ¹⁸Ne (α, p)²¹Na reaction cross section calculations in the present work with the previous measurements by Salter et al. [29], Groombridge et al. [20], and Anastasiou et al. [21] is shown.

4.2 R-matrix analysis and α-cluster structure

The excitation function of ¹⁸Ne + α elastic scattering obtained at the higher excitation energy region E_x ∼ 11–16 MeV is shown in Figure 6. The black circles represent the differential cross sections of the ¹⁸Ne (α, α)¹⁸Ne obtained at 0° ≤ θ_lab ≤ 7°. Several peaks were evident in the spectrum, which implies the existence of resonances with large Γ_α. Since the strength of the α-clustering feature of a resonance state is reflected by its α width, observed peaks in the present work are possible candidates of α-cluster states. To constrain the energy level properties of ²²Mg including Γ_α, an analysis using the R-matrix calculation code SAMMY8 [38, 39] has been in progress. A channel radius of R_c = 5.0 fm was adopted in the calculation, which is the same value used in the GCM calculation [11]. We calculated the excitation function at an average angle of θ_c.m. = 173 °, and the result was then broadened considering the experimental energy resolution.

FIGURE 6

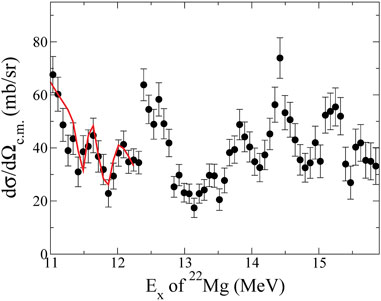
FIGURE 6. The excitation function of the elastic scattering of α particles on ¹⁸Ne obtained at 0°≤ θ_lab ≤7° (black circles) with the R-matrix fit with three resonances (red solid line) is shown.

By introducing three resonances in the R-matrix calculation, the fitting curve was obtained at E_x ≤ 12.3 MeV, which is plotted as red solid line in Figure 6. The resonance parameters are summarized in Table 2. Since the spectroscopic information of ²²Mg nucleus in this energy region is very limited, an intensive R-matrix analysis with all possible spin and natural parity combinations for observed resonances should be carefully performed until the experimental excitation function is well-reproduced. The resonance parameters with best fitting result will be provided in the future. The χ² analysis will be performed to deduce possible parameters for each peak. The dimensionless partial width ${\theta }_a^2$ for each level will be calculated by ${\theta }_a^2$ = Γ_α/Γ_W, where Γ_W is the Wigner limit of Γ_α, which can provide a direct comparison with theoretical predictions in [11]. More detailed calculations would be necessary to reveal the nature of those levels, if they are shell-model-like or cluster-like states.

TABLE 2

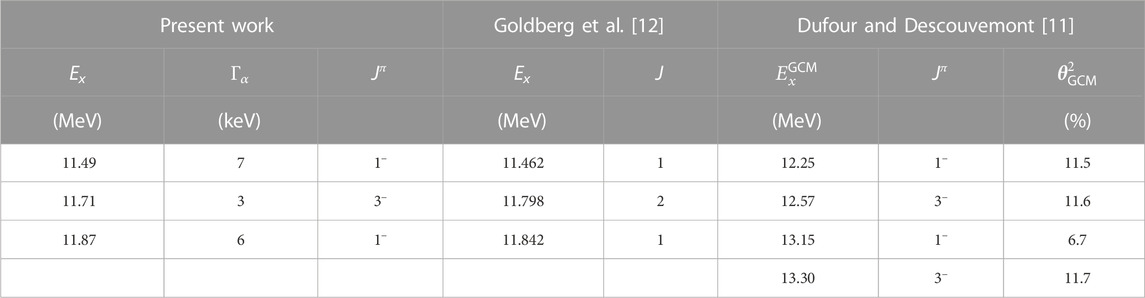
TABLE 2. Resonance properties of ²²Mg extracted from the present work are summarized. Results from the previous works are listed for comparison.

5 Summary

We measured α resonant elastic scattering on ¹⁸Ne using the thick-target method in inverse kinematics technique to improve our knowledge of the α-cluster structure of proton-rich ²²Mg nucleus. The excitation function for ¹⁸Ne (α, α)¹⁸Ne in the energy range of E_x ∼ 10–16 MeV was obtained at 0° ≤ θ_lab ≤ 7°. Several levels with large α widths were evident in our result, which can be candidates for the α-cluster states. To clarify the energy level properties of ²²Mg and to investigate α-clustering features, the R-matrix analysis is in progress. The resonance parameters will be extracted considering all possible combinations of spin and parity for observed peaks. The first experimental constraints on spectroscopic information of ²²Mg above E_x ∼ 13 MeV will be provided. To better understand the experimental results, complete theoretical descriptions are required in the future.

No levels were evident at E_x < 11 MeV in the present work, even though two small bumps were observed in the cross section spectrum. Therefore, we set upper limits on the ¹⁸Ne (α, α)¹⁸Ne cross section, which indicate the possible maximum resonant cross section assuming the hypothetical levels at E_x = 10.772 and 10.892 MeV (E_c.m. = 2.63 and 2.75 MeV). We also estimated the astrophysically important ¹⁸Ne (α, p)²¹Na reaction cross section based on our experimental data. The calculation indicates that the ¹⁸Ne (α, p)²¹Na cross section depends on the proton widths of the resonances as well. Experimental studies on Γ_p are necessary to evaluate the ¹⁸Ne (α, p)²¹Na reaction cross section conclusively.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

KC was the spokesperson of the experiment. All authors contributed to the setup of the experiment and the measurements. SMC wrote the first draft, the revised versions, and the final version of the manuscript. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the Institute for Basic Science (IBS) funded by the Ministry of Science and ICT, Korea (Grant No. IBS-R031-D1). This work was also supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (MSIT) Nos. 2020R1A2C1005981 and 2019K2A9A2A10018827. This work has been supported by the Rare Isotope Science Project of Institute for Basic Science funded by the Ministry of Science and NRF of Korea (2013M7A1A1075765). AK acknowledges the National Research Foundation of Korea (NRF) grants funded by the Korean Government (Grant No. 2018R1A5A1025563). LHK acknowledges the support of the International Centre of Physics at the Institute of Physics (Grant No. ICP.2023.04).

Acknowledgments

The experiment was performed at the RIBF operated by RIKEN Nishina Center and CNS, University of Tokyo. The authors are grateful to the RIKEN and CNS accelerator staff for their technical support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ikeda K, Takigawa N, Horiuchi H. The systematic structure-change into the molecule-like structures in the self-conjugate $4n$ nuclei. Prog Theor Phys Suppl (1968) E68:464–75. doi:10.1143/PTPS.E68.464

CrossRef Full Text | Google Scholar

2. Freer M. The clustered nucleus—Cluster structures in stable and unstable nuclei. Rep Prog Phys (2007) 70:2149–210. doi:10.1088/0034-4885/70/12/R03

CrossRef Full Text | Google Scholar

3. Horiuchi H, Ikeda K, Katō K. Recent developments in nuclear cluster physics. Prog Theor Phys Suppl (2012) 192:1–238. doi:10.1143/PTPS.192.1

CrossRef Full Text | Google Scholar

4. Freer M, Angélique JC, Axelsson L, Benoit B, Bergmann U, Catford WN, et al. Exotic molecular states in ¹²Be. Phys Rev Lett (1999) 82:1383–6. doi:10.1103/PhysRevLett.82.1383

CrossRef Full Text | Google Scholar

5. Freer M, Angélique JC, Axelsson L, Benoit B, Bergmann U, Catford WN, et al. Helium breakup states in ¹⁰Be and ¹²Be. Phys Rev C (2001) 63:034301. doi:10.1103/PhysRevC.63.034301

CrossRef Full Text | Google Scholar

6. Yamaguchi H, Kahl D, Hayakawa S, Sakaguchi Y, Abe K, Nakao T, et al. Experimental investigation of a linear-chain structure in the nucleus ¹⁴C. Phys Lett B (2017) 766:11–6. doi:10.1016/j.physletb.2016.12.050

CrossRef Full Text | Google Scholar

7. Yamaguchi H, Hashimoto T, Hayakawa S, Binh DN, Kahl D, Kubono S, et al. α resonance structure in ¹¹B studied via resonant scattering of ⁷Li+α. Phys Rev C (2011) 83:034306. doi:10.1103/PhysRevC.83.034306

CrossRef Full Text | Google Scholar

8. Yamaguchi H, Kahl D, Wakabayashi Y, Kubono S, Hashimoto T, Hayakawa S, et al. α-resonance structure in ¹¹C studied via resonant scattering of ⁷Be + α and with the ⁷Be(α, p) reaction. Phys Rev C (2013) 87:034303. doi:10.1103/PhysRevC.87.034303

CrossRef Full Text | Google Scholar

9. Descouvemont P. Microscopic investigation of the α+¹⁸O system in a three-cluster model. Phys Rev C (1988) 38:2397–407. doi:10.1103/PhysRevC.38.2397

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Rogachev GV, Goldberg VZ, Lönnroth T, Trzaska WH, Fayans SA, Källman KM, et al. Doubling of α-cluster states ²²Ne. Phys Rev C (2001) 64:051302. doi:10.1103/PhysRevC.64.051302

CrossRef Full Text | Google Scholar

11. Dufour M, Descouvemont P. Microscopic study of α-cluster states in ²²Ne. Nucl Phys A (2003) 726:53–66. doi:10.1016/j.nuclphysa.2003.07.004

CrossRef Full Text | Google Scholar

12. Goldberg VZ, Rogachev GV, Trzaska WH, Kolata JJ, Andreyev A, Angulo C, et al. Investigation of the α-cluster structure of ²²Ne and ²²Mg. Phys Rev C (2004) 69:024602. doi:10.1103/PhysRevC.69.024602

CrossRef Full Text | Google Scholar

13. Kimura M. Molecular orbitals and α +¹⁸O molecular bands of ²²Ne. Phys Rev C (2007) 75:034312. doi:10.1103/PhysRevC.75.034312

CrossRef Full Text | Google Scholar

14. Scholz W, Neogy P, Bethge K, Middleton R. 0⁺ state at 6.24 MeV in ²²Ne excited by the reaction ¹⁸O(⁷Li,t)²²Ne. Phys Rev Lett (1969) 22:949–51. doi:10.1103/PhysRevLett.22.949

CrossRef Full Text | Google Scholar

15. Scholz W, Neogy P, Bethge K, Middleton R. Rotational bands in ²²Ne excited by the ¹⁸O(⁷Li,t)²²Ne reaction. Phys Rev C (1972) 6:893–900. doi:10.1103/PhysRevC.6.893

CrossRef Full Text | Google Scholar

16. Chen AA, Lewis R, Swartz KB, Visser DW, Parker PD. Structure of ²²Mg and its implications for explosive nucleosynthesis. Phys Rev C (2001) 63:065807. doi:10.1103/PhysRevC.63.065807

CrossRef Full Text | Google Scholar

17. Chae KY, Bardayan DW, Blackmon JC, Chipps KA, Hatarik R, Jones KL, et al. Constraint on the astrophysical ¹⁸Ne(α,p)²¹Na reaction rate through a ²⁴Mg(p,t)²²Mg measurement. Phys Rev C (2009) 79:055804. doi:10.1103/PhysRevC.79.055804

CrossRef Full Text | Google Scholar

18. Matic A, Berg AM, Harakeh MN, Wörtche HJ, Berg GPA, Couder M, et al. High-precision (p, t) reaction measurement to determine ¹⁸ Ne(α,p)²¹Na reaction rates. Phys Rev C (2009) 80:055804. doi:10.1103/PhysRevC.80.055804

CrossRef Full Text | Google Scholar

19. Bradfield-Smith W, Davinson T, DiPietro A, Laird AM, Ostrowski AN, Shotter AC, et al. Breakout from the hot CNO cycle via the ¹⁸ Ne(α,p)²¹Na reaction. Phys Rev C (1999) 59:3402–9. doi:10.1103/PhysRevC.59.3402

CrossRef Full Text | Google Scholar

20. Groombridge D, Shotter AC, Bradfield-Smith W, Cherubini S, Davinson T, Di Pietro A, et al. Breakout from the hot CNO cycle via the ¹⁸ Ne(α,p)²¹Na reaction. II. Extended energy range E_c.m. ∼ 1.7 − 2.9MeV. Phys Rev C (2002) 66:055802. doi:10.1103/PhysRevC.66.055802

CrossRef Full Text | Google Scholar

21. Anastasiou M, Wiedenhöver I, Blackmon JC, Baby LT, Caussyn DD, Hood AA, et al. Measurement of the ¹⁸ Ne(α,p)²¹Na reaction with the ANASEN active-target detector system at E_c.m. = 2.5 − 4MeV. Phys Rev C (2022) 105:055806. doi:10.1103/PhysRevC.105.055806

CrossRef Full Text | Google Scholar

22. He JJ, Kubono S, Teranishi T, Hu J, Notani M, Baba H, et al. Investigation of excited states in ²²Mg via resonant elastic scattering of ²¹Na + p and its astrophysical implications. Phys Rev C (2009) 80:015801. doi:10.1103/PhysRevC.80.015801

CrossRef Full Text | Google Scholar

23. He JJ, Zhang LY, Parikh A, Xu SW, Yamaguchi H, Kahl D, et al. The ¹⁸ Ne(α,p)²¹Na breakout reaction in x-ray bursts: Experimental determination of spin-parities for α resonances in ²²Mg via resonant elastic scattering of ²¹Na + p. Phys Rev C (2013) 88:012801. doi:10.1103/PhysRevC.88.012801

CrossRef Full Text | Google Scholar

24. Zhang LY, He JJ, Parikh A, Xu SW, Yamaguchi H, Kahl D, et al. Investigation of the thermonuclear ¹⁸ Ne(α,p)²¹Na reaction rate via resonant elastic scattering of ²¹Na + p. Phys Rev C (2014) 89:015804. doi:10.1103/PhysRevC.89.015804

CrossRef Full Text | Google Scholar

25. Wallace RK, Woosley SE. Explosive hydrogen burning. Astrophys J Suppl Ser (1981) 45:389–420. doi:10.1086/190717

CrossRef Full Text | Google Scholar

26. Schatz H, Aprahamian A, Görres J, Wiescher M, Rauscher T, Rembges J, et al. rp-process nucleosynthesis at extreme temperature and density conditions. Phys Rep (1998) 294:167–263. doi:10.1016/S0370-1573(97)00048-3

CrossRef Full Text | Google Scholar

27. Woosley SE, Heger A, Cumming A, Hoffman RD, Pruet J, Rauscher T, et al. Models for type I x-ray bursts with improved nuclear physics. Astrophys J Suppl Ser (2004) 151:75–102. doi:10.1086/381533

CrossRef Full Text | Google Scholar

28. Cyburt RH, Amthor AM, Heger A, Johnson E, Keek L, Meisel Z, et al. Dependence of x-ray burst models on nuclear reaction rates. Astrophys J (2016) 830:55. doi:10.3847/0004-637X/830/2/55

CrossRef Full Text | Google Scholar

29. Salter PJC, Aliotta M, Davinson T, Al Falou H, Chen A, Davids B, et al. Measurement of the 18 \mathrm{Ne}({\alpha}{,p_{0}})^{21}\mathrm{Na} reaction cross section in the burning energy region for x-ray bursts. Phys Rev Lett (2012) 108:242701. doi:10.1103/PhysRevLett.108.242701

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kubono S, Yanagisawa Y, Teranishi T, Kato S, Kishida Y, Michimasa S, et al. New low-energy RIB separator CRIB for nuclear astrophysics. Eur Phys J A (2002) 13:217–20. doi:10.1140/epja1339-36

CrossRef Full Text | Google Scholar

31. Yanagisawa Y, Kubono S, Teranishi T, Ue K, Michimasa S, Notani M, et al. Low-energy radioisotope beam separator CRIB. Nucl Instrum Methods Phys Res Sect A (2005) 539:74–83. doi:10.1016/j.nima.2004.09.041

CrossRef Full Text | Google Scholar

32. Vorozhtsov S, Perepelkin E, Vorozhtsov A, Watanabe S, Kubono S, Goto A. Beam simulations in computer-modelled 3d fields for riken avf cyclotron upgrade. In: Proceedings of Particle Accelerator Society Meeting; August 1-3, 2017; Sapporo, Japan (2009). p. 240–3.

Google Scholar

33. Yamaguchi H, Wakabayashi Y, Amadio G, Hayakawa S, Fujikawa H, Kubono S, et al. Development of a cryogenic gas target system for intense radioisotope beam production at CRIB. Nucl Instrum Methods Phys Res Sect A (2008) 589:150–6. doi:10.1016/j.nima.2008.02.013

CrossRef Full Text | Google Scholar

34. Kumagai H, Ozawa A, Fukuda N, Sümmerer K, Tanihata I. Delay-line PPAC for high-energy light ions. Nucl Instrum Methods Phys Res Sect A (2001) 470:562–70. doi:10.1016/S0168-9002(01)00804-X

CrossRef Full Text | Google Scholar

35. Artemov KP, Belyanin OP, Vetoshkin AL, Wolski R, Golovkov MS, Goldberg VZ, et al. Effective method of study of α-cluster states. Sov J Nucl Phys (1990) 52:408.

Google Scholar

36. Ziegler JF, Ziegler M, Biersack J. Srim – the stopping and range of ions in matter. Nucl Instrum Methods Phys Res Sect B 268 (2010) 1818–23. doi:10.1016/j.nimb.2010.02.091

CrossRef Full Text | Google Scholar

37. Rolfs CE, Rodney WS. Cauldrons in the cosmos. Chicago and London: The University of Chocago Press (1988).

Google Scholar

38. Lane AM, Thomas RG. R-matrix theory of nuclear reactions. Rev Mod Phys (1958) 30:257–353. doi:10.1103/RevModPhys.30.257

CrossRef Full Text | Google Scholar

39. Larson N. A code system for multilevel R-matrix fits to neutron data using bayes’ equations. unpublished: ORNL/TM-9179/R5 (2000).

Google Scholar

40. Longland R, Iliadis C, Champagne A, Newton J, Ugalde C, Coc A, et al. Charged-particle thermonuclear reaction rates: I. Monte carlo method and statistical distributions. Nucl Phys A (2010) 841:1–30. doi:10.1016/j.nuclphysa.2010.04.008

CrossRef Full Text | Google Scholar

41. Illiadis C. Nuclear Physics of stars. New York: VCH (2007).

Google Scholar