- 1Engineering Laboratory of Spatial Information Technology of Highway Geological Disaster Early Warning in Hunan Province, Changsha University of Science and Technology, Changsha, Hunan, China
- 2School of Computer and Communication Engineering, Changsha University of Science and Technology, Changsha, China
- 3Hunan University of Science and Technology, Xiangtan, Hunan, China
This study proposes a novel color image encryption algorithm based on a 3D chaotic Hopfield neural network and random row–column permutation. First, a 3D chaotic Hopfield neural network is proposed to produce the random sequence for generating the diffusion and permutation keys. Then, the rows and columns of the original image are randomly arranged according to the permutation key in the permutation process. Three subgraphs are formed by separating the R, G, and B components of the color image in the diffusion process. Each of the three subgraphs is split along the columns to form three parts; the left and middle parts are exchanged. Three diffusion keys are used to encrypt each of the three parts. Finally, the individually encrypted subgraphs are stitched together to obtain the final encrypted image. Simulation results using MATLAB and FPGA and security analysis demonstrate that the encryption scheme has good performance.
1 Introduction
In recent years, communication technology has made significant progress. At the same time, the security of information distribution has been raised to a new level. Digital images are an important means of multimedia expression [1, 2], which are widely used in clinical medicine, astronomy, inspection, and other regions. In conclusion, image information transmission urgently needs a set of new, more stable, not-easy-to-be-cracked image encryption algorithms.
Chaos is a non-linear dynamical phenomenon that exists in a wide variety of natural fields [3–6], such as biology, meteorology, and economics. Interestingly, chaos is not a pure disorder but rather an ordered state that does not possess periodic changes and other notable symmetrical features. One distinctive feature of chaotic systems is that they are extremely sensitive to the initial values and parameters, and the dynamics and values of the system can vary considerably for different initial values of the same parameters. These characteristics of chaotic systems are well suited to the needs of image encryption algorithms [7, 8], and that is the reason why many researchers have applied chaotic systems to image encryption in recent years. Wang et al. [9] proposed a new image-encryption algorithm based on iterating chaotic maps. Using the pseudorandom sequence generated by a group of one-dimensional chaotic maps, Li et al. [10] used a 1-D chaotic tent map to generate a chaos-based key stream for image encryption. Lai et al. [11] proposed a novel image encryption based on the 2D Salomon map.
Many image-encryption studies now combine chaotic systems with other methods, such as DNA sequences [12–15] and diffusion-permutation [16–18]. Enayatifar et al. [15]proposed a novel image-encryption algorithm based on the deoxyribonucleic acid (DNA) masking hybrid model, genetic algorithm (GA), and logical map. Chai et al. [19]designed an encryption algorithm based on a chaotic system and DNA sequence operations. Liu et al. proposed an image-encryption algorithm based on one-time keys and robust chaotic maps and designed a novel encryption algorithm based on the spatial bit-level permutation and high-dimension chaotic system in Refs. 20, 21, respectively. Chen et al. [22] proposed a complete cryptosystem, which is built by using Bake maps for image permutations, and Diab et al. [23] improved it.
In recent years, some research studies on artificial neural networks and their applications [24–29] have been widely discussed. With the creation of the first memristor [30], many researchers have used memristors to simulate synapses [31–33] between neurons in the human brain and to analyze the dynamical behavior [34–38] of artificial neuronal networks. The combination of chaotic systems and artificial neural networks has become a hot research topic nowadays [39, 40], and due to the nonlinear characteristic of the Hopfield neural network model, this model is capable of generating abundant chaotic behavior and is often used by researchers to simulate the various dynamic behaviors of neurons in the brain [41]. Using the Hopfield chaotic neural network model, a random sequence can be generated, and the more random the generated random sequence, the better the encryption of the image. There are many works in the field of random number generation using chaotic models [42, 43]. Wang et al. [44] proposed a novel encryption algorithm based on a new fractional-order chaotic system.
Before our work, Wang et al. [45] proposed a new color image encryption, which uses Hopfield chaotic neural networks to generate the self-diffusion chaotic matrix. Chen et al. [46] proposed a three-dimensional fractional-order discrete Hopfield neural network. Wu et al. [47] applied the Hopfield chaotic neural network together with the novel hyperchaotic system to propose a new color image encryption algorithm. The purpose of this study is to investigate a simple but efficient image-encryption algorithm based on a chaotic Hopfield neural network model.
This study proposed an image encryption based on a 3D chaotic Hopfield neural network and random row–column permutation. In this diffusion process, we separate the RGB components of the color image. Each component is split into three equal parts along the columns and then the middle and left parts are swapped. Three different random sequences are obtained by the proposed chaotic Hopfield neural network to encrypt the three parts of each component. Finally, the R, G, and B components of the ciphertext image are combined into the ciphertext image. Most of the previous image-encryption algorithms [48–51] either encrypted the RGB components using the same set of random sequences or encrypted the RGB using three different sets of random sequences separately. The association of each element of RGB in the relative position of the image is ignored, which would make the image easier to crack. Therefore, this study splits the RGB subgraphs separately and then uses different encryption sequences for each part of the subgraph. The experimental results are obtained by using MATLAB and FPGA. The extensive security analysis shows that the proposed algorithm improves encryption efficiency and has good security performance.
The rest of this paper is organized as follows. Section 2 describes the Hopfield neural network system. Section 3 presents the image-encryption and -decryption algorithm. Section 4 shows the simulation result of the image encryption and decryption. Section 5 analyzes the safety of this algorithm. Section 6 concludes this paper.
2 Hopfield neural network systems
The Hopfield neural network was proposed by the American physicist J. Hopfield [52]. In this study, the Hopfield neural network model of three neurons with self-feedback is adopted. We can see that the three neurons have the ability to connect together and influence each other. The Hopfield neural network model is shown as follows:
where
In this study, the weight matrix [53] is expressed as follows:
The weight matrix w is obtained through constant exploration and verification. The initial states of the system are x1(0), x2(0), and x3(0). The system state changes continuously under the action of the weight matrix and the excitation function. After continuous iteration, the system gradually enters a chaotic state.
The 3D chaotic Hopfield neural network of this study can be presented as follows:
where x1(t), x2(t), and x3(t) represent the state variables of the three neurons, respectively, and the activation function Ui is represented as follows:
Equation 3 represents first-order ordinary differential equations. With the forementioned weight matrix (2) and the activation Eq. 4, we find that the system is chaotically optimal at initial values around [−0.215, −0.127, and 1.530] after continuous experimentation and verification using MATLAB. To use different keys for each encrypted image, we have changed the initial value to a variable in the neighborhood of [−0.215, −0.127, and 1.53], with two decimal places tending to be constant. Such changes to the initial values are minimal, and the system still eventually enters a chaotic state.
The initial values are chosen as follows:
where sum represents the function of summing over pixel values, p represents the 3D array of plaintext images, and mod represents the residual function.
The phase diagrams of the system are shown in Figure 1, and the initial values of the system are x1(0) = −0.123, x2(0) = −0.127, and x3(0) = 1.530, respectively. The neural network system consisting of three neurons enters a chaotic state with the presence of chaotic attractors.
To further confirm whether the system is in a chaotic state, we take the method of whether there exists a positive Lyapunov exponent [54] to judge. As the weights are determined and the initial values of the system are changed slightly, the Lyapunov exponent is always larger than zero. So, we can consider the proposed Hopfield neural network as a chaotic system [55].
3 Image-encryption and -decryption algorithms
In this section, the encryption process and decryption process of images are introduced.
3.1 Image encryption
Images are made up of pixels in electronics and are divided into color and grayscale images. Each pixel of a grayscale image contains only one pixel value, while every pixel of a color image consists of three pixel values of RGB. The grayscale image can be regarded as a two-dimensional array that contains the horizontal coordinates, vertical coordinates, and pixel value information for every pixel. The color image can be considered a three-dimensional array that contains the horizontal coordinates, vertical coordinates, and the RGB pixel values of every pixel. This study proposes a method to separate the RGB components of the color image and then perform the encryption operation. Equation 6 is used to separate the RGB component of the color image, which is shown as follows:
where P represents the original image. PR, PG, and PB represent the R, G, and B components of the original image, respectively.
This study proposes an image-encryption algorithm based on a 3D chaotic Hopfield neural network and random row–column permutation. Row–column permutation is the process of changing the position of the pixel without changing the value. The chaotic sequences are generated by the proposed chaotic Hopfield neural network for producing the permutation keys and diffusion keys. In the permutation process, the positions of the ranks of the pixels will be changed according to the permutation keys. Image diffusion is the process of changing the pixel values of RGB with the diffusion keys.
The chaotic sequences are obtained through continuously iterating the proposed 3D chaotic neural network system. The length of the intercepted chaotic sequences depends on the number of pixels in the image. Here, the first 3,000 numbers should be removed from the sequences, which are generated before the chaotic neural network system is stabilized with some error and poor randomness. The intercepted sequences will stay within the interval [0,255] by taking the absolute value, expanding by 1015, and taking the remainder. The permutation keys and diffusion keys are both obtained from the chaotic sequences.
The encryption algorithm in this study consists of two main steps: random row–column permutation and image diffusion. Details of the process can be described as follows: First, the rows and columns of the image are distorted through the permutation keys. Next, the RGB components of the image are separated by the method shown in Eq. 6. Each subgraph is formed by dividing the RGB components into three parts along columns and exchanging the middle and left part. The three parts of the subgraphs are encrypted with three different sets of diffusion keys. Finally, the subgraphs are synthesized to yield the encrypted images. The image encryption flowchart is shown in Figure 2.
3.1.1 Permutation process
The process of image permutation is to change the position of the image pixels without changing the values. First of all, the chaotic sequences are generated by the 3D chaotic Hopfield neural network (3) for producing the permutation keys, which are combined with the increasing sequences of length and width of the corresponding image to form 2 × M and 2 × N key pairs, respectively. Then, the permutation process is achieved by the determinant transformation of the original image through the key pairs.
Step 1: The length M and width N of the image are obtained at first. Then, the chaotic sequences x1(i) and x2(j) (i = 1,2,…,M and j = 1,2,…,N) are generated through the 3D chaotic Hopfield network system, respectively.
Step 2: The permutation keys are obtained through the chaotic sequences, and the expression of the generated function is as follows:
where RandM(i) and RandN(j) (i = 1,2,…,M and j = 1,2,…,N) represent the permutation keys of the row and column, respectively. The floor is the downward-rounding function. x1(i) and x2(j) are the chaotic sequences.
Step 3: Duplicate numbers are discarded when the permutation keys are obtained. For each number stored in RandM(i) or RandN(j), the corresponding position variables i or j increases by 1. This step is repeated until i and j have reached the values of M and N, or the chaotic sequences have been taken.
Step 4: The numbers in RandM(i) and RandM(j) are complemented because there is no guarantee that all non-repeating numbers from 1 to M or 1 to N will be taken; we need to find numbers that do not exist in the arrays and add them to the arrays until they are filled
Step 5: The key pairs are formed through the permutation keys and increasing sequences. The generating function of the key pairs is shown as follows:
Specifically, Mchange and Nchange are 2 × M and 2 × N arrays, respectively. The first row is an increasing sequence of 1 ∼ M or 1 ∼ N, and the second row is the sequence of RandM(i) or RandM(j), respectively. Ultimately, the mappings are formed by key pairs to perform permutation.
Step 6: The rows and columns of pixels are randomly permutated to get the permuted image. The permutation method can be shown as follows:
The outline and main information of the permuted image are obscured after this process. However, there is still some plaintext image information that can be captured by illegal hackers. At the same time, the correlation between the pixel points of the adjacent is still at a high level. To make the encryption system works better, the diffusion process is performed.
3.1.2 Segmentation and diffusion process
The difference between image permutation and image diffusion is that image diffusion needs to change the original pixel value, which will completely distort the information of the whole image. The main information and details of the image are completely invisible, and the cryptographer cannot find any useful information.
Three subgraphs are generated by separating the R, G, and B components of the color image in the diffusion process. Each subgraph is split along the columns to form three equal parts. The primary information of the daily photos or machine-made images is usually centered. So, the left and middle parts are exchanged in this process. Three different chaotic sequences y1, y2, y3 are obtained through the 3D chaotic Hopfield neural network system to produce the diffusion keys, which are used to encrypt the three parts, respectively. The experimental results obtained using MATLAB and FPGA prove that our proposed encryption algorithm has a good encryption effect. The detailed steps are as follows:
Step 1: First, RGB components of the permuted image are separated to form three subgraphs, which are divided along columns into three parts to exchange the left part and middle part. Three parts of the RGB components are generated by Eq. 10:
where j1 = 1,3…,
Step 2: The diffusion keys are obtained by Eq. 11:
where n1 = 1,2,…,
Step 3: Three different diffusion keys are used to encrypt the three parts of the subgraph, which is shown as follows:
where CLR, CCR, and CRR represent the left, middle, and right parts of the encrypted subgraph R, respectively. bixor(P, k) represents the XOR operation. The pixel value of the cipher image is formed by the XOR operation between the original pixel value and the diffusion key. The information in the plaintext image is completely hidden.
Step 4: Splicing the three encrypted parts of the subgraph together, we get
where CR represents the R component of the ciphertext image. The positions of CCR and CLR are exchanged to obtain a better encryption effect.
Step 5: Step 1 to Step 4 is repeated to realize the encryption of the G and B components.
Step 6: The encrypted RGB components are combined to form the final encrypted image. Furthermore, three two-dimension arrays are merged into one three-dimensional array, which is shown as follows:
where C represents the ciphertext images after the diffusion process and cat represents the splicing function.
3.2 Image decryption
The image decryption is the inverse process of the image encryption. In this process, the ciphertext image is obtained at first. Then, the R, G, and B components of the ciphertext image are divided into three parts by columns, and then the middle part and left part are exchanged. After that, the inverse diffusion process is performed, and the RGB components are stitched to obtain the complete images. In image encryption, the column-transformed operation happens behind the row-transformed operation in the permutation process. So, the inverse operation is done in the inverse permutation process. Finally, the plaintext image is obtained. The flowchart of the image decryption is shown in Figure 3.
4 Simulation results
In this study, we selected four color images with a resolution of 512 × 512 for encryption.
4.1 Simulation results using MATLAB
The images with a clear outline, dense pixel distribution, uniform color, and uniform light and dark are selected as the test images because they are representative and better reflect the performance of the encryption algorithm. From Figure 4, we can see that the outline of the ciphertext image is invisible, and the pixels are equally distributed. So, it is almost impossible to obtain plaintext image information from the ciphertext image. The decrypted image is exactly the same as the plaintext image. It can be said that the encryption algorithm has excellent encryption performance.
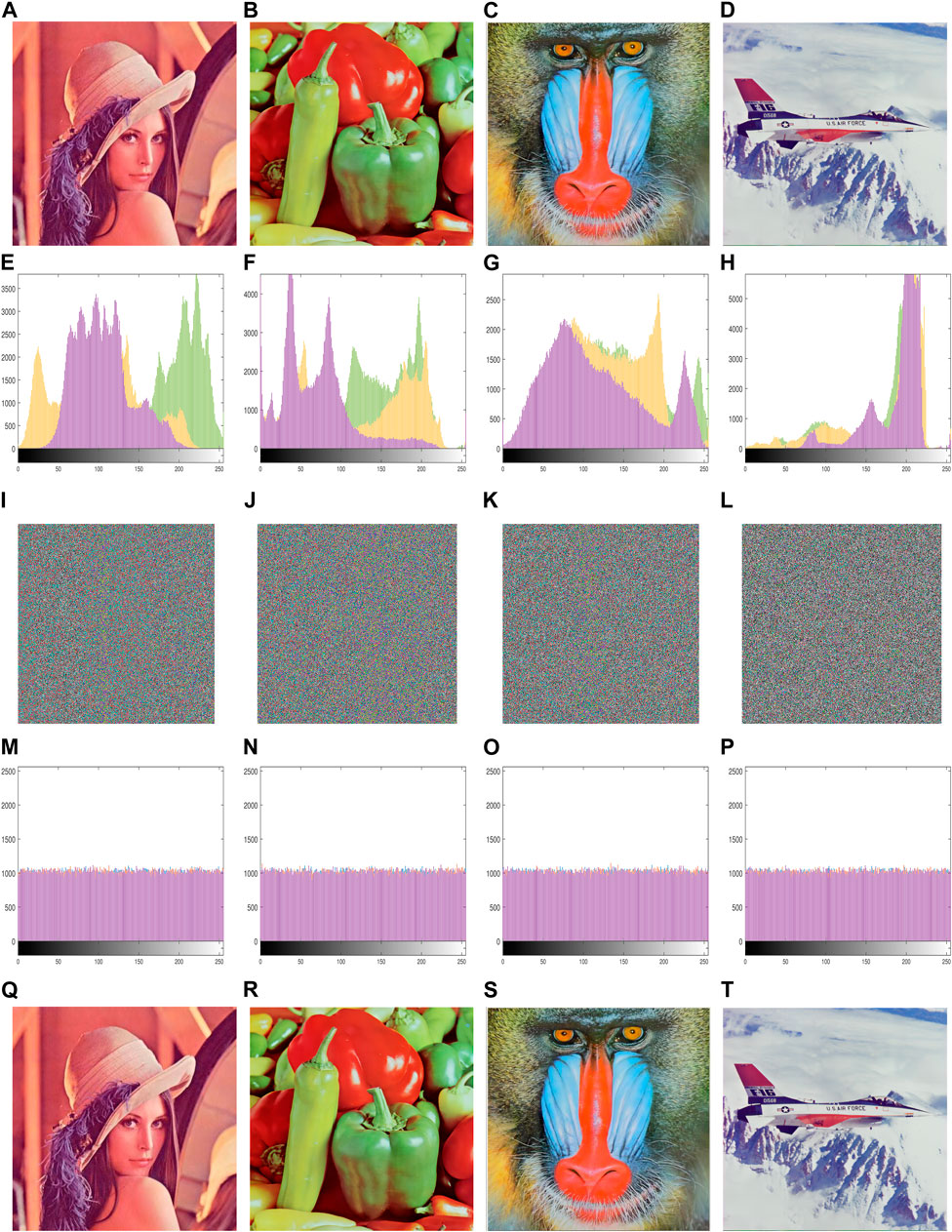
FIGURE 4. Simulation result: (A–D) plaintext images, (E–H) histograms of the plaintext images, (I–L) ciphertext images, (M–P) histograms of the ciphertext images, and (Q–T) decrypted images of ciphertext images.
4.2 Simulation results in FPGA
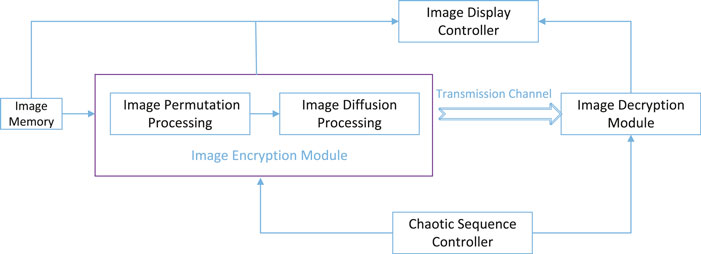
In this section, FPGA-based implementation of the proposed image cryptosystem is introduced. We have implemented FPGA debugging by using a Xilinx Zynq-7000 series XC7Z020 FPGA chip and an AN9767 dual-port parallel 14-bit digital-to-analog converter module with a maximum conversion rate of 125MHz, Vivado17.4, and a system generator. The proposed image encryption scheme is implemented on an FPGA platform with the hardware design shown in Figure 5, consisting of five components: image memory, image encryption, image decryption, image display controller, and chaotic sequence controller. The image memory module is used to store plaintext images. The keys are obtained from the chaotic sequence controller. The plaintext image and the chaotic sequences are transferred to the image encryption module, which is used to generate the ciphertext image. The image encryption module consists of the image permutation process and the image diffusion process module. The image decryption module is the inverse of the encryption module and decrypts the ciphertext image into a plaintext image. The image display controller module is used to display both plaintext and ciphertext images.
FPGA-based implementation result of the proposed image cryptosystem is shown in Figure 6. From Figures 6A, B, the plaintext image and the encrypted image are shown on the screen. The images on the right in Figure 6A and on the left in Figure 6B are the permutated images, and the image on the right in Figure 6B is the ciphertext image. Figure 6C is the decryption result of the FPGA-based implementation. Experiments have demonstrated no significant difference between the FGPA platform and MATLAB regarding the effectiveness of image encryption and decryption.

FIGURE 6. FPGA-based implementation results of the proposed image cryptosystem: (A, B) process of image encryption; (C) process of image decryption and (D) experimental equipment and environment.
5 Performance analysis
This section is to verify the security and efficiency of the proposed encryption algorithm. The simulation test is performed on a computer using MATLAB R2020b.
5.1 Histogram analysis
The histogram can reflect the distribution of the overall pixel values of the image accurately and intuitively. There is only one component of the pixel value in a grayscale image, so the greyscale image has only one histogram. However, the pixel value of the color image consists of R, G, and B components. Therefore, a color image has three histograms, representing the occurrence of R, G, and B pixel values, respectively. The histogram is a two-dimensional statistical map, where the abscissa represents each pixel value in the color image and the ordinate indicates the frequency of each pixel value appearing in the color image. The analysis of the histogram can capture information about the images. The encryption system with high security should make the histograms of the ciphertext image as uniform as possible. Four color images are selected for histogram analysis; the histograms of plaintext images are shown in Figures 4E–H, and the histograms of the ciphertext images are shown in Figures 4M–P.
The histograms of R, G, and B components of the plaintext images show a mountainous pattern with an uneven distribution of the pixels, while the histograms of the ciphertext images are very uniform and the characteristics of the distribution of the image pixels are well hidden. It is difficult for a cracker to obtain any useful information from the histograms. It can be inferred that this encryption scheme has great security.
5.2 Correlation analysis
Correlation analysis reflects the degree of correlation of pixel values at adjacent positions in the image. The size of the correlation coefficient of adjacent pixel values in the ciphertext image can better reflect the effects of the encryption algorithm. The lower the correlation, the better the encryption effects of the ciphertext image obtained by the proposed encryption algorithm. The correlation coefficient of a good color image-encryption algorithm should be close to zero. The correlation analysis equation is as follows:
where ui and vi represent the adjacent pixel values in the image and n is the number of pixels sampled. E(u) and E(v) represent the expectation of u and v. cov(u, v) represents the covariance, and r is the correlation coefficient.
The correlations should be analyzed in the R, G, and B components separately in the color images, and we need to analyze the four directions of the image: horizontal, vertical, positive-diagonal, and negative angles. Here, 10,000 pixels of the components R, G, and B are randomly taken. If the coordinate point of ui is (xi, yi), then the adjacent coordinate point in the horizontal direction is set to vi (xi + 1, yi). Similarly, the adjacent coordinate point we set in the vertical direction is vi (xi, yi + 1), in the positive-diagonal direction; we set vi (xi + 1, yi + 1), and the adjacent coordinate points in the opposite angular direction were set as vi (xi − 1, yi + 1).
The correlation coefficient of the plaintext image is almost close to 1, which indicates that the correlation of the pixels in the plaintext image is extremely strong. However, the ciphertext image is almost close to 0, indicating the adjacent pixels in the ciphertext image have almost no correlation. The correlation test in plaintext and ciphertext images is shown in Figure 7, which contains the distributions in those four directions, respectively. The ciphertext image shows the irregular distribution in four directions, and the pixel values around each pixel point are arbitrarily random. However, most of the points in Figures 7A, C, E, G are around a straight line, indicating there is a significant correlation in the plaintext image.
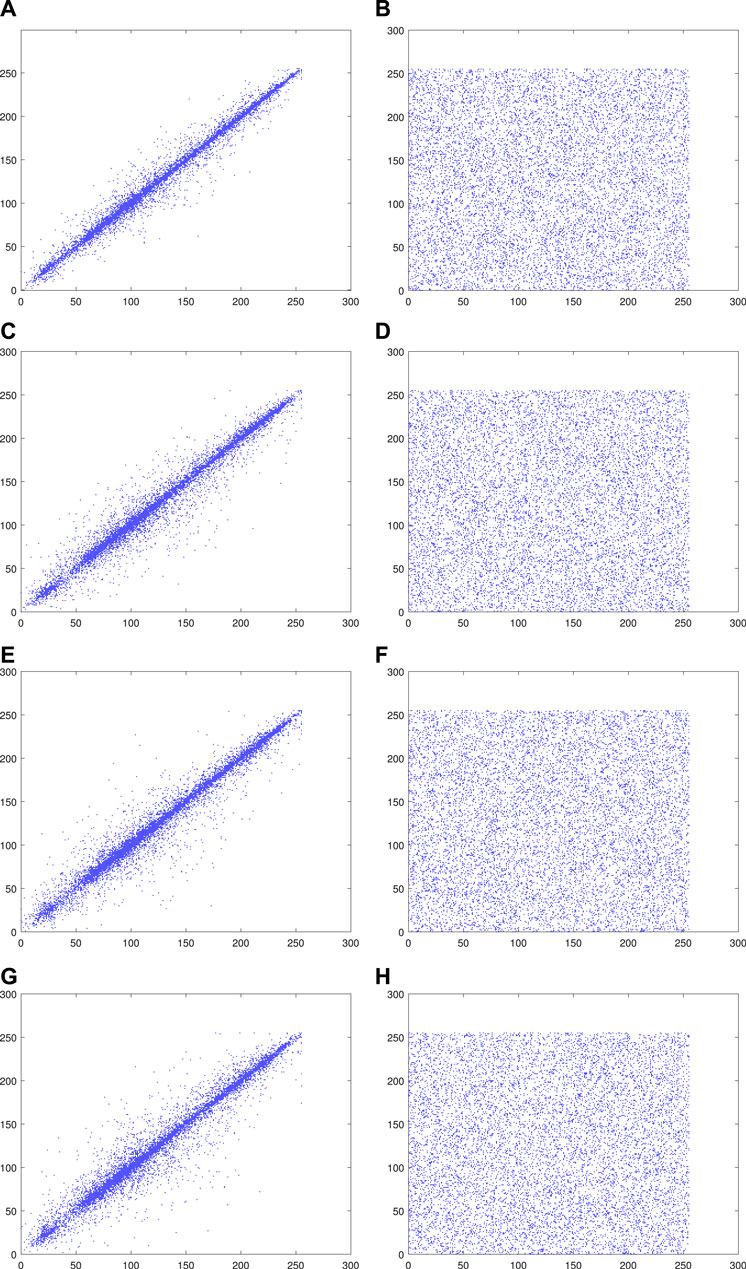
FIGURE 7. Correlation test result of Lena: (A) Horizontal diagonal of the plaintext image, (B) horizontal diagonal of the ciphertext image, (C) vertical diagonal of the plaintext image, (D) vertical diagonal of the ciphertext image, (E) positive diagonal of the plaintext image, (F) positive diagonal of the ciphertext image, (G) opposition diagonal of the plaintext image, and (H) opposition diagonal of the ciphertext image.
The results of the correlation coefficient in different directions are shown in Table 1. We can see that the proposed scheme has a remarkable performance. Only one of the correlation coefficients obtained by the proposed algorithm is higher than others.
5.3 Analysis of information entropy
Information entropy is an index to evaluate the performance of the encryption algorithm. The higher the information entropy index, the better the performance of this encryption algorithm. The information entropy equation is as follows:
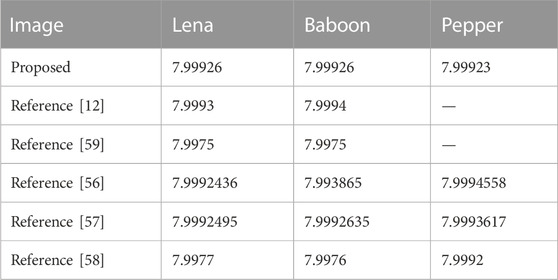
where P(i) represents the probability of the occurrence of the pixel value of i. The ideal entropy for the R, G, and B components of the color image should be equal to 8. The color Lena graph, Baboon graph, Pepper graph, and plane graph are chosen as the test images, which are encrypted by the proposed encryption algorithm. The information entropy of R, G, and B components are analyzed by Eq. 16. The test results are shown in Table 2.
The table clearly shows the information entropies of the R, G, and B components of the encrypted images Cipher-Lena, Cipher-Baboon, Cipher-Pepper, and Cipher-plane. The entropies obtained by the proposed algorithm are close to the ideal value. From Table 3, we can see that most of the entropies are larger than those obtained by other algorithms. This feature prevents information leakage during the encryption process. So, we can infer that the proposed algorithm is significantly secure.
5.4 Analysis of PSNR and MSE
PSNR and MSE are used to describe the difference between the original and encrypted images. The greater the difference between the plaintext image and the ciphertext image, the better the performance of the encryption algorithm. PSNR is the peak signal-to-noise ratio, which is an index of distortion between the plaintext and ciphertext images. The lower the PSNR value, indicating that the greater the difference between plaintext and ciphertext images, the better the encryption algorithm is.
MSE is the mean squared error, which is used to calculate the cumulative squared error between plaintext and ciphertext images. The larger the MSE, the better the encryption effect. The PSNR and MSE are defined as follows:
where P and C represent the plaintext and the ciphertext images, respectively. In addition, (i,j) stands for the position of each pixel.
The comparison of PSNR and MSE among the proposed and other algorithms is shown in Tables 4, 5, respectively. Most of the PSNR and MSE indices of our proposed algorithm are superior compared to those of others. The results show that the proposed encryption scheme has better performance.
5.5 Sensitivity analysis
Sensitivity analysis is decrypting the encrypted image with the keys whose initial values are slightly different from the original keys to see if the encrypted image can be decrypted correctly. The Lena plaintext image is encrypted by using the keys. Then, the ciphertext image is decrypted with the pseudo-keys of three very close key values Y1, Y2, and Y3, respectively. The initial values of the pseudo-keys are as follows:
where x1(0), x2(0), and x3(0) are the initial values of the keys. The three aforementioned sets of pseudo-keys with slightly different initial values are used to decrypt the Lena ciphertext image. The results of decrypting are shown in Figure 8. The plaintext image cannot be recovered correctly. Therefore, the encryption system proposed in this study satisfies the requirement of key sensitivity.

FIGURE 8. Test results of sensitivity analysis. (A) Plaintext image. (B) Decryption result of Y1. (C) Decryption result of Y2 (D) Decryption result of Y3.
5.6 Analysis of key space
A good image-encryption algorithm must have the ability to withstand outside attacks. Therefore, the key space must be large enough to ensure the security of the encryption algorithm. The key space of an ideal image encryption is larger than 2100.
The computer computational accuracy is about 1015, and the compression rate CR is 105. In this study, the key generation process consists of the following: 1) the initial values of x1(0), x2(0), and x3(0) are used for the chaotic Hopfield system iteration and the sampling time point, and 2) chaotic sequences y1(t), y2(t), and y3(t) are also used. So the key space is calculated by Eq. 19:
This shows that the encryption algorithm has a large enough key space to resist exhaustive attacks.
6 Conclusion
This study proposes a color image-encryption algorithm based on random row–column permutation and a 3D chaotic Hopfield neural network. The 3D chaotic Hopfield neural network is used to generate chaotic sequences to ensure the randomness of keys. After the permutation process, three subgraphs are formed by separating the R, G, and B components of the color image, and then, the subgraphs are cut along the columns for swapping the middle part and the left part. Three diffusion keys are produced through the chaotic sequence, and then the three parts of the subgraphs are encrypted separately. In this study, we consider the interrelationship of the pixel values of the RGB components in the plaintext image, so three sets of diffusion keys are used to encrypt the three parts of the split RGB subgraphs. This measure effectively reduces the interconnection of pixel values. Through extensive simulations and security analysis, the simulation results in MATLAB and FPGA show that the encryption algorithm has superior performance and high security.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Ethics statement
Ethical review and approval were not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author contributions
Conceptualization: WY, KG, ZZ, LC, and JZ. Methodology: WY. Hardware: LC. Validation: KG, ZZ, LC, and JZ. Formal analysis: KG, ZZ, LC, and JZ. Investigation: ZZ. Resources: WY, KG, LC, and JZ. Data curation: JZ and ZZ. Writing—original draft preparation: KG. Writing—review and editing: WY, JZ, and LC. Visualization: JZ and ZZ. Supervision: JZ and LC. Project administration: JZ and WY. Funding acquisition: JZ and WY. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Open Fund of Engineering Laboratory of Spatial Information Technology of Highway Geological Disaster Early Warning in Hunan Province, Changsha University of Science & Technology under Grant No. kfj220603, Hunan Provincial Natural Science Foundation of China, under Grant No. 2022JJ40514, the Scientific research project of Hunan Provincial Department of Education, China under Grant No. 21C0200.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Gui Y, Zeng G. Joint learning of visual and spatial features for edit propagation from a single image. Vis Comput (2019) 36:469–82.
2. Long M, Peng F, Li H. Separable reversible data hiding and encryption for hevc video. J Real Time Image Process (2018) 14:171–82.
3. Hirata Y, Oku M, Aihara K. Chaos in neurons and its application: Perspective of chaos engineering. Chaos: Interdiscip J Nonlinear Sci (2012) 22(4):047511. doi:10.1063/1.4738191
4. Mcneal P, Petcovic H, Bals-Elsholz T, Ellis T. Seeing weather through chaos: A case study of disembedding skills in undergraduate meteorology students. Bull Am Meteorol Soc (2019) 100(6):997–1010. doi:10.1175/bams-d-18-0015.1
5. Wan Q, Li F, Chen S, Yang Q. Symmetric multi-scroll attractors in magnetized hopfield neural network under pulse controlled memristor and pulse current stimulation. Chaos Solitons Fractals (2023) 169:113259.
6. Spelta A, Pecora N, Pagnottoni P. Chaos based portfolio selection: A nonlinear dynamics approach. Expert Syst Appl (2022) 188:116055. doi:10.1016/j.eswa.2021.116055
7. Lai Q, Yang L, Liu Y. Design and realization of discrete memristive hyperchaotic map with application in image encryption. Chaos, Solitons & Fractals (2022) 165:112781. doi:10.1016/j.chaos.2022.112781
8. Han X, Mou J, Jahanshahi H, Cao Y, Bu F. A new set of hyperchaotic maps based on modulation and coupling. The Eur Phys J Plus (2022) 137:523. doi:10.1140/epjp/s13360-022-02734-3
9. Wang X, Zhao J, Liu H. A new image encryption algorithm based on chaos. Opt Commun (2012) 285(5):562–6. doi:10.1016/j.optcom.2011.10.098
10. Li C, Luo G, Qin K, Li C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn (2017) 87(1):127–33. doi:10.1007/s11071-016-3030-8
11. Lai Q, Hu G, Erkan U, Toktas A. 2023, A novel pixel-split image encryption scheme based on 2D salomon map. Expert Syst Appl, 213:118845, doi:10.1016/j.eswa.2022.118845
12. Chai X, Gan Z, Yuan K, Chen Y, Liu X. A novel image encryption scheme based on DNA sequence operations and chaotic systems. Neural Comput Appl (2017) 31(1):219–37. doi:10.1007/s00521-017-2993-9
13. Yu J, Xie W, Zhong Z, Wang H. Image encryption algorithm based on hyperchaotic system and a new DNA sequence operation. Chaos, Solitons & Fractals (2022) 162:112456. doi:10.1016/j.chaos.2022.112456
14. Wu J, Liao X, Bo Y. Image encryption using 2D hénon-sine map and DNA approach. Signal Process. (2018) 153:11–23. doi:10.1016/j.sigpro.2018.06.008
15. Enayatifar R, Abdullah A, Isnin I. Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence. Opt Lasers Eng (2014) 56:83–93. doi:10.1016/j.optlaseng.2013.12.003
16. Chen J, Zhu Z, Zhang L, Zhang B, Yang Y. Exploiting self-adaptive permutation–diffusion and DNA random encoding for secure and efficient image encryption. Signal Process. (2018) 142:340–53. doi:10.1016/j.sigpro.2017.07.034
17. Li M, Lu D, Xiang Y, Zhang Y, Ren H. Cryptanalysis and improvement in a chaotic image cipher using two-round permutation and diffusion. Nonlinear Dyn (2019) 96:31–47. doi:10.1007/s11071-019-04771-7
18. Wang M, Wang X, Zhang Y, Gao Z. A novel chaotic encryption scheme based on image segmentation and multiple diffusion models. Opt Laser Technol (2018) 108:558–73. doi:10.1016/j.optlastec.2018.07.052
19. Chai X, Chen Y, Broyde L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt Lasers Eng (2017) 88:197–213. doi:10.1016/j.optlaseng.2016.08.009
20. Liu H, Wang X. Color image encryption based on one-time keys and robust chaotic maps. Comput Maths Appl (2010) 59(10):3320–7. doi:10.1016/j.camwa.2010.03.017
21. Liu H, Wang X. Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Opt Commun (2011) 284(16-17):3895–903. doi:10.1016/j.optcom.2011.04.001
22. Chen J, Zhu Z, Chong F, Hai Y, Zhang Y. Reusing the permutation matrix dynamically for efficient image cryptographic algorithm. Signal Process. (2015) 111:294–307. doi:10.1016/j.sigpro.2015.01.003
23. Diab H, El-Semary A. Cryptanalysis and improvement of the image cryptosystem reusing permutation matrix dynamically. Signal Process. Official Publ Eur Assoc Signal Process (2018) 148:172–92. doi:10.1016/j.sigpro.2018.02.011
24. Yao W, Wang C, Sun Y, Zhou C, Lin H. Exponential multistability of memristive cohen-grossberg neural networks with stochastic parameter perturbations. Appl Maths Comput (2020) 386:125483. doi:10.1016/j.amc.2020.125483
25. Yao W, Yu F, Zhang J, Zhou L. Asymptotic synchronization of memristive cohen-grossberg neural networks with time-varying delays via event-triggered control scheme. Micromachines (2022) 13:726. doi:10.3390/mi13050726
26. Yu F, Shen H, Yu Q, Kong X, Sharma P, Cai S. Privacy protection of medical data based on multi-scroll memristive hopfield neural network. IEEE Trans Netw Sci Eng (2023) 10(2):845–58. doi:10.1109/tnse.2022.3223930
27. Wang J, Zou Y, Lei P, Simon Sherratt R, Wang L. Research on recurrent neural network based crack opening prediction of concrete dam. J Internet Technol (2020) 21(4):1161–9.
28. Wang J, Wu Y, He S, Sharma P, Yu X, AlFarraj O, et al. Lightweight single image super-resolution convolution neural network in portable device. KSII Trans Internet Inf Syst (2021) 115:4065–83.
29. Long M, Zeng Y. Detecting iris liveness with batch normalized convolutional neural network. Comput Mater Continua (2019) 58(2):493–504. doi:10.32604/cmc.2019.04378
30. Strukov D, Snider G, Stewart D, Williams R. The missing memristor found. Nature (2008) 453:80–3. doi:10.1038/nature06932
31. Yao W, Wang C, Sun Y, Zhou C. Robust multimode function synchronization of memristive neural networks with parameter perturbations and time-varying delays. IEEE Trans Syst Man, Cybernetics: Syst (2022) 52(1):260–74. doi:10.1109/tsmc.2020.2997930
32. Lai Q, Wan Z, Zhang H, Chen G. Design and analysis of multiscroll memristive hopfield neural network with adjustable memductance and application to image encryption. IEEE Trans Neural Networks Learn Syst (2022)(99) 1–14. doi:10.1109/tnnls.2022.3146570
33. Lai Q, Wan Z, Kuate P. Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans Circuits Syst Regular Pap (2023) 70(3):1324–36. doi:10.1109/tcsi.2022.3228566
34. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. A new multi-scroll chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics, hardware implementation and image encryption application. Integration, VLSI J (2021) 81:71–83. doi:10.1016/j.vlsi.2021.05.011
35. Cui L, Luo W, Ou Q. Analysis and implementation of new fractional-order multi-scroll hidden attractors. Chin Phys B (2021) 30(2):020501. doi:10.1088/1674-1056/abbbe4
36. Cui L, Luo W, Ou Q. Analysis of basins of attraction of new coupled hidden attractor system. Chaos, Solitons & Fractals (2021) 146:110913. doi:10.1016/j.chaos.2021.110913
37. Yu F, Liu L, Xiao L, Li K, Cai S. A robust and fixed-time zeroing neural dynamics for computing time-variant nonlinear equation using a novel nonlinear activation function. Neurocomputing (2019) 350:108–16. doi:10.1016/j.neucom.2019.03.053
38. Ren L, Mou J, Banerjee S, Zhang Y. A hyperchaotic map with a new discrete memristor model: Design, dynamical analysis, implementation and application. Chaos, Solitons & Fractals (2023) 167:113024. doi:10.1016/j.chaos.2022.113024
39. Wang X, Zhao Y, Zhang H, Guo K. A novel color image encryption scheme using alternate chaotic mapping structure. Opt Lasers Eng (2016) 82:79–86. doi:10.1016/j.optlaseng.2015.12.006
40. Zhu H, Ge J, Qi W, Zhang X, Lu X. Dynamic analysis and image encryption application of a sinusoidal-polynomial composite chaotic system. Mathematics Comput Simulation (2022) 198:188–210. doi:10.1016/j.matcom.2022.02.029
41. Lin H, Wang C, Deng Q, Xu C, Deng Z, Zhou C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn (2021) 106(1):959–73. doi:10.1007/s11071-021-06853-x
42. Sang L, Guo Y, Liu H, Zhang J, Wang Y. Real-time all-optical random numbers based on optical Boolean chaos. Opt Express (2021) 29(5):7100–9. doi:10.1364/oe.420010
43. Li S, Liu Y, Ren F, Yang Z. Design of a high throughput pseudo-random number generator based on discrete hyper-chaotic system. IEEE Trans Circuits Syst Express Briefs (2023) 70(2):806–10. doi:10.1109/tcsii.2022.3178103
44. Xu S, Wang X, Ye X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos, Solitons & Fractals (2022) 157:111889. doi:10.1016/j.chaos.2022.111889
45. Wang X, Li Z. A color image encryption algorithm based on hopfield chaotic neural network. Opt Lasers Eng (2019) 115:107–18. doi:10.1016/j.optlaseng.2018.11.010
46. Chen L, Hao Y, Huang T, Yuan L, Yin L. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Networks (2020) 125:174–84. doi:10.1016/j.neunet.2020.02.008
47. Wu Y, Zeng J, Dong W, Li X, Qin D, Ding Q. A novel color image encryption scheme based on hyperchaos and hopfield chaotic neural network. Entropy (2022) 24(10):1474. doi:10.3390/e24101474
48. Zhang Z, Tang J, Zhang F, Ni H, Chen J, Huang Z. Color image encryption using 2D sine-cosine coupling map. IEEE Access (2022) 10:67669–85. doi:10.1109/access.2022.3185229
49. Rani N, Sharma S, Mishra V. Grayscale and colored image encryption model using a novel fused magic cube. Nonlinear Dyn (2022) 108:1773–96. doi:10.1007/s11071-022-07276-y
50. Hosny K, Kamal S, Darwish M. A novel color image encryption based on fractional shifted gegenbauer moments and 2D logistic-sine map. Vis Comput (2023) 39:1027–44. doi:10.1007/s00371-021-02382-1
51. Chen L, Hao Y, Yuan L, Machado J, Alam Z. Double color image encryption based on fractional order discrete improved henon map and rubik’s cube transform. Signal Processing: Image Commun (2021) 97:116363. doi:10.1016/j.image.2021.116363
52. Hopfield J. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci (1982) 79:2554–8. doi:10.1073/pnas.79.8.2554
53. Wang Y, Li J, Wang Y. Hyperchaotic image encryption algorithm based on 4D of hopfield-type neural network and AES algorithm. Comput Eng Appl (2018) 54:202–7.
54. Eckhardt B, Yao D. Local lyapunov exponents in chaotic systems. Physica D Nonlinear Phenomena (1993) 65(1-2):100–8. doi:10.1016/0167-2789(93)90007-n
55. Koçak H, Palmer K. Lyapunov exponents and stability in interval maps. SeMA J (2010) 51:79–82. doi:10.1007/bf03322557
56. Liu L, Zhang Z, Chen R. Cryptanalysis and improvement in a plaintext-related image encryption scheme based on hyper chaos. IEEE Access (2019) 7:126450–63. doi:10.1109/access.2019.2938181
57. Zhang W, Yu H, Zhao Y, Zhu Z. Image encryption based on three-dimensional bit matrix permutation. Signal Process. (2016) 118:36–50. doi:10.1016/j.sigpro.2015.06.008
58. Benaissi S, Chikouche N, Hamza R. A novel image encryption algorithm based on hybrid chaotic maps using a key image. Optik (2023) 272:170316. doi:10.1016/j.ijleo.2022.170316
Keywords: image encryption, non-linear dynamics, diffusion and permutation, chaotic Hopfield neural network, random row–column permutation
Citation: Yao W, Gao K, Zhang Z, Cui L and Zhang J (2023) An image encryption algorithm based on a 3D chaotic Hopfield neural network and random row–column permutation. Front. Phys. 11:1162887. doi: 10.3389/fphy.2023.1162887
Received: 10 February 2023; Accepted: 03 March 2023;
Published: 22 March 2023.
Edited by:
Viet-Thanh Pham, Ton Duc Thang University, VietnamReviewed by:
Qiang Lai, East China Jiaotong University, ChinaJun Mou, Dalian Polytechnic University, China
Copyright © 2023 Yao, Gao, Zhang, Cui and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Yao, eWFvd2VpQGNzdXN0LmVkdS5jbg==
 Wei Yao
Wei Yao Kai Gao2
Kai Gao2