Numerical approach for the fractional order cable model with theoretical analyses

This study, considers the fractional order cable model (FCM) in the sense of Riemann–Liouville fractional derivatives (R-LFD). We use a modified implicit finite difference approximation to solve the FCM numerically. The Fourier series approach is used to examine the proposed scheme’s theoretical analysis, including stability and convergence. The scheme is shown to be unconditionally stable, and the approximate solution converges to the exact solution. To demonstrate the application and feasibility of the proposed approach, a numerical example is provided.

1 Introduction

Real-life phenomena have been modeled in a variety of ways, and partial differential equations (PDEs) and ordinary differential equations (ODEs) can be used to model some of these phenomena. For the phenomena that are not sufficiently modeled by PDEs, fractional PDEs have been developed by replacing the non-integers order derivative [1]. Fractional calculus can be applied to every field of science, such as biology, engineering, image processing, wave propagation, rheology, viscoelasticity, etc.

Fractional diffusion equations are a type of fractional differential equation that has sparked a lot of interest due to their various applications. By adding a variable lower limit of integration Rajkovic [2] generalized the notions of fractional the g-integral and g-derivative, and came up with a q-Taylor definition that contains fractional-order q-derivatives of the function. Yakar [3] considered a fractional boundary value problem with a two-part operator. The main problem’s eigenvalues with Eigen functions are the same as the constructed operator’s eigenvalues and corresponding Eigen functions in Hilbert spaces. The non-integers order Cable model is derived from the circuit model based on intracellular and extracellular space [4]. Vitali [5] introduced a Caputo formula as an extension of the FCE, obtained the analytical solution using the Laplace transform, and obtained results in terms of special functions. Yu [6] used the compact difference method and the Fourier method for stability and convergence in his computational treatment of the two-dimensional FCE. Liu et al. [7] discussed the FCE having two fractional temporal derivatives, and proposed implicit schemes with convergence orders of $O\left(\tau +h^2\right)$ and $O\left({\tau }^2+h^2\right)$, respectively. The energy approach was used to investigate the stability and convergence analysis. Lin et al. [8] devised a numerical schema for FCE discretization. They analyzed the proposed schema by providing theoretical and error estimates. The schema was unconditionally stable. Liu et al. [9] used a two-grid approach with the finite element scheme to solve the non-linear FCM, and the stability based on the fully discrete two-grid method was derived. A semi-discrete approach was used for time, and the Galerkin finite element approach was used for space Zhuang [10]. To approximate the time of the FCE involving two fractional temporal derivatives, Nikan [11] proposed a computational scheme for the radial basis function-generated finite difference (RBF-FD). The Grünwald–Letnikov expansion was used to discretize the time domain of the TFCM, and the RBF-FD was used to discretize the spatial derivatives. They demonstrated that the method can easily be implemented on such types of fractional PDEs. The orthogonal spline collocation with a complete theoretical analysis with order $O\left({\tau }^{\min (2-{\gamma }_1,2-{\gamma }_2}+h^{r+1}\right)$ was used by Zhang [12]. Quintana-Murillo [13] researched two temporal R-LFD for explicit numerical approaches to solve FCE. The numerical solution was obtained by using the forward difference formula, the Grünwald–Letnikov formula for the first-order derivative and Riemann–Liouville derivatives, respectively, and the three-point centered formula for the spatial derivative. The stability was tested by the von Neumann technique. Baleanu [14] proposed computational schemes for the optimal control problems of fractional order in the R-LFD sense. The approximations were replaced into optimal control equations of fractional order, and an algebraic equation was obtained, which can be solved by a numerical technique. To model the electrodiffusion of ions in nerve cells with anomalous sub-diffusion along and through the nerve cells, Henry [15] introduced fractional Nernst–Planck equations and related FCE. They analyzed fundamental solutions after modeling the sub-diffusion in two different ways, leading to two FCE. The solution approaches the normal non-zero steady state with uniform sub-diffusion along and around the nerve cells, but the approach is delayed by the anomalous sub-diffusion. Realistic electrophysiological studies on actual dendrites may be related to these solutions. Langlands [16] introduced fractional Nernst–Planck equations and derived FCE as macroscopic models for the electro diffusion of ions in nerve cells. They calculated the power lessening along dendrites in response to synaptic inputs of the alpha function. Easy integration and fire variants of the models were also used to calculate action potential firing rates. Tomovski [17] discussed Laplace and Fourier transforms to formulate the Green function of the generalized space-time FCE, and then examined the even moments to demonstrate that it can have a negative sign, indicating that the Green function does not always flow in one direction and that the current can switch directions. Bhrawy [18] used the collocation method in combination with the Shifted-Jacobi operational matrix in the sense of the Caputo fractional derivative. The results of their suggested approach are much more efficient for solving variable-order non-linear PDEs with high accuracy. Liu [19] presented a discrete numerical formula obtained by finite difference and finite element approximation in time and space, respectively, for the FCE. Liang-lian [20] considered the finite volume approach to solving the FCE using an implicit difference scheme. The approach was also convergent and unconditionally stable. Zhang [21] suggested an unconditionally numerical approach for the convection-diffusion of the fractional order problem. A novel shifted version of the Grünwald–Letnikov formula for the fractional order derivatives was used to prove the accuracy, and for theoretical analysis. Hu [22] implemented compact schemes for the FCE, and utilized the energy method to prove that the first scheme is stable and convergent in ${\mathrm{l}}_{\infty }$-norm with the order $\mathrm{O}\left(\mathrm{\tau }+{\mathrm{h}}^4\right)$, while the second one is an inner product. The computed result indicates that both schemes are accurate and effective. Moshtaghi and Saadatmandi [23] researched the cable model of fractional order and solved using the collocation-type approach. They converted the fractional order model into a set of algebraic equations and presented two numerical examples to confirm the accuracy and efficiency. Aslefallah et al. [24] studied the 2D time-fractional order cable model with Dirichlet boundary conditions and implemented the singular boundary method to split the solution of the inhomogeneous governing equation. More studies related to the fractional order differential equation can be seen in [25–35].

The aim of this study is to find out the numerical solution of the fractional-order cable model. The fractional derivative is approximated by the discretized Riemann–Liouville derivative and for the space derivative use the finite difference approximation. For the proposed approach’s complete theoretical analysis as stability and convergence are discussed. The theoretical analysis, confirms the efficiency and effectiveness of the proposed approach.

Suppose the following fractional order cable model [36] as:

$\frac{\partial w\left(x,t\right)}{\partial t}={}_0{}^{}{D}_t^{1-{\rho }_1}\left(K\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^2}\right)-{\mu }^2{}_0{}^{}{D}_t^{1-{\rho }_2}w\left(x,t\right)+h\left(x,t\right),(1)$

with initial and boundary conditions

$w\left(x,0\right)=\beta \left(x\right),0\le x\le L,(2)$

$w\left(0,t\right)={\beta }_1\left(t\right),w\left(L,t\right)={\beta }_2\left(t\right),0<t\le T,(3)$

where $0<{\rho }_1,{\rho }_2<1,K>0and\mu$ are constants and $\beta ,{\beta }_{1}and{\beta }_2$ are known functions and the unknown function $w$ is to be determined $.$

The ${}_0{}^{}{D}_t^{1-{\rho }_1}w\left(x,t\right)$ is the Riemann–Liouville fractional derivative of fraction order $1-{\rho }_1$ defined by [37]:

${}_0{D}_t^{1-{\rho }_1}w\left(x,t\right)=\frac{1}{\mathrm{\Gamma }\left({\rho }_1\right)}\frac{d}{dt}{\displaystyle \underset{0}{\overset{t}{\int }}}\frac{w\left(x,\eta \right)}{{\left(t-\eta \right)}^{1-{\rho }_1}}d\eta =\frac{\partial }{\partial t}{I}_0^{{\rho }_1}w\left(x,t\right).(4)$

The Riemann–Liouville fractional integral can be discretized [38] as:

$I_0^{{\rho }_1}w\left(x,t\right)=\frac{1}{\mathrm{\Gamma }\left({\rho }_1\right)}{\displaystyle \underset{0}{\overset{t}{\int }}}\frac{w\left(x,\eta \right)}{{\left(t-\eta \right)}^{1-{\rho }_1}}d\eta ,$

discretizing the equation at the grid point $\left(x_i,t_k\right).$

$I_0^{{\rho }_1}w\left(x_i,t_k\right)=\frac{1}{\mathrm{\Gamma }\left({\rho }_1\right)}{\displaystyle \underset{0}{\overset{t_k}{\int }}}{\left(t_k-\eta \right)}^{{\rho }_1-1}w\left(x_i,\eta \right)d\eta .$

As by Jumarie property [39] as:

$=\frac{1}{{\rho }_1\mathrm{\Gamma }\left({\rho }_1\right)}{\displaystyle \underset{0}{\overset{t_k}{\int }}}w\left(x_i,\eta \right){\left(d\eta \right)}^{{\rho }_1},$

$=\frac{1}{\mathrm{\Gamma }\left(1+{\rho }_1\right)}{\displaystyle \sum _{j=0}^{k-1}}{\displaystyle \underset{t_j}{\overset{t_{j+1}}{\int }}}w\left(x_i,\eta \right){\left(d\eta \right)}^{{\rho }_1},$

$=\frac{1}{\mathrm{\Gamma }\left(1+{\rho }_1\right)}{\displaystyle \sum _{j=0}^{k-1}}w\left(x_i,t_{k-j}\right){\displaystyle \underset{t_j}{\overset{t_{j+1}}{\int }}}1{\left(d\eta \right)}^{{\rho }_1}.$

Again, by Jumarie property as:

$=\frac{1}{\mathrm{\Gamma }\left(1+{\rho }_1\right)}{\displaystyle \sum _{j=0}^{k-1}}w\left(x_i,t_{k-j}\right)\left({\tau }^{{\rho }_1}{\left(j+1\right)}^{{\rho }_1}-{\tau }^{{\rho }_1}{\left(j\right)}^{{\rho }_1}\right),$

$=\frac{{\tau }^{{\rho }_1}}{\mathrm{\Gamma }\left(1+{\rho }_1\right)}{\displaystyle \sum _{j=0}^{k-1}}w\left(x_i,t_{k-j}\right)\left({\left(j+1\right)}^{{\rho }_1}-{\left(j\right)}^{{\rho }_1}\right),$

$I_0^{{\rho }_1}w\left(x_i,t_k\right)=\frac{{\tau }^{{\rho }_1}}{\mathrm{\Gamma }\left({1+\rho }_1\right)}{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_1\right)}w\left(x_i,t_{k-j}\right),(5)$

where $d_j^{\left({\rho }_1\right)}={\left(j+1\right)}^{{\rho }_1}-{\left(j\right)}^{{\rho }_1}.$ The same procedure can be followed for ${\rho }_2$.

Lemma 1:. The coefficients $d_k^{\left({\rho }_1\right)}$ $\left(k=0,1,2,\dots \right)$ satisfy the following properties [35]:

(i) $d_0^{\left({\rho }_1\right)}=1,d_k^{\left({\rho }_1\right)}>0,k=1,2,\dots$

(ii) $d_{k-1}^{\left({\rho }_1\right)}>d_k^{\left({\rho }_1\right)},k=1,2,3,\dots$

(iii) There exists a positive constant $C>0$, such that $\tau \le C{d}_k^{\left({\rho }_1\right)}{\tau }^{{\rho }_1},$ $k=1,2,3,\dots$

(iv) ${\sum }_{j=0}^k{d}_j^{\left({\rho }_1\right)}{\tau }^{{\rho }_1}={\left(k+1\right)}^{{\rho }_1}\le T^{{\rho }_1}$

2 Methodology

We implement an implicit numerical approximation for the FCE in Eqs 1–3, utilizing the discretization of the Riemann–Liouville integral with backward difference approximation for the partial derivative using central difference approximation. The steps as $x_i=i∆x$ along x-axis, where $i=1,2,\dots ,M_x-1,∆x=\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$M_x$}\right.$ and the step $t_k=k\tau ,$ $k=1,2,3,\dots ,N$ where $\tau =\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$N$}\right..$ Letting the obtained numerical solution be $w_i^k$ to $w\left(x_i,t_k\right)$, and using Eq. 4 in Eq. 1, we have

$\frac{\partial w\left(x,t\right)}{\partial t}=K\left[\frac{\partial }{\partial t}{I}_0^{{\rho }_1}\frac{{\partial }^2}{{\partial x}^2}w\left(x,t\right)\right]-{\mu }^2\frac{\partial }{\partial t}{I}_0^{{\rho }_2}w\left(x,t\right)+h\left(x,t\right).(6)$

Further, applying Eq. 5 in Eq. 6, we can write

$\frac{\partial w\left(x_i,t_k\right)}{\partial t}=\frac{\partial }{\partial t}{m}_1{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_1\right)}{\delta }_x^{2}w\left(x_i,t_{k-j}\right)-\frac{\partial }{\partial t}{m}_2{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_2\right)}w\left(x_i,t_{k-j}\right)+h\left(x_i,t_{k-j}\right),(7)$

Where

$m_1=\frac{K{\tau }^{{\rho }_1}}{{\left(∆x\right)}^2\mathrm{\Gamma }\left({\rho }_1+1\right)},m_2=\frac{{\mu }^2{\tau }^{{\rho }_2}}{\mathrm{\Gamma }\left({\rho }_2+1\right)}.(8)$

By using implicit discretization with respect to time ‘$t$’, we have

$w_i^k-w_i^{k-1}=m_1{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_1\right)}{\delta }_x^2\left[w_i^{k-j}-w_i^{k-j-1}\right]-m_2{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_2\right)}\left[w_i^{k-j}-w_i^{k-j-1}\right]+{\tau h}_i^k,(9)$

Simplifying Eq. 9, we obtained

$\begin{array}{c}{w}_i^k=w_i^{k-1}+m_1{d}_0^{\left({\rho }_1\right)}\left[w_{i+1}^k-2w_i^k+w_{i-1}^k\right]-m_1{d}_{k-1}^{\left({\rho }_1\right)}\left[w_{i+1}^0-2w_i^0+w_{i-1}^0\right]-m_1\hfill \\ {\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]\left[w_{i+1}^{k-j}-2w_i^{k-j}+w_{i-1}^{k-j}\right]+m_2\left[d_{k-1}^{\left({\rho }_2\right)}{w}_i^0-d_0^{\left({\rho }_2\right)}{w}_i^k\right]+m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]\left[w_i^{k-j}\right]+{\tau h}_i^k,\hfill \end{array}(10)$

With

$w_i^0=\beta \left(x_i\right),0\le x\le L,(11)$

$w_0^k={\beta }_1\left(t_k\right),w_{M_x}^k={\beta }_2\left(t_k\right),0\le t\le T.(12)$

where $i=1,2,\dots ,M_x-1,k=1,2,3,\dots ,N.$

3 Stability

In this section, we use the Fourier series method to analyze the stability of the implicit numerical scheme. Letting $W_i^k$ be the approximate solution for Eq. 10, we have

$\begin{array}{c}{W}_i^k=W_i^{k-1}+m_1{d}_0^{\left({\rho }_1\right)}\left[W_{i+1}^k-2W_i^k+W_{i-1}^k\right]-m_1{d}_{k-1}^{\left({\rho }_1\right)}\left[W_{i+1}^0-2W_i^0+W_{i-1}^0\right]-m_1\hfill \\ {\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]\left[W_{i+1}^{k-j}-2W_i^{k-j}+W_{i-1}^{k-j}\right]+m_2\left[d_{k-1}^{\left({\rho }_2\right)}{W}_i^0-d_0^{\left({\rho }_2\right)}{W}_i^k\right]+m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]\left[W_i^{k-j}\right]+{\tau h}_i^k.\hfill \end{array}(13)$

The error is defined as:

${\mathit{E}}_i^k={w_i^k-W}_i^k,(14)$

where ${\mathit{E}}_i^k$ satisfies $\left(13\right)$ and

$\begin{array}{c}{\mathit{E}}_i^k={\mathit{E}}_i^{k-1}+m_1{d}_0^{\left({\rho }_1\right)}\left[{\mathit{E}}_{i+1}^k-2{\mathit{E}}_i^k+{\mathit{E}}_{i-1}^k\right]-m_1{d}_{k-1}^{\left({\rho }_1\right)}\left[{\mathit{E}}_{i+1}^0-2{\mathit{E}}_i^0+{\mathit{E}}_{i-1}^0\right]-m_1\hfill \\ {\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]\left[{\mathit{E}}_{i+1}^{k-j}-2{\mathit{E}}_i^{k-j}+{\mathit{E}}_{i-1}^{k-j}\right]+m_2\left[d_{k-1}^{\left({\rho }_2\right)}{\mathit{E}}_i^0-d_0^{\left({\rho }_2\right)}{\mathit{E}}_i^k\right]+m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]\left[{\mathit{E}}_i^{k-j}\right].\hfill \end{array}(15)$

The error and initial conditions are

${\mathit{E}}_0^k={\mathit{E}}_{M_x}^k={\mathit{E}}_i^0=0.(16)$

Here, $i=1,2,\dots ,M_x-1.$

Here, we need to define grid functions for $k=1,2,\dots ,N,$ as the following:

${\mathit{E}}^k\left(x\right)=\left\{\begin{array}{c}{\mathit{E}}_i^k,when{x}_{i-\frac{∆x}{2}}<x<x_{i+\frac{∆x}{2}},\\ 0,when0\le x\le \frac{∆x}{2}orL-\frac{∆x}{2}\le x\le L.\end{array}\right.(17)$

Then, ${\mathit{E}}^k\left(x\right)$ can be written in Fourier series, such as

${\mathit{E}}^k\left(x\right)={\displaystyle \sum _{l_1=-\infty }^{\infty }}{\lambda }^k\left(l_1\right)e^{2\sqrt{-1}\pi \left(l_1\frac{x}{L}\right)},(18)$

Here

${\lambda }^k\left(l_1\right)=\frac{1}{L}{\int }_0^L{\mathit{E}}^k\left(x\right)e^{-2\sqrt{-1}\pi \left(l_1\frac{x}{L}\right)}.(19)$

From the definition of $l^2$ norm and Parseval equality, we have

$‖{\mathit{E}}^k‖\begin{array}{l}2\\ \infty \end{array}={\displaystyle \sum _{i=1}^{M_x-1}}∆x{\left|{\mathit{E}}_i^k\right|}^2={\displaystyle \sum _{l_1=-\infty }^{\infty }}{\left|{\lambda }^k\left(l_1\right)\right|}^2.(20)$

Supposing that

${\mathit{E}}_i^k={\lambda }^k{e}^{\sqrt{-1}\left(\sigma i∆x\right)}.(21)$

where $\sigma =\frac{2\pi l_1}{L}$ and by substituting $\left(18\right)-\left(21\right)$ in Eq. 15, we have

${\lambda }^k=\frac{1}{\left[1+m_2+4m_1\left({\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right)\right)\right]}\left[{\lambda }^{k-1}+{\lambda }^0\left[m_2{d}_{k-1}^{\left({\rho }_2\right)}+m_1{d}_{k-1}^{\left({\rho }_1\right)}\left(4{\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right)\right)\right]+{\lambda }^{k-j}\left[m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]+m_{1}4{\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right){\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]\right]\right],(22)$

Proposition 1: If ${\lambda }^k\left(K=1,2,\dots ,N\right)$ satisfies Eq. 22, then $\left|{\lambda }^k\right|\le \left|{\lambda }^0\right|$.

Proof:. To prove the above equality based on mathematical induction, we take $k=1$ in Eq. 22.

$\left|{\lambda }^1\right|\le \frac{1}{\left[1+m_2+4m_1\left({\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right)\right)\right]}\left[\left|{\lambda }^{1-1}\right|+\left|{\lambda }^0\right|\left[m_2{d}_{1-1}^{\left({\rho }_2\right)}+m_1{d}_{1-1}^{\left({\rho }_1\right)}\left(4{\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right)\right)\right]+\left|{\lambda }^{k-j}\right|\left[m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]+m_{1}4{\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right){\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]]\right]]\right],$

As $d_0^{\left({\rho }_1\right)}=d_0^{\left({\rho }_2\right)}=1$ and $0<{\gamma }_1,{\gamma }_2<1$, we have

$\left|{\lambda }^1\right|\le \left|{\lambda }^0\right|.$

Now consider,

$\left|{\lambda }^m\right|\le \left|{\lambda }^0\right|,m=1,2,\dots ,k-1.$

As $0<{\rho }_1,{\rho }_2<1,$ from $\left(22\right)$ and Lemma 1

$\begin{array}{c}\left|{\lambda }^k\right|\le \frac{1}{\left[1+m_2\left({\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)\right]}\left[\begin{array}{l}\left|{\lambda }^{k-1}\right|+\left|{\lambda }^0\right|\left[m_2{d}_{k-1}^{\left({\rho }_2\right)}+m_1{d}_{k-1}^{\left({\rho }_1\right)}\left(4{\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)\right]+\\ \left|{\lambda }^{k-j}\right|\left[m_2{\sum }_{j=1}^{k-1}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]+m_1\left(4{\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)\right]\end{array}\right],\hfill \\ \le \frac{1}{\left[1+m_2+4m_1\left({\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)\right]}\left[1+m_2{d}_{k-1}^{\left({\rho }_2\right)}+m_1{d}_{k-1}^{\left({\rho }_1\right)}\left(4{\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)+m_2{d}_0^{\left({\rho }_2\right)}+m_2{d}_{k-1}^{\left({\rho }_2\right)}+m_1{d}_0^{\left({\rho }_1\right)}\left(4{\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)-m_1{d}_{k-1}^{\left({\rho }_1\right)}\left(4{\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)\right]\left|{\lambda }^0\right|,\hfill \\ \le \frac{1}{\left[1+m_2+4m_1\left({\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)\right]}\left[1+m_2{d}_0^{\left({\rho }_2\right)}+m_1{d}_0^{\left({\rho }_1\right)}\left(4{\mathit{sin}}^2\left(\frac{\sigma \Delta x}{2}\right)\right)\right]\left|{\lambda }^0\right|,\hfill \end{array}$

Here, $d_0^{\left({\rho }_1\right)}=d_0^{\left({\rho }_2\right)}=1$, we have

$\le \frac{1}{\left[1+m_2+4m_1\left({\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right)\right)\right]}\left[1+m_2+m_{1}4{\mathit{sin}}^2\left(\frac{\sigma ∆x}{2}\right)\right]\left|{\lambda }^0\right|,\left|{\lambda }^k\right|\le \left|{\lambda }^0\right|.(23)$

By using proposition 1 and Eq. 20

${‖{\lambda }^k‖}_2\le {‖{\lambda }^0‖}_2.$

The implicit numerical scheme in Eq. 10 is unconditionally stable.

4 Convergence

To investigate the convergence of the proposed implicit scheme. Let $w\left(x_i,t_k\right)$ be the exact solution represented by Taylor series, then the local truncation error is obtained as

$Q_i^k=w\left(x_i,t_k\right)-w\left(x_i,t_{k-1}\right)-m_1{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_1\right)}{\delta x}^2\left[w\left(x_i,t_{k-j}\right)-w\left(x_i,t_{k-j-1}\right)\right]+m_2{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_2\right)}\left[w\left(x_i,t_{k-j}\right)-w\left(x_i,t_{k-j-1}\right)\right]-\tau h\left(x_i,t_k\right),(24)$

From Eq. 1

$\begin{array}{c}{Q}_i^k=\frac{w\left(x_i,t_k\right)-w\left(x_i,t_{k-1}\right)}{\tau }-\frac{\partial w\left(x_i,t_k\right)}{\partial t}+{}_0{}^{}{D}_t^{1-{\rho }_1}\left(K\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^2}\right)-m_1{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_1\right)}{\delta x}^2\left(w_i^{k-j}-w_i^{k-j-1}\right)\hfill \\ -{}_0{}^{}{D}_t^{1-{\rho }_2}w\left(x_i,t_k\right)+m_2{\displaystyle \sum _{j=0}^{k-1}}{d}_j^{\left({\rho }_2\right)}\left(w_i^{k-j}-w_i^{k-j-1}\right),=O\left(\tau +{\left(∆x\right)}^2\right)\hfill \end{array}(25)$

Since $i$ and $k$ are finite, then there exist a positive constant $C_1$, then we have

$\left|Q_i^k\right|\le C_1\left(\tau +{\left(∆x\right)}^2\right),(26)$

The error is defined as

${\psi }_i^k=w\left(x_i,t_k\right)-w_i^k.(27)$

From Eq. 24, as

$\begin{array}{c}{\psi }_i^k={\psi }_i^{k-1}{+m}_1{d}_0^{\left({\rho }_1\right)}\left[{\psi }_{i+1}^k-2{\psi }_i^k+{\psi }_{i-1}^k\right]-m_1{d}_{k-1}^{\left({\rho }_1\right)}\left[{\psi }_{i+1}^0-2{\psi }_i^0+{\psi }_{i-1}^0\right]-m_1\hfill \\ {\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]\left[{\psi }_{i+1}^{k-j}-2{\psi }_i^{k-j}+{\psi }_{i-1}^{k-j}\right]-m_2\left[d_0^{\left({\rho }_2\right)}{\psi }_i^k-d_{k-1}^{\left({\rho }_2\right)}{\psi }_i^0\right]+m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]{\psi }_i^{k-j}+\tau Q_i^k.\hfill \end{array}(28)$

With error conditions that are

${\psi }_i^0=0,{\psi }_0^k={\psi }_M^k=0,$

Next, we define the following grid functions for $k=1,2,\dots ,N.$

${\psi }^k\left(x\right)=\left\{\begin{array}{c}{\psi }_i^k,when{x}_{i-\frac{∆x}{2}}<x<x_{i+\frac{∆x}{2}},\\ 0,when0\le x\le \frac{∆x}{2}orL-\frac{∆x}{2}\le x\le L.\end{array}\right.$

And

$Q^k\left(x\right)=\left\{\begin{array}{c}{Q}_i^k,when{x}_{i-\frac{∆x}{2}}<x<x_{i+\frac{∆x}{2}},\\ 0,when0\le x\le \frac{∆x}{2}orL-\frac{∆x}{2}\le x\le L.\end{array}\right.$

Here, ${\psi }^k\left(x\right)$ and $Q^k\left(x\right)$ can be expanded in Fourier series such as

${\psi }^k\left(x\right)={\displaystyle \sum _{l_1=-\infty }^{\infty }}{\xi }^k\left(l_1\right)e^{2\sqrt{-1}\pi \left(l_1\frac{x}{L}\right)},k=1,2,\dots ,N,$

$Q^k\left(x\right)={\displaystyle \sum _{l_1=-\infty }^{\infty }}{\phi }^k\left(l_1\right)e^{2\sqrt{-1}\pi \left(l_1\frac{x}{L}\right)},k=1,2,\dots ,N.$

where

${\xi }^k\left(l_1\right)=\frac{1}{L}{\int }_0^L{\psi }^k\left(x\right)e^{-2\sqrt{-1}\pi \left(l_1\frac{x}{L}\right),}(29)$

${\phi }^k\left(l_1\right)=\frac{1}{L}{\int }_0^L{Q}^k\left(x\right)e^{-2\sqrt{-1}\pi \left(l_1\frac{x}{L}\right)}.(30)$

From the definition of $l^2$ norm and the Parseval equality, we have

$‖{\psi }^k‖\begin{array}{l}2\\ l^2\end{array}={\displaystyle \sum _{i=1}^{M_x-1}}∆x{\left|{\mathbf{E}}_i^k\right|}^2={\displaystyle \sum _{l_1=-\infty }^{\infty }}{\left|{\xi }^k\left(l_1\right)\right|}^2,(31)$

$‖Q^k‖\begin{array}{l}2\\ l^2\end{array}={\displaystyle \sum _{i=1}^{M_x-1}}∆x{\left|{\mathbf{E}}_i^k\right|}^2={\displaystyle \sum _{l_1=-\infty }^{\infty }}{\left|{\phi }^k\left(l_1\right)\right|}^2.(32)$

Based on the above, supposing that

${\psi }_i^k={\xi }^k{e}^{\sqrt{-1}\left({\sigma }_{1}i∆x\right)},(33)$

$Q_i^k={\phi }^k{e}^{\sqrt{-1}\left({\sigma }_{1}i∆x\right)},(34)$

where ${\sigma }_1=\frac{{2\pi l}_1}{L}$, by using $\left(33\right)$ and ($34)$ in Eq. 28, we have

${\xi }^k=\frac{1}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]}\left[{\xi }^{k-1}+{\xi }^0\left[{m_2{d}_{k-1}^{\left({\rho }_2\right)}+4m}_1{d}_{k-1}^{\left({\rho }_1\right)}{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]+{\xi }^{k-j}\left[m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right){\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]]\right]+\tau {\phi }^k]\right],(35)$

Proposition 2: If ${\xi }^k$ is the solution of $\left(35\right)$, then there exists a positive constant $C_2$ such that $\left|{\xi }^k\right|\le C_{2}k\tau \left|{\phi }^1\right|$.

Proof: From ${\psi }^0=0$ and Eq. 29 we have

${\xi }^0={\xi }^0\left(l_1\right)=0.(36)$

From ($29)$ and ($30)$, there exists positive constant $C_2$, such that

$\left|{\phi }^1\right|\le C_2\left|{\phi }^1\left(l_1\right)\right|.(37)$

Using mathematical induction, for $k=1$, then from $\left(35\right),$

$\left|{\xi }^1\right|\le \frac{1}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]}\left[\left|{\xi }^0\right|+\left|{\xi }^0\right|\left[{m_2{d}_0^{\left({\rho }_2\right)}+4m}_1{d}_0^{\left({\rho }_1\right)}{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]+C_2\tau \left|{\phi }^1\right|\right],$

From Eq. 36

$\left|{\xi }^1\right|\le {\frac{1}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]}C}_2\tau \left|{\phi }^1\right|,\left|{\xi }^1\right|\le C_2\tau \left|{\phi }^1\right|.$

Now suppose

$\left|{\xi }^m\right|\le C_{2}m\tau \left|{\phi }^1\right|,m=1,2,\dots ,k-1.$

From Eq. 34 and Lemma 1

$\left|{\xi }^k\right|\le \frac{1}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]}\left[\left|{\xi }^{k-1}\right|+\left|{\xi }^0\right|\left[{m_2{d}_{k-1}^{\left({\rho }_2\right)}+4m}_1{d}_{k-1}^{\left({\rho }_1\right)}{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]+m_2{\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]\left|{\xi }^{k-j}\right|+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right){\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]\left|{\xi }^{k-j}\right|+\tau \left|{\phi }^k\right|]\right],$

from Eq. 36

$\left|{\xi }^k\right|\le \frac{1}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]}\left[k-1+4m_1\left(k-1\right){\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right){\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_1\right)}-d_j^{\left({\rho }_1\right)}\right]+m_2\left(k-1\right){\displaystyle \sum _{j=1}^{k-1}}\left[d_{j-1}^{\left({\rho }_2\right)}-d_j^{\left({\rho }_2\right)}\right]+1\right]C_2\tau \left|{\phi }^1\right|,$

$\left|{\xi }^k\right|\le \frac{1}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]}\left[k+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\left(k-1\right)\left(1-d_{k-1}^{\left({\rho }_1\right)}\right)+m_2\left(k-1\right)\left(1-d_{k-1}^{\left({\rho }_2\right)}\right)+]\right]C_2\tau \left|{\phi }^1\right|,$

$\left|{\xi }^k\right|\le \frac{1}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]}\left[k\left(1+m_2\left(1-d_{k-1}^{\left({\rho }_2\right)}\right)+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\left(1-d_{k-1}^{\left({\rho }_1\right)}\right)\right)-\left(m_2\left(1-d_{k-1}^{\left({\rho }_2\right)}\right)+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\left(1-d_{k-1}^{\left({\rho }_1\right)}\right)\right)]\right]C_2\tau \left|{\phi }^1\right|.$

Here, $\left(1-d_{k-1}^{\left({\rho }_1\right)}\right)\cong 1,$ $\left(1-d_{k-1}^{\left({\rho }_2\right)}\right)\cong 1$ because $d_{k-1}^{\left({\rho }_1\right)}\cong 0,$ and $d_{k-1}^{\left({\rho }_1\right)}\cong 0.$

$\left|{\xi }^k\right|\le \frac{\left[k\left(1+m_2+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right)-\left(m_2+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right)\right]C_2\tau \left|{\phi }^1\right|}{\left[1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)\right]},$

$\left|{\xi }^k\right|\le \left[k-\frac{m_2+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)}{1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)}\right]C_2\tau \left|{\phi }^1\right|,$

The value of $(\left(\frac{m_2+4m_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)}{1{+m_2+4m}_1{\mathit{sin}}^2\left(\frac{{\sigma }_1∆x}{2}\right)})\right)$ is very small, lying between 0 and 1. So, we obtained

$\left|{\xi }^k\right|\le k{C}_2\tau \left|{\phi }^1\right|.$

5 Numerical tests

In this study, the numerical result of an implicit scheme for one-dimensional FCE are discussed numerically and graphically. The examples are as following.

Example 1. Consider the fractional-order cable model [15] with the closed-form solution is given as:

$\frac{\partial w\left(x,t\right)}{\partial t}={}_0{}^{}{D}_t^{1-{\rho }_1}\left(K\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^2}\right)-{\mu }^2{}_0{}^{}{D}_t^{1-{\rho }_2}w\left(x,t\right)+2\left(t+\frac{{\pi }^2{t}^{1+{\rho }_1}}{\mathrm{\Gamma }\left(2+{\rho }_1\right)}+\frac{t^{1+{\rho }_2}}{\mathrm{\Gamma }\left(2+{\rho }_2\right)}\right)\sin \left(\pi x\right),$

with initial and boundary conditions

$w\left(x,0\right)=0,0\le x\le 1,$

$w\left(0,t\right)=0,w\left(1,t\right)=0,0<t\le 1.$ Where $\left.{\rho }_1,{\rho }_2\in (0,1\right]$ and $K=1,\mu =1.$ The closed-form solution is $w\left(x,t\right)=t^2\sin \left(\pi x\right).$

Example 2. Consider the 1D fractional Stokes’ first problem for the heated generalized second-grade equation [40].

$\frac{\partial w\left(x,t\right)}{\partial t}={}_0{}^{}{D}_t^{1-{\mathrm{\rho }}_3}\left(\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^2}\right)+\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^2}+\left(\left(2+{\rho }_3\right)t^{1+{\rho }_3}-\frac{\mathrm{\Gamma }\left(3+{\rho }_3\right)}{\mathrm{\Gamma }\left(2+2{\rho }_3\right)}{t}^{1+{2\rho }_3}-t^{2+{\rho }_3}\right)e^x,$

with initial and boundary conditions

$w\left(x,0\right)=0,0\le x\le 1,$

$w\left(0,t\right)=t^{1+{\rho }_3},w\left(1,t\right)=e{t}^{1+{\rho }_3},0<t\le 1.$ Where $\left.{\rho }_3\in (0,1\right]$ and $K=1,\mu =1.$ The closed-form solution is $w\left(x,t\right)=e^x{t}^{1+{\rho }_3}.$The errors between a numerical and an exact solution are defined as follows:

$E_{\infty }=\underset{1<i\le M_x-1}{\max }\left\{w\left(x_i,t_k\right)-w_i^k\right\}.(38)$

$E_2={\left({\displaystyle \sum _{k=1}^{M_x-1}}{\left(w\left(x_i,t_k\right)-w_i^k\right)}^2∆x\right)}^{1/2}.(39)$

The above problem is solved using the modified implicit scheme. The errors $E_{\infty }and{E}_2$ at $T=1.0$ and for different values of $∆x$ and $N$. The time step $\tau$ is defined by $\tau =\frac{T}{N}$.

6 Results and discussion

The modified implicit finite difference approximation is used to solve the numerical example of fractional order, such as fractional cable model and the fractional order Stokes’ first problem for the heated generalized second grade equation. Numerical results are presented in the form of tables and figures for various values of space and time steps in order to demonstrate the efficiency of the suggested numerical scheme.

In Tables 1–3, the exact and the numerical solution are compared of the given example 1 for fixed values ${\rho }_1=0.5$ and ${\rho }_2=0.75,0.5,0.25$, and different values of $N$ and $h$. The error decreases as the value of $N$ increases. Similarly, as the time and space step size $\tau$ and $\Delta x,\Delta y$ reduce, the errors decrease for a fixed value of ${\rho }_{1}and{\rho }_2$. In Table 4, the exact and the numerical solution of example 1 are compared for ${\rho }_1,{\rho }_1=0.25$, ${\rho }_1,{\rho }_1=0.5$, and ${\rho }_1,{\rho }_1=0.95$, and for different values of $N$ and $∆x$. The results show that as we increase the value of N, i.e., reduce the time and space step size $\tau$ and $h_x$, the errors decrease for different values of ${\rho }_{1}and{\rho }_2$. In Table 5, the numerical results are explained for example, 2 of the suggested scheme for the fractional order first problem for a heated generalized second-grade fluid for various values of order ${\rho }_3$, step size $\tau$, and $∆x$. Figures 1–3 show the comparison of the numerical and the exact solution of example 1 in Figure 1 at ${\rho }_1$, ${\rho }_2$ = 0.5, $T=1.0$, $∆x$ = 1/10, and $N=40.$ For Figure 2, at ${\rho }_1$, ${\rho }_2$ = 0.5, $T=1.0$, $∆x$ = 1/20, and $N=80$. For Figure 3, at ${\rho }_1$, ${\rho }_2$ = 0.5, $T=1.0$, $∆x$ = 1/40, and $N=250$. Furthermore, added Figure 4 which shows the graphical representation of example 2 for ${\rho }_3=.6,\Delta x=1/8,T=1.0$ and $N=64$, which confirmed our theoretical analysis and demonstrated that the proposed approach is very powerful and efficient.

TABLE 1

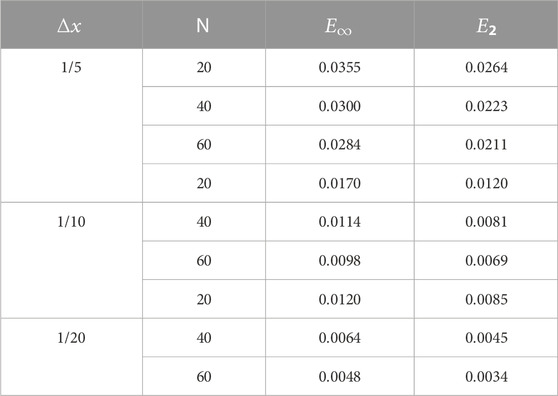
TABLE 1. Numerical results for example, 1 of the modified implicit scheme for various values of $,$ $∆\mathit{x}$, and fixed values of ${\mathit{\rho }}_{\mathbf{1}}=\mathbf{0.5},{\mathit{\rho }}_{\mathbf{2}}=\mathbf{0.75}$.

TABLE 2

TABLE 2. Numerical results example 1 of the modified implicit scheme for various values of $,$ $∆x$, and fixed value of ${\rho }_1,{\rho }_2=0.5$.

TABLE 3

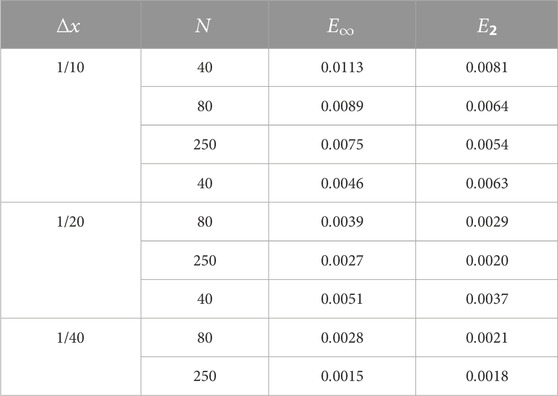
TABLE 3. Numerical results example 1 of the modified implicit scheme for various values of $N,∆x$, and for fixed value of ${\rho }_1=0.5,{\rho }_2=0.25$.

TABLE 4

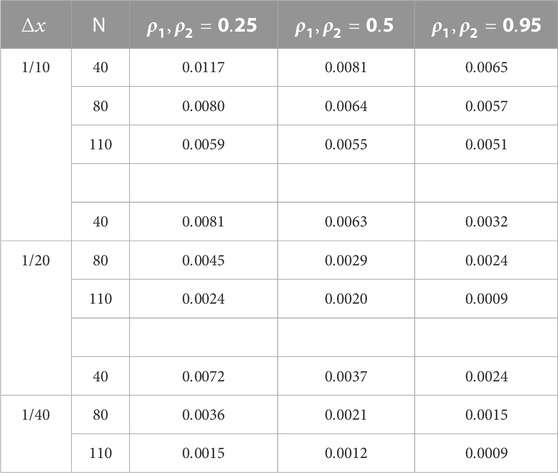
TABLE 4. Numerical results example 1 of the modified implicit scheme for various values of ${\rho }_1,{\rho }_2$, $N$, and $∆x$.

TABLE 5

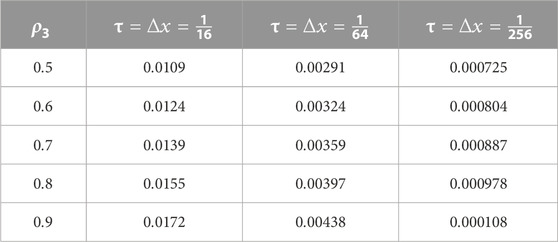
TABLE 5. Numerical results for example 2 of the modified implicit scheme for various values of ${\rho }_3$, $\tau$, and $∆x$.

FIGURE 1

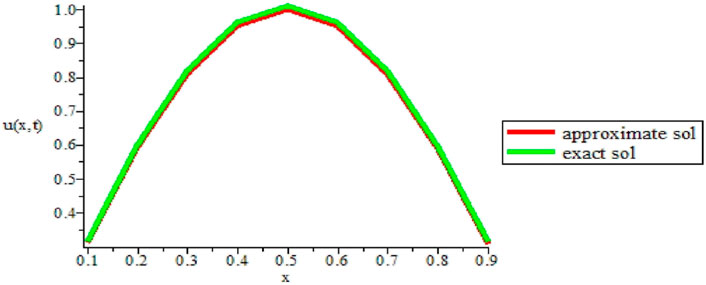
FIGURE 1. Comparison of the numerical and exact solution of the given example 1 at ${\rho }_1$, ${\rho }_2$ = 0.5, $T=1.0$, $∆x$ = 1/10, and $N=40.$

FIGURE 2

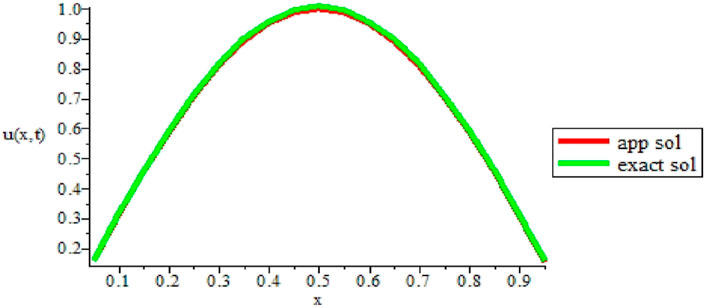
FIGURE 2. Comparison of the numerical and exact solution of the given example 1 at ${\rho }_1$, ${\rho }_2$ = 0.5, $T=1.0$, $∆x$ = 1/20, and $N=80.$

FIGURE 3

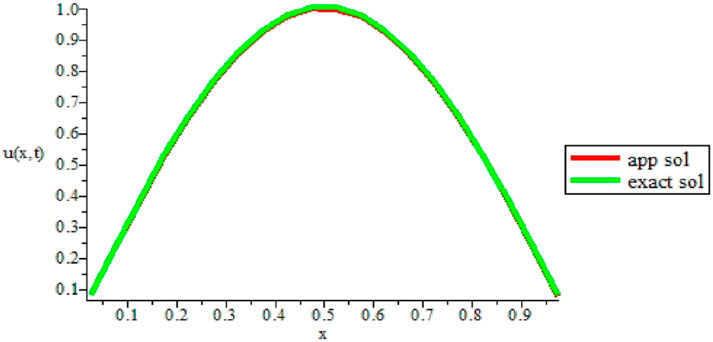
FIGURE 3. Comparison of the numerical and exact solution of the given example 1 at ${\rho }_1$, ${\rho }_2$ = 0.5, $T=1.0$, $∆x$ = 1/40, and $N=250.$

FIGURE 4

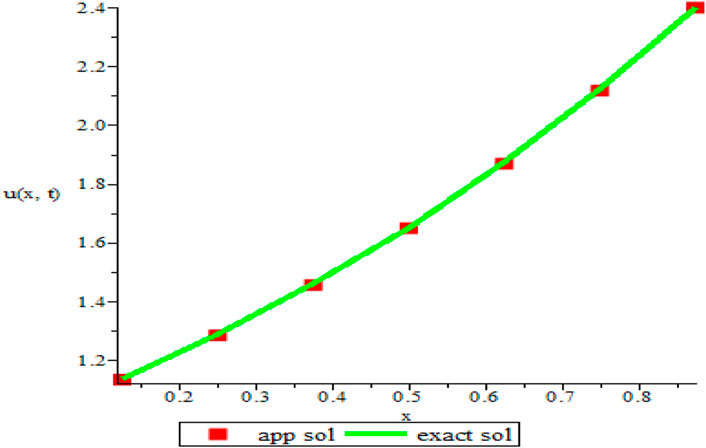
FIGURE 4. Comparison of the numerical and exact solution of the given example 1 at ${\rho }_3$ = 0.6, $T=1.0$, $∆x$ = 1/8, and $N=64.$

7 Conclusion

This paper presented the modified implicit numerical approximation for a fractional one-dimensional linear Cable model. The scheme is convergent and unconditionally stable, as seen by the investigation using the Fourier series method. The time-fractional derivative was calculated using the Riemann–Liouville formula. The outcome of an application to specific examples of fractional order one-dimensional linear Cable model and the fractional order Stokes’ first problem for the heated generalized second-grade equation have been explored graphically and numerically. The scheme is verified through the comparison of the numerical solution with the exact solution, which shows an agreement with the theoretical analysis and the numerical experiment, confirming that the approximate solution converges to the exact solution. This modified approach can also extend to other types of two and three dimensional fractional order differential models.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work under Grant code: 22UQU4310396DSR58.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhuang P, Liu F. Finite difference approximation for two-dimensional time fractional diffusion equation. J Algorithms Comput Technol (2007) 1:1–16. doi:10.1260/174830107780122667

CrossRef Full Text | Google Scholar

2. Rajković PM, Marinković SD, Stanković MS. Fractional integrals, and derivatives in q-calculus. Appl Anal Discret Math (2007) 1:311–23. doi:10.2298/aadm0701311r

CrossRef Full Text | Google Scholar

3. Yakar A, Akdogan Z. On the fundamental solutions of a discontinuous fractional boundary value problem. Adv Differ Equ (2017) 1:378–15. doi:10.1186/s13662-017-1433-6

CrossRef Full Text | Google Scholar

4. Holmes WR. Cable equation. New York: Springer (2014).

Google Scholar

5. Vitali S, Castellani G, Mainardi F. Time fractional cable equation, and applications in neurophysiology. Chaos Solitons Fractals (2017) 102:467–72. doi:10.1016/j.chaos.2017.04.043

CrossRef Full Text | Google Scholar

6. Yu B, Jiang X. Numerical identification of the fractional derivatives in the two-dimensional fractional cable equation. J Sci Comput (2016) 68:252–72. doi:10.1007/s10915-015-0136-y

CrossRef Full Text | Google Scholar

7. Liu F, Yang Q, Turner I. Two new implicit numerical methods for the fractional cable equation. J Comput Nonlinear Dyn (2011) 6(1-7):011009. doi:10.1115/1.4002269

CrossRef Full Text | Google Scholar

8. Lin Y, Li X, Xu C. Finite difference/spectral approximations for the fractional cable equation. Math Comput (2011) 80:1369–96. doi:10.1090/s0025-5718-2010-02438-x

CrossRef Full Text | Google Scholar

9. Liu Y, Du YW, Li H, Wang JF. A two-grid finite element approximation for a nonlinear time-fractional Cable equation. Nonlinear Dyn (2016) 85:2535–48. doi:10.1007/s11071-016-2843-9

CrossRef Full Text | Google Scholar

10. Zhuang P, Liu F, Turner I, Anh V. Galerkin finite element method and error analysis for the fractional cable equation. Numer Algorithms (2016) 72:447–66. doi:10.1007/s11075-015-0055-x

CrossRef Full Text | Google Scholar

11. Nikan O, Golbabai A, Machado JT, Nikazad T. Numerical approximation of the time fractional cable model arising in neuronal dynamics. Eng Comput (2020) 1–19.

CrossRef Full Text | Google Scholar

12. Zhang H, Yang X, Han X. Discrete-time orthogonal spline collocation method with application to two-dimensional fractional cable equation. Comput Math Appl (2014) 68:1710–22. doi:10.1016/j.camwa.2014.10.019

CrossRef Full Text | Google Scholar

13. Quintana-Murillo J, Yuste SB. An explicit numerical method for the fractional cable equation. Int J Differ Equ (2011) 2011:1–12. doi:10.1155/2011/231920

CrossRef Full Text | Google Scholar

14. Baleanu D, Defterli O, Agrawal OP. A central difference numerical scheme for fractional optimal control problems. J Vib Control (2009) 15:583–97. doi:10.1177/1077546308088565

CrossRef Full Text | Google Scholar

15. Langlands TAM, Henry BI, Wearne SL. Fractional cable equation models for anomalous electrodiffusion in nerve cells: Finite domain solutions. SIAM J Appl Math (2011) 71:1168–203. doi:10.1137/090775920

CrossRef Full Text | Google Scholar

16. Langlands TAM, Henry BI, Wearne SL. Fractional cable equation models for anomalous electrodiffusion in nerve cells: Infinite domain solutions. J Math Biol (2009) 59:761–808. doi:10.1007/s00285-009-0251-1

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Saxena RK, Tomovski Z, Sandev T. Analytical solution of generalized space-time fractional cable equation. Mathematics (2015) 3:153–70. doi:10.3390/math3020153

CrossRef Full Text | Google Scholar

18. Bhrawy AH, Zaky MA. Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn (2015) 80:101–16. doi:10.1007/s11071-014-1854-7

CrossRef Full Text | Google Scholar

19. Liu J, Li H, Liu Y. A new fully discrete finite difference/element approximation for fractional cable equation. J Appl Math Comput (2016) 52:345–61. doi:10.1007/s12190-015-0944-0

CrossRef Full Text | Google Scholar

20. Ma L, Liu D. An implicit difference approximation for fractional cable equation in high-dimensional case. J Liaoning Tech Univ Nat Sci (2014) 4.

Google Scholar

21. Zhang Y. A finite difference method for the fractional partial differential equation. Appl Math Comput (2009) 215:524–9.

CrossRef Full Text | Google Scholar

22. Hu X, Zhang L. Implicit compact difference schemes for the fractional cable equation. Appl Math Model (2012) 36:4027–43. doi:10.1016/j.apm.2011.11.027

CrossRef Full Text | Google Scholar

23. Moshtaghi N, Saadatmandi A. Numerical solution of time fractional cable equation via the sinc-Bernoulli collocation method. J Appl Comput Mech (2020) 7:1–9.

Google Scholar

24. Aslefallah M, Abbasbandy S, Shivanian E. Fractional cable problem in the frame of meshless singular boundary method. Eng Anal Bound Elem (2019) 108:124–32. doi:10.1016/j.enganabound.2019.08.003

CrossRef Full Text | Google Scholar

25. Ali U, Sohail M, Usman M, Abdullah FA, Khan Nisar KS. Fourth-order difference approximation for time-fractional modified sub-diffusion equation. Symmetry (2020) 12:691. doi:10.3390/sym12050691

CrossRef Full Text | Google Scholar

26. Kumar S, ChauhanMomani RPS, Hadi S. Numerical investigations on COVID-19 model through singular and non-singular fractional operators. Numer Methods Partial Differential Equations (2020). doi:10.1002/num.22707

CrossRef Full Text | Google Scholar

27. Kumar S, Kumar A, Samet B, Dutta H, A study on fractional host–parasitoid population dynamical model to describe insect species, Numer Methods Partial Differential Equations 37 (2), 1673–92. doi:10.1002/num.226032021). A study on fractional host–parasitoid population dynamical model to describe insect species,

CrossRef Full Text | Google Scholar

28. Khan MA, Ullah S, S. K. A robust study on 2019-nCOV outbreaks through non-singular derivative. The Eur Phys J Plus (2021) 136:168.

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kumar S, Kumar R, Osman MS. A wavelet based numerical scheme for fractional orderSEIRepidemic of measles by using Genocchi polynomials. Numer Methods Partial Differential Equations (2021) 37(2):1250–68. doi:10.1002/num.22577

CrossRef Full Text | Google Scholar

30. Mohammadi H, Kumar S, Rezapour S, Etemad S, A theoretical study of the Caputo–Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control, Chaos, Solitons and Fractals (2021) 144, 110668 doi:10.1016/j.chaos.2021.110668

CrossRef Full Text | Google Scholar

31. Kumar S, Kumar R, Cattani C, Samet B, Chaotic behaviour of fractional predator-prey dynamical system, Chaos Solitons Fractals (2020)135, 109811 doi:10.1016/j.chaos.2020.109811

CrossRef Full Text | Google Scholar

32. Ali U, Kamal R, Mohyud-Din ST. On nonlinear fractional differential equations. Int J Mod Math Sci (2012) 3(3):116–24.

Google Scholar

33. Zubair T, Usman M, Ali U, Mohyud-Din ST. Homotopy analysis method for a system of partial differential equations. Int J Mod Eng Sci (2012) 1:67–79.

Google Scholar

34. Ali U, Abdullah FA. Explicit Saul’yev finite difference approximation for the two-dimensional fractional sub-diffusion equation. In: AIP Conference Proceedings. AIP Publishing LLC (2018). 020111.

Google Scholar

35. Ali U, Sohail M, Abdullah FA. An efficient numerical scheme for variable-order fractional sub-diffusion equation. Symmetry (2020) 12:1437. doi:10.3390/sym12091437

CrossRef Full Text | Google Scholar

36. Yang Q. Novel analytical and numerical methods for solving fractional dynamical systems. Dr Diss Qld Univ Technol (2010) 1–201.

Google Scholar

37. Povstenko Y, Ostoja-Starzewski M. Fractional telegraph equation under moving time-harmonic impact. Int J Heat Mass Transfer (2022) 182:121958. doi:10.1016/j.ijheatmasstransfer.2021.121958

CrossRef Full Text | Google Scholar

38. Khater M, Ali U, Khan MA, Mousa AA, Attia RA. A new numerical approach for solving 1D fractional diffusion-wave equation. J Funct Spaces (2021) 2021:1–7. doi:10.1155/2021/6638597

CrossRef Full Text | Google Scholar

39. Jumarie G. Modified Riemann-Liouville derivative and fractional Taylor series of non-differentiable functions further results. Comput Math Appl (2006) 51:1367–76. doi:10.1016/j.camwa.2006.02.001

CrossRef Full Text | Google Scholar

40. Chunhong W. Numerical solution for Stocks’ first problem for a heated generalized second grade fluid with fractional derivative. Appl Numer Math (2009) 59:2571–83.

Google Scholar