Multiparty quantum contract signing

Quantum contract signing has the advantage of unconditional security compared with classical one. However, the prior works focus on two clients’ case. In this paper, we give a multiparty quantum contract signing protocol, which allows multiparty clients to sign an electronic contract simultaneously. The analysis shows that it not only satisfies the requirements for optimism and fairness but also can be realized with current technology.

1 Introduction

Contract signing is considered as a basic procedure in commercial transactions [1]. Traditional contract signing protocols are constrained by time, place and cost. With the emergence of e-commerce and other online transactions, the traditional contract signing protocols have been unable to meet the demand for online transactions. Therefore, the concept of electronic contract signing protocol was proposed [2]. Since fairness is the primary principle that electronic contract signing protocols must require, more electronic contract signing protocols took fairness as the research focus [3–7].

However, there exists an important problem that one client may commit on contract but not get the other’s commitment in the initial electronic contract signing protocols. Moreover, because of the non-synchronization of the network [8], one client always has more advantages than other clients. This unfair situation will cause serious outcomes, especially in a stock market [9]. A possible solution is to introduce a trusted third party (TTP). Furthermore, Even and Pagnia [10, 11] pointed out that without the involvement of a TTP, both truly fair electronic contract signing and fair exchange are not feasible. Therefore, electronic contract signing protocol with TTP is particularly important. Nevertheless, the involvement of TTP may lead to cryptographic attacks and higher communication costs; in addition, TTP may become a key factor that restricts the efficiency of the protocol. Therefore, how to optimize TTP participation becomes an important issue. The participation of TTP is optimized from the initial online mode to the off-line mode with stronger practicability [12, 13]. The electronic contract signing protocol with off-line TTP is more advantageous for TTP is not involved in other stages when no dispute happens.

Many classic electronic contract signing protocols involving three or more clients have been reported due to its application in real scenarios [14–17], but most of them are based on mathematical difficult problems and therefore is computationally secure. With the fast development of computing technology, their security is seriously challenged. Quantum cryptography are unconditionally secure in theory [18–22]. This is also the case for quantum contract signing, and therefore it has attracted much attention from researchers and many quantum electronic contract signing protocols have been presented [23–27]. Nevertheless, the prior works mainly deal with the application scenarios that two clients sign an electronic contract, but the multiparty case are not covered except a simple discussion in [9].

In this paper, we firstly study the design for multiparty quantum contract signing and give a specific protocol, which inherits the advantages of the prior works such as its unconditional security in theory and high fairness and so on. Furthermore, this protocol does not need long-time quantum storage and therefore can be realized with current technology.

This rest of this paper is organized as follows. In Section 2, we introduce the general model of multiparty quantum contract signing, and then present a multiparty quantum contract signing protocol in Section 3. In Section 4, we analyse its correctness, security and efficiency. Finally, we draw a conclusion in Section 5.

2 The model

The model of quantum contract signing includes n clients and a off-line TTP, who communicate with each other via classical and quantum channels. The channels are required to be authenticated in the model. The model consists of three phases: initializing phase, exchanging phase and binding phase. Specifically, in the initializing phase, the keys used for clients’ commitment on an electronic contract are established with the help of TTP. Then the clients exchange their commitment on the contract using the way of bit by bit in the exchanging phase, and TTP does not participate in the phase. When there is a dispute among clients, the binding phase is activated and TTP makes a judgement on the valid of commitment according to the testimonies submitted by the clients.

2.1 The initializing phase

• Preparing and distributing quantum states. TTP prepares n sets of quantum states ${\otimes }_{i=1}^N|{\phi \rangle }_i^{P_j}(j=\mathrm{1,2},\dots ,n)$, and then sends them to n clients P₁, P₂, …, P_n, respectively.

• Providing state information. TTP provides each client P_j with $\frac{N}{n}$ of the classical description $C^{P_k}$ for k = 1, 2, …, j − 1, j + 1, …, n, corresponding to a set ${\mathrm{\Gamma }}^{P_j}$, denoted as $C^{P_k{P}_j}$.

• Measuring quantum states. Each client P_j measures the quantum states distributed by TTP and keeps the measurement outcome $C^{P_j^{\prime }}$.

• Assigning identifier number. TTP assigns a unique identifier number I to all the data, which is used to link a specific contract C in the exchanging phase.

2.2 The exchanging phase

• Computing Hash value. All the clients compute the Hash value of the contract C, the identifier number I and some restriction.

• Exchanging information. All clients exchange their respective measurement results with each other in the way of 2 bits by 2 bits.

• Completing commitment. Each of clients gets the others’ commitments on the contract C.

2.3 The binding phase

When a dispute happens, the binding phase is activated.

• Submitting testimonies. TTP requires that all clients send their respective testimonies to him.

• Making judgement. TTP makes a judgement on the valid of commitment according to the testimonies submitted by the clients.

3 The protocol

Assume that n + 1 participants are P₁, P₂, …, P_n in the protocol, and they will sign an electronic contract as follows.

3.1 The initializing phase

This phase can be divided into four steps (please see Figure 1).

(1) TTP prepares n sets of quantum states ${\otimes }_{i=1}^N|{\phi \rangle }_i^{P_1}$, ${\otimes }_{i=1}^N|{\phi \rangle }_i^{P_2}$, ⋯, ${\otimes }_{i=1}^N|{\phi \rangle }_i^{P_n}$, and each state $|{\phi \rangle }_i^{P_j}$ is randomly chosen from the set {|0⟩, |1⟩, | + ⟩, | − ⟩} for i = 1, 2, …, N and j = 1, 2, …, n, where N = kn. Moreover, quantum states |0⟩, |1⟩, | + ⟩ and | − ⟩ are denoted as classical bits 00, 01, 10 and 11, respectively, and thus the corresponding classical description for the n sets of quantum states can be represented as $C^{P_1}=C_1^{P_1}\Vert C_2^{P_1}\Vert \cdots \Vert C_N^{P_1}$, $C^{P_2}=C_1^{P_2}\Vert C_2^{P_2}\Vert \cdots \Vert C_N^{P_2}$, …, $C^{P_n}=C_1^{P_n}\Vert C_2^{P_n}\Vert \cdots \Vert C_N^{P_n}$, where $C_i^{P_j}=C_{i_1}^{P_j}\Vert C_{i_2}^{P_j}\in \{\mathrm{00,01,10,11}\}$ for i = 1, 2, …, N and j = 1, 2, …, n, the notation ‖ denotes the concatenation between bits. Then he assigns a unique identifier number I to all data so that it can be linked to a specific contract C in the exchanging phase.

(2) TTP provides a set ${\mathrm{\Gamma }}^{P_j}$ that includes $\frac{N}{n}$ indices randomly chosen from a set Γ for each client P_j (j = 1, 2, …, n), where Γ = {1, 2, …, N}.

(3) For each client P_j (j = 1, 2, …, n), TTP provides P_j with $\frac{N}{n}$ of the classical description $C^{P_k}$ for k = 1, 2, …, j − 1, j + 1, …, n corresponding to the set ${\mathrm{\Gamma }}^{P_j}$, denoted as $C^{P_k{P}_j}$. Then TTP sends the identifier number I and quantum states ${\otimes }_{i=1}^N|{\phi \rangle }_i^{P_j}$ to P_j while keeping the remaining classical description $C^{P_{j}T}$ for j = 1, 2, …, n.

(4) For each client P_j (j = 1, 2, …, n), when receiving the quantum sates ${\otimes }_{i=1}^N|{\phi \rangle }_i^{P_j}$, P_j immediately measures each $|{\phi \rangle }_i^{P_j}$ with Z-basis or X-basis randomly for i = 1, 2, …, N, and then uses the classical bits 00, 01, 10 and 11 to represent the measurement outcome |0⟩, |1⟩, | + ⟩ and | − ⟩, respectively, denoted as $C_i^{P_j^{\prime }}=C_{i_1}^{P_j^{\prime }}\Vert C_{i_2}^{P_j^{\prime }}\in \{\mathrm{00,01,10,11}\}$. Finally, P_j keeps the measurement outcome $C^{P_j^{\prime }}=C_1^{P_j^{\prime }}\Vert C_2^{P_j^{\prime }}\Vert \cdots \Vert C_N^{P_j^{\prime }}$, the identifier number I, the classical description $C^{P_k{P}_j}$ and the indices ${\mathrm{\Gamma }}^{P_j}$.

FIGURE 1

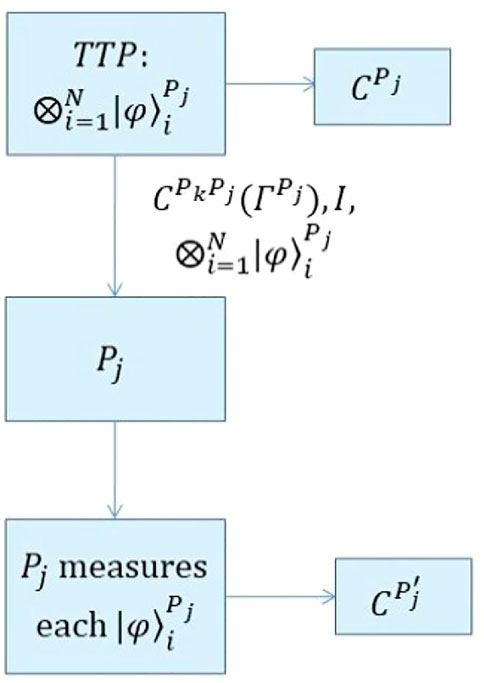
FIGURE 1. Depiction of initializing phase. TTP prepares n sets of quantum states. Then TTP sends the identifier number I, ${\otimes }_{i=1}^N|{\phi \rangle }_i^{P_j}$ and classical description of other clients’ states corresponding to the set ${\mathrm{\Gamma }}^{P_j}$ to P_j. P_j measures each $|{\phi \rangle }_i^{P_j}$ with Z-basis or X-basis randomly for i = 1, 2, …, N, and then keeps the measurement outcome $C^{P_j^{\prime }}$.

3.2 The exchanging phase

Suppose that all the n clients P₁, P₂, …, P_n agree on a contract C, the identifier number I that they want to use, and the time duration restriction t. Then they commit the contract C by the following exchange phase (please see Figure 2). Without loss of generality, assume that P₁ is the initiator.

(1) All the clients compute the Hash value

$H\left(C\Vert I\Vert t\right)=h_1\Vert h_2\Vert \cdots \Vert h_{2N},(1)$

where H(⋅): (0,1)* → (0,1)^2N is a collision-free hash function, used to generate a digest.

(2) If P₁ agrees to sign the contract C, he computes

$C_1^{\widetilde{P_1^{\prime }}}=C_1^{P_1^{\prime }}\oplus h_1\Vert h_2;(2)$

otherwise, he computes

$C_1^{\widetilde{P_1^{\prime }}}=C_1^{P_1^{\prime }}\oplus h_1\Vert h_2\oplus 01.(3)$

FIGURE 2

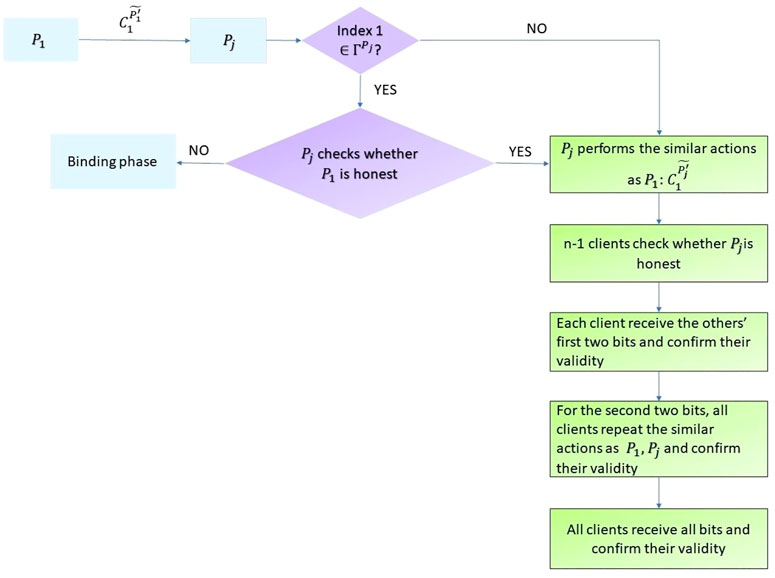
FIGURE 2. Depiction of exchanging phase. All clients simultaneously commit on the contract C through exchanging their classical information with the way of 2 bits by 2 bits.

Then he sends $C_1^{\widetilde{P_1^{\prime }}}$ to other n − 1 clients.

(3) For each P_j (j = 2, 3, …, n), if he has not received $C_1^{\widetilde{P_1^{\prime }}}$ in the time duration restriction t, he immediately contacts TTP to perform the binding phase. Otherwise, he checks whether the index 1 is in ${\mathrm{\Gamma }}^{P_j}$ or not. If the index 1 is not in ${\mathrm{\Gamma }}^{P_j}$, P_j performs the similar actions as P₁ does in Step (2), i.e., if he agrees to sign the contract C, he computes

$C_1^{\widetilde{P_j^{\prime }}}=C_1^{P_j^{\prime }}\oplus h_1\Vert h_2;(4)$

otherwise, he computes

$C_1^{\widetilde{P_j^{\prime }}}=C_1^{P_j^{\prime }}\oplus h_1\Vert h_2\oplus 01.(5)$

Then he sends $C_1^{\widetilde{P_j^{\prime }}}$ to other n − 1 clients. If the index 1 is in ${\mathrm{\Gamma }}^{P_j}$, he computes

$C_1^{\widetilde{P_1}}=C_1^{P_1}\oplus h_1\Vert h_2,(6)$

and then checks whether

$C_1^{\widetilde{P_1}}=C_1^{\widetilde{P_1^{\prime }}}(7)$

holds or not. If the first bit of $C_1^{\widetilde{P_1}}$ is the same as that of $C_1^{\widetilde{P_1^{\prime }}}$ but Eq.7 does not hold, P_j also immediately contacts TTP to perform the binding phase. In other cases, P_j also performs the similar actions as P₁ does in Step (2). This step is sequentially executed until each client has received the others’ first 2 bits and confirmed their validity.

(4) P₁ performs the similar actions as that he does in Step (2), i.e., if he agrees to sign the contract C, he computes

$C_2^{\widetilde{P_1^{\prime }}}=C_2^{P_1^{\prime }}\oplus h_3\Vert h_4;(8)$

otherwise, he computes

$C_2^{\widetilde{P_1^{\prime }}}=C_2^{P_1^{\prime }}\oplus h_3\Vert h_4\oplus 01.(9)$

Then he sends $C_2^{\widetilde{P_1^{\prime }}}$ to other n − 1 clients. Other n − 1 clients performs the similar actions as that they does in Step (3). This step is also sequentially executed until each client has received the others’ second 2 bits and confirmed their validity.

(5) The similar procedure is repeated until each client has received all the others’ bits and confirmed their validity.

3.3 The binding phase

Without loss of generality, suppose that dispute appears at the mth round and TTP requires that all clients send their respective testimonies to him. After receiving all the clients’ testimonies, if all of them accept the validity of the contract C or reject it, then TTP confirms and keeps it in case of possible dispute in future. Otherwise, TTP just considers the testimonies submitted by the clients who want to bind the contract C. Furthermore, as long as one of the testimonies passes his verification, TTP declares the contract C is valid. Specifically, after receiving all clients’ testimonies, TTP only checks the part submitted by P₁, P₂, …, P_k who want to bind the contract C. The check process can be described as follows (please see Figure 3).

(1) For the testimonies I, H(C, I, t) and $C^{\widetilde{P_j^{\prime }}}=C_1^{\widetilde{P_j^{\prime }}}\Vert C_2^{\widetilde{P_j^{\prime }}}\Vert \cdots \Vert C_m^{\widetilde{P_j^{\prime }}}(j=\mathrm{1,2},\dots ,n)$ submitted by P₁, TTP computes

$C_i^{P_j^{″}}=C_i^{\widetilde{P_j^{\prime }}}\oplus h_{2i-1}\Vert h_{2i}\mathtt{f}\mathtt{o}\mathtt{r}i=\mathrm{1,2},\dots ,m\mathtt{a}\mathtt{n}\mathtt{d}j=\mathrm{1,2},\dots ,n,(10)$

FIGURE 3

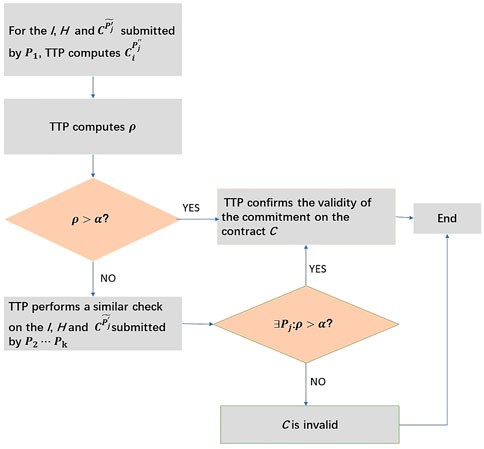
FIGURE 3. Depiction of binding phase. TTP checks the testimonies submitted by the clients who want to bind the contract C and then gives a verdict on the validity of all clients’ commitment according to the check outcome.

For each $i\in \{\mathrm{1,2},\dots ,m\}\cap (\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_1})$, if the first bit of $C_i^{P_j^{″}}$ is equal to the one of $C_i^{P_j}$, i.e., $C_{i_1}^{P_j^{″}}=C_{i_1}^{P_j}$, TTP checks whether $C_i^{P_j^{″}}=C_i^{P_j}$, then he counts the number n_e of $C_i^{P_j^{″}}$ that satisfies this condition. After that, he computes the ratio $\rho =\frac{n_e}{n_t}$, where n_t is the total number of $C_i^{P_j^{″}}$ that should satisfy $C_{i_1}^{P_j^{″}}=C_{i_1}^{P_j}(i\in (\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_1}))$. By simply computing, it can be found $n_t\approx \frac{N}{4}$. Finally, he checks whether the in equation

$\rho >\alpha (11)$

holds or not, where α is a parameter independently chosen by TTP according to some publicly-known distribution p_m(α). If Eq.11 holds for j = 1, 2, …, n, then TTP confirms the validity of the commitment on the contract C while signing an authorized document for all clients to declare that the hash value H(C, I, t) is valid, and the binding phase is completed. Otherwise, TTP continues to perform the next step.

(2) TTP performs a similar check on the testimonies I, H(C, I, t) and $C^{\widetilde{P_j^{\prime }}}=C_1^{\widetilde{P_j^{\prime }}}\Vert C_2^{\widetilde{P_j^{\prime }}}\Vert \cdots \Vert C_m^{\widetilde{P_j^{\prime }}}(j=\mathrm{1,2},\dots ,n)$ submitted by P₂.

(3) The similar procedure is repeated until the check on the last client P_k’s testimonies is completed.

Finally, if all the k clients’ testimonies cannot pass the check, TTP declares that the commitment on the contract C is invalid. Finally, he keeps the verdict in both cases.

4 The analysis

4.1 Correctness

Theorem 1. Either each of n clients gets the other n − 1 ones’ commitment on the contract C, or none of them gets any commitment on the contract C in the above protocol.

Proof. It can be seen that if all n clients perform this protocol honestly in the exchanging phase, then each of them will get the other n − 1 clients’ commitment on the contract C. In the binding phase, TTP signs an authorized document for all clients to confirm the validity of commitment on the contract C, or declares that the commitment on the contract C is invalid, which means that either each of n clients gets the others’ commitment, or none of them gets any commitment in both cases.

Therefore, this protocol can be correctly completed.

4.2 Optimistic

In an ideal scenario, all clients perform this protocol honestly, then each will get the other n − 1 clients’ commitment on the contract C simultaneously. In this case, TTP does not need to be involved, and therefore this protocol is optimistic.

4.3 Fairness

As we know, if a cryptographic protocol is secure against participant attacks, then it must be also secure for external opponents. This is also the case for quantum contract signing, and therefore the main security goal of this protocol is to prevent the attacks from legal participants, i.e., how to guarantee the fairness that each client will get the others’ commitment or none of them will get the commitment from anyone else [9, 23–27].

As mentioned in Section 2, a cryptographic hash function H(⋅) is used to generate a digest in this protocol. Clearly, if a dishonest client has unlimited computational resources, then he can find a collision, i.e., H(C‖I‖t) = H(C′‖I‖t), which will give him a good chance to bind a different contract C′. Nevertheless, as pointed out in [24], “given a particular hash function H(⋅), it is negligible that other collisions different from the contract C would still represent meaningful contracts, let alone contracts that would be favorable to the dishonest one”. Consequently, we do not consider the collision attack any longer here.

Before proving the fairness, we firstly define some probabilities as follows.$P_{P_{a}T{P}_b}(m,\alpha )$: Probability that P_a passes TTP’s test on P_b’s bits $C^{\widetilde{P_b^{\prime }}}=C_1^{\widetilde{P_b^{\prime }}}\Vert C_2^{\widetilde{P_b^{\prime }}}\Vert \cdots \Vert C_m^{\widetilde{P_b^{\prime }}}$ for $i\in \{\mathrm{1,2},\dots ,m\}\cap (\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_a})$, hereafter a, b ∈ {1, 2, …, n}.$P_{P_{b}T{P}_a}(m,\alpha )$: Probability that P_b passes TTP’s test on P_a’s bits $C^{\widetilde{P_a^{\prime }}}=C_1^{\widetilde{P_a^{\prime }}}\Vert C_2^{\widetilde{P_a^{\prime }}}\Vert \cdots \Vert C_m^{\widetilde{P_a^{\prime }}}$ for $i\in \{\mathrm{1,2},\dots ,m\}\cap (\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_b})$.$P_{P_b{P}_{a}S}(m,\alpha )$: Probability that P_b passes P_a’s test on his bits $C^{\widetilde{P_b^{\prime }}}=C_1^{\widetilde{P_b^{\prime }}}\Vert C_2^{\widetilde{P_b^{\prime }}}\Vert \cdots \Vert C_m^{\widetilde{P_b^{\prime }}}$ for $i\in \{\mathrm{1,2},\dots ,m\}\cap {\mathrm{\Gamma }}^{P_a}$.$P_{P_a{P}_{b}S}(m,\alpha )$: Probability that P_a passes P_b’s test on his bits $C^{\widetilde{P_a^{\prime }}}=C_1^{\widetilde{P_a^{\prime }}}\Vert C_2^{\widetilde{P_a^{\prime }}}\Vert \cdots \Vert C_m^{\widetilde{P_a^{\prime }}}$ for $i\in \{\mathrm{1,2},\dots ,m\}\cap {\mathrm{\Gamma }}^{P_b}$.

It should be noted that the communication channels in this protocol are authenticated, and thus the attacks from external opponents need not be considered. Consequently, we only consider the possible participant attacks: one is dishonest clients want to get the others’ commitment on the contract C but make the others not obtain theirs by sending fake bits in the exchanging phase, and the other is that they send forgery testimonies to TTP in the binding phase in order to get a certified copy of the different contract C′.

Firstly, we analyze the possibility of the first kind of attack. Without loss of generality, assume that P_b is a dishonest client who wants to get P_a’s commitment on the contract C but make P_a not obtain his in the exchanging phase. To attain this goal, a possible way is to send some fake bits to P_a in the exchanging phase. Nevertheless, he must make P_a’s testimony $C^{\widetilde{P_b^{\prime }}}=C_1^{\widetilde{P_b^{\prime }}}\Vert C_2^{\widetilde{P_b^{\prime }}}\Vert \cdots \Vert C_m^{\widetilde{P_b^{\prime }}}$ sent by himself not satisfy Eq.13, i.e.,

$\rho =\frac{n_e}{n_t}\le \alpha \iff n_e\le \alpha n_t,(12)$

which means when the communication was interrupted at the mth round, he must send at least (1 − α)n_t such $C_i^{\widetilde{P_b^{\prime }}}$ that satisfies $C_i^{P_b^{″}}=C_i^{\widetilde{P_b^{\prime }}}\oplus h_{2i-1}\Vert h_{2i}$and$C_{i_1}^{P_b^{″}}=C_{i_1}^{P_b}$,but$C_{i_2}^{P_b^{″}}\ne C_{i_2}^{P_b}$, $i\in \{\mathrm{1,2},\dots ,m\}\cap (\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_a})$. Since P_b has no way to distinguish the index i of $C_i^{\widetilde{P_b^{\prime }}}$ from ${\mathrm{\Gamma }}^{P_a}$ and $\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_a}$, his deception will be detected by P_a with the probability

$\begin{array}{ccc}\hfill P_{f_{P_a}}& =\hfill & 1-P_{P_b{P}_{a}S}\left(m,\alpha \right)\hfill \\ \hfill & =\hfill & 1-{\left(\frac{3}{4}\right)}^{4\left(1-\alpha \right)n_t}\hfill \\ \hfill & \approx \hfill & 1-{\left(\frac{3}{4}\right)}^{\left(1-\alpha \right)N},\hfill \end{array}(13)$

which is exponentially close to 1. Therefore, the successful probability

$\begin{array}{ccc}\hfill P_{ch}\left(m,\alpha \right)& =\hfill & 1-P_{f_{P_a}}\hfill \\ \hfill & =\hfill & {\left(\frac{3}{4}\right)}^{4\left(1-\alpha \right)n_t}\hfill \\ \hfill & \approx \hfill & {\left(\frac{3}{4}\right)}^{\left(1-\alpha \right)N}\hfill \end{array}(14)$

for P_b to cheat is negligible. Furthermore, when a dispute appears, TTP will sign an authorized document for all clients to declare that the hash value h* = H(C, I, t) is valid, whereby each can obtain a certified copy of the contract C, which implies that the difference between P_a’s probability $P_{\mathit{bind}}^{P_a}(m,\alpha )$ and P_b’s probability $P_{\mathit{bind}}^{P_b}(m,\alpha )$ to bind the contract C is equal to P_ch(m, α), i.e.,

$|P_{\mathit{bind}}^{P_b}\left(m,\alpha \right)-P_{\mathit{bind}}^{P_a}\left(m,\alpha \right)|=P_{ch}\left(m,\alpha \right)<\epsilon ,(15)$

here ɛ is any given real positive number.

Secondly, we analyze the possibility of the second kind of attack. Without loss of generality, we also assume that P_b is dishonest. Differing from the first one, P_b directly forges the testimonies H(C′, I, t) and $C^{\widetilde{P_a^{\prime }}}$ in this case, and then sends them to TTP for getting a certified copy of forgery contract C′. To attain this goal, he must make them satisfy Eq. 12, i.e.,

$\rho =\frac{n_e}{n_t}>\alpha \iff n_e>\alpha n_t\approx \frac{N}{4}\alpha .(16)$

That is to say, when the communication is interrupted at the mth round, he must forge at least αn_t such $C_i^{\widetilde{A^{\prime }}}$ that satisfies $C_i^{P_a^{″}}=C_i^{\widetilde{P_a^{\prime }}}\oplus h_{2i-1}\Vert h_{2i}$, $C_{i_1}^{P_a^{″}}=C_{i_1}^{P_a}$, and $C_{i_2}^{P_a^{″}}=C_{i_2}^{P_a}$, $i\in \{\mathrm{1,2},\dots ,m\}\cap (\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_b})$. For each $i\in \{\mathrm{1,2},\dots ,m\}\cap (\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_b})$, it will be in ${\mathrm{\Gamma }}^{P_b}$ and $\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_b}$ with the probability $\frac{1}{n}$ and $\frac{n-1}{n}$, respectively. Furthermore, when the index i is in $\mathrm{\Gamma }-{\mathrm{\Gamma }}^{P_b}$, the probability that $C_i^{\widetilde{P_a^{\prime }}}$ matches with $C_i^{P_a}$ is not more than $\frac{1}{4}$. Therefore, the successful probability is

$\begin{array}{ll}\hfill P_{ch}^{\prime }\left(m,\alpha \right)& =C_m^r{\left(\frac{1}{4n}\right)}^r{\left(\frac{4n-1}{4n}\right)}^{m-r}+C_m^{r+1}{\left(\frac{1}{4n}\right)}^{r+1}{\left(\frac{4n-1}{4n}\right)}^{m-r-1}\hfill \\ \hfill & +\cdots +C_m^{m-1}{\left(\frac{1}{4n}\right)}^{m-1}\left(\frac{4n-1}{4n}\right)+C_m^m{\left(\frac{1}{4n}\right)}^m\hfill \\ \hfill & <\left(m-r+1\right)C_m^r{\left(\frac{1}{4n}\right)}^r{\left(\frac{4n-1}{4n}\right)}^{m-r}\hfill \\ \hfill & \approx \left(m-\lceil \alpha \frac{N}{4}\rceil +1\right)C_m^{\lceil \alpha \frac{N}{4}\rceil }{\left(\frac{1}{4n}\right)}^{\lceil \alpha \frac{N}{4}\rceil }{\left(\frac{4n-1}{4n}\right)}^{m-\lceil \alpha \frac{N}{4}\rceil },\hfill \end{array}(17)$

which is exponentially close to 0, here $r=\lceil \alpha \frac{N}{4}\rceil$, the notation ⌈⋅⌉ denotes the top integral function, and $C_m^r=\frac{m\times (m-1)\times \cdots \times (m-r+1)}{r\times (r-1)\times \cdots \times 1}$. Accordingly, the successful probability $P_{ch}^{\prime }(m,\alpha )$ for P_b to cheat is also negligible. Note that we can adjust the threshold value α according to both the practical noise and measurement errors to guarantee its security in a non-ideal case, the analysis is similar.

4.4 Efficiency

Compared with two-party protocols in [23–27], the number n of clients in this protocol can be larger than three and is flexible. Nevertheless, this protocol needs to prepare and transit o(nN) qubits, which is about $\frac{n}{2}$ times of two-party protocols. At the same time, it requires to transit o(2N(n + 1) (n − 1)) bits, which is also about $\frac{n}{2}$ times of two-party protocols. Therefore, both the communication complexity and resource consumption is about $\frac{n}{2}$ times of two-party protocols, which means its efficiency is about $\frac{2}{n}$ of two-party protocols.

5 Conclusion

To sum up, we firstly study the design of multiparty quantum contract signing and give a specific protocol. The analysis shows that it is optimistic and fair. Furthermore, this protocol does not need long-time quantum storage, and therefore can be realized with current technology. We hope this work can provide more enlightenment for the future practicability of multiparty electronic contract signing protocol.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Z-FL, Analyzed the protocol, Prepared the figures, Wrote the main manuscript text. R-JY: Analyzed the protocol. X-QC: Proposed the protocol. T-YW: Analyzed the protocol.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 62272208, 62172196 and 61902166), the Guangxi Key Laboratory of Trusted Software (Grant No. KX202040), the Postgraduate Education Reform Project of Henan Province (Grant No. 2019-SJGLX094Y), and the Natural Science Foundation of Henan Province (Grant No. 212300410062).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1154415/full#supplementary-material

References

1. Asokan N, Shoup V, Waidner M Optimistic fair exchange of digital signatures. IEEE J Selected Areas Commun (2000) 18(4):593–610. doi:10.1109/49.839935

CrossRef Full Text | Google Scholar

2. Ben-Or M, Goldreich O, Micali S, Rivest R. A fair protocol for signing contracts. IEEE Trans Inf Theor (1990) 36(1):40–6. doi:10.1109/18.50372

CrossRef Full Text | Google Scholar

3. Asokan N, Schunter M, Waidner M Optimistic protocols for fair exchange. In: Proceedings of the 4th ACM Conference on Computer and Communications Security. New York: ACM (1997). p. 7–17.

CrossRef Full Text | Google Scholar

4. Zhang L, Zhang HL, Yu J, Xian H. Blockchain-based two-party fair contract signing scheme. Inf Sci (2020) 535:142–55. doi:10.1016/j.ins.2020.05.054

CrossRef Full Text | Google Scholar

5. Wang GL An abuse-free fair contract-signing protocol based on the rsa signature. IEEE Trans Inf Forensics Security (2010) 5(1):158–68. doi:10.1109/tifs.2009.2035972

CrossRef Full Text | Google Scholar

6. Ray I, Ray I Fair exchange in e-commerce. SIGecom Exch (2002) 3(2):9–17. doi:10.1145/844340.844345

CrossRef Full Text | Google Scholar

7. Ray I, Ray I An optimistic fair exchange e-commerce protocol with automated dispute resolution. In: K Bauknecht, S Kumar Madria, and G Pernul, editors. Electronic commerce and web technologies. Berlin, Heidelberg: Springer Berlin Heidelberg (2000). p. 84–93.

CrossRef Full Text | Google Scholar

8. Zhou NR, Zhang TF, Xie XW, Wu JY. Hybrid quantum–classical generative adversarial networks for image generation via learning discrete distribution. Signal Processing: Image Commun (2023) 110:116891. doi:10.1016/j.image.2022.116891

CrossRef Full Text | Google Scholar

9. Paunković N, Bouda J, Mateus P Fair and optimistic quantum contract signing. Phys Rev A (2011) 84:062331. doi:10.1103/physreva.84.062331

CrossRef Full Text | Google Scholar

10. Even S, Yacobi Y Relations among public key signature systems. Technical report. Haifa: Computer Science Department, Technion (1980).

Google Scholar

11. Pagnia H, Gärtner FC On the impossibility of fair exchange without a trusted third party. Citeseer: Technical report (1999).

Google Scholar

12. Zhou JY, Gollman D A fair non-repudiation protocol. In: Proceedings 1996 IEEE Symposium on Security and Privacy; May 1996; Oakland, CA, USA. IEEE (1996). p. 55–61.

Google Scholar

13. Feng B, Robert HD, Mao WB Efficient and practical fair exchange protocols with off-line ttp. In: Proceedings. 1998 IEEE Symposium on Security and Privacy (Cat. No. 98CB36186); May 1998; Oakland, CA, USA. IEEE (1998). p. 77–85.

Google Scholar

14. Garay JA, MacKenzie P Abuse-free multi-party contract signing. In: J Prasad, editor. Distributed computing. Berlin, Heidelberg: Springer Berlin Heidelberg (1999). p. 151–66.

CrossRef Full Text | Google Scholar

15. Baum-Waidner B Optimistic asynchronous multi-party contract signing with reduced number of rounds. In: Automata, Languages and Programming: 28th International Colloquium, ICALP 2001 Crete; July 8–12, 2001; Greece. Springer (2001). p. 898–911. Proceedings.

CrossRef Full Text | Google Scholar

16. Ferrer-Gomila JL, Hinarejos MF, Andreu-Pere ID A fair contract signing protocol with blockchain support. Electron Commerce Res Appl (2019) 36:100869. doi:10.1016/j.elerap.2019.100869

CrossRef Full Text | Google Scholar

17. Guo LJ, Li XL, Gao JT Multi-party fair exchange protocol with smart contract on bitcoin. Int J Netw Secur (2019) 21(1):71–82.

Google Scholar

18. Chen YA, Zhang Q, Chen TY, Cai WQ, Liao SK, Zhang J, et al. An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature (2021) 589(7841):214–9. doi:10.1038/s41586-020-03093-8

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chen LL, Li Q, Liu CD, Peng Y, Yu F. Efficient mediated semi-quantum key distribution. Physica A: Stat Mech its Appl (2021) 582:126265. doi:10.1016/j.physa.2021.126265

CrossRef Full Text | Google Scholar

20. Cai XQ, Liu ZF, Wei CY, Wang TY. Long distance measurement-device-independent three-party quantum key agreement. Physica A: Stat Mech its Appl (2022) 607:128226. doi:10.1016/j.physa.2022.128226

CrossRef Full Text | Google Scholar

21. Liu J, Li Q, Quan JY, Wang C, Shi J, Situ H. Efficient quantum homomorphic encryption scheme with flexible evaluators and its simulation. Designs, Codes and Cryptography (2022) 90(3):577–91. doi:10.1007/s10623-021-00993-2

CrossRef Full Text | Google Scholar

22. Wang Y, Lou XP, Zhou F, Wang S, Huang S. Verifiable multi-dimensional (t,n) threshold quantum secret sharing based on quantum walk. Int J Theor Phys (2022) 61(2):1–17. doi:10.1007/s10773-022-05009-w

CrossRef Full Text | Google Scholar

23. Chou YH, Tsai IM, Ko CM, Kou S, Chen I Quantum oblivious transfer and fair digital transactions. In: Proceeding of the 2006 12th Pacific Rim International Symposium on Dependable Computing (PRDC’06); December 2006; Riverside, CA, USA. IEEE (2006). p. 121–8.

CrossRef Full Text | Google Scholar

24. Yadav P, Mateus P, Paunković N, Souto A. Quantum contract signing with entangled pairs. Entropy (2019) 21(9):821. doi:10.3390/e21090821

CrossRef Full Text | Google Scholar

25. Cai XQ, Wang XX, Wang TY Fair and optimistic contract signing based on quantum cryptography. Int J Theor Phys (2019) 58(11):3677–83. doi:10.1007/s10773-019-04236-y

CrossRef Full Text | Google Scholar

26. Cao T, Chang Y, Yan LL, Wang Q. Quantum electronic contract scheme based on single photon. CMC-Computers Mater Continua (2020) 65(2):1507–17. doi:10.32604/cmc.2020.010213

CrossRef Full Text | Google Scholar

27. Cai XQ, Wang TY, Wei CY, Gao F. Practical quantum contract signing without quantum storage. Quan Inf Process (2022) 21(2):58. doi:10.1007/s11128-021-03406-4

CrossRef Full Text | Google Scholar