Nonlinear stretched flow of a radiative MHD Prandtl fluid with entropy generation and mixed convection

This paper examines the analysis of entropy generation in the flow of an MHD Prandtl fluid over a nonlinear stretching sheet. Heat transfer is developed through a convectively heated sheet. The impacts of nonlinear radiation and nonlinear mixed convection are considered. The resulting nonlinear systems are computed for the unique solutions of velocity and temperature profiles. Effects of thermal radiation, the Prandtl number, Prandtl fluid parameters, and the Biot number are discussed. Results for the Nusselt number and skin friction coefficient are analyzed. The impact of the radiation parameter is to improve the rate of heat transport to the flow region. It is stated that temperature distribution increases for greater values of θ_f. We state that the fluid temperature decreases with the increasing importance of the Prandtl number Pr. Growth in the Prandtl number decreases the rate of thermal diffusion. It shows that the magnitude of drag forces decreases for larger values of Prandtl fluid parameters. Furthermore, curvature and mixed convection parameters boost the flow and heat transfer rate near the cylinder wall. The entropy generation grew up rapidly with larger values of magnetic and Brinkman numbers. The temperature ratio parameter and Prandtl fluid parameters reduce the entropy generation rate. These parameters are also used to control the entropy generation process.

1 Introduction

In recent years, non-Newtonian fluid with boundary layer approximation over the moving surface has gained considerable attention due to its extensive applications. In [1], the Couette flow of a viscoelastic fluid with thermal convection was studied. In [2], the micropolar fluid flow in a channel was analytically investigated. In [3], the flow and heat transfer of a viscoelastic electrically conducting fluid over a stretching/shrinking sheet was reported. In [4], the exact solution of a rate-type fluid in a circular duct was developed. Coupled flow and heat transfer of a Maxwell fluid over a stretching sheet was discussed in [5, 6], where the mixed convection flow of power-law fluids past an inclined sheet was explored. The effects of shear flow and power-law viscosity on the temperature field were also considered. MHD boundary layer stagnation point flow of a Jeffrey fluid over a moving sheet was analyzed in [7].

Convective heat transfer has great interest among researchers, both theoretical and practical, and also has many applications in engineering and geophysical fields. Initially, in [8], the convective heat transfer flow over a moving sheet was reported. In [9], the convective heat transfer over a stretching/shrinking surface was numerically examined. In [10], the steady flow of double-diffusive mixed convection boundary layer flow through convective boundary conditions was numerically reported. The flow of a Maxwell fluid due to constantly moving radiative surfaces with the convective condition was reported in [11, 12],where numerical analysis over a continuous stretching sheet with nonlinear thermal radiation was performed. In [13], the flow of a nanofluid in the existence of nonlinear thermal radiation was numerically analyzed. In [14], the three-dimensional flow of a Jeffrey nanofluid subject to thermal radiation effects was explored. In [15], the analysis of MHD flow and heat transfer with nonlinear radiation in a viscoelastic fluid was performed. The study of three-dimensional magnetohydrodynamics with thermophoresis and Brownian motion aspects was extended in [16].

In the present study, we explore the entropy generation in the flow of an MHD Prandtl fluid with nonlinear thermal radiation. Although the stretching problems are explored extensively for linear thermal radiation, much less emphasis has been given to the flow problems with nonlinear thermal radiation. Such information is further scarce when heat transfer through convective conditions is considered. The radiation effect in the flow of a pseudo-plastic nanofluid was examined in [17]. The MHD stretched flow of a nanofluid in the presence of buoyancy and thermal radiation was analyzed in [18]. A salient feature of radiation in nanofluid flow over an unsteady stretching sheet was reported in [19, 20],where the thermal radiation effect in time-dependent MHD flow with variable viscosity was analyzed. The hydromagnetic flow of a second-grade fluid in the presence of thermal radiation was examined in [21]. The effect of thermal radiation in the flow of a micropolar fluid was considered in [22, 23],where entropy generation in nonlinear radiative flow in the direction of a variable thick surface was reported. A mathematical model for entropy generation with variable fluid properties was examined in [24]. The impact of mixed convection and nonlinear radiation was further considered. The results of surface drag forces, entropy generation rate, heat/mass transfer, and the Bejan number were presented numerically in [25], where the entropy generation in an MHD micropolar nanofluid was analyzed using a nonlinear stretching sheet.

We explore the nonlinear effects of radiation, mixed convection, and stretching sheet with an MHD [26–31] Prandtl fluid and heat transfer on entropy generation. The first objective of the current article is to venture further into the regime of the nonlinear stretched flow of the Prandtl fluid with convective heat transfer [32–41] effects. Thus, the Prandtl fluid dealt with the nonlinear flow of thermal radiation. Our second objective is to consider the nonlinear mixed convection in the entropy generation by nonlinear stretching. Having such an incentive in mind, the reason here is to model first the appropriate problem and then compute it. Nonlinear radiation properties are also incorporated. Governing differential systems are solved for the unique solution of velocity and temperature fields. Velocity, temperature, and entropy generation are sketched and examined for different emerging parameters. The local Nusselt number and skin friction coefficient are studied by graphical illustrations and tabular values.

2 Mathematical construction

We consider the 2D flow of an MHD Prandtl fluid over a stretching sheet. The flow is induced by using a nonlinear stretching sheet. The x- and y-axis are taken along and perpendicular correspondingly. Furthermore, the effects of nonlinear radiation, mixed convection, and convective condition are considered. The Cauchy stress tensor for the Prandtl fluid is given by

$S=\frac{A{\sin }^{-1}\left\{\frac{1}{C}{\left[{\left(\frac{\partial u_i}{\partial x_j}\right)}^2+{\left(\frac{\partial u_j}{\partial x_i}\right)}^2\right]}^{\frac{1}{2}}\right\}}{{\left[{\left(\frac{\partial u_i}{\partial x_j}\right)}^2+{\left(\frac{\partial u_j}{\partial x_i}\right)}^2\right]}^{\frac{1}{2}}}{A}_1,(1)$

where A and C are the material parameters and A₁ is the first Rivlin–Erickson tensor. The boundary layer equations containing the stability of mass, linear momentum, and energy can be written as follows:

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(2)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left(\frac{A}{C}\right)\frac{{\partial }^{2}u}{\partial y^2}+\frac{A}{2C^3}{\left(\frac{\partial u}{\partial y}\right)}^2\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B_0}{\rho }u+g\left\{{\wedge }_1\left(T-T_{\infty }\right)+{\wedge }_2{\left(T-T_{\infty }\right)}^2\right\},(3)$

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{\partial }{\partial y}\left\{\alpha +\frac{16{\sigma }^{*}{T}^3}{3\rho c_p{k}^{*}}\right\}\frac{\partial T}{\partial y}+\frac{1}{\rho c_p}\left[\frac{A}{C}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{A}{6C^3}{\left(\frac{\partial u}{\partial y}\right)}^4\right]+\sigma B_0{u}^2,(4)$

with the subjected boundary conditions

$U_w\left(x\right)=\frac{\nu }{L^{\frac{4}{3}}}{x}^{\frac{1}{3}},v=0,-k\frac{\partial T}{\partial y}=h\left(T_f-T\right)\text{\hspace{0.17em}at\hspace{0.17em}}y=0,$

$u\to 0,T\to T_{\infty }\text{\hspace{0.17em}\hspace{0.17em}as\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}y\to \infty .(5)$

In the aforementioned expressions, ν = (μ/ρ) is the kinematic viscosity, μ is the dynamic viscosity, k is the thermal conductivity of the fluid, ρ is the fluid density, T is the fluid temperature, c_p is the specific heat, $q_r=-\frac{16{\sigma }^{*}{T}^3}{3k^{*}}\frac{\partial T}{\partial y}$ is the radiative heat flux, k* is the mean absorption coefficient, σ* is the Stefan–Boltzmann constant, and Bi is the Biot number.

Setting

$\begin{array}{ccc}\hfill u& =\hfill & \frac{\upsilon }{L^{\frac{4}{3}}}{x}^{\frac{1}{3}}{f}^{\prime }\left(\eta \right),v=-\frac{\upsilon }{L^{\frac{2}{3}}}{x}^{-\frac{1}{3}}\frac{\left(2f-\eta f\right)}{3},\hfill \\ \hfill \theta & =\hfill & \frac{T-T_{\infty }}{T_f-T_{\infty }},\eta =y\frac{x^{\frac{-1}{3}}}{L^{\frac{2}{3}}},{\theta }_f=\frac{T_f}{T_{\infty }},\hfill \end{array}(6)$

equation 2 is identically satisfied, and Eqs.3−5) give

$\alpha f^{\prime \prime \prime }-f^{\prime 2}+\frac{2}{3}f{f}^{\prime \prime }-\beta f^{\prime \prime 2}{f}^{\prime \prime \prime }-M{f}^{\prime }+\lambda \left(1+{\beta }_t\theta \right)\theta =0,(7)$

$\left(1+R\right){\theta }^{\prime \prime }+R\left({\theta }_f-1\right)\left\{{\theta }^{\prime \prime }{\theta }^3{\left({\theta }_f-1\right)}^2+3{\theta }^{\prime \prime }{\theta }^2\left({\theta }_f-1\right)+3\theta {\theta }^{\prime \prime }\right\},$

$+3R\left({\theta }_f-1\right)\left\{{\theta }^{{\prime }^2}+{\theta }^2{\theta }^{{\prime }^2}{\left({\theta }_f-1\right)}^2+2{\theta }^{{\prime }^2}\theta \left({\theta }_f-1\right)\right\}+\frac{2}{3}\mathrm{Pr}f{\theta }^{\prime }+\mathrm{Pr}Ec\left(\alpha f^{\prime \prime }+\frac{\beta }{3}{f}^{\prime \prime 4}\right)+\mathrm{Pr}EcM{f}^{\prime 2}=0,(8)$

$\begin{array}{ccc}\hfill f& =\hfill & 0,f^{\prime }=1,{\theta }^{\prime }=-Bi\left(1-\theta \right)\text{\hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\eta =0,\hfill \\ \hfill f^{\prime }& \to \hfill & 0,\theta \to 0\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}as\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\eta \to \infty ,\hfill \end{array}(9)$

where prime denotes the differentiation with respect to η, f is the dimensionless stream function, θ is the dimensionless temperature, and θ_f is the temperature ratio parameter; the dimensionless numbers are

$\alpha =\frac{A}{\mu C},R=\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k{k}^{*}},\beta =\frac{A\nu }{2\rho L^4{C}^3},Bi=\frac{h}{k}\text{,\hspace{0.17em}}\mathrm{Pr}=\frac{\mu c_p}{k},E_k=\frac{U_w\left(x\right)}{c_p\left(T_f-T_{\infty }\right)}.(10)$

Here, α and β are the dimensionless Prandtl parameters, R is the radiation parameter, Bi is the Biot number, and Pr is the Prandtl number.

The local Nusselt number Nu_x and skin friction coefficient C_f are defined as follows:

$N{u}_x=\frac{x{q}_w}{k\left(T_f-T_{\infty }\right)},C_f=\frac{{\tau }_w}{\rho U_w^2},(11)$

where ρ is the fluid density, τ_w is the surface shear stress, and q_w is the surface heat flux. These quantities are defined by

$q_w=-k{\left(\frac{\partial T}{\partial y}\right)}_{y=0}+{\left(q_r\right)}_w,{\tau }_w=\frac{A}{C}\frac{\partial u}{\partial y}+\frac{A}{6C^3}{\left(\frac{\partial u}{\partial y}\right)}^3.(12)$

The dimensionless Nusselt number and skin friction coefficient are

${\mathrm{R}\mathrm{e}}_x^{1/2}N{u}_x=-\left(1+R{\theta }_f^3\right){\theta }^{\prime }\left(0\right),(13)$

$\mathrm{R}\mathrm{e}x{C}_f=\alpha f^{\prime \prime }\left(0\right)+\frac{\beta }{3}{\left(f^{\prime \prime }\left(0\right)\right)}^3,(14)$

where ${\mathrm{R}\mathrm{e}}_x=\frac{U_w(x)L}{\upsilon }$ is the local Reynolds number.

3 Entropy generation

This sector is associated with the influence of the MHD Prandtl fluid with heat transfer on entropy generation. The local volumetric rate of entropy generation is defined as

$\begin{array}{ccc}\hfill S_{\mathit{gen}}^{\prime \prime \prime }& =\hfill & \frac{k}{T_{\infty }^2}\left[{\left(\frac{\partial T}{\partial y}\right)}^2+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}}{\left(\frac{\partial T}{\partial y}\right)}^2\right]+\frac{\sigma B_0^2{u}^2}{T_{\infty }}\hfill \\ \hfill & \hfill & +\frac{\mu }{T_{\infty }}\left[\frac{A}{C}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{A}{6C^3}{\left(\frac{\partial u}{\partial y}\right)}^4\right].\hfill \end{array}(15)$

The aforementioned equation is the combination of three different phenomena. The first is heat transfer, the second is due to the magnetic field, and the third one is due to viscous dissipation of Walter’s B fluid. The characteristic entropy generation rate is defined as

${\dot{S}}_0^{\prime \prime \prime }=\frac{k{\left(\mathrm{\Delta }T\right)}^2}{l^2{T}_{\infty }^2}.(16)$

Thus, the dimensionless form of entropy generation is obtained by taking a ratio of Eqs 21 and 22.

$\begin{array}{ccc}\hfill N_G& =\hfill & \frac{S_{\mathit{gen}}^{\prime \prime \prime }}{{\dot{S}}_0^{\prime \prime \prime }}=\mathrm{R}\mathrm{e}\left[\left(1+R\right){\theta }^{\prime \prime }+R\left({\theta }_f-1\right)\{{\theta }^{\prime \prime }{\theta }^3{\left({\theta }_f-1\right)}^2+3{\theta }^{\prime \prime }{\theta }^2\left({\theta }_f-1\right)+3\theta {\theta }^{\prime \prime }\}\right]+\frac{1}{{\theta }_f^2}\mathrm{R}\mathrm{e}BrM{f}^{\prime 2}\hfill \\ \hfill & \hfill & -\frac{1}{{\theta }_f^2}\mathrm{R}\mathrm{e}Br\left[\alpha f^{\prime \prime 2}+\beta f^{\prime \prime 4}\right],\hfill \end{array}(17)$

where $\mathrm{R}\mathrm{e}=\frac{U_w(x)x}{\upsilon }$, $Br=\frac{\mu {(U_w(x))}^2}{k\mathrm{\Delta }T}$, and ${\theta }_f=\frac{\mathrm{\Delta }T}{T_{\infty }}$.

4 Convergent series solutions

Convergent series solutions depend on the non-zero auxiliary parameters. The convergence of solution is checked by drawing the h-curves for the velocity and temperature distributions. Figures (a and b) show the h-curves of velocity and temperature profiles for fixed values of other physical parameters. The admissible ranges are h_f and h_θ, respectively. It is observed that the solutions converge for the complete region. Table 1 illustrates the convergence of solutions for various orders of approximations. Tabular values elucidate that 15th and 30th order of approximations are enough for the convergence of series solutions of momentum and energy equations, respectively.

TABLE 1

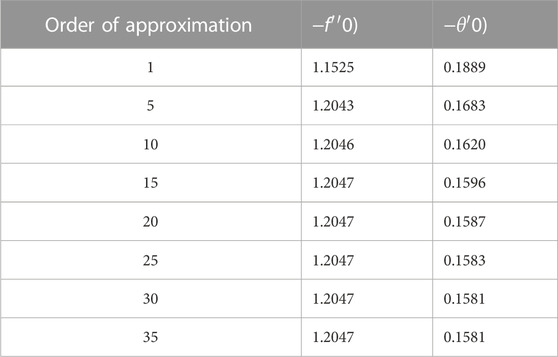
TABLE 1. Homotopic convergence for various orders of approximations when a =0.4, θ_f =1.03, R =0.2, Pr=1.0, Bi =0.3, h_f =−0.9, and h_θ =−1.7.

Figures a and b show the ℏ-curves for velocity and temperature profiles.

5 Results and discussion

To analyze the physical aspects of the considered problem, we discuss the effects of dimensionless parameters α, β, R,θ_f, Bi, and Pr on the velocity f′η) and temperature θ(η) distributions. The influence of Prandtl fluid parameters α and β on the velocity profile is presented in Figures 1, 2. It is inspected that the velocity profile increases for greater α and β. The increment in velocity for larger values of β is smaller when compared with α. The effect of thermal radiation parameter R on the temperature profile is displayed in Figure 3. It represents the increasing behavior of thermal radiation parameters when α = 0.4, β = 0.3, Bi = 0.3, Pr = 1.0, and θ_f = 1.03. There is heat transfer from the flow region to the wall, indicating that the boundary layer thickness increases throughout the region. Physically, the effect of the radiation parameter is to increase the rate of heat transport to the flow region. Figure 4 illustrates the behavior of ratio parameter θ_f on the thermal profile. It is observed that temperature distribution increases for greater values of θ_f. Figure 5 shows the effect of the Biot number on the temperature field. A larger Biot number Bi boosts the temperature profile. Here, a gradual increase in Bi results in the larger convection at the stretching sheet which increases the temperature. This outcome leads to the conclusion that the heat transfer rate at the sheet is enhanced by increasing the velocity of the stretching sheet. Figure 6 depicts the temperature distribution for different values of the Prandtl number. We observe that the fluid temperature decreases with the increase in the value of the Prandtl number Pr. Growth in the Prandtl number decreases the rate of thermal diffusion. Consequently, the boundary layer thickness becomes thinner due to the reduction in thermal conductivity. The Nusselt number characterizes the heat flux from a solid surface to a fluid. Here, we see graphical effects of radiation parameter R, Prandtl number Pr, and Prandtl fluid parameters on the Nusselt number. Figures 7–10 reveal the influences of emerging parameters on the Nusselt number. Figure 7 describes the variation of the Nusselt number. Physically, a larger-Prandtl number fluid has a relatively lower thermal conductivity; thus, an increase in Pr decreases conduction and, thereby, increases the variations of thermal characteristics. This results in the reduction of the thermal boundary layer thickness and an increase in the heat transfer rate at the bounding surface. We can see that the heat transfer rate increases for greater values of α and Pr. Figure 8 depicts that the Nusselt number increases for radiation parameter R. An increase in R enhances the heat flux from the sheet which increases the fluid’s velocity and temperature. Figure 9 depicts that the Nusselt number increases for a larger temperature ratio parameter. Figure 10 shows that the Nusselt number increases with an increase in the Biot number. The values of drag forces are given in Table 2. It shows that the magnitude of drag forces decreases for larger values of Prandtl fluid parameters. Table 3 shows the validation of the method, and we found good agreement with the published work.

FIGURE 1

FIGURE 1. f′(η) versus α.

FIGURE 2

FIGURE 2. f′(η) versus β.

FIGURE 3

FIGURE 3. f′(η) versus R.

FIGURE 4

FIGURE 4. f′(η) versus θ_f.

FIGURE 5

FIGURE 5. θ(η) versus Bi.

FIGURE 6

FIGURE 6. θ(η) versus Pr.

FIGURE 7

FIGURE 7. Nusselt number versus Pr.

FIGURE 8

FIGURE 8. Nusselt number versus R.

FIGURE 9

FIGURE 9. Nusselt number versus θ_f.

FIGURE 10

FIGURE 10. Nusselt number versus Bi.

TABLE 2

TABLE 2. Values of drag forces for various fluid parameters.

TABLE 3

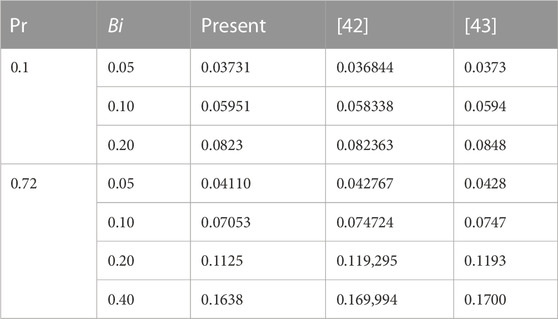
TABLE 3. Comparison of the Nusselt number at the wall for the present results and those of Ishak [42] and Aziz [43] for Pr and Biot number Bi.

Deviation of entropy generation with η is represented in Figure 11 for different values of Eckert’s number. Growth in Eckert’s number leads to a decrease in entropy generation. It is also observed that near-the-surface variation is almost negligible. Figure 12 shows the dual behavior of the radiation parameter: a small increase is displayed near the wall, but far away from the wall, entropy generation increases rapidly. Figures 13,14 exhibit the influence of fluid parameters α and β which boost the entropy generation. The distribution of the magnetic framework on entropy generation is displayed in Figure 15. The magnetic parameter persuades Lorentz force which boosts the entropy generation. The effect of the temperature ratio framework on entropy generation is shown in Figure 16. From this figure, it can be seen that entropy generation decreases when the temperature ratio parameter increases. The effect of the Brickman number is discussed in Figure 17. The Brickman number produces heat transport by viscous heating, which leads to the development in entropy generation. The variation of entropy generation with the Reynolds number is discussed in Figure 18. It is distinguished that entropy generation increases with a larger Reynolds number because a larger Reynolds number corresponds to a larger inertia and smaller viscous force.

FIGURE 11

FIGURE 11. Entropy generation versus Ec.

FIGURE 12

FIGURE 12. Entropy generation versus R.

FIGURE 13

FIGURE 13. Entropy generation versus β.

FIGURE 14

FIGURE 14. Entropy generation versus α.

FIGURE 15

FIGURE 15. Entropy generation versus M.

FIGURE 16

FIGURE 16. Entropy generation versus θ_f.

FIGURE 17

FIGURE 17. Entropy generation versus Br.

FIGURE 18

FIGURE 18. Entropy generation versus Re.

6 Conclusion

Important features of the heat transfer flow of an MHD Prandtl fluid past a stretching are investigated. Important points are mentioned as follows.

■ By increasing α and β, the velocity field increases.

■ Larger values of radiation parameter enhance the temperature distribution.

■ The temperature field decreases by increasing the Prandtl number.

■ Larger Biot number enhances the temperature and thermal boundary thickness.

■ The effect of fluid parameters α and β on the magnitude of the skin friction coefficient is quite the opposite.

■ Entropy generation develops with the magnetic parameter, Reynolds number, curvature parameter, and Brinkman number, while contrary behavior is detected for larger values of the temperature ratio parameter.

■ Nusselt number enhances when R and Bi are enhanced.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Acknowledgments

The author would like to thank Deanship of Scientific Research at Majmaah University for supporting this work under Project Number (R-2023-787).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yin C, Niu J, Fu C, Tan W, Thermal convection of viscoelastic fluid in porous system subjected to horizontal plane Couette flow. Int J Heat Fluid Flow (2013) 44, 711 − 8. doi:10.1016/j.ijheatfluidflow.2013.10.002

CrossRef Full Text | Google Scholar

2. Sheikholeslami M, Ashorynejad HR, Ganji DD, Rashidi MM, Heat and mass transfer of a micropolar fluid in a porous channel. Commun Numer Anal (2014) 2014, 1 − 20. doi:10.5899/2014/CNA-00166

CrossRef Full Text | Google Scholar

3. Turkyilmazoglu M, Three dimensional MHD flow and heat transfer over a stretching/shrinking surface in viscoelastic fluid with various physical effects. Int J Heat Mass Transfer (2014) 78, 150 − 5. doi:10.1016/j.ijheatmasstransfer.2014.06.052

CrossRef Full Text | Google Scholar

4. Fetecau C, Rana M, Nigar N, Fetecau C, First exact solutions for flows of rate type fluids in a circular duct that applies a constant couple to the fluid. Z Naturforschung Section A J Phys Sci (2014) 69, 232 − 8. doi:10.5560/zna.2014-0022

CrossRef Full Text | Google Scholar

5. Han S, Zheng L, Li C, Zhang X. Coupled flow and heat transfer in viscoelastic fluid with Cattaneo-Christov heat flux model. Appllied Maths Lett (2014) 38:87–93. doi:10.1016/j.aml.2014.07.013

CrossRef Full Text | Google Scholar

6. Sui J, Zheng L, Zheng X, Chen G, Mixed convection heat transfer in power law fluids over a moving conveyor along an inclined plate. Int J Heat Mass Transfer (2015) 85, 1023 − 33. doi:10.1016/j.ijheatmasstransfer.2015.02.014

CrossRef Full Text | Google Scholar

7. Hayat T, Sad S, Mustafa M, Alsaedi A, MHD stagnation point flow of Jeffrey fluid over convectively heated stretching sheet. Comput Fluids (2015) 108, 179 − 85. doi:10.1016/j.compfluid.2014.11.016

CrossRef Full Text | Google Scholar

8. Ishak A. Similarity solutions for flow and heat transfer over a permeable stretching surface with convective boundary condition. Appllied Maths Compution (2010) 217:837–42. doi:10.1016/j.amc.2010.06.026

CrossRef Full Text | Google Scholar

9. Bachok N, Ishak A, Pop I, Stagnation point flow toward a stretching/shrinking sheet with a convective surface boundary condition. J Franklin Inst (2013) 350, 2736 − 44. doi:10.1016/j.jfranklin.2013.07.002

CrossRef Full Text | Google Scholar

10. Patil PM, Omoniat E, Roy S, Influence of convective boundary condition on double diffusive mixed convection flow from a permeable vertical surface. Int J Heat Mass Transfer (2014) 70, 313 − 21. doi:10.1016/j.ijheatmasstransfer.2013.11.021

CrossRef Full Text | Google Scholar

11. Mustafa M, Khan JA, Hayat T, Alsaedi A. Sakiadis flow of Maxwell fluid considering magnetic field and convective boundary conditions. AIP Adv (2015) 5. doi:10.1063/1.4907927.027106

CrossRef Full Text | Google Scholar

12. Cortell R, Fluid flow and radiative nonlinear heat transfer over stretching sheet. J King Saud University-Science (2013) 26, 161 − 7. doi:10.1016/j.ijheatmasstransfer.2013.11.021

CrossRef Full Text | Google Scholar

13. Mushtaq A, Mustafa M, Hayat T, Alsaedi A. Nonlinear radiative heat transfer in the flow of nanofluid due to solar energy: a numerical study. J Taiwan Inst Chem. Eng (2014) 45:1176–83. doi:10.1016/j.jtice.2013.11.008.1176-1183

CrossRef Full Text | Google Scholar

14. Shehzad SA, Hayat T, Alsaedi A, Obid MA, Nonlinear thermal radiation in three-dimensional flow of Jeffrey nanofluid: a model for solar energy. Appllied Maths Compution (2014) 248. 273 − 86. doi:10.1016/j.amc.2014.09.091(2014)

CrossRef Full Text | Google Scholar

15. Cortell R. MHD (magneto-hydrodynamic) flow and radiative nonlinear heat transfer of a viscoelastic fluid over a stretching sheet with heat generation/absorption. Energy (2014) 74:896–905. doi:10.1016/j.energy.2014.07.069.896-905

CrossRef Full Text | Google Scholar

16. Hayat T, Muhammad T, Alsaedi A, Alhuthali MS, Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. J Magnetism Magn Mater (2015) 385, 222 − 9. doi:10.1016/j.jmmm.2015.02.046(2015)

CrossRef Full Text | Google Scholar

17. Lin Y, Zheng L, Zhang X. Radiation effects on Marangoni convection flow and heat transfer in pseudo-plastic non-Newtonian nanofluids with variable thermal conductivity. Int J Heat Mass Transfer (2014) 77:708–16. doi:10.1016/j.ijheatmasstransfer.2014.06.028

CrossRef Full Text | Google Scholar

18. Rashidi MM, Ganesh NV, Hakeem AKA, Ganga B. Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J Mol Liquids (2014) 198:234–8. doi:10.1016/j.molliq.2014.06.037

CrossRef Full Text | Google Scholar

19. Das K, Duari PR, Kundu PK. Nanofluid flow over an unsteady stretching surface in presence of thermal radiation. Alexandria Eng J (2014) 53:737–45. doi:10.1016/j.aej.2014.05.002

CrossRef Full Text | Google Scholar

20. Turkyilmazoglu M. Thermal radiation effects on the time-dependent MHD permeable flow having variable viscosity. Int J Therm Sci (2011) 50:88–96. doi:10.1016/j.ijthermalsci.2010.08.016

CrossRef Full Text | Google Scholar

21. Olajuwon BI. Convection heat and mass transfer in a hydromagnetic flow of a second grade fluid in the presence of thermal radiation and thermal diffusion. Int Commun Heat Mass Transfer (2011) 38:377–82. doi:10.1016/j.icheatmasstransfer.2010.11.006

CrossRef Full Text | Google Scholar

22. Bhattacharyya K, Mukhopadhyay S, Layek GC, Pop I. Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int J Heat Mass Transfer (2012) 55:2945–52. doi:10.1016/j.ijheatmasstransfer.2012.01.051

CrossRef Full Text | Google Scholar

23. Hayat T, Khan MWA, Khan MI, Alsaedi A. Nonlinear radiative heat flux and heat source/sink on entropy generation minimization rate. Phys B: Condensed Matter (2018) 538:95–103. doi:10.1016/j.physb.2018.01.054

CrossRef Full Text | Google Scholar

24. Khan MI, Hayat T, Khan MI, Waqas M, Alsaedi A. Numerical simulation of hydromagnetic mixed convective radiative slip flow with variable fluid properties: a mathematical model for entropy generation. J Phys Chem Sol (2019) 125:153–64. doi:10.1016/j.jpcs.2018.10.015

CrossRef Full Text | Google Scholar

25. Almakki M, Mondal H, Sibanda P. Entropy generation in magneto nanofluid flow with Joule heating and thermal radiation. World J Eng (2020) 17:1–11. doi:10.1108/wje-06-2019-0166

CrossRef Full Text | Google Scholar

26. Devi SPA, Kumar PS. Effect of magnetic field on Blasius and Sakiadis flow of nanofluids past on inclined plate. J Taibah Univ Sci (2017) 11:1275–88. doi:10.1016/j.jtusci.2017.03.004

CrossRef Full Text | Google Scholar

27. Disu AB, Dada MS. Rynolds model viscosity of radiative MHD flow in porous medium between two vertical wavy walls. J Taibah Univ Sci (2017) 11:548–65. doi:10.1016/j.jtusci.2015.12.001

CrossRef Full Text | Google Scholar

28. Ganga B, Ansari SMY, Ganesh NV, Hakeem AKA. Hydromagnetic flow and radiative heat transfer of nanofluid past a vertical plate. J Taibah Univ Sci (2017) 11:1200–13. doi:10.1016/j.jtusci.2015.12.005

CrossRef Full Text | Google Scholar

29. Waqas M, Shehzad SA, Hayat T, Ijaz Khan M, Alsaedi A. Simulation of magnetohydrodynamics and radiative heat transport in convectively heated stratified flow of Jeffrey nanofluid. J Phys Chem Sol (2019) 133:45–51. doi:10.1016/j.jpcs.2019.03.031

CrossRef Full Text | Google Scholar

30. Waqas M, Khan M, Farooq M, Alsaedi A, Hayat T, Yasmeen T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretching sheet with convective condition. Int J Heat Mass Transfer (2016) 102:766–72. doi:10.1016/j.ijheatmasstransfer.2016.05.142

CrossRef Full Text | Google Scholar

31. Asad S. Radiative analysis of entropy generation on MHD Walters-B fluid with heat and mass transfer. Int J Bulgarian Chem Commun (2021) 53:343–54. doi:10.34049/bcc.53.3.5390.343

CrossRef Full Text | Google Scholar

32. Alharbi SO, Khan U, Zaib A, Ishak A, Raizah Z, Ishak S, et al. Heat transfer analysis of buoyancy opposing radiated flow of alumina nanoparticles scattered in water-based fluid past a vertical cylinder. Scientific Rep (2023) 13:10725. doi:10.1038/s41598-023-37973-6

CrossRef Full Text | Google Scholar

33. Khan U, Zaib A, Ishak A, ElSHERIF SM, Sarris IE, Eldin SM, et al. Analysis of assisting and opposing flows of the Eyring-Powell fluid on the wall jet nanoparticles with significant impacts of irregular heat source/sink. Case Stud Therm Eng (2023) 49:103209. doi:10.1016/j.csite.2023.103209

CrossRef Full Text | Google Scholar

34. Khan U, Zaib A, Madhukesh JK, Elattar S, Eldin SM, Ishak A, et al. Features of radiative mixed convective heat transfer on the slip flow of nanofluid past a stretching bended sheet with activation energy and binary reaction. Energies (2022) 15:7613. doi:10.3390/en15207613

CrossRef Full Text | Google Scholar

35. Khan U, Zaib A, Ishak A, Eldin SM, Alotaibi AM, Raizah Z, et al. Features of hybridized AA7072 and AA7075 alloys nanomaterials with melting heat transfer past a movable cylinder with Thompson and Troian slip effect. Arabian J Chem (2023) 16:104503. doi:10.1016/j.arabjc.2022.104503

CrossRef Full Text | Google Scholar

36. Roy NC, Pop I. Dual solutions of a nanofluid flow past a convectively heated nonlinearly shrinking sheet. Chin J Phys (2023) 82:31–40. doi:10.1016/j.cjph.2022.12.008

CrossRef Full Text | Google Scholar

37. Roy NC, Pop I. Dual solutions of magnetohydrodynamic mixed convection flow of an Oldroyd-B nanofluid over a shrinking sheet with heat source/sink. Alexandria Eng J (2022) 61:5939–48. doi:10.1016/j.aej.2021.11.021

CrossRef Full Text | Google Scholar

38. Roy NC, Hossain A, Pop I. Flow and heat transfer of MHD dusty hybrid nanofluids over a shrinking sheet. Chin J Phys (2022) 77:1342–56. doi:10.1016/j.cjph.2021.12.012

CrossRef Full Text | Google Scholar

39. Roy NC, Pop I. Exact solutions of Stokes’ second problem for hybrid nanofluid flow with a heat source. Phys Fluids (2021) 33:063603. doi:10.1063/5.0054576

CrossRef Full Text | Google Scholar

40. Roy NC, Pop I. Unsteady magnetohydrodynamic stagnation point flow of a nanofluid past a permeable shrinking sheet. Chin J Phys (2022) 75:109–19. doi:10.1016/j.cjph.2021.12.018

CrossRef Full Text | Google Scholar

41. Roy NC, Pop I. Heat and mass transfer of a hybrid nanofluid flow with binary chemical reaction over a permeable shrinking surface. Chin J Phys (2022) 76:283–98. doi:10.1016/j.cjph.2021.10.041

CrossRef Full Text | Google Scholar

42. Ishak A. Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Appl Maths Comput (2010) 217:837–42. doi:10.1016/j.amc.2010.06.026

CrossRef Full Text | Google Scholar

43. Aziz A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Commun Nonlinearsci Numer Simul (2009) 14:1064–8. doi:10.1016/j.cnsns.2008.05.003

CrossRef Full Text | Google Scholar

Nomenclature