Lie symmetry and exact homotopic solutions of a non-linear double-diffusion problem

The Lie symmetry method is applied, and exact homotopic solutions of a non-linear double-diffusion problem are obtained. Additionally, we derived Lie point symmetries and corresponding transformations for equations representing heat and mass transfer in a thin liquid film over an unsteady stretching surface, using MAPLE. We used these symmetries to construct new (Lie) similarity transformations that are different from those that are commonly used for flow and mass transfer problems. These new (Lie) similarity transformations map the partial differential equations of a mathematical model under consideration to ordinary differential equations along with boundary conditions. Lie similarity transformations are shown to lead to new solutions for the considered flow problem. These solutions are obtained using the homotopy analysis method to analytically solve the ordinary differential equations that resulted from the reduction of considered flow equations through Lie similarity transformations. With the aid of these solutions, effects of various parameters on the flow and heat transfer are discussed and presented graphically in this study.

1 Introduction

Fluid flow and heat transfer phenomena have a wide range of applications in engineering. By varying these transporters and enforcing various physical conditions, it is possible to produce a variety of industrial products at their best. As a result, it has drawn a significant amount of attention during the past several decades. The Navier–Stokes equations are used to quantitatively represent these heat and flow exchanges, with the appropriate circumstances. These are extremely non-linear partial differential equations (PDEs) of order two or higher. Such non-linearities lessen the likelihood of obtaining precise results. As a result, flow studies are related to approximation techniques and analytical solution schemes, and heat transfer techniques are frequently used.

The Runge–Kutta and shot method are combined for the derivation of the former type of solutions, whereas homotopy analysis and perturbation techniques are frequently used for the latter.

These problem-solving methods are not directly related to the PDEs that describe the flow problems. The system of ordinary differential equations (ODEs) relating to these flow issues is, nevertheless, solved using these methods. The similarity transformation is the technology that makes this kind of reduction possible. The dependent and/or independent variables of flow equations are reduced using these adjustments.

First, the fact that there are more established and diverse solution methods for ODEs than PDEs accounts for this reduction. Second, running ODEs through mathematical symbolic and numeric software requires less time and equipment compared to other approaches. Following the reduction of flow equations to ODEs via similarity transformations, one finds several applications of such solution algorithms in the literature.

With this procedure, the flow and heat transfers have been studied under different sets of conditions, for example, in a liquid film on an unsteady stretching surface [1, 2], under the effects of variable fluid properties and thermo capillarity [3], with Soret and Dufour effects on a viscoelastic fluid in three dimensions [4], in a rotating channel three-dimensional squeezing flow [5], in a three-dimensional flow of a nanofluid over a non-linearly stretching sheet [6], and for an Oldroyd-B nanofluid thin film over an unsteady stretching sheet [7]. Likewise, magnetohydrodynamic (MHD) flow and heat transfer have been studied for the following: thermosolutal Marangoni convection with heat generation [8], viscoelastic fluid flow over a vertical stretching sheet under the effects of Soret and Dufour [9], Jeffrey fluid over a stretching sheet considering the chemical reaction and thermal radiation [10], three-dimensional flow of an Oldroyd-B nanofluid on a radiative surface [11], thermally radiative flow in three dimensions of a Jeffrey nanofluid under internal heat generation [12], a shrinking sheet with thermal slip [13], a vertical stretching sheet under the effects of heat sink or source [14], mixed convection on the inclined stretching plate in the Darcy porous medium with a Soret effect considering variable surface conditions [15], and mixed convective flow of a Maxwell nanofluid past a porous vertical stretching sheet with a chemical reaction [16].

There are countless studies through an area of research known as the Lie symmetry method, which helps to accurately derive the analytical or approximate solutions for flow and heat transfer equations. For instance, Lie group theory has been employed to study the flow and heat transfer in a non-Newtonian fluid over a stretching surface with thermal radiation [17], MHD boundary layer flow over a stretching sheet with viscous dissipation and uniform heat source/sink [18], MHD mixed flow of unsteady convection on a vertical porous plate with radiation [19], MHD double-diffusion convection of a Casson nanofluid on a vertical stretching/shrinking surface under the effects of thermal radiation and chemical reaction [20], heat flux effect on MHD second slip flow past a stretching sheet along with heat generation [21], MHD Casson fluid flow near a stagnation point on a linearly stretching sheet taking variable viscosity and thermal conductivity into account [22], thermophysical properties of a magnetized Williamson fluid subject to porous/non-porous surfaces [23], two-parameter Lie scaling approach on an unsteady MHD Casson fluid over a porous rigid plate with a stagnation point flow [24], double-diffusive MHD tangent hyperbolic fluid flow on a stretching sheet [25], MHD thermally slip Carreau fluid subject to multiple flow regimes [26], and for a liquid film on an unsteady stretching sheet using Lie point symmetries [27].

The governing equations in the aforementioned flow models are non-linear. Therefore, numerous approaches are adopted to deal with the non-linearity of the governing equations. The Lie symmetry method is one of those that provide a systematic procedure to construct similarity transformation that is a pivotal component of solution schemes employed on fluid flows mentioned previously. Non-linear phenomena impose constraints on the studies conducted to analyze physical models appearing in numerous applications due to the availability of few techniques that are employed to deal with it. As far as the Lie approach is concerned, one may linearize the governing equations (28)–(31). There are many non-Lie procedures that are also available in the literature, for example, effective treatments of the non-linearity of differential equations have been reported in [32–34].

A Lie point symmetry transformation can be associated with a differential or an algebraic equation if it leaves it form invariant. It implies that a heat equation remains a heat equation after mapping it under its Lie point transformation. Every Lie point transformation possesses a Lie symmetry generator. For basic theory and the algebraic computations of the Lie symmetry generators and transformation, readers are referred to [35, 36]. MAPLE contains all these procedures to build symmetry transformations in the “PDEtools” package, which, on applying “Infinitesimals” on differential equations, reveals their symmetries. MAPLE is used to find out symmetry generators and corresponding transformations for flow problems that are being taken into consideration in this study.

We deduce Lie point symmetries for the momentum, energy, and concentration equations representing the flow problem under consideration. There exist nine Lie symmetries, and by using them, Lie similarity transformations are obtained. However, we employ only those symmetries which leave the associated boundary conditions in a particular form. Based on these constraints, we consider three linear combinations (that are also Lie point symmetries) of the derived Lie symmetries. In one of these, we combine two symmetries, while the remaining two consist of three symmetries. These three combinations provided a different type of similarity transformation which transformed flow equations into three different types of ODE systems. Arbitrary constants are used in the linear combinations of the Lie point symmetries, and these constants also appear in the resulting system of ODEs due to their presence in the Lie similarity transformations we construct. We use them to control the convergence of solutions of the flow model we are considering.

The outline of the paper is as follows. The second section is about flow equations and their Lie symmetries. The subsequent section is on similarity transformations and mapping of flow PDEs to ODEs. In the fourth section, analytical solutions are constructed and presented with graphs and tables. The last section is the conclusion.

2 Flow equations

The flow of heat and mass in a thin liquid film has been studied [37] on an unsteady stretching surface with thermosolutal capillarity and variable magnetic field. Here, we are considering the flow model without the magnetic field and thermosolutal capillarity. The governing equations for the flow of heat and mass transfer in a thin liquid film over an unsteady surface are given by the following system of PDEs:

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}-\nu \frac{{\partial }^{2}u}{\partial y^2}=0,(1)$

$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}-\kappa \frac{{\partial }^{2}T}{\partial y^2}=0,$

$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}-D\frac{{\partial }^{2}C}{\partial y^2}=0,$

subject to boundary conditions as follows:

$u\left(t,x,y\right)=U_s\left(t,x\right),v\left(t,x,y\right)=0,T\left(t,x,y\right)=T_s\left(t,x\right),C\left(t,x,y\right)=C_s\left(t,x\right),\mathrm{a}\mathrm{t}y=0,$

$\frac{\partial u\left(t,x,y\right)}{\partial y}=0,\frac{\partial T\left(t,x,y\right)}{\partial y}=0,\frac{\partial C\left(t,x,y\right)}{\partial y}=0,v\left(t,x,y\right)=\frac{dh}{dt},\mathrm{a}\mathrm{t}y=h\left(t\right).(2)$

The Lie point symmetries of the flow mathematical model (Eq. 1) are derived by using the MAPLE “PDEtools” package and the built-in command “Infinitesimals.”

${\mathrm{X}}_1=\frac{\partial }{\partial t},{\mathrm{X}}_2=\frac{\partial }{\partial x},{\mathrm{X}}_3=\frac{\partial }{\partial T},{\mathrm{X}}_4=\frac{\partial }{\partial C},{\mathrm{X}}_5=t\frac{\partial }{\partial x}+\frac{\partial }{\partial u},{\mathrm{X}}_6=T\frac{\partial }{\partial T},{\mathrm{X}}_7=C\frac{\partial }{\partial C},{\mathrm{X}}_8=x\frac{\partial }{\partial x}+u\frac{\partial }{\partial u},{\mathrm{X}}_9=t\frac{\partial }{\partial t}+\frac{y}{2}\frac{\partial }{\partial y}-u\frac{\partial }{\partial u}-\frac{v}{2}\frac{\partial }{\partial v}.(3)$

However, for a detailed algebraic procedure to obtain symmetries of system (Eq. 1), the reader is referred to [27]. The Lie symmetry transformations corresponding to symmetry generators (Eq. 3) leave equations of system (Eq. 1) form invariant. These Lie transformations are given in Table 1. Furthermore, all the associated conditions (Eq. 2) should also remain invariant. For this purpose, we employ each

$X_m^{\left[l\right]}{\left.\left({\zeta }_n\right)\right|}_{{\zeta }_n=0}=0,(4)$

where $l$ denotes the extension of the symmetry generator; here, we require the first extension of $X_m$, for m $=\mathrm{1,2},\dots ,9$, and ${\zeta }_n$ denotes the conditions (Eq. 2) for $n=\mathrm{1,2},\dots ,8$, e.g., ${\zeta }_1≔u\left(t,x,0\right)=U_s\left(t,x\right)$, and vice versa.

TABLE 1

Table 1. Lie symmetry generators and transformations.

3 Lie similarity transformations of flow equations

We construct the Lie similarity transformations corresponding to a few linear combinations for the derived Lie point symmetries ${\mathbf{X}}_1,{\mathbf{X}}_2,...,{\mathbf{X}}_9$. These combinations are based on the unknown functions they determine for $U_s\left(t,x\right)$, $T_s\left(t,x\right)$, $C_s\left(t,x\right)$, and $h\left(t\right)$. In this work, only those cases are of interest in which all these functions remain dependent on their arguments. Hence, we consider the combination ${k_1\mathbf{X}}_8+{k_2\mathbf{X}}_9$ of Lie symmetries in Case-I, ${k_1\mathbf{X}}_6+{k_2\mathbf{X}}_7+{k_3\mathbf{X}}_8$ in Case-II, and ${k_1\mathbf{X}}_6+{k_2\mathbf{X}}_7+{k_3\mathbf{X}}_9$ in Case-III, where ${\mathrm{k}}_1$, ${\mathrm{k}}_2$, and ${\mathrm{k}}_3$ are any non-zero real numbers. All other symmetries from the list (Eq. 3) are not suitable in any form to construct the similarity transformations due to stretching sheet velocity and temperature obtained for these symmetries and their combinations. Hence, we consider only those linear combinations that are mentioned previously. These three linear combinations of symmetries leave both $x$ and $t$ in the stretching sheet velocity $U_s=U_s\left(t,x\right)$ and temperature $T_s=T_s\left(t,x\right)$; i.e., we want to keep them as functions of time $t$ and space variable $x$. Moreover, $h\left(t\right)$ is also left as a function of $t$.

In the study conducted earlier on this type of fluid and heat transports [38], both the said quantities are set to be dependent on both $t$ and $x$.

3.1 Case-I: Similarity transformations for ${k_1\mathbf{X}}_8+{k_2\mathbf{X}}_9$

These symmetry generators provided the similarity transformations

$y=\beta \sqrt{\frac{\alpha \nu t}{b}}\eta ,u=-\frac{bx}{\alpha t}\frac{df}{d\eta },v=\beta \sqrt{\frac{b\nu }{\alpha t}}f\left(\eta \right),T=x{t}^{\frac{-k_1}{k_2}}\theta \left(\eta \right)-1,C=x{t}^{\frac{-k_1}{k_2}}\varphi \left(\eta \right)-1(5)$

which map the system of PDEs (Eq. 1) into the following system of ODEs:

$\frac{d^{3}f}{d{\eta }^3}+{\beta }^2\left(S\frac{df}{d\eta }+\frac{S\eta }{2}\frac{d^{2}f}{d{\eta }^2}+{\left(\frac{df}{d\eta }\right)}^2-f\left(\eta \right)\frac{d^{2}f}{d{\eta }^2}\right)=0,$

$\frac{1}{P_r}\frac{d^2\theta }{d{\eta }^2}+{\beta }^2\left(\frac{df}{d\eta }\theta \left(\eta \right)-f\left(\eta \right)\frac{d\theta }{d\eta }+\frac{S\eta }{2}\frac{d\theta }{d\eta }+\frac{k_1}{k_2}S\theta \left(\eta \right)\right)=0,(6)$

$\frac{1}{S_c}\frac{d^2\varphi }{d{\eta }^2}+{\beta }^2\left(\frac{df}{d\eta }\varphi \left(\eta \right)-f\left(\eta \right)\frac{d\varphi }{d\eta }+\frac{S\eta }{2}\frac{d\varphi }{d\eta }+\frac{k_1}{k_2}S\varphi \left(\eta \right)\right)=0,$

where $\eta$ is the new independent variable. The associated boundary conditions are

$f\left(0\right)=0,\theta \left(0\right)=\varphi \left(0\right)=1,\frac{df\left(0\right)}{d\eta }=1,f\left(1\right)=\frac{S}{2},$

$\frac{d^{2}f\left(1\right)}{d{\eta }^2}=\frac{d\theta \left(1\right)}{d\eta }=0,\frac{d\varphi \left(1\right)}{d\eta }=0.(7)$

3.2 Case-II: Similarity transformations for ${k_1\mathbf{X}}_6+{k_2\mathbf{X}}_7+{k_3\mathbf{X}}_8$

In this case, the following similarity transformations are obtained:

$y=\beta \sqrt{\frac{\alpha \nu \left(1+t\right)}{b}}\eta ,u=-\frac{bx}{\alpha \left(1+t\right)}\frac{df}{d\eta },v=\beta \sqrt{\frac{b\nu }{\alpha \left(1+t\right)}}f\left(\eta \right),T=\left(1+t\right)x^{\frac{k_1}{k_3}}\theta \left(\eta \right),C=\left(1+t\right)x^{\frac{k_2}{k_3}}\varphi \left(\eta \right).(8)$

These similarity transformations map the system of PDEs (Eq. 1) into the following system of ODEs:

$\frac{d^{3}f}{d{\eta }^3}+{\beta }^2\left(S\frac{df}{d\eta }+\frac{S\eta }{2}\frac{d^{2}f}{d{\eta }^2}+{\left(\frac{df}{d\eta }\right)}^2-f\left(\eta \right)\frac{d^{2}f}{d{\eta }^2}\right)=0,$

$\frac{1}{P_r}\frac{d^2\theta }{d{\eta }^2}+{\beta }^2\left(\frac{k_1}{k_3}\frac{df}{d\eta }\theta \left(\eta \right)-f\left(\eta \right)\frac{d\theta }{d\eta }+\frac{S\eta }{2}\frac{d\theta }{d\eta }-S\theta \left(\eta \right)\right)=0,(9)$

$\frac{1}{S_c}\frac{d^2\varphi }{d{\eta }^2}+{\beta }^2\left(\frac{k_2}{k_3}\frac{df}{d\eta }\varphi \left(\eta \right)-f\left(\eta \right)\frac{d\varphi }{d\eta }+\frac{S\eta }{2}\frac{d\varphi }{d\eta }-S\varphi \left(\eta \right)\right)=0,$

and the associated boundary conditions are given as follows:

$f\left(0\right)=0,\frac{df\left(0\right)}{d\eta }=\theta \left(0\right)=\varphi \left(0\right)=1,f\left(1\right)=\frac{S}{2},\frac{d^{2}f\left(1\right)}{d{\eta }^2}=\frac{d\theta \left(1\right)}{d\eta }=\frac{d\varphi \left(1\right)}{d\eta }=0.(10)$

3.3 Case-III: Similarity transformations for ${k_1\mathbf{X}}_6+{k_2\mathbf{X}}_7+{k_3\mathbf{X}}_9$

Here, we obtain the following similarity transformations:

$y=\beta \sqrt{\frac{\alpha \nu t}{b}}\eta ,u=-\frac{b\left(1+x\right)}{\alpha t}\frac{df}{d\eta },v=\beta \sqrt{\frac{b\nu }{\alpha t}}f\left(\eta \right),$

$T=\left(1+x\right)t^{\frac{k_1}{k_3}}\theta \left(\eta \right),C=\left(1+x\right)t^{\frac{k_2}{k_3}}\varphi \left(\eta \right).(11)$

These similarity transformations map the system of PDEs (Eq. 1) into the following system of ODEs:

$\frac{d^{3}f}{d{\eta }^3}+{\beta }^2\left(S\frac{df}{d\eta }+\frac{S\eta }{2}\frac{d^{2}f}{d{\eta }^2}+{\left(\frac{df}{d\eta }\right)}^2-f\left(\eta \right)\frac{d^{2}f}{d{\eta }^2}\right)=0,$

$\frac{1}{P_r}\frac{d^2\theta }{d{\eta }^2}+{\beta }^2\left(\frac{df}{d\eta }\theta \left(\eta \right)-f\left(\eta \right)\frac{d\theta }{d\eta }+\frac{S\eta }{2}\frac{d\theta }{d\eta }-\frac{k_1}{k_3}S\theta \left(\eta \right)\right)=0,(12)$

$\frac{1}{S_c}\frac{d^2\varphi }{d{\eta }^2}+{\beta }^2\left(\frac{df}{d\eta }\varphi \left(\eta \right)-f\left(\eta \right)\frac{d\varphi }{d\eta }+\frac{S\eta }{2}\frac{d\varphi }{d\eta }-\frac{k_2}{k_3}S\varphi \left(\eta \right)\right)=0.$

The associated boundary conditions map to

$f\left(0\right)=0,\frac{df\left(0\right)}{d\eta }=\theta \left(0\right)=\varphi \left(0\right)=1,f\left(1\right)=\frac{S}{2},\frac{d^{2}f\left(1\right)}{d{\eta }^2}=\frac{d\theta \left(1\right)}{d\eta }=\frac{d\varphi \left(1\right)}{d\eta }=0.(13)$

4 Analytic solution by the homotopy analysis method

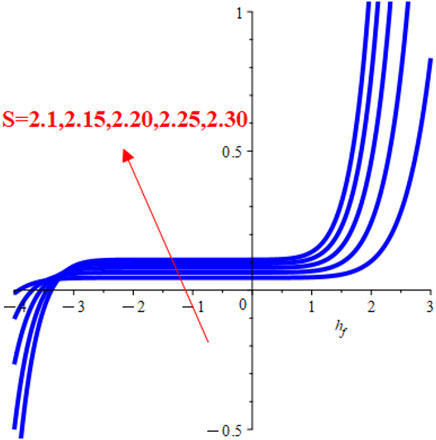
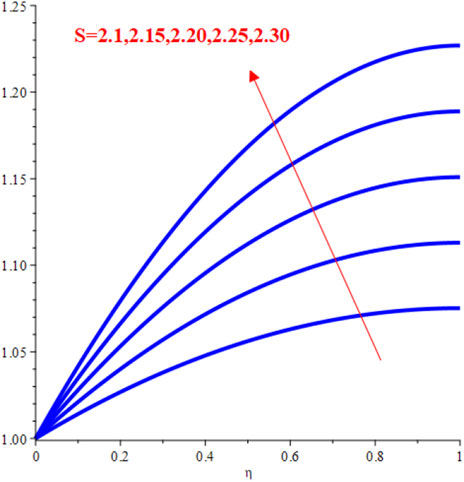
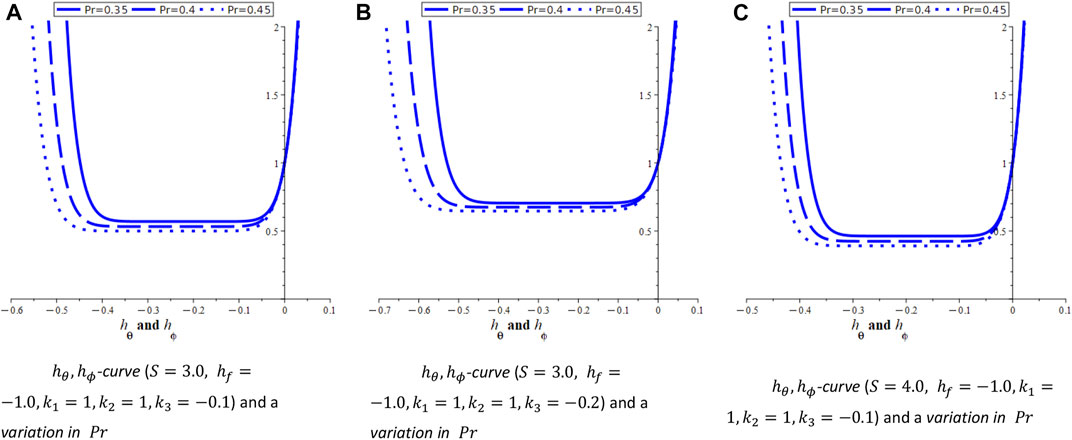
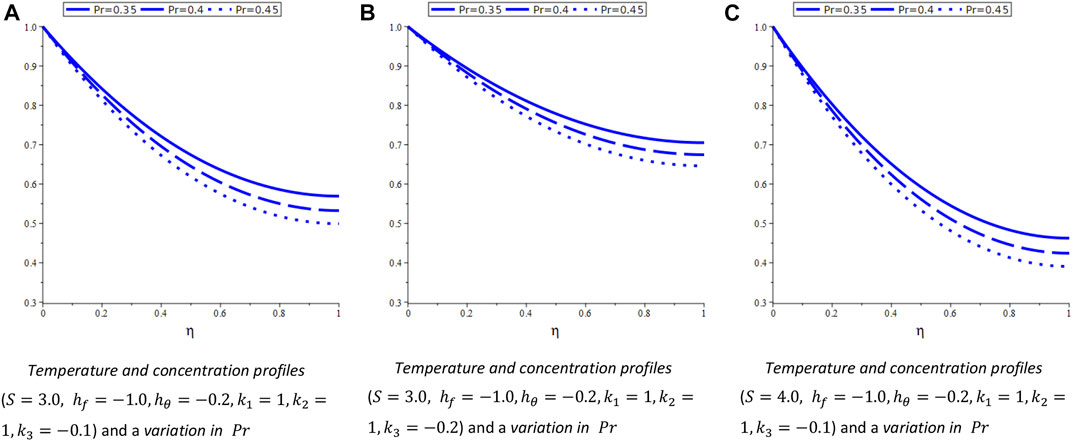
In this section, the velocity and temperature profiles are constructed with the aid of the analytical solution of order ten derived through the HAM. It has been observed that the first equation in all three cases that are under consideration here is the same. First, we draw $h_f$-curves that are presented graphically for $2.10<S<2.30$ in Figure 1. The reason to consider this range is the dimensionless film thickness which remains negative or zero for $S\le 2.0$. Hence, all the velocity, temperature, and concentration profiles are presented here for $S>2.0$. The dimensionless film thickness increases with an increase in $S$, under the conditions provided by Lie similarity conditions. This situation changes and opposite trends have been found in [39] using Lie similarity transformations with an introduction of a magnetic term. Figure 2 shows the velocity profiles for the same range of an unsteadiness parameter, which shows an increase in the velocity with this parameter. The temperature and concentration profiles are expected to be different in all three cases as, apparently, the second and third equations in the systems of ODEs (Eq. 6), (Eq. 9), and (Eq. 12) are different. Hence, they are written separately in the following cases to present the trends that are followed by these quantities under the influence of $S$, $P_r$, and $S_c$. Moreover, the constants $k_1$, $k_2$, and $k_3$ that are used in forming the linear combinations of the Lie symmetry generators (Eq. 3) also affect the temperature and concentration profiles. These are all present in the second and third equations of the systems in Case (3.1)–(3.3).

FIGURE 1

FIGURE 1. $h_f$-curves ($S=2.10-2.30)$.

FIGURE 2

FIGURE 2. Velocity profiles ($S=2.10-2.30)$.

4.1 Velocity and concentration profiles for Case-I

For system (Eq. 6), we draw the $h_{\theta }$-curves in Figures 3A–C, for $S=2.5,h_f=-1.0,k_2=1$ and for three different values of $P_r=0.25,0.35,0.45$. The $h_{\theta }$-curves show a decline for $k_1<0.$ From these curves, we select a value for $h_{\theta }=-0.003$ to construct the temperature profiles in Figures 4A–C, which also exhibit a decreasing trend with a decrease in the values of $k_1.$ Likewise, we draw $h_{\varphi }-$ curves in Figures 5A–C for $S=3.5,h_f=-1.0,k_2=1$ and for multiple values of $k_1$. These figures show a decrease in the $h_{\varphi }-$ curves with a decrease in $k_1$ and an increase in ${\mathrm{P}}_r=0.025,0.035,0.045$. The concentration profiles behave in a similar manner as $h_{\varphi }-$ curves. Here, we present these profiles for $S=3.5,h_f=-1.0,h_{\varphi }=-0.025,k_2=1$ and a variation in $k_1$ and ${\mathrm{S}}_c=0.025,0.035,0.045.$ The temperature and concentration profiles follow the same trends as system (Eq. 6) equations for both are the same; however, we are presenting them here separately. In both the mentioned set of figures, we considered different values of the unsteadiness parameter $S$. It can be observed from these figures that the unsteadiness parameter and concentration are inversely proportional, i.e., $S\propto \frac{1}{T}$.

FIGURE 3

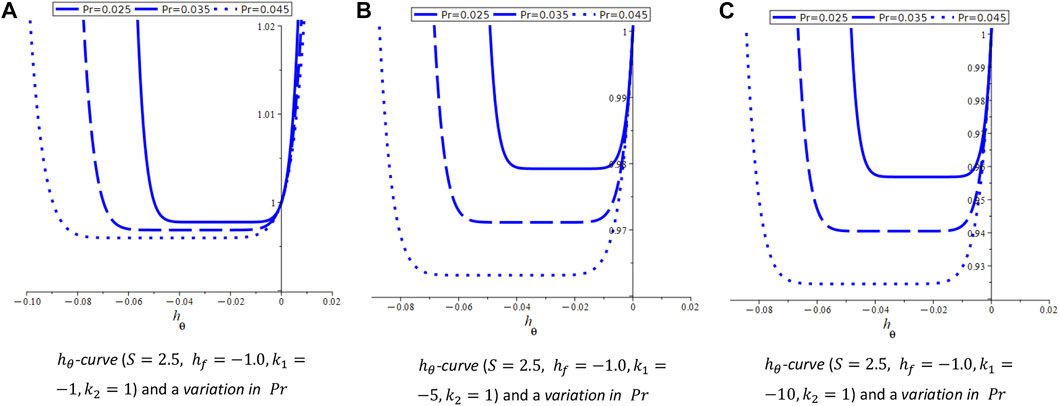
FIGURE 3. Different h-curves. (A) $h_{\theta }$-curve ($S=2.5,h_f=-1.0,k_1=-1,k_2=1$) and a variation in $\mathit{Pr}$. (B) $h_{\theta }$-curve ($S=2.5,h_f=-1.0,k_1=-5,k_2=1$) and a variation in $\mathit{Pr}$. (C) $h_{\theta }$-curve ($S=2.5,h_f=-1.0,k_1=-10,k_2=1$) and a variation in $\mathit{Pr}$.

FIGURE 4

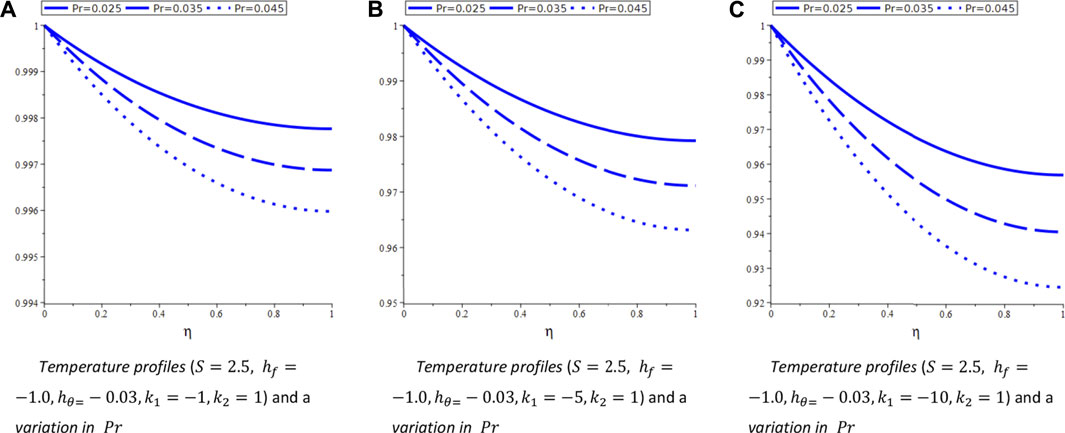
FIGURE 4. Different temperature profiles. (A) Temperature profiles ($S=2.5,h_f=-1.0,h_{\theta =}-0.03,k_1=-1,k_2=1$) and a variation in $\mathit{Pr}$. (B) Temperature profiles ($S=2.5,h_f=-1.0,h_{\theta =}-0.03,k_1=-5,k_2=1$) and a variation in $\mathit{Pr}$. (C) Temperature profiles ($S=2.5,h_f=-1.0,h_{\theta =}-0.03,k_1=-10,k_2=1$) and a variation in $\mathit{Pr}$.

FIGURE 5

FIGURE 5. Different h-curves.

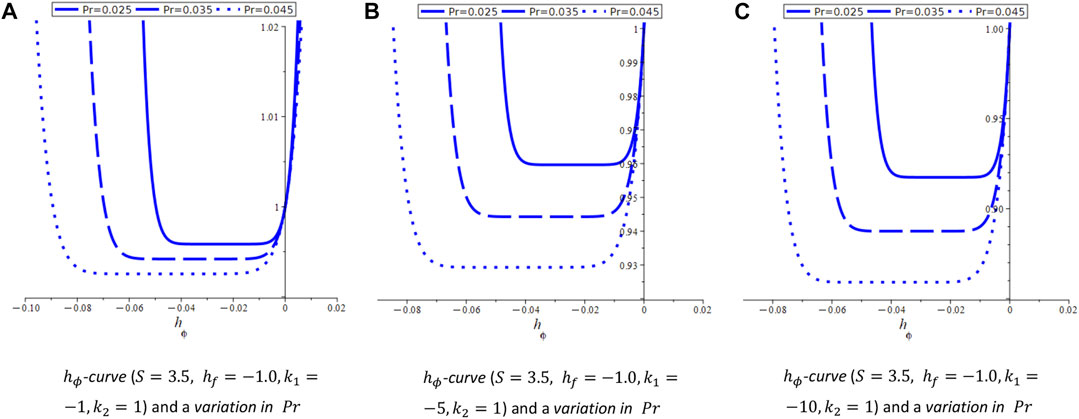
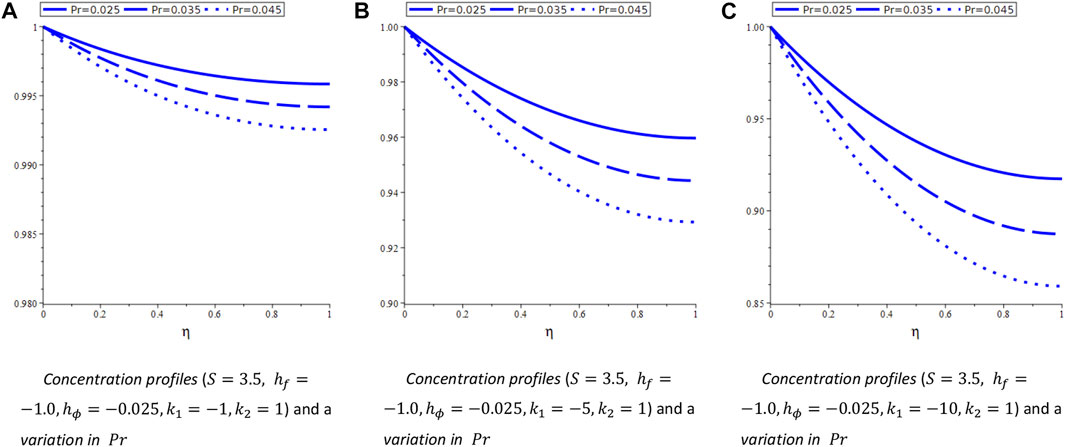
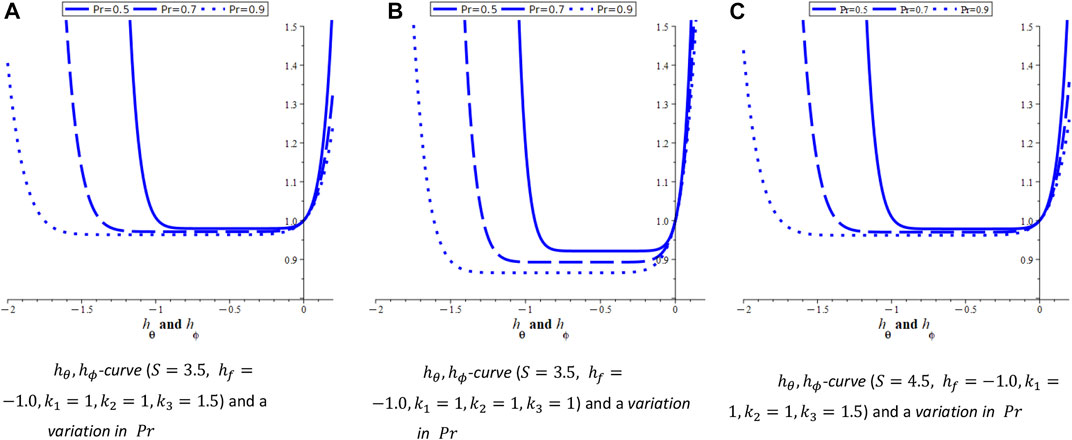
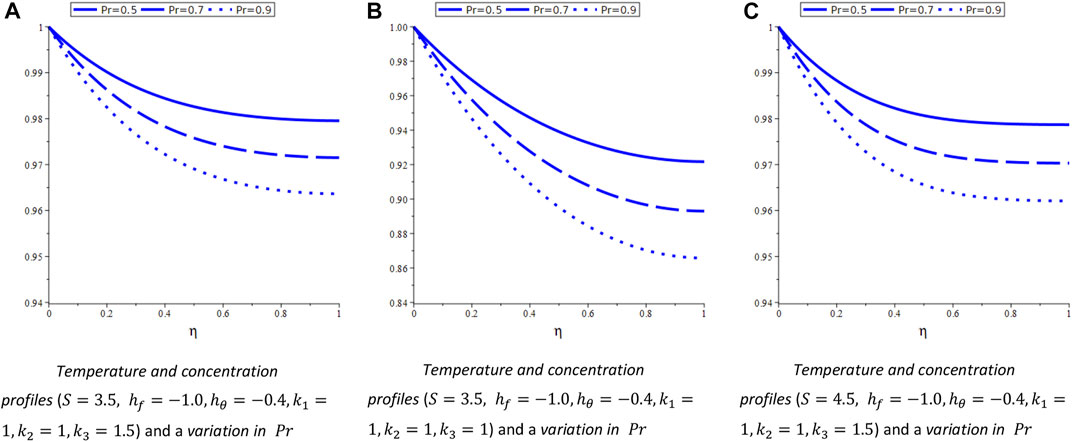
4.2 Velocity and concentration profiles for Case-II

System (Eq. 9) involves three arbitrary constants $k_1,k_2$, and $k_3$, which appear here due to the linear combination of Lie point symmetries we used to construct the corresponding Lie similarity transformation. We draw common curves for $h_{\theta }$ and $h_{\varphi }$ as $h$-curves for this system in Figures 6A–C. These curves are drawn for $h_f=-1.0,k_1=1,k_2=1$ and a variation in the unsteadiness parameter $S=3.0$ and $4.0$, $k_3=-0.2$ and $-0.1$, and a range of $P_r=0.35,0.40,0.45$ and $S_c=0.35,0.40,0.45$. These curves and corresponding set of graphs for temperature and concentration show an increase when the unsteadiness parameter decreases from $S=4.0$ to $S=3.0.$ Similar is the case when $k_3$ goes from $-0.1$ to $-0.2$, as shown in Figures 7A–C and Figures 8A–8C.

FIGURE 6

FIGURE 6. Different concentration profiles.

FIGURE 7

FIGURE 7. Different h-curves.

FIGURE 8

FIGURE 8. Different temperature and concentration profiles.

4.3 Velocity and concentration profiles for Case-III

System (Eq. 12) involves three arbitrary constants $k_1,k_2$, and $k_3$ that are also part of the associated Lie similarity transformation. Figures 9A–C show the $h$-curves for both $h_{\theta }$ and $h_{\varphi }.$ These curves are constructed with the same values of $h_f,k_1,k_2$ as in the previous case and for a different value of the unsteadiness parameter $S$. When the unsteadiness parameter decreases from $4.5$ to $3.5$, the $h_{\theta }$- and $h_{\varphi }$-curves are decreasing. Similar behavior is shown by temperature and concentration profiles in Figures 10A–C; that is, for $1.0<k_3<1.5$, the temperature and concentration are increasing. However, for $P_r=0.5,\mathrm{0.7,0.9}$, a decrease in the temperature and concentration is evident from these figures.

FIGURE 9

FIGURE 9. Different h-curves.

FIGURE 10

FIGURE 10. Different temperature and concentration profiles.

5 Conclusion

Lie point symmetries for heat and mass transfer in a thin liquid film on an unsteady stretching sheet are derived. These symmetries are used to construct Lie similarity transformations which map the PDEs representing the heat and flow model to ODE systems. We showed that there exist three different types of such reductions of the considered flow equations. In the Lie similarity transformation derivation, linear combinations of Lie symmetry generators are utilized. These linear combinations are derived with the help of arbitrary constants, which gives rise to multiple solutions of the flow and heat equations. We use the HAM to analytically solve the obtained non-linear ODEs with a ${10}^{th}$-order of approximation. Velocity, temperature, and concentration profiles are drawn with the aid of these ${10}^{th}$-order HAM solutions. These profiles are presented graphically with variations in the unsteadiness parameter $S$, Prandtl number $P_r$, Schmidt number $S_c$, and the arbitrary constants used in the linear combinations of the Lie point symmetries.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

RK designed and analyzed the results; ST prepared the figures and was involved in discussion; SA was responsible for software and coding; IK analyzed and wrote the manuscript and discussed the results; and SE was responsible for software and coding, supervised the research, and acquired funding.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Andersson HI, Aarseth JB, Dandapat BS. Heat transfer in a liquid film on an unsteady stretching surface. Int J Heat Mass Transfer (2000) 43(1):69–74. doi:10.1016/s0017-9310(99)00123-4

CrossRef Full Text | Google Scholar

2. Wang C. Analytic solutions for a liquid film on an unsteady stretching surface. Heat Mass Transfer (2006) 42(8):759–66. doi:10.1007/s00231-005-0027-0

CrossRef Full Text | Google Scholar

3. Dandapat B, Santra B, Vajravelu K. The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet. Int J Heat Mass Transfer (2007) 50(5-6):991–6. doi:10.1016/j.ijheatmasstransfer.2006.08.007

CrossRef Full Text | Google Scholar

4. Hayat T, Safdar A, Awais M, Mesloub S. Soret and Dufour effects for three-dimensional flow in a viscoelastic fluid over a stretching surface. Int J Heat Mass Transfer (2012) 55(7-8):2129–36. doi:10.1016/j.ijheatmasstransfer.2011.12.016

CrossRef Full Text | Google Scholar

5. Munawar S, Mehmood A, Ali A. Three-dimensional squeezing flow in a rotating channel of lower stretching porous wall. Comput Math Appl (2012) 64(6):1575–86. doi:10.1016/j.camwa.2012.01.003

CrossRef Full Text | Google Scholar

6. Khan JA, Mustafa M, Hayat T, Alsaedi A. Three-dimensional flow of nanofluid over a non-linearly stretching sheet: An application to solar energy. Int J Heat Mass Transfer (2015) 86:158–64. doi:10.1016/j.ijheatmasstransfer.2015.02.078

CrossRef Full Text | Google Scholar

7. Zhang Y, Zhang M, Bai Y. Flow and heat transfer of an Oldroyd-B nanofluid thin film over an unsteady stretching sheet. J Mol Liquids (2016) 220:665–70. doi:10.1016/j.molliq.2016.04.108

CrossRef Full Text | Google Scholar

8. Zhang Y, Zheng L. Analysis of MHD thermosolutal Marangoni convection with the heat generation and a first-order chemical reaction. Chem Eng Sci (2012) 69(1):449–55. doi:10.1016/j.ces.2011.10.069

CrossRef Full Text | Google Scholar

9. Rashidi MM, Ali M, Rostami B, Rostami P, Xie GN. Heat and mass transfer for MHD viscoelastic fluid flow over a vertical stretching sheet with considering Soret and Dufour effects. Math Probl Eng (2015) 2015:1–12. doi:10.1155/2015/861065

CrossRef Full Text | Google Scholar

10. Narayana PS, Babu DH. Numerical study of MHD heat and mass transfer of a Jeffrey fluid over a stretching sheet with chemical reaction and thermal radiation. J Taiwan Inst Chem Eng (2016) 59:18–25. doi:10.1016/j.jtice.2015.07.014

CrossRef Full Text | Google Scholar

11. Shehzad S, Abdullah Z, Abbasi F, Hayat T, Alsaedi A. Magnetic field effect in three-dimensional flow of an Oldroyd-B nanofluid over a radiative surface. J Magnetism Magn Mater (2016) 399:97–108. doi:10.1016/j.jmmm.2015.09.001

CrossRef Full Text | Google Scholar

12. Shehzad S, Abdullah Z, Alsaedi A, Abbasi F, Hayat T. Thermally radiative three-dimensional flow of Jeffrey nanofluid with internal heat generation and magnetic field. J Magnetism Magn Mater (2016) 397:108–14. doi:10.1016/j.jmmm.2015.07.057

CrossRef Full Text | Google Scholar

13. Ahmad S, Yousaf M, Khan A, Zaman G. Magnetohydrodynamic fluid flow and heat transfer over a shrinking sheet under the influence of thermal slip. Heliyon (2018) 4(10):e00828. doi:10.1016/j.heliyon.2018.e00828

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Alarifi IM, Abokhalil A, Osman M, Lund L, Ayed M, Belmabrouk H, et al. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry (2019) 11(3):297. doi:10.3390/sym11030297

CrossRef Full Text | Google Scholar

15. Mandal B, Bhattacharyya K, Banerjee A, Kumar Verma A, Kumar Gautam A. MHD mixed convection on an inclined stretching plate in Darcy porous medium with Soret effect and variable surface conditions. Nonlinear Eng (2020) 9(1):457–69. doi:10.1515/nleng-2020-0029

CrossRef Full Text | Google Scholar

16. Dessie H, Fissha D. MHD mixed convective flow of Maxwell nanofluid past a porous vertical stretching sheet in presence of chemical reaction. Appl Appl Math Int J (2020) 15(1):31.

Google Scholar

17. Tufail MN. Group theoretical analysis of non-Newtonian fluid flow, heat and mass transfer over a stretching surface in the presence of thermal radiation. Appl Fluid Mech (2016) 9:1515. doi:10.18869/acadpub.jafm.68.228.24069

CrossRef Full Text | Google Scholar

18. Metri PG, Guariglia E, Silvestrov S. Lie group analysis for MHD boundary layer flow and heat transfer over stretching sheet in presence of viscous dissipation and uniform heat source/sink. AIP Conf Proc (2017) 1798:020096. doi:10.1063/1.4972688

CrossRef Full Text | Google Scholar

19. Rajput GR, Patil V, Jadhav B. MHD mixed flow of unsteady convection with radiation over a vertical porous plate: Lie group symmetry analysis. Appl Comput Mech (2017) 11(2):1–12. doi:10.24132/acm.2017.380

CrossRef Full Text | Google Scholar

20. Pal D, Roy N. Lie group transformation on MHD double-diffusion convection of a Casson nanofluid over a vertical stretching/shrinking surface with thermal radiation and chemical reaction. Int J Appl Comput Math (2018) 4(1):13–23. doi:10.1007/s40819-017-0449-7

CrossRef Full Text | Google Scholar

21. Megahed AM, Abdel-Rahman RG. Lie group analysis of heat flux effect on MHD second slip flow for a slightly rarefied gas past a stretching sheet with heat generation. Tech Sci (2019) 22(1):45–59. doi:10.31648/ts.4347

CrossRef Full Text | Google Scholar

22. Nazim Tufail M, Zaib F. Symmetry analysis of MHD Casson fluid flow for heat and mass transfer near a stagnation point over a linearly stretching sheet with variable viscosity and thermal conductivity. Heat Transfer (2021) 50(6):5418–38. doi:10.1002/htj.22131

CrossRef Full Text | Google Scholar

23. Rehman KU, Shatanawi W, Abodayeh K. Thermophysical aspects of magnetized Williamson fluid flow subject to both porous and non-porous surfaces: A lie symmetry analysis. Case Stud Therm Eng (2021) 28:101688. doi:10.1016/j.csite.2021.101688

CrossRef Full Text | Google Scholar

24. Saleem M, Tufail MN, Chaudhry QA. Unsteady MHD Casson fluid flow with heat transfer passed over a porous rigid plate with stagnation point flow: Two-parameter Lie scaling approach. Pramana (2021) 95(1):28–9. doi:10.1007/s12043-020-02054-0

CrossRef Full Text | Google Scholar

25. Zeb S, Khan S, Ullah Z, Yousaf M, Khan I, Alshammari N, et al. Lie group analysis of double diffusive MHD tangent hyperbolic fluid flow over a stretching sheet. Math Probl Eng (2022) 2022:1–14. doi:10.1155/2022/9919073

CrossRef Full Text | Google Scholar

26. Rehman KU, Shatanawi W, Abodayeh K. A group theoretic analysis on heat transfer in MHD thermally slip Carreau fluid subject to multiple flow regimes (MFRs). Case Stud Therm Eng (2022) 30:101787. doi:10.1016/j.csite.2022.101787

CrossRef Full Text | Google Scholar

27. Safdar M, Ijaz Khan M, Taj S, Malik M, Shi QH. Construction of similarity transformations and analytic solutions for a liquid film on an unsteady stretching sheet using lie point symmetries. Chaos, Solitons and Fractals (2021) 150:111115. doi:10.1016/j.chaos.2021.111115

CrossRef Full Text | Google Scholar

28. Soh CW, Mahomed F. Linearization criteria for a system of second-order ordinary differential equations. J Int J Non-Linear Mech (2001) 36(4):671–7. doi:10.1016/s0020-7462(00)00032-9

CrossRef Full Text | Google Scholar

29. Maharaj A, Leach P. The method of reduction of order and linearization of the two-dimensional Ermakov system. J Math Methods Appl Sci (2007) 30(16):2125–45. doi:10.1002/mma.919

CrossRef Full Text | Google Scholar

30. Ayub M, Khan M, Mahomed F. Algebraic linearization criteria for systems of ordinary differential equations. J Nonlinear Dyn (2012) 67(3):2053–62. doi:10.1007/s11071-011-0128-x

CrossRef Full Text | Google Scholar

31. Dutt HM, Safdar M, Qadir A. Linearization criteria for two-dimensional systems of third-order ordinary differential equations by complex approach. J Arabian J Math (2019) 8(3):163–70. doi:10.1007/s40065-019-0238-8

CrossRef Full Text | Google Scholar

32. Song L-M, Yang ZJ, Li XL, Zhang SM. Coherent superposition propagation of Laguerre–Gaussian and Hermite–Gaussian solitons. J Appl Math Lett (2020) 102:106114. doi:10.1016/j.aml.2019.106114

CrossRef Full Text | Google Scholar

33. Shen S, Yang Z, Li X, Zhang S. Periodic propagation of complex-valued hyperbolic-cosine-Gaussian solitons and breathers with complicated light field structure in strongly nonlocal nonlinear media. J Commun Nonlinear Sci Numer Simulation (2021) 103:106005. doi:10.1016/j.cnsns.2021.106005

CrossRef Full Text | Google Scholar

34. Shen S, Yang ZJ, Pang ZG, Ge YR. The complex-valued astigmatic cosine-Gaussian soliton solution of the nonlocal nonlinear Schrödinger equation and its transmission characteristics. J Appl Math Lett (2022) 125:107755. doi:10.1016/j.aml.2021.107755

CrossRef Full Text | Google Scholar

35. Stephani H. Differential equations: Their solution using symmetries. Cambridge, United Kingdom: Cambridge University Press (1989).

Google Scholar

36. Ibragimov NH. CRC handbook of Lie group analysis of differential equations. Florida, United States: CRC Press (1995).

Google Scholar

37. Zhang Y, Zhang M, Qi S. Heat and mass transfer in a thin liquid film over an unsteady stretching surface in the presence of thermosolutal capillarity and variable magnetic field. Math Probl Eng (2016) 2016:8521580. doi:10.1155/2016/8521580

CrossRef Full Text | Google Scholar

38. Wu Y, Zhang X, Zhang X. Simplified analysis of heat and mass transfer model in droplet evaporation process. Appl Therm Eng (2016) 99:938–43. doi:10.1016/j.applthermaleng.2016.01.020

CrossRef Full Text | Google Scholar

39. Safdar M, Khan MI, Khan RA, Taj S, Abbas F, Elattar S, et al. Analytic solutions for the MHD flow and heat transfer in a thin liquid film over an unsteady stretching surface with Lie symmetry and homotopy analysis method. Waves in Random Complex Media (2022) 2022:1–19. doi:10.1080/17455030.2022.2073402

CrossRef Full Text | Google Scholar