- 1School of Science, Hainan University, Haikou, China
- 2Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan, China
- 3University of Chinese Academy of Science, Beijing, China
- 4Graduate School of China Academy of Engineering Physics, Beijing, China
- 5Beijing Computational Science Research Center, Beijing, China
- 6Center for Theoretical Physics, Hainan University, Haikou, China
We present sympathetic cooling in an optomechanical system consisting of two coupled cantilevers. The hybridization of the cantilevers creates a symmetric mode, which is feedback cooled, and an anti-symmetric mode not directly controllable by the feedback. The scheme of sympathetic cooling is adopted to cool the anti-symmetric mode indirectly by parametrically coupling to the feedback-cooled symmetric mode, from which the cooling power can be transferred. Experiment shows that the realization of coherent dynamics plays an essential role in sympathetic cooling, in which optimal cooling is achieved when the mechanical dissipation rate and the strength of coupling become comparable. The sympathetic cooling is improved by increasing the strength of mode coupling to enhance the transfer of cooling power. Also, the limit of sympathetic cooling imposed by the capacity of feedback cooling is reached as the effective temperatures of the two modes approach the strong coherent coupling condition. Our research provides the prospect of extending the cooling techniques to coupled mechanical resonators for a broad application in sensing and information processing.
1 Introduction
Cooling of the mechanical resonator is of great significance in improving the sensitivity of mechanical sensors [1–6] and a prerequisite for exploring the intriguing quantum phenomena at a macroscale [7–12]. Recent advances on cavity optomechanics that integrates the unique capacity on sensing and controlling mechanical motions have allowed cooling mechanical resonators of different types by means of either laser cooling [13–16] or feedback control [17–21]. For example, the scheme of measurement-based feedback has demonstrated the potential on realizing quantum control of a room-temperature mechanical resonator by developing a sensor capable of resolving the zero-point fluctuation at its thermal decoherence rate [22–24]. With respect to the great successes on cooling of the mechanical resonator, significant efforts have been devoted to scaling up the system by connecting additional mechanical resonators for applications ranging from high-precision measurement [25–27] to scalable phonon-based information processing devices [28–31]. Nevertheless, cooling of coupled mechanical resonators remains a primary obstacle in scaling up the system because the hybridization of mechanical resonators typically creates mechanical modes with shapes that are not directly controllable. Examples include distant mechanical resonators that cannot be addressed by laser [32, 33], optomechanical mode that appears dark to the probe [34, 35], and mechanical modes with symmetries that can balance the actuation force [36].
The realization of cooling in the coupled mechanical resonators beyond that which can be directly cooled would require a controllable coupling between mechanical modes [37–40]. The concept of sympathetic cooling has been achieved in systems such as trapped ions and atoms to cool degrees of freedom that are inaccessible to direct laser cooling [41, 42]. In micro- and nanomechanical systems, coherent coupling between mechanical modes of either distinct mechanical resonators or different modes of the same resonator have been achieved so far by optical [43, 44], electrical [45, 46], and elastic means [47]. Also, dynamical manipulation [48–51], geometric control [52, 53], and topological transfer [54, 55] of mechanical motions have been demonstrated in coupled mechanical resonators. The ability in coherent transfer of motions between the mechanical resonator opens the possibility to sympathetic cooling in coupled mechanical resonators by transferring the cooling power to mechanical modes which is impossible for direct cooling.
In this paper, we present sympathetic feedback cooling in the optomechanical system consisting of two mechanical modes. The scheme of measurement-based feedback is implemented to cool one of the mechanical modes directly. Also, the mechanical mode, which is unable to be actuated by the feedback force due to the symmetry of its oscillation shape, is cooled sympathetically by coupling to the feedback-cooled mode. The coherent dynamics of the sympathetic feedback cooling is investigated by changing the strength of feedback cooling. Also, the strength of mode coupling is enhanced to improve the sympathetic cooling to the limit imposed by the capacity of feedback cooling.
2 Methods
The mechanical resonators used in our experiment are two elastically coupled cantilevers with dimensions of 200 μm in length, 10 μm in width, and 200 nm in thickness. As illustrated in Figure 1A, one of the cantilevers (cantilever 1) is inserted into a fiber-based cavity to form a membrane-in-the-middle optomechanical system, in which the cantilever is trapped by a 1,064 nm laser. Consequently, the resonant frequency of cantilever 1 becomes trap power P dependent
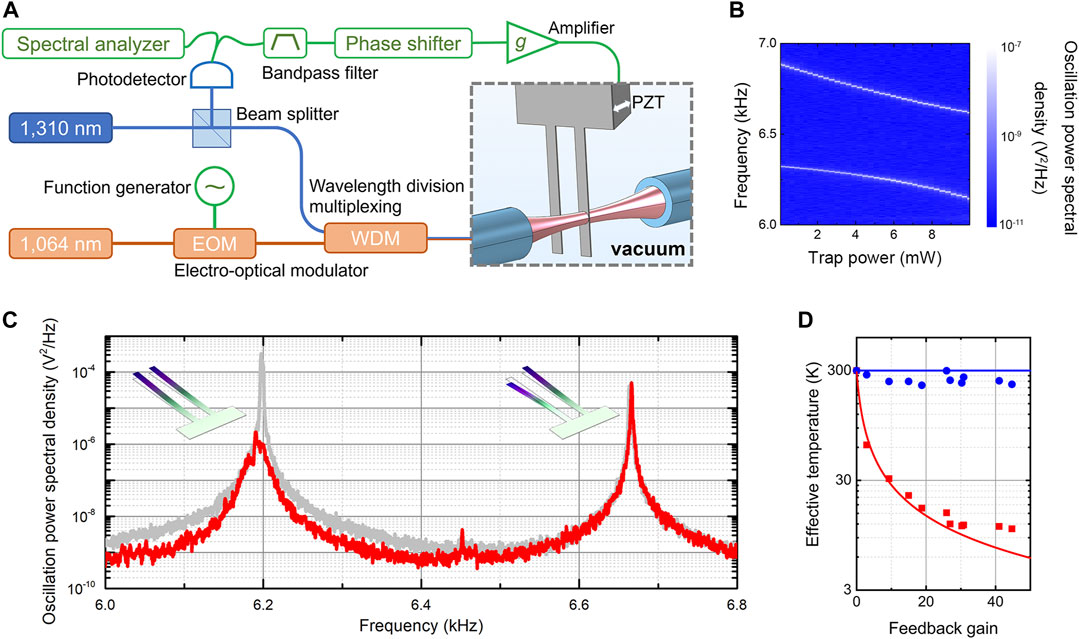
FIGURE 1. (A) Schematic illustration of the experimental setup. The power of the 1,310 nm probe is 0.12 mW. A bandpass filter with pass band from 1 kHz to 10 kHz is used to filter out the motion signal of higher-order mechanical modes. Also, the motion signal shifted by a phase of
The mechanical resonator is cooled at the anti-crossing point using the scheme of measurement-based feedback, in which a force proportional to the oscillation velocity
where J denotes the strength of elastic coupling, and the effective mass and the intrinsic damping rate of the two cantilevers are assumed to be nearly identical with
3 Results and discussion
In order to cool the anti-symmetric mode, a parametric pump is applied to couple the anti-symmetric mode to the feedback-cooled symmetric mode by modulating the trap power
with
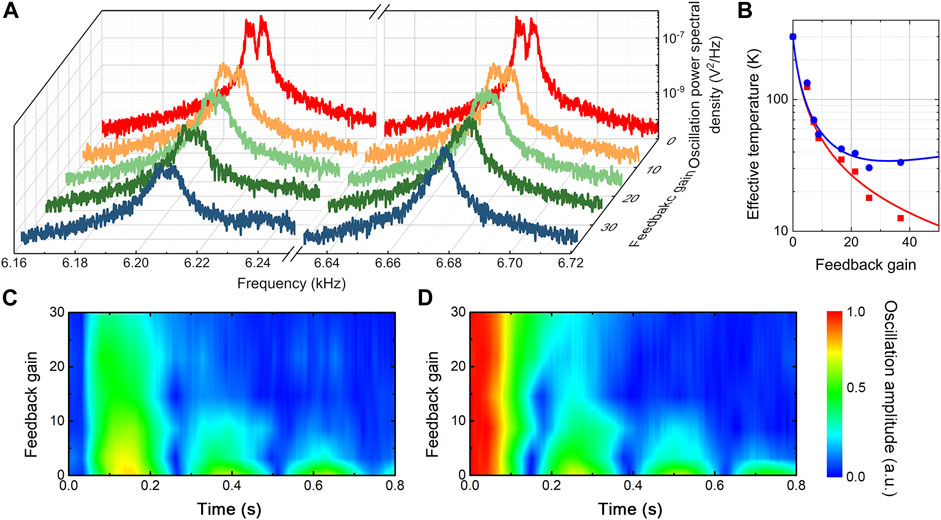
FIGURE 2. (A) Thermal oscillation power spectral density of the modes cooled sympathetically at different feedback gains. The spectra for different feedback gains are recorded at the pump power of
For a given parametric coupling strength
The dependence of the optimal feedback gain on the parametric coupling strength reveals that the coherent dynamics plays an essential role in transferring the cooling power between the parametrically coupled modes. The real-time dynamics of the motion transduction is investigated by initializing the system through resonantly actuating the anti-symmetric mode to an oscillation amplitude of approximately 50 nm. After the initialization, the parametric pump with
We demonstrate that sympathetic cooling can be improved by increasing the strength of parametric coupling to enhance the transfer of cooling power. The strength of parametric coupling for each pump power
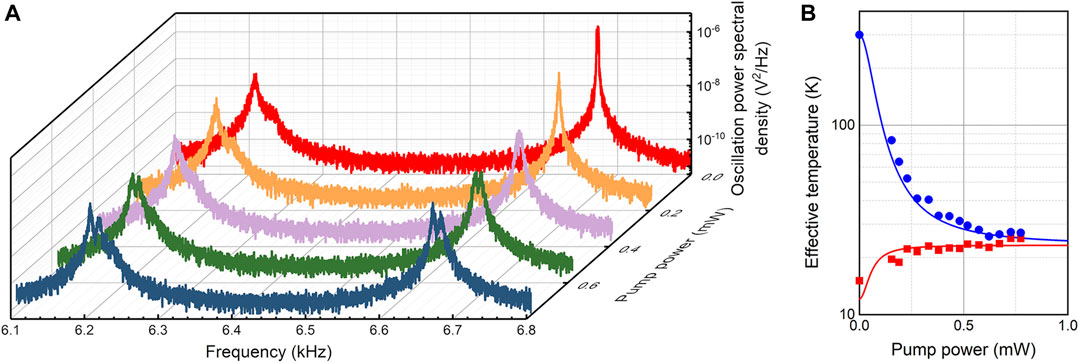
FIGURE 3. (A) Thermal oscillation power spectral density of the modes cooled sympathetically at different pump powers. The spectra for different pump powers are recorded at the feedback gain of
4 Conclusion
In summary, we have presented sympathetic feedback cooling of elastically coupled mechanical resonators in an optomechanical system, which allows for sensing and coherent controlling of mechanical motions simultaneously. The complete hybridization between cantilevers creates two normal modes with the cantilevers oscillating symmetrically and anti-symmetrically. In order to cool the anti-symmetric mode that is beyond direct control due to its oscillation shape, a parametric pump is applied to resonantly couple the two modes. As a result, when the symmetric mode is feedback cooled, the cooling power can be transferred to the anti-symmetric mode. We demonstrate that the coherent dynamics plays an essential role in sympathetic cooling with an optimal cooling achieved when the mechanical dissipation becomes comparable to the strength of parametric coupling. The sympathetic cooling is improved by increasing the strength of parametric coupling to enhance the transfer of cooling power. Also, sympathetic cooling of the anti-symmetric mode to the limit imposed by the capacity of feedback is achieved when the effective temperatures of the two modes approach.
Although the sympathetic cooling of the anti-symmetric mode, which has been widely adopted in mechanical sensors for its resilience to vibration noises [36, 56–58], is demonstrated in our experiment, the scheme can be generally extended to coupled mechanical resonator array to transfer cooling power to distant mechanical resonators that are inaccessible by direct cooling. Also, significant improvement on the limit of sympathetic cooling can be expected under the condition of deep feedback cooling, in which the measurement noises, such as shot noise and photodetector noise, should be taken into account. With respect to the great advances on the measurement-based feedback control, our research on sympathetic feedback cooling provides a feasible scheme to cool coupled mechanical resonators for scalable phonon information processing.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
HF and Z-CG designed and conceived the experiment. C-YS, Z-CG, and QY carried out the measurements. C-YS proceeded and analyzed the experimental data. YL provided theoretical support. HF and YL wrote the paper. C-PS and HF supervised the project. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China (grant nos. U2130117, 12074030, 12274107, U1930403, U1930402, and 12088101), the Natural Science Foundation of Hubei Province (grant no. 2020CFB830), and the Research Funds of Hainan University [grant no. KYQD (ZR) 22170].
Acknowledgments
Z-CG gratefully acknowledges the helpful discussion with Jie-qiao Liao at Hunan Normal University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Chen Y. Macroscopic quantum mechanics: Theory and experimental concepts of optomechanics. J Phys B-at Mol Opt (2013) 46(10):104001. doi:10.1088/0953-4075/46/10/104001
2. Lei CU, Weinstein AJ, Suh J, Wollman EE, Kronwald A, Marquardt F, et al. Quantum nondemolition measurement of a quantum squeezed state beyond the 3 dB limit. Phys Rev Lett (2016) 117(10):100801. doi:10.1103/PhysRevLett.117.100801
3. Miao H, Srinivasan K, Aksyuk V. A microelectromechanically controlled cavity optomechanical sensing system. New J Phys (2012) 14(7):075015. doi:10.1088/1367-2630/14/7/075015
4. Yi S, Xiang J, Zhou M, Wu Z, Yang L, Yu Z. Angle-based wavefront sensing enabled by the near fields of flat optics. Nat Commun (2021) 12(1):6002. doi:10.1038/s41467-021-26169-z
5. Jiang X, Qavi AJ, Huang SH, Yang L. Whispering-gallery sensors. Matter (2020) 3(2):371–92. doi:10.1016/j.matt.2020.07.008
6. Tang SJ, Liu S, Yu XC, Song Q, Gong Q, Xiao YF. On-chip spiral waveguides for ultrasensitive and rapid detection of nanoscale objects. Adv Mater (2018) 30(25):e1800262. doi:10.1002/adma.201800262
7. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev Mod Phys (2014) 86(4):1391–452. doi:10.1103/RevModPhys.86.1391
8. Barzanjeh S, Redchenko ES, Peruzzo M, Wulf M, Lewis DP, Arnold G, et al. Stationary entangled radiation from micromechanical motion. Nature (2019) 570(7762):480–3. doi:10.1038/s41586-019-1320-2
9. Safavi-Naeini AH, Chan J, Hill JT, Alegre TP, Krause A, Painter O. Observation of quantum motion of a nanomechanical resonator. Phys Rev Lett (2012) 108(3):033602. doi:10.1103/PhysRevLett.108.033602
10. Ockeloen-Korppi CF, Damskagg E, Pirkkalainen JM, Asjad M, Clerk AA, Massel F, et al. Stabilized entanglement of massive mechanical oscillators. Nature (2018) 556(7702):478–82. doi:10.1038/s41586-018-0038-x
11. Poot M, van der Zant HSJ. Mechanical systems in the quantum regime. Phys Rep (2012) 511(5):273–335. doi:10.1016/j.physrep.2011.12.004
12. Riedinger R, Hong S, Norte RA, Slater JA, Shang J, Krause AG, et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature (2016) 530(7590):313–6. doi:10.1038/nature16536
13. Chan J, Alegre TP, Safavi-Naeini AH, Hill JT, Krause A, Groblacher S, et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature (2011) 478(7367):89–92. doi:10.1038/nature10461
14. Qiu L, Shomroni I, Seidler P, Kippenberg TJ. Laser cooling of a nanomechanical oscillator to its zero-point energy. Phys Rev Lett (2020) 124(17):173601. doi:10.1103/PhysRevLett.124.173601
15. Teufel JD, Donner T, Li D, Harlow JW, Allman MS, Cicak K, et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature (2011) 475(7356):359–63. doi:10.1038/nature10261
16. Clark JB, Lecocq F, Simmonds RW, Aumentado J, Teufel JD. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature (2017) 541(7636):191–5. doi:10.1038/nature20604
17. Kleckner D, Bouwmeester D. Sub-kelvin optical cooling of a micromechanical resonator. Nature (2006) 444(7115):75–8. doi:10.1038/nature05231
18. Poggio M, Degen CL, Mamin HJ, Rugar D. Feedback cooling of a cantilever's fundamental mode below 5 mK. Phys Rev Lett (2007) 99(1):017201. doi:10.1103/PhysRevLett.99.017201
19. Schmid G-L, Ngai CT, Ernzer M, Aguilera MB, Karg TM, Treutlein P. Coherent feedback cooling of a nanomechanical membrane with atomic spins. Phys Rev X (2022) 12(1):011020. doi:10.1103/PhysRevX.12.011020
20. Zhang J, Liu Y, Wu RB, Jacobs K, Nori F. Quantum feedback: Theory, experiments, and applications. Phys Rep (2017) 679(17):1–60. doi:10.1016/j.physrep.2017.02.003
21. Schafermeier C, Kerdoncuff H, Hoff UB, Fu H, Huck A, Bilek J, et al. Quantum enhanced feedback cooling of a mechanical oscillator using nonclassical light. Nat Commun (2016) 7:13628. doi:10.1038/ncomms13628
22. Guo J, Norte R, Groblacher S. Feedback cooling of a room temperature mechanical oscillator close to its motional ground state. Phys Rev Lett (2019) 123(22):223602. doi:10.1103/PhysRevLett.123.223602
23. Wilson DJ, Sudhir V, Piro N, Schilling R, Ghadimi A, Kippenberg TJ. Measurement-based control of a mechanical oscillator at its thermal decoherence rate. Nature (2015) 524(7565):325–9. doi:10.1038/nature14672
24. Rossi M, Mason D, Chen J, Tsaturyan Y, Schliesser A. Measurement-based quantum control of mechanical motion. Nature (2018) 563(7729):53–8. doi:10.1038/s41586-018-0643-8
25. Lin Y, Yabuno H, Liu X, Yamamoto Y, Matsumoto S. Highly sensitive AFM using self-excited weakly coupled cantilevers. Appl Phys Lett (2019) 115(13):133105. doi:10.1063/1.5115836
26. Manav M, Phani AS, Cretu E. Mode localized MEMS transducers with voltage-controlled linear coupling. J Micromech Microeng (2017) 27(5):055010. doi:10.1088/1361-6439/aa6652
27. Marquez S, Alvarez M, Plaza JA, Villanueva LG, Dominguez C, Lechuga LM. Asymmetrically coupled resonators for mass sensing. Appl Phys Lett (2017) 111(11):113101. doi:10.1063/1.5003023
28. Habraken SJM, Stannigel K, Lukin MD, Zoller P, Rabl P. Continuous mode cooling and phonon routers for phononic quantum networks. New J Phys (2012) 14(11):115004. doi:10.1088/1367-2630/14/11/115004
29. Fu H, Gong ZC, Yang LP, Mao TH, Sun CP, Yi S, et al. Coherent optomechanical switch for motion transduction based on dynamically localized mechanical modes. Phys Rev Appl (2018) 9(5):054024. doi:10.1103/PhysRevApplied.9.054024
30. Barzanjeh S, Wulf M, Peruzzo M, Kalaee M, Dieterle PB, Painter O, et al. Mechanical on-chip microwave circulator. Nat Commun (2017) 8(1):953. doi:10.1038/s41467-017-01304-x
31. Huang P, Zhang L, Zhou J, Tian T, Yin P, Duan C, et al. Nonreciprocal radio frequency transduction in a parametric mechanical artificial lattice. Phys Rev Lett (2016) 117(1):017701. doi:10.1103/PhysRevLett.117.017701
32. Luo G, Zhang ZZ, Deng GW, Li HO, Cao G, Xiao M, et al. Strong indirect coupling between graphene-based mechanical resonators via a phonon cavity. Nat Commun (2018) 9(1):383. doi:10.1038/s41467-018-02854-4
33. Lin S, Tian T, Huang P, Yin P, Zhang L, Du J. Realization of programmable nanomechanical lattice with both nearest-neighboring and next-nearest-neighboring couplings. Appl Phys Lett (2020) 117(9):093503. doi:10.1063/5.0009302
34. Dong C, Fiore V, Kuzyk MC, Wang H. Optomechanical dark mode. Science (2012) 338(6114):1609–13. doi:10.1126/science.1228370
35. Wang Y-D, Clerk AA. Using dark modes for high-fidelity optomechanical quantum state transfer. New J Phys (2012) 14(10):105010. doi:10.1088/1367-2630/14/10/105010
36. Pachkawade V. State-of-the-Art in mode-localized mems coupled resonant sensors: A comprehensive review. IEEE Sens J (2021) 21(7):8751–79. doi:10.1109/JSEN.2021.3051240
37. Frimmer M, Gieseler J, Novotny L. Cooling mechanical oscillators by coherent control. Phys Rev Lett (2016) 117(16):163601. doi:10.1103/PhysRevLett.117.163601
38. Lai DG, Huang J, Hou BP, Nori F, Liao JQ. Domino cooling of a coupled mechanical-resonator chain via cold-damping feedback. Phys Rev A (2021) 103(6):063509. doi:10.1103/PhysRevA.103.063509
39. Lai DG, Zou F, Hou BP, Xiao YF, Liao JQ. Simultaneous cooling of coupled mechanical resonators in cavity optomechanics. Phys Rev A (2018) 98(2):023860. doi:10.1103/PhysRevA.98.023860
40. Jockel A, Faber A, Kampschulte T, Korppi M, Rakher MT, Treutlein P. Sympathetic cooling of a membrane oscillator in a hybrid mechanical-atomic system. Nat Nanotechnol (2015) 10(1):55–9. doi:10.1038/nnano.2014.278
41. Bohman M, Grunhofer V, Smorra C, Wiesinger M, Will C, Borchert MJ, et al. Sympathetic cooling of a trapped proton mediated by an LC circuit. Nature (2021) 596(7873):514–8. doi:10.1038/s41586-021-03784-w
42. Christoph P, Wagner T, Zhong H, Wiesendanger R, Sengstock K, Schwarz A, et al. Combined feedback and sympathetic cooling of a mechanical oscillator coupled to ultracold atoms. New J Phys (2018) 20(9):093020. doi:10.1088/1367-2630/aadf20
43. Lin Q, Rosenberg J, Chang D, Camacho R, Eichenfield M, Vahala KJ, et al. Coherent mixing of mechanical excitations in nano-optomechanical structures. Nat Photon (2010) 4(4):236–42. doi:10.1038/nphoton.2010.5
44. Shkarin AB, Flowers-Jacobs NE, Hoch SW, Kashkanova AD, Deutsch C, Reichel J, et al. Optically mediated hybridization between two mechanical modes. Phys Rev Lett (2014) 112(1):013602. doi:10.1103/PhysRevLett.112.013602
45. Huang P, Wang P, Zhou J, Wang Z, Ju C, Wang Z, et al. Demonstration of motion transduction based on parametrically coupled mechanical resonators. Phys Rev Lett (2013) 110(22):227202. doi:10.1103/PhysRevLett.110.227202
46. Okamoto H, Schilling R, Schütz H, Sudhir V, Wilson DJ, Yamaguchi H, et al. A strongly coupled Λ-type micromechanical system. Appl Phys Lett (2016) 108(15):153105. doi:10.1063/1.4945741
47. Gong ZC, Fu H, Mao TH, Yuan Q, Shen CY, Sun CP, et al. Coherent phonon-mediated dynamics for an addressable transducer of coupled micro-mechanical resonators. Appl Phys Lett (2021) 118(20):203505. doi:10.1063/5.0044428
48. Faust T, Rieger J, Seitner MJ, Kotthaus JP, Weig EM. Coherent control of a classical nanomechanical two-level system. Nat Phys (2013) 9(8):485–8. doi:10.1038/nphys2666
49. Okamoto H, Gourgout A, Chang C-Y, Onomitsu K, Mahboob I, Chang EY, et al. Coherent phonon manipulation in coupled mechanical resonators. Nat Phys (2013) 9(8):480–4. doi:10.1038/nphys2665
50. Fu H, Gong ZC, Mao TH, Sun CP, Yi S, Li Y, et al. Classical analog of Stückelberg interferometry in a two-coupled-cantilever–based optomechanical system. Phys Rev A (2016) 94(4):043855. doi:10.1103/PhysRevA.94.043855
51. Zhang Z-Z, Song X-X, Luo G, Su Z-J, Wang K-L, Cao G, et al. Coherent phonon dynamics in spatially separated graphene mechanical resonators. P Natl Acad Sci USA (2020) 117(11):5582–7. doi:10.1073/pnas.1916978117
52. Fu H, Gong ZC, Mao TH, Shen CY, Sun CP, Yi S, et al. Geometric energy transfer in a stückelberg interferometer of two parametrically coupled mechanical modes. Phys Rev Appl (2019) 11(3):034010. doi:10.1103/PhysRevApplied.11.034010
53. Yuan Q, Gong ZC, Gao YZ, Mao TH, Shen CY, Sun CP, et al. Geometric motion transfer between two indirectly coupled mechanical resonators. Appl Phys Lett (2021) 119(14):143504. doi:10.1063/5.0060300
54. Xu H, Mason D, Jiang L, Harris JG. Topological energy transfer in an optomechanical system with exceptional points. Nature (2016) 537(7618):80–3. doi:10.1038/nature18604
55. Xu H, Jiang L, Clerk AA, Harris JGE. Nonreciprocal control and cooling of phonon modes in an optomechanical system. Nature (2019) 568(7750):65–9. doi:10.1038/s41586-019-1061-2
56. Giner J, Zhang Y, Maeda D, Ono K, Shkel AM, Sekiguchi T. Dynamicaly balanced degenerate mode gyro with sub-hz frequency symmetry and temperature robustness. In: 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS); 22-26 January 2017; Las Vegas (2017).
57. Senkal D, Efimovskaya A, Shkel AM. Miniature origami-like folded MEMS TIMU. In: 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings; 21-25 June 2015; Anchorage (2015).
Keywords: sympathetic cooling, optomechanical system, coupled mechanical resonators, coherent coupling, feedback control
Citation: Gong Z-C, Shen C-Y, Yuan Q, Sun C-P, Li Y and Fu H (2023) Sympathetic feedback cooling in the optomechanical system consisting of two coupled cantilevers. Front. Phys. 11:1149337. doi: 10.3389/fphy.2023.1149337
Received: 21 January 2023; Accepted: 13 March 2023;
Published: 29 March 2023.
Edited by:
Zhangqi Yin, Beijing Institute of Technology, ChinaCopyright © 2023 Gong, Shen, Yuan, Sun, Li and Fu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hao Fu, aC5mdUBsaXZlLmNu
†These authors contributed equally to this work
 Zhi-Cheng Gong
Zhi-Cheng Gong Cheng-Yu Shen2,3†
Cheng-Yu Shen2,3† Hao Fu
Hao Fu