Polarization singularities: Topological and dynamical aspects

The review describes general principles and characteristics of inhomogeneously polarized paraxial optical fields and, especially, the polarization singularities (PSs). Main parameters of the optical vector waves are discussed, with the emphasis on the physical relevance and topological distinctiveness of the PSs. Special features of the stochastic vector fields are considered in the context of the PSs’ genericity and structural stability. A detailed attention is paid to interrelations between the PSs and the phase singularities of scalar fields formed by the orthogonal polarization projections of the total field, and their derivatives (complex Stokes fields, phase-difference fields, etc.). On this base, the practical approaches are discussed for the experimental PS identification and characterization. A particular examination of the internal energy flows associated with the PSs, and accompanying distributions of the optical momentum and angular momentum, reveals meaningful dynamical features of PSs and supplies additional physically transparent and informative means for their studies and characterization.

1 Introduction

During the past years, an especial progress in optical research and technologies is associated with the development of singular optics (SO). The corresponding literature is practically spanless, but we can mention some most recent and popular review publications [1–21]. The fruitful and meaningful concepts of SO deal with special points of a light field, at which certain definitive field parameters (phase, direction or handedness of polarization, etc.) are indeterminate, or “singular.” Such singular points, or “singularities,” are exceptional in the sense that each such point, with its morphology and topological characteristics, determines qualitatively the whole optical field in adjacent points of space. Accordingly, the spatial distribution of separate singularities is not arbitrary but obey certain topologically motivated laws due to which the singular points, lines and surfaces form a coherent and interdependent network—“singular skeleton” which supplies a succinct and meaningful characterization of the field as a whole. The SO, as a branch of physical optics, is, first of all, the system of relations between the definitive elements of the optical-field fine structure, and gives a general understanding of its physical nature and the mechanisms of its formation, existence, and development [1–21].

Especially intricate and rich of details singular networks are coupled with the vector nature of the electromagnetic field. A generic electromagnetic field represents a vector wave with spatially-variable polarization parameters, and its singularities are classified as polarization singularities (PSs). Being the basic structure elements of complex optical fields, the PSs have attracted scrupulous attention of the research community since the early 80-ies of the past century. Many exquisite studies were dedicated to the description of PSs, identification and analysis of their main characteristics, specific details of their formation, detection, diagnostics and applications. The PSs and associated issues are discussed in a huge massive of works among which we would like to emphasize the brilliant book by J. F. Nye [22] and works performed by his colleagues, founders of the SO as a scientific direction, J. V. Hajnal, M. V. Berry, M. R. Dennis, I. Freund, etc. [23–33].

However, to the best of our knowledge, some important aspects related to the PSs are presented incompletely or even arguably. Namely, we can formulate several topics where, in our opinion, there are gaps in the cited literature. In the most general form, such “imperfect” topics can be combined into the following items:

• Any vector field can be represented as a superposition of “partial” fields of the basic orthogonal polarization components [34]. Accordingly, a PS is always associated with a singularity in a certain (scalar) partial field [1, 2, 5, 35–39], and there is no clear and consistent understanding of the seemingly obvious connection between the PS characteristics and the parameters of these scalar phase singularities.

• Especially, a phase singularity is characterized by the specific mechanical features of the field: emergence of the orbital angular momentum (OAM) and the circulatory character of the energy flows [5, 9, 35, 36, 40, 41] in its vicinity. Naturally, the questions appear relating the mechanical features and the structure of energy flows in the vicinity of a PS.

• As topological objects, the PSs are structurally stable against weak perturbations, e.g., the slight symmetry breaking. This property makes them “generic” [22, 38, 42] which means that they occur naturally in optical fields, without further specific requirements. However, there are special “non-generic” sorts of singularities which only exist under special conditions, concerning, e.g., the spatial symmetry of the field. In this context, important questions arise relating the “genericity” and structural stability of the PSs.

Therefore, in this paper, without claiming to be comprehensive (for example, the problems of synthesizing fields with PSs are not considered), we try to clarify, supplement, and, probably, correct the understanding of certain PS-associated issues, briefly characterized in the above points. The main materials of the present article are of a review nature; however, they are mainly based on the results obtained by the authors earlier.

The review is organized as follows. We start with a short introduction to paraxial optics, general description of the polarization state and the brief inventory of the polarization-ellipse parameters, spatial distributions of which form the mathematical fields whose singularities are studied as the PSs (Section 2). Section 3 outlines the main types of the paraxial PSs, their genesis, properties and characteristic features, including the topological principles of their existence and combinations. A special subsection of Section 3 is devoted to the interferometric methods of the PS detection and experimental diagnostics as well as to questions of their informativity and practical implementation. More general questions of the PS genericity and structure stability are briefly discussed in Section 4 based on their topological properties discussed above. The PS-associated dynamical features of optical fields (specific energy flows, mechanical momentum and angular momentum) are considered in Section 5. Here, the special attention is paid to singularities of the energy flow pattern and their relations with the “usual” PSs. The whole presentation is summarized and accentuated in Section 6.

2 Paraxial fields and the polarization parameters

Prior to proceed with a detailed discussion of the PSs, it is convenient to summarize the main ideas and parameters usually employed for the description of the optical field’s polarization. Note that in view of the vector nature of electromagnetic waves, the polarization structure is essentially three-dimensional; however, in a lot of practical situations, the field can be described by the paraxial approximation [35, 36, 40]. As was shown at the dawn of the SO era [22–25, 28], the PS systems in the 3D and paraxial case are rather different. In this review, our subjects are the paraxial light fields whose main properties and principles of characterization are briefly outlined in this Section.

We consider monochromatic light fields in which the instant electric and magnetic vectors can be represented as $\mathcal{E}\left(t\right)=\mathrm{R}\mathrm{e}\left({\mathbf{E}e}^{-iwt}\right)$, $\mathcal{H}\left(t\right)=\mathrm{R}\mathrm{e}\left({\mathbf{H}e}^{-iwt}\right)$ where ω is the light frequency, and E(R), H(R) are the vector complex amplitudes [34] depending only on the spatial coordinates R = (x, y, z) ≡ (r, z). In paraxial light beams, the well-defined physically selected longitudinal direction z exists, and the field behavior along the z-coordinate is qualitatively different from that in the transverse plane r = (x, y). In such fields, the complex amplitudes E and H are “almost transverse” and can be described through the paraxial complex amplitude u (r, z) by equations [35, 36, 40]

$\mathbf{E}={\mathbf{E}}_{\perp }+{\mathbf{e}}_z{E}_z=\left[\mathbf{u}+\frac{i}{kn}{\mathbf{e}}_z\left({\nabla }_{\perp }\cdot \mathbf{u}\right)\right]e^{iknz},$(2.1)

$\mathbf{H}={\mathbf{H}}_{\perp }+{\mathbf{e}}_z{H}_z=\sqrt{\frac{\epsilon }{\mu }}\left[\left({\mathbf{e}}_z\times \mathbf{u}\right)+\frac{i}{kn}{\mathbf{e}}_z\left({\nabla }_{\perp }\cdot \left({\mathbf{e}}_z\times \mathbf{u}\right)\right)\right]e^{iknz}$(2.2)

where k = ω/c is the vacuum wavenumber, ε and μ are the medium permittivity and permeability, $n=\sqrt{\epsilon \mu }$ is the refractive index, ${\nabla }_{\perp }={\mathbf{e}}_x\left(\partial /\partial x\right)+{\mathbf{e}}_y\left(\partial /\partial y\right)$ is the transverse gradient, e_x, e_y and e_z are the unit vectors of the Cartesian coordinates. The main (first) terms in brackets of Eqs 2.1, 2.2 describe the predominant transverse field components, whereas the longitudinal components (second terms) are of the relative order $\gamma ={\left(kb\right)}^{-1}$ in magnitude, with b being the characteristic transverse scale of the complex amplitude u (r, z) inhomogeneity. The quantity γ is the small parameter of the paraxial approximation; the longitudinal characteristic scale of a paraxial beam variations (usually called “Rayleigh length” [5, 40]) is much higher and equals to $z_R=k{b}^2$.

Equations 2.1, 2.2 clearly show that an optical field can be equally characterized via the electric or magnetic vector distributions. The electric and magnetic fields are interrelated but can be considered independently, with revealing their separate polarization structures and systems of singularities, sometimes rather different [26, 31]. However, the principles of their description and the physical contents are common, and in this review, the optical fields are considered in terms of the electric vector distribution.

The total vector complex amplitude u (r, z) of the field can be represented in the transverse bases as [5, 37, 40, 42]

$\mathbf{u}={\mathbf{e}}_x{u}_x+{\mathbf{e}}_y{u}_y={\mathbf{e}}_{+}{u}_{+}+{\mathbf{e}}_{-}{u}_{-}=\mathbf{P}+i\mathbf{Q}={\mathbf{e}}_x\left(P_x+i{Q}_x\right)+{\mathbf{e}}_y\left(P_y+i{Q}_y\right),$(2.3)

where

${\mathbf{e}}_{+}=\frac{1}{\sqrt{2}}\left({\mathbf{e}}_x+i{\mathbf{e}}_y\right){,\hspace{0.17em}\hspace{0.17em}\mathbf{e}}_{-}=\frac{1}{\sqrt{2}}\left({\mathbf{e}}_x-i{\mathbf{e}}_y\right)$(2.4)

are the unit vectors of right and left circular polarization. The functions u_x, u_y and u₊, u_–describe the partial field contributions in Cartesian (x, y) and complex Eq. 2.4 orthogonal frames and can be called “planar” (u_x, u_y) and “circular” (u₊, u_–) polarization projections of the field. Eq. 2.4 mean that in the right-polarized wave, the field vector $\mathbf{u}={\mathbf{e}}_{+}{u}_{+}$ rotates positively (counter-clockwise) when observed against the beam propagation (from the positive end of axis z). This convention contradicts to the classical-optics tradition associating the “right” circular polarization with the clockwise rotation [34, 43] but fully complies with the standard concepts of wave-field helicity and spin in quantum physics and electromagnetic theory, and dominates in the modern literature [see, for example, (1, 2, 4, 7, 13, 35, 36, 40, 42)]. That is why it is accepted in this review.

The state of polarization in the transverse plane is completely determined by the complex vector Eq. 2.3 or its components

$u_x=a_x\exp \left(i{\epsilon }_x\right),\hspace{0.17em}\hspace{0.17em}{u}_y=a_y\exp \left(i{\epsilon }_y\right),\hspace{0.17em}{u}_{+}=a_{+}\exp \left(i{\epsilon }_{+}\right),u_{-}=a_{-}\exp \left(i{\epsilon }_{-}\right),$(2.5)

and can be exhaustively characterized by the Stokes parameters [1, 9, 22, 42]

$S_0={\left|\mathbf{u}\right|}^2={\left|u_x\right|}^2+{\left|u_y\right|}^2={\left|u_{+}\right|}^2+{\left|u_{-}\right|}^2=P_x^2+P_y^2+Q_x^2+Q_y^2;$

$S_1={\left|u_x\right|}^2-{\left|u_y\right|}^2=2\mathrm{R}\mathrm{e}\left(u_{+}^{*}{u}_{-}\right)=P_x^2+Q_x^2-P_y^2-Q_y^2;$

$S_2=2\mathrm{R}\mathrm{e}\left(u_x^{*}{u}_y\right)=2\mathrm{I}\mathrm{m}\left(u_{+}^{*}{u}_{-}\right)=2\left(P_x{P}_y+Q_x{Q}_y\right);$

$S_3=2\mathrm{I}\mathrm{m}\left(u_x^{*}{u}_y\right)={\left|u_{+}\right|}^2-{\left|u_{-}\right|}^2=2\left(P_x{Q}_y-Q_x{P}_y\right)=2{\mathbf{e}}_z\cdot \left(\mathbf{P}\times \mathbf{Q}\right).$(2.6)

The zero-index Stokes parameter coincides with the local intensity of the wave; for the coherent beams

$S_1^2+S_2^2+S_3^2=S_0^2;$(2.7)

the last Stokes parameter S₃ expresses the field “helicity” (degree of circular polarization; see, for example, [34, 36]). In many cases, where the field spatial distribution is important but its absolute values are of minor interest, the normalized Stokes parameters are introduced, $s_j=S_j/S_0$ (s₀ = 1).

In addition to the usual Stokes parameters, complex Stokes fields can be introduced:

$S_{12}=S_1+i{S}_2=2u_{+}^{*}{u}_{-},\hspace{0.17em}\hspace{0.17em}{S}_{23}=S_2+i{S}_3=2u_x^{*}{u}_y,$

$S_{31}=S_3+i{S}_1=2\left[\mathrm{I}\mathrm{m}\left(u_x^{*}{u}_y\right)+i\mathrm{R}\mathrm{e}\left(u_{+}^{*}{u}_{-}\right)\right]={\left|u_{+}\right|}^2-{\left|u_{-}\right|}^2+i\left({\left|u_x\right|}^2-{\left|u_y\right|}^2\right).$(2.8)

Instantaneous behavior of the electric field in the beam Eq. 2.3 cross section can be seen from equations

$P_x\cos \omega t+Q_x\sin \omega t={\mathcal{E}}_x\left(t\right),\hspace{0.17em}\hspace{0.17em}{P}_y\cos \omega t+Q_y\sin \omega t={\mathcal{E}}_y\left(t\right).$(2.9)

This is a parametric representation of an ellipse in coordinates ${\mathcal{E}}_x,{\mathcal{E}}_y$ (see Figure 1); for example, at the moment t = 0, vector $\mathcal{E}\left(0\right)$ coincides with P whereas at t = t_i = π/(2ω), $\mathcal{E}\left(t_i\right)=\mathbf{Q}$. Excluding the time variable t, one can derive an explicit equation of the ellipse in the form

${\mathcal{E}}_x^2{\left|u_y\right|}^2+{\mathcal{E}}_y^2{\left|u_x\right|}^2-2{\mathcal{E}}_x{\mathcal{E}}_y\left(P_x{P}_y+Q_x{Q}_y\right)={\left(P_x{Q}_y-Q_x{P}_y\right)}^2$

or

${\mathcal{E}}_x^2{\left|u_y\right|}^2+{\mathcal{E}}_y^2{\left|u_x\right|}^2-{\mathcal{E}}_x{\mathcal{E}}_y{S}_2=\frac{1}{4}{S}_3^2.$(2.10)

FIGURE 1

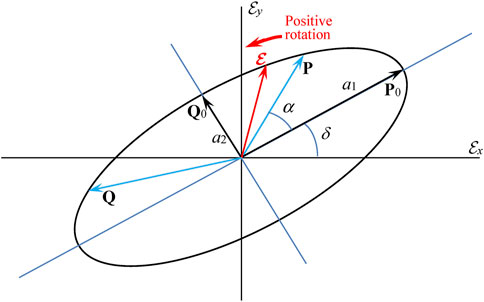
FIGURE 1. “Polarization ellipse” (Eq. 2.10) seen against the beam propagation axis z, and its main parameters. During the oscillation period, the end of the instantaneous electric field vector $\mathcal{E}$ (Eq. 2.9) (red arrow) slides along the ellipse: anti-clockwise (clockwise) rotation corresponds to the right-hand (left-hand) polarization. The meanings of the parameters $a_1$, ${\mathrm{a}}_2$, α, δ, P, P₀, and Q₀ are explained in the text.

The ellipse configuration is usually characterized by the set of parameters [9, 22, 30, 42]:

(1) major and minor semi-axes a₁ = |P₀|, |a₂| = |Q₀|, equal to

$a_{\mathrm{1,2}}=\frac{1}{\sqrt{2}}\left(\left|u_{+}\right|\pm \left|u_{-}\right|\right)=\frac{1}{\sqrt{2}}{\left(S_0\pm \sqrt{S_0^2-S_3^2}\right)}^{1/2}$(2.11)

where the sign of a₂ gives the sense of the instantaneous field vector $\mathcal{E}$ rotation;

(2) azimuth (orientation of the ellipse main axes with respect to the Cartesian axes)

$\delta =\frac{1}{2}\left(\arg u_{-}-\arg u_{+}\right)=\frac{1}{2}\arctan \left(\frac{S_2}{S_1}\right);$(2.12)

(3) the ellipse eccentricity ε

${\epsilon }^2=\frac{4\left|u_{+}\right|\left|u_{-}\right|}{{\left(\left|u_{+}\right|+\left|u_{-}\right|\right)}^2}=\frac{2}{S_3^2}\left(S_0-\sqrt{S_0^2-S_3^2}\right)\sqrt{S_0^2-S_3^2};$(2.13)

(4) the main phase (“phase of vibration”, “rectifying phase”) χ is defined by the condition that in the phase-transformed function ${\mathbf{u}}_0=\mathbf{u}{e}^{-i\chi }={\mathbf{P}}_0+i{\mathbf{Q}}_0$, the vectors P₀ and Q₀ are orthogonal, P₀⋅Q₀ = 0:

$\chi =\frac{1}{2}\arctan \frac{2\mathbf{P}\cdot \mathbf{Q}}{P^2-Q^2}=\frac{1}{2}\left(\arg u_{+}+\arg u_{-}\right).$(2.14)

The vectors P₀ and Q₀ determine the orthogonal semi-axis frame of the ellipse. The phase transformation $\mathbf{u}\to \mathbf{u}{e}^{-i\chi }$ of the field Eq. 2.3 is equivalent to the time shift, $\omega t\to \omega t+\chi$, and specifies the starting point for the instantaneous vector motion Eq. 2.9 along the elliptic trajectory. The value Eq. 2.14 means that the initial phase of the oscillations Eq. 2.9 is chosen such that for t = 0, the instantaneous vector $\mathcal{E}\left(0\right)={\mathbf{P}}_0$ and coincides with the major semi-axis of the polarization ellipse. Geometrically, χ is proportional to the ellipse area between P and P₀ and can be linked to the angle α counted from P to P₀,

$\chi =\arctan \left(\frac{a_1}{a_2}\tan \alpha \right),$(2.15)

while the positive rotation is dictated by the polarization handedness (in Figure 1, the positive rotation is counter-clockwise, and χ, α are thus negative).

3 Classification and characterization of the polarization singularities

In paraxial fields, the polarization structure is always considered in the transverse (x, y)-plane, and the small longitudinal component, inevitably present in the field according to Eqs 2.1, 2.2, 2.3, is discarded. This fact stipulates two important aspects of the “paraxial” singularities: (i) only the singularities of the transverse field described by the transverse complex amplitude u (x, y) are discussed, and (ii) the field pattern observed in a single transverse plane is, actually, a planar section of a 3D pattern evolving with the beam propagation along the longitudinal direction. Accordingly, each singular structure observed in the transverse plane is, generally, a “part” of the “genuine” spatial singularity with the dimension exceeding the dimension of its “planar” counterpart by 1: viz., a singular point (line) in the plane corresponds to the singular line (surface) in the 3D space, etc.

Another general note is that each PS, as a singularity of a vector field, is associated with certain singularities in the scalar fields of the partial polarization projections u_x, u_y and u₊, u_– Eq. 2.3. The scalar point-like singularities of a 2D fields are the prototype of other, more complex, singularities, and the corresponding ideas and concepts [1, 2, 5, 9, 35, 40] are widely used in the studies of PSs. For this reason, we remind that the generic scalar singularity of a complex field u (x, y) is associated with the isolated zero of the function u (x, y) where its phase is indeterminate (phase singularity). Upon a round trip near the singular point, the phase acquires an increment 2πl where l is the positive or negative integer topological charge (TC) of the singularity (generically, l = ±1). Accordingly, the surface of constant phase (wavefront) possesses a helical shape forming the “screw wavefront (phase) dislocation”. As the wave energy propagates, normally, along the wavefront normals, the phase dislocation inspires the helical pattern of the energy propagation (“optical vortex”). These terms and notions will be frequently employed in the following presentation.

3.1 Disclinations, s-contours and C-points

We start the discussion of planar polarization singularities with singling out the “temporary zero” singularities—so called “disclinations” [22–27]. These are the points where the instantaneous field $\mathcal{E}$(r, t) = 0 and, consequently, the field-vector direction is indeterminate. In contrast to other characteristics of monochromatic light fields, the disclinations are essentially non-stationary objects that move during the oscillation and restore periodically with the oscillation frequency.

Eq. 2.9 and the polarization ellipse they describe (see Figure 1) testify that, generically, the transverse electric field never takes a zero value. Therefore, the sets of points in which the total field vanishes at certain moments of time (this event may only occur twice during the oscillation period) should also be considered as singularities—and these singularities are stationary. The existence of such structures can be easily understood by referring to Figure 2A.

FIGURE 2

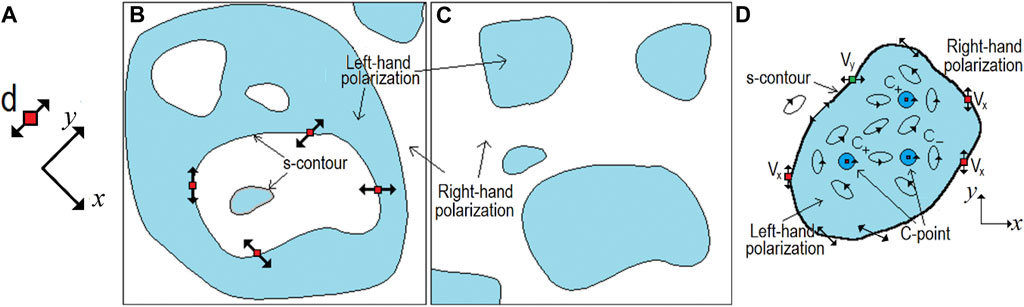
FIGURE 2. (A) Illustration of the transverse-field disclination; (B) s-contour structure of the “matryoshka” type; (C) the structure of s-contours (“islands in the ocean”), forbidden for an absolutely random field, but which can be realized in fields with predominantly circular polarization; (D) area of the field containing C-points enclosed by the s-contour where the field is linearly polarized with variable azimuth; points of x-oriented (y-oriented) polarization are highlighted as vortices of the vanishing component V_y (V_x).

Let the field be linearly polarized at some point d (Figure 2A). Let us decompose the total transverse-field vector u (Eqs 2.1, 2.2, 2.3) into orthogonal linearly polarized components with projections u_x, u_y in accordance with the basis shown in the figure. As follows from the figure, the x-component is identically equal to zero: ${\mathcal{E}}_x(d,t)=u_x\left(d\right)\times e^{i(kz-wt)}\equiv 0$, i.e., the orthogonal component ${\mathcal{E}}_y(d,t)$ represents the total transverse field. Obviously, ${\mathcal{E}}_y(d,t)$ vanishes twice during the oscillation period, and so does the total transverse electric field. As a result, a disclination is observed in the point d twice per period.

Note that the disclinations may only exist in points where the field is linearly polarized. It can be easily shown that, due to the field continuity, such points form closed, simply connected lines in the transverse plane, separating regions with different polarization handedness (see Figures 2B, C). These lines are sometimes called l-lines (see, for example, Refs. [4, 29, 31]), or, according to the terminology of the authors who first considered them [22–27], s-contours (s-surfaces in 3D [22–25]). The latter terminology is accepted here. Generally, the s-contours appear as transverse cross sections of the 3D s-surfaces, on which the field polarization is linear.

At different time moments, the field vanishes in different points, and the disclinations “run” along the s-contour. Sometimes, the disclination pairs may emerge and/or annihilate. At a fixed moment of time, the spatial structure of the field near the disclination can be analyzed with employing the full set of vector-field singularity parameters, which will be considered below. This practice is important for various physical wave fields [22] but in optics, the stationary singularities are of the main interest, and disclinations appear only in discussion for indirect illustrations and supplemental reasonings.

The possibility of the disclination “presence” on an s-contour imposes no restrictions on the polarization azimuth at its points. Moreover, it can be argued that the azimuth of this linear polarization continuously changes along a s-contour, since otherwise one would have to admit that one of the plane polarization projections of the field identically vanishes on the s-contour. That means the existence of an edge phase dislocation [5] for this polarization projection, i.e., a 3D surface, at each point of which the field projection is equal to zero. However, the existence of such field structures is problematic.

The relation between the s-contours and disclinations is natural and serves a manifestation of the fact that all special manifolds of the same physical field are interrelated [22–28]. The proper singular nature of s-contours, as well as their belonging to the PS family, is expressed by the fact that in points where the field is polarized linearly, the polarization handedness is indeterminate.

The length of s-contours can generally vary from zero (the degenerate case, where an s-contour transforms into a point) to infinity, and the mean length of the s-contour depends on the predominant polarization of the vector field [8, 44]. This mean length reaches minimum (maximum) when the polarization of the inhomogeneous field is predominantly circular (linear).

The separate s-contours are not independent and obey the laws of topological compatibility. In particular, for absolutely random fields (globally depolarized with Gaussian statistical characteristics [8, 45–47]), only the structure of s-contours is possible where a region with a certain polarization handedness (or several such regions) is embedded inside a region with the opposite polarization (Figure 2B), which, in turn, is surrounded by a region in which the handedness of the field-vector rotation reverses again, and so on. Figuratively speaking, for such a field, the structure of s-contours of the “matryoshka” type is realized. At the same time, the maximum size of the “largest” s-contour is not limited. Another possible type of s-contour structure (“islands in the ocean”) is realized in fields with predominantly circular polarization (Figure 2C) [8].

s-Contours constitute the first main type of the paraxial PSs; another type is the C-points [4, 8, 22, 31, 38] (see Figure 2D). In such points, the polarization ellipse degenerates into the circle, and, accordingly, the orientation of the polarization ellipse main axis (see Figure 1) is indeterminate. Simultaneously, there become indeterminate the polarization azimuth δ Eq. 2.12 together with the main phase (vibration phase) χ Eq. 2.14 which determines the position of the vector P = Re(u) Eq. 2.3 with respect to the ellipse’s main axes [8, 39].

The s-contours and C-points illustrate the relations of the PSs with the scalar singularities in the partial fields of orthogonally polarized components, discussed in the Introduction. Each point of an s-contour is a phase singularity of a certain plane-polarization projection of the field (in Figure 2D, the points with vertical polarization are highlighted as the vortices V_x of the planar x-projection u_x, and the points with horizontal polarization—as the vortices V_y of the planar y-projection u_y, see Eq. 2.3), and a C-point coincides with the phase singularity of a circular-polarization projection Eqs 2.3, 2.4 [4, 8, 22].

As the point of indeterminacy of the polarization azimuth δ Eq. 2.12 and the main phase χ Eq. 2.14, the C-point topology can be characterized by the corresponding phase increment on a round trip along any trajectory enclosing the C-point [8, 39, 42]. Accordingly, the 2 TCs can be introduced: the TC of the main phase

$S_C=\frac{1}{2\pi }\oint d\chi$(3.1)

and the TC of the azimuth

$I_C=\frac{1}{2\pi }\oint d\delta .$(3.2)

The quantity I_C Eq. 3.2 coincides with the Hopf—Poincare index of the C-point [30, 42]. In what follows, S_C will be called the C-point charge and I_C—its index. As both δ and χ are determined modulo π, the integer and half-integer values of S_C and I_C are admissible (this is in contrast to the phase singularities of scalar fields where only the integer TC values are possible [4–7]). For example, the polarization azimuth may rotate by ±π, ±2π, … ±Nπ on a loop around a C-point [4, 8, 42]. In principle, any natural number N is possible but only the case of N = ±1 is topologically and physically stable (generic) and occurs in general optical fields without special symmetry.

Obviously, the charge and index of the same C-point are interrelated [34, 47], and their connection can be easily seen from Eqs 2.12, 2.14. Near a left-handed C-point, u_–(r) is regular while u₊(r) possesses a phase dislocation, S_C and I_C are determined solely by arg (u₊) and differ by sign; near a right-handed C-point, the situation is opposite, which leads to a conclusion

$S_C=h{I}_C.$(3.3)

Here, h is the handedness factor, h = ±1 for the right (left) handedness of the elliptical polarization (counter-clockwise or clockwise motion of the instant field vector $\mathcal{E}$ in Figure 1).

Contrary to the scalar field singularities, the index (or charge) provides inexhaustive characterization of the PS: for any index value, three topologically different types of the polarization-ellipse behavior near a C-point are possible. These structures are known as “star”, “monstar”, and “lemon” [4, 7–9, 48] (see Figure 3).

FIGURE 3

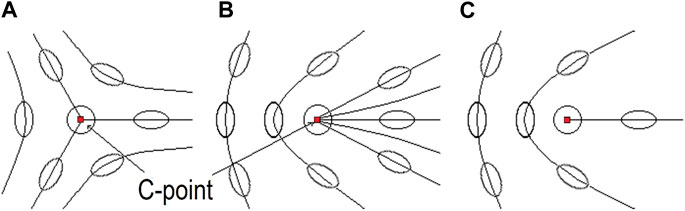
FIGURE 3. Possible structures of the polarization-ellipse field near a C-point (A) “star” (the index I_C Eq. 3.2 is negative); (B) “monstar” and (C) “lemon” (I_C is positive).

For cases (b) and (c), the major axis of polarization ellipses rotates in a counter-clockwise sense for a counter-clockwise circulation around the C-point. Conversely, in case (a), ellipses rotate in the opposite, clockwise sense, for a counter-clockwise circulation. The lemons (Figure 3C) have only one direction where the major semi-axis is radial: the major semi-axis rotates at half the rate of circulation about the C-point, and so there is undoubtedly one direction where the axis points to the centre (C-point). The same is true with the star (Figure 3A): since here the ellipses rotate in the sense opposite to the path, the axis must be radial in three places. For the monstar (Figure 3B) the pattern is not obvious. This is because the monstar is part of a more general class of C-points where the rate of rotation is not constant: the rotation rate may be greater and lower than the circulation rate, creating more than one angular direction where the polarization ellipses axes are radial. In Figure 3B, there are three angles where this is true. These radial directions are separatrices of line morphologies. Also, in the monstar of Figure 3B, in two of the sectors delineated by the separatrices, all the lines, along which the major axes are oriented, have the C-point as an end point.

Note that the TC Eq. 3.1 and index Eq. 3.2 can be defined for any area including any number of singularities. For this, the contour integral should be calculated along a singly connected closed trajectory l enclosing the considered area (see, e.g., Refs. [8, 22]):

$I_{C\mathrm{t}\mathrm{o}\mathrm{t}}=\frac{1}{2\pi }{\oint }_{l}d\delta .$(3.4)

If an s-contour is taken as the integration trajectory l, then Eq. 3.4 dictates the relationship between the s- and C-singularities, the essence of which is that the total number and the sense of revolutions of the linear polarization vector along the s-contour coincides with the sum of indices of all C-points I_Ctot bounded by this contour [8, 39, 47]. For example, in Figure 2D, the total topological index of the C-points situated inside the s-contour is I_Ctot = +1/2, which corresponds to the rotation of the field vector by π on the complete counter-clockwise circulation along the s-contour. In other words, the polarization structure inside a region enclosed by an s-contour is homomorphically “mapped” on the s-contour, and the parameters of both the s- and C-singularities determine the characteristic behavior of the whole field in any point of the region. One can state that, as in case of scalar optical fields, the set of PSs form a coherent and self-consistent “singular skeleton” of the vector field qualitatively determining the whole field in each its point.

3.2 Relations between the C-points and the singularities of partial scalar fields of the components

It was mentioned in previous sections that PSs are related with the phase singularities of scalar partial fields of the separate orthogonal projections of the field Eq. 2.3. In particular, the C-point where the field possesses a perfect circular polarization (u(r) = e_±u_±(r)), spatially coincides with the isolated zero of the opposite polarization component ($u_{\mp }\left(\mathbf{r}\right)=0$) associated with the phase dislocation and optical vortex in the field $u_{\mp }\left(\mathbf{r}\right)$ [1, 2, 5]. Similarly, the s-contours are the locus of the vortices of linearly polarized components for any orientation of the planar decomposition basis (see Eqs. 2.3, 2.4 and the discussion nearby).

Obviously, the topological characteristics of the accompanying vortices are related with the C-point morphology, which is illustrated by examples presented in Figure 4. The images represent the polarization ellipses at eight angular positions surrounding the C-point. For each ellipse, the local vectors P = Reu (red arrows) and Q = Imu (red lines without arrows) are shown as well as the ellipse major-axis orientation vectors P₀ (blue arrows). Vector P indicates the instantaneous electric field at the time moment t = 0. The polarization-ellipse azimuth δ (see Figure 1) is merely the angle between the axis X and P₀ counted from the axis X in the counter-clockwise direction (it changes by ±π on a full circulation). The main (rectifying) phase χ can be seen in the ellipses of Figure 4 from the angle α (see Eq. 2.15) counted from P to P₀, with the positive direction dictated by the polarization handedness (e.g., in Figures 4A, B, the positive direction for χ is counter-clockwise whereas in Figures 4C, D the positive direction is clockwise). According to these rules, the charge and index Eqs 3.1, 3.2 of the C-point can be determined geometrically from the images presented, and their values are indicated in the legends of each Figures 4A–D.

FIGURE 4

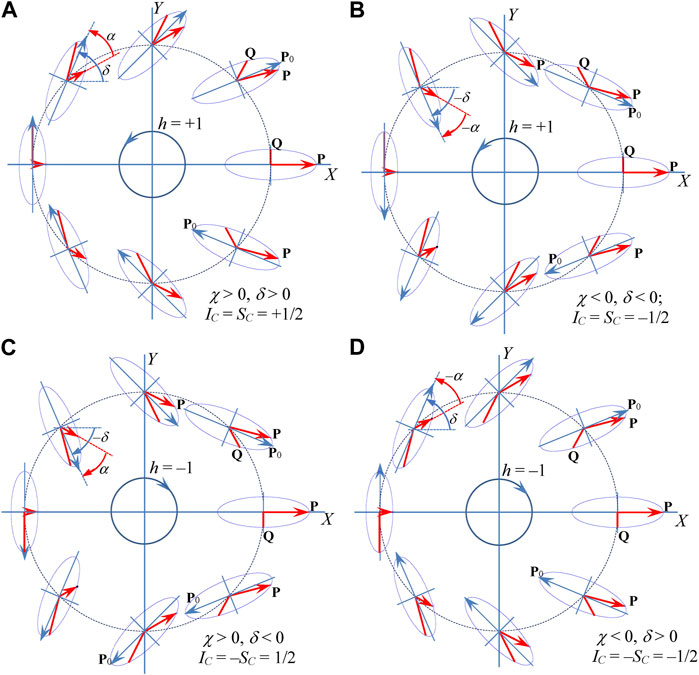
FIGURE 4. Polarization structure of the field near a C-point depending on the polarization handedness (central circle with an arrow) and on the TC l of the singular component: (A) right polarization, u₊(r) ≠ 0, u_–(r) ∼ x + iy (l = +1); (B) right polarization, u₊(r) ≠ 0, u_–(r) ∼ x—iy (l = −1); (C) left polarization, u_–(r) ≠ 0, u₊(r) ∼ x + iy (l = +1); (D) left polarization, u_–(r) ≠ 0, u₊(r) ∼ x—iy (l = −1). Upper left ellipses of each panel illustrate the geometric definitions of the polarization azimuth δ and the angle α corresponding to the main phase χ Eq. 2.15; further explanations see in text.

One can see that not only the C-point morphology but even its type (as classified in Figure 3) are determined by the common influence of the C-point handedness and the opposite-component singularity. The “lemon” structure (Figure 3C) is realized when the signs of the C-point handedness h and of the accompanying-vortex TC coincide (Figures 4A, D). If the signs are opposite, the C-point of the star type (Figure 3A) takes place (Figures 4B, C).

Other interesting aspects of the PS morphology concern the important circumstance, already mentioned in Section 3.1, that the polarization situation inside the region (in the vicinity of a C-point) can be homomorphically, along lines of the same azimuth, reflected onto the s-contour enclosing this C-point. Accordingly, one can expect a closer relationship between the characteristics of the field at the s-contour points and the C-point parameters. It turns out that this is indeed the case. In any case, such a statement is true, and emerges from the analysis of the main phase behavior on the s-contour with considering the disclinations moving along it [26]. By using Eqs 3.1, 3.2, 3.3, 3.4, one can derive the expression for the total index of such an s-contour

$I_{C\mathrm{t}\mathrm{o}\mathrm{t}}=h{S}_{C\mathrm{t}\mathrm{o}\mathrm{t}}=\frac{h}{2\pi }{\oint }_{s}d\chi .$(3.5)

Generally, the rectifying phase χ is not constant along the s-contour but varies smoothly with position. The field zeros (disclinations) exist in points and moments at which the following condition holds:

$\chi -\omega t=\frac{\pi }{2}+m\pi ,\hspace{0.17em}\hspace{0.17em}m=0,\pm 1,\pm 2,...$(3.6)

Where the distribution of χ on the s-contour has a minimum, pairs of disclinations are born, and then move off along in opposite directions. Likewise, maxima of χ on the s-contour result in annihilation events in which two disclinations move towards one another, coalesce and then disappear. The number n_d of disclinations on a closed s-contour depends on the total index Eq. 3.5 of the C-points enclosed by the contour:

$n_d=2\left|I_{C\mathrm{t}\mathrm{o}\mathrm{t}}\right|+2l\left(t\right)$(3.7)

where $2l\left(t\right)$ is the variable in time number of “temporary” disclinations caused by the “birth” and “annihilation” events during the period.

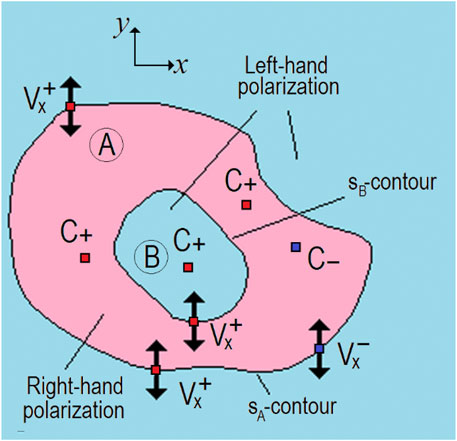
The Eq. 3.7 establishes an interesting and meaningful connection between the stationary and instantaneous (“temporary”) singularities of the field. Additionally, direct relations exist between the characteristics of C-points, enclosing s-contours, and the partial vortices of orthogonal field components. Now turn to Figure 5 where a certain region of a vector field with two s-contours and several C-points is depicted.

FIGURE 5

FIGURE 5. A region of the field cross section with left-hand (blue) and right-hand (pink) areas.

The area of left-hand polarization with one positive C-point is surrounded by the s_B-contour. This area, in turn, is enclosed by the right-hand polarization area with the s_A-contour. It was shown in Ref. [39] that, for any linearly polarized projection, the equality takes place:

$S_{C\mathrm{t}\mathrm{o}\mathrm{t}}=\frac{1}{2}{S}_{x\mathrm{t}\mathrm{o}\mathrm{t}}=\frac{1}{2}\left(S_{Ax\mathrm{t}\mathrm{o}\mathrm{t}}+S_{Bx\mathrm{t}\mathrm{o}\mathrm{t}}\right)$(3.8)

where $S_{Ax\mathrm{t}\mathrm{o}\mathrm{t}}$, $S_{Bx\mathrm{t}\mathrm{o}\mathrm{t}}$ are the total TCs of the vortex singularities of the polarization projections u_x, u_y Eq. 2.3 on the s_A- and s_B-contours, respectively. In Eq. 3.8, neither the number of vortices nor the number of s-contours is specified. In other words, the total TC of all C-points contained in a certain region is determined by the sum TC of all vortices lying on the s-contours bounding this region. Moreover, this statement remains valid if the inner regions, in turn, contain regions with a different type of polarization.

As will be shown below, the relation Eq. 3.8 has a fundamental character, which determines the mechanism of transformation of the OAM carried by the orthogonal components u_x, u_y into the OAM of the whole vector field.

3.3 V-points

Another type of singularity that should be mentioned is the singularity that occurs in fields with inhomogeneous but everywhere linear polarization, where the polarization azimuth varies from point to point. Naturally, this type of field cannot emerge as a random field. However, it can be realized in common practice: examples are the radially (azimuthally) polarized beams (“cylindrical vector beams”) described by many authors, e.g., [4, 8, 49–62]. The polarization structures characteristic for some of these beams are shown in Figures 6A–D. The corresponding beams can be obtained as superpositions of orthogonally linearly polarized TE₀₁ and TE₁₀ mode beams with different phase shifts. For example, the Gaussian beam with radial polarization (Figure 6A) is nothing but the superposition of Hermite-Gaussian TE₀₁ and TE₁₀ modes [63] in the forms Eq. 2.3 where

$u_x\left(x,y\right)=x{u}_0\left(x,y\right),\hspace{0.17em}\hspace{0.17em}{u}_y\left(x,y\right)=y{u}_0\left(x,y\right),$(3.9)

or

$u_{+}\left(x,y\right)=\left(x-iy\right)u_0\left(x,y\right){,\hspace{0.17em}\hspace{0.17em}u}_{-}\left(x,y\right)=\left(x+iy\right)u_0\left(x,y\right),$(3.10)

and $u_0\left(x,y\right)=A_0\exp \left(-\frac{x^2+y^2}{2b^2}\right)$ is the fundamental Gaussian mode. Likewise, the azimuthally polarized beam of Figure 6B represents a superposition Eq. 2.3 with

$u_x\left(x,y\right)=-y{u}_0\left(x,y\right),\hspace{0.17em}\hspace{0.17em}{u}_y\left(x,y\right)=x{u}_0\left(x,y\right)$(3.11)

and

$u_{+}\left(x,y\right)=\left(-y-ix\right)u_0\left(x,y\right),\hspace{0.17em}\hspace{0.17em}{u}_{-}\left(x,y\right)=\left(-y+ix\right)u_0\left(x,y\right),$(3.12)

and similar simple representations can be written for other beams of Figure 6. In point (x, y) = (0, 0) the polarization azimuth of the fields described by Figures 6A–D is indeterminate, and this point is thus a PS usually called “V-point”—a singularity of the continuous field of 2D vectors with variable directions and moduli. The wave structures corresponding to Figures 6E, F also contain a singularity at the beam center, but this is another class of fields (not the field of vectors but of ellipses, the polarization is not everywhere linear), and another type of PS.

FIGURE 6

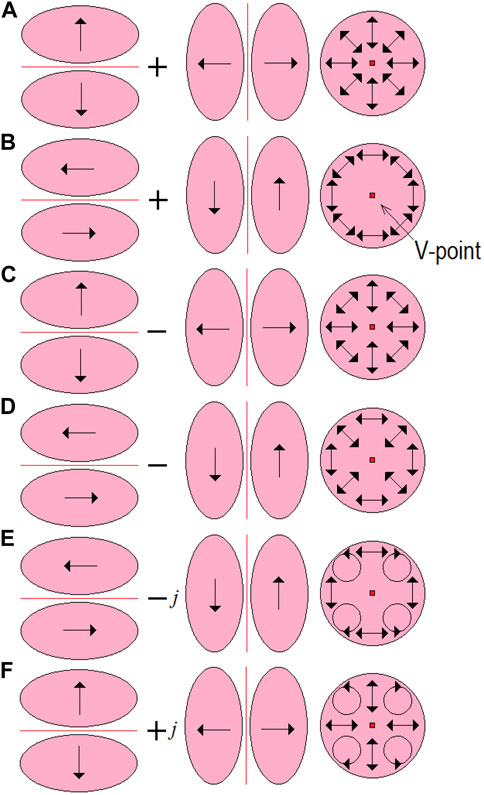
FIGURE 6. Polarization structure of some cylindrical vector beams formed as superpositions of the modes ТЕ₀₁ (TE₁₀). (A, B) Beams with radial and azimuthal polarizations (phase difference between the TE components Eq. 3.9 equals to zero); (C, D) beams with “twisting” polarization (phase difference between the TE components is π); (E, F) beams with variable elliptic polarization (phase difference between the TE components is $-\pi /2$ and $+\pi /2$, coorrespondingly).

For fields of Figures 6A–D, the definitive parameter of the vector field is the polarization direction (azimuth δ, see Eq. 2.12; Figure 1; the polarization ellipse degenerates into the rectilinear segment). The vibration phase Eq. 2.14 of a V-point is constant, so its charge Eq. 3.1 vanishes. In contrast to the C-point, the Poincare—Hopf index Eq. 3.2 of the V-points is integer. For example, it equals to +1 for the fields with radial and azimuthal polarizations of Figures 6A, B and −1 for the fields of Figures 6C, D. Note that one can imagine radially and azimuthally polarized beams with any integer index (|I_C| > 1)—such beams are admitted by the Maxwell equations or the wave equation. The possibility of such wave formations will be discussed below in the context of the PS genericity.

3.4 Stokes-formalism of the polarization singularities. Stokes-vortices

In Section 2, the description of the state of polarization by means of the Stokes parameters was discussed (Eq. 2.6). Also, the Stokes-formalism extension with the help of complex Stokes parameters Eq. 2.8 has been introduced. This procedure offers specific conveniences in the PS characterization [4, 64–66], especially when the normalized Stokes parameters $s_j=S_j/S_0$ are employed. The corresponding complex Stokes fields are defined as

$s_{12}=s_1+i{s}_2,\hspace{0.17em}{s}_{23}=s_2+i{s}_3,\hspace{0.17em}{s}_{31}=s_3+i{s}_1$(3.13)

where

$s_1=S_0^{-1}\left({\left|u_x\right|}^2-{\left|u_y\right|}^2\right),\hspace{0.17em}\hspace{0.17em}{s}_2=2S_0^{-1}\mathrm{R}\mathrm{e}\left(u_x^{*}{u}_y\right),\hspace{0.17em}{s}_3=2S_0^{-1}\mathrm{I}\mathrm{m}\left(u_x^{*}{u}_y\right).$(3.14)

Obviously, the fields Eqs 3.13, 3.14 are complex scalar fields that can possess their own systems of singularities (“Stokes-vortices”) but are interrelated and keep close connections to the partial complex amplitudes u_x, u_y. In particular, the complex Stokes field s₂₃(r) is equivalent to the off-diagonal element of the coherence matrix [67], s₂₃ = 2J_xy. The coordinates of the Stokes-vortices (phase singularities of the fields s_jk(r) (k, j = 1, 2, 3)) are determined as solutions of the system of equations

$s_j\left(\mathbf{r}\right)=0,\hspace{0.17em}\hspace{0.17em}{s}_k\left(\mathbf{r}\right)=0.$(3.15)

It follows from Eqs 3.13, 3.15 that in the points of Stokes-vortices, only one of the Stokes parameters s_j does not vanish; moreover, its absolute value equals to 1. For example, in the singular point of the field s₁₂(r), s₁ = s₂ = 0, and |s₃| = 1. Therefore, vortices of the field s₁₂(r) coincide with the C-points.

For description of the vortices of complex Stokes fields s_jk(r), it is reasonable to introduce an additional parameter ϑ = ±1 which specifies the sign of the non-vanishing Stokes parameter. Then, the vortex of the field s₁₂(r) with ϑ = 1 (ϑ = −1) corresponds to the C-point with the right-hand (left-hand) polarization.

Similarly, for the field s₂₃(r), Eq. 3.15 dictate |s₁| = 1, i.e., |u_x| = 0 or |u_y| = 0. This means that the phase singularities (vortices) of the field s₂₃(r) occur in points where at least one of the planar polarization projections of the field is singular (has a screw or edge phase dislocation [1, 2, 5]).

Now consider Eq. 3.15 separately. Each of them determines certain systems of closed contours in the (x, y) plane. For example, the condition s₁(r) = 0 determines the contours along which the intensities of the u_x and u_y components are equal, while the condition s₂(r) = 0 specifies a system of so called C-contours along which the phase difference between u_x and u_y equals to ±π/2. On the contrary, the condition s₃(r) = 0 distinguishes the lines where their phases arg (u_x) and arg (u_y) coincide.

Finally, vortices of the field s₃₁(r), accompanied by the condition |s₂(r)| = 1, appear at the intersections of s-contours and lines |u_x| = |u_y| along which the intensities of the planar polarization projections are equal. These vortices have no correspondence among the traditional PS or scalar optical singularities but single out the “reference” points of the s-contours with the polarization azimuth π/4 or 3π/4.

Naturally, using the “complex Stokes formalism”, one can formulate various kinds of the sign principles [68] that relate to C-points, or to the phase-difference vortices (see Section 3.5), and obtain various topological invariants for such fields. Note that the properties of Stokes vortices enable identification and full characterization of the traditional PSs, once the distributions of the local Stokes parameters are known. Accordingly, there is a real possibility of analyzing the features of a vector field using the methods of traditional Stokes polarimetry (see, for example, Refs. [34, 43]). However, such approaches not always lead to success, since the traditional PSs, by their nature, are phase objects (for example, the C-points can be considered as singularities of the main phase χ or the azimuth δ). As a consequence, the only unambiguous methods for identifying PS are those based on the phase-metric approaches.

Indeed, determination of the Stokes parameters relies on the intensity measurements [34, 43]. But the C-points have no direct relation to the field intensity; these can appear both in locations with a relatively high intensity and in regions where the intensity is low. Moreover, for generic fields with predominantly circular polarization, approximately 50% of the C-points are located in regions of extremely low intensity in the zone of so-called scalar zeros [8, 26]. Accordingly, because the intensity measurements in low-intensity areas suffer from significant measurement errors caused by the photodetector noise and/or external hindrances, at least half of the C-points cannot be accurately identified by the Stokes-polarimetry methods.

That is why we believe that the only relatively reliable approach for measuring the PS characteristics should involve the phase-metric methods based on the use of certain interferometric schemes, which will be considered below (Section 3.6).

3.5 Phase-difference vortices

Let us again consider the vector field decomposition into the planar polarization projections introduced by Eqs 2.3, 2.5, that is, $\mathbf{u}={\mathbf{e}}_x{u}_x+{\mathbf{e}}_y{u}_y$ where $u_x=a_x\exp \left(i{\epsilon }_x\right)$, $u_y=a_y\exp \left(i{\epsilon }_y\right)$, and define a “characteristic function”

$W_{xy}\left(x,y\right)=u_x{u}_y^{*}=a_x{a}_y\exp \left(i\Delta {\epsilon }_{xy}\right)$(3.16)

where $\Delta {\epsilon }_{xy}={\epsilon }_x-{\epsilon }_y$. Note that the characteristic function (Eq. 3.16) is, in fact, the complex conjugated Stokes parameter S₂₃ (see Eq. 2.8) which, in turn, coincides with the off-diagonal element of the 2D coherence matrix J_xy (0) [67], and expresses the same physical meaning.

The characteristic function Eq. 3.16 can be interpreted as a complex amplitude of a certain scalar field whose phase equals to the phase difference between the planar polarization components u_x and u_y. The wavefront dislocations (vortices) of the field W_xy (x, y) are situated in points where u_x = 0 or/and u_y = 0, i.e., in points where these components have their own vortices. Naturally, the phase difference $\Delta {\epsilon }_{xy}={\epsilon }_x-{\epsilon }_y$ is indeterminate in these points, so they can be considered as the phase-difference singularities (vortices), and, moreover, the topology of the characteristic function phase completely specifies the topology of the phase difference between the components of the “original” vector field. Just like the vortices of scalar fields, the phase-difference vortices are characterized by the TC; it equals to the TC of the vortex of field u_x or is opposite to the TC of u_y, regarding which of the components is singular in this point.

Obviously, the phase-difference singularity positions are determined by equations

$\mathrm{R}\mathrm{e}{W}_{xy}\left(\mathbf{r}\right)=0,\hspace{0.17em}\hspace{0.17em}\mathrm{I}\mathrm{m}{W}_{xy}\left(\mathbf{r}\right)=0.$(3.17)

Solutions of 2^nd the equation correspond to the s-contours. By the analogy, the curves determined by the 1^st Eq. 3.17, can be called “C-contours”. Along these lines, |Δε_x,y| = π/2, and points where a_x = a_y coincide with C-points.

A similar reasoning can be applied to the circular components of the decomposition Eqs 2.3, 2.4 [8]: $\mathbf{u}={\mathbf{e}}_{+}{u}_{+}+{\mathbf{e}}_{-}{u}_{-}$, $u_{+}=a_{+}\exp \left(i{\epsilon }_{+}\right)$, $u_{-}=a_{-}\exp \left(i{\epsilon }_{-}\right)$, and the analog of function Eq. 3.16 appears in the form

$W_{\pm }\left(x,y\right)=u_{+}{u}_{-}^{*}=a_{+}{a}_{-}\exp \left(i\Delta {\epsilon }_{\pm }\right).$(3.18)

Here, due to Eq. 2.12, the phase difference Δε_± = ε₊—ε_– dictates the local polarization azimuth δ. As a result, the phase-difference vortices of function Eq. 3.18 are the C-points of the “original” field u (x, y) while the contours of constant phase difference are the loci of constant polarization azimuth. With such a decomposition, the s-contours are the lines determined by the equation $a_{+}\left(x,y\right)=a_{-}\left(x,y\right)$. The TC of such a “circular” phase-difference vortex has the same sign as the index of the accompanying C-point, and its modulus is twice as large. The main consequence of such a representation of vector fields, involving the phase-difference characteristic functions Eqs 3.16, 3.18, is the validity of the “sign principle” analogous to the sign principle ruling the phase vortices of scalar fields [38, 68, 69]:

1. There is an even number of C-points on a closed equal-azimuth contour.

2. Neighboring C-points, which are located on the same equal-azimuth line, are characterized by I_C indices of different signs. Herewith, neighboring C-points can be located in areas with different directions of field vector circulation.

3.6 Interference methods of the PS investigation. Principles of the vortex analysis of vector fields

In this Section, we briefly outline some principles and results of the interferometric approaches to the PS detection and characterization [8, 44, 69, 70] which are still not well known and, to the best of our knowledge, remain underestimated by the research community.

3.6.1 Determination of the s-contour characteristics

Let us consider a vector field of the general form (for example, a random spatially-inhomogeneous in intensity and polarization optical beam) with the complex amplitude distribution u (x, y), and, again, turn to its decomposition into plane-polarized components, $\mathbf{u}={\mathbf{e}}_x{u}_x+{\mathbf{e}}_y{u}_y$. Now take an arbitrary point of the s-contour and define the Cartesian frame such that in this point u_x ≡ 0, and the corresponding instantaneous electric field $\mathcal{E}$_x(t) ≡ 0 at any moment of time. This means that, in such a basis, a vortex singularity of u_x occurs in this point. The whole instantaneous electric field is then determined by the u_y component and, according to Eqs 2.3, 2.9,

${\mathcal{E}}_y\left(t\right)=P_y\cos \omega t+Q_y\sin \omega t=\mathrm{R}\mathrm{e}\left\{a_y\exp \left[i\left({\epsilon }_y-\omega t\right)\right]\right\}.$(3.19)

Hence, the condition for the emergence of a disclination (instantaneous field zero [22]) in this point appears in the form similar to Eq. 3.6:

${\epsilon }_y-\omega t=\frac{\pi }{2}+m\pi ,\hspace{0.17em}\hspace{0.17em}m=0,\pm 1,\pm 2,...$(3.20)

Therefore, if the field is observed through a polarizer selecting the x-component, one sees the optical vortex of the u_x field; the permanent amplitude zero at the vortex axis actually “visualizes” the disclination position at the time moments $t_m=\left({\epsilon }_y-\pi /2-m\pi \right)/\omega$. (The phase ε_y can be determined with the polarizer orientation changed by 90°—of course, with respect to the reference wave phase.) Then, rotating the polarizer a little, one may single out another x-axis slightly different from the initial one. The “new” x-component vortex emerges in another point of the s-contour which indicates the disclination position at another time moment. Thus operating, one can establish the correspondence between the time-dependent position of the disclination, space-dependent position of the vortex on the s-contour and the polarizer orientation.

Experimental observations of the processes of birth, migration and annihilation of partial vortices of the polarization projections of optical fields can be performed with the Mach-Zander interferometer illustrated in Figure 7. The patterns observed when the quarter-wave plate 7 is removed, are presented in Figure 8.

FIGURE 7

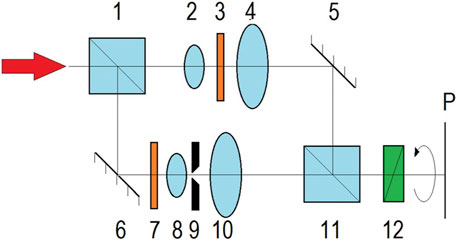
FIGURE 7. Arrangement for the experimental investigation of vortices of the planar polarization projections of an optical field (1, 11) beam-splitters; (2) micro-objective; (3) Teflon (PTFE) plate; (4) objective; (5, 6) mirrors; (7) quarter-wave plate; (8, 9, 10) beam expander; (12) analyzer.

FIGURE 8

FIGURE 8. Results of the experimental investigation of the s-contour and the points of birth and annihilation of the vortices in planar polarization projections. Interferograms (A–F) correspond to different orientations of the polarizer 12 (Figure 7); light arrows on the left side of the images indicate the spatial reference. The detected s-contour is shown in the panel (F) by the light-blue line.

On the panel (a), all fringes of the interference pattern seen in the interferogram are continuous. With a certain rotation of the polarizer 12 (Figure 7), a pronounced bending of the interference fringes is observed in the area marked in images B—E by the blue rectangle, indicating a sharp change of the optical-field phase in this region (a precursor to the vortex birth). With further rotation of the polarizer 12, a fringe break occurs in this place, which corresponds to the point of vortex birth (Figure 8C). At this point, a local extremum of the polarization azimuth takes place. In the same panel Figure 8C, one can see that a new vortex V₁ enters the observed zone; it can be identified via a downwardly directed interference “fork”. Further rotation of the analyzer demonstrates that vortices V₂ and V₃ of opposite TCs become distinguishable and move in opposite directions from the “point of birth” (Figure 8D). Simultaneously, in the same panel, one can observe a new “break” of the interference fringe (marked by the light rectangle), corresponding to the birth of another pair of vortices, V₄ and V₅. In the panel E, the vortex V₁ has annihilated with the vortex V₅ whose birth was expected in panel (d), but the vortex V₄ moves towards V₃. The image F illustrates the situation when the annihilation of V₃ and V₄ has already occurred, and continuous interference fringes are observed over the entire area of analysis, except the vicinity of the vortex V₂, that continues the migration towards the left upper corner of the interferogram. The light line in Figure 8F indicates the s-contour detected.

3.6.2 Detection and characterization of C-points

The simplest method of interference identification of C-points [8, 39] can be realized with the scheme shown in Figure 7 where the quarter-wave plate 7 is active and oriented at an angle of ±45° with respect to the analyzer 12. In other words, a pair of elements, plate λ/4 and analyzer 12, form a circular polarizer, at the output of which a linearly polarized projection will be formed, which coincides in structure with the right (left) circularly polarized component of the analyzed optical field. Due to the fact that the polarization is circular at the C-point, a vortex will appear in one or another planar projection of the field, which can be identified interferometrically. Accordingly, the sign of the vortex TC can be determined via the interference fork orientation [5] with account for the mutual orientation of the object and reference beams. The sign of such a vortex coincides with the sign of the C-point charge Eq. 3.1. Accordingly, the C-point index Eq. 3.2 can be determined from the relationship Eq. 3.3.

Figure 9 shows the results obtained from the experimental study of a spatially inhomogeneous field with predominantly circular polarization. In this case, significant differences in the polarization characteristics are concentrated in regions of low intensity, in the zone of “scalar zeros” (regions where zeros of the planar polarization components are observed). The sizes of s-contours are small and coincide, in the order of magnitude, with the sizes of these regions [8, 69]. Figure 9A presents the interferogram of a planar polarization projection with the vortices detected at the centers of the corresponding interference forks. Figure 9B shows the topological results extracted from the interferogram, with detected positions of the C-points, s-contours and locations of the vortices for some linearly polarized field projections.

FIGURE 9

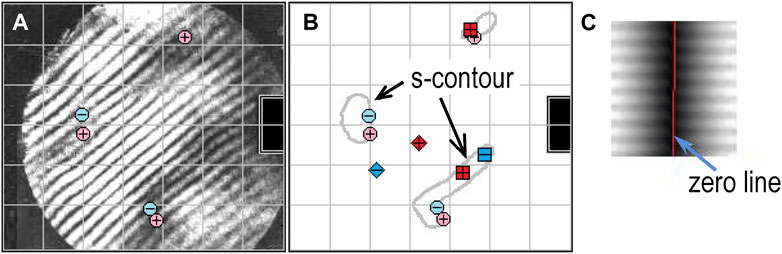
FIGURE 9. Experimental characterization of C-points: (A) interferogram of a certain planar-polarization projection of a vector field with predominantly circular polarization; (B) reconstructed positions of C-points, s-contours, and vortices of the observed projection. Symbols

,

denote the right-handed C-points with right circular polarization.

,

mark the left-handed C-points.

,

denote the vortices of the polarization projection analyzed; “+, −” inside the square (circle) corresponds to the positive or negative TC of the C-point (vortex). (C) Interference pattern of the edge phase dislocation. Fringes on opposite sides of the dislocation line (red) are shifted by half a period.

Note that the analysis of spatial distribution of C-points and their reconstructed characteristics confirms the validity of relation Eq. 3.8, which establishes a connection between the TCs of C-points and the TCs of vortices located on the s-contour surrounding the region in which these C-points are situated. The vortices located on the s-contour on the left side of Figure 9B deserve special attention. One can see that there is no C-point inside the contour; however, two vortices are observed with opposite TC signs on the s-contour. Accordingly, their total TC is equal to zero, which corresponds to the zero-value total TC of the enclosed C-points, or to their absence in the enclosed region.

3.6.3 Identification of V-points

The identification of V-points and similar singular structures can be performed in the same scheme of Figure 7, if the selected planar polarization projection forms an interference pattern characteristic for the edge wavefront dislocation [5] (see Figure 9C).

In this case, such a pattern for an azimuthally (radially) polarized beam (Figures 6A, B) and beams of the types presented in Figures 6C, D, is formed in any planar polarization projection for arbitrary orientation of the output polarizer. All beams can be distinguished if the orientation of the polarizer axis is known, by rotating it with a small step within 180°. Beams of the types E, F of Figure 6 can be identified in the same way if, after analyzing planar polarization projections (that will form an edge dislocation only for two orientations of the output polarizer), an additional λ/4 plate is inserted after the objective 4 (see Figure 7), and a circular polarizer is thus formed. As in the previous case, to completely identify the wave structures, it is necessary to know the orientations of the axes of the output polarizer and the quarter-wave plate.

4 Genericity and stability of the polarization singularities

In the early doctrine of scalar wave-field singularities, it was recognized that, despite the great diversity of topologically feasible singular structures, only a small subset of them, having the simplest forms, can be observed in common practice [4–6, 8, 9]. The reason is that the higher-order complex singularities are characterized by a higher-order symmetry, which can be destroyed under a minor perturbation which is inevitable in any real situation. Under such perturbations, the usual (non-singular) physical structures experience certain deformations but preserve their main physical features and can be described by symmetric models, at least approximately. For example, the circular intensity spot of a Gaussian beam can be slightly deformed, and the intensity maximum shifted from the nominal axis by 1% of its radius but this does not affect its qualitative identity of a “circular Gaussian beam” for the most practical needs. As a topological structure, an optical singularity differs from this example in two aspects: (1) being topologically stable, the singularity “per se” survives even through rather strong perturbations (it can be displaced, deformed but never disappears completely), and (2) being the objects of high symmetry, the higher-order singularities are topologically forbidden as soon as the ideal symmetry is destroyed, i.e., in any practical situation. This fact is usually expressed in terms of “generic” (existing spontaneously in occasionally taken optical fields) and “non-generic” (specially prepared by experimenter’s efforts and destroyable by a smallest perturbation) singularities [8].

Obviously, for the PSs, the issues of their genericity and stability are also relevant [22, 71]). Indeed, can PSs arise and exist with charges (indices) (see Eqs. 3.1, 3.2) whose module values are greater than the minimum ones? Some authors consider, in great detail, the polarization-inhomogeneous fields containing the PSs with the Poincaré-Hopf index |I_C| > 1/2 (for C-points), or |I_C| > 1 (for V-points), as the wave formations that can be realized in practice (examples can be seen in Refs. [4, 13]). Indeed, such wave formations can only be realized as a certain type of model, which can exist in the laboratory, and even employed for some practical applications but are structurally unstable both in the topological and physical sense.

Let us make a reservation right away that in real random inhomogeneously polarized fields, only PSs with the minimum values of the topological indices |I_C|, |S_C| may exist. It is also known that stable intensity zeros do not exist in vector fields [22, 72], at least, beyond the paraxial approximation (moreover, in the 3D picture, the system of PSs is completely different from the paraxial analogs [22, 35] but this topic is beyond our present consideration). However, it is interesting to inspect some aspects of “artificially” created non-generic wave structures, which can arise due to the “tricks” of an experimenter.

In general, the concepts of genericity and structural stability, introduced in [8, 22, 72, 73]), indicate that generic objects are structurally stable (in space and time) natural realizations of certain physical models that exist in a self-governed physical field without special external actions. Naturally, under certain influences on the physical process (for example, with a specific phase modulation of the field or its part, etc.), a non-generic structure can arise at some point (region) of the field, at least, because its occurrence and existence does not contradict the Maxwell equations and other fundamental laws of the electromagnetic field theory.

However, the “lifetime” of such a structure occupies only a point on the time axis. Therefore, despite that the field properties in the considered point (region) of the field dramatically change at the time of the structure’s implementation, its physical impact, as well as its “time of existence” (births, development, decay) are infinitely small. Moreover, the probability of simultaneous implementation of at least two non-generic structures is zero, and it can be argued that in a fixed plane of observation for any field and any physical impact, only one non-generic structure can exist at a given moment of time.

The concept of genericity is closely related with the concept of structural stability: the latter differs by a special emphasize of the physical processes underlying the structure’s existence. For example, a single vortex of a scalar field, or a group of vortices of the same sign are absolutely stable field objects, since their disappearance requires the implementation of a special process—annihilation. The combination of two closely spaced vortices, the specific field morphology in the vicinity of the vortex annihilation point [74–78] are absolutely generic situations, but structurally unstable, since a relatively small field perturbation can cause disintegration of such field formations. Note also that the observation of the “birth–annihilation” processes of specific field structures is strictly “tied” to the position of the “analysis plane”—the “selected” cross section of the beam that can translate along the longitudinal z-axis (see Section 2). In this context, the “point-like” nature of the “near-birth” or “near-decay” structures underlies their extreme sensitivity to the plane of analysis, since its arbitrarily small longitudinal displacement can be associated with an effective perturbation of the field.

In view of the above reasoning, practical realization of a non-generic PS (e.g., C-point with a high absolute TC) can be deemed as a system of closely positioned PSs of the same sign. In such situations, if the distance between the singularities is less than the wavelength, then:

• the field in the vicinity of this system looks as if it is the field formed near a high-index PS;

• no optical experiment is able to distinguish this system of singularities from the high-index PS.

At the same time, further wave propagation (shift of the observation plane) and even weak physical perturbations cause the transformation of this “visually non-generic” singularity into a quite common combination of simple generic PSs.

4.1 Genericity and stability of V-points

The especial attention should be paid to the V-singularities of cylindrical vector beams (see Figure 6). Indeed, according to Eqs 3.9, 3.11, such a beam can be represented as a superposition of two linearly polarized components possessing orthogonal polarizations and non-parallel edge dislocations (ED) of the phase distributions (the lines of zero amplitude which in cases of Eqs 3.9, 3.11 coincide with the (x, y) Cartesian axes) such that at their intersection the V-point is formed. However, the edge dislocation, as a scalar-field singularity, has zero TC. As a consequence, it is not protected topologically from a decay: an ED of the phase has no structural stability. The question naturally arises of how wave formations with ED (for example, beams of the TE₀₁ (TE₁₀) type) retain their basic properties during propagation.

As is known, an ED can be observed in a certain observation plane in two cases [5]:

(1) The zero-line (ZL) of the field is localized in the observation plane (see Figure 10A);

(2) There exists a zero-surface (ZS), where the wave has zero amplitude, in 3D space, and it is crossed by the observation plane (Figure 10C).

FIGURE 10

FIGURE 10. Manifestations of zero-lines (ZLs) and zero-surfaces (ZSs) regarding their positions with respect to the observation plane (horizontal plane): (A) ZL, or its segment, lies completely in the observation plane (non-generic case); (B) ZL crosses the observation plane several times; (C) ZS is decomposed into a set of adjacent ZL crossing the observation plane.

Naturally, the first case is practically not realized, since the field in which the ZL lies strictly in the observation plane, generally is not observed. The more real situation that arises in optical fields is illustrated by Figure 10B: the ZL intersects with the observation plane in a number of points, thus forming a set of vortices alternating in sign (Figure 10B). At best, the observation plane can be tangent to the ZL. At this point, an infinitesimal translation of the observation plane may cause the events of vortices’ birth or annihilation. Such a point can be conventionally called a “zero-length ED” (ZLED) [79], see Figure 10B.

At first glance, the second case—the case of ZS—is even more exotic than the ZL, since the ZS can be considered as a degenerate wave object, and such a structure should naturally decay under an infinitesimal physical perturbation. At the same time, such a transformation leads to the emergence of a bunch of ZLs located close enough and forming bunches of closely spaced vortices with an alternating TCs (see Figure 10C). Such structures, due to the topological stability of the vortices, can propagate infinitely without changing their topological characteristics.

The conclusions of the above paragraphs are confirmed by the results of numerical simulations (Figure 11). Here, the situation is considered where the initial beam with the ED (a Hermite-Gaussian beam of the form Eq. 3.9) is transmitted through a thin phase plate introducing a small random modulation of phase (Figures 11A, D); the mean value of the phase modulation is << π/2. According to the Rayleigh criterion [80], this procedure practically does not affect the beam profile immediately behind the plate (Figures 11B, C). Moreover, at a distance z from the plate corresponding to the far field (Fraunhofer zone), the overall intensity and phase profiles are still close to those of the incident Hermite-Gaussian beam (Figures 11E, F). However, the dramatic changes do occur on the geometric projection of the ED and its nearest vicinity: instead of the expected ZL, a system of vortices with alternating TC signs is formed. In other words, the ED really decays into a set of screw phase dislocations, as is well seen in Figures 11F, G.

FIGURE 11

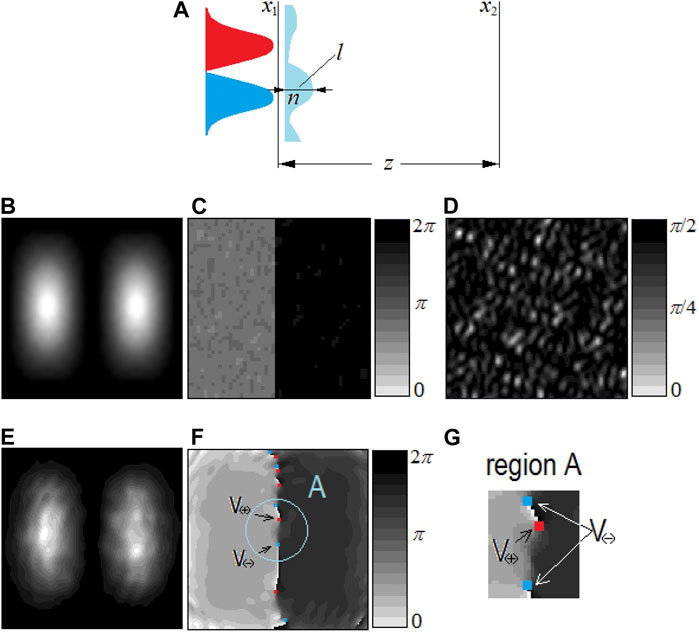
FIGURE 11. Transformation of the ED after passing through a thin random phase plate. (A) The model illustration; (B) intensity distribution immediately behind the phase plate; (C) phase distribution immediately behind the phase plate; (D) the phase modulation implemented by the phase plate; (E) intensity distribution in the far field behind the phase plate; (F) phase distribution in the far field behind the phase plate; (G) magnified region of the field marked by the light ring in (F). Red (blue) square denotes the vortex of positive (negative) TC.

Accordingly, if such individual vortices on the “zero-intensity surface” ZS (Figure 10C) are located close enough, the resulting field structure appears to look very similar to the field formed by an edge dislocation experienced weak phase perturbations. Consequently, a superposition of the similar linearly polarized beams, like those considered in Section 3.3, leads to a formation of stable vector fields with the azimuthal and radial polarizations (Figures 6A, B), and more complex fields of Figures 6C, D. This testifies for the structural stability and genericity of V-points.

5 Dynamical manifestations of the electromagnetic field near polarization singularities. Relations between the singularities and energy flows

5.1 Energy flow and momentum in paraxial fields with polarization singularities

At first glance, the presence of a PS in a vector wave does not lead to any specific physical features. Indeed, the field in a C-point, or at the points of an s-contour, is practically indistinguishable from the field in its nearest neighborhood in the traditional sense. For example, the instantaneous electric field in any point of the immediate vicinity of the C-point oscillates with describing an elliptic trajectory (see Figure 1) that differs very little from a circle. In this sense, the fields at the C-point itself and in its vicinity are almost identical. At the same time, any C-point coincides with the vortex in the partial field of the oppositely-polarized circular projection of the field; likewise, points of the s-contour are coupled with vortices of certain planar polarization projections. As is well known, in scalar fields, the vortex singularities are associated with the specific energy flow patterns, manifested as the transverse energy circulation and the local OAM of the optical field [1, 2, 5, 35, 36]. Accordingly, a specific behavior of energy flows can be expected in the PS regions, as well as the presence of the mechanical angular momentum with respect to the singularity “center”. This, in turn, leads to deep relations between the PS characteristics and the singularities of the transverse energy flow (Poynting vector) of the field [8, 37, 47, 81–87].

Prior to discuss the angular-momentum and energy-flow features associated with PSs, we establish explicit relations between the main dynamical characteristics of paraxial light beams [35, 36] and the Stokes parameters being the basis of the polarization-optics formalism (see Section 2). In paraxial fields described by Eqs. 2.1, 2.2, the energy density can be expressed as

$w=g\epsilon \left({\mathbf{u}}^{*}\cdot \mathbf{u}\right)=g\epsilon S_0,$(5.1)

where $g={\left(8\pi \right)}^{-1}$, and the Gaussian system of units is used. The energy flow density is determined by the Poynting vector U proportional to the field momentum density p:

$\mathbf{U}=\frac{c^2}{\epsilon \mu }\mathbf{p}={\mathbf{e}}_z{U}_{\parallel }+{\mathbf{U}}_{O\perp }+{\mathbf{U}}_S$(5.2)

(in view of some general considerations, we accept the Minkowski form of the electromagnetic momentum [36]; however, the accurate momentum definition and the Abraham—Minkowski dilemma [88–90] it is not important in the present context, especially when the PS phenomena in the vacuum or air are considered, and the condition ε = μ = 1 is valid). In Eq. 5.2, the first term proportional to

$U_{\parallel }=gc\sqrt{\frac{\epsilon }{\mu }}{S}_0$(5.3)

(S₀ is the zeroth Stokes parameter Eq. 2.6) describes the longitudinal energy flow associated with the usual beam intensity. (Note that sometimes the Stokes parameters are re-normalized such that to incorporate the coefficient of Eq. 5.3, after which it looks as an identity $U_{\parallel }=S_0$, but we preserve the definitions of Section 2). The main interest focuses on other terms originating from the spin-orbital decomposition of the momentum (energy flow) [35–37, 91–94]. The first of them expresses the transverse part of the “orbital” energy flow,

${\mathbf{U}}_{O\perp }=\frac{cg}{k\mu }\mathrm{I}\mathrm{m}\left({\mathbf{u}}^{*}\cdot \left({\nabla }_{\perp }\right)\mathbf{u}\right)=\frac{c^{2}g}{2\omega \mu }\left[\left(S_1+S_2\right){\nabla }_{\perp }{\epsilon }_x+\left(S_1-S_2\right){\nabla }_{\perp }{\epsilon }_y\right]=\frac{c^{2}g}{2\omega \mu }\left[\left(S_0+S_3\right){\nabla }_{\perp }{\epsilon }_{+}+\left(S_0-S_3\right){\nabla }_{\perp }{\epsilon }_{-}\right]$(5.4)

(∇_⊥ = e_x∂/∂x + e_y∂/∂y means the transverse gradient, ε_x, ε_y and ε₊, ε_– are the phases of the planar and circular polarization projections Eq. 2.5); the second is the “spin” flow [37, 91, 92] existing due to inhomogeneity of the “helicity-dependent” Stokes parameter S₃:

${\mathbf{U}}_S=-\frac{i{c}^2}{2\omega \mu }g\left({\nabla }_{\perp }\times \left[{\mathbf{u}}^{*}\times \mathbf{u}\right]\right)=\frac{c^{2}g}{2\omega \mu }\left({\mathbf{e}}_x\frac{\partial }{\partial y}-{\mathbf{e}}_y\frac{\partial }{\partial x}\right)S_3.$(5.5)

According to Eqs 5.2, 5.4, 5.5, the total transverse energy flow is determined by equation

${\mathbf{U}}_{\perp }={\mathbf{e}}_x{U}_x+{\mathbf{e}}_y{U}_y=\frac{c^{2}g}{2\omega \mu }\left[\left(S_1+S_2\right){\nabla }_{\perp }{\epsilon }_x+\left(S_1-S_2\right){\nabla }_{\perp }{\epsilon }_y+\left({\mathbf{e}}_x\frac{\partial }{\partial y}-{\mathbf{e}}_y\frac{\partial }{\partial x}\right)S_3\right].$(5.6)

Notably, Eq. 5.6 only includes partial derivatives of the phases, i.e., the initial phase is not important, and the vector field (U_x, U_y) can be restored from experimental data based on the interferometry of the polarization components and polarimetric measurements [95].

According to Eq. 5.2, transverse flows are associated with the transverse momentum components, and transverse energy circulation “generates” the optical angular momentum with respect to the longitudinal axis z. This angular momentum includes the orbital part (OAM) with the density

$\mathbf{L}=\frac{\epsilon \mu }{c^2}\left(\mathbf{r}\times {\mathbf{U}}_{O\perp }\right),$(5.7)

and the spin angular momentum (SAM) part entailed by the presence of circular polarization:

$\mathbf{J}=\frac{g\epsilon }{\omega }{\mathbf{e}}_z{S}_3+\frac{g}{2\omega k}\sqrt{\frac{\epsilon }{\mu }}\left[\left(S_0+S_3\right){\nabla }_{\perp }{\epsilon }_{+}-\left(S_0-S_3\right){\nabla }_{\perp }{\epsilon }_{-}\right].$(5.8)

The first summand of this equation represents the usual longitudinal spin momentum density of a field with circular polarization whereas the second one characterizes its relatively small variations caused by the spatial inhomogeneity of the beam.

Based on the representations Eqs 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8 and using the field decomposition into orthogonal circularly polarized components, a conclusion can be derived that in the vicinity of a C-point, optical angular momentum arises from two sources. First obvious source is the SAM caused by the field helicity (1^st summand of Eq. 5.8), and the second is the orbital flow Eq. 5.4 of a vortex that exists in one of the components, u₊ or u_–. The optical angular momentum is not an additive quantity, and the fact that it is carried by some field components does not warrants that the whole field also possesses a non-zero angular momentum, but makes this conclusion rather likely. An opposite example is the field near an s-contour: at any point of this contour, the vortex of a certain linearly-polarized component is situated (see, for example, Ref. [8]) but in the resulting vector wave, the angular momentum can hardly reach any significant value near the s-contour.

On the other hand [8, 39], indeed, there exists a direct relationship between the indices and charges of C-points, on the one hand, and the vortices of separate polarization projections of the field, on the other. As was noted in Section 3.2, the total TC Eq. 3.1 and index Eq. 3.2 of C-points situated in the area enclosed by s-contours (including internal ones, characterized by different senses of the field vector circulation, cf. Figures 2B; 5) is determined by the total TC of all vortices of an arbitrary planar polarization projection of the field, located on the s-contours enclosing this area. In this case, relation Eq. 3.8 is satisfied, which can be rewritten as:

${\displaystyle \sum }_j^N{h}_j{I}_{C\mathrm{t}\mathrm{o}\mathrm{t}}=S_{C\mathrm{t}\mathrm{o}\mathrm{t}}=\frac{1}{2}{S}_{\mathrm{t}\mathrm{o}\mathrm{t}}$(5.9)

where h_j is the handedness factor in the j-th area equal to +1 (−1) in areas with right (left) handedness, N is the number of areas with different senses of the field vector circulation.

Equation 5.9 expresses the specific form of the angular momentum conservation in the fields with inhomogeneous polarization. Due to a more complex relationship between the component vortices and the characteristics of polarization singularities, the general conclusion about the conservation of angular momentum cannot be applied to individual structures (regions) of the vector field. However, it remains valid for the entire vector field as a whole, i.e., a rather complicated transformation is observed of the angular momentum of partial field components into the angular momentum of the whole vector field.

5.2 Poynting singularities

The OAM definition Eq. 5.7 implies that it depends on the coordinate origin and can be considered for arbitrary field region, with respect to an arbitrary point. However, physically meaningful OAM values are associated with some special points of the optical field, and, particularly, special points of the Poynting-vector distribution, so called Poynting singularities (P-singularities) [8, 35, 37, 39, 47, 81–83, 95, 96]. The P-singularities are interesting not only as physically meaningful and intuitively conceivable examples of the vector-field singularities but also as light structures suitable for trapping and manipulation of micro- and nanoparticles [97–100].

Poynting singularities emerge in the field U_⊥ = (U_x, U_y) just like in other 2D vector fields [8, 35, 82], in points where both components of U_⊥ vanish: there, the vector azimuth is indeterminate. The classification of singular points is common for any 2D vector fields [101] and includes nodes (sinks and sources), saddle points, vortices (circulation points) and attractive or repelling focuses (spiral points). These are illustrated in Figure 12, and more details can be found, for example, in Refs; [2, 8, 35, 37]. In scalar beams, the Poynting singularities normally coincide with the corresponding phase singularities. For vector beams, the P-singularities of the partial fields, belonging to separate polarization projections, in many cases can be associated with the usual PSs (C-points and s-contours) [8, 37, 38]. However, for P-singularities of the total transverse flow Eq. 5.6, this association is mostly indirect: their positions and classes generally cannot be related to certain PS [37], although some definite correlations are well established [83, 91, 92].

FIGURE 12

FIGURE 12. Behavior of the transverse Poynting vector component near the P-singularity: (A) vortex-type singularity, (B) saddle, (C) attractive focus, (D) source; (B–D) represent passive singularities.

The vortex-type P-singularity is exceptional by its physical manifestations, so it is specially highlighted among other—“passive”—singularities (Figure 12). Near P-vortices, the energy circulation takes place, which is coupled with the angular momentum Eq. 5.7. That is why the vortex points can be called “application points of the momentum”, keeping in mind their specific role for the field OAM. In the vortex-singularity area, the OAM takes on a maximum value, whereas in the vicinity of a passive singularity, the OAM reaches the minimum.

Naturally, the P-singularities are characterized by the Poincaré-Hopf index Eq. 3.2 involving the flow-line azimuth. For all types of singularities presented in Figure 12, |I_C| = 1; moreover, its sign is positive for all P-singularities, except the saddle (Figure 12B) for which I_C = −1. To distinguish the vortex singularities with opposite directions of circulation, an additional characteristic is introduced: the chirality V, which equals to +1 if the component circulates counter-clockwise and −1 in the opposite case (Figure 12A).

Remarkably, any pattern of the energy flow can be associated with the specific spatial behavior of the instantaneous field distribution $\mathcal{E}$_x (x, y, t), $\mathcal{E}$_y (x, y, t) Eq. 2.9 [81, 102–104]. It was found that any time-average “stationary” energy flow can be treated as a manifestation of the “running” features of the instantaneous field oscillations, and the local energy flow density provides a natural criterion of this instantaneous motion. In particular, if the instantaneous intensity circulates around a certain point of the field, then this point is a vortex singularity of the type of Figure 12A, and the OAM arises in its vicinity.

In view of the spin-orbital momentum decomposition Eqs 5.4, 5.5 and Eqs 5.7, 5.8, it is reasonable to consider separately the singularities of the orbital Eqs 5.4 and spin Eq. 5.5 flow contributions which occur in points where

${\mathbf{U}}_{O\perp }=0,\hspace{0.17em}\hspace{0.17em}{\mathbf{U}}_S=0.$(5.10)

Accordingly, different types of singularities may exist in the fields ${\mathbf{U}}_{O\perp }$ and ${\mathbf{U}}_S$, and the points of vortex singularity, like in Figure 12A, can be considered as “application points” of the separate orbital and spin momenta.

5.3 Relations between the transverse energy flows and polarization singularities

The detailed description of the P-singularities is beyond the scope of the present review; moreover, this task is still a problem for further research efforts. Here we only mention some correlations and interactions between them and the PSs of the same field, with the special attention to the vortex-type singularities, which serve “application points” for the corresponding momentum contributions.

Naturally, in the general case, the singularities (“application points”) of different momentum contributions Eqs 5.4, 5.5, 5.6 do not coincide. All application points merge only in the beams with central symmetry. In this case, the association of the field-momentum application point with the PS, for example, with the C-point, becomes physically transparent and informative [8, 84]. Figure 13 illustrates the situation where the right-hand C-point is formed at the coordinate origin $\left(x,y\right)=\left(\mathrm{0,0}\right)$. In its vicinity, the field is formed by a superposition of two circularly polarized components Eq. 2.3, and the right-hand component is smooth and regular,

$u_{+}\left(x,y\right)=a_{+}\exp \left(i{\epsilon }_{+}\right)\approx \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t},$(5.11)

while the left-hand one takes on the form of a positive-TC vortex:

$u_{-}\left(x,y\right)=u_0\left(x+iy\right)=u_{0}r\exp \left(i\phi \right)$(5.12)

(u₀ is the normalization constant, (r, ϕ) is the polar frame). At a certain distance from the C-point, where the component amplitudes are equal, the s-contour takes place (Figures 13B, C). Between the C-point and s-contour, all states of polarization are realized that are mapped on the upper Poincare hemisphere [34], which enables to characterize such a beam as the “full Poincare beam” [66, 105–110]. According to Eqs 5.4, 5.5, 5.6,

${\mathbf{U}}_{O\perp }={\mathbf{U}}_S\propto u_0\left(-{\mathbf{e}}_{x}y+{\mathbf{e}}_{y}x\right)=u_{0}r{\mathbf{e}}_{\phi }$(5.13)

where ${\mathbf{e}}_{\phi }$ is the unit vector of the azimuthal direction, i.e., the central-symmetric energy flow circulates around the C-point (Figure 13C). Note that in this result, the contribution of the smooth component Eq. 5.11 vanishes, and the whole observable transverse energy flow Eq. 5.13 is due to the singular component Eq. 5.12. Additionally, the spin and orbital contributions in Eq. 5.13 coincide because the polarization handedness (h = −1) and the vortex TC (l = +1) in the variable component Eq. 5.12 are opposite [111]; otherwise, when the signs of h and l are the same, the resulting momentum in the nearest C-point vicinity would vanish [84, 111].

FIGURE 13

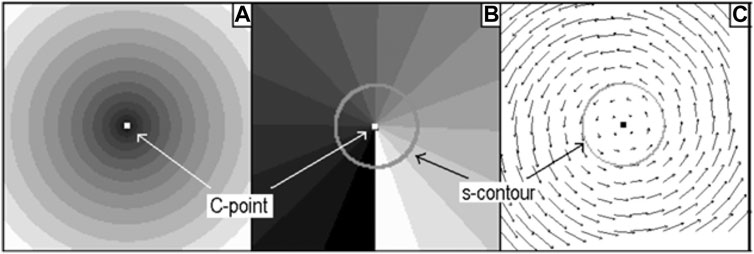
FIGURE 13. Spatial distribution of the transverse Poynting vector U_⊥ Eq. 5.6 for the symmetric field of Eqs 5.11, 5.12: (A) distribution of the modulus |U_⊥|, brighter colors denote higher values; (B) distribution of the vector azimuth, from white (ϕ = 0) to black (ϕ = 2π); (C) explicit vector-field pattern (local directions and strengths are indicated by the orientations and lengths of the arrows).

In other situations, if at least one of the main parameters (amplitude, phase) of any polarization projection shows spatial asymmetry, the application point of the total transverse momentum shifts from the C-point. For example, if in Eq. 5.11 the amplitude a₊(x, y) and phase ε₊(x, y) of the smooth component are variable, additional terms appear in the total transverse flow:

$\Delta {\mathbf{U}}_{\perp }\propto {\mathbf{e}}_x{a}_{+}\left(a_{+}\frac{\partial {\epsilon }_{+}}{\partial x}+\frac{\partial a_{+}}{\partial y}\right)+{\mathbf{e}}_y{a}_{+}\left(a_{+}\frac{\partial {\epsilon }_{+}}{\partial y}-\frac{\partial a_{+}}{\partial x}\right)$(5.14)

which should be added to Eq. 5.13. They destroy the symmetry of Figure 13, and the new situation is shown in Figure 14.

FIGURE 14

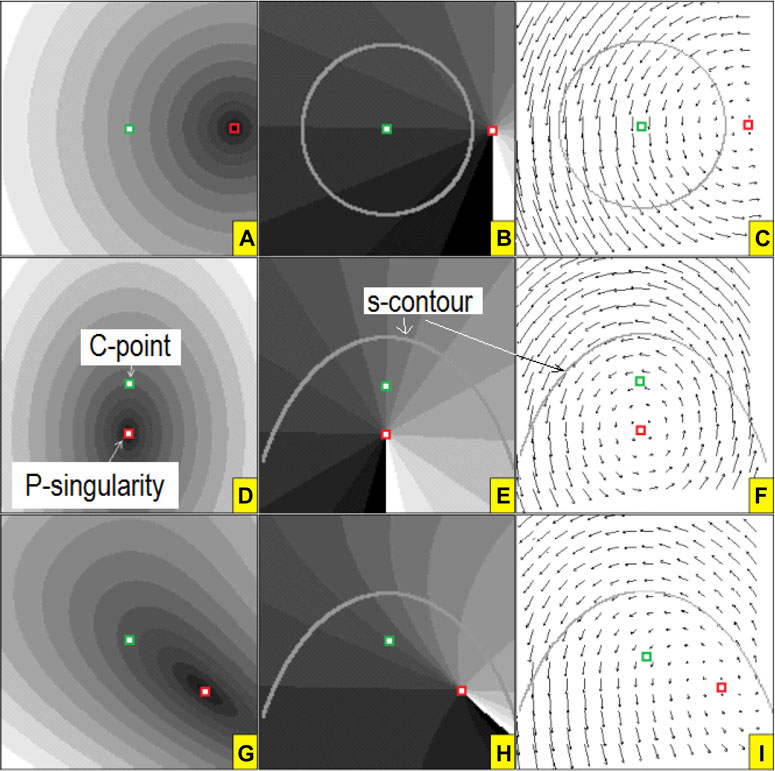
FIGURE 14. Shift of the P-singularity (vortex of the transverse Poynting vector Eq. 5.6) in the full Poincare beam [84, 105] due to asymmetry of amplitude $a$₊(x, y) and phase ε₊(x, y) of the smooth polarization component Eq. 5.11. Only the asymmetry in horizontal direction is considered (∂$a$₊/∂y = ∂ε₊/∂y = 0). Panels (A, D, G): distribution of the modulus |U_⊥|; (B, E, H): distribution of the U_⊥ azimuth (color-encoding conventions are the same as in Figure 13); (C, F, I): full vector plots with local strengths and orientations depicted by arrows. 1^st row (А–C) illustrate the influence of amplitude asymmetry ($a$₊ variable, ε₊ = const); 2^nd row (D–F)—effect of the phase asymmetry (ε₊ is variable, $a$₊ = const); 3^rd row (G–I)—combined effect of the phase and amplitude asymmetries. Symbols

,

denote the C-point and P-singularity, respectively. The gray line in figures (B, C, E, F, H, I) indicates the s-contour.

It is seen that both the phase ε₊(x, y) and the amplitude a₊(x, y) asymmetry lead to the field deformation and the P-singularity shifts with respect to the PS. The only difference is that x-dependent (y-dependent) variations of the phase (1^st row of Figure 14) induce the x-dependent (y-dependent) deformations of the U_⊥ distribution, whereas, in case of the amplitude perturbations, horizontal deformations of the amplitude invoke the vertical changes in the U_⊥ distribution, and vice versa. Note that the application point of the total transverse momentum (P-singularity) can cross the s-contour and move even to a region with an opposite field handedness (see Figures 14A–C).

At the same time, relations between the characteristics of C-points and P-singularities are preserved even in random non-uniformly polarized fields. Negative (positive) C-points and vortex (passive) P-singularities form associated pairs which can be considered as results of symmetry-breaking perturbations of initially symmetric structures of the type shown in Figure 13 with initially “merged” C- and P-singularities. The distance between the P-singularity and the corresponding C-point is determined by the degree of asymmetry of the orthogonal components u₊(x, y) and u_–(x, y) Eq. 2.3 of the total vector field. The situation is illustrated by the results of numerical simulation for a random vector field [112] presented in Figure 15 where a part of the beam cross section is shown with C-points and P-singularities.

FIGURE 15

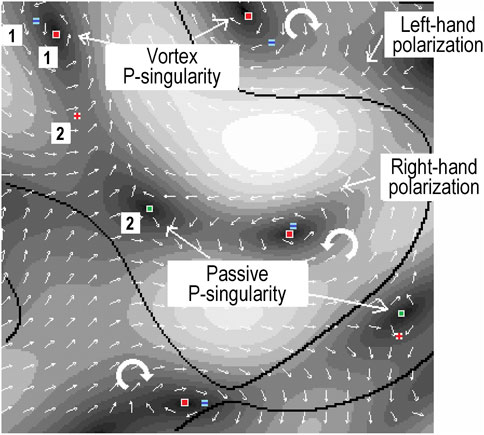
FIGURE 15. Correspondence between the С-points and Р-singularities. Symbols

,

denote the positive and negative С-points,

,

are the vortex and passive Р-singularities. Numerals 1 and 2 indicate the pairs of associated C- and Р-singularities. Local directions of the Poynting vector are indicated by arrows, black lines are the s-contours, background shows the grayscale-encoded intensity distribution with dark minima.

6 Conclusion

In the above Sections, the general description and discussion of the PSs have been presented based on the universal model of paraxial light fields. In this context, the specific properties of vector light fields appear as a generalization and further development of the scalar models where the vector nature of electromagnetic waves supplies additional internal degree of freedom. The vector field is considered as a superposition of orthogonally polarized projections, both planar and circular, and the partial fields of separate projections can be treated as scalar wave fields. Accordingly, the specific singularities of the vector fields can be analyzed with the well-developed scalar models, and each PS appears as a special point of a certain scalar field. This approach enables to consider the PSs, their structure, topological and morphology properties following to the common schemes developed for the simpler case of scalar wave fields.

This way of reasoning makes the relations between the PSs and the “underlying” scalar singularities more obvious and involve the heuristic arguments based on the pictorial and intuitive models of scalar singular optics: optical vortex, screw or edge phase dislocation, their numerical characteristics such as topological charge, Hopf–Poincare index, etc. On the other hand, it naturally invokes the dynamical features of optical fields, including the internal energy flows, momentum and angular momentum distributions. Simultaneously, this approach reveals the unique descriptive abilities of the optical dynamical characteristics for meaningful characterization of the PSs, their evolution, propagation and physical properties.

Another aspect, scrutinized in this review, embraces the issues of genericity and observability of PSs with regard to their types and physical nature, possibilities of their experimental detection and characterization by using interferometric approaches. We hope that the review has exposed additional consistent arguments to the validity and diagnostic abilities of these methods, which can be used in the future research activity addressing the PSs.

However, the knowledge associated with singular phenomena in physics, and the PS-oriented studies in particular, are still at the early stages of their potential development, and new results, ideas and concepts emerge with growing intensity. Therefore, this review is forcedly restricted to a limited number of issues which are especially close and deeply connected with the authors’ previous activity.

To conclude the review, we would like to outline some of the main milestones indicating the current state of the art and the general trends in the PS research and applications, which are left beyond its scope. First of all, we must emphasize that, due to the vector nature of electromagnetic fields, the PSs are essentially 3D objects, and their 2D models, considered here, offer sometimes very useful and suitable but inevitably simplified characterization of real physical processes. Investigation of the 3D features associated with the PSs is one of the most promising directions of physical optics discovering new impressive phenomena. Among them, studies of the dynamic behavior of PSs propagating in 3D space should be mentioned first (a succinct but informative review of them was recently published [13]). The essentially 3D structures of optical fields attract growing attention; as an example, such exotic polarization constructions as Mobius strips [113, 114] can be mentioned. Remarkable efforts are being applied to studies of the PSs dynamics in non-linear media [115, 116] and, more generally, to identification of mechanisms determining the evolution of non-generic singularities into stable generic systems. Particularly, the PS analogs of the “fractional optical vortex” [17] reveal interesting and fundamental mathematical attributes of their “life” [117].

Another consistent aspect of the PS investigation, only slightly touched in this review, concerns the transformations and mutual conversion processes of the PSs [13], which can be useful, e.g., for many practical needs. The patterns of the PS dynamics and evolution are especially interesting in partially coherent beams (see, for example, Refs. [118–122]); in particular, the PS control offers efficient channels to manipulate the beam intensity and phase profiles [121, 122]. However, the PSs in partially coherent stochastic fields are also outside our present scope.

Generally, the practical applications of the PSs are just at the beginning of the potentially brilliant development, which differs them from the scalar optical singularities whose utilitarian qualities are widely recognized [1, 2, 4, 7, 18]. Nevertheless, various practical aspects of the PSs are intensively studied, aimed, for example, at the image filtering and pattern recognition, measuring the optical activity of chiral media, as well as at the “classic” goal of the singular optics—“robust” information encoding with enhanced stability, capacity, and hindrance protection for optical communication through turbulent media, under conditions of external interference, etc. [4, 13]. Specific features of the PSs make them valuable instruments of optical metrology [123–125]. Like the familiar scalar singularities (e.g., optical vortices), the PSs create conditions for specific energy flow distributions favorable for the particles’ trapping, guiding and manipulation in nanoengineering techniques [13, 106, 126, 127].

Unfortunately, the limited frame of the present review gives no possibility to describe the vivid and informative research activity relating the practical applications of the PSs in more detail. Like many other useful and relevant data, these can be found in other recent publications, for example, Refs. [4, 7, 9, 11, 13].

Author contributions

OA, IM, and JZ contributed to conception and design of the study; IM and CZ wrote the first draft of the manuscript; AB and JZ wrote Section 1, Section 2 and Conclusion; IM and OA wrote Section 3, Section 4; IM, AB, and CZ wrote Section 5. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

Research Institute of Zhejiang University—Taizhou, Center for Modern Optical Technology, China; Ministry of Education and Science of Ukraine (project 610/22, ^#0122U001830).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Angelsky OV, Bekshaev AY, Vasnetsov MV, Zenkova CY, Maksimyak PP, Zheng J. Optical phase singularities: Physical nature, manifestations and applications. Front Phys (2022) 10:1168. doi:10.3389/fphy.2022.1060787

CrossRef Full Text | Google Scholar

2. Angelsky OV, Bekshaev AY, Mokhun , Vasnetsov MV, Zenkova CY, Hanson SG, et al. Review on the structured light properties: Rotational features and singularities. Opto-Electronics Rev (2022) 30:e140860. doi:10.24425/opelre.2022.140860

CrossRef Full Text | Google Scholar

3. Angelsky OV, Bekshaev AY, Zenkova CY, Ivansky DI, Zheng J. Correlation optics, coherence and optical singularities: Basic concepts and practical applications. Front Phys (2022) 10:924508. doi:10.3389/fphy.2022.924508

CrossRef Full Text | Google Scholar

4. Senthilkumaran P. Singularities in physics and engineering: Properties, methods, and applications. Bristol, UK: IOP Publishing (2018). doi:10.1088/978-0-7503-1698-9

CrossRef Full Text | Google Scholar

5. Soskin MS, Vasnetsov MV. Singular optics. Prog Opt (2001) 42:219–76. doi:10.1016/S0079-6638(01)80018-4

CrossRef Full Text | Google Scholar

6.OV Angelsky, editor. Introduction to singular correlation optics. Bellingham: SPIE Press (2019).

Google Scholar

7. Ruchi , Senthilkumaran P, Pal SK. Phase singularities to polarization singularities. Int J Opt (2020) 2020:1–33. doi:10.1155/2020/2812803

CrossRef Full Text | Google Scholar

8. Mokhun . Introduction to linear singular optics. In: O Angelsky, editor. Optical correlation: Techniques and applications. Bellingham, Washington: SPIE Press (2007). p. 1–131. doi:10.1117/3.714999

CrossRef Full Text | Google Scholar

9. Dennis MR, O’Holleran K, Padgett MJ. Singular optics: Optical vortices and polarization singularities. Prog Opt (2009) 53:293–363. doi:10.1016/S0079-6638(08)00205-9

CrossRef Full Text | Google Scholar

10. Gbur GJ. Singular optics. Boca Raton: CRC Press (2016). doi:10.1201/9781315374260

CrossRef Full Text | Google Scholar

11. Liu W, Liu W, Shi L, Kivshar Y. Topological polarization singularities in metaphotonics. Nanophotonics (2021) 10(5):1469–86. doi:10.1515/nanoph-2020-0654

CrossRef Full Text | Google Scholar

12. Ni J, Huang C, Zhou LM, Gu M, Song Q, Kivshar Y, et al. Multidimensional phase singularities in nanophotonics. Science (2021) 374(6566):eabj0039. doi:10.1126/science.abj0039

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang Q, Tu CH, Li YN, Wang HT. Polarization singularities: Progress, fundamental physics, and prospects. Apl Photon (2021) 6(4):040901. doi:10.1063/5.0045261

CrossRef Full Text | Google Scholar

14. Porfirev AP, Kuchmizhak AA, Gurbatov SO, Juodkazis S, Khonina SN, Kul’chin YN. Phase singularities and optical vortices in photonics. Phys Uspekhi (2021) 65(8):789–811. doi:10.3367/UFNe.2021.07.039028

CrossRef Full Text | Google Scholar

15. Andrews DL. Symmetry and quantum features in optical vortices. Symmetry (2021) 13(8):1368. doi:10.3390/sym13081368

CrossRef Full Text | Google Scholar

16. Forbes A, de Oliveira M, Dennis MR. Structured light. Nat Photon (2021) 15(4):253–62. doi:10.1038/s41566-021-00780-4

CrossRef Full Text | Google Scholar

17. Zhang H, Zeng J, Lu X, Wang Z, Zhao C, Cai Y. Review on fractional vortex beam. Nanophotonics (2022) 11(2):241–73. doi:10.1515/nanoph-2021-0616

CrossRef Full Text | Google Scholar

18. Lian Y, Qi X, Wang Y, Bai Z, Wang Y, Lu Z. OAM beam generation in space and its applications: A review. Opt Lasers Eng (2022) 151:106923. doi:10.1016/j.optlaseng.2021.106923

CrossRef Full Text | Google Scholar

19. Lian Y, Yu Y, Han S, Luan N, Wang Y, Lu Z. OAM beams generation Technology in optical fiber: A review. IEEE Sensors J (2022) 22(5):3828–43. doi:10.1109/JSEN.2022.3145833

CrossRef Full Text | Google Scholar

20. Shen Y, Pidishety S, Nape IM, Dudley A. Self-healing of structured light: A review. J Opt (2022) 24:103001. doi:10.1088/2040-8986/ac8888

CrossRef Full Text | Google Scholar

21. Bai Y, Yan J, Lv H, Yang Y. Plasmonic vortices: A review. J Opt (2022) 24:084004. doi:10.1088/2040-8986/ac7d5f

CrossRef Full Text | Google Scholar

22. Nye JF. Natural focusing and fine structure of light. Caustics and wave dislocations. Bristol: Institute of Physics Publishing (1999).

Google Scholar

23. Nye JF. Polarization effects in the diffraction of electromagnetic waves: The role of disclinations. Proc R Soc Lond A (1983) 387:105–32. doi:10.1098/rspa.1983.0053

CrossRef Full Text | Google Scholar

24. Nye JF. Lines of circular polarization in electromagnetic wave fields. Proc R Soc Lond A (1983) 389:279–90. doi:10.1098/rspa.1983.0109

CrossRef Full Text | Google Scholar

25. Nye JF, Hajnal JV. The wave structure of monochromatic electromagnetic radiation. Proc R Soc Lond A (1987) 409:21–36. doi:10.1098/rspa.1987.0002

CrossRef Full Text | Google Scholar

26. Hajnal JV. Singularities in the transverse fields of electromagnetic waves. I. Theory. Proc R Soc Lond A (1987) 414:433–46. doi:10.1098/rspa.1987.0153

CrossRef Full Text | Google Scholar

27. Hajnal JV. Singularities in the transverse fields of electromagnetic waves. II. Observations on the electric field. Proc R Soc Lond A (1987) 414:447–68. doi:10.1098/rspa.1987.0154

CrossRef Full Text | Google Scholar

28. Nye JF. Line singularities in wave fields. Phil Trans R Soc Lond A (1997) 355:2065–9. –9. doi:10.1098/rsta.1997.0107

CrossRef Full Text | Google Scholar

29. Berry MV, Dennis MR. Polarization singularities in isotropic random vector waves. Proc R Soc Lond A (2001) 457:141–55. doi:10.1098/rspa.2000.0660

CrossRef Full Text | Google Scholar

30. Dennis MR. Polarization singularities in paraxial vector fields: Morphology and statistics. Opt Commun (2002) 213:201–21. doi:10.1016/S0030-4018(02)02088-6

CrossRef Full Text | Google Scholar

31. Berry MV. The electric and magnetic polarization singularities of paraxial waves. J Opt A: Pure Appl Opt (2004) 6:475–81. doi:10.1088/1464-4258/6/5/030

CrossRef Full Text | Google Scholar

32. Freund I. Polarization singularity indices in Gaussian laser beams. Opt Commun (2002) 201:251–70. doi:10.1016/S0030-4018(01)01725-4

CrossRef Full Text | Google Scholar

33. Freund I. Polarization flowers. Opt Commun (2001) 199:47–63. doi:10.1016/S0030-4018(01)01533-4

CrossRef Full Text | Google Scholar

34. Born M, Wolf E. Principles of optics. 7th ed. Cambridge: Cambridge University Press (1999). p. 952.

Google Scholar

35. Bekshaev A, Bliokh K, Soskin M. Internal flows and energy circulation in light beams. J Opt (2011) 13(5):053001. doi:10.1088/2040-8978/13/5/053001

CrossRef Full Text | Google Scholar

36. Angelsky O, Bekshaev A, Hanson SG, Zenkova CY, Mokhun I, Zheng J. Structured light: Ideas and concepts. Front Phys (2020) 8:114. doi:10.3389/fphy.2020.00114

CrossRef Full Text | Google Scholar

37. Bekshaev AY, Soskin MS. Transverse energy flows in vectorial fields of paraxial beams with singularities. Opt Commun (2007) 271:332–48. doi:10.1016/j.optcom.2006.10.057

CrossRef Full Text | Google Scholar

38. Freund I, Soskin MS, Mokhun AI. Elliptic critical points in paraxial optical fields. Opt Commun (2002) 208:223–53. doi:10.1016/S0030-4018(02)01585-7

CrossRef Full Text | Google Scholar

39. Angelsky O, Mokhun A, Mokhun I, Soskin M. The relationship between topological characteristics of component vortices and polarization singularities. Opt Commun (2002) 207:57–65. doi:10.1016/S0030-4018(02)01479-7

CrossRef Full Text | Google Scholar

40. Bekshaev A, Soskin M, Vasnetsov M. Paraxial light beams with angular momentum. New York: Nova Science Publishers (2008). p. 112.

Google Scholar

41. Rubinsztein-Dunlop H, Forbes A, Berry MV, Dennis MR, Andrews DL, Mansuripur M, et al. Roadmap on structured light. J Opt (2017) 19:013001. doi:10.1088/2040-8978/19/1/013001

CrossRef Full Text | Google Scholar

42. Dennis MR. Topological singularities in wave fields. PhD Thesis. Bristol: University of Bristol (2001).

43. Azzam RMA, Bashara NM. Ellipsometry and polarized light. Amsterdam: North-Holland (1977).

Google Scholar

44. Angelsky O, Besaha R, Mokhun A, Mokhun I, Sopin M, Soskin M, et al. Singularities in vectoral fields. Proc SPIE (1999) 3904:40–55. doi:10.1117/12.370443

CrossRef Full Text | Google Scholar

45. Apostol A, Dogariu A. First- and second-order statistics of optical near fields. Opt Lett (2004) 29:235–7. doi:10.1364/OL.29.000235

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ellis J, Dogariu A. Discrimination of globally unpolarized fields through Stokes vector element correlations. J Opt Soc Am A (2005) 22:491–6. doi:10.1364/JOSAA.22.000491

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Mokhun I, Mokhun A, Ju V, Cojoc D, Angelsky O, Di Fabrizio E. Orbital angular momentum of inhomogeneous electromagnetic field produced by polarized optical beams. Proc SPIE (2004) 5514:652–62. doi:10.1117/12.559628

CrossRef Full Text | Google Scholar

48. Galvez EJ, Rojec BL, Beach K, Cheng X. C-Point singularities in Poincaré beams. Available at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.712.1192&rep=rep1&type=pdf (2014).

49. Tidwell SC, Ford DH, Kimura WD. Generating radially polarized beams interferometrically. Appl Opt (1990) 29:2234–9. doi:10.1364/AO.29.002234

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Tidwell SC, Kim GH, Kimura WD. Efficient radially polarized laser beam generation with a double interferometer. Appl Opt (1993) 32:5222–9. doi:10.1364/AO.32.005222

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Ruchi , Pal SK, Senthilkumaran P. C-point and V-point singularity lattice formation and index sign conversion methods. Opt Commun (2017) 393:156–68. doi:10.1016/j.optcom.2017.02.048

CrossRef Full Text | Google Scholar

52. Vyas S, Kozawa Y, Sato S. Polarization singularities in superposition of vector beams. Opt Express (2013) 21:8972–86. doi:10.1364/oe.21.008972

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Ruchi , Pal SK, Senthilkumaran P. Generation of V-point polarization singularity lattices. Opt Express (2017) 25:19326. doi:10.1364/oe.25.019326

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Bhargava Ram BS, Sharma A, Senthilkumaran P. Diffraction of V-point singularities through triangular apertures. Opt Express (2017) 25:10270–5. doi:10.1364/OE.25.010270

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Armstrong DJ, Phillips MC, Smith AV. Generation of radially polarized beams with an image-rotating resonator. Appl Opt (2003) 42:3550–4. doi:10.1364/AO.42.003550

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Oron R, Blit S, Davidson N, Friesem AA, Bomzon Z, Hasman E. The formation of laser beams with pure azimuthal or radial polarization. Appl Phys Lett (2000) 77:3322–4. doi:10.1063/1.1327271

CrossRef Full Text | Google Scholar

57. Chang KC, Lin T, Wei M-D. Generation of azimuthally and radially polarized offaxis beams with an intracavity large-apex-angle axicon. Opt Express (2013) 21:16035–42. doi:10.1364/OE.21.016035

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Kozawa Y, Sato S. Generation of a radially polarized laser beam by use of a conical Brewster prism. Opt Lett (2005) 30:3063–5. doi:10.1364/OL.30.003063

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Meier M, Romano V, Feurer T. Material processing with pulsed radially and azimuthally polarized laser radiation. Appl Phys A (2007) 86:329–34. doi:10.1007/s00339-006-3784-9

CrossRef Full Text | Google Scholar

60. Doerr CR, Buhl LL. Circular grating coupler for creating focused azimuthally and radially polarized beams. Opt Lett (2011) 36:1209–11. doi:10.1364/OL.36.001209

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Ma P, Zhou P, Ma Y, Wang X, Su R, Liu Z. Generation of azimuthally and radially polarized beams by coherent polarization beam combination. Opt Lett (2012) 37:2658–60. doi:10.1364/OL.37.002658

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Karpeev SV, Paranin VD, Khonina SN. Generation of nonuniformly polarised vortex Bessel beams by an interference polariser. Quant Electron (2018) 48:521–6. doi:10.1070/QEL16603

CrossRef Full Text | Google Scholar

63. Kogelnik H, Li T. Laser beams and resonators. Appl Opt (1966) 5(10):1550–67. doi:10.1364/AO.5.001550

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Freund I, Mokhun AI, Soskin MS, Angelsky OV, Mokhun . Stokes singularity relations. Opt Lett (2002) 27:545–7. doi:10.1364/OL.27.000545

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Pal SK, Senthilkumaran P. Synthesis of Stokes vortices. Opt Lett (2019) 44:130–3. doi:10.1364/OL.44.000130

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Arora G, Ruchi , Senthilkumaran P. Full Poincaré beam with all the Stokes vortices. Opt Lett (2019) 44:5638–41. doi:10.1364/OL.44.005638

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Perina J. Coherence of light. Berlin, Heidelberg: Springer (1985).

Google Scholar

68. Freund I, Shvartsman N. Wave-field phase singularities: The sign principle. Phys Rev A (1994) 50(6):5164–72. doi:10.1103/PhysRevA.50.5164

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Angelsky O, Besaha R, Mokhun I, Sopin M, Soskin M. Synguliarnosti u vektornykh poliakh (Singularities in vector fields). Naukovyi Visnyk Chernivetskogo Universytety Fizyka, Elektronika (1999) 57:88–99. (Scientific Gerald of Chernivtsi University, Physics, Electronics)(In Ukrainian).

Google Scholar

70. Angelsky O, Mokhun A, Mokhun I, Soskin M. Interferometric methods in diagnostics of polarization singularities. Phys Rev E (2002) 65:036602. doi:10.1103/PhysRevE.65.036602

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Nye JF. Unfolding of higher-order wave dislocations. J Opt Soc Am A (1998) 15:1132–8. doi:10.1364/JOSAA.15.001132

CrossRef Full Text | Google Scholar

72. Angelsky O, Besaha R, Mokhun I. Statistical optical fields in the vicinity of zero crossing. Proc SPIE (1997) 3317:88–96. doi:10.1117/12.295665

CrossRef Full Text | Google Scholar

73. Abramochkin E, Volostnikov V. Structurally stable singular wavefields. Proc SPIE (1998) 3487:20–8. doi:10.1117/12.317710

CrossRef Full Text | Google Scholar

74. Bekshaev A, Chernykh A, Khoroshun A, Mikhaylovskaya L. Localization and migration of phase singularities in the edge-diffracted optical-vortex beams. J Opt (2016) 18(2):024011. doi:10.1088/2040-8978/18/2/024011

CrossRef Full Text | Google Scholar

75. Bekshaev A, Chernykh A, Khoroshun A, Mikhaylovskaya L. Displacements and evolution of optical vortices in edge-diffracted Laguerre-Gaussian beams. J Opt (2017) 19(5):055605. doi:10.1088/2040-8986/aa6352

CrossRef Full Text | Google Scholar

76. Bekshaev A, Chernykh A, Khoroshun A, Mikhaylovskaya L. Singular skeleton evolution and topological reactions in edge-diffracted circular optical-vortex beams. Opt Commun (2017) 397:72–83. doi:10.1016/j.optcom.2017.03.062

CrossRef Full Text | Google Scholar

77. Bekshaev AY, Mikhaylovskaya LV. Displacements of optical vortices in Laguerre–Gaussian beams diffracted by a soft-edge screen. Opt Commun (2019) 447:80–8. doi:10.1016/j.optcom.2019.04.085

CrossRef Full Text | Google Scholar

78. Bekshaev AY, Khoroshun AN, Mikhaylovskaya LV. Transformation of the singular skeleton in optical-vortex beams diffracted by a rectilinear phase step. J Opt (2019) 21:084003. doi:10.1088/2040-8986/ab2c5b

CrossRef Full Text | Google Scholar

79. Angelsky OV, Besaha RN, Mokhun . Appearance of wave front dislocations under interference among beams with simple wave fronts. Optica Applicata (1997) 27:273–8.

CrossRef Full Text | Google Scholar

80. Rayleigh L. XXXI. Investigations in optics, with special reference to the spectroscope. Lond Edinb Dublin Phil Mag J Sci (1879) 8(49):261–74. doi:10.1080/14786447908639684

CrossRef Full Text | Google Scholar

81. Mokhun , Arkhelyuk AD, Brandel RO, Ju V. Angular momentum of electromagnetic field in areas of optical singularities. Proc SPIE (2004) 5577:47–54. doi:10.1117/12.558754

CrossRef Full Text | Google Scholar

82. Mokhun I, Brandel R, Ju V. Angular momentum of electromagnetic field in areas of polarization singularities. Ukr J Phys Opt (2006) 7:63–73. doi:10.3116/16091833/7/2/63/2006

CrossRef Full Text | Google Scholar

83. Mokhun I, Mokhun A, Ju V. Singularities of Poynting vector and the structure of optical fields. Ukr J Phys Opt (2006) 7:129–41. doi:10.3116/16091833/7/3/129/2006

CrossRef Full Text | Google Scholar

84. Mokhun , Khrobatin RI. Shift of application point of angular momentum in the area of elementary polarization singularity. J Opt A: Pure Appl Opt (2008) 10:064015. doi:10.1088/1464-4258/10/6/064015

CrossRef Full Text | Google Scholar

85. Wang XL, Chen J, Li Y, Ding J, Guo CS, Wang HT. Optical orbital angular momentum from the curl of polarization. Phys Rev Lett (2010) 105(25):253602. doi:10.1103/PhysRevLett.105.253602

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Angelsky OV, Gorsky MP, Maksimyak PP, Maksimyak AP, Hanson SG, Cyu Z. Investigation of optical currents in coherent and partially coherent vector fields. Opt Express (2011) 19:660–72. doi:10.1364/OE.19.000660

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Angelsky OV, Maksimyak PP, Bekshaev AY, Dragan GS, Maksymyak P, Zenkova CY, et al. Structured light control and diagnostics using optical crystals. Front Phys (2021) 9:715045. doi:10.3389/fphy.2021.715045

CrossRef Full Text | Google Scholar

88. Milonni PW, Boyd RW. Momentum of light in a dielectric medium. Adv Opt Photon (2010) 2(4):519–53. doi:10.1364/AOP.2.000519

CrossRef Full Text | Google Scholar

89. Barnett SM, Loudon R. The enigma of optical momentum in a medium. Phil Trans R Soc A (2010) 368:927–39. doi:10.1098/rsta.2009.0207

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Brevik I. Analysis of recent interpretations of the Abraham-Minkowski problem. Phys Rev A (2018) 98(4):043847. doi:10.1103/PhysRevA.98.043847

CrossRef Full Text | Google Scholar

91. Berry MV. Optical currents. J Opt A: Pure Appl Opt (2009) 11:094001. doi:10.1088/1464-4258/11/9/094001

CrossRef Full Text | Google Scholar

92. Bekshaev A, Soskin M. Transverse energy flows in vectorial fields of paraxial light beams. Proc SPIE (2007) 6729:67290G. doi:10.1117/12.751952

CrossRef Full Text | Google Scholar

93. Angelsky OV, Zenkova CY, Hanson SG, Zheng J. Extraordinary manifestation of evanescent wave in biomedical application. Front Phys (2020) 8:159. doi:10.3389/fphy.2020.00159

CrossRef Full Text | Google Scholar

94. Angelsky OV, Hanson SG, Maksimyak PP, Maksimyak AP, Cyu Z, Polyanskii P, et al. Influence of evanescent wave on birefringent microplates. Opt Express (2017) 25(3):2299. doi:10.1364/OE.25.002299

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Mokhun I, Arkhelyuk A, Yu G, Ye K, Yu V. Experimental analysis of the Poynting vector characteristics. Appl Opt (2012) 51:C158–62. doi:10.1364/AO.51.00C158

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Novitsky AV, Barkovsky LM. Poynting singularities in optical dynamic systems. Phys Rev A (2009) 79:033821. doi:10.1103/PhysRevA.79.033821

CrossRef Full Text | Google Scholar

97. Dienerowitz M, Mazilu M, Dholakia K. Optical manipulation of nanoparticles: A review. J Nanophoton (2008) 2(1):021875. doi:10.1117/1.2992045

CrossRef Full Text | Google Scholar

98. Otte E, Denz C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl Phys Rev (2020) 7(4):041308. doi:10.1063/5.0013276

CrossRef Full Text | Google Scholar

99. Angelsky OV, Maksymyak PP, Zenkova CY, Maksymyak AP, Hanson SG, Ivanskyi DI. Peculiarities of control of erythrocytes moving in an evanescent field. J Biomed Opt (2019) 245(5):055002. doi:10.1117/1.JBO.24.5.055002

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Angelsky OV, Zenkova CY, Maksymyak PP, Maksymyak AP, Ivanskyi DI, Tkachuk VM. Peculiarities of energy circulation in evanescent field. Application for red blood cells. Inf Optics) (2019) 28(1):11–20. doi:10.3103/s1060992x19010028

CrossRef Full Text | Google Scholar

101. Andronov AA, Vitt AA, Khaikin SE. Theory of oscillators. New York: Dover (1987).

Google Scholar

102. Bekshaev AY. Transverse rotation of the instantaneous field distribution and the orbital angular momentum of a light beam. J Opt A: Pure Appl Opt (2009) 11(9):094004. doi:10.1088/1464-4258/11/9/094004

CrossRef Full Text | Google Scholar

103. Bekshaev AY. Internal energy flows and instantaneous field of a monochromatic paraxial light beam. Appl Opt (2012) 51(10):C13–6. doi:10.1364/AO.51.000C13

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Mokhun I. Validity of running criterion. Proc SPIE (2015) 9809:20–6. doi:10.1117/12.2228955

CrossRef Full Text | Google Scholar

105. Beckley AM, Brown TG, Alonso MA. Full Poincare beams. Opt Express (2010) 18:10777–85. doi:10.1364/OE.18.010777

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Wang L-G. Optical forces on submicron particles induced by full Poincaré beams. Opt Express (2012) 20:20814–26. doi:10.1364/OE.20.020814

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Galvez E, Khadka S, Schubert W, Nomoto S. Poincaré-beam patterns produced by nonseparable superpositions of Laguerre–Gauss and polarization modes of light. Appl Opt (2012) 51:2925–34. doi:10.1364/AO.51.002925

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Ling X, Yi X, Dai Z, Wang Y, Chen L. Characterization and manipulation of full Poincaré beams on the hybrid Poincaré sphere. J Opt Soc Am B (2016) 33:2172–6. doi:10.1364/JOSAB.33.002172

CrossRef Full Text | Google Scholar

109. Krasnoshchekov YA, Yaparov VV, Taranenko VB. Rotating full Poincaré beams. Ukr J Phys Opt (2017) 18:1–8. doi:10.3116/16091833/18/1/1/2017

CrossRef Full Text | Google Scholar

110. Liu M, Huo P, Zhu W, Zhang C, Zhang S, Song M, et al. Broadband generation of perfect Poincaré beams via dielectric spin-multiplexed metasurface. Nat Commun (2021) 12:2230–9. doi:10.1038/s41467-021-22462-z

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Bekshaev A, Vasnetsov M. Vortex flow of light: “Spin” and “orbital” flows in a circularly polarized paraxial beam. In: JP Torres, and L Torner, editors. Twisted photons. Applications of light with orbital angular momentum. Weinheim: Wiley VCH (2011). p. 13–24. doi:10.1002/9783527635368.ch2

CrossRef Full Text | Google Scholar

112. Mokhun I, Galushko Y, Kharitonova Y, Viktorovskaya Y. Poynting singularities, angular momentum and “anticorrelation” in heterogeneously polarized vector field. J Optoelecronics Adv Mater (2010) 12:79–84.

Google Scholar

113. Bauer T, Banzer P, Karimi E, Orlov S, Rubano A, Marrucci L, et al. Observation of optical polarization Möbius strips. Science (2015) 347:964–6. doi:10.1126/science.1260635

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Bauer T, Neugebauer M, Leuchs G, Banzer P. Optical polarization Möbius strips and points of purely transverse spin density. Phys Rev Lett (2016) 117:013601. doi:10.1103/PhysRevLett.117.013601

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Bouchard F, Larocque H, Yao AM, Travis C, De Leon I, Rubano A, et al. Polarization shaping for control of nonlinear propagation. Phys Rev Lett (2016) 117:233903. doi:10.1103/PhysRevLett.117.233903

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Gibson CJ, Bevington P, Oppo GL, Yao AM. Control of polarization rotation in nonlinear propagation of fully structured light. Phys Rev A (2018) 97:033832. doi:10.1103/PhysRevA.97.033832

CrossRef Full Text | Google Scholar

117. Wang Y, Gbur G. Hilberts hotel in polarization singularities. Opt Lett (2017) 42:5154–7. doi:10.1364/OL.42.005154

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Felde CV, Chernyshov AA, Bogatyryova GV, Polyanskii PV, Soskin MS. Polarization singularities in partially coherent combined beams. JETP Lett (2008) 88:418–22. doi:10.1134/S002136400819003X

CrossRef Full Text | Google Scholar

119. Soskin MS, Polyanskii PV. New polarization singularities of partially coherent light beams. Proc SPIE (2010) 7613:129–39. doi:10.1117/12.840197

CrossRef Full Text | Google Scholar

120. Raburn WS, Gbur G. Singularities of partially polarized vortex beams. Front Phys (2020) 8:168. doi:10.3389/fphy.2020.00168

CrossRef Full Text | Google Scholar

121. Joshi S, Khan SN, Senthilkumaran P, Kanseri B. Statistical properties of partially coherent polarization singular vector beams. Phys Rev A (2021) 103(5):053502. doi:10.1103/PhysRevA.103.053502

CrossRef Full Text | Google Scholar

122. Zhang H, Wang H, Lu X, Zhao X, Hoenders BJ, Zhao C, et al. Statistical properties of a partially coherent vector beam with controllable spatial coherence, vortex phase, and polarization. Opt Express (2022) 30:29923–39. doi:10.1364/OE.465274

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Angelsky OV, Hanson SG, Zenkova CY, Gorsky MP, Gorodyns’ka NV. On polarization metrology (estimation) of the degree of coherence of optical waves. Opt Express (2009) 17:15623–34. doi:10.1364/OE.17.015623

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Angelsky O, Maksymyak P, Zenkova C, Ushenko O, Zheng J. New trends of optical measurements. In: O Velychko, editor. Applied aspects of modern metrology. London, UK: IntechOpen (2021). doi:10.5772/intechopen.100589

CrossRef Full Text | Google Scholar

125. Angelsky OV, Maksymyak PP, Zenkova CY, Hanson SG, Zheng J. Current trends in development of optical metrology. Opt Mem Neural Networks (2020) 29(4):269–92. doi:10.3103/S1060992X20040025

CrossRef Full Text | Google Scholar

126. Vernon AJ, Dennis MR, Rodríguez-Fortuño FJ. 3D zeros in electromagnetic fields (2023). arXiv [Preprint]. arXiv:2301.03540.

Google Scholar

127. Xu X, Nieto-Vesperinas M. Azimuthal imaginary Poynting momentum density. Phys Rev Lett (2019) 123:233902. doi:10.1103/PhysRevLett.123.233902

PubMed Abstract | CrossRef Full Text | Google Scholar