- 1Dipartimento di Scienze Matematiche ed Informatiche, Scienze Fisiche e della Terra, Università Degli Studi di Messina, Messina, Italy
- 2CAFPE and Departamento de Física Teórica y del Cosmos, Universidad de Granada, Granada, Spain
- 3Laboratory of High Energy and Comp. Physics, Tallinn, Estonia
We explore a simple and renormalizable model which incorporates a new stable fermion that accounts for the dark matter in the universe and which, at the same time, provides an interpretation of two recent measurements that deviate from the expectation in the Standard Model: the muon anomalous magnetic moment and the mass of the W boson recently recorded by the CDF collaboration. The model has a fermionic sector that involves singlet and doublet fields, in which the lightest state is the DM and interacts mainly through the Higgs portal. Two realizations of such a possibility are considered: one in which the Higgs sector is minimal and another in which it is extended to contain two doublet fields.
1 Introduction
There is a large consensus that the Standard Model (SM) of particle physics, although chiefly confirmed by the recent campaign of direct and indirect searches performed at the CERN LHC [1, 2], cannot be the ultimate theory and should only be valid at currently explored energies. One of the main reasons is that it does not involve an electrically neutral, weakly interacting massive particle (WIMP) that could account for the dark matter that apparently forms 25% of the energy budget of the universe [3]. New physics beyond the SM that incorporates such a particle is thus highly expected [4, 5]. Most interesting are the scenarios in which this WIMP interacts mainly or exclusively through the Higgs sector of the theory, the so-called Higgs portal models; see Ref. 6 for a recent review.
The need for new physics beyond the SM recently received a further boost with some unexpected experimental results performed at Fermilab and which cannot be interpreted strictly within the context of the model. The most surprising one is a new and more precise determination of the mass of the W boson performed by the CDF collaboration [7]
which not only deviates by about 7σ with respect to the SM value but is also in conflict with similar measurements performed at other colliders, such as LEP and LHC [8]. Another less surprising result is the latest Fermilab measurement of the anomalous magnetic moment of the muon,
confirming and magnifying the long-standing (g − 2)μ anomaly [10], as the deviation from the consensus theory prediction in the SM [25] is now 4.2σ,
Despite the fact that these two results are still controversial and require further experimental and theoretical scrutiny, it is tempting to interpret them as the first of the long-awaited hints of new physics beyond the SM. Nevertheless, one should at least try to relate the two anomalies and explore the possibility of embedding them into model extensions that address also some important shortcomings of the SM, in particular, those which include a viable DM candidate. This is what we attempt and explore in the present work.
We consider a rather simple particle physics scenario dubbed the singlet–doublet model [27–29] in which the DM is the lightest electrically neutral state of a new fermionic sector consisting of an admixture of SU(2) singlet and doublet fields. The new fermions obey a discrete symmetry which forces the DM to be stable and to interact with the SM particle mainly through the Higgs sector. This singlet–doublet model is thus an economical and renormalizable realization of a Higgs portal to a fermionic DM [6]. The SM extension with these fermions charged under the SU(2) group implies new contributions that could provide a theoretical interpretation of the
Two realizations of this possibility will be considered. In the first and minimal one, the DM state interacts with the SM via the single SM Higgs particle [36] with a mass of 125 GeV observed at the LHC. We will show that, although it could lead to a correct DM cosmological relic abundance assuming the freeze-out paradigm [4, 5], the model is severely constrained, in particular, by direct DM detection in astroparticle physics experiments, which excludes most of its parameter space. In addition, such a minimal extension, while it can indeed address the MW anomaly, does not explain the (g − 2)μ value. Therefore, we also consider an extension of the model in which the Higgs sector is enlarged and includes two Higgs-doublet fields to break the electroweak symmetry. This two-Higgs-doublet model (2HDM) [37] allows evading the constraints from DM direct searches while leading to a correct DM relic density and, at the same time, addressing both the MW and (g − 2)μ anomalies via the new contributions of the richer Higgs sector.
The paper is organized as follows: we introduce the fermionic singlet–doublet model with the minimal SM Higgs sector in the next section and the 2HDM extension in Section 3. In both sections, we discuss the impact on DM phenomenology and attempt to explain the values of
2 The singlet–doublet model with an SM-like Higgs sector
2.1 The theoretical setup
The so-called fermionic singlet–doublet model [27–29] [6, 38, 39] is one of the most minimal ultraviolet-complete realizations of the Higgs portal framework for dark matter, enabling the possibility of renormalizable interactions between a fermionic DM candidate and the SM Higgs doublet field. In this scenario, the spectrum of the SM is extended by two additional SU(2)L doublet fields and one singlet fermionic field
which are described by the following Lagrangian
with the implicit assumption that the new states are odd under a Z2 symmetry that forbids mixing with the SM fermions. Φ is the SM Higgs doublet which, in the unitary gauge, is
After electroweak symmetry breaking, mixing occurs between the electrically neutral components of the new fermionic fields. The mass eigenstates will be assumed to be three Majorana fermions2, whose masses are obtained by diagonalizing the mass matrix
The mass eigenstates, using the unitary 3 × 3 matrix U diagonalizing
with, by convention,
In the physical basis, the interaction Lagrangian of the new fermions reads [5]
with g the SU(2)L gauge coupling and
From the aforestated equations, one notices in particular that given its Majorana nature, the DM couples in pairs with the Z boson only via the vector–axial interaction; there are also couplings to the W boson. The model is thus not strictly of the Higgs portal type, and this will have an impact on the phenomenology, as will be seen shortly. Following Ref. 29, we will trade the parameters y1, y2 with a single coupling y and a mixing angle θ
With these elements, one can start discussing the phenomenology of the model and, in particular, the way it addresses the DM issue and the CDF measurement of MW.
2.2 The DM relic density and constraints from direct detection
In order to be a viable DM candidate, the lightest Majorana fermion should have a primordial abundance which is compatible with the measurement ΩDMh2 ≈ 0.12 ± 0.0012 performed by the Planck experiment [3]. Throughout this work, we will assume that the DM relic density is accounted for in the standard thermal freeze-out paradigm in which it is related to a thermally averaged annihilation cross-section of the order of ⟨σv⟩∝ 10−26cm3s−1 [4, 5]. In our singlet–doublet model, the DM annihilates mostly into SM fermion pairs via s-channel exchange of the H and Z bosons and, for larger DM masses, into WW, ZZ and Zh final states. The latter channels occur not only through Z and H boson exchange but also through t-channel exchange of the new fermions.
It is of note that if the DM is very close in mass to some of its fermionic partners, coannihilation processes involving the DM and these fermions, or these fermions alone, come as a supplement to DM annihilation and could, in any case, provide the correct relic density. In order to determine it with sufficient accuracy and match it with the Planck value, we have implemented the model into the numerical package micrOMEGAs [40, 41], which includes all (co)annihilation channels and all relevant effects.
There are other constraints on the DM mass and couplings beyond the one from the relic density, and the strongest one comes from direct detection in astroparticle experiments, i.e., in elastic scattering of the DM with nuclei. Our singlet–doublet DM model features both spin-independent (SI) and spin-dependent (SD) interactions. The former are due to the interaction of the DM with the Higgs boson and are described by the following DM-nucleon scattering cross-section (for simplicity, we explicitly report only the more important proton case).
where
from which one can see that it can be set to zero if the term
A blind spot
2.3 The CDF W-mass anomaly and the new fermionic sector
We come now to the discussion of the new contributions to the W boson mass and confront them with the recent CDF measurement. In leading order, the variation of the electroweak observables and, in particular, MW with respect to the SM prediction can be related to a deviation from the custodial limit Δρ = 1/(ρ − 1) = 0 of the ρ parameter, which measures the strength of the neutral to charged currents ratio at zero-momentum transfer [44, 45]:
To also take into account subleading contributions to ΔMW, one can, e.g., consider the Peskin–Takeuchi approach with the S, T, U parameters [46]. In this scheme, the largest contribution T is, in fact, simply Δρ, T ∝Δρ − Δρ|SM, while S describes new contributions from neutral current processes at different energies and U is the contribution to MW from new charged currents (this last correction is in general small and we will neglect it here). In our singlet–doublet model, the contributions to the S and T parameters originate from the new fermionic sector that couples to the W and Z bosons [47–51].
The new fermion (NF) contributions can be schematically written as [50]
where the functions F and G are given by (αEM is the fine structure constant)
As an illustration, in Figure 1, we show the regions of the [mD, mS] and [y, tan θ] planes, which provide a viable fit of the
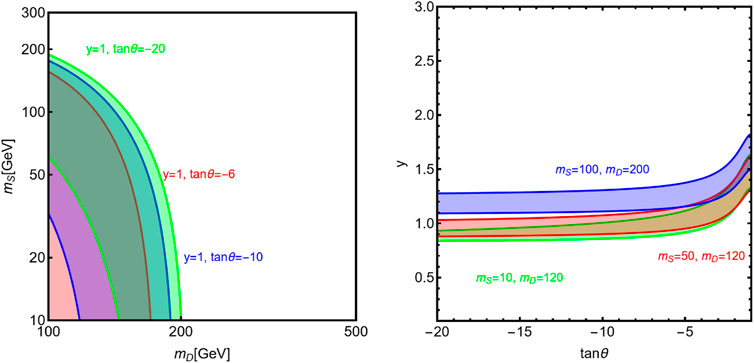
FIGURE 1. Regions of the [mD, mS] (left) and [tan θ, y] (right) planes for the singlet–doublet model with an SM-like Higgs sector which comply with the
As evidenced by Figure 1, the CDF MW measurement seems to favor relatively low values of the masses mS and mD, implying a rather light DM candidate. In such a case, a relevant complementary constraint would be represented by the invisible widths of the Z and H bosons, as both particles can decay into a pair of the escaping DM candidate if such processes are kinematically allowed, i.e., when
Additional decay processes of the Z boson are strongly constrained by precision measurements performed at LEP, which can be summarized by the upper bound Γ(Z → inv) < 2.3 MeV for mS ≤ 45 GeV [8]. Likewise, extra exotic decays of the 125 GeV Higgs boson are disfavored by LHC measurements of the H couplings to fermions and gauge bosons. The most recent results lead to an upper bound on the Higgs invisible decay branching ratio of BR(H → inv) < 0.11 [1, 2]. Additional constraints on the masses mS and mD, and on the parameters y and θ, could come from direct searches at LEP2 and at the LHC, but they are model dependent and we will ignore them here for simplicity.
Before moving to the combination of our results, we note that as the new fermionic sector does not couple or mix with SM fermions, it does not contribute to (g − 2)μ and, thus, the anomalous Fermilab result cannot be explained in this minimal model.
2.4 Combined numerical results
We now have all the elements to discuss our main numerical results that combine all collider and astroparticle physics constraints, which are reported in Figure 2. The figure compares the regions of parameter space in the [mD, mS] plane accounting for the
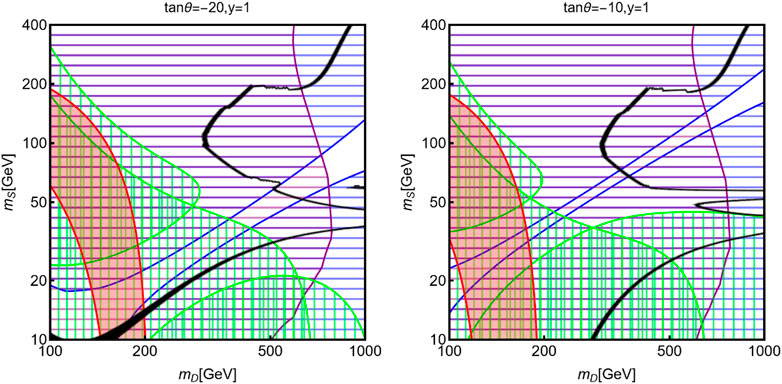
FIGURE 2. Summary of constraints for the singlet–doublet model: the black isocontour corresponds to the correct relic density, while the red regions provide a viable interpretation of the
The green regions are, instead, excluded by searches of invisible decay branching fractions of the SM Higgs and Z bosons. A given benchmark will be regarded as viable if there is a non-zero intersecting area between the red and black contours and outside the colored regions corresponding to the experimental exclusions. As can be seen, this is not the case for the benchmarks shown in the figure. This is mostly due to the very strong constraints from DM detection, which rule out most of the [mD, mS] plane. Indeed, given the different interactions responsible for the spin-independent and spin-dependent cross-sections, it is very difficult to achieve blind spots for both of them at the same time. Given also the low mS and mD values needed to reproduce the
To assess our results in a more systematic way, we have conducted a parameter scan over the following ranges for the model parameters
retaining the points complying with the CDF anomaly, the correct DM relic density, and the constraints from the Z/H invisible decay widths. The lower limit of 100 GeV on mD has been chosen to account for the LEP bound on exotic charged particle searches. These model points are shown in Figure 3 in the
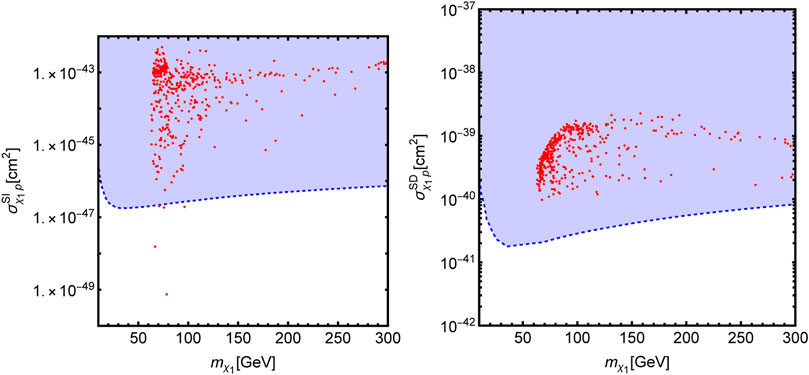
FIGURE 3. Model points of the minimal singlet–doublet model complying with CDF excess and DM relic density shown in the
As one can see, even if it is possible to achieve a small population of points, mostly around the Higgs pole
An extension of the model is thus required to bypass these limitations. An interesting possibility would be a Higgs sector with two doublets to which we turn our attention now.
3 The singlet–doublet fermion case in a 2HDM
3.1 The 2HDM and its ingredients
We consider the case that the scalar sector of the theory is composed of two doublet fields Φ1 and Φ2
After electroweak symmetry breaking, the two doublets can be decomposed as
with v1 and v2 vacuum expectation values satisfying
with
In order to be theoretically consistent, the parameters of the scalar potential should comply with a series of constraints (see, for instance, Ref. 55): i) the scalar potential should be bound from below, ii) it obeys s-wave unitarity at the tree level, iii) the electroweak vacuum should be a stable global minimum, and finally, iv) the couplings should stay perturbative, i.e., |λi| ≤ 4π. These constraints have been discussed in the literature, and a recent account has been given, e.g., in Ref. 35. They can be translated into constraints on the masses of the various Higgs mass eigenstates using relations also given in Ref. 35. We will include all these constraints in our numerical analysis.
Turning to the couplings between the physical Higgs bosons and the SM fermions, they are described by the following Yukawa-type Lagrangian:
with
To avoid the emergence of tree-level flavor-changing neutral currents, only four possible sets of assignments of the couplings can be considered [37, 56]; they are dubbed type-I, type-II, type-X (or lepton-specific), and type-Y (or flipped) 2HDMs. The corresponding couplings are summarized in Table 1. It is of note that the angle α, which determines the mixing between the neutral CP-even states h and H, is constrained by the measurement of the couplings of the h state at the LHC, which should be SM-like. The statement is enforced quantitatively by allowing only small deviations from the so-called alignment limit

TABLE 1. Couplings of the 2HDM Higgs bosons to fermions, normalized to those of the SM-like Higgs boson, as a function of the angles α and β. In the case of the CP-even Higgs states, their values in the alignment limit
Considering the interactions of the Higgs sector with the singlet–doublet fermionic states, the relevant Lagrangian is a straightforward generalization of the one presented in the previous section and can be written as (a, b = 1, 2) [39, 58]
The fermionic physical eigenstates will be still represented by three neutral Majoranas and one electrically charged Dirac fermion. This time, the neutral mixing matrix will depend on the two different vacuum expectation values: v1 and v2. Consequently, the singlet and doublet components of the DM and its couplings will also be sensitive to the angles α and β, in addition to the masses mS and mD. In the fermion mass basis, the interaction Lagrangian reads
where the Higgs couplings in the case of ϕ = h, H, A and H± are given by
with δh = δH = −1 and δA = −i. Similar to what occurs for the SM fermions, one should not assume arbitrary couplings of the new fermions with the Φ1 and Φ2 doublet fields. The simplest way to proceed would consist of extending to the new fermionic sector the same symmetries which define the four flavor-conserving 2HDMs defined earlier [39, 58]. This leads to two possible assignments of the
which will be dubbed type-A for the first one and type-B for the second configuration.
This completes the necessary ingredients to study the phenomenology of the model.
3.2 The DM sector
The phenomenology of the DM particle in the present case bears many similarities with the already-discussed minimal singlet–doublet model. We thus simply point out the additional features that are due to the extended Higgs sector. Starting with DM direct detection, the spin-independent cross-section receives an additional contribution from the t-channel exchange of the heavy CP-even H state and will be then given by [39, 58]
In contrast, the functional form of the spin-dependent cross-section is unchanged with respect to the one in the minimal model presented in Section 2.2. Again, the spin-independent cross-section can be set to zero at the tree level by choosing vanishing Higgs couplings
For what concerns the relic density, there are mostly two relevant changes with respect to the minimal model. First, we have the possibility of the extra s-channel exchange of the pseudoscalar boson A (in addition to that of the H state) in DM annihilation into SM fermion final states. This additional contribution has no counterpart in the interactions relevant to DM direct detection and, hence, could potentially alleviate the tensions that are present in the minimal model. A further relevant impact on the DM relic density would appear when one of the extra Higgs bosons is lighter than the DM particle, implying the possibility of additional annihilation channels for the latter.
Finally, there are also bounds on the DM mass and couplings from collider searches, as already discussed in the previous section when we considered the invisible decay widths of the h and Z bosons that would also apply in the 2HDM realization. One additional feature not presented earlier is that, in the case of a light pseudoscalar state, the width of the 125 GeV Higgs boson can get additional exotic contributions corresponding to the h → ZA and h → AA channels. The former is absent in the alignment limit as ghZA = 0, and the latter is subject to a very active search program at the LHC, see, e.g., Refs. 59–61.
The partial decay width of the 125 Higgs into two light pseudoscalars is given by [62]
where, using the abbreviation
One can see that it is possible to set the λhAA coupling to zero, i.e., to achieve a kind of blind spot, by imposing the relation [63]
3.3 Interpreting the CDF W-mass anomaly
We now come to the contributions of the new particles of this extended singlet–doublet scenario to the electroweak observables and, in particular, to the mass MW. In addition to the new fermion contributions to the S and T parameters, which have exactly the same functional form given in Section 2.3, one needs to include those of the extended Higgs sector. The contribution to the S and T parameters from a 2HDM can be written as [48]
where we have assumed the alignment limit
We show in Figure 4 how a viable fit of the
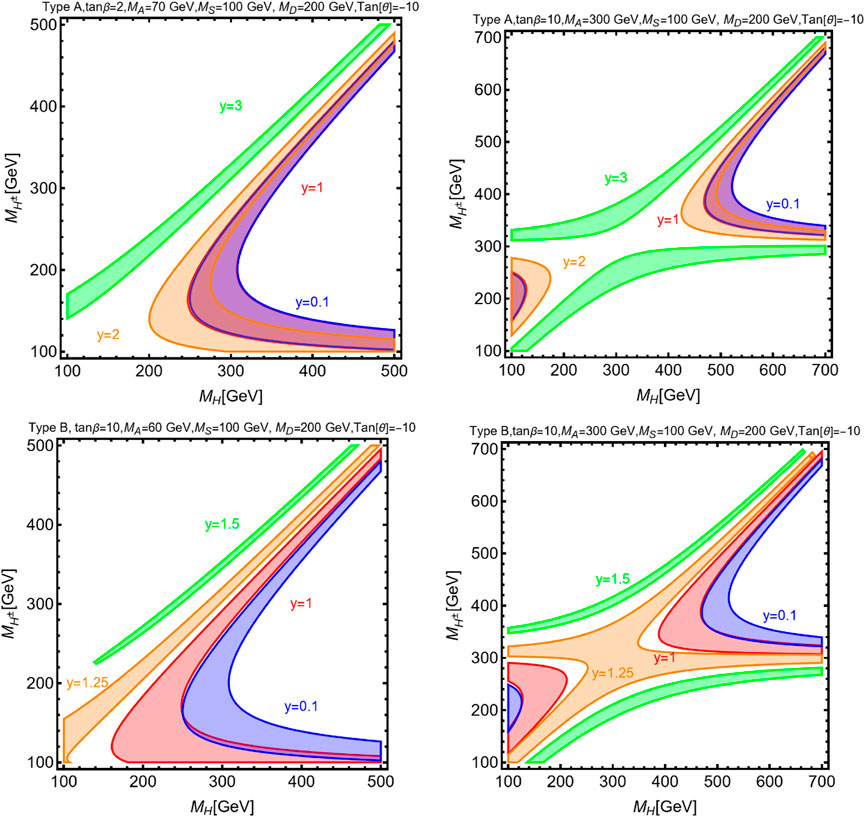
FIGURE 4. Regions in the
For what concerns the fermionic sector, we have taken for panels mS = 100 GeV, mD = 200 GeV, and tan θ = −10 and considered four values of y, corresponding to the different colored contours. We have focused again on a negative value for tan θ so that a blind spot can be enforced in DM direct detection.
The pattern in the figures can be understood as follows. For the lowest values of the DM Yukawa coupling y, the contributions of the new fermions to the electroweak observables and, hence, to MW are very small. The
3.4 Addressing the muon g-2 anomaly
In contrast to the minimal singlet–doublet model discussed in the previous section, the presence of an extended Higgs sector also allows to generate an additional contribution to the anomalous magnetic moment of the muon, which could potentially reproduce the recent experimental result. Such a contribution actually emerges from the combination of two types of terms. The first one, which appears at the one-loop level, scales as
Given the already-mentioned suppression, a proper computation of Δaμ should also include the two-loop level contribution which arises from Barr–Zee-type diagrams [66] in which there is a heavy fermion loop with an enhanced
Our numerical determination of Δaμ is nonetheless obtained by considering the full computation, as given, for example, in Ref. 69, which includes the contribution of all Higgs bosons of the 2HDM. It is arguable from the aforestated expressions that sizable couplings of the new Higgs bosons with the muons are needed to account for the (g − 2)μ anomaly; for a more detailed discussion, see, for example, Ref. 33. This requirement selects the type-II and the type-X among the flavor-preserving Yukawa configurations as they involve enhanced Higgs couplings to muons at high tan β values, gAℓℓ ∝ tan β. However, in the type-II scenario, the presence of light neutral Higgs bosons is disfavored by direct Higgs searches at the LHC, in particular, in the production processes
We show in Figure 5 the regions of the [MA, tan β] plane which provide a viable fit of the (g − 2)μ anomaly at the 1σ (green) and 2σ (yellow) levels. The two panels differ by the assignments of the
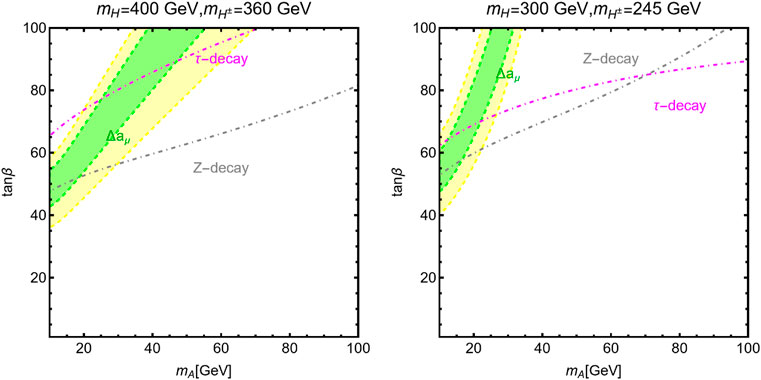
FIGURE 5. Regions providing a viable fit of the (g − 2)μ anomaly at 1σ(green) and 2σ (yellow) in the plane [MA, tan β] for two assignments of
The different shapes of the (g − 2)μ contours can be explained as follows. The value of aμ in the 2HDM is due to a non-trivial interplay between 1- and 2-loop contributions, as the latter one can potentially exceed the former since the suppression by the factor αEM is compensated by an
It is of note that the constraints from Z-decays are stronger when the hierarchy between MA and MH increases, while constraints from τ decays become weaker with increasing
3.5 LHC searches of additional Higgs bosons
Additional Higgs bosons are actively searched by the ATLAS and CMS collaborations. The strongest constraints are typically associated with searches of electrically neutral resonances. Among them, the most constraining and typically most relevant in our context are the ones coming from the processes H/A → τ+τ−; see, e.g., Ref. 70 for the most recent results. As discussed in, e.g., Refs. 33, 35 and mentioned previously, these bounds are generally rather severe in the type-II scenario at sufficiently high tan β values. Indeed, in this case, both the production cross-sections in the fusion processes gg → H/A (mediated by loops of b-quark with strongly enhanced couplings),
In turn, these bounds sensitively weaken in the case of the type-X or the lepton-specific scenario in which the H/A couplings to b-quarks are not enhanced, thus lowering the production cross-section rates (albeit also increasing the decay branching ratios). For this reason, bounds from processes not involving fermions in the final state, such as H → ZZ [76], H → AZ [77], A → HZ [78], and A → hZ [79], could become more relevant.
We have therefore computed the production cross-sections’ time decay branching ratios of all the processes mentioned previously as function of the model parameters. We have used the numerical package SuSHI [80, 81] and compared the obtained results with the corresponding bounds given by the two LHC teams. The outcome of such a comparison, when combined with other constraints, will be discussed at the end of the next subsection.
3.6 Combined results
We are now ready to combine the individual constraints previously discussed to obtain the global picture that is shown in Figure 6. We have considered three benchmarks for the singlet–doublet 2HDM model in the type-X configuration and with the tan β and Mϕ values listed on each plot and imposed the various constraints in the [mD, mS] plane. The color code is the same as the one adopted in the minimal singlet–doublet case (Figure 2). A combined fit of the correct relic density and of the
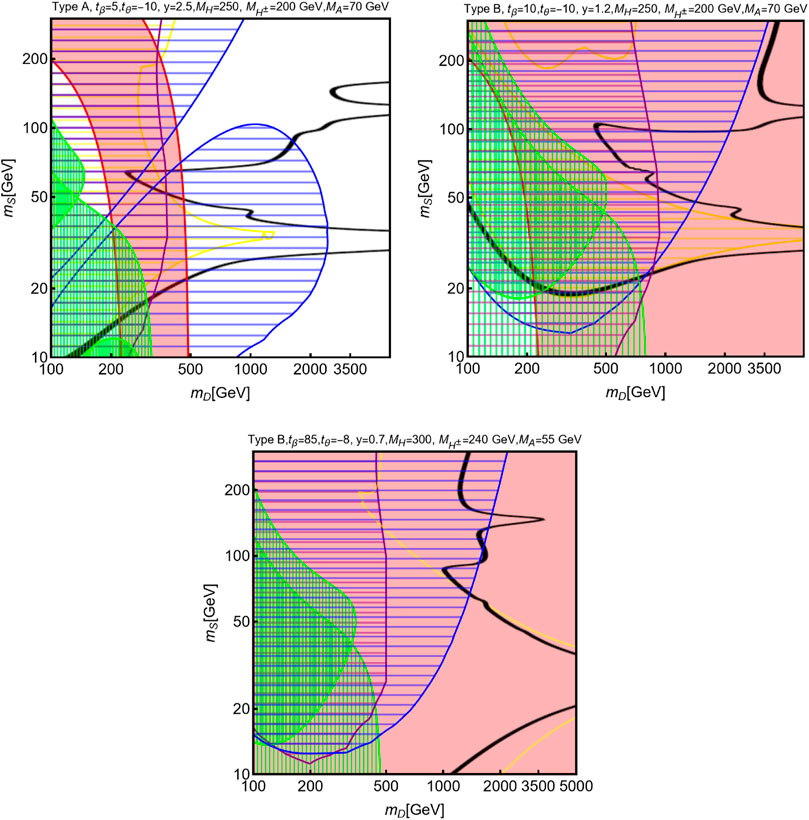
FIGURE 6. Combined constraints on the singlet–double 2HDM scenario in the [mD, mS] plane for three benchmarks in the type-X configuration, with input parameters given on top of each plot. The color convention is the same as that in Figure 2.
In the three selected benchmarks, the first two allow simply combining the CDF result for MW with DM phenomenology, and similar parameter assignments as in Figure 1 of the minimal singlet–doublet model have been adopted. Comparing the outcome with the analogous one given in the previous section, one first notices that the relic density contours have a richer pattern. This is due to the presence of the possibly light extra Higgs bosons which could meet the resonance condition,
A second notable difference with respect to the minimal model is that due to the dependence of the entries of the Majorana mixing matrix U on tan β, it is possible to further reduce the impact of the bounds from DM direct detection and from the invisible Higgs decay branching ratio, in addition to the blind spot condition (the latter is particularly evident in the first panel of the figure, showing similarly to the previous section, the excluded regions separated in two “islands”) for negative tan θ values. It is of note that for these first two benchmarks, we have considered only values
In turn, the third benchmark of Figure 6 is characterized by a very high value of tan β and a light A boson, tan β = 85 (which allows a perturbativity of all couplings in the type-X case) and MA = 55 GeV (which is not excluded by pp → A → ττ, μμ searches). As can be seen from the last panel of Figure 6, this benchmark leads at the same time to a correct DM relic density and provides viable interpretations of both the (g − 2)μ and
In addition to the study of these three specific benchmarks, we have conducted a parameter scan to provide a more complete and systematic illustration of our results. The model parameters have been varied within the following ranges:
Again, the ranges of the parameters associated with the new fermionic sector have been limited to automatically encompass the LEP bound on new charged particles, mD > 100 GeV. Furthermore, we have limited ourselves to negative values of tan θ to more easily evade DM direct detection constraints. For what concerns the 2HDM sector, we have again accounted for the LEP bound on the mass of the charged Higgs and considered only the value of MA above
The first one consists of imposing a viable fit of
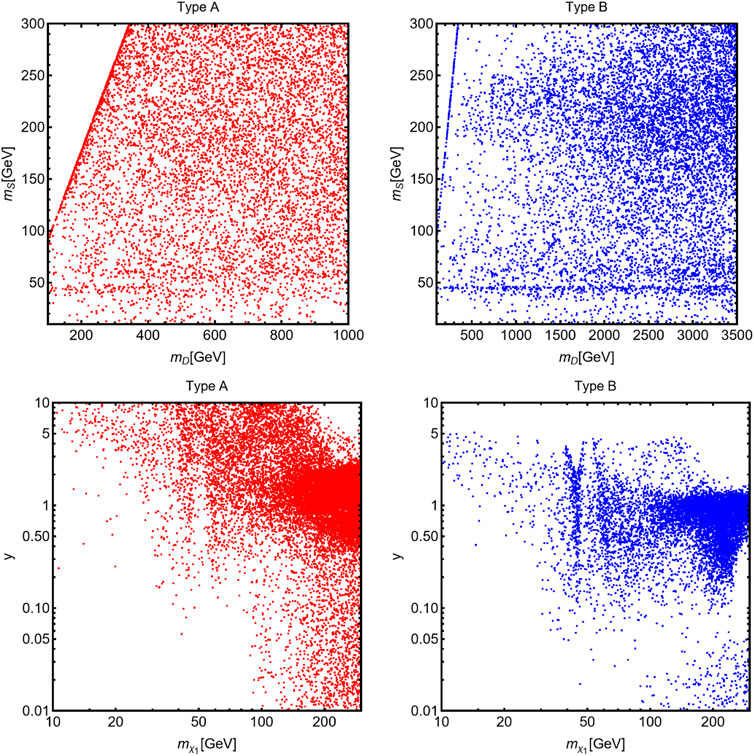
FIGURE 7. Outcome of the large parameter scan of the singlet–doublet fermionic model coupled with two Higgs-doublet fields. The model points compatible with the CDF MW value and the DM constraints are shown in the (mD, mS) plane (first row) and
In an analogous fashion, we see that the viable model points span large regions of the
To complete our analysis, we have therefore applied the constraints from the searches of neutral Higgs bosons at the LHC to the model points already shown in Figure 7, the impact of which is illustrated in Figure 8. In the left panel of the figure, we show all the model points (marked in red) already reported in Figure 7 but, this time, in the

FIGURE 8. Another view of the model points that have been shown in Figure 7 (red points) and those that are also complying with the LHC constraints from additional Higgs boson searches (green points) in the
A clearer picture is provided by the right panel of Figure 8, which shows the viable model points after applying the LHC Higgs search constraints in the (MA, tan β) bidimensional plane. From this figure, one can argue that the most relevant constraints are the ones coming from searches of A → Zh and A → ZH decay channels, as the viable points lie mostly in areas in which such decay processes are kinematically forbidden. From the figure, one can thus conclude that dedicated searches for additional Higgs bosons with couplings, as in the type-X or lepton-specific configurations, have the highest potential in constraining the scenario under investigation.
4 Conclusion
In this work, we have considered the relatively simple fermionic singlet–doublet model for dark matter, first with a minimal Higgs sector and then with an extended one to include two doublets. We have explored the possibility of simultaneously fulfilling the collider and astroparticle physics constraints that allow us to obtain a successful DM candidate with the correct relic density and addressing two recent experimental anomalies, namely, the discrepancies with respect to the prediction in the SM of the muon anomalous magnetic moment (g − 2)μ and the mass of the W boson MW measured by the CDF collaboration.
We have shown that in the minimal singlet–doublet model with an SM-like Higgs sector, as a result of the presence of a new fermionic sector coupled with the SM gauge bosons, one can address only the
Extending the Higgs sector of the singlet–doublet model to contain a second scalar doublet field is doubly beneficial. On the one hand, it allows one to evade the constraints from DM direct detection, and, on the other hand, one can also achieve a viable interpretation of the muon (g − 2) anomaly, besides the interpretation of the CDF MW measurement. This is carried out by means of a light pseudoscalar A boson that strongly couples to muons. In this case, significant parts of the parameter space of the model are still allowed, but they will be challenged by the next round of collider and astroparticle physics experiments.
Author contributions
GA, as the corresponding author, proposed the idea of the manuscript and contributed to the analysis of dark matter phenomenology and to the fit of the anomalies. AD contributed to the building of the model and assessment of theoretical constraints and constraints from Higgs physics, due to his expertise in the field. Both authors contributed equivalent amounts to the editing of the text.
Funding
AD is supported by the Estonian Research Council (ERC) grant MOBTT86 and by the Junta de Andalucia through the Talentia Senior program grants PID2021-128396NB-I00, A-FQM-211-UGR18, and P18-FR-4314 with ERDF.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Other extensions, for instance, the ones discussed Refs. 33–35, in which the DM is an isosinglet fermion and the Higgs sector is enlarged to contain two doublet fields and a singlet pseudoscalar Higgs field, can also achieve this goal.
2The possibility of Dirac fermions was proposed in Ref. 38 and leads to a similar picture compared to the Majorana case.
References
1.The ATLAS Collaboration. A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery. Nature (2022) 607:52–9. [Erratum: Nature 612, E24 (2022)]. doi:10.1038/s41586-022-04893-w
2.The CMS Collaboration. A portrait of the Higgs boson by the CMS experiment ten years after the discovery. Nature (2022) 607:60–8. doi:10.1038/s41586-022-04892-x
3. Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. VI. Cosmological parameters. Astron Astrophys (2020) 641:A6. [Erratum: Astron.Astrophys. 652, C4 (2021)]. doi:10.1051/0004-6361/201833910
4. Bertone G, Hooper D, Silk J. Particle dark matter: Evidence, candidates and constraints. Phys Rept (2005) 405:279–390. doi:10.1016/j.physrep.2004.08.031
5. Arcadi G, Dutra M, Ghosh P, Lindner M, Mambrini Y, Pierre M, et al. The waning of the WIMP? A review of models, searches, and constraints. Eur Phys J C (2018) 78:203. doi:10.1140/epjc/s10052-018-5662-y
6. Arcadi G, Djouadi A, Raidal M. Dark matter through the Higgs portal. Phys Rept (2020) 842:1–180. doi:10.1016/j.physrep.2019.11.003
7. Aaltonen T, Amerio S, Amidei D, Anastassov A, Annovi A, Antos J, et al. High-precision measurement of the W boson mass with the CDF II detector. Science (2022) 376:170–6. doi:10.1126/science.abk1781
8. Zyla PA, Barnett RM, Beringer J, Dahl O, Dwyer DA, Groom DE, et al. Review of particle physics. PTEP (2020) 2020:083C01. doi:10.1093/ptep/ptaa104
9. Abi B, Albahri T, Al-Kilani S, Allspach D, Alonzi L, Anastasi A, et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys Rev Lett (2021) 126:141801. doi:10.1103/PhysRevLett.126.141801
10. Bennett GW, Bousquet B, Brown HN, Bunce G, Carey RM, Cushman P, et al. Final report of the E821 muon anomalous magnetic moment measurement at BNL. Phys Rev D (2006) 73:072003. doi:10.1103/PhysRevD.73.072003
11. Davier M, Hoecker A, Malaescu B, Zhang Z. Reevaluation of the hadronic vacuum polarisation contributions to the Standard Model predictions of the muon g − 2 and ${\alpha (m_{Z}^2)}$ using newest hadronic cross-section data. Eur Phys J (2017) C77:827. doi:10.1140/epjc/s10052-017-5161-6
12. Keshavarzi A, Nomura D, Teubner T. Muon g − 2 and $\alpha(M_{Z}^2)$: A new data-based analysis. Phys Rev (2018) D97:114025. doi:10.1103/PhysRevD.97.114025
13. Colangelo G, Hoferichter M, Stoffer P. Two-pion contribution to hadronic vacuum polarization. J High Energ Phys (2019) 02:006. doi:10.1007/JHEP02(2019)006
14. Hoferichter M, Hoid BL, Kubis B. Three-pion contribution to hadronic vacuum polarization. J High Energ Phys (2019) 08:137. doi:10.1007/jhep08(2019)137
15. Davier M, Hoecker A, Malaescu B, Zhang Z. A new evaluation of the hadronic vacuum polarisation contributions to the muon anomalous magnetic moment and to $\boldsymbol{\alpha}(\mathbf{m}_{\spmathbf{Z}}^{\spmathbf{2}})$. Eur Phys J (2020) C80:241. [Erratum: Eur. Phys. J. C80, 410 (2020)]. doi:10.1140/epjc/s10052-020-7792-2
16. Keshavarzi A, Nomura D, Teubner T. The g − 2 of charged leptons, $\alpha(M_{Z}^2)$ and the hyperfine splitting of muonium. Phys Rev (2020) D101:014029. doi:10.1103/PhysRevD.101.014029
17. Kurz A, Liu T, Marquard P, Steinhauser M. Hadronic contribution to the muon anomalous magnetic moment to next-to-next-to-leading order. Phys Lett (2014) B734:144–7. doi:10.1016/j.physletb.2014.05.043
18. Melnikov K, Vainshtein A. Hadronic light-by-light scattering contribution to the muon anomalous magnetic moment revisited. Phys Rev (2004) D70:113006. doi:10.1103/PhysRevD.70.113006
19. Masjuan P, Sánchez-Puertas P. Pseudoscalar-pole contribution to the (gμ − 2): A rational approach. Phys Rev (2017) D95:054026. doi:10.1103/PhysRevD.95.054026
20. Colangelo G, Hoferichter M, Procura M, Stoffer P. Dispersion relation for hadronic light-by-light scattering: Two-pion contributions. J High Energ Phys (2017) 04:161. doi:10.1007/jhep04(2017)161
21. Hoferichter M, Hoid BL, Kubis B, Leupold S, Schneider SP. Dispersion relation for hadronic light-by-light scattering: Pion pole. J High Energ Phys (2018) 10:141. doi:10.1007/jhep10(2018)141
22. Gérardin A, Meyer HB, Nyffeler A. Lattice calculation of the pion transition form factor with Nf = 2 + 1 Wilson quarks. Phys Rev (2019) D100:034520. doi:10.1103/PhysRevD.100.034520
23. Bijnens J, Hermansson-Truedsson N, Rodríguez-Sánchez A. Short-distance constraints for the HLbL contribution to the muon anomalous magnetic moment. Phys Lett (2019) B798:134994. doi:10.1016/j.physletb.2019.134994
24. Colangelo G, Hagelstein F, Hoferichter M, Laub L, Stoffer P. Longitudinal short-distance constraints for the hadronic light-by-light contribution to (g − 2)μ with large-Nc Regge models. J High Energ Phys (2020) 03:101. doi:10.1007/jhep03(2020)101
25. Aoyama T, Asmussen N, Benayoun M, Bijnens J, Blum T, Bruno M, et al. The anomalous magnetic moment of the muon in the Standard Model. Phys Rept (2020) 887:1–166. doi:10.1016/j.physrep.2020.07.006
26. Borsanyi S, Fodor Z, Guenther JN, Hoelbling C, Katz SD, Lellouch L, et al. Leading hadronic contribution to the muon magnetic moment from lattice QCD. Nature (2021) 593:51–5. doi:10.1038/s41586-021-03418-1
27. Cohen T, Kearney J, Pierce A, Tucker-Smith D. Singlet-doublet dark matter. Phys Rev D (2012) 85:075003. doi:10.1103/PhysRevD.85.075003
28. Cheung C, Sanford D. Simplified models of mixed dark matter. J Cosmology Astroparticle Phys (2014) 02:011. doi:10.1088/1475-7516/2014/02/011
29. Calibbi L, Mariotti A, Tziveloglou P. Singlet-Doublet Model: Dark matter searches and LHC constraints. J High Energ Phys (2015) 10:116. doi:10.1007/jhep10(2015)116
30. Crivellin A, Heeck J, Stoffer P. Perturbed lepton-specific two-Higgs-doublet model facing experimental hints for physics beyond the standard model. Phys Rev Lett (2016) 116:081801. doi:10.1103/PhysRevLett.116.081801
31. Crivellin A, Kirk M, Kitahara T, Mescia F. Large t→cZ as a sign of vectorlike quarks in light of the W mass. Phys Rev D (2022) 106:L031704. doi:10.1103/PhysRevD.106.L031704
32. de Giorgi A, Merlo L, Pokorski S. The low-scale seesaw solution to the MW and (g − 2)μ anomalies. Fortschritte der Physik (2022). doi:10.1002/prop.202300020
33. Arcadi G, Djouadi A, Queiroz FDS. Models with two Higgs doublets and a light pseudoscalar: A portal to dark matter and the possible (g−2)μ excess. Phys Lett B (2022) 834:137436. doi:10.1016/j.physletb.2022.137436
34. Arcadi G, Djouadi A. 2HD plus light pseudoscalar model for a combined explanation of the possible excesses in the CDF MW measurement and (g-2)μ with dark matter. Phys Rev D (2022) 106:095008. doi:10.1103/PhysRevD.106.095008
35. Arcadi G, Benincasa N, Djouadi A, Kannike K. The 2HD+a model: Collider, dark matter and gravitational wave signals. arXiv (2022). doi:10.48550/arXiv.2212.14788
36. Djouadi A. The Anatomy of electro-weak symmetry breaking. I: The Higgs boson in the standard model. Phys Rept (2008) 457:1–216. doi:10.1016/j.physrep.2007.10.004
37. Branco GC, Ferreira PM, Lavoura L, Rebelo MN, Sher M, Silva JP. Theory and phenomenology of two-Higgs-doublet models. Phys Rept (2012) 516:1–102. doi:10.1016/j.physrep.2012.02.002
38. Yaguna CE. Singlet-doublet Dirac dark matter. Phys Rev D (2015) 92:115002. doi:10.1103/PhysRevD.92.115002
39. Arcadi G. 2HDM portal for singlet-doublet dark matter. Eur Phys J C (2018) 78:864. doi:10.1140/epjc/s10052-018-6327-6
40. Belanger G, Boudjema F, Pukhov A, Semenov A. MicrOMEGAs: A program for calculating the relic density in the MSSM. Comput Phys Commun (2002) 149:103–20. doi:10.1016/S0010-4655(02)00596-9
41. Belanger G, Boudjema F, Pukhov A, Semenov A. micrOMEGAs 2.0.7: A program to calculate the relic density of dark matter in a generic model. Comput Phys Commun (2007) 177:894–5. doi:10.1016/j.cpc.2007.08.002
42. Choudhury A, Kowalska K, Roszkowski L, Sessolo EM, Williams AJ. Less-simplified models of dark matter for direct detection and the LHC. J High Energ Phys (2016) 04:182. doi:10.1007/JHEP04(2016)182
43. Choudhury A, Kowalska K, Roszkowski L, Sessolo EM, Williams AJ. Blind spots for direct detection with simplified DM models and the LHC. Universe (2017) 3:41. doi:10.3390/universe3020041
44. Veltman MJG. Limit on mass differences in the weinberg model. Nucl Phys B (1977) 123:89–99. doi:10.1016/0550-3213(77)90342-X
45. Toussaint D. Renormalization effects from superheavy Higgs particles. Phys Rev D (1978) 18:1626–31. doi:10.1103/PhysRevD.18.1626
46. Peskin ME, Takeuchi T. Estimation of oblique electroweak corrections. Phys Rev D (1992) 46:381–409. doi:10.1103/PhysRevD.46.381
47. He HJ, Polonsky N, Su SF. Extra families, Higgs spectrum and oblique corrections. Phys Rev D (2001) 64:053004. doi:10.1103/PhysRevD.64.053004
48. Barbieri R, Hall LJ, Nomura Y, Rychkov VS. Supersymmetry without a light Higgs boson. Phys Rev D (2007) 75:035007. doi:10.1103/PhysRevD.75.035007
49. Enberg R, Fox PJ, Hall LJ, Papaioannou AY, Papucci M. LHC and dark matter signals of improved naturalness. J High Energ Phys (2007) 11:014. doi:10.1088/1126-6708/2007/11/014
50. D’Eramo F. Dark matter and Higgs boson physics. Phys Rev D (2007) 76:083522. doi:10.1103/PhysRevD.76.083522
51. Joglekar A, Schwaller P, Wagner CEM. Dark matter and enhanced Higgs to di-photon rate from vector-like leptons. J High Energ Phys (2012) 12:064. doi:10.1007/JHEP12(2012)064
52. Aalbers J, Akerib DS, Akerlof CW, Al Musalhi AK, Alder F, Alqahtani A, et al. First dark matter search results from the LUX-ZEPLIN (LZ) experiment (2022).
53. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro F, et al. Constraining the spin-dependent WIMP-nucleon cross sections with XENON1T. Phys Rev Lett (2019) 122:141301. doi:10.1103/PhysRevLett.122.141301
54. Davidson S, Haber HE. Erratum: Basis-independent methods for the two-Higgs-doublet model [Phys. Rev. D72, 035004 (2005)]. Phys Rev D (2005) 72:035004. [Erratum: Phys.Rev.D 72, 099902 (2005)]. doi:10.1103/PhysRevD.72.099902
55. Barroso A, Ferreira PM, Ivanov IP, Santos R. Metastability bounds on the two Higgs doublet model. J High Energ Phys (2013) 06:045. doi:10.1007/JHEP06(2013)045
56. Glashow SL, Weinberg S. Natural conservation laws for neutral currents. Phys Rev D (1977) 15:1958–65. doi:10.1103/PhysRevD.15.1958
57. Pich A, Tuzon P. Yukawa alignment in the two-Higgs-doublet model. Phys Rev D (2009) 80:091702. doi:10.1103/PhysRevD.80.091702
58. Berlin A, Gori S, Lin T, Wang LT. Pseudoscalar portal dark matter. Phys Rev D (2015) 92:015005. doi:10.1103/PhysRevD.92.015005
59. Aad G, Abbott B, Abbott D, Abed Abud A, Abeling K, Abhayasinghe D, et al. Search for Higgs boson decays into two new low-mass spin-0 particles in the 4b channel with the ATLAS detector using pp collisions at \sqrt{s}= 13 TeV. Phys Rev D (2020) 102:112006. doi:10.1103/PhysRevD.102.112006
60.The CMS collaboration Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Bergauer T, et al. Search for a light pseudoscalar Higgs boson in the boosted μμττ final state in proton-proton collisions at $\sqrt{s}=$ 13 TeV. J High Energ Phys (2020) 08:139. doi:10.1007/JHEP08(2020)139
61. Tumasyan A, Adam W, Bergauer T, Dragicevic M, Ero J, Valle AED, et al. Search for low-mass dilepton resonances in Higgs boson decays to four-lepton final states in proton–proton collisions at $$\sqrt{s}=13\,\text {TeV}. Eur Phys J C (2022) 82:290. doi:10.1140/epjc/s10052-022-10127-0
62. Djouadi A. The anatomy of electroweak symmetry breaking Tome II: The Higgs bosons in the Minimal Supersymmetric Model. Phys Rept (2008) 459:1–241. doi:10.1016/j.physrep.2007.10.005
63. Abe T, Sato R, Yagyu K. Lepton-specific two Higgs doublet model as a solution of muon g − 2 anomaly. J High Energ Phys (2015) 07:064. doi:10.1007/JHEP07(2015)064
64. Dedes A, Haber HE. Can the Higgs sector contribute significantly to the muon anomalous magnetic moment? J High Energ Phys (2001) 05:006. doi:10.1088/1126-6708/2001/05/006
65. Djouadi A, Kohler T, Spira M, Tutas J. (e t) type leptoquarks at e p colliders. Z Phys C (1990) 46:679–86. doi:10.1007/BF01560270
66. Barr SM, Zee A. Electric dipole moment of the electron and of the neutron. Phys Rev Lett (1990) 65:21–4. [Erratum: Phys.Rev.Lett. 65, 2920 (1990)]. doi:10.1103/PhysRevLett.65.21
67. Chang D, Chang WF, Chou CH, Keung WY. Large two-loop contributions tog−2from a generic pseudoscalar boson. Phys Rev D (2001) 63:091301. doi:10.1103/PhysRevD.63.091301
68. Larios F, Tavares-Velasco G, Yuan CP. Very lightCP-odd scalar in the two-Higgs-doublet model. Phys Rev D (2001) 64:055004. doi:10.1103/PhysRevD.64.055004
69. Ilisie V. New Barr-Zee contributions to (g −2)μ in two-Higgs-doublet models. J High Energ Phys (2015) 04:077. doi:10.1007/JHEP04(2015)077
70. Aad G, Abbott B, Abbott D, Abed Abud A, Abeling K, Abhayasinghe D, et al. Search for heavy Higgs bosons decaying into tau leptons with the ATLAS detector using pp collisions at \sqrt{s}=13 TeV. Phys Rev Lett (2020) 125:051801. doi:10.1103/PhysRevLett.125.051801
71.CMS Collaboration. Searches for additional Higgs bosons and vector leptoquarks in ττ final states in proton-proton collisions at $\sqrt{s}=13∼\mathrm{TeV}$ (2022).
72. Argyropoulos S, Haisch U. Benchmarking LHC searches for light 2HDM+a pseudoscalars. Scipost Phys (2022) 13:007. doi:10.21468/SciPostPhys.13.1.007
73. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Bergauer T, Dragicevic M, et al. Search for a narrow resonance lighter than 200 GeV decaying to a pair of muons in proton-proton collisions at s=13 TeV. Phys Rev Lett (2020) 124:131802. doi:10.1103/PhysRevLett.124.131802
74.The LHCb collaboration Aaij R, Abellán Beteta C, Ackernley T, Adeva B, Adinolfi M, et al. Searches for low-mass dimuon resonances. J High Energ Phys (2020) 10:156. doi:10.1007/JHEP10(2020)156
75. Chun EJ, Kim J. Leptonic precision test of leptophilic two-Higgs-doublet model. J High Energ Phys (2016) 07:110. doi:10.1007/jhep07(2016)110
76. Aad G, Abbott B, Abbott DC, Abud AA, Abeling K, et al. ATLAS Collaboration Search for heavy resonances decaying into a pair of Z bosons in the ℓ+ℓ−ℓ′+ℓ′− and \ell ^+\ell ^-\nu {{\bar{\nu }}} final states using 139 fb−1 of proton–proton collisions at \sqrt{s} = 13TeV with the ATLAS detector. Eur Phys J C (2021) 81:332. doi:10.1140/epjc/s10052-021-09013-y
77.The CMS collaboration Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Bergauer T, et al. Search for new neutral Higgs bosons through the H → ZA $\to \ell^{+}\ell^{-} \mathrm{b}\bar{\mathrm{b}}$ process in pp collisions at $\sqrt{s} =$ 13 TeV. J High Energ Phys (2020) 03:055. doi:10.1007/JHEP03(2020)055
78. Aad G, Abbott B, Abbott DC, Abed Abud A, Abeling K, Abhayasinghe DK, et al. Search for a heavy Higgs boson decaying into a Z boson and another heavy Higgs boson in the ℓℓbb and ℓℓWW final states in pp collisions at \sqrt{s}=13\ \text {TeV} with the ATLAS detector. Eur Phys J C (2021) 81:396. doi:10.1140/epjc/s10052-021-09117-5
79.ATLAS Collaboration. Search for heavy resonances decaying into a Z or W boson and a Higgs boson in final states with leptons and b-jets in 139 fb−1 of pp collisions at $\sqrt{s}=13∼$TeV with the ATLAS detector (2022).
80. Harlander RV, Liebler S, Mantler H. SusHi: A program for the calculation of Higgs production in gluon fusion and bottom-quark annihilation in the standard model and the MSSM. Comput Phys Commun (2013) 184:1605–17. doi:10.1016/j.cpc.2013.02.006
81. Harlander RV, Liebler S, Mantler H. SusHi Bento: Beyond NNLO and the heavy-top limit. Comput Phys Commun (2017) 212:239–57. doi:10.1016/j.cpc.2016.10.015
82. Ackermann M, Ajello M, Albert A, Atwood WB, Baldini L, Ballet J, et al. Search for gamma-ray emission from the Coma Cluster with six years of Fermi-LAT data. Astrophys J (2016) 819:149. [Erratum: Astrophys.J. 860, 85 (2018)]. doi:10.3847/0004-637X/819/2/149
Keywords: dark matter theory, dark matter phenomenology, beyond the Standard Model of physics, dark matter experiment, experimental searches of new physics
Citation: Arcadi G and Djouadi A (2023) A model for fermionic dark matter addressing both the CDF MW and the (g − 2)μ anomalies. Front. Phys. 11:1143932. doi: 10.3389/fphy.2023.1143932
Received: 13 January 2023; Accepted: 02 March 2023;
Published: 21 March 2023.
Edited by:
Debasish Borah, Indian Institute of Technology Guwahati, IndiaReviewed by:
Soumya Sadhukhan, Ramakrishna Mission Residential College, Narendrapur, IndiaCopyright © 2023 Arcadi and Djouadi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giorgio Arcadi, Z2lvcmdpby5hcmNhZGlAdW5pbWUuaXQ=
 Giorgio Arcadi
Giorgio Arcadi Abdelhak Djouadi
Abdelhak Djouadi