Consistent assessment of neutron-induced activation of 93Nb

A concurrent assessment of all measured excitation functions for various reactions induced by neutrons on ⁹³Nb, in addition to the results of TENDL-2021 and default parameters in TALYS-1.96, is given in this work. We use consistent parameter sets that were formerly obtained or validated by the analysis of other independent data, while no empirical rescaling factors of γ and/or neutron widths have been used. The correlation between the measured error bars of the primary data providing the consistent input parameters and the final uncertainty bands of the calculated results have been pointed out. At the same time, a proper account in this work of all available data for competitive reaction channels prevented compensation effects of less accurate model parameters. Remaining questions and the need for additional measurements are emphasized.

1 Introduction

The interest in niobium has followed its application in structural materials of nuclear reactors, activation monitor in reactor dosimetry, 14 MeV neutron flux determination, and element of superconductor alloys in fusion reactors. A consequent large body of experimental data for neutron interactions with the ⁹³Nb nucleus also guided its use as a “sample problem” [1] in statistical Hauser–Feshbach (HF) [2] and pre-equilibrium emission (PE) [3] model calculations [4–10]. However, rather sparse measured data, for neutron-induced reactions on this only Nb natural isotope are yet pointing out a need of more accurate measurements to settle its evaluation [11–13].

Moreover, the concurrent assessment of all measured excitation functions for various reactions induced by neutrons on ⁹³Nb, in addition to the results of using default parameters within the worldwide used computer code TALYS-1.96 [14] and the currently related TENDL-2021 evaluation [15], remains an actual goal of further nuclear model analysis. This demand has been confirmed within a recent assessment of the α-particle emission in neutron-induced reactions on Zr, Nb, and Mo stable isotopes [16]. Furthermore, we look for a proper account of all available data for competitive reaction channels to prevent compensation effects of less accurate model parameters.

Consequently, we have paid more attention to the use of consistent parameter sets that are formerly obtained or validated by the analysis of other independent data [17]. Thus, no empirical rescaling factors of γ and/or neutron widths are involved. On the other hand, detailed analyses based on consistent input parameter sets are needed to eventually improve the global parameters for involvement in large-scale evaluations. Such a case has been that of the α-particle optical model potential [18] adopted as the corresponding default option of TALYS, whose suitable setup and confirmation [19–22] made use of consistent parameter sets.

Nonetheless, the accuracy of the independent data formerly involved in the setup of a consistent parameter set entirely determines the appropriateness of these parameters and, finally, the uncertainties of the calculated reaction cross-sections. Thus, the use of consistent parameters leads to increased accuracy of model calculations, but only within the limits of actual knowledge about the primary data triggering the input parameters. This is why, in this work, we look for the definite relation between the measured error bars of the primary data providing the consistent input parameters, the corresponding limits of these parameters, and, finally, the uncertainty bands of the calculated results. On the other hand, the use of no empirical rescaling factors completes the consistency of both input parameters and calculation results by agreeing with something previously obtained and always behaving in a similar way.

This work completes Ref. [16] with reference to the target nucleus ⁹³Nb, and the only additional HF+PE model parameters for neutron-induced reactions on this nucleus are given in Section 2. Comparison of HF+PE results and all available related data are discussed in Section 3. Conclusions are finally given in Section 4.

2 Nuclear models and parameters

The HF+PE reaction analysis and collective inelastic scattering cross-section assessment have been carried out using the same models, codes [14, 23–25], and previous local approaches [16, 26]. Moreover, the same parameters, consistently established or validated by means of distinct data, have been involved for the 1) back-shifted Fermi gas (BSFG) [27] nuclear-level density (NLD), 2) particle transmission coefficients through optical model potentials (OMPs) [18, 28], and 3) γ-ray transmission coefficients through radiative strength functions (RSFs) [29, 30]. The same NLD and OMP parameters have been used in the framework of the HF+PE models, with additional pickup direct-reaction (DR) contribution to the α-particle emission.

NLD parameters for the main reaction products concerned in the present work in addition to Ref. [16] are given in Table 1, including the corresponding uncertainties. The last ones correspond first to the fit of the s-wave nucleon-resonance spacing $D_0^{\exp }$ [33] in ΔE energy range [34] above separation energy S, for the target-nucleus ground state (g.s.) spin I₀. The additional uncertainty of the fitted number of low-lying levels N_d, up to excitation energy $E_d^{*}$ [31], led to enlarged BSFG model parameter uncertainties (second pair of brackets in Table 1). The smooth-curve method [35] was applied for nuclei without resonance data, and an average of fitted a-values of nearby nuclei was used to obtain only the Δ values by fitting low-lying discrete levels alone. Larger uncertainties of averaged a-values have resulted in this case, due to the spread of the former ones. Finally, the NLD-parameter uncertainties have been used to illustrate the NLD effects on calculated cross-sections (Section 3).

TABLE 1

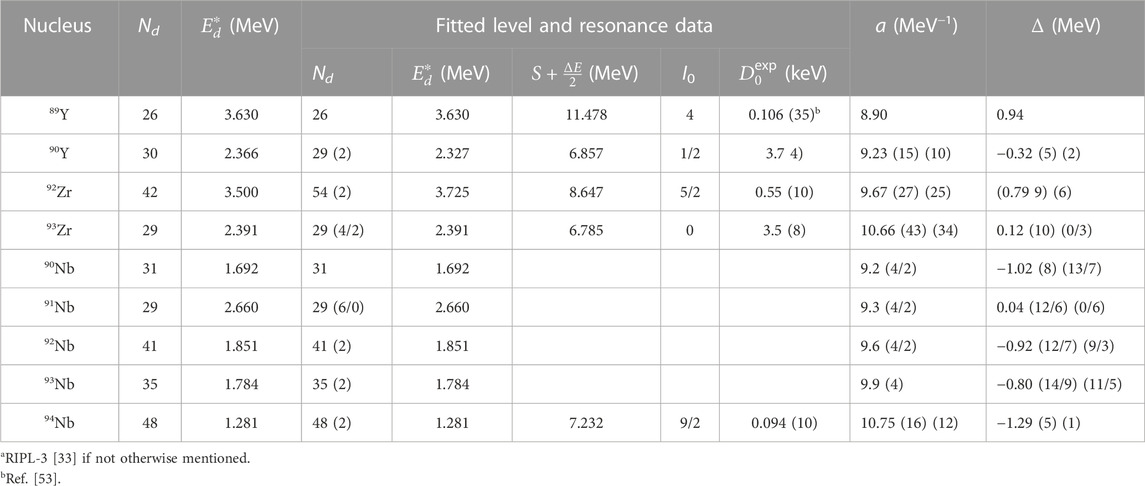
TABLE 1. Low-lying levels number N_d up to excitation energy $E_d^{*}$ [31] used in SM calculations, and N_d and s-wave nucleon-resonance ${\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}}^a{D}_0^{\exp }$ (with uncertainties given in units of the last digit in parentheses) in the energy range ΔE above the separation energy S, for target nucleus g.s. spin I₀, fitted to obtain BSFG level-density parameter a and g.s. shift Δ (for a spin cut-off factor corresponding to a variable moment of inertia [32] between half and 75% of the rigid-body value, from g.s. to S, and reduced radius r₀ = 1.25 fm).

The neutron transmission coefficients have been obtained using the global and local OMPs of Koning and Delaroche [28], and their additional analysis by means of the SPRT method [36] within the energy range of this work. Thus, these OMP results for the s- and p-wave neutron strength functions S₀ and S₁, respectively; the potential scattering radius R′; and the energy dependence of the neutron total cross-section σ_T(E) are compared in Figure 1 with the available data [32, 33, 36]. We found that the global parameter set [28] provides a particularly better agreement of the measured and calculated σ_T(E) in comparison to the related local parameter set within this energy range. So, we used the aforementioned global parameter set [28]. Nevertheless, the corresponding changes also shown in Figure 1 for the reaction cross-sections σ_R(E), of notable importance around 1 MeV for the competition between the neutron and charged-particle decay of excited compound nuclei (CNs), have no importance.

FIGURE 1

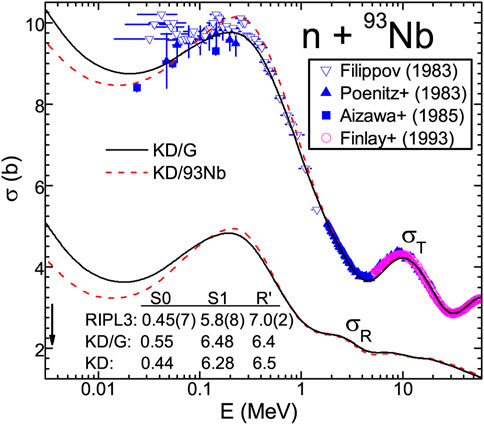
FIGURE 1. Comparison of measured [37] and calculated neutron total cross-sections (upper curves) of ⁹³Nb using the global (solid curves) and local (dashed curves) OMP parameters [28]. The calculated reaction cross-sections (lower similar curves) corresponding to the same OMPs are also shown.

Moreover, the same OMP parameters provided the collective inelastic scattering component within the distorted-wave Born approximation (DWBA) method, the code DWUCK4 [24], and the deformation parameters [4] of the first 2⁺ and 3⁻ collective states. It goes up to ∼7% of σ_R for incident energies around 4 MeV and then decreases slightly below 5% at energies above 20 MeV. A corresponding decrease in σ_R has been then taken into account within the PE+HF analysis of various reaction channels.

The proton transmission coefficients of a similar alternative have been solved by the usual analysis of the (p,n) cross-sections at energies (≥3 MeV) where this reaction channel has cross-sections close to the optical potential σ_R. However, because only earlier measured data have been available for this reaction on neighboring Zr isotopes (Figure 2B,C), more recent data on the (p,γ) reaction have been used below the (p,n) reaction effective threshold, where its cross-sections are yet to come close to σ_R values. Then, the comparison of measured and calculated cross-sections shown in Figure 2A led to the further involvement in this work of the global proton OMP [28].

FIGURE 2

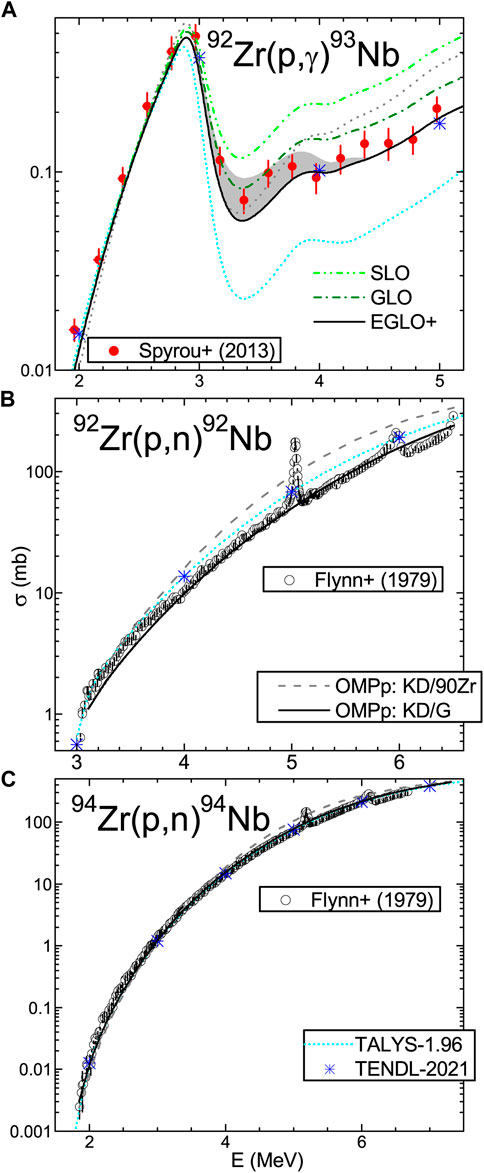
FIGURE 2. Comparison of cross-sections measured [37], evaluated [15] (*), and calculated with the code TALYS-1.96 [14] (short-dotted curves) and in this work, using proton global OMP parameters [28] and E1-radiation EGLO strength functions (solid curves) for (A) (p,γ) reaction on ⁹²Zr, and (B, C) (p,n) reaction on ^92,94Zr, respectively. (A) The results for the alternative use of E1-radiation GLO (dash-dotted) and SLO (dash-dot-dotted) models are also shown, and the uncertainty band corresponds to values between 1 and 2 of the WFC number of degrees of freedom for the χ² partial-width distribution.

The α-particle transmission coefficients corresponding to the α-particle OMP [18] have just been proved to be well suited for α-emission in neutron-induced reactions in the mass range A ∼90 including ⁹³Nb nucleus [16]. A still-open question to be answered in this work may concern only the role of the uncertainties related to the competitive reaction channels (Section 3).

The γ-ray transmission coefficients involve RSFs, which unfortunately have no confident parametrization despite the widespread systematics [30, 37] performed even recently. So, we have adopted the giant dipole resonance (GDR) parameters of Kopecky and Uhl [39] within the former Lorentzian (SLO) [40], the generalized Lorentzian (GLO) [39], and the enhanced generalized Lorentzian (EGLO) [41] models for the electric-dipole RSF. The additional M1 upbend parameters found recently to describe the RSF data for ^92,94Mo nuclei, i.e., the middle resonance parameters given in Table II of Ref. [42], have been used for ^93,94Nb nuclei too.

Comparison of the results obtained within the aforementioned models for the E1-radiation in Figure 2A showed that the EGLO model has led to an enhanced RSF description over the whole energy range of the measured (p,γ) cross-sections [43]. Furthermore, an eventual uncertainty band of the calculated results corresponding to the values between 1 and 2 for the number of degrees of freedom for the χ² partial-width distribution within Moldauer’s width fluctuation correction (WFC) [44] has fully covered the scattered experimental data around the excitation function minimum just above the (p,n) reaction threshold.

A similar analysis to be shown hereafter for the neutron capture on ⁹³Nb comes to the same conclusion concerning the average s-wave radiation widths Γ_γ. Thus, the SLO and GLO models have led to larger captured cross-sections and Γ_γ values in comparison to the measured data [33, 36].

The pre-equilibrium emission account within the geometry-dependent hybrid (GDH) model [45], generalized through the inclusion of the angular momentum and parity conservation [46] and knockout α-particle emission, has a main parameter of pre-formation probability φ [3]. Its suitable values have been recently obtained [16] by the analysis of several energy spectra measurements around the incident energy of 14 MeV. On the other hand, the GDH intra-nuclear transition rates were calculated also using the aforementioned imaginary OMP parameters within the local density approximation ([45] and Refs. therein). Local-density Fermi energy was similarly related to various partial waves and a central-well Fermi energy value F = 40 MeV.

Moreover, the revised version of the advanced particle-hole-level densities (PLD) [47, 48] was used with the Fermi–gas energy dependence of the single-particle level (s.p.l) density [49]. The s.p.l. density g_α of the pre-formed α-cluster, which behaves like an exciton [3, 45], has been related to the level-density parameter a through the usual equidistant spacing–model relation g=(6/π²)a.

The DR pickup mechanism has also been used to describe the α-particle emission in neutron-induced reactions, similar to recent analyses in the mass ranges A ∼60 [21, 22] and A ∼90 [16] including ⁹³Nb. However, the lack of measured angular distributions for the (n, α) reaction again made impossible the current DWBA assessment of related pickup cross-sections using spectroscopic factors (SFs) obtained by the analysis of α-particle angular distributions.

Thus, one-step reaction has also been considered through the pickup of ³He clusters. However, the “spectator model” [50, 51] was used for the pair of transferred protons in ⁹³Nb(n,α)⁹⁰Y reaction, with the corresponding SFs given by Glendenning [52]. Then, the SFs for the picked neutron were obtained on account of their similarity with the picked-proton SFs found by the analysis of the α-particle angular distributions of the pickup reaction ⁹¹Zr (t,α)⁹⁰Y toward the same residual nucleus [16]. The DWBA formalism with prior-form transition amplitudes and finite-range interactions within the code FRESCO [25] have been used. Last, the description of the α-particle angle–integrated energy distributions around 14 MeV induced by neutrons on ⁹³Nb has validated the α-particle’s both PE and DR components [16].

3 Results and discussion

The (n, γ) excitation-function analysis is of general interest due to the significant activation of various isomeric states by neutrons incident on ⁹³Nb. The former validation of the γ-ray transmission coefficients has confirmed the adopted NLD spin cut-off factors, which then trigger all isomeric cross-sections. Therefore, a good agreement between the more recent experimental data and the calculated results shown in Figure 3 is particularly important.

FIGURE 3

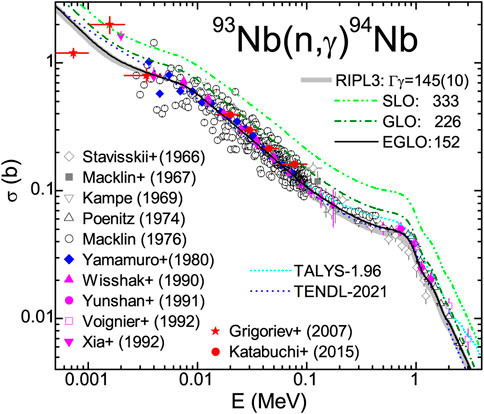
FIGURE 3. Figure 2A includes evaluated cross-sections [15] (short-dashed curve), but for (n, γ) reaction on ⁹³Nb [37], with the uncertainty band of the calculated cross-sections corresponding to the error bar of RIPL-3 average s-wave radiation widths Γ_γ [33]. The Γ_γ values provided by the use of E1-radiation RSF of EGLO (solid curve), GLO (dash-dotted), and SLO (dash-dot-dotted) models are also included.

At the same time, it should be pointed out that a good agreement has also been obtained for the related RIPL-3 average s-wave radiation width, even within quite a narrow error bar [33]. Actually, the narrow uncertainty band of the calculated cross-sections corresponding to the Γ_γ limits (Figure 3) is close to the more recently measured data. On the other hand, replacing the EGLO model for the E1-radiation RSF with GLO and especially SLO models, a notable overestimation follows both for the calculated excitation function and Γ_γ values. Thus, the use of the GLO model leads to increased cross-sections and Γ_γ values by ∼37% and ∼50%, respectively, around the incident energy of 1 MeV, while the SLO model corresponds to over two times larger values.

The (n, 2n) reaction analysis has the shortcoming of no total cross-section data available within the last 40 years. Fortunately, there are recent measurements for the isomeric cross-sections corresponding to the 2⁺ state of ⁹²Nb nucleus at 136 keV, as shown in Figure 4A. First, the agreement between the calculated and recently measured isomeric cross-section at the incident energy of ∼14 MeV, i.e., on the flat maximum of this excitation function should be noted. Second, it is also notable that the concurrent suitable account of both the isomeric state and total (n, 2n) excitation functions is obtained. At the same time, the TALYS-1.96 results are in better agreement with only the latter data, while TENDL-2021 fits to a greater extent the former excitation function. There is thus support for the neutron OMP and the NLD spin distribution corresponding to the aforementioned spin cut-off factors.

FIGURE 4

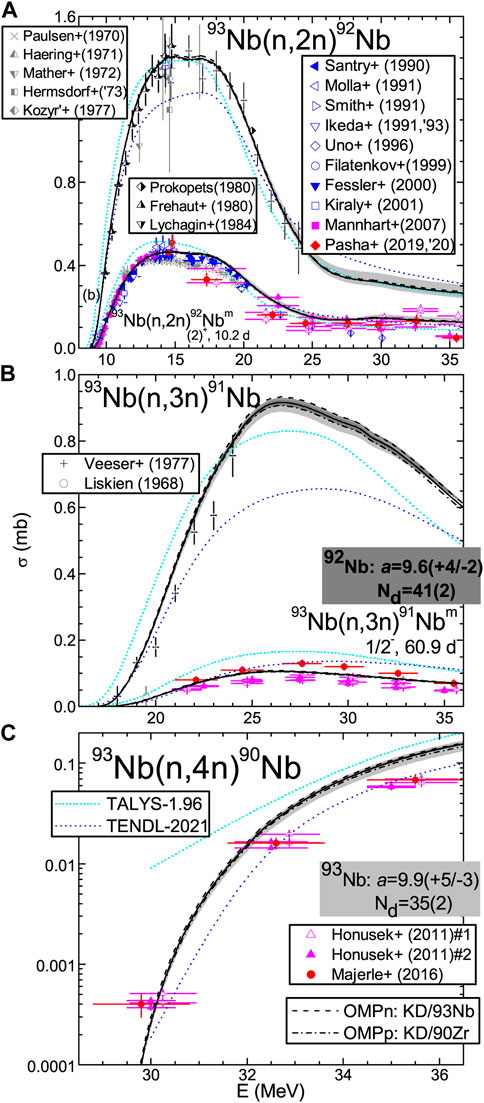
FIGURE 4. Comparison of cross-sections measured [37], evaluated [15] (short-dashed curves), and calculated with the code TALYS-1.96 [14] (short-dotted curves) and in this work, using proton global OMP parameters [28] (solid curves) for (A) (n, 2n), (B) (n, 3n), and (C) (n, 4n) reactions on ⁹³Nb. Results obtained with the alternative use of the corresponding local OMP parameters [28] of either neutrons on ⁹³Nb (dashed) or protons on ⁹⁰Zr (dash-dotted) are shown, and the uncertainty bands related to NLD-parameter error bars (Table 1) of the target nucleus (light gray) and residual nucleus ⁹²Nb (gray) are also shown.

The size of the NLD effects on calculated cross-sections closely follows the NLD-parameter uncertainty related to the error bars of the fitted $D_0^{\exp }$ and low-lying levels (Table 1). Moreover, the spread of the formerly fitted LD parameters a is also quite important within the smooth-curve method involved for nuclei without the resonance data. It determines the adopted limits of the average a-values, given in Table 1 as well, and finally the corresponding uncertainty bands of the calculated excitation functions. On the other hand, the particular minimum of the a-systematics for nuclei around the magic number N = 50, as the Nb residual nuclei, has eventually led to adopted upper deviations from the average a-value, which are larger than the lower deviations, e.g., a = [9.2 ± (0.4/0.2)] MeV⁻¹ for ⁹²Nb nucleus (Table 1).

Thus, Figure 4A shows the bands related to the NLD-parameter limits of the residual nuclei ^92,93Nb, which deserve the following comments. The wider uncertainty bands are related to the limits of the NLD parameters for ⁹³Nb nucleus populated through the excited nucleus ⁹⁴Nb decay by neutron emission. However, even these bands, rather similar for the total and isomeric cross-sections, are larger than ∼1% only for incident energies above 20 MeV. Then, it becomes either higher or lower than the calculated cross-sections at the incident energy of 37 MeV by ∼14% and ∼8%, respectively. At the same time, the uncertainty bands corresponding to the limits of the NLD parameters for the residual nucleus ⁹²Nb of the (n, 2n) reaction are overall below 1%.

The changes in the calculated (n, 2n) reaction cross-sections due to an eventual use of the neutron local OMP [28] have also been only from about 1% at the excitation function maximum to ∼2% around 35 MeV. The replacement of the aforementioned proton local OMP [28] has led to the changes below 1% at all incident energies. One may thus conclude that there is quite a low model–parameter dependence of the calculated (n, 2n) cross-sections, particularly below the incident energy of 20 MeV, for the case of consistent parameters determined formerly by the analysis of independent data.

The (n, 3n) reaction analysis has shown quite similar results in Figure 4B, particularly for the agreement with the recently measured isomeric cross-sections. Uncertainty bands similar to the case of the (n, 2n) reaction have been obtained, with only about 1% larger limits. Comparable changes have followed the use of either neutron or proton local OMPs [28]. The latter now becomes distinct from those related to the global proton OMP for ⁹³Zr, for the total (n, 3n) excitation function, but close to it. On the other hand, the uncertainty bands corresponding to the NLD parameters of the residual nucleus ⁹¹Nb have widths within 3% of the calculated excitation functions and thus cannot be distinguished.

The (n, 4n) reaction-calculated cross-sections shown in Figure 4C are in good agreement with the measured data around the incident energy of 30 MeV but overestimated around 35 MeV. This disagreement remains even beyond the uncertainty band related to the NLD parameters of the residual nucleus ⁹³Nb within the (n, n′) reaction. Despite the width of this band going from 14% to 23%, for energies from 30 to 37 MeV, it is yet above the measured data by 2–3 times, while the threshold energy for the (n, 5n) reaction is above 39 MeV. Lower changes due to the use of local OMPs [28] for either neutrons or protons, of only about +2% and −6%, respectively, cannot improve the measured data description. Eventually, a less suitable PE energy-dependence account at these higher energies may explain this variance and should be a concern within further studies.

The (n, xp) reaction analysis has to overcome the shortcoming of no measured excitation function. Only several angle-integrated energy distributions of proton emission induced by neutrons on ⁹³Nb around the incident energy of 14 MeV have provided proton total-emission cross-sections at this energy. On the other hand, the overall account of the measured energy spectra, in the limit of the error bars (Figure 11D of Ref. [16]), have particularly supported an appropriate description of proton PE in neutron-induced reactions on ⁹³Nb at least within this energy range. Moreover, there is a good agreement between the corresponding measured proton total-emission cross-sections and the model calculation results, as shown in Figure 5.

FIGURE 5

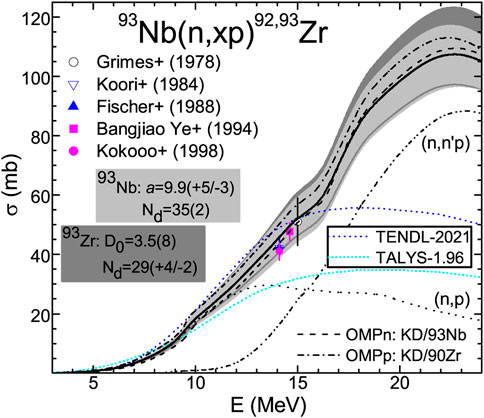
FIGURE 5. Comparison of cross-sections measured [37] and calculated in this work using proton global OMP parameters [28] (solid curves) for (n, xp) reactions on ⁹³Nb. Results obtained with the alternative use of the corresponding local OMP parameters [28] of either neutrons on ⁹³Nb (dashed) or protons on ⁹⁰Zr (dash-dotted) are shown, and the uncertainty bands related to NLD-parameter error bars (Table 1) of the residual nuclei ⁹³Nb (light gray) and ⁹³Zr (gray) are also shown. The (n, p) and (n, n′p) components are shown as well (dotted and dash-dot-dotted curves, respectively), with a comparison of the former with the evaluated [15] (short-dashed curve) and calculated with the code TALYS-1.96 [14] (short-dotted curve) results, too.

In this case, a comparison is possible between the NLD effects on calculated cross-sections due to NLD-parameter uncertainty related to either the adopted limits of the average a-value for the residual nucleus ⁹³Nb, or the error bars of the fitted $D_0^{\exp }$ for the proton-emission residual ⁹³Zr. While the numbers of low-lying levels also fitted for these, both odd A nuclei are rather similar, and the average a-value for ⁹³Nb has the aforementioned rather large limits, whereas $D_0^{\exp }$ value for ⁹³Zr has a 23% singular uncertainty (Table 1).

Under these conditions, the corresponding uncertainty bands of the calculated excitation functions (Figure 5) are both large compared to those for the (n, xn) reactions. Thus, the uncertainty band related to NLD parameters for ⁹³Nb has a width going from 29%, at the incident energy of 14.8 MeV, to 19% at the maximum of the proton-emission excitation function, which is around 23 MeV. The width of the uncertainty band related to NLD parameters for ⁹³Zr, from 28% to 25% between the same incident energies, is evidently larger at the higher energies. It thus pointed out the importance of the higher accuracy of the $D_0^{\exp }$ measurements for improvement of the calculated reaction cross-sections with consistent parameters sets.

On the other hand, changes due to the use of the neutron local OMP [28] are only between −2% and 4% for the same incident energies from 14.8 to 23 MeV. Somewhat larger ones, from 9% to −6%, correspond to the use of the local OMP [28] for protons. Nevertheless, while the former are yet within the error bars of the measured proton total-emission cross-sections, the latter match similarly only to the larger earlier data errors.

The (n, xα) reaction analysis has already been discussed [16], with the main points only briefly mentioned hereafter. Thus, the spectroscopic factors provided by an analysis of the α-particle angular distributions from ⁹¹Zr (t,xα)^89,90Y led to a significant DR component for only 14 levels up to ∼ 2.5 MeV excitation energy by the ⁹³Nb(n,α)⁹⁰Y reaction. Therefore, a minor pickup DR contribution has been found to the total cross-sections of this reaction in Figure 6A. The same is the case of the 7⁺ isomer of the residual nucleus ⁹⁰Y, which was also recently measured, as shown in Figure 6B, for energies from the effective threshold to above 20 MeV. On the other hand, the suitable account of the whole higher energy side of the emitted α-spectrum around 14 MeV validated the value φ = 0.14 of the aforementioned α-particle PE parameter [3, 45]. Then, the agreement of the measured and CN + PE calculated cross-sections within the error bars of the recent data made possible the assessment of a PE uncertainty band corresponding to Δφ = 0.02 [16]. The width of this uncertainty band increases from ∼19%, around the incident energy of 10 MeV, to ∼30% at 20 MeV.

FIGURE 6

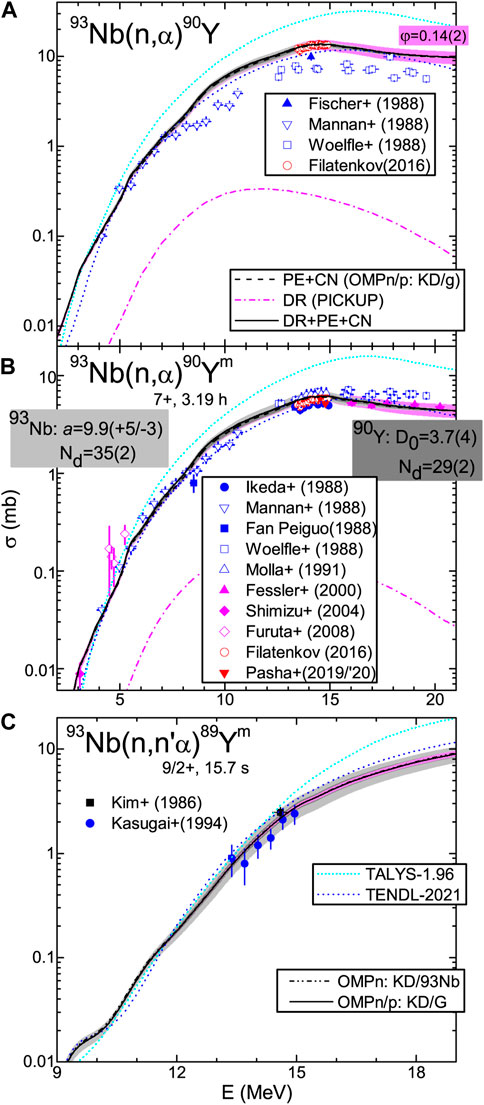
FIGURE 6. Similar to that shown in Figure 4, but for (A) ⁹³Nb(n,α)⁹⁰Y reaction [37], (B) the corresponding 7+ isomeric state ⁹⁰Y^m activation, and (C) ⁹³Nb(n,n′α)⁸⁹Y^m reaction [37]. (A, B) The DR (dash-dotted curve) and PE + CN (dashed) components of (n, α) reaction are additionally shown, while PE + CN uncertainty bands also related to NLD-parameter error bars (Table 1) of the residual nucleus ⁹⁰Y (gray) and PE parameter φ (magenta) are also shown. (C) The alternative use of the local OMP parameters [28] of neutrons on ⁹³Nb (dash-dot-dotted) is shown as well.

Similar results were obtained for the 7⁺ isomeric-state ⁹⁰Y^m activation and that of the 9/2⁺ isomer through the ⁹³Nb(n,n′α)⁸⁹Y^m reaction shown in Figure 6C. The only difference in the latter case is that there is no distinct PE uncertainty band. A related parallel with the accuracy of the measured data was thus not possible either, while the main aim to validate the α-particle OMP [18] was entirely proved by the suitable CN + PE account of all α-emission data.

Moreover, a comparison has been possible between the NLD effects due to uncertainties of the average a-value for the residual nucleus ⁹³Nb, and the a-value of the residual ⁹⁰Y, which corresponds to the error bar of the fitted $D_0^{\exp }$. However, the numbers of low-lying levels also fitted for these nuclei are rather similar, and the average a-value for ⁹³Nb has the aforementioned rather large limits whereas the $D_0^{\exp }$ value for ⁹⁰Y has only 11% uncertainty (Table 1). Consequently, the uncertainty band related to NLD parameters for ⁹³Nb has the width from around 26%–6%, for incident energies between 10 and 20 MeV. The width of the uncertainty band related to NLD parameters for ⁹⁰Y, from ∼8%–6% between the same incident energies, is indeed smaller at lower energies. It is thus evident that there is a correlation between the accuracy of the HF model parameters, given in turn by the distinct data taken previously into account, and the final uncertainties of the calculated reaction cross-sections. So, the importance of $D_0^{\exp }$ measurements with a higher accuracy, for more accurate calculated reaction cross-sections using consistent parameter sets, is again pointed out.

Hence, larger calculated cross-section uncertainties are at lower energies, due to average level-density parameters, while rather similar values are related to the PE account at higher energies. Notably, the former aforementioned uncertainties become comparatively much lower as the energy increases, whereas the latter have significant values also at lower energies. Nevertheless, changes due to the use of local OMPs [28] for neutrons are higher than 1% only from the incident energy of 14 MeV and up to 2% at 20 MeV. At the same time, the local OMP [28] for protons led to the changes below 1% in the whole energy range.

Finally, the same analysis of the activation of 9/2⁺ isomers through the ⁹³Nb(n,n′α)⁸⁹Y^m reaction makes possible a better understanding of the balance between the experimental and calculated cross-sectional uncertainties. Its enlarged illustration in Figure 6C facilitates the note of the calculated cross-section PE uncertainty band with a width from ∼2%–16% for incident energies between 10 and 20 MeV. However, it is well below the uncertainty band related to NLD parameters for ⁹³Nb, with a width of around 23% at the same energy, but rather close to that related to NLD parameters for ⁹⁰Y. For the sake of completeness, an increase due to the use of the local OMP [28] for neutrons from 4%– 2% within the same energy range should be mentioned. Therefore, one may see, in this case, a close matching of the experimental and calculated cross-section uncertainties and the latter truly corresponding to the limits of the distinct data that are previously involved within the consistent parameter assessment.

4 Conclusion and outlook

A concurrent assessment of all measured excitation functions for various reactions induced by neutrons on ⁹³Nb, in addition to the results of using default parameters within the worldwide used computer code TALYS-1.96 [14] and the currently related TENDL-2021 evaluation [15], is reported. The use of consistent parameter sets that are formerly obtained or validated by analysis of other independent data is mainly concerned. Moreover, no empirical rescaling factors of the γ and/or neutron widths have been used.

A proper account of all available data for competitive reaction channels has prevented compensation effects of less accurate model parameters. On the other hand, detailed analyses based on consistent input parameter sets are really needed to eventually improve the global parameters for involvement in large-scale evaluations. Moreover, the consistency of input parameters may lead to a similar condition of the model calculation results, agreeing with the data obtained previously and always behaving in a similar way.

The correlation between the measured error bars of the primary data providing the consistent input parameters and the final uncertainty bands of the calculated results has been pointed out. Thus, e.g., comparison between the nuclear-level density effects due to the uncertainty of either the average-level density parameter a for the residual nucleus ⁹³Nb or the fitted $D_0^{\exp }$ for the residual nuclei ⁹³Zr and ⁹⁰Y has been carried out.

Finally, matching of the experimental and calculated cross-section uncertainties has been obtained and its correspondence to the limits of the distinct data previously involved in the consistent parameter assessment. Remaining questions and the need for additional measurements are emphasized.

Data availability statement

The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work has been partly supported by the Executive Unit for the Financing of Higher Education, Research, Development and Innovation (UEFISCDI) (Project No. PN-III-ID-PCE-2021-1260) and carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200—EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.

Acknowledgments

The support by the Nuclear Energy Agency (NEA) Data Bank, Paris, in providing their services hosting the progress meetings, is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Gruppelaar H, Nagel P. International nuclear model and code comparison on pre-equilibrium effects. In: Tech. rep. Vienna, Austria: INDC(NEA)6, IAEA (1985). Available from: https://www-nds.iaea.org/publications/indc/indc-nea-0006/ (Accessed 15 10, 2022).

Google Scholar

2. Hauser W, Feshbach H. The inelastic scattering of neutrons. Phys Rev (1952) 87:366–73. doi:10.1103/PhysRev.87.366

CrossRef Full Text | Google Scholar

3. Gadioli E, Hodgson PE. Pre-equilibrium nuclear reactions. Oxford: Clarendon (1992).

Google Scholar

4. Kalbach C. Surface and collective effects in preequilibrium reactions. Phys Rev C (2000) 62:044608. doi:10.1103/PhysRevC.62.044608

CrossRef Full Text | Google Scholar

5. Watanabe Y, Aoto A, Kashimoto H, Chiba S, Fukahori T, Hasegawa K, et al. Feshbach-Kerman-Koonin model analysis of preequilibrium (p,p’) and (p,n) reactions at 12 to 26 MeV. Phys Rev C (1995) 51:1891–907. doi:10.1103/PhysRevC.51.1891

CrossRef Full Text | Google Scholar

6. Demetriou P, Hodgson PE, Marcinkowski A, Watanabe Y. A consistent analysis of (n, n′), (p, p′), (n, p), and (p, n) multistep reactions using the Feshbach - kerman - Koonin theory. J Phys G: Nucl Part Phys (1996) 22:629–40. doi:10.1088/0954-3899/22/5/010

CrossRef Full Text | Google Scholar

7. Avrigeanu M, Harangozo A, Avrigeanu V, Antonov AN. Nuclear surface localization of preequilibrium reactions at low energies. Phys Rev C (1996) 54:2538–46. doi:10.1103/PhysRevC.54.2538

CrossRef Full Text | Google Scholar

8. Avrigeanu M, Harangozo A, Avrigeanu V, Antonov AN. Average strength of the effective interaction in multistep direct reactions. Phys Rev C (1997) 56:1633–6. doi:10.1103/PhysRevC.56.1633

CrossRef Full Text | Google Scholar

9. Kalbach C. Toward a global exciton model; lessons at 14 MeV. J Phys G: Nucl Part Phys (1998) 24:847–66. doi:10.1088/0954-3899/24/4/014

CrossRef Full Text | Google Scholar

10. Koning A, Rochman D. Modern nuclear data evaluation with the talys code system. Nucl Data Sheets (2012) 113:2841–934. doi:10.1016/j.nds.2012.11.002

CrossRef Full Text | Google Scholar

11. Ichihara A. Calculation of cross sections for metastable state production in the (n, γ), (n, n′), (n, 2n) and (n, 3n) reactions of ⁹³Nb. J Nucl Sci Tech (2016) 53:2049–55. doi:10.1080/00223131.2016.1192005

CrossRef Full Text | Google Scholar

12. Liang H, Wu Z, Zhang Z, Han Y, Jiao X. Calculations and analysis of n+93Nb reaction. Nucl Sci Eng (2017) 187:107–26. doi:10.1080/00295639.2017.1295699

CrossRef Full Text | Google Scholar

13. Naik H, Kim G, Kim K, Zaman M, Nadeem M, Sahid M. Neutron-induced reaction cross-sections of 93Nb with fast neutron based on 9Be(p,n) reaction. Nucl Phys A (2018) 970:156–68. doi:10.1016/j.nuclphysa.2017.11.011

CrossRef Full Text | Google Scholar

14. Koning AJ, Hilaire S, Duijvestijn MC. Talys-1.0. In: O Bersillon, F Gunsing, E Bauge, R Jacqmin, and S Leray, editors. Proceedings of the International Conference on Nuclear Data for Science and Technology - ND2007; April 22-27, 2007; Nice, France. Les Ulis, France: EDP Sciences (2008). p. 211–4. Available from: http://www.talys.eu (Accessed 15 10, 2022).

Google Scholar

15. Koning A, Rochman D, Sublet JC, Dzysiuk N, Fleming M, van der Marck S. TENDL: Complete nuclear data library for innovative nuclear science and technology. Nucl Data Sheets (2019) 155:1–55. doi:10.1016/j.nds.2019.01.002

CrossRef Full Text | Google Scholar

16. Avrigeanu M, Avrigeanu V. Optical potential for incident and emitted low-energy α particles. III. Non-statistical processes induced by neutrons on Zr, Nb, and Mo nuclei (2022). Submitted to Phys. Rev. C; Report arXiv:2302.09845 [nucl-th]. doi:10.48550/arXiv.2302.09845

CrossRef Full Text | Google Scholar

17. Arthur ED. Parameter determination and application to nuclear model calculations of neutron-induced reactions on yttrium and zirconium isotopes. Nucl Sci Eng (1980) 76:137–47. doi:10.13182/NSE80-A19446

CrossRef Full Text | Google Scholar

18. Avrigeanu V, Avrigeanu M, Mănăilescu C. Further explorations of the α-particle optical model potential at low energies for the mass range A ≈ 45–209. Phys Rev C (2014) 90:044612. doi:10.1103/PhysRevC.90.044612

CrossRef Full Text | Google Scholar

19. Avrigeanu V, Avrigeanu M. Analysis of uncertainties in α-particle optical-potential assessment below the coulomb barrier. Phys Rev C (2016) 94:024621. doi:10.1103/PhysRevC.94.024621

CrossRef Full Text | Google Scholar

20. Avrigeanu V, Avrigeanu M. Role of consistent parameter sets in an assessment of the α-particle optical potential below the coulomb barrier. Phys Rev C (2019) 99:044613. doi:10.1103/PhysRevC.99.044613

CrossRef Full Text | Google Scholar

21. Avrigeanu V, Avrigeanu M. Validation of an optical potential for incident and emitted low-energy α-particles in the A ≈ 60 mass range. Eur Phys J A (2021) 57:54. doi:10.1140/epja/s10050-020-00336-0

CrossRef Full Text | Google Scholar

22. Avrigeanu V, Avrigeanu M. Validation of an optical potential for incident and emitted low-energy α-particles in the A ≈ 60 mass range. II. Neutron–induced reactions on Ni isotopes. Eur Phys J A (2022) 58:189. doi:10.1140/epja/s10050-022-00831-6

CrossRef Full Text | Google Scholar

23. Avrigeanu M, Avrigeanu V. Recent improvements of the STAPRE-H95 preequilibrium and statistical model code. In: Tech. rep. Bucharest: Institute for Physics and Nuclear Engineering Report NP-86-1995 (1995). Available from: http://www.oecd-nea.org/tools/abstract/detail/iaea0971/ (Accessed 15 10, 2022).

Google Scholar

24.[Dataset] Kunz PD. DWUCK4 user manual (1984). Available from: http://spot.colorado.edu/∼kunz/DWBA.html, http://www.oecd-nea.org/tools/abstract/detail/nesc9872/ (Accessed 15 10, 2022).

Google Scholar

25. Thompson IJ. Coupled reaction channels calculations in nuclear physics. Comp Phys Rep (1988) 7:167–212. doi:10.1016/0167-7977(88)90005-6

CrossRef Full Text | Google Scholar

26. Avrigeanu V, Avrigeanu M. Consistent optical potential for incident and emitted low-energy α particles. II. α emission in fast-neutron-induced reactions on Zr isotopes. Phys Rev C (2017) 96:044610. doi:10.1103/PhysRevC.96.044610

CrossRef Full Text | Google Scholar

27. Vonach H, Uhl M, Strohmaier B, Smith BW, Bilpuch EG, Mitchell GE. Comparison of average s-wave resonance spacings from proton and neutron resonances. Phys Rev C (1988) 38:2541–9. doi:10.1103/PhysRevC.38.2541

CrossRef Full Text | Google Scholar

28. Koning AJ, Delaroche JP. Local and global nucleon optical models from 1 keV to 200 MeV. Nucl Phys A (2003) 713:231–310. doi:10.1016/S0375-9474(02)01321-0

CrossRef Full Text | Google Scholar

29.[Dataset] UiO/OCL. UiO/OCL Level densities and gamma-ray strength functions (2022). Available from: http://ocl.uio.no/compilation (Accessed 15 10, 2022).

Google Scholar

30. Kawano T, Cho Y, Dimitriou P, Filipescu D, Iwamoto N, Plujko V, et al. IAEA photonuclear data library 2019. Nucl Data Sheets (2020) 163:109–62. doi:10.1016/j.nds.2019.12.002

CrossRef Full Text | Google Scholar

31.[Dataset] ENSDF. Evaluated nuclear structure data file (ENSDF) (2022). Available from: https://www.nndc.bnl.gov/ensdf/(Accessed 15 10, 2022).

Google Scholar

32. Avrigeanu V, Glodariu T, Plompen AJM, Weigmann H. On consistent description of nuclear level density. J Nucl Sci Tech (2002) 39:746–9. doi:10.1080/00223131.2002.10875205

CrossRef Full Text | Google Scholar

33. Capote R, Herman M, Obložinský P, Young PG, Goriely S, Belgya T, et al. RIPL – reference input parameter library for calculation of nuclear reactions and nuclear data evaluations. Nucl Data Sheets (2009) 110:3107–214. doi:10.1016/j.nds.2009.10.004

CrossRef Full Text | Google Scholar

34.[Dataset] Nuclear Data Services. Average neutron resonance parameters and other data collected in Beijing (1998). Available from: https://www-nds.iaea.org/ripl/resonances/other_files/beijing_dat.htm (Accessed 15 10, 1998).

Google Scholar

35. Johnson CH. Statistical model radiation widths for 75 < A < 130 and the enhancement of P-wave neutron capture for A ≈ 90. Phys Rev C (1977) 16:2238–48. doi:10.1103/PhysRevC.16.2238

CrossRef Full Text | Google Scholar

36. Delaroche JP, Lagrange C, Salvy J. Handbook for calculations of nuclear reaction data, RIPL-2. In: Tech. rep. Vienna, Austria: IAEA-190, IAEA (1976). Available from: https://www-nds.iaea.org/publications/tecdocs/iaea-0190-vol.1/ (Accessed 15 10, 2022).

Google Scholar

37. Otuka N, Dupont E, Semkova V, Pritychenko B, Blokhin A, Aikawa M, et al. Towards a more complete and accurate experimental nuclear reaction data library (EXFOR): International collaboration between nuclear reaction data centres (NRDC). Nucl Data Sheets (2014) 120:272–6. doi:10.1016/j.nds.2014.07.065

CrossRef Full Text | Google Scholar

38. Goriely S, Dimitriou P, Wiedeking M, Belgya T, Firestone R, Kopecky J, et al. Reference database for photon strength functions. Eur Phys J A (2019) 55:172. doi:10.1140/epja/i2019-12840-1

CrossRef Full Text | Google Scholar

39. Kopecky J, Uhl M. Test of gamma-ray strength functions in nuclear reaction model calculations. Phys Rev C (1990) 41:1941–55. doi:10.1103/PhysRevC.41.1941

CrossRef Full Text | Google Scholar

40. Axel P. Electric dipole ground-state transition width strength function and 7-mev photon interactions. Phys Rev (1962) 126:671–83. doi:10.1103/PhysRev.126.671

CrossRef Full Text | Google Scholar

41. Kopecky J, Uhl M, Chrien RE. Radiative strength in the compound nucleus ¹⁵⁷Gd. Phys Rev C (1993) 47:312–22. doi:10.1103/PhysRevC.47.312

CrossRef Full Text | Google Scholar

42. Tveten GM, Spyrou A, Schwengner R, Naqvi F, Larsen AC, Eriksen TK, et al. Completing the nuclear reaction puzzle of the nucleosynthesis of ⁹²Mo. Phys Rev C (2016) 94:025804. doi:10.1103/PhysRevC.94.025804

CrossRef Full Text | Google Scholar

43. Spyrou A, Quinn SJ, Simon A, Rauscher T, Battaglia A, Best A, et al. Measurement of the ^90,92Zr(p, γ)^91,93Nb reactions for the nucleosynthesis of elements near A = 90. Phys Rev C (2013) 88:045802. doi:10.1103/PhysRevC.88.045802

CrossRef Full Text | Google Scholar

44. Moldauer P. Statistics and the average cross section. Nucl Phys A (1980) 344:185–95. doi:10.1016/0375-9474(80)90671-5

CrossRef Full Text | Google Scholar

45. Blann M, Vonach HK. Global test of modified precompound decay models. Phys Rev C (1983) 28:1475–92. doi:10.1103/PhysRevC.28.1475

CrossRef Full Text | Google Scholar

46. Avrigeanu M, Ivascu M, Avrigeanu V. Nuclear level densities below 40 MeV excitation energy in the mass region A ∼50. Z Phys A - At Nuclei (1990) 335:299–313. doi:10.1007/BF01304709

CrossRef Full Text | Google Scholar

47. Avrigeanu M, Avrigeanu V. Partial level densities for nuclear data calculations. Comp Phys Commun (1998) 112:191–226. doi:10.1016/S0010-4655(98)00050-2

CrossRef Full Text | Google Scholar

48. Harangozo A, Şteţcu I, Avrigeanu M, Avrigeanu V. Particle-hole state densities with nonequidistant single-particle levels. Phys Rev C (1998) 58:295–306. doi:10.1103/PhysRevC.58.295

CrossRef Full Text | Google Scholar

49. Kalbach C. Surface effects in the exciton model of preequilibrium nuclear reactions. Phys Rev C (1985) 32:1157–68. doi:10.1103/PhysRevC.32.1157

CrossRef Full Text | Google Scholar

50. Smits J, Siemssen R. Semi-microscopic description of three-nucleon transfer and the Sn(p,α)In reaction. Nucl Phys A (1976) 261:385–412. doi:10.1016/0375-9474(76)90154-8

CrossRef Full Text | Google Scholar

51. Smits J, Siemssen R, Van Der Werf S, Van Der Woude A. The 58,60,62,64ni(p,α)55,57,59,61co reactions and their description by the semi-microscopic model for three-nucleon transfer. Nucl Phys A (1979) 319:29–49. doi:10.1016/0375-9474(79)90169-6

CrossRef Full Text | Google Scholar

52. Glendenning NK. Tables of nuclear structure amplitudes for two-nucleon transfer involving light projectiles (a ≤ 4). At Data Nucl Data Tables (1975) 16:1–134. doi:10.1016/0092-640X(75)90031-5

CrossRef Full Text | Google Scholar

53. Guttormsen M, Larsen AC, Garrote FLB, Byun Y, Eriksen TK, Giacoppo F, et al. Shell-gap-reduced level densities in ^89,90Y. Phys Rev C (2014) 90:044309. doi:10.1103/PhysRevC.90.044309

CrossRef Full Text | Google Scholar