Variational Bayesian cardinalized probability hypothesis density filter for robust underwater multi-target direction-of-arrival tracking with uncertain measurement noise

The direction-of-arrival (DOA) tracking of underwater targets is an important research topic in sonar signal processing. Considering that the underwater DOA tracking is a typical multi-target problem under unknown underwater environment with missing detection, false alarm, and uncertain measurement noise, a robust underwater multi-target DOA tracking method for uncertain measurement noise is proposed. First, a kinematic model of the multiple underwater targets and bearing angle measurement model with missing detection and false alarms are established. Then, the multi-target DOA tracking algorithm is derived by using the cardinalized probability hypothesis density (CPHD) filter, the performance of which largely depends on the accuracy of the parameter of measurement noise variance. In addition, the variational Bayesian approach is used to adaptively estimate the uncertain measurement of noise variance for each measurement of target in the real time of tracking. Thus, the robust underwater multi-target DOA tracking is carried out. Finally, comprehensive experimental validations and discussions are made to prove that the proposed algorithm can provide robust DOA tracking in the multi-target tracking scenario with uncertain measurement noise.

1 Introduction

The direction-of-arrival (DOA) estimation and tracking is an important research topic in sonar signal processing [1–5]. For the scenario of moving targets, the traditional DOA estimation methods cut the measurement of the output of sonar array signal into small periods in time to process, which ignores the kinematic characteristics of the targets [6–8]. The DOA tracking methods not only use the measurement information but also rely on the kinematic characteristics of the underwater targets [9–18]. Therefore, by not only depending on the current measurements but also utilizing the prior kinematic information of an unknown underwater target, the DOA tracking methods can provide more robust and accurate results than the traditional DOA estimation methods.

In view of the advantages of the DOA tracking methods, researchers have carried out a lot of work around DOA tracking. The DOA tracking methods first take the outputs of the sonar array signals or results of the traditional DOA estimation methods as the measurements. Then, considering the typical kinematics of the underwater targets, the kinematic model by the bearing angle is established. Then, based on the framework of the Bayesian filter theory [19], the bearing angle of the target can be recursively estimated from the current measurements. Depending on the bearing angle measurements obtained by the traditional DOA estimation methods, the Kalman filter (KF) is always utilized as the DOA tracking algorithm [9, 10] for the linear relationship between the measurement and bearing angle of the target. Besides utilizing the bearing angle measurements, some research take the outputs of sonar array signals as measurements. However, under such a circumstance, the mathematical relationship between the bearing angle of the target and the measurement is non-linear. For such non-linear problems, many tracking algorithms based on the non-linear Bayesian filter have proposed the extended Kalman filter (EKF) [11, 12].The first-order Taylor series expansion of the measurement model was used to approximate the non-linear model to a linear model. The unscented Kalman filter (UKF) [20, 21] uses a group of determined sigma points to linearize the non-linear model. The particle filter (PF) [22] generates and transforms a large number of arbitrary particles to represent the distribution of the target state. Thus, the PF can theoretically achieve accurate tracking in any non-linear tracking system with any distribution of the uncertainties, while the computational complexity of the PF stays significant.

Although the tracking techniques are widely utilized in the scenario of underwater target tracking, most of them are only applicable to the single-target tracking scenario [9–12, 20–22]. However, the underwater DOA tracking issue is a typical multi-target tracking scenario where the multi-target tracking techniques should be considered and proposed. The methods for multi-target tracking problem can be divided into two categories: the traditional data association methods and random finite set (RFS)–based multi-target tracking methods. The data association methods establish the association between measurements and targets, so as to transform the multi-target tracking problem into a single-target tracking problem to use the abovementioned single-target tracking methods. However, these data association techniques have to match every measurement with its target which can make computation highly complex with large number of targets or false alarms caused by uncertain measurement noise [23, 24]. From the beginning of this century, the RFS-based multi-target tracking methods have developed rapidly to overcome the drawbacks caused by the data association techniques. The RFS can be defined by a set with elements along with the number of the elements which are subjected to random distributions. The RFS-based multi-target tracking methods define the states and measurements of targets as RFSs such that the data association procedure can be avoided. As a result, by utilizing the RFS technique, the computational complexity of multi-target tracking can be hugely reduced, especially when the number of targets and false alarms is large. For the RFS-based multi-target tracking, Mahler first proposed the concept of “first-order moment filter,” also known as probability hypothesis density (PHD) filter [25]. Since, the PHD filter has no closed-form solution in general, Vo et al. [26] proposed sequential Monte Carlo solution for the PHD filter (SMC-PHD), and Clark et al. [27] proposed the Gaussian mixture model implementation of the PHD filter (GM-PHD), which push the PHD filter from theory to application. The GM-PHD filter requires both the kinematic model of targets and the measurement model to be linear. The SMC-HD filter represents the distribution of the states of the targets by generating and transferring many of the particles, which is suitable for non-linear models. However, the calculation of the particles leads to high computation overload. Subsequently, Mahler [28, 29] introduced the cardinality distribution to describe the number of targets on the basis of the PHD filter to make a more accurate estimation of the number of targets and proposed the CPHD filter. Similar to the PHD filter, the CPHD filter also has no closed-form solution in general and has to be implemented on the basis of the SMC or GM model [30]. Considering that the computational complexity of the RFS-based method is lower than that of the data association method, researchers have proposed many multi-target DOA tracking methods based on the PHD and CPHD filters [13–16]. These methods use the output of the array signal as measurements with the non-linear measurement model, thus implementing them based on SMC.

Due to high-dimension array signal–based measurements and the large number of particles for the SMC method, the existing RFS-based multi-target DOA tracking methods get a large computation overload. Moreover, in the real scenario of underwater tracking, the unknown ocean environment always results in uncertain measurement noise. Thus, besides considering the computational complexity, accomplishing robust and accurate tracking when the measurements are in a low SNR scenario is also important, especially in the underwater target tracking case. However, most of the existing DOA tracking methods assume the measurement noise to be a certain stochastic process which leads to the degradation of the tracking performance in the real scenario of uncertain measurement noise. To deal with the uncertain measurement noise, Zhang et al. [12] derived a robust single-target DOA tracking method based on the EKF by estimating the measurement noise covariance matrix (MNCM) by using the improved Sage-Husa algorithm. By estimating the MNCM in a maximum-likelihood (ML) framework, the expectation-maximum adaptive Kalman filter (EM-AKF) was proposed [31, 32]. Sarkka and Hartikainen [33, 34] assumed the MNCM to be subject to an inverse Wishart distribution and iteratively estimated the MNCM by using variational Bayesian approach, namely, the variational Bayesian adaptive Kalman filter (VB-AKF). Huang et al. [37] assumed the mean square error matrix (MSEM) to also be subjected to an inverse Wishart distribution and jointly estimated it along with the MNCM to improve the performance of VB-AKF. In the existing works, the superior accuracy and stability of the VB-AKF has been demonstrated [33–37]. However, the MNCM estimation method has not been applied to robust multi-target DOA tracking yet. Thus, considering the uncertain underwater environment and its influences on the underwater target tracking missions, adopting variational Bayesian online estimation technique into the multitarget tracking scenario is inspiring and necessary.

In this article, the bearing angle estimates obtained by using the traditional DOA estimation method are regarded as the measurements, and the multi-target DOA tracking algorithm is derived by using the GM-CPHD filter. Different from most of the existing tracking algorithms, we considered the uncertain measurement noise caused by the unknown underwater environment, which always makes a certain tracking algorithm diverge. Thus, the variational Bayesian approach is utilized to estimate the covariance matrix of the measurement noise along with the states of targets in the framework of the GM-CPHD filter. In this way, the variational Bayesian GM-CPHD filter (VB-GMCPHD) for robust underwater multi-target DOA tracking is proposed for the scenario of robust tracking under uncertain measurement noise. Finally, the results of the experiment show the robustness and accuracy of the proposed method in real underwater multi-target DOA tracking scenario. The contributions of this article are summarized as follows:

First, the multi-target DOA tracking algorithm is derived by using the GM-CPHD filter for the real underwater tracking scenario with missing detection and false alarm.

Second, the issue of uncertain measurement noise is addressed by using the variational Bayesian approach to estimate the measurement noise variance. Thus, the VB-GMCPHD for robust underwater multi-target DOA tracking is proposed.

Finally, the real experimental data is utilized to verify the superior accuracy and robustness of the proposed method in real underwater DOA tracking scenario.

The rest of this article is organized as follows: in Section 2, the problem of underwater multi-target DOA tracking with missing detection and false alarm is formulated. In Section 3, the GM-CPHD filter for DOA tracking is described. In Section 4, based on the variational Bayesian approach, an innovative multi-target DOA tracking method for uncertain measurement noise scenario, namely the VB-GMCPHD, is proposed. In Section 5, experimental validations are made and the results are proved, demonstrating the superior performance of the proposed VB-GMCPHD. Finally, the conclusions are drawn in Section 6.

2 Multi-target tracking models

The sets of the states of the targets and the measurements are assumed to be RFSs. Assuming that $n_k$ targets exist within the detection range of the sonar at time step k and the state of the $i_n$-th target is ${\mathit{x}}_k^{i_n}$, the set of the states of targets at time step k is expressed as ${\mathit{X}}_k=\left\{{\mathit{x}}_k^1,{\mathit{x}}_k^2,...,{\mathit{x}}_k^{n_k}\right\}$. Let ${\theta }_k$ denote the bearing angle of the $i_n$-th target (${\theta }_k^{i_n}$ is the angle between the target and positive x-axis with respect to the positive counterclockwise.) and ${\dot{\theta }}_k^{i_n}$ denote the change rate of ${\theta }_k^{i_n}$, then the state of the $i_n$-th target is expressed as ${\mathit{x}}_k^{i_n}={\left({\theta }_k^{i_n},{\dot{\theta }}_k^{i_n}\right)}^{\mathrm{T}}$, where ${\left(\cdot \right)}^{\mathrm{T}}$ denotes the matrix transposition. Since the underwater targets are usually not maneuvering to save energy and keep concealed, the bearing angles of the targets are assumed to be subject to the constant velocity (CV) model. The CV model of the state of the $i_n$-th target is expressed as

$\left\{\begin{array}{l}{\mathit{x}}_k^{i_n}={\mathit{F}}_{k|k-1}{\mathit{x}}_{k-1}^{i_n}+{\mathit{G}}_k{w}_k\\ {\mathit{F}}_{k|k-1}=\left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right],{\mathit{G}}_k=\left[\begin{array}{c}{T}^2/2\\ T\end{array}\right]\end{array}\right.,(1)$

where ${\mathit{F}}_{k|k-1}$ and ${\mathit{G}}_k$ are the state transition matrix and the noise driving matrix, $w_k$ denotes the zero-mean Gaussian process noise with the covariance matrix $Q_k$ caused by the unknown underwater environment, and T is the interval between the adjacent time steps.

The estimates of the bearing angles of the targets with error obtained by the traditional DOA estimation methods are taken as measurements. Considering the probability of missing detection and false alarm, the number of measurements and the states of the targets are always different in a multi-target tracking problem. It is assumed that $m_k^d$ targets are detected and $m_k^f$ false alarms exist, i.e., $m_k=m_k^d+m_k^f$ measurements are obtained at time step k. The set of measurements at time step k are expressed as ${\mathit{Z}}_k=\left\{{\mathit{z}}_k^1,{\mathit{z}}_k^2,...,{\mathit{z}}_k^{m_k}\right\}$. Then the measurement of the $i_m^d$-th detected target ${\mathit{z}}_k^{i_m^d}$ at time step k can be expressed as

${\mathit{z}}_k^{i_m^d}={\mathit{H}}_k{\mathit{x}}_k^{i_m^d}+v_k,(2)$

where ${\mathit{H}}_k$ denotes the measurement matrix and ${\mathit{H}}_k=\left[\mathrm{1,0}\right]$, $v_k$ is the error of the bearing angle estimate obtained by using traditional DOA estimation, which is subject to Gaussian distribution with zero mean and variance of ${\sigma }_{r,k}^2$. The false alarms ${\mathit{z}}_k^1,{\mathit{z}}_k^2,...,{\mathit{z}}_k^{m_k^f}$ are assumed to be subject to Poisson distribution with intensity of ${\kappa }_k$.

3 GM-CPHD filter for multi-target DOA tracking

The CPHD filter performs multi-target tracking by recursively calculating the PHD and the cardinality distribution to represent the distribution of the states and the number of the targets, respectively. The closed-form solution of the CPHD filter is given in the assumption of the linear Gaussian mixture (GM) model, which is called the GM-CPHD filter. Each component of the Gaussian mixture model represents the respective states of the targets [30].

The cardinality distribution $p_{k-1}\left(n\right)$ and the PHD $v_{k-1}\left(x\right)$ are assumed to be known, and $v_{k-1}\left(x\right)$ is subject to the Gaussian mixture model as

$v_{k-1}\left(x\right)={\displaystyle \sum }_{i=1}^{J_{k-1}}{w}_{k-1}^{\left(i\right)}N\left({\mathit{x}}_k;{\mathit{m}}_{k-1}^{\left(i\right)},{\mathit{P}}_{k-1}^{\left(i\right)}\right),(3)$

where $w_{k-1}^{\left(i\right)}$ denotes the weight, $N\left(\cdot ;\mathit{m},\mathit{P}\right)$ denotes the Gaussian distribution with the mean of m and covariance matrix of P, and ${\mathit{m}}_{k-1}^{\left(i\right)}$ and ${\mathit{P}}_{k-1}^{\left(i\right)}$ denote the estimate of the state of the target and the mean square error matrix (MSEM), respectively. Then, the process of the GM-CPHD filter at time step k is divided into prediction and update as follows:

(1) Prediction

Once the cardinality distribution $p_{k-1}\left(n\right)$ at time step $k-1$ is given, the predicted cardinality distribution is expressed as

$p_{k|k-1}\left(n\right)={\displaystyle \sum }_{j=0}^n{p}_{\mathrm{\Gamma },k}\left(n-j\right){\displaystyle \sum }_{l=j}^{\infty }{C}_l^j{p}_{k-1}\left(l\right)p_{s,k}^j{\left(1-p_{s,k}\right)}^{l-j},(4)$

where $C_l^j=l!/\left(j!\left(l-j\right)!\right)$, $p_{\mathrm{\Gamma },k}\left(\cdot \right)$ is the cardinality distribution of birth targets, and $p_{s,k}$ is the probability of targets surviving.

Once the PHD $v_{k-1}\left(x\right)$ at time step $k-1$ is given, the predicted PHD is expressed as

$v_{k|k-1}\left(x\right)=v_{s,k|k-1}\left(x\right)+{\gamma }_k\left(x\right),(5)$

where $v_{s,k|k-1}\left(x\right)$ and ${\gamma }_k\left(x\right)$ denote the PHD of surviving targets and birth targets, respectively. $v_{s,k|k-1}\left(x\right)$ is expressed as

$v_{s,k|k-1}\left(x\right)=p_{s,k}{\displaystyle \sum }_{j=1}^{J_{k-1}}{w}_{k-1}^{\left(j\right)}N\left(x;{\mathit{m}}_{s,k|k-1}^{\left(j\right)},{\mathit{P}}_{s,k|k-1}^{\left(j\right)}\right),(6)$

where the predicted state ${\mathit{m}}_{s,k|k-1}^{\left(j\right)}$ and predicted MSEM ${\mathit{P}}_{s,k|k-1}^{\left(j\right)}$ of the j-th surviving target is given as follows:

${\mathit{m}}_{s,k|k-1}^{\left(j\right)}={\mathit{F}}_{k-1}{\mathit{m}}_{k-1}^{\left(j\right)},(7)$

${\mathit{P}}_{s,k|k-1}^{\left(j\right)}={\mathit{G}}_k{\mathit{\sigma }}_q^2{\mathit{G}}_k^T+{\mathit{F}}_{k-1}{\mathit{P}}_{k-1}^{\left(j\right)}{\mathit{F}}_{k-1}^T.(8)$

The PHD of birth targets ${\gamma }_k\left(x\right)$ is also subject to the Gaussian mixture model as follows:

${\gamma }_k\left(x\right)={\displaystyle \sum }_{i=1}^{J_{\gamma ,k}}{w}_{\gamma ,k}^{\left(i\right)}N\left(x;{\mathit{m}}_{\gamma ,k}^{\left(i\right)},{\mathit{P}}_{\gamma ,k}^{\left(i\right)}\right).(9)$

where $J_{\gamma ,k}$ denotes the number of components of the Gaussian mixture model for ${\gamma }_k\left(x\right)$, and $w_{\gamma ,k}^{\left(i\right)}$, ${\mathit{m}}_{\gamma ,k}^{\left(i\right)}$, and ${\mathit{P}}_{\gamma ,k}^{\left(i\right)}$ denote the weight, state, and MSEM of the i-th birth target, respectively.

According to Equations 5, 6, and 9, the predicted PHD can be expressed as follows:

$v_{k|k-1}\left(x\right)={\displaystyle \sum }_{i=1}^{J_{k|k-1}}{w}_{k|k-1}^{\left(i\right)}N\left(x;{\mathit{m}}_{k|k-1}^{\left(i\right)},{\mathit{P}}_{k|k-1}^{\left(i\right)}\right),(10)$

where $w_{k|k-1}^{\left(i\right)}$, ${\mathit{m}}_{k|k-1}^{\left(i\right)}$, and ${\mathit{P}}_{k|k-1}^{\left(i\right)}$ denote the weight, predicted estimate of the state, and predicted MSEM of the i-th target, respectively.

(2) Update

The cardinality distribution $p_k\left(n\right)$ and PHD $v_k\left(x\right)$ at time step k are obtained by using the measurement set ${\mathit{Z}}_k$ to update $p_{k|k-1}\left(n\right)$ and $v_{k|k-1}\left(x\right)$ as follows:

$p_k\left(n\right)=\frac{{\mathrm{\Psi }}_k^0\left[{\mathit{w}}_{k|k-1},{\mathit{Z}}_k\right]\left(n\right)p_{k|k-1}\left(n\right)}{〈{\mathrm{\Psi }}_k^0\left[{\mathit{w}}_{k|k-1},{\mathit{Z}}_k\right],p_{k|k-1}〉},(11)$

$v_k\left(x\right)=\frac{〈{\mathrm{\Psi }}_k^1\left[{\mathit{w}}_{k|k-1},{\mathit{Z}}_k\right],{\mathit{p}}_{k|k-1}〉}{〈{\mathrm{\Psi }}_k^0\left[{\mathit{w}}_{k|k-1},{\mathit{Z}}_k\right],{\mathit{p}}_{k|k-1}〉}\left(1-p_{D,k}\right)v_{k|k-1}\left(x\right)+{\displaystyle \sum }_{z\in Z_k}{\displaystyle \sum }_{j=1}^{J_{k|k-1}}{w}_k^{\left(j\right)}\left(\mathit{z}\right)N\left(\mathit{x};{\mathit{m}}_k^{\left(j\right)},{\mathit{P}}_k^{\left(j\right)}\right),(12)$

where $〈\mathit{\alpha },\mathit{\beta }〉$ denotes the inner product of $\mathit{\alpha }$ and $\mathit{\beta }$, i.e., $〈\mathit{\alpha },\mathit{\beta }〉={\sum }_{l=1}^L{\alpha }_l{\beta }_l$ ($\mathit{\alpha }=\left[{\alpha }_1,{\alpha }_2,...,{\alpha }_L\right]$, $\mathit{\beta }=\left[{\beta }_1,{\beta }_2,...,{\beta }_L\right]$), and $p_{D,k}$ denotes the detection probability, and

${\mathrm{\Psi }}_k^u\left[\mathit{w},\mathit{Z}\right]\left(n\right)={\displaystyle \sum }_{j=0}^{\min \left(\left|\mathit{Z}\right|,n\right)}\left(\left|\mathit{Z}\right|-j\right)p_{K,k}\left(\left|\mathit{Z}\right|-j\right)A_n^{j+u}\frac{{\left(1-p_{D,k}\right)}^{n-\left(j+u\right)}}{{〈1,\mathit{w}〉}^{j+u}}{e}_j\left({\mathrm{\Lambda }}_k\left(\mathit{w},\mathit{Z}\right)\right),(13)$

${\mathrm{\Lambda }}_{k,z}\left(x\right)=\left\{\frac{〈1,{\kappa }_k〉}{{\kappa }_k\left(z\right)}{p}_{D,k}{\mathit{w}}^T{\mathit{q}}_k\left(z\right):z\in Z\right\},(14)$

${\mathit{w}}_{k|k-1}={\left[w_{k|k-1}^{\left(1\right)},\dots ,w_{k|k-1}^{\left(J_{k|k-1}\right)}\right]}^T,(15)$

${\mathit{q}}_k\left(z\right)={\left[q_k^{\left(1\right)}\left(z\right),\dots ,q_k^{\left(J_{k|k-1}\right)}\left(z\right)\right]}^T,(16)$

$q_k^{\left(j\right)}\left(\mathit{z}\right)=N\left(\mathit{z};{\mathit{\eta }}_{k|k-1}^{\left(j\right)},{\mathit{S}}_{k|k-1}^{\left(j\right)}\right),(17)$

${\mathit{\eta }}_{k|k-1}^{\left(j\right)}={\mathit{H}}_k{\mathit{m}}_{k|k-1}^{\left(j\right)},(18)$

${\mathit{S}}_{k|k-1}^{\left(j\right)}={\mathit{H}}_k{\mathit{P}}_{k|k-1}^{\left(j\right)}{\mathit{H}}_k^T+{\sigma }_{r,k}^2,(19)$

$w_k^{\left(j\right)}\left(\mathit{z}\right)=p_{D,k}{w}_{k|k-1}^{\left(j\right)}{q}_k^{\left(j\right)}\left(\mathit{z}\right)\frac{〈{\mathrm{\Psi }}_k^1\left[w_{k|k-1},{\mathit{Z}}_k\backslash \left\{\mathit{z}\right\}\right],p_{k|k-1}〉}{〈{\mathrm{\Psi }}_k^0\left[w_{k|k-1},{\mathit{Z}}_k\right],p_{k|k-1}〉}\frac{〈1,{\kappa }_k〉}{{\kappa }_k\left(\mathit{z}\right)},(20)$

${\mathit{m}}_k^{\left(j\right)}\left(\mathit{z}\right)={\mathit{m}}_{k|k-1}^{\left(j\right)}+{\mathit{K}}_k^{\left(j\right)}\left(\mathit{z}-{\mathit{\eta }}_{k|k-1}^{\left(j\right)}\right),(21)$

${\mathit{P}}_k^{\left(j\right)}=\left[\mathit{I}-{\mathit{K}}_k^{\left(j\right)}{\mathit{H}}_k\right]{\mathit{P}}_{k|k-1}^{\left(j\right)},(22)$

${\mathit{K}}_k^{\left(j\right)}={\mathit{P}}_{k|k-1}^{\left(j\right)}{\mathit{H}}_k^T{\left[{\mathit{S}}_{k|k-1}^{\left(j\right)}\right]}^{-1},(23)$

where $\left|\mathit{Z}\right|$ denotes the number of the elements of the set Z, $p_{K,k}$ denotes the cardinality distribution of false alarm at time step k, $e_j\left(\cdot \right)$ denotes elementary symmetric function of order j, and $e_j\left(Z\right)={{\displaystyle \sum }}_{S\subseteq Z,\left|S\right|=j}{\prod }_{\zeta \in S}\zeta$, $e_0\left(Z\right)=1$, $A_l^j=l!/\left(l-j\right)!$, and ${\mathit{Z}}_k\backslash \left\{\mathit{z}\right\}$ denotes the set ${\mathit{Z}}_k$ without element z.

At last, the components with tiny weight are pruned away, the components with uniform distribution are combined, and the maximum number of components is limited [27]. Then, the updated PHD at time step k is expressed in the Gaussian mixture model as follows:

$v_k\left(x\right)={\displaystyle \sum }_{i=1}^{J_k}{w}_k^{\left(i\right)}N\left(x;{\mathit{m}}_k^{\left(i\right)},{\mathit{P}}_k^{\left(i\right)}\right),(24)$

where $w_k^{\left(i\right)}$, ${\mathit{m}}_k^{\left(i\right)}$, and ${\mathit{P}}_k^{\left(i\right)}$ denote the weight, estimate of the state, and MSEM of the i-th target at time step k, respectively.

The n corresponding to the maximum value of the cardinality distribution $p_k\left(n\right)$ is the estimate of the number of targets. The ${\mathit{m}}_k^{\left(i\right)}$ corresponding to the components with the ${\widehat{N}}_k$ largest weight in the PHD $v_k\left(x\right)$ is the estimate of the target states. The first element of the estimated state vector is the estimate of the bearing angle of the target. By substituting $p_k\left(n\right)$ and $v_k\left(x\right)$ into the next time step, the GM-CPHD filter can be used to recursively estimate the state of the target to carry out DOA tracking.

4 VB-GMPHD filter for robust multi-target DOA tracking with uncertain measurement noise

The existing DOA tracking techniques usually assume that the measurement noise is a certain stochastic process, which means the MNCM is constant. However, in the real scenario of underwater tracking, the unknown underwater environment always results in uncertain measurement noise, which means the MNCM is time varying. Thus, the assumption of the existing DOA tracking technology on constant MNCM is inconsistent with the real scenario, which results in the decline of tracking performance. In order to improve the robustness of multi-target DOA tracking, variational Bayesian approach is used to estimate the MNCM in the real time of tracking. In this article, the measurement is a number instead of a vector, thus the MNCM reduces to the measurement noise variance.

4.1 Choice of prior distribution

In the multi-target DOA tracking scenario, when using the $i_m$-th measurement to estimate the corresponding $i_n$-th target, the one-step predicted probability density distribution (PDF) $p\left({\mathit{x}}_k^{i_n}|{\mathit{z}}_{1:k-1}^{i_m}\right)$ and the likelihood PDF $p\left({\mathit{z}}_k^{i_m}|{\mathit{x}}_k^{i_n}\right)$ are assumed to be subject to Gaussian distributions in the framework of the KF [35] as follows:

$p\left({\mathit{x}}_k^{i_n}|{\mathit{z}}_{1:k-1}^{i_m},{\mathit{P}}_{k|k-1}\right)=\mathrm{N}\left({\mathit{x}}_k^{i_n};{\widehat{\mathit{x}}}_{k|k-1}^{i_n},{\mathit{P}}_{k|k-1}^{i_n}\right),(25)$

$p\left({\mathit{z}}_k^{i_m}|{\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2\right)=\mathrm{N}\left({\mathit{z}}_k^{i_m};{\mathit{H}}_k{\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2\right),(26)$

where $\mathrm{N}\left(\cdot ;\mu ,\mathit{\Sigma }\right)$ denotes the PDF of the Gaussian distribution with mean μ and covariance matrix Σ, ${\mathit{H}}_k$ is the measurement matrix given in Equation 2, and ${\sigma }_{r,k}^2$ denotes the measurement noise variance. ${\widehat{\mathit{x}}}_{k|k-1}^{i_n}$ and ${\mathit{P}}_{k|k-1}^{i_n}$ denote the predicted state and predicted MSEM of the $i_n$-th target, respectively, which are expressed as

${\widehat{\mathit{x}}}_{k|k-1}^{i_n}={\mathit{F}}_{k|k-1}{\widehat{\mathit{x}}}_{k-1|k-1}^{i_n},(27)$

${\mathit{P}}_{k|k-1}^{i_n}={\mathit{F}}_{k|k-1}{\mathit{P}}_{k-1|k-1}^{i_n}{\mathit{F}}_{k|k-1}^{\mathrm{T}}+{\mathit{Q}}_{k-1},(28)$

where ${\widehat{\mathit{x}}}_{k-1|k-1}^{i_n}$ and ${\mathit{P}}_{k-1|k-1}^{i_n}$ are the estimates of the state and MSEM of the $i_n$-th target at time step k-1, respectively.

In order to infer ${\mathit{x}}_k^{i_n}$ along with ${\sigma }_{r,k}^2$, a conjugate prior distribution has to be selected for the fluctuant ${\sigma }_{r,k}^2$, since a conjugate distribution can guarantee the same functional forms of the prior distribution and posterior distribution. In the Bayesian theory, the inverse Wishart distribution is usually used as the conjugate prior for the covariance matrix of a Gaussian distribution with known mean [36]. Since ${\sigma }_{r,k}^2$ is the variance of the Gaussian distribution, the prior distribution $p\left({\sigma }_{r,k}^2|{\mathit{z}}_{1:k-1}^{i_m}\right)$ is selected as the inverse Wishart distribution, given by

$p\left({\sigma }_{r,k}^2|{\mathit{z}}_{1:k-1}^{i_m}\right)=\mathrm{I}\mathrm{W}\left({\sigma }_{r,k}^2;{\widehat{u}}_{k|k-1},{\widehat{\mathit{U}}}_{k|k-1}\right),(29)$

where $\mathrm{I}\mathrm{W}\left(\cdot ;\lambda ,\mathit{\Psi }\right)$ denotes the PDF of the inverse Wishart distribution with degree of freedom (dof) λ and inverse scale matrix Ψ [37], ${\widehat{u}}_{k|k-1}$ and ${\widehat{\mathit{U}}}_{k|k-1}$ are the dof and inverse scale matrix of $p\left({\sigma }_{r,k}^2|{\mathit{z}}_{1:k-1}^{i_m}\right)$, respectively.

The posterior distribution $p\left({\sigma }_{r,k-1}^2|{\mathit{z}}_{1:k-1}^{i_m}\right)$ is also subject to an inverse Wishart distribution as follows:

$p\left({\sigma }_{r,k-1}^2|{\mathit{z}}_{1:k-1}^{i_m}\right)=\mathrm{I}\mathrm{W}\left({\sigma }_{r,k-1}^2;{\widehat{u}}_{k-1|k-1},{\widehat{\mathit{U}}}_{k-1|k-1}\right).(30)$

To guarantee that $p\left({\sigma }_{r,k-1}^2|{\mathit{z}}_{1:k-1}^{i_m}\right)$ is the inverse Wishart distribution given by Equation 29, the previous approximate posterior distribution is spread through a forgetting factor $\rho \in \left.\left(\mathrm{0,1}\right.\right]$, which indicates the extent of time fluctuations of the MNCM. Then, the prior dof ${\widehat{u}}_{k|k-1}$ and prior inverse scale matrix ${\widehat{\mathit{U}}}_{k|k-1}$ are given as follows [34]:

${\widehat{u}}_{k\mid k-1}=\rho \left({\widehat{u}}_{k-1\mid k-1}-r-1\right)+r+1,(31)$

${\widehat{\mathit{U}}}_{k\mid k-1}=\rho {\widehat{\mathit{U}}}_{k-1\mid k-1}.(32)$

where r denotes the order of the MNCM ${\sigma }_{r,k}^2$.

4.2 Variational approximations of posterior PDFs

According to the variational Bayesian approximation, the joint posterior PDF of the state of the $i_n$-th target ${\mathit{x}}_k^{i_n}$ and MNCM ${\sigma }_{r,k}^2$ is approximated to

$p\left({\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2\mid {\mathit{z}}_{1:k}^{i_m}\right)\approx q\left({\mathit{x}}_k^{i_n}\right)q\left({\sigma }_{r,k}^2\right),(33)$

where $q\left({\mathit{x}}_k^{i_n}\right)$ and $q\left({\sigma }_{r,k}^2\right)$ are the approximate posterior PDFs of ${\mathit{x}}_k^{i_n}$ and ${\sigma }_{r,k}^2$, respectively [38, 39]. The variational Bayesian approximation is formed by minimizing the Kullback–Leibler divergence (KLD) between the true joint distribution $p\left({\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2\mid {\mathit{z}}_{1:k}^{i_m}\right)$ and the approximate distribution $q\left({\mathit{x}}_k^{i_n}\right)q\left({\sigma }_{r,k}^2\right)$, i.e.,

$\left\{q\left({\mathit{x}}_k^{i_n}\right),q\left({\sigma }_{r,k}^2\right)\right\}=\mathrm{arg\; min}\mathrm{K}\mathrm{L}\mathrm{D}\left(q\left({\mathit{x}}_k^{i_n}\right)q\left({\sigma }_{r,k}^2\right)\parallel p\left({\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2\mid {\mathit{z}}_{1:k}^{i_m}\right)\right),(34)$

where $\mathrm{K}\mathrm{L}\mathrm{D}\left(q\left(x\right)\parallel p\left(x\right)\right)$ denotes the KLD between $q\left(x\right)$ and $p\left(x\right)$ [38, 39], and

$\mathrm{K}\mathrm{L}\mathrm{D}\left(q\left(x\right)\parallel p\left(x\right)\right)=\int q\left(x\right)\log \frac{q\left(x\right)}{p\left(x\right)}dx.(35)$

The optimal solution of Equation 34 satisfies the following equations [39]:

$\log q\left({\mathit{x}}_k^{i_n}\right)={\mathrm{E}}_{{\sigma }_{r,k}^2}\left[\log p\left({\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2,{\mathit{z}}_{1:k}^{i_m}\right)\right]+c_{\mathit{x}},(36)$

$\log q\left({\sigma }_{r,k}^2\right)={\mathrm{E}}_{{\mathit{x}}_k^{i_n}}\left[\log p\left({\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2,{\mathit{z}}_{1:k}^{i_m}\right)\right]+c_{\mathit{R}},(37)$

where ${\mathrm{E}}_{{\mathit{x}}_k^{i_n}}\left[\cdot \right]$ and ${\mathrm{E}}_{{\sigma }_{r,k}^2}\left[\cdot \right]$ denote the expectation with regard to ${\mathit{x}}_k^{i_n}$ and ${\sigma }_{r,k}^2$, respectively, and $c_{\mathit{x}}$ and $c_{\mathit{R}}$ denote the constants with respect to ${\mathit{x}}_k^{i_n}$ and ${\sigma }_{r,k}^2$, respectively. Since the variational parameters of $q\left({\mathit{x}}_k^{i_n}\right)$ and $q\left({\sigma }_{r,k}^2\right)$ are coupled, a fixed point iteration process is applied to solve Equations 36, 37, i.e., the approximate posterior PDF $q\left({\mathit{x}}_k^{i_n}\right)$ is updated to $q^{\left(n+1\right)}\left({\mathit{x}}_k^{i_n}\right)$ at the $n+1$-th iteration using the posterior PDF $q^{\left(n\right)}\left({\sigma }_{r,k}^2\right)$, and $q\left({\sigma }_{r,k}^2\right)$ is updated to $q^{\left(n+1\right)}\left({\sigma }_{r,k}^2\right)$ using the posterior $q^{\left(n\right)}\left({\mathit{x}}_k^{i_n}\right)$.

According to Equations 25, 26, 29, the joint PDF is expressed as

$\begin{array}{l}p\left({\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2,{\mathit{z}}_{1:k}^{i_m}\right)\\ =p\left({\mathit{z}}_k^{i_m}|{\mathit{x}}_k^{i_n},{\sigma }_{r,k}^2\right)p\left({\mathit{x}}_k^{i_n}|{\mathit{z}}_{1:k-1}^{i_m}\right)p\left({\sigma }_{r,k}^2|{\mathit{z}}_{1:k-1}^{i_m}\right)p\left({\mathit{z}}_{1:k-1}^{i_m}\right)\\ =\mathrm{N}\left({\mathit{z}}_k^{i_m};h\left({\mathit{x}}_k^{i_n}\right),{\sigma }_{r,k}^2\right)\mathrm{N}\left({\mathit{x}}_k^{i_n};{\widehat{\mathit{x}}}_{k|k-1}^{i_n},{\mathit{P}}_{k|k-1}^{i_n}\right)\times \mathrm{I}\mathrm{W}\left({\sigma }_{r,k}^2;{\widehat{u}}_{k|k-1},{\widehat{\mathit{U}}}_{k|k-1}\right)p\left({\mathit{z}}_{1:k-1}^{i_m}\right)\end{array}(38)$

(1) Update of ${\mathit{x}}_k^{i_n}$

The posterior $q^{\left(n+1\right)}\left({\mathit{x}}_k^{i_n}|{\mathit{z}}_{1:k-1}^{i_m}\right)$ is updated according to the extended Kalman filter equations as

$q^{\left(n+1\right)}\left({\mathit{x}}_k^{i_n}|{\mathit{z}}_{1:k-1}^{i_m}\right)=\mathrm{N}\left({\mathit{x}}_k^{i_n};{\widehat{\mathit{x}}}_{k|k}^{\left(n+1\right)},{\widehat{\mathit{P}}}_{k|k}^{\left(n+1\right)}\right),(39)$

where the mean vector ${\widehat{\mathit{x}}}_{k|k}^{\left(n+1\right)}$ and the covariance matrix ${\widehat{\mathit{P}}}_{k|k}^{\left(n+1\right)}$ are given as follows:

${\mathit{K}}_k^{\left(n+1\right)}={\mathit{P}}_{k|k-1}^{i_n}{\left({\mathit{H}}_k\right)}^{\mathrm{T}}{\left({\mathit{H}}_k{\mathit{P}}_{k|k-1}^{i_n}{\left({\mathit{H}}_k\right)}^{\mathrm{T}}+{\left({\sigma }_{r,k}^{\left(n\right)}\right)}^2\right)}^{-1},(40)$

${\widehat{\mathit{x}}}_{k|k}^{\left(n+1\right)}={\widehat{\mathit{x}}}_{k|k-1}^{i_n}+{\mathit{K}}_k^{\left(n+1\right)}\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k-1}\right),(41)$

${\mathit{P}}_{k|k}^{\left(n+1\right)}={\mathit{P}}_{k|k-1}^{i_n}-{\mathit{K}}_k^{\left(n+1\right)}{\mathit{H}}_k^{\left(n\right)}{\mathit{P}}_{k|k-1}^{i_n}.(42)$

(2) Update of ${\sigma }_{r,k}^2$

According to Equation 38, $\log q^{\left(n\right)}\left({\sigma }_{r,k}^2\right)$ is given by

$\begin{array}{l}\log q^{\left(n+1\right)}\left({\sigma }_{r,k}^2\right)\\ =-0.5\left(r+{\widehat{u}}_{k|k-1}+2\right)\log \left|{\sigma }_{r,k}^2\right|-0.5\mathrm{t}\mathrm{r}\left({\widehat{\mathit{U}}}_{k|k-1}{\left({\sigma }_{r,k}^2\right)}^{-1}\right)-0.5{\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right)}^{\mathrm{T}}{\left({\sigma }_{r,k}^2\right)}^{-1}\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right)+c_{\mathit{R}}\\ =-0.5\left(r+{\widehat{u}}_{k|k-1}+2\right)\log \left|{\sigma }_{r,k}^2\right|-0.5\mathrm{t}\mathrm{r}\left(\left({\mathit{B}}_k^{\left(n\right)}+{\widehat{\mathit{U}}}_{k|k-1}\right){\left({\sigma }_{r,k}^2\right)}^{-1}\right)+c_{\mathit{R}}\end{array}(43)$

where

$\begin{array}{l}{\mathit{B}}_k^{\left(n\right)}={\mathrm{E}}^{\left(n\right)}\left[\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right){\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right)}^{\mathrm{T}}\right]\\ ={\mathrm{E}}^{\left(n\right)}\left[({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}+{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right)\left.{\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}+{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right)}^{\mathrm{T}}\right]\\ =\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}\right){\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}\right)}^{\mathrm{T}}+{\mathit{H}}_k{\mathrm{E}}^{\left(n\right)}\left[\left({\mathit{x}}_k^{i_n}-{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}\right){\left({\mathit{x}}_k^{i_n}-{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}\right)}^{\mathrm{T}}\right]{\mathit{H}}_k^{\mathrm{T}}\\ =\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}\right){\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k}^{\left(n\right)}\right)}^{\mathrm{T}}+{\mathit{H}}_k{\mathit{P}}_{k|k}^{\left(n\right)}{\mathit{H}}_k^{\mathrm{T}}\end{array}.(44)$

From Equation 43, $q^{\left(n+1\right)}\left({\sigma }_{r,k}^2\right)$ is updated as

$q^{\left(n+1\right)}\left({\sigma }_{r,k}^2\right)=\mathrm{I}\mathrm{W}\left({\sigma }_{r,k}^2;{\widehat{u}}_k^{\left(n+1\right)},{\widehat{\mathit{U}}}_k^{\left(n+1\right)}\right),(45)$

where the dof ${\widehat{u}}_k^{\left(n+1\right)}$ and the inverse scale matrix ${\widehat{\mathit{U}}}_k^{\left(n+1\right)}$ are given as follows:

${\widehat{u}}_k^{\left(n+1\right)}={\widehat{u}}_{k\mid k-1}+1,(46)$

${\widehat{\mathit{U}}}_k^{\left(n+1\right)}={\mathit{B}}_k^{\left(n\right)}+{\widehat{\mathit{U}}}_{k\mid k-1}.(47)$

Then, according to Equation 38, $\log q^{\left(n\right)}\left({\mathit{x}}_k^{i_n}\right)$ is given by

$\begin{array}{l}\log q^{\left(n+1\right)}\left({\mathit{x}}_k\right)=-0.5{\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right)}^{\mathrm{T}}{\mathrm{E}}^{\left(n+1\right)}\left[{\left({\sigma }_{r,k}^2\right)}^{-1}\right]\left({\mathit{z}}_k^{i_m}-{\mathit{H}}_k{\mathit{x}}_k^{i_n}\right)\\ -0.5{\left({\mathit{x}}_k^{i_n}-{\widehat{\mathit{x}}}_{k|k-1}^{i_n}\right)}^{\mathrm{T}}{\mathit{P}}_{k|k-1}^{-1}\left({\mathit{x}}_k^{i_n}-{\widehat{\mathit{x}}}_{k|k-1}^{i_n}\right)+c_{\mathit{x}}\end{array}(48)$

where ${\mathrm{E}}^{\left(n+1\right)}\left[{\left({\sigma }_{r,k}^2\right)}^{-1}\right]$ is given by

${\mathrm{E}}^{\left(n+1\right)}\left[{\left({\sigma }_{r,k}^2\right)}^{-1}\right]=\left({\widehat{u}}_k^{\left(n+1\right)}-m-1\right){\left({\widehat{\mathit{U}}}_k^{\left(n+1\right)}\right)}^{-1}.(49)$

The modified one-step predicted PDF $p^{\left(n+1\right)}\left({\mathit{z}}_k|{\mathit{x}}_k\right)$ at the $n+1$-th iteration is defined as

$p^{\left(n+1\right)}\left({\mathit{z}}_k^{i_m}|{\mathit{x}}_k^{i_n}\right)=\mathrm{N}\left({\mathit{z}}_k^{i_m};{\mathit{H}}_k{\mathit{x}}_k^{i_n},{\left({\widehat{\sigma }}_{r,k}^{\left(n+1\right)}\right)}^2\right),(50)$

where the modified MNCM ${\left({\widehat{\sigma }}_{r,k}^{\left(n+1\right)}\right)}^2$ is formulated as

${\left({\widehat{\sigma }}_{r,k}^{\left(n+1\right)}\right)}^2={\left\{{\mathrm{E}}^{\left(n+1\right)}\left[{\left({\sigma }_{r,k}^2\right)}^{-1}\right]\right\}}^{-1}={\widehat{\mathit{U}}}_k^{\left(n+1\right)}/\left({\widehat{u}}_k^{\left(n+1\right)}-m-1\right).(51)$

Finally, after N fixed-point iterations, the variational approximations of the posterior PDFs for the $i_n$-th target are given as follows:

$q\left({\mathit{x}}_k^{i_n}\right)\approx q^{\left(N\right)}\left({\mathit{x}}_k^{i_n}\right)=\mathrm{N}\left({\mathit{x}}_k^{i_n};{\widehat{\mathit{x}}}_{k|k}^{\left(N\right)},{\mathit{P}}_{k|k}^{\left(N\right)}\right)=\mathrm{N}\left({\mathit{x}}_k^{i_n};{\widehat{\mathit{x}}}_{k|k}^{i_n},{\mathit{P}}_{k|k}^{i_n}\right),(52)$

$q\left({\sigma }_{r,k}^2\right)\approx q^{\left(N\right)}\left({\sigma }_{r,k}^2\right)=\mathrm{I}\mathrm{W}\left({\sigma }_{r,k}^2;{\widehat{u}}_k^{\left(N\right)},{\widehat{\mathit{U}}}_k^{\left(N\right)}\right)=\mathrm{I}\mathrm{W}\left({\sigma }_{r,k}^2;{\widehat{u}}_{k\mid k},{\widehat{\mathit{U}}}_{k\mid k}\right).(53)$

4.3 Algorithm of VB-GMCPHD filter

According to the above derivation, the pseudo-code of the variational Bayesian GM-CPHD filter (VB-GMCPHD) for DOA tracking at one time step is given in Algorithm 1.

Algorithm 1. VB-CPHD filter for Robust multi-target DOA tracking

1. Initialize GM components ${\left\{w_0^{\left(i\right)},{\mathit{m}}_0^{\left(i\right)},{\mathit{P}}_0^{\left(i\right)}\right\}}_{i=1}^{J_0}$ and cardinality distribution $p_0\left(n\right)$;

For $k=1:K$

Prediction:

2. Predict the cardinality distribution $p_{k|k-1}\left(n\right)$ by using Equation 4;

3. Calculate the components of survive targets:

 For $i=1:J_{k-1}$

  $w_{s,k|k-1}^{\left(i\right)}=p_{s,k}{w}_{k-1}^{\left(i\right)}$, ${\mathit{m}}_{s,k|k-1}^{\left(i\right)}={\mathit{F}}_{k-1}{\mathit{m}}_{k-1}^{\left(i\right)}$, ${\mathit{P}}_{s,k|k-1}^{\left(i\right)}={\mathit{G}}_k{\sigma }_q^2{\mathit{G}}_k^T+{\mathit{F}}_{k-1}{\mathit{P}}_{k-1}^{\left(i\right)}{\mathit{F}}_{k-1}^T$;

  ${\widehat{u}}_{k|k-1}^{\left(i\right)}=\rho \left({\widehat{u}}_{k-1}^{\left(i\right)}-r-1\right)+r+1$, ${\widehat{\mathit{U}}}_{k|k-1}^{\left(i\right)}=\rho {\widehat{\mathit{U}}}_{k-1}^{\left(i\right)}$.

 End

4. Add the components of birth targets ${\left\{w_{\gamma ,k}^{\left(i\right)},{\mathit{m}}_{\gamma ,k}^{\left(i\right)},{\mathit{P}}_{\gamma ,k}^{\left(i\right)}\right\}}_{i=J_{k-1}+1}^{i=J_{k-1}+J_{\gamma ,k}}$;

5. Express the predicted GM components as ${\left\{w_{k|k-1}^{\left(i\right)},{\mathit{m}}_{k|k-1}^{\left(i\right)},{\mathit{P}}_{k|k-1}^{\left(i\right)}\right\}}_{i=1}^{i=J_{k|k-1}}$, where $J_{k|k-1}=J_{k-1}+J_{\gamma ,k}$;

Update:

6. Update the cardinality distribution $p_k\left(n\right)$ by using Equation 11;

7. Update GM components of targets:

 For $i=1:J_{k|k-1}$

  $w_k^{\left(i\right)}=\frac{〈{\mathrm{\Psi }}_k^1\left[{\mathit{w}}_{k|k-1},{\mathit{Z}}_k\right],p_{k|k-1}〉}{〈{\mathrm{\Psi }}_k^0\left[{\mathit{w}}_{k|k-1},{\mathit{Z}}_k\right],p_{k|k-1}〉}\left(1-p_{D,k}\right)w_{k-1}^{\left(i\right)}$, ${\mathit{m}}_k^{\left(i\right)}={\mathit{m}}_{k|k-1}^{\left(i\right)}$, ${\mathit{P}}_k^{\left(i\right)}={\mathit{P}}_{k|k-1}^{\left(i\right)}$;

 End

 For $m=1:m_k$

  For $i=1:J_{k|k-1}$

8. Estimate ${\sigma }_{r,k}^2$ along with states of targets by using VB iterations

Initialization: ${\widehat{\mathit{m}}}_{k|k}^{\left(0\right)}={\mathit{m}}_{k|k-1}^{\left(i\right)}$, ${\left({\widehat{\sigma }}_{r,k}^{\left(0\right)}\right)}^2={\widehat{\mathit{U}}}_{k|k-1}/{\widehat{u}}_{k|k-1}$.

 For $n=0:N-1$

  ${\mathit{S}}_{k|k-1}^{\left(n\right)}={\mathit{H}}_k{\mathit{P}}_{k|k-1}^i{\mathit{H}}_k^T+{\left({\widehat{\sigma }}_{r,k}^{\left(n\right)}\right)}^2$

  ${\mathit{K}}_k^{\left(n+1\right)}={\mathit{P}}_{k|k-1}^{\left(i\right)}{\left({\mathit{H}}_k\right)}^{\mathrm{T}}{\left({\mathit{S}}_{k|k-1}^{\left(n\right)}\right)}^{-1}$, ${\widehat{\mathit{m}}}_{k|k}^{\left(n+1\right)}={\widehat{\mathit{m}}}_{k|k-1}+{\mathit{K}}_k^{\left(n+1\right)}\left(z_m-{\mathit{H}}_k{\widehat{\mathit{m}}}_{k|k}^{\left(n\right)}\right)$,

  ${\mathit{P}}_{k|k}^{\left(n+1\right)}={\mathit{P}}_{k|k-1}^{\left(i\right)}-{\mathit{K}}_k^{\left(n+1\right)}{\mathit{H}}_k{\mathit{P}}_{k|k-1}^{\left(i\right)}$.

  ${\mathit{B}}_k^{\left(n+1\right)}=\left(z_m-{\mathit{H}}_k{\widehat{\mathit{m}}}_{k|k}^{\left(n+1\right)}\right){\left(z_m-{\mathit{H}}_k{\widehat{\mathit{m}}}_{k|k}^{\left(n+1\right)}\right)}^{\mathrm{T}}+{\mathit{H}}_k{\mathit{P}}_{k|k}^{\left(n+1\right)}{\left({\mathit{H}}_k\right)}^{\mathrm{T}}$,

  ${\widehat{\mathit{U}}}_{k|k}^{\left(n+1\right)}={\widehat{\mathit{U}}}_{k|k-1}+{\mathit{B}}_k^{\left(n+1\right)}$, ${\widehat{u}}_{k|k}^{\left(n+1\right)}={\widehat{u}}_{k|k-1}+1$,

  ${\left({\widehat{\sigma }}_{r,k}^{\left(n+1\right)}\right)}^2={\widehat{\mathit{U}}}_{k|k}^{\left(n+1\right)}/{\widehat{u}}_{k|k}^{\left(n+1\right)}$.

End

${\mathit{S}}_{k|k-1}={\mathit{S}}_{k|k-1}^{\left(N\right)}$

${\mathit{m}}_k^{\left(J_{k|k-1}+\left(m-1\right)m_k+i\right)}={\widehat{\mathit{m}}}_{k|k}^{\left(N\right)}$,

${\mathit{P}}_k^{\left(J_{k|k-1}+\left(m-1\right)m_k+i\right)}={\mathit{P}}_{k|k}^{\left(N\right)}$;

$w_k^{\left(J_{k|k-1}+\left(m-1\right)m_k+i\right)}=p_{D,k}{w}_{k|k-1}^{\left(i\right)}{q}_k^{\left(i\right)}\left({\mathit{z}}_m\right)\frac{〈{\mathrm{\Psi }}_k^1\left[w_{k|k-1},{\mathit{Z}}_k\backslash \left\{{\mathit{z}}_m\right\}\right],p_{k|k-1}〉}{〈{\mathrm{\Psi }}_k^0\left[w_{k|k-1},{\mathit{Z}}_k\right],p_{k|k-1}〉}\frac{〈1,{\kappa }_k〉}{{\kappa }_k\left({\mathit{z}}_m\right)}$

  End

 End

9. $J_{k|k}=J_{k|k-1}+J_{k|k-1}{m}_k$, Prune, merge, and limit the $J_{k|k}$ components, and new $J_k$ components are obtained;

10. Express the updated GM components as ${\left\{w_k^{\left(i\right)},{\mathit{m}}_k^{\left(i\right)},{\mathit{P}}_k^{\left(i\right)}\right\}}_{i=1}^{i=J_k}$;

11. The n corresponding to the peak of $p_k\left(n\right)$ is the estimate of the target number;

12. The ${\mathit{m}}_k^{\left(i\right)}$ corresponding to the ${\widehat{N}}_k$ components with the largest weight is the estimate of target states.

End

5 Results and discussion

5.1 Experimental setup

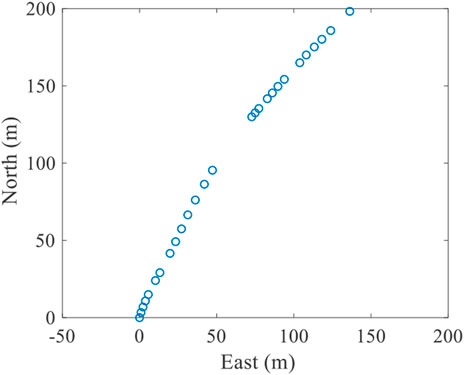
The open experimental data set SWellEx-96 [40] is used to verify the tracking performance of the proposed VB-GMCPHD filter for robust DOA tracking. The experiment was performed at the United States Marine Physical Laboratory from 10 to 18 May 1996, approximately 12 km from the tip of Point Loma near San Diego, California. The data of the north horizontal linear array of the S59 event of the experiment is used in this section. 900 s of experimental data is used to test the proposed method in this section. Before the experiment, a CTD is used to obtain the sound velocity in the experimental area. The experimental ship tows a continuous sound source at a depth of 54 m at a speed of 5 knots and sails north, which is named target 1 in this article. In addition, an uncooperative ship sails from northwest to southeast with continuous radiating noise, which is named target 2 in this article. The radar system of an experimental ship records the distance and bearing of the uncooperative ship and derives the latitude and longitude of the uncooperative ship. The horizontal linear array is placed on the seafloor at a depth of 213 m and continuously records the received acoustic signal at a sampling frequency of 3,276.8 Hz. The horizontal array consists of 32 elements, among which 27 elements provide effective data. The positions of the effective elements are shown in Figure 1, where the position of the first element is taken as the origin of coordinates. Figure 1 shows that the elements are actually not arranged in a straight line but in a slight curve. Therefore, the port and starboard ambiguity problem of a linear array is avoided.

FIGURE 1

FIGURE 1. Position of the horizontal linear array.

To evaluate the difference between the real set and estimated set of the states of the targets, an evaluation has to be chosen. Because the number of elements of the real set and estimated set of the states of the targets is different, the root-mean-square type of evaluation (such as the root mean square error) is not usable. In this article, optimal sub-pattern assignment (OSPA) error is selected to evaluate the multi-target tracking performance, which is defined as follows [41]:

$\left\{\begin{array}{cc}{d}_p^{\left(c\right)}\left(\mathit{X},\mathit{Y}\right)={\left(\frac{1}{n}\underset{\pi \in \mathrm{\Pi }}{\min }{\displaystyle \sum }_{i=1}^m{d}^{\left(c\right)}{\left(x_i,y_{\pi \left(i\right)}\right)}^p+c^p\left(n-m\right)\right)}^{1/p},& m\le n\\ d_p^{\left(c\right)}\left(\mathit{X},\mathit{Y}\right)=d_p^{\left(c\right)}\left(\mathit{Y},\mathit{X}\right),& m>n\end{array}\right.(54)$

where $d_p^{\left(c\right)}\left(\mathit{X},\mathit{Y}\right)$ is the OSPA error, $\mathit{X}=\left\{x_1,x_2,...,x_m\right\}$ and $\mathit{Y}=\left\{y_1,y_2,...,y_n\right\}$ are RFSs, $\mathrm{\Pi }$ denotes the set made up with m elements from $\left\{\mathrm{1,2},...,n\right\}$, and $d^{\left(c\right)}\left(x,y\right)=\min \left\{d\left(x,y\right),c\right\}$, $d\left(x,y\right)$ is the Euclidean distance between x and y, while c and p denote the truncation parameter and order, and are set to 5 and 1, respectively. The smaller the OSPA error means the higher the precision.

5.2 Experimental results

The minimum variance distortionless response (MVDR) was used to obtain the measurement of the bearing angles of the targets at 48 Hz–52 Hz every 10 s, and the bearing angle scans from 0 to 360° every 1°. According to the CTD data, the sound velocity was set to 1,493 m/s. The bearing time recording (BTR) obtained by the MVDR is given by the background 3D color diagram of Figure 2A. The true bearing angles of the two targets are given by the black line. The bearing angles corresponding to the peaks of the spectrum are extracted at each moment, and the obtained measurements of bearing angles of targets are shown by red dots in Figure 2A. Figure 2A shows trajectories of three targets. The bearing angle of target 1 moves from 135° to 50°, the bearing angle of target 2 moves from 285° to 275°, and the bearing angle of an unknown uncooperative target stays near 320°, which is named target 3 in this article. Figure 2A also shows some error, missing detection, and false alarm in the measurements.

FIGURE 2

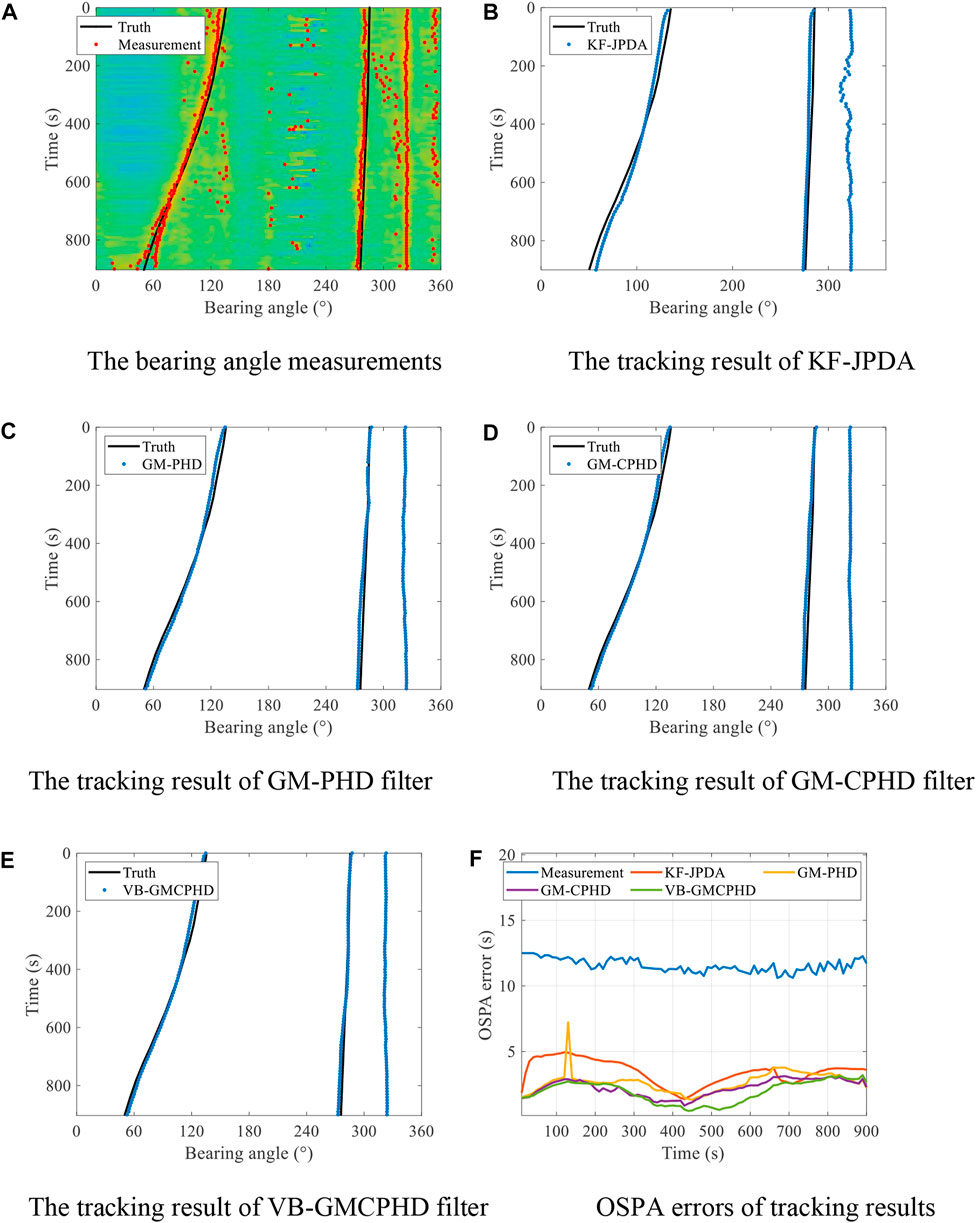
FIGURE 2. Bearing angle measurements, tracking results, and the OSPA errors of KF-JPDA, GM-PHD filter, GM-CPHD filter, and VB-GMCPHD filter. (A) Bearing angle measurements. (B) Tracking result of KF-JPDA. (C) The tracking result of GM-PHD filter. (D) The tracking result of GM-CPHD filter. (E) The tracking result of VB-GMCPHD filter. (F) OSPA errors of tracking results.

The proposed robust multi-target DOA tracking method is used to process the bearing angle measurements, and the results of KF-JPDA [42], GM-PHD filter [27], and GM-CPHD filter [30] are also given for comparison. The process noise variance of the CV model is set to $2.5\times {10}^{-4}$. The detection probability and false alarm probability are set to 0.9 and 0.1, respectively. The measurement noise variance ${\sigma }_{r,k}^2$ of KF-JPDA, GM-PHD filter, and GM-CPHD filter is set to 25. The parameters ${\widehat{u}}_0$, ${\widehat{\mathit{U}}}_0$, and ρ of the VB- GMCPHD are set to 12, 12 ${\sigma }_{r,k}^2$, and 0.95, respectively, and the number of VB iterations N is set to 5.

The tracking results of KF-JPDA, GM-PHD filter, GM-CPHD filter, and VB-GMCPHD filter are shown in Figures 2B–E, and the OSPA errors are shown in Figure 2F. The average OSPA errors tracking step are shown in Table 1; Figures 2B–E show that all multi-target DOA tracking methods carried out stable tracking of the three targets, and the tracking trajectories are consistent with the real trajectories. Figure 2F and Table 1 show that KF-JPDA, GM-PHD filter, GM-CPHD filter, and the proposed VB-GMCPHD filter significantly reduce OSPA errors on the basis of measurements, and the OSPA errors of the VB-GMCPHD filter are slightly smaller than those of the KF-JPDA, GM-PHD filter, and GM-CPHD filter.

TABLE 1

TABLE 1. The average OSPA errors of the tracking results of KF-JPDA, GM-PHD filter, GM-CPHD filter, and VB- GMCPHD filter in one tracking step.

Since the power of measurement noise hardly varies in the experiment, the performance of the proposed VB-GMCPHD filter for the robust multi-target DOA tracking improves slightly when compared to the other methods. In order to further test the robustness of the proposed robust underwater multi-target DOA tracking method in the scenario of uncertain measurement noise, a period of high-power noise was added to the experimental data from 500 s to 600 s. Then, the abovementioned process was repeated for the data with added noise.

The BTR and bearing angle measurements obtained by MVDR are shown in Figure 3A. The tracking results of KF-JPDA, GM-PHD filter, GM-CPHD filter, and VB-GMCPHD filter are shown in Figures 3B–E, respectively. The OSPA errors of the tracking results are shown in Figure 3F, and the average OSPA errors per tracking step are shown in Table 2.

FIGURE 3

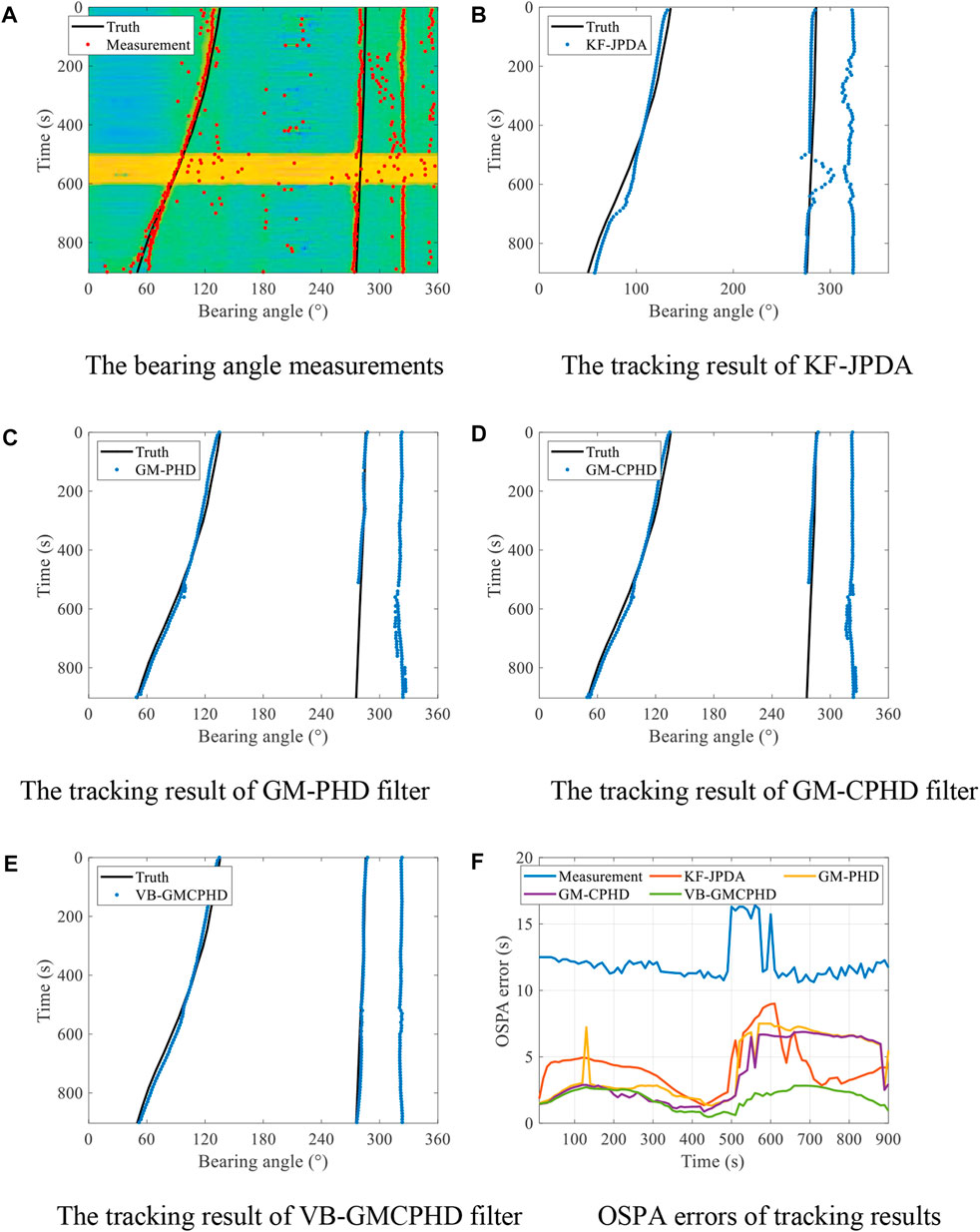
FIGURE 3. Bearing angle measurements, tracking results, and OSPA errors of KF-JPDA, GM-PHD filter, GM-CPHD filter, and VB-GMCPHD filter when processing the experimental data with added noise. (A) Bearing angle measurements. (B) Tracking result of KF-JPDA. (C) Tracking result of GM-PHD filter. (D) Tracking result of GM-CPHD filter. (E) Tracking result of VB-GMCPHD filter. (F) OSPA errors of tracking results.

TABLE 2

TABLE 2. The average OSPA errors of the tracking results of KF-JPDA, GM-PHD filter, GM-CPHD filter, and VB-GMCPHD filter in one tracking step when processing the experimental data with added noise.

Figure 3 shows that KF-JPDA, GM-PHD filter, and GM-CPHD filter provide stable tracking of the bearing angles of the three targets when the measurement noise variance is stationary from 0 to 500 s. However, when the measurement noise variance increases from 500 s to 600 s, the assumption of fixed measurement noise variance of KF-JPDA, GM-PHD filter, and GM-CPHD filter becomes inconsistent with the real increasing measurement noise variance, which results in inaccurate Kalman filter gain. Therefore, the KF-JPDA, GM-PHD filter, and GM-CPHD filter carry out fluctuating tracking trajectory or even miss tracking, which results in an increasing of the OSPA error. The OSPA error of the proposed VB-GMCPHD filter for robust multi-target DOA tracking is significantly less than that of the KF-JPDA, GM-PHD filter, and GM-CPHD filter. The reason is that the VB-GMCPHD filter estimates the measurement noise variance in the real time of tracking so the Kalman filter gain calculated by using the estimate of measurement noise variance is more accurate. Therefore, the increasing measurement noise variance hardly affects the performance of the VB-GMCPHD filter, and the robust DOA tracking with uncertain measurement noise is carried out. Table 2 proves the superiority of the proposed VB-GMCPHD filter in robustness again.

6 Conclusion

The robust multi-target underwater DOA tracking problem in uncertain measurement noise scenario is studied in this article. In order to solve the underwater multi-target DOA tracking problem, a multi-target DOA tracking technique is derived on the basis of the GM-CPHD filter, which is combined the kinematics of the target, the bearing angle measurements, and the multi-target tracking scheme at the same time. Then, considering the uncertain measurement noise results from unknown underwater environment, the online measurement estimator is designed on the basis of the variational Bayesian approach to estimate the measurement noise variance along with the states of the targets as an integrated part during the multi-target DOA tracking procedure. Thus, a robust underwater multi-target DOA tracking method with uncertain measurement noise, named VB-GMCPHD filter, is proposed. From the experiment results validated by real sea trial data, the accuracy and robustness of the proposed VB-GMCPHD is verified and comprehensive discussions are made. From the experimental results and discussions, the proposed VB-GMCPHD can be regarded as an alternative method to accomplish DOA tracking missions, especially when the underwater environment is uncertain.

Data availability statement

Publicly available data sets were analyzed in this study. These data can be found at http://swellex96.ucsd.edu/.

Author contributions

BZ, XH, and YY contributed to the conception and design of the study. XH, YY, JZ, and SX contributed to the investigation of the study. BZ performed the experimental data analysis and wrote the first draft of the manuscript. XH wrote sections of the manuscript. All authors contributed to manuscript revision, and read and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 12104113), the Shanghai Aerospace Science and Technology Innovation Foundation (Grant No. SAST2022-011), the foundation of Central University Operating Expenses Project (Grant No. G2022KY05102), and the Natural Science Basic Research Program of Shaanxi (Grant No. 2023-JC-JQ-07).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hou X, Yang L, Yang Y, Zhou J, Qiao G. Bearing-only underwater uncooperative target tracking for non-Gaussian environment using fast particle filter. IET Radar Sonar Nav (2022) 16:501–14. doi:10.1049/rsn2.12198

CrossRef Full Text | Google Scholar

2. Hou X, Zhou J, Yang Y, Yang L, Qiao G. 3D underwater uncooperative target tracking for a time-varying non-Gaussian environment by distributed passive underwater buoys. Entropy (2021) 23:902. doi:10.3390/e23070902

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Li Y, Tang B, Yi Y. A novel complexity-based mode feature representation for feature extraction of ship-radiated noise using VMD and slope entropy. Appl Acoust (2022) 196:108899. doi:10.1016/j.apacoust.2022.108899

CrossRef Full Text | Google Scholar

4. Li Y, Geng B, Jiao S. Dispersion entropy-based lempel-ziv complexity: A new metric for signal analysis. Chaos solitons fractals (2022) 161:112400. doi:10.1016/j.chaos.2022.112400

CrossRef Full Text | Google Scholar

5. Li Y, Jiao S, Geng B. Refined composite multiscale fluctuation-based dispersion Lempel–Ziv complexity for signal analysis. ISA Trans (2022). in press. doi:10.1016/j.isatra.2022.06.040

CrossRef Full Text | Google Scholar

6. Yang Y, Zhang Y, Yang L. Wideband sparse spatial spectrum estimation using matrix filter with nulling in a strong interference environment. J Acoust Soc Am (2018) 143:3891–8. doi:10.1121/1.5042406

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yan F, Jin M, Qiao X. Low-complexity DOA estimation based on compressed MUSIC and its performance analysis. IEEE Trans Signal Process (2013) 61:1915–30. doi:10.1109/TSP.2013.2243442

CrossRef Full Text | Google Scholar

8. Cao R, Liu B, Gao F, Zhang X. A low-complex one-snapshot DOA estimation algorithm with massive ULA. IEEE Commun Lett (2017) 21:1071–4. doi:10.1109/LCOMM.2017.2652442

CrossRef Full Text | Google Scholar

9. Yan H, Fan HH. Signal-selective DOA tracking for wideband cyclostationary sources. IEEE Trans Signal Process (2007) 55:2007–15. doi:10.1109/TSP.2007.893204

CrossRef Full Text | Google Scholar

10. Chen W, Zhang W, Wu Y, Chen T, Hu Z. Joint algorithm based on interference suppression and Kalman filter for bearing-only weak target robust tracking. IEEE Access (2019) 7:131653–62. doi:10.1109/ACCESS.2019.2940956

CrossRef Full Text | Google Scholar

11. Kong D, Chun J. A fast DOA tracking algorithm based on the extended Kalman filter. In: Proceedings of the IEEE 2000 National Aerospace and Electronics Conference (NAECON); October 2000; Dayton, OH, USA. IEEE (2000). p. 235–8. doi:10.1109/NAECON.2000.894916

CrossRef Full Text | Google Scholar

12. Zhang B, Hou X, Yang Y. Robust underwater direction-of-arrival tracking with uncertain environmental disturbances using a uniform circular hydrophone array. J Acoust Soc Am (2022) 151:4101–13. doi:10.1121/10.0011730

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Saucan AA, Chonavel T, Sintes C, Le Caillec JM. Marked Poisson point process PHD filter for DOA tracking. In: Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO); September 2015; Nice, France. IEEE (2015). p. 2621–5. doi:10.1109/EUSIPCO.2015.7362859

CrossRef Full Text | Google Scholar

14. Saucan AA, Chonavel T, Sintes C, Le Caillec JM. Track before detect DOA tracking of extended targets with marked Poisson point processes. In: Proceedings of the 2015 18th International Conference on Information Fusion (Fusion); July 2015; Washington, DC. IEEE (2015). p. 754–60.

Google Scholar

15. Saucan AA, Chonavel T, Sintes C, Le Caillec JM. CPHD-DOA tracking of multiple extended sonar targets in impulsive environments. IEEE Trans Signal Process (2016) 64:1147–60. doi:10.1109/TSP.2015.2504349

CrossRef Full Text | Google Scholar

16. Masnadi-Shirazi A, Rao BD. A covariance-based superpositional CPHD filter for multisource DOA tracking. IEEE Trans Signal Process (2018) 66:309–23. doi:10.1109/TSP.2017.2768025

CrossRef Full Text | Google Scholar

17. Li G, Wei P, Li Y, Chen Y. A labeled multi-Bernoulli filter for multisource DOA tracking. In: Proceedings of the 2019 International Conference on Control, Automation and Information Sciences (ICCAIS); October 2019; Chengdu, China. IEEE (2019). p. 1–6. doi:10.1109/ICCAIS46528.2019.9074552

CrossRef Full Text | Google Scholar

18. Zhao J, Gui R, Dong X. A new measurement association mapping strategy for DOA tracking. Digit Signal Process (2021) 118:103228. doi:10.1016/j.dsp.2021.103228

CrossRef Full Text | Google Scholar

19. Yardim C, Michalopoulou ZH, Gerstoft P. An overview of sequential Bayesian filtering in ocean acoustics. IEEE J Ocean Eng (2011) 36:71–89. doi:10.1109/JOE.2010.2098810

CrossRef Full Text | Google Scholar

20. Koteswara Rao S, Raja Rajeswari K, Lingamurty KS. Unscented Kalman filter with application to bearings-only target tracking. IETE J Res (2009) 55:63–7. doi:10.4103/0377-2063.53236

CrossRef Full Text | Google Scholar

21. Leong PH, Arulampalam S, Lamahewa TA, Abhayapala TD. A Gaussian-sum based cubature Kalman filter for bearings-only tracking. IEEE T Aero Elec Sys (2013) 49:1161–76. doi:10.1109/TAES.2013.6494405

CrossRef Full Text | Google Scholar

22. Orton M, Fitzgerald W. A Bayesian approach to tracking multiple targets using sensor arrays and particle filters. IEEE Trans Signal Process (2002) 50:216–23. doi:10.1109/78.978377

CrossRef Full Text | Google Scholar

23. Qiu W, Li L, Lei P, Wang Z. Multiple targets tracking by using probability data association and cubature Kalman filter. In: Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP); October 2018; Hangzhou, China. IEEE (2018). p. 1–5. doi:10.1109/WCSP.2018.8555720

CrossRef Full Text | Google Scholar

24. Li X, Willett P, Baum M, Baum M, Li Y. PMHT approach for underwater bearing-only multisensor–multitarget tracking in clutter. IEEE J Oceanic Eng (2016) 41:831–9. doi:10.1109/JOE.2015.2506220

CrossRef Full Text | Google Scholar

25. Mahler RPS. Multitarget Bayes filtering via first-order multitarget moments. IEEE T Aero Elec Sys (2003) 39:1152–78. doi:10.1109/TAES.2003.1261119

CrossRef Full Text | Google Scholar

26. Vo BN, Singh S, Doucet A. Sequential Monte Carlo methods for multitarget filtering with random finite sets. IEEE T Aero Elec Sys (2005) 41:1224–45. doi:10.1109/TAES.2005.1561884

CrossRef Full Text | Google Scholar

27. Clark DE, Panta K, Vo BN. The GM-PHD filter multiple target tracker. In: Proceedings of the 2006 9th International Conference on Information Fusion; July 2006; Florence, Italy. IEEE (2006). p. 1–8. doi:10.1109/ICIF.2006.301809

CrossRef Full Text | Google Scholar

28. Mahler R. A theory of PHD filters of higher order in target number. In: Signal processing, sensor fusion, and target recognition XV. SPIE, 6235. Orlando (Kissimmee) Florida, United States (2006). p. 193–204. doi:10.1117/12.667083

CrossRef Full Text | Google Scholar

29. Mahler R. PHD filters of higher order in target number. IEEE T Aero Elec Sys (2007) 43:1523–43. doi:10.1109/TAES.2007.4441756

CrossRef Full Text | Google Scholar

30. Vo BT, Vo BN, Cantoni A. Analytic implementations of the cardinalized probability hypothesis density filter. IEEE T Signal Proces (2007) 55:3553–67. doi:10.1109/TSP.2007.894241

CrossRef Full Text | Google Scholar

31. Huang D, Leung H, Naser ES. Expectation maximization based GPS/INS integration for land-vehicle navigation. IEEE Trans Aerosp Electron Syst (2007) 43:1168–77. doi:10.1109/TAES.2007.4383607

CrossRef Full Text | Google Scholar

32. Huang Y, Zhang Y, Xu B, Wu Z, Chambers JA. A new adaptive extended Kalman filter for cooperative localization. IEEE Trans Aerosp Electron Syst (2017) 54:353–68. doi:10.1109/TAES.2017.2756763

CrossRef Full Text | Google Scholar

33. Sarkka S, Nummenmaa A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans Autom Control (2009) 54:596–600. doi:10.1109/TAC.2008.2008348

CrossRef Full Text | Google Scholar

34. Hartikainen SSJ. Variational Bayesian adaptation of noise covariances in non-linear Kalman filtering (2013). arXiv (2013). preprint arXiv:1302.0681. doi:10.48550/arXiv.1302.0681

CrossRef Full Text | Google Scholar

35. Mohinder SG. Kalman filtering: Theory and practice using MATLAB. Hoboken, NJ: Wiley (2001).

Google Scholar

36. O’Hagan A, Forster JJ. Kendall’s advanced theory of statistics: Bayesian inference. London, U.K.: Edward Arnold (2004).

Google Scholar

37. Huang Y, Zhang Y, Wu Z, Li N, Chambers J. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans Autom Control (2017) 63:594–601. doi:10.1109/TAC.2017.2730480

CrossRef Full Text | Google Scholar

38. Bishop CM. Pattern recognition and machine learning. Berlin, Germany: Springer (2007).

Google Scholar

39. Tzikas DG, Likas AC, Galatsanos NP. The variational approximation for Bayesian inference. IEEE Signal Proc Mag (2008) 25:131–46. doi:10.1109/MSP.2008.929620

CrossRef Full Text | Google Scholar

40. Booth NO, Hodgkiss WS, Ensberg DE. SWellEx-96 experiment acoustic data. San Diego. UC San Diego Library Digital Collections (2015). doi:10.6075/J0MW2F21

CrossRef Full Text | Google Scholar

41. Song Y, Hu Z, Li T, Fan H. Performance evaluation metrics and approaches for target tracking: A survey. Sensors (2022) 22:793. doi:10.3390/s22030793

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Fortmann T, Bar-Shalom Y, Scheffe M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J Oceanic Eng (1983) 8:173–84. doi:10.1109/JOE.1983.1145560

CrossRef Full Text | Google Scholar