A discrete side-lobe clutter recognition method based on sliding filter response loss for space-based radar

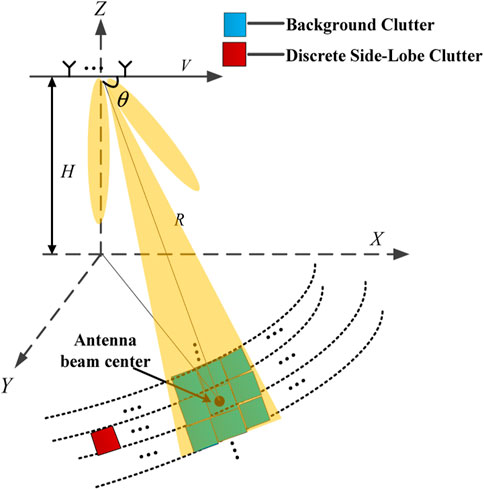
Different from ground-based or airborne early warning radar, space-based radar (SBR) possesses large coverage capability. As a result, several discrete strong scatter points from the antenna side-lobe shares the same feature with the real targets in range-Doppler domain, which leads to false alarms when conducting constant false alarm rate (CFAR) detection process, and the detection performance with regard to SBR deteriorates seriously. In this paper, a discrete side-lobe clutter recognition method based on sliding filter response loss is proposed for space-based radar. Firstly, considering both the echo inhomogeneity and the limited degrees of freedom (DOFs) after dimension-reduced space-time adaptive processing (STAP), the sliding window design strategy is employed to segment range cells for the observation scene. Then, the images related to different range segments are registered after clutter suppression, in this way, the candidate target parameters, including the position information and the amplitude information are counted. On this basis, the reliable recognition scheme between the real target and the discrete side-lobe clutter can be realized by comparing these filter response losses. Compared with recent works, experimental results based on real measured data show that the proposed method significantly improves the fault-tolerant discrimination ability, which possesses high robustness in algorithm performance as well as good prospect in engineering application.

1 Introduction

For space-based radar, due to its wide detection range, there exist a large number of discrete strong scatter points in the echo data, including iron towers, telegraph poles, tall buildings, isolated islands and marine targets [1]. These discrete side-lobe clutters, which come from the antenna side-lobe, cannot be distinguished from the real targets as they are located outside the main lobe clutter in Doppler domain. Space-time adaptive processing (STAP) [2–6] is currently one of the effective means for clutter suppression. However, the reason for the emergence of discrete side-lobe clutters in heterogeneous environment lies in the sample selection strategy when constructing the clutter covariance matrix (CCM). The amplitude of discrete side-lobe clutters is affected several factors, i.e., radar detection range, antenna side-lobe level, self-scattering cross section, and hence resulting in a certain amplitude randomness after clutter suppression. That is, in order to alleviate the influence of non-independent identical distribution (IID) samples on clutter suppression performance, strong scatter points may be regarded as heterogeneous samples, and thus the corresponding resolution cells cannot be suppressed effectively for their CCM have a bad match with the cell under test (CUT) [7, 8].

Presently, the discrete side-lobe clutter recognition researches can be divided into two categories. The first one is the synthetic channel gain method [9, 10], in which the candidate targets are identified through comparing the output of the synthetic channel gain and that of the auxiliary channel gain. If the candidate target is located at the antenna beam pointing position, the synthetic channel gain is $10{\mathit{log}}_{10}{N}^2$ without considering the system errors, where $N$ stand for the channel number. Instead, if the candidate target comes from the antenna side-lobe, the synthetic channel gain declines obviously for the channel amplitude cannot be coherently accumulated. Thus, discrete side-lobe clutters can be recognized according to the increased channel gain value. The other one is the filter response loss method [11], in which the energy loss of the candidate target are counted in the STAP process. Compared with the real target, discrete side-lobe clutters suffer more energy loss as the target steering vector is pointed at the main lobe area. On this basis, multiple space-time steering vector constraint methods are presented to identify discrete side-lobe clutter [12]. Firstly, two steering vectors related to the target and main-lobe clutter regions are employed to construct the optimal weight vectors. Then, the energy loss of candidate targets after STAP processing is compared, where these resolution cells with large energy loss are judged as the real targets, others are regarded as the discrete side-lobe clutters. To a certain extent, the above two methods provide an effective means for discrete side-lobe clutter recognition. However, the real targets generally do not come from the antenna beam center pointing direction, and hence the synthetic channel gain method cannot achieve the ideal value. In addition, although the discrete side-lobe clutters share apparent amplitude attenuation with regard to filter response loss method, there also exist energy loss for the real target. Therefore, the existing methods cannot significantly enhance the fault-tolerant capability when conducting discrete side-lobe clutter recognition process. It is necessary to further explore the robust discrete side-lobe clutter recognition method for space-based radar with wide area coverage. Aiming at the above problems, a discrete side-lobe clutter recognition method based on sliding filter response loss for space-based radar is proposed in this paper, in which the wide area detection ability and the sample inhomogeneity characteristics are combined, and the filter response losses corresponding to different segmented data are evaluated to achieve the recognition capability between the real targets and discrete side-lobe clutters. Meanwhile, this method introduces the sample segmentation registration strategy, and thus to alleviate the poor clutter suppression ability at the scene edge area, which possesses simple implementation and high robustness characteristics. Experimental results with airborne measured data verify the effectiveness of this method.

2 STAP model

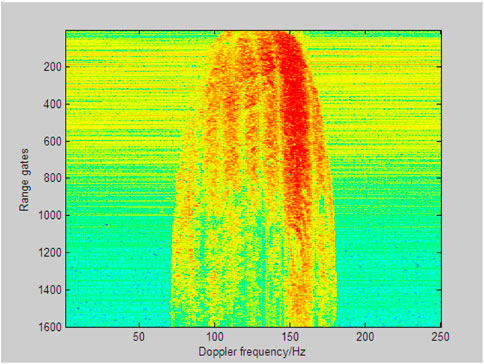
Space-based radar (SBR) generally operates under down-looking mode, and there exists strong ground clutter or sea clutter in the echo data. Besides, due to its wide coverage capability, a large number of isolated scattering points from the antenna side-lobe are collected by the receiver, as demonstrated in Figure 1. Thus, clutter suppression is important to meet the requirements of moving target detection.

FIGURE 1

FIGURE 1. STAP model of SBR.

Assume that $C_l$ denotes the scatter number in the $l$ th range bin, where $1\le l\le L$. $G_i$ and $G_{tar}$ denote the complex amplitude of the $i$ th scatter and the target, respectively. $N_l$ represents the Gaussian white noise. Thus, the echo data of the $l$ th range bin can be expressed as

${\mathit{x}}_{\mathit{l}}={\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{{\mathit{C}}_{\mathit{l}}}{\mathit{G}}_{\mathit{i}}\left({\mathit{s}}_{\mathit{t}}^{\mathit{i}}\otimes {\mathit{s}}_{\mathit{s}}^{\mathit{i}}\right)+{\mathit{G}}_{\mathit{t}\mathit{a}\mathit{r}}\left({\mathit{s}}_{\mathit{t}}^{\mathit{t}\mathit{a}\mathit{r}}\otimes {\mathit{s}}_{\mathit{s}}^{\mathit{t}\mathit{a}\mathit{r}}\right)+{\mathit{N}}_{\mathit{l}}(1)$

where symbol $\otimes$ denotes the Kronecker product operation, and $j=sqrt\left(-1\right)$. Let the normalized temporal steering vector and spatial steering vector of clutter cell be ${\mathit{s}}_t^i$ and ${\mathit{s}}_s^i$ in turn. The antenna array is composed of $N$ elements with an interval of $d$, and the number of pulses during one coherent processing interval (CPI) is $K$. Thus, the normalized temporal steering vector and spatial steering vector with regard to the target are given by

${\mathit{s}}_{\mathit{t}}^{\mathit{t}\mathit{a}\mathit{r}}={\left[\mathbf{1},\mathit{exp}\left[\mathit{j}\mathbf{2}\mathit{\pi }\left(\frac{\mathbf{2}\mathit{V}}{\mathit{\lambda }\cdot {\mathit{f}}_{\mathit{r}}}\mathit{cos}{\mathit{\theta }}_{\mathit{t}\mathit{a}\mathit{r}}+\frac{\mathbf{2}\mathit{v}}{\mathit{\lambda }\cdot {\mathit{f}}_{\mathit{r}}}\right)\right],...,\mathit{exp}\left[\mathit{j}\mathbf{2}\mathit{\pi }\left(\frac{\mathbf{2}\mathit{V}}{\mathit{\lambda }\cdot {\mathit{f}}_{\mathit{r}}}\mathit{cos}{\mathit{\theta }}_{\mathit{t}\mathit{a}\mathit{r}}+\frac{\mathbf{2}\mathit{v}}{\mathit{\lambda }\cdot {\mathit{f}}_{\mathit{r}}}\right)\left(\mathit{K}-\mathbf{1}\right)\right]\right]}^{\mathit{T}}(2)$

${\mathit{s}}_{\mathit{s}}^{\mathit{t}\mathit{a}\mathit{r}}={\left[\mathbf{1},\mathit{exp}\left[\mathit{j}\mathbf{2}\mathit{\pi }\frac{\mathit{d}}{\mathit{\lambda }}\mathit{cos}{\mathit{\theta }}_{\mathit{t}\mathit{a}\mathit{r}}\right],...,\mathit{exp}\left[\mathit{j}\mathbf{2}\mathit{\pi }\frac{\mathit{d}}{\mathit{\lambda }}\mathit{cos}{\mathit{\theta }}_{\mathit{t}\mathit{a}\mathit{r}}\left(\mathit{N}-\mathbf{1}\right)\right]\right]}^{\mathit{T}}(3)$

In Eqs 2, 3, $f_r$ stands for the pulse repetition frequency (PRF), $V$ represents the platform velocity, $\lambda$ is the signal wave length, ${\theta }_{tar}$ is the cone angle, $v$ is the target velocity, $\mathit{exp}$ and $\mathit{cos}$ indicate the exponential operation and the cosine operation, respectively. The subscript $T$ denotes the transpose operation. If $v=0$, the steering vectors of clutter echo are consistent with that of the target. Instead, if $v\ne 0$, the temporal steering vector caused by the Doppler component will lead to the separation of the target and the echo data in space-time domain. However, the discrete side-lobe clutters come from the antenna side-lobe may result in similar distribution characteristics, compared with the real target, in which these candidate targets cannot be distinguished in the STAP process.

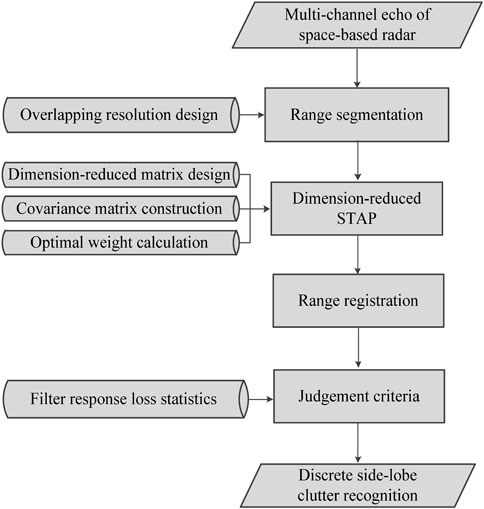
3 A discrete side-lobe clutter recognition method based on sliding filter response loss for space-based radar

For full-dimensional STAP methods, it is not conductive to real-time processing due to the high computational complexity in the order of $\mathrm{{\rm O}}{\left(NK\right)}^3$. Further, the number of independent identically distributed (IID) samples should be more than $2NK$ to minimize the optimal detection performance loss to less than 3 dB. However, the actual observation environment is difficult to meet this requirement, especially for the heterogeneous scene with massive discrete strong scattering points. In order to reduce the full-dimensional STAP computational complexity and achieve reasonable clutter suppression performance, the dimension-reduced strategy is employed. Assume that $\mathit{T}\in {\mathbb{C}}^{NM\times PQ}$ is the dimension-reduced matrix, where $P$; $Q$ denote the degrees of freedom (DOFs) with regard to the spatial domain and the temporal domain in turn. The adaptive weight based on the linear constraint minimum variance (LCMV) criterion can be rewritten as

${\mathit{w}}_{\mathit{T}}=\mathit{\mu }{\mathit{R}}_{\mathit{T}}^{-\mathbf{1}}{\mathit{s}}_{\mathit{T}}(4)$

where $\mathit{m}=\frac{\mathbf{1}}{{\mathit{s}}_{\mathit{T}}^{\mathit{H}}{\mathit{R}}_{\mathit{T}}^{-\mathbf{1}}{\mathit{s}}_{\mathit{T}}}{\left(\cdot \right)}^{-\mathbf{1}}$ is the matrix inverse operation. The dimension-reduced matrix ${\mathit{R}}_{\mathit{T}}$ and the target steering vector $s_T$ can be re-represented as

${\mathit{R}}_{\mathit{T}}={\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{\mathit{L}}\left({\mathit{T}}^{\mathit{H}}{\mathit{x}}_{\mathit{l}}\right){\left({\mathit{T}}^{\mathit{H}}{\mathit{x}}_{\mathit{l}}\right)}^{\mathit{H}}(5)$

${\mathit{s}}_{\mathit{T}}={\mathit{T}}^{\mathit{H}}\left({\mathit{s}}_{\mathit{t}}^{\mathit{t}\mathit{a}\mathit{r}}\otimes {\mathit{s}}_{\mathit{s}}^{\mathit{t}\mathit{a}\mathit{r}}\right)(6)$

Here, ${\left(\cdot \right)}^H$ stand for the conjugate transpose operation.

Without loss of generality, EFA methods are adopted in the dimension-reduced STAP. The filter response loss is defined as

$\mathit{L}\mathit{o}\mathit{s}\mathit{s}=\frac{\mathit{E}\_\mathit{o}\mathit{u}\mathit{t}}{\mathit{E}\_\mathit{i}\mathit{n}}(7)$

where $E\_in$ represents echo power of the target resolution cell before clutter suppression, while $\mathit{E}\_\mathit{o}\mathit{u}\mathit{t}$ denotes that after clutter suppression. Let $\mathit{x}$ be the echo data of the cell under detected (CUT) in range-Doppler domain, the above variables can be expressed as $\mathit{E}\_\mathit{i}\mathit{n}=\left|{\mathit{x}}^{\mathit{H}}\mathit{x}\right|$, $\mathit{E}\_\mathit{o}\mathit{u}\mathit{t}={\left|{\mathit{w}}_{\mathit{T}}^{\mathit{H}}\mathit{x}\right|}^{\mathbf{2}}$.

Space-based radars possess wide coverage capability as its high orbit height, and the echo data shares strong fluctuation characteristics. As a result, the sliding window needs to be employed to segment the range rings in heterogeneous environment. On one hand, these resolution cells within a limited scene have relatively consistent distribution characteristics by means of range segmentation process. On the other hand, the number of available samples for constructing clutter covariance matrix (CCM) will be reduced after range segmentation strategy, which may lead to clutter suppression performance deterioration with regard to the scene edge resolution cells. In this paper, a discrete side-lobe clutter recognition method based on the sliding window is proposed for space-based radar system, in which both the sample number for building CCM and the filtering performance with regard to scene edge area are taken into account. Firstly, the sliding window is presented to segment the observation scene into the identical range intervals. Assuming these two sample sets are denoted as $X_1$ and $X_2$ before and after the sliding process, the corresponding CCMs are expressed as $R_1$ and $R_2$, and the optimal weight vectors are indicated as $w_1$ and $w_2$, respectively. Thus, the STAP results related to different range intervals are given by

$\mathit{r}\mathit{e}\mathit{s}\mathit{u}\mathit{l}{\mathit{t}}_{\mathbf{1}}={\mathit{w}}_{\mathbf{1}}^{\mathit{T}}{\mathit{X}}_{\mathbf{1}}(8)$

$\mathit{r}\mathit{e}\mathit{s}\mathit{u}\mathit{l}{\mathit{t}}_{\mathbf{2}}={\mathit{w}}_{\mathbf{2}}^{\mathit{T}}{\mathit{X}}_{\mathbf{2}}(9)$

For the two $resul{t}_1$ and $resul{t}_2$ generated by the sliding window, the range cells are registered according to mark the range cell number. In this way, the amplitudes of the resolution cells which exceed the CFAR threshold are added to the candidate target set [13]. Assume that judgment threshold of filter response loss is $\eta$. For any candidate target, the STAP filter response loss before and after the sliding process are $Los{s}_1$ and $Los{s}_2$, respectively, and the corresponding judgment criteria is given by

$\mathbf{c}\mathbf{a}\mathbf{n}\mathbf{d}\mathbf{i}\mathbf{d}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{t}\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{e}\mathbf{t}=\left\{\begin{array}{c}\mathbf{d}\mathbf{i}\mathbf{s}\mathbf{c}\mathbf{r}\mathbf{e}\mathbf{t}\mathbf{e}\mathbf{s}\mathbf{i}\mathbf{d}\mathbf{e}-\mathbf{l}\mathbf{o}\mathbf{b}\mathbf{e}\mathbf{c}\mathbf{l}\mathbf{u}\mathbf{t}\mathbf{t}\mathbf{e}\mathbf{r}\mathbf{s},\mathbf{min}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)>\mathbf{\eta }\\ \mathbf{d}\mathbf{i}\mathbf{s}\mathbf{c}\mathbf{r}\mathbf{e}\mathbf{t}\mathbf{e}\mathbf{s}\mathbf{i}\mathbf{d}\mathbf{e}-\mathbf{l}\mathbf{o}\mathbf{b}\mathbf{e}\mathbf{c}\mathbf{l}\mathbf{u}\mathbf{t}\mathbf{t}\mathbf{e}\mathbf{r}\mathbf{s},\left\{\mathbf{max}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)>\mathbf{\eta }>\mathbf{min}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)\right\}\\ \&\&\left\{\frac{\mathbf{max}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)+\mathbf{min}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)}{\mathbf{2}}>\mathbf{\eta }\right\}\\ \mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}\mathbf{t}\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{e}\mathbf{t}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\left\{\mathbf{max}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)>\mathbf{\eta }>\mathbf{min}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)\right\}\\ \&\&\left\{\frac{\mathbf{max}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)+\mathbf{min}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)}{\mathbf{2}}\le \mathbf{\eta }\right\}\\ \mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}\mathbf{t}\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{e}\mathbf{t}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\mathbf{max}\left(\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{1}},\mathbf{L}\mathbf{o}\mathbf{s}{\mathbf{s}}_{\mathbf{2}}\right)\le \mathbf{\eta }\end{array}\right.(10)$

The background clutter suppression as well as the target energy accumulation can be achieved by employing the optimal weight vector when conducting STAP algorithm. Generally, the filter energy loss of the moving target is small, while that of the discrete side-lobe clutter is large. However, the moving target is not necessarily located in the antenna beam center, and the suppression degree of discrete side-lobe clutter show randomness due to the heterogeneous environment, which resulting in the limited fault tolerance with regard to filter response loss method for distinguishing the real targets from discrete side-lobe clutters [12].

Space-based radar possesses wide area coverage and complex regional distribution, in which the discrete side-lobe clutters mainly generate from the heterogeneous area with discrete strong scattering points. Considering that the samples corresponding to different range segments present quite different characteristics, the category judgment results of these samples are uncertain for a specific sample discrimination criterion. In this paper, the sliding window strategy is proposed to process the segmented echo data. As the clutter covariance matrices before and after the sliding window operation are constructed by adopting different sample sets, the filter response loss value in regard of a discrete side-lobe clutter suppression is also different. Thus, the maximum filter response loss of each discrete side-lobe clutter can be statistically obtained based on the above sample sets. Besides, the real target is located in the main antenna lobe direction, as a result, the target steering vectors are identical for different sample sets, and the filtering response losses of the real target is relatively small compared with discrete side-lobe clutters. If the candidate target within the CUT is a discrete side-lobe clutter, which comes from the antenna side-lobe direction, the target steering vector has a limited constraint ability to this area. However, the suppression ability to the discrete side-lobe clutter shows great fluctuation with regard to different samples sets. That is, for a specific candidate target, the significance of energy loss characteristics can be enhanced through analyzing the filter response losses. Conversely, if the candidate target within the CUT is a real target, which comes from the antenna main-lobe direction, the target steering vector has a strong constraint ability to this region. As the real target and its competitive clutter have obvious differences in spatial domain, the filter response losses of the real target can be maintained at a small level. Therefore, the proposed filter response loss method based on the given sliding window can effectively improve the diversity between the discrete side-lobe clutter and the real target. Especially for heterogeneous environment, this method has extremely robust recognition ability for discrete side-lobe clutters. Figure 2 demonstrates the flow chart of discrete side-lobe clutter recognition method.

FIGURE 2

FIGURE 2. Flow chart of discrete side-lobe clutter recognition method.

4 Experimental results

4.1 Airborne scheme design

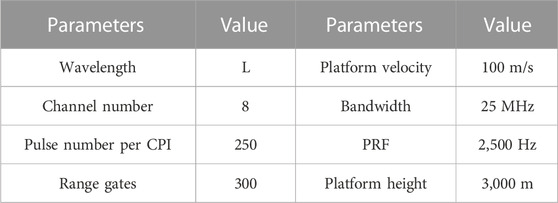
In this section, the effectiveness of the proposed method is validated by utilizing the real measured data with an airborne radar system. Radar system parameters are shown in Table 1.

TABLE 1

TABLE 1. Airborne radar system parameters.

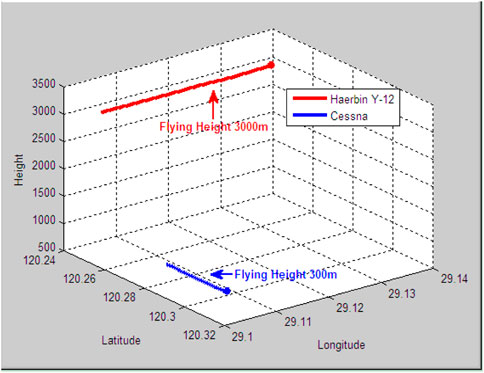
In order to simulate the SBR operating mode more realistically, a drone aircraft is designed to fly below the carrier aircraft, as shown in Figure 3. Here, Haerbin Y-12 and Cessna are selected as the carrier aircraft and the drone aircraft, respectively. Figure 4 shows the Range-Doppler data of channel 1 with 250 pulses. One can see that the interferences and discrete terrain clutters exist in most of the Range-Doppler image. As a result, the measured data is composed of real target echo, real clutter echo and real interference echo, with which the performance of the proposed method could be varified reliably.

FIGURE 3

FIGURE 3. Target detection scheme design.

FIGURE 4

FIGURE 4. Range-Doppler data of channel 1.

4.2 Clutter suppression and discrete side-lobe clutter recognition

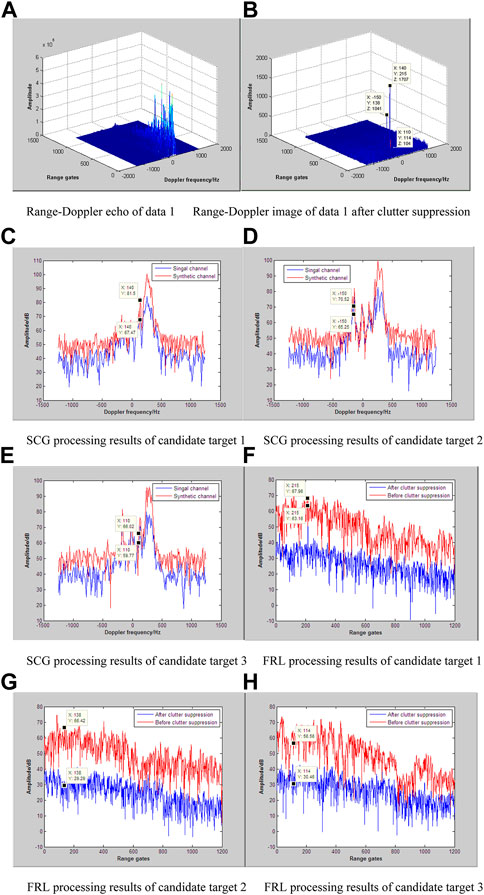
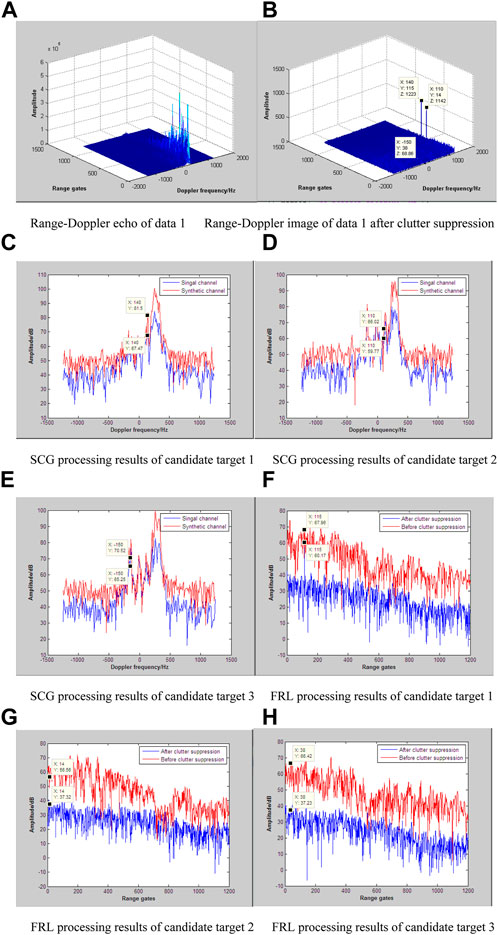
In this section, FSA algorithm is adopted as the dimension-reduced method for STAP. In order to achieve robust clutter suppression performance, the heterogeneous samples are eliminated when constructing the CCM. As a result, the real target and discrete side-lobe clutters may coexist in the image after clutter suppression. During the data processing procedure, the range segment unit is set to 400, and that of the overlapping range units in regard of adjacent data sets is set to 100. For the two data sets before and after the sliding window strategy, the corresponding clutter suppression results is shown in Figures 5, 6 respectively. From Figures 5B, 6B, there exist two candidate targets for different data set, where the candidate target coordinates of the first data segment are given by (140, 215), (−150, 138), and those of the second data segment are given by (140, 115), (110, 14). Considering that only one drone aircraft is arranged in the experiment, it is necessary to identify the categories of the candidate targets. By employing the range registration process, one candidate target is generated in each image, which are indicated as (110, 114), (−150, 38) in turn. Meanwhile, the candidate points (140, 215) within the first image and the candidate points (140, 115)within the second image has a good match after image registration. Therefore, there are three candidate targets in the observation scene. Figures 5C, 5H, 6C, 6H represent the processing results of these candidate targets with the Synthetic channel gain (SCG) method, the filter response loss (FRL) method and the sliding filter response loss (SFRL) method. Here, the sliding window size is set to 400 range cells, and the overlapping range number between adjacent sliding windows is set to 100.

FIGURE 5

FIGURE 5. Processing results of data 1.

FIGURE 6

FIGURE 6. Processing results of data 2.

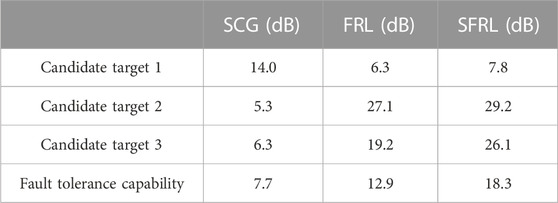
The data processing results of the real measured data are shown in Table 2. According to the judging criteria, candidate target one is recognized as a real target, candidate target two and candidate target three are recognized as discrete side-lobe clutters. Among the above three methods, SFRL method has the best fault tolerance performance, while SCG method has the worst fault tolerance performance. Here, the fault tolerance capability is defined as the desirable dynamic interval of the decision threshold, that is, it can be regarded as the reliable threshold setting interval to distinguish the real target from the discrete side-lobe clutter.

TABLE 2

TABLE 2. Processing results of candidate targets with different methods.

5 Conclusion

For space-based radar, a discrete side-lobe clutter recognition method based on sliding filter response loss is demonstrated to separate the targets from abundant discrete side-lobe clutters in heterogeneous environment, in which the filter response losses corresponding to different segmented data are calculated, and thus the fault tolerance capability for real target recognition can be effectively enhanced. Meanwhile, the insufficient clutter suppression ability at the scene edge areas is significantly alleviated by means of the range segmentation strategy. Theoretical analysis and experimental results based on real measured data verify the reliability of the proposed method.

Data availability statement

The datasets presented in this article are not immediately available because of sensitive information. Requests to access the datasets should be directed to the corresponding author.

Author contributions

Conceptualization YL investigation JC methodology YL and WY Visualization WW validation QL writing-original draft, JC writing-review and editing CL and CD All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (NNSFC) (No. 62107033) and the National Defense Science and Technology Foundation Strengthening Plan Fund (No. 2022-JCJQ-JJ-0202) and the Sustainedly Supported Foundation by National Key Laboratory of Science and Technology on Space Microwave (No. HTKJ2022KL504004) and the CAST Foundation of the Fifth Academy (No. Y22-CASTJJ-02) and the Outstanding Youth Foundation of the Fifth Academy, Aerospace Science and Technology Group (No. Y22-RCWYJQ1-01).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Li HY, Bao WW, Hu JF, Xie J, Liu R. A training samples selection method based on system identification for STAP. Signal Process. (2018) 142(3):119–24. doi:10.1016/j.sigpro.2017.07.008

CrossRef Full Text | Google Scholar

2. Wu YF, Wang T, Wu JX, Duan J. Robust training samples selection algorithm based on spectral similarity for space-time adaptive processing in heterogeneous interference environments. IET Radar Sonar & Navig (2015) 9(7):778–82. doi:10.1049/iet-rsn.2014.0285

CrossRef Full Text | Google Scholar

3. Guo JJ, Liao GS, Yang ZW, Du WT. Iterative weighted covariance matrix estimation method for STAP based on generalized inner products. J Electro Inf Technol (2014) 36(2):422–7. doi:10.3724/SP.J.1146.2013.00426

CrossRef Full Text | Google Scholar

4. Yang XP, Liu YX, Hu XN. Robust generalized inner products algorithm using prolate spheroidal wave functions. In: Radar Conference (RADAR) on Aerospace, Components and Signal Processing; 2012; Atlanta, US (2012).

Google Scholar

5. Sun GH, He ZS, Tong J, Zhang X. Knowledge-aided covariance matrix estimation via kronecker product expansions for airborne STAP. IEEE Geosci Remote Sensing Lett (2018) 15(4):527–31. doi:10.1109/lgrs.2018.2799329

CrossRef Full Text | Google Scholar

6. Wen C, Peng JY, Zhou Y, Wu JX. Enhanced three-dimensional joint domain localized STAP for airborne FDA-MIMO radar under dense false-target jamming scenario. IEEE sensors J (2018) 18(10):4154–66. doi:10.1109/jsen.2018.2820905

CrossRef Full Text | Google Scholar

7. Duan CD, Li Y, Wang WW. An intelligent sample selection method for space-time adaptive processing in heterogeneous environment. IEEE Access (2019) 7(1):30321–30. doi:10.1109/access.2019.2902218

CrossRef Full Text | Google Scholar

8. Jing H, Hu MK, Wang ZW. A improved knowledge-aided space time adaptive signal processing algorithm for MIMO radar. J Electro Inf Technol (2019) 41(4):795–800. doi:10.11999/JEIT180557

CrossRef Full Text | Google Scholar

9. Shnidman DA, Toumodge SS. Sidelobe blanking with integration and target fluctuation. IEEE Trans Aerospace Electron Syst (2002) 38(3):1023–37. doi:10.1109/taes.2002.1039418

CrossRef Full Text | Google Scholar

10. Narasimhan RS, Engadarajan AV, Ramakrishnan KR. Mitigation of sidelobe clutter discrete using sidelobe blanking technique in airborne radars. In: IEEE Aerospace Conference; 2018; Big Sky, US (2018).

CrossRef Full Text | Google Scholar

11. Tian M, Yang ZW, Dang HX, Xu HJ, Huang PH. A two-step detector based on point spread function feature for multi-channel SAR-GMTI radar. In: 2016 CIE International Conference on Radar; 2016; Guangzhou, China (2016).

CrossRef Full Text | Google Scholar

12. Wang WW, Duan CD, Zhang X. A discrete side-lobe clutter recognition method using space-time steering vectors for space-based radar system. J Electro Inf Technol (2020) 42(11):2592–2599. doi:10.11999/JEIT190562

CrossRef Full Text | Google Scholar

13. He Y, Guan J, Meng XW. Radar target detection and CFAR processing. Beijing: Tsinghua University Press (2011). p. 40–50.

Google Scholar