- 1Institute of Applied Physics and Computational Mathematics, Beijing, China
- 2HEDPS, Center for Applied Physics and Technology, Peking University, Beijing, China
- 3Graduate School, China Academy of Engineering Physics, Beijing, China
Hybrid fluid-PIC simulations aimed at a better understanding of the implosion physics and the material mixing into the hot spot are described. The application of a hybrid fluid-PIC code is motivated by the difficulty of modeling the material mixing by the commonly used radiation hydrodynamic simulations. Hybrid fluid-PIC techniques, which treat the ions with the traditional particle-in-cell method, and electrons with a massless fluid, are more adaptable to handle the heating of DT fuel through PdV work and the material mixing near the DT ice-gas interface and ablator-fuel interface of a compressed capsule. During implosion shock convergence, significant reactant temperature separation and a noticeable amount of material mixing are observed, both of which have important consequences for estimating neutron yield and the understanding of implosions. Physical explanations for these phenomena are discussed, with the non-equilibrium effect in the hotspot and hydrodynamic instabilities at the interface as the likely explanation, respectively. The hybrid fluid-PIC method would be helpful to test the phenomenological fluid model describing the material mixing in ICF implosion.
1 Introduction
Recently, inertial confinement fusion (ICF) [1, 2] experiments have reached a record fusion yield of nearly 3.15 MJ [3]. For the first time, the laser fusion experiments have passed the unity fusion conditions that the energy generated by fusion reactions is larger than that was put into the system [4]. However, experiments showed that the implosion performance of capsules is limited by the material mixing inside the hotspot, which is usually seeded by capsule imperfections amplified by hydrodynamic instabilities during acceleration and convergence. The hotspot mix degrades yield by increasing radiative losses and conductive, as well as displacing fuel [5]. Furthermore, the determination of the transport coefficients, e.g., viscosity and diffusivity, is also sensitive to the distribution of ion mix [6]. Therefore, it is crucially important to understand the amount of material mixing in the hotspot region, which is challenging to model and has not been demonstrated yet.
ICF experiments usually generate a broad range of plasma conditions, ranging in temperature of 0.01–10 keV, ranging in density of 1019–1026 cm−3. Consequentially, ICF experiments often contain a wide range of physical phenomena [7]: non-degenerate to degenerate, kinetic to fluid. The Knudsen number
Here, we use hybrid fluid-PIC techniques to model the material mixing and ion kinetic effects in an indirect-drive implosion. Its development is motivated by the kinetic plasma effects that are found to play important roles in several regions inside ICF hohlraums. For example, for shock wave propagation across the inner surface of the implosion capsule and in the rebound of this shock wave at the capsule center [12, 13], etc. In our hybrid code [14], ions are treated using the traditional particle-in-cell method, while electrons are carefully modeled as a massless fluid. The kinetic treatment of multi-species ions allows an assessment of the material mixing and ion kinetic effects in an indirect-drive implosion. And, it is more reliable and adaptable to handle the heating of deuterium-tritium (DT) fuel through PdV work. However, our code does not have enough ICF capabilities since some required physics input is yet to be implemented at present, e.g., radiation ablation-driven shock wave. To solve this problem and save computational resources, the implosion physics in an early stage of compression is still simulated by the radiation hydrodynamic code RDMG [15, 16], which models well the whole ablation process. The remaining deceleration and stagnation phases of the implosion are then simulated with our hybrid fluid-PIC code Ascent-H. Here, the conditions from the RDMG simulation at the deceleration time are linked to the hybrid code Ascent-H.
2 Simulation setup
This work addresses ion kinetic effects, and hydrodynamic instabilities in the hot spot of an indirect-drive implosion target, using the state-of-art hybrid fluid-PIC code Ascent-H [14]. In distinction to most simulation tools that have been used to simulate the ICF implosion processes, Ascent-H treats the ions with large numbers of computation particles, and the collisions between different particles are modeled with the binary Monte Carlo method [17]. For this sake, the ion viscosity and typical ionic kinetic effects are self-consistently included. Because we mainly focus on the time scales of ions, it is reasonable to treat the electrons as a massless fluid. In Ascent-H, the ion motion equation, electron pressure equation, and electromagnetic fields can be described by:
Here, we discuss 2D indirect-drive implosion simulations following the typical parameters of ICF experiments on the Shenguang laser facility. For the sake of simplicity, it is a cylindrical symmetric CH shell (2D disk) with a radius of
Figure 1 shows the trajectories of the hydrodynamic fronts in the time-space plane, one can see a clear view of the shock dynamics from the shock convergence time to bangtime. The merged strong shock, which propagates through the gas, travels to the center and rebounds at t = 2 ns. The reflected shock then bounces back and forth inside the gas between the target center and the inner surface of the shell. At t = 2.22 ns, the reflected shock wave collides with the imploding shell. This is the beginning of the shell deceleration phase. During this stage, the target converges significantly, and the shell acts like a piston which compresses the central gas and creates a hot spot. Meanwhile, the kinetic energy of the shell is then gradually converted to the internal energy of the hot spot. During the deceleration stage, the ice-gas interface is Rayleigh-Taylor (RT) unstable [20]. RT instabilities might result in an undesirable ion mix at the ice-gas interface which increases energy loss and tends to create a warm-spot instead of a designed hot-spot. Thus, the combination of hydrodynamic instabilities and ion mixing would lead to complex shock behavior whose impact is inadequately captured by the usual RH simulations. Here, we use the hybrid-fluid PIC code to simulate the implosion physics starting from the deceleration stage.
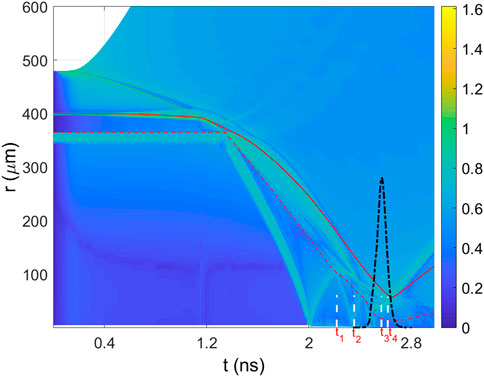
FIGURE 1. Evolution of the hydrodynamic fronts represented by the fluid velocity gradient (
The initial conditions (density profiles, temperature, and velocity) are extracted from the RDMG simulation and remapped onto the Ascent-H grid at the beginning of the deceleration stage (t = 2.22 ns), as shown in Figure 2. At this time, the DT ice has already been compressed to a high-density spike of
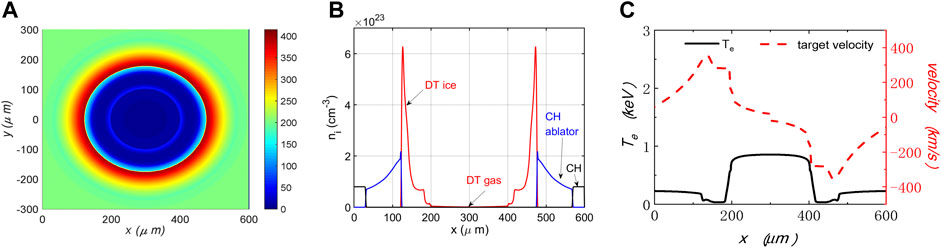
FIGURE 2. The initial pressure and density profiles of the hybrid fluid-PIC simulations, which are extracted from the RDMG simulation. (A) the 2D pressure profile in a unit of Mbar, (B) slice of the density profile, (C) slice of electron temperature and target velocity along x-axis.
3 Hybrid fluid-PIC simulation results
An overview of the implosion dynamics from Ascent-H kinetic simulations is shown in Figure 3, which shows the density (Figures 3A–C), ion temperature (Figures 3D–F), and pressure (Figures 3G–I) at three typical times. One can see that the outer edge of the dense carbon shell has abundant filament-like structures (Figure 3A) that are not shown in usual RH simulations. These filament-like structures result from RTIs that are associated with a rarefaction wave. In Figure 3, the first row shows the density, temperature, and pressure at shock collision time t = 2.41 ns. We observe that a peak ion temperature of 3∼6 keV is formed at the center, but the density and pressure are still low. This ion temperature approximately matches the measured integrated implosion observables (hot-spot temperature, neutron yield) in the Shenguang laser facility [21, 22]. Usually, the ion temperature in the hot spot would be overestimated by the RH simulations due to the mishandling of conductivity, ion kinetic effect, self-generated electromagnetic fields, and so on. Here, in our hybrid simulations, the ion kinetic effect and electromagnetic fields are self-consistently included, which reduced the discrepancies between the simulated and measured ion temperatures.
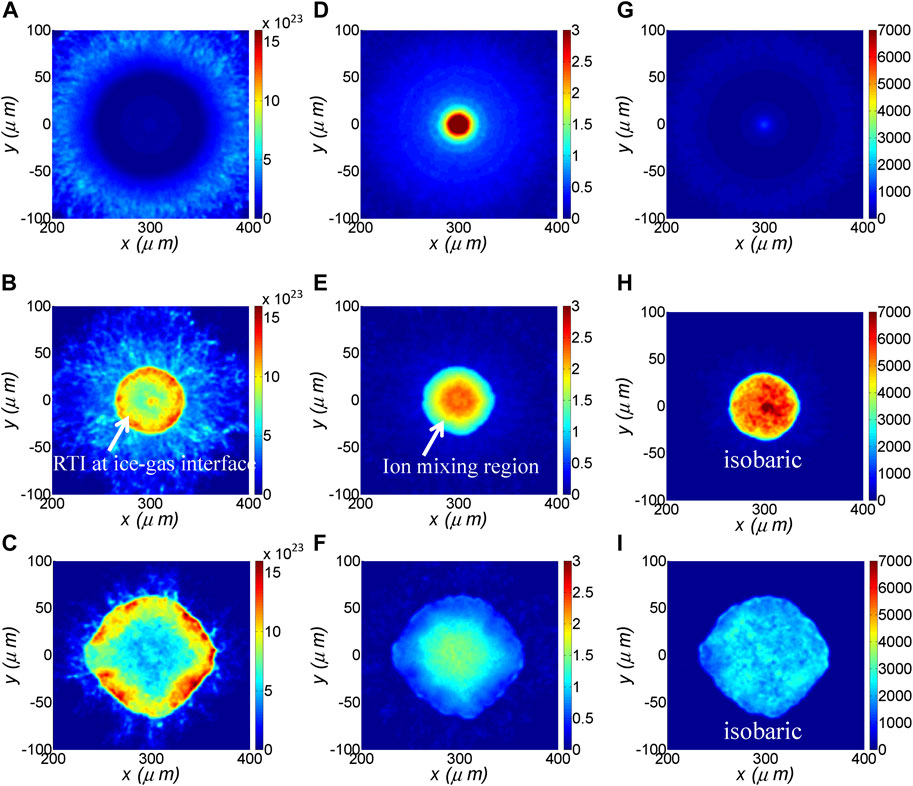
FIGURE 3. Snapshots of the 2D density in unit of cm−3 (A–C), ion temperature in unit of keV (D–F), and pressure in unit of Mbar (G–I) at three typical times. The simulation uses 0.43 billion particles and applies a similar setup as RH simulation.
The second row shows the density, temperature, and pressure at bang time t = 2.57 ns. One can see that a hot spot is created in the center, which is surrounded by the cold DT fuel (Figure 3E). And, the pressure reaches its peak value although the ion temperature drops down (Figure 3H). At this moment, the implosion reaches a peak neutron production rate. Although the ablator is affected by the RTI and ion mixing, the temperature and isobaric pressure equilibrium conditions are maintained well in the hot spot region. More importantly, the ice-gas interface is also Rayleigh-Taylor (RT) unstable [23, 26] during the deceleration stage of the implosion, which is shown in Figure 3B. The seeds for this RT instability growth include the engineering features, such as a fill tube, shell roughness, and bulk inhomogeneities [24]. RT instabilities result in an undesirable mixing of the cold and hot fuel at the ice-gas interface, which increases energy loss and tends to produce a smaller hot-spot volume. In our hybrid simulation, the radius of the hot-spot is only
Figure 4 shows the evolution of the density and ion temperature at the target center of the hotspot. Figure 4A shows that the density of DT plasma increases with time after the shock wave convergence. It increases quite abruptly after around the Bangtime, and eventually decreases again in the disassembly phase. Interestingly, ion temperature reaches a peak value of Ti,D∼5 keV when the shock wave converges at the center at time t = 2.41 ns. After the rebounding of the shock at the center, the ion temperature drops quickly by approximately 50%. It is known that the reflected shock bounces back and forth inside the gas between the target center and the inner surface of the shell, decreasing in strength after every reflection. At t∼2.57 ns, the ion temperature increases again around the Bangtime. By comparing the ion temperature of D and T in Figure 4B, we find a non-equilibrium effect in the hotspot. At the center, the temperature of T is higher than that of D. The physics of this non-equilibrium effect can be explained by the formula below. In the laboratory frame, one can estimate the shock speed and Mach number for different ion species by [25],
where
here, T1 and T2 denote the ion temperature in the upstream and downstream regions. During the shock convergence phase, the temperature separation of D and T in the hot spot volume is most significant, which is consistent with Le’s simulation [27]. Assuming Maxwellian reactivity-weighted averages, one can find
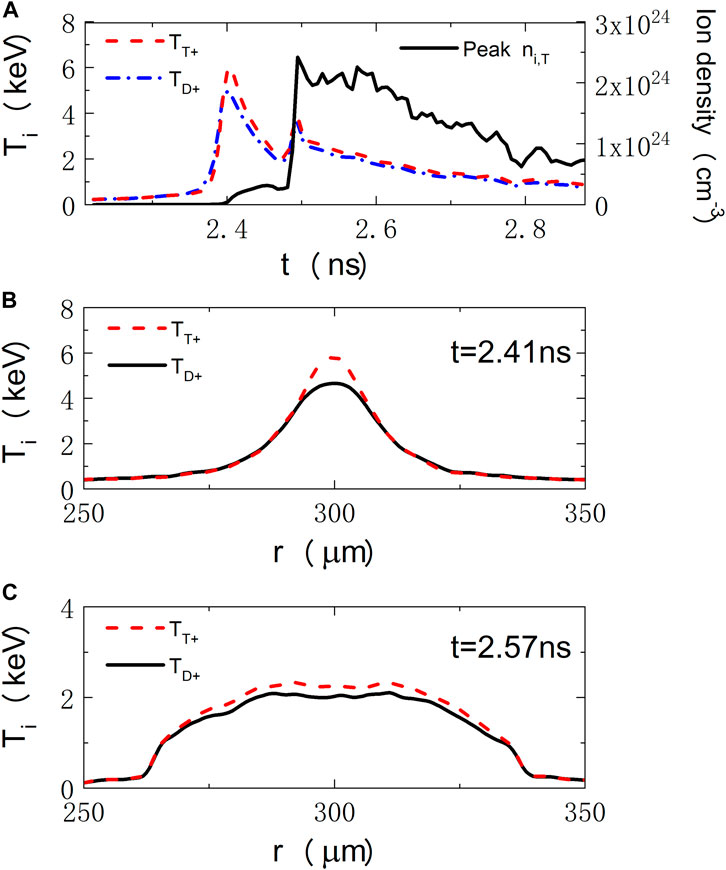
FIGURE 4. (A) Time evolution of the density and ion temperature at the target center. For comparison, we plot the D (solid black) and T (red-dashed line) temperatures at (B) t = 2.41 ns and (C) t = 2.57 ns.
Hence, the total evaluated fusion yield would be overestimated by ∼15% with
In order to show the development of the hydrodynamic instabilities during the implosion, we plot the snapshot of the carbon and tritium number densities at the shock collision time (t = 2.41 ns) and the Bangtime (t = 2.57 ns) in Figure 5. The hydrodynamic instabilities at the ablator-DT interface are seen. For the hybrid fluid-PIC studies, the instability can be linked to the Richtmyer-Meshkov instability (RMI) that is produced during shock breakout from the ablator into DT layer. The RMI is barely visible at t = 2.41 ns but, by t = 2.57 ns, has been amplified via interaction with the reflected shock. This instability is also shown in the snapshot of the density of T (see Figures 5B, D). As a result, during the deceleration of the DT fuel layer, ablator material jets can penetrate the hot spot, which might cool the hot spot and degrade the neutron yield.
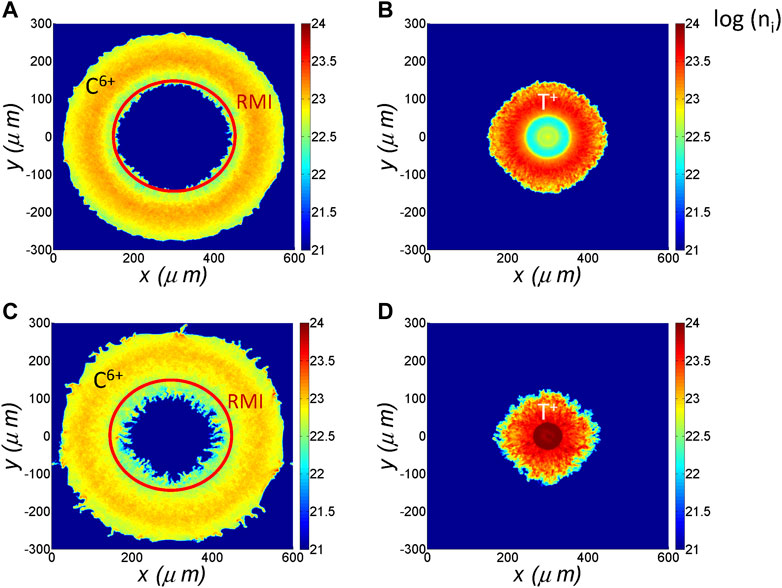
FIGURE 5. Snapshots of the 2D density of (A,C) carbon (ablator) and (B,D) tritium (fuel) in logarithm scale at (A,B) the shock collision time t = 2.41 ns and (C,D) the Bangtime t = 2.57 ns. The hydrodynamic instabilities at the ablator-DT interface are marked inside the red circles.
Note that the hybrid fluid-PIC simulations are prone to creating hydrodynamic instabilities seeds due to ion thermal fluctuation. This fluctuation could be technically reduced by setting more meshes and particles but is limited by computational capability. Since the PIC approach tracks all ion motions, all non-equilibrium physical processes such as diffusion, and dissipation, which are difficult to be accurately captured by the traditional hydrodynamic simulations, are involved naturally in the evolution of RMI. At the late time, the short-wavelength hydrodynamic instabilities interact with each other. While in the hybrid fluid-PIC simulations, the bubble/spike amplitude could be lower due to the ion mixing. The physics of the suppression of RMI could be explained by the increase of viscosity due to the ion mixing. One can estimate the kinematic viscosity by the formula of Braginskii [29],
If the DT ions mix into the carbon plasma, the viscosity of carbon will be significantly increased due to the decreasing of number-density-weighted average charge [30]
Here,
In ICF implosion, the mixing of the ablator material mass into the fuel is also an important factor in reducing the neutron yield. Ion mixing between ablator material and fuel is usually not uniform and incomplete. How much mix occurs and how this mix is distributed are crucial to evaluate what the effects are on the neutron yield. To achieve a better quantitative evaluation of the mixing, we draw the product of the T+ and C6+ number densities,
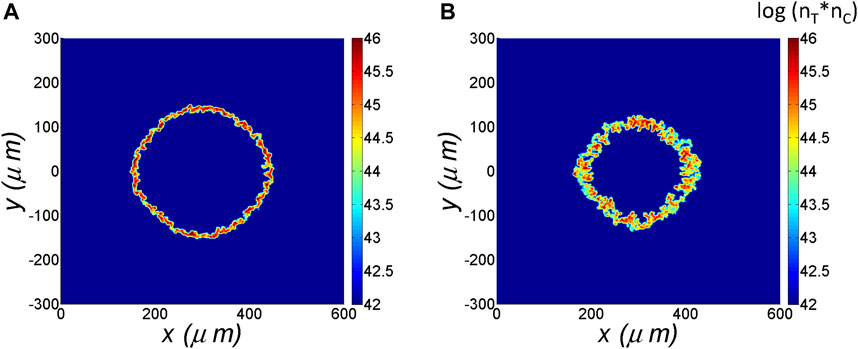
FIGURE 6. The product of the tritium and carbon number densities (nT)*(nC) in logarithm scale at the time (A) t = 2.41 ns and (B) t = 2.57 ns.
The slice of the density profiles also indicates that the width of the mixing region increases over time. The full width of the mixed region, which is defined by 10% and 90% Carbon contours in Figure 7, depends on the density profile. A crude estimate of the width of the mixed ablator-fuel region can be obtained by finding the typical perturbation amplitude, which grows linearly as time goes on:
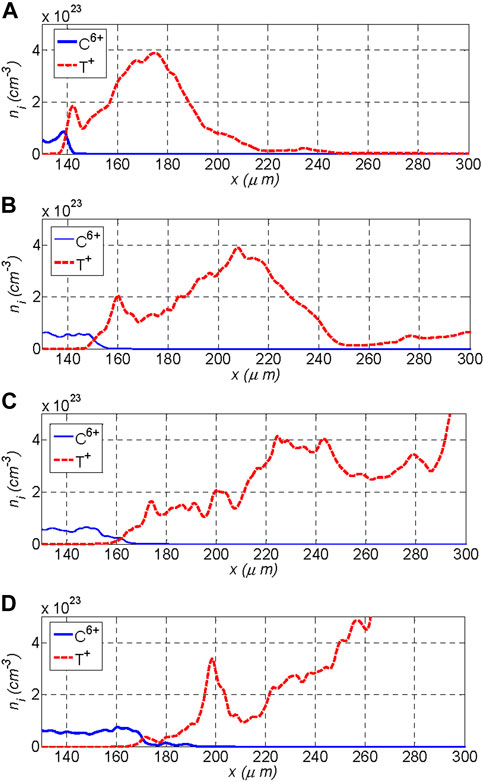
FIGURE 7. The slice of the ion density profile of C6+/T+ around the ablator-fuel interface at different times: (A) t = 2.32 ns, (B) t = 2.41 ns, (C) t = 2.49 ns, (D) t = 2.57 ns.
It should be pointed out that the hybrid fluid-PIC simulations are prone to creating hydrodynamic instability seeds due to the statistical noise (finite particle number and grid effect). The mixing ratio of the materials can be related to the statistical noise since the hydrodynamic instabilities are dependent on the instability seeds. Thus, the hydrodynamic instability seeds can be reduced by using a larger number of particles and higher resolution in hybrid simulations, however, most likely they cannot be completely eliminated. This is the characteristic of all particle-based methods, in which the statistical noise is present in the thermodynamic properties of the kinetic simulations. In our hybrid simulations, to reduce the statistical noise, we adopted a fourth-order spline interpolation for the currents and spatial smoothing for the physical quantities.
4 Summary
In summary, we modeled an indirect-drive cylindrical implosion using a hybrid fluid-PIC model with a kinetic treatment of both the plastic shell and DT fuel ions. The primary advancement of our work is that the injection and mixing between the ablator and fuel are self-consistently included. It is found that RTI at the ice-gas interface leads to an undesirable mixing of the cold and hot fuel, which tends to produce a smaller hot-spot volume and reduce the neutron yield. Furthermore, it is found that the RMI can be developed at the ablator-fuel interface. Although the growth rate reduction is self-consistently included in the simulation, the instability still brings significant ion mixing at the ablator-fuel interface. It is also demonstrated that reactant temperature separation (
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
HC, SYZ, and SPZ conceived of the presented paper. HC constructed the hybrid-PIC simulations and wrote this article, FG and ZD constructed hydrodynamic simulations. WZ and BD assisted with the data analysis. All other authors contributed to the discussion of the results.
Funding
This work was supported by the National Natural Science Foundation of China (Grants No. 11975055), and the National Key Programme for S&T Research and Development (Grant No. 2022YFA1603200).
Acknowledgments
The authors thank C. Y. Li, X. Li, J. W. Li, and Y. K. Ding for helpful discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Hurricane OA, Callahan DA, Casey DT, Celliers PM, Cerjan C, Dewald EL, et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature (2014) 506:343–8. doi:10.1038/nature13008
2. Zylstra AB, Hurricane OA, Callahan DA, Kritcher AL, Ralph JE, Robey HF, et al. Burning plasma achieved in inertial fusion. Nature (London) (2022) 2601:542–8. doi:10.1038/s41586-021-04281-w
3.The U.S. Department of Energy (DOE), National Ignition Facility achieves fusion ignition Available at: https://www.llnl.gov/news/national-ignition-facility-achieves-fusion-ignition.
4. Abu-Shawareb H, Acree R, Adams P, Adams J, Addis B, Aden R, et al. Lawson criterion for ignition exceeded in an inertial fusion experiment. Phys Rev Lett (2022) 129:075001–19. doi:10.1103/PhysRevLett.129.075001
5. Haines BM, Shah RC, Smidt JM, Albright BJ, Cardenas T, Douglas MR, et al. Observation of persistent species temperature separation in inertial confinement fusion mixtures. Nat Commun (2022) 11:544–9. doi:10.1038/s41467-020-14412-y
6. Simakov AN, Molvig K. Hydrodynamic description of an unmagnetized plasma with multiple ion species. I. General formulation. Phys Plasmas (2016) 23:032115. doi:10.1063/1.4943894
7. Rinderknecht HG, Amendt PA, Wilks SC, Collins G. Kinetic physics in ICF: Present understanding and future directions. Plasma Phys Control Fusion (2018) 60:064001–14. doi:10.1088/1361-6587/aab79f
8. Shan LQ, Cai HB, Zhang WS, Tang Q, Zhang F, Song ZF, et al. Experimental evidence of kinetic effects in indirect-drive inertial confinement fusion hohlraums. Phys Rev Lett (2018) 120:195001–5. doi:10.1103/PhysRevLett.120.195001
9. Inglebert A, Canaud B, Larroche O. Species separation and modification of neutron diagnostics in inertial-confinement fusion. Eur Phys Lett (2014) 107:65003–p6. doi:10.1209/0295-5075/107/65003
10. Lautenbach S, Grauer R. Multiphysics simulations of collisionless plasmas. Frontier Phys (2018) 6:113–9. doi:10.3389/fphy.2018.00113
11. Sagert I, Even WP, Strother TT. Two-dimensional implosion simulations with a kinetic particle code. Phys Rev E (2017) 95:053206–15. doi:10.1103/PhysRevE.95.053206
12. Rosenberg MJ, Rinderknecht HG, Hoffman NM, Amendt NM, Atzeni S, Zylstra AB, et al. Exploration of the transition from the hydrodynamiclike to the strongly kinetic regime in shock-driven implosions. Phys Rev Lett (2014) 112:185001–6. doi:10.1103/PhysRevLett.112.185001
13. Rygg JR, Frenje JA, Li CK, Seguin FH, Petrasso RD, Marshall FJ, et al. Observations of the collapse of asymmetrically driven convergent shocks. Phys Plasmas (2008) 15:034505. doi:10.1063/1.2892025
14. Cai HB, Yan XX, Yao PL, Zhu SP. Hybrid fluid–particle modeling of shock-driven hydrodynamic instabilities in a plasma. Matt Rad Extremes (2021) 6:035901–9. doi:10.1063/5.0042973
15. Feng TG, Lai DX, Xu Y. An artifical-scatteriong interaction method for calculating multi-group radiation transfer problems. Chin J Comput Phys (1999) 16:199–205. Available at: http://www.cjcp.org.cn/CN/abstract/abstract1870.shtml.
16. Song P, Zhai CL, Li SG, Yong H, Qi J, Hang XD, et al. LARED–Integration code for numerical simulation of the whole process of the indirect-drive laser inertial confinement fusion[J]. High Power Laser Part Beams (2015) 27:032007–7. doi:10.11884/HPLPB201527.032007
17. Nanbu K. Yonemura weighted particles in coulomb collision simulations based on the theory of a cumulative scattering angle S. Weighted particles in coulomb collision simulations based on the theory of a cumulative scattering angle. J Comput Phys (1998) 145:639–54.
18 . Jones ME, Lemons DS, Mason RJ, Thomas VA, Winske D. A gridbasedCoulomb collision model for PIC codes. J Comput Phys (1996) 123:169–81. doi:10.1006/jcph.1996.0014
19. Lindl J, Landen O, Edwards J. Moses ed, and NIC teams, review of the national ignition campaign 2009-2012. Phys Plasmas (2014) 21:020501–72. doi:10.1063/1.4865400
20. Haines BH, Olson RE, Sweet W, Yi SA, Zylstra AB, Bradley PA, et al. Robustness to hydrodynamic instabilities in indirectly driven layered capsule implosions. Phys Plasmas (2019) 26:012707–15. doi:10.1063/1.5080262
21. Li X, Dong YS, Kang DG, Jiang W, Shen H, Kuang LY, et al. First indirect drive experiment using a six-cylinder-port hohlraum. Phys Rev Lett (2022) 128:195001–5. doi:10.1103/PhysRevLett.128.195001
22. Lan K, Dong YS, Wu JF, Li ZC, Chen YH, Cao H, et al. First inertial confinement fusion implosion experiment in octahedral spherical hohlraum. Phys Rev Lett (2021) 127:245001–7. doi:10.1103/PhysRevLett.127.245001
23. Fu JY, Zhang HS, Cai HB, Yao PL, Zhu SP. Effect of ablation on the nonlinear spike growth for the single-mode ablative Rayleigh–Taylor instability. Matter Radiat Extremes (2023) 8:016901–10. doi:10.1063/5.0106832
24. Liu MF, Ai X, Liu YH, Chen Q, Zhang S, He ZB, et al. Fabrication of solid CH-CD multilayer microspheres for inertial confinement fusion. Matter and Radiation at Extremes. Fabrication of solid CH-CD multilayer microspheres for inertial confinement fusion (2021) 6:025901. doi:10.1063/5.0033103
25. Bellei C, Amendt PA. Asymptotic separation in multispecies collisional plasma shocks. Phys Rev E (2014) 90:013101–5. doi:10.1103/PhysRevE.90.013101
26. Vidal F, Matte JP, Casanova M, Larroche O. Ion kinetic simulations of the formation and propagation of a planar collisional shock wave in a plasma. Phys Fluids B (1993) 5:3182–90. doi:10.1063/1.860654
27. Le A, Kwan JT, Schmitt MJ, Herrmann HW, Batha SH. Simulation and assessment of ion kinetic effects in a direct-drive capsule implosion experiment. Phys Plasmas (2016) 23:102705–5. doi:10.1063/1.4965913
30. Simakov N, Molvig K. Hydrodynamic description of an unmagnetized plasma with multiple ion species. II. Two and three ion species plasmas. Phys Plasmas (2016) 23:032116–2. doi:10.1063/1.4943895
31. Mikaelian KO. Effect of viscosity on Rayleigh-Taylor and Richtmyer-Meshkov instabilities. Phys Rev E (1993) 47:375–83. doi:10.1103/PhysRevE.47.375
32. Brouillette M, Sturtevant B. Experiments on the richtmyer-meshkov instability: Single-scale perturbations on a continuous interface. J Fluid Mech (1994) 263:271–92. doi:10.1017/s0022112094004118
Keywords: hybrid fluid-PIC, ion mixing, indirect-drive implosion, hydrodynamic instability, inertial confinement fusion (ICF)
Citation: Cai H, Zhang W, Ge F, Du B, Dai Z, Zou S and Zhu S (2023) Simulation and assessment of material mixing in an indirect-drive implosion with a hybrid fluid-PIC code. Front. Phys. 11:1140383. doi: 10.3389/fphy.2023.1140383
Received: 09 January 2023; Accepted: 07 February 2023;
Published: 16 February 2023.
Edited by:
Bing Guo, China Institute of Atomic Energy, ChinaReviewed by:
Fuyuan Wu, Shanghai Jiao Tong University, ChinaXiaohu Yang, National University of Defense Technology, China
Copyright © 2023 Cai, Zhang, Ge, Du, Dai, Zou and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hongbo Cai, Y2FpX2hvbmdib0BpYXBjbS5hYy5jbg==; Shaoping Zhu, emh1X3NoYW9waW5nQGlhcGNtLmFjLmNu
 Hongbo Cai
Hongbo Cai Wenshuai Zhang1
Wenshuai Zhang1