Alternative schemes for twin-field quantum key distribution with discrete-phase-randomized sources

The twin-field quantum key distribution (TF-QKD) protocol and its variants can overcome the well-known rate-loss bound without quantum repeaters, which have attracted significant attention. Generally, to ensure the security of these protocols, weak coherent states with continuous randomized phases are always assumed in the test mode. However, this assumption is difficult to meet in practice. To bridge the gap between theory and practice, we propose two alternative discrete-phase-randomized (DPR)-twin-field quantum key distribution protocols, which remove the phase sifting procedure in the code mode. Simulation results show that when compared with previous discrete-phase-randomized-twin-field quantum key distribution protocols, our modified protocols can significantly improve the secret key rate in the low channel loss range, which is very promising for practical twin-field quantum key distribution systems.

1 Introduction

Based on the laws of quantum mechanics, quantum key distribution (QKD) [1] can provide secret keys for two distant parties, Alice and Bob, even in the presence of an eavesdropper Eve. Since the first protocol [1] was proposed in 1984, many achievements [2–6] have been made to promote the procedure of QKD. However, the fundamental rate-loss bound [7,8] limits the performance of these QKD protocols. Surprisingly, based on the single-photon interference at the third untrusted party Eve, the twin-field QKD (TF-QKD) protocol [9] shows the possibility of overcoming this limit.

Inspired by the revolutionary idea of TF-QKD [9], many variant protocols [10–19] have been proposed to strengthen the security, and some variants have been demonstrated in experiments [20–26]. To ensure the security of these protocols, quantum states should be randomly switched between the code mode and the test mode. Generally, the decoy-state method [27–29] is adopted in the test mode to estimate the eavesdropper’s information on raw keys.

However, the standard decoy-state method assumes that the phases of coherent states should be continuously randomized, which is very difficult to achieve in practical experiments. Fortunately, [30,31] proposed the discrete-phase-randomized (DPR) scheme to bypass the requirement of continuous phase randomization. Subsequently, researchers have generalized the DPR source to various TF-QKD protocols [32–35] to improve their practical security. In particular, [33] requires phase post-selection both in the code mode and the test mode, and [35] needs phase post-selection only in the code mode. Nevertheless, the secret key rate of [33,35] is lower due to phase sifting in the code mode, especially in the low channel loss range. Hence, it is necessary to further promote the performance of these two DPR-TF-QKD protocols.

In this paper, by removing the phase post-selection procedure of the code mode [33,35], we propose two alternative DPR-TF-QKD protocols. In our protocols, if Alice and Bob choose the code mode, the classical bits 0,1 are encoded into the 0, π phases of a coherent state, respectively; and if Alice and Bob choose the test mode, they modulate the phases of a coherent state with a random phase $0,\frac{2\pi }{M},\frac{4\pi }{M},\dots ,\frac{\left(M-1\right)2\pi }{M}$. Simulation results show that only with a small number of discrete phases, our protocols can overcome the rate-loss bound; and compared with [33,35], our protocols perform much better in the low channel loss range.

2 Protocols

We introduce the procedure of our modified DPR-TF-QKD protocols, which are named as Protocol I and Protocol II in the following context. Compared with [33,35], our protocols I and II remove the phase sifting procedure in the code mode, which can improve the secret key rate of DPR-TF-QKD protocols in the low channel loss range.

2.1 Protocol I

2.1.1 Step 1

Alice (Bob) chooses the code mode or the test mode in each trial. If the code mode is selected, Alice (Bob) randomly generates a key bit $b_A\left(b_B\right)$ to prepare a coherent state $\left|{(-1)}^{b_A}\sqrt{\mu }\right.⟩\left(\left|{(-1)}^{b_B}\sqrt{\mu }\right.⟩\right)$. If the test mode is selected, Alice (Bob) randomly chooses a number $x\left(y\right)$ and an intensity ${\xi }_a\left({\xi }_b\right)$ to prepare a coherent state $\left|\sqrt{{\xi }_a}{\mathrm{e}}^{i\frac{2\pi x}{M}}\right.⟩\left(\left|\sqrt{{\xi }_b}{\mathrm{e}}^{i\frac{2\pi y}{M}}\right.⟩\right)$, where x, y ∈ {0, 1, 2, … , M − 1}, ${\xi }_a,{\xi }_b\in \left\{\mu ,\nu ,\omega \right\}$, and M denotes the number of discrete phases modulated by Alice (Bob).

2.1.2 Step 2

Alice and Bob send the prepared states to the untrusted party Eve. Eve interferes with the received states on a 50:50 beam splitter, measures output pulses with two threshold detectors L and R, and announces the corresponding results. Only three results are acceptable, including only detector L clicks, only detector R clicks, or no detectors click. If both detectors click, it is considered to be no detectors click. Notably, the events of only detector L or R clicking are considered successful measurements.

2.1.3 Step 3

Alice and Bob repeat the aforementioned steps numerous times. For those successful events, Alice and Bob announce their chosen mode. For trials in the code mode, they keep b_A and b_B as their sifted key bits. Moreover, Bob should flip his key bits b_B for those events that detector R clicks. For trials in the test mode, they announce the values of ξ_a, ξ_b, x and y and only keep the trials that are ξ_a = ξ_b and x = y or $x=y\pm \frac{M}{2}$.

2.1.4 Step 4

Alice and Bob perform error correction and privacy amplification to get final secret keys.

The final secret key rate of Protocol I is

$K\ge Q^{\mu }\left[1-fH\left(e^{\mu }\right)-I_{AE}^{\mu }\right],(1)$

where $H\left(X\right)=-X{\log }_{2}X-\left(1-X\right){\log }_2\left(1-X\right)$ is the binary Shannon entropy, Q^μ and e^μ denote the gain and error rate of quantum states, respectively, with intensity μ in the code mode, f denotes the inefficiency of error correction, and $I_{AE}^{\mu }$ denotes the upper bound of Eve’s Holevo information. Notably, the procedure and secret key rate of our Protocol I are the same as [32], while [32] estimates the eavesdropper’s information by obtaining the upper bounds of the phase error, which is different from our security analysis. The detailed analysis of our Protocol I is shown in Supplementary Appendix A.

For the simplicity of practical implementations, we can further remove the phase post-selection step of the test mode in Protocol I, which will be reduced to Protocol II. The procedure of Protocol II runs as follows.

2.2 Protocol II

2.2.1 Step 1

This step is similar to that of Protocol I.

2.2.2 Step 2

Alice and Bob send the prepared states to the untrusted party Eve. Eve interferes with the received states on a 50:50 beam splitter, measures output pulses with two threshold detectors L and R, and announces the corresponding results. Only three results are acceptable, including only detector L clicks, only detector R clicks, or no detectors click. Here, the event that both detectors click is considered to be no detectors click for the code mode and is randomly assigned as only detector L or R clicks for the test mode. Notably, the events of only detector L or R clicking are considered successful measurements.

2.2.3 Step 3

Alice and Bob repeat the aforementioned steps numerous times. For those successful events, Alice and Bob announce their chosen mode. For trials in the code mode, they keep b_A and b_B as their sifted key bits. Moreover, Bob should flip his key bits b_B for those events that detector R clicks. For trials in the test mode, they announce the values of ξ_a and ξ_b to calculate gains $Q^{{\xi }_a{\xi }_b}$.

2.2.4 Step 4

This step is similar to that of Protocol I.

The final secret key rate of Protocol II is the same as that of Protocol I, and the corresponding analysis is shown in Supplementary Appendix B.

3 Simulation

For typical TF-QKD systems [36], we assume that the detection efficiency and the dark count rate per pulse of single-photon detectors are 20% and 10^–8, respectively, the inefficiency of key reconciliation is 1.1, and the intrinsic misalignment error is 1.5%. With these system parameters, we investigate the performance of our protocols. Moreover, we optimize the intensities of μ and ν by a coarse-grained exhaustive search, and the intensity ω is simply fixed to be 0.

The simulation results of Protocol I are shown in Figure 1, and the Pirandola–Laurenza–Ottaviani–Banchi (PLOB) bound [8] is plotted in comparison. It can be seen that, with M = 4, Protocol I cannot break the PLOB bound; however, with the increase of M which can estimate Eve’s information more accurately, Protocol I can break the PLOB bound, and the maximal channel loss becomes higher.

FIGURE 1

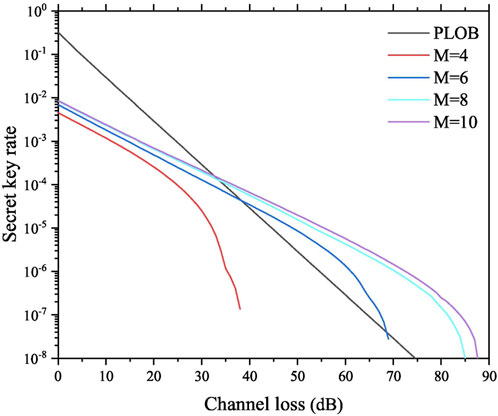
FIGURE 1. Results of the secret key rate versus channel loss for Protocol I with different M values. The black line represents the PLOB bound, and the curves from the bottom to the top represent the secret key rates of Protocol I with M = 4, 6, 8, and 10.

Moreover, we compare the performance of Protocol I and [33], and the corresponding results are shown in Figure 2. The difference between them is the preparation of the code mode. Specifically, in Protocol I, Alice (Bob) prepares a coherent state $\left|{(-1)}^{b_A}\sqrt{\mu }\right.⟩\left(\left|{(-1)}^{b_B}\sqrt{\mu }\right.⟩\right)$ for the code mode, while in [33], Alice (Bob) prepares a coherent state $\left|{\mathrm{e}}^{i\left[b_A\pi +\left(\frac{2\pi x}{M}\right)\right]}\sqrt{\mu }\right.⟩\left(\left|{\mathrm{e}}^{i\left[b_B\pi +\left(\frac{2\pi y}{M}\right)\right]}\sqrt{\mu }\right.⟩\right)$. Compared to [33], which requires phase sifting in the code mode and introduces the sifting factor 2/M in the key generation rate, Protocol I removes the phase sifting procedure and thus naturally bypasses the sifting factor 2/M in the key rate. Hence, the key rate of Protocol I is higher than that of [33] in the relatively low channel loss range. On the other hand, Protocol I modulates only two phases in the code mode, which leads to the tolerable channel loss is relatively lower than that of [33].

FIGURE 2

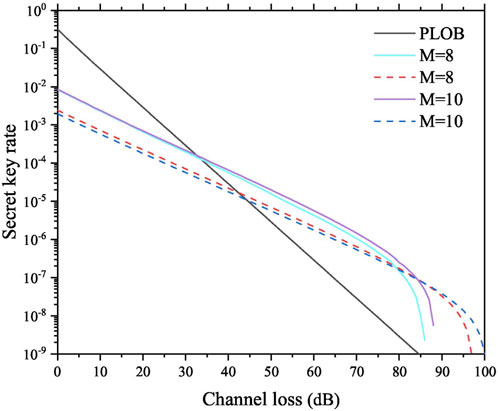
FIGURE 2. Comparison results of Protocol I and [33] with M = 8 and 10. The solid curves represent the results of Protocol I, and the dashed curves represent the results of [33].

Figure 3 shows the simulation results of Protocol II. Protocol II cannot break the PLOB bound with M = 4; however, with the increase of M, Protocol II can break the PLOB bound, and the maximal channel loss becomes higher as well. It should be noted that the secret key rates of M = 8 and M = 10 are almost overlapped, which indicates that modulating only eight phases in the test mode is adequate to ensure both the performance and security of Protocol II. Furthermore, we compare the performance of Protocol II and [35], and the results are shown in Figure 4. Similar to the analysis of Figure 2, [35] requires phase sifting in the code mode, while Protocol II removes phase sifting in the code mode. Consequently, the secret key rate of Protocol II is higher than that of [35] in the relatively low channel loss range, and the tolerable channel loss of Protocol II is lower than that of [35].

FIGURE 3

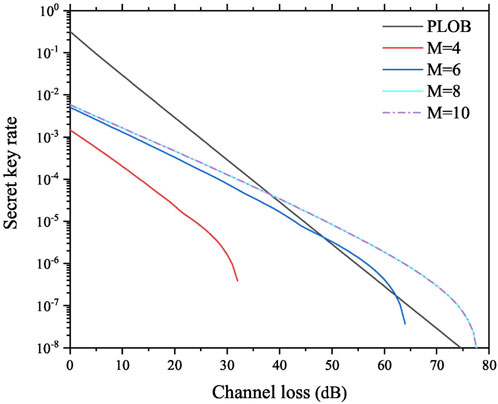
FIGURE 3. Results of the secret key rate versus channel loss for Protocol II with different M values. The black line represents the PLOB bound, and the curves represent the secret key rates of Protocol II with M = 4, 6, 8, and 10.

FIGURE 4

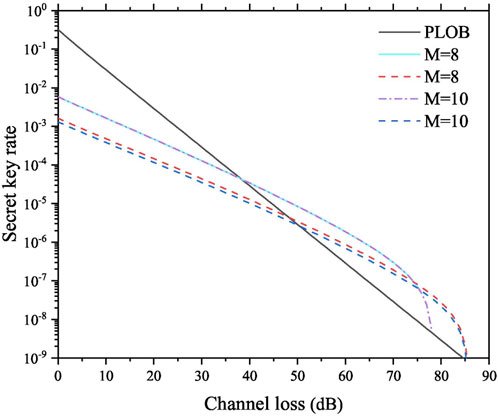
FIGURE 4. Comparison results of Protocol II and [35] with M = 8 and 10. The solid curve and the dot–dash curve represent the results of Protocol II, and the dashed curves represent the results of [35].

4 Conclusion

Briefly, we have proposed two alternative DPR-TF-QKD protocols, which removed the phase sifting procedure in the code mode. In our security analysis, we only consider the security against collective attacks, which can be extended to the security against coherent attacks with the post-selection technique in [37]. Simulation results show that our protocols can break the PLOB bound with only a small number of discrete phases. Also, compared with the previous protocols which required phase post-selection in the code mode, our protocols performed much better, especially in the low channel loss range. In addition, the finite key effect plays an important role in the practical implementation of the QKD system [38–41], and we will leave this issue for future research.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CZ proposed the presented idea. HL and CZ developed the protocols and proofs. HL simulated the protocols, and CZ verified the simulation results. All authors discussed the results and contributed to the final manuscript.

Funding

This work was supported by the China Postdoctoral Science Foundation (2019T120446 and 2018M642281), the Jiangsu Planned Projects for Postdoctoral Research Funds (2018K185C), and the Natural Science Foundation of Nanjing University of Posts and Telecommunications (NY221058 and 1311).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1140156/full#supplementary-material

References

1. Bennett CH, Brassard G. Quantum cryptography: Public key distribution and coin tossing. Proc IEEE Int Conf Comput Syst Signal Process (1984) 560:7–11. doi:10.1016/j.tcs.2014.05.025

CrossRef Full Text | Google Scholar

2. Fröhlich B, Lucamarini M, Dynes JF, Comandar LC, Tam WW-S, Plews A, et al. Long-distance quantum key distribution secure against coherent attacks. Optica (2017) 4:163. doi:10.1364/OPTICA.4.000163

CrossRef Full Text | Google Scholar

3. Boaron A, Boso G, Rusca D, Vulliez C, Autebert C, Caloz M, et al. Secure quantum key distribution over 421 km of optical fiber. Phys Rev Lett (2018) 121:190502. doi:10.1103/PhysRevLett.121.190502

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yin H-L, Chen T-Y, Yu Z-W, Liu H, You L-X, Zhou Y-H, et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys Rev Lett (2016) 117:190501. doi:10.1103/PhysRevLett.117.190501

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Pirandola S, Ottaviani C, Spedalieri G, Weedbrook C, Braunstein SL, Lloyd S, et al. High-rate measurement-device-independent quantum cryptography. Nat Photon (2015) 9:397–402. doi:10.1038/nphoton.2015.83

CrossRef Full Text | Google Scholar

6. Gu J, Cao X-Y, Fu Y, He Z-W, Yin Z-J, Yin H-L, et al. Experimental measurement-device-independent type quantum key distribution with flawed and correlated sources. Sci Bull (2022) 67:2167–75. doi:10.1016/j.scib.2022.10.010

CrossRef Full Text | Google Scholar

7. Takeoka M, Guha S, Wilde MM. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat Commun (2014) 5:5235. doi:10.1038/ncomms6235

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Pirandola S, Laurenza R, Ottaviani C, Banchi L. Fundamental limits of repeaterless quantum communications. Nat Commun (2017) 8:15043. doi:10.1038/ncomms15043

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lucamarini M, Yuan ZL, Dynes JF, Shields AJ. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature (2018) 557:400–3. doi:10.1038/s41586-018-0066-6

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Tamaki K, Lo H-K, Wang W, Lucamarini M (2018). Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. arXiv preprint arXiv:1805.05511

Google Scholar

11. Wang X-B, Yu Z-W, Hu X-L. Twin-field quantum key distribution with large misalignment error. Phys Rev A (2018) 98:062323. doi:10.1103/PhysRevA.98.062323

CrossRef Full Text | Google Scholar

12. Ma X, Zeng P, Zhou H. Phase-matching quantum key distribution. Phys Rev X (2018) 8:031043. doi:10.1103/PhysRevX.8.031043

CrossRef Full Text | Google Scholar

13. Cui C, Yin Z-Q, Wang R, Chen W, Wang S, Guo G-C, et al. Twin-field quantum key distribution without phase postselection. Phys Rev Appl (2019) 11:034053. doi:10.1103/PhysRevApplied.11.034053

CrossRef Full Text | Google Scholar

14. Curty M, Azuma K, Lo H-K. Simple security proof of twin-field type quantum key distribution protocol. npj Quan Inf (2019) 5:64. doi:10.1038/s41534-019-0175-6

CrossRef Full Text | Google Scholar

15. Lin J, Lütkenhaus N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys Rev A (2018) 98:042332. doi:10.1103/PhysRevA.98.042332

CrossRef Full Text | Google Scholar

16. Yin H-L, Fu Y. Measurement-device-independent twin-field quantum key distribution. Scientific Rep (2019) 9:3045. doi:10.1038/s41598-019-39454-1

CrossRef Full Text | Google Scholar

17. Wang R, Yin Z-Q, Lu F-Y, Wang S, Chen W, Zhang C-M, et al. Optimized protocol for twin-field quantum key distribution. Commun Phys (2020) 3:149. doi:10.1038/s42005-020-00415-0

CrossRef Full Text | Google Scholar

18. Xie Y-M, Lu Y-S, Weng C-X, Cao X-Y, Jia Z-Y, Bao Y, et al. Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quan (2022) 3:020315. doi:10.1103/PRXQuantum.3.020315

CrossRef Full Text | Google Scholar

19. Zeng P, Zhou H, Wu W, Ma X. Mode-pairing quantum key distribution. Nat Commun (2022) 13:3903. doi:10.1038/s41467-022-31534-7

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Minder M, Pittaluga M, Roberts GL, Lucamarini M, Dynes J, Yuan Z, et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat Photon (2019) 13:334–8. doi:10.1038/s41566-019-0377-7

CrossRef Full Text | Google Scholar

21. Wang S, He D-Y, Yin Z-Q, Lu F-Y, Cui C-H, Chen W, et al. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys Rev X (2019) 9:021046. doi:10.1103/PhysRevX.9.021046

CrossRef Full Text | Google Scholar

22. Zhong X, Hu J, Curty M, Qian L, Lo H-K. Proof-of-principle experimental demonstration of twin-field type quantum key distribution. Phys Rev Lett (2019) 123:100506. doi:10.1103/PhysRevLett.123.100506

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Fang X-T, Zeng P, Liu H, Zou M, Wu W, Tang Y-L, et al. Implementation of quantum key distribution surpassing the linear rate-transmittance bound. Nat Photon (2020) 14:422–5. doi:10.1038/s41566-020-0599-8

CrossRef Full Text | Google Scholar

24. Liu Y, Yu Z-W, Zhang W, Guan J-Y, Chen J-P, Zhang C, et al. Experimental twin-field quantum key distribution through sending or not sending. Phys Rev Lett (2019) 123:100505. doi:10.1103/PhysRevLett.123.100505

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chen J-P, Zhang C, Liu Y, Jiang C, Zhang W, Hu X-L, et al. Sending-or-not-sending with independent lasers: Secure twin-field quantum key distribution over 509 km. Phys Rev Lett (2020) 124:070501. doi:10.1103/PhysRevLett.124.070501

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wang S, Yin Z-Q, He D-Y, Chen W, Wang R-Q, Ye P, et al. Twin-field quantum key distribution over 830-km fibre. Nat Photon (2022) 16:154–61. doi:10.1038/s41566-021-00928-2

CrossRef Full Text | Google Scholar

27. Hwang W-Y. Quantum key distribution with high loss: Toward global secure communication. Phys Rev Lett (2003) 91:057901. doi:10.1103/PhysRevLett.91.057901

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Lo H-K, Ma X, Chen K. Decoy state quantum key distribution. Phys Rev Lett (2005) 94:230504. doi:10.1103/PhysRevLett.94.230504

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang X-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys Rev Lett (2005) 94:230503. doi:10.1103/PhysRevLett.94.230503

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Cao Z, Zhang Z, Lo H-K, Ma X. Discrete-phase-randomized coherent state source and its application in quantum key distribution. New J Phys (2015) 17:053014. doi:10.1088/1367-2630/17/5/053014

CrossRef Full Text | Google Scholar

31. Cao Z. Discrete-phase-randomized measurement-device-independent quantum key distribution. Phys Rev A (2020) 101:062325. doi:10.1103/PhysRevA.101.062325

CrossRef Full Text | Google Scholar

32. Currás-Lorenzo G, Wooltorton L, Razavi M. Twin-field quantum key distribution with fully discrete phase randomization. Phys Rev Appl (2021) 15:014016. doi:10.1103/PhysRevApplied.15.014016

CrossRef Full Text | Google Scholar

33. Zhang C-M, Xu Y-W, Wang R, Wang Q. Twin-field quantum key distribution with discrete-phase-randomized sources. Phys Rev Appl (2020) 14:064070. doi:10.1103/PhysRevApplied.14.064070

CrossRef Full Text | Google Scholar

34. Jiang C, Yu Z-W, Hu X-L, Wang X-B. Sending-or-not-sending twin-field quantum key distribution with discrete-phase-randomized weak coherent states. Phys Rev Res (2020) 2:043304. doi:10.1103/PhysRevResearch.2.043304

CrossRef Full Text | Google Scholar

35. Xu Y-W, Wang R, Zhang C-M. Discrete-phase-randomized twin-field quantum key distribution without phase postselection in the test mode. Quan Inf Process (2021) 20:199. doi:10.1007/s11128-021-03135-8

CrossRef Full Text | Google Scholar

36. Zeng P, Wu W, Ma X. Symmetry-protected privacy: Beating the rate-distance linear bound over a noisy channel. Phys Rev Appl (2020) 13:064013. doi:10.1103/physrevapplied.13.064013

CrossRef Full Text | Google Scholar

37. Christandl M, König R, Renner R. Postselection technique for quantum channels with applications to quantum cryptography. Phys Rev Lett (2009) 102:020504. doi:10.1103/physrevlett.102.020504

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Yin H-L, Zhou M-G, Gu J, Xie Y-M, Lu Y-S, Chen Z-B. Tight security bounds for decoy-state quantum key distribution. Scientific Rep (2020) 10:14312. doi:10.1038/s41598-020-71107-6

CrossRef Full Text | Google Scholar

39. Maeda K, Sasaki T, Koashi M. Repeaterless quantum key distribution with efficient finite-key analysis overcoming the rate-distance limit. Nat Commun (2019) 10:3140. doi:10.1038/s41467-019-11008-z

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Yin H-L, Chen Z-B. Finite-key analysis for twin-field quantum key distribution with composable security. Scientific Rep (2019) 9:17113. doi:10.1038/s41598-019-53435-4

CrossRef Full Text | Google Scholar

41. Currás-Lorenzo G, Navarrete Á, Azuma K, Kato G, Curty M, Razavi M. Tight finite-key security for twin-field quantum key distribution. npj Quan Inf (2021) 7:22. doi:10.1038/s41534-020-00345-3

CrossRef Full Text | Google Scholar