Comparative study of surface integral methods in aeroacoustic prediction

Introduction: Surface integral methods based on the acoustic analogy and Kirchhoff formulation are widely employed in computational aeroacoustics. The computational accuracy is usually highly dependent on the selections of the acoustic prediction method and of the integral surfaces.

Methods: This paper analyzes the pros and cons of each aeroacoustic prediction method and studies numerically sound generated from flow past a circular cylinder by employing different surface integral methods. The acoustic analogy based on the impermeable solid surfaces either ignores the quadrupole contribution or needs high computational cost to calculate the quadrupole contribution, and the acoustic analogy based on the permeable integral surfaces usually suffers from the spurious source issue.

Results: Both the pressure-based or density-based Kirchhoff formulations can be used in aeroacoustic prediction, however, the numerical results indicate that the pressure-based Kirchhoff formulation also suffers from the issue of the spurious sound because the pressure fluctuations at the permeable integral surfaces are contaminated by hydrodynamic component.

Discussion: It seems that only the density-based Kirchhoff formulation does not suffer from the issue of the spurious sound, but this formulation requires the acoustic sources should be extracted from compressible flow simulations.

1 Introduction

Sound generated from turbulence and its interaction with solid boundaries can be predicted with either integral methods or differential methods [1, 2]. Compared with differential methods, integral methods cannot consider the effect of shear mean flow on sound propagation outside the integral surfaces [3]. However, the integral methods usually need less computational cost than the differential methods because the integral methods do not need to discretize the entire domain of acoustic propagation. Therefore, the integral methods are more widely employed in various engineering applications [4].

All integral methods can be classified into the following two types. The first method is based on the acoustic analogy proposed by Lighthill [5] and developed by Ffowcs Williams and Hawkings (FW-H) [6]. In numerical calculations, the integral solutions of FW-H equation, such as time-domain formulations developed by Farassat [7–10], are utilized to predict sound radiated from sources located on and outside the integral surfaces. Since calculation of sound radiated from the quadupole sources located outside the integral surfaces usually costs much more time than calculations of monopole and dipole sources on the integral surfaces do, permeable integral surfaces are widely employed in order to reduce or avoid the time consumed at quadrupole calculation.

The second method is based on the Kirchhoff formulation [11, 12], which is derived from the linearized acoustic theory. Therefore, the integral surfaces of the Kirchhoff formulation should enclose all non-linear sources for predicting aerodynamic noise. Detailed reviews of Kirchhoff formulation in computational aeroacoustics can be found in [13].

Both methods have been widely used in computational aeroacoustics, such as jet noise [14–16] and rotor noise [17–19]. Analytical comparison of these two methods have been performed by Brentener and Farassat [20], and they concluded the integral method based on the FW-H equation is superior to that based on the Kirchhoff formulation because the acoustic results based on the FW-H equation is less sensitive than the Kirchhoff formulation to placement of integral surfaces.

However, this conclusion is not supported by all numerical results. For examples, studies of some investigators, such as Wang et al. [21], Sinayoko et al. [22] and Zhong and Zhang [23], have revealed that the FW-H equation with permeable surfaces suffer from the issue of spurious sound owing to vortical disturbances passing through the permeable integral surfaces. Therefore, the acoustic calculation result based on the FW-H equation is still highly dependent on the position of the permeable integral surfaces. In order to reduce the acoustic contamination caused by the spurious sources located at permeable surfaces, various methods, such as, open integral surfaces [24], outflow-disk-averaging technique [25–27], have been developed to supress the spurious sound radiated from the permeable surfaces over past decades. Detailed reviews can be found in [28].

On the other hand, the input variables of the Kirchhoff formulation do not include the velocity disturbances, thus the Kirchhoff formulation is thought to do not suffer the issue of spurious sound. The static pressure and its gradient are usually used as the input variables of the Kirchhoff formulation in previous numerical studies, such as [20, 29, 30]. However, we must emphasize that the Kirchhoff formulation is derived based on the linearized acoustic theory, thus both the input and output variables should be only acoustic components. In prediction of aerodynamic sound generated from turbulence, the static pressure extracted from the flow simulation results includes not only acoustic but also hydrodynamic (vortical) components [31–33]. Therefore, the pressure-based Kirchhoff formulation is actually also contaminated by the vortical component which is similar to that encountered by the FW-H formulation with permeable integral surfaces. The density fluctuation and its gradient are only relevant to acoustic process in turbulence without external heat sources. Therefore, the density-based Kirchhoff formulation can avoid the issue of spurious sound, to the best knowledge of authors, but no comparative studies on this topic have been performed so far.

This paper aims to perform comparative studies on surface integral methods in aeroacoustic prediction. Aerodynamic sound generated from compressible flow past a circular cylinder is studied numerically using different surface integral methods. The remainder of this paper is structured as follows. Section 2 describes the numerical case. In Section 3, simulation and validation of unsteady flow are performed through comparing the numerical results with previous numerical and experimental data. Acoustic results calculated from different aeroacoustic prediction methods are compared in Section 4. Conclusion are drawn in Section 5.

2 Description of numerical case

Sound generated from compressible flow past a circular cylinder is predicted, where the free stream Mach number and Reynolds number are 0.75 and 2*10⁵, respectively.

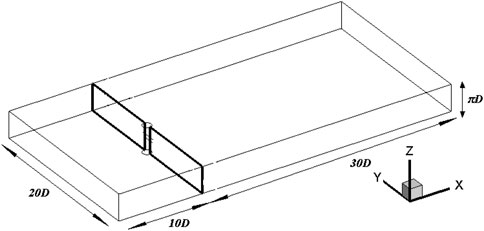
Flow physics at this operating condition has been studied numerically and experimentally by some investigators, such as Rodriguez [34], Murthy et al. [35], Xu et al. [36] and Hong et al. [37]. Thus abundant experimental database and numerical results can be used to validate the numerical method used in this paper. The computational domain is 40D*20D*πD as shown in Figure 1, where D represents the diameter of the circular cylinder. The upstream and downstream boundaries are 10D and 30D away from the center of the cylinder surface, respectively. A spanwise length of πD is chosen according to recommendation of numerical studies performed by Breuer [38] and Lysenko [39].

FIGURE 1

FIGURE 1. Global view of the computational domain for flow simulation.

3 Simulation and validation of unsteady flow

3.1 Flow simulation setup

Large eddy simulation (LES) technique is employed to solve three-dimensional unsteady compressible Navier-Stokes equations. The well-known Smagorinsky model [40] is used to consider the influence of small scale eddies and to calculate the subgrid scale tensor. All computations are carried out with a Smagroinsky constant of Cs = 0.1 [41], which is an empirical value mostly used for practical applications.

Different spatial and temporal discretization schemes are used for the governing equations, in which spatial discretization is achieved by using the bounded central differencing scheme for the convection terms and second-order central difference for the diffusion terms, and an implicit second-order scheme is utilized for the temporal discretization. The SIMPLE algorithm is used for pressure-velocity coupling.

In present study, the initial and boundary conditions are presented as follows. The constant free-stream quantities, i.e., the mass flow and static temperature, are imposed at the inlet boundary without any perturbation. The non-reflecting boundary condition is used at the downstream boundary of the computational domain to avoid acoustic reflection at this surface. No-slip and adiabatic boundary conditions are applied on the solid wall of the cylinder and periodic boundary conditions are used at the rest pairs of surfaces of the computational domain.

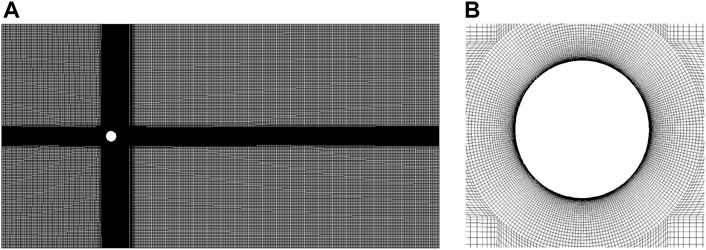
The computational domain is discretized with hexahedral meshes and the total number of mesh cells is around 5.8 million, as shown in Figure 2. To avoid any kind of wall functions, the detailed flow inside boundary layer is solved directly using fine grids in the vicinity of the cylinder surface, and the normal distance between the first layer mesh nodes and the cylinder surface is set to be 0.002 mm, with a stretching factor of 1.08.64 and 320 nodes are distributed uniformly along the spanwise and circumferential directions, respectively, which are similar to the grid numbers and distributions utilized in previous simulations [38, 39, 42, 43]. The above grid distribution ensures that the non-dimensional nearest wall distance $y^{+}$ is smaller than 1. Figure 3 illustrates the distribution of $y^{+}$, which satisfies the requirement of the LES. Time step $\Delta t=4.7\times {10}^{-6}$ s is used to ensure temporal resolution of the numerical result, which corresponds to the non-dimensional parameter $U_{\infty }\Delta t/D=0.006$.

FIGURE 2

FIGURE 2. Computational mesh for the circular cylinder: (A) entire domain; (B) near-wall region.

FIGURE 3

FIGURE 3. y⁺distribution of the circular cylinder.

3.2 Validation of flow simulation results

Based on numerical simulation results, distribution features of the normalized wall pressure, i.e., time-averaged and root-mean-square (RMS) values, are compared with experimental data from Rodriguez [34] as well as the numerical data from Xu et al; [36] and Hong et al; [37]; Figures 4A, B compare time-averaged and root-mean-square (RMS) values from different sources, where $\theta =0$ and $\theta ={180}^{\circ }$ represent the stagnation point and rear point of the cylinder wall, respectively.

FIGURE 4

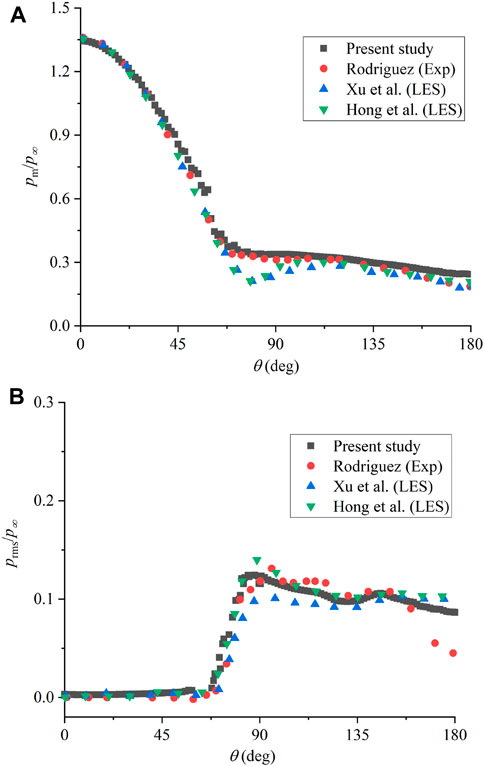
FIGURE 4. Comparison of the calculated results with experimental data: (A) time-averaged wall pressure; (B) RMS of pressure fluctuation.

In Figure 4A, the time-averaged pressure obtained from present numerical simulation has a good agreement with experimental data of Rodriguez [34], but has a little deviation from the numerical results from Xu et al; [36] and Hong et al [37]; Figure 4B shows that the RMS values from different sources have a disperse feature, but all the numerical results can reach a fair consistency.

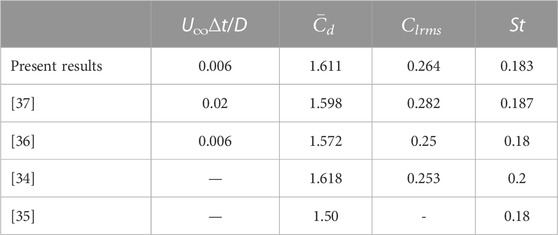
To further assess reliability of present numerical results, some quantities together with previous experimental [34, 35] and numerical studies [36, 37] have conducted at the same Reynolds number, including the time-averaged and root-mean square values of lift and drag coefficients based on spanwise length of the cylinder, as well as the Strouhal number, are summarized in Table 1. It can be seen that both the time-average drag coefficient ${\overline{C}}_d$ and RMS value of the lift coefficient $C_{lrms}$ fall in the range of the existing experimental and numerical results. As is well known, the pressure fluctuation on a cylinder is associated with the alternating vortex shedding. To identify the frequency of the vortex shedding, the power spectral density (PSD) of the instantaneous lift coefficient is shown in Figure 5. The characteristic Strouhal number is defined based on the free stream velocity of U_∞ and the diameter of the cylinder D. As exhibited in Figure 5, an obviously frequency peak value is about 233 Hz corresponding to the highest peak value St ≈ 0.183, which is consistent with experimental data in the range from 0.18 to 0.2. Moreover, The time histories of the lift and drag coefficients from the present study are given in Figure 6, and features are consistent with the previous literatures [36, 37].

TABLE 1

TABLE 1. Comparison of main flow quantities at Re = 2 × 10⁵.

FIGURE 5

FIGURE 5. Power spectral density of unsteady lift coefficient.

FIGURE 6

FIGURE 6. Time histories of lift and drag coefficients.

4 Comparative study of aeroacoustic prediction

4.1 Acoustic formulations

The convective wave equation of the acoustic analogy, developed independently by Najafi-Yazdi et al. [44] and Ghorbaniasl et al. [45] based on the equation of Ffowcs Williams and Hawkings [6], is used to describe sound, generated by turbulence and its interaction with solid boundaries, propagation in a uniform mean flow, which is expressed by

$\left(\frac{D^2}{D{t}^2}-c_0^2{\nabla }^2\right)\left[H\left(f\right){\rho }^{\prime }\right]=\frac{D}{Dt}\left[Q\delta \left(f\right)\right]-\nabla \cdot \left[\mathbf{L}\delta \left(f\right)\right]+\nabla \cdot \left\{\nabla \cdot \left[H\left(f\right)\mathbf{T}\right]\right\}(1)$

where three terms at right hand side of Eq. 1 are named as monopole, dipole and quadrupole sources, respectively. These sources are expressed by

$Q={\rho }_0\left(v_n-U_{\infty n}\right)+\rho \left(u_n+U_{\infty n}-v_n\right)(2)$

$\mathbf{L}=\left(\left(p-p_0\right)\mathbf{I}-\mathbf{\sigma }\right)\cdot \mathbf{n}+\rho \mathbf{u}\left(u_n+U_{\infty n}-v_n\right)(3)$

$\mathbf{T}=\left[\left(p-p_0\right)-c_0^2\left(\rho -{\rho }_0\right)\right]\mathbf{I}-\mathbf{\sigma }+\rho \mathbf{u}\mathbf{u}(4)$

where $f=0$ can be either the solid surface or the permeable surface enclosing all solid surfaces, $H\left(\cdot \right)$ and $\delta \left(\cdot \right)$ respectively represent the Heaviside and Dirac Delta functions, ${\mathbf{U}}_{\infty }$ is the velocity of uniform mean flow, $\mathbf{u}$ denotes the fluctuation of the local flow velocity, $\mathbf{v}$ represents the velocity of the surface $f=0$, n is the unit vector normal to surface $f=0$, $\mathbf{\sigma }$ is the viscous stress tensor, $c_0$ and ${\rho }_0$ are respectively the speed of sound and density of undisturbed fluid.

By following the derivation method of the time-domain acoustic pressure integral formulations 1 and 1A of Farassat [46], the acoustic pressure integral formulations corresponding to the convective FW-H equations have been derived in [44, 45]. Especially, when the integral surfaces are stationary, the frequency-domain acoustic pressure formulations of the monopole and dipole surface sources can be expressed by:

$4\pi {{\stackrel{\sim }{p}}^{\prime }}_T\left(\mathbf{x},\omega \right)=-\underset{f=0}{{\displaystyle \int }}\frac{\mathrm{i}k{c}_0\stackrel{\sim }{Q}\left(1-M_{\infty R}\right)}{R^{*}}{\mathrm{e}}^{\mathrm{i}kR}\mathrm{d}S-\underset{f=0}{{\displaystyle \int }}\frac{c_0\stackrel{\sim }{Q}{M}_{\infty R^{*}}}{R^{*2}}{\mathrm{e}}^{\mathrm{i}kR}\mathrm{d}S(5)$

$4\pi {{\stackrel{\sim }{p}}^{\prime }}_L\left(\mathbf{x},\omega \right)=-\underset{f=0}{{\displaystyle \int }}\frac{ik{\stackrel{\sim }{L}}_R}{R^{*}}{\mathrm{e}}^{\mathrm{i}kR}\mathrm{d}S+\underset{f=0}{{\displaystyle \int }}\frac{{\stackrel{\sim }{L}}_{R^{*}}}{R^{*2}}{\mathrm{e}}^{\mathrm{i}kR}\mathrm{d}S(6)$

where subscripts T and L, respectively, represent the monopole and dipole source, and $R$, which means the acoustic distance between the source and observer in the mean flow, is expressed by

$R={\gamma }^2\left(R^{*}-r{M}_{\infty r}\right)(7)$

with $\gamma =\sqrt{\left.1/\left(1-M_{\infty }^2\right.\right)}$, $M_{\infty r}=M_{\infty i}{\widehat{r}}_i$, $M_{\infty i}=U_{\infty i}/c_0$, and $L_R=L_j{R}_j$, $L_{R^{*}}=L_j{R}_j^{*}$, $M_R=M_j{R}_j$, $M_{R^{*}}=M_j{R}_j^{*}$ and

$R^{*}=\frac{\sqrt{r^2+{\gamma }^2{\left(M_{\infty }\cdot \mathbf{r}\right)}^2}}{\gamma }=\frac{r\sqrt{1+{\gamma }^2{M}_{\infty r}^2}}{\gamma }(8)$

where $\mathbf{r}=\mathbf{x}-\mathbf{y}$ is the position vector from the source to the observer, and $r=\left|\mathbf{r}\right|$ is the geometrical distance between the source and the observer. Usually, a permeable surface enclosing all solid surfaces can be used to calculate far-field sound in order to reduce the computational time consumed at the volume integral over the quadrupole sources. However, the issue of the spurious sound must be treated carefully in this situation due to vortical disturbances passing through the permeable surface.

Alternative acoustic prediction method is based on the following convective formulation of Kirchhoff formulation [28]:

$\begin{array}{l}4\pi \stackrel{\sim }{p^{\prime }}\left(\mathbf{x},\omega \right)=-\underset{f=0}{{\displaystyle \int }}\left(\frac{\partial \stackrel{\sim }{p^{\prime }}}{\partial \mathbf{n}}+ik\stackrel{\sim }{p^{\prime }}{R}_n\right)\frac{e^{ikR}}{R^{*}}dS+\underset{f=0}{{\displaystyle \int }}\stackrel{\sim }{p^{\prime }}{R}_n^{*}\frac{e^{ikR}}{R^{*2}}dS\\ +M_{\infty n}\left[\underset{f=0}{{\displaystyle \int }}\left(-2ik\stackrel{\sim }{p^{\prime }}+ik{M}_{\infty R}\stackrel{\sim }{p^{\prime }}+{\mathbf{M}}_{\infty }\cdot \nabla \stackrel{\sim }{p^{\prime }}\right)\frac{e^{ikR}}{R^{*}}dS-\underset{f=0}{{\displaystyle \int }}\stackrel{\sim }{p^{\prime }}{M}_{\infty R^{*}}\frac{e^{ikR}}{R^{*2}}dS\right]\end{array}(9)$

with $R_n={\widehat{R}}_j{\widehat{n}}_j$ and $R_n^{*}={\widehat{R}}_j^{*}{\widehat{n}}_j$ . From Eq. 9 we can find that once variables, including the pressure and its spatial derivative in the flow field are known, the acoustic pressure in the far field can be calculated. The pressure fluctuation in the terms at the right hand side of Eq. 9 should be strictly acoustic component, but the pressure fluctuation obtained from the unsteady flow simulation includes both the acoustic and vortical components, thus aeroacoustic prediction results based on Eq. 9 is also prone to be contaminated by the vortical component of the pressure fluctuation. In order to avoid this issue, the following density-based version of the convective Kirchhoff formulation is recommended

$\begin{array}{l}\frac{4\pi \stackrel{\sim }{p^{\prime }}\left(\mathbf{x},\omega \right)}{c_0^2}=-\underset{f=0}{{\displaystyle \int }}\left(\frac{\partial \stackrel{\sim }{{\rho }^{\prime }}}{\partial \mathbf{n}}+ik\stackrel{\sim }{{\rho }^{\prime }}{R}_n\right)\frac{e^{ikR}}{R^{*}}dS+\underset{f=0}{{\displaystyle \int }}\stackrel{\sim }{{\rho }^{\prime }}{R}_n^{*}\frac{e^{ikR}}{R^{*2}}dS\\ +M_{\infty n}\left[\underset{f=0}{{\displaystyle \int }}\left(-2ik\stackrel{\sim }{{\rho }^{\prime }}+ik{M}_{\infty R}\stackrel{\sim }{{\rho }^{\prime }}+{\mathbf{M}}_{\infty }\cdot \nabla \stackrel{\sim }{{\rho }^{\prime }}\right)\frac{e^{ikR}}{R^{*}}dS-\underset{f=0}{{\displaystyle \int }}\stackrel{\sim }{{\rho }^{\prime }}{M}_{\infty R^{*}}\frac{e^{ikR}}{R^{*2}}dS\right]\end{array}(10)$

Eq. 9 is mathematically equivalent to Eq. 10 as the acoustic pressure and density fluctuation has the relationship of $\stackrel{\sim }{p^{\prime }}=\stackrel{\sim }{{\rho }^{\prime }}{c}_0^2$. Compared Eq. 9 with Eq. 10, density fluctuation in Eq. 10 can be extracted directly from simulation of the unsteady compressible flow but the acoustic pressure component in Eq. 9 could be contaminated by the hydrodynamic component.

4.2 Computational methods

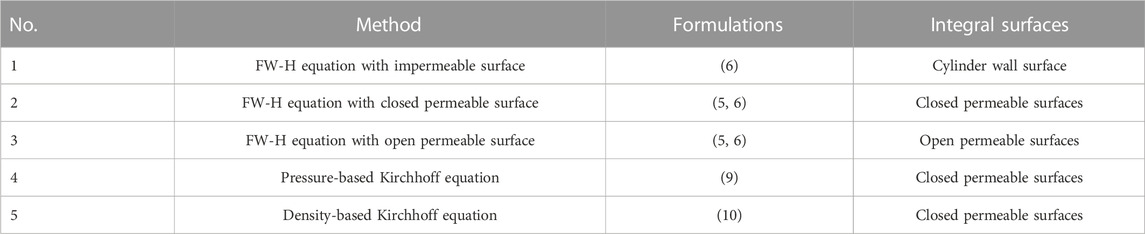
Sound radiated from flow past a circular cylinder is predicted using five numerical methods to compare their pros and cons. Details on these five methods are described below.

In the first method, sound radiated from a stationary solid surface is calculated by means of the convective FW-H equation, where the integral surface f is the stationary cylinder surface. Thereby, the monopole source disappears and acoustic contribution from only the dipole source is calculated using Eq. 6 when the quadrupole contribution is ignored to save the computational cost.

In the second method, sound is still calculated with the convective FW-H equation but the integral surfaces f corresponds to six permeable surfaces of the computational domain. Aeroacoustic prediction is performed based on formulations (5) and (6), which is capable of reducing the computational time consumed at the volume integral over the quadrupole sources. However, this method is prone to cause the issue of spurious sound owing to vortical velocity disturbances passing through the downstream permeable surface, as discussed by previous investigators, such as [21].

In the present case, the acoustic prediction result is mainly contaminated by the spurious sources located at the downstream permeable surface. Therefore, acoustic computations over the upstream permeable surface and four side permeable surfaces can be calculated based on the formulations (5) and (6). In the third method, the acoustic contribution from the downstream permeable surface is ignored directly, thus this method is usually named open-surface FW-H method.

In the fourth and fifth methods, the acoustic contribution from the closed permeable surfaces is calculated with the pressure-based Kirchhoff formulation (9) and the density-based Kirchhoff formulation (10). As mentioned above, the pressure fluctuation is still contaminated by the hydrodynamic component but the density fluctuation is only related to acoustic process.

All surface integral methods in aeroacoustic prediction are compared and summarized in Table 2.

TABLE 2

TABLE 2. Comparison of surface integral methods in computational aeroacoustics.

4.3 Comparison of computational results

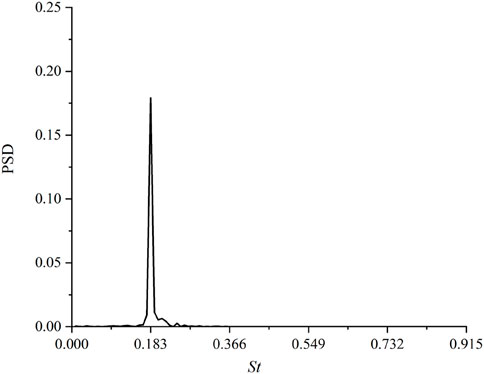
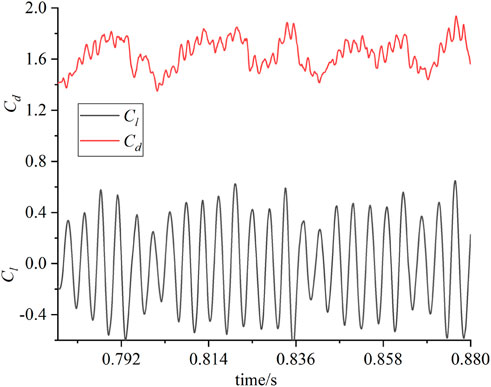
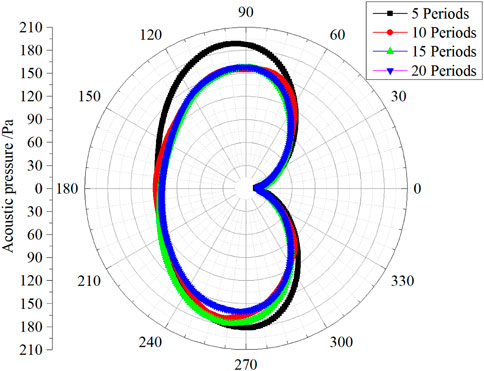
Aeroacoustic prediction is performed by means of five methods mentioned above, where the prediction results should be independent of the length of sampling time used in the calculation. Therefore, the effect of the sampling time on the acoustic prediction results should be investigated in advance. The flow simulation results shown in Figure 5 indicate that the period of vortex shedding is about 430 time steps, thus unsteady flow simulation results based on 5, 10, 15 and 20 periods are, respectively, used as the input data to predict the acoustic pressure. 36 acoustic sampling points are uniformly distributed at a circle with a radius of R = 1 m in the XY plane and its center is the same as that circular cylinder.

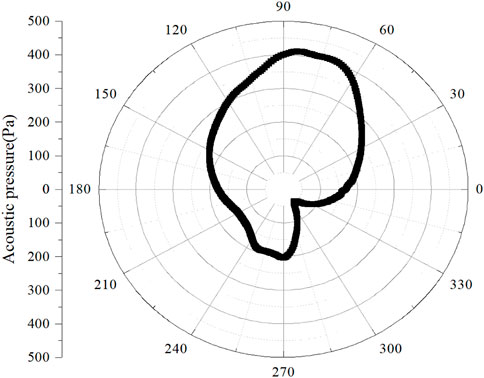
Figure 7 illustrates the directivity pattern of the acoustic pressure calculated from the first acoustic prediction method, i.e., the FW-H equation with the cylinder wall surface. The results indicate that the computational results can reach a converged solution when the sampling times is not smaller than 10 periods of vortex shedding. Therefore, in the following analysis, the aeroacoustic prediction results are performed by extracting sources from 10 periods of vortex shedding.

FIGURE 7

FIGURE 7. Acoustic results for the FW-H equation with impermeable wall surface.

The FW-H equation with the solid surface does not suffer from the issue of spurious sources but ignores the contribution from the quadrupole sources. The acoustic prediction result is very similar to sound radiated from a compact dipole source immersed in a uniform mean flow, where acoustic pressure at the upstream sampling point is usually higher than that at the downstream sampling point owing to the connective amplification.

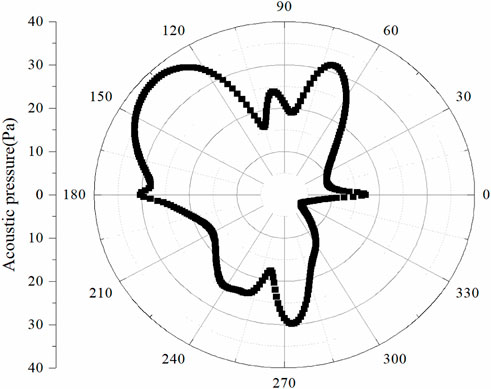
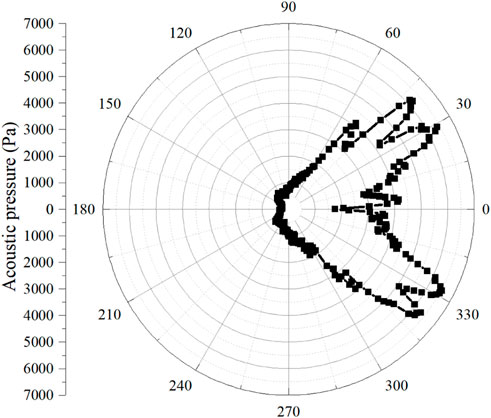
Figures 8, 9 illustrate the acoustic results calculated from the FW-H equation with closed and open permeable surfaces, respectively. The results presented in these two figures show a great deviation, implying that the acoustic prediction results are very sensitive to the sources located at the downstream permeable integral surface. It should be noted that the results in both Figures 8, 9 have an obvious difference from that in Figure 7, implying that the FW-H equation with either closed permeable integral surfaces or open permeable integral surfaces cannot output an accurate acoustic prediction result.

FIGURE 8

FIGURE 8. Acoustic results for the FW-H equation with closed permeable integral surfaces.

FIGURE 9

FIGURE 9. Acoustic results for the FW-H equation with open permeable integral surfaces.

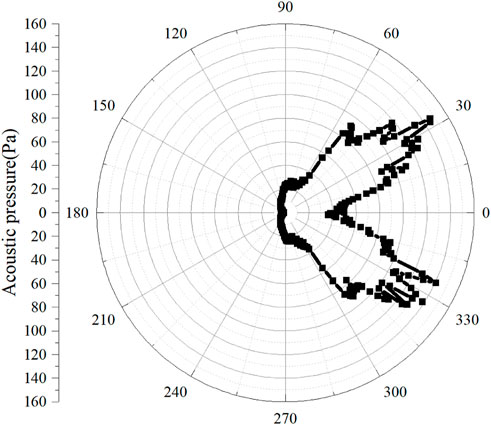
Figures 10, 11 display the acoustic pressure prediction results based on the pressure-based Kirchhoff formulation and the density-based Kirchhoff formulation, respectively. The results show that the directivity patterns calculated from two methods are very similar, but the amplitudes of the acoustic pressure have a distinct difference. The reason causing this difference is that the pressure fluctuations at the permeable integral surface are contaminated by the hydrodynamic component, therefore, the acoustic pressure calculated from the pressure-based Kirchhoff formulation is much higher than that from the density-based Kirchhoff formulation.

FIGURE 10

FIGURE 10. Acoustic results for the pressure-based Kirchhoff formulation.

FIGURE 11

FIGURE 11. Acoustic results for the density-based Kirchhoff formulation.

Moreover, compared Figure 7 with Figure 11, the directivity pattern calculated from these two methods has a distinct difference, which implies that the acoustic contribution from quadrupole sources has a great impact on the acoustic radiation.

5 Conclusion

Sound radiated from flow past a circular cylinder is studied numerically to investigate the effect of different surface integral methods on the prediction results. Conclusions are drawn as follows.

(1) Acoustic calculation results are highly dependent on selections of the aeroacoustic prediction method and the integral surfaces. The FW-H equation combined with the impermeable wall surface is a suitable choice if the acoustic contribution from the quadrupole sources can be ignored. However, the permeable integral surfaces are recommended in a high-Mach number flow because the acoustic contribution from quadrupole sources has a great impact on acoustic radiation.

(2) Compared with the FW-H equation with the impermeable wall surfaces, the FW-H equation with the permeable integral surfaces is computationally efficient to predict sound generated from turbulence and its interaction with wall surfaces. However, numerical simulations validate that the acoustic result predicted from the later method has visible computational errors owing to that the monopole and dipole sources are contaminated by vortical velocity at the permeable integral surfaces.

(3) Acoustic results calculated from the pressure-based Kirchhoff formulation with the permeable integral surfaces also suffers from the issue of spurious sound, but the mechanics of the spurious sound is different from the FW-H equation with the permeable integral surfaces. In the pressure-based Kirchhoff formulation, the spurious sound is caused by the hydrodynamic pressure fluctuations located at the permeable integral surfaces, but the spurious sources in the FW-H equation is caused by the vortical velocity fluctuations located at the permeable integral surfaces.

(4) Density fluctuation is contributed only from acoustic waves in turbulence without heat transfer. Therefore, the density-based Kirchhoff formulation with the permeable integral surfaces does not suffer from the issue of spurious sound. Difference of acoustic results between the density-based Kirchhoff formulation and the FW-H equation with impermeable wall integral surface can be regarded as the contribution from the quadrupole located in the region between the impermeable wall integral surface and permeable integral surfaces.

However, the density-based Kirchhoff formulation requires that the acoustic sources should be obtained from the compressible flow simulation. Therefore, this method is not suitable for low-Mach-number flows, in which aeroacoustic sources are usually obtained by solving incompressible Navier-Stokes equations.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CX and SW, Numerical simulation and Analysis; DY and RZ, Formal analysis, YM, Prgramming; SJ and CX, Writing. All authors have read and agreed to the published version of the manuscript.

Funding

The research is supported by the National Natural Science Foundation of China (No. 52076086) and Laboratory of Aerodynamic Noise Control of China Aerodynamics Research and Development Center (Nos ANCL20220302, SKLA-20200302).

Acknowledgments

The authors gratefully acknowledge high-performance computing facilities IRIDIS4 at the University of Southampton in the completion of this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hardin JC, Hussaini MY. Computational aeroacoustics. Hampton, Springer New York: Springer Science and Business Media (1993).

Google Scholar

2. Tam CKW. Computational aeroacoustics: A wave number approach. New York: Cambridge University Press (2012).

Google Scholar

3. Pan FL, Uzun A, Lyrintzis AS. Surface integral methods in jet aeroacoustics: Refraction corrections. J Aircraft (2008) 45:381–7. doi:10.2514/1.23513

CrossRef Full Text | Google Scholar

4. Lyrintzis AS. Surface integral methods in computational aeroacoustics—from the (CFD) near-field to the (acoustic) far-field. Int J Aeroacoust (2003) 2:95–128. doi:10.1260/147547203322775498

CrossRef Full Text | Google Scholar

5. Lighthill MJ. On sound generated aerodynamically. I. General theory. Proc R.Soc Lond Ser A, Math Phys Sci (1952) 211:564–87. doi:10.1098/rspa.1952.0060

CrossRef Full Text | Google Scholar

6. Ffowcs Williams J, Hawkings D. Sound generation by turbulence and surfaces in arbitrary motion. Philos Trans R Soc Lond A, Math Phys Eng.Sci (1969) 264:321–42. doi:10.1098/rsta.1969.0031

CrossRef Full Text | Google Scholar

7. Farassat F, Succi GP. A review of propeller discrete frequency noise prediction technology with emphasis on two current methods for time domain calculations. J Sound Vib (1980) 71:399–419. doi:10.1016/0022-460x(80)90422-8

CrossRef Full Text | Google Scholar

8. Farassat F. Linear acoustic formulas for calculation of rotating blade noise. AIAA J (1981) 19:1122–30. doi:10.2514/3.60051

CrossRef Full Text | Google Scholar

9. Farassat F, Brentner KS. Supersonic quadrupole noise theory for high-speed helicopter rotors. J Sound Vib (1998) 218:481–500. doi:10.1006/jsvi.1998.1836

CrossRef Full Text | Google Scholar

10. Farassat F, Farris M. Verification and analysis of Formulation 4 of Langley for the study of noise from high speed surfaces. Bellevue: AIAA paper (1999). p. 99–1881.

Google Scholar

11. Farassat F, Myers MK. Extension of Kirchhoffs formula to radiation from moving surfaces. J Sound Vib (1988) 123:451–60. doi:10.1016/s0022-460x(88)80162-7

CrossRef Full Text | Google Scholar

12. Lyrintzis A, Xue Y. Versatile Kirchhoff code for aeroacoustic predictions. AIAA J (1997) 35:198–200. doi:10.2514/3.13484

CrossRef Full Text | Google Scholar

13. Lyrintzis AS. Review: The use of Kirchhoffs method in computational aeroacoustics. J Fluid Eng-t ASME (1994) 116:665–76. doi:10.1115/1.2911834

CrossRef Full Text | Google Scholar

14. Rahier G, Prieur J, Vuillot F, Lupoglazoff N, Biancherin A. Investigation of integral surface formulations for acoustic post-processing of unsteady aerodynamic jet simulations. Aerosp Sci Technol (2004) 8:453–67. doi:10.1016/j.ast.2004.04.005

CrossRef Full Text | Google Scholar

15. Bodony DJ, Lele SK. Current status of jet noise predictions using large-eddy simulation. AIAA J (2008) 46:364–80. doi:10.2514/1.24475

CrossRef Full Text | Google Scholar

16. Uzun A, Lyrintzis AS, Blaisdell GA. Coupling of integral acoustics methods with LES for jet noise prediction. Int J Aeroacoust (2004) 3:297–346. doi:10.1260/1475472043499290

CrossRef Full Text | Google Scholar

17. Xue Y, Lyrintzis AS. Rotating Kirchhoff method for 3-dimensional transonic blade-vortex interaction hover noise. AIAA J (1994) 32:1350–9. doi:10.2514/3.12202

CrossRef Full Text | Google Scholar

18. Lyrintzis AS, Koutsavdis EK. Rotorcraft impulsive noise prediction using a rotating Kirchhoff formulation. J Aircraft (1996) 33:1054–61. doi:10.2514/3.47057

CrossRef Full Text | Google Scholar

19. Strawn RC, Biswas R, Lyrintzis AS. Helicopter noise predictions using Kirchhoff methods. J Comput Acoust (1996) 4:321–39. doi:10.1142/s0218396x96000106

CrossRef Full Text | Google Scholar

20. Brentner KS, Farassat F. Analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces. AIAA J (1998) 36:1379–86. doi:10.2514/3.13979

CrossRef Full Text | Google Scholar

21. Wang M, Lele SK, Moin P. Computation of quadrupole noise using acoustic analogy. AIAA J (1996) 34:2247–54. doi:10.2514/3.13387

CrossRef Full Text | Google Scholar

22. Sinayoko S, Wright M, Sandberg R. A generalised Ffowcs-Williams and Hawkings formulation applied to flow simulations with vorti-cal outflow. In: The 22nd congress on sound and vibration. Florence, Italy (2015).

Google Scholar

23. Zhong S, Zhang X. A sound extrapolation method for aeroacoustics far-field prediction in presence of vortical waves. J Fluid Mech (2017) 820:424–50. doi:10.1017/jfm.2017.219

CrossRef Full Text | Google Scholar

24. Colonius T, Lele SK. Computational aeroacoustics: Progress on nonlinear problems of sound generation. Prog Aerosp Sci (2004) 40:345–416. doi:10.1016/j.paerosci.2004.09.001

CrossRef Full Text | Google Scholar

25. Shur ML, Spalart PR, Strelets MK. Noise prediction for increasingly complex jets. Part I: Methods and tests. Int J Aeroacoust (2005) 4:213–45. doi:10.1260/1475472054771376

CrossRef Full Text | Google Scholar

26. Spalart PR, Shur ML, Strelets MK, Travin AK. Initial noise predictions for rudimentary landing gear. J Sound Vib (2011) 330:4180–95. doi:10.1016/j.jsv.2011.03.012

CrossRef Full Text | Google Scholar

27. Spalart P, Shur M. Variants of the Ffowcs Williams-Hawkings equation and their coupling with simulations of hot jets. Int J Aeroacoust (2009) 8:477–91. doi:10.1260/147547209788549280

CrossRef Full Text | Google Scholar

28. Mao Y, Hu Z. Analysis of spurious sound due to vortical flow through permeable surfaces. Aerosp Sci Technol (2020) 96:105544. doi:10.1016/j.ast.2019.105544

CrossRef Full Text | Google Scholar

29. Farassat F. Acoustic radiation from rotating blades - the Kirchhoff method in aeroacoustics. J Sound Vib (2001) 239:785–800. doi:10.1006/jsvi.2000.3221

CrossRef Full Text | Google Scholar

30. Wang B, Zhao QJ, Xu GH, Ye L, Wang JY. Numerical analysis on noise of rotor with unconventional blade tips based on CFD/Kirchhoff method. Chin J Aeronaut (2013) 26:572–82. doi:10.1016/j.cja.2013.04.045

CrossRef Full Text | Google Scholar

31. Felli M, Grizzi S, Falchi M. A novel approach for the isolation of the sound and pseudo-sound contributions from near-field pressure fluctuation measurements: Analysis of the hydroacoustic and hydrodynamic perturbation in a propeller-rudder system. Exp Fluids (2014) 55:1651. doi:10.1007/s00348-013-1651-y

CrossRef Full Text | Google Scholar

32. Mancinelli M, Pagliaroli T, Di Marco A, Camussi R, Castelain T. Wavelet decomposition of hydrodynamic and acoustic pressures in the near field of the jet. J Fluid Mech (2017) 813:716–49. doi:10.1017/jfm.2016.869

CrossRef Full Text | Google Scholar

33. Mancinelli M, Pagliaroli T, Camussi R, Castelain T. On the hydrodynamic and acoustic nature of pressure proper orthogonal decomposition modes in the near field of a compressible jet. J Fluid Mech (2018) 836:998–1008. doi:10.1017/jfm.2017.839

CrossRef Full Text | Google Scholar

34. Rodriguez O. The circular cylinder in subsonic and transonic flow. AIAA J (1984) 22:1713–8. doi:10.2514/3.8842

CrossRef Full Text | Google Scholar

35. Murthy VS, Murthy WC. Detailed measurements on a circularcylinder in cross flow. AIAA J (1978) 16:549–50. doi:10.2514/3.60930

CrossRef Full Text | Google Scholar

36. Xu CY, Chen LY, Lu XY. Large-eddy simulation of the compressible flow past a wavy cylinder. J Fluid Mech (2010) 665:238–73. doi:10.1017/s0022112010003927

CrossRef Full Text | Google Scholar

37. Hong R, Xia Z, Shi Y, Xiao Z, Chen S. Constrained large-eddy simulation of compressible flow past a circular cylinder. Commun Comput Phys (2014) 15:388–421. doi:10.4208/cicp.050513.270513a

CrossRef Full Text | Google Scholar

38. Breuer M. Large eddy simulation of the subcritical flow past a circular cylinder: Numerical and modeling aspects. Int J Numer Methods Fluids (1998) 28:1281–302. doi:10.1002/(sici)1097-0363(19981215)28:9<1281::aid-fld759>3.0.co;2-#

CrossRef Full Text | Google Scholar

39. Lysenko DA, Ertesvåg IS, Rian KE. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFOAM toolbox. Turbul Combust (2012) 89:491–518. doi:10.1007/s10494-012-9405-0

CrossRef Full Text | Google Scholar

40. Smagorinsky J. General circulation experiments with the primitive equations: I. The basic experiment. Mon Weather Rev (1963) 91:99–164. doi:10.1175/1520-0493(1963)091<0099:gcewtp>2.3.co;2

CrossRef Full Text | Google Scholar

41. Rogallo RS, Moin P. Numerical simulation of turbulent flows. Annu Rev Fluid Mech (1984) 16:99–137. doi:10.1146/annurev.fl.16.010184.000531

CrossRef Full Text | Google Scholar

42. Sarkar S. Large-eddy simulation of wake and boundary layer interactions behind a circular cylinder. J Fluids Eng (2009) 131. doi:10.1115/1.3176982

CrossRef Full Text | Google Scholar

43. Breuer M. A challenging test case for large eddy simulation: High Reynolds number circular cylinder flow. Int J Heat Fluid Flow (2000) 21:648–54. doi:10.1016/s0142-727x(00)00056-4

CrossRef Full Text | Google Scholar

44. Najafi-Yazdi A, Bres GA, Mongeau L. An acoustic analogy formulation for moving sources in uniformly moving media. P Roy Soc A: Math Phy (2011) 467:144–65. doi:10.1098/rspa.2010.0172

CrossRef Full Text | Google Scholar

45. Ghorbaniasl G, Lacor C. A moving medium formulation for prediction of propeller noise at incidence. J Sound Vib (2012) 331:117–37. doi:10.1016/j.jsv.2011.08.018

CrossRef Full Text | Google Scholar

46. Farassat F. Derivation of formulations 1 and 1A of Farassat. Hampton: NASA TM, 2007-214853 (2007).

Google Scholar