Hybrid weighted communication network node importance evaluation method

Communication networks are used as an important guarantee for information interaction and efficient collaboration within many fields and systems; however, under information technology conditions, the destruction of a number of nodes in a network may have a great impact on the overall operation of the network. Therefore, it is important to accurately determine the critical nodes in the network to enhance the network’s resistance to destruction. Combining the characteristic attributes of the communication network, a node contribution evaluation matrix is proposed based on the efficiency matrix, from the perspective of node receiving information; a node value evaluation matrix is proposed from the perspective of a node providing information to neighboring nodes, and node importance is calculated by integrating the evaluation results of the two matrices and the node’s own attributes. The algorithm is suitable for directed-weighted network node value evaluation, and the effectiveness and accuracy of the algorithm are verified by comparing other algorithms for a small-scale network. In further experimental validation, a hybrid weighted communication network evolution model based on organizational structured networks is proposed, and networks of different sizes are generated for experimental simulation. The results show that when nodes with high importance are removed from the network, they can cause a rapid decrease in the network efficiency and maximum connectivity, confirming the accuracy of the algorithm in evaluating the importance of nodes and identifying critical nodes in the network.

1 Introduction

Following the rapid development of information technology, communication networks have become an indispensable and important part of many systems and fields [1, 2]. A communication network refers to a complex network with topology and specific functions and is composed of multiple nodes with information transmission functions that are interconnected by communication links. The communication network is the basis for information transmission, close collaboration, and efficient cooperation among the components within the system [3, 4]. Differences in hierarchical relationships, location effects, and information interaction capabilities of the nodes in a communication network result in nodes having different values and varying influence on the whole network [5–7]. Evaluating the importance of nodes in communication networks, detecting critical nodes in the network, and protecting them are important for improving networks’ resilience to damage [8].

At present, evaluating the importance of network nodes is generally based on complex network theory, mainly focusing on the study of undirected and unweighted networks, while results from the study of directed-weighted networks are rare [9–13]. The connection between communication network nodes represents a link for information transmission and defines the direction of information flow; the strength of information interaction between nodes; and the connectivity of communication links, transmission rate, communication capacity, and other various indicators [14, 15]. This causes specificity of the connected edges between nodes, which need to be assigned different weights for consideration; therefore, evaluation methods in undirected and unweighted networks cannot be simply applied to communication networks.

[16] proposed the DWCN_NodeRank metric to evaluate the importance of nodes in directed-weighted networks from the perspective of information transmission based on the idea of the PageRank algorithm. However, the algorithm was not well-distinguished for partial nodes and it converged slowly, making it difficult to guarantee accuracy. Wang et al. [17] constructed multiple influence matrices for directed-weighted networks; however, the algorithm needed to calculate both the shortest path and the number of path entries between nodes, making it highly time-consuming, complex, and difficult to apply to large-scale networks. Ma et al. [3] introduced a mutual information (MI) algorithm [18] to communication networks to measure node importance; however, the algorithm did not take the mutual influence between non-adjacent nodes into account, while the consideration of edge weights was neglected in the calculation process and the measured results were unconvincing. The literature [19–22] used a node importance contribution matrix and a network efficiency matrix to evaluate the value of nodes; however, the former only considered the influence between neighboring nodes, while the latter ignored the weakening effect of intermediate nodes on information transmission when considering the interaction between non-adjacent nodes, and both did not take the directedness of the network into account.

In this article, complex network theory is used to evaluate the importance of nodes in communication networks. To address the problem that most current node importance evaluation algorithms are not applicable to directed-weighted networks, we combine the characteristics of communication networks and, first, complete the construction of a topological model of a communication network. Second, considering the directedness of the network, the importance of nodes in the network is divided into the importance of receiving information from other nodes and the importance generated by providing information to adjacent nodes. From the above two different perspectives, CEM and VEM are proposed to measure the node importance. Finally, a hybrid weighted communication network evolution model based on OSN is proposed to determine the characteristics of communication network hierarchy, and experimental simulations are performed in the model to verify the effectiveness of the algorithm.

2 Communication network and its node importance

2.1 Communication network topology model construction

In communication networks, information transmission between nodes occurs both bidirectionally and unidirectionally, and the weights of two edges in bidirectional communication transmission may not be the same. Based on this, the communication network is abstracted as a hybrid weighted network with both undirected and directed edges [3].

For the convenience of research, the bidirectional link in the communication network, i.e., the undirected edges in the network, is transformed into two directed edges with opposite directions, thus transforming the hybrid weighted network into a directed-weighted network with only directed edges. The weights of communication links represent the flow of information transmitted between nodes, so the principle of similar weights is used [23], i.e., the larger the weight, the stronger the connection between nodes. On this basis, the nodes in the network can then be studied using a directed-weighted network node importance assessment method.

In the directed-weighted network model, $G=\left(\mathit{V},\mathit{E},\mathit{W}\right)$, where $\mathit{V}=\left\{v_1,v_2,\cdots ,v_n\right\}$ is the set of nodes in the network, the number of nodes is n, $\mathit{E}=\left\{e_1,e_2,\cdots ,e_m\right\}$ is the set of directed edges with the number of edges m, $\mathit{W}={\left(w_{ij}\right)}_{n\times n}$ is the edge weight matrix, and if there exists a directed edge pointing from node $v_i$ to node $v_j$, then $w_{ij}$ denotes the weight of the edge, and if not, then $w_{ij}=0$. The node strength can be divided into in-strength $S_{in}\left(i\right)$ and out-strength $S_{out}\left(i\right)$. $S_{in}\left(i\right)$ is the sum of the weights of all edges pointing to node $v_i$, which can be obtained by summing the ith column of $\mathit{W}$ and $S_{out}\left(i\right)$ is the sum of the weights of edges connected from node $v_i$, which can be obtained by summing the ith row of $\mathit{W}$. The total strength of the nodes is $S_i=S_{in}\left(i\right)+S_{out}\left(i\right)$. The connectivity of nodes in a network is usually represented by the adjacency matrix $\mathit{A}={\left(a_{ij}\right)}_{n\times n}$, which can be regarded as a mapping of the edge weight matrix $\mathit{W}$. When $W_{ij}$ is not 0, there exists a directed edge $\left(v_i,v_j\right)$ pointing from $v_i$ to $v_j$, then $a_{ij}=1$, and vice versa, $a_{ij}=0$. In a directed network, $\mathit{A}$ is not always a symmetric matrix, i.e., $a_{ij}$ is not necessarily equal to $a_{ji}$. Summing the ith row of the adjacency matrix $\mathit{A}$ represents the out-degree $D_{out}\left(i\right)$ of node $v_i$ and summing the ith column of A represents the in-degree $D_{in}\left(i\right)$ of node $v_i$.

2.2 Related metrics

Based on the network model constructed above and considering the operational characteristics of the communication network [15, 24, 25], the following definitions are given to measure the individual nodes in the network as well as the network globally.

2.2.1 Node importance metrics

Metric 1: Node efficiency $I_k$ [15]. The average of the sum of the inverse of the distances from a node to other nodes in the network can be calculated as:

$I_k=\frac{1}{n-1}{\displaystyle \sum _{i=1,i\ne k}^n}\frac{1}{d_{ki}},(1)$

where $d_{ki}$ is the shortest path distance from node $v_k$ to node $v_i$. In a weighted network, the closeness of node connections is measured by the weights of the edges between nodes, and, based on the principle of similar weights, the node distance is the minimum value of the sum of the inverse of the weights of the edges contained in the node path; the calculation for which is as follows:

$d_{ki}=\min \left(\frac{1}{w_{k{j}_1}}+\frac{1}{w_{j_1{j}_2}}+\cdots +\frac{1}{w_{j_{n}i}}\right),(2)$

where $j_1,j_2,\cdots ,j_n$ denote the intermediate nodes through the path from node $v_k$ to node $v_i$. If there is no path between nodes $v_k$ and $v_i$, then $d_{ki}\to \infty$. Node efficiency reflects the difficulty of nodes to transmit information to other nodes in the network as well as the contribution of nodes to network information transmission. The larger the value of node efficiency, the greater the role played by nodes in network information transmission.

Metric 2: DWCN_NodeRank (NR). Zhang et al. [16] proposed the NR method, an evaluation metric for the importance of nodes in directed-weighted network; the $NR\left(v\right)$ value of a node is calculated as follows:

$NR\left(v\right)=\frac{1-\sigma }{n}+\sigma {\displaystyle \sum }_{v_i\in V_{in}\left(v\right)}\frac{w\left(v_i,v\right)}{{\sum }_{j=1}^{k_i}w\left(v_i,z_i\right)}NR\left(v_i\right),(3)$

where $\sigma \left(0<\sigma <1\right)$ is the damping coefficient, which indicates the resistance to continue propagation when the information flow reaches a node. The larger the damping coefficient, the greater the benefit of the information flow to the node. $v_i\in V_{in}\left(v\right)$ is the incoming node of node $v$. ${\sum }_{j=1}^{k_i}w\left(v_i,z_i\right)$ denotes the sum of all the connected edge weights with node $v_i$ as the source node, i.e., the out-strength $S_{out}\left(i\right)$ of node $v_i$.The $NR\left(v\right)$ value is calculated by the iterative method, which is related to the in-degree of the node and the proportion of the node to the out-strength of the source node; the larger the $NR\left(v\right)$ value, the more important the node is in the network.

2.2.2 Network global efficiency metrics

Metric 3: Maximum connectivity $C$ [24]. The ratio of the number of nodes contained in the maximum connected subgraph to the total number of network nodes in the directed graph network is called the maximum connectivity, and can be calculated as:

$C=\frac{\max ‖Z_i‖}{n},(4)$

where $Z_i\in G$ denotes a connected subgraph in the network, where a connected path exists between any nodes in the subgraph. $\max ‖Z_i‖$ denotes the number of nodes in the maximum connectivity subgraph of the network and the maximum connectivity $C\in \left.\left(\mathrm{0,1}\right.\right]$ reflects the difficulty of information transmission in the network. When $C=1$ the network is fully connected.

Metric 4: Network efficiency $E$ [25]. The average of the summation of the inverse of the distances of all nodes in the network represents the efficiency of the entire network and is calculated as follows:

$E=\frac{{\displaystyle \sum }_{i\ne j,i,j\in \mathit{V}}\frac{1}{d_{ij}}}{n\left(n-1\right)}(5)$

The higher the efficiency of the network, the smoother the transmission of information in the network and the stronger the connectivity of the network.

3 Node importance evaluation method based on importance evaluation matrix

In complex communication networks, nodes interact with each other through paths composed of directed edges to complete an information interaction. The variability of node connectivity in the network and the fact that the edges connecting nodes have different weights and directions cause the strength of interaction between different nodes and their contribution to the overall information flow efficiency of the network to be strong or weak. The node importance contribution matrix [20] mainly describes the contribution of nodes to adjacent nodes without taking the interaction effects between non-adjacent nodes into account, and it is only researched for undirected networks. The efficiency matrix [22] takes the influence of non-adjacent nodes through the shortest path between nodes into account. However, this method just considers the influence of the nodes in the shortest path on network information transmission and only for undirected networks.

In this article, we believe that the importance of nodes in the process of information transmission in the network is mainly reflected in two aspects: one is the contribution value from other nodes in the network. In a directed network, when there exists a path from node $v_i$ to node $v_j$, information can be transmitted through node $v_i$ to node $v_j$, and node $v_i$ can be considered to make a contribution to node $v_j$. Therefore, the contribution of all nodes in the network to $v_j$ can be used to evaluate the importance of node $v_j$. However, it is not comprehensive enough to use only the contribution degree of other nodes as the basis of measurement. In a directed communication network, there are some nodes which in-degree are 0, and these nodes do not receive information from other nodes, such as from some sub-nodes located at the bottom of the intelligence reconnaissance network. These nodes only transmit information to the higher-level nodes and do not receive information from other nodes; all nodes in the network do not contribute to this node and it is difficult to distinguish the importance of such nodes by only using the above method [26, 27]. Therefore, we believe that another aspect that reflects the importance of a node lies in its ability to provide information to its neighboring nodes. When the amount of information provided by node $v_i$ to its neighboring nodes is greater, the node is more important.

In this article, CEM and VEM are proposed to measure the value of nodes in the above two aspects in directed-weighted networks.

4 Node contribution evaluation matrix (CEM)

For directed-weighted networks, the transmission efficiency between nodes forms the network efficiency matrix $\mathit{E}={\left(e_{ij}\right)}_{n\times n}$, where $e_{ij}=\frac{1}{d_{ij}}$ is the information transmission efficiency between node $v_i$ and node $v_j$. The traditional efficiency matrix does not consider the influence of intermediate nodes contained in the information transmission path on the transmission efficiency, so we redefine the transmission efficiency matrix $\text{EN}$ as follows:

$\mathit{\text{EN}}=\left[\begin{array}{cccc}0& e_{12}{\alpha }^{l_{12}}& \cdots & e_{1n}{\alpha }^{l_{1n}}\\ e_{21}{\alpha }^{l_{21}}& 0& \cdots & e_{2n}{\alpha }^{l_{2n}}\\ ⋮& ⋮& \ddots & ⋮\\ e_{n1}{\alpha }^{l_{n1}}& e_{n2}{\alpha }^{l_{n2}}& \cdots & 0\end{array}\right],(6)$

where $l_{ij}$ is the number of intermediate nodes contained in the shortest path from node $v_i$ to node $v_j$. $\alpha \left(0<\alpha <1\right)$ is the fading rate, which indicates the amount of information remaining when the message continues to propagate backward through each intermediate node. $e_{ij}{\alpha }^{l_{ij}}$ is used to denote the transmission efficiency of information from node $v_i$ to node $v_j$. The higher the transmission efficiency, the smoother the information transmission from node $v_i$ to node $v_j$. Each row of the efficiency matrix $\text{EN}$ is multiplied with the total strength of the corresponding node to obtain the CEM as follows:

${\mathit{H}}_{\text{CEM}}=\left[\begin{array}{cccc}0& e_{12}{S}_1{\alpha }^{l_{12}}& \cdots & e_{1n}{S}_1{\alpha }^{l_{1n}}\\ e_{21}{S}_2{\alpha }^{l_{21}}& 0& \cdots & e_{2n}{S}_2{\alpha }^{l_{2n}}\\ ⋮& ⋮& \ddots & ⋮\\ e_{n1}{S}_n{\alpha }^{l_{n1}}& e_{n2}{S}_n{\alpha }^{l_{n2}}& \cdots & 0\end{array}\right](7)$

where $e_{ij}{S}_i{\alpha }^{l_{ij}}$ is the contribution of node $v_i$ to node $v_j$, which is influenced by the strength of the source node and the transmission efficiency. After obtaining the CEM, the contribution importance of the node $h_{CEM}\left(j\right)$ can be obtained by calculating the contribution of all nodes in the network as follows:

$h_{CEM}\left(j\right)={\displaystyle \sum _{i=1,i\ne j}^n}{e}_{ij}{S}_i{\alpha }^{l_{ij}}(8)$

A larger value of node $h_{CEM}\left(j\right)$ indicates that the more information node $v_j$ receives from other nodes in the network, the more important the node is.

4.1 Node value evaluation matrix (VEM)

The CEM measures the node importance from the point of view that the node receives contributions from other nodes. In this section, the node value is measured from the point of view that the node provides information for its adjacent nodes, and the VEM is proposed as follows:

${\mathit{H}}_{\text{VEM}}=\left[\begin{array}{cccc}0& a_{12}\cdot \frac{w\left(v_1,v_2\right)}{S_{in}\left(2\right)}& \cdots & a_{1n}\cdot \frac{w\left(v_1,v_n\right)}{S_{in}\left(n\right)}\\ a_{21}\cdot \frac{w\left(v_2,v_1\right)}{S_{in}\left(1\right)}& 0& \cdots & a_{2n}\cdot \frac{w\left(v_2,v_n\right)}{S_{in}\left(n\right)}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}\cdot \frac{w\left(v_n,v_1\right)}{S_{in}\left(1\right)}& a_{n2}\cdot \frac{w\left(v_n,v_2\right)}{S_{in}\left(2\right)}& \cdots & 0\end{array}\right](9)$

In this matrix, $a_{ij}$ reflects the connection between nodes, $w\left(v_i,v_j\right)$ denotes the weight of edge $\left(v_i,v_j\right)$, $S_{in}\left(j\right)$ is the in-strength of node $v_j$. The ratio of the two can represent the proportion of the information provided by node $v_i$ to the information received by node $v_j$. The higher the ratio is, the more valuable node $v_i$ is to node $v_j$, so the value importance of node $v_i$ can be expressed as:

$h_{VEM}\left(i\right)={\displaystyle \sum _{j=1,j\ne i}^n}{a}_{ij}\frac{w\left(v_i,v_j\right)}{S_{in}\left(j\right)}(10)$

A higher $h_{VEM}\left(i\right)$ value means the node is more valuable to its adjacent nodes, and the node is more important.

4.2 Evaluation the node importance

CEM and VEM measure the importance of nodes from different perspectives, and obtain the contribution evaluation vector ${\mathit{h}}_{CEM}$ and value evaluation vector ${\mathit{h}}_{VEM}$. The two vectors are normalized and the comprehensive importance of the node is determined by considering the above two measurement methods:

${\mathit{h}}_{\mathit{I}}=\theta \cdot {\mathit{h}}_{\text{CEM}}+\left(1-\theta \right)\cdot {\mathit{h}}_{\text{VEM}}(11)$

Combining Eq. 11–13, the above equation can be expressed as:

$h_I\left(i\right)=\theta \cdot {\displaystyle \sum _{j=1,j\ne i}^n}{e}_{ji}{S}_j{\alpha }^{l_{ji}}+\left(1-\theta \right)\cdot {\displaystyle \sum _{j=1,j\ne i}^n}{a}_{ij}\frac{w\left(v_i,v_j\right)}{S_{in}\left(j\right)},(12)$

where $\theta \left(0<\theta <1\right)$ is an adjustable parameter used to adjust the proportion of evaluation results based on different methods. CEM and VEM have different emphases in evaluating the importance of nodes. The former considers the influence of non-adjacent nodes and evaluates the importance of nodes from the perspective of nodes receiving global network information. The latter only considers the influence of adjacent nodes, and evaluates the importance of nodes from the perspective of nodes providing information locally to the network.

After obtaining the comprehensive importance of the node, it is also necessary to take the node’s own strength information into consideration in the calculation of the node importance. The importance of the node $v_i$ can be finally expressed as:

$I\left(i\right)=h_I\left(i\right)\cdot S_i(13)$

4.3 Algorithm steps and complexity analysis

In a communication network, the most direct form of information exchange and dissemination exists between adjacent nodes; however, when the strength of a node and the efficiency of information transmission are high, this will also have a greater influence on non-adjacent nodes, which makes the evaluation results inaccurate if only node importance is evaluated in terms of nodes receiving or outputting information. Therefore, this article comprehensively considers the characteristics of the above two aspects in a directed-weighted network. The information flow and interaction of the communication network, CEM, and VEM are proposed. Combining the node importance obtained by the two matrixes, a comprehensive evaluation of the node importance is finally realized. The specific steps of the algorithm are as follows.

Step 1:. Preparation stage. According to the network edge weight matrix $\mathit{W}$, the out-strength $S_{out}\left(i\right)$, in-strength $S_{in}\left(i\right)$, and total strength $S_i$ of each node in the network are calculated. Using the Floyd algorithm, the shortest path length $d_{ij}$ between all node pairs in the network and the number of intermediate nodes $l_{ij}$ included are calculated according to Eq. 2.

Step 2:. Constructing CEM and calculating the node contribution importance. Fill the obtained $S_i$, $e_{ij}$, $l_{ij}$ values into the matrix, sum each column element of the matrix, and then convert it into a column vector, thereby obtaining the node contribution evaluation vector ${\mathit{h}}_{CEM}$.

Step 3:. Constructing VEM and calculating the node value importance. Fill the elements $\mathit{W}$ and ${\mathit{S}}_{\text{in}}$ into the corresponding positions of the matrix and sum up each row of the matrix to obtain the node value evaluation vector ${\mathit{h}}_{VEM}$.

Step 4:. Importance integration. Normalize the vectors ${\mathit{h}}_{CEM}$ and ${\mathit{h}}_{VEM}$ and fuse them according to Eq. 11 to obtain the comprehensive importance vector ${\mathit{h}}_{\mathit{I}}$ of the node.

Step 5:. Node importance calculation. The importance of the node $v_i$ is obtained by multiplying the node strength $S_i$ and the node comprehensive importance $h_I\left(i\right)$, according to Eq. 13.The framework chart of the proposed algorithm and a comparison of the two evaluation methods are shown in Figure 1.From the above algorithm steps, the time complexity of the entire algorithm is mainly concentrated in the calculation of the node distance in step 1. The time complexity of the Floyd algorithm is $O\left(n^3\right)$, so the time complexity of the entire algorithm is $O\left(n^3\right)$. Previous studies [19, 20] optimized the design of the Floyd algorithm to reduce the time complexity of the algorithm to $O\left(n^2\right)$, In this article, the improved method in Ref. [20] is adopted and the final computational complexity of the algorithm $O\left(n^2\right)$ is obtained.

FIGURE 1

FIGURE 1. Framework chart of the proposed algorithm and a comparison of the two evaluation methods.

5 Experiment analysis

5.1 Algorithm effectiveness analysis

The ARPA (advanced research project agency) network is a typical network model, which is often used to verify the evaluation results of the importance of complex networks. As shown in Figure 2 the network has 21 nodes and 26 edges. This article takes the directed-weighted ARPA network as an example to analyze the effectiveness of the algorithm employed here. The node deletion (ND) method, NR method (σ = 0.85) [16], MI method [3], our algorithm (α = 0.8, θ = 0.7), and only the evaluation results of the CEM method are used for comparison. The experimental results are shown in Table 1.

FIGURE 2

FIGURE 2. Directed-weighted network obtained by the ARPA network.

TABLE 1

TABLE 1. Results of node importance evaluation in ARPA networks.

From the comparison results in Table 1, the calculation results of the algorithm in this study have a higher distinguishing effect for nodes than the NR method and only the CEM method; the above two methods have the same evaluation results for 8 nodes with an in-degree of 0 in the network, especially for the evaluation of nodes 1, 5, 9, and 16. The above four nodes are located in different positions in the network, and the edge weights of the nodes are different. However, the NR values of the four nodes and the evaluation results using only the CEM cannot effectively distinguish them. Therefore, it is not comprehensive enough to consider the importance of nodes in directed-weighted communication network only from the perspective of nodes receiving contributions from other nodes. Comparing the algorithm in this study with the evaluation results using only the CEM, the first four nodes with the highest importance are the same, and they are all nodes 2, 14, 3, and 19. For the node ranked fifth in importance, the CEM considered to be node 6, and the algorithm in this study considered to be node 15 after the comprehensive VEM. Comparing the evaluation of the above two nodes by the node deletion method, the importance of node 15 is obviously better than node 6. Therefore, the algorithm in this study considers the importance of two aspects of the node, which not only strengthens the distinction of the algorithm for node identification, but also makes the evaluation results more accurate. At the same time, taking the evaluation results of the node deletion method as a reference, comparing our algorithm with the MI method, the evaluation result of our algorithm is more relevant to the node deletion method.

The algorithm based on CEM and VEM measures the importance of nodes from the two aspects of receiving information and outputting information. We proved using examples that the algorithm has better applicability to the directed-weighted network, and the accuracy of measuring the importance of nodes.

5.2 Further analysis in simulated network

5.2.1 Construction of hybrid weighted communication network

Most of the real-world communication networks have an obvious organizational hierarchy [28], such as the combat command network, which has obvious hierarchical characteristics between nodes and contains tree skeletons and implicit connections [29, 30]. Such networks can be classified as Organizational Structure Networks (OSNs) [31]. In order to better simulate the hybrid weighted communication network with organizational structure characteristics, this study proposes an OSN-based hybrid weighted network evolution model for the characteristics of the communication network. The construction process of the model is as follows.

Step 1:. Generate nodes and establish a communication network skeleton with a hierarchical structure. First, add a central node to the network and randomly generate m $\left(m\in \left[a,b\right]\right)$ nodes under the central node; the layer of these nodes is 1. Then, take each node in the first layer as the central node and randomly generate m nodes below. In this step, the number of layers of generated nodes is 2 and this process is repeated until the number of network nodes reaches N.

Step 2:. Assign weights to the skeleton network and define the edge connecting the node and the parent node in the skeleton network as an undirected edge. The edge weight is $w_0\cdot {\beta }^{d_i}$, where $\beta \left(0<\beta <1\right)$ is the weight weakening value and $d_i$ is the layers of child nodes. The lower the number of layers the node is in, the more valuable the connection between the node and the upper-level node; therefore, a higher weight is given.

Step 3:. Generate implicit connections for the skeleton network and assign edges between nodes according to the probability given by the following formula:

$P\left(i,j\right)=e^{-\frac{D_{ij}}{\lambda }}\cdot e^{-\frac{{\left(d_i^2+d_j^2-2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\xi }}(14)$

where $\lambda$ and $\xi$ are adjustable parameters that are used to adjust the probability of implicit connection and $D_{ij}$ is the number of layers of the common parent node of node $v_i$ and node $v_j$. We believe that the lower layers a node is located in, the more frequent the information interaction between nodes, and the greater the probability of generating implicit connections.

Step 4:. Determine the direction and weight of implied edges. The direction of the edge is divided into the following three cases: i) when $d_i<d_j$ the implied edge points to node $v_i$, ii) when $d_i=d_j$ the implied edge is an undirected edge, and iii) when $d_i>d_j$ the implied edge points to node $v_j$. In this study, we believe that implicit connections are generally directed from lower-level nodes to upper-level nodes, that is, nodes with higher layers provide information to nodes with lower layers and newly generated edges are given weights $w_0^2\cdot {\beta }^{\left(d_i+d_j+2\right)}$.

5.2.2 Simulation experiment analysis

Taking the parameters $a=4$, $b=6$, $\lambda =0.8$, $\xi =0.8$, and $\beta =0.7$ in the above network evolution model, three hybrid weighted OSN communication network models with N = 100, 200, 300, 500, and 1000 nodes are generated. Figure 3 shows a simulation network with 100 nodes generated according to the model rules. The lower the number of node layers in the figure, the larger the node. Table 2 shows the number of directed and undirected edges in the three generated networks.

FIGURE 3

FIGURE 3. Hybrid weighted OSN communication network model (N = 100).

TABLE 2

TABLE 2. Distribution of edges in the hybrid weighted network generated by the model.

In order to further verify the effectiveness of the algorithm, according to the ranking results of the importance of the nodes, the nodes in the network are deleted in turn, and the changes of the maximum connectivity $C$ and the network efficiency $E$ of the network are observed. The NR method (σ = 0.85), the MI method, and the CEM are also used as comparisons. In addition to this, we added two different mechanisms of node importance evaluation algorithms for directed-weighted networks: the K-Order Propagation Number (WKPN) algorithm [11] and WVoteRank algorithm [32]. The accuracy of the different evaluation algorithms was further compared in OSN networks by the node deletion method. The experimental results are shown in Figures 4, 5.

FIGURE 4

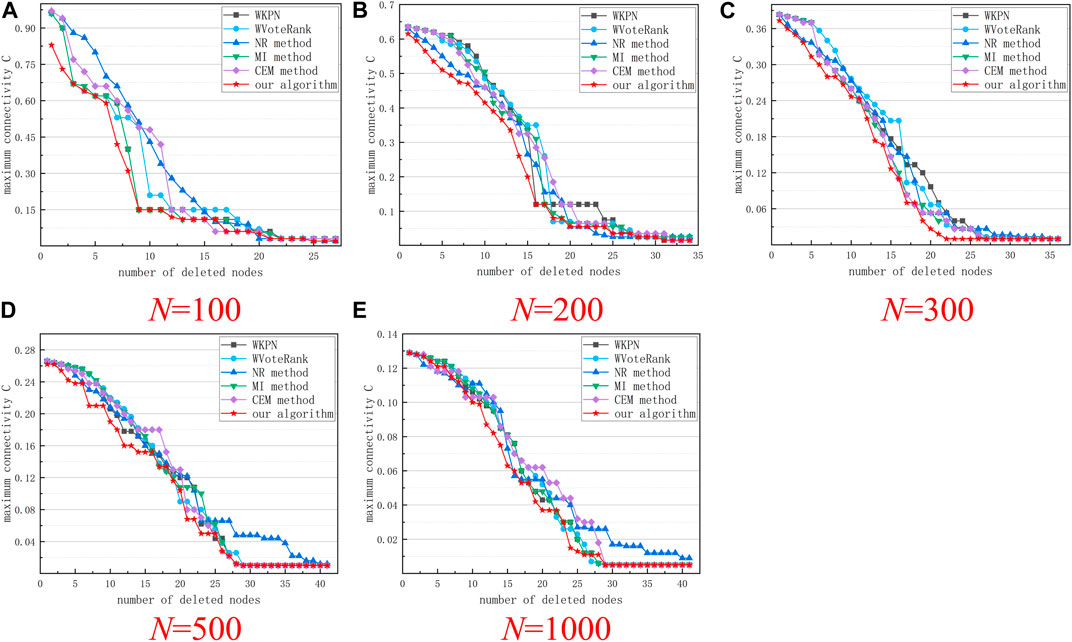
FIGURE 4. Maximum connectivity curves of the network after removing nodes according to the ranking results of different algorithms. (A–E) respectively show the results of five groups of experiments with a network size of 100 to 1000.

As can be seen from Figure 4, removing the nodes in the network according to the sorting results of the algorithm in this study (α = 0.8, θ = 0.7) can rapidly decreases the network connectivity, which has a significant impact on the transmission of information in the network. Compared with other algorithms, this algorithm also has certain advantages. As can be seen from Figure 5, in networks of different scales, the network efficiency decline curves obtained by our algorithm can maintain a rapid downward trend in the initial stage, indicating that after these nodes are removed from the network, the network will be rapidly destroy.

FIGURE 5

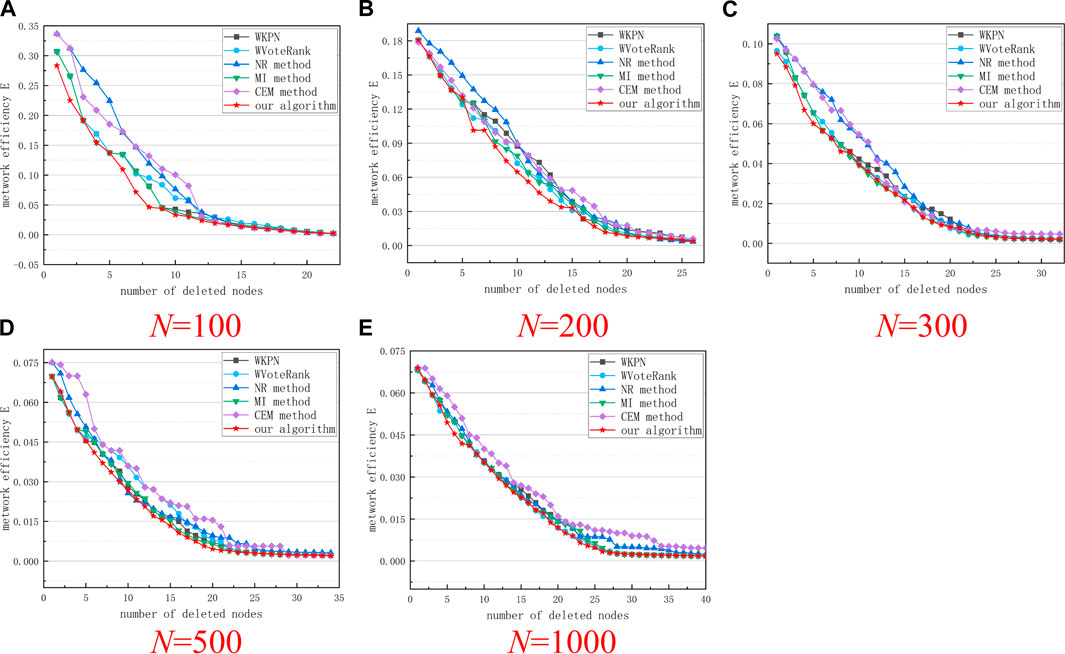
FIGURE 5. Network efficiency changing curves after removing nodes according to the ranking results of different algorithms. (A–E) respectively show the results of five groups of experiments with a network size of 100 to 1000.

As shown in Figures 4, 5, the algorithm in this study deletes the same number of nodes in most cases, which can cause greater damage to the network. Therefore, using the algorithm in this article, and considering the importance of the two aspects of the node, the node can be measured more accurately.

6 Conclusion

In this article, a communication network is abstracted as a hybrid weighted network for analysis and the CEM and the VEM are respectively proposed to evaluate the importance of nodes from the perspective of nodes receiving and output information. The effectiveness of the algorithm is proved in a small network. A hybrid weighted network evolution model based on OSN is proposed to verify the efficacy of the algorithm.

The experimental results show that the algorithm proposed in this study can better distinguish the nodes in the network and is more suitable for evaluating the importance of different types of nodes in a directed network. The validity of the algorithm is verified in the ARPA network. Compared with other directed-weighted network node value evaluation algorithms, the measurement results of the node value of the algorithm in this study have a higher correlation with the measurement results based on the ND method, indicating that the algorithm is more accurate in identifying key nodes in the network. At the same time, according to the sorting result of the algorithm in this study, when the node is deleted from the OSN-based hybrid weighted network model, the maximum connectivity and network efficiency drop rapidly, which shows that the important nodes identified by our algorithm have great value in the network. Through experimental simulation, the accuracy of the algorithm in discovering critical nodes in the network is further verified, which has certain application value for improving the invulnerability of communication networks.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GT and XY performed the analysis. GT validated the analysis and drafted the manuscript. ZY reviewed the manuscript. YL and GC designed the research. All authors have read and approved the content of the manuscript.

Funding

This work was financially supported by the regional foundation of the Shaanxi Natural Science Foundation (2021JM-250).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ren D, Lin Z. Analysis of computer communication network and its security technology framework. In: Innovative computing: Proceedings of the 4th international conference on innovative computing (IC 2021). Singapore: Springer (2022).

CrossRef Full Text | Google Scholar

2. Chen G, Sun P, Zhang J. Repair strategy of military communication network based on discrete artificial bee colony algorithm. IEEE Access (2020) 8:73051–60. doi:10.1109/access.2020.2987860

CrossRef Full Text | Google Scholar

3. Yang Y-Z, Hu M, Huang T-Y. Influential nodes identification in complex networks based on global and local information. Chin Phys B (2020) 29(8):088903. doi:10.1088/1674-1056/ab969f

CrossRef Full Text | Google Scholar

4. Lu Y, Zhao Y-J, Sun F-C, Liang R. Measuring and improving communication robustness of networks. IEEE Commun Lett (2019) 23(12):2168–71. doi:10.1109/lcomm.2019.2941940

CrossRef Full Text | Google Scholar

5. Hu T-R, Wang R, Huang X-H. Node importance evaluation method for command information system communication network. Command Inf Syst Tech (2019) 10(5):95–100.

Google Scholar

6. Lü L, Zhang YC, Yeung CH, Zhou T. Leaders in social networks, the delicious case. PloS one (2011) 6(6):e21202. doi:10.1371/journal.pone.0021202

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Li C, Wang L, Sun S, Xia C. Identification of influential spreaders based on classified neighbors in real-world complex networks. Appl Math Comput (2018) 320:512–23. doi:10.1016/j.amc.2017.10.001

CrossRef Full Text | Google Scholar

8. Wang Z-Q, Zhang Y, Zhang S, Guo Q-Q, Chen S-D. DJ-1 can inhibit microtubule associated protein 1 B formed aggregates. J Beijing Univ Posts Telecommunications (2011) 34(4):38–42. doi:10.1186/1750-1326-6-38

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sun H, Chen D, He J, Ch’ng E. A voting approach to uncover multiple influential spreaders on weighted networks. Physica A: Stat Mech its Appl (2019) 519:303–12. doi:10.1016/j.physa.2018.12.001

CrossRef Full Text | Google Scholar

10. Gao L, Cao J-H, Song T-L, Xing B, Yan X. Evolution model of equipment support system of systems based on complex network theory. Acta Armamentarii (2017) 38(10):2019–30.

Google Scholar

11. Tang P-C, Song C-C, Ding W-W, Ma J, Dong J, Huang L. Research on the node importance of a weighted network based on the K-Order propagation number algorithm. Entropy (2020) 22(3):364. doi:10.3390/e22030364

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li Z-Y, Xiong F, Wang X-M, Chen H-S, Xiong X. Topological influence-aware recommendation on social networks. New York: John Wiley (2019). Complexity.

Google Scholar

13. Xiong F, Shen W, Chen H, Pan S, Wang X, Yan Z. Exploiting implicit influence from information propagation for social recommendation. IEEE Trans Cybernetics (2019) 50(10):4186–99. doi:10.1109/tcyb.2019.2939390

CrossRef Full Text | Google Scholar

14. Yang Z-R, Zhang H, Liu J. Optimization algorithm of military communication network structure under node attack strategy. Syst Eng Elect (2021) 43(7):1848–55.

Google Scholar

15. Chandrasekharan S, Gomez K, Al-Hourani A, Kandeepan S, Rasheed T, Goratti L, et al. Designing and implementing future aerial communication networks. IEEE Commun Mag (2016) 54(5):26–34. doi:10.1109/mcom.2016.7470932

CrossRef Full Text | Google Scholar

16. Zhang K, Li P, Zhu B, Hu M. Evaluation method for node importance in directed-weighted complex networks based on PageRank. J Nanjing Univ Aeronautics Astronautics (2013) 45(3):429–34.

Google Scholar

17. Wang Y, Guo J-L. Evaluation method of node importance in directed-weighted complex network based on multiple influence matrix. Acta Physica Sinica (2017) 66(5):050201. doi:10.7498/aps.66.050201

CrossRef Full Text | Google Scholar

18. Liu Y, Jin J, Zhang Y, Xu C. A new clustering algorithm based on data field in complex networks. The J Supercomputing (2014) 67(3):723–37. doi:10.1007/s11227-013-0984-x

CrossRef Full Text | Google Scholar

19. Xuan Z, Zhang F-M, Li K-W, Hui X-B, Wu H-S. Finding vital node by node importance evaluation matrix in complex networks. Acta Physica Sinica (2012) 61(5):1–7.

Google Scholar

20. Zhou X, Zhang J-W. A new node importance evaluating method for complex weighted networks. Acta Armamentarii (2015) 36(S2):268–73.

Google Scholar

21. Fan W-L, Liu Z-G. An evaluation method for node importance based on efficiency matrix. Chin J Comput Phys (2013) 30(5):714–9.

Google Scholar

22. Fan W-L, Liu Z-G. Ranking method for node importance based on efficiency matrix. J Southwest Jiaotong Univ (2014) 49(2):337–42.

Google Scholar

23. Zhong C, Xiong F, Pan S, Wang L, Xiong X. Hierarchical attention neural network for information cascade prediction. Inf Sci (2023) 622:1109–27. doi:10.1016/j.ins.2022.11.163

CrossRef Full Text | Google Scholar

24. Zhang H, Lü Y-J. Vulnerability of vehicular ad hoc network based on complex network. J Beijing Univ Aeronautics Astronautics (2021) 47(8):1543–9.

Google Scholar

25. Liu J, Xiong Q, Shi W, Shi X, Wang K. Evaluating the importance of nodes in complex networks. Physica A: Stat Mech its Appl (2016) 452:209–19. doi:10.1016/j.physa.2016.02.049

CrossRef Full Text | Google Scholar

26. Liu J-X. A regulative arithmetic on the contingency communication in the damaged military communication networks. Appl Mech Mater (2014) 364:571–2.

Google Scholar

27. Yu J, Xiao B, Cui Y. Cascading failure model and robustness of heterogeneous interdependent combat network. arXiv preprint arXiv:2205.04099 (2022).

Google Scholar

28. Wang W, Mosse D, Cole D, Pickel J-G. Dynamic wireless network reconfiguration for control system applied to a nuclear reactor case study. Proc 26th Int Conf Real-Time Networks Syst (2018) 30–40.

CrossRef Full Text | Google Scholar

29. Li J-C, Jiang J, Yang K-W, Chen Y. Research on functional robustness of heterogeneous combat networks. IEEE Syst J (2019) 13(2):1487–95. doi:10.1109/jsyst.2018.2828779

CrossRef Full Text | Google Scholar

30. Qiu T, Liu J, Si W, Wu DO. Robustness optimization scheme with multi-population Co-evolution for scale-free wireless sensor networks. IEEE/ACM Trans Networking (2019) 27(3):1028–42. doi:10.1109/tnet.2019.2907243

CrossRef Full Text | Google Scholar

31. Li E-Y, Gong J-X, Huang J, Kong J-T. Node importance analysis of complex networks for combat systems based on function chain. J Command Control (2018) 4(1):42–9.

Google Scholar

32. Kumar S, Panda A. Identifying influential nodes in weighted complex networks using an improved WVoteRank approach. Appl Intelligence (2022) 52(2):1838–52. doi:10.1007/s10489-021-02403-5

CrossRef Full Text | Google Scholar