Passive control of wake flow behind a square cylinder using a flat plate

In this study, control over the wake flow of a single square cylinder exercised by a flat plate attached to the rear side of the cylinder is analyzed numerically via the lattice Boltzmann method. The Reynolds number ($Re$) is fixed at 150, and the length of the plate is varied from 0.1 to 8.5. Three distinct flow modes are observed in this study: unsteady, transient, and steady flow in the cases of plate lengths ($L$) in the ranges 0.1 $\le$ $L$ $\le$ 6.5, 6.75 $\le$ $L$ $\le$ 7.5, and 7.75 $\le$ $L$ $\le$ 8.5, respectively. The streamlines exhibit different flow structures, termed hairpin-like, ellipse-like, and elongated bubble-like, at different values of L. Complete wake control is achieved at plate lengths beyond 7.75. This study reveals that the drag and lift coefficients exhibit unsteadiness at short plate lengths in early time steps, but as the plate length increases, unsteadiness slows down and eventually disappears, confirming the steady flow pattern. The mean drag coefficient ($C{D}_m$), Strouhal number ($St$), and root-mean-square value of drag and lift coefficients ($C{D}_{rms}$; $C{L}_{rms}$) are reduced by maximums of 23.5%, 100%, 84.6%, and 99.5%, respectively, as a result of the presence of the plate.

1 Introduction

Numerous natural processes and engineering applications involve fluid flows. These applications include high-rise structures, bridges, submarines, and chimneys, among many others. The dynamics of such flows are so complex that understanding them requires the development and implementation of efficient flow models. Researchers have reported on several experimental and computational approaches to understanding flow action under various flow conditions. The study of flow across a bluff body is mainly concerned with the analysis of flow-induced vibrations and their effects on bluff structures. In addition, the dependency of wake patterns and force characteristics on various parameters such as Reynolds numbers ($Re$) and the size, shape, orientation, and number of bodies in the flow stream is also important. Most published research relating to bluff-body flow dynamics focuses on the flow structure mechanism, vorticity behavior, velocity and pressure fluctuations, variations in fluid forces, and so on. Several experimental and numerical studies regarding the fluid flow characteristics of a single bluff body are worth mentioning [1–7]. Gera et al. [1] conducted a numerical study for two-dimensional (2$d$) unsteady flow around a square cylinder considering $Re$ in the range from 50 to 250 to keep flow laminar. They found that the flow was steady up to $Re$ = 50, minor unsteadiness occurred between $Re$ = 50–55, and after this, range flow became completely unsteady. Golani and Dhiman [2] numerically investigated 2$d$ flow and heat transfer around a circular cylinder at $Re$ = 50–180. Their findings showed that drag coefficient ($CD$), lift coefficient ($CL$), Strouhal number ($St$), and vortex shedding frequency $\left(f_s\right)$ depended strongly on the $Re$. Zdravkovich [3] experimentally measured forces, in a wind tunnel, on a circular cylinder near a plane wall at a range of $Re$ values, 4.8 $\times$ 10⁴ $\le$ $Re$ $\le$ 3 $\times$ 10⁵. He examined the $CD$ and $CL$ and found that the $CL$ was affected by the gap-to-diameter ratio ($S/D$), while the $CD$ was affected by the gap-to-boundary layer thickness ($\delta /D$). Park et al. [4] numerically examined flow past a circular cylinder with $Re$ up to 160. Flow quantities including $St$, $CD$, and $CL$, and base pressure around the cylinder at low $Re$ were recorded. They noted that, as $Re$ increased, the total drag coefficient and pressure drag coefficient $\left(C{D}_P\right)$ also increased. Saha et al. [5] investigated the transitions and chaos in the wake of a square cylinder. They observed steady flow at $Re$ = 40, and periodicity was seen in the wake at $Re$ $>$ 45, while chaos was expected to occur in the range of $Re$ = 500–600. Sohankar et al. [6] investigated 2$d$ and 3$d$ unsteady flow across a square cylinder at $Re$ = 150–500. They observed stable 2d laminar shedding flow at $Re$ = 150, while at $Re$ = 200, the effects of 3$d$ flow appeared. Perumal et al. [7] investigated the properties of 2d flow past an elliptical cylinder. They found that at $Re$ = 78, periodicity appeared more quickly as the cylinder was positioned closer to the entrance of the flow domain. Additionally, it was observed that $f_s$ increased with increase in the blockage ratio.

In addition to the analysis of fluid flow physics around cylinders, many researchers have used various control mechanisms to prevent vortex shedding and reduce fluid forces. It is a well-known fact that vortex shedding and flow-induced forces may result in detrimental effects on structures placed in flow streams. Therefore, through use of various strategies to control these effects, the drastic effects of fluids on solid bodies can be prevented. Flow-control methods are generally classified as either active or passive methods of control. In active control methods, flows around bluff bodies are controlled in various ways, for example, through rotation of the bluff bodies, oscillations, jet-blowing, or suction. The main objective of active control techniques is fluid flow control through the provision of external energy. Active control techniques require relatively complex procedures that supply external power to the flow. In contrast, passive flow control methods involve shape modification or the introduction of additional devices, such as thin plates or small control cylinders of different dimensions and sizes. These techniques are, therefore, energy-free and often easier to implement. Saha and Shrivastava [8] observed the suppression of vortex shedding in a case of flow past a square cylinder at $Re$ = 100 using blowing. At various jet velocities, they found that vortex shedding vanished along with major reductions in $CD$. Abograis and Alshayji [9] studied the reduction of the fluid forces acting on a square cylinder in a laminar flow using a passive control method at $Re$ = 160. They found that placing control plates at both upstream and downstream positions resulted in more reduction in the $CL$ and $CD$ on the cylinder as compared to placement of plates at one side only. Chen et al. [10] tested different shapes of 2$d$ riser fairing for the suppression of vortex-induced vibration (VIV) faced by marine risers. These included water-drop-shaped fairings and caudal fin-like fairings. They concluded that all optimal shapes played important roles in VIV suppression at some range of fluid velocity. Dey and Das [11] analyzed the reduction of forces in the case of flow around a square cylinder by attaching a triangular-shaped thorn. They observed that $CD$ and $CL$ were reduced by 16$\%$ and 46%, respectively, for $Re$ = 100, while for $Re$ = 180, the reduction was 22$\%$ and 60$\%$, respectively. Furquan and Mittal [12] performed numerical simulations for flow around two square cylinders, placed side by side, with attached flexible splitter plates at $Re$ = 100. The effect of separation between the cylinders was also examined. It was found that greater separation between the two cylinders reduced the oscillation amplitude of the plates and increased the oscillation frequency. Ghadimi et al. [13] numerically investigated vortex shedding around a square cylinder with a detached splitter plate at $Re$ = 100–200. They concluded that $CD$ and $f_s$ were significantly reduced by the splitter plate and that vortex shedding was suppressed in the wake. Chauhan et al. [14] experimentally investigated flow over a square cylinder with an attached splitter plate at $Re$ = 485. They observed a reduction in $CD$ and $St$ with increasing plate length. Gallegos and Sharma [15] studied the effects of channel blockage on the dynamic behavior of a flexible plate attached to a circular cylinder. It was observed that the frequency and oscillation amplitude of the flexible plate were greatly affected by the size of the cylinder and the effects of blockages. Ali et al. [16] numerically examined the effect of the control plate on flow past a square cylinder with fixed $Re$ = 150. They identified three flow regimes depending on the length of the control plate: the first flow regime was observed for $L\le 1.0D$, where $St$ decreased with an increase in plate length; the second flow regime was observed for $1.25D\le L\le 4.75D$, where $St$ first increased and then started decreasing with an increase in plate length; and the third flow regime was observed for $L\ge 5D$, where $St$ remained unchanged when the plate length increased. Mansy et al. [17] studied the effect of a splitter plate, placed upstream, on flow around a square cylinder. They considered different velocity ratios at $Re$ = 56 and 200 and found that the splitter plate stabilized the incoming flow to a greater extent at low velocity ratios than at high velocity ratios. Barman and Bhattacharyya [18] studied the effect of dual splitter plates on flow around a square cylinder at $Re$ = 150. They found that splitter plates controlled both drag force and $f_s$. In the case of the plate placed at the upstream location, drag decreased with increased plate length; in the case of the downstream location, vortex shedding suppression was observed. Bao and Tao [19] attached dual splitter plates at the rear surface of a circular cylinder to investigate wake flow behavior. Their findings showed that the use of dual splitter plates caused higher drag reduction and powerful wake suppression at comparatively shorter plate lengths as compared to the use of a single plate. Kumar et al. [20] also investigated the control of drag force on a square cylinder using two detached splitter plates at Re = 150–200. In addition to these studies, other studies have also used new active methods such as a modulated pulse jet (MPJ) [21–23] or plasma operators [24–28] to control fluid flows around solid structures. Several further studies indicating the use of surface acoustic waves and other flow control mechanisms include [29–34].

From the above mentioned discussion and to the best of our knowledge, it can be concluded that fluid flow and wake behavior of a square cylinder with an attached splitter at the rear side have been less investigated and analyzed in the available literature. In particular, there is no corresponding work employing the lattice Boltzmann method (LBM) in the case of such geometry. Therefore, the current investigation was carried out from the perspective of these applications and limitations in the literature. More precisely, the current study emphasized five main points: 1) the development of a flat plate-based control mechanism that is more effective and useful for bluff bodies; 2) understanding of the extent to which such a plate suppresses flow-induced forces and controls the vortex shedding process; 3) comparison of the flow structure around a square cylinder with an attached plate to that around a single square cylinder without a plate in order to thoroughly observe the changes in the flow structure mechanism due to the plate; 4) analysis of the optimum conditions for maximum reduction in fluid forces; and 5) applicability of the lattice Boltzmann method for simulating such flow control problems. It is important to mention here that flow control in the laminar regime is of particular relevance in the case of low Re flows, such as those occurring in electronic devices [35].

2 Numerical method

The governing continuity and momentum equations for the laminar, incompressible, and unsteady fluid flow models considered in the current study are as follows:

$\mathbf{\nabla }.\mathit{u}=0,(1)$

$\frac{\partial \mathit{u}}{\partial t}+\left(\mathit{u}.\mathbf{\nabla }\right)\mathit{u}=-\frac{1}{\rho }\mathbf{\nabla }p+\nu {\mathbf{\nabla }}^2\mathit{u},(2)$

where $\mathit{u}$ is the velocity vector, $\rho$ is the fluid density, $p$ is pressure, $\nu$ is kinematic viscosity, and $t$ is time.

In this study, the well-known mesoscopic-level-based technique, the lattice Boltzmann method, is used to capture the important fluid flow characteristics. The LBM is a non-traditional method, as it replaces the Navier–Stokes equations with the discrete Boltzmann equation in fluid flow simulations. Furthermore, the salient features of the LBM include second-order accuracy, ease of implementation for complex boundaries, parallel computations, quasi-non-linearity, and a relatively easy process for computation of the pressure term; these make it more prominent than other CFD approaches [36]. It is important to mention here that the compressibility and discretization errors play an important role in the overall accuracy of the method. The Mach number (Ma) controls the compressibility error in the LBM, which is of the order O (Ma²). The discretization error in the LBM is of the order O (Ma⁻¹h^δ), where δ represents the order of the underlying finite difference scheme. For stable and accurate computation, we have chosen e = 1, leading to Ma = 0.1. It should be noted that all the results in subsequent sections were obtained using code developed in-house in the FORTRAN language.

It is well-proven in the literature that Eqs 1, 2 can be derived from the discrete Boltzmann equation by using the Chapman–Enskog expansion [37], which is an asymptotic expansion relating statistical mechanics with the theory of continuum fluid dynamics. Due to this fact, in the lattice Boltzmann method, the discrete Boltzmann equation is solved, instead of directly dealing with Eqs. 1, 2, along different lattice links to analyze the fluid flow dynamics. The discrete form of the Boltzmann equation is

$f_j\left(x+v_j\Delta t,t+\Delta t\right)=f_j\left(x,t\right)+\frac{1}{\tau }\left[f_j^{eq}\left(x,t\right)-f_j\left(x,t\right)\right],(3)$

where $j$ ranging from 0 to n indicates the lattice links, the discrete velocity directions are $v_j=e\frac{\Delta x}{\Delta t}$, and the parameter $\tau >0.5$ is the dimensionless relaxation time, which is also termed the stability control parameter. In Eq. 3, $f_j$ is the particle distribution function, whereas $f_j^{eq}$ is the equilibrium distribution function, defined for two-dimensional problems as

$f_j^{eq}=\rho w_j\left[1+3\left(\mathit{v}.\mathit{u}\right)-\frac{3}{2}\left(\mathit{u}.\mathit{u}\right)+\frac{9}{2}{\left(\mathit{v}.\mathit{u}\right)}^2\right],(4)$

where $w_j$ indicate the weights whose values are associated with the nature of lattice models [38].

The macroscopic quantities are linked to $f_j$ by the following constraints:

$\rho \left(x,t\right)={\displaystyle \sum _{j=0}^n}{f}_j={\displaystyle \sum _{j=0}^n}{f}_j^{eq},(5)$

$\rho u\left(x,t\right)={\displaystyle \sum _{j=0}^n}{v}_j{f}_j={\displaystyle \sum _{j=0}^n}=v_j{f}_j^{eq}.(6)$

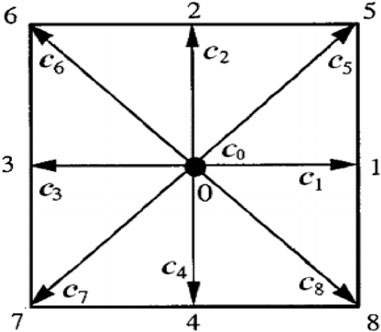
Based on the nature and dimensions of the problem, different models are used in the LBM [38], which, in general form, are specified as DmQn, where m indicates the dimension and n indicates the number of lattice links. In the current study, the D2Q9 model is used, which is a two-dimensional model with a square lattice and nine velocity directions (Figure 1). As mentioned earlier, the weights are specific to the model and are derived by evaluating the moments of distribution functions satisfying certain isotropy conditions [38, 39]. For the D2Q9 model, the weights and velocity directions are

$w_j=\left\{\begin{array}{ll}4/9,& j=0\\ 1/9,& j=\mathrm{1,2,3,4}\\ 1/36,& j=\mathrm{5,6,7,8}.\end{array}\right.(7)$

and

$v_j=\left\{\begin{array}{ll}v\left(\mathrm{0,0}\right),& j=0\\ v\left(\cos \left(\frac{\pi }{2}\left(j-1\right)\right),\sin \left(\frac{\pi }{2}\left(j-1\right)\right)\right),& j=\mathrm{1,2,3,4}\\ \sqrt{2}v\left(\cos \left(\frac{\pi }{2}\left(j-\frac{9}{2}\right)\right),\left(\sin \left(\frac{\pi }{2}\left(j-\frac{9}{2}\right)\right)\right.\right.& j=\mathrm{5,6,7,8}\end{array}\right..(8)$

FIGURE 1

FIGURE 1. Two-dimensional nine-velocity particle model.

3 Problem description

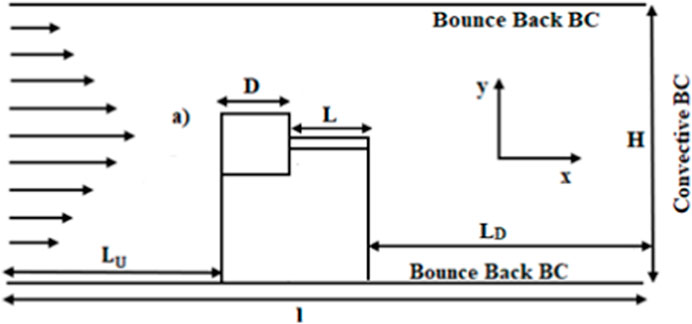
The geometry of the problem under consideration is presented in Figure 2. A fixed square cylinder with an attached flat plate is placed inside a channel having length l and height H. D is the size of the cylinder, and L is the non-dimensional length of the plate. The length of the plate is systematically varied in the range 0.1–8.5. Specifically, plate length is varied with step size 0.1 in the range 0.1–2, with step size 0.2 in the range 2–6, and with step size 0.25 in the range 6–8.5. It is of note that the height of the plate is fixed at 0.2 throughout this study. The height H of the channel is fixed at 21, while the length l of the channel varies depending on the length of the plate. Furthermore, we selected an upstream distance, from the inlet to the cylinder, of L_U = 10 times the size of the cylinder and a downstream distance, from the plate rear end to the outlet, of L_D = 20 times the size of the cylinder. These domain locations are fixed for all chosen lengths of the attached plate. All the domain locations and plate lengths are non-dimensionalized using the size D of the cylinder.

FIGURE 2

FIGURE 2. Schematic flow diagram.

The flow at the inlet is prescribed by the parabolic velocity (u = 4U_in (y/H)(1 – y/H); v = 0). One reason for choosing this velocity profile is that parabolic incoming flows are of practical relevance in most fluid flow problems. A second is that, in most previously published work, a uniform inflow velocity was chosen for flow control-related problems. We attempted to address the flow control mechanism around a square cylinder when the inflow velocity is parabolic. At the upper and lower channel walls and the cylinder surface, a no-slip boundary condition ($u=v=0$) is applied using the bounce-back rule, in which the fluid particles hitting the solid walls bounce back in the opposite direction [38]. A convective boundary condition [40] is used at the outlet position of the channel to ensure that the fluid particles leave the channel without causing significant changes in the flow domain.

4 Grid independence and code validation

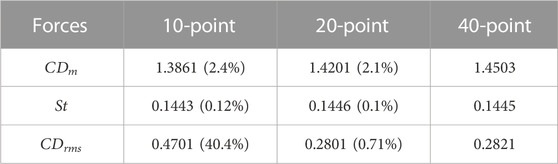
To ensure that the results of the current study were not influenced by the number of grid points on the surface of the square cylinder, a grid independence analysis was performed for flow past a single square cylinder at Re = 150. For this analysis, the mean drag coefficient, Strouhal number, and root-mean-square values of the drag coefficient were computed by dividing the cylinder’s surface into 10, 20, and 40 grid points (Table 1). In comparison to the other schemes, the results for the 20-point grid were more appropriate in terms of computation time and accuracy. Although a 40-point grid may produce more accurate results, it takes a great deal of computation time to reach convergence, and there is not much difference in results between the 20- and 40-point grids. On the other hand, a 10-point grid suffers from a lack of accuracy. Thus, all computations in this study were performed on a 20-point grid, D = 20. Islam et al. [40] and Guo et al. [41] also proposed a 20-point grid for convergence.

TABLE 1

TABLE 1. Comparison of physical parameters for different grid sizes at $\mathit{R}\mathit{e}$ = 150.

To confirm the validity of the code, the computations were performed for flow around a single square cylinder without a plate at Re = 150 to test whether our code is capable of capturing the important physics of flow around bluff bodies. The results are illustrated in terms of instantaneous contours of vorticity, streamlines, drag and lift coefficients, and power spectrum in Figure 3. In the vorticity graph (Figure 3A), the dashed lines indicate the clockwise vortices and the solid lines show the anticlockwise vortices. It can be noted that the incoming flow detaches from the front edges of the cylinder and rolls up to form vortices in the wake of a cylinder. These vortices move alternately in the domain, exhibiting the well-known Kármán vortex street behavior. In the streamlines graph (Figure 3B), a recirculating eddy can be observed adjacent to the rear lower corner of the cylinder, indicating vortex formation due to the merging of shear layers detaching from the upper and lower sides of the cylinder. The alternate movement of vortices is indicated by the waviness of streamlines in the wake region of the cylinder. Due to the unsteadiness in flow, $CD$ and $CL$ exhibit periodic behavior, as shown in Figures 3C, D. The $CD$ value initially oscillates randomly, jumps to a higher value, and then stabilizes after reaching a steady oscillating state over time. Figure 3D shows that $CL$ at Re = 150 starts with minor oscillations, which can be attributed to parabolic inflow velocity, and as time passes, CL signals oscillate in the range [−0.4, 0.4] with a mean value of zero, which confirms the complete unsteadiness in the flow produced. To determine the vortex shedding frequency, the power spectrum analysis of $CL$ is carried out by applying a fast Fourier transformation technique. The resulting $St$ is characterized by a single dominant peak indicating uniform unsteadiness in flow without any chaos (Figure 3E). This flow behavior is commonly observed in the case of bluff bodies [2, 8, 11, 13]. Further information on qualitative and quantitative validation of the code in terms of statistical parameters such as average drag coefficient, Strouhal number, and RMS values of drag and lift coefficients can be found in most of our previously published papers [42–47]. These observations indicate the capacity of our code to capture the important characteristics of fluid flows around bluff bodies.

FIGURE 3

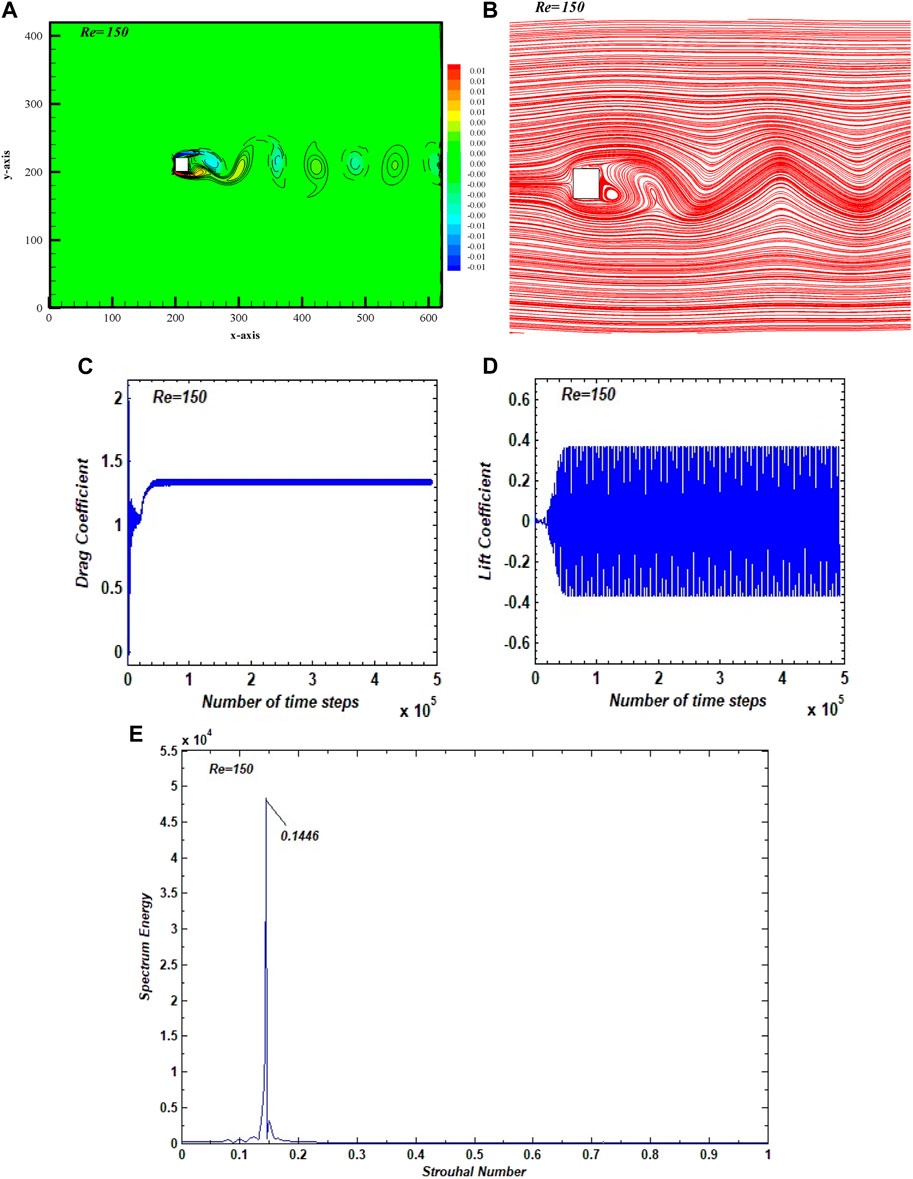
FIGURE 3. (A) Vorticity, (B) streamline, (C) drag coefficient, and (D) lift coefficient. (E) Power spectrum graphs for the flow past a single square cylinder for Re = 150.

5 Results and discussion

Flow around a square cylinder exhibits different modes with fluid force modifications in a case in which a controlling device is introduced in the wake [16, 48]. In the present case, when the length of the plate attached to the cylinder is systematically varied from 0.1 to 8.5, three major flow modes are observed. In accordance with certain characteristics of these flow modes, they are named the unsteady, transitional, and steady flow modes. These classifications depend on the flow structure observed in vorticity contours, behavior of streamlines behavior, temporal variations in the drag and lift coefficients, power spectrum analysis of the lift coefficient, Strouhal number, and RMS values of the drag and lift coefficients. This section presents only representative cases for each flow mode, keeping in mind the fact that all simulation results cannot be included in the manuscript for purposes of brevity and to avoid repetition. The effect of plate length on important flow parameters such as $C{D}_m$, $St$, $C{D}_{rms}$, and $C{L}_{rms}$ is also analyzed and compared to the values of these parameters in the case of a single cylinder to examine the trend in fluid force suppression.

5.1 Flow mode analysis

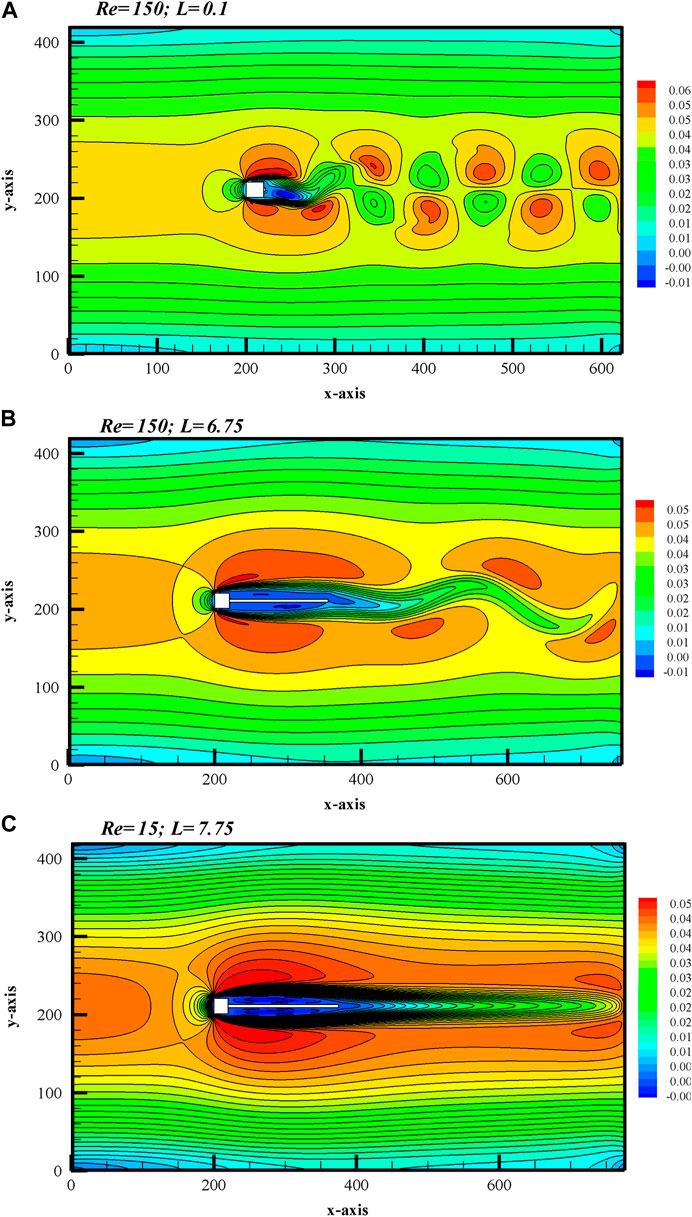
Figures 4A–F show observed vorticity contours for the different flow modes, corresponding to different plate lengths, at Re = 150. For the values of plate length $L$ = 0.1–6.5, a completely developed unsteady flow can be observed (see Figures 4A, B). At smaller plate lengths (less than 1.0), the shear layers separated from upstream corners of the cylinder roll up at a moderated distance from the plate tip, but as the plate length increases, the roll up of shear layers occurs immediately after the tip of the plate to form vortices. These vortices move alternately in the wake forming the von Kármán vortex street, which is a very common flow pattern in the case of single bluff bodies. Resilient vortex shedding with larger recirculation regions can be seen at smaller plate lengths.

FIGURE 4

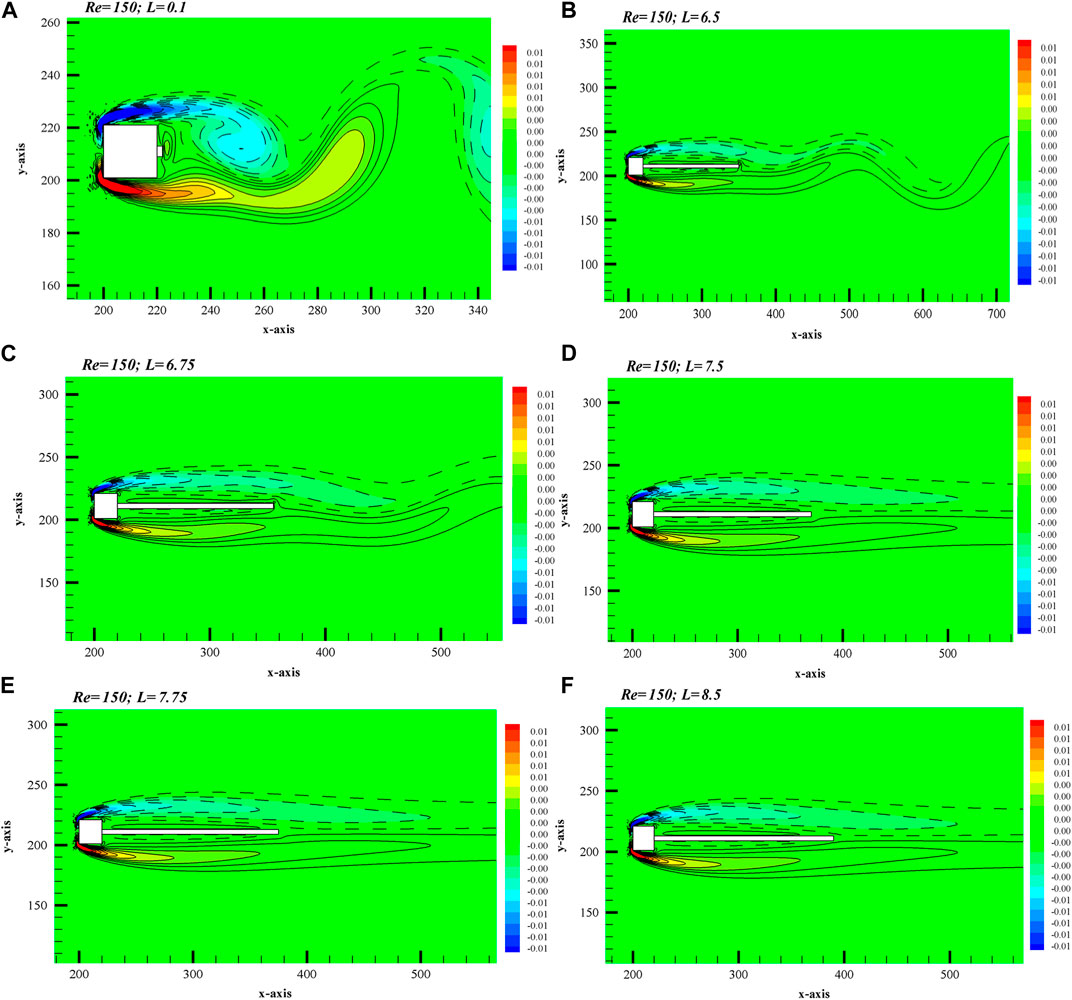
FIGURE 4. Vorticity graphs corresponding to different flow modes: (A,B) Unsteady, (C,D) Tranisent, and (E,F) Steady flow mode.

With each increment in plate length, the cross-wake region is minimized and comes closer to the plate surface. Due to the increased length of the plate, the merging of shear layers of opposite signs is delayed. It seems that the plate gradually controls the unsteadiness in flow. With plate lengths beyond 6.5, the transitional flow mode can be observed in the range $L$ = 6.75–7.5 (Figures 4C, D). The flow in the wake region is initially steady, thus generating a longer shear layer, and minor oscillations in shear layers occur near the outlet of the channel. With these minor oscillations, the unsteady flow seen at smaller plate lengths, seems to be in a transitional phase toward steadiness, which leads to the first Hopf bifurcation. This is evidence that the plate attached to the cylinder has systematically controlled the unsteadiness in flow.

With a further increment in plate length ($L$ = 7.75), it can be observed that a second Hopf bifurcation arises, which results in the transitional flow being turned into a steady flow, and vortex shedding completely disappears (Figures 4E, F). The shear layers emerge only horizontally, without any cross-flow variations, and exhibit symmetry about the plate. Saha and Shrivastava [8] also observed similar flow modes while working on flow control around a square cylinder using the jet-blowing technique. It should be noted that the upper bound of $L$ = 8.5 for steady flow is according to the plate length cases considered in the current study. In general, it can be inferred that the steady flow mode occurs for all $L$ ≥ 7.75. Ali et al. [16] also categorized wake flow into three different regimes depending on the length of plate attached to a square cylinder. Finally, Shahab et al. [49] also characterized the flow around a square cylinder with an attached upstream T-shaped control plate into three different flow regimes.

Figures 5A–C show the streamlines corresponding to different flow modes observed from vorticity contours. In Figure 5A, the streamline pattern indicates periodic flow at the down-wake region for plate length $L$ = 0.1. The region of formation of vortices is indicated by a recirculating bubble that resembles a hairpin-like structure. The hairpin vortex model was first reported by Dousset and Pothérat [50] in the wake of a truncated cylinder positioned in a duct. Another tiny recirculating bubble also appears near the lower back corner of the cylinder due to the merging of shear layers detached from the upper and lower sides of the cylinder. An almost similar streamline trend was observed in the case of the bare cylinder, which indicates that, at these shorter lengths, the plate is unable to modify the fluid flow movement. Furthermore, the cross-flow variation in streamlines in the wake of the cylinder is evidence of the von Kármán vortex street observed from the vorticity graph (Figure 4A). Figure 5B shows the representative case of the transitional flow mode observed at plate lengths in the range $L$ = 6.75–7.5. From Figure 5B, it can be seen that the unsteadiness in flow is abridged by the plate, due to which the hairpin-like structure disappears, and instead, an elongated bubble shape appears, similar to an ellipse-like structure that remains attached to both the upper and lower sides of the plate. The length of the bubbles increases in the direction of flow, while wake width decreases in a cross-flow direction contrary to what is seen at $L$ = 0.1. Additionally, the cross-flow variation in streamlines adjacent to the tip of the plate seems to be shortened as compared to the unsteady flow case ($L$ = 0.1). Graphs illustrating the streamlines conforming to the steady flow mode are presented in Figure 5C for plate length $L$ = 7.75. In this case, two stable, symmetrical, and long recirculation zones appear at the upper and lower sides of the plate, and the waviness in streamlines that is observed in the case of unsteady and transitional flow modes disappears, which indicates a completely steady flow mode (Figure 5C).

FIGURE 5

FIGURE 5. Streamlines graphs corresponding to different flow modes: (A) Unsteady, (B) Tranisent, and (C) Steady flow mode.

Figure 6; Figure 7 show the time-dependent variations in $CD$ and $CL$, respectively, for the different flow modes discussed above. Upon closer examination, the change in behavior of these force coefficients reveals a significant effect of plate length on these force coefficients. In particular, the frequency and amplitude of both $CD$ and $CL$ decrease with increase in the length of the plate. As illustrated in Figure 6A, $CD$ oscillates randomly at the initial stages. Subsequently, its magnitude increases and settles into an unsteady stable state at a time step of approximately 0.5 $\times$ 10⁵ (see the close-up view in Figure 6A). At similar plate lengths, $CL$ exhibits periodicity caused by an alternating trend of positive and negative vortices at shorter plate lengths (Figure 7A). This starts with minor variations initially, confirming the initial parabolic nature of the incoming flow. These minor oscillations jump to high-amplitude variations at nearly 0.5 $\times$ 10⁵ time steps with almost the same amplitude. With the gradual increase in plate length, the amplitude of both $CD$ and $CL$ drops. This trend can be attributed to the increasing length and decreasing width of the wake, observed from the vorticity and streamline graphs, owing to the transitional flow mode (Figure 6B; 7B). It is evident from these figures that, in this flow mode, the amplitude of both of these force coefficients is significantly decreased as compared to the case of the unsteady flow mode, whereas at $L$ = 7.75, both $CD$ and $CL$ turn out to be constant without any degree of variation owing to the steady flow mode. The minor random fluctuations seen initially are due to randomness in the initial iterations of the data (Figure 6C; 7C). This constant behavior of force coefficients is due to the fact that the plate fully controls the vortex shedding process, and as a result, the fluid forces are also suppressed completely. It is a well-known fact that drag force is induced by the fluid on the bluff body due to pressure and viscous forces. Furthermore, according to Dey and Das [11], the periodic variation in drag coefficient occurs mainly due to the formation of vortex shedding, because vortex shedding results in periodic pressure variations. In the present case, due to the attached plate, with a sufficiently long length, vortex shedding is unable to develop, which is why the periodicity of drag force disappears.

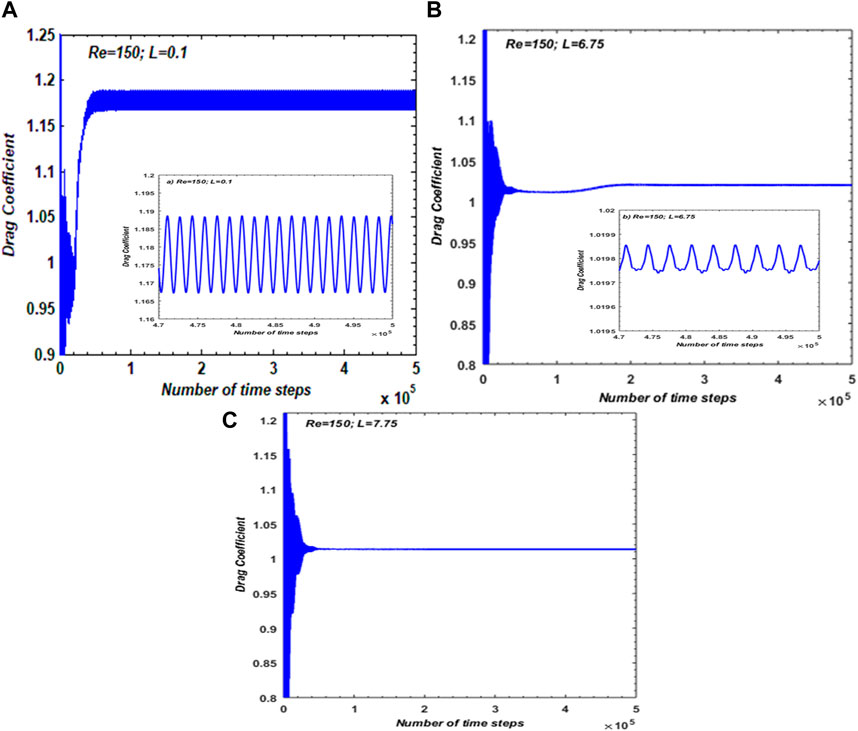
FIGURE 6

FIGURE 6. $\mathit{C}\mathit{D}$ graphs corresponding to different flow modes: (A) Unsteady, (B) Tranisent, and (C) Steady flow mode.

FIGURE 7

FIGURE 7. $\mathit{C}\mathit{L}$ graphs corresponding to different flow modes: (A) Unsteady, (B) Tranisent, and (C) Steady flow mode.

The power spectra of $CL$ corresponding to different plate lengths (and, hence, flow modes) are shown in Figures 8A–C. Since for plate lengths 0.1 $\le$ $L$ $\le$ 6.5, periodicities are observed in $CL$ because of alternate movement of vortices, the power spectrum graphs show a single peak for this range, indicating that the primary vortex shedding frequency is dominant for all cases of unsteady flow mode (Figure 8A). According to Dey and Das [11], the single peak in the lift coefficient spectra indicates the periodic nature of the flow. The values of $St$, corresponding to the shedding frequencies, are also given on power spectrum graphs peaks. It can be observed that with each increment in the length of the plate attached at the downstream location, the spectrum energy and frequency of shed vortices are both reduced as the interaction between the shear layers is delayed, and thus, the $St$ starts dropping. A representative case of the power spectrum graph for transitional flow mode is shown in Figure 8B at $L$ = 6.75. There is only one prominent dominant peak, with an $St$ value of 0.0694, significantly less than that at $L$ = 0.1. This shows that the distortion in wake flow is sufficiently controlled by the plate. In the case of steady flow ($L$ = 7.75), the fact that no oscillations are observed in $CL$ accounts for the power spectrum graph indicating an almost flattened graph without a prominent peak. In the steady flow case, the power spectrum peak does not appear, and hence, the value of $St$ cannot be calculated because of the absence of vortex shedding. 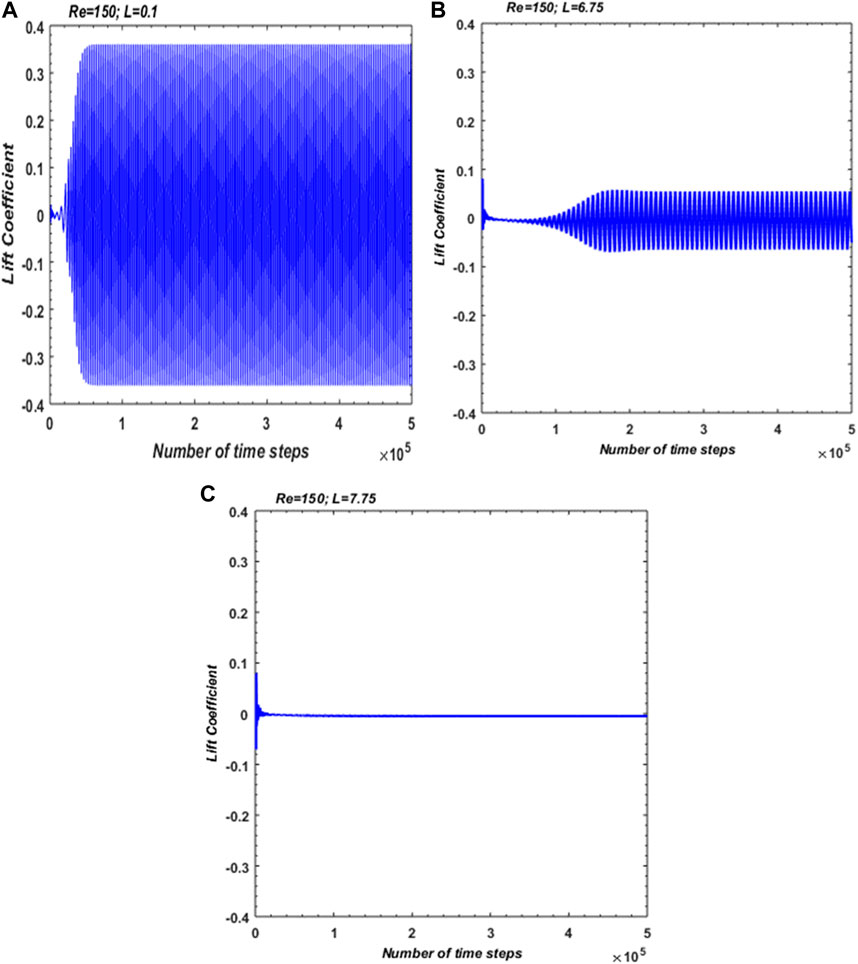This interpretation indicates that the different flow modes observed on the basis of vorticity and streamlines are also well-evidenced by the power spectra of $CL$.

FIGURE 8

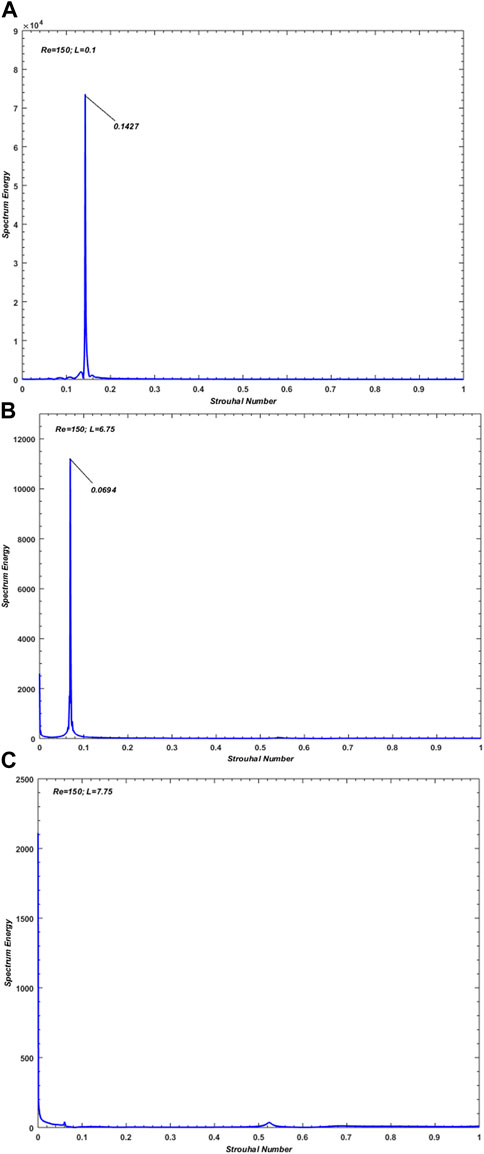
FIGURE 8. Power Spectrum graphs corresponding to different flow modes: (A) Unsteady, (B) Tranisent, and (C) Steady flow mode.

5.2 Statistical analysis of physical parameters

In this section, the effects of plate length on physical parameters such as $C{D}_m$, $St$, $C{D}_{rms}$, and $C{L}_{rms}$ are discussed.

The variations in $C{D}_m$, $St$, $C{D}_{rms}$, and $C{L}_{rms}$ against the different plate lengths are shown in Figure 9. Figure 9A shows a gradual decrement in $C{D}_m$ as plate length increases from $L$ = 0.1 to $L$ = 7.75. As described earlier, the variations in drag force are directly associated with pressure variations around the sides of the cylinder. Therefore, the minimization of drag force can be attributed to pressure control by the plate. The maximum value of $C{D}_m$ is 1.1666 at $L$ = 0.1, where an unsteady flow pattern is observed. $C{D}_m$ then drops gradually with increments in plate length until it reaches its minimum value of 1.0096 at L = 7.75, where the flow changes its behavior from the transient to steady mode. From the vorticity graphs, in the range $L$ = 6.75–7.5, the transitional flow mode is observed. $C{D}_m$ decreases monotonically with increments in the value of $L$ in this range also. In the range $L$ = 7.75–8.5 (the case of steady flow mode), it can be observed that the $C{D}_m$ values are almost constant. This indicates that the plate attached to the cylinder significantly minimizes the drag force. Dousset and Pothérat [50] reported that as the flow modes changes from unsteady to steady, the CD_m decreases, and a similar trend can also be seen in Figure 9A.

FIGURE 9

FIGURE 9. Variation of (A) average $\mathit{C}\mathit{D}$, (B) $\mathit{S}\mathit{t}$, (C) $\mathit{C}{\mathit{D}}_{\mathit{r}\mathit{m}\mathit{s}}$ and (D) $\mathit{C}{\mathit{L}}_{\mathit{r}\mathit{m}\mathit{s}}$ with plate length.

Figure 9B represents the variations in $St$ under the effects of different plate lengths. The maximum value of $St$ is 0.1431, which can be observed at $L$ = 0.1. It is important to mention here that at this sufficiently short plate length, the incoming flow interacts strongly with the cylinder, and the amplitude of the $CL$ cycle is also at its maximum at this plate length as compared to all other plate lengths. This is why $St$ is also at its maximum here; however, with increasing plate lengths, $St$ drops gradually, except in the range of $L$ = 1.1 to 2.0, where it first increases and then decreases, but the value of $St$ in this range is still smaller than its value at $L$ = 0.1. The reason for this behavior of $St$ is that cross-flow variations of shear layers are minimized due to increasing plate length, which results in a reduction in vortex shedding frequency and hence in $St$ values. This graph also shows that the $St$ values are higher in the unsteady flow mode as compared to the transitional and steady flow modes. For the steady flow mode ($L$ = 7.75–8.5), $St$ values are not shown due to the fact that here the vortex shedding stops due to significantly higher plate lengths, and there is no variation in lift force. Islam et al. [40] also reported similar behavior of $St$ for different plate lengths. According to Ali et al. [16], with a plate attached to a cylinder, $St$ decreases for $L\le 1.0D$; for $1.25D\le L\le 4.75D$, $St$ first increases and then starts decreasing; and for $L\ge 5D$, $St$ remains unchanged when the length of the plate increases.

The variation in $C{D}_{rms}$ against different plate lengths is shown in Figure 9C. This graph shows that $C{D}_{rms}$ values do not follow a regular pattern of behavior (increasing or decreasing) as was observed in case of $C{D}_m$ and $St$. The value increases at first, but a sudden fall in values of $C{D}_{rms}$ can be seen for increasing plate lengths. The minimum value of $C{D}_{rms}$ is 0.0518 at $L$ = 0.1. In the range $L$ = 1–7.5, $C{D}_{rms}$ shows mixed (increasing or decreasing) behavior. It is of note that this range of $L$ corresponds to the unsteady and transitional flow modes. This graph also indicates that the maximum value of $C{D}_{rms}$ of 0.0924 occurs at $L=$ 8.5, where steady flow is observed (see Figure 9C).

Figure 9D shows $C{L}_{rms}$ as a function of plate length for lengths in the range $L$ = 0.1–8.5. For the unsteady flow mode ($L$ = 0.1–6.5), $C{L}_{rms}$ initially decreases with increase in plate length in the range $L$ = 0.1–1.9. After that point, it increases up to $L$ = 3.2. After that, a consistent decrease can be seen with each increment in plate length, except at $L$ = 6.5, which produces a slightly higher value. It is of note that at this particular value of the $L$, the unsteady flow pattern changes to the transitional flow pattern. For $L$ = 6.75–7.5, the value exhibits decreasing behavior and then settles to a constant value in the range $L$ = 7.75–8.5, where steady flow is observed. A maximum value of 0.2496 for $C{L}_{rms}$ can be observed at $L$ = 0.1 and a minimum value of 0.0014 at $L$ = 8.5. This indicates that the plate attached to the cylinder has sufficiently reduced the $C{L}_{rms}$ value, which is mainly due to the control of cross-flow variations offered by the plate.

5.3 Analysis of reduction in physical parameters

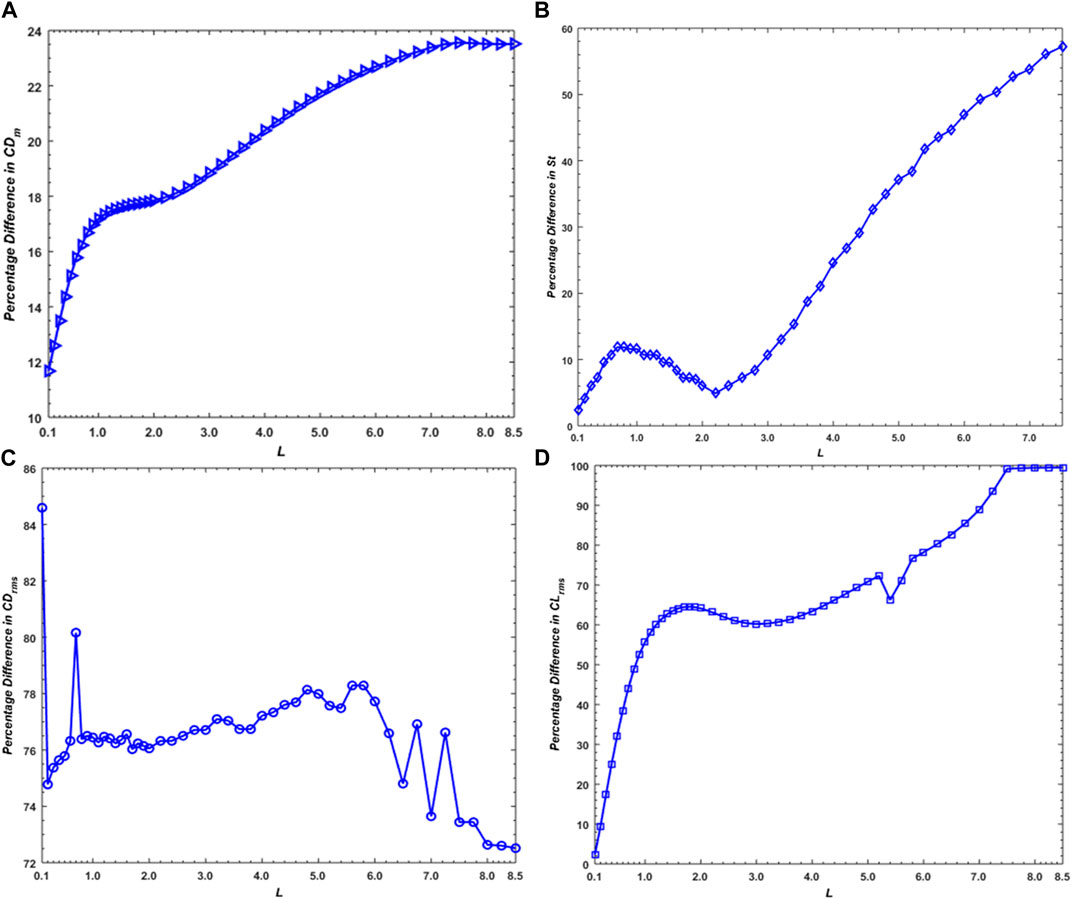
Figure 10 shows the percentage differences in $C{D}_m$, $St$, $C{D}_{rms}$, and $C{L}_{rms}$ of a square cylinder with and without the flat plate. The purpose of the comparison is to examine how the plate attached at a downstream location affects the $C{D}_m$, $St$, $C{D}_{rms}$, and $C{L}_{rms}$ of a square cylinder.

FIGURE 10

FIGURE 10. Percentage difference graphs: (A) $\mathit{C}{\mathit{D}}_{\mathit{m}}$, (B) $\mathit{S}\mathit{t}$, (C) $\mathit{C}{\mathit{D}}_{\mathit{r}\mathit{m}\mathit{s}}$, and (D) $\mathit{C}{\mathit{L}}_{\mathit{r}\mathit{m}\mathit{s}}$.

Note that the values of $C{D}_m$, $St$, $C{D}_{rms}$, and $C{L}_{rms}$ in the SCWP case are 1.3208, 0.1466, 0.3362, and 0.2528, respectively. It is important to note in Figure 10 that reduction in physical parameters occurs at all plate lengths, which indicates that attaching a flat plate to a square cylinder always minimizes these fluid force parameters. Figure 10A shows the reduction in $C{D}_m$ against various plate lengths considered in this study. With each increment in plate length, the percentage reduction in $C{D}_m$ as compared to the SCWP case increases. This implies that as plate length increases, the drag force that the fluid exerts on the cylinder surfaces is decreased due to the weakening of vortices. The minimum reduction in $C{D}_m$ (of 11.7%) can be seen at $L$ = 0.1, where unsteady flow mode is observed, while the maximum reduction value (of approximately 23.5%) can be seen at $L$ = 8.5, where steady flow mode is observed. The reason for this maximum reduction is that the vortex shedding is completely controlled by the plate, resulting in no disruptions in flow and no oscillations in $CD$. Dey and Das [11] reported a maximum reduction of 16% and 22% in the drag coefficient of a square cylinder at $Re$ = 100 and 180, respectively, when a triangle-shaped thorn.

Similar to $C{D}_m$, $St$ is also significantly reduced due to the plate, as shown in Figure 10B. For the unsteady flow mode ($L$ = 0.1–6.5), it can be observed that $St$ undergoes a minimum reduction of 2.4% at $L$ = 0.1, and in this range, the maximum reduction is 43.5% at $L$ = 6.5. Subsequently, the flow pattern changes from unsteady to transitional mode at $L$ = 6.75, and in this flow mode ($L$ = 6.75–7.5), the $St$ value is reduced by 57% in comparison to the case of the single cylinder without the plate (SCWP). In the range $L$ = 7.75–8.5, where steady flow mode is observed, a 100% reduction in $St$ can be seen. It is of note that the reduction in $St$ is directly associated with $CL$ due to the fact that, in the current study, $St$ is computed by applying a fast Fourier transform to $CL$ signals. According to Dey and Das [11], a maximum reduction of 46% and 60% in $CL$ of a square cylinder due to use of a triangular thorn occurs at $Re$ = 100 and 180, respectively. Ali et al. [16] also observed reduction in $St$ with increments in splitter plate lengths.

From Figure 10C, it can be seen that the highest-percentage reduction as compared to the SCWP in the case of $C{D}_{rms}$ is 84.6%, which occurs in the unsteady flow mode range ($L$ = 0.1–6.5), while the minimum reduction of 72.5% occurs at plate length $L$ = 8.5, where steady flow mode is observed. For $C{D}_{rms}$, the percentage difference values randomly fluctuate (either increasing or decreasing) without following any consistent trend. This indicates that the $C{D}_{rms}$ values are greatly influenced by change in the flow structure mechanism in the wake due to addition of the plate.

Figure 10D shows that in the unsteady flow mode range ($L$ = 0.1–6.5), $C{L}_{rms}$ is reduced from its values in the SCWP case by a minimum of 2.4% and a maximum of 71%. Furthermore, significant reduction in $C{L}_{rms}$ occurs in the transitional flow mode range ($L$ = 6.75–7.5) as compared to the unsteady flow mode range ($L$ = 6.75–7.5). In contrast, in steady flow mode, when the length of plate increases, approximately a 99.5% reduction in $C{L}_{rms}$ can be observed up to $L$ = 8.5.

5.4 Effect of the plate on velocity fluctuations

The effect of increasing plate length on horizontal velocity fluctuations is depicted in Figures 11A–C, corresponding to the three observed flow modes as representative cases. Similar to the cases of other fluid flow parameters, these graphs also indicate the damping of velocity due to increasing plate length. Figure 11 shows the maximum velocity at the front corners of the cylinder regardless of increasing plate length. This is due to detachment of shear layers from the front corners of the cylinder. The minimum velocity can be observed in the wake region adjacent to the cylinder, which is due to the shielding effect of the cylinder. The velocity is then distributed randomly as the fluid flows in the wake of the cylinder. The plate plays a role in stabilizing the randomness of velocity, and the steady flow region and minimum velocity region are enlarged as its length increases. At L = 0.1, the velocity fluctuates unsteadily; this is then sufficiently controlled by the plate at L = 7.75 owing to the establishment of steady flow mode.

FIGURE 11

FIGURE 11. Velocity contours for (A) unsteady, (B) transient, and (C) steady flow modes.

6 Conclusion

The current study investigated the capacity of a flat plate attached to the rear side of a square cylinder to control the fluctuating forces and regulate vortex shedding using the lattice Boltzmann method. The plate length was varied in the range 0.1 $\le$ $L$ $\le$ 8.5, and the Reynolds number was fixed at 150. The effects of the plate on flow characteristics were observed in terms of vorticity contours, streamline visualization, variation of time-dependent force coefficients, energy spectrum, and velocity variations. In addition, the influence of plate length on major flow parameters such as $C{D}_m$, $C{D}_{rms}$, $C{L}_{rms}$, and $St$ was also investigated. Furthermore, the percentage difference in these values was calculated by comparing the values of these parameters to those in the case of a single square cylinder without the plate. Some of the key findings of this study are as follows:

1  Depending on the plate length, three different flow modes were observed: unsteady flow ($L$ = 0.1–6.5), transitional flow ($L$ = 6.75–7.5), and steady flow ($L$ = 7.75–8.5). In the unsteady flow mode, vortices exhibited von Kármán street behavior in the wake of the cylinder starting from the trailing edge of the plate. For the transitional flow mode, minor transverse oscillations in the wake were observed near the exit of the computational domain. However, vortex shedding in the wake region was observed to be completely suppressed for the steady flow mode.

2  The amplitudes of the drag and lift force coefficients were found to be significantly reduced as plate length gradually increased and eventually became constant in the steady flow mode.

3  For the unsteady and transitional flow modes, the power spectrum of CL exhibited a single peak owing to the chaos-free behavior of the flow. However, due to the steadiness in $CL$, no peak was observed in the steady flow mode.

4  As plate length increased, flow parameters such as $C{D}_m$, $C{D}_{rms}$, and $St$ were observed to decrease in general, but $C{L}_{rms}$ showed a mixed trend. It was observed that when the plate was attached downstream of the cylinder, the values of $C{D}_m$, $St$, $C{D}_{rms}$, and $C{L}_{rms}$ values were reduced by a maximum of 23.5%, 100%, 84.6%, and 99.5%, respectively.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

WA, AM, and SI performed modelling, computed results and prepared initial draft of manuscript. HR, IK, SN, and AM reviewed the draft for improvement. AM and IK improve results. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Gera B, Pavan K, Singh RK. CFD analysis of 2D unsteady flow around a square cylinder. J Appl Eng (2010) 1(3):602–10.

Google Scholar

2. Golani R, Dhiman AK. Fluid flow and heat transfer across a circular cylinder in the unsteady flow regime. J Eng Sci (2014) 3(3):08–19.

Google Scholar

3. Zdravkovich MM. Forces on a circular cylinder near a plane wall. Appl Ocean Res (1985) 7(4):197–201. doi:10.1016/0141-1187(85)90026-4

CrossRef Full Text | Google Scholar

4. Park J, Kwon K, Choi H. Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160. KSME Int J (1998) 12(6):1200–5. doi:10.1007/bf02942594

CrossRef Full Text | Google Scholar

5. Saha AK, Muralidhar K, Biswas G. Transition and chaos in two-dimensional flow past a square cylinder. J Eng Mech (2000) 2000(126):523–32. doi:10.1061/(asce)0733-9399(2000)126:5(523)

CrossRef Full Text | Google Scholar

6. Sohankar A, Norberg C, Davidsona L. Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys Fluids (1999) 11(2):288–306. doi:10.1063/1.869879

CrossRef Full Text | Google Scholar

7. Perumal DA, Kumar GVS, Dass AK. Lattice Boltzmann simulation of viscous flow past elliptical cylinder. J Mech Eng (2012) 4(3):127–39.

Google Scholar

8. Saha AK, Shrivastava A. Suppression of vortex shedding around a square cylinder using blowing. Sadhana (2015) 40(3):769–85. doi:10.1007/s12046-014-0331-9

CrossRef Full Text | Google Scholar

9. Abograis AS, Alshayji AE. Reduction of fluid forces on a square cylinder in a laminar flow using passive control methods. In: COMSOL Conference in Boston (2013).

Google Scholar

10. Chen M, Liua X, Liu F, Lou M. Optimal design of two-dimensional riser fairings for vortex-induced vibration suppression based on genetic algorithm. Fluid Dyn (2018) 1–25. arXiv:1801.03792.

Google Scholar

11. Dey P, Das AK. Numerical analysis of drag and lift reduction of square cylinder. Eng Sci Technol Int J (2015) 18(4):758–68. doi:10.1016/j.jestch.2015.05.007

CrossRef Full Text | Google Scholar

12. Furquan M, Mittal S. Flow past two square cylinders with flexible splitter plates. Comput Mech (2015) 55:1155–66. doi:10.1007/s00466-014-1110-5

CrossRef Full Text | Google Scholar

13. Ghadimi P, Djeddi SR, Oloumiyazdi RH, Dashtimanesh A. Simulation of ow over a confined square cylinder and optimal passive control of vortex shedding using a detached splitter plate. Trans B: Mech Eng (2015) 22(1):175–86.

Google Scholar

14. Chauhan MK, Dutta S, Singh B, Gandhi BK. Experimental investigation of flow over a square cylinder with an attached splitter plate at intermediate Reynolds number. J Fluids Structures (2018) 76:319–35. doi:10.1016/j.jfluidstructs.2017.10.012

CrossRef Full Text | Google Scholar

15. Gallegos RKB, Sharma RN (2016). “ Dynamic behaviour of a flexible plate behind a circular cylinder: Numerical study on the effects of blockage and cylinder size.” Australasian Fluid Mechanics Conference, pp. 5–8.

Google Scholar

16. Ali MSM, Doolan CJ, Wheatley C. Low Reynolds number flow over a square cylinder with splitter plate. Phys Fluids (2011) 23:1–12.

Google Scholar

17. Mansy RE, Sarwar W, Rodriguez I, Bergada JM. Three dimensional structures of flow through a square cylinder with an upstream splitter plate and for several velocity ratios. In: Tenth International Conference on Computational Fluid Dynamics; Barcelona, Spain (2018). p. 1–13.

Google Scholar

18. Barman B, Bhattacharyya S. Control of vortex shedding and drag reduction through dual splitter plates attached to a square cylinder. J Mar Sci Appl (2015) 14:138–45. doi:10.1007/s11804-015-1299-5

CrossRef Full Text | Google Scholar

19. Bao Y, Tao J. The passive control of wake flow behind a circular cylinder by parallel dual plates. J Fluids Structures (2013) 37:201–19. doi:10.1016/j.jfluidstructs.2012.11.002

CrossRef Full Text | Google Scholar

20. Kumar R, Selokar GR, Jhavar P, Kalariya S. Drag estimation of flow past a square cylinder using two splitter plate. Int J Adv Res Innovative Ideas Edu (2016) 2(1):371–80.

Google Scholar

21. Abdolahipour S, Mani M, Taleghani AS. Pressure improvement on a supercritical high-lift wing using simple and modulated pulse jet vortex generator. Flow Turbulence Combustion (2022) 109:65–100. doi:10.1007/s10494-022-00327-9

CrossRef Full Text | Google Scholar

22. Abdolahipour S, Mani M, Taleghani AS. Experimental investigation of flow control on a high-lift wing using modulated pulse jet vortex generator. J Aerospace Eng (2022) 35(5):05022001. doi:10.1061/(asce)as.1943-5525.0001463

CrossRef Full Text | Google Scholar

23. Abdolahipour S, Mani M, Taleghani AS. Parametric study of a frequency-modulated pulse jet by measurements of flow characteristics. Physica Scripta (2021) 96(12):125012. doi:10.1088/1402-4896/ac2bdf

CrossRef Full Text | Google Scholar

24. Taleghani AS, Shadaram A, Mirzaei M. Effects of duty cycles of the plasma actuators on improvement of pressure distribution above a NLF0414 airfoil. IEEE Trans Plasma Sci (2012) 40(5):1434–40. doi:10.1109/tps.2012.2187683

CrossRef Full Text | Google Scholar

25. Salmasi A, Shadaram A, Taleghani AS. Effect of plasma actuator placement on the airfoil efficiency at poststall angles of attack. IEEE Trans Plasma Sci (2013) 41(10):3079–85. doi:10.1109/tps.2013.2280612

CrossRef Full Text | Google Scholar

26. Mohammadi M, Taleghani AS. Active flow control by dielectric barrier discharge to increase stall angle of a NACA0012 airfoil. Arabian J Sci Eng (2014) 39:2363–70. doi:10.1007/s13369-013-0772-1

CrossRef Full Text | Google Scholar

27. Mirzaei M, Taleghani AS, Shadaram A. Experimental study of vortex shedding control using plasma actuator. Appl Mech Mater (2012) 186:75–86. doi:10.4028/www.scientific.net/amm.186.75

CrossRef Full Text | Google Scholar

28. Taleghani AS, Shadaram A, Mirzaei M, Abdolahipour S. Parametric study of a plasma actuator at unsteady actuation by measurements of the induced flow velocity for flow control. J Braz Soc Mech Sci Eng (2018) 40(4):173–13. doi:10.1007/s40430-018-1120-x

CrossRef Full Text | Google Scholar

29. Sheikholeslam M, NooriTaleghani AS, Rahni MT. Surface acoustic waves as control actuator for drop removal from solid surface. Fluid Dyn Res (2021) 53(4):045503. doi:10.1088/1873-7005/ac12af

CrossRef Full Text | Google Scholar

30. Rahni MT, Taleghani AS, Sheikholeslam M, Ahmadi G. Computational simulation of water removal from a flat plate, using surface acoustic waves. Wave Motion (2022) 111:102867. doi:10.1016/j.wavemoti.2021.102867

CrossRef Full Text | Google Scholar

31. Malekzadeh S, Sohankar A. Reduction of fluid forces and heat transfer on a square cylinder in a laminar flow regime using a control plate. Int J Heat Fluid Flow (2021) 34:15–27. doi:10.1016/j.ijheatfluidflow.2011.12.008

CrossRef Full Text | Google Scholar

32. Canpolat C, Sahin B. Influence of single rectangular groove on the flow past a circular cylinder. Int J Heat Fluid Flow (2017) 64:79–88. doi:10.1016/j.ijheatfluidflow.2017.02.001

CrossRef Full Text | Google Scholar

33. Sohankar A, Khodadi M, Rangraz E, Alam MM. Control of flow and heat transfer over two inline square cylinders. Phys Fluids (2019) 31:123604. doi:10.1063/1.5128751

CrossRef Full Text | Google Scholar

34. Zhou L, Li H, Tse TKT, He X, Maceda GYC, Zhang H. Sensitivity-aided active control of flow past twin cylinders. Int J Mech Sci (2023) 242:108013. doi:10.1016/j.ijmecsci.2022.108013

CrossRef Full Text | Google Scholar

35. Chan AS. Control and suppression of laminar vortex shedding off two-dimensional bluff bodies. PhD Dissertation. Stanford, CA: Department of Mechanical Engineering, Stanford University (2012).

36. Wolf-Gladrow DA. Lattice-gas cellular automata and lattice Boltzmann models-an introduction. Berlin, Germany: Springer (2005).

Google Scholar

37. Chapman S, Cowling TG. Mathematical theory of non-uniform gases. 3rd ed. Cambridge, UK: Cambridge University Press (1970).

Google Scholar

38. Mohamad AA. Lattice Boltzmann method: Fundamentals and engineering applications with computer codes. 2nd ed. Berlin, Germany: Springer (2019).

Google Scholar

39. Viggen EM. The lattice Boltzmann method with applications in acoustics. Master’s thesis. Trondheim, Norway: NTNU (2009).

40. Islam S, U, Manzoor R, Ying Z, C, Rashdi M, M, Khan A. Numerical investigation of fluid flow past a square cylinder using upstream, downstream and dual splitter plates. J Mech Sci Tech (2017) 31(2):669–87. doi:10.1007/s12206-017-0119-z

CrossRef Full Text | Google Scholar

41. Guo Z, Liu H, Luo L-S, Xu K. A comparative study of the LBE and GKS methods for 2D near incompressible laminar flows. Comput Phys (2008) 227:4955–76. doi:10.1016/j.jcp.2008.01.024

CrossRef Full Text | Google Scholar

42. Abbasi WS, Islam SU, Faiz L, Rahman H. Numerical investigation of transitions in flow states and variation in aerodynamic forces for flow around square cylinders arranged inline. Chin J Aeronautics (2018) 31(11):2111–23. doi:10.1016/j.cja.2018.08.020

CrossRef Full Text | Google Scholar

43. Abbasi WS, Islam SU. Transition from steady to unsteady state flow around two inline cylinders under the effect of Reynolds numbers. J Braz Soc Mech Sci Eng (2018) 40:168. doi:10.1007/s40430-018-1083-y

CrossRef Full Text | Google Scholar

44. Abbasi WS, Islam SU, Rahman H, Manzoor R. Numerical investigation of fluid-solid interaction for flow around three square cylinders. AIP Adv (2018) 8:025221. doi:10.1063/1.5004631

CrossRef Full Text | Google Scholar

45. Abbasi WS, Naheed A, Islam SU, Rahman H. Investigation of optimum conditions for flow control around two inline square cylinders. Arabian J Sci Eng (2021) 46:2845–64. doi:10.1007/s13369-020-05303-x

CrossRef Full Text | Google Scholar

46. Islam SU, Rahman H, Abbasi WS, Shahina T. Lattice Boltzmann study of wake structure and force statistics for various gap spacings between a square cylinder with a detached flat plate. Arabian J Sci Eng (2015) 40:2169–82. doi:10.1007/s13369-015-1648-3

CrossRef Full Text | Google Scholar

47. Islam SU, Abbasi WS, Ying ZC. Transitions in the unsteady wakes and aerodynamic characteristics of the flow past three square cylinders aligned inline. Aerospace Sci Tech (2016) 50:96–111. doi:10.1016/j.ast.2015.12.004

CrossRef Full Text | Google Scholar

48. Islam SU, Rahman H, Abbasi WS, Noreen U, Khan A. Suppression of fluid force on flow past a square cylinder with a detached flat plate at low Reynolds number for various spacing ratios. J Mech Sci Tech (2014) 28(12):4969–78. doi:10.1007/s12206-014-1118-y

CrossRef Full Text | Google Scholar

49. Shahab M, Islam SU, Nazeer G. T-shaped control plate effect on flow past a square cylinder at low Reynolds numbers. Math Probl Eng (2021) 2021:1–19. doi:10.1155/2021/7562460

CrossRef Full Text | Google Scholar

50. Dousset V, Pothérat A. Formation mechanism of hairpin vortices in the wake of a truncated square cylinder in a duct. J Fluid Mech (2010) 653:519–36. doi:10.1017/s002211201000073x

CrossRef Full Text | Google Scholar