- School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Khurda, India
We review recent studies of contact and thermodynamic geometry for black holes in AdS spacetimes in the extended thermodynamics framework. The cosmological constant gives rise to the notion of pressure P = −Λ/8π and, subsequently a conjugate volume V, thereby leading to a close analogy with hydrostatic thermodynamic systems. To begin with, we review the contact geometry approach to thermodynamics in general and then consider thermodynamic metrics constructed as the Hessians of various thermodynamic potentials. We then study their correspondence to statistical ensembles for systems with two-dimensional spaces of equilibrium states. From the zeroes and divergences of the curvature scalar obtained from the metric, we carefully analyze the issue of ensemble non-equivalence and show certain complimentary behaviors in the description of a thermodynamic system. Following a thorough analysis of the familiar van der Waals system, we turn our attention to black holes in extended phase space. Considering the example of charged AdS black holes, we discuss the generic features of their thermodynamic geometry in detail. The relationship of the thermodynamic curvature(s) with critical points as well as microscopic interactions in black holes is also briefly explored. We finally set up the thermodynamic geometry for finite temperature gauge theories dual to black holes in AdS via holographic correspondence and comment on recent progress.
1 Introduction
It is well appreciated that black holes are associated with entropy and temperature, being given by the relations [1–5] (in units ℏ = kB = c = G = 1):
where
The introduction of geometrical ideas into thermodynamics have led to several interesting physical insights (see for example, the reviews [22, 23]). Of particular interest is the concept of a length between different thermodynamic states [24–26]. A good starting point leading to the notion of thermodynamic length is Einstein’s fluctuation theory which can be motivated as follows. It is a well understood fact that the entropy of a thermodynamic system is a measure of the number of ways the system can arrange itself microscopically. One can then invert the Boltzmann’s formula for entropy (we shall set kB = 1 throughout the paper): S = ln Ω where Ω is the thermodynamic probability or equivalently the number of accessible microstates to obtain
We may then expand the entropy S about its equilibrium value S0, i.e. about the point at which all its first derivatives vanish so that we have up to the second order:
where {xi} are suitable thermodynamic variables specified by external baths or boundary conditions defining the ensemble. With this, one can re-write Eq. 2 as
with,
Clearly,
The curvature scalar associated with the Ruppeiner metric, known as the Ruppeiner curvature or simply the thermodynamic curvature possesses an intriguing behavior. The empirical understanding obtained from studying several thermodynamic systems is as follows. It typically diverges at critical points and possibly also at points where the thermodynamic system exhibits strong microscopic correlations. This has been verified for several systems including the van der Waals fluid [27, 28] and model magnetic systems [29–31] (see also [32–34]). In fact, it has been argued [22, 35] that close to the critical point, the Ruppeiner curvature scales with the correlation volume, i.e. R ∼ ξd where ξ is the correlation length and d is the number of spatial dimensions. Another interesting aspect of the Ruppeiner curvature is that its sign seems to have a connection with the nature of dominant interactions between the microscopic degrees of freedom in a given thermodynamic system [35]. In the sign convention that we adopt in this paper, the curvature scalar is negative (R < 0) for the attractive van der Waals gas [27, 28] or an ideal gas of bosons [36]. In the latter, the attractive interactions are of quantum mechanical origin. Similarly, for the ideal gas of fermions, one has R > 0 which may be taken to signal the existence of quantum mechanical repulsive interactions whose origin can be traced back into the exclusion principle [36]. This feature has indeed been verified for several systems where independent microscopic calculations can be performed (see [35] and references therein). Therefore, the Ruppeiner curvature seems to be a powerful diagnostic tool whose behavior may reveal early insights into the microscopic physics of systems such as black holes where a satisfactory microscopic theory is not yet available [27, 28, 37–67] (see also [68–72]).
In recent times, there has been an ongoing debate about the applicability of geometric methods for understanding the physics of thermodynamic systems [73, 74, 76, 77], including black holes. Thermodynamic or information geometry has been shown to be a powerful diagnostic tool, with the divergences of the associated curvature scalar capturing the critical points in various thermodynamic systems. The connection between thermodynamic curvature and the specific heat capacities has also been explored, particularly because the divergences of these quantities typically signal the onset of instabilities and phase transitions in a system. Despite these advantages, there have been a few longstanding unresolved issues concerning the lack of diffeomorphism invariance [42, 78] and non-equivalence of thermodynamic curvatures constructed out of different thermodynamic potentials [79], among others. It has been noted in several papers in the past that thermodynamic Hessian metrics are not Legendre invariant (see for example [42, 79, 80]) and we can understand it by considering thermodynamic curvatures constructed from two different thermodynamic potentials. Without loss of generality, for example, one can construct a certain thermodynamic curvature RU by taking the internal energy U as the fundamental potential with the divergences of RU capturing the critical point of the system. Performing a partial Legendre transform and using instead enthalpy H as the potential, leads to a different thermodynamic curvature (call it, RH), which may not capture the critical point exactly (as we show later). Thus, the features exhibited by thermodynamic curvatures computed using different potentials may be different. This has been termed as ensemble non-equivalence in thermodynamic geometry [79]. While a large body of work is devoted to probing the connection of the divergences of thermodynamic curvatures to phase transitions, there has been a relatively less focus on the study of their zeroes, until recently [27, 28, 55, 59, 61].
One of the major goals of this article is to pedagogically introduce thermodynamic geometry with black holes in mind, and to perform a critical analysis of the thermodynamic curvatures obtained in different statistical ensembles related by (partial) Legendre transforms. It is demonstrated that if RU captures the divergences of a certain specific heat, RH (obtained by a Legendre transform) contains information about the zeroes of that specific heat and vice versa. This suggests a complimentary nature of RU and RH (see also [79]). Different parametrizations of thermodynamic Hessian metrics in a given ensemble are elaborately discussed. We follow the general route discussed by Mrugala [82] (discussed in section-(II)) to obtain thermodynamic metrics in a given ensemble, once the first law satisfied at thermodynamic equilibrium is known. We particularly focus on entropic metrics which are generated from the derivatives of the entropy or the free entropy and highlight some key features of such metrics and their relationship with energy metrics (those which are generated from the derivatives of energy functions). The geometry described by entropic metrics is explored in some detail, particularly in the context of black hole chemistry.
The paper is organized as follows. In section-(II), we start by setting up our notation and summarize some basic aspects of the contact geometry approach to thermodynamic phase spaces followed by the notion of Hessian metrics defined on spaces of equilibrium states [73–77]. Then, in section-(III), we discuss some key ideas on thermodynamic Hessian metrics and their reparametrizations. The issue of ensemble non-equivalence is analyzed very carefully. For two-dimensional spaces of thermodynamic equilibrium states, we follow closely the earlier analysis in [79] (see also [80, 81]) and study the (Ruppeiner) thermodynamic curvatures in two different ensembles contrasting their behavior. The possible sources of singularities of the Ruppeiner metric are identified in the two ensembles related by a (partial) Legendre transform. As a model hydrostatic system, we consider the van der Waals fluid and discuss its thermodynamic geometry. In section-(IV), we apply the ideas developed earlier to explore the thermodynamic geometry of black holes in AdS spacetimes in the extended thermodynamics framework. This section contains two subsections, i.e. (A) and (B), where the thermodynamic geometries of the bulk and the boundary (via the gauge/gravity duality) settings are discussed respectively. We end with comments and a summary of the paper in the concluding section-(V).
2 Contact and metric structures on thermodynamic phase spaces
In this section, we shall very briefly review some basic aspects of the geometry of thermodynamics. The reader is referred to [83–87] for the details. Thermodynamic phase spaces assume the structure of a contact manifold, i.e. a (2n + 1)-dimensional smooth manifold
Clearly, η ∧ (dη)n is a volume form on
In other words, the vector field ξ can be understood to be dual to the one form field η. Analogous to the one on symplectic manifolds, there exists a Darboux theorem on contact manifolds which states that on any local patch on a contact manifold
There exist a very special class of submanifolds of a contact manifold
In this context F = F (qi, pj) is known as the generator of L and it should be clear that all Legendre submanifolds are n-dimensional. It was shown long back that any contact manifold can be associated with a Riemannian metric structure which satisfies some compatibility conditions with the contact form. The reader is referred to the works [88–90] for details on compatible metric structures on contact manifolds. The metric is a bilinear, symmetric as well as non-degenerate structure. It can be verified that the generic choice due to Mrugala [82]: G = η2 + dqi ⊗ dpi satisfies all these three basic requirements and also the compatibility condition presented in [88]. Since for an arbitrary Legendre submanifold L, one has η|L = 0 by definition, therefore restricting G to L gives the local expression from Eq. 9:
The metric on a Legendre submanifold L is therefore defined from the Hessian of the generator of L. Such a metric will be called a Hessian metric on L. There are of course other ways of defining a symmetric, bilinear and non-degenerate metric structure on a contact manifold but that would not be of interest to us in the present work.
With this background, we can now make connection with thermodynamics (also see [73, 74, 76, 77]). We start by recalling the first law of thermodynamics for a hydrostatic (P, V, T) system described by the microcanonical ensemble:
A direct comparison between the first of Eqs 8, 11 leads to the immediate identification that the thermodynamic variables are local coordinates on a 5-dimensional contact manifold. Explicitly, one identifies s = U while (q1, q2) = (S, V) and (p1, p2) = (T, − P). Further, Eq. 11 which holds at equilibrium implies that the system’s state is represented by a point on a Legendre submanifold of the thermodynamic phase space. Such a Legendre submanifold has the following local structure [Eq. 9]:
Legendre submanifolds therefore represent spaces of thermodynamic equilibrium states in the sense that each point on the Legendre submanifold represents an equilibrium state of the system. Thus, even though apriori all the coordinates of the thermodynamic phase space are independent, thermodynamic equilibrium or equivalently the first law puts an on-shell condition such that the system lives on a Legendre submanifold with just n independent coordinates while the other n are derived by taking derivatives of the thermodynamic potential (the generator) with respect to the independent thermodynamic variables. A thermodynamic system is therefore a triplet
3 Two ensembles related by a Legendre transform
We shall begin by analyzing two generic ensembles which in the thermodynamic limit are related by a Legendre transform (see also [79] and references therein). Let us say that at equilibrium, the entropy can be expressed as S = S(xi) with i = 1, …., n where xi are suitable state variables characterzing the system’s equilibrium state. For the sake of simplicity, we take the case with n = 2 so that we have, S = S (E, X) where E is the energy function (for example, internal energy U) and X can be a suitable thermodynamic variable.
3.1 Ensemble
In the thermodynamic limit, we consider the first law with E = U:
where Y = (∂U/∂X)S is the variable conjugate to X. For a hydrostatic system where X = V (imposed by boundary conditions), one has Y = −P. On the other hand, for a magnetic system one has X = η (the magnetization) and Y = h (magnetic intensity). Comparison with the first of Eq. 8 leads us to the identification that s = U and (q1, q2) = (S, X) whereas (p1, p2) = (T, Y). The condition, dU − TdS − YdX = 0 defines the space of equilibrium states on which it is most natural to choose S and X as the independent coordinates whereas, T and Y are defined on-shell as derivatives of the generator function U with respect to the independent ones. The thermodynamic metric [Eq. 10] is then (in our notation, (dx)2 = dx ⊗ dx)
This is known as the Weinhold metric [25]. Note that here CX is the specific heat at constant X. Noting that the function U = U(S, X) is obtained by inverting the relation S = S(U, X) in favour of U, then since S(U, X) is a concave function, U(S, X) is convex ensuring that the metric given above is positive. This happens because of positivity of temperature, which implies that entropy is a monotonically increasing function of U [105]. Now, since S and X are the independent thermodynamic coordinates on the 2-dimensional space of equilibrium states, such that U = U(S, X), one has T = T (S, X) = ∂SU(S, X) and Y = Y(S, X) = ∂XU(S, X). These are the equations of state. Using this, Eq. 14 is equivalent to
This is also easily obtained from Eq. 10:
with q1 = S, p1 = T, q2 = X, p2 = Y. Eq. 15 is the line element of the natural metric on the Legendre submanifold LX representing the system described by this ensemble.
Now, because of the equations of state (the on-shell relations between thermodynamic quantities such that only two of them are independent), one can write T = T(S, X) and Y = Y(S, X). These can in principle be inverted to obtain S = S(T, Y) and X = X(T, Y). One may also obtain S = S(T, X) and Y = Y(T, X) or even T = T (S, X) and Y = Y(S, X). This means that by suitably inverting the equations of state on the space of equilibrium states LX, we can pick any two among S, T, X or Y to be independent and re-express our metric [Eq. 15] in four different ways. One is of course Eq. 14. The other three are
Here, CX and CY are the specific heats at constant X and Y respectively. It should be specially emphasized that we have not performed any Legendre transformation in deriving these line elements. They are simply Eq. 15 in different coordinate parameterizations. One goes from one set of independent coordinates to another by exploiting the equations of state while still being on the Legendre submanifold LX. All these line elements therefore, represent the same length on LX but expressed in different fluctuation coordinates. This is possible because the fluctuations in the natural coordinates (S, X) are related to those of the dependent coordinates (T, Y) via the equations of state. Therefore, one expects that the Ricci scalars associated with the line elements given in Eqs. 14, 17–19 are all equivalent to each other. For example, one can compute the scalar curvature on the (S, X) plane [Eq. 14] and then using the equations of state re-express it as a function of say, T and Y. It then means that the curvature scalar so obtained would be the same as that directly calculated using the line element given in Eq. 19.
Since there is a natural first law associated with a given ensemble, this introduces a set of natural coordinates on the Legendre submanifold or the space of thermodynamic equilibrium states on which the system of interest is described. For example, for the present case the natural coordinates are S and X although as we saw, by using the on-shell equations of state T and/or Y could be made independent on LX. The choice of natural coordinates does not depend on the specific functional form of the thermodynamic potential (in this case, the internal energy U = U(S, X)). In an arbitrary case with n independent variables, one has S = S (E, Xj) where j = 1, 2, …., n − 1. One can therefore write E = E(S, Xj) giving the first law:
This sets the natural coordinates to {S, Xj} and the Legendre submanifold describing the system is n-dimensional. Keeping in mind that the exact form of E is not relevant here (as long as it is well behaved), one may assert that a given statistical ensemble describes a family of Legendre submanifolds in the thermodynamic limit. The choice of natural coordinates is specified by the ensemble of interest.
3.2 Ensemble
Let us consider the case where the system is in contact with a reservoir for the variable X. For a hydrostatic system, with our usual identification that Y is the pressure, the bath is a barostat with which the system can exchange its volume. If on the other hand, the system was a magnetic system with Y being the magnetic intensity, one can think about the system attaining thermodynamic equilibrium in the presence of a constant external field. In the present case, the first law is given by
for some energy function E = E(S, Y). The first laws given in Eqs 13, 21 can be related by the Legendre transformation, E(S, Y) = U(S, X) − XY provided it exists. For a usual hydrostatic system, E(S, P) = U(S, V) + PV ≔ H(S, P) which is the enthalpy whereas for a magnetic system, E(S, h) = U(S, η) − ηh.
Inspecting Eq. 21, we arrive at the following identifications: (q1, q2) = (S, Y) and (p1, p2) = (T, − X) on the space of equilibrium states (say) LY. The thermodynamic length [Eq. 10] is then
or in the natural coordinates,
Clearly, the thermodynamic lengths on Legendre submanifolds LX and LY given respectively in Eqs 15, 22 are not the same. It can be shown [77] that two Legendre submanifolds are diffeomorphic to each other if the Legendre transformation connecting them is regular. Even then, the thermodynamic lengths for two ensembles do not coincide. In other words, in the thermodynamic limit where the ensembles become equivalent (up to Legendre transformations), the lengths are not! We strongly emphasize on the fact that this non-equivalence has nothing to do with the microscopic description of a particular system. It is well appreciated that the presence of long ranged interactions may render different ensembles inequivalent to each other [94, 95] (see also [96]). However, the non-equivalence which is being discussed here follows from the basic structure of the thermodynamic phase space and shall continue to be there even when there are no long range interactions between the microscopic degrees of freedom. Thus, non-equivalence in the present context shall refer to the fact that some of the geometrical properties of the two Legendre submanifolds representing the same system but in two different ensembles are not the same. It can be intuitively understood on physical grounds by noting that although one is finally working in the thermodynamic limit, the Hessian metrics are all derived generically based on thermodynamic fluctuations which are not equivalent in different ensembles. As it is clear, the two distinct ensembles are associated with different system-boundary conditions. For example, in ensemble
Now for the present case, it is possible to re-express the length [Eq. 22] in different coordinate parameterizations. One of them is Eq. 23. The other three are
It turns out that the Ricci scalars of the line elements given in Eqs 23–26 are equivalent to one another. However, the line elements with the same fluctuation coordinates (say (T, X)) are not equivalent in the two ensembles. Therefore, to summarize, the Ricci scalars associated with thermodynamic metrics corresponding to different ensembles (hence, different families of Legendre submanifolds) are in general inequivalent.
3.3 Entropic metrics
So far we saw that it is possible to construct various thermodynamic metrics by taking Hessians of different thermodynamic potentials. Typically, such potentials are the energy functions of the system such as the internal energy or the enthalpy. However, it is often physically more intuitive to consider entropic potentials (those with dimensions of entropy) in the construction of such metrics. Among them the Ruppeiner metric is special because it is directly linked with the probability of fluctuations rendering a physical meaning to the length between two thermodynamic states. Furthermore, its Ricci scalar, i.e. the Ruppeiner curvature or the thermodynamic curvature bears a nice physical interpretation as was pointed out in the introduction.
As it turns out, Eq. 13 can be re-written as
This is clearly a microcanonical description where the entropy is given by the Boltzmann formula S = ln Ω(U, X). From the point of view of statistical mechanics, this is a more fundamental form of the first law as compared to Eq. 13 because all the equilibrium properties including the specific heats and susceptibilities can be computed from the knowledge of S derived from microscopic details (via Ω). The Ruppeiner metric is then defined as the negative Hessian of the entropy or equivalently, the Hessian of the negative entropy. In order to derive an expression for the Ruppeiner metric in ensemble
Now, since dzi = gijdxj, we must have
From the first law given in Eq. 13, one can write
which means that z1 = 1/T and z2 = −Y/T whereas x1 = U and x2 = X. With these identifications,
The line element given in Eq. 28 can now be expressed as
which from the first law reduces to
We can now turn to ensemble
where the entropy of the system is of the generic form S = S(E, Y). This is different from the microcanonical or (V, U)-description. The first law in terms of the entropy can be re-written as
which is equivalent to rearranging Eq. 27 and defining E = U − YX. Since X is an extensive variable, its conjugate, Y is intensive and consequently S has been expressed as a function of an intensive and an extensive variable as opposed to the microcanonical description where it is a function of U and X, both being extensive. It therefore follows that in ensemble
As it turns out, the curvature scalar associated with the Ruppeiner metric has a peculiar behavior close to critical points or even the points at which the system gets strongly correlated [24]. Let us examine the case of a system described by the ensemble
where g is the determinant of the metric tensor. This means that calculations are a lot simpler if the metric is diagonal. For the sake of simplicity, let us consider the ensemble
Clearly, one finds that the metric is singular if CX = 0 or (∂Y/∂X)T = 0. Taking the Ruppeiner line element obtained by dividing Eq. 18 by a factor of T, it also follows that the curvature scalar say RU in ensemble
Next, let us consider the ensemble
3.4 (U, V) and (H, P)-ensembles
In this subsection, we shall make our assertions concrete by considering the van der Waals model, which exhibits features of the liquid-gas phase transition. Then, ensemble
The van der Waals (vdW) fluid is a prototypical example of a model fluid exhibiting features of the liquid-gas phase transition. The attractive interactions among the fluid molecules can be summarized by the van der Waals potential V(r) = −k/r6 for some constant k > 0 acting between pairs of molecules. Furthermore, the molecules are modelled as impenetrable hard spheres and therefore, if σ be the distance at which two molecules touch each other, the potential is infinite. Such a description of intermolecular interactions is mean field. The fluid is described by the equation of state:
Taking Cv = 3/2, one has the following expression for CP:
Note that putting a = b = 0, one has CP − Cv = 1 as expected from the ideal gas. In the microcanonical ensemble, the thermodynamic curvature reads (see also [27, 28])
whereas, in the isoenthalpic-isobaric ensemble, the curvature scalar of the Ruppeiner metric reads the following when expressed in T and v coordinates:
where the subscript H signifies that in this case, the energy function E is equal to the enthalpy. The thermodynamic curvatures RU and RH have been plotted as a function of v in Figure 1. Clearly, the divergences in CP and RU exactly coincide as was expected. With v > b = 1, CP has divergences at v = 1.21, 37.9 and RU diverges exactly at these points. We mention that the plots are for a temperature below the critical temperature. The curvature scalar RU becomes zero at the point v = b where the specific volume and the co-volume coincide putting a lower cutoff to the physical values v can take. However, this point lies in the negative bulk modulus range below the critical temperature. We also note that RU crosses zero for two values of v > b. However, both of them occur in the region where the isothermal bulk modulus is negative thus falling in a thermodynamically unstable region. For T = 0.1, a = 2 and b = 1, the isothermal bulk modulus is negative (shaded in grey in the plots) between v = 1.210 and 37.918). Such crossings are therefore not considered to be of physical interest. It is then simple to check that the thermodynamic curvature is negative definite over the entire thermodynamically stable region with v > b and (∂P/∂v)T ≤ 0. This can empirically be taken to signal the existence of attractive interactions between molecules. It may be shown that near the critical temperature Tc, the specific heat CP and thermodynamic curvature RU scale as [28]
The exponent ‘2’ for the thermodynamic curvature near the critical point has been obtained earlier in other contexts [27, 33, 34, 64, 72].
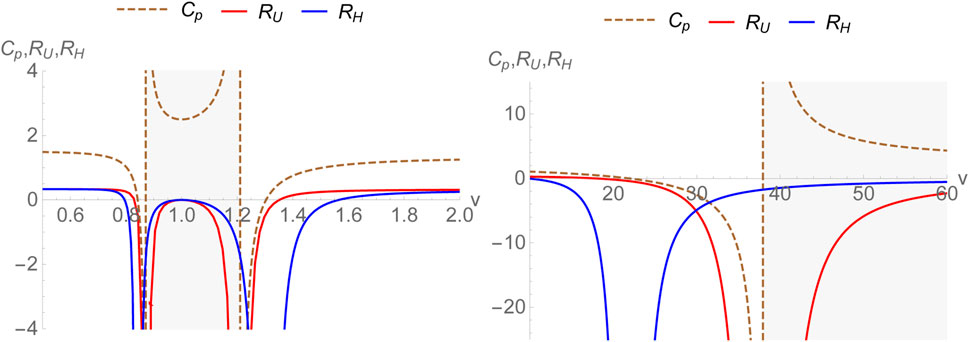
FIGURE 1. Thermodynamic curvatures RU, RH and specific heat CP for the van der Waals fluid plotted versus specific volume with a = 2, b =1 below the critical temperature. The region(s) with negative bulk modulus are shaded in grey.
As for RH, the divergences of RH do not correspond to those of CP. As a matter of fact, if Cv had divergences, one could expect such divergences to coincide with those of the thermodynamic curvature RH. In the present case where Cv is a constant it can be clearly seen that the divergences of RH correspond to the zeroes of CP. It should be emphasized that the constancy of one of the specific heats (here Cv) originates from the specific choice X = v for the (U, X) ensemble where Cv is a constant due to the equipartition theorem for the van der Waals fluid. For v > b = 1, CP has zeroes at v = 21.8 and 1.3. RH diverges at both these points. This is expected from the generic structure of the line elements presented earlier. Let us also note that RH consistently goes to zero at v = b. Finally, we point out that the other crossings of RH fall into the region of negative isothermal bulk modulus (shaded in grey) and are therefore discarded. Thus, RH is negative over the entire physically interesting region possibly signifying the attractive nature of van der Waals interactions between the molecules. Furthermore, let us note that as one takes v → ∞, both RU and RH approach zero. This is the ideal gas limit where the thermodynamic geometry is flat.
Some discussion is in order. Although we find that for the van der Waals model, the physically interesting zero of both RU and RH agree, irrespective of their inequivalence, this is not true in general. For example, if we use the fact that the specific heat at fixed volume is a constant (certainly true for several model systems), then RH and RU have the following general expressions (written in terms of specific volume):
and,
Now, using the fact that ∂T,T,vP = 0 (the equation of state is linear in T), it is simple to check that both RU = RH = 0 when
The above condition, gives one physical solution at which both RU and RH vanish, both below and above the critical point. Other zero crossings are physically not quite interesting because they lie in the range of negative bulk modulus. Although the above result proving the equivalence of the zero crossing(s) of RU and RH looks appealing, let us emphasize that it is based on two crucial assumptions about the fluid system. First, we have assumed that Cv is a constant, independent of T and v. Although this follows from the equipartition theorem, this is certainly not true for a general fluid with complicated microscopic interactions where the virial coefficients are temperature dependent. The second assumption is that the equation of state is linear in T, i.e. ∂T,T,vP = 0. While this is true for the ideal gas and several model fluid systems (such as van der Waals), this is not the case for a general fluid where the virial coefficients do not depend on temperature linearly. Thus, the zero crossing behavior of RU and RH are indeed not equivalent in the general case. Nevertheless, they do follow some general trends as far as their divergences are concerned.
4 Black holes in AdS spacetimes
We shall consider black holes in AdS spacetimes. In the extended thermodynamics framework [12], the cosmological constant is treated as thermodynamic pressure via the relation
Here d is the number of spacetime dimensions. For charged black holes, the first law of thermodynamics takes the following form:
where, Q is the electric charge (U (1) charge) of the black hole, and Φ is the corresponding potential. The thermodynamic variables satisfy the Smarr relation [12, 15, 16]:
which can be obtained via scaling arguments. Thermodynamic geometry of black holes was first studied in [37] wherein the BTZ black hole was considered and it was found that the curvature scalar diverges at extremality. This was followed by a series of papers (see for instance [38, 39, 41, 42]) where the thermodynamic curvature for various black holes were computed and analyzed. It was found that upon suitably choosing the thermodynamic potential, the thermodynamic curvature is divergent along the Davies line [39] (see also [79]). The most natural choice of energy metric for black holes is defined as the Hessian of the mass [37–39], i.e.
where M = M(yi) with y1 = S (entropy). One may invert this fundamental relation, to express the entropy as the potential, ie. S = S(M, ⋯) and subsequently define the Ruppeiner metric
In the extended thermodynamics framework, thermodynamic geometry for BTZ black holes (d = 3) has been studied in [59, 60] (also see [37, 40] for older studies). It has been found that for the neutral and non-rotating BTZ black hole, the thermodynamic geometry is Ricci flat, empirically indicating towards the absence of net microscopic interactions. However, for black holes with electric charge and/or angular momentum, the geometry is curved with a positive thermodynamic curvature. This may be taken to indicate towards the presence of repulsive microscopic interactions and is consistent with the fact that the BTZ black hole does not admit a phase transition [18]. For charged and/or rotating BTZ black holes, the scalar RH has been found to diverge at the extremal point [59], consistent with a much older result [37]. The thermodynamic curvature RH was obtained for the case of exotic BTZ black holes in [59], and it was found that RH could be both positive and negative with a zero crossing between the two regimes. The origin of such a crossing is not well understood, partly because exotic BTZ black holes do not admit a fluid-like equation of state. On the other hand, thermodynamic curvatures obtained for black holes in higher dimensions exhibit richer features. Below, we shall consider charged AdS black holes in four dimensions.
4.1 Bulk
The solution to Einstein-Maxwell equations with a negative cosmological constant in four dimensions (d = 4) reads [15]:
where
Here, M is the ADM mass and q is the U (1) charge of the spacetime. The event horizon is defined as the largest root of the relation f (r+) = 0. In terms of r+, the black hole mass can be expressed as
It should be remarked that here, the mass takes the role of the enthalpy of the system, i.e. M≔H(S, P, q) [12]. In terms of thermodynamic variables
Temperature and thermodynamic volume can be computed by differentiating the enthalpy giving
which upon elimination of S, gives the equation of state:
This provides an on-shell relationship between P, V and T for the charged AdS black hole. Thermodynamic geometry of the system has been studied earlier in both the (U, V)-ensemble [27, 28] and the (H, P)-ensemble [48, 55]. Let us note that the thermodynamic volume turns out to be (see also [14])
which is only a function of entropy (no pressure dependence). Therefore, the specific heat at constant volume CV identically vanishes ensuring that RU is divergent for all thermodynamic equilibrium states. The authors of [27, 28] have suggested a remedy by considering CV to be a vanishingly small number (rather than zero), of the order of kB and then one may define a normalized curvature as
which is finite. As a matter of fact, in black hole chemistry with d ≥ 3, CV vanishes for all black holes with spherical symmetry and as such the procedure described above works for all such cases. In what follows, we compare and contrast the behavior of the curvature scalars obtained in (U, V) and (H, P)-ensembles [48, 55].
The specific heat CP turns out to be
and we have the following expression for
where,
This in terms of the horizon radius r+ is equivalent to the condition:
where,
This expression coincides with the one obtained earlier in [55] for the choice CV = 0. Since, the limit CV → 0+ is smooth for RH, we can very well set it equal to zero without the need of normalizing the thermodynamic curvature unlike the case of RU. The scalar RH diverges as V → 0. This corresponds to the limit CP → 0 and is consistent with our expectations. Remarkably, even for the black hole, the two thermodynamic curvatures have identical crossing points within the region of thermodynamic stability (corresponding to the horizon radius r+ satisfying
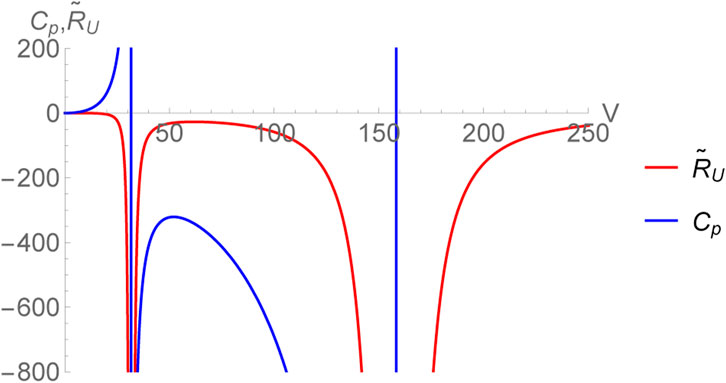
FIGURE 2. Normalized thermodynamic curvature
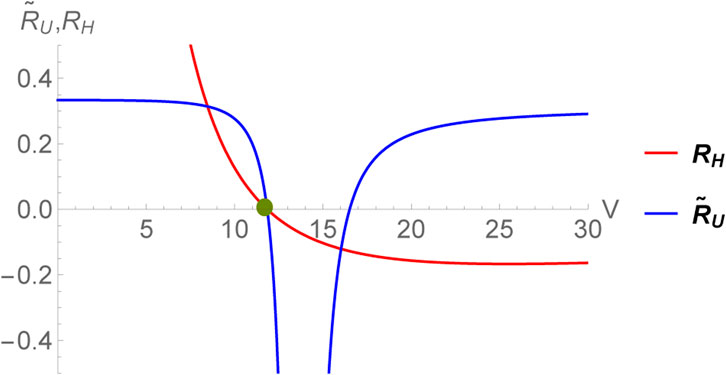
FIGURE 3. Zero crossing of
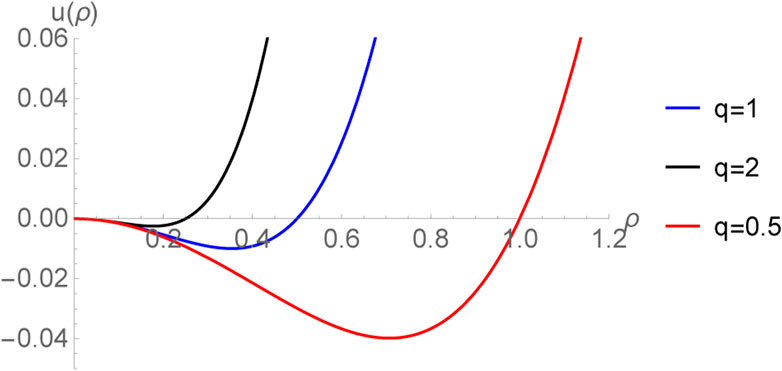
Interestingly, the existence the zero crossings for black holes may be explained naively as follows. If we define a specific volume v = 2r+ = 2(3V/4π)1/3, then Eq. 56 becomes [15]
which resembles the equation of state of a non-ideal fluid, i.e. a fluid with interactions among its molecules. Since v is the specific volume, its reciprocal, i.e. ρ = 1/v can be interpreted as a density of the degrees of freedom [49]. In terms of ρ, the equation of state takes the following intuitive form [61]:
It may be speculated that the underlying degrees of freedom have some resemblance with those of a fluid. Noting that by the equipartition theorem, the kinetic energy of molecules is proportional to T, the first term appearing in the RHS of Eq. 64 can be interpreted as a kinetic energy density of the degrees of freedom. Then, it is natural to interpret the remaining terms as a potential energy density, i.e. one defines the potential energy density:
which has been plotted in Figure 4.
If the sign of the thermodynamic curvatures indicates towards the nature of microscopic interactions, then the point of zero crossing
The condition above gives
Therefore, the Lennard-Jones potential describes the interactions between the microscopic degrees of freedom, at least at a mean field level [28, 61, 99, 100].
The remarks made above may be generalized straightforwardly to the case of charged AdS black holes in an arbitrary number of spacetime dimensions. It should be mentioned that similar studies have been performed for black holes in higher curvature theories, such Einstein-Gauss-Bonnet theory [54–58]. The analysis of the thermodynamic curvatures for such systems can be done in a similar manner as described above for charged AdS black holes in Einstein gravity. Although we do not pursue it further, we summarize the sign of the thermodynamic curvature for several black holes in AdS in the extended thermodynamic framework in Table 2. In the next subsection, we shall consider an alternate set-up, where black hole chemistry has been studied in the context of the AdS/CFT correspondence.
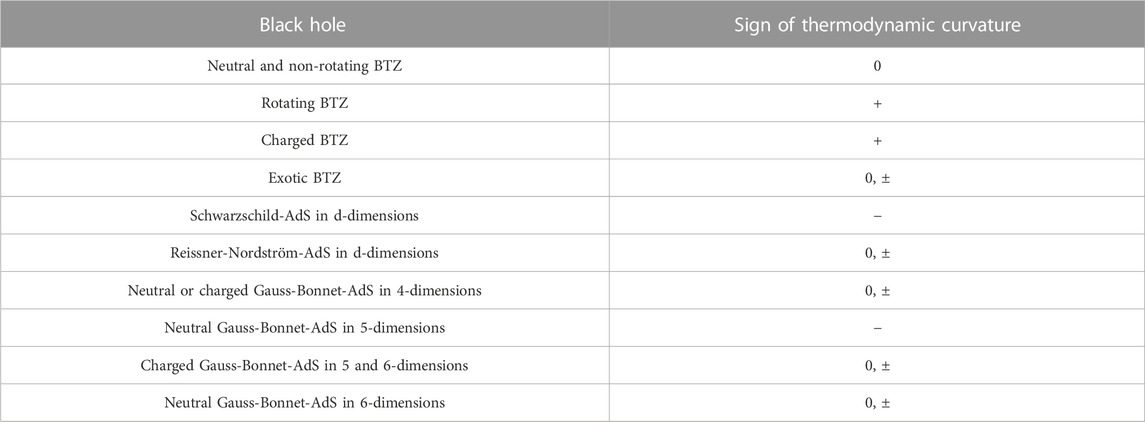
TABLE 2. Sign of Ruppeiner curvature for some black holes in AdS [27, 28, 37–42, 44–49, 51–55, 57–72]. In the table below, by “neutral” we mean the absence of electric charge.
4.2 Boundary
A deep motivation for studying the thermodynamics of black holes in AdS, is the all too important AdS/CFT correspondence [7–9], which is a duality relating: a certain (quantum) theory of gravity in d-dimensional AdS spacetime (known as the bulk) to a conformal field theory (CFT) which is defined on the (d − 1)-dimensional boundary. One of the remarkable checks of this correspondence is the identification of the cross-over from thermal AdS phase to the black hole phase (the Hawking-Page transition), with the large N confinement-deconfinement transition in the boundary field theory [8]. This correspondence has of course received continuous attention with the most well studied case being the correspondence between string theory in AdS5 × S5 and
Here, l gives a measure of number of degrees of freedom via N which is the number of colors of the boundary gauge theory with
Now, with regards to extended thermodynamics motivated above, we saw the possibility of having new pressure P and thermodynamic volume V, variables in the bulk (gravity) description. It is tempting to ask what these quantities correspond to in the holographic dual field theory via the AdS/CFT correspondence. There are several arguments which reveal that the pressure P in bulk introduced as above, is not the usual pressure of the boundary field theory [19–21]. The pressure of the boundary theory is fully determined from the partition function of the theory. However, in the bulk, the pressure comes from a different notion of a variable Λ. Gauge/gravity duality is well studied in the large N limit giving several clarifying results, which is the limit of large l or small curvature limit. On the field theory side, N is generally the rank of the gauge group and sets the number of degrees of freedom (which are actually proportional to N2 for the U(N) gauge group). This means that a dynamical Λ, giving pressure P = −Λ/8πGd in the bulk, should correspond to a dynamical N on the holographic dual side [20]. Varying the number of branes N, might mean holographic renormalization group (RG) flow and more interestingly, to a tour in the space of dual field theories [19]. It is well known that RG flow changes the effective cosmological constant of the underlying theory and also plays an active role in changing the number of degrees of freedom.
It is important to note here that: in traditional black hole thermodynamics (when Λ is not dynamical), the gauge/gravity correspondence suggests identifying the bulk quantities such as temperature T and entropy S with the quantities in the boundary. What changes now, in the context of a dynamical Λ is that, although black hole mass M continues get identified with internal energy U of the boundary [19]; in the bulk M is identified with enthalpy H = U + PV. This holographic interpretation was argued in several works to be a plausible starting point to discuss holographic aspects of black hole heat engines, most notably in [19]. There are further subtleties such as the role of the Newton’s constant Gd in the extended first law of black hole thermodynamics. Such questions are currently being explored [101–103].
Let us consider the approach adopted in [68–72], where a dynamical cosmological constant in the bulk corresponds to varying the number of colours on the boundary [20]. For definiteness, we shall consider black holes in AdS5× S5. The bulk metric field reads [10]
where,
with
where l is the radius of the AdS5 spacetime related to the cosmological constant as
Here, it is the ten dimensional Newton’s constant G(10) and the ten dimensional Planck length lP (linked as
where
Thus, from Eq. 73, the Hawking temperature is calculated to be
which has a minimum value, Tmin at
Before computing the thermodynamic curvatures, it is important to find the specific heats.
It diverges at T = Tmin and is positive in the region of the large black hole while it is negative for that of the small black hole [6]. In a fixed chemical potential setting, Cμ is calculated to be
where h = u − μN2. Thus, we now have two ensembles, one with fixed N2 while the other is with fixed μ. In the latter, the first law reads: dh = Tds − N2dμ.
Let us begin with the fixed N2 ensemble, in which following the treatment presented in section-(III), we have
and this can be written in different parametrizations. The associated thermodynamic curvature, Ru takes the following form:
where,
The thermodynamic curvature Ru has been plotted in Figure 5, together with the specific heats Cμ and
thereby giving the same exponents as found in the bulk concerning the divergence of CP and the normalized curvature
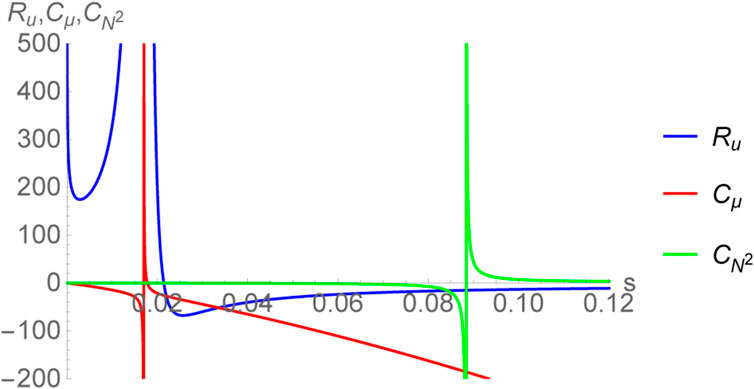
FIGURE 5. Plot of thermodynamic curvature Ru together with the specific heats
In the fixed μ ensemble, the Ruppeiner metric turns out to have the following form:
The associated curvature scalar, labelled as Rh is computed to be
where,
The curvature scalar Rh has been plotted in Figure 6, together with the specific heats
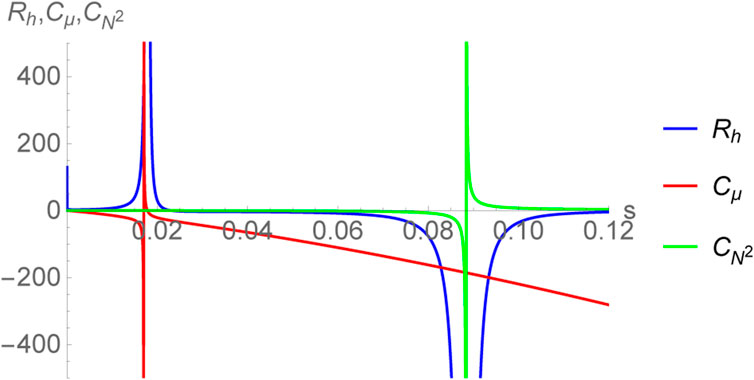
FIGURE 6. Plot of thermodynamic curvature Rh together with the specific heats
Now, if one considers the sign of the thermodynamic curvature to be an empirical indicator of the nature of microscopic interactions, then clearly for the large black hole branch (s > 0.0883883) one has Ru, Rh < 0 suggesting that the system is attraction dominated, reminiscent of an ideal gas of bosons. Moreover, it was shown in [72] (see also [20]) that |Ru| increases as one approaches towards z → 1 where z = eμ/T is the fugacity parameter. For an ideal gas of bosons, this limit indicates Bose condensation wherein the absolute value of the thermodynamic curvature grows indicating the growth of inter-particle correlations [36]. The fact that the same behavior is observed for black holes in AdS5 × S5 may suggest that the degrees of freedom undergo an analogous condensation [20]. However, a satisfactory understanding of this can only be achieved via computations performed in a quantum theory of gravity. Nevertheless, the study of the thermodynamic curvature may reveal early insights into the physics of black holes.
5 Discussion
Geometrical approaches to thermodynamics and in particular, thermodynamics of black holes have received constant attention due to their potential to provide a unique perspective on connecting the microscopic to macroscopic physics [27, 28, 37–49, 51–55, 57–72]. As summarised in this review, methods of contact and metric geometry have given novel insights (though qualitative in nature) on the nature of dominant interactions and phase transitions in black holes in AdS in the extended thermodynamics set up. It should be mentioned here that the thermodynamic metrics explored in this review have been generalized further by several groups with varied advantages, such as [42–44, 78], among others. For instance, in the framework of geometrothermodynamics [42, 78], the thermodynamic metric is Legendre invariant, i.e. it is invariant under Legendre transformations. However, the metric is not a Hessian although there have been recent attempts to derive it from statistical mechanics [104].
In this review, we considered Hessian thermodynamic metrics in different ensembles connected by (partial) Legendre transforms and discussed their complimentary behavior as far as divergences are concerned [79]. While such metrics are not Legendre invariant, they are physically straightforward to motivate on the grounds of thermodynamic fluctuation theory. We have emphasized upon ensemble non-equivalence and reparametrizations of Hessian metrics in various choices of independent coordinates. We then considered the most widely used Hessian metric, the Ruppeiner metric [22, 24] and listed the sources of its divergences from general considerations. They were then verified through various examples considered subsequently. It was mentioned that the sign of the thermodynamic curvature could possibly indicate towards the nature of microscopic interactions in a thermodynamic system. While this can indeed be verified for the van der Waals fluid or ideal quantum gases [36], one cannot yet ascertain its validity for a general thermodynamic system. However, keeping in mind that black holes in the extended thermodynamics framework do admit a van der Waals-like behavior, one may gain early insights into the microscopic interactions from studying the behavior of the thermodynamic curvature. In this sense, it is encouraging to explore the thermodynamic geometry of black holes in various settings.
In section-(IV), we applied the ideas developed in sections-(II) to (III), to study thermodynamic geometry of black holes in AdS spacetimes in the extended thermodynamics framework. In subsections-(A) and (B), the thermodynamic geometries of the bulk and the boundary (via the gauge/gravity duality) settings were discussed respectively. We briefly touched upon the applications of thermodynamic geometry in a holographic setting where the black hole in the AdS bulk is dual to a finite temperature gauge theory on the boundary. While some consistent results were demonstrated including the exponent ‘2’ for the thermodynamic curvature, it should be pointed out that in the context of extended thermodynamics, there have been recent developments on new ideas in relating the holographic dual theories [101–103]. It would be interesting to extend the methods summarized in this review to such situations.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
AG. would like to thank the Ministry of Education (MoE), Government of India for financial support in the form of a Prime Minister’s Research Fellowship (ID: 1200454). CB. Gratefully acknowledges the support received from DST (S.E.R.B.), Government of India, MATRICS (Mathematical Research Impact Centric Support) Grant No. MTR/2020/000135.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bardeen JM, Carter B, Hawking SW. The four laws of black hole mechanics. Commun Math Phys (1973) 31:161–70. doi:10.1007/bf01645742
3. Bekenstein JD. Generalized second law of thermodynamics in black-hole physics. Phys Rev D (1974) 9:3292–300. doi:10.1103/physrevd.9.3292
4. Hawking SW. Particle creation by black holes. Commun Math Phys (1975) 43:199. Erratum: [Commun. Math. Phys. 46, 206 (1976)]. doi:10.1007/bf01608497
5. Hawking SW. Black holes and thermodynamics. Phys Rev D (1976) 13:191–7. doi:10.1103/physrevd.13.191
6. Hawking SW, Page DN. Thermodynamics of black holes in anti-de Sitter space. Commun Math Phys (1983) 87:577–88. doi:10.1007/bf01208266
7. Maldacena JM. The large-N limit of superconformal field theories and supergravity. Int J Theor Phys (1999) 38:1113. [Adv. Theor. Math. Phys. 2, 231 (1998)]. doi:10.1023/A:1026654312961
8. Witten E. Anti-de Sitter space and holography. Adv Theor Math Phys (1998) 2:253. doi:10.4310/ATMP.1998.v2.n2.a2
9. Witten E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv Theor Math Phys (1998) 2:505. doi:10.4310/ATMP.1998.v2.n3.a3
10. Chamblin A, Emparan R, Johnson CV, Myers RC. Charged AdS black holes and catastrophic holography. Phys Rev D (1999) 60:064018. doi:10.1103/physrevd.60.064018
11. Chamblin A, Emparan R, Johnson CV, Myers RC. Holography, thermodynamics, and fluctuations of charged AdS black holes. Phys Rev D (1999) 60:104026. doi:10.1103/physrevd.60.104026
12. Kastor D, Ray S, Traschen J. Enthalpy and the mechanics of AdS black holes. Class Quant Grav (2009) 26:195011. doi:10.1088/0264-9381/26/19/195011
13. Dolan BP. The cosmological constant and black-hole thermodynamic potentials. Class Quant Grav (2011) 28:125020. doi:10.1088/0264-9381/28/12/125020
14. Cvetic M, Gibbons G, Kubiznak D, Pope C. Black hole enthalpy and an entropy inequality for the thermodynamic volume. Phys Rev D (2011) 84:024037. doi:10.1103/physrevd.84.024037
15. Kubiznak D, Mann RB. P − V criticality of charged AdS black holes. J High Energ Phys (2012) 07:033. doi:10.1007/JHEP07(2012)033
16. Gunasekaran S, Mann RB, Kubiznak D. Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. J High Energ Phys (2012) 11:110. doi:10.1007/JHEP11(2012)110
17. Cai RG, Cao LM, Li L, Yang RQ. Measurements of branching fractions of leptonic and hadronic Ds+ meson decays and extraction of the Ds+ meson decay constant. J High Energ Phys (2013) 09:005. doi:10.1007/JHEP09(2013)139
18. Frassino AM, Mann RB, Mureika JR. Lower-dimensional black hole chemistry. Phys Rev D (2015) 92:124069. doi:10.1103/physrevd.92.124069
19. V Johnson C. Holographic heat engines. Class Quan Grav (2014) 31:205002. doi:10.1088/0264-9381/31/20/205002
20. Dolan BP. Entanglement entropy: A perturbative calculation. J High Energ Phys (2014) 10:179. doi:10.1007/JHEP12(2014)179
21. Karch A, Robinson B. Holographic black hole chemistry. J High Energ Phys (2015) 12:073. doi:10.1007/JHEP12(2015)073
22. Ruppeiner G. Erratum: Riemannian geometry in thermodynamic fluctuation theory. Rev Mod Phys (1995) 67:605. [Erratum: Rev. Mod. Phys. 68, 313 (1996)]. doi:10.1103/revmodphys.68.313
23. Aman J, Bengtsson I, Pidokrajt N. Thermodynamic metrics and black hole physics. Entropy (2015) 17(9):6503–18. doi:10.3390/e17096503
24. Ruppeiner G. Thermodynamics: A riemannian geometric model. Phys Rev A (1979) 20:1608–13. doi:10.1103/physreva.20.1608
25. Weinhold F. Metric geometry of equilibrium thermodynamics. J Chem Phys (1975) 63:2479–83. doi:10.1063/1.431689
26. Crooks GE. Measuring thermodynamic length. Phys Rev Lett (2007) 99:100602. doi:10.1103/physrevlett.99.100602
27. Wei SW, Liu YX, Mann RB. Repulsive interactions and universal properties of charged anti–de Sitter black hole microstructures. Phys Rev Lett (2019) 123:071103. doi:10.1103/physrevlett.123.071103
28. Wei SW, Liu YX, Mann RB. Ruppeiner geometry, phase transitions, and the microstructure of charged AdS black holes. Phys Rev D (2019) 100:124033. doi:10.1103/physrevd.100.124033
29. Janyszek H, Mrugala R. Riemannian geometry and the thermodynamics of model magnetic systems. Phys Rev A (1989) 39:6515–23. doi:10.1103/physreva.39.6515
30. Dolan BP. Geometry and thermodynamic fluctuations of the Ising model on a Bethe lattice. Proc Roy Soc Lond A (1998) 454:2655–65. doi:10.1098/rspa.1998.0274
31. Dolan BP, Johnston DA, Kenna R. The Information geometry of the one-dimensional Potts model. J Phys A (2002) 35:9025–36. doi:10.1088/0305-4470/35/43/303
32. Janke W, Johnston DA, Kenna R. Information geometry and phase transitions. Physica A (2004) 336:181–6. doi:10.1016/j.physa.2004.01.023
33. Kumar P, Sarkar T. Geometric critical exponents in classical and quantum phase transitions. Phys Rev E (2014) 90:042145. doi:10.1103/physreve.90.042145
34. Maity R, Mahapatra S, Sarkar T. Information geometry and the renormalization group. Phys Rev E (2018) 98:052112.
35. Ruppeiner G. Thermodynamic curvature measures interactions. Am J Phys (2010) 78:1170–80. doi:10.1119/1.3459936
36. Janyszek H, Mrugala R. Riemannian geometry and stability of ideal quantum gases. J Phys A: Math Gen (1990) 23:467–76. doi:10.1088/0305-4470/23/4/016
37. Cai RG, Cho JH. Thermodynamic curvature of the BTZ black hole. Phys Rev D (1999) 60:067502. doi:10.1103/physrevd.60.067502
38. Aman JE, Bengtsson I, Pidokrajt N. Geometry of black hole thermodynamics. Gen Rel Grav (2003) 35:1733–43. doi:10.1023/a:1026058111582
39. Shen Jy., Cai RG, Wang B, Su RK. Int J Mod Phys A (2007) 22:11–27. doi:10.1142/s0217751x07034064
40. Sarkar T, Sengupta G, Tiwari BN. On the thermodynamic geometry of BTZ black holes. J High Energ Phys (2006) 11:015. doi:10.1088/1126-6708/2006/11/015
41. Mirza B, Zamani-Nasab M. Ruppeiner geometry of RN black holes: Flat or curved? J High Energ Phys (2007) 06:059. doi:10.1088/1126-6708/2007/06/059
42. Quevedo H. Geometrothermodynamics of black holes. Gen Rel Grav (2008) 40:971–84. doi:10.1007/s10714-007-0586-0
43. Hendi SH, Panahiyan S, Eslam Panah B, Momennia M. A new approach toward geometrical concept of black hole thermodynamics. Eur Phys J C (2015) 75:507. doi:10.1140/epjc/s10052-015-3701-5
44. Mansoori SAH, Mirza B, Sharifian E. Extrinsic and intrinsic curvatures in thermodynamic geometry. Phys Lett B (2016) 759:298–305. doi:10.1016/j.physletb.2016.05.096
45. Banerjee R, Ghosh S, Roychowdhury D. New type of phase transition in Reissner Nordström–AdS black hole and its thermodynamic geometry. Phys Lett B (2011) 696:156–62. doi:10.1016/j.physletb.2010.12.010
46. Sahay A, Sarkar T, Sengupta G. On the thermodynamic geometry and critical phenomena of AdS black holes. J High Energ Phys (2010) 07:082. doi:10.1007/JHEP07(2010)082
47. Liu H, Lu H, Luo M, Shao KN. Measuring black hole formations by entanglement entropy via coarse-graining. J High Energ Phys (2010) 12:054. doi:10.1007/JHEP11(2010)054
48. Guo XY, Li HF, Zhang LC, Zhao R. Microstructure and continuous phase transition of a Reissner-Nordstrom-AdS black hole. Phys Rev D (2019) 100:064036. doi:10.1103/physrevd.100.064036
49. Wei SW, Liu YX. Erratum: Insight into the microscopic structure of an AdS black hole from a thermodynamical phase transition [Phys. Rev. Lett. 115, 111302 (2015)]. Phys Rev Lett (2015) 115:111302. [Erratum: Phys. Rev. Lett. 116, 169903 (2016)]. doi:10.1103/physrevlett.116.169903
50. Belhaj A, Chabab M, El Moumni H, Masmar K, Sedra MB. On thermodynamics of AdS black holes in M-theory. Eur Phys J C (2016) 76(2):73. doi:10.1140/epjc/s10052-016-3928-9
51. Bhattacharya K, Majhi BR. Thermogeometric description of the van der Waals like phase transition in AdS black holes. Phys Rev D (2017) 95:104024. doi:10.1103/physrevd.95.104024
52. Miao YG, Xu ZM. Thermal molecular potential among micromolecules in charged AdS black holes. Phys Rev D (2018) 98:044001. doi:10.1103/physrevd.98.044001
53. Xu ZM, Wu B, Yang WL. Ruppeiner thermodynamic geometry for the Schwarzschild-AdS black hole. Phys Rev D (2020) 101:024018. doi:10.1103/physrevd.101.024018
54. Wei SW, Liu YX. Intriguing microstructures of five-dimensional neutral Gauss-Bonnet AdS black hole. Phys Lett B (2020) 803:135287. doi:10.1016/j.physletb.2020.135287
55. Ghosh A, Bhamidipati C. Thermodynamic geometry for charged Gauss-Bonnet black holes in AdS spacetimes. Phys Rev D (2020) 101:046005. doi:10.1103/physrevd.101.046005
56. Zhou R, Liu YX, Wei SW. Phase transition and microstructures of five-dimensional charged Gauss-Bonnet-AdS black holes in the grand canonical ensemble. Phys Rev D (2020) 102:124015. doi:10.1103/physrevd.102.124015
57. Wei SW, Liu YX. Extended thermodynamics and microstructures of four-dimensional charged Gauss-Bonnet black hole in AdS space. Phys Rev D (2020) 101:104018. doi:10.1103/physrevd.101.104018
58. Mansoori SAH. Thermodynamic geometry of the novel 4-D Gauss–Bonnet AdS black hole. Phys Dark Universe (2021) 31:100776. doi:10.1016/j.dark.2021.100776
59. Ghosh A, Bhamidipati C. Thermodynamic geometry and interacting microstructures of BTZ black holes. Phys Rev D (2020) 101:106007. doi:10.1103/physrevd.101.106007
60. Xu ZM, Wu B, Yang WL. Diagnosis inspired by the thermodynamic geometry for different thermodynamic schemes of the charged BTZ black hole. Eur Phys J C (2020) 80:997. doi:10.1140/epjc/s10052-020-08563-x
61. Singh A, Ghosh A, Bhamidipati C. Thermodynamic curvature of AdS black holes with dark energy. Front Phys (2021) 9:631471. doi:10.3389/fphy.2021.631471
62. Dehyadegari A, Sheykhi A, Wei SW. Microstructure of charged AdS black hole via P−V criticality. Phys Rev D (2020) 102:104013. doi:10.1103/physrevd.102.104013
63. Mansoori SAH, Rafiee M, Wei SW. Universal criticality of thermodynamic curvatures for charged AdS black holes. Phys Rev D (2020) 102:124066. doi:10.1103/physrevd.102.124066
64. Rafiee M, Mansoori SAH, Wei SW, B Mann R. Universal criticality of thermodynamic geometry for boundary conformal field theories in gauge/gravity duality. Phys Rev D (2022) 105:024058. doi:10.1103/physrevd.105.024058
65. Kumara AN, Rizwan CLA, Hegde K, Ali MS, Ajith KM. Ruppeiner geometry, reentrant phase transition, and microstructure of Born-Infeld AdS black hole. Phys Rev D (2021) 103:044025. doi:10.1103/physrevd.103.044025
66. Wei SW, Liu YX, Mann RB. Novel dual relation and constant in Hawking-Page phase transitions. Phys Rev D (2020) 102:104011. doi:10.1103/physrevd.102.104011
67. Yerra PK, Bhamidipati C. Ruppeiner curvature along a renormalization group flow. Phys Lett B (2021) 819:136450. doi:10.1016/j.physletb.2021.136450
68. Zhang JL, Cai RG, Yu H. Phase transition and thermodynamical geometry for Schwarzschild AdS black hole in AdS5 × S5 spacetime. J High Energ Phys (2015) 02:143. doi:10.1007/JHEP02(2015)143
69. Zhang JL, Cai RG, Yu H. Phase transition and thermodynamical geometry of Reissner-Nordström-AdS black holes in extended phase space. Phys Rev D (2015) 91:044028. doi:10.1103/physrevd.91.044028
70. Maity R, Roy P, Sarkar T. Black hole phase transitions and the chemical potential. Phys Lett B (2017) 765:386–94. doi:10.1016/j.physletb.2016.12.004
71. Wei SW, Liang B, Liu YX. Critical phenomena and chemical potential of a charged AdS black hole. Phys Rev D (2017) 96:124018. doi:10.1103/physrevd.96.124018
72. Mahish S, Ghosh A, Bhamidipati C. Thermodynamic curvature of the Schwarzschild-AdS black hole and Bose condensation. Phys Lett B (2020) 811:135958. doi:10.1016/j.physletb.2020.135958
74. Mrugala R. Recent developments in semiclassical floquet theories for intense-field multiphoton processes. Rep Math Phys (1985) 21:197. doi:10.1016/S0065-2199(08)60143-8
75. Mrugala R, Nulton JD, Schön JC, Salamon P. Statistical approach to the geometric structure of thermodynamics. Phys Rev A (1990) 41:3156–60. doi:10.1103/physreva.41.3156
76. Mrugala R, Nulton JD, Schön JC, Salamon P. Contact structure in thermodynamic theory. Rep Math Phys (1991) 29:109–21. doi:10.1016/0034-4877(91)90017-H
77. Bravetti A, Lopez-Monsalvo CS, Nettel F. Contact symmetries and Hamiltonian thermodynamics. Ann Phys (2015) 361:377–400. doi:10.1016/j.aop.2015.07.010
79. Bravetti A, Nettel F. Thermodynamic curvature and ensemble nonequivalence. Phys Rev D (2014) 90:044064. doi:10.1103/physrevd.90.044064
80. Lopez-Monsalvo CS, Nettel F, Pineda-Reyes V, Escamilla-Herrera LF. Contact polarizations and associated metrics in geometric thermodynamics. J Phys A: Math Theor (2021) 54:105202. doi:10.1088/1751-8121/abddeb
81. Pineda-Reyes V, Escamilla-Herrera LF, Gruber C, Nettel F, Quevedo H. Reparametrizations and metric structures in thermodynamic phase space. Physica A (2021) 563:125464. doi:10.1016/j.physa.2020.125464
82. Mrugala R. On a Riemannian metric on contact thermodynamic spaces. Rep Math Phys (1996) 38:339. doi:10.1016/S0034-4877(97)84887-2
83. Geiges H. An introduction to contact topology. Cambridge, UK: Cambridge University Press (2008).
84. Arnold VI. Singularities of caustics and wave fronts. Berlin, Germany: Springer Netherlands (1990).
85.VI Arnold, editor. Mathematical methods of classical mechanics. Graduate texts in mathematics. 2nd ed. New York, NY: Springer (1989). p. 60. doi:10.1007/978-1-4757-1693-1
86. De Leon M, Sardon C. Cosymplectic and contact structures for time-dependent and dissipative Hamiltonian systems. J Phys A (2017) 50:255205. doi:10.1088/1751-8121/aa711d
87. Bravetti A, Cruz H, Tapias D. Contact Hamiltonian mechanics. Ann Phys (2017) 376:17–39. doi:10.1016/j.aop.2016.11.003
88. Sasaki S. On differentiable manifolds with certain structures which are closely related to almost contact structure, I. Tohoku Math J (1960) 12:459. doi:10.2748/tmj/1178244407
89. Hatakeyama Y. On the existence of Riemann metrics associated with a 2-form of rank 2r. Tohoku Math J (1962) 14:162. doi:10.2748/tmj/1178244171
90. Sasaki S, Hatakeyama Y. On differentiable manifolds with contact metric structures. J Math Sot Jpn (1962) 14:249. doi:10.2969/jmsj/01430249
91. Rajeev SG. A Hamilton–Jacobi formalism for thermodynamics. Ann Phys (2008) 323:2265–85. doi:10.1016/j.aop.2007.12.007
92. Ghosh A, Bhamidipati C. Contact geometry and thermodynamics of black holes in AdS spacetimes. Phys Rev D (2019) 100:126020. doi:10.1103/physrevd.100.126020
93. Baldiotti MC, Fresneda R, Molina C. A Hamiltonian approach for the Thermodynamics of AdS black holes. Ann Phys (2017) 382:22–35. doi:10.1016/j.aop.2017.04.009
94. Barré J, Mukamel D, Ruffo S. Inequivalence of ensembles in a system with long-range interactions. Phys Rev Lett (2001) 87:030601. doi:10.1103/physrevlett.87.030601
95. Leyvraz F, Ruffo S. Ensemble inequivalence in systems with long-range interactions. J Phys A: Math Gen (2002) 35:285–94. doi:10.1088/0305-4470/35/2/308
96. Rottman C, Wortis M. Statistical mechanics of equilibrium crystal shapes: Interfacial phase diagrams and phase transitions. Phys Rep (1984) 103:59–79. doi:10.1016/0370-1573(84)90066-8
98. Andersen HC. Molecular dynamics simulations at constant pressure and/or temperature. J Chem Phys (1980) 72:2384–93. doi:10.1063/1.439486
99. Dutta S, Singh Punia G. Interactions between AdS black hole molecules. Phys Rev D (2021) 104:126009. doi:10.1103/physrevd.104.126009
100. Wei SW, Liu YX, Mann RB. Characteristic interaction potential of black hole molecules from the microscopic interpretation of Ruppeiner geometry (2021). arXiv:2108.07655 [gr-qc].
101. Visser MR. Holographic thermodynamics requires a chemical potential for color. Phys Rev D (2022) 105:106014. doi:10.1103/physrevd.105.106014
102. Cong W, Kubiznak D, Mann RB. Thermodynamics of AdS black holes: Critical behavior of the central charge. Phys Rev Lett (2021) 127:091301. doi:10.1103/physrevlett.127.091301
103. Cong W, Kubiznak D, Mann RB, Visser MR. Holographic CFT phase transitions and criticality for charged AdS black holes. J High Energ Phys volume (2022) 2022:174. doi:10.1007/jhep08(2022)174
Keywords: thermodynamic curvature, black hole chemistry, contact geometry, phase transitions, black hole thermodynamics, AdS/CFT, holography
Citation: Ghosh A and Bhamidipati C (2023) Contact and metric structures in black hole chemistry. Front. Phys. 11:1132712. doi: 10.3389/fphy.2023.1132712
Received: 27 December 2022; Accepted: 30 January 2023;
Published: 16 February 2023.
Edited by:
Mohamed Chabab, Cadi Ayyad University, MoroccoReviewed by:
Samir Iraoui, Cadi Ayyad University, MoroccoEkrem Aydiner, Istanbul University, Türkiye
Copyright © 2023 Ghosh and Bhamidipati. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aritra Ghosh, YWczNEBpaXRiYnMuYWMuaW4=
†These authors have contributed equally to this work
 Aritra Ghosh
Aritra Ghosh Chandrasekhar Bhamidipati
Chandrasekhar Bhamidipati