Scaling laws of out-of-time-order correlators in a non-Hermitian kicked rotor model

We investigate the dynamics of the out-of-time-order correlators (OTOCs) via a non-Hermitian extension of the quantum kicked rotor model, where the kicking potential satisfies $\mathcal{PT}$-symmetry. The spontaneous $\mathcal{PT}$-symmetry breaking emerges when the strength of the imaginary part of the kicking potential exceeds a threshold value. We find, both analytically and numerically, that in the broken phase of $\mathcal{PT}$ symmetry, the OTOCs rapidly saturate with time evolution. Interestingly, the late-time saturation value scales as a pow-law in the system size. The mechanism of such scaling law results from the interplay between the effects of the nonlocal operator in OTOCs and the time reversal induced by non-Hermitian-driven potential.

1 Introduction

In recent years, the out-of-time-order correlators (OTOCs) C = −⟨[A(t),B]²⟩ have attracted extensive attention in diverse fields of physics, ranging from quantum chaos [1,2] and quantum information [3] to black hole physics [4]. A fundamental concept in these fields is information scrambling, namely, the spread of information encoding in local degrees of freedoms over the entire system to be inaccessible by local measurement [5–7]. This progress is quantified by the growth of local operators with time evolution, due to which it will be no longer commutable with other operators, separated by a long distance [8,9]. The operator growth is dominated by the classical chaos in such a way that the rate of exponential growth of OTOCs is proportional to the classical Lyapunov exponent [10,11]. Nowadays, the OTOCs are being widely used to diagnose the many-body localization [12,13], quantum entanglement [14–16], quantum thermalization [17–19], and many-body chaos [20–22], hence promoting intensive investigations in the field of many-body physics [23,24]. Interestingly, experimental advances have observed both the quantum information scrambling and quantum phase transition by measuring the OTOCs in the system of the quantum circuit [25,26] and a nuclear magnetic resonance quantum simulator [27].

For $\mathcal{PT}$-symmetric systems, the dynamics of OTOCs signals the Yang–Lee edge singularity [28] of phase transition and shows the quantized response to external driven potential [29]. It is now widely accepted that the non-Hermiticity is a fundamental modification to conventional quantum mechanics [30–36] since many systems, such as optics propagation in the “gain-or-loss” medium [37–39], the electronics transport in the dissipative circuit [40–43], and cold atoms in the tailored magneto-optical trap [44–48], are described by a non-Hermitian theory. The extension of Floquet systems to non-Hermitian regimes uncovers rich understandings of physics [49–53]. For example, the scaling of the spontaneous $\mathcal{PT}$-symmetry breaking and its relation with classical chaos are revealed in a non-Hermitian chaotic system [54]. The ballistic energy diffusion [55] and quantized acceleration of momentum current [56] are reported in a $\mathcal{PT}$-symmetric kicked rotor (PTKR) model. The quantum kicked rotor (QKR) and its variants provide ideal platforms for investigating fundamental problems, such as the quantum transport in momentum-space lattice [57,58], the quantum-to-classical transition of chaotic systems [59,60], and the quantum thermalization in many-body systems [61]. The operator growth and chaotic information scrambling in different variations of QKR are still open issues and require urgent investigations.

In this context, we investigate, both analytically and numerically, the dynamics of OTOCs in a PTKR model, with focus on the broken phase of $\mathcal{PT}$ symmetry. We observed that the OTOCs rapidly saturate with time evolution. Interestingly, the saturation value is the power-law function of the dimension of the system, which demonstrates a kind of scaling-law of the OTOCs with the system size. The mechanism of such scaling law results from two aspects. One is that the action of the non-local operators constructing the OTOCs on the state leads to a power-law decayed distribution in momentum space. The other is that the non-Hermitian kicking potential induces the perfect time reversal of thequantum state in momentum space. Using the power-law decayed quantum state, we analytically obtain the scaling of OTOCs with the size of momentum space, for which the OTOCs is the power-law function of the dimension of the system. This demonstrates that the OTOCs unboundedly increase with the system size, revealing a kind of fast scrambling [62,63]. Our result sheds light on the Floquet engineering of the fast scramblers in the non-Hermitian map systems.

The paper is organized as follows. In Section 2, we show our model and the scaling-law of OTOCs. In Section 3, we present the theoretical analysis of the scaling law. Section 4 contains the conclusion and discussion.

2 Model and results

The Hamiltonian of a PTKR reads

$H=\frac{p^2}{2}+V_K\left(\theta \right)\sum _{n=0}^{\infty }\delta \left(t-t_n\right),(1)$

with the kicking potential

$V_K\left(\theta \right)=K\left[\cos \left(\theta \right)+i\lambda \sin \left(\theta \right)\right],(2)$

which satisfies the $\mathcal{PT}$ symmetry $V_K(\theta )=V_K^{*}(-\theta )$ [55]. Here, p = −iℏ_eff∂/∂θ is the angular momentum operator and θ is the angle coordinate, which obey the communication relation [θ, p] = iℏ_eff with ℏ_eff, the effective Planck constant. The parameters K and λ control the strength of the real and imaginary part of the kicking potential, respectively. The time t_n is integer, i.e., t_n = 1, 2 … , indicating the kicking number. All variables are properly scaled and thus in dimensionless units. The eigenequation of the angular momentum operator is p|ϕ_n⟩ = p_n|ϕ_n⟩ with eigenstate $⟨\theta |{\varphi }_n⟩=e^{in\theta }/\sqrt{2\pi }$ and eigenvalue p_n = nℏ_eff. On the basis of |ϕ_n⟩, an arbitrary quantum state can be expanded as $|\psi \rangle ={\sum }_{n=-\infty }^{\infty }\psi (p_n)|{\varphi }_n\rangle$.

The evolution of the quantum state from t_j to t_j+1 is given by |ψ(t_j+1)⟩ = U|ψ(t_j)⟩, where the Floquet operator U takes the form

$U=\exp \left(-i\frac{p^2}{2{\hslash }_{\text{eff}}}\right)\exp \left[-i\frac{V_K\left(\theta \right)}{{\hslash }_{\text{eff}}}\right].(3)$

In numerical simulations, one period evolution splits into two steps, namely, the kicking evolution $U_K(\theta )=\exp \left(-i{V}_K(\theta )/{\hslash }_{\text{eff}}\right)$ and the free evolution $U_f(p_n)=\exp \left(-i{p}_n^2/2{\hslash }_{\text{eff}}\right)$ [57–59]. At first, we construct the kicking evolution in angle coordinate space, ψ′(θ_l) = U_K(θ_l)ψ(θ_l, t_j) with discrete grids θ_l = −π + 2πl/N (0 ≤ l < N) and N = 2^m. Then, the fast Fourier transform is used to realize the transformation of the state |ψ′⟩ to momentum space yielding the state ψ′(p_n) with −Nℏ_eff/2 ≤ p_n ≤ (N − 1)ℏ_eff/2. Finally, we take the free evolution, i.e., ψ(p_n, t_j+1) = U_f(p_n)ψ′(p_n). By repeating the same procedure, one can get the state |ψ(t_n)⟩ at an arbitrary time. In the experiment, the PTKR model can be realized by an optical platform with a Fabry–Perot resonator consisting of two plane mirrors, one of which is equipped with a mixed-loss phase grating to mimic the periodic kicking sequence of PT-symmetric potential [55]. It is found that in the broken phase of PT-symmetry, the light propagation in the Fabry–Perot resonator demonstrates the unidirectional transport in frequency domain.

The eigenequation of the Floquet operator has the expression U|φ_ɛ⟩ = e^−iɛ|φ_ɛ⟩, where the eigenvalue ɛ is named as quasienergy. Intrinsically, the quasienergy of the PTKR model is complex, i.e., ɛ = ɛ_r + iɛ_i, when the value λ exceeds a threshold value, i.e., λ > λ_c [54,55], which is a signature of the spontaneous $\mathcal{PT}$-symmetry breaking of Floquet systems. Based on the relation $|\psi (t_n)\rangle ={\sum }_{\epsilon }{C}_{\epsilon }{e}^{-i{\epsilon }_r{t}_n}{e}^{{\epsilon }_i{t}_n}|{\epsilon }_{\epsilon }\rangle$, the norm $\mathcal{N}=⟨\psi (t_n)|\psi (t_n)⟩$ exponentially increases with time for positive ɛ_i. We numerically investigate the time evolution of $\mathcal{N}$ for different λ. Figure 1A shows that for very small λ (e.g., λ = 10^–4), the norm remains at unity $\mathcal{N}=1$ with the time evolution, which implies that ɛ_i = 0 and the system is in the unbroken phase of $\mathcal{PT}$ symmetry. Interestingly, for sufficiently large λ (e.g., λ = 0.002), the norm exponentially increases with time, i.e., $\mathcal{N}=e^{\gamma t}$, signaling the occurrence of the spontaneous $\mathcal{PT}$ symmetry breaking. The growth rate γ increases with the increase of λ. In order to quantify the phase transition point λ_c, we numerically investigate the time-averaged value of norm $\bar{\mathcal{N}}={\sum }_{j=1}^M\mathcal{N}(t_j)/M$ for different values of λ. Our results show that for a specific ℏ_eff, the average value $\bar{\mathcal{N}}$ equals to unity for λ smaller than a critical value λ_c, beyond which the $\bar{\mathcal{N}}$ gradually increases (see Figure 1B). Moreover, the λ_c increases with the increase of ℏ_eff.

FIGURE 1

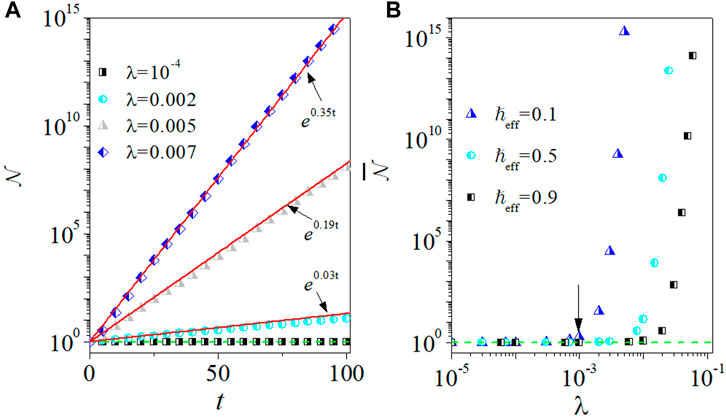
FIGURE 1. (A) Time dependence of $\mathcal{N}$ for ℏ_eff = 0.1 with λ = 10^–4 (squares), 0.002 (circles), 0.005 (triangles), and 0.007 (diamonds). Solid lines indicate the exponential fitting $\mathcal{N}=e^{\gamma t}$. (B) The average value $\bar{\mathcal{N}}$ versus λ with ℏ_eff = 0.1 (squares), 0.5 (circle), and 0.9 (triangles). Arrows mark the phase transition point λ_c for ℏ_eff = 0.1. Horizontal dashed lines in (A,B) denote $\mathcal{N}=1$ and $\bar{\mathcal{N}}=1$, respectively. The parameter is K = 2π.

The OTOCs are defined as the average of the squared commutator, i.e., C(t) = −⟨[A(t),B]²⟩, where both operators A(t) = U^†(t)AU(t) and B are evaluated in the Heisenberg picture, and ⟨⋯ ⟩ = ⟨ψ(t₀)|⋯|ψ(t₀)⟩ indicates the expectation value taken over the initial state |ψ(t₀)⟩ [23]. It usually uses the thermal states for taking the average in the investigation of OTOCs of lattice systems. For the Floquet-driven system, however, there are no well-defined thermal states, as the temperature tends to be infinity as time evolves [64]. Without loss of generality, we choose a Gaussian wavepacket as an initial state, i.e., ψ(θ, 0) = (σ/π)^1/4 exp (−σθ²/2) with σ = 10. We consider the case as A = θ and B = p^m $(m\in \mathbb{N})$, hence $C(t)=-⟨{[\theta (t),p^m]}^2⟩$.

Our main result is the scaling law of the late-time behavior of the OTOCs

$C\left(t\right)\sim N^{2m-1}{\theta }_c^2,(4)$

where N is the dimension of the momentum space of the PTKR model, and θ_c = π/2. This prediction is verified by numerical results in Figure 2. As an illustration, we consider m = 1, 2, and 3 in numerical simulations. Figure 2A shows that for a specific m, the C(t) saturates rapidly as time evolves, which is in perfect agreement with our theoretical prediction in Eq. 4. The critical time for the saturation of C decreases with the increase of λ, until saturation (as shown in Figure 2A). In order to further confirm the scaling law of C(t), we numerically investigate the C at a specific time for different values of N. Figure 2B shows that for t = t₁₀, the value of C increases in the power-law of N, which coincides with the theoretical prediction in Eq. 4. The scaling of C(t) with dimensions of the system demonstrates that it diverges as N → ∞, which is of interest in the study of fast scrambling [63]. We would like to mention that we previously found the scaling law for the OTOCs constructed by A = θ and B = p, in a Gross–Pitaevskii map system [65]. Our present work explores the scaling law for B = p^m with the arbitrary integer m; moreover, it extends the investigation to non-Hermitian systems, which is evidently a significant advance in the fields of operator growth in chaotic systems.

FIGURE 2

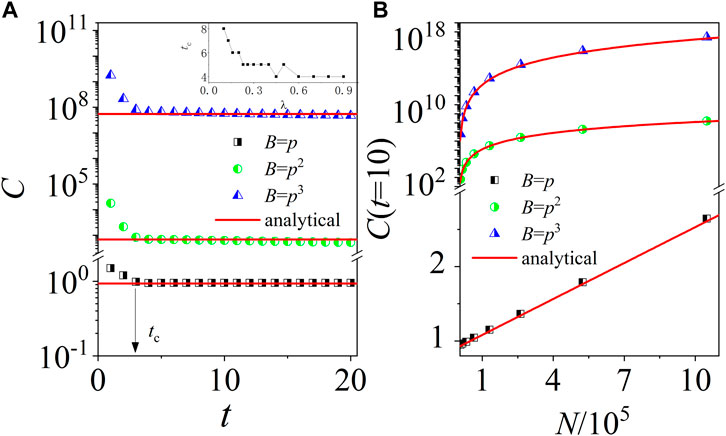
FIGURE 2. (A) Time dependence of C(t) with B = p (squares), p² (circles), and p³ (triangles) with N = 2¹³. The arrow marks the critical time t_c for B = p. Inset: Critical time t_c versus λ. (B) C(t) at the time t = t₁₀ versus N. Solid lines in (A,B) denote our theoretical prediction in Eq. 4. The parameters are K = 2π, λ = 0.9, and ℏ_eff = 0.1.

3 Theoretical analysis

3.1 Scaling law of the C₁(t)

Straightforward derivation yields the expression of OTOCs

$C\left(t\right)=C_1\left(t\right)+C_2\left(t\right)-2\text{Re}\left[C_3\left(t\right)\right],(5)$

where the three terms in right side are defined by

$C_1\left(t\right)=⟨{\psi }_R\left(t_0\right)|p^{2m}|{\psi }_R\left(t_0\right)⟩,(6)$

$C_2\left(t\right)=⟨{\phi }_R\left(t_0\right)|{\phi }_R\left(t_0\right)⟩,(7)$

and

$C_3\left(t\right)=⟨{\psi }_R\left(t_0\right)|p^m|{\phi }_R\left(t_0\right)⟩,(8)$

with |ψ_R (t₀)⟩ = U^†(t_n, t₀)θU (t_n, t₀)|ψ(t₀)⟩ and |φ_R (t₀)⟩ = U^†(t_n, t₀)θU (t_n, t₀)p^m|ψ(t₀)⟩.

To get the state |ψ_R (t₀)⟩, one needs three steps: 1) forward evolution t₀ → t_n, i.e., |ψ(t_n)⟩ = U (t_n, t₀)|ψ(t₀); 2) action of the operator θ on |ψ(t_n)⟩, i.e., $|\tilde{\psi }(t_n)\rangle =\theta |\psi (t_n)\rangle$; and 3) backward evolution t_n → t₀, i.e., $|{\psi }_R(t_0)\rangle =U^{†}(t_{\mathrm{n}},t_0)|\tilde{\psi }(t_n)\rangle$. C₁ (t_n) (see Eq. 6) is just the expectation value of the p^2m taken over the state |ψ_R (t₀)⟩. For the numerical calculation of the state |φ_R (t₀)⟩, one should first construct the operation of p^m on the initial state |ψ(t₀)⟩, i.e., |φ(t₀)⟩ = p^m|ψ(t₀)⟩. Then, forward evolution from t₀ to t_n yields the state |φ(t_n)⟩ = U (t_n, t₀)|φ(t₀)⟩. At time t = t_n, the action of θ on the state |φ(t_n)⟩ results in a new state $|\tilde{\phi }(t_n)\rangle =\theta |\phi (t_n)\rangle$, starting from which the time-reversal process t_n → t₀ yields the state $|{\phi }_R(t_0)\rangle =U^{†}(t_{\mathrm{n}},t_0)|\tilde{\phi }(t_n)\rangle$. The norm of |φ_R (t₀)⟩ is just the C₂ (t_n) (see Eq. 7). As the two states |ψ_R (t₀)⟩ and |φ_R (t₀)⟩ are available at the end of time reversal, one can calculate the C₃ (t_n) according to Eq. 8.

It is known that in the $\mathcal{PT}$-symmetry breaking phase, the norm of quantum state ${\mathcal{N}}_{\psi }(t_n)=⟨\psi (t_n)|\psi (t_n)⟩$ exponentially increases for both the forward and backward time evolutions. To eliminate the contribution of norm to OTOCs, it is necessary to take the normalization for the time-evolved state. Specifically, for the forward evolution t₀ → t_n, we set the norm of the quantum state equals to that of the initial state, i.e., ${\mathcal{N}}_{\psi }(t_j)=⟨\psi (t_0)|\psi (t_0)⟩$ with 0 ≤ j ≤ n. The backward evolution starts from the time t = t_n with the state $|\tilde{\psi }(t_n)\rangle$, whose norm ${\mathcal{N}}_{\tilde{\psi }}(t_n)=⟨\psi (t_n)|{\theta }^2|\psi (t_n)⟩$ is expectation value of θ² with the state |ψ(t_n)⟩. It is evident that the value of ${\mathcal{N}}_{\tilde{\psi }}(t_n)$ is important information encoded by the operation of θ on the state |ψ(t_n)⟩. Based on this, we take the normalization of the quantum state in the backward evolution t_n → t₀ in such a way that its norm equals to ${\mathcal{N}}_{\tilde{\psi }}(t_n)$, i.e., ${\mathcal{N}}_{{\psi }_R}(t_j)={\mathcal{N}}_{\tilde{\psi }}(t_n)$. One can find that for both the forward and backward evolutions, the norm of a time-evolved state always equals that of the state which the time evolution starts from. The same procedure of normalization is applied in calculating C₂ (t_n). Therefore, we have the equivalence ${\mathcal{N}}_{\phi }(t_j)=⟨\phi (t_0)|\phi (t_0)⟩$ and ${\mathcal{N}}_{{\phi }_R}(t_j)=⟨\tilde{\phi }(t_n)|\tilde{\phi }(t_n)⟩$ (0 ≤ j ≤ n) for the forward evolution and time reversal, respectively.

We rewrite the C₁ as

$C_1\left(t\right)=\langle {\psi }_R\left(t_0\right)|p^{2m}|{\psi }_R\left(t_0\right)\rangle =\langle p^{2m}{\left(t_0\right)\rangle }_R{\mathcal{N}}_{{\psi }_R}\left(t_0\right),(9)$

where ${\mathcal{N}}_{{\psi }_R}(t_0)=⟨{\psi }_R(t_0)|{\psi }_R(t_0)⟩$ is the norm of the quantum state |ψ_R (t₀)⟩ and ${⟨p^{2m}(t_0)⟩}_R=⟨{\psi }_R(t_0)|p^{2m}|{\psi }_R(t_0)⟩/{\mathcal{N}}_{{\psi }_R}(t_0)$ indicates the exception value of p^2m of the state |ψ_R (t₀)⟩ with the division of its norm. We numerically investigate both the forward and backward evolutions of the norm $\mathcal{N}$, and the mean values ⟨θ⟩ and ⟨p⟩ for a specific time, e.g., t = t₁₀. It should be noted that we define the expectation value of observable Q as $⟨Q⟩=⟨\psi (t)|Q|\psi (t)⟩/\mathcal{N}(t)$ with $\mathcal{N}(t)=⟨\psi (t)|\psi (t)⟩$. It is evident that such kind of definition eliminates the contribution of norm to mean value. Figure 3A shows that the norm is in unity during the forward time evolution (i.e., t₀ → t₁₀) and remains at a fixed value, i.e., ${\mathcal{N}}_{{\psi }_R}(t_0)\approx {\theta }_c^2$ during the backward evolution (i.e., t₁₀ → t₀). For t₀ → t₁₀, the value of norm equals to that of the normalized initial state, so $\mathcal{N}(t_j)=1$. For the time reversal t₁₀ → t₀, our normalization procedure results in the equivalence ${\mathcal{N}}_{{\psi }_R}(t_j)=⟨\psi (t_n)|{\theta }^2|\psi (t_n)⟩$. Interestingly, our numerical investigations in Figures 4A, C, E show that for the forward evolution, the initial Gaussian wavepacket rapidly moves to the position θ_c = π/2; it should be noted that the initial Gaussian wavepacket has not moved to the position θ_c before t₄. This is the reason why C(t) decays sharply before t₄. During the time reversal, it remains localized at θ_c with the width of distribution being much smaller than that of the state of forward evolution. Correspondingly, the mean value ⟨θ⟩ has very slight differences with θ_c (see Figure 3A). Since the quantum state is extremely localized at θ_c, one can get the approximation

${\mathcal{N}}_{{\psi }_R}\left(t_0\right)=⟨\psi \left(t_n\right)|{\theta }^2|\psi \left(t_n\right)⟩\approx {\theta }_c^2.(10)$

FIGURE 3

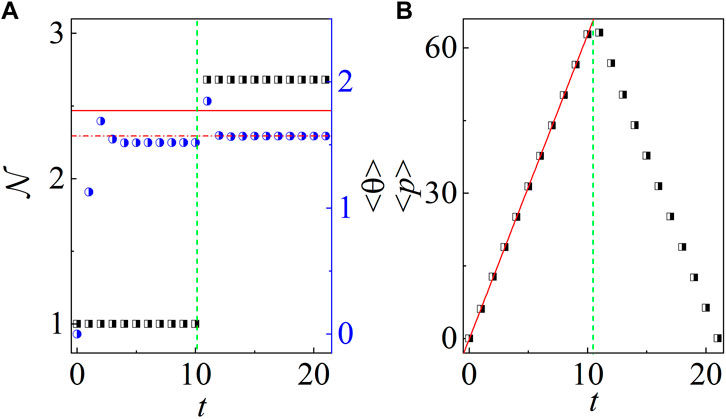
FIGURE 3. Time evolution of $\mathcal{N}$ (A), ⟨θ⟩ (A), and ⟨p⟩ (B) with t = t₁₀. In (A), solid and dash-dotted lines indicate $\mathcal{N}={\theta }_c^2$ and ⟨θ⟩ = θ_c (= π/2), respectively. In (B), solid line indicates ⟨p⟩ = Kt. Green dashed lines in (A,B) are auxiliary lines. The parameters are the same as in Figure 2.

FIGURE 4

FIGURE 4. Distributions in real (left panels) and momentum (right panels) space. In (A–D), black and red lines indicate the distribution of the states at the forward |ψ(t_j)⟩ and backward |ψ_R (t_j)⟩ evolution, respectively, with t = t₀ (top panels), t = t₅ (middle panels), and t = t₁₀ (bottom panels). In (E–F), red and black lines indicate the distribution of the states |ψ(t₁₀)⟩ and $|\tilde{\psi }(t_{10})\rangle =\theta |\psi (t_{10})\rangle$. Blue dashed lines indicate the power-law decay $|\psi {|}^2\propto {(p-p_c)}^{-2}$. The parameters are the same as in Figure 2.

Figures 4B, D, F show the momentum distribution of the state during both forward and backward evolutions. For the forward evolution, the quantum state behaves like a soliton which moves to a positive direction in momentum space, resulting in the linear increase of the mean momentum, i.e., ⟨p⟩ = Kt (see Figure 3B). The mechanism of the directed acceleration has been unveiled in our previous investigations [29,56]. Intriguingly, at time t = t₁₀, the action of θ yields a state with a power-decayed shape, i.e., $|{\psi }_R(p,t_0){|}^2\propto {(p-p_c)}^{-2}$ (see Figure 4F). Most importantly, during the backward evolution, the quantum state still retains the power-law decayed shape, for which the center p_c decreases with time and almost overlaps with that of the state of the forward evolution. This clearly demonstrates a kind of time reversal of transport behavior in momentum space.

In the aspect of the mean momentum ⟨p⟩, we find that the value of ⟨p⟩ linearly decreases during the backward evolution and is in perfect symmetry with that of the forward evolution, which is a solid evidence of time reversal. In the end of the backward evolution, the quantum state |ψ_R (t₀)⟩ is localized at the point p = 0 (see Figure 4B). By using the power-law distribution |ψ_R (p, t₀)|² ∼ p⁻², it is straightforward to get the estimation of the expectation value of p^2m, i.e., ${⟨p^{2m}⟩}_{{\psi }_R}={\int }_{p_{-N/2}}^{p_{N/2}}{p}^{2m}|{\psi }_R(p,t_0){|}^{2}dp\propto N^{2m-1}$. Taking both ${⟨p^{2m}⟩}_{{\psi }_R}$ and ${\mathcal{N}}_{{\psi }_R}(t_0)$ in Eq. 10 into Eq. 9 yields the relation

$C_1\left(t\right)\propto N^{2m-1}{\theta }_c^2,(11)$

which is verified by our numerical results in Figure 5. As an illustration, we consider the cases with m = 1, 2, and 3. Our numerical results of the late-time saturation values of C₁ are in good agreement with Eq. 11. It is now clear that the scaling of C(t) with N originates from the power-law decay of the state |ψ_R (t₀)⟩. The reason for the formation of power-law decayed wavefunction has been uncovered in Ref. 65.

FIGURE 5

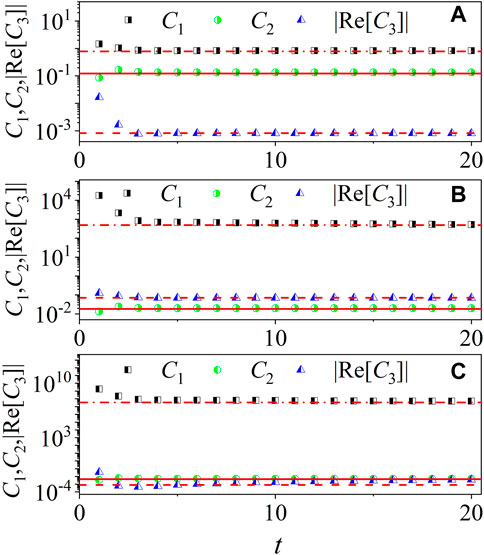
FIGURE 5. C₁ (squares), C₂ (circles), and $\left|\text{Re}[C_3]\right|$ (triangles) versus time with B = p (A), p² (B), and p³ (C). Dash-dotted, solid, and dashed lines indicate our theoretical prediction in Eq. 11 for C₁, Eq. 13 for C₂, and Eq. 15 for C₃, respectively. The parameters are the same as in Figure 2.

3.2 Analytical analysis of C₂(t)

We proceed to evaluate the time dependence of C₂(t) in Eq. 7, which is just the norm of the state |φ_R (t₀)⟩ at the end of backward evolution. According to our normalization procedure, the value of C₂ equals to the norm of the state $|\tilde{\phi }(t_n)\rangle =\theta |\phi (t_n)\rangle$, hence

$C_2=\langle \phi \left(t_n\right)|{\theta }^2|\phi \left(t_n\right)\rangle =\langle {\theta }^2\rangle {\mathcal{N}}_{\phi }\left(t_n\right),(12)$

with ${\mathcal{N}}_{\phi }(t_n)=⟨\phi (t_n)|\phi (t_n)⟩$ and $⟨{\theta }^2⟩=⟨\phi (t_n)|{\theta }^2|\phi (t_n)⟩/\mathcal{N}(t_n)$. We numerically find that the state |φ(t_n)⟩ is extremely localized at the position θ_c during the forward evolution (see Figure 6). Then, a rough estimation yields $⟨{\theta }^2⟩\sim {\theta }_c^2$. The norm ${\mathcal{N}}_{\phi }(t_n)$ equals that of the initial state |φ(t₀)⟩ = p^m|ψ(t₀)⟩. By using the initial Gaussian wavepacket $\psi (p,t_0)={(1/\sigma {\hslash }_{\text{eff}}^2\pi )}^{1/4}\exp (-p^2/2\sigma {\hslash }_{\text{eff}}^2)$, one can straightforwardly obtain

${\mathcal{N}}_{\phi }\left(t_n\right)={\int }_{-\infty }^{\infty }{p}^{2m}|\psi \left(p,t_0\right){|}^{2}dp=\frac{\left(2m-1\right)‼}{2^m{\alpha }^m},$

where α = 1/(σℏ²) and (…)!! denote a double factorial. Taking both the ⟨θ⟩ and ${\mathcal{N}}_{\phi }(t_n)$ into Eq. 12 yields the late-time saturation value

$C_2\left(t\right)\sim {\theta }_c^2\frac{\left(2m-1\right)‼}{2^m{\alpha }^m},(13)$

which is in good agreement with our numerical results in Figure 5.

FIGURE 6

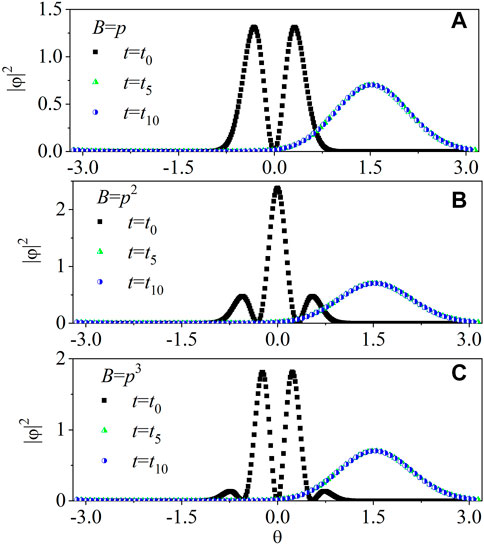
FIGURE 6. Probability density distributions in real space at the time t = t₀ (squares), t₅ (triangles), and t₁₀ (circles) with B = p (A), p² (B), and p³ (C). The parameters are the same as in Figure 2.

3.3 Scaling law of C₃(t)

The value of C₃(t) depends on both the states |ψ_R (t₀)⟩ and |φ_R (t₀)⟩ (see Eq. 8). Figure 7 shows the probability density distributions of the two states in both the real space and momentum space. For comparison, the two states are normalized to unity. One can find the perfect consistence between |ψ_R (t₀)⟩ and |φ_R (t₀)⟩. Then, we roughly regard C₃ as the expectation value of the p^m taking over the state ψ_R (t₀) or φ_R (t₀), i.e., $C_3(t)\approx {⟨p^m(t_0)⟩}_{{\psi }_R}\sqrt{{\mathcal{N}}_{{\psi }_R}(t_0)}\sqrt{{\mathcal{N}}_{{\phi }_R}(t_0)}$, where according to aforementioned derivations ${\mathcal{N}}_{{\psi }_R}(t_0)={\theta }_c^2$ and ${\mathcal{N}}_{{\phi }_R}(t_0)=C_2(t)$. By using the power-law decayed wavepacket |ψ_R (t₀)|² ∝ p⁻², one can obtain the estimation

$\begin{array}{cc}\hfill {⟨p^m\left(t_0\right)⟩}_{{\psi }_R}& \approx {\int }_{p_{-N/2}}^{p_{N/2}}{p}^m|{\psi }_R\left(p,t_0\right){|}^{2}dp\hfill \\ \hfill & \sim \left\{\begin{array}{cc}0\hfill & \text{for odd}m,\hfill \\ N^{m-1}\hfill & \text{for even}m.\hfill \end{array}\right.\hfill \end{array}.(14)$

Accordingly, the C₃ is approximated as

$C_3\left(t\right)\sim \left\{\begin{array}{cc}0\hfill & \text{for odd}m,\hfill \\ \eta N^{m-1}\hfill & \text{for even}m.\hfill \end{array}\right..(15)$

with the prefactor $\eta \propto {\theta }_c^2{\left[(2m-1)!!/2^m{\alpha }^m\right]}^{\frac{1}{2}}$.

FIGURE 7

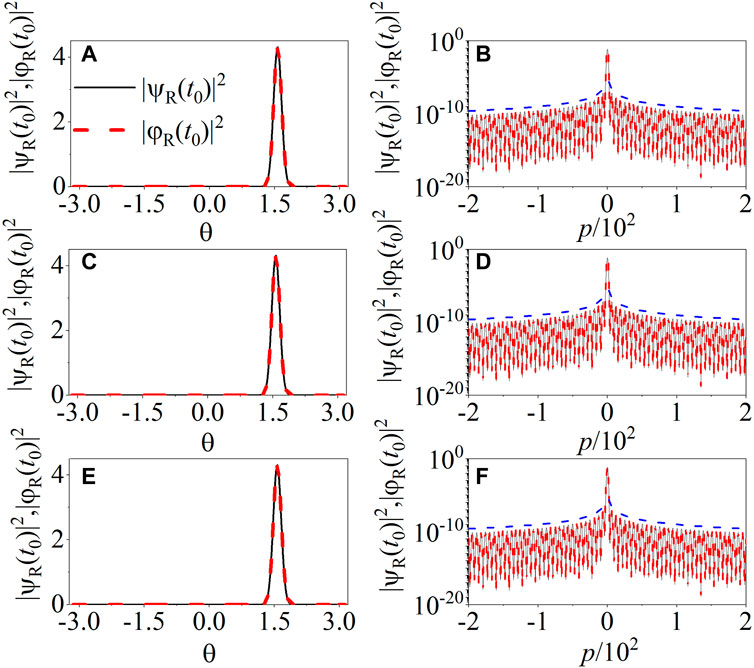
FIGURE 7. Comparison of the distribution of states |ψ_R (t₀)⟩ (solid lines) and |φ_R (t₀)⟩ (dashed lines) in real (A, C, E) and momentum space (B, D, F) with B = p (top panels), p² (middle panels), and p³ (bottom panels). Blue dashed lines in (B, D, F) indicate the power-law decay |ψ_R (t₀)|² (|φ_R (t₀)|²) ∝ p⁻². The parameters are the same as in Figure 2.

We numerically calculate the absolute value of the real part of C₃. Interestingly, our numerical results of |Re [C₃]| is in good agreement with the analytical prediction in Eq. 15 (see Figure 5), which proves the validity of our theoretical analysis. We further numerically investigate the |Re [C₃(t)]| at a specific time for different N. Figure 8 shows that for B = p, the value of |Re [C₃(t)]| is nearly zero with varying N, which is consistent with our theoretical prediction in Eq. 15. For B = p³, the value of |Re [C₃(t)]| has slight difference with zero for large values of N, signaling the derivations with Eq. 15. This is due to the fact the quantum state |ψ_R (t₀)|² is not exactly symmetric around p. In order to quantify such asymmetry, we numerically investigate the difference of the sum of the probability between the positive and negative momentums ${\mathrm{\Delta }}_{\rho }={\sum }_{n=0}^{\frac{N}{2}-1}|{\psi }_R(t_0,p_n){|}^2-{\sum }_{n=-\frac{N}{2}}^{-1}|{\psi }_R(t_0,p_n){|}^2$ and find that it is non-zero Δ_ρ = 0.13. Interestingly, for B = p², the value of |Re [C₃(t)]| increases linearly with increasing N, which is clear evidence of the validity of our theoretical prediction.

FIGURE 8

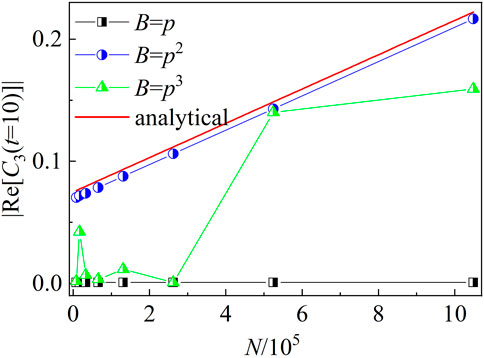
FIGURE 8. |Re [C₃(t)]| at the time t = t₁₀ versus N with B = p (squares), p² (circles), and p³ (triangles). Red solid line indicates our theoretical prediction in Eq. 15 with η = 6.05 × 10⁻⁷ for B = p². The parameters are the same as in Figure 2.

4 Conclusion and discussion

In the present work, we investigate the dynamics of the C(t) = −⟨[θ(t), p^m]⟩ in a PTKR model. The spontaneous $\mathcal{PT}$-symmetry breaking is assured by the condition λ > λ_c. In the broken phase of $\mathcal{PT}$-symmetry, we find, both analytically and numerically, the scaling law of C(t) with the dimension of the momentum space, i.e., $C(t)\sim N^{2m-1}{\theta }_c^2$. This demonstrates that the value of C increases unboundedly with N, which implies that the local perturbation can spread to the entire system very rapidly. In order to reveal the mechanism of the scaling, we make detailed investigations on both the forward and backward evolutions of the quantum state. Our investigations show that the action of θ on a quantum state leads to the formation of the power-law decayed momentum distribution $|\psi (p){|}^2\propto {(p-p_c)}^{-2}$. Interestingly, such a shape retains during the time reversal, in addition to the decrease of p_c to almost zero. Based on the power-law decayed state, we analytically derive the late-time saturation values of the three parts of the C, which is confirmed by numerical results.

In recent years, fruitful physics of quantum many-body systems, such as dynamical phase transition, many-body localization, and thermalization have received extensive studies. It is found that the energy conservation of chaotic systems leads to the scaling law of OTOCs, for which the late-time saturation of OTOCs scales as the inverse polynomial with the system size [66]. For chaotic systems with long-range interaction, the late-time saturation values of OTOCs obey the dynamical scaling law near the phase transition point [67]. Accordingly, our finding of the power-law scaling of OTOCs with the system size of the PTKR model serves as a new element of the quantum information scrambling in non-Hermitian map systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

W-LZ proposed ideas and revised the manuscript. R-RW conducted the numerical simulation and wrote the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (grant no. 12065009), the Science and Technology Planning Project of Jiangxi province (grant no. 20224ACB201006), and the Science and Technology Planning Project of Ganzhou City (grant no. 202101095077).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Maldacena J, Shenker SH, Stanford D. A bound on chaos. J High Energ Phys. (2016) 08:106. doi:10.1007/jhep08(2016)106

CrossRef Full Text | Google Scholar

2. Rozenbaum EB, Ganeshan S, Galitski V. Lyapunov exponent and out-of-time-ordered correlator’s growth rate in a chaotic system. Phys Rev Lett (2017) 118:086801. doi:10.1103/physrevlett.118.086801

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Harris J, Yan B, Sinitsyn NA. Benchmarking information scrambling. Phys Rev Lett (2022) 129:050602. doi:10.1103/physrevlett.129.050602

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Hayden P, Preskill J. Black holes as mirrors: Quantum information in random subsystems. J High Energ Phys. (2007) 09:120. doi:10.1088/1126-6708/2007/09/120

CrossRef Full Text | Google Scholar

5. Zanardi P, Anand N. Information scrambling and chaos in open quantum systems. Phys Rev A (2021) 103:062214. doi:10.1103/physreva.103.062214

CrossRef Full Text | Google Scholar

6. Touil A, Deffner S. Information scrambling versus decoherence—two competing sinks for entropy. PRX QUANTUM (2021) 2:010306. doi:10.1103/prxquantum.2.010306

CrossRef Full Text | Google Scholar

7. Prakash R, Lakshminarayan A. Scrambling in strongly chaotic weakly coupled bipartite systems: Universality beyond the Ehrenfest timescale. Phys Rev B (2020) 101:121108. doi:10.1103/physrevb.101.121108

CrossRef Full Text | Google Scholar

8. Zhou T, Xu S, Chen X, Guo A, Swingle B. Operator lé vy flight: Light cones in chaotic long-range interacting systems. Phys Rev Lett (2020) 124:180601. doi:10.1103/physrevlett.124.180601

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhao SK, Ge ZY, Xiang Z, Xue GM, Zhao SP, Wang Z, et al. Probing operator spreading via Floquet engineering in a superconducting circuit. Phys Rev Lett (2022) 129:160602. doi:10.1103/physrevlett.129.160602

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Yin C, Lucas A. Quantum operator growth bounds for kicked tops and semiclassical spin chains. Phys Rev A (2021) 103:042414. doi:10.1103/physreva.103.042414

CrossRef Full Text | Google Scholar

11. Moudgalya S, Devakul T, Keyserlingk CV, Sondhi SL. Operator spreading in quantum maps. Phys Rev B (2019) 99:094312. doi:10.1103/physrevb.99.094312

CrossRef Full Text | Google Scholar

12. Fan R, Zhang P, Shen H, Zhai H. Out-of-time-order correlation for many-body localization. Sci Bull (2017) 62(10):707–11. doi:10.1016/j.scib.2017.04.011

CrossRef Full Text | Google Scholar

13. Smith A, Knolle J, Moessner R, Kovrizhin DL. Logarithmic spreading of out-of-time-ordered correlators without many-body localization. Phys Rev Lett (2019) 123:086602. doi:10.1103/physrevlett.123.086602

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Gärttner M, Hauke P, Rey AM. Relating out-of-time-order correlations to entanglement via multiple-quantum coherences. Phys Rev Lett (2018) 120:040402. doi:10.1103/physrevlett.120.040402

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Keyserlingk CV, Rakovszky T, Pollmann F, Sondhi SL. Operator hydrodynamics, OTOCs, and entanglement growth in systems without conservation laws. Phys Rev X (2018) 8:021013. doi:10.1103/physrevx.8.021013

CrossRef Full Text | Google Scholar

16. Lerose A, Pappalardi S. Bridging entanglement dynamics and chaos in semiclassical systems. Phys Rev A (2020) 102:032404. doi:10.1103/physreva.102.032404

CrossRef Full Text | Google Scholar

17. Lewis-Swan RJ, Safavi-Naini A, Bollinger JJ, Rey AM. Unifying scrambling, thermalization and entanglement through measurement of fidelity out-of-time-order correlators in the Dicke model. Nat Commun (2019) 10:1581. doi:10.1038/s41467-019-09436-y

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhu Q, Sun ZH, Gong M, Chen F, Zhang YR, Wu Y, et al. Observation of thermalization and information scrambling in a superconducting quantum processor. Phys Rev Lett (2022) 128:160502. doi:10.1103/physrevlett.128.160502

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Balachandran V, Benenti G, Casati G, Poletti D. From the eigenstate thermalization hypothesis to algebraic relaxation of OTOCs in systems with conserved quantities. Phys Rev B (2021) 104:104306. doi:10.1103/physrevb.104.104306

CrossRef Full Text | Google Scholar

20. Kobrin B, Yang Z, Kahanamoku-Meyer GD, Olund CT, Moore JE, Stanford D, et al. Many-body chaos in the sachdev-ye-kitaev model. Phys Rev Lett (2021) 126:030602. doi:10.1103/physrevlett.126.030602

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Borgonovi F, Izrailev FM, Santos LF. Timescales in the quench dynamics of many-body quantum systems: Participation ratio versus out-of-time ordered correlator. Phys Rev E (2019) 99:052143. doi:10.1103/physreve.99.052143

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Xu S, Swingle B. Scrambling dynamics and out-of-time ordered correlators in quantum many-body systems: A tutorial. arXiv:2202.07060 quant-ph. (2022).

Google Scholar

23. Heyl M, Pollmann F, Dóra B. Detecting equilibrium and dynamical quantum phase transitions in Ising chains via out-of-time-ordered correlators. Phys Rev Lett (2018) 121:016801. doi:10.1103/physrevlett.121.016801

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zamani S, Jafari R, Langari A. Out-of-time-order correlations and Floquet dynamical quantum phase transition. Phys Rev B (2022) 105:094304. doi:10.1103/physrevb.105.094304

CrossRef Full Text | Google Scholar

25. Mi X, Roushan P, Quintana C, Mandra S, Marshall J, Neill C, et al. Information scrambling in quantum circuits. Science (2021) 374:1479–83. doi:10.1126/science.abg5029

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Weinstein Z, Kelly SP, Marino J, Altman E. Scrambling transition in a radiative random unitary circuit. arXiv:2210.14242 quant-ph. (2022)

Google Scholar

27. Nie X, Wei BB, Chen X, Zhang Z, Zhao X, Qiu C, et al. Experimental observation of equilibrium and dynamical quantum phase transitions via out-of-time-ordered correlators. Phys Rev Lett (2020) 124:250601. doi:10.1103/physrevlett.124.250601

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhai LJ, Yin S. Out-of-time-ordered correlator in non-Hermitian quantum systems. Phys Rev B (2020) 102:054303. doi:10.1103/physrevb.102.054303

CrossRef Full Text | Google Scholar

29. Zhao WL. Quantization of out-of-time-ordered correlators in non-Hermitian chaotic systems. Phys Rev Res (2022) 4:023004. doi:10.1103/physrevresearch.4.023004

CrossRef Full Text | Google Scholar

30. Berry M. Physics of nonhermitian degeneracies. Czech J Phys (2004) 54:1039–47. doi:10.1023/b:cjop.0000044002.05657.04

CrossRef Full Text | Google Scholar

31. Ashida Y, Gong Z, Ueda M. Non-Hermitian physics. Adv Phys (2020) 69:249–435. doi:10.1080/00018732.2021.1876991

CrossRef Full Text | Google Scholar

32. Bender CM, Boettcher S. Real spectra in non-hermitian Hamiltonians HavingPTSymmetry. Phys Rev Lett (1998) 80:5243–6. doi:10.1103/physrevlett.80.5243

CrossRef Full Text | Google Scholar

33. Bender CM, Brody DC, Jones HF. Complex extension of quantum mechanics. Phys Rev Lett (2002) 89:270401. doi:10.1103/physrevlett.89.270401

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhao XM, Guo CX, Yang ML, Wang H, Liu WM, Kou SP. Anomalous non-Abelian statistics for non-Hermitian generalization of Majorana zero modes. Phys Rev B (2021) 104:214502. doi:10.1103/physrevb.104.214502

CrossRef Full Text | Google Scholar

35. Yu ZF, Xue JK, Zhuang L, Zhao J, Liu WM. Non-Hermitian spectrum and multistability in exciton-polariton condensates. Phys Rev B (2021) 104:235408. doi:10.1103/physrevb.104.235408

CrossRef Full Text | Google Scholar

36. Zhao XM, Guo CX, Kou SP, Zhuang L, Liu WM. Defective Majorana zero modes in a non-Hermitian Kitaev chain. Phys Rev B (2021) 104:205131. doi:10.1103/physrevb.104.205131

CrossRef Full Text | Google Scholar

37. Pino JD, Slim JJ, Verhagen E. Non-Hermitian chiral phononics through optomechanically induced squeezing. Nature (London) (2022) 606:82–7. doi:10.1038/s41586-022-04609-0

CrossRef Full Text | Google Scholar

38. El-Ganainy R, Makris KG, Khajavikhan M, Musslimani ZH, Rotter S, Christodoulides DN. Non-Hermitian physics and PT symmetry. Nat Phys (2018) 14:11–9. doi:10.1038/nphys4323

CrossRef Full Text | Google Scholar

39. Xia S, Danieli C, Zhang Y, Zhao X, Lu H, Tang L, et al. Higher-order exceptional point and Landau–Zener Bloch oscillations in driven non-Hermitian photonic Lieb lattices. APL Photon (2021) 6:126106. doi:10.1063/5.0069633

CrossRef Full Text | Google Scholar

40. Zhang Y, Xia S, Zhao X, Qin L, Feng X, Qi W, et al. Symmetry-protected third-order exceptional points in staggered flatband rhombic lattices. Photon Res (2023) 11(3):225. doi:10.1364/PRJ.478167

CrossRef Full Text | Google Scholar

41. Xiao Z, Li H, Kottos T, Al u A. Enhanced sensing and nondegraded thermal noise performance based on PT-symmetric electronic circuits with a sixth-order exceptional point. Phys Rev Lett (2019) 123:213901. doi:10.1103/physrevlett.123.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Chitsazi M, Li H, Ellis FM, Kottos T. Experimental realization of Floquet PT-symmetric systems {PT}}-Symmetric systems. Phys Rev Lett (2017) 119:093901. doi:10.1103/physrevlett.119.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zou D, Chen T, He W, Bao J, Lee CH, Sun H, et al. Observation of hybrid higher-order skin-topological effect in non-Hermitian topolectrical circuits. Nat Commun (2021) 12:7201. doi:10.1038/s41467-021-26414-5

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kreibich M, Main J, Cartarius H, Wunner G. Tilted optical lattices with defects as realizations ofPTsymmetry in Bose-Einstein condensates. Phys Rev A (2016) 93:023624. doi:10.1103/physreva.93.023624

CrossRef Full Text | Google Scholar

45. Keller C, Oberthaler MK, Abfalterer R, Bernet S, Schmiedmayer J, Zeilinger A. Tailored complex potentials and friedel’s law in atom optics. Phys Rev Lett (1997) 79:3327–30. doi:10.1103/physrevlett.79.3327

CrossRef Full Text | Google Scholar

46. Li J, Harter AK, Liu J, Melo LD, Joglekar YN, Luo L. Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat Commun (2019) 10:855. doi:10.1038/s41467-019-08596-1

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Xue Y, Hang C, He Y, Bai Z, Jiao Y, Huang G, et al. Experimental observation of partial parity-time symmetry and its phase transition with a laser-driven cesium atomic gas. Phys Rev A (2022) 105:053516. doi:10.1103/physreva.105.053516

CrossRef Full Text | Google Scholar

48. Ren Z, Liu D, Zhao E, He C, Pak KK, Li J, et al. Chiral control of quantum states in non-Hermitian spin–orbit-coupled fermions. Nat Phys (2022) 18:385–9. doi:10.1038/s41567-021-01491-x

CrossRef Full Text | Google Scholar

49. Zhou L, Han W. Driving-induced multiple PT-symmetry breaking transitions and reentrant localization transitions in non-Hermitian Floquet quasicrystals PT-symmetry breaking transitions and reentrant localization transitions in non-Hermitian Floquet quasicrystals. Phys Rev B (2022) 106:054307. doi:10.1103/physrevb.106.054307

CrossRef Full Text | Google Scholar

50. Zhou L. Floquet engineering of topological localization transitions and mobility edges in one-dimensional non-Hermitian quasicrystals. Phys Rev Res (2021) 3:033184. doi:10.1103/physrevresearch.3.033184

CrossRef Full Text | Google Scholar

51. Zhou L, Gu Y, Gong J. Dual topological characterization of non-Hermitian Floquet phases. Phys Rev B (2021) 103:L041404. doi:10.1103/physrevb.103.l041404

CrossRef Full Text | Google Scholar

52. Zhang DJ, Wang Q, Gong J. Time-dependent PT-symmetric quantum mechanics in generic non-Hermitian systems-symmetric quantum mechanics in generic non-Hermitian systems. Phys Rev A (2019) 100:062121. doi:10.1103/physreva.100.062121

CrossRef Full Text | Google Scholar

53. Longhi S. Oscillating potential well in the complex plane and the adiabatic theorem. Phys Rev A (2017) 96:042101. doi:10.1103/physreva.96.042101

CrossRef Full Text | Google Scholar

54. West CT, Kottos T, Prosen T. PT-symmetric wave chaos. Phys Rev Lett (2010) 104:054102. doi:10.1103/physrevlett.104.054102

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Longhi S. Localization, quantum resonances, and ratchet acceleration in a periodically kickedPT-symmetric quantum rotator. Phys Rev A (2017) 95:012125. doi:10.1103/physreva.95.012125

CrossRef Full Text | Google Scholar

56. Zhao WL, Wang J, Wang X, Tong P. Directed momentum current induced by the PT-symmetric driving. Phys Rev E (2019) 99:042201. doi:10.1103/physreve.99.042201

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Santhanam MS, Paul S, Kannan JB. Quantum kicked rotor and its variants: Chaos, localization and beyond. Phys Rep (2022) 956:1–87. doi:10.1016/j.physrep.2022.01.002

CrossRef Full Text | Google Scholar

58. Ho DYH, Gong J. Quantized adiabatic transport in momentum space. Phys Rev Lett (2012) 109:010601. doi:10.1103/physrevlett.109.010601

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Gadway B, Reeves J, Krinner L, Schneble D. Evidence for a quantum-to-classical transition in a pair of coupled quantum rotors. Phys Rev Lett (2013) 110:190401. doi:10.1103/physrevlett.110.190401

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Huang KQ, Zhao WL, Li Z. Effective protection of quantum coherence by a non-Hermitian driving potential. Phys Rev A (2021) 104:052405. doi:10.1103/physreva.104.052405

CrossRef Full Text | Google Scholar

61. Vuatelet V, Rançon A. Effective thermalization of a many-body dynamically localized Bose gas. Phys Rev A (2021) 104:043302. doi:10.1103/physreva.104.043302

CrossRef Full Text | Google Scholar

62. Belyansky R, Bienias P, Kharkov YA, Gorshkov AV, Swingle B. Minimal model for fast scrambling. Phys Rev Lett (2020) 125:130601. doi:10.1103/physrevlett.125.130601

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Kuwahara T, Saito K. Absence of fast scrambling in thermodynamically stable long-range interacting systems. Phys Rev Lett (2021) 126:030604. doi:10.1103/physrevlett.126.030604

PubMed Abstract | CrossRef Full Text | Google Scholar

64. D’Alessio L, Rigol M. Long-time behavior of isolated periodically driven interacting lattice systems. Phys Rev X (2014) 4:041048. doi:10.1103/physrevx.4.041048

CrossRef Full Text | Google Scholar

65. Zhao WL, Hu Y, Li Z, Wang Q. Super-exponential growth of out-of-time-ordered correlators. Phys Rev B (2021) 103:184311. doi:10.1103/physrevb.103.184311

CrossRef Full Text | Google Scholar

66. Huang Y, Brandão FGSL, Zhang YL. Finite-size scaling of out-of-time-ordered correlators at late times. Phys Rev Lett (2019) 123:010601. doi:10.1103/physrevlett.123.010601

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Wei BB, Sun G, Hwang MJ. Dynamical scaling laws of out-of-time-ordered correlators. Phys Rev B (2019) 100:195107. doi:10.1103/physrevb.100.195107

CrossRef Full Text | Google Scholar